Non-Absorbing Dielectric Materials for Surface-Enhanced Spectroscopies and Chiral Sensing in the UV
Abstract
:1. Introduction
2. Methods
2.1. Mie Theory
2.2. Optical Chirality
3. Materials under Study
4. Results
4.1. Near-Field Enhancement and Absorption Efficiency
4.2. Chirality
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NFE | Near-field enhancement |
| OCD | Optical chirality density |
| HRI | High refractive index |
| MRI | Medium refractive index |
| LRI | Low refractive index |
| BOD | Bulk optical devices |
| CS | Coatings and substrates |
| FO | Fiber Optics |
| DRAM | Dynamic random access memories |
| RRAM | Resistive random access memories |
| MRAM | Magnetoresistive random access memories |
| ISFET | Ion sensitive field effect transistor |
| TCF | Transparent conductive films |
| GS | Gas sensors |
| Pcat | Photocatalysis |
| HT | High temperatures |
| HPD | High power devices |
| PD | Photodetectors |
| MOSFET | Metal-oxide-semiconductor field effect transistor |
| SBF | Schottky barrier diodes |
| LED | Light-emitting diode |
| DSSC | Dye Synthesize Solar Cells |
| WBS | Wide Bandgap Semiconductor |
| LumD | Luminescent devices |
| OQC | Optical quantum computing |
| MD | Magnetic dipole |
| MQ | Magnetic quadrupole |
| MO | Magnetic octopole |
| ED | Electric dipole |
| EQ | Electric quadrupole |
| EO | Electric octopole |
References
- Stiles, P.L.; Dieringer, J.A.; Shah, N.C.; Van Duyne, R.P. Surface-Enhanced Raman Spectroscopy SERS: Surface-enhanced Raman spectroscopy Raman scattering: Inelastic scattering of a photon from a molecule in which the frequency change precisely matches the difference in vibrational energy levels. Annu. Rev. Anal. Chem. 2008, 1, 601–626. [Google Scholar] [CrossRef] [PubMed]
- Caldarola, M.; Albella, P.; Cortés, E.; Rahmani, M.; Roschuk, T.; Grinblat, G.; Oulton, R.F.; Bragas, A.V.; Maier, S.A. Non-plasmonic nanoantennas for surface enhanced spectroscopies with ultra-low heat conversion. Nat. Commun. 2015, 6, 7915. [Google Scholar] [CrossRef]
- Pirotta, S.; Xu, X.G.; Delfan, A.; Mysore, S.; Maiti, S.; Dacarro, G.; Patrini, M.; Galli, M.; Guizzetti, G.; Bajoni, D.; et al. Surface-Enhanced Raman Scattering in Purely Dielectric Structures via Bloch Surface Waves. J. Phys. Chem. C 2013, 117, 6821–6825. [Google Scholar] [CrossRef]
- Mayerhöfer, T.G.; Popp, J. Periodic array-based substrates for surface-enhanced infrared spectroscopy. Nanophotonics 2018, 7, 39–79. [Google Scholar] [CrossRef]
- Yang, X.; Sun, Z.; Low, T.; Hu, H.; Guo, X.; García de Abajo, F.J.; Avouris, P.; Dai, Q. Nanomaterial-Based Plasmon-Enhanced Infrared Spectroscopy. Adv. Mater. 2018, 30, 1–23. [Google Scholar] [CrossRef]
- Subramanian, A.Z.; Ryckeboer, E.; Dhakal, A.; Peyskens, F.; Malik, A.; Kuyken, B.; Zhao, H.; Pathak, S.; Ruocco, A.; Groote, A.D.; et al. Silicon and silicon nitride photonic circuits for spectroscopic sensing on-a-chip. Photon. Res. 2015, 3, B47–B59. [Google Scholar] [CrossRef]
- Taliercio, T.; Biagioni, P. Semiconductor infrared plasmonics. Nanophotonics 2019, 8, 949–990. [Google Scholar] [CrossRef]
- Li, J.F.; Li, C.Y.; Aroca, R.F. Plasmon-enhanced fluorescence spectroscopy. Chem. Soc. Rev. 2017, 46, 3962–3979. [Google Scholar] [CrossRef]
- Frascella, F.; Ricciardi, S.; Rivolo, P.; Moi, V.; Giorgis, F.; Descrovi, E.; Michelotti, F.; Munzert, P.; Danz, N.; Napione, L.; et al. A Fluorescent One-Dimensional Photonic Crystal for Label-Free Biosensing Based on Bloch Surface Waves. Sensors 2013, 13, 2011–2022. [Google Scholar] [CrossRef]
- Sinibaldi, A.; Fieramosca, A.; Rizzo, R.; Anopchenko, A.; Danz, N.; Munzert, P.; Magistris, C.; Barolo, C.; Michelotti, F. Combining label-free and fluorescence operation of Bloch surface wave optical sensors. Opt. Lett. 2014, 39, 2947–2950. [Google Scholar] [CrossRef]
- Ray, K.; Badugu, R.; Lakowicz, J.R. Bloch surface wave-coupled emission from quantum dots by ensemble and single molecule spectroscopy. RSC Adv. 2015, 5, 54403–54411. [Google Scholar] [CrossRef] [PubMed]
- Bochenkov, V.E.; Shabatina, T.I. Chiral plasmonic biosensors. Biosensors 2018, 8, 120. [Google Scholar] [CrossRef] [PubMed]
- Vestler, D.; Ben-moshe, A.; Markovich, G. Enhancement of Circular Dichroism of a Chiral Material by Dielectric Nanospheres Published as part of The Journal of Physical Chemistry virtual special issue “Abraham Nitzan Festschrift”. J. Phys. Chem. C 2019, 123, 5017–5022. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, J.; Yoon, J. Recent Advances in Development of Chiral Fluorescent and Colorimetric Sensors. Chem. Rev. 2014, 114, 4918–4959. [Google Scholar] [CrossRef]
- Barron, L.D. (Ed.) Molecular Light Scattering and Optical Activity, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Tang, Y.; Cohen, A.E. Optical chirality and its interaction with matter. Phys. Rev. Lett. 2010, 104, 163901. [Google Scholar] [CrossRef]
- Taniguchi, M.; Lindsey, J.S. Database of Absorption and Fluorescence Spectra of >300 Common Compounds for use in PhotochemCAD. Photochem. Photobiol. 2018, 94, 290–327. [Google Scholar] [CrossRef]
- Amdursky, N.; Stevens, M.M. Circular Dichroism of Amino Acids: Following the Structural Formation of Phenylalanine. ChemPhysChem 2015, 16, 2768–2774. [Google Scholar] [CrossRef]
- Okuom, M.O.; Burks, R.; Naylor, C.; Holmes, A.E. Applied Circular Dichroism: A Facile Spectroscopic Tool for Configurational Assignment and Determination of Enantiopurity. J. Anal. Methods Chem. 2015, 2015, 865605. [Google Scholar] [CrossRef]
- Lemesle-Lamache, V.; Wouessidjewe, D.; Chéron, M.; Duchêne, D. Study of β-cyclodextrin and ethylated β-cyclodextrin salbutamol complexes, in vitro evaluation of sustained-release behaviour of salbutamol. Int. J. Pharm. 1996, 141, 117–124. [Google Scholar] [CrossRef]
- Nagai, M.; Nagai, Y.; Imai, K.; Neya, S. Circular Dichroism of Hemoglobin and Myoglobin. Chirality 2014, 26, 438–442. [Google Scholar] [CrossRef]
- Kypr, J.; Kejnovska, I.; Renciuk, D.; Vorlickova, M. Circular dichroism and conformational polymorphism of DNA. Nucleic Acids Res. 2009, 37, 1713–1725. [Google Scholar] [CrossRef] [PubMed]
- Chin, D.H.; Woody, R.W.; Rohl, C.A.; Baldwin, R.L. Nonlinear partial differential equations and applications: Circular dichroism spectra of short, fixed-nucleus alanine helices. Proc. Natl. Acad. Sci. USA 2002, 99, 15416–15421. [Google Scholar] [CrossRef] [PubMed]
- Sellmer, A.; Terpetschnig, E.; Wiegrebe, W.; Wolfbeis, O.S. UV/Vis and fluorescence study on anthralin and its alkylated derivatives. J. Photochem. Photobiol. A Chem. 1998, 116, 39–45. [Google Scholar] [CrossRef]
- Singh, G.; Abbas, J.; Dogra, S.D.; Sachdeva, R.; Rai, B.; Tripathi, S.; Prakash, S.; Sathe, V.; Saini, G. Vibrational and electronic spectroscopic studies of melatonin. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2014, 118, 73–81. [Google Scholar] [CrossRef]
- Barden, J.A.; Wu, C.S.C.; Remedios, C.G.D. Actin monomer conformation under polymerizing conditions studied by proton nuclear magnetic resonance and circular dichroism spectroscopy. Biochim. Biophys. Acta (BBA) Protein Struct. Mol. Enzymol. 1983, 748, 230–235. [Google Scholar] [CrossRef]
- Bonvicini, A.; Guilhaudis, L.; Tognetti, V.; Desmaële, D.; Sauvonnet, N.; Oulyadi, H.; Joubert, L. Revisiting absorption and electronic circular dichroism spectra of cholesterol in solution: A joint experimental and theoretical study. Phys. Chem. Chem. Phys. 2018, 20, 5274–5284. [Google Scholar] [CrossRef]
- Sanz, J.M.; Ortiz, D.; de la Osa, R.A.; Saiz, J.M.; González, F.; Brown, A.S.; Losurdo, M.; Everitt, H.O.; Moreno, F. UV Plasmonic Behavior of Various Metal Nanoparticles in the Near- and Far-Field Regimes: Geometry and Substrate Effects. J. Phys. Chem. C 2013, 117, 19606–19615. [Google Scholar] [CrossRef]
- Gutiérrez, Y.; Losurdo, M.; González, F.; Everitt, H.O.; Moreno, F. Nanoplasmonic Photothermal Heating and Near-Field Enhancements: A Comparative Survey of 19 Metals. J. Phys. Chem. C 2020, 124, 7386–7395. [Google Scholar] [CrossRef]
- Lereu, A.L.; Farahi, R.H.; Tetard, L.; Enoch, S.; Thundat, T.; Passian, A. Plasmon assisted thermal modulation in nanoparticles. Opt. Express 2013, 21, 12145–12158. [Google Scholar] [CrossRef] [PubMed]
- Baffou, G.; Bordacchini, I.; Baldi, A.; Quidant, R. Simple experimental procedures to distinguish photothermal from hot-carrier processes in plasmonics. Light. Sci. Appl. 2020, 9, 108. [Google Scholar] [CrossRef]
- Plech, A.; Kotaidis, V. Laser-induced heating and melting of gold nanoparticles studied by time-resolved x-ray scattering. Phys. Rev. B 2004, 70, 195423. [Google Scholar] [CrossRef]
- King, M.D.; Khadka, S.; Craig, G.A.; Mason, M.D. Effect of Local Heating on the SERS Efficiency of Optically Trapped Prismatic Nanoparticles. J. Phys. Chem. C 2008, 112, 11751–11757. [Google Scholar] [CrossRef]
- Decker, M.; Staude, I. Resonant dielectric nanostructures: A low-loss platform for functional nanophotonics. J. Opt. 2016, 18, 103001. [Google Scholar] [CrossRef]
- Baranov, D.G.; Zuev, D.A.; Lepeshov, S.I.; Kotov, O.V.; Krasnok, A.E.; Evlyukhin, A.B.; Chichkov, B.N. All-dielectric nanophotonics: The quest for better materials and fabrication techniques. Optica 2017, 4, 814–825. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef]
- Delfan, A.; Liscidini, M.; Sipe, J.E. Surface enhanced Raman scattering in the presence of multilayer dielectric structures. J. Opt. Soc. Am. B 2012, 29, 1863–1874. [Google Scholar] [CrossRef]
- Mayerhöfer, T.G.; Pahlow, S.; Popp, J. Structures for surface-enhanced nonplasmonic or hybrid spectroscopy. Nanophotonics 2020, 9, 741–760. [Google Scholar] [CrossRef]
- Gomez-Medina, R.; Garcia-Camara, B.; Suarez-Lacalle, I.; González, F.; Moreno, F.; Nieto-Vesperinas, M.; Saenz, J.J. Electric and magnetic dipolar response of germanium nanospheres: Interference effects, scattering anisotropy, and optical forces. J. Nanophotonics 2011, 5, 053512. [Google Scholar] [CrossRef]
- Geffrin, J.M.; García-Cámara, B.; Gómez-Medina, R.; Albella, P.; Froufe-Pérez, L.S.; Eyraud, C.; Litman, A.; Vaillon, R.; González, F.; Nieto-Vesperinas, M.; et al. Magnetic and electric coherence in forward-and back-scattered electromagnetic waves by a single dielectric subwavelength sphere. Nat. Commun. 2012, 3, 1–8. [Google Scholar] [CrossRef]
- Nieto-Vesperinas, M. Chiral optical fields: A unified formulation of helicity scattered from particles and dichroism enhancement. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20160314. [Google Scholar] [CrossRef]
- Zhao, X.; Reinhard, B.M. Switchable Chiroptical Hot-Spots in Silicon Nanodisk Dimers. ACS Photonics 2019, 6, 1981–1989. [Google Scholar] [CrossRef]
- Ho, C.S.; Garcia-Etxarri, A.; Zhao, Y.; Dionne, J. Enhancing Enantioselective Absorption Using Dielectric Nanospheres. ACS Photonics 2017, 4, 197–203. [Google Scholar] [CrossRef]
- Baibakov, M.; Barulin, A.; Roy, P.; Claude, J.B.; Patra, S.; Wenger, J. Zero-mode waveguides can be made better: Fluorescence enhancement with rectangular aluminum nanoapertures from the visible to the deep ultraviolet. Nanoscale Adv. 2020, 2, 4153–4160. [Google Scholar] [CrossRef]
- Gutierrez Vela, Y.; Ortiz, D.; Saiz, J.; González, F.; Albella, P.; Moreno, F. The Quest for Low Loss High Refractive Index Dielectric Materials for UV Photonic Applications. Appl. Sci. 2018, 8, 2065. [Google Scholar] [CrossRef]
- Hervé, P.; Vandamme, L. General relation between refractive index and energy gap in semiconductors. Infrared Phys. Technol. 1994, 35, 609–615. [Google Scholar] [CrossRef]
- Hu, J.; Lawrence, M.; Dionne, J.A. High Quality Factor Dielectric Metasurfaces for Ultraviolet Circular Dichroism Spectroscopy. ACS Photonics 2020, 7, 36–42. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. (Eds.) Absorption and Scattering of Light by Small Particles; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. der Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Lu, H.L.; Scarel, G.; Alia, M.; Fanciulli, M.; Ding, S.J.; Zhang, D.W. Spectroscopic ellipsometry study of thin NiO films grown on Si (100) by atomic layer deposition. Appl. Phys. Lett. 2008, 92, 222907. [Google Scholar] [CrossRef]
- Nigara, Y. Measurement of the Optical Constants of Yttrium Oxide. Jpn. J. Appl. Phys. 1968, 7, 404–408. [Google Scholar] [CrossRef]
- Paskaleva, A.; Spassov, D.; Terziyska, P. Electric, dielectric and optical properties of Ga2O3 grown by metal organic chemical vapour deposition. J. Phys. Conf. Ser. 2017, 794, 012017. [Google Scholar] [CrossRef]
- Serényi, M.; Lohner, T.; Petrik, P.; Zolnai, Z.; Horváth, Z.; Khánh, N. Characterization of sputtered and annealed niobium oxide films using spectroscopic ellipsometry, Rutherford backscattering spectrometry and X-ray diffraction. Thin Solid Film. 2008, 516, 8096–8100. [Google Scholar] [CrossRef]
- Palik, E.D.; Addamiano, A. Zinc Sulfide (ZnS). In Handbook of Optical Constants of Solids; Palik, E.D., Ed.; Academic Press: Burlington, ON, Canada, 1997; pp. 597–619. [Google Scholar] [CrossRef]
- Bäuerle, D.; Braun, W.; Saile, V.; Sprüssel, G.; Koch, E.E. Vacuum ultraviolet reflectivity and band structure of SrTiO3 and BaTiO3. Z. Für Phys. B Condens. Matter Quanta 1978, 29, 179–184. [Google Scholar] [CrossRef]
- Çetinörgü, E.; Gümüş, C.; Goldsmith, S.; Mansur, F. Optical and structural characteristics of tin oxide thin films deposited by filtered vacuum arc and spray pyrolysis. Phys. Status Solidi (a) 2007, 204, 3278–3285. [Google Scholar] [CrossRef]
- Guo, L.; Hu, G.; Zhang, S.; Feng, W.; Zhang, Z. Structural, elastic, electronic and optical properties of beryllium chalcogenides BeX (X=S, Se, Te) with zinc-blende structure. J. Alloys Compd. 2013, 561, 16–22. [Google Scholar] [CrossRef]
- Synowicki, R.; Tiwald, T.E. Optical properties of bulk c-ZrO2, c-MgO and a-As2S3 determined by variable angle spectroscopic ellipsometry. Thin Solid Films 2004, 455–456, 248–255. [Google Scholar] [CrossRef]
- de Marcos, L.V.R.; Larruquert, J.I.; Méndez, J.A.; Aznárez, J.A. Self-consistent optical constants of SiO2 and Ta2O5 films. Opt. Mater. Express 2016, 6, 3622–3637. [Google Scholar] [CrossRef]
- Daimon, M.; Masumura, A. High-accuracy measurements of the refractive index and its temperature coefficient of calcium fluoride in a wide wavelength range from 138 to 2326 nm. Appl. Opt. 2002, 41, 5275–5281. [Google Scholar] [CrossRef]
- Dodge, M.J. Refractive properties of magnesium fluoride. Appl. Opt. 1984, 23, 1980–1985. [Google Scholar] [CrossRef]
- Pervak, V.; Krausz, F.; Apolonski, A. Hafnium oxide thin films deposited by reactive middle-frequency dual-magnetron sputtering. Thin Solid Films 2007, 515, 7984–7989. [Google Scholar] [CrossRef]
- Malitson, I.H.; Murphy, F.V.; Rodney, W.S. Refractive Index of Synthetic Sapphire. J. Opt. Soc. Am. 1958, 48, 72–73. [Google Scholar] [CrossRef]
- Miyata, N.; Moriki, K.; Mishima, O.; Fujisawa, M.; Hattori, T. Optical Constants of Cubic Boron Nitride. Phys. Rev. B Condens. Matter 1990, 40, 12028–12029. [Google Scholar] [CrossRef] [PubMed]
- Philipp, H. Silicon Nitride (Si3N4) (Noncrystalline). In Handbook of Optical Constants of Solids; Palik, E.D., Ed.; Academic Press: Burlington, ON, Canada, 1997; pp. 771–774. [Google Scholar] [CrossRef]
- Phillip, H.R.; Taft, E.A. Kramers-Kronig Analysis of Reflectance Data for Diamond. Phys. Rev. 1964, 136, A1445–A1448. [Google Scholar] [CrossRef]
- Mochalin, V.N.; Shenderova, O.; Ho, D.; Gogotsi, Y. The properties and applications of nanodiamonds. Nat. Nanotechnol. 2012, 7, 11–23. [Google Scholar] [CrossRef]
- Lenzini, F.; Gruhler, N.; Walter, N.; Pernice, W.H.P. Diamond as a Platform for Integrated Quantum Photonics. Adv. Quantum Technol. 2018, 1, 1800061. [Google Scholar] [CrossRef]
- Solomon, M.L.; Hu, J.; Lawrence, M.; Garc, A.; Dionne, J.A. Enantiospecific Optical Enhancement of Chiral Sensing and Separation with Dielectric Metasurfaces. ACS Photonics 2018, 6, 43–49. [Google Scholar] [CrossRef]
- Palik, E. (Ed.) Handbook of Optical Constants of Solids; Academic Press: Millbrae, CA, USA, 1997. [Google Scholar]
- Whispering gallery mode microresonators: Fundamentals and applications. La Rivista del Nuovo Cimento 2011, 34, 435–488. [CrossRef]
- Krüger, H.; Kemnitz, E.; Hertwig, A.; Beck, U. Transparent MgF2-films by sol–gel coating: Synthesis and optical properties. Thin Solid Film. 2008, 516, 4175–4177. [Google Scholar] [CrossRef]
- Pilvi, T.; Arstila, K.; Leskelä, M.; Ritala, M. Novel ALD Process for Depositing CaF2Thin Films. Chem. Mater. 2007, 19, 3387–3392. [Google Scholar] [CrossRef]
- Salisbury, I.G.; Timsit, R.S.; Berger, S.D.; Humphreys, C.J. Nanometer scale electron beam lithography in inorganic materials. Appl. Phys. Lett. 1984, 45, 1289–1291. [Google Scholar] [CrossRef]
- Bensalah, A.; Mortier, M.; Patriarche, G.; Gredin, P.; Vivien, D. Synthesis and optical characterizations of undoped and rare-earth-doped CaF2 nanoparticles. J. Solid State Chem. 2006, 179, 2636–2644. [Google Scholar] [CrossRef]
- Pantelides, S.T.; Wang, S.; Franceschetti, A.; Buczko, R.; Ventra, M.D.; Rashkeev, S.N.; Tsetseris, L.; Evans, M.; Batyrev, I.; Feldman, L.C.; et al. Si/SiO2 and SiC/SiO2 Interfaces for MOSFETs—Challenges and Advances. Mater. Sci. Forum 2006, 527–529, 935–948. [Google Scholar] [CrossRef]
- Miya, T.; Terunuma, Y.; Hosaka, T.; Miyashita, T. Ultimate low-loss single-mode fibre at 1.55 μm. Electron. Lett. 1979, 15, 106. [Google Scholar] [CrossRef]
- Yi, K.J.; Wang, H.; Lu, Y.F.; Yang, Z.Y. Enhanced Raman scattering by self-assembled silica spherical microparticles. J. Appl. Phys. 2007, 101, 063528. [Google Scholar] [CrossRef]
- Bose, S.; Cunha, J.M.V.; Suresh, S.; Wild, J.D.; Lopes, T.S.; Barbosa, J.R.S.; Silva, R.; Borme, J.; Fernandes, P.A.; Vermang, B.; et al. Optical Lithography Patterning of SiO2 Layers for Interface Passivation of Thin Film Solar Cells. Solar RRL 2018, 2, 1800212. [Google Scholar] [CrossRef]
- Miguez, H.; López, C.; Meseguer, F.; Blanco, A.; Vázquez, L.; Mayoral, R.; Ocaña, M.; Fornés, V.; Mifsud, A. Photonic crystal properties of packed submicrometric SiO2 spheres. Appl. Phys. Lett. 1997, 71, 1148–1150. [Google Scholar] [CrossRef]
- Silva, C.M.; Varisco, P.; Moehlecke, A.; Fichtner, P.; Papaléo, R.; Eriksson, J. Processing of nano-holes and pores on SiO2 thin films by MeV heavy ions. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2003, 206, 486–489. [Google Scholar] [CrossRef]
- Rahman, I.A.; Padavettan, V. Synthesis of Silica Nanoparticles by Sol-Gel: Size-Dependent Properties, Surface Modification, and Applications in Silica-Polymer Nanocomposites—A Review. J. Nanomater. 2012, 2012, 132424. [Google Scholar] [CrossRef]
- Huang, R.; Kitai, A.H. Preparation and characterization of thin films of MgO, Al2O3 and MgAl2O4 by atomic layer deposition. J. Electron. Mater. 1993, 22, 215–220. [Google Scholar] [CrossRef]
- Yaoi, T.; Ishio, S.; Miyazaki, T. Dependence of magnetoresistance on temperature and applied voltage in a 82Ni-Fe/Al-Al2O3/Co tunneling junction. J. Magn. Magn. Mater. 1993, 126, 430–432. [Google Scholar] [CrossRef]
- Chen, S.; Bomer, J.G.; Carlen, E.T.; van den Berg, A. Al2O3/Silicon NanoISFET with Near Ideal Nernstian Response. Nano Letters 2011, 11, 2334–2341. [Google Scholar] [CrossRef]
- Ganesan, R.; Dinachali, S.S.; Lim, S.H.; Saifullah, M.S.M.; Chong, W.T.; Lim, A.H.H.; Yong, J.J.; Thian, E.S.; He, C.; Low, H.Y. Direct nanoimprint lithography of Al2O3 using a chelated monomer-based precursor. Nanotechnology 2012, 23, 315304. [Google Scholar] [CrossRef] [PubMed]
- Yuasa, S.; Nagahama, T.; Fukushima, A.; Suzuki, Y.; Ando, K. Giant room-temperature magnetoresistance in single-crystal Fe/MgO/Fe magnetic tunnel junctions. Nat. Mater. 2004, 3, 868–871. [Google Scholar] [CrossRef]
- Moussavi, G.; Mahmoudi, M. Removal of azo and anthraquinone reactive dyes from industrial wastewaters using MgO nanoparticles. J. Hazard. Mater. 2009, 168, 806–812. [Google Scholar] [CrossRef]
- Dixon, S.C.; Scanlon, D.O.; Carmalt, C.J.; Parkin, I.P. n-Type doped transparent conducting binary oxides: An overview. J. Mater. Chem. C 2016, 4, 6946–6961. [Google Scholar] [CrossRef]
- Das, S.; Jayaraman, V. SnO2: A comprehensive review on structures and gas sensors. Prog. Mater. Sci. 2014, 66, 112–255. [Google Scholar] [CrossRef]
- Candeloro, P.; Comini, E.; Baratto, C.; Faglia, G.; Sberveglieri, G.; Kumar, R.; Carpentiero, A.; Fabrizio, E.D. SnO2 lithographic processing for nanopatterned gas sensors. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. 2005, 23, 2784. [Google Scholar] [CrossRef]
- Kim, S.P.; Choi, M.Y.; Choi, H.C. Photocatalytic activity of SnO2 nanoparticles in methylene blue degradation. Mater. Res. Bull. 2016, 74, 85–89. [Google Scholar] [CrossRef]
- Long, Z.; Xu, X.; Yang, W.; Hu, M.; Shtansky, D.V.; Golberg, D.; Fang, X. Cross-Bar SnO2-NiO Nanofiber-Array-Based Transparent Photodetectors with High Detectivity. Adv. Electron. Mater. 2019, 6, 1901048. [Google Scholar] [CrossRef]
- Gu, F.; Wang, S.F.; Lü, M.K.; Zhou, G.J.; Xu, D.; Yuan, D.R. Photoluminescence Properties of SnO2 Nanoparticles Synthesized by Sol-Gel Method. J. Phys. Chem. B 2004, 108, 8119–8123. [Google Scholar] [CrossRef]
- Xue, H.; He, Q.; Jian, G.; Long, S.; Pang, T.; Liu, M. An Overview of the Ultrawide Bandgap Ga2O3 Semiconductor-Based Schottky Barrier Diode for Power Electronics Application. Nanoscale Res. Lett. 2018, 13, 290. [Google Scholar] [CrossRef]
- Orita, M.; Ohta, H.; Hirano, M.; Hosono, H. Deep-ultraviolet transparent conductive β-Ga2O3 thin films. Appl. Phys. Lett. 2000, 77, 4166–4168. [Google Scholar] [CrossRef]
- Zhong, M.; Wei, Z.; Meng, X.; Wu, F.; Li, J. High-performance single crystalline UV photodetectors of β-Ga2O3. J. Alloys Compd. 2015, 619, 572–575. [Google Scholar] [CrossRef]
- Zhang, W.; Naidu, B.S.; Ou, J.Z.; O’Mullane, A.P.; Chrimes, A.F.; Carey, B.J.; Wang, Y.; Tang, S.Y.; Sivan, V.; Mitchell, A.; et al. Liquid Metal/Metal Oxide Frameworks with Incorporated Ga2O3 for Photocatalysis. ACS Appl. Mater. Interfaces 2015, 7, 1943–1948. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yamazaki, T.; Shen, Y.; Kikuta, T.; Nakatani, N.; Li, Y. O2 and CO sensing of Ga2O3 multiple nanowire gas sensors. Sens. Actuators BChem. 2008, 129, 666–670. [Google Scholar] [CrossRef]
- Li, X.; Zhen, X.; Meng, S.; Xian, J.; Shao, Y.; Fu, X.; Li, D. Structuring β-Ga2O3 Photonic Crystal Photocatalyst for Efficient Degradation of Organic Pollutants. Environ. Sci. Technol. 2013, 47, 9911–9917. [Google Scholar] [CrossRef]
- Lee, S.Y.; Gao, X.; Matsui, H. Biomimetic and Aggregation-Driven Crystallization Route for Room-Temperature Material Synthesis: Growth of β-Ga2O3 Nanoparticles on Peptide Assemblies as Nanoreactors. J. Am. Chem. Soc. 2007, 129, 2954–2958. [Google Scholar] [CrossRef]
- Zareiee, M. A novel high performance nano-scale MOSFET by inserting Si3N4 layer in the channel. Superlattices Microstruct. 2015, 88, 254–261. [Google Scholar] [CrossRef]
- Altun, A.O.; Jeong, J.H.; Rha, J.J.; Kim, K.D.; Lee, E.S. Boron nitride stamp for ultra-violet nanoimprinting lithography fabricated by focused ion beam lithography. Nanotechnology 2007, 18, 465302. [Google Scholar] [CrossRef] [PubMed]
- Aradi, E.; Erasmus, R.M.; Derry, T.E. Formation of c-BN nanoparticles by helium, lithium and boron ion implantation. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2012, 272, 57–60. [Google Scholar] [CrossRef]
- kumar, J.P.; Ramgopal, G.; Vidya, Y.; Anantharaju, K.; Prasad, B.D.; Sharma, S.; Prashantha, S.; Premkumar, H.; Nagabhushana, H. Bio-inspired synthesis of Y2O3: Eu3+ red nanophosphor for eco-friendly photocatalysis. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2015, 141, 149–160. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Hou, X.; Liu, M.; Lv, Y.; Hou, X. Controllable Synthesis of Y2O3 Microstructures for Application in Cataluminescence Gas Sensing. Chem. A Eur. J. 2011, 17, 7105–7111. [Google Scholar] [CrossRef] [PubMed]
- Rubio, E.J.; Atuchin, V.V.; Kruchinin, V.N.; Pokrovsky, L.D.; Prosvirin, I.P.; Ramana, C.V. Electronic Structure and Optical Quality of Nanocrystalline Y2O3 Film Surfaces and Interfaces on Silicon. J. Phys. Chem. C 2014, 118, 13644–13651. [Google Scholar] [CrossRef]
- Ko, K.Y.; Her, E.J.; Nichols, W.T.; Lee, H.; Do, Y.R.; Ahn, J. Fabrication of 2D photonic crystal assisted Y2O3:Eu3+ thin-film phosphors by direct nano-imprinting. Microelectron. Eng. 2011, 88, 2930–2933. [Google Scholar] [CrossRef]
- Traina, C.A.; Schwartz, J. Surface Modification of Y2O3 Nanoparticles. Langmuir 2007, 23, 9158–9161. [Google Scholar] [CrossRef] [PubMed]
- Beck, U.; Smith, D.; Reiners, G.; Dapkunas, S. Mechanical properties of SiO2 and Si3N4 coatings: A BAM/NIST co-operative project. Thin Solid Film. 1998, 332, 164–171. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, Z.; Yang, X.; Zhou, D.; Qian, X.; Zhang, J.; Zhang, D. Facile synthesis of Si3N4 nanowires with enhanced photocatalytic application. Mater. Lett. 2018, 212, 41–44. [Google Scholar] [CrossRef]
- Ayari-Kanoun, A.; Jaouad, A.; Souifi, A.; Drouin, D.; Beauvais, J. Silicon nitride nanotemplate fabrication using inductively coupled plasma etching process. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2011, 29, 051802. [Google Scholar] [CrossRef]
- Gwo, S.; Wu, C.L.; Chien, F.S.S.; Yasuda, T.; Yamasaki, S. Scanning Probe Microscopy and Lithography of Ultrathin Si3N4Films Grown on Si(111) and Si(001). Jpn. J. Appl. Phys. 2001, 40, 4368–4372. [Google Scholar] [CrossRef]
- Chaneliere, C.; Autran, J.; Devine, R.; Balland, B. Tantalum pentoxide (Ta2O5) thin films for advanced dielectric applications. Mater. Sci. Eng. R Rep. 1998, 22, 269–322. [Google Scholar] [CrossRef]
- Sreethawong, T.; Ngamsinlapasathian, S.; Suzuki, Y.; Yoshikawa, S. Nanocrystalline mesoporous Ta2O5-based photocatalysts prepared by surfactant-assisted templating sol-gel process for photocatalytic H2 evolution. J. Mol. Catal. A Chem. 2005, 235, 1–11. [Google Scholar] [CrossRef]
- Nagaraju, G.; Karthik, K.; Shashank, M. Ultrasound-assisted Ta2O5 nanoparticles and their photocatalytic and biological applications. Microchem. J. 2019, 147, 749–754. [Google Scholar] [CrossRef]
- Wahlbrink, T.; Bolten, J.; Mollenhauer, T.; Kurz, H.; Baumann, K.; Moll, N.; Stöferle, T.; Mahrt, R. Fabrication and characterization of Ta2O5 photonic feedback structures. Microelectron. Eng. 2008, 85, 1425–1428. [Google Scholar] [CrossRef]
- Ganesan, R.; Lim, S.H.; Saifullah, M.S.M.; Hussain, H.; Kwok, J.X.Q.; Tse, R.L.X.; Bo, H.A.P.; Low, H.Y. Direct nanoimprinting of metal oxides by in situ thermal co-polymerization of their methacrylates. J. Mater. Chem. 2011, 21, 4484. [Google Scholar] [CrossRef]
- Zhu, H.; Tang, C.; Fonseca, L.R.C.; Ramprasad, R. Recent progress in ab initio simulations of hafnia-based gate stacks. J. Mater. Sci. 2012, 47, 7399–7416. [Google Scholar] [CrossRef]
- Benedicto, M.; Galiana, B.; Molina-Aldareguia, J.M.; Monaghan, S.; Hurley, P.K.; Cherkaoui, K.; Vazquez, L.; Tejedor, P. Fabrication of HfO2 patterns by laser interference nanolithography and selective dry etching for III-V CMOS application. Nanoscale Res. Lett. 2011, 6, 400. [Google Scholar] [CrossRef] [PubMed]
- Ramadoss, A.; Kim, S.J. Synthesis and characterization of HfO2 nanoparticles by sonochemical approach. J. Alloys Compd. 2012, 544, 115–119. [Google Scholar] [CrossRef]
- Panda, D.; Tseng, T.Y. Growth, dielectric properties, and memory device applications of ZrO2 thin films. Thin Solid Films 2013, 531, 1–20. [Google Scholar] [CrossRef]
- Kohno, Y.; Tanaka, T.; Funabiki, T.; Yoshida, S. Identification and reactivity of a surface intermediate in the photoreduction of CO2 with H2 over ZrO2. J. Chem. Soc. Faraday Trans. 1998, 94, 1875–1880. [Google Scholar] [CrossRef]
- Park, H.H.; Zhang, X.; Lee, S.W.; don Kim, K.; Choi, D.G.; Choi, J.H.; Lee, J.; Lee, E.S.; Park, H.H.; Hill, R.H.; et al. Facile nanopatterning of zirconium dioxide films via direct ultraviolet-assisted nanoimprint lithography. J. Mater. Chem. 2011, 21, 657–662. [Google Scholar] [CrossRef]
- Liang, J.; Deng, Z.; Jiang, X.; Li, F.; Li, Y. Photoluminescence of Tetragonal ZrO2 Nanoparticles Synthesized by Microwave Irradiation. Inorg. Chem. 2002, 41, 3602–3604. [Google Scholar] [CrossRef]
- Lin, Z.; Du, C.; Yan, B.; Wang, C.; Yang, G. Two-dimensional amorphous NiO as a plasmonic photocatalyst for solar H2 evolution. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Sato, H.; Minami, T.; Takata, S.; Yamada, T. Transparent conducting p-type NiO thin films prepared by magnetron sputtering. Thin Solid Film. 1993, 236, 27–31. [Google Scholar] [CrossRef]
- Hasan, M.R.; Xie, T.; Barron, S.C.; Liu, G.; Nguyen, N.V.; Motayed, A.; Rao, M.V.; Debnath, R. Self-powered p-NiO/n-ZnO heterojunction ultraviolet photodetectors fabricated on plastic substrates. APL Mater. 2015, 3, 106101. [Google Scholar] [CrossRef]
- Hotovy, I.; Rehacek, V.; Siciliano, P.; Capone, S.; Spiess, L. Sensing characteristics of NiO thin films as NO2 gas sensor. Thin Solid Films 2002, 418, 9–15. [Google Scholar] [CrossRef]
- Liu, H.; Wang, G.; Liu, J.; Qiao, S.; Ahn, H. Highly ordered mesoporous NiO anode material for lithium ion batteries with an excellent electrochemical performance. J. Mater. Chem. 2011, 21, 3046. [Google Scholar] [CrossRef]
- Bandara, J.; Weerasinghe, H. Solid-state dye-sensitized solar cell with p-type NiO as a hole collector. Solar Energy Mater. Sol. Cells 2005, 85, 385–390. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, J.; Yang, X.; Lu, L.; Wang, X. Preparation of NiO nanoparticles and their catalytic activity in the thermal decomposition of ammonium perchlorate. Thermochim. Acta 2005, 437, 106–109. [Google Scholar] [CrossRef]
- Aharonovich, I.; Neu, E. Diamond Nanophotonics. Adv. Opt. Mater. 2014, 2, 911–928. [Google Scholar] [CrossRef]
- Werner, M.; Fahrner, W. Review on materials, microsensors, systems and devices for high-temperature and harsh-environment applications. IEEE Trans. Ind. Electron. 2001, 48, 249–257. [Google Scholar] [CrossRef]
- Taniguchi, J.; Tokano, Y.; Miyamoto, I.; Komuro, M.; Hiroshima, H. Diamond nanoimprint lithography. Nanotechnology 2002, 13, 592–596. [Google Scholar] [CrossRef]
- Viet, A.L.; Jose, R.; Reddy, M.V.; Chowdari, B.V.R.; Ramakrishna, S. Nb2O5 Photoelectrodes for Dye-Sensitized Solar Cells: Choice of the Polymorph. J. Phys. Chem. C 2010, 114, 21795–21800. [Google Scholar] [CrossRef]
- Prado, A.G.; Bolzon, L.B.; Pedroso, C.P.; Moura, A.O.; Costa, L.L. Nb2O5 as efficient and recyclable photocatalyst for indigo carmine degradation. Appl. Catal. B Environ. 2008, 82, 219–224. [Google Scholar] [CrossRef]
- Lopes, O.F.; Paris, E.C.; Ribeiro, C. Synthesis of Nb2O5 nanoparticles through the oxidant peroxide method applied to organic pollutant photodegradation: A mechanistic study. Appl. Catal. B Environ. 2014, 144, 800–808. [Google Scholar] [CrossRef]
- Lee, G.J.; Wu, J.J. Recent developments in ZnS photocatalysts from synthesis to photocatalytic applications—A review. Powder Technol. 2017, 318, 8–22. [Google Scholar] [CrossRef]
- Xu, X.; Li, S.; Chen, J.; Cai, S.; Long, Z.; Fang, X. Design Principles and Material Engineering of ZnS for Optoelectronic Devices and Catalysis. Adv. Funct. Mater. 2018, 28, 1802029. [Google Scholar] [CrossRef]
- Kim, J.H.; Rho, H.; Kim, J.; Choi, Y.J.; Park, J.G. Raman spectroscopy of ZnS nanostructures. J. Raman Spectrosc. 2012, 43, 906–910. [Google Scholar] [CrossRef]
- Park, W.; King, J.; Neff, C.; Liddell, C.; Summers, C. ZnS-Based Photonic Crystals. Phys. Status Solidi (b) 2002, 229, 949–960. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, W. Synthesis and properties of transition metals and rare-earth metals doped ZnS nanoparticles. Opt. Mater. 2006, 28, 536–550. [Google Scholar] [CrossRef]
- Wang, D.; Ye, J.; Kako, T.; Kimura, T. Photophysical and Photocatalytic Properties of SrTiO3 Doped with Cr Cations on Different Sites. J. Phys. Chem. B 2006, 110, 15824–15830. [Google Scholar] [CrossRef]
- Phoon, B.L.; Lai, C.W.; Juan, J.C.; Show, P.L.; Chen, W.H. A review of synthesis and morphology of SrTiO3 for energy and other applications. Int. J. Energy Res. 2019, 43, 5151–5174. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Boston, MA, USA, 2007. [Google Scholar] [CrossRef]
- Prasad, P.N. Nanophotonics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Sharma, B.; Frontiera, R.R.; Henry, A.I.; Ringe, E.; Van Duyne, R.P. SERS: Materials, applications, and the future. Mater. Today 2012, 15, 16–25. [Google Scholar] [CrossRef]
- Jahn, M.; Patze, S.; Hidi, I.J.; Knipper, R.; Radu, A.I.; Mühlig, A.; Yüksel, S.; Peksa, V.; Weber, K.; Mayerhöfer, T.; et al. Plasmonic nanostructures for surface enhanced spectroscopic methods. Analyst 2016, 141, 756–793. [Google Scholar] [CrossRef] [PubMed]
- Fort, E.; Grésillon, S. Surface enhanced fluorescence. J. Phys. D Appl. Phys. 2008, 41, 013001. [Google Scholar] [CrossRef]
- Beltrán, C.; Etayo, U. The diamond ensemble: A constructive set of spherical points with small logarithmic energy. J. Complex. 2020, 59, 101471. [Google Scholar]
- Meier, M.; Wokaun, A. Enhanced fields on large metal particles: Dynamic depolarization. Opt. Lett. 1983, 8, 581. [Google Scholar] [CrossRef] [PubMed]
- Maier, N.M.; Franco, P.; Lindner, W. Separation of enantiomers: Needs, challenges, perspectives. J. Chromatogr. A 2001, 906, 3–33. [Google Scholar] [CrossRef]
- Balavoine, G.; Moradpour, A.; Kagan, H.B. Preparation of chiral compounds with high optical purity by irradiation with circularly polarized light, a model reaction for the prebiotic generation of optical activity. J. Am. Chem. Soc. 1974, 96, 5152–5158. [Google Scholar] [CrossRef]
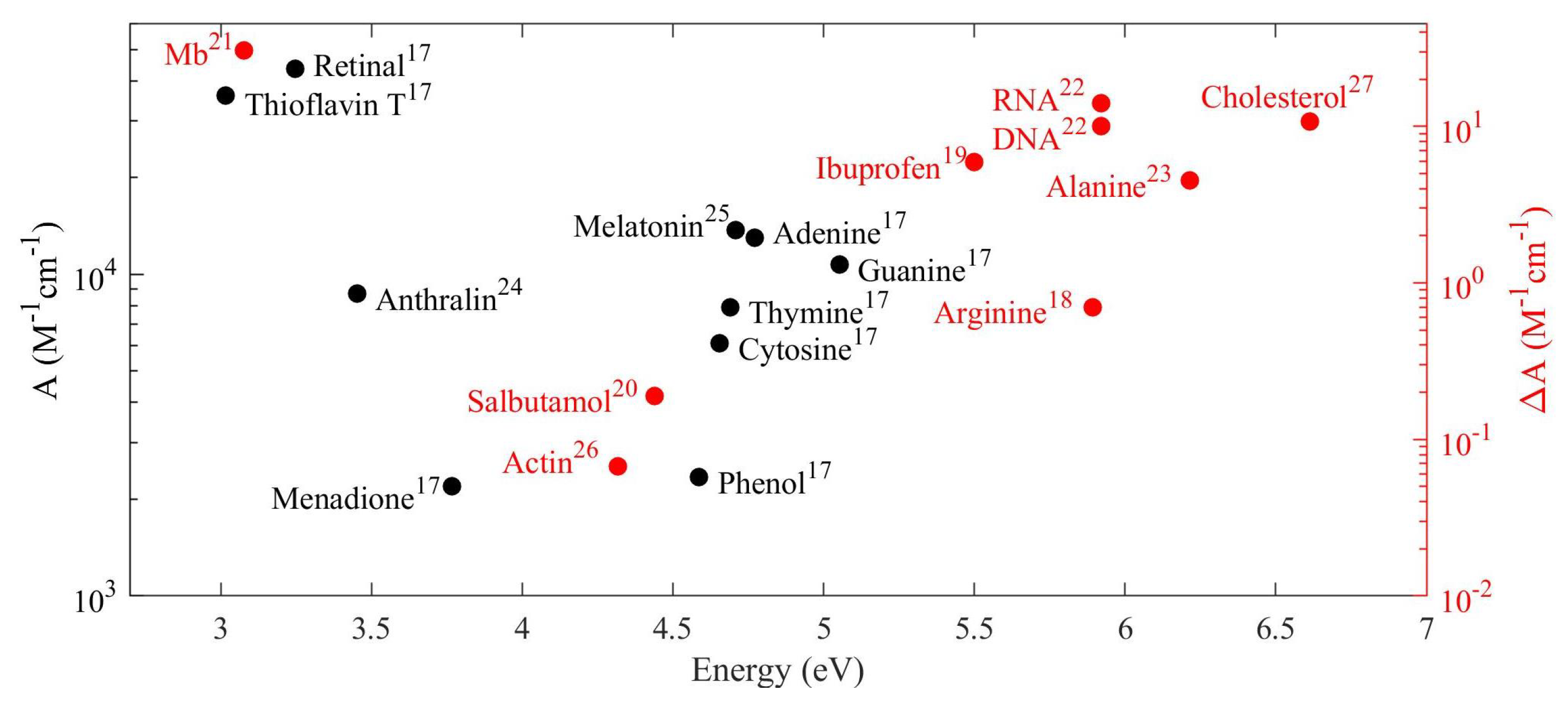
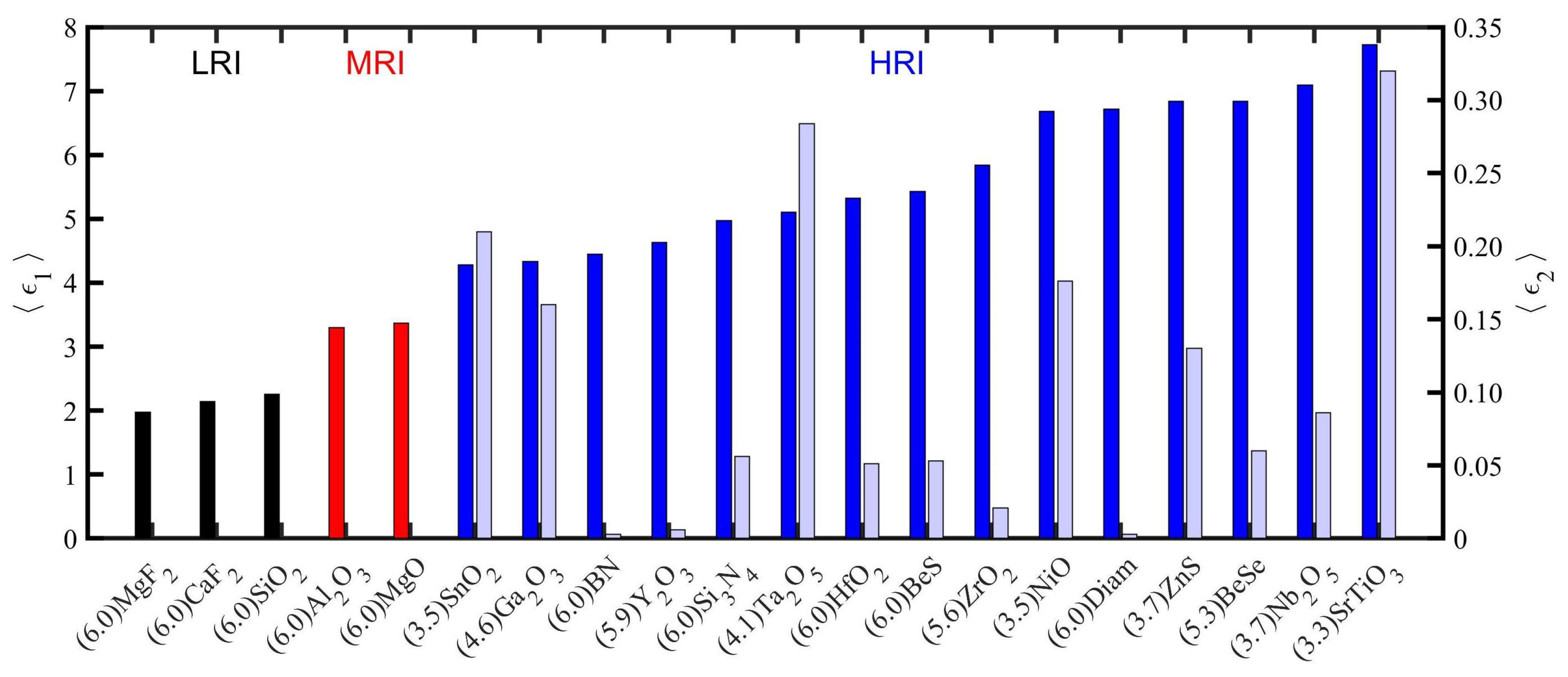
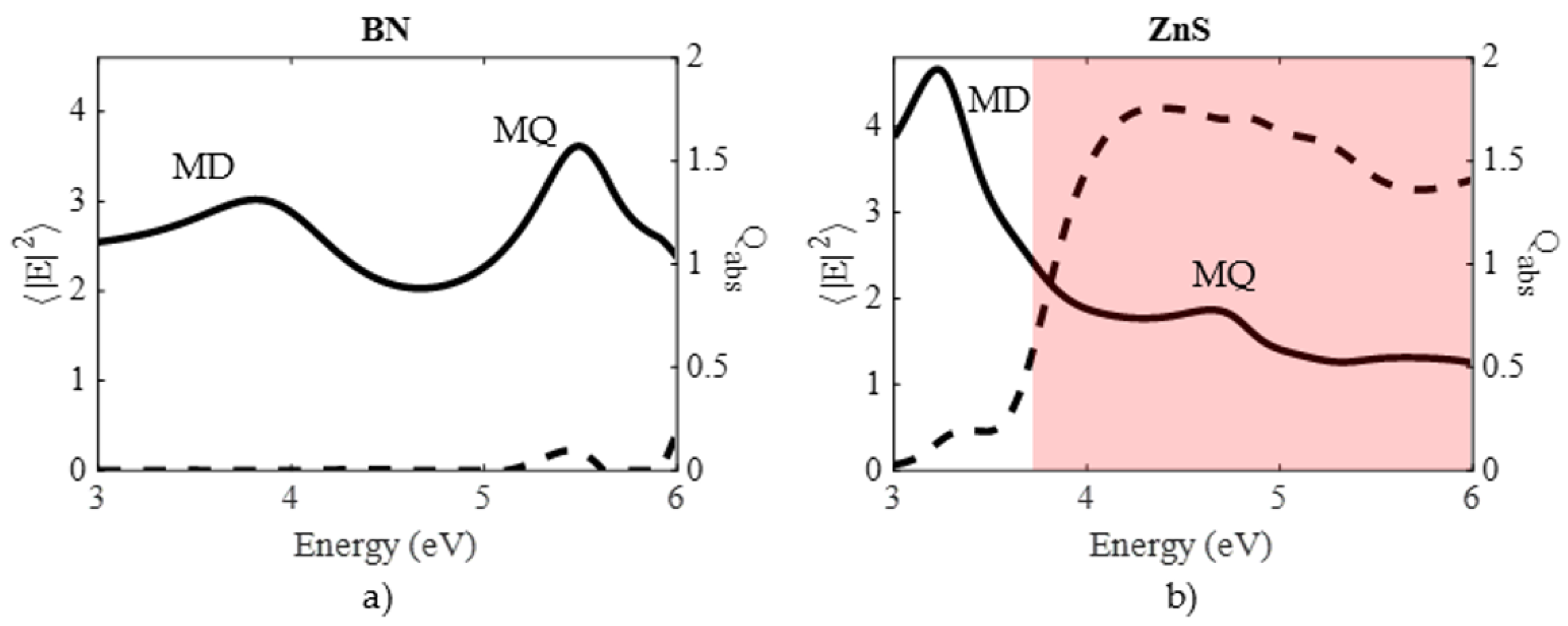
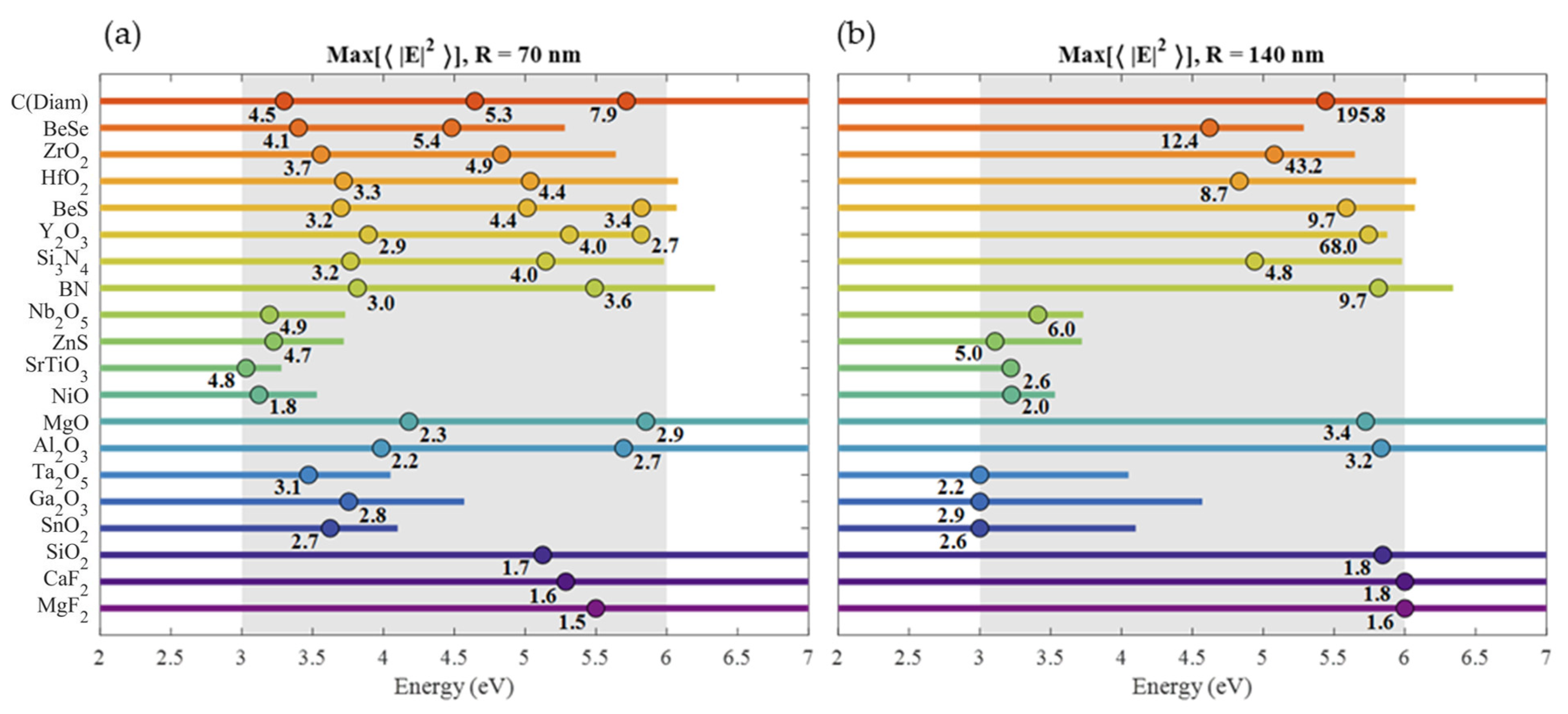
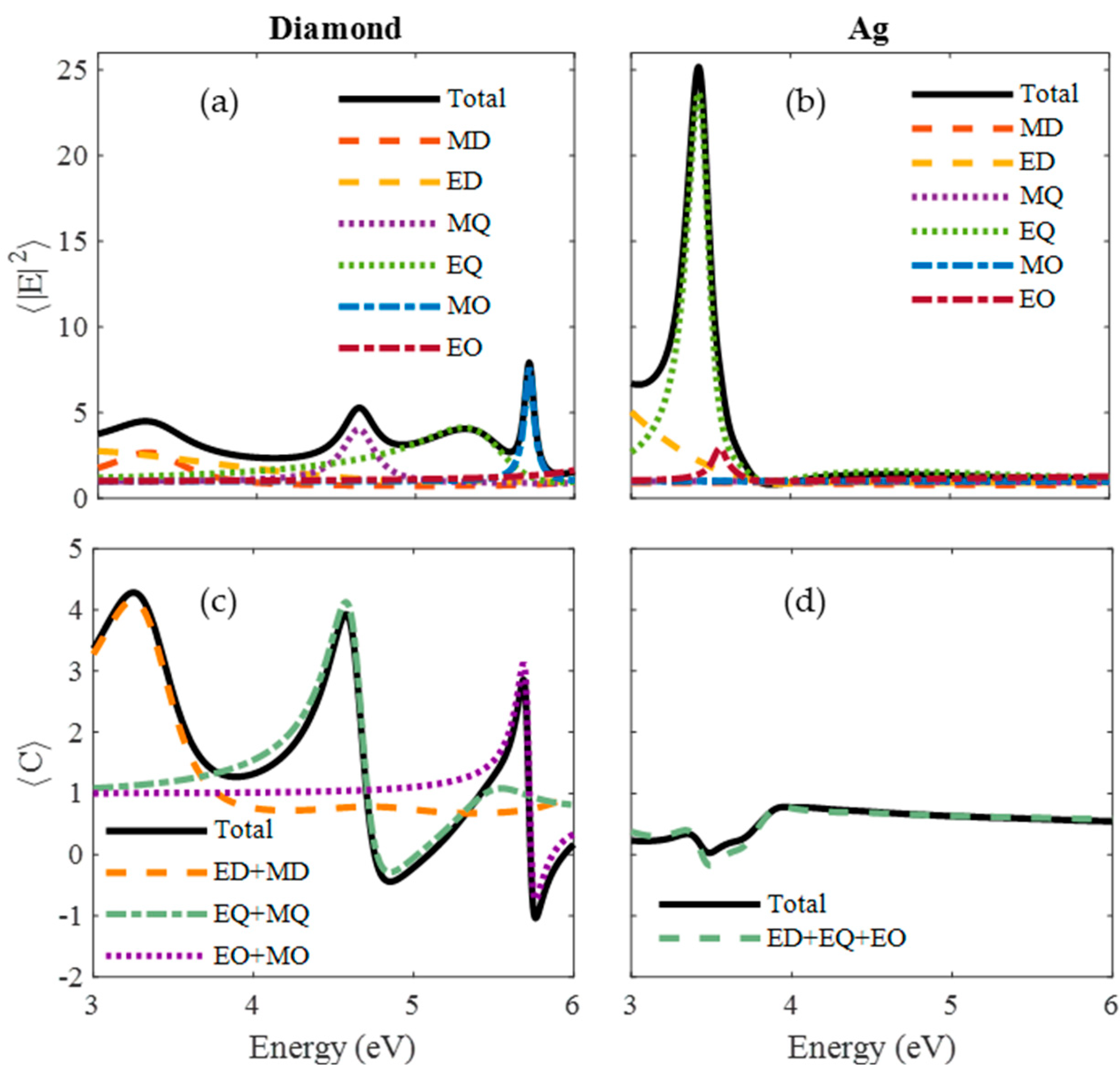
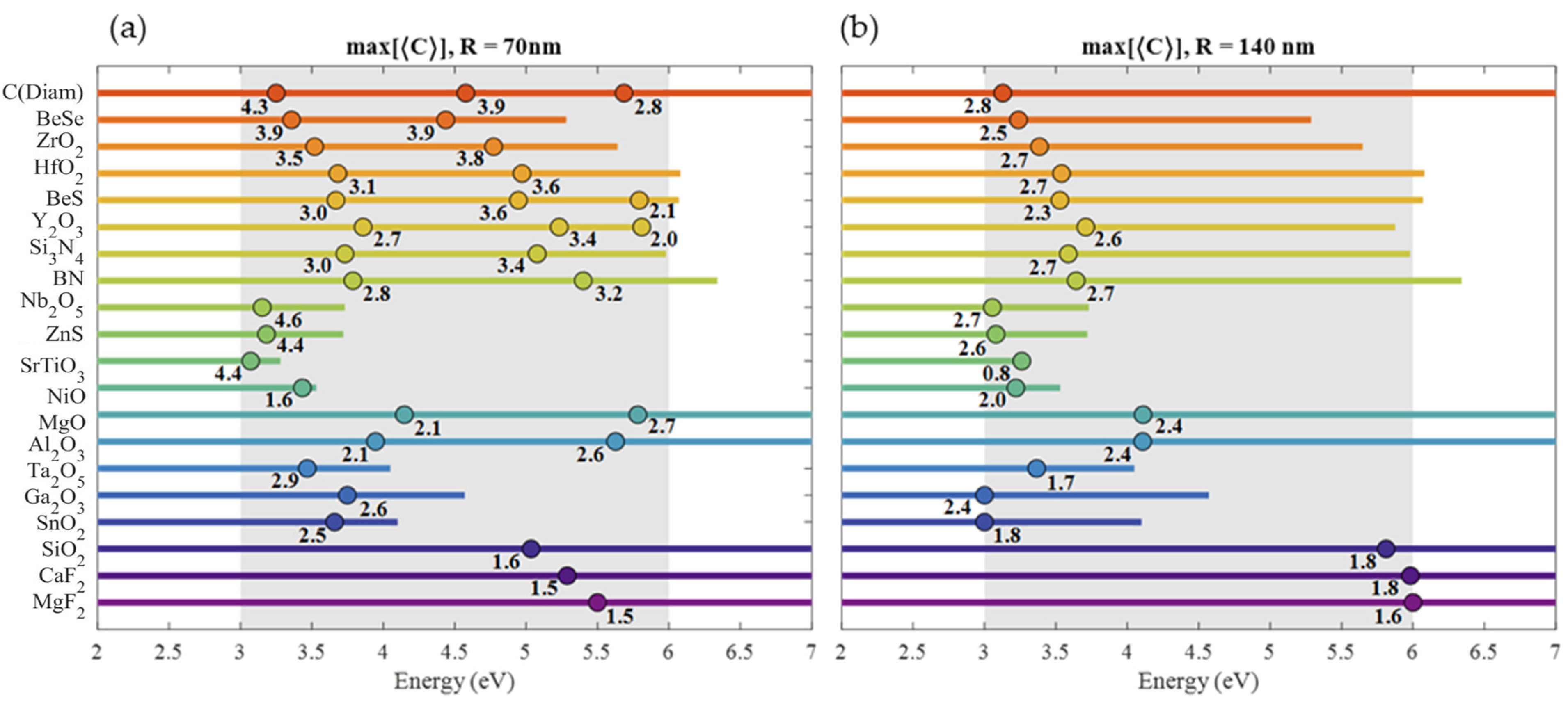
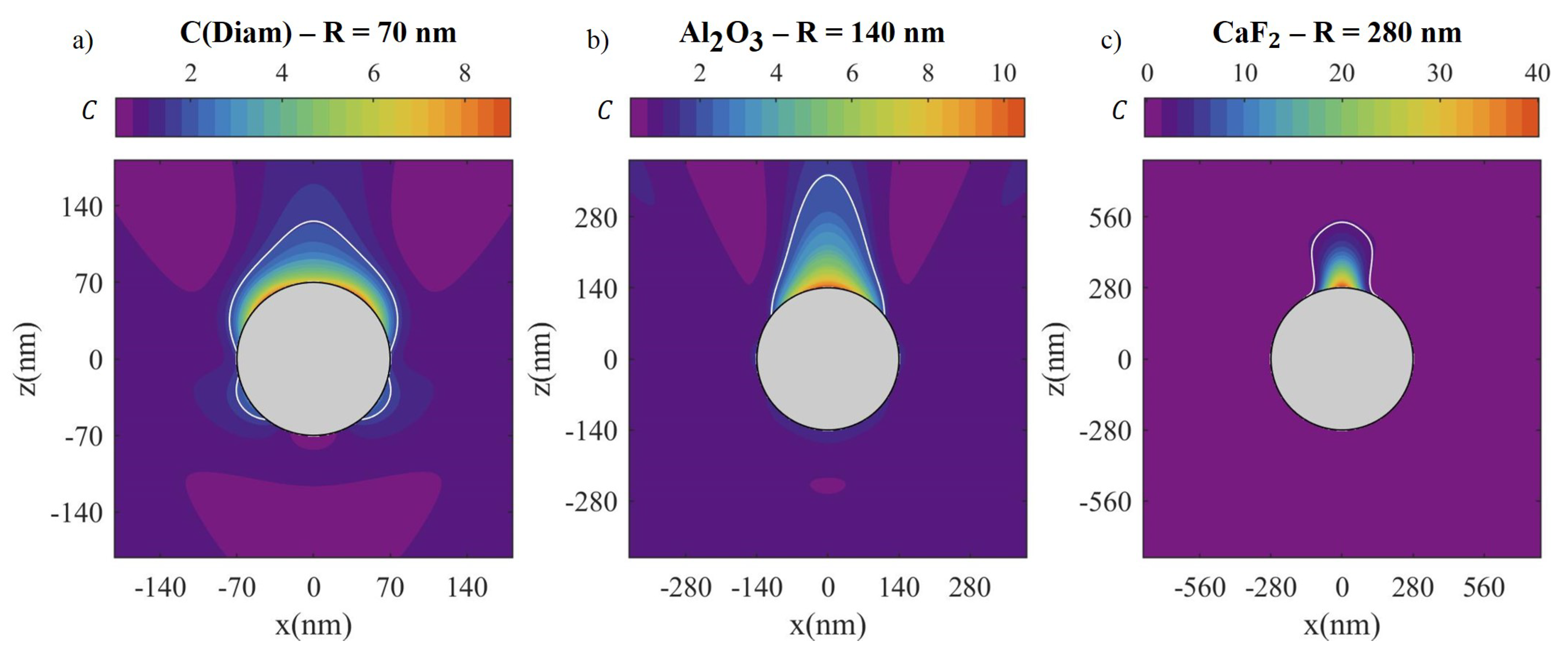
| Material | Applications | Lithography | Nanoparticles (Colloidal) |
|---|---|---|---|
| MgF2 | BOD(UV-IR), CS [71,72] | - | - |
| CaF2 | BOD(UV-IR), CS [71,73] | [74] | [75] |
| SiO2 | CS, BOD(VIS-IR), MOSFET, FO, SES [59,71,76,77,78] | [79,80,81] | [82] |
| Al2O3 | CS, MRAM, ISFET [83,84,85] | [74,86] | - |
| MgO | CS, MRAM [83,87] | [74] | [88] |
| SnO2 | n-TCF, GS, Pcat, UV-PD [89,90,91,92,93] | [91] | [94] |
| Ga2O3 | MOSFET, SBD, HPD, n-TCF, UV-PD, Pcat, GS [95,96,97,98,99] | [100] | [101] |
| BN | HT-HPD, HT-UV-PD [102] | [103] | [104] |
| Y2O3 | SS-LASER, Pcat, GS, HT-CS [51,105,106,107] | [108] | [109] |
| Si3N4 | SES, CS, Pcat, [6,110,111] | [112,113] | - |
| Ta2O5 | DRAM, MOSFET, ISFET, CS, Pcat [114,115,116] | [117,118] | [116] |
| HfO2 | MOSFET, RRAM [119] | [120] | [121] |
| BeS | Blue and green LED [57] | - | - |
| ZrO2 | DRAM, Pcat [122,123] | [118,124] | [125] |
| NiO | Pcat, p-TCF, UV-PD, GS, Battery anode, DSSC-electroanode [126,127,128,129,130,131] | - | [132] |
| C(Diam) | OQC, LumD, HT-HPD [68,133,134] | [68,135] | [67] |
| BeSe | Blue and green LED [57] | - | - |
| Nb2O5 | DSSC-electroanode, Pcat [136,137,138] | [118] | [138] |
| ZnS | Pcat, p and n-TCF, LumD, UV-PD, SES [139,140,141] | [140,142] | [143] |
| SrTiO3 | Pcat, GS [144,145] | - | [99] |
| Material | R (nm) | (eV) | (μm2) | (μm2) | (μm2) | (μm2) | |
|---|---|---|---|---|---|---|---|
| C(Diam) | 70 | 4.58 | 3.9 | 0.062 | 0.021 (33%) | 0.060 (97%) | 0 |
| Al2O3 | 140 | 4.1 | 2.4 | 0.246 | 0.046 (19%) | 0.246 (100%) | 0 |
| CaF2 | 280 | 5.7 | 1.6 | 0.985 | 0.097 (10%) | 0.409 (41%) | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosales, S.A.; González, F.; Moreno, F.; Gutiérrez, Y. Non-Absorbing Dielectric Materials for Surface-Enhanced Spectroscopies and Chiral Sensing in the UV. Nanomaterials 2020, 10, 2078. https://doi.org/10.3390/nano10102078
Rosales SA, González F, Moreno F, Gutiérrez Y. Non-Absorbing Dielectric Materials for Surface-Enhanced Spectroscopies and Chiral Sensing in the UV. Nanomaterials. 2020; 10(10):2078. https://doi.org/10.3390/nano10102078
Chicago/Turabian StyleRosales, Saúl A., Francisco González, Fernando Moreno, and Yael Gutiérrez. 2020. "Non-Absorbing Dielectric Materials for Surface-Enhanced Spectroscopies and Chiral Sensing in the UV" Nanomaterials 10, no. 10: 2078. https://doi.org/10.3390/nano10102078
APA StyleRosales, S. A., González, F., Moreno, F., & Gutiérrez, Y. (2020). Non-Absorbing Dielectric Materials for Surface-Enhanced Spectroscopies and Chiral Sensing in the UV. Nanomaterials, 10(10), 2078. https://doi.org/10.3390/nano10102078






