Additive Manufacturing Gyroid Structures Used as Crash Energy Management
Abstract
1. Introduction
- Assess the impact of fabrication direction on the energy capabilities of Gyroid structures in compression.
- Evaluate the scalability of Gyroid structures to achieve the desired force or deceleration.
- Derive power-law coefficients to estimate forces and energies for different relative densities.
- Evaluate the estimation of deceleration impacting Gyroids, assuming constant deceleration.
- Simulate compression and impact tests with a simplified model.
- Design a tailored deformation element that meets two distinct deceleration requirements.
- Analyze computational stability results using data from the open material database instead of compression of real lattice structures.
2. Materials and Methods
2.1. Fabrication of PLA Gyroid Structures
2.2. Compression Tests
2.3. Estimation of Impact Tests with Various Mass and Initial Velocity
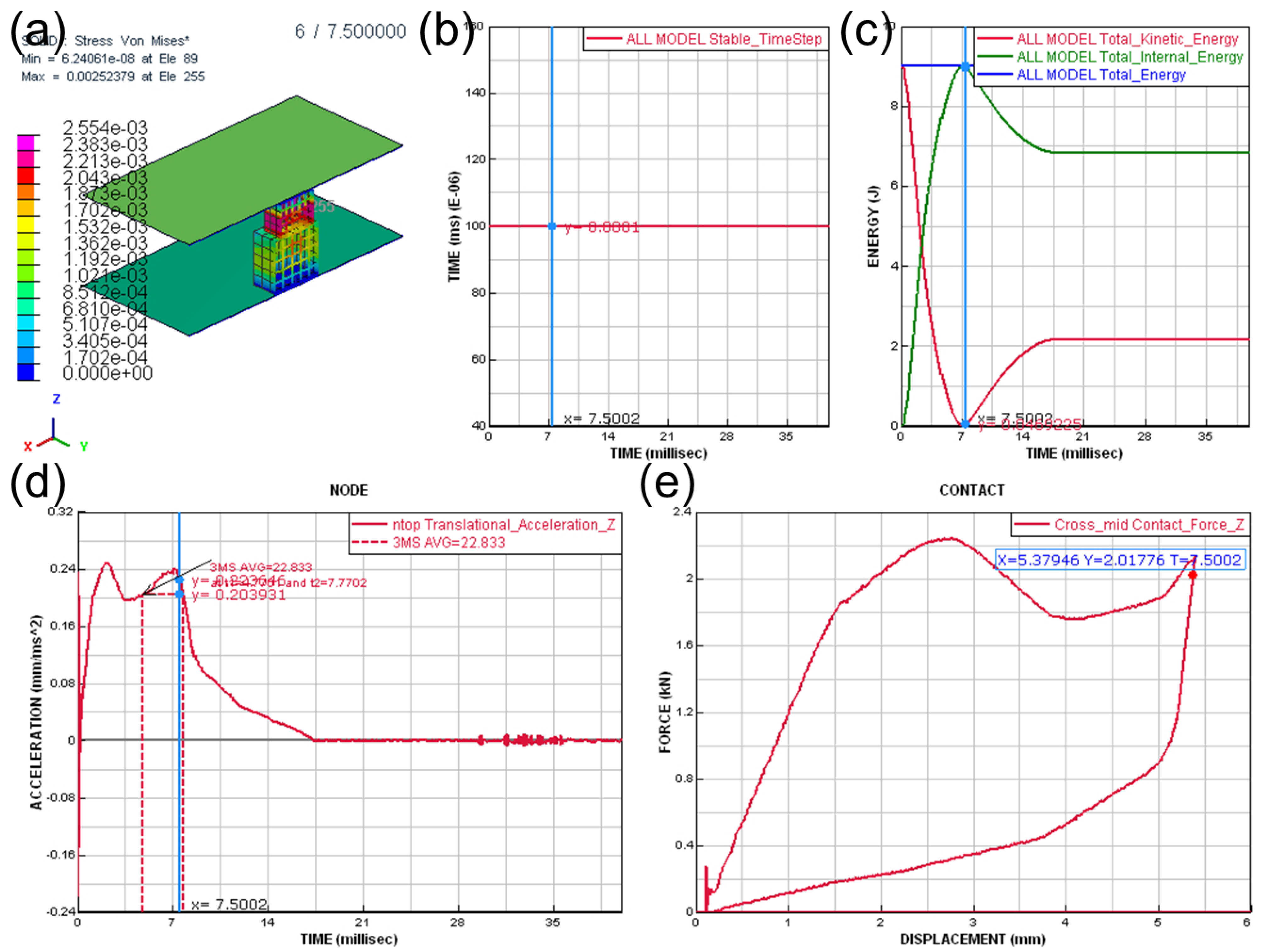
2.4. Simulation Model for Compression and Impact Tests
3. Results
3.1. Compression Results Depending on Fabrication Direction
3.2. Scalability of Quasistatic Compression Results
3.3. Power-Law Coefficients for Relative Density Based on Quasistatic Compression Tests
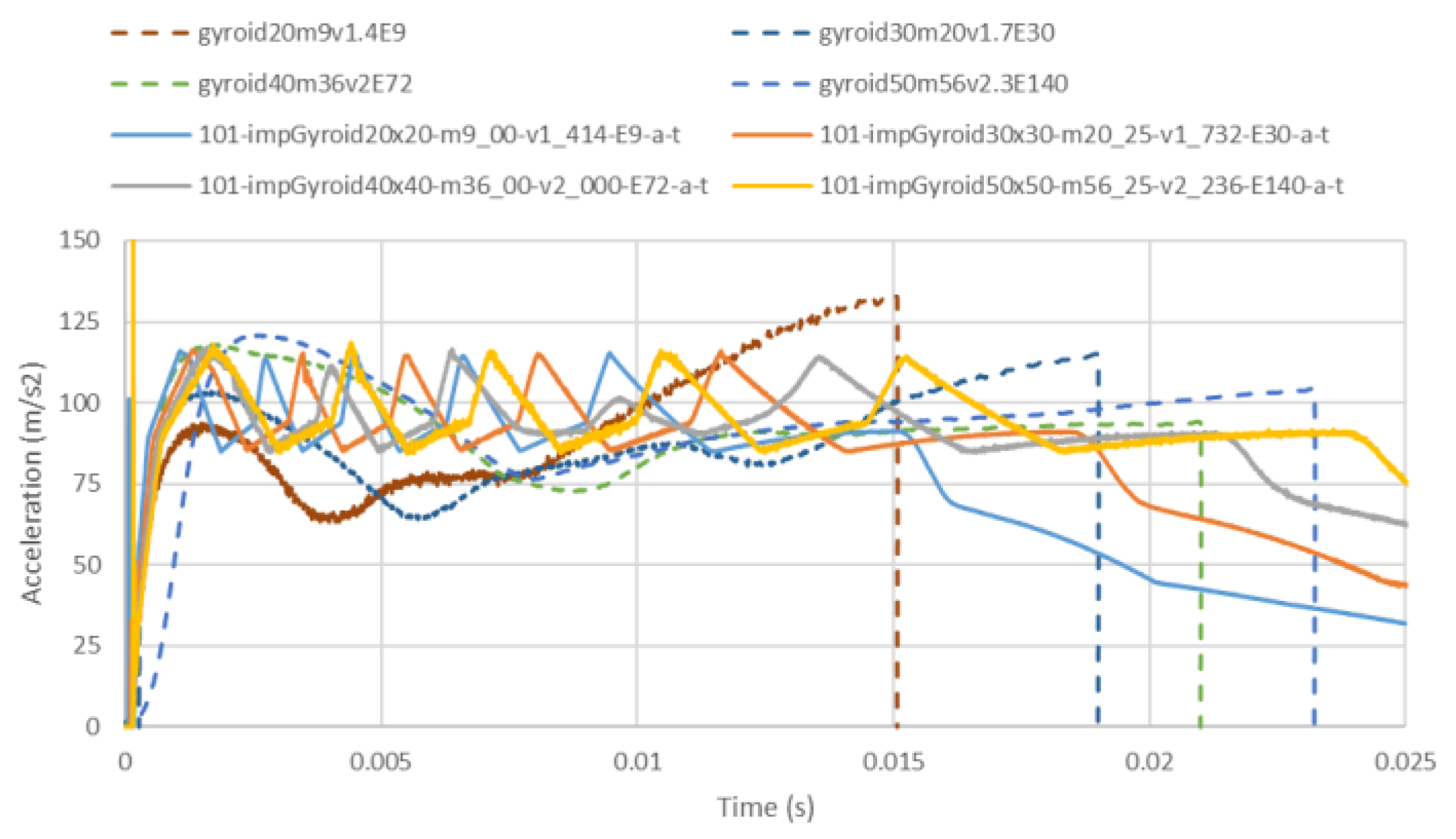
3.4. Estimation of Acceleration Impacting Gyroids
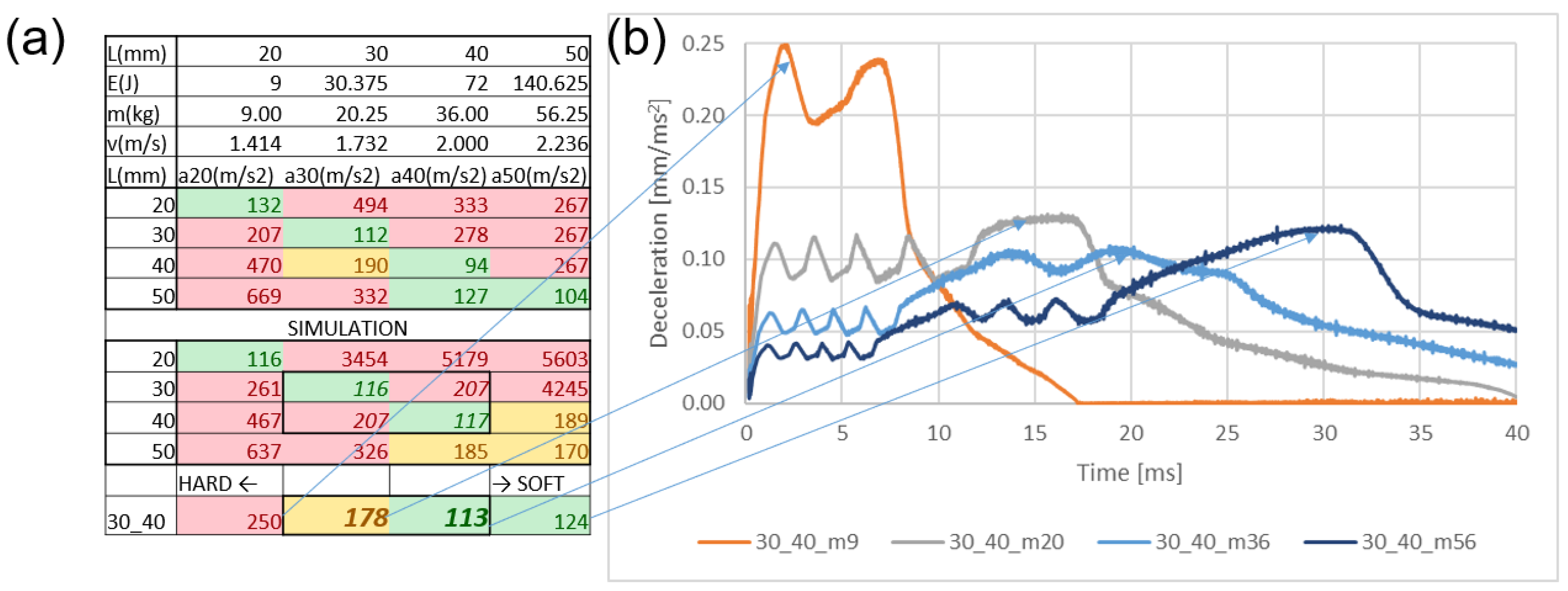
3.5. Simulation of Compression of Gyroids
3.6. Design to Meet Two Different Requirements of Decelerations
3.7. Computation Results for Mesh Type, Hardening, and Strain Rate
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Doubrovski, Z.; Verlinden, J.C.; Geraedts, J.M. Optimal Design for Additive Manufacturing: Opportunities and Challenges. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; Volume 54860, pp. 635–646. [Google Scholar]
- Yang, S.; Tang, Y.; Zhao, Y.F. A New Part Consolidation Method to Embrace the Design Freedom of Additive Manufacturing. J. Manuf. Process. 2015, 20, 444–449. [Google Scholar] [CrossRef]
- Efa, D.A.; Gutema, E.M.; Lemu, H.G.; Gopal, M. Optimization of Titanium Alloy-Ti-6Al-4V to Minimize Mass, Maximize Stiffness and Frequency in Additive Manufacturing. Key Eng. Mater. 2024, 980, 3–13. [Google Scholar] [CrossRef]
- Khan, N.A.; Sankar, M.R.; Kumar, A. State of the Art on Additive Manufacturing of Moulding Dies with Conformal Cooling Channels. In International Conference on Processing and Fabrication of Advanced Materials; Springer Nature: Singapore, 2023; pp. 63–83. [Google Scholar] [CrossRef]
- Pietropaoli, M.; Ahlfeld, R.; Montomoli, F.; Ciani, A.; D’Ercole, M. Design for Additive Manufacturing: Internal Channel Optimization. J. Eng. Gas Turbines Power 2017, 139, 102101. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Dai, N.; Dong, G.; Tang, Y.; Xie, Y.M. Optimal Design and Modeling of Gyroid-Based Functionally Graded Cellular Structures for Additive Manufacturing. Comput. Aided Des. 2018, 104, 87–99. [Google Scholar] [CrossRef]
- Zhang, B.; Mhapsekar, K.; Anand, S. Design of Variable-Density Structures for Additive Manufacturing Using Gyroid Lattices. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Naghavi, S.A.; Tamaddon, M.; Marghoub, A.; Wang, K.; Babamiri, B.B.; Hazeli, K.; Xu, W.; Lu, X.; Sun, C.; Wang, L.; et al. Mechanical Characterisation and Numerical Modelling of TPMS-Based Gyroid and Diamond Ti6Al4V Scaffolds for Bone Implants: An Integrated Approach for Translational Consideration. Bioengineering 2022, 9, 504. [Google Scholar] [CrossRef] [PubMed]
- Maskery, I.; Sturm, L.; Aremu, A.O.; Panesar, A.; Williams, C.B.; Tuck, C.J.; Wildman, R.D.; Ashcroft, I.; Hague, R.J.M. Insights into the Mechanical Properties of Several Triply Periodic Minimal Surface Lattice Structures Made by Polymer Additive Manufacturing. Polymer 2018, 152, 62–71. [Google Scholar] [CrossRef]
- Chouhan, G.; Murali, G.B. Designs, Advancements, and Applications of Three-Dimensional Printed Gyroid Structures: A Review. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2024, 238, 965–987. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Dai, N.; Xie, Y.M. Comparison of Mechanical Properties and Energy Absorption of Sheet-Based and Strut-Based Gyroid Cellular Structures with Graded Densities. Materials 2019, 12, 2183. [Google Scholar] [CrossRef]
- Zisopol, D.G.; Minescu, M.; Iacob, D.V. A Study on the Evaluation of the Compression Behavior of PLA Lattice Structures Manufactured by FDM. Eng. Technol. Appl. Sci. Res. 2023, 13, 11801–11806. [Google Scholar] [CrossRef]
- Weber, D.; Sundarram, S.S. 3D-Printed and Foamed Triply Periodic Minimal Surface Lattice Structures for Energy Absorption Applications. Polym. Eng. Sci. 2023, 63, 1133–1145. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved mechanical properties and energy absorption of BCC lattice structures with triply periodic minimal surfaces fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Granada, A.-A. High-Compression Crash Simulations and Tests of PLA Cubes Fabricated Using Additive Manufacturing FDM with a Scaling Strategy. Computation 2024, 12, 40. [Google Scholar] [CrossRef]
- Kim, G.-W.; Park, Y.-I.; Park, K. Topology Optimization and Additive Manufacturing of Automotive Component by Coupling Kinetic and Structural Analyses. Int. J. Automot. Technol. 2020, 21, 1455–1463. [Google Scholar] [CrossRef]
- Ramos, H.; Santiago, R.; Soe, S.; Theobald, P.; Alves, M. Response of Gyroid Lattice Structures to Impact Loads. Int. J. Impact Eng. 2022, 164, 104202. [Google Scholar] [CrossRef]
- Silva, C.; Pais, A.I.; Caldas, G.; Gouveia, B.P.P.A.; Alves, J.L.; Belinha, J. Study on 3D Printing of Gyroid-Based Structures for Superior Structural Behaviour. Prog. Addit. Manuf. 2021, 6, 689–703. [Google Scholar] [CrossRef]
- Rostro-González, H.; Puigoriol-Forcada, J.M.; Pérez-Peña, A.; Menacho, J.; Garcia-Granada, A.-A. Optimizing Crash Box Design to Meet Injury Criteria: A Protocol for Accurate Simulation and Material Selection. Struct. Multidiscip. Optim. 2024, 67, 1–17. [Google Scholar] [CrossRef]
- Association, European Automobile Manufacturers. ACEA-Regulatory-Guide-2023. 2024. Available online: https://www.acea.auto/files/ACEA-Regulatory-Guide-2023.pdf (accessed on 1 October 2024).
- Wang, D.; Deng, W.; Wu, L.; Xin, L.; Xie, L.; Zhang, H. Impact of Vehicle Steering Strategy on the Severity of Pedestrian Head Injury. Biomimetics 2024, 9, 593. [Google Scholar] [CrossRef] [PubMed]












| L (mm) | 20 | 30 | 40 | 50 | 10 | 15 | 20 | 25 |
|---|---|---|---|---|---|---|---|---|
| Mass of a Gyroid Structure | Mass of a Cube Structure | |||||||
| Min (g) | 1.82 | 6.13 | 14.86 | 29.49 | 1.21 | 4.09 | 9.62 | 18.71 |
| Max (g) | 1.88 | 6.48 | 15.30 | 29.66 | 1.27 | 4.11 | 9.70 | 18.90 |
| Avg (g) | 1.858 | 6.351 | 15.096 | 29.583 | 1.241 | 4.100 | 9.660 | 18.820 |
| Std (g) | 0.02630 | 0.11328 | 0.13640 | 0.08622 | 0.01798 | 0.00816 | 0.03651 | 0.08206 |
| Std (%) | 1.416% | 1.784% | 0.904% | 0.291% | 1.449% | 0.199% | 0.378% | 0.436% |
| Density (kg/m3) | 232.19 | 235.22 | 235.89 | 236.67 | 1240.56 | 1214.81 | 1207.50 | 1204.48 |
| Relative density (-) | 0.19 | 0.20 | 0.20 | 0.20 | 1.03 | 1.01 | 1.00 | 1.00 |
| Strategy | Gyroid (mm) | Mass (kg) | Velocity (m/s) | Energy (J) | Time (ms) | Deceleration (m/s2) | Penetration (mm) | Penetration (%) |
|---|---|---|---|---|---|---|---|---|
| Time | 20 | 8 | 1.4 | 7.84 | 14 | 100 | 9.80 | 49% |
| 30 | 12 | 2.1 | 26.46 | 14 | 150 | 14.70 | 49% | |
| 40 | 16 | 2.8 | 62.72 | 14 | 200 | 19.60 | 49% | |
| 50 | 20 | 3.5 | 122.5 | 14 | 250 | 24.50 | 49% | |
| Deceleration | 20 | 9 | 1.4 | 9 | 13.3 | 105 | 9.33 | 47% |
| 30 | 20 | 1.7 | 30 | 16.2 | 105 | 13.76 | 46% | |
| 40 | 36 | 2 | 72 | 19.0 | 105 | 19.05 | 48% | |
| 50 | 56 | 2.3 | 140 | 21.9 | 105 | 25.19 | 50% |
| Size Gyroid (mm) | Peak Force (N) | Plateau Force at 50% (N) | Energy at 50% (J) | Peak Stress (MPa) | Plateau Stress at 50% (MPa) | Energy by Weight (J/kg) | Size Cube (mm) | Plateau Stress at 50% (MPa) | Energy by Weight (J/kg) | Stress Ratio Cube/Gyroid (-) | Energy Ratio Cube/Gyroid (J-) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 895 | 856 | 7 | 2.24 | 2.14 | 3528 | 10 | 80.1 | 22,100 | 37.43 | 6.26 |
| 30 | 2050 | 1653 | 24 | 2.28 | 1.84 | 3584 | 15 | 82.2 | 24,912 | 44.67 | 6.95 |
| 40 | 4210 | 3352 | 63 | 2.63 | 2.10 | 3969 | 20 | 81.4 | 25,001 | 38.76 | 6.30 |
| 50 | 6920 | 5373 | 127 | 2.77 | 2.15 | 4097 | 30 | 80.2 | 25,026 | 37.30 | 6.11 |
| avg | 2.48 | 2.058 | 3795 | 80.98 | 24,260 | 39.36 | 6.39 | ||||
| estimate | 2.3 | 2.3 | 4791 | 80 | 33,333 | 34,78 | 6.95 |
| Solid | Shell–Fine | Shell–Fine/Solid | Shell–Coarse | Shell–Coarse/Solid | |
|---|---|---|---|---|---|
| Elements | 125 | 9278 | 74.2 | 2237 | 17.9 |
| CPU Time (s) | 46 | 372 | 8.1 | 105 | 2.3 |
| Elapsed time (s) | 20 | 184 | 9.2 | 55 | 2.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rostro-González, H.; Reyes-Pozo, G.; Puigoriol-Forcada, J.M.; López-Valdés, F.-J.; Sundarram, S.S.; Garcia-Granada, A.-A. Additive Manufacturing Gyroid Structures Used as Crash Energy Management. Computation 2024, 12, 248. https://doi.org/10.3390/computation12120248
Rostro-González H, Reyes-Pozo G, Puigoriol-Forcada JM, López-Valdés F-J, Sundarram SS, Garcia-Granada A-A. Additive Manufacturing Gyroid Structures Used as Crash Energy Management. Computation. 2024; 12(12):248. https://doi.org/10.3390/computation12120248
Chicago/Turabian StyleRostro-González, Horacio, Guillermo Reyes-Pozo, Josep Maria Puigoriol-Forcada, Francisco-José López-Valdés, Sriharsha Srinivas Sundarram, and Andres-Amador Garcia-Granada. 2024. "Additive Manufacturing Gyroid Structures Used as Crash Energy Management" Computation 12, no. 12: 248. https://doi.org/10.3390/computation12120248
APA StyleRostro-González, H., Reyes-Pozo, G., Puigoriol-Forcada, J. M., López-Valdés, F.-J., Sundarram, S. S., & Garcia-Granada, A.-A. (2024). Additive Manufacturing Gyroid Structures Used as Crash Energy Management. Computation, 12(12), 248. https://doi.org/10.3390/computation12120248








