Abstract
Advanced finite element (FE) modeling and simulations were performed on vehicular crashes into a three-bar metal bridge rail (TMBR). The FE models of a sedan, a pickup truck, and a TMBR section were adopted in the crash simulations subject to Manual for Assessing Safety Hardware (MASH) Test Level 2 (TL-2) and Test Level 3 (TL-3) requirements. The test vehicle models were first validated using full-scale physical crash tests conducted on a two-bar metal bridge using a sedan and a pickup truck with similar overall physical properties and sizes to their respective vehicles used in the simulations. The validated vehicular models were then used to evaluate the crash performance of the TMBR using MASH evaluation criteria for structural adequacy, occupant risk, and post-impact trajectory. The TMBR met all MASH TL-2 requirements but failed to meet the MASH TL-3 Criteria H and N requirements when impacted by the sedan. The TMBR was also evaluated under in-service conditions (behind a 1.52 m wide sidewalk) and impacted by the sedan under MASH TL-3 conditions. The simulation results showed that the TMBR behind a sidewalk met all safety requirements except for the occupant impact velocity in the longitudinal direction, which exceeded the MASH limit by 3.93%.
1. Introduction
Bridge rails are important roadside safety devices used to protect errant vehicles, and their occupants, from catastrophes. Commonly used bridge rails include concrete bridge rails, metal bridge rails, and hybrid bridge rails (i.e., metal rails anchored onto a concrete parapet). While concrete bridge rails have higher rigidity than metal bridge rails, they have higher initial and repair costs. Bridge rails are considered longitudinal barriers and like all other roadside safety devices, they must be tested to pass the safety requirements issued by the American Association of State Highway and Transportation Officials (AASHTO). Figure 1 shows a three-bar metal bridge rail (TMBR) adopted by the North Carolina Department of Transportation (NCDOT). This bridge rail has two oval-shaped rails and one flat rail, all made of aluminum and constrained to metal posts that are affixed to the concrete footings along the edges of the bridge deck.

Figure 1.
A three-bar metal bridge rail [1].
The TMBR was originally tested and passed the safety requirements of the National Cooperative Highway Research Program (NCHRP) Report 350 [2], which was later replaced by the new AASHTO standards, Manual for Assessing Safety Hardware (MASH) 2016 [3]. With the issuance of the new standards, the performance of the TMBR should be re-evaluated to provide guidance for usage, design improvements, and physical crash testing.
Bridge rail evaluations began in the early 1960s with physical crash tests as the primary method to study bridge structure performance [4]. Since then, full-scale crash testing has been the predominant approach for design validation and performance assessment. Over the years, a variety of bridge rails have been tested across different states, such as the California Type 9 [5] and Type 115 [6] bridge rails, the Wyoming tube-type bridge rail [7], two types of Texas bridge rails [8], Texas T-1F bridge rail [9] and T202 bridge rail [10], the Tennessee bridge rail [11], and many other bridge rails [12,13,14,15,16,17,18,19,20]. Most of these bridge rails were crash tested using a small passenger car as well as a pickup truck. Over the years, many bridge rails were also tested under more severe crash conditions such as impacts by a single-unit truck [21,22,23,24,25,26,27]. All these crash tests provided valuable data and insights into bridge rail designs and performance under vehicular crashes. However, full-scale physical tests are extremely expensive and time-consuming to conduct. Although they are useful for design validation, they are prohibitively expensive for design exploration when many different designs/options are to be evaluated.
Since the early 1990s, the use of computer modeling and simulation in transportation safety has dramatically increased [28,29,30]. Significant effort was put into model development, particularly on vehicle models [31,32,33,34,35], to improve the fidelity of numerical simulations. In the past few decades, computer modeling and simulations for vehicular crashes have seen significant growth in modeling capabilities and model complexity, attributed to the technological advancement of computing hardware and numerical codes. Full-scale crash simulations have been used on a variety of roadside safety devices and infrastructures such as cable barriers [36,37,38,39,40,41,42], W-beam and Thrie-beam guardrails [43,44,45,46,47,48,49,50,51,52], concrete barriers [53,54,55,56,57], crush cushions [58,59,60,61], bus shelters and cluster mailboxes [62], and various bridge rails [63,64,65,66,67]. Numerical modeling and simulations, specifically finite element analysis (FEA), have provided alternative and viable means for studying the crash mechanisms and performance of highway safety devices.
In the work by Wekezer et al. [63], they used LS-DYNA simulations to study the safety performance of Florida beam-and-post reinforced concrete bridge barriers under the Test Level 3 (TL-3) impact of a Chevy pickup truck according to the NCHRP Report 350 [2]. The study revealed severe snagging of the vehicle and provided input for retrofit recommendations. Ray et al. [64] performed FEA on an extruded aluminum truss-work bridge railing subject to TL-3 and Test Level 4 (TL-4) impacts specified in the NCHRP Report 350. An AASHTO LRFD analysis conducted in the study confirmed the results of LS-DYNA simulations, and the bridge rail design was found to have comparable strength to other F-shaped bridge railings in terms of structural rigidity. Atahan and Cansiz [65] used FEA to study a concrete bridge rail-to-guardrail transition that failed to pass the TL-3 requirements of NCHRP Report 350. After validating the simulations using qualitative and quantitative comparisons, an examination of the physical test and simulation results was performed. It was determined that the W-beam height of 685 mm was the main cause of vehicle rollover. It was suggested to modify the W-beam height to 810 mm and subsequent simulation results predicted that the modified design contained and stably redirected the impacting vehicle without wheel snagging. Atahan [66] subsequently performed FEA on the modified bridge rail-to-guardrail transition and determined that the vehicle trajectory, occupant risk, guardrail displacements, and vehicle redirections matched well with the results from a similar transition previously tested under TL-4 conditions specified in NCHRP Report 350. Atahan [67] later studied a high-containment-level rail (i.e., under impacts of tractor-trailers) for bridges and viaducts using LS-DYNA simulations and a physical crash test. The numerical simulation results were validated using test data, and the rail was determined to meet the EN1317 Standard [68].
Bocchieri and Kirkpatrick [69] used LS-DYNA simulation combined with the design of experiments to identify the critical modeling parameters on several bridge railing designs impacted by a Chevrolet C2500 truck. By evaluating the effect of parameter variation on bridge railing performance, they selected the best bridge rail design choice, and a second experimental design was used to determine the bounds of the predicted performance. Abu-Odeh [70] used LS-DYNA simulation to study the T501 steel-reinforced concrete bridge rail under a 2268 kg bogie’s impact at different speeds. The study evaluated the usability of three LS-DYNA material models and suggested the use of small-scale material tests such as triaxial tests to improve the predictability of these material models. Thanh and Itoh [71] used FEA to study the performance of curved steel railings subjected to collisions of trucks at large impact angles. Their simulation results showed that curved railings absorbed less energy than straight railings under the same impact conditions, but they were still capable of guiding the truck’s subsequent movements as long as the initial impact angles were within the limit by the design specification. They also pointed out that the impact angle at curved bridge sites sometimes might be larger than the 15° allowable impact angle, meaning that the curved railing would not be capable of guiding the truck back to the travel lane.
Fang et al. [72] evaluated an NCDOT two-bar metal bridge rail using both FEA and physical crash tests of two vehicles, i.e., a 2010 Toyota Yaris passenger car and a 2014 Chevy Silverado pickup truck. Their finite element (FE) models were validated using test data. The study confirmed the validity of simulation results and high fidelity of FE models of both the vehicles and the two-bar metal rail.
A characteristic feature of full-scale crash tests is that roadside barriers are typically evaluated under predefined impact conditions specified by relevant standards. However, questions remain regarding how these barriers will perform under different, untested impact conditions. To address this issue, this study aimed to evaluate the safety performance of the TMBR under MASH standard Test Level 2 (TL-2) and TL-3 impact conditions, as well as under real-world in-service conditions. The research results would help identify performance issues and guide necessary design improvements of the TMBR before conducting expensive full-scale crash tests.
The research plan assumed the use of FE models of the two validated vehicle models from Fang et al. [72] (Section 3.2). Having reliable FE models, simulations of the test vehicles impacting the TMBR on flat terrain were performed under MASH TL-2 and TL-3 conditions (Section 4.2 and Section 4.3, respectively). Given that the TMBR was often installed behind sidewalks, the study evaluated its performance in this configuration. Specifically, the TMBR behind a sidewalk was assessed when impacted by a 2010 Toyota Yaris under MASH TL-3 conditions (Section 4.4). The safety evaluation focused on the structural adequacy of the TMBR, the risks posed to vehicle occupants, and the trajectories of vehicles after impacts. These analyses aimed to identify potential issues and safety concerns related to barrier installations behind sidewalks, which have not been previously assessed in full-scale crash tests. The findings could contribute to future improvements in roadside barrier designs and crash test requirements. The modeling and simulation methodology from this research is expected to contribute significantly to roadside barrier designs, and the research findings could provoke necessary adjustments to crash testing requirements or standards.
All numerical simulations for this study were conducted using LS-DYNA R11.2.0. Consequently, the description of the FE models employs nomenclature consistent with this software to describe the types of finite elements and the material models used.
2. FE Modeling of TMBR
The FE model of TMBR was based on 9.14 m (30 ft) long sections according to NCDOT specifications. Figure 2 shows a 27.4 m (90 ft) long TMBR model that consists of three sections connected by two expansion joints.
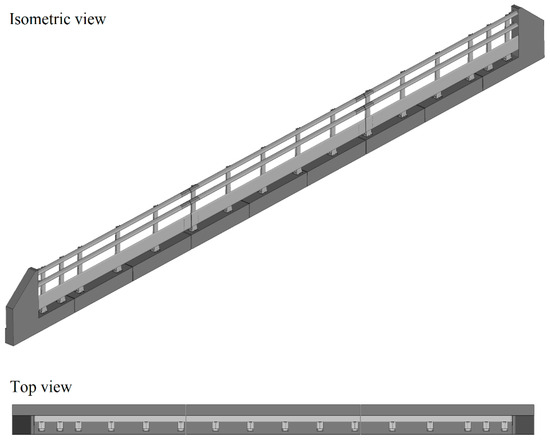
Figure 2.
FE model of the TMBR.
2.1. Modeling of Metal Rails
Each section of the TMBR comprised three horizontal aluminum rails attached to aluminum posts via clamping bars, as depicted in the post assembly in Figure 3. The cross-sections of the top two rails were oval-shaped, while the bottom rail had a trapezoidal cross-section. The TMBR post featured a thin, T-shaped front plate backed by a solid, trapezoidal support, both welded to a base plate. Six clamping bars were used to secure the three rails to the post, and the bars were affixed to the post with twelve 12.7 mm diameter bolts. The base plate was anchored to the concrete parapet using three 19.05 mm bolts and two 15.875 mm bolts, which were connected to wire struts within the concrete parapet to form the anchor assembly. In this study, aluminum alloy 6061-T6 was selected for all aluminum components in the FE model of the TMBR, while carbon steel was used for the bolts, nuts, washers, and reinforcement bars within the concrete.
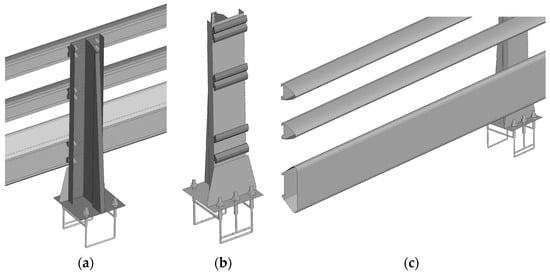
Figure 3.
Rail–post assembly of TMBR: (a) Rear view; (b) front view of the post without rails; (c) front view of rails.
Fully integrated membrane elements, i.e., the Belytschko–Tsay membrane in LS-DYNA with elform 2, were used to model the aluminum rails, the T-shaped front posts, and the base plates, while the trapezoidal supports of the posts were meshed using constant stress solid elements with elform 1. The bolts were modeled using Hughes–Liu beams with a single integration point along the length, while the nuts were treated as the same solid elements used for the trapezoidal supports. The bolt-and-nut fastening mechanism was implemented in the FE model through pre-tensioned bolts, designed to provide clamping forces. For each of the bolted connections, a discrete element was used to connect the bolt head and the nut. The clamping force is activated upon the start of the crash simulation by an elongation prescribed to the discrete element. An automatic surface-to-surface contact definition was defined between the nut and the bolt since the nut can slide along the bolt.
At each expansion joint, the aluminum rails from the two sections were connected using extension bars. Figure 4 shows the cross-sectional profiles of three extension bars inserted into one side of the horizontal rails. The extension bars for the top and middle rails were modeled as solid elements, while the bottom extension bar was modeled as shell elements.
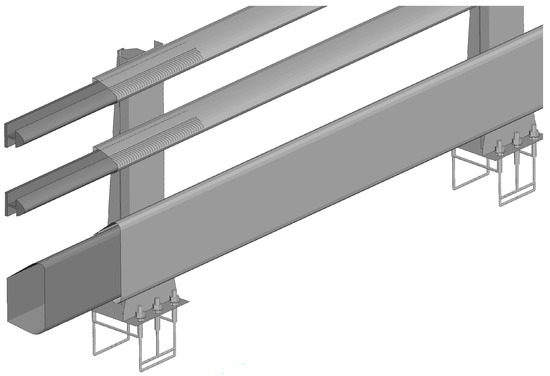
Figure 4.
Expansion joint of the TMBR.
2.2. Modeling of Concrete Parapet and Terminals
The aluminum rail assembly was fastened to the concrete parapet through the anchor assembly shown in Figure 3. At the end of the aluminum rails, a concrete terminal is installed to secure the aluminum rails through brackets (see Figure 5). The brackets were bolted to the clamping bars inserted in the horizontal rails with four bolts and nuts for each rail. The brackets were connected to the concrete parapet using bolts and nuts. One pair of bolts and nuts were used for each of the top and middle rails, and two pairs for the bottom rail. All the brackets were modeled using the same membrane elements introduced previously.
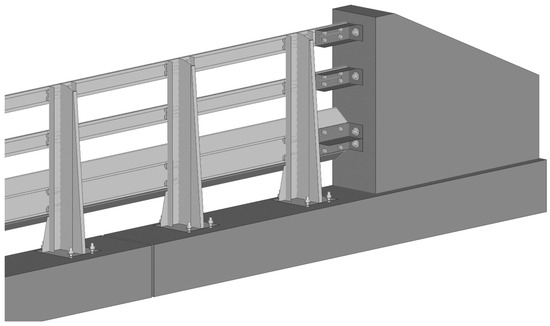
Figure 5.
Rail connections to the concrete parapet and terminal of the TMBR.
The steel reinforcing bars cast in concrete terminals and parapet of the TMBR were explicitly modeled using beam elements, as shown in Figure 6 and Figure 7. The concrete terminals and parapet were modeled as constant-strain solid elements. The meshes of the concrete and steel reinforcing bars were carefully created such that the nodes of beam elements (representing the reinforcing bars) coincided with the nodes on the solid elements (representing the concrete). This node-sharing technique for modeling reinforced concrete was effective and eliminated the need for contact definitions between the steel bars and concrete.
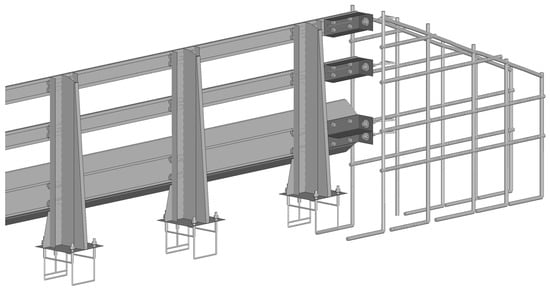
Figure 6.
Beam elements for the reinforcing bars embedded in a concrete terminal of the TMBR.

Figure 7.
Beam elements for the reinforcing bars embedded in the concrete parapet of the TMBR.
The entire TMBR model consisted of 1530 components that were meshed with 1,111,527 elements (680,653 solid, 416,056 shell, 14,514 beam, and 304 discrete elements) and 1,244,441 nodes. The following is a list of the seven material models for the TMBR model:
- MAT_PIECEWISE_LINEAR_PLASTICITY (MAT_024): for all aluminum components (rails, posts, clamping bars, extension bars, and brackets).
- MAT_CSCM (MAT_159): for the concrete parapet and terminals.
- MAT_PLASTIC_KINEMATIC (MAT_003): for steel bolts and reinforcement bars.
- MAT_LINEAR_ELASTIC_DISCRETE_BEAM (MAT_066): for discrete elements.
- MAT_RIGID (MAT_020): for nuts and washers.
- MAT_NULL (MAT_009): for contact purposes.
- MAT_ELASTIC (MAT_001): for the road surface.
Table 1 gives the basic material properties of the steel, aluminum, and concrete components of the TMBR. The material model of steel components (MAT_003) includes a damage mechanism that removes elements upon reaching a failure strain of 0.4. Aluminum components are modeled by MAT_024 in LS-DYNA, incorporating a damage model with a plastic strain threshold value of 0.06 for element deletion upon reaching this value. The CSCM model (MAT_159) in LS-DYNA was employed to represent the concrete parapet. It incorporated isotropic constitutive equations, yield and hardening surfaces, and damage formulations to simulate material softening and modulus reduction. The CSCM model required thirty-seven input values and seven control parameters. A detailed review and validation of this model can be found in references [73,74].

Table 1.
Basic material properties of TMBR components.
3. FE Modeling of Test Vehicles
3.1. FE Vehicle Models
In this study, the vehicle models employed were a 2010 Toyota Yaris passenger car and a 2014 Chevy Silverado pickup truck, corresponding to the MASH 1100C and 2270P test vehicle specifications, respectively. The FE models of the vehicles were originally developed at the National Crash Analysis Center (NCAC) and previously validated using the standard tests for crashworthiness. Fang et al. [72] enhanced the numerical stability of these models by remeshing and adding hourglass controls to handle large deformations. Some of the contact definitions between dissimilar materials, such as between metals and plastic bumpers, were updated using pinball segment-based single-surface contact definitions to overcome premature terminations of the simulations caused by contact instabilities. The initial penetrations, which were due to small errors in geometry caused by meshing, were removed by separating those components involved. The improved vehicle models were validated using physical crash tests on another bridge rail system (also with a metal rail anchored on a concrete parapet) and were shown to have good accuracy and numerical stability [72]. Figure 8 shows the vehicle models used in this study and Table 2 summarizes the detailed information of the two models. These models are available from the National Highway Traffic Safety Administration (NHTSA) [75].
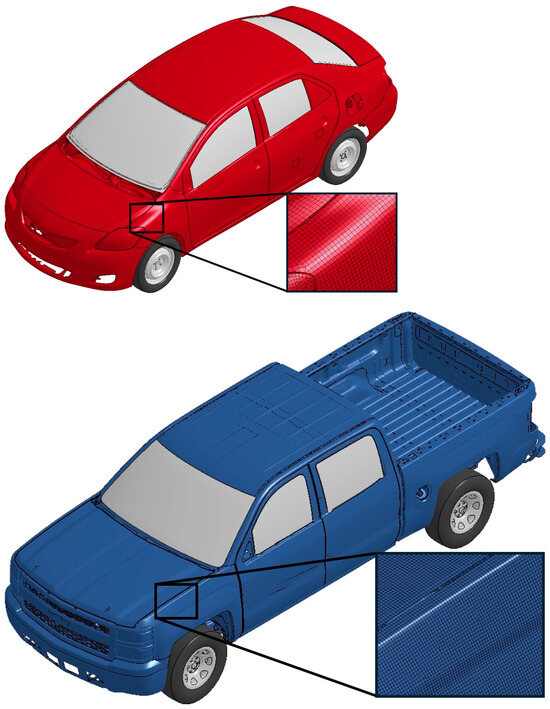
Figure 8.
Vehicle models of a 2010 Toyota Yaris (top) and a 2014 Chevy Silverado (bottom).

Table 2.
FE model attributes of the two test vehicles used in simulation.
The vehicle models included fully functional suspensions and steering systems. The following is a list of the main material models for both vehicle models:
- MAT_PIECEWISE_LINEAR_PLASTICITY (MAT_024): for all steel components.
- MAT_RIGID (MAT_020): for accelerometers and non-deformable materials.
- MAT_ELASTIC (MAT_001): for rubber components.
- MAT_LINEAR_ELASTIC_DISCRETE_BEAM (MAT_066): for shock absorbers with viscous damping effects.
- MAT_LOW_DENSITY_VISCOUS_FOAM (MAT_073): for the radiator.
- MAT_SPOTWELD (MAT_100): for sheet metal connections.
- MAT_NULL (MAT_009): for contact definitions.
- MAT_SPRING_NONLINEAR_ELASTIC (MAT_S04): for the suspensions.
3.2. Model Validation
The test vehicle models were validated using crash tests conducted at the Midwest Roadside Safety Facilities (MwRSF) in 2019 [76]. A 27.4 m (90 ft) long NCDOT two-bar metal rail was constructed and impacted by two test vehicles in accordance with MASH TL-3 requirements. The two-bar metal rail was made of aluminum rails attached to aluminum posts that were supported by a concrete parapet. The FE model of the two-bar metal rail was created using similar modeling techniques and material models to that for the TMBR. Due to challenges in obtaining test vehicles over five years old, test vehicles with the exact models and years of the FE vehicle models could not be acquired. Consequently, alternative vehicles were utilized for the testing: a 2010 Hyundai Accent sedan and a 2015 Chevy Silverado pickup truck. Despite variations in make and model year, these vehicles exhibited comparable dimensions, body structures, and mass relative to the FE models. Figure 9 demonstrates the correlation between vehicular responses in the simulations and those observed in the actual crash tests.

Figure 9.
Comparison of simulation results and physical tests in MASH TL-3 conditions [72]: (a) 2010 Hyundai Assent (test) and 2010 Toyota Yaris (simulation); (b) 2015 Chevy Silverado (test) and 2014 Chevy Silverado (simulation).
The boundary conditions used in the simulations were set to match the test conditions. In the simulation model, the road surface and the bottom of the concrete parapet were constrained for all degrees of freedom to prevent any translational or rotational displacements. An initial translational velocity was assigned to all vehicle components in the global coordinate system to initiate the motion.
It can be seen from Figure 9 that the 2010 Toyota Yaris and 2014 Chevy Silverado exhibited similar overall responses to their respective test vehicles in terms of vehicular redirection characteristics and structural deformations. Subsequently, Figure 10 and Figure 11 provide detailed visual representations of the trajectories of these two vehicles, capturing data from both the crash tests and the simulations to facilitate a comprehensive analysis of the dynamics involved. Note that the rectangular boxes in Figure 10b and Figure 11b are the exit boxes corresponding to those shown in Figure 10a and Figure 11a, respectively.
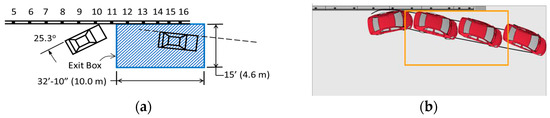
Figure 10.
Comparison of vehicle trajectories for the 1100C test vehicles: (a) Crash test with 2010 Hyundai Accent [76]; (b) simulation with 2010 Toyota Yaris [72].
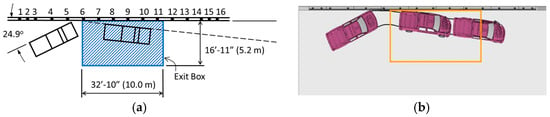
Figure 11.
Comparison of vehicle trajectories for the 2270P test vehicles: (a) Crash test with 2015 Chevy Silverado [76]; (b) simulation with 2014 Chevy Silverado [72].
Figure 12 and Figure 13 show the comparison of FE simulation results to test data of vehicle accelerations of the 1100C and 2270P vehicles, respectively. The longitudinal and lateral accelerations from the simulations had similar trends to those from test data.
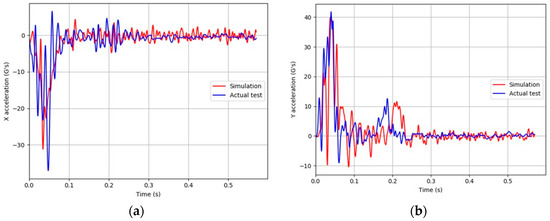
Figure 12.
Accelerations histories of the 2010 Hyundai Accent (test) and 2010 Toyota Yaris (simulation): (a) Longitudinal “x” acceleration; (b) Lateral “y” acceleration.
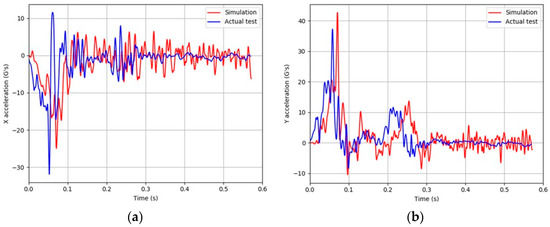
Figure 13.
Acceleration histories of 2015 Chevy Silverado (test) and 2014 Chevy Silverado (simulation): (a) Longitudinal “x” acceleration; (b) Lateral “y” acceleration.
The simulated vehicles’ roll, pitch, and yaw angles, as well as the values of occupant impact velocity (OIV) and occupant ride-down accelerations (ORAs), were found to generally match well with physical test data. The validated vehicle models were then used in the crash simulations of the TMBR.
4. Evaluation of TMBR
4.1. Simulation Setup and Evaluation Criteria
Crash simulations of the TMBR under the impact of the 1100C and 2270P test vehicles were conducted. In alignment with MASH TL-2 and TL-3 standards, the impacts were conducted at an angle of 25°. For both vehicle models, MASH TL-2 required an impact speed of 44 mph (70 km/h), and MASH TL-3 specified a speed of 62 mph (100 km/h). The expansion joint of the TMBR was used as the reference point to determine the critical impact points (CIPs) for all the impact cases. The distances from the CIPs to the reference point were specified in MASH for each of the test cases as listed in Table 3.

Table 3.
MASH TL-2 and TL-3 requirements for 1100C and 2270P test vehicles.
The following performance evaluation criteria were used on the TMBR:
- Structural Adequacy by MASH Criterion A. The TMBR was designed to ensure that vehicles were contained and redirected without overriding, underriding, or penetrating the bridge rail.
- Occupant Risk by MASH Criteria D, F, H, I: These criteria define the assessed risk to occupants during a crash.
- Criterion D: No debris from the TMBR should enter the passenger compartment during the crash;
- Criterion F: Maximum pitch and roll angles of the vehicle must not exceed 75°; and
- Criteria H and I: Two risk factors for occupant safety were considered: occupant impact velocity (OIV) and occupant ride-down acceleration (ORA). The acceptable and preferred limits for OIV are 12.2 m/s and 9.1 m/s, respectively. The acceptable and preferred limits of ORA are 20.5 G and 15.0 G, respectively, where G is the acceleration of gravity.
- Post-Impact Trajectory by MASH Criterion N. This criterion, also known as the exit box criterion, assesses the risk of the vehicle crashing into other vehicles after being redirected back to the travel lane. The exit box is a rectangular box with its long side along the traffic side of the barrier (Figure 14). The top-left corner of the exit box was the final point of contact of the rear wheel with the initial, undeformed barrier face. The dimensions of the exit boxes for the two test vehicles are listed in Table 4.
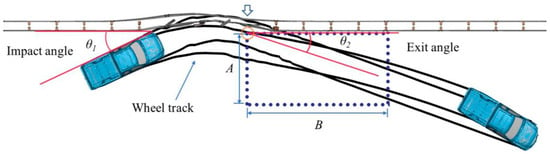 Figure 14. Definition of the MASH exit box criterion.
Figure 14. Definition of the MASH exit box criterion. Table 4. MASH exit box dimensions.
Table 4. MASH exit box dimensions.- The width of the exit box, A, was calculated using the width and length of the vehicle (VW and VL) by (7.2 + VW + 0.16VL);
- the length of the exit box, B, had a specified value for each type of vehicle; and
- all four wheels of the impact vehicle are required to remain inside the exit box to ensure a small exit angle for the vehicle to safely return to the roadway.
4.2. Vehicular Crashes According to MASH TL-2 Requirements
The TMBR was subjected to the impacts at a 25° angle by both vehicles traveling at 70 km/h in accordance with the MASH TL-2 condition. The vehicle trajectories of the 2010 Toyota Yaris and 2014 Chevy Silverado are shown in Figure 15, with the exit boxes marked along with the original, undeformed TMBR. For both impact cases, the MASH Criterion N was met since both vehicles were redirected, as shown in Figure 15. The exit angles were 20° and 2.2° for the 2010 Toyota Yaris and 2014 Chevy Silverado, respectively. Although the exit angle of the Yaris is much larger than that of the Silverado, it was considered a safe redirection by the post-impact trajectory.

Figure 15.
Vehicle trajectories impacting the TMBR in MASH TL-2 conditions: (a) 1100C; (b) 2270P.
Figure 16 shows the angular motion histories of test vehicles impacting the TMBR. The 2010 Toyota Yaris recorded maximum roll and pitch angles of 5.3° and 3.6°, respectively. In comparison, the 2014 Chevy Silverado exhibited maximum roll and pitch angles of 7.1° and 2.2°, respectively. For both test vehicles, these values confirm compliance with MASH Criterion F, which requires that roll and pitch angles do not exceed 75°, thereby ensuring the safety effectiveness of the TMBR under these specific impact conditions.
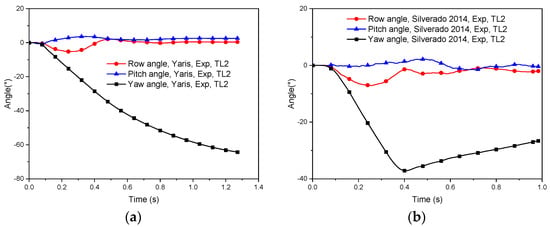
Figure 16.
Angular motion of test vehicles at MASH TL-2 conditions: (a) 1100C; (b) 2270P.
The risk factors for occupant safety, OIVs and ORAs, were determined using the longitudinal and lateral accelerations of the test vehicles, as shown in Table 5. Along with the evaluation results for MASH Criteria A, D, F, and N in Table 6 and Table 7, the TMBR satisfied all safety requirements under MASH TL-2 test conditions. The maximum deflections of the TMBR, both permanent and dynamic, were found negligible in both impact scenarios.

Table 5.
Performance evaluation of TMBR by MASH TL-2 Criteria H and I.

Table 6.
Performance evaluation of TMBR by MASH TL-2 Criterion A.

Table 7.
Performance evaluation of TMBR by MASH TL-2 Criteria D, F, and N.
4.3. Vehicular Crashes According to MASH TL-3 Requirements
The vehicle trajectories under TL-3 conditions are shown in Figure 17. The 2010 Toyota Yaris was minimally redirected before it rebounded towards the travel lane, leading to a failure to meet the MASH Criterion N for the TMBR in this instance. For the impact case by the 2014 Chevy Silverado, the exit angle was 16°, confirming that MASH Criterion N was satisfied as the vehicle was successfully redirected.

Figure 17.
Vehicle trajectories impacting the TMBR in MASH TL-3 conditions: (a) 1100C; (b) 2270P.
Figure 18 shows angular motion histories of test vehicles impacting the TMBR. The maximum roll and pitch angles were 6.0° and 10.8°, respectively, for the 2010 Toyota Yaris. For the 2014 Silverado, the maximum roll and pitch angles were determined to be 5.0° and 4.1°, respectively, meeting the requirement of MASH Criterion F.
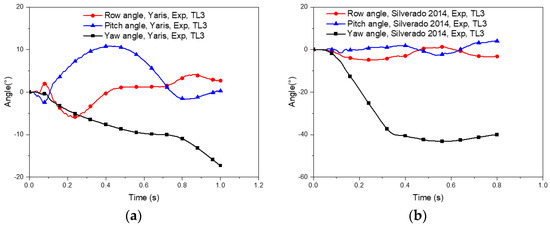
Figure 18.
Angular motion of test vehicles at MASH TL-3 conditions: (a) 1100C; (b) 2270P.
The risk factors for occupant safety (OIVs and ORAs) were calculated for both impact cases and are summarized in Table 8, along with the results for MASH Criteria A, D, F, and N given in Table 9 and Table 10. The results indicate that the TMBR did not meet the requirements of MASH Criterion H in the case of the 2010 Toyota Yaris due to the high longitudinal OIV value (OIVx). Additionally, as previously mentioned, the TMBR also failed to meet MASH Criterion N in the same case. Despite these issues, all other safety requirements were satisfied under MASH TL-3 test conditions. The maximum deflections of the TMBR were calculated for both impact scenarios and were found to be insignificant.

Table 8.
Performance evaluation of TMBR by MASH TL-3 Criteria H and I.

Table 9.
Performance evaluation of TMBR by MASH TL-3 Criterion A.

Table 10.
Performance evaluation of TMBR by MASH TL-3 Criteria D, F, and N.
4.4. Vehicular Crash into TMBR behind a Sidewalk
Under in-service conditions, the TMBR requires a sidewalk with a minimum width of 1.52 m. This is different from the flat-terrain condition specified in MASH; therefore, the performance of the TMBR could be different from that without the sidewalk. Since the TMBR failed to pass Criteria H and N when impacted by the 2010 Toyota Yaris subject to TL-3 requirements, the FE model of the TMBR was updated to include a 1.52 m wide sidewalk and re-evaluated under the impact of the 2010 Toyota Yaris subject to TL-3 requirements (see Figure 19). In this simulation, the vehicle would first hit the curb face of the sidewalk, ride up the sidewalk, and impact the TMBR. The CIP was the same as that in Section 4.3, with the reference point at the expansion joint of the TMBR.
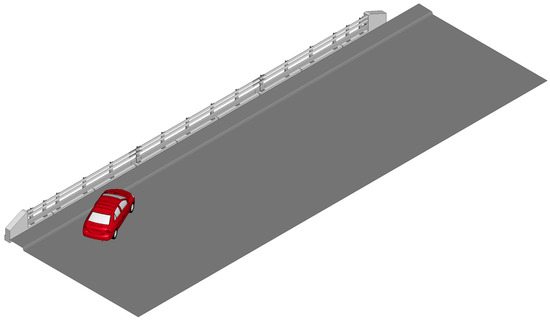
Figure 19.
FE model of the TMBR with a (1.52 m) sidewalk under impact by a 2010 Toyota Yaris.
Figure 20 shows the 2010 Toyota Yaris trajectory impacting the TMBR with a sidewalk. Redirection of the vehicle with a 15° exit angle was observed; therefore, the TMBR met MASH Criterion N. The angular motion histories of the 2010 Toyota Yaris were obtained and the maximum roll and pitch angles were determined to be 6.6° and 3.8°, respectively, not exceeding the 75° limit according to the MASH Criterion F.
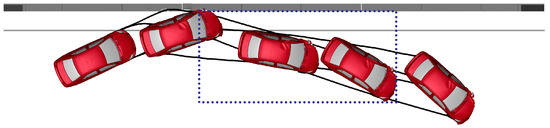
Figure 20.
Trajectory of 1100C vehicle impacting the TMBR behind a curb in MASH TL-3 conditions.
Table 11, Table 12 and Table 13 summarize the results of the performance evaluation for the TMBR with a sidewalk impacted by a 2010 Toyota Yaris. The TMBR met all MASH safety requirements, except for the longitudinal OIV value that exceeded the limit by 3.93%. When compared to the results for the TMBR without a sidewalk (Table 8), it was observed that the presence of the sidewalk significantly reduced the longitudinal OIV value from 15.28 m/s to 12.68 m/s. This was due to the initial contact of the vehicle with the curb face of the sidewalk, which reduced the peak acceleration of the vehicle in the longitudinal direction upon impacting the TMBR. Although the OIV value in the case with a sidewalk still exceeded the MASH limit, the small percentage (3.93%) could be considered well within the margin of error and would not raise serious concerns.

Table 11.
Performance evaluation of TMBR with sidewalk by MASH TL-3 Criteria H and I.

Table 12.
Performance evaluation of TMBR with sidewalk by MASH TL-3 Criterion A.

Table 13.
Performance evaluation of TMBR with sidewalk by MASH TL-3 Criteria D, F, and N.
5. Major Research Findings
The performance of TMBR was evaluated using finite element simulations of vehicular crashes based on MASH TL-2 and TL-3 requirements. Two vehicle models and the TMBR model were used in the simulations. The major findings of the study are summarized as follows:
- Under MASH TL-2 test conditions, the TMBR was shown to pass all the safety requirements on structural adequacy (MASH Criterion A), occupant risk (MASH Criteria D, F, H, and I), and post-impact trajectory (MASH Criterion N). The damage to the rails was acceptable and no debris entered the occupant compartments of the vehicles.
- For MASH TL-3 test conditions, the TMBR met all safety requirements subject to the impact of the 2014 Chevy Silverado. However, the TMBR failed to pass the safety requirements of MASH Criteria H and N under the impact of the 2010 Toyota Yaris. Specifically, the longitudinal OIV value did not satisfy the MASH limit requirement. Moreover, the vehicle was bounced back and unable to be redirected, indicating failure of MASH Criterion N.
- Under in-service conditions (i.e., the TMBR was installed behind a 1.52 m wide sidewalk), the impact severity on the TMBR was reduced in the case of the 2010 Toyota Yaris according to MASH TL-3 requirements. The TMBR with the sidewalk passed all safety requirements except for the longitudinal OIV value that exceeded the MASH limit by 3.93%. This small percentage could be considered well within the error margins and would not cause serious safety concerns.
- The numerical models and modeling techniques adopted in this study were shown to be effective through model valuation using full-scale physical crash test data. Although the makes and/or years of the vehicles in the physical tests and FE simulations were different, the numerical simulation results and test data generally agreed well in overall vehicular responses. More full-scale crash tests, particularly those with the same or similar vehicles as the FE models, would be extremely useful and important to further fine-tune the FE models and improve their accuracy and fidelity.
6. Conclusions
In this study, FE simulations of vehicles crashing into a three-bar metal bridge rail (TMBR) were performed. The FE models of two test vehicles were validated, and the FE model of the TMBR was constructed. Vehicular crash simulations were performed per both MASH TL-2 and TL-3 requirements, and the performance of the TMBR was evaluated according to MASH criteria on structural adequacy, risks of occupants in the vehicle, and trajectories of vehicles after impacts. It is concluded that the TMBR met all evaluation criteria under MASH TL-2 impacts. However, the TMBR failed to pass all safety requirements under MASH TL-3 conditions, due to a large longitudinal OIV value and failure to stay within the exit box. The TMBR was also evaluated under in-service conditions, i.e., installed behind a 1.52 m wide sidewalk, when impacted by 1100C under MASH TL-3 conditions. The sidewalk reduced the impact severity on the TMBR, and MASH Criterion N was met under the in-service conditions. Although the longitudinal OIV value still exceeded the MASH limit, the value 3.93% over the limit was small enough to be considered within the error margins without serious safety concerns.
The simulation results provide insights into general trends of vehicular responses and TMBR performance but should not be used as definitive conclusions about TMBR performance under specific impact scenarios. The potential issues or safety concerns identified in the simulations can guide future designs, improvements, and further testing. Full-scale crash tests are essential for validating simulation results and assessing real-world performance. Numerical simulations have proven to be a valuable tool in crashworthiness and transportation safety studies, complementing physical tests by providing cost-effective ways to explore various design options for different crash scenarios.
Author Contributions
Conceptualization, H.F.; methodology, H.F.; software, E.P. and L.P.; validation, E.P., L.P. and D.B.; formal analysis, E.P. and L.P.; investigation, H.F., E.P. and Q.W.; resources, H.F.; data curation, E.P., L.P. and D.B.; writing—original draft preparation, H.F. and Q.W.; writing—review and editing, H.F., C.J., Q.W., E.P., L.P. and D.B.; visualization, E.P., Q.W. and L.P.; supervision, H.F.; project administration, H.F.; funding acquisition, H.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the North Carolina Department of Transportation, grant number RP2019-23.
Data Availability Statement
The research data are available upon reasonable requests to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- NCDOT Structures Bridge Sites Images. Available online: https://connect.ncdot.gov/resources/Structures/Structures%20Bridge%20Sites%20Images/14_Site15A_5488.JPG (accessed on 15 July 2024).
- Ross, H.E., Jr.; Sicking, D.L.; Zimmer, R.A.; Michie, J.D. Recommended Procedures for the Safety Performance Evaluation of Highway Features; NCHRP Report 350; Transportation Research Board, National Research Council: Washington, DC, USA, 1993. [Google Scholar]
- AASHTO. Manual for Assessing Safety Hardware (MASH), 2nd ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2016. [Google Scholar]
- Nordlin, E.F.; Field, R.N.; Hackett, R.P. Dynamic Full-Scale Impact Tests of Bridge Barrier Rails. In Proceedings of the 43rd Transportation Research Board Annual Meeting, Washington, DC, USA, 1965; Available online: https://onlinepubs.trb.org/Onlinepubs/hrr/1965/83/83-007.pdf (accessed on 13 August 2024).
- Nordlin, E.F.; Hackett, R.P.; Folsom, J.J. Dynamic tests of California Type 9 bridge barrier rail and Type 8 bridge approach guardrail. In Proceedings of the 49th Transportation Research Board Annual Meeting, Washington, DC, USA, 1970; Available online: https://onlinepubs.trb.org/Onlinepubs/hrr/1970/302/302-001.pdf (accessed on 13 August 2024).
- Jewell, J.; Stoughton, R.L.; Glauz, D. Vehicle crash tests of Type 115 barrier rail systems for use on secondary highways. Transp. Res. Rec. 1993, 1419, 86–94. [Google Scholar]
- Mak, K.K.; Bligh, R.P.; Pope, D.H. Wyoming tube-type bridge rail and box-beam guardrail transition. Transp. Res. Rec. 1990, 1258, 61–70. [Google Scholar]
- Rails, A.B.; Bullard Jr, D.L.; Williams, W.F.; Menges, W.L.; Haug, R.R. Design and Evaluation of the TxDOT F411 and T77 Aesthetic Bridge Rails; FHWA/TX-03/4288-1; Texas Department of Transportation: Austin, TX, USA, 2002. [Google Scholar]
- Williams, W. New aesthetic Type T-1F bridge rail from the Texas Department of Transportation: Design and Test Level 3 crash testing. Transp. Res. Rec. 2008, 2050, 39–46. [Google Scholar] [CrossRef]
- Buth, C.E.; Williams, W.F.; Bligh, R.P.; Menges, W.L.; Haug, R.R. Performance of the TxDOT T202 (MOD) Bridge Rail Reinforced with Fiber Reinforced Polymer Bars; FHWA/TX-03/0-4138-3; Texas Transportation Institute (TTI): Austin, TX, USA, 2003. [Google Scholar]
- Bligh, R.P.; Mak, K.K.; Hirsch, T.J. Evaluation of Tennessee Bridge Rail Designs; RF 7199; Texas Transportation Institute (TTI): Austin, TX, USA, 1994. [Google Scholar]
- Buth, E.C.; Hirsch, T.J.; Menges, W.L. Testing of New Bridge Rail and Transition Designs; FHWA-RD-93-058; Texas Transportation Institute (TTI): Austin, TX, USA, 1993. [Google Scholar]
- Alberson, D.C.; Williams, W.F.; Menges, W.L.; Haug, R.R. Testing and Evaluation of the Florida Jersey Safety Shaped Bridge Rail; FHWA/TX-04/9-8132-1; Texas Transportation Institute: Austin, TX, USA, 2004. [Google Scholar]
- Whitesel, D.; Jewell, J.R. Development and Crash Testing of an Aesthetic, See-Through Bridge Rail, Type 90; California Department of Transportation: Sacramento, CA, USA, 2008. [Google Scholar]
- Williams, W.F.; Bligh, R.P.; Menges, W.L. MASH Test 3-11 of the TxDOT Single Slope Bridge Rail (Type SSTR) on Pan-Formed Bridge Deck; FHWA/TX-11/9-1002-3; Texas Transportation Institute (TTI): Austin, TX, USA, 2010. [Google Scholar]
- Thiele, J.C.; Sicking, D.L.; Faller, R.K.; Bielenberg, R.W.; Lechtenberg, K.A.; Reid, J.D.; Rosenbaugh, S.K. Development of a Low-Cost, Energy-Absorbing Bridge Rail; TRP-03-226-10; Midwest Roadside Safety Facility (MwRSF): Lincoln, NE, USA, 2010. [Google Scholar]
- Williams, W.F.; Holt, J. Design and Full-Scale Testing of Texas Department of Transportation Type T131RC Bridge Rail; FHWA/TX-12/9-1002-12-1; Texas Department of Transportation: Austin, TX, USA, 2013. [Google Scholar]
- Whitesel, D.; Jewell, J.; Meline, R. Compliance Crash Testing of the Type 732sw Bridge Rail; FHWA/CA15-2181; California Department of Transportation: Sacramento, CA, USA, 2016. [Google Scholar]
- Williams, W.F.; Bligh, R.P.; Odell, W.; Smith, A.; Holt, J. Design and full-scale testing of low-cost Texas Department of Transportation Type T631 bridge rail for MASH Test Level 2 and 3 Applications. Transp. Res. Rec. 2015, 2521, 117–127. [Google Scholar] [CrossRef]
- Williams, W.F.; Bligh, R.P.; Menges, W.L.; Kuhn, D.L. Crash Test and Evaluation of the TxDOT T224 Bridge Rail; FHWA/TX-15/9-1002-15-5; Texas Transportation Institute (TTI): Austin, TX, USA, 2018. [Google Scholar]
- Polivka, K.A.; Faller, R.K.; Keller, E.A.; Sicking, D.L.; Rohde, J.R.; Holloway, J.C. Design and Evaluation of the TL-4 Minnesota Combination Traffic/Bicycle Bridge Rail; SPR-3(017); Midwest Roadside Safety Facility (MwRSF): Lincoln, NE, USA, 1998. [Google Scholar]
- Faller, R.K.; Ritter, M.A.; Rosson, B.T.; Fowler, M.D.; Duwadi, S.R. Two test level 4 bridge railing and transition systems for transverse timber deck bridges. Transp. Res. Rec. 2000, 1696, 334–351. [Google Scholar] [CrossRef]
- Sheikh, N.M.; Bligh, R.P.; Menges, W.L. Determination of Minimum Height and Lateral Design Load for MASH Test Level 4 Bridge Rails; FHWA/TX-12/9-1002-5; Texas Transportation Institute (TTI): Austin, TX, USA, 2011. [Google Scholar]
- Rasmussen, J.D.; Rosenbaugh, S.K.; Faller, R.K.; Bielenberg, R.W.; Steelman, J.S.; Pena, O.; Mauricio, P. Development of a Test Level 4, side-mounted, steel tube bridge rail. Transp. Res. Rec. 2020, 2674, 525–537. [Google Scholar] [CrossRef]
- Pena, O.; Faller, R.K.; Rasmussen, J.D.; Steelman, J.S.; Rosenbaugh, S.K.; Bielenberg, R.W.; Mauricio, P.; Duren, J.T. Development of a MASH Test Level 4 Steel, Side-Mounted, Beam-And-Post, Bridge Rail; TRP-03-410-20; Midwest Roadside Safety Facility (MwRSF): Lincoln, NE, USA, 2020. [Google Scholar]
- Rosenbaugh, S.K.; Rasmussen, J.D.; Faller, R.K. Development and testing of a Test Level 4 concrete bridge rail and deck overhang. Transp. Res. Rec. 2020, 2674, 455–465. [Google Scholar] [CrossRef]
- Rosenbaugh, S.K.; Faller, R.K.; Dixon, J.; Loken, A.; Rasmussen, J.D.; Flores, J. Development and Testing of an Optimized MASH TL-4 Bridge Rail; TRP-03-415-21; Midwest Roadside Safety Facility (MwRSF): Lincoln, NE, USA, 2021. [Google Scholar]
- Wekezer, J.W.; Oskard, M.S.; Logan, R.W.; Zywicz, E. Vehicle impact simulation. J. Transp. Eng. 1993, 119, 598–617. [Google Scholar] [CrossRef]
- Mendis, K.; Mani, A.; Shyu, S.C. Finite Element Crash Models of Motor Vehicles; FHWA-RD-016; Federal Highway Administration: Washington, DC, USA, 1995. [Google Scholar]
- Cofie, E. Finite Element Model of a Small Automobile Impacting a Rigid Pole; FHWA-RD-94-151; Federal Highway Administration: Washington, DC, USA, 1995. [Google Scholar]
- Zaouk, A.K.; Bedewi, N.E.; Kan, C.D.; Marzougui, D. Development and evaluation of a C-1500 pick-up truck model for roadside hardware impact simulation. In Proceedings of FHWA Vehicle Crash Analysis Conference, Langley, VA, USA, 13 December 1997. FHWA-RD-96-212. [Google Scholar]
- Mohan, P.; Marzougui, D.; Arispe, E.; Story, C. Component and Full-Scale Tests of the 2007 Chevrolet Silverado Suspension System; NCAC-2009-R-004; National Crash Analysis Center: Washington, DC, USA, 2009. [Google Scholar]
- Marzougui, D.; Samaha, R.R.; Cui, C.; Kan, C.D.; Opiela, K.S. Extended Validation of the Finite Element Model for the 2010 Toyota Yaris Passenger Sedan (MASH 1100kg Vehicle); NCAC-2012-W-005; National Crash Analysis Center: Washington, DC, USA, 2012. [Google Scholar]
- Marzougui, D.; Kan, C.D.; Samaha, R.R.; Cui, C.; Nix, L. Extended Validation of the Finite Element Model for the 2007 Chevrolet Silverado Pick-Up Truck (MASH 2270kg Vehicle); National Crash Analysis Center: Washington, DC, USA, 2012; NCAC 2012-W-003. [Google Scholar]
- CCSA. 2014 Chevrolet Silverado 1500 Detailed Finite Element Model; Center for Collision Safety and Analysis, George Mason University: Fairfax, VA, USA, 2018. [Google Scholar] [CrossRef]
- Stolle, C.; Reid, J.D. Development of a wire rope model for cable guardrail simulation. Int. J. Crashworthiness 2011, 16, 331–341. [Google Scholar] [CrossRef]
- Wang, Q.; Fang, H.; Li, N.; Weggel, D.C.; Wen, G. An efficient FE model of slender members for crash analysis of cable barriers. Eng. Struct. 2013, 52, 240–256. [Google Scholar] [CrossRef]
- Fang, H.; Wang, Q.; Weggel, D.C. Crash analysis and evaluation of cable median barriers on sloped medians using an efficient finite element model. Adv. Eng. Softw. 2015, 82, 1–13. [Google Scholar] [CrossRef]
- Bruski, D.; Burzyński, S.; Chróścielewski, J.; Jamroz, K.; Pachocki, Ł.; Witkowski, W.; Wilde, K. Experimental and numerical analysis of the modified TB32 crash tests of the cable barrier system. Eng. Fail. Anal. 2019, 104, 227–246. [Google Scholar] [CrossRef]
- Wilde, K.; Bruski, D.; Budzyński, M.; Burzyński, S.; Chróścielewski, J.; Jamroz, K.; Pachocki, Ł.; Witkowski, W. Numerical analysis of TB32 crash tests for 4-cable guardrail barrier system installed on the horizontal convex curves of road. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 65–81. [Google Scholar] [CrossRef]
- Bruski, D.; Burzyński, S.; Witkowski, W. Analysis of passenger car crash with a cable barrier installed with anti-glare screens on a horizontal convex road curve with 400 m radius. Int. J. Impact Eng. 2023, 173, 104486. [Google Scholar] [CrossRef]
- Wang, Q.; Palta, E.; Fang, H. Numerical modeling and simulation of cable barriers under vehicular impacts on a sloped median. Int. J. Prot. Struct. 2024. [Google Scholar] [CrossRef]
- Borovinšek, M.; Vasenjak, M.; Ulbin, M.; Ren, Z. Simulation of crash tests for high containment levels of road safety barriers. Eng. Fail. Anal. 2007, 14, 1711–1718. [Google Scholar] [CrossRef]
- Li, N.; Fang, H.; Zhang, C.; Gutowski, M.; Palta, E.; Wang, Q. A numerical study of occupant responses and injuries in vehicular crashes into roadside barriers based on finite element simulations. Adv. Eng. Softw. 2015, 90, 22–40. [Google Scholar] [CrossRef]
- Teng, T.-L.; Liang, C.-C.; Tran, T.-T. Effect of various W-beam guardrail post spacings and rail heights on safety performance. Adv. Mech. Eng. 2015, 7, 1–16. [Google Scholar] [CrossRef]
- Gutowski, M.; Palta, E.; Fang, H. Crash analysis and evaluation of vehicular impacts on W-beam guardrails placed on sloped medians using finite element simulations. Adv. Eng. Softw. 2017, 112, 88–100. [Google Scholar] [CrossRef]
- Gutowski, M.; Palta, E.; Fang, H. Crash analysis and evaluation of vehicular impacts on W-beam guardrails placed behind curbs using finite element simulations. Adv. Eng. Softw. 2017, 114, 85–97. [Google Scholar] [CrossRef]
- Yin, H.; Xiao, Y.; Wen, G.; Fang, H. Design optimization of a new w-beam guardrail for enhanced highway safety performance. Adv. Eng. Softw. 2017, 112, 154–164. [Google Scholar] [CrossRef]
- Soltani, M.; Topa, A.; Karim, M.R.; Ramli Sulong, N.H. Crashworthiness of G4(2W) guardrail system: A finite element parametric study. Int. J. Crashworthiness 2017, 22, 169–189. [Google Scholar] [CrossRef]
- Li, Z.; Fang, H.; Fatoki, J.; Gutowski, M.; Wang, Q. A numerical study of strong-post double-faced W-beam and Thrie-beam guardrails under impacts of vehicles of multiple size classes. Accid. Anal. Prev. 2021, 159, 106286. [Google Scholar] [CrossRef] [PubMed]
- Wolny, R.; Bruski, D.; Budzyński, M.; Pachocki, L.; Wilde, K. Influence of a lighting column in the working width of a W-beam barrier on TB51 crash test. Materials 2022, 15, 4926. [Google Scholar] [CrossRef] [PubMed]
- Bruski, D.; Pachocki, L.; Sciegaj, A.; Witkowski, W. Speed estimation of a car at impact with a W-beam guardrail using numerical simulations and machine learning. Adv. Eng. Softw. 2023, 184, 103502. [Google Scholar] [CrossRef]
- Yin, H.; Fang, H.; Wang, Q.; Wen, G. Design optimization of a MASH TL-3 concrete barrier using RBF based metamodels and nonlinear finite element simulations. Eng. Struct. 2016, 114, 122–134. [Google Scholar] [CrossRef]
- Wang, Q.; Fang, H.; Yin, H. Reliability analysis of concrete barriers under vehicular crashes using augmented RBFs. Struct. Multidiscip. Optim. 2020, 61, 1215–1228. [Google Scholar] [CrossRef]
- Pachocki, Ł.; Bruski, D. Modeling, simulation, and validation of a TB41 crash test of the H2/W5/B concrete vehicle restraint system. Arch. Civ. Mech. Eng. 2020, 20, 62. [Google Scholar] [CrossRef]
- Li, Z.; Gao, X.; Tang, Z. Safety performance of a precast concrete barrier: Numerical study. CMES-Comput. Model. Eng. Sci. 2020, 123, 1105–1129. [Google Scholar] [CrossRef]
- Pachocki, L.; Daszkiewicz, K.; Łuczkiewicz, P.; Witkowski, W. Biomechanics of lumbar spine injury in road barrier collision–finite element study. Front. Bioeng. Biotechnol. 2021, 9, 760498. [Google Scholar] [CrossRef]
- Budzynski, M.; Jamroz, K.; Jelinski, L.; Bruski, D.; Pachocki, L.; Baginski, G. Assessing roadside hybrid energy absorbers using the example of SafeEnd. Materials 2022, 15, 1712. [Google Scholar] [CrossRef]
- Büyük, M.; Atahan, A.O.; Kurucuoglu, K. Impact Performance Evaluation of a crash cushion design using finite element simulation and full-scale crash testing. Safety 2018, 4, 48. [Google Scholar] [CrossRef]
- Atahan, A.O.; Erdem, M.M. Evaluation of 12 m long turned down guardrail end terminal using full-scale crash testing and simulation. Lat. Am. J. Solids Struct. 2016, 13, 3107–3125. [Google Scholar] [CrossRef][Green Version]
- Meng, Y.; Hu, W.; Untaroiu, C. An examination of the performance of damaged energy-absorbing end terminals. Accid. Anal. Prev. 2020, 147, 105789. [Google Scholar] [CrossRef] [PubMed]
- Fang, H.; Li, Z.; Fatoki, O.; Palta, E. Risk Assessment of Roadside Utility Structures under Vehicular Impacts; NCDOT Research Report FHWA/NC/2018-24; North Carolina Department of Transportation: Raleigh, NC, USA, 2020. [Google Scholar]
- Wekezer, J.W.; Kreja, I.; Issa, M. Retrofit analysis of Florida beam-and-post reinforced concrete bridge barriers. Eng. Transp. 2002, 50, 187–211. [Google Scholar]
- Ray, M.H.; Oldani, E.; Plaxico, C.A. Design and analysis of an aluminum F-shape bridge railing. Int. J. Crashworthiness 2004, 9, 349–363. [Google Scholar] [CrossRef]
- Atahan, A.O.; Cansiz, O.F. Impact analysis of a vertical flared back bridge rail-to-guardrail transition structure using simulation. Finite Elem. Anal. Des. 2005, 41, 371–396. [Google Scholar] [CrossRef]
- Atahan, A.O. Crashworthiness analysis of a bridge rail-to-guardrail transition. Int. J. Crashworthiness 2016, 21, 423–434. [Google Scholar] [CrossRef]
- Atahan, A.O. Development of a heavy containment level bridge rail for Istanbul. Lat. Am. J. Solids Struct. 2018, 15. [Google Scholar] [CrossRef]
- ERF. EN1317; European Road Restraint Systems, European Union Road Federation: Brussels, Belgium, 1998; Available online: https://erf.be/en-1317/ (accessed on 13 August 2024).
- Bocchieri, R.; Kirkpatrick, S. Evaluation of bridge rail designs using probabilistic finite element crash simulations. In Proceedings of the International Crashworthiness Conference (ICrash2006), Athens, Greece, 4–7 July 2006. [Google Scholar]
- Abu-Odeh, A. Modeling and simulation of bogie impacts on concrete bridge rails using LS-DYNA. In Proceedings of the 10th International LS-DYNA Users Conference, Detroit, MI, USA, 8–10 June 2008. [Google Scholar]
- Thanh, L.; Itoh, Y. Performance of curved steel bridge railings subjected to truck collisions. Eng. Struct. 2013, 54, 34–46. [Google Scholar] [CrossRef]
- Fang, H.; Li, Z.; Fatoki, O.; Stolle, C. Evaluation of Four Bridge Rail Systems for Compliance with the 2016 Edition of Manual for Assessing Safety Hardware (MASH); NCDOT Research Report FHWA/NC/2019-23; North Carolina Department of Transportation: Raleigh, NC, USA, 2022. [Google Scholar]
- Murray, Y.D. User’s Manual for LS-DYNA Concrete Material Model 159; Report No. FHWA-HRT-05-062; Federal Highway Administration: Washington, DC, USA, 2007. [Google Scholar]
- Murray, Y.D.; Abu-Odeh, A.; Bligh, R. Evaluation of Concrete Material Model 159; Report No. FHWA-HRT-05-063; Federal Highway Administration: Washington, DC, USA, 2006. [Google Scholar]
- NHTSA. Crash Simulation Vehicle Models. Available online: https://www.nhtsa.gov/crash-simulation-vehicle-models (accessed on 13 August 2024).
- Dowler, N.; Stolle, C.; Hinojosa, M.; Fang, H. Full-Scale Crash Test of a Two-Bar Metal Bridge Rail; Report No. TRP-03-419-19; Midwest Roadside Safety Facility, University of Nebraska-Lincoln: Lincoln, NE, USA, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).