Abstract
In this article, we analyze the - and -convergence, using the data of the socio-economic development of Russian areas, and discover the role of spatial autocorrelation in regional economic development. We are considering 80 areas of the Russian Federation for the period of 2010–2017. Moran coefficients were used to estimate spatial autocorrelation. We compare the Moran scatterplots for GDP per capita and GDP growth rates per capita in 2017 and in 2014. We study the impact on raising investment in leading capital and the costs of technological innovation. We evaluate a wide range of specifications of spatial econometric models for all kinds of weight matrices. We combine standard geographical proximity with specialization proximity to assess whether they are substitutes or additions to converging economic growth rates. The weight matrix of the neighborhood and specialization similarities are used. The weight matrix of specialization similarities of the regional economies is based on data on the structure of tax payments in 82 industries. The specialization structure of the region’s economy is related to its location. Clusters obtained by matrices of specialization proximity are well separable from each other in space. The connectivity within clusters and the boundaries between them become more apparent over time. It is shown that according to the results of estimation of conditional -convergence models, the models of 2010–2014 and 2014–2017 differ significantly. There is a statistically significant -convergence for the period 2010–2014. There is also the presence of spatial autocorrelation. Based on the results of valuation models constructed from data after 2014, it can be concluded that the coefficient estimates for the explanatory variables are not significantly different from zero, and accordingly there is no tendency towards regional convergence in terms of economic development. The results obtained in the work are stable for the proposed models and spatial weight matrices. Territorial proximity is a more important factor than the similarity of specialization for explanation the economic growth rates of Russian regions.
1. Introduction
The economic development of Russian regions is very disproportional due to distances, climatic zones, proximity to borders, historical differences in development, etc. While in some regions there is a marked increase in production and investment inflows, other regions face serious economic and social problems. Therefore, models of spatial econometrics are attractive for the analysis of social and economic processes occurring in large territories. The influence of neighboring more developed technological regions means that the regional activities of enterprises benefit from proximity to other firms generating innovations. Territorial interaction can be expressed through institutional, technological and social ties that affect the convergence of economic development levels in regions. The goal of our work is to assess the impact of technological innovation on the economic growth of regions using spatial econometrics models for various options of weight matrices.
2. The Theoretical Model
In the study of convergence, its presence is checked in two forms: and . The -convergence implies a decrease in differences between regions over time. That is, we can talk about the presence of a trend towards equalization of economic development levels in a long-term opportunity. Appropriate measurements are used to measure the -convergence of the unweighted ordinary difference, variant coefficient, Gini index, Tail index, etc. The -convergence suggests that poor regions grow faster than rich ones and therefore catch up with them. -convergence is based on the Solow model [1], which implies that production factors tend to have diminishing returns. Thus, the growth process should bring the economies of the regions to a long-term stable state, the growth rates of which depend only on the (exogenous) rates of technological progress and labor force growth.
where i is the region number, ; is the time interval; is GDP per capita in region i, respectively, of the base and current year; is a decreasing function.
The basic econometric model is:
where is GDP per capita in region i at time t; are parameters to be estimated; is error term.
The convergence rate is calculated:
time to overcome half of the initial GDP per capita inequalities:
If there is absolute convergence, then the coefficient estimates for all areas will become similar. If this is not so, then they are different and depend on the socio-economic data of the ranges. That is, the hypothesis of conditional convergence implies, in fact, that convergence occurs when the structural properties of the economy (for example, demographic situation, municipal political figure, human capital, investments, etc.) affect the rate of GDP growth. In this case, the model of conditional convergence contains the form:
where is the vector of regression coefficients for control variables [2].
Convergence models were tested on various types of data: cross sections, time series, panels. It was found that the -convergence is characterized by a negative correlation between the average per capita GDP growth over the period k and the base GDP. However, several works show that a negative value of the convergence parameter does not necessarily indicate a decrease in the variance of the level of GDP per capita in cross-sectional data or -convergence. For example, Quah [3] notes that cross-sectional data have a negative correlation between growth rates and the initial level. This is achieved by a stable dispersion of income levels, which is explained by the presence of shocks in the growth rates in a particular country, which can compensate for the negative coefficients of . The problem of convergence of economic growth of territories is widely discussed in the scientific literature. We note several concepts that have their own methodology. R. Barro and H. Sala-i-Martin suggest considering the -convergence and the -convergence [4] separately. -convergence is characterized by a gradual decrease in the spread of development indicators (for example, GDP or per capita income). The presence of -convergence means the existence of -convergence, but not vice versa. The -convergence suggests a tendency toward a decrease in the differentiation of economic development. That is, lagging countries or regions will have higher rates of economic growth than more developed territories. This should lead to a narrowing gap in the economic development level. The concept of convergence in the Solow model is to change the ratio of capital to labor when the country goes to a stationary state. Iodchin A.A. offers models for assessing the relative convergence of economic growth of countries [5]. The basic concepts of convergence, methods for its measurement, as well as the analysis of scientific articles in this field of knowledge were described in the article by Yu.A. Pshenichnykh [6].
Many scientific papers have tested hypotheses about the presence or absence of convergence at the regional level [7]. Such work involves various research methods. These are neoclassical models of endogenous economic growth, empirical research, based on the analysis of statistical data for one period and panel data [7]. The study of income convergence at the regional level, as a rule, is based on traditional methods of -convergence analysis. However, in the last decade, the majority of papers took into account the spatial component.
Lopez-Rodriguez in his work explores the regional convergence of [8]. Fischer and Stirbeck [9] examine the spatial effects of per capita income convergence in the EU. Scientists Egger and Pfaffermayr based on data on GDP per capita investigate the influence of spatial interdependence of the countries of the European Union. They note that convergence rate is affected by the location of the region. The paper [10] highlights the influence of the remoteness of the region, the actual rate of convergence and the significance of the initial gap in economic development. Thus, the question of similarity or difference in convergence rates in regions located close to each other can be raised. It is also necessary to take into account the territorial aspects of uneven economic development.
Ray, Furness, and Maccab examine a spatial model of inequality in per capita GDP growth in India and China [11,12]. The problems of convergence and spillover effect of Turkey are studied in the work of Kindap and Dogan [13].
Finglengton and Lopez-Bazo examine the relationship of external factors affecting the economies of neighboring countries using spatial econometrics tools [14,15]. Ertur and Koch examine the interdependence of technological development level in neighboring countries. The authors note that technological interdependence is an external spatial factor, and geographical proximity is important for the development of the country’s technologies [16]. Lesage and Fischer, in their study, conclude that spatial dependence between regions and their structure are an indicator that determines the long-term regional income level [17].
Coe and Helpman (1995) studied the impact of the level of innovation development of neighboring countries. Studying the influence of R&D reserves in the country and abroad on the total productivity of factors of production, the paper concluded that the total factor productivity of a country depends not only on the level of development of innovations in a given country, but also on the development of innovations of neighboring countries [18].
Spatial effects in econometric models of convergence of the Russian regions are considered in the research of O.S. Balash [19,20], N. Gichiev [21], Demidova O.A. [22,23]. The conducted studies allow us to conclude that the geographical position plays an important role for the development of the territories of the Volga and Southern Federal Districts territories.
Using econometric methods, Kolomak E.A. considered in her study the dynamics of the regional budget development, as well as the impact of the existing fiscal policy on the presence or absence of regional convergence [24].
3. Methodology
The weights express the neighbor structure between the observations as a matrix W in which the elements of the matrix are the spatial weights:
The size of the matrix is equal to the number of regions.
The spatial weights are non-zero when i and j are neighbors, and zero otherwise. By convention, the self-neighbor relation is excluded, so that the elements in the diagonal of W are equal to zero. This is quite natural, since the weight matrix is designed to reflect the influence of other regions.
In our analyses we use the spatial weights in so-called row-standardized form. Row-standardization takes the given weights (e.g., the binary zero-one weights) and divides them by the row sum:
As a result, each row sum of the row-standardized weights equals one. In addition, the sum of all weights, , equals n, the total number of observations [25].
Contiguity means that two spatial units share a common border of non-zero length. Operationally, we can further distinguish between a rook and a queen criterion of contiguity, in analogy to the moves allowed for the such-named pieces on a chess board. The rook criterion defines neighbors by the existence of a common edge between two spatial units. The queen criterion is somewhat more encompassing and defines neighbors as spatial units sharing a common edge or a common vertex. Therefore, the number of neighbors according to the queen criterion will always be at least as large as for the rook criterion. When constructing a geographic adjacency matrix for regions with a common border, we used queen criterion [26].
When studying spatially distributed phenomena, it is important in one way or another to take into account the mutual influence of processes occurring in different regions. The economic processes taking place in a particular territory are often interdependent, and the strength of interaction is largely determined by the spatial closeness of regions, for example, increases with common borders, decreases with increasing distance between administrative centers or centroids of regional economic activity, etc.
In addition to spatial, many other factors affect the cross-correlation of processes occurring within regions. Therefore, many authors try to use alternative methods of indirectly assessing the intensity of interactions between territories. By analogy with the presence of a common border, it is assumed that the relationship between the regions is significant if the level of interaction exceeds a predetermined threshold. In many cases, this allows one to take into account cross-correlations between the observed values of the dependent variable more accurately. Many authors use of non-geographically based proximity matrices or compositions of geographic and non-geographic patterns in spatial econometrics models.
Spatial econometric models suggest the use of spatial weight matrices W. Most often, square matrices of adjacency (neighborhood), reciprocal distances or square of reciprocal distances are used. When using the inverse matrix of distances as weights, we can take the distances between capitals or centroids of regions. You can calculate distances by road or rail.
In addition, they often calculate the matrix of squared distances between regions .
Many authors argue that the occurrence of spillover effects of economic development can be facilitated by the presence of spatial proximity and networks in the social, institutional, technological, and organizational “space”. Haining discussed such opportunities in relation to modeling income changes between urban areas in Pennsylvania [27]. Holmes and Haggett suggested using the number of trips or trade flows to reflect social or economic interactions between regions [28], Bavaud [29] use spatial weights based on export and import flows.
Territories with a similar specialization structure can share knowledge more easily and cheaper, which can contribute to innovation. Marrocu, Paci, Usai [30] calculated numbers similarity indices to measure technological, social and organizational proximity between regions. Measure of technological proximity was based on the distribution of patenting activity among 44 sectors, organizational proximity based on the affiliation to the same organization by the applicant, and the inventors of a patent when they are located in different regions.
We followed an approach to measuring the similarity of regional specialization based on tax statistics industry data [31]. We suggest that tax data are reasonable proxy variables for assessing regional specialization.
We denote as the amount of tax payments to the budget in the region i and industry r, as the total payments in Russia.
Then is the share of taxes on the r industry in the i region.
The weight matrix W was calculated in two ways. First, as the Euclidean distance between vectors describing the structure of payments:
In the second calculation method, the concept of distinguishing the “leading” sectors of the economy was used. We will call the economic sector leading if its share in tax revenues in the region exceeds the national average:
The elements of the weight matrix were calculated as the Manhattan distance between the corresponding vectors:
Thus, two variants of weight matrices reflecting the specialization of the regions were calculated.
To detect spatial autocorrelation between regions using the Moran’s coefficient (Global Moran’s):
where is the GDP per capita; is the sum of the weights of the matrix W; n is the number of regions [32,33].
The value of the Moran’s coefficient depends on spatial weights matrix W. As a rule, one of the following options is used: an adjacency matrix (neighborhood), inverse distance spatial matrix, or matrix of squared inverse distances [2].
An important step in the analysis of the obtained data is the construction of a spatial Moran scattering diagram. The standardized Z-values of the studied parameter are ploted along the abscissa, and the spatial factor is plotted along the ordinates.
The diagram shows the regression line by Z, the slope of which is equal to the coefficient of total spatial autocorrelation I with a standardized matrix of weights. The spatial autocorrelation coefficient shows the degree of linear relationship between the vector Z of centered values of the studied parameter and the vector of spatially weighted centered values of the studied indicator in neighboring territories (areas), which is called the spatially lagged vector [34].
Spatial models suggest that the economic development of regions depends on the level of economic development of neighboring territories. Neighboring regions have an impact both directly, for example, through innovation, investment flows, the labor market, and indirectly, for example, through interaction at the level of enterprises or government institutions. Econometric modeling with a spatial weight matrix provides an opportunity to take into account the mutual influence of economic growth factors. External spatial effects are explained by a similar reaction to external macroeconomic shocks and territorial heterogeneity [2].
The conditional -convergence model with autoregressive spatial lag (SAR) suggests that there is interdependence between the values of the dependent variable in neighboring regions. The mutual influence depends on the elements of the weights matrix W and the value of the spatial autocorrelation coefficient :
where is the logarithm of the GDP growth rate per capita, N is the number of regions, is the spatial autocorrelation coefficient, is the weighted average of the logarithm of the GDP growth rate in all regions with weights , are variables included to control the impact of innovation and investment on the economic growth of the regions [2].
The spatial error model (SEM) can be written as follows:
This model assumes that spatial dependence exists in the unexplained part of the change in GDP per capita of the base year.
The Durbin model (SDM) can be considered if it is assumed that there is no endogenous interaction and that the emphasis is placed on neighbourhood externalities:
where K is number of independent variable, is value of the k-th independent variable [2].
General Nesting Spatial model (GNS) includes both a spatially lagged dependent variable and a spatially auto-correlated error term:
Models are estimated using maximum likelihood. One of the major benefits of spatial regression models is their ability to quantify spatial spillovers. For this, direct, indirect, and cumulative effects are calculated [35]. The direct effect is found as the average change across the regions in the growth rate of GDP per capita in the region when the basic level of GDP per capita in the same region changes. An indirect effect, or an overflow effect, is the average change in the growth rate in a region with a change in the GDP of the base year in all other regions. The overall effect is the sum of the direct and indirect effects [2].
Using the values of direct and indirect effects, we can calculate the proportion of direct and indirect effects in the total effect. The proportion of direct effects shows the influence of one’s own region on neighboring ones. The greater the value of the share of indirect effects, the greater the impact of this region on what is happening in other regions [2].
4. Empirical Analysis
The aim of the study is to test conditional -convergence models that take into account the spatial interdependence of regional economic growth rates and assess the values of direct and indirect (spillover) effects of investments and innovations.
At present, in Russia there are 89 administrative units—republics, regions, autonomous okrugs. However, due to the lack of statistics from 2010 to 2015 for the Republic of Crimea, the city of Sevastopol, as well as the disaggregation of the Tyumen and Arkhangelsk regions since 2012, we analyzed data for 80 regions. That does not affect the results.
We use official data of the Russian statistical data service (Rosstat) for 80 Russian regions from 2010 to 2017. Detailed descriptions of variables are as follows::
y is GDP per capita in roubles,
Cap is investments in fixed capital in million roubles,
Tech is the expenditure on technological innovation in the regions in million roubles.
Weight matrices were calculated based on data on the geographical boundaries of the regions, and the distances between regional centers (capitals) by road [2]. When calculating Adjacency Matrix, we assumed that for the Kaliningrad region, the closest neighbor is the Leningrad region. This route involves the least number of crossings of border control points.
Let us consider how stable the topology of economic communication systems is reflected in the specialization matrices and .
Weight matrices according to the similarity of regional specialization were calculated according to tax statistics by sectors of the economy. If in the region the tax payments received from the sector were higher than the national average, then it was assumed that this sector was the leader in the region (the value was assigned 1, otherwise 0). To calculate the similarity matrix of regional specialization, the Manhattan metric was used.
To construct weight matrices of proximity to regional specialization, we used data on tax revenues by region of the Russian Federation for 82 sectors. Information from the site https://www.nalog.ru/ from 2010 to 2018 was used as a database.
Obviously, the territorial weight matrix is constant, and the specialization matrix can change over time. The study will also propose to form a linear combination of weight matrices (spatial proximity and similarity of specialization). This will allow us to distinguish the relative contribution of the two types of proximity. The literature suggests that relationships are more likely to occur between geographically close regions. For example, despite the globalization of trade, the purchase and sale of goods are still significantly affected by physical distance, as gravity models show [36]. On the other hand, it is necessary to take into account the similarity of regional specialization. This will help to distinguish the special role played by cooperation in research and development between regions. We note that the specialization of regions may change over a seven-year period of time for which we have data. Since our empirical model is static, we used weight matrices of industry similarity created in 2010 and 2014.
As can be seen from Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, the industry structure was quite stable over the period under review. At the same time, the regions that passed from one specialization cluster to another are well traced. The most clearly flowing regions from one cluster to another can be observed on dendrograms.
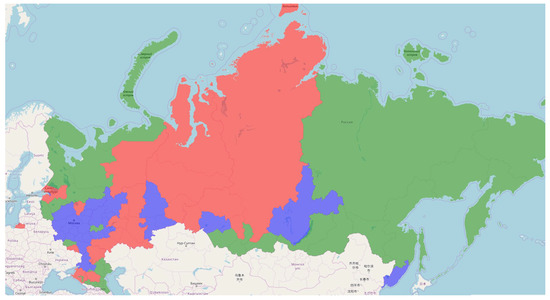
Figure 1.
Regions of Russia, clustering by specialization, 2010.
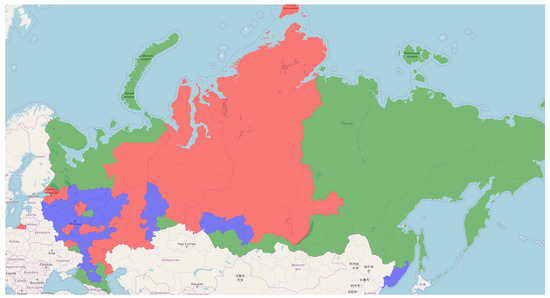
Figure 2.
Regions of Russia, clustering by specialization, 2014.
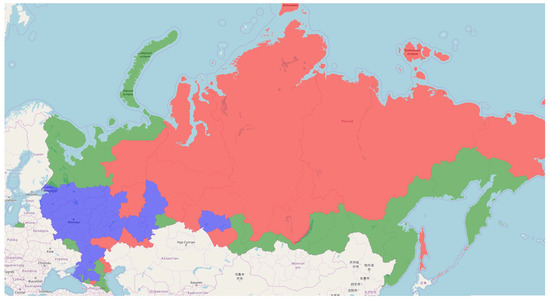
Figure 3.
Regions of Russia, clustering by specialization, 2017.
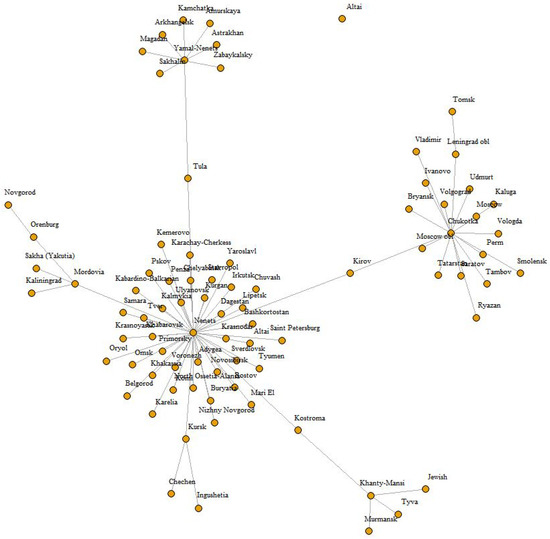
Figure 4.
Minimum spanning tree for 2010.
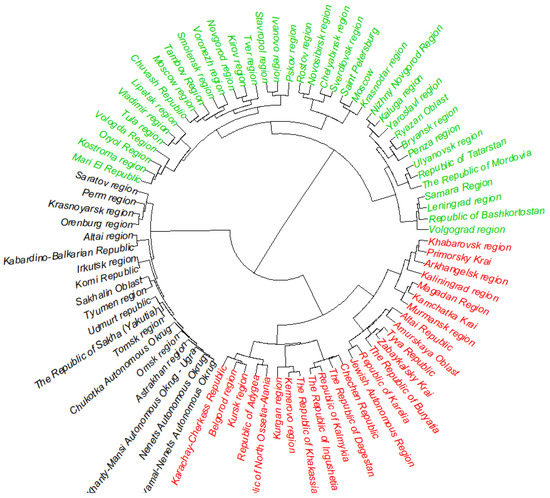
Figure 5.
Hierarchical classification tree, 2017.
In general, clusters are quite compact and even have some territorial affinity. For example, every year the central European cluster becomes more compact.
Let us characterize the territorial composition and specialization features of the resulting clusters (Figure 6). The first cluster built according to 2017 data includes 36 regions located in the center and south of the European part of the Russian Federation and the Southern Urals. These regions are characterized by a high share of manufacturing, trade, and services in the sectoral structure of gross value added (green boxplot).
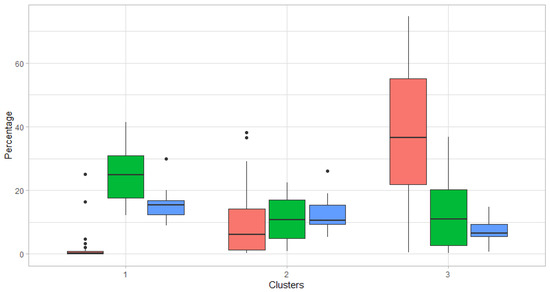
Figure 6.
Share of manufacturing, trade, and services, mining in gross value added by cluster in 2017.
The second cluster included 24 regions: the north of the European part, the Caucasus, the south of Siberia, and the Far East. The share of manufacturing and mining industries in this cluster is close to the national average.
The third cluster included 19 regions of the Northern Urals, Siberia, and certain regions of the Volga region. These regions mostly specialize in mining (red boxplot).
The Table 1 shows the regions that consistently fell into the same cluster during the considered period of time.

Table 1.
Stable regions.
4.1. -Convergence
The differences in the amount of GDP per capita in the regions of Russia are great. In 2010, almost 20.2 times the GDP per capita of the “rich” regions exceeded the “poor” ones in 2010, in 2017 it was 16.5 times.
To study -convergence, the dynamics of different indicators of variation and inequality is usually analyze.
The box plot presented in Figure 7 shows that differentiation of regions increased in the period under review. Six regions with the highest GDP per capita: Tyumen Region, Sakhalin Region, Chukotka Autonomous Okrug, Moscow, Magadan Region, Republic of Sakha (Yakutia), St. Petersburg. The value of GDP per capita is taken for the Tyumen and Arkhangelsk regions within the boundaries until 2012 [2].
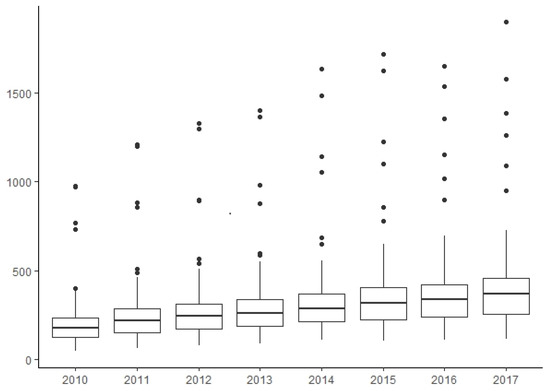
Figure 7.
Dispersion of GDP per capita in the regions of Russia for 2010–2017.
As can be seen from Figure 7 at current prices, GDP per capita for the period from 2010 to 2017 increased in all regions.
Figure 8 shows the coefficients of variation unweighted and weighted in terms of population. The fact that the values of the weighted coefficient of variation is greater than the unweighted one is due to the fact that regions with high GDP per capita, as a rule, are regions with a larger population. The values of the coefficients of variation fluctuate slightly in time, so there is no reason to talk about the manifestation of the effects of -convergence in the period under consideration.
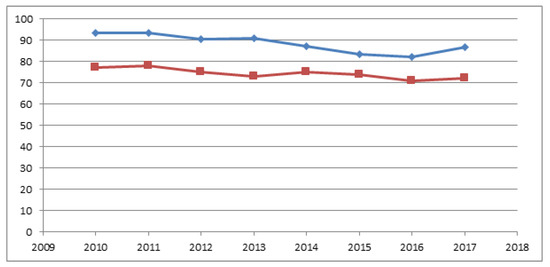
Figure 8.
Dynamics of the coefficient of variation (bottom) and the weighted coefficient of variation of the GDP per capita of Russia in 2010–2017, %.
A similar conclusion is drawn from a study of the dynamics of the values of the Gini coefficient (Figure 9). The tendency to reduce inequality was manifested in 2010–2013, but since 2014 there increased the polarization of regions in terms of GDP per capita.
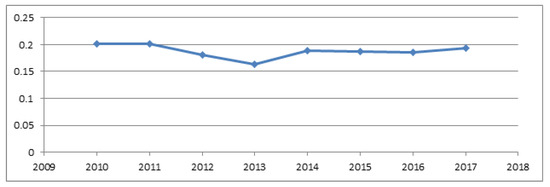
Figure 9.
Dynamics of the Gini coefficient of GDP of Russia for 2010–2017.
Let us present the results of estimation the indicators of spatial interdependence of the studied indicators [2].
Table 2 presents the values of the Moran’s coefficient for the growth rate of GDP per capita. The weights matrix was calculated based on the adjacency matrix of regions (the presence of a border between them). For all the considered periods, there is a significant positive spatial autocorrelation between the growth rates of GDP per capita in the regions of Russia.

Table 2.
Moran’s coefficient for GDP per capita.
Figure 10 shows the Moran Scatter Plot, in which the standardized values of the spatial lag of GDP per capita growth rate of 2017 plotted along the axis are compared to 2014, and the standardized values of GDP per capita growth rate of 2017 shown along the axis are compared to 2014, the regression line is the slope coefficient corresponding to the value of the Moran’s spatial autoregression coefficient for the GDP per capita growth rate in 2017 compared to 2014.
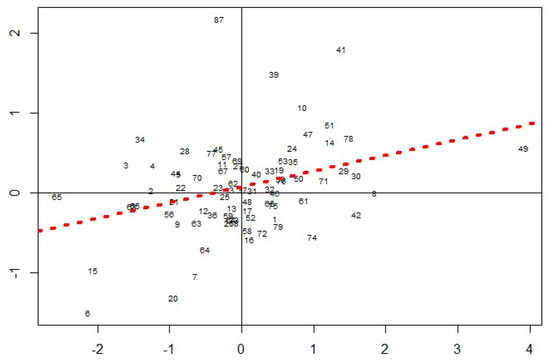
Figure 10.
Moran Scatter Plot of per capita GDP growth rates for 2014–2017.
As it can be seen from Figure 10, the Kamchatka Territory (41), Kaliningrad Oblast (39), St. Petersburg (78), Moscow Oblast (51), Republic of Karelia (10), etc. fell into the first quadrant of regions with high GDP per capita growth rates, surrounded by the same neighbors.
The third quadrant includes regions with low per capita GDP growth, surrounded by the same neighbors: the Republic of Ingushetia (6), the Republic of North Ossetia-Alania (15), the Chechen Republic (20), Saratov Region (64), etc.
In the second quadrant (regions with low GDP per capita, surrounded by neighbors with high growth rates): Chukotka Autonomous Okrug (87), Volgograd Oblast (34) and others, in the fourth quadrant of regions with low GDP per capita, surrounded by neighbors with high growth rates, Kemerovo (42), Chelyabinsk (74) regions, Jewish Autonomous Region (49), and others [2].
4.2. -Convergence
-convergence captures regional differences in the variance of regional GDP per capita. However, this is not enough for convergence analysis. The -convergence model suggests faster growth in lagging regions. If the -convergence hypothesis is true, we expect to see a negative correlation between the growth rate of GDP per capita and the initial levels of GDP per capita in the regions [2].
There are two varieties of beta convergence: absolute (unconditional) and conditional convergence. We study conditional regional convergence, including and the logarithm of the growth rate of expenditure on technological innovation the regions as control variables. Different durations of the periods were chosen by us in order to track the possible difference in the trends of the studied process before and after 2014. We split the estimations in 2 periods: 2010–2014 and 2014–2017, because we were interested to see how economic sanctions against Russia affected the interaction between its regions.

Table 3.
Conditional -convergence models for 2010–2014. The weight matrix is adjacency matrix.

Table 4.
Conditional -convergence models for 2010–2014. The weight matrix is specialization matrix.

Table 5.
Conditional -convergence models for 2014–2017. The weight matrix is adjacency matrix.

Table 6.
Conditional -convergence models for 2014–2017. The weight matrix is specialization matrix.
In addition, we present the results for spatial models estimated by including two different proximity matrices in order to take into account the complementarity between spatial and specialized secondary channels. Table 7 and Table 8 show the log likelihood values for different values of the parameter. Territorial proximity is a more important factor than the similarity of specialization for explanation the economic growth rates of Russian regions.

Table 7.
Log likelihood for conditional -convergence models for 2010–2014. The weight matrix is matrix combination, .

Table 8.
Log likelihood for conditional -convergence models for 2014–2017. The weight matrix is matrix combination, .
The results of the estimation of models according to 2010–2014 and 2014–2017 differ significantly. In the first subperiod, the coefficients of the explanatory variables are significantly different from zero. The sign of the coefficient in the logarithm of GDP in the base period is negative, which corresponds to the assumption of the presence of beta convergence. In addition, the growth rate of investment in fixed assets and the expenditure on technological innovation had a significant impact on economic growth.
In the case of spatial proximity between regions, there is a positive correlation between economic growth rates. However, in the case of the specializations proximity, the spatial correlation coefficients become insignificant. Consequently, territorial proximity is more important than the similarity of specialization in explaining the interdependence of the rates of economic growth of Russian regions.
The significance and positive value of the spatial lag in the rate of growth of expenditure on technological innovations confirms the hypothesis that there is a dependence of the average GDP growth per capita on the rate of growth of expenditure on technological innovations in neighboring regions. These conclusions are resistant to the specification of the model and the choice of spatial weights matrices. Note that the hypothesis of the substantial presence of spatial autocorrelation (non-zero coefficient ) is confirmed for the SEM and SAR models, but not for the SDM. However, in the SDM model, spatial interdependence is taken into account by including regressors in the spatial lag model. Our results are consistent with the findings of previous studies on the presence of -convergence of Russian regions in the period 1990–2010 [19,20].
That said, the estimates of the coefficients of the explanatory variables obtained from the results of evaluating models constructed from data after 2014 are not significant nonzero. It is not possible to confirm the conclusions about the preservation of the trend towards the rapprochement of regions in terms of the level of economic development; rather, we can talk about its deceleration or reversal of the trend.
Table 9 shows the indirect, direct, and cumulative effects of the Durbin model for the adjacency weights matrix.

Table 9.
Direct, indirect, and cumulative effects for Durbin models.
In this article, we use the Akaike information criterion (AIC) to obtain a possible ranking of evaluation models. The computed AIC values for the evaluation models indicate that the “best” model is a model based on geographical and specialization proximity.
If we compare the direct and indirect effects calculated for the adjacency matrix, then the influence of the logarithm of the base 2010 GDP per capita and the logarithms of the growth rate of investment in fixed capital on the change in the growth rate of GDP per capita is much greater in the own region than in the neighboring ones. The expenditure on technological innovation, on the contrary, have a greater impact on neighboring regions than on their own. The share of the impact that the amount of fixed capital investments in our own region has on the economic growth reaches 92%, while the share of the technological innovation expenditure makes 44% for our own region effect and 56% for neighboring territories influence.
The use of different weights matrices makes it possible to estimate the robustness of the results for the choice of weights. For all three options for the selection of weights matrices, the results are quite similar and do not affect the conclusions for the periods from 2010 to 2014, and from 2014 to 2017.
5. Conclusions
In this study we compared the power of spillover effects arising from territorial adjacency and similarity of specialization of Russian regions, as applied to economic growth models. Using methods of spatial econometrics, we tested hypotheses about the conditional -convergence of Russian regions by GDP per capita.
To simulate spatial effects, we used the following options for constructing weight matrices: according to data on the geographical boundaries of regions and distances between regional centers (capitals) by road. Similarity weighted matrices of regional specialization were estimated by similarity indices of the regional specialization according to tax statistics.
It is known that spatial weight matrices are exogenous and practically unchanged in time. We analyzed the stability of the elements of the weight matrix of specialization. The topological structure defined by such matrices changed rather weakly in the studied period. We found several stable territorial clusters located in the European, Asian, northwestern and Far Eastern parts of Russia.
We also found that spatial models of conditional -convergence, which used the growth rates of investments in fixed assets and the costs of technological innovations as control variables, differ significantly according to 2010–2014 and 2014–2017. There is a statistically significant -convergence for the period 2010–2014. It has been established that the growth rate of investment in fixed assets and the costs of technological innovation have an impact on economic growth. A statistically significant dependence of the average GDP per capita growth rate on the growth rate of technological innovation costs in neighboring regions was found. Our conclusions are resistant to the selection of weight matrices and model specifications for this period of time. We found a statistically significant dependence of the average per capita GDP growth rate on the growth rate of technological innovation costs in neighboring regions.
However, according to the results of evaluating models constructed from data after 2014, the estimates of the coefficients for the explanatory variables do not significantly differ from zero. There is no trend towards regional convergence in terms of economic development.
Author Contributions
Conceptualization, V.B. and O.B.; methodology, V.B. and O.B.; software, A.F.; resources, A.F.; data curation, A.F.; writing—Original draft preparation, V.B., O.B., and E.C.; project administration, V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation according to the research project 19-18-00199.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Solow, R. A Contribution to the Theory of Economic Growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Balash, V.A.; Balash, O.S.; Faizliev, A.; Chistopolskaya, E.V. Modeling the Spatial Effects of the Impact of Innovation on Regional Economic Growth. In Fourth Workshop on Computer Modelling in Decision Making (CMDM 2019); Atlantis Press: Paris, France, 2019; pp. 108–114. [Google Scholar] [CrossRef]
- Quah, D. Empirical cross-section dynamics in economic growth. Eur. Econ. Rev. 1993, 37, 426–434. [Google Scholar]
- Barro, R.; Sala-i Martin, X. Convergence across States and Regions. Brook. Papers Econ. Act. 1991, 22, 107–182. [Google Scholar]
- Iodchin, A. Decomposition of regional convergence in Russia. In Audit and Financial Analysis; 2007; pp. 475–482. [Google Scholar]
- Pshenichnykh, J. Methodological foundations of convergence research. In Bulletin of the Taganrog Institute of Management and Economics; Cambridge University Press: Cambridge, UK, 2015; pp. 114–118. [Google Scholar]
- Baumol, W.J. Productivity Growth, Convergence, and Welfare: What the Long-Run Data Show. Am. Econ. Rev. 1986, 76, 1072–1085. [Google Scholar]
- Lopez-Rodriguez, J. Regional Convergence in the European Union: Results from a Panel Data Model. Econ. Bull. 2008, 18, 1–7. [Google Scholar]
- Fischer, M.M.; Stirböck, C. Regional Income Convergence in the Enlarged Europe, 1995–2000: A Spatial Econometric Perspective. In ZEW—Centre for European Economic Research Discussion; ZEW: Manheim, Germany, 2004; pp. 1–28. [Google Scholar]
- Egger, P.; Pfaffermayr, M. Spatial convergence*. Pap. Reg. Sci. 2006, 85, 199–215. [Google Scholar] [CrossRef]
- Rohan, R.; Cledwyn, F. India and China’s Growth Spillover in Asia: A Spatial Panel Econometric Approach. In Proceedings of the 14th Annual Conference on Economic Growth and Development, New Delhi, India, 9 December 2018; pp. 1–28. [Google Scholar]
- Mccabe, A. Economy on Pace to Become World; Gazette Montreal: Montreal, QC, Canada, 2010; pp. 1–2. [Google Scholar]
- Kýndap, A.; Dogan, T. Regional Economic Convergence and Spatial Spillovers in Turkey. Int. Econ. Rev. (IER) 2019, 11, 1–23. [Google Scholar]
- Fingleton, B.; López-Bazo, E. Empirical growth models with spatial effects*. In Papers in Regional Science; Wiley: New York, NY, USA, 2006; Volume 85, pp. 177–198. [Google Scholar]
- López-Bazo, E.; Vayá, E.; Artís, M. Regional Externalities And Growth: Evidence From European Regions*. J. Reg. Sci. 2004, 44, 43–73. [Google Scholar]
- Ertur, C.; Koch, W. Growth, technological interdependence and spatial externalities: Theory and evidence. J. Appl. Econ. 2007, 22, 1033–1062. [Google Scholar] [CrossRef]
- Lesage, J.P.; Fischer, M.M. Spatial Growth Regressions: Model Specification, Estimation and Interpretation. Spat. Econ. Anal. 2008, 3, 275–304. [Google Scholar] [CrossRef]
- Coe, D.T.; Helpman, E. International R and D spillovers. Eur. Econ. Rev. 1995, 39, 859–887. [Google Scholar] [CrossRef]
- Balash, O. Convergence Spatial Analysis of Russia’s Regions. Izvestiya Saratov Univ. New Ser. Ser. Econ. Manag. Law 2012, 12, 45–52. [Google Scholar]
- Balash, O.; Chistopolskaya, E. The Spatial Approach to the Analysis of Economic Growth in the Regions of Russia. In Proceedings of the International Scientific and Economics Conference Named after Academicial P.P. Maslov, Berlin, Germany, 22–24 May 2013; pp. 12–20. [Google Scholar]
- Gichiev, N. Regional convergence of economic growth: Spatial econometrics. Reg. Econ. Theory Pract. 2018, 16, 58–67. [Google Scholar] [CrossRef]
- Demidova, O. Spatial effects for the eastern and western regions of Russia: A comparative analysis. Int. J. Econ. Policy Emerg. Econ. 2015, 8, 153–168. [Google Scholar] [CrossRef]
- Demidova, O.; Daddi, P.; Medvedeva, E.; Signorelli, M. Modeling the Employment Rate in Russia: A Spatial-Econometric Approach. Econ. Reg. 2018, 1, 1383–1398. [Google Scholar] [CrossRef]
- Kolomak, E. Models of regional policy: Convergence or divergence. Reg. Econ. Theory Pract. 2009, 9, 113–120. [Google Scholar]
- Anselin, L.; Rey, S.J. Modern Spatial Econometrics in Practice: A Guide to GeoDa, GeoDaSpace and PySAL; GeoDa Press LLC: Chicago, IL, USA, 2014. [Google Scholar]
- Anselin, L.; Smirnov, O. Efficient algorithms for constructing proper higher order spatial lag operators*. J. Reg. Sci. 1996, 36, 67–89. [Google Scholar] [CrossRef]
- Haining, R. Income Diffusion and Spatial Econometric Models. Geograph. Anal. 1987, 19, 57–68. [Google Scholar] [CrossRef]
- Holmes, J.H.; Haggett, P. Graph Theory Interpretation of Flow Matrices: A Note on Maximization Procedures for Identifying Significant Links. Geograph. Anal. 1977, 9, 388–399. [Google Scholar] [CrossRef]
- Bavaud, F. Models for Spatial Weights: A Systematic Look. Geograph. Anal. 1998, 30, 153–171. [Google Scholar] [CrossRef]
- Paci, R.; Marrocu, E.; Usai, S. The Complementary Effects of Proximity Dimensions on Knowledge Spillovers. Spat. Econ. Anal. 2014, 9, 9–30. [Google Scholar] [CrossRef]
- Afanasyev, M.; Kudrov, A. Structures of strong sectors of the regional economy and estimates of their economic complexity. In Proceedings of the 2nd International Scientific and Practical Conference “Modern Management Trends and the Digital Economy: From Regional Development to Global Economic Growth” (MTDE 2020), Yekaterinburg, Russia, 16–17 April 2020; pp. 55–63. [Google Scholar]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Geary, R.C. The Contiguity Ratio and Statistical Mapping. Inc. Stat. 1954, 5, 115–146. [Google Scholar]
- Anselin, L. The Moran scatterplot as an ESDA tool to assess local instability in spatial association. Spatial Analytical; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- LeSage, J.; Pace, R. Introduction to Spatial Econometrics; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2009. [Google Scholar]
- Anderson, J.E.; van Wincoop, E. Trade Costs. J. Econ. Lit. 2004, 42, 691–751. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).