1. Introduction
The role of rubble-mound low-crested breakwaters (LCBs) in coastal protection, whose main advantage is their mild aesthetic impact on the natural environment, is to partially dissipate incident waves. Consequently, in the seaward region of LCBs, the most important wave processes are breaking and reflection, while in their leeward region, the most important ones are overtopping, transmission, and setup. These wave processes induce also significant flow processes in the vicinity of LCBs. The influence of the geometrical characteristics of LCBs on wave and flow processes has been studied extensively for emerged or submerged LCBs. The case of zero-freeboard breakwaters (ZFBs), where the crest level of the structure is at the still water level (SWL), is the subject of the present study. In the following literature review, the focus is on experimental and numerical (only depth-resolving flow models) studies of rubble-mound, two-dimensional vertical (2-DV) LCBs.
In terms of wave reflection in the seaward region of permeable LCBs with rock armor, Zanuttigh and Van der Meer [
1] analyzed several experimental datasets and derived an empirical formula for the prediction of the reflection coefficient
Kr. Specifically for ZFBs, the formula in [
1] becomes:
where
A = 0.167(1 − exp(−3.2
γf)) and
b = 1.49(
γf − 0.38)
2 + 0.86 are calibration parameters related to the roughness factor
γf,
C < 1 is a reduction parameter necessary for LCBs,
ξ0 = tan
a(
gT2/2
πHi)
1/2 is the breaker parameter, tan
a is the seaward slope of the ZFB,
T is the wave period of the incident waves, and
Hi is the wave height of the incident waves at the seaward toe of the ZFB. In terms of wave transmission in the leeward region of LCBs, empirical formulas for the prediction of the transmission coefficient:
where
Ht is the wave height at the leeward toe of the LCB, derived in [
2,
3,
4,
5]. Specifically for ZFBs with rock armor, the corresponding empirical formulas are:
where
B is the crest width of the ZFB,
dS is the water depth at the seaward toe of the ZFB, and
λ0 =
gT2/2
π is the deep-water wavelength. The empirical formulas in [
2,
3] were derived using experimental datasets of LCBs with impermeable core, while the empirical formulas in [
4,
5] used practically the same datasets as reported in [
4]. In all cases of Equation (3), the important effect of
ξ0 and/or
B on the wave transmission is noted.
In terms of the mean overtopping discharge over rubble-mound ZFBs, the following empirical formula is suggested in EurOtop [
6]:
where
fq is an adjustment factor that accounts for scale effect corrections. In terms of the wave setup,
δ, at the leeward toe of rubble-mound, permeable LCBs, experimental data were presented in [
7,
8]. In both studies, several cases of ZFBs were included, and the following empirical formulas were derived:
where
D50 is the mean diameter of the rubble rocks and
λi is the wavelength at the seaward toe of the ZFB. Semi-analytical models for the prediction of
δ were also presented [
9,
10], but they refer to submerged barriers and are not considered here where the focus is on ZFBs.
The influence of the geometrical characteristics of rubble-mound, permeable, submerged breakwaters on wave transmission was investigated numerically (potential flow theory in the fluid region and viscous flow in the permeable trunk of the breakwater) in [
11]. It was concluded that increasing the crest width and/or decreasing the crest submergence depth results in the reduction of
Kt, while increasing the permeability of the breakwater, i.e., increasing the porosity or the size of the rubble rocks, results in the increase of
Kt and the reduction of
Kr. The Navier-Stokes equations were solved numerically in [
12] to simulate the interaction between a solitary wave and a permeable submerged bar. It was found that the increase of porosity from 0.4 to 0.52 results in the reduction of
Kt, while if the porosity is further increased up to 0.7, the transmission coefficient increases, indicating that an optimum porosity value seems to exist.
Near-field flow processes that occur due to the interaction between regular waves and rubble-mound, permeable LCBs were studied experimentally and numerically in [
13]. The numerical model was based on the “Cornell Breaking Waves and Structures” (COBRAS) software [
14]. In both the experiments and the simulations, a recirculation system was devised to return flow to the seaward region of the LCB to balance the non-realistic pilling of water in the leeward region of the LCB; this system was found to be crucial in the modeling of 2-DV LCBs. Specifically for the ZFB case in [
13], it was tan
a = 1/2,
ds = 25 cm,
B = 100 cm, while the median diameter,
D50, of the rocks was 4.80 cm in the armor layer and 1.47 cm in the core. Several regular wave cases were examined, which for the ZFB case corresponded to the ranges 0.20 ≤
Hi/
ds ≤ 0.78 and 9.38 ≤
λi/
ds ≤ 19.63. It was observed that breaking waves collapsed on the seaward edge of the ZFB crest inducing a strong vortex cell in this zone, a strong mean shoreward current developed over the ZFB crest, a primary vortex cell was formed in the leeward region of the ZFB, a weak mean seaward current developed in the ZFB trunk, and a secondary vortex cell was formed near the seaward toe of the ZFB.
Losada et al. [
15] focused on the submerged breakwater cases in [
13] with crest height
hc = 25 cm,
ds = 30 cm resulting into crest elevation
Rc = −5 cm, and
Rc/
Hi = −0.52. They performed numerical simulations using the COBRAS model and found that the resulting
Kr does not depend on B, while the shear stress field attains its maximum values along the armor layer of the crest. Losada et al. [
15] also studied numerically a submerged breakwater case at a prototype scale with tan
a = 2/3,
dS = 5 m,
B = 5 m,
RC = −0.5 m. The trunk of the breakwater was homogeneous with
D50 = 1.44 m, while the incident wave parameters at the seaward toe of the breakwater were
Hi = 0.97 m (
Rc/
Hi = −0.52) and
T = 6 s. It was found that the velocity of the flow over the crest was about one order of magnitude larger than the one in the permeable trunk of the breakwater.
Lara et al. [
16] exploited the capability of COBRAS to study irregular wave interaction with the submerged permeable breakwater case in [
13], and they presented regular wave interaction with an LCB of permeable armor layer and less permeable core. The latter case corresponded to the LCB studied experimentally at the Maritime Engineering Laboratory of the Polytechnic University of Catalunya (Spain) as described in [
17]. This LCB had tan
a = 1/2,
hc = 1.59 m,
B = 1.825 m, while the median diameter,
D50, of the rocks was 10.82 cm in the armor layer and 3 ± 1 cm in the core. No ZFB case was considered; the only submerged case had
Rc = −0.13 m,
Hi = 0.286 cm (
Rc/
Hi = −0.45) and
T = 2.18 s. The transmitted wave height in the leeward region of the LCBs was, in general, under-predicted by the numerical simulations in comparison to the experimental data; this discrepancy was attributed to several factors, including the inaccurate replication of the experimental LCB geometry in the numerical model.
In this paper, the interaction of regular waves with rubble-mound, permeable ZFBs was studied numerically using a two-phase flow model in the air-water region and a porous flow model in the trunk of the ZFBs. The objective was to reveal the effect of crest width and trunk permeability on the main wave (reflection, transmission, and leeward setup) and flow (vortex generation, mean currents, and overtopping discharge) processes for ZFBs. The formulations are based on the Navier-Stokes equations, and not on a depth-averaged approach, to capture the vertical variability of flow phenomena. At present, the computational cost of using solvers based on the Navier-Stokes equations in large-scale coastal problems is high, but it is reasonable for smaller scale problems such as the present one.
3. Results
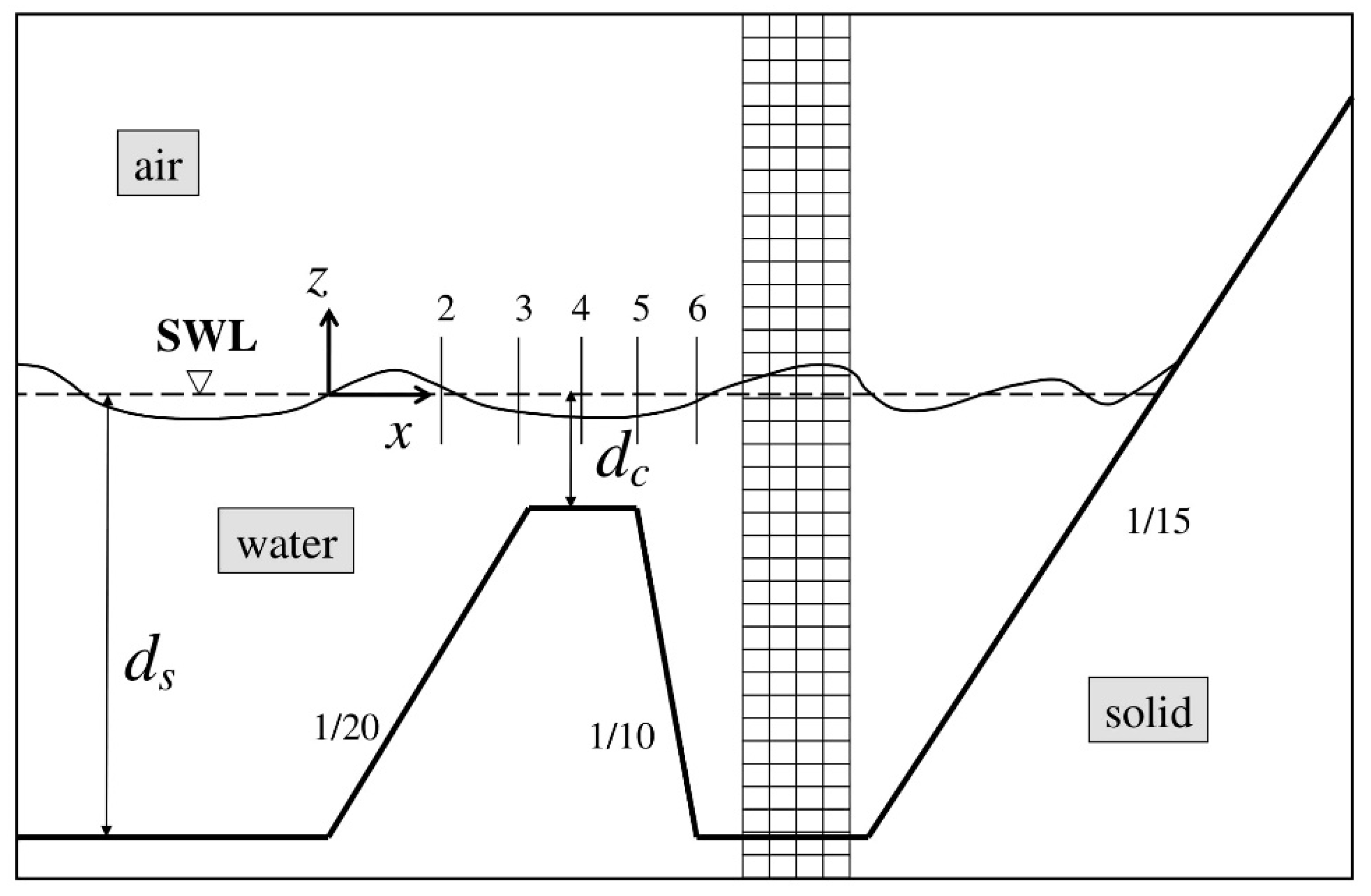
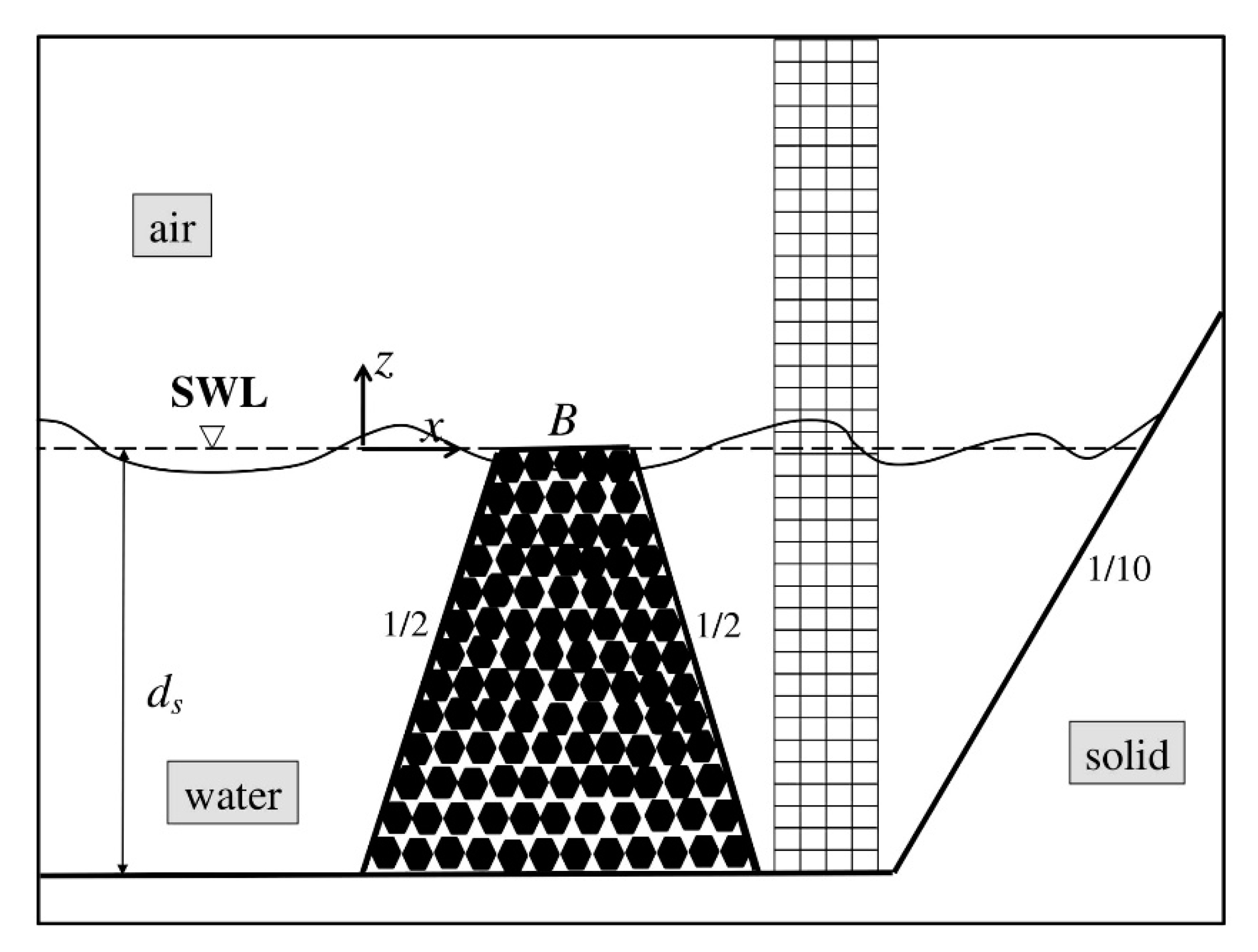
All ZFBs in the present study were rubble mound and permeable with tan
a = 1/2 for both seaward and leeward slopes. A sketch of the computational domain is shown in
Figure 5. First, three different setups were considered to examine the effect of crest width (cases 1–3 in
Table 1) on the hydrodynamic processes of wave reflection, overtopping, transmission, and setup, as well as the flow behavior in the seaward and leeward regions of these structures. In cases 1–3, the ZFBs were fully-permeable (homogeneous trunk permeability), while the crest width,
B, was set equal to
dS, 2
dS, and 3
dS, respectively, where
dS is the constant water depth between the wavemaker and the seaward ZFB toe. Then, the effect of the incident wave period (cases 1 and 4 in
Table 1) and the ZFB trunk permeability (cases 1 and 5 in
Table 1) were also investigated for the ZFB case with
B =
dS.
In dimensional terms,
dS was selected to be equal to 0.4 m, which corresponds to Reynolds number Re
d = 800,000. The geometrical details and the incident wave parameters for all cases are summarized in
Table 1. For all cases, a grid independence study was performed, and the selected computational grid had a uniform size of Δ
x/
dS = 0.02 along
x (300–450 grid points per wavelength of the incident waves), and a non-uniform size in
z; Δ
z/
dS = 0.0025 in the water and increasing to Δ
z/
dS = 0.01 in the air. The corresponding values in the water with respect to the Stokes length,
δ, were Δ
x/
δ = 10.1 ÷ 12.1 and Δ
z/
δ = 1.27 ÷ 1.51 according to the wave length, which were sufficient to get a good resolution with at least four grid points in the wave boundary layer over the bed. The small flow scales occurring during breaking at the ZFB seaward slope are modeled by the SGS eddy-viscosity model. In all simulations, the CFL and VSL criteria were equal to 2.0 × 10
−2 and 5 × 10
−4, respectively. In order for the flow field not to be affected by the height of the air layer in the computational domain, this was selected to be 1.5
dS above the SWL (after trial and error). The calibration values
αp = 1000 and
βp = 1.1, according to [
19,
20], were used in Equation (7).
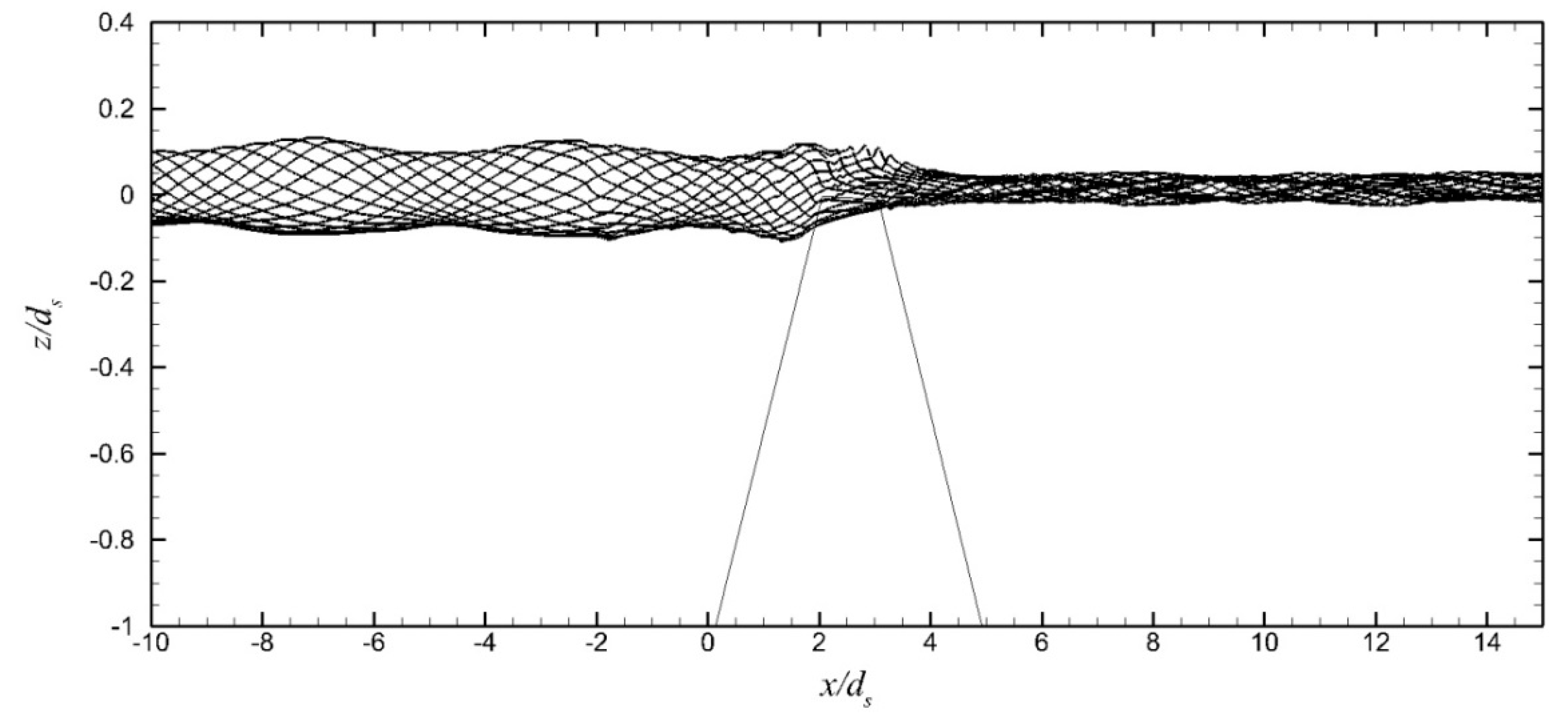
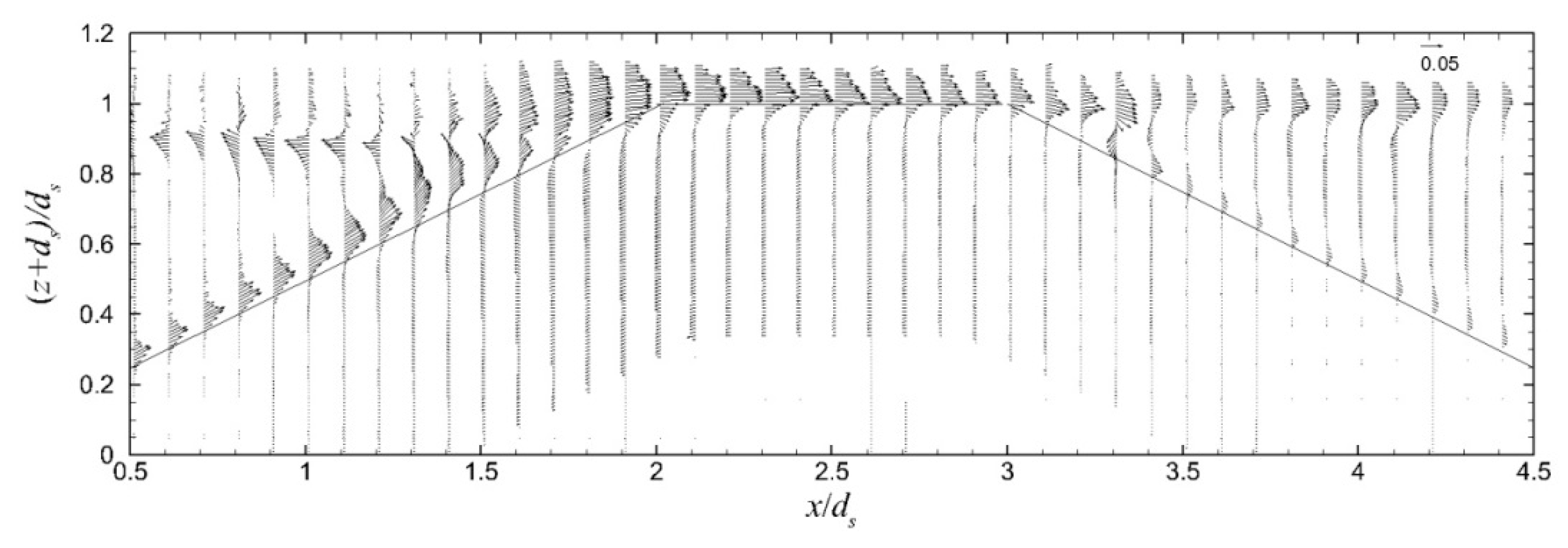
Typical crest and trough elevation envelopes during 10 wave periods, after 20 wave periods of simulation (1 wave period per 6 h on ARIS), are shown in
Figure 6 for case 1. From such envelope results, the breaking depth on the seaward ZFB slope and the corresponding wave height were identified at the location of the maximum wave crest elevation. In all cases, wave breaking occurred on the seaward slope and near the crest of the ZFBs; these results are summarized in
Table 1. In cases 1–3, which correspond to the same incident wave and different crest width, the waveform in the seaward region of the ZFBs is similar, and a partially standing wave is generated due to reflection. In the leeward region of the ZFBs, the wave height, i.e., the wave energy, is different between cases 1–3 as it decreases with the increase of the crest width. In case 4, a decreased wave height is observed in the seaward region, while less wave energy is transmitted to the leeward region in comparison to case 1, which has the same crest width but larger incident wave period, i.e., a longer incident wavelength. In case 5, where the ZFB has a less permeable core, a slightly increased wave height is observed in the seaward region and slightly less wave energy is transmitted to the leeward region in comparison to case 1, which has the same crest width but larger ZFB trunk permeability.
The behavior of wave height in the seaward and leeward side of all ZFB cases is also demonstrated in terms of the reflection and transmission coefficients presented in
Table 2. For the reflection coefficient, surface elevation time series at three locations in the seaward region of the ZFBs were obtained, and a reflection analysis was performed using the method in [
28]. For the transmission coefficient, the surface elevation time series, recorded at the seaward and leeward toe of the ZFBs, were used to calculate the wave height at each position through spectral analysis. It is observed that wave transmission decreased, while wave reflection did not vary, with the increase of the crest width (cases 1–3) when incident wave height, incident wave period, and trunk permeability did not change. The decrease of wave transmission is attributed to the increase of wave dissipation over the ZFB crest as
B increased. Decreasing the incident wave period (cases 1 and 4) results in the decrease of wave reflection and the decrease of wave transmission when the crest width and trunk permeability did not change. These decreases are associated with the decrease of
ξ0. Finally, reducing trunk permeability (cases 1 and 5) also increased the wave reflection and decreased the wave transmission when crest width and incident waves did not change. Wave energy transmission was affected by both the overtopping over the ZFB crest and the porous flow in the ZFB trunk. In case 5, the less permeable ZFB trunk inhibited the transmission of kinetic energy through the trunk from the seaward to the leeward region of the ZFB in comparison to case 1, thus, the resulting reflection coefficient,
Kr, was larger and the transmission coefficient,
Kt, was smaller.
Apart from the computed reflection and transmission coefficients, the corresponding values predicted by widely used empirical formulas are also presented in
Table 2. For wave reflection, the empirical formula of Equation (1) was used, with
γf = 0.40, for the fully-permeable ZFB cases 1–4, and
γf = 0.5, for the partially-permeable ZFB case 5, according to [
1]. To achieve the best possible agreement to the computed results, the reduction parameter was set to
C = 0.43 instead of the value
C = 0.67 suggested in [
1] for ZFBs. For wave transmission, the empirical formulas of Equation (3) were used. Overall, better prediction seems to be achieved by the empirical formula in [
5].
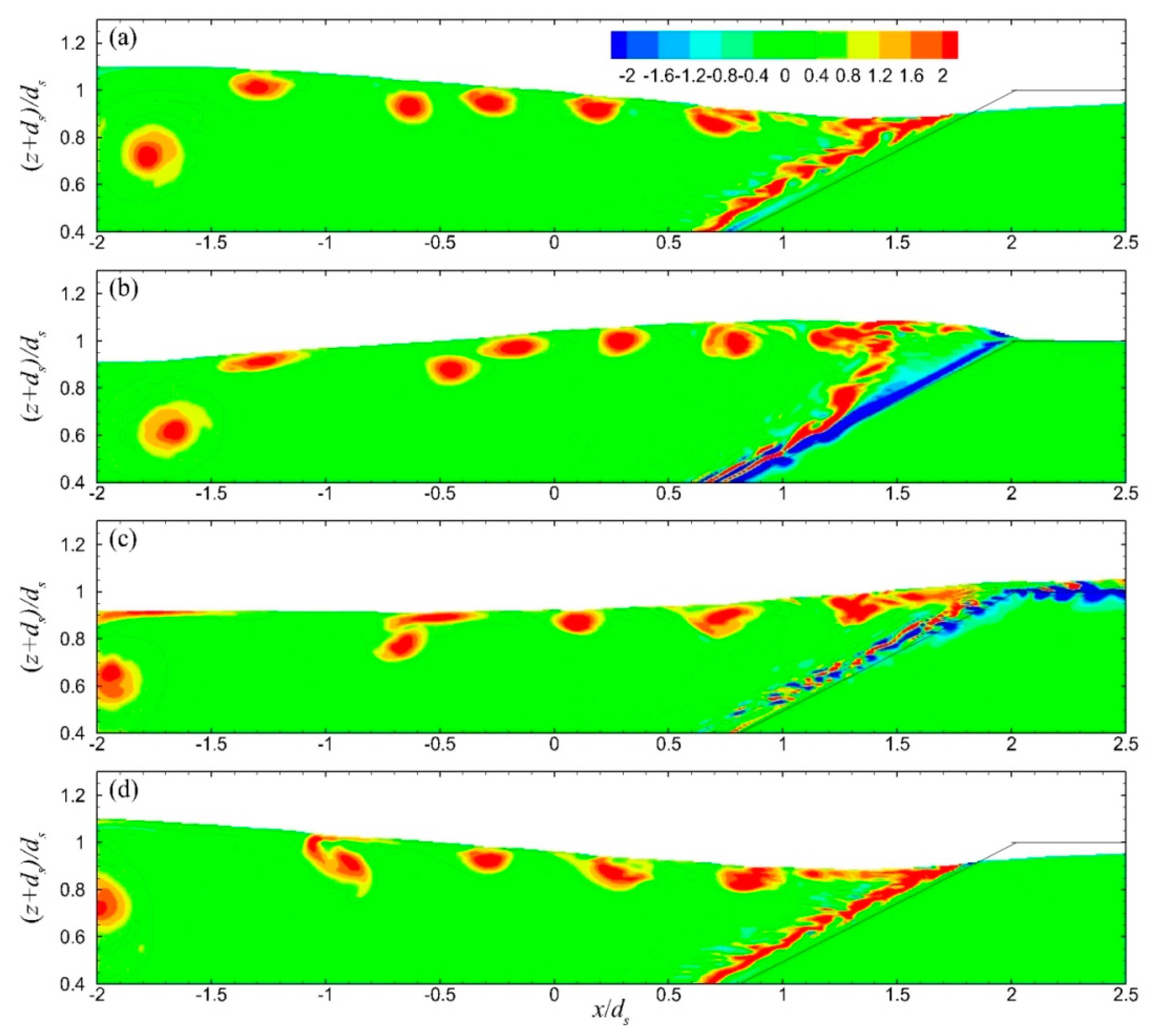
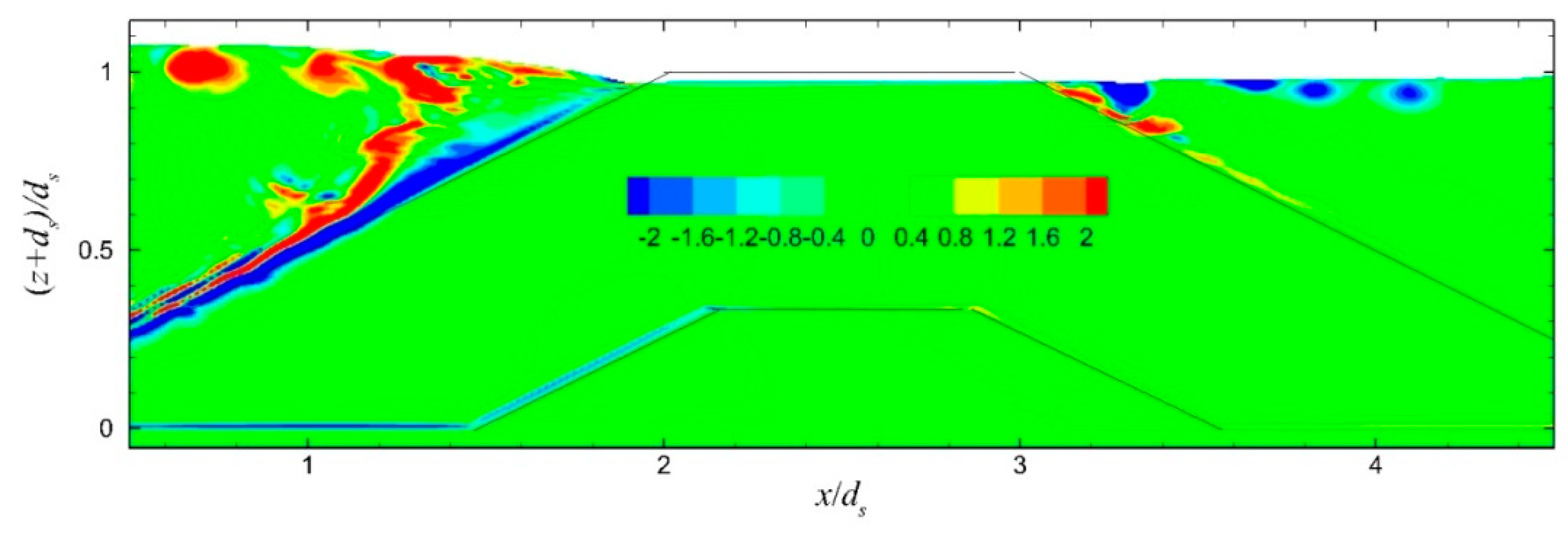
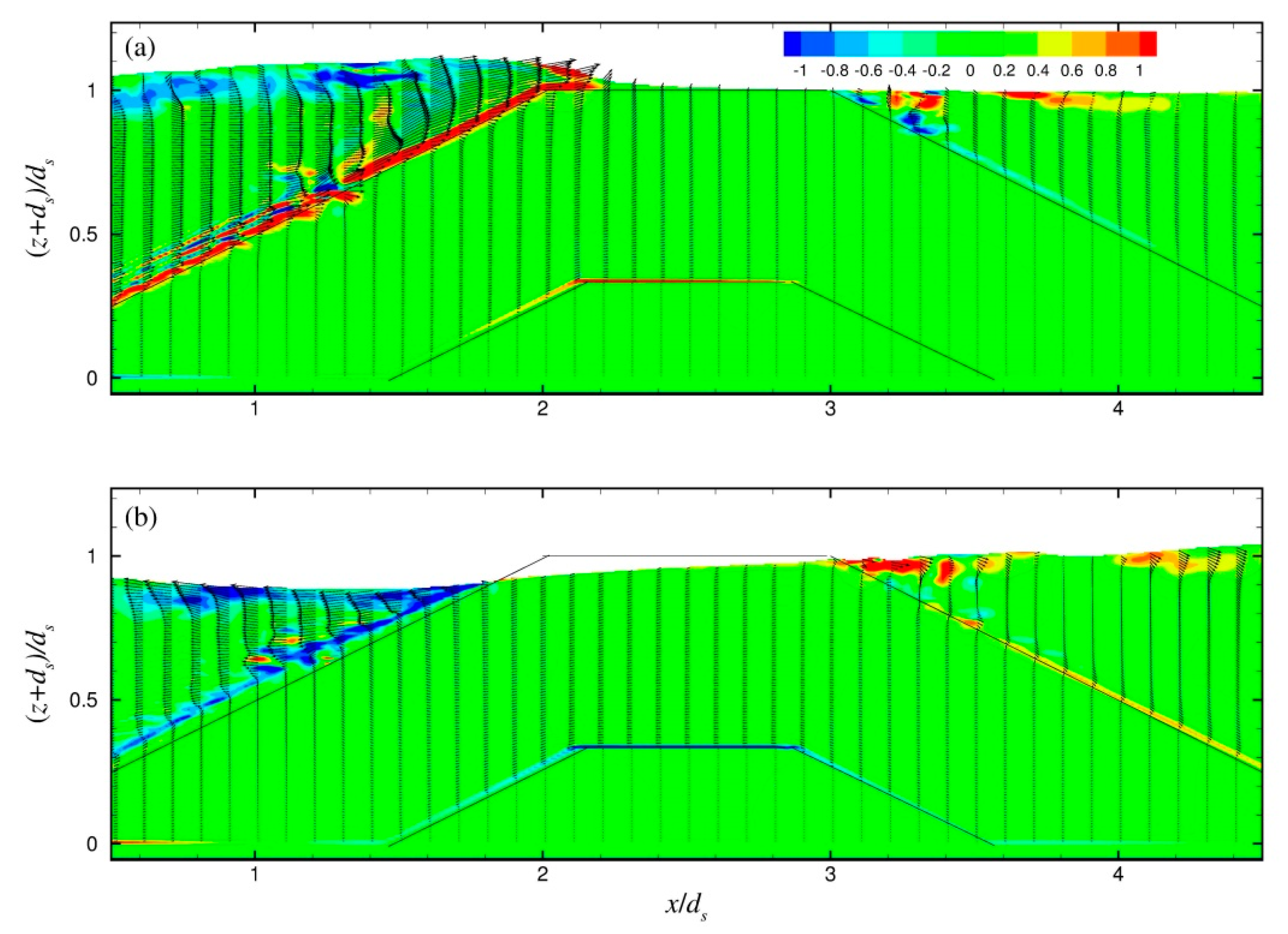
The distribution of the instantaneous vorticity field in the vicinity of the ZFB case 1, at four instants during the 30th wave period of the simulation, is presented in
Figure 7. It is shown that as the wave trough reached the breakwater crest (down-rush flow phase), strong anti-clockwise vorticity developed near above the seaward slope of the structure. As the wave propagated and the flow reversed (up-rush flow phase), this vorticity layer was separated from the slope and vortices were generated and transported offshore, while a new vorticity layer of opposite sign (clockwise) formed near above the slope. During the down-rush flow phase, there was no separation of this vorticity layer. In cases 2 and 3, there were no notable differences in the vorticity behavior above the seaward slope of the ZFBs. In case 4, with a shorter wavelength in comparison to case 1, the vorticity behavior was similar, but the offshore transportation of the vortices was extended to a shorter distance (
Figure 8). In case 5, with a less permeable ZFB trunk in comparison to case 1, the vorticity behavior near the crest was similar, while a weak vorticity layer was generated at the interface between the armor layer and the core in the ZFB trunk (
Figure 9).
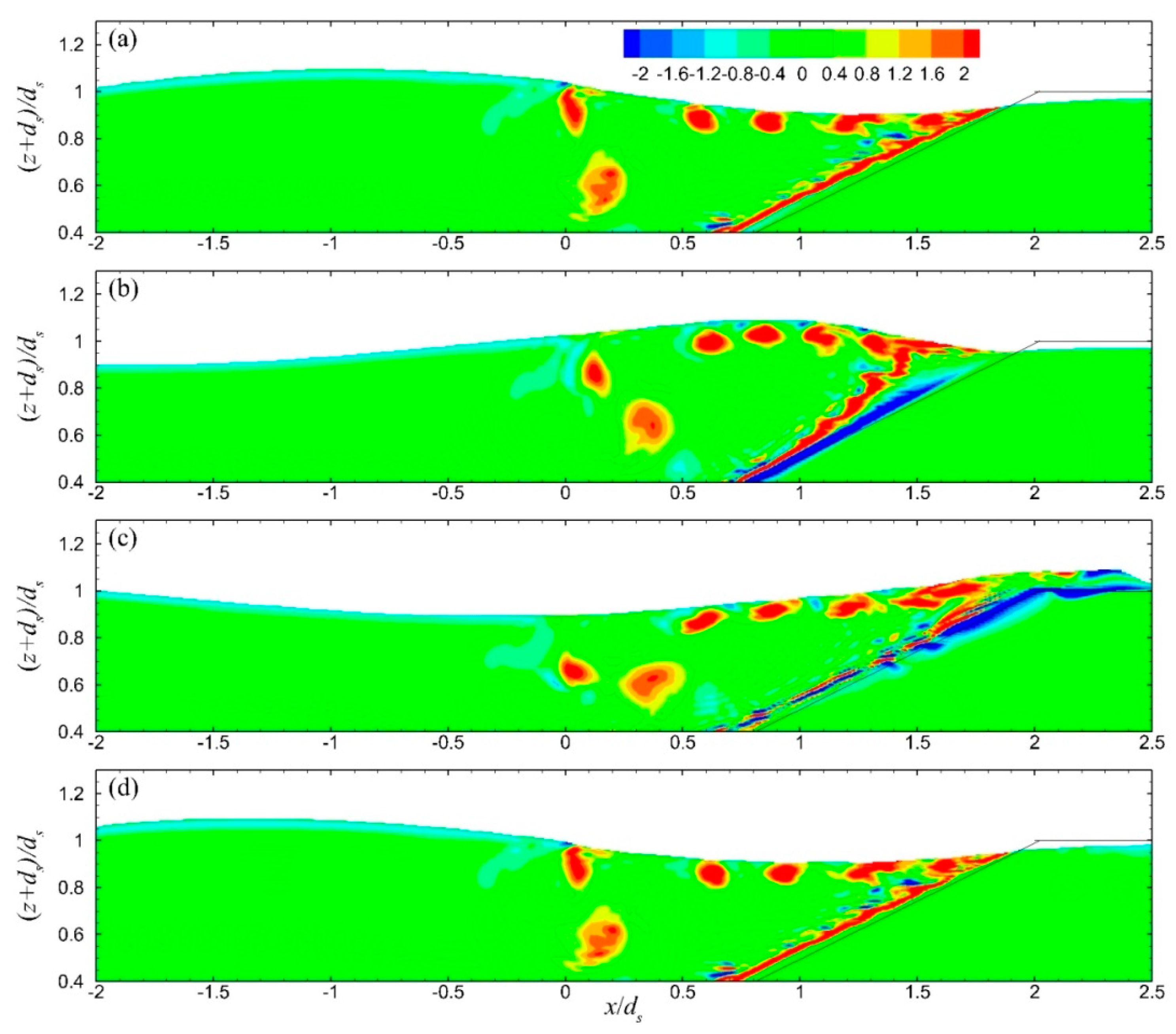
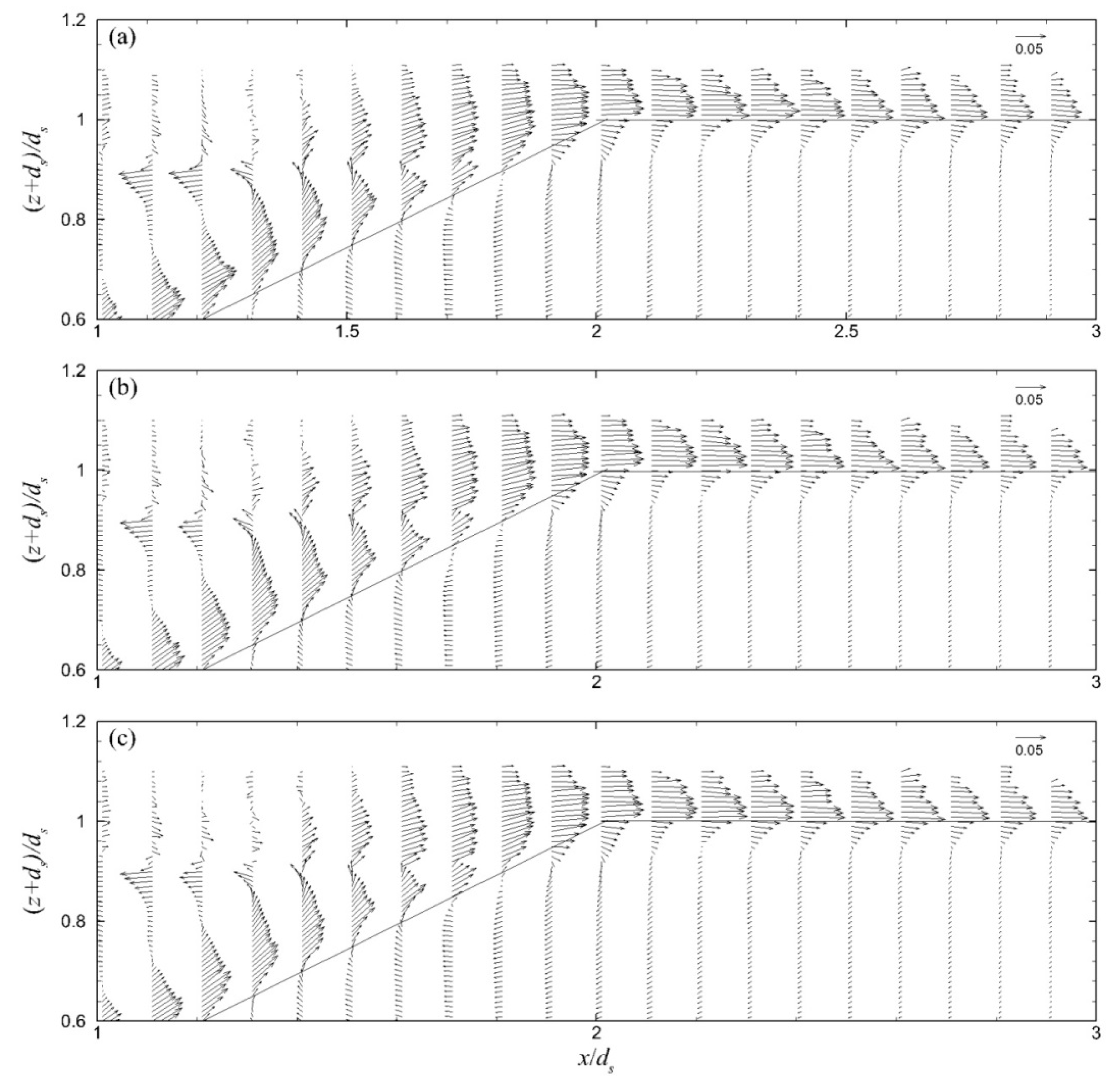
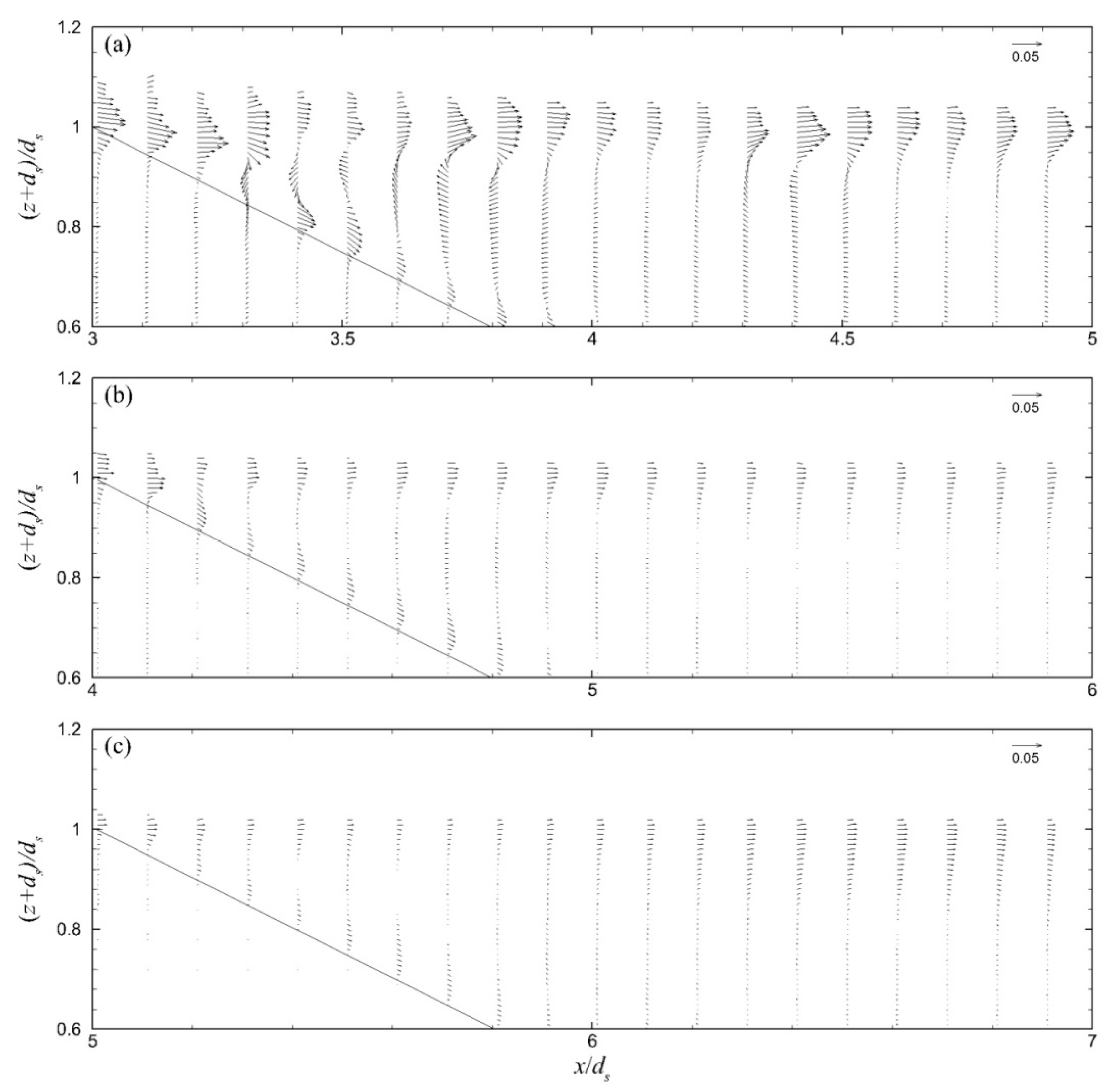
The period-mean velocity field (of 10 wave periods after 20 wave periods of simulation) in the seaward region of the ZFBs in cases 1–3 is presented in
Figure 10. It is highlighted that in these cases, the generated currents above the ZFB seaward slope and crest were directed onshore due to wave overtopping, while the currents in the ZFB trunk were weaker and directed offshore. In the leeward region of these ZFBs, the period-mean velocity field is presented in
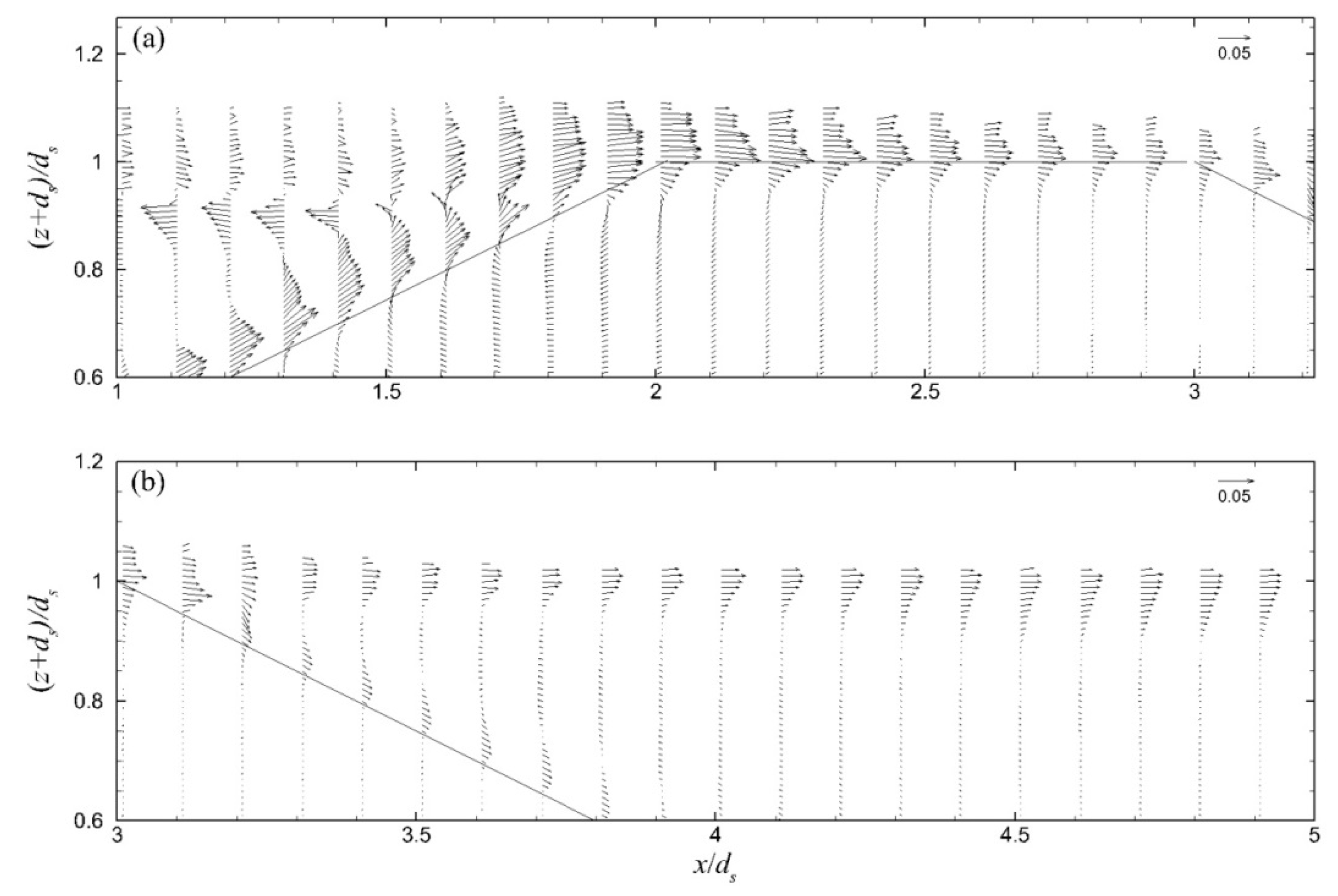
Figure 11. It is shown that as the crest width increased, the magnitude of the velocities became weaker. The period-mean velocity in the seaward and leeward regions of the ZFB case 4 is presented in
Figure 12. The direction of the currents in the seaward and leeward regions of the ZFB follows the same pattern as in case 1, but their magnitude was smaller in both regions due to the lower energy transmission onshore. The period-mean velocity field for the ZFB case 5 is presented in
Figure 13. The magnitude of the currents in the seaward and leeward regions and the ZFB trunk was slightly larger in comparison to case 1.
The period-mean flow pattern in the vicinity of the ZFBs for cases 1–3 is illustrated through streamlines in
Figure 14. It is demonstrated that in the ZFB trunk, the flow was directed offshore in all cases. Part of the flow that overtops the crest of the ZFBs returned offshore through the ZFB trunk; as a result, the water renewal was facilitated in the ZFB leeward region. This process is obvious in cases 1 and 2. Further increase of the crest width though (case 3) results in the limitation of the flow circulation cell in the ZFB trunk and the interruption of water renewal in the ZFB leeward region through the ZFB trunk. The pattern of the streamlines in ZFB case 4 does not differ from the one in case 1, and it is not shown. For the ZFB case 5 (
Figure 15), the return flow from the leeward to the seaward region through the ZFB trunk is inhibited by the presence of a less permeable core than in case 1.
The mean overtopping discharge,
q, over and through the ZFBs, and the wave setup,
δ, in the leeward region of the ZFBs are shown in
Table 3. The overtopping discharge was computed as the period-mean (of 10 wave periods after 20 wave periods of simulation) flux through the vertical cross-section at the leeward end of the ZFB crest. The instantaneous flux is:
where
dlc(
t) is the instantaneous water level at the leeward end of the ZFB crest. The mean overtopping discharge comprises the discharge through the ZFB trunk and the crest discharge over the ZFB crest. The corresponding results are also shown in
Table 3. The wave setup,
δ, was computed as the period-mean (of 10 wave periods after 20 wave periods of simulation) free-surface level over the SWL at the leeward ZFB toe.
For ZFB case 1, the trunk discharge is in the offshore direction (negative), while the one over the crest is in the onshore direction (positive). As
B increased, for ZFB cases 2 and 3, the negative trunk discharge weakened and even turned positive in case 3, while the one over the crest weakened as well but remained positive. The overall mean overtopping discharge was always onshore and it decreased, albeit weakly, with the increase of the ZFB crest width. The decrease of
ξ0 in ZFB case 4, in comparison to case 1, also resulted in the weak decrease of the mean overtopping discharge. In ZFB case 5, both the trunk discharge and the one over the crest strengthened in comparison to the ones in case 1, but the mean overtopping discharge decreased. To apply Equation (4) in the present cases, which were laboratory-scale ones since
dS = 0.4 m, an adjustment factor of
fq = 8.2 was used, which is lower than the maximum value of 11 suggested in EurOtop [
6] for tan
a = 1/2. The mean overtopping discharge predicted by Equation (4) was constant for all ZFB cases, as shown in
Table 3, reflecting the strong dependence of
q on
Hi but not the one on
B,
ξ0, and permeability as the present results suggest.
The wave setup increases with increasing
B, for ZFB cases 1 and 2, but it decreases again for ZFB case 3 despite the further increase of
B because of the interruption of the flow circulation cell in the ZFB trunk for case 3 as shown in
Figure 14c. The decrease of
ξ0 in ZFB case 4, in comparison to case 1, resulted in the decrease of the wave setup, while the decrease of permeability in ZFB case 5 increased the wave setup. The corresponding wave setup predicted by the empirical formulas of Equation (5) overestimated
δ (
Table 3) since they were both based on experiments without the recirculation system described in the Wave Generation subsection.
Finally, the instantaneous shear stress field for ZFB case 5 at two instants during the 30th wave period of the simulation is presented in
Figure 16. During the up-rush flow phase and as the wave crest approaches the breakwater crest, significant positive shear stress was observed near the seaward slope of the structure, while a positive layer was also developed in between the two different materials inside the porous media. Shear stress of opposite sign was developed in the same areas during the down rush flow phase. As expected, the seaward slope of the ZFB was the most crucial part of the structure in terms of hydraulic stability, as it experienced larger values of the developing shear stress, i.e., the destabilizing force due to wave breaking.
4. Discussion
In the present work, the effect of ZFB crest width, breaking parameter, and ZFB trunk permeability on wave reflection, crest overtopping, wave transmission, wave setup, and wave-generated currents were studied numerically.
The results indicate that the size of the crest width,
B, did not notably affect wave (reflection coefficient) and flow (instantaneous vorticity and period-mean currents) processes in the seaward region of ZFBs. However, the processes in the leeward region of ZFBs were significantly affected by
B; wave transmission and magnitude of currents decreased with increasing
B. In addition, the mean overtopping discharge heading onshore decreased, albeit weakly, with increasing
B. The effect of
B on the wave setup was not monotonic as it depended on the pattern of the flow circulation in the ZFB trunk, but eventually this also decreased with increasing
B. The effect of the breaking parameter,
ξ0, and the ZFB trunk permeability on wave and flow processes were significant both in the seaward and leeward regions of ZFBs. As
ξ0 decreased, the wave reflection, wave transmission, magnitude of currents, mean overtopping discharge, and wave setup all decreased; this observation is in accordance with the relevant empirical formulas (
Table 2 and
Table 3) considered in this study. Finally, decreasing the ZFB trunk permeability led to the increase of wave reflection, the magnitude of currents, and wave setup, but to the decrease of wave transmission and mean overtopping discharge.
Therefore, for the design of ZFBs, decreasing trunk permeability is equivalent to increasing crest width in terms of the wave and hydrodynamic processes in the leeward region of ZFBs as far as wave transmission and mean overtopping discharge are concerned, but not equivalent for wave setup and magnitude of currents. If the latter parameters are not critical, decreasing the ZFB trunk permeability is a more economical option compared to the increase of crest width.