Abstract
Between external position updates, the most useful technique for trajectory estimation of a submerged drifter is dead reckoning (DR). These devices drift with the water current to measure the current’s velocity or to observe physical phenomena. We focus on the specific but important case of when the drifter, due to its size and shape, experiences acceleration by the water current, an effect that must be taken into account during the DR. The force induced by the water current over the drifter is translated into a shift in the heading direction, thus creating a horizontal (sideslip) and a vertical (angle of attack) directional angles between the drifter’s moving direction and its body frame. In this paper, we extend and modify techniques used for pedestrian DR and propose PCA-DR: a principle component analysis-based DR algorithm to estimate the directional angles. Used for cases where the water current is significant such that its force induces acceleration over the drifter and used only for short time periods of a few seconds between navigation fixes, PCA-DR uses acceleration measurements only and does not assume knowledge of the drifter’s dynamics. Instead, as part of the DR process, PCA-DR estimates the directional angles induced by the water current. Compared to the traditional DR approach, our results demonstrate good navigation performance. A designated sea experiment demonstrates the applicability of PCA-DR in a realistic sea environment.
1. Introduction
Subsea drifters (drift with the water current) are used for a variety of applications, including the gathering of scientific data and climate monitoring, to name a few [1,2]. In all applications, the device has no positioning aided solutions while being submerged, so the navigation system is critical, enabling the user to infer the drifter’s measurements with its geographic location. The role of the navigation system is to determine the position, velocity, and attitude of the device while being submerged and while drifting or maneuvering. We consider freely drifting devices that are not connected to, e.g., a surface buoy. Due to the water conductivity, GPS signals are not received by these drifters, so GPS positioning is not available. In such situations, the main underwater navigation techniques fall into one of the following three categories [3]:
- Inertial Navigation Systems (INSs): An INS uses accelerometers and gyroscopes and requires initial conditions to calculate the device state through dead reckoning (DR). Although the full state can be determined by the INS, it suffers from an inherent drift. This is because the INS-measured quantities contain noises and biases that are integrated to obtain the device state [4]. Therefore, INSs are usually fused with external sensors [5] or information about the environment [6,7] to compensate for this drift.
- Acoustic Localization: Acoustic localization provides the navigation system with position fixes by measuring the device’s range to nodes of known positions, referred to as anchors. Acoustic ranging is based on measuring the time-of-flight (TOF), the time-difference-of-flight (TDOF), or the signal strength of an acoustic signal from the anchor to the submerged device. Ranging can be carried out passively or actively, but in either case requires the existence of at least one anchor in the acoustic range [8,9].
- Geophysical Navigation: In geophysical navigation, features from the environment are used as navigation reference points, usually employing cameras [10] or different types of sonar [11] for terrain-based tracking [12] or simultaneous localization and mapping [13].
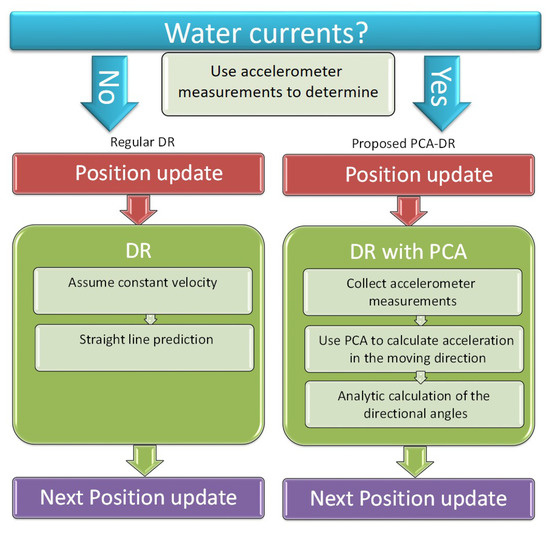
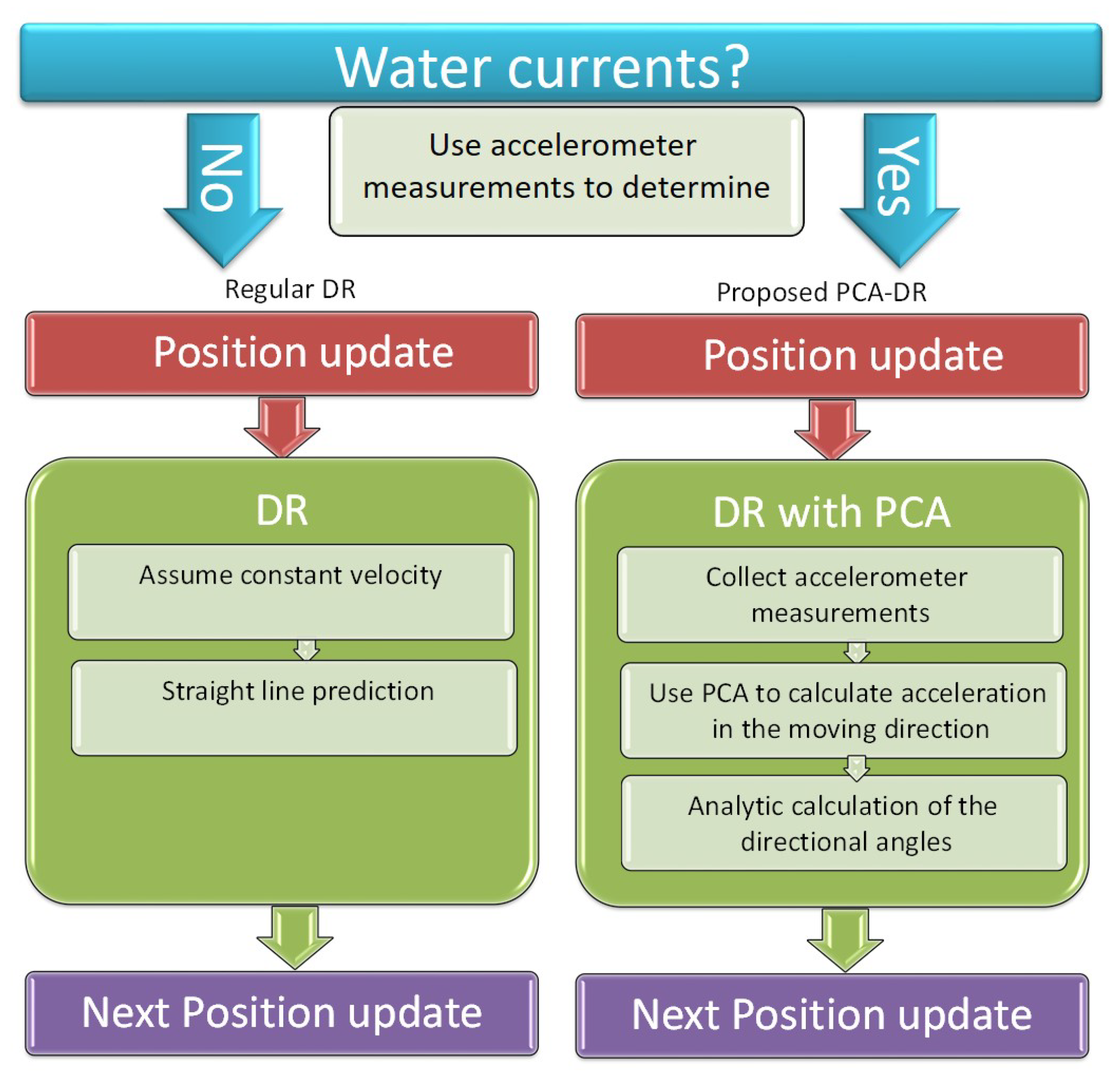
In addition, underwater navigation is often performed by means of sensor fusion. For example, frameworks for the navigation of autonomous underwater vehicles (AUVs) based on, e.g., an extended Kalman filter or an Unscented Kalman filter combine data from inertial measurements, acoustic beacons, Doppler velocity loggers, and others, and obtain high performance. Yet, multimodal navigation aid sensors are often scarce in low-cost systems such as drifters. Out of the three categories, the INS is the most popular since it does not require specific knowledge of the environment or uses external sources of information. Consequently, the context of this work is a DR navigation of a subsea drifter using only the device’s self-measured accelerometers. In this context, a DR approach for the self-navigation of submerged drifting nodes is a cost-effective solution with several advantages. First, it is a standalone system that uses only an inertial navigation unit and does not require any information/transmissions from external sources. Second, different from filtering techniques, DR does not require information about the mobility pattern of the tracked device or on the hydrodynamics of the device. As such, DR is a cost-effective robust navigation solution that best fits low-cost systems such as submerged drifters. Moreover, DR navigation is needed for short time periods between external position updates such as long baseline systems (LBLs) or from global navigation satellite systems (GNSSs). Trajectory estimation using DR does not require the modeling of the drifter’s dynamics, nor does it require a prior assumption about the motion type of the drifter. Instead, it updates the dynamic state on the fly based on the INS measurements.
1.1. Scope of Work
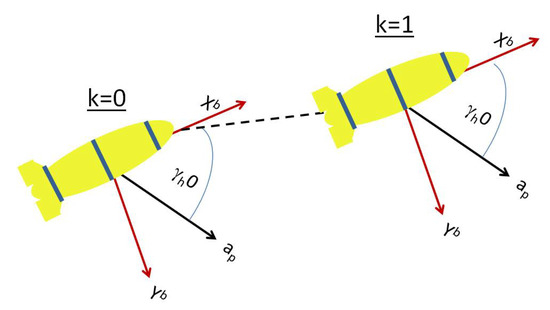
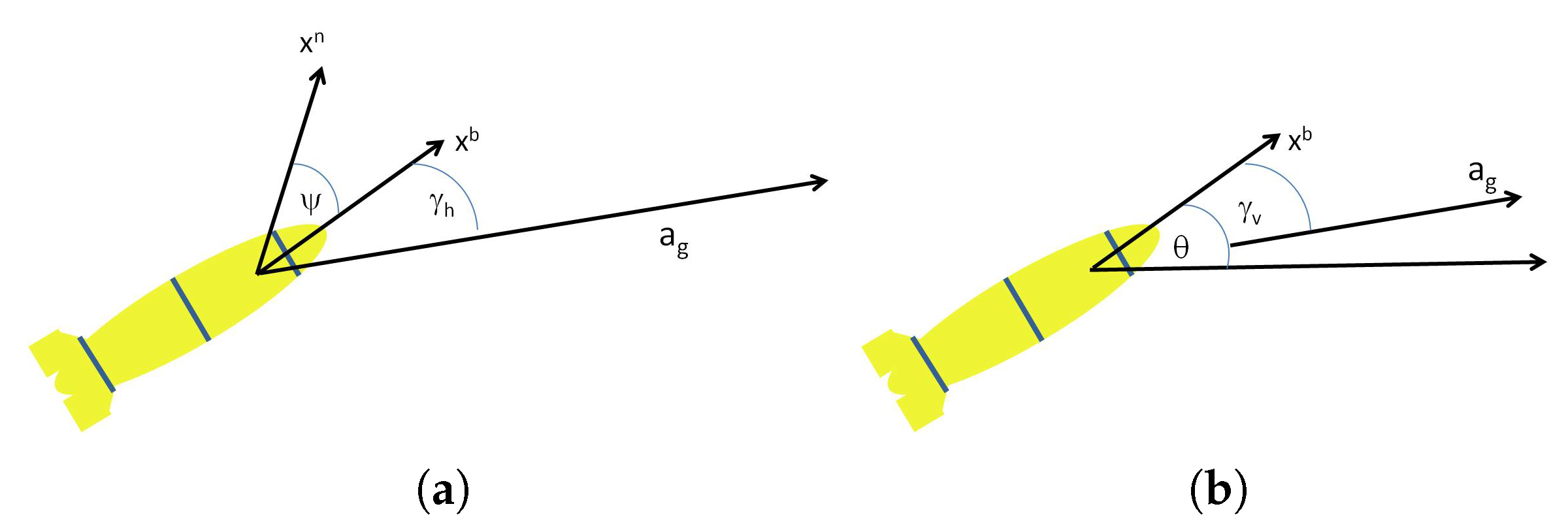
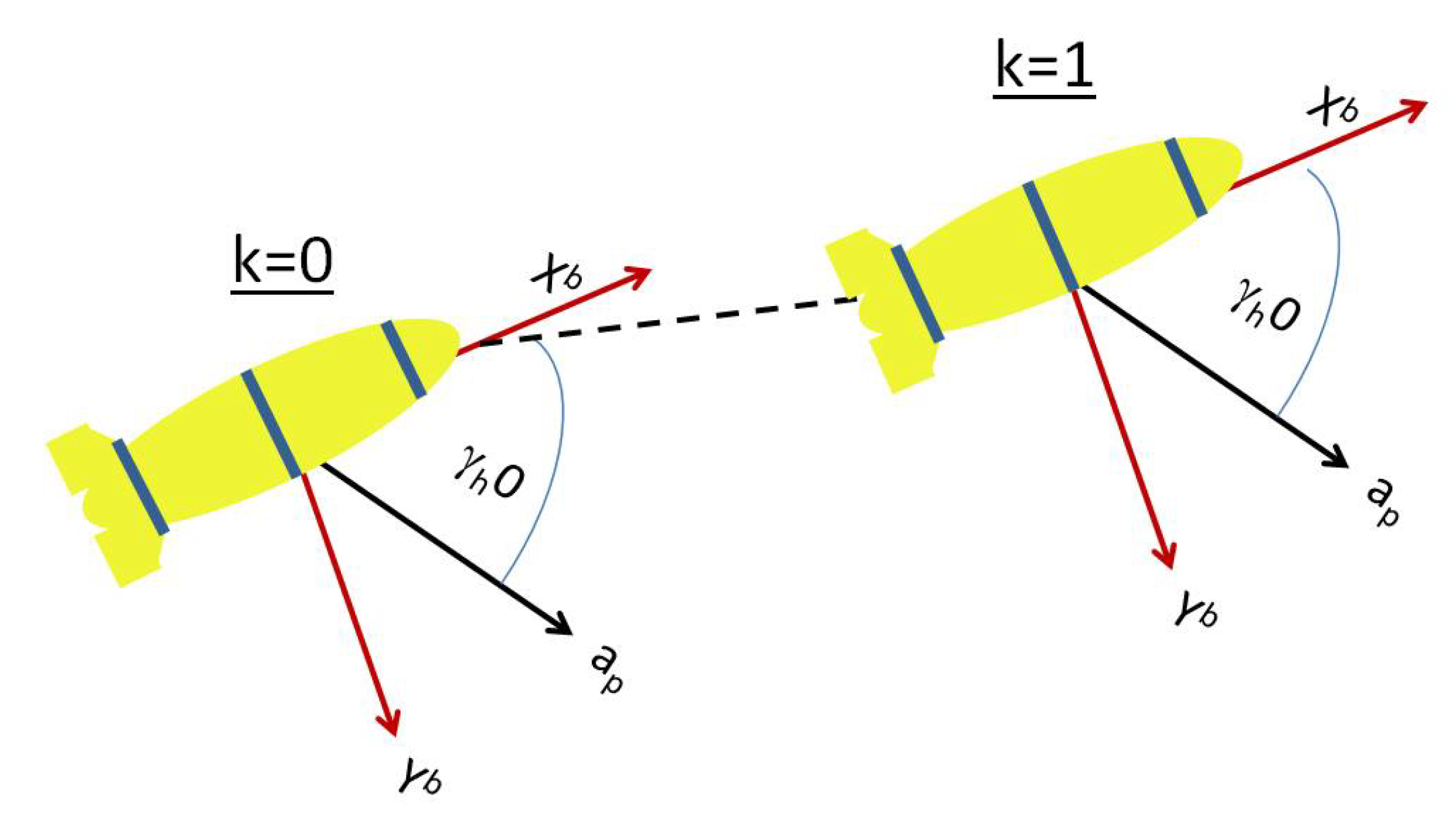
DR assumes that the underwater platform nominally follows a dynamic model between two successive position updates; yet, as a result of water currents, in practice, the device is subject to an unknown moving direction, whose estimation is crucial to the success of the DR process. Since the drifter’s motion is affected only by the motion of the water current, which, due to the non-negligible size and shape of the drifter, is an acceleration-driving force [14], this uncertainty in the moving direction occurs when the induced force operates at certain horizontal and vertical angles with respect to the body frame of the drifter. As illustrated in Figure 1a,b, the angles considered are and . We refer to these angles as the directional angles, and consider the case where directional angles are formed by the water current.
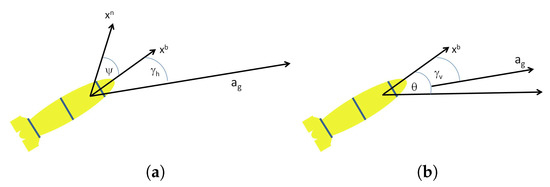
Figure 1.
Illustration of the acceleration triangle experienced by a subsea device. The force induced by the water current over the drifter is translated into a shift in the heading direction, thus creating an horizontal and/or vertical directional angles between the drifter’s moving direction and its body frame. (a) Horizontal plane; (b) vertical plane.
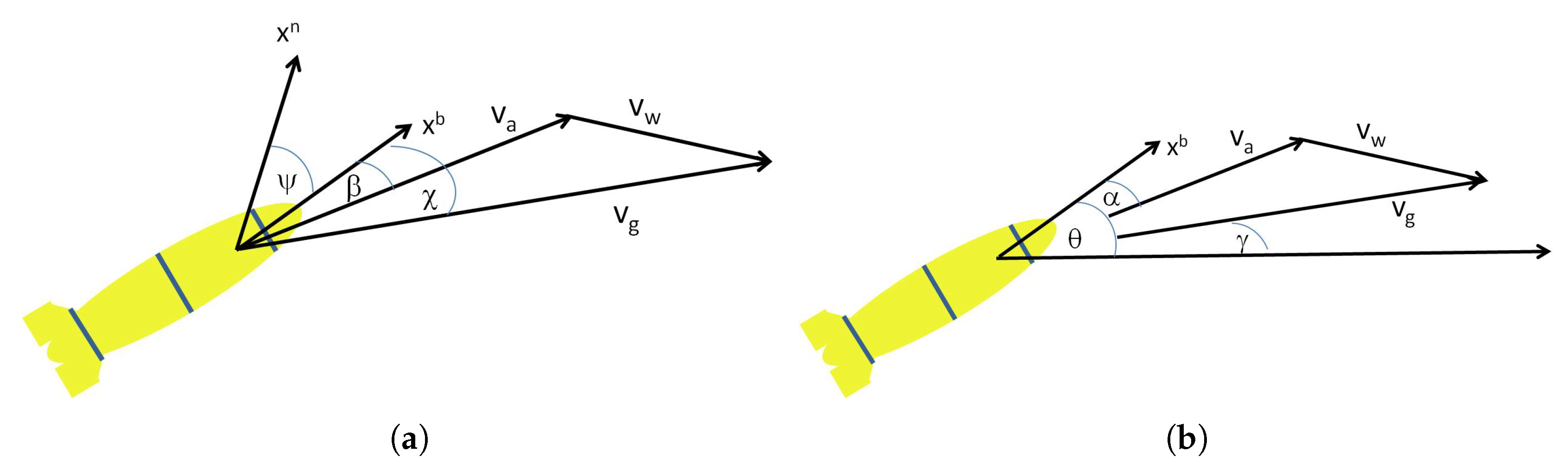
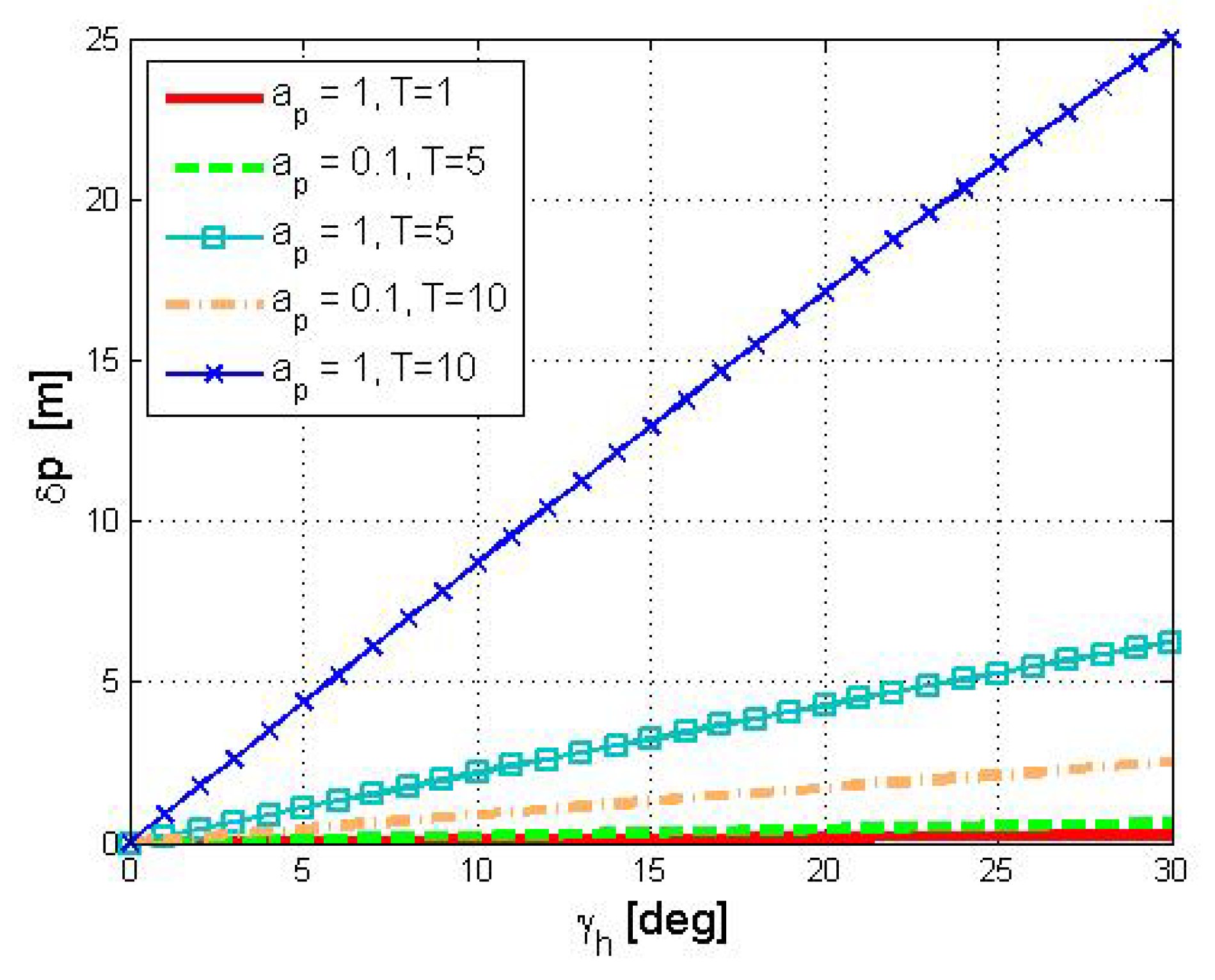
Performing DR directly on the acceleration measurements without compensating for the directional angles would result in large errors. This is evident by the velocity triangle illustrated in Figure 2a,b. In the horizontal plane, the directional angles result in a sideslip angle, denoted by in Figure 2a, which is the angle between the drifter’s horizontal velocity with respect to the water and its horizontal velocity in the body frame. In the vertical plane, the directional angles render an angle of attack, denoted by in Figure 2b, which is the angle between the drifter’s vertical velocity with respect to the water and its vertical velocity in the body frame. The result of the existence of both a sideslip angle and an angle of attack is a shift in the drifter’s moving direction, which must be compensated for in the DR process. More specifically, since both the horizontal and vertical directional angles affect the acceleration measurements that are measured in the body frame, without estimating the current’s acceleration, , or the values of and from Figure 1a,b, respectively, DR is not possible. To further support this claim, in Figure 3, we show the results of the DR position error as a function of the directional angle on the horizontal plane, , when this angle is not compensated (results are obtained using the simulation setup reported in Section 5). As expected, the results show that DR performance greatly deteriorates with the increase of . Besides the need to estimate the directional angles for DR navigation, evaluating their value has the practical implementation of path planning in case the drifter can control its depth (e.g., [2]).
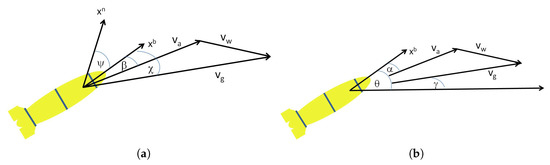
Figure 2.
Illustration of the projected velocity triangle. (a) Horizontal plane; (b) vertical plane.
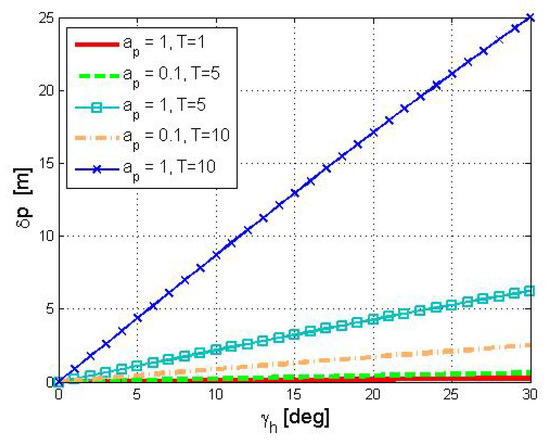
Figure 3.
Dead reckoning (DR) position error when the horizontal directional angle is not compensated.
The effect of the directional angles on the drifter’s motion is very similar to the effect an aircraft experiences, due to the wind factor. However, unlike in aircrafts, where the wind speed and direction can be measured directly using the pitot tube [15], direct measurement of the water current is challenging and is generally performed by maneuvering. This, of course, is not possible in the case of drifters. Traditionally, the sideslip angle can be estimated by gyroscopes, by magnetometers, or by GNSSs, as will be elaborated in Section 2.2. Yet, while the drifter is submerged, the GNSS is not available, and the magnetometer measurements are subject to varying interferences from the surrounding environment. Additionally, high precision gyroscopes are very expensive, and simple submerged floaters use low grade gyroscopes whose noise cannot be filtered easily, due to the rapidly changing marine environment that include thermoclines and turbulances. As a result, it is challenging to accurately measure the directional angles. Considering the problem of obtaining cost-effective gyroscopes and magnetometers, we propose a method that estimates the directional angles between two successive position updates based only on acceleration measurements and performs DR based on this type of estimation. Our method becomes effective for drifters with low-to-moderate gyroscope sensors in the common scenario when the device’s motion is set by the water currents. Our work is limited to the cases where an acceleration force operates on submerged drifters, such that DR can be performed.
1.2. Contribution
Our contribution is in the trajectory estimate for submerged drifters between two known locations, while taking into account the effect of the water current on the drifter’s velocity. Due to the limitation of the acceleration-only DR approach, the time period considered for performing the DR is on the order of a few seconds. This is applicable in cases where periodic location fixes are received. For example, the work in [2] presents an application for a flock of submerged drifters aiming to estimate ocean currents and to track migration patterns of biofauna. These drifters include an acoustic recorder to receive signals from a set of on-surface anchored acoustic beacons. These beacons generate periodic acoustic emissions every few seconds such that, using long baseline acoustic positioning, the drifters can be localized offline. Between such acoustic-based fixes, there is a need to estimate the trajectory of the drifters.
Our approach does not require the estimation or prediction of the water current, nor does it need the information of the drifter’s dimensions, thereby achieving robustness to the shape of the drifter in use and to the sea conditions. We offer this capability based on low-cost accelerometers only, which is important since long deployment drifters do not allow for the insertion of energy-hungry and expensive instruments such as acoustic Doppler current profiling (ADCP). Consequently, when the water current is substantial, to the best of our knowledge, ours is the only approach that allows subsea positioning for drifters.
Our method, referred to as PCA-DR, makes use of the principle component analysis (PCA) method to estimate the moving direction of the drifter. Once the moving direction is determined, we derive the DR algorithm and its closed form expressions to evaluate its performance as a function of the involved parameters. PCA-DR is inspired by the successful application of DR-based pedestrian navigation in [16], where PCA is used to estimate the walking direction regardless of the smartphone direction. Yet, while most of the time a pedestrian is moving horizontally and thus only the horizontal angle needs to be determined, an underwater platform can also move in a vertical direction. Hence, the vertical directional angle should also be considered to determine the moving direction. Moreover, while pedestrian navigation can be aided by reference points at times when the foot touches the ground and the velocity is zero, the motion of a submerged floater is continuous. Considering these challenges, we derive a modification to the PCA approach, which enables the estimation of the angles affecting the submerged device’s moving direction based on accelerometer readings. When the platform applies no acceleration but undergoes accelerations due to water currents, the proposed approach can also estimate the angles between the moving direction of the platform and its x-axis in the body frame. Like all DR approaches, PCA-DR is limited to short time intervals, usually on the order of a few seconds, before the navigation solution drifts. However, different from common DR, PCA-DR also provides a navigation solution in the presence of a water current’s force. This also means that PCA-DR is applicable only in the presence of an observable acceleration-induced force over the submerged drifter.
While both DR and PCA are well explored techniques, ours is the first method to combine the two for the task of location-tracking drifters in the presence of a water current. For drifters, the effect of the water current has not been explored, although, as we show in our analysis, navigation fails if this effect is neglected. Moreover, while previous approaches have used PCA and DR sequentially, ours is the first work to use PCA as part of the DR process. The result is an iterative estimation of water-current-induced directional angles. This task is performed using only acceleration measurements. This is mostly appealing for drifters whose cost and energy limitations are substantial and thus cannot support maneuvering or Doppler shift measurements.
Our list of contributions is threefold:
- a compensation for the directional angles when DR navigation is required;
- the estimation of directional angles using acceleration measurements only for short time periods of a few seconds between two successive position updates;
- a simplified DR approach for submerged floaters under the effect of directional angles for online/offline trajectory estimation.
We evaluate the performance of the proposed approach in the presence of a water current in both numerical and experimental investigations including a drifting buoy with a self-made INS. The results show a great improvement over benchmark DR solutions.
The remainder of this paper is organized as follows: In Section 2, we describe current approaches for sideslip angle estimation and for transformation, to coordinate between the navigation frames used in the paper. In Section 3, our proposed approach for estimating directional angles is described, and in Section 4 the DR algorithm and its derivations are presented. Section 5 shows the analysis and numerical and experimental results. Conclusions are presented in Section 6.
2. Preliminaries
Different from filtering-based navigation techniques that require modeling of the dynamics of the submerged platform, DR does not follow a specific model. As a result, DR is robust to the navigating platform and does not require knowledge of its hydro-dynamic profile. For this reason, DR is accepted as the most practical solution for subsea navigation. In basic terms, DR is the process whereby the current position of a tracked platform is calculated based on its last known position. With no dynamic model to follow, the tracking is based on measurements of speed and direction. One of the most common implementations of DR is inertial navigation. Here, inertial sensors (accelerometers and gyroscopes) provide measurements of rotational and translational motion of the tracked platform, and additional information in the form of external sensors or movement type can be added (see our analysis in [17]). Our PCA-DR is a DR process that takes into account the effect of the water current. In PCA-DR, we consider DR between two successive position measurements using only accelerometers.
In the following, we describe current works for pedestrian navigation using the PCA method, and briefly review two related subjects used in the derivation of the methodology presented herein: (1) the transformation of coordinate frames, and (2) principle component analysis. We then present our system’s model.
2.1. Approaches for Underwater Dead Reckoning
While the challenge of geo-locating a drifter is not fully addressed, a large body of literature offers solutions for the location tracking of autonomous underwater vehicles (AUVs). In [18], a few filtering approaches are compared for the location estimate of an AUV. The methods assume a motion model whose parameters are updated by filtering techniques, and the work in [19] uses the motion model to identify faulty sensory information. Considering the challenge in determining a motion model, the methods in [20,21] use unconventional filtering techniques with the aim of being robust to various dynamics and noise distribution types. Instead, the works in [22,23,24] use the known dimensions of the AUV to form a hydrodynamic model, which, in turn is used in the filtering scheme to obtain a better dynamic model. Results from sea experiments show good performance. However, we suspect these are performed in low water currents, as almost no consideration is given to the water current that introduces an external force, and can significantly affect small devices such as drifters.
While in PCA-DR we do not assume knowledge of the water current, some approaches have been suggested to compensate for a given or directly measured water current. The work in [25] takes into account the water current along the water column during the DR operation. The solution offered directly measures the water current using a Doppler velocity logger or an acoustic Doppler current profiler positioned on an AUV, and integrates this data in the filtering scheme. However, such systems are energy- and cost-expensive and may not fit the case of low-cost drifters such as Argo floats, cf. [1]. External forces are also considered in [26], where a full-scaled inertial measurement unit is employed to combine acceleration measurements, gyrocompasses, and magnetometers in a filtering scheme. Experiments show results when an external magnetic force is present. Yet, here too, a motion model is employed, and directional angles induced by the water current are ignored. The need for data about the water current is acknowledged in [27], where a group of AUVs cooperates by sharing information about mismatches found from a water current forecast. Similarly, in [28], we tracked the location of a submerged node also using drifting information from nearby beacons. However, the success of these approaches largely depends on the spatial stability of the water current, and requires prior knowledge of the environment, e.g., bathymetry, temperature, and tied fluctuations, which are often hard to obtain.
2.2. Common Approaches for Sideslip Angle Estimation
For land vehicles, the sideslip angle must be evaluated to guarantee the vehicle’s stability. Considering the problematic fact that the drifter’s sideslip angle cannot be measured directly, several approaches have been suggested to estimate the sideslip angle [29] or, equivalently, to evaluate the lateral velocity [30,31]. These approaches rely on modeling the device’s dynamics, and require measurements from sensors such as gyroscopes, accelerometers, magnetometers and GPS. Similar to underwater navigation, in the pedestrian navigation context, obtaining such measurements requires high-precision and expensive sensors. Therefore, different approaches have been suggested for the same problem of estimating the walking direction.
We find that the most promising methods for estimating directional angles are the PCA method [16,32], Forward and Lateral Accelerations modeling (FLAM) [33], and the Frequency analysis of Inertial Signals (FIS), as indicated in [34]. The PCA approach is further elaborated in Section 2.4; however, we emphasize here that the PCA approach requires only accelerometer data and thus is most suitable for underwater navigation, which bears a low cost and is short on energy and on accurate sensors. In FLAM, the approach models the forward and lateral accelerations by the sum of sinusoids. The angle pointing towards the heading direction is found to be the one that maximizes the correlation of the estimated acceleration and the pre-determined model. As in the PCA approach, only accelerometer data are required from the sensors, but, in addition, walking pattern modeling is also needed. This may result in model mismatch for underwater maneuvering, which is affected by non-linear complex phenomena such as water currents, turbulence, and sea waves. In the FIS approach, both accelerometer and gyroscope outputs are used. The main idea is to find the direction that maximizes the spectral density of the accelerometer and gyroscope signals’ energy for the step/stride frequency [35,36].
The sideslip angle estimation for underwater navigation is thus far handled in the context of path-following controller design [37]. In this case, the sideslip angle is treated as an unknown, small, and constant parameter during straight line paths. The switching between the segments appears as steps in the parameter update law. For vehicles traversing a non-circular path, the method utilizes the fact that the sideslip angle varies much more slowly than the control bandwidth to estimate the varying sideslip using a nonlinear adaptation law. Other works use a zero sideslip angle assumption supported by sea experiments to carry out controller design analysis [38] or parameter identification for a nonlinear simulation [39]. However, as we show in our analysis, neglecting the sideslip and the directional angles may result in large navigation errors.
2.3. Coordinate Frames and Transformations
To manage directional angle estimations, we need to coordinate the body reference frame (b-frame) with the stability frame (s-frame) and the current reference frame (c-frame). While the acceleration measurements are given in the b-frame, for navigation purposes they should be translated onto the s-frame. This transformation should take into account the effect of the water current, which resides in the c-frame. Referring to Figure 2a,b, the b-frame is the drifter’s fixed coordinate system. The origin of the coordinates is located at a convenient position in relation to the device, usually the center of buoyancy. The axis points towards the front of the drifter, the axis points towards the right of the drifter (starboard), and the axis completes the right-handed orthogonal frame pointing to the bottom (the keel). The s-frame is fixed to the drifter at the same origin as the b-frame. The axis points along the speed vector projection onto the - plane, the axis coincides with the axis, and the axis completes the right-handed coordinate system. The c-frame, like the b-frame and s-frame, has its origin fixed. The axis is aligned with the current’s speed vector, coincides with , and completes the right-handed coordinate system.
To transfer between these three coordinate frames, we use two angles: the angle of attack, denoted by , and the sideslip angle, denoted by . The angle of attack is shown in the vertical plane (Figure 2b), together with the pitch angle . The sideslip angle is shown in the horizontal plane (Figure 2a) with the heading angle, . The angle of attack is defined as being positive for a right-handed rotation from the stability frame’s axis to the body frame’s axis. Hence, a left-handed rotation is needed for the transformation between the b- and s-frames such that
The sideslip angle is the angle between the water current speed vector and the - plane. The sideslip is used to define the transformation between the s- and w-frames through
Finally, the transformation between the b-frame and the c-frame is obtained by multiplying matrix from Equation (1) with matrix from Equation (2). Denoting and , this multiplication yields the transformation
The inertial forces experienced by the underwater platform are dependent on the velocities and accelerations, relative to the inertial frame. On the contrary, the hydrodynamic forces depend on the velocity of the frame, relative to the surrounding water. When a water current is not present, these velocities coincide. However, this is not the case in the presence of a water current. Particularly with small platforms, such as drifters, the speed difference may be significant. Considering this difference, we distinguish between the current speed, represented by the velocity with respect to the surrounding water,, and the ground speed, , represented by the velocity with respect to the inertial frame. The velocity triangle is given by
where is the velocity of the water current. The velocity triangle in Equation (4), projected into both vertical and horizontal planes, is presented in Figure 2a,b.
The connection between the velocity vector expressed in the b-frame and the velocity vector expressed in the c-frame is , or
From Equation (5), we can express the angle of attack with the body velocity vector components as
as well as the sideslip angle with both the body and water current velocity components,
2.4. Principle Component Analysis (PCA)
The method of PCA is mostly used to dilute the number of dimensions within a given set of observations while still maintaining most of the information. The dimension reduction is possible if the rank of the observations’ covariance matrix can be reduced. Geometrically, the PCA rotates the axis of the original coordinate system into a new orthogonal axes, such that the new axes correspond to the direction of maximal variability of the observations. This is performed statistically by an orthogonal transformation to convert a set of observations of possibly correlated variables (which hence can be diluted) onto a set of linearly uncorrelated variables called principal components. This transformation is defined in such a way that the first principal component has the largest possible variance and that each succeeding component, in turn, has the highest variance possible, under the constraint that it is orthogonal to the preceding components. The resulting vectors form a set of uncorrelated orthogonal bases. In other words, the principal components are eigenvectors of the symmetric covariance matrix, and are thus orthogonal.
Applying the PCA to the accelerometer outputs from the inertial measurement unit, we find the acceleration in the moving direction, thereby estimating the vertical directional angle. We perform PCA through eigenvalue decomposition of a data covariance as follows. Let be a matrix consisting of acceleration measurements for a defined time span , such that each row i, , of is the measured acceleration vector at the ith time epoch. The covariance of is defined by
Given the data covariance, the corresponding eigenvectors, , can be calculated from the eigenvalue problem
where each column is an eigenvector of . Finally, the PCA matrix is obtained by projecting using such that
5. Analysis and Results
In this section, we report results from numerical and field work performance investigation. In all cases, due to the limitation of DR to perform navigation over long periods of time, we consider only short time intervals of a few seconds from the last navigation update. Further, since the water current on the vertical axis is usually weak (accept in the rare cases of being affected by an internal wave or in areas where hot water is cooling down) and since our PCA-DR approach is suitable for cases of significant water currents, in our investigation we consider the private case of a water current acting on the submerged platform in the horizontal plane such that while is non-zero.
5.1. Numerical Investigation
We now show a simulative investigation of the performance of PCA-DR. We employ a 1000 Monte-Carlo runs in which is uniformly randomized over a range of . Unless mentioned otherwise, in each simulation, , , and are estimated over a navigation period of during which 50 acceleration measurements are obtained. The acceleration noise for the three dimensions, , is randomized according to a zero-mean i.i.d. Gaussian distribution with a fixed variance, , that is characteristic of the inertial sensor. The roll and pitch angles are assumed known and constant throughout the DR period, so the gravity vector can be expressed in the body frame. For this case, we use Equation (18) for the calculation of . According to the procedure described in Section 3, using the acceleration matrix , is calculated based on Equations (8)–(10).
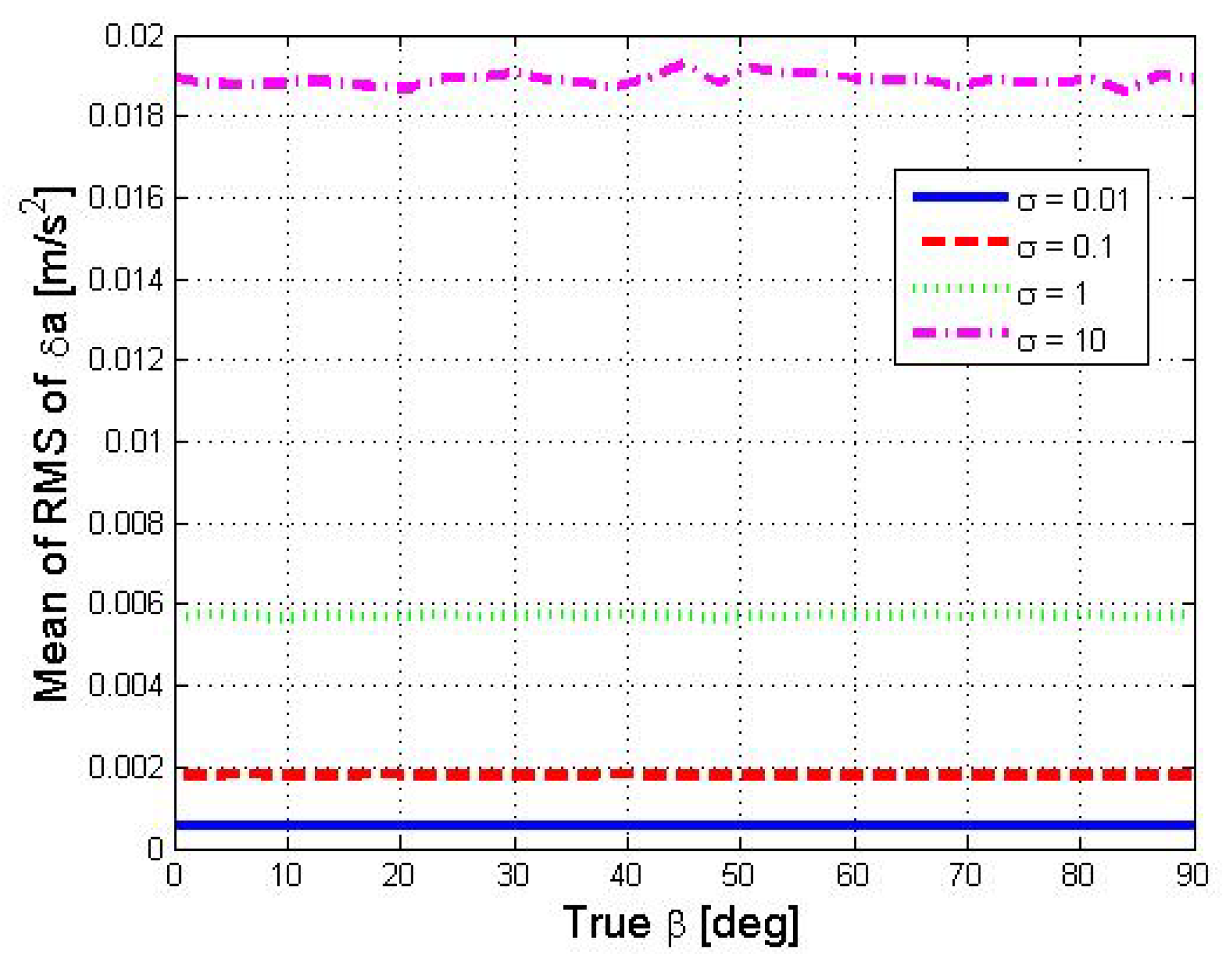
The performance of estimating is given in Figure 6, where we show the average of the RMS of the estimation error at each time step for a given value with perfect initial conditions, i.e., . As expected, we observe that does not depend on . That is, for a , the projection of the acceleration measurements in the body frame, only the stability-frame is error free.
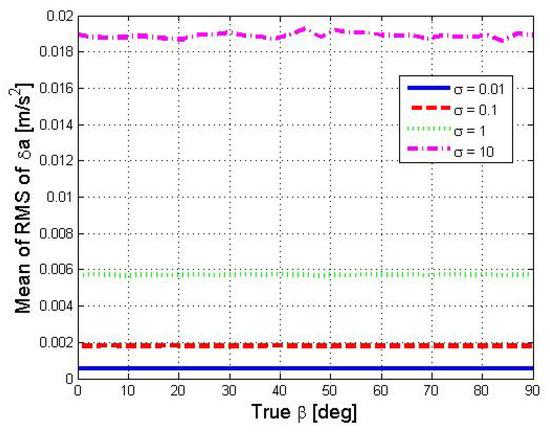
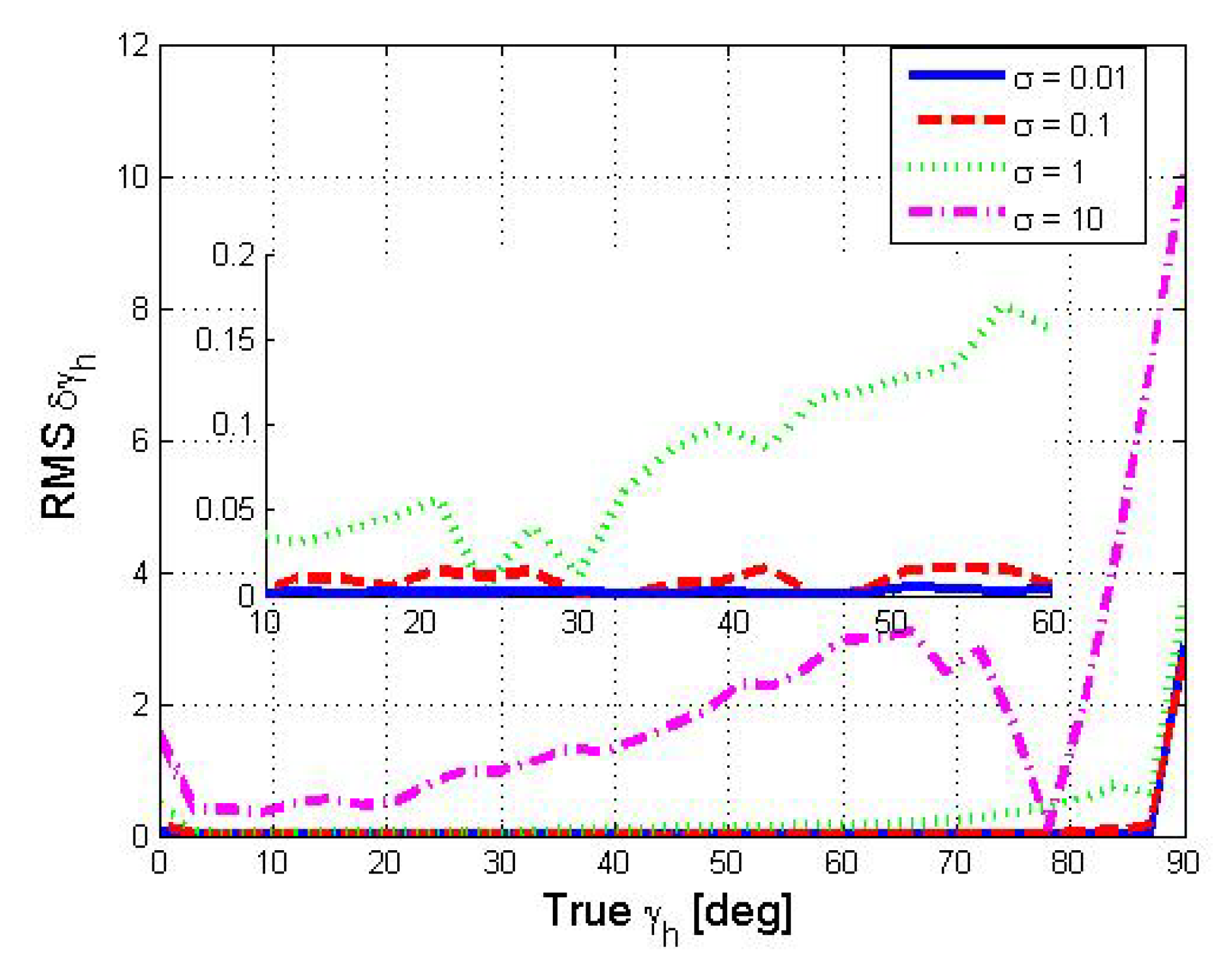
Figure 6.
Average of the RMS of as a function of . Curves represent different accelerometers’ noise variance in units of . The inner plot zooms in an area of interest in the figure.
In Figure 7, we show the error in estimating the directional angle using Equation (18). Here, we assume . We observe that, while does not depend on , for large values of the noise variance , error does change with . This is because the estimation of in Equation (18) depends not only on the acceleration measurements, but also on . Nevertheless, for reasonable values [40], the change of with is not significant, and an error of less than is observed for up to degrees. To comment on the impact of the navigation period on performance, in Figure 8, we change to obtain 150 acceleration measurements and show the error as a function of . An improvement of more than for most values of is observed.
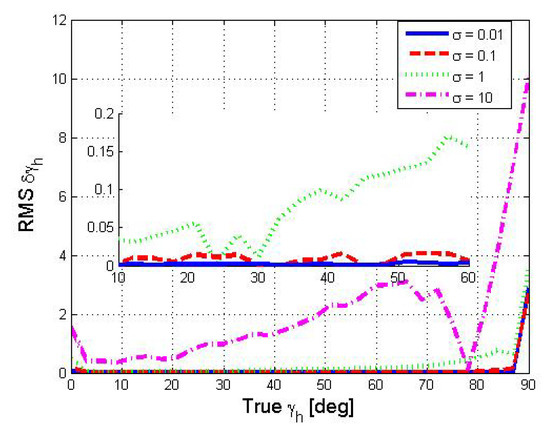
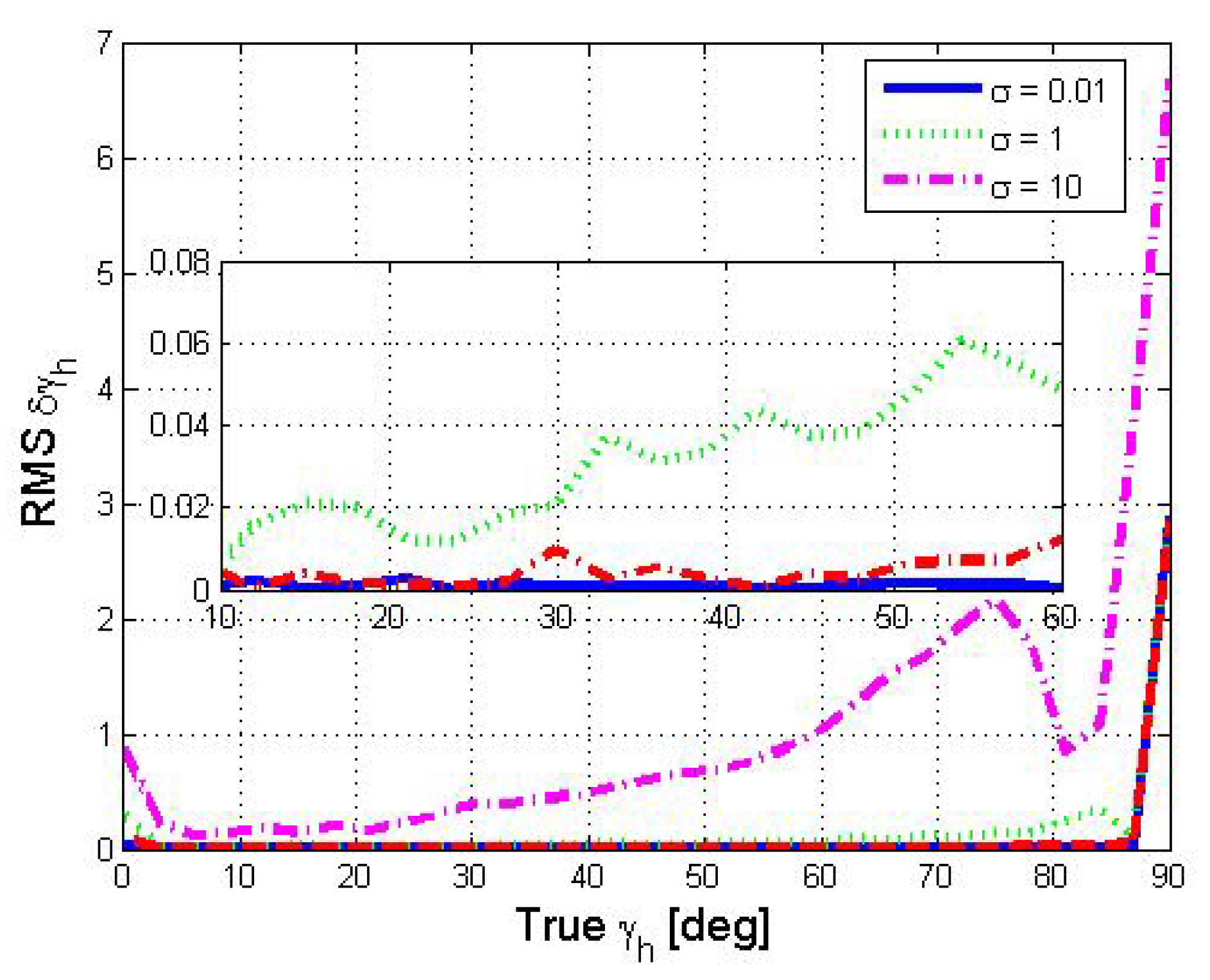
Figure 7.
RMS of as a function of . Curves represent different accelerometer variance values in units of
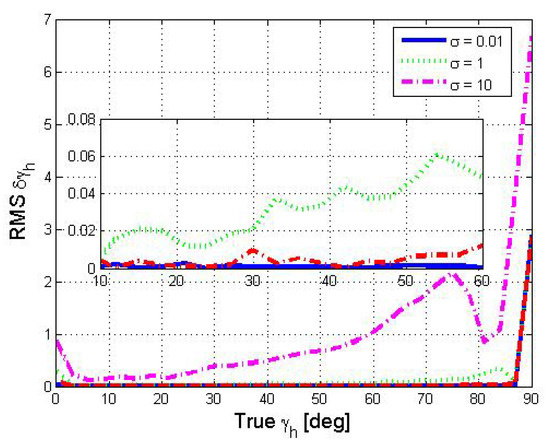
Figure 8.
RMS of as a function of . Use of 150 acceleration measurements. Curves represent different accelerometer variance values in units of .
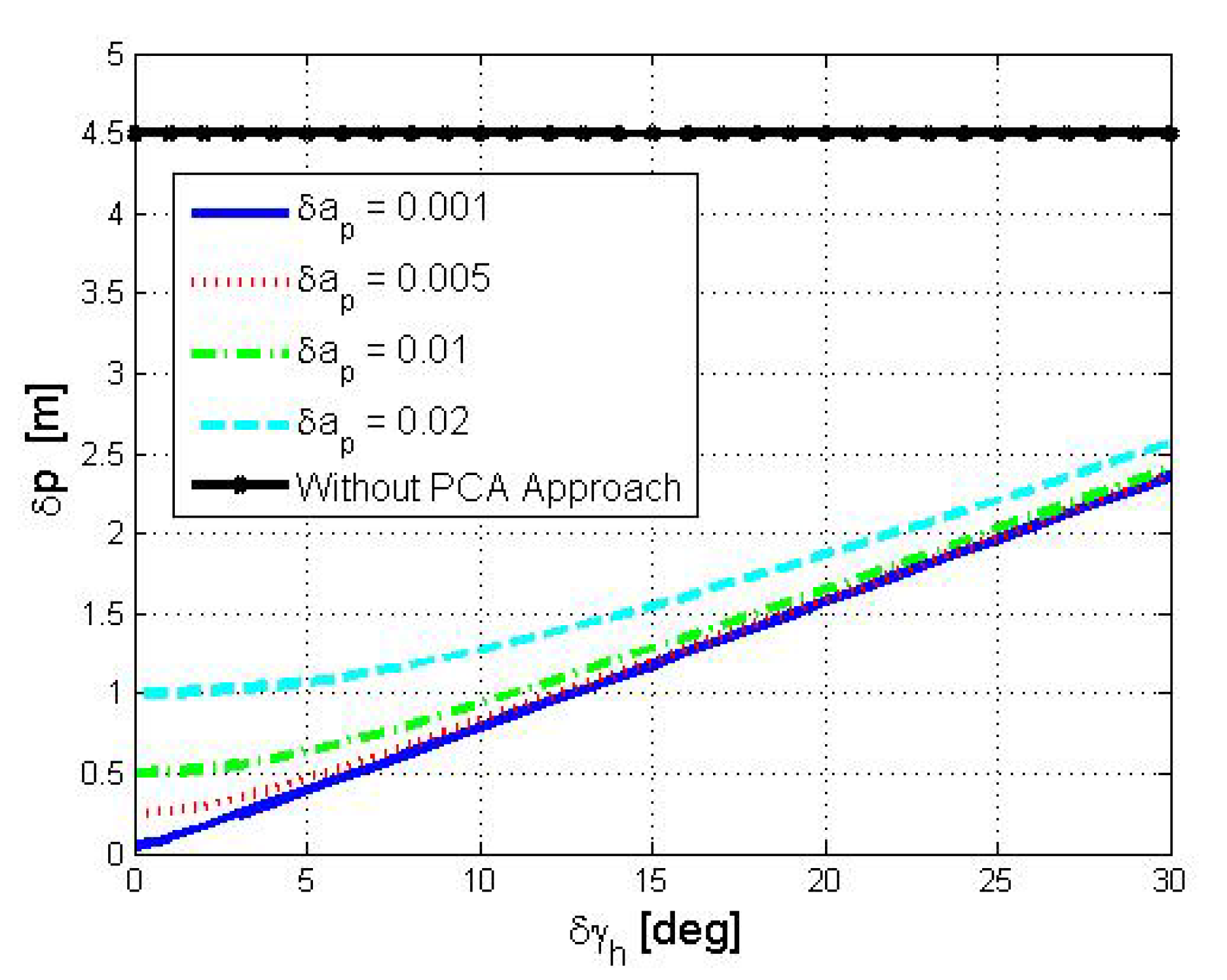
Next, we evaluate the performance of PCA-DR using the closed form expressions in Equation (31). Numerical values for the position error are shown in Figure 9. Results are shown as a function of the two error terms of the PCA-DR approach, namely, and . We examine a scenario with true values of deg and m/ and for a navigation period . We collect 1000 acceleration measurements for data analysis. In Figure 9, the initial position and velocity errors were nullified. Figure 9 also includes (solid line with marker) the performance of the traditional DR, that is, when the directional angles are neglected. The results show that, without compensating for the directional angles, the DR error is roughly 4.5 m. This positioning error depends only on the actual water current acting on the drifter and, clearly, is not sensitive to the two error sources of PCA-DR. This is the reason why the positioning error of the traditional DR remains constant in Figure 9. We also observe the strong dependency between the positioning error of the traditional DR and the error in estimating the directional angles. This result motivates the need for an accurate estimation of the latter.
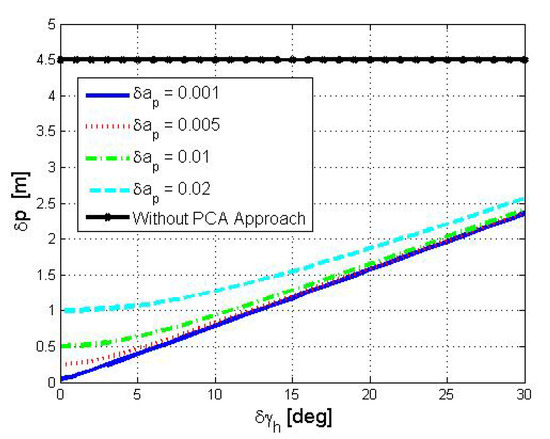
Figure 9.
Numerical positioning error of the DR procedure.
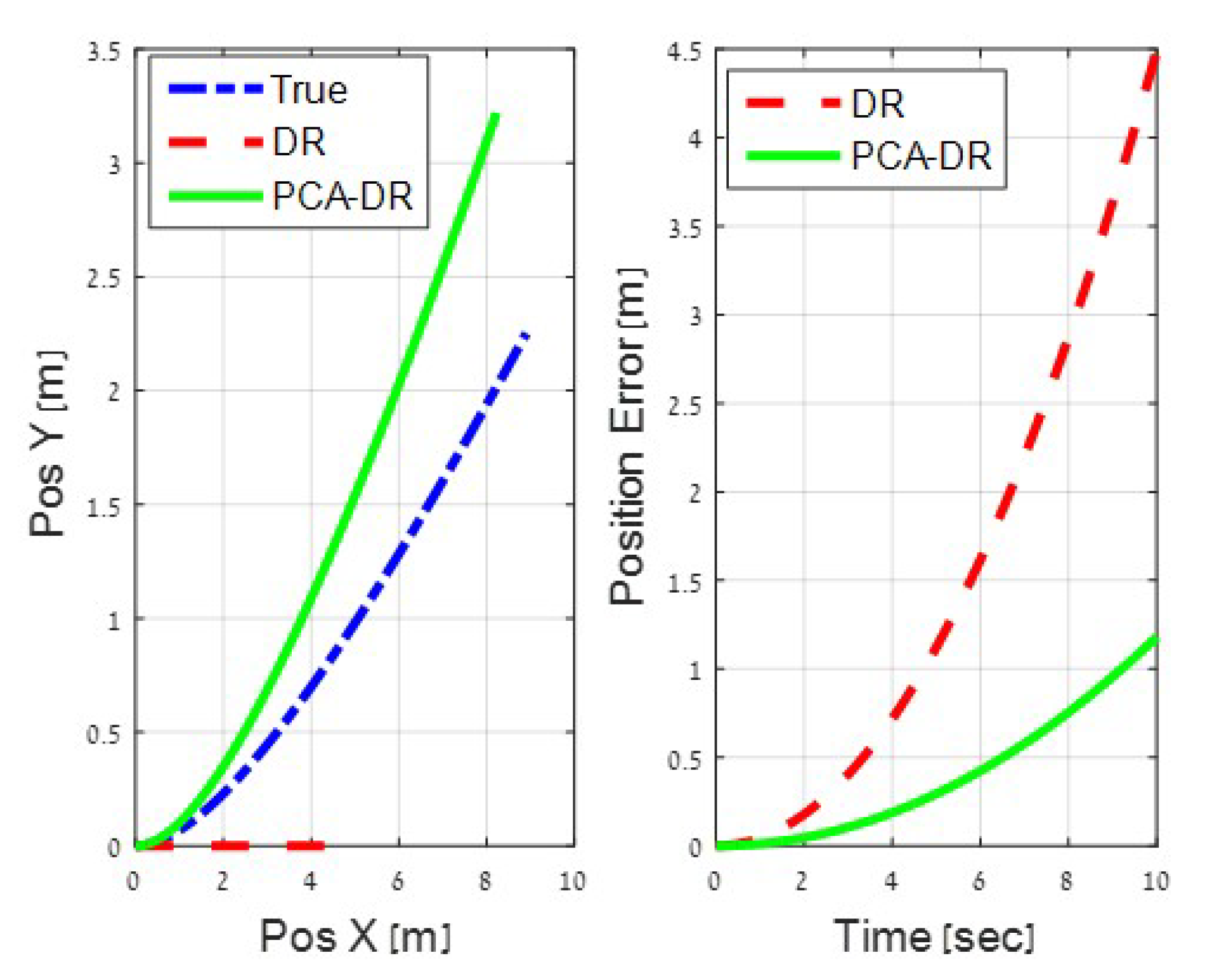
To further illustrate the difference between PCA-DR and other DR approaches, we examine the navigation performance for a single data point from Figure 9. We consider the case where = 0.001 m/s2 and deg and a scenario of 10s between two position updates. In the DR implementation, we assume perfect knowledge of the initial position and velocity of the drifter. The comparison between the navigation performance over time of the DR and the PCA-DR approaches for this scenario is shown in Figure 10. On the left panel, we show the estimated position of the drifter using the two approaches relative to the true position. Notice that, using the DR approach, the position remains in a straight line. This is excepted due to the assumption of no water current. Differently, the performance of the PCA-DR approach depends on the values of and . On the right panel of Figure 10, we show the position error of the two approaches. We observe that PCA-DR offers a significant improvement of the position error by more than compared to that of the traditional DR approach.
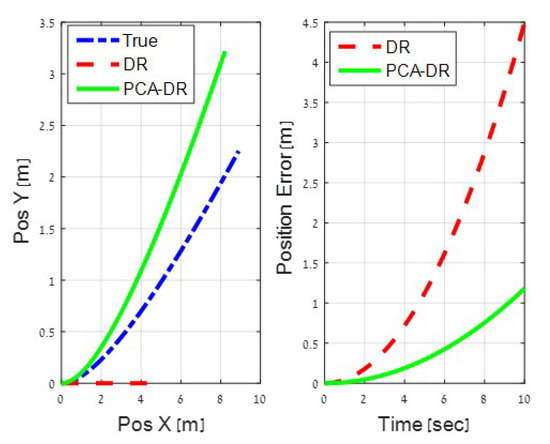
Figure 10.
Comparison between traditional DR and PCA-DR. Left panel: actual position of the two approaches relative to the true position. Right panel: position error of the two approaches.
Based on the above discussion, we claim that, when a water current exists, the traditional DR approach fails, while PCA-DR retains good DR performance. We also observe that, due to overfitting, when no water current exists, the performance of PCA-DR is inferior to that of the traditional DR. However, the performance degradation is not substantial.
The results of the comparison between PCA-DR and the traditional DR also highlight the robustness of the former. This is because exploring different directional angles corresponds to either different water current forces or different drifter designs.
5.2. Experimental Investigation
In our simulations, we assumed that and that the water current induces an acceleration force that results only in a non-zero . To test the validity of these assumptions, and to demonstrate the performance of PCA-DR in a realistic scenario, we performed a designated sea experiment. The experiment was conducted on December 2018 across the shoreline of Haifa. The water depth was roughly 12 [m]. The sea conditions can be characterized as Beaufort force Level 1, and a significant water current of roughly 1 knot was present. Together with the north–south direction of the Eastern Mediterranean sea current, the area of the experiment is affected by two main local water current sources originating from the nearby Haifa harbor and from the estuary of the nearby Kishon river.
The experiment involved in a single submerged water-proof tube including an industrial-graded VectorNav vn-300 INS. The specifications of the INS includes a 5° per hour gyro in-run bias and a 0.04 mg accelerometer in-run bias. Only the VectorNav accelerometers are used for the experiments. Those are indeed better than the ones found, for example, in our smartphones. Further, we did not calibrate for sensor biases nor filter out the noises; rather, only the raw measurements were used. For the examined time period (1–10 s), this is almost identical to taking low-cost sensors after bias calibration.
We used the INS at a rate of 10 [Hz], and recorded its data for offline processing. The tube was lowered by scuba divers to the middle of the water current, and was then released to freely drift. To have the tube maintain its depth, weights were carefully added to the drifter by the scuba divers. Ground truth information about the location of the drifter was obtained by having the divers follow the tube (without effecting its motion) while dragging a buoy with a GPS logger. As the direction and magnitude of the water current in the tested area highly varied in space, this procedure was performed a few times to test the performance of PCA-DR for different water current conditions. A picture of the deployed tube is shown in Figure 11.

Figure 11.
Pictures of the deployed drifter with the self-made INS in the test tank (a)) and at sea (b)).
Due to the limitation of the acceleration-only DR approach to perform tracking until the navigation error drifters, we conducted sea experiments for very short time periods of a few seconds. Specifically, we consider eight trajectories for our evaluation, with a minimum time duration of 3 s and a maximum of 10 s. First, we examine the directional angle accuracy followed by DR analysis. To calculate the actual direction of the tube, we used the GPS start and end points measured position, while the estimated direction is obtained from the PCA analysis. Results are summarized in Table 1. For a short time duration, an error of 0.02° was obtained, and for the 10 [s] trajectory, an error of 2.55° was obtained. This result emphasizes the strength of the PCA-DR approach since, in regular DR, the direction cannot be estimated.

Table 1.
Directional angles recorded from the sea experiments.
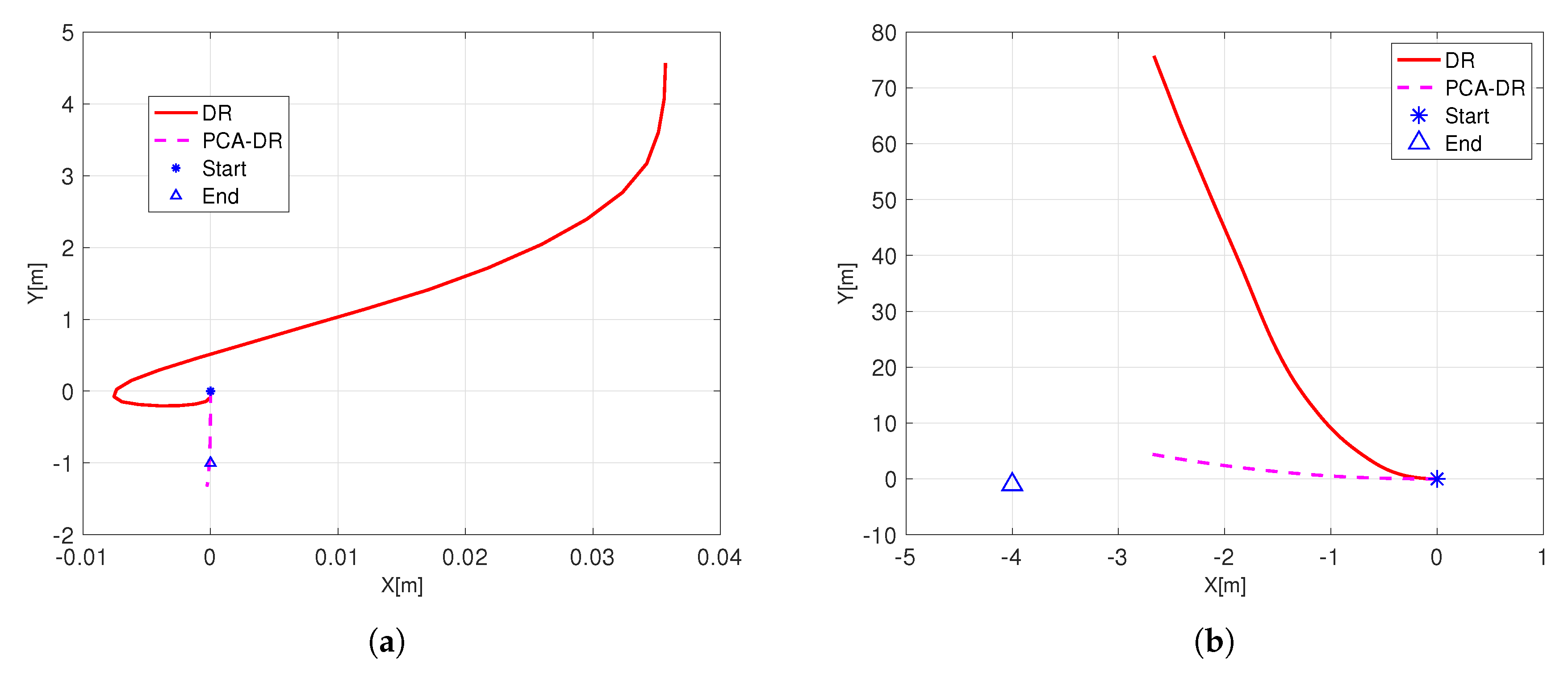
Further, in Figure 12, we show the trajectory estimate of the drifter using our PCA-DR approach, and compare it to the performance of the traditional DR approach that does not take into account the water current. We note that, in both approaches, only acceleration data is used. Two trajectories are shown for 3 s (Figure 12a,b) intervals, and the ground truth start and end positions are marked. The ground truth was determined using the GPS receiver onboard the buoy. For both trajectories, we observe that the traditional DR completely fails to follow the path of the drifter, and highly drifts both in terms of the heading angle and in terms of the traveled distance. Due to the significant water current, this drift starts already from the beginning of the motion. Contrarily, we observe that PCA-DR successfully follows the path of the drifter, and manages to accurately calculate its heading angle. This result supports the analysis shown in Figure 10. Notice that the GPS receiver used for ground truth has a 5 m error; thus, the starting point of the trajectory is expected to have this range of error. Yet, what is important is the behavior of the two approaches: the DR solution shows a traveled distance of tens of meters (which of course was not the case), while our PCA-DR approach shows a traveled distance of a few meters. Our point is that, while ground thruthing was not accurate, given the outcome, we argue that our approach well outperforms classical DR.
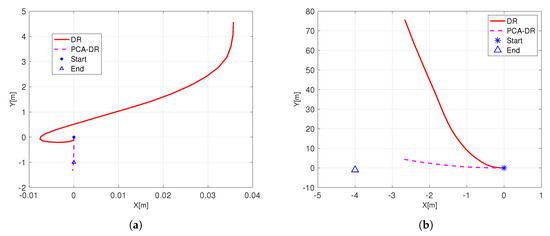
Figure 12.
Results from the sea experiment comparing PCA-DR with the traditional DR approach. (a) Trajectory A. Data collected for 3 s. (b) Trajectory B. Data collected for 10 s.
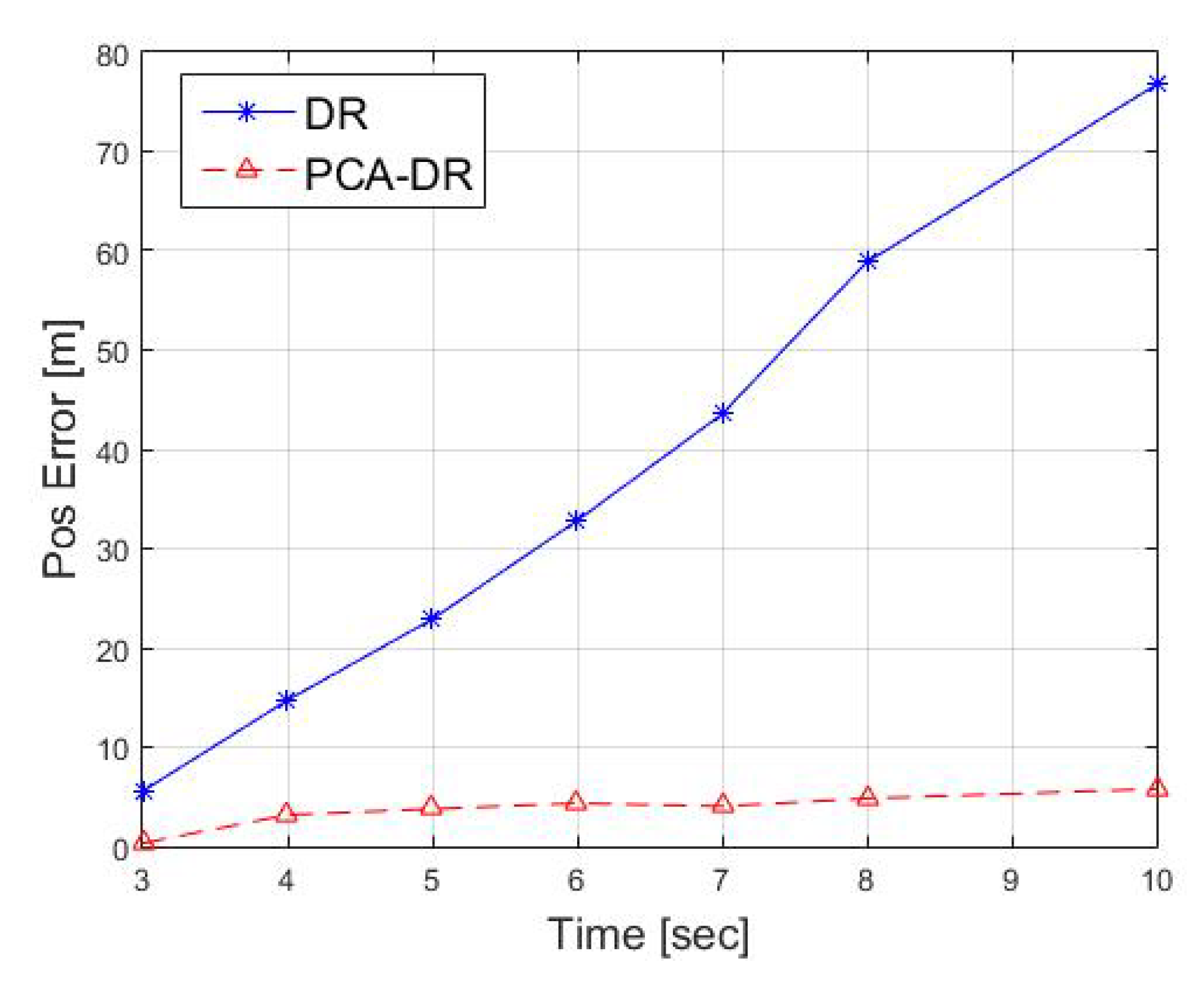
In addition, using Equation (13), we calculated the position error at the end of the trajectories for both regular DR and PCA-DR. The results are plotted in Figure 13. As expected, the DR solution error drifts with time much more quickly than the PCR-DR approach. For the 10 s trajectory, the DR has a position error of 76.6 m, while the PCA-DR has an error of 5.8 m. While this error may seem high, we note that DR is performed over short periods of time before obtaining location fixes. Still, the focus of our work is on considering induced acceleration force on the drifter, so the results should be considered with respect to performing DR without such consideration. Here, the performance in Figure 13 shows a huge improvement.
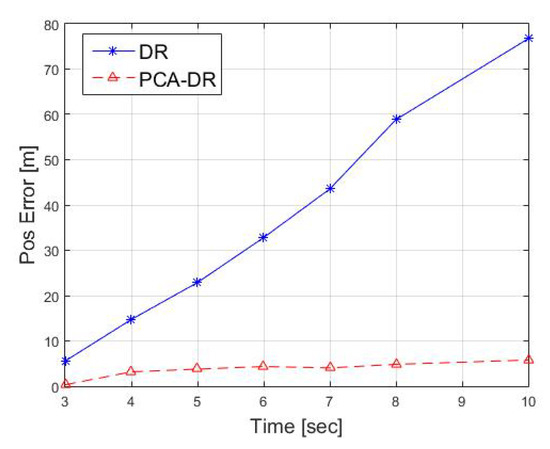
Figure 13.
Position error results from the sea experiment comparing PCA-DR with the traditional DR approach.
5.3. Discussion
Without a water current acting on the drifter, DR methods will give a satisfactory performance between two successive position updates. Yet, as we show by the results of Figure 9 and Figure 12, for scenarios including an acceleration-induced water current force, even for short periods of time of a few seconds, traditional DR approaches will result in large position errors. These errors dramatically grow as a function of the time between position updates and the magnitude of the water current acceleration force. In this respect, whenever the water current is substantial, it must be considered in the DR process. Indeed, as we showed in numerical simulations and as we demonstrated in our sea experiment, in such cases, PCA-DR performance far exceeds that of the traditional DR approach. However, relying only on acceleration measurements, PCA-DR is limited to short time periods of a few seconds. It should therefore be used within navigation fixes as an aid to either evaluate the water current, or gap time instances without navigation assistance from, e.g., DVL. The accuracy of PCA-DR depends on the accelerometer grade, the number of measurements used in the process of PCA evaluation, and the value of the actual directional angle. In that context, the performance improvement of PCA-DR might be obtained by analyzing the optimal number of acceleration measurements required for the PCA evaluation. Further, PCA-DR can be extended for situations where the drifter also experiences a vertical directional angle.
6. Conclusions
In this paper, we considered the problem of DR navigation for submerged drifters. These devices drift with the water current to measure the current’s velocity or to observe certain phenomena. Hence, they are not connected to, e.g., a surface buoy, but rather drift freely in the water column. Due to their non-negligible size and shape, they are under the influence of an acceleration-driving force by the water current. The water current affects the horizontal and vertical angles between the x-body frame and the stability frame. These angles, referred to as the directional angles, must be estimated in order to allow for DR navigation. Instead of directly estimating the directional angles through gyrocompasses or magnetometers that may not be available or may be of low accuracy, for the short time periods of a few seconds required for the DR calculation, we use a PCA-based approach to obtain an estimate of the directional angles using the three-dimensional acceleration measurements only. Applying the proposed approach enables online/offline trajectory estimation between two successive position updates. To comment on the effect of such an estimation on the DR navigation, we derived closed form expressions for the positioning error under a mismatch in the estimation of the directional angles. Results of both numerical simulations and sea experiments showed that, without compensating for the directional angles, a large positioning error exists. However, using our PCA-DR method, the positioning error is reduced into a reasonable acceleration noise level. Further work would also include an extension of the suggested method for cases where the drifter changes its heading direction during the navigation period, and for long-term time periods of navigation.
Author Contributions
The authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the MOST-BMBF German-Israeli Cooperation in Marine Sciences 2018–2020 and by the MOST action for Agriculture Environment and Water for year 2019.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- Roemmich, D.; Johnson, G.; Riser, S.; Davis, R.; Gilson, J.; Owens, W.; Garzoli, S.; Schmid, C.; Ignaszewski, M. The argo program: Observing the global ocean with profiling floats. Oceanography 2009, 22, 34–43. [Google Scholar] [CrossRef]
- Jaffe, J.; Franks, P.; Roberts, P.; Mirza, D.; Schurgers, C.; Kastner, R.; Boch, A. A swarm of autonomous miniature underwater robot drifters for exploring submesoscale ocean dynamics. Nat. Commun. 2017, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV Navigation and Localization—A review. IEEE J. Ocean. Eng. 2014, 39, 221–231. [Google Scholar] [CrossRef]
- Titterton, D.; Weston, J. Strapdown Inertial Navigation Technology, 2nd ed.; The Institution of Engineering and Technology: Stevenage, UK, 2004. [Google Scholar]
- Farrell, J. Aided Navigation GPS with High Rate Sensors; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Hegrenaes, A.; Hallingstad, O. Model aided INS with sea current estimation for robust underwater navigation. IEEE J. Ocean. Eng. 2011, 36, 316–337. [Google Scholar] [CrossRef]
- Klein, I.; Filin, S.; Toledo, T. Pseudo-measurements as aiding to INS during GPS outages. NAVIGATION 2010, 57, 25–34. [Google Scholar] [CrossRef]
- Morgado, M.; Oliveira, P.; Silvestre, C. Tightly coupled ultrashort baseline and inertial navigation system for underwater vehicles: An experimental validation. J. Field Robot. 2013, 30, 142–170. [Google Scholar] [CrossRef]
- Lee, P.; Jun, B.; Kim, K.; Lee, J.; Aoki, T.; Hyakudome, T. Simulation of an inertial acoustic navigation system with range aiding for an autonomous underwater vehicle. IEEE J. Ocean. Eng. 2007, 32, 327–345. [Google Scholar] [CrossRef]
- Eustice, R.; Pizarro, O.; Singh, H. Visually augmented navigation for autonomous underwater vehicles. IEEE J. Ocean. Eng. 2008, 33, 103–122. [Google Scholar] [CrossRef]
- Ribas, D.; Ridao, P.; Neira, J.; Tardos, J. SLAM using an imaging sonar for partially structured underwater environments. In Intelligent Robots and Systems; IEEE/RSJ: Sendai, Japan, 2006; pp. 5040–5045. [Google Scholar]
- Casagrande, D.; Krasnosky, K.; Roman, C. Localization of a drifting underwater vehicle using a terrain-based particle filter. In OCEANS 2019 MTS/IEEE SEATTLE; IEEE: Piscataway, NJ, USA, 2019; pp. 1–8. [Google Scholar]
- Fallon, M.; Folkesson, J.; McClelland, H.; Leonard, J. Relocating underwater features autonomously using sonar-based SLAM. IEEE J. Ocean. Eng. 2013, 38, 500–513. [Google Scholar] [CrossRef]
- Neumann, G. Ocean Currents; Elsevier: Amsterdam, The Netherlands, 2014; Volume 4. [Google Scholar]
- Beard, R.; McLain, T. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Deng, Z.; Guofeng, W.; Ying, H.; Di, W. Heading estimation for indoor pedestrian navigation using a smartphone in the pocket. Sensors 2015, 15, 21518–21536. [Google Scholar] [CrossRef] [PubMed]
- Klein, I.; Diamant, R. Observability analysis of DVL/PS aided INS for a maneuvering AUV. Sensors 2015, 15, 26818–26837. [Google Scholar] [CrossRef] [PubMed]
- Costanzi, R.; Fanelli, F.; Meli, E.; Ridolfi, A.; Caiti, A.; Allotta, B. UKF-based navigation system for AUVs: Online experimental validation. IEEE J. Ocean. Eng. 2018, 44, 1–9. [Google Scholar] [CrossRef]
- Filaretov, V.F.; Zhirabok, A.N.; Zyev, A.V.; Protsenko, A.A.; Tuphanov, I.E.; Scherbatyuk, A.F. Design and investigation of dead reckoning system with accommodation to sensors errors for autonomous underwater vehicle. In OCEANS 2015—MTS/IEEE Washington; IEEE: Piscataway, NJ, USA, 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Li, Q.; Ben, Y.; Naqvi, S.M.; Neasham, J.A.; Chambers, J.A. Robust student’s t-based cooperative navigation for autonomous underwater vehicles. IEEE Trans. Instrum. Meas. 2018, 67, 1762–1777. [Google Scholar] [CrossRef]
- Chu, Z.; Zhu, D.; Sun, B.; Nie, J.; Xue, D. Design of a dead reckoning based motion control system for small autonomous underwater vehicle. In Proceedings of the 2015 IEEE 28th Canadian Conference on Electrical and Computer Engineering (CCECE), Halifax, NS, Canada, 3–6 May 2015; pp. 728–733. [Google Scholar] [CrossRef]
- Fagogenis, G.; Flynn, D.; Lane, D.M. Improving Underwater Vehicle navigation state estimation using Locally Weighted Projection Regression. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 6549–6554. [Google Scholar] [CrossRef]
- Sabet, M.T.; Daniali, H.M.; Fathi, A.; Alizadeh, E. Identification of an autonomous underwater vehicle hydrodynamic model using the extended, cubature, and transformed unscented kalman filter. IEEE J. Ocean. Eng. 2018, 43, 457–467. [Google Scholar] [CrossRef]
- Sabet, M.T.; Sarhadi, P.; Zarini, M. Extended and unscented Kalman filters for parameter estimation of an autonomous underwater vehicle. Ocean Eng. 2014, 91, 329–339. [Google Scholar] [CrossRef]
- Medagoda, L.; Kinsey, J.C.; Eilders, M. Autonomous underwater vehicle localization in a spatiotemporally varying water current field. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–4 June 2015; pp. 565–572. [Google Scholar] [CrossRef]
- Sabet, M.T.; Daniali, H.M.; Fathi, A.; Alizadeh, E. A low-cost dead reckoning navigation system for an AUV using a robust AHRS: Design and experimental analysis. IEEE J. Ocean. Eng. 2018, 43, 927–939. [Google Scholar] [CrossRef]
- Song, Z.; Mohseni, K. FACON: A flow-aided cooperative navigation scheme. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 6251–6256. [Google Scholar] [CrossRef]
- Diamant, R.; Wolff, L.M.; Lampe, L. Location Tracking of Ocean-Current-Related Underwater Drifting Nodes Using Doppler Shift Measurements. IEEE J. Ocean. Eng. 2015, 40, 887–902. [Google Scholar] [CrossRef]
- Chen, B.; Hsien, F. Sideslip angle estimation using extended Kalman filter. Veh. Syst. Dyn. 2008, 46, 353–364. [Google Scholar] [CrossRef]
- Ryu, J.; Rossetter, E.; Gerdes, J. Vehicle Sideslip and Roll Parameter Estimation using GPS. In Proceedings of the 2002 International Symposium on Advanced Vehicle Control, Hiroshima, Japan, 9–13 September 2002. [Google Scholar]
- Yoon, J.H.; Peng, H. Sideslip Angle Estimation Based on GPS and Magnetometer Measurements. In Proceedings of the 11th International Symposium on Advanced Vehicle Control, Seoul, Korea, 9–12 September 2006. [Google Scholar]
- Kunze, K.; Lukowicz, P.; Partridge, K.; Begole, B. Which way am I facing: Inferring horizontal device orientation from an accelerometer signal. In Proceedings of the 2009 International Symposium on Wearable Computers, Linz, Austria, 4–7 September 2009; pp. 149–150. [Google Scholar]
- Combettes, C.; Renaudin, V. Comparison of Misalignment Estimation Techniques Between Handheld Device and Walking Directions. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation, Calgary, AL, Canada, 13–16 October 2015; pp. 13–16. [Google Scholar]
- Steinhoff, U.; Bernt, S. Dead reckoning from the pocket-an experiment study. In Pervasive Computing and Communications (PerCom); IEEE: Piscataway, NJ, USA, 2010; pp. 162–170. [Google Scholar]
- Han, R.; Ortiz, M. Smartphone based gait analysis using STFT and wavelet transform for indoor navigation. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation, Busan, Korea, 27–30 October 2014. [Google Scholar]
- Kourogi, M.; Kurata, T. A method of pedestrian dead reckoning for smart phones using frequency domain analysis on patterns of acceleration and angular velocity. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 5–8 May 2014; pp. 164–168. [Google Scholar]
- Fossen, T.; Pettersen, K.; Galeazzi, R. Line-of-Sight Path Following for Dubins Paths with Adaptive Sideslip Compensation of Drift Forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef]
- Bender, A.; Steinberg, D.M.; Friedman, A.; Williams, S. Analysis of an Autonomous Underwater Glider. In Proceedings of the 2008 Australasian Conference on Robotics and Automation, Canberra, ACT, Australia, 3–5 December 2008; pp. 1–10. [Google Scholar]
- Graver, J.; Bachmayer, R.; Leonard, N. Underwater Glider Model Parameter Identification. In Proceedings of the 2003 International Symposium on Unmanned Untethered Submersible Technology, Durham, NH, USA, 21–24 August 2003. [Google Scholar]
- Groves, D.; Pulford, W.; Littlefield, A.; Nash, L.; Mather, J. Inertial Navigation Versus Pedestrian Dead Rreckoning: Optimizing the Integration; Institute of Navigation GNSS; ION: Fort Worth, TX, USA, 2007. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).