Optimal State Estimation in Underwater Vehicle Discrete-Continuous Measurements via Augmented Hybrid Kalman Filter
Abstract
1. Introduction
- Navigation systems. Modern requirements for autonomous underwater vehicles (AUVs) are characterized by strict limitations on the deviation values from the specified trajectory. At the same time, the coordinates’ determination accuracy requirements have significantly increased [3,4]. In this regard, complex methods for determining the AUV position coordinates based on the combination and optimal navigation information processing (from DVL, IMU, PS, GPS), which contribute to a significant increase in motion accuracy, are increasingly used [5,6,7,8].
- Simultaneous Localization and Mapping (SLAM). Simultaneous localization and mapping (SLAM) is a fundamental problem in robotics, including underwater robotics, in which the vehicle simultaneously builds an environmental map and estimates its position in it. Nonlinear state-estimation filters are widely used to solve the SLAM problem due to nonlinearity and uncertainty [9,10,11,12].
- Autonomous underwater vehicle control. Nonlinear state-estimation filters are widely used for closed-loop autonomous underwater vehicle (AUV) control. By accurately estimating the vehicle state, including position, orientation, and velocity, the filters provide precise control in complex underwater environments [13,14,15,16].
- Optimal data fusion from different navigation sources. When using navigation aids for determining the AUV location, special attention should be paid to the weight of each information source. The optimum in the meaning of coordinate determination accuracy should be provided by data fusion from all sources instead of separation into two subsystems, as in the classical case [23,24,25].
2. Theoretical Frameworkand Methods
2.1. Problem Statement for Fusion Task
2.2. Green–Lagrange Characteristic Identity
2.3. Optimal State Estimation in Linear Nonstationary Continuous-Discrete Systems
- 1.
- Hybrid Dynamics: The continuous-time term accounts for system evolution between discrete measurements, while the discrete-term handles abrupt updates at measurement times .
- 2.
- Multi-Rate Updates: The Kalman gain depends on both continuous () and discrete () noise covariances, unlike classical filters.
- 3.
- Cross-Term Handling: The term explicitly couples continuous predictions with discrete process noise, which is absent in purely continuous/discrete Riccati Equations.
2.4. Discrete and Continuous Fusion
2.5. Hydrodynamic Parameters Estimation
- —the solid-body inertia matrix ( is the DoF number),
- —added-mass matrix,
- —solid-body Coriolis matrix,
- —added-mass Coriolis matrix,
- —dissipative-coefficient matrix,
- —gravitational-forces-and-moments vector,
- —vector (of forces and moments) of the controls applied to the body expressed in the body-fixed frame,
- —vector (of forces and moments) of external disturbances applied to the body expressed in the inertial frame,
- —is a vector that describes the thrusters’ load ( is the number of thrusters).
- —dynamics matrix,
- —control matrix,
- —output matrix (—number of system outputs),
- —input-output coupling matrix,
- —control vector, including the vector of external perturbations .
3. Results
4. Discussion
- The state-vector augmentation was used to improve the estimation convergence, as evidenced by the reduction in errors (RMSE) compared to the method without augmentation. This is in agreement with previous studies such as [17,18,19,20,21,22], where augmentation was used to estimate hydrodynamic parameters.
- Like other Kalman filters, the proposed method is sensitive to the model precision. Unaccounted nonlinearities or significant deviations from the noise Gaussianity may reduce the estimation quality.
- The augmented state vector’s high dimensionality can increase the computational load, although this was balanced in this study by optimizing the algorithm.
5. Conclusions
- Computational Load: State augmentation increases dimensionality, making the method less suitable for ultra-low-power embedded systems without hardware acceleration.
- Synchronization Assumption: The filter assumes perfectly synchronized continuous/discrete measurements. Performance may degrade with significant sensor latency.
- Nonlinearity Handling: Strong nonlinearities (e.g., complex noise, turbulent flow beyond quadratic damping) requires additional linearization steps, akin to EKF/UKF.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUV | Autonomous Underwater Vehicle |
| CKF | Cubature Kalman Filter |
| DVL | Doppler Velocity Logger |
| EKF | Extended Kalman Filter |
| EnKF | Ensemble Kalman Filter |
| GPS | Global Positioning System |
| IMU | Inertial Measurement Unit |
| KF | Kalman Filter |
| PF | Particle Filter |
| PS | Pressure Sensor |
| RMSE | Root Mean Square Error |
| SLAM | Simultaneous Localization and Mapping |
| UKF | Unscented Kalman Filter |
References
- Kramar, V.; Kabanov, A.; Alchakov, V. Multiloop Multirate Continuous-Discrete Drone Stabilization System: An Equivalent Single-Rate Model. Drones 2021, 5, 129. [Google Scholar] [CrossRef]
- Ju, C.; Son, H.I. A Hybrid Systems-Based Hierarchical Control Architecture for Heterogeneous Field Robot Teams. IEEE Trans. Cybern. 2023, 53, 1802–1815. [Google Scholar] [CrossRef] [PubMed]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control, 2nd ed.; Wiley: Hoboken, NJ, USA; Chichester, UK, 2021; ISBN 978-1-119-57503-0. [Google Scholar]
- Antonelli, G. Underwater Robots; Springer Tracts in Advanced Robotics; Springer International Publishing: Cham, Switzerland, 2018; Volume 123, ISBN 978-3-319-77898-3. [Google Scholar]
- Kramar, V.; Kabanov, A.; Dementiev, K. Autonomous Underwater Vehicle Navigation via Sensors Maximum-Ratio Combining in Absence of Bearing Angle Data. JMSE 2023, 11, 1847. [Google Scholar] [CrossRef]
- Scherbatyuk, A.F. Multiple AUV Navigation without Using Acoustic Beacons. Gyroscopy Navig. 2022, 13, 253–261. [Google Scholar] [CrossRef]
- Jeong, D.B.; Ko, N.Y. Sensor Fusion for Underwater Vehicle Navigation Compensating Misalignment Using Lie Theory. Sensors 2024, 24, 1653. [Google Scholar] [CrossRef]
- Filaretov, V.F.; Zhirabok, A.N.; Zyev, A.V.; Protsenko, A.A.; Tuphanov, I.E.; Scherbatyuk, A.F. Design and Investigation of Dead Reckoning System with Accommodation to Sensors Errors for Autonomous Underwater Vehicle. In Proceedings of the OCEANS 2015—MTS/IEEE Washington; IEEE: Washington, DC, USA, 2015; pp. 1–4. [Google Scholar]
- Yuan, X.; Martínez-Ortega, J.-F.; Fernández, J.; Eckert, M. AEKF-SLAM: A New Algorithm for Robotic Underwater Navigation. Sensors 2017, 17, 1174. [Google Scholar] [CrossRef]
- Merveille, F.F.R.; Jia, B.; Xu, Z.; Fred, B. Advancements in Sensor Fusion for Underwater SLAM: A Review on Enhanced Navigation and Environmental Perception. Sensors 2024, 24, 7490. [Google Scholar] [CrossRef]
- Luo, J.; Ko, H.-L. UKF-Based Inverted Ultra-Short Baseline SLAM With Current Compensation. IEEE Access 2022, 10, 67329–67337. [Google Scholar] [CrossRef]
- Mu, P.; Zhang, X.; Qin, P.; He, B. A Variational Bayesian-Based Simultaneous Localization and Mapping Method for Autonomous Underwater Vehicle Navigation. JMSE 2022, 10, 1563. [Google Scholar] [CrossRef]
- Liu, Q.; Li, M. Position Control for an Autonomous Underwater Vehicle under Noisy Conditions. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2022, 236, 1119–1132. [Google Scholar] [CrossRef]
- Liu, Q.; Li, M. Discrete-Time Position Control for Autonomous Underwater Vehicle under Noisy Conditions. Appl. Sci. 2021, 11, 5790. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Li, S.; Wang, J.; Fang, L.; Ning, L.; Feng, J.; Zhang, J. An Improved Unscented Kalman Filter Applied to Positioning and Navigation of Autonomous Underwater Vehicles. Sensors 2025, 25, 551. [Google Scholar] [CrossRef] [PubMed]
- Zhang, A.; Wu, Y.; Zhi, C.; Yang, R. A Novel Adaptive Factor-Based H∞ Cubature Kalman Filter for Autonomous Underwater Vehicle. JMSE 2022, 10, 326. [Google Scholar] [CrossRef]
- Deng, F.; Levi, C.; Yin, H.; Duan, M. Identification of an Autonomous Underwater Vehicle Hydrodynamic Model Using Three Kalman Filters. Ocean. Eng. 2021, 229, 108962. [Google Scholar] [CrossRef]
- Sajedi, Y.; Bozorg, M. Robust Estimation of Hydrodynamic Coefficients of an AUV Using Kalman and H∞ Filters. Ocean. Eng. 2019, 182, 386–394. [Google Scholar] [CrossRef]
- Guan, Y.; Qin, H.; Hu, M.; Cui, Q.; Zheng, H.; Ding, R. Hydrodynamic Parameter Identification of Deep-Sea Mining Vehicle during Deployment and Retrieval Using a Nonlinear Filter. Adv. Theory Simul. 2024, 7, 2400066. [Google Scholar] [CrossRef]
- Shariati, H.; Moosavi, H.; Danesh, M. Application of Particle Filter Combined with Extended Kalman Filter in Model Identification of an Autonomous Underwater Vehicle Based on Experimental Data. Appl. Ocean. Res. 2019, 82, 32–40. [Google Scholar] [CrossRef]
- Sabet, M.T.; Daniali, H.M.; Fathi, A.; Alizadeh, E. Identification of an Autonomous Underwater Vehicle Hydrodynamic Model Using the Extended, Cubature, and Transformed Unscented Kalman Filter. IEEE J. Ocean. Eng. 2018, 43, 457–467. [Google Scholar] [CrossRef]
- Lu, S.; Wang, B.; Dong, Z.; Hu, Z.; Ding, Y.; Liu, W. Parameter Identification of an Unmanned Surface Vessel Nomoto Model Based on an Improved Extended Kalman Filter. Appl. Sci. 2024, 15, 161. [Google Scholar] [CrossRef]
- Shaukat, N.; Otero, P. Underwater Vehicle Positioning by Fuzzy and Neural Adaptive Kalman Sensor Fusion. In Proceedings of the OCEANS 2021: San Diego—Porto, San Diego, CA, USA, 20–23 September 2021; pp. 1–7. [Google Scholar]
- Shaukat, N.; Ali, A.; Javed Iqbal, M.; Moinuddin, M.; Otero, P. Multi-Sensor Fusion for Underwater Vehicle Localization by Augmentation of RBF Neural Network and Error-State Kalman Filter. Sensors 2021, 21, 1149. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, C.; Liu, Y.; Zhu, J.; Qin, J. A Multi-Sensor Fusion Underwater Localization Method Based on Unscented Kalman Filter on Manifolds. Sensors 2024, 24, 6299. [Google Scholar] [CrossRef] [PubMed]
- Kulikov, G.Y.; Kulikova, M.V. State Estimation for Nonlinear Continuous–Discrete Stochastic Systems: Numerical Aspects and Implementation Issues; Studies in Systems, Decision and Control; Springer International Publishing: Cham, Switzerland, 2024; Volume 539, ISBN 978-3-031-61370-8. [Google Scholar]
- Shmaliy, Y.S.; Zhao, S. Optimal and Robust State Estimation: Finite Impulse Response (FIR) and Kalman Approaches, 1st ed.; Wiley: Hoboken, NJ, USA, 2022; ISBN 978-1-119-86307-6. [Google Scholar]
- Barfoot, T.D. State Estimation for Robotics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2024; ISBN 978-1-009-29990-9. [Google Scholar]
- Potokar, E.; Norman, K.; Mangelson, J. Invariant Extended Kalman Filtering for Underwater Navigation. IEEE Robot. Autom. Lett. 2021, 6, 5792–5799. [Google Scholar] [CrossRef]
- Singh, R.K.; Saha, J.; Bhaumik, S. Maximum Correntropy Polynomial Chaos Kalman Filter for Underwater Navigation. Digit. Signal Process. 2024, 155, 104774. [Google Scholar] [CrossRef]
- Sheng, G.; Liu, X.; Sheng, Y.; Cheng, X.; Luo, H. Cooperative Navigation Algorithm of Extended Kalman Filter Based on Combined Observation for AUVs. Remote Sens. 2023, 15, 533. [Google Scholar] [CrossRef]
- Allotta, B.; Costanzi, R.; Fanelli, F.; Monni, N.; Paolucci, L.; Ridolfi, A. Sea Currents Estimation during AUV Navigation Using Unscented Kalman Filter. IFAC-PapersOnLine 2017, 50, 13668–13673. [Google Scholar] [CrossRef]
- Lewis, F.L.; Xie, L.; Popa, D. Optimal and Robust Estimation: With an Introduction to Stochastic Control Theory, 2nd ed.; Automation and Control Engineering; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2008; ISBN 978-0-8493-9008-1. [Google Scholar]
- Tijjani, A.S.; Chemori, A.; Ali, S.A.; Creuze, V. Continuous–Discrete Observation-Based Robust Tracking Control of Underwater Vehicles: Design, Stability Analysis, and Experiments. IEEE Trans. Contr. Syst. Technol. 2023, 31, 1477–1492. [Google Scholar] [CrossRef]
- Särkkä, S.; Solin, A. On Continuous-Discrete Cubature Kalman Filtering. IFAC Proc. Vol. 2012, 45, 1221–1226. [Google Scholar] [CrossRef]
- Bhase, S.; Bhushan, M.; Kadu, S.; Mukhopadhyay, S. Continuous–Discrete Filtering Techniques for Estimating States of Nonlinear Differential–Algebraic Equations (DAEs) Systems. Int. J. Dynam. Control 2023, 11, 162–182. [Google Scholar] [CrossRef]
- Feddaoui, A.; Boizot, N.; Busvelle, E.; Hugel, V. High-Gain Extended Kalman Filter for Continuous-Discrete Systems with Asynchronous Measurements. Int. J. Control. 2020, 93, 2001–2014. [Google Scholar] [CrossRef]
- Kramar, V.; Alchakov, V.; Karapetian, V. The Models of Non-Stationary End Position Control Systems with Digital Corrective Circuits. In Proceedings of the 2023 International Conference on Ocean Studies (ICOS), Vladivostok, Russian, 3–6 October 2023; pp. 144–149. [Google Scholar] [CrossRef]
- Zhang, B.; Ji, D.; Liu, S.; Zhu, X.; Xu, W. Autonomous Underwater Vehicle Navigation: A Review. Ocean. Eng. 2023, 273, 113861. [Google Scholar] [CrossRef]
- Kumari, N.; Kulkarni, R.; Ahmed, M.R.; Kumar, N. Use of Kalman Filter and Its Variants in State Estimation: A Review. In Artificial Intelligence for a Sustainable Industry 4.0; Awasthi, S., Travieso-González, C.M., Sanyal, G., Kumar Singh, D., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 213–230. ISBN 978-3-030-77069-3. [Google Scholar]
- Jin, X.-B.; Robert Jeremiah, R.J.; Su, T.-L.; Bai, Y.-T.; Kong, J.-L. The New Trend of State Estimation: From Model-Driven to Hybrid-Driven Methods. Sensors 2021, 21, 2085. [Google Scholar] [CrossRef] [PubMed]
- Elfring, J.; Torta, E.; Van De Molengraft, R. Particle Filters: A Hands-On Tutorial. Sensors 2021, 21, 438. [Google Scholar] [CrossRef] [PubMed]
- Simon, D. Optimal State Estimation: Kalman, H∞, and Nonlinear Approaches, 1st ed.; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-0-471-70858-2. [Google Scholar]
- Gao, Z. Cubature Kalman Filters for Nonlinear Continuous-Time Fractional-Order Systems with Uncorrelated and Correlated Noises. Nonlinear Dyn. 2019, 96, 1805–1817. [Google Scholar] [CrossRef]
- Urrea, C.; Agramonte, R. Kalman Filter: Historical Overview and Review of Its Use in Robotics 60 Years after Its Creation. J. Sens. 2021, 2021, 9674015. [Google Scholar] [CrossRef]
- Zorich, V.A. Mathematical Analysis II; Universitext; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-662-48991-8. [Google Scholar]
- Alekseev, V.M.; Tihomirov, V.M.; Fomin, S.V. Optimal Control; Izd. 2, pererab. i dopoln.; Fizmatlit: Moskva, Russia, 2005; ISBN 978-5-9221-0589-7. [Google Scholar]
- Aström, K.J. Introduction to Stochastic Control Theory; Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1970; ISBN 978-0-12-065650-9. [Google Scholar]
- Casti, J. The Linear-Quadratic Control Problem: Some Recent Results and Outstanding Problems. SIAM Rev. 1980, 22, 459–485. [Google Scholar] [CrossRef]
- Zelikin, M.I. Optimalʹnoe Upravlenie i Variacionnoe Isčislenie; Izd. 2., ispr. i dop.; URSS: Moskva, Russia, 2004; ISBN 978-5-354-00622-9. [Google Scholar]

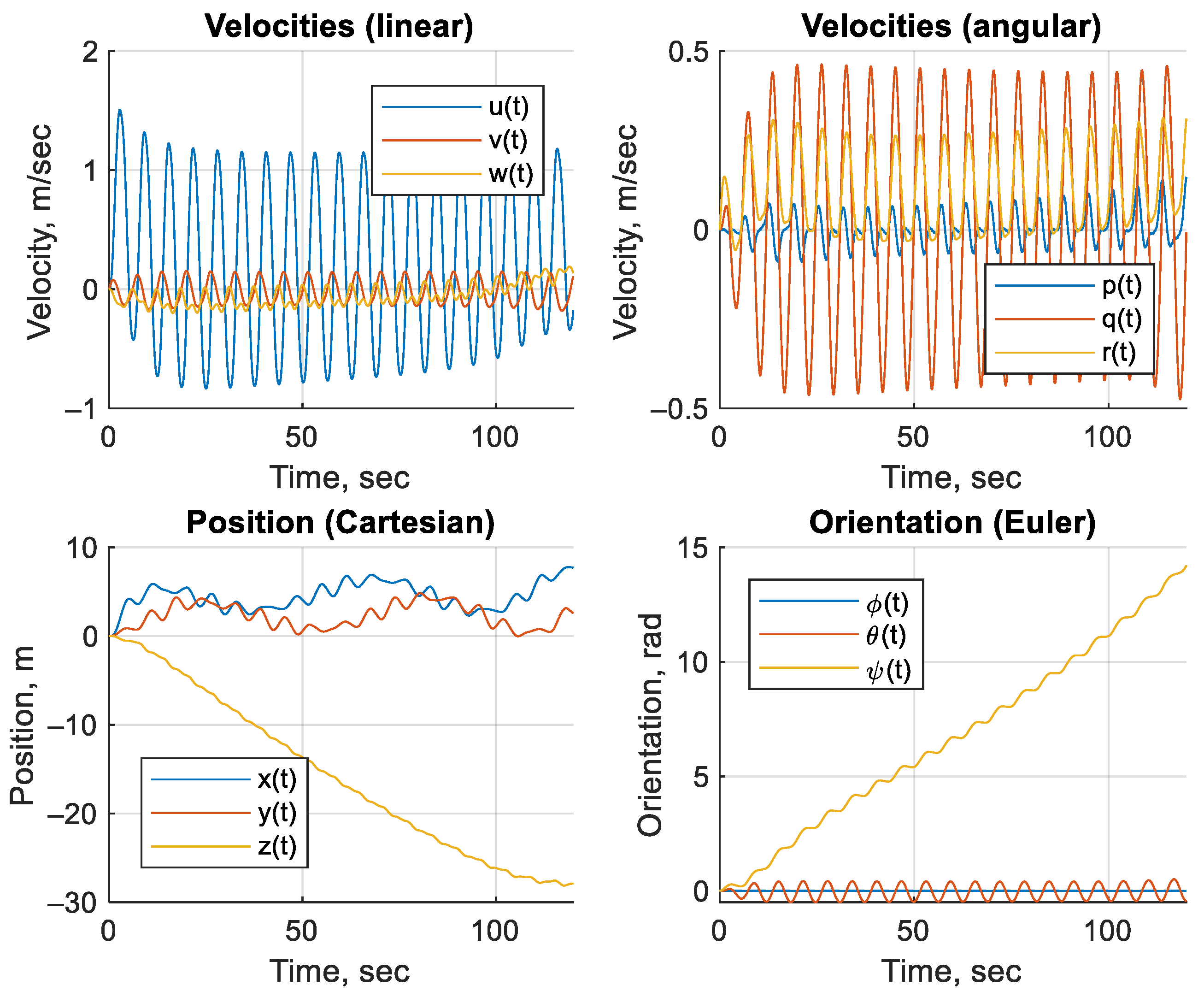
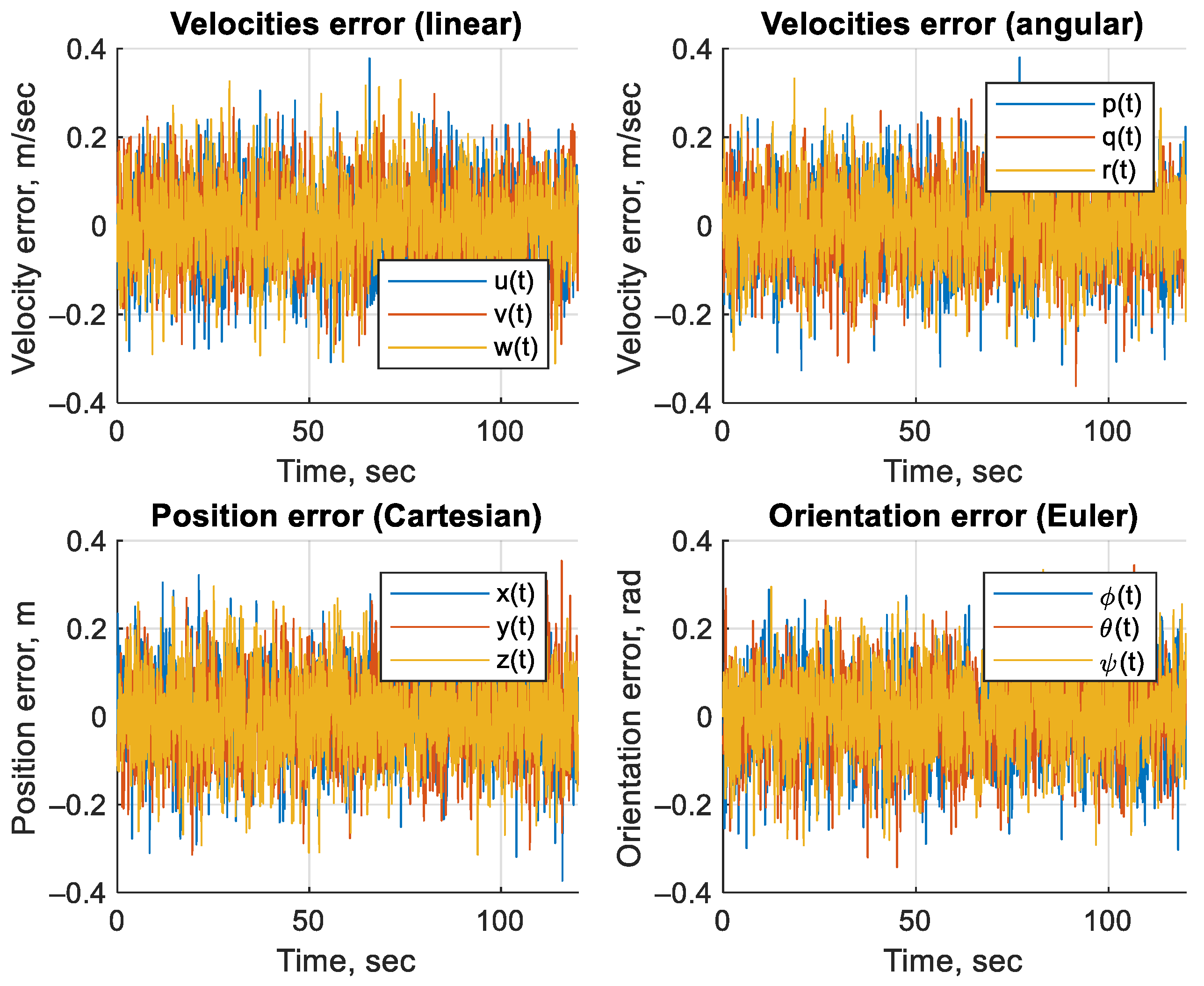
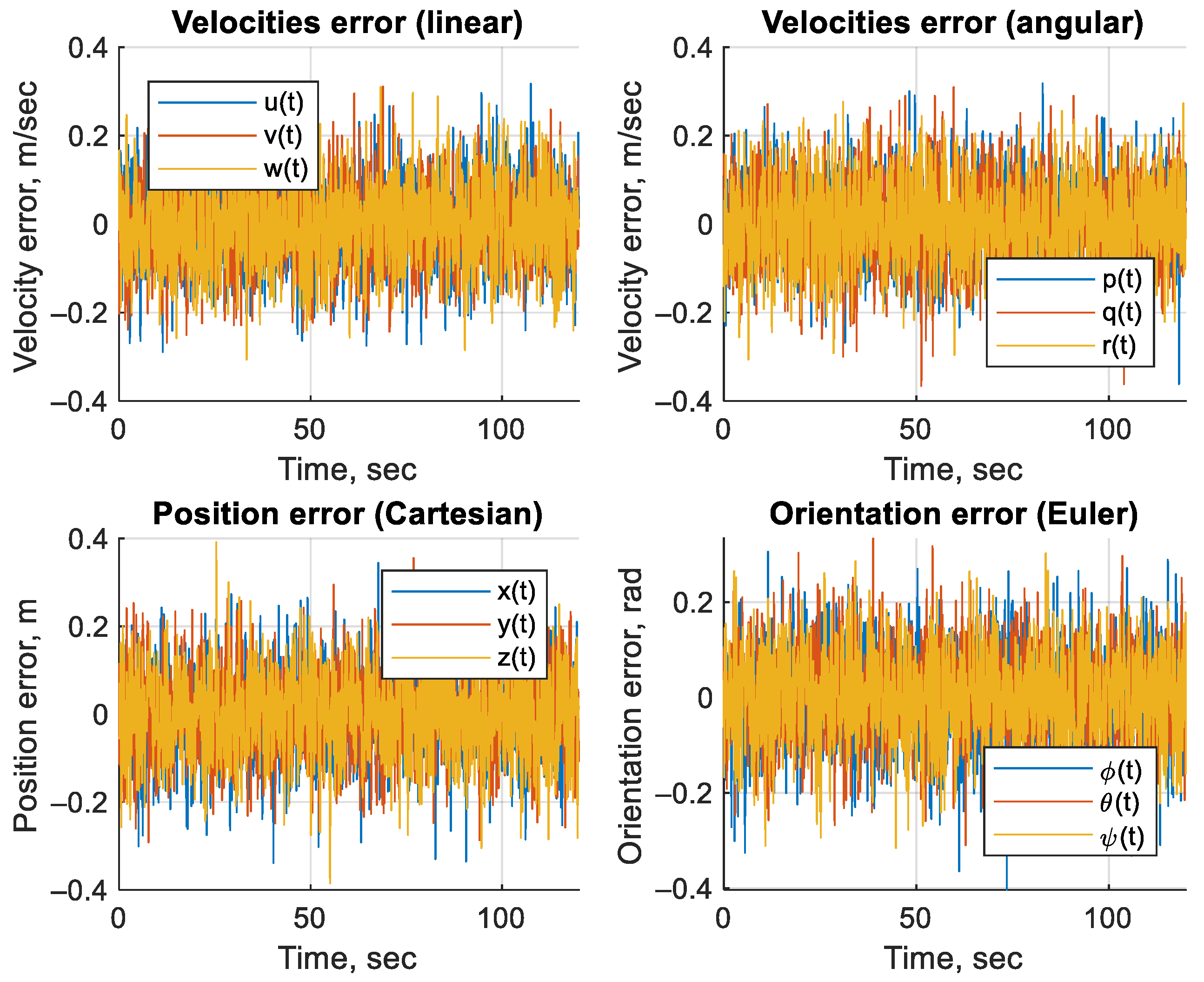
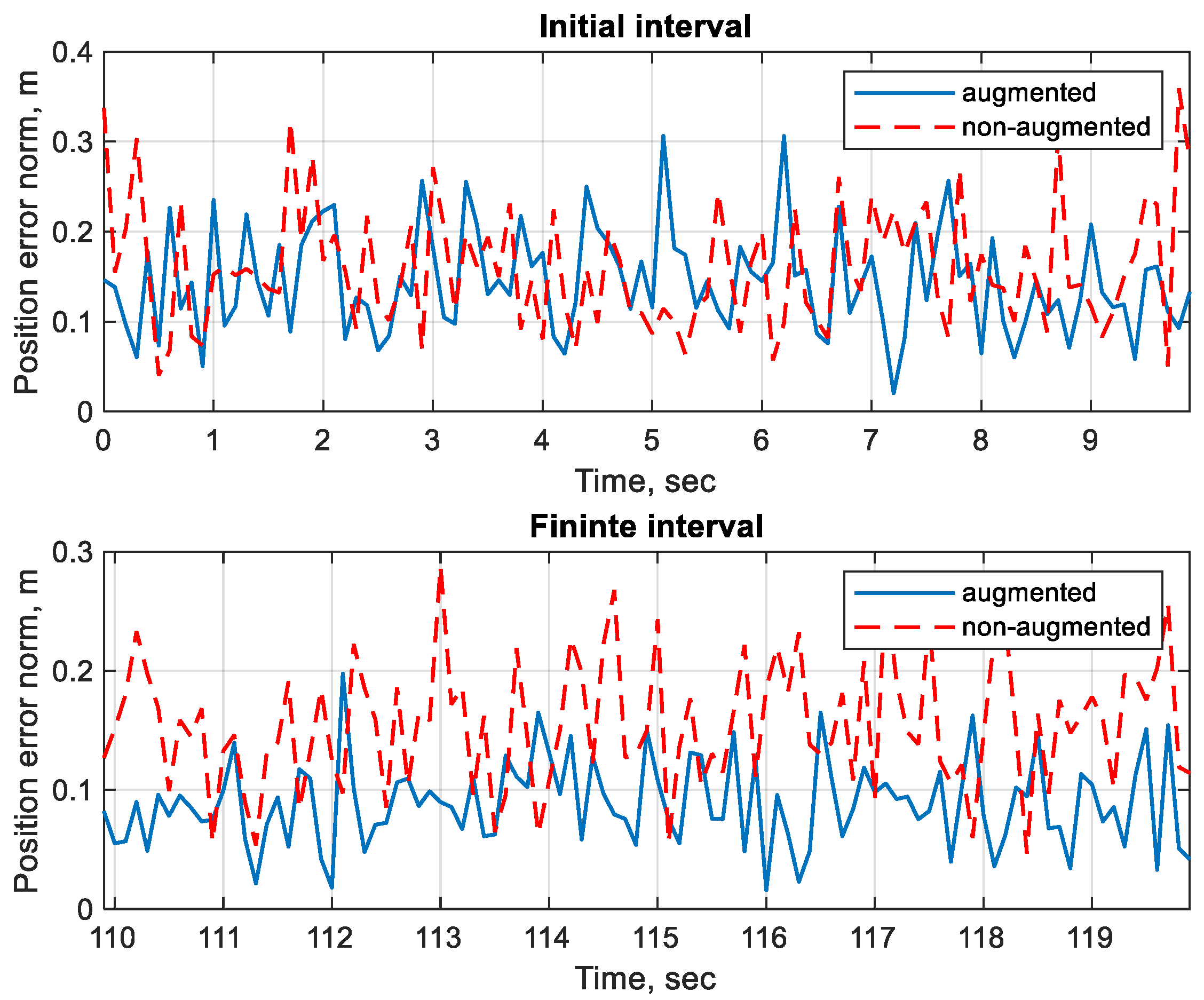
| Filter | Assumed Distribution | Computational Costs | Remarks |
|---|---|---|---|
| EKF | Gaussian | Low | Not appropriate for large systems, divergence may occur due to linearization |
| UKF | Gaussian | Medium | Performance degrades as the state variables increase in number |
| CKF | Gaussian | Medium | The error for higher degree cubature is smaller, and the accuracy and stability under abrupt load changes are higher |
| EnKF | Non-Gaussian | High | Suitable for highly nonlinear systems, measurement interpolation does not affect its performance |
| PF | Non-Gaussian | High | Suitable for more complex system models that are not uniquely defined, nor robust to emissions |
| H∞ | Non-Gaussian | High | Most robust to model uncertainties, but difficult to set up and compute |
| Sensor | Update Rate | Measurements |
|---|---|---|
| IMU | 50 Hz | , , |
| GPS | 1 Hz | , |
| DVL | 25 Hz | |
| PS | 50 Hz |
| Measurements | Continuous | Discrete |
|---|---|---|
| ZOH | 1 Hz | |
| ZOH | 1 Hz | |
| 50 Hz | ||
| ZOH | 50 Hz | |
| ZOH | 50 Hz | |
| 50 Hz | ||
| 25|50 Hz | ||
| 25|50 Hz | ||
| 25|50 Hz | ||
| Case | RMSE |
|---|---|
| Proposed Hybrid Kalman Filter | |
| Non-augmentation | |
| Augmentation | |
| Hybrid Unscented Kalman Filter | |
| Non-augmentation | |
| Augmentation | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kramar, V.; Dementiev, K.; Kabanov, A. Optimal State Estimation in Underwater Vehicle Discrete-Continuous Measurements via Augmented Hybrid Kalman Filter. J. Mar. Sci. Eng. 2025, 13, 933. https://doi.org/10.3390/jmse13050933
Kramar V, Dementiev K, Kabanov A. Optimal State Estimation in Underwater Vehicle Discrete-Continuous Measurements via Augmented Hybrid Kalman Filter. Journal of Marine Science and Engineering. 2025; 13(5):933. https://doi.org/10.3390/jmse13050933
Chicago/Turabian StyleKramar, Vadim, Kirill Dementiev, and Aleksey Kabanov. 2025. "Optimal State Estimation in Underwater Vehicle Discrete-Continuous Measurements via Augmented Hybrid Kalman Filter" Journal of Marine Science and Engineering 13, no. 5: 933. https://doi.org/10.3390/jmse13050933
APA StyleKramar, V., Dementiev, K., & Kabanov, A. (2025). Optimal State Estimation in Underwater Vehicle Discrete-Continuous Measurements via Augmented Hybrid Kalman Filter. Journal of Marine Science and Engineering, 13(5), 933. https://doi.org/10.3390/jmse13050933






