Hybrid Path Planning Method for USV Based on Improved A-Star and DWA
Abstract
1. Introduction
- Improve the search strategy of the A-Star algorithm to avoid passing through the vertices of obstacles and narrow passages between obstacles during the path search process, thereby enhancing the safety and feasibility of path planning;
- Optimize the nodes and use the Bezier curve smoothing method to smooth the path, proposing an adaptive strategy for selecting control points to improve the smoothness and driving stability of the path;
- The improved A-Star algorithm is combined with the DWA to comprehensively consider the kinematic characteristics and various physical limitations of USVs, generate a global path, and use the DWA algorithm to achieve dynamic obstacle avoidance to handle obstacles in dynamic environments and ensure the safe navigation of unmanned vessels.
2. Global Path Planning
2.1. Traditional A-Star Algorithm
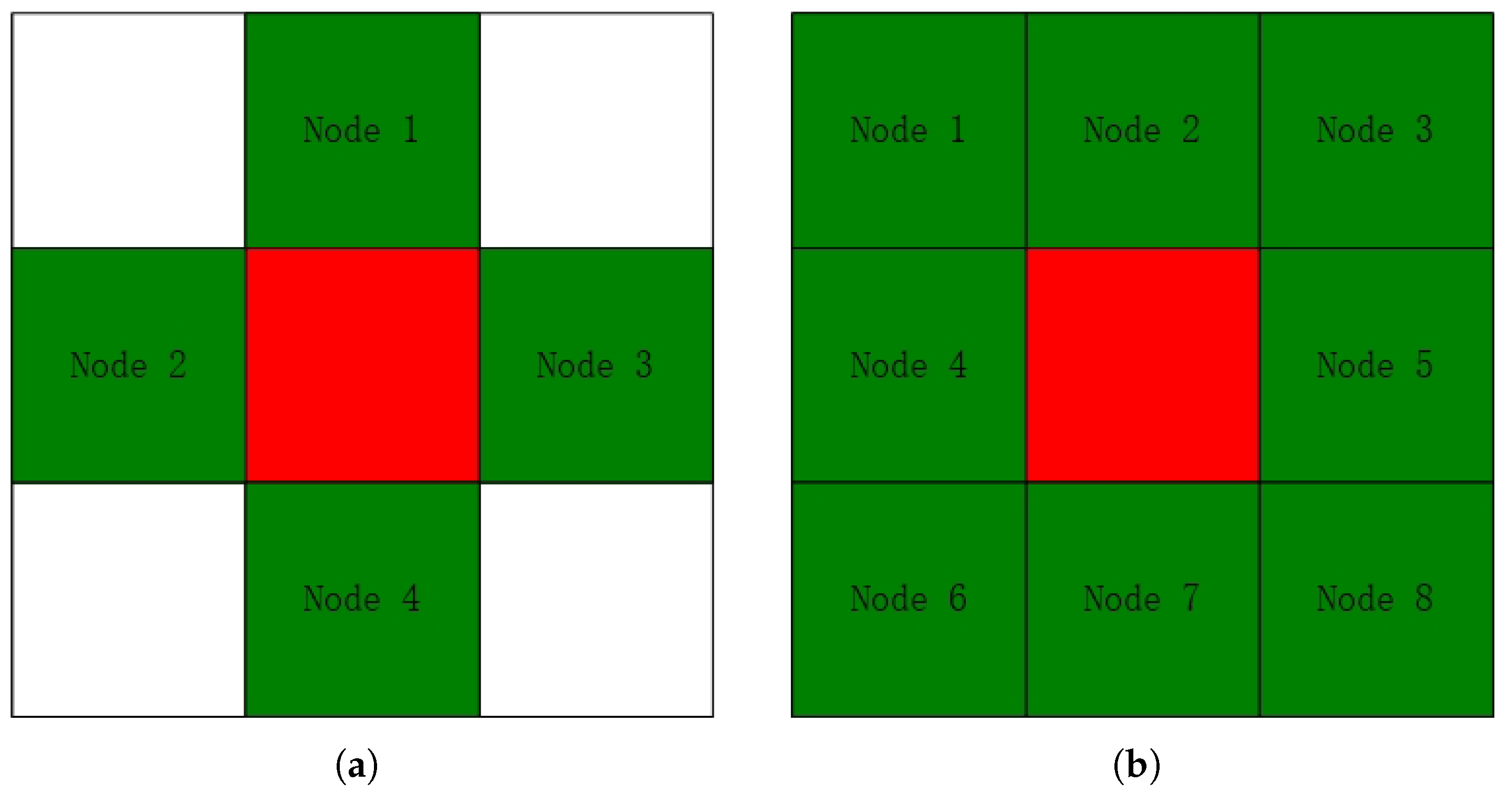
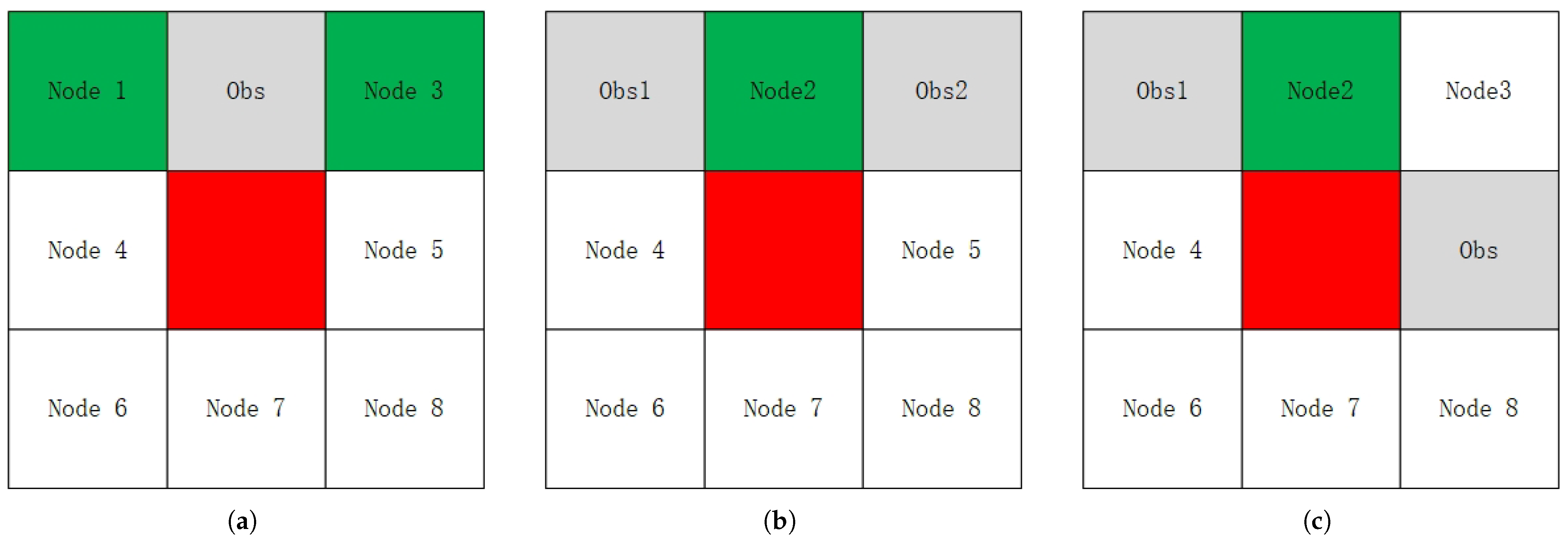
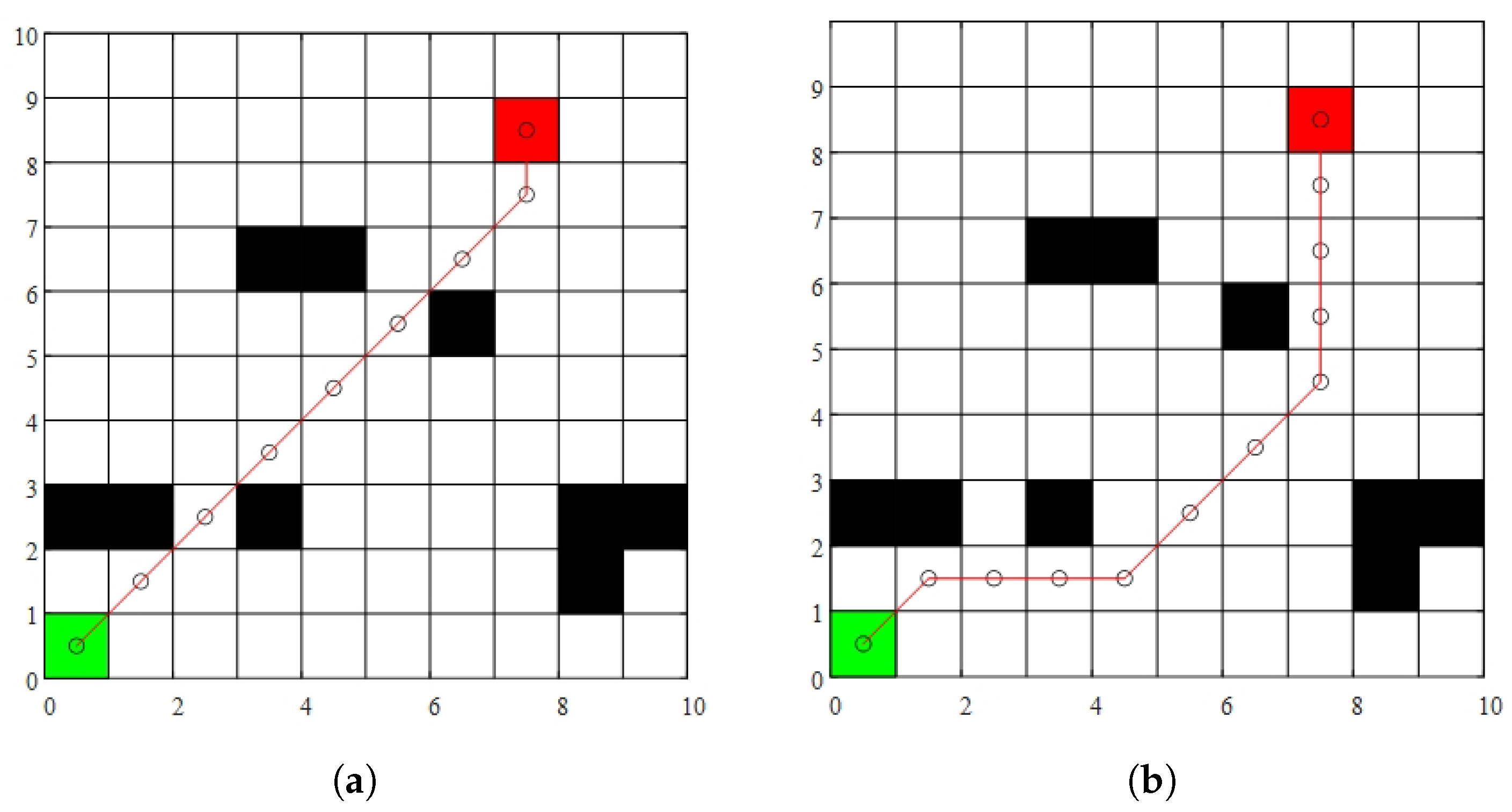
2.2. Improvement of Search Strategy
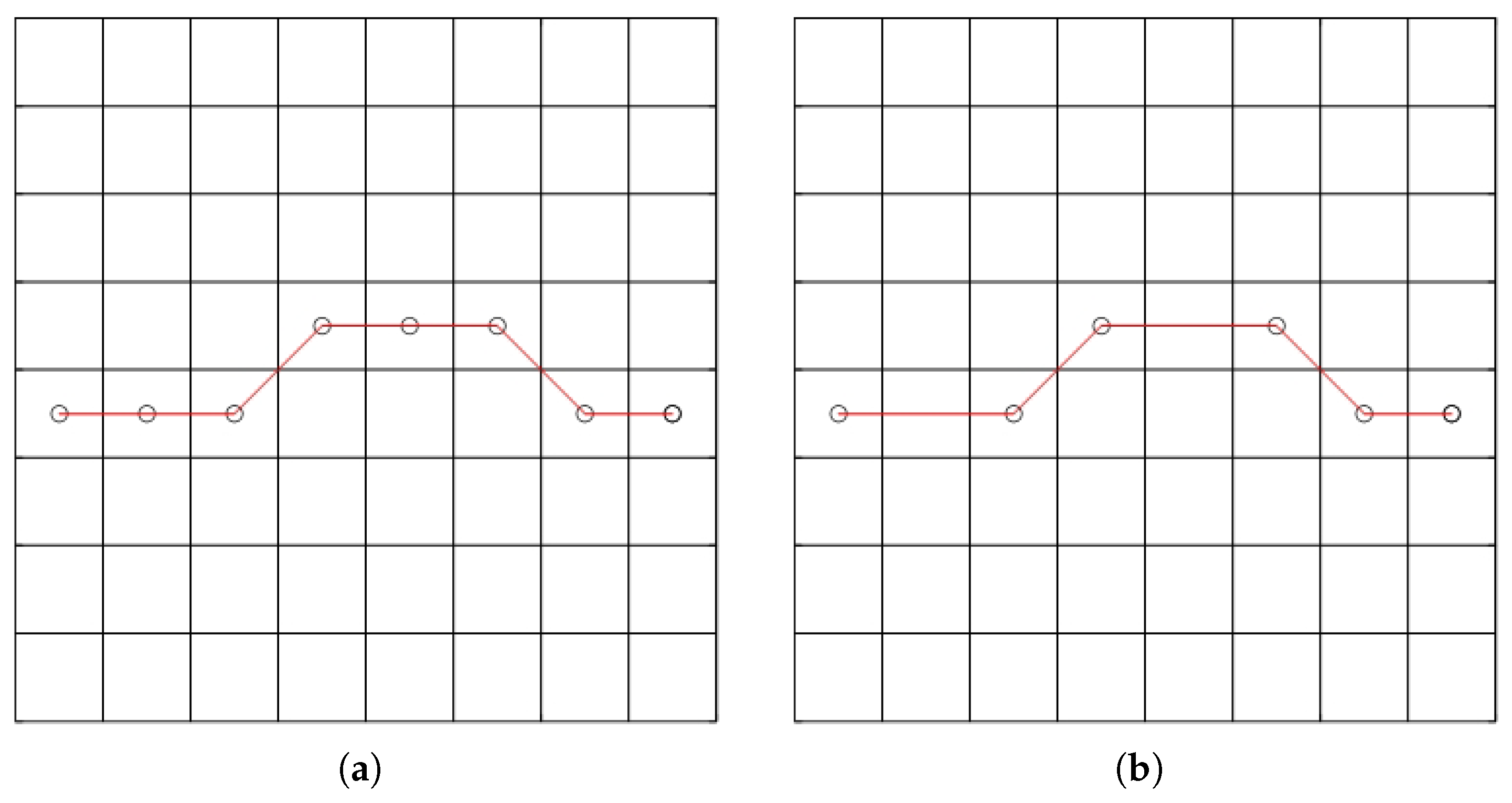
2.3. Node Optimization Strategy
2.4. Path Smoothing
- Node extraction: Extract a series of optimized path nodes ,,,…, from Section 2.3. Starting from the starting point , divide these nodes into three consecutive groups of three nodes each. For example, the first group , . If there are (where k is a positive integer) nodes and there is only one node left that cannot form three nodes, then is taken as a group. If there are nodes in total, they can be divided into groups of three. Each group of three nodes will be used to generate a Bézier curve.
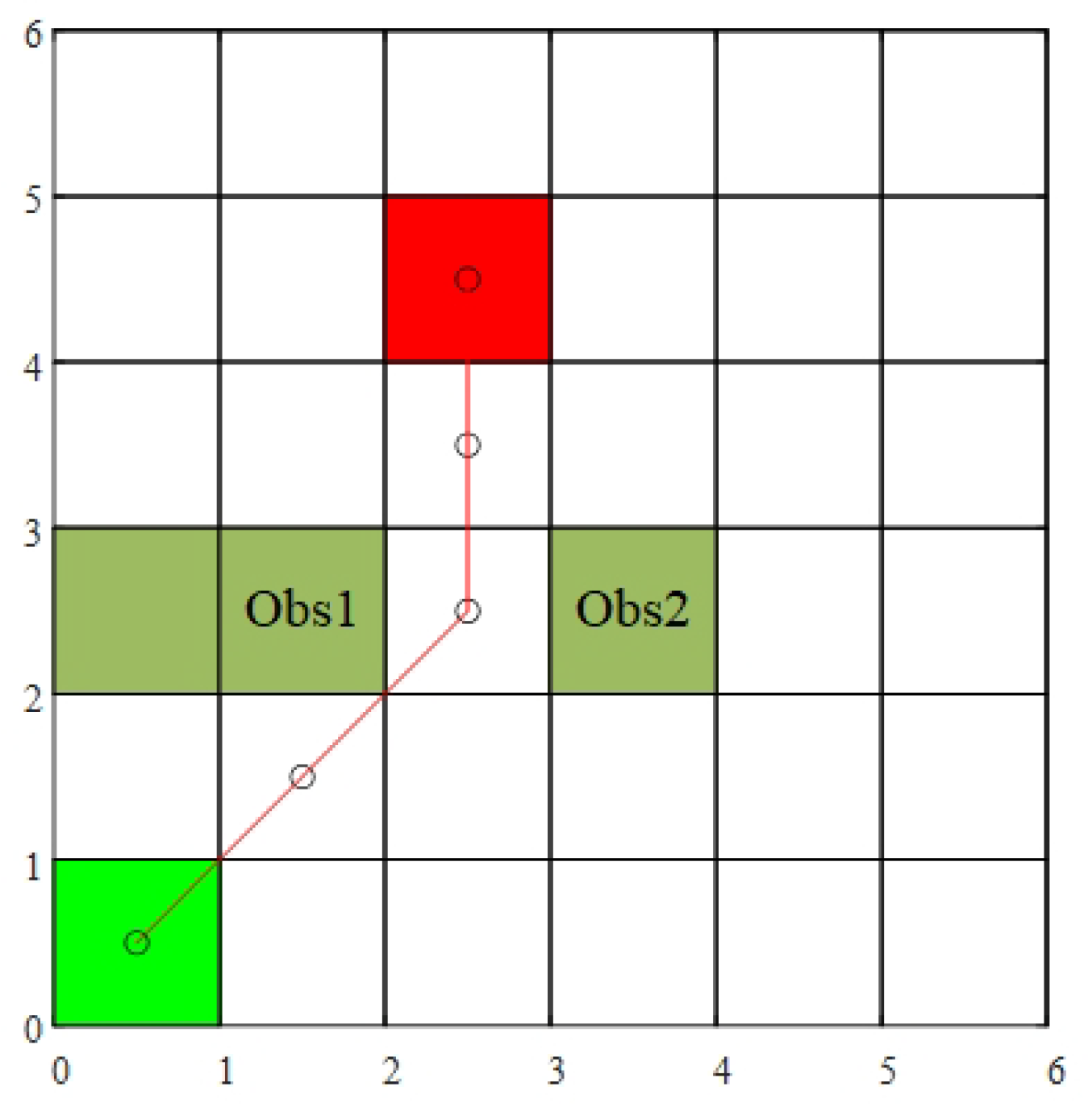
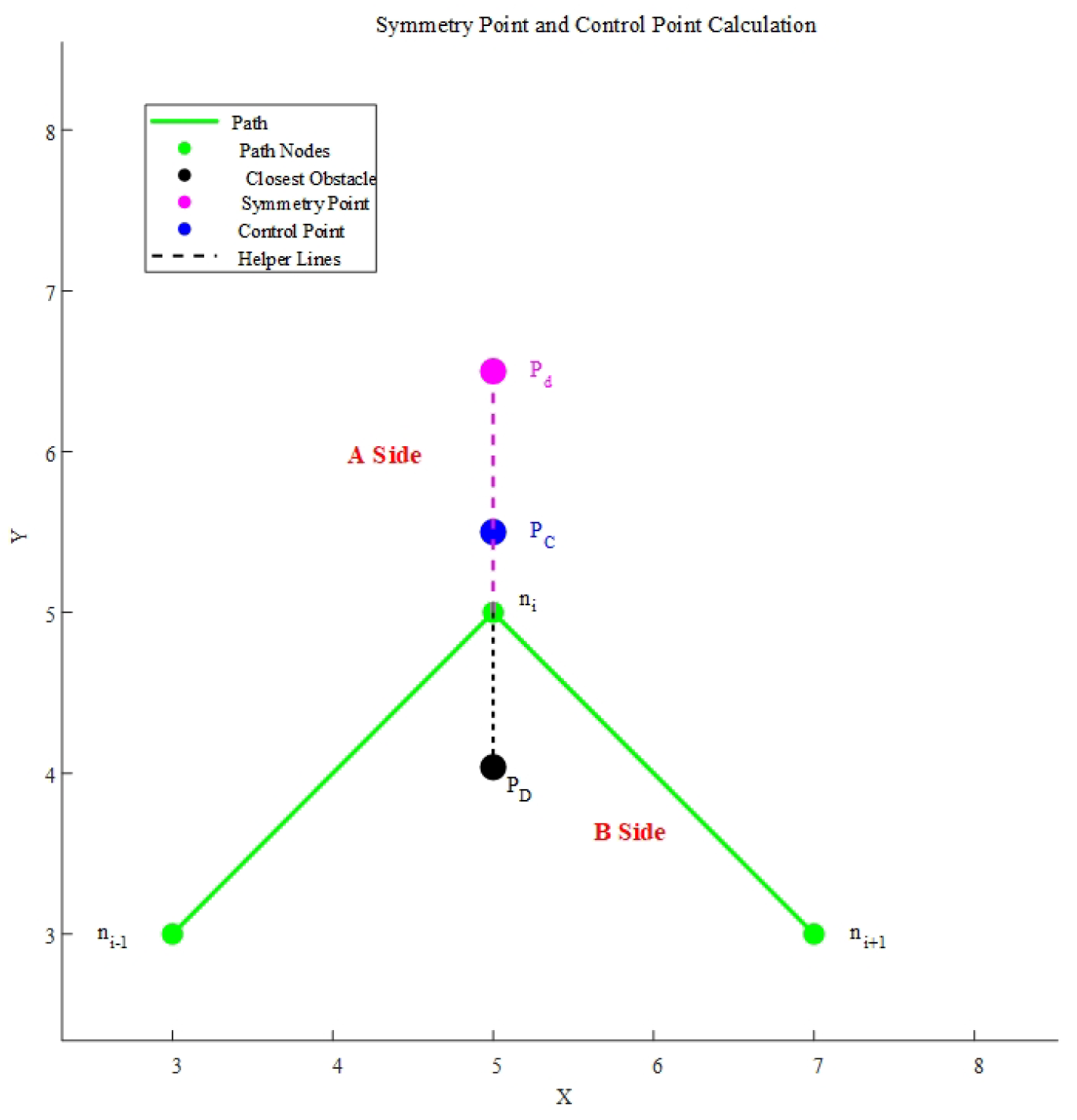
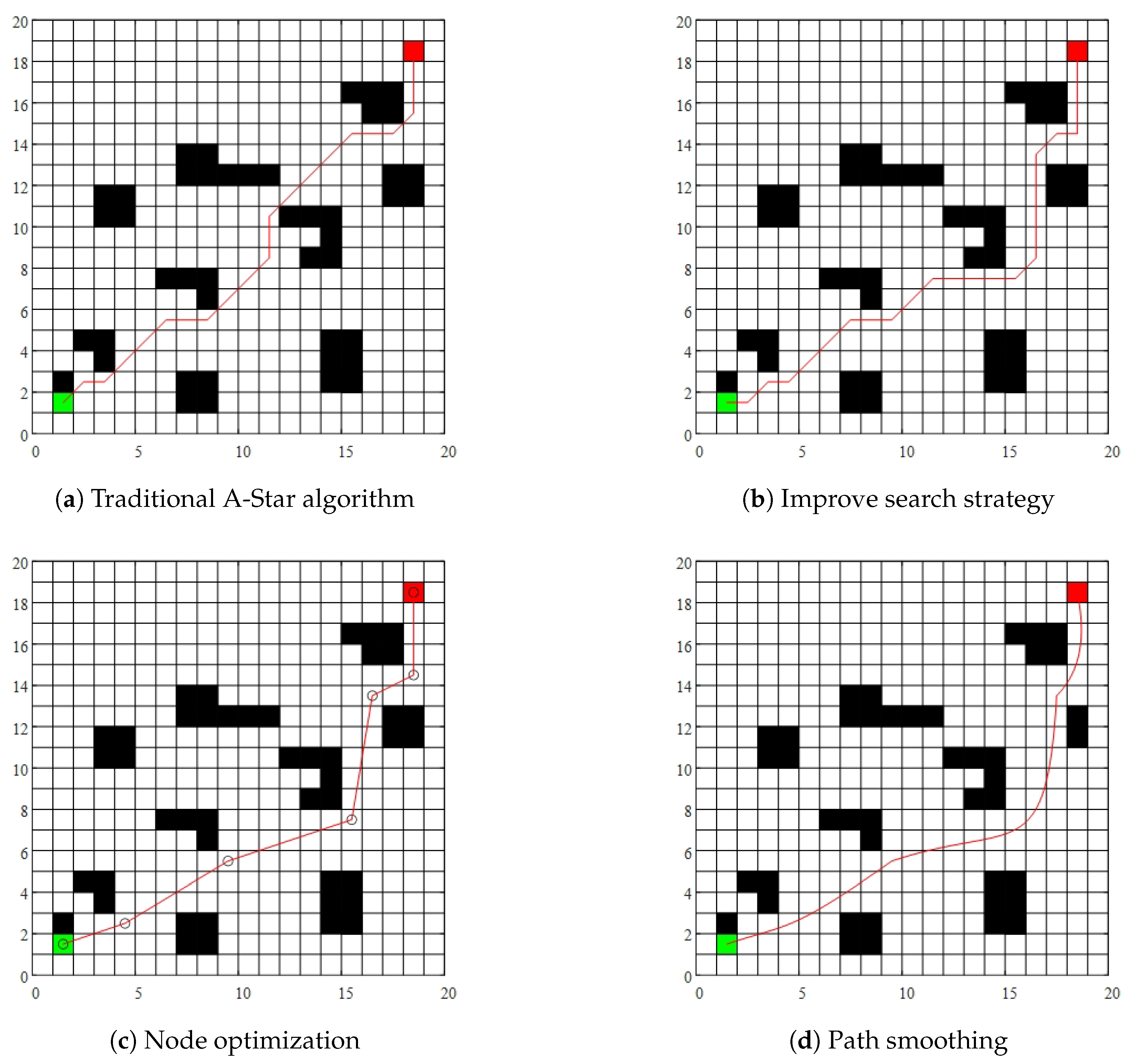
- Selection of control points: The position of control points is crucial for path smoothness and obstacle avoidance performance. This paper proposes a dynamic adjustment method based on obstacle distribution. Select a set of nodes from the previous step, . Define the path composed of this group of nodes as . Select the middle node , check the obstacles on both sides of path , and calculate the distance between the obstacles on both sides and the middle node . Calculate the distance from the obstacle on side A to , and calculate the distance from the obstacle on side B of the path to . Determine the difference between and . If , it indicates that the intermediate node is closer to the obstacle on side B, and the control point needs to be shifted to side A to ensure the path avoids the obstacle. Conversely, if , the control point should be shifted to side B.Assume that the nearest obstacle coordinate to is . The control point can be determined by calculating the symmetry point of and . The formula for isIf and , thenThe final position of the control point is chosen between the middle node and the symmetry point . Specifically,This formula ensures that the control point is biased towards one-third of the distance between the middle node and the symmetry point, thereby controlling the smoothness of the path while effectively avoiding obstacles. Figure 9 illustrates the method for selecting control points for the Bézier curve, where represents the obstacle closest to node , denotes the symmetry point of relative to , and represents the position of the control point.If there are only nodes in the path, the last two points cannot form a set of three nodes, so no control points are added, and the last two points are directly smoothed to form the path. When the distance between the obstacle and the intermediate node is greater than 1.5 grid sizes, the surrounding environment of the node is considered relatively safe, and no additional control points are needed. In this case, the nodes are directly used for path smoothing without introducing additional control points, ensuring the smoothness of the path while avoiding unnecessary complex calculations.
3. Dynamic Obstacle Avoidance
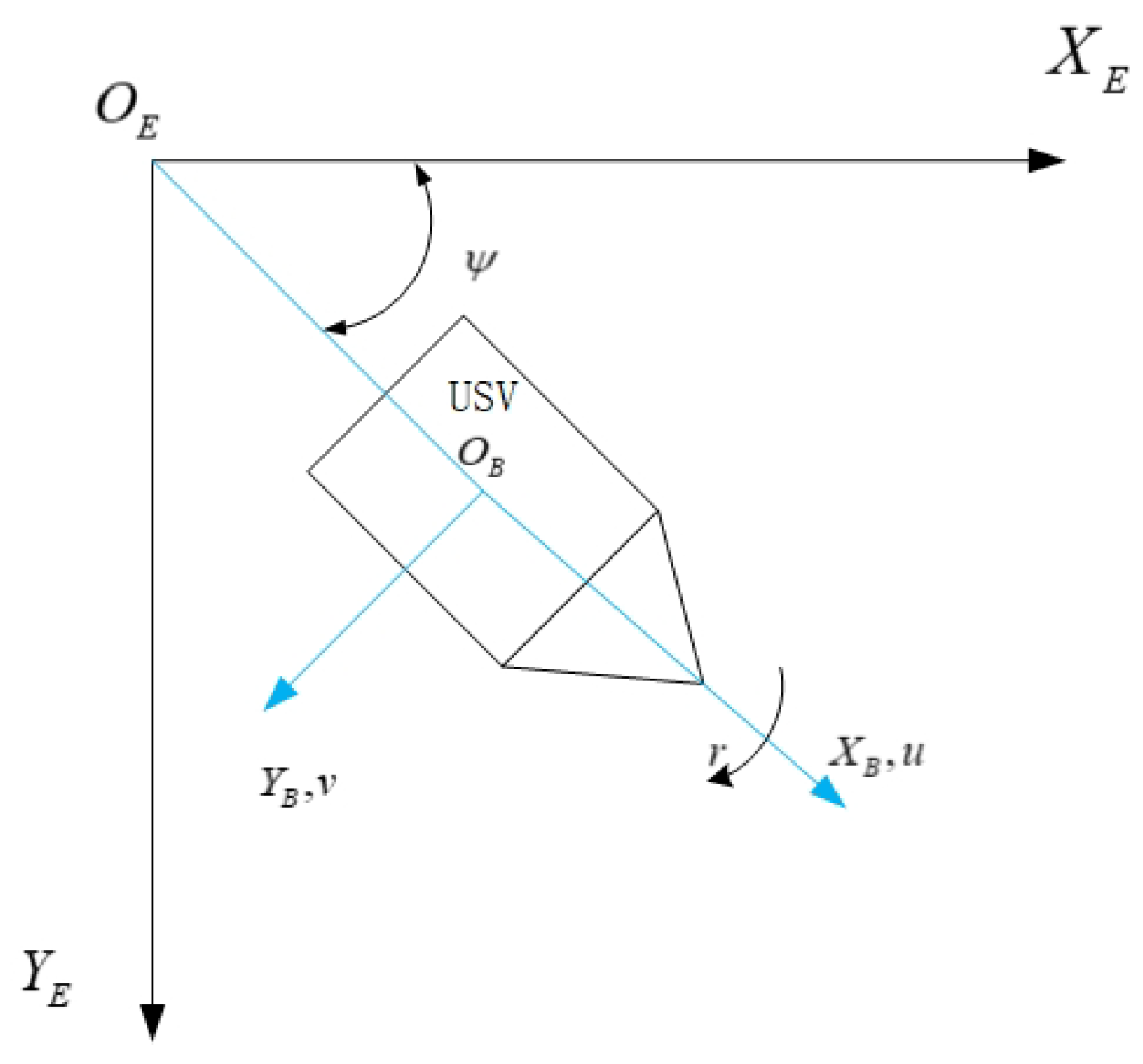
3.1. Modeling of Unmanned Surface Vessels
3.2. Dynamic Window Approach
3.2.1. Speed Sampling
3.2.2. Trajectory Prediction
3.2.3. Evaluation Function
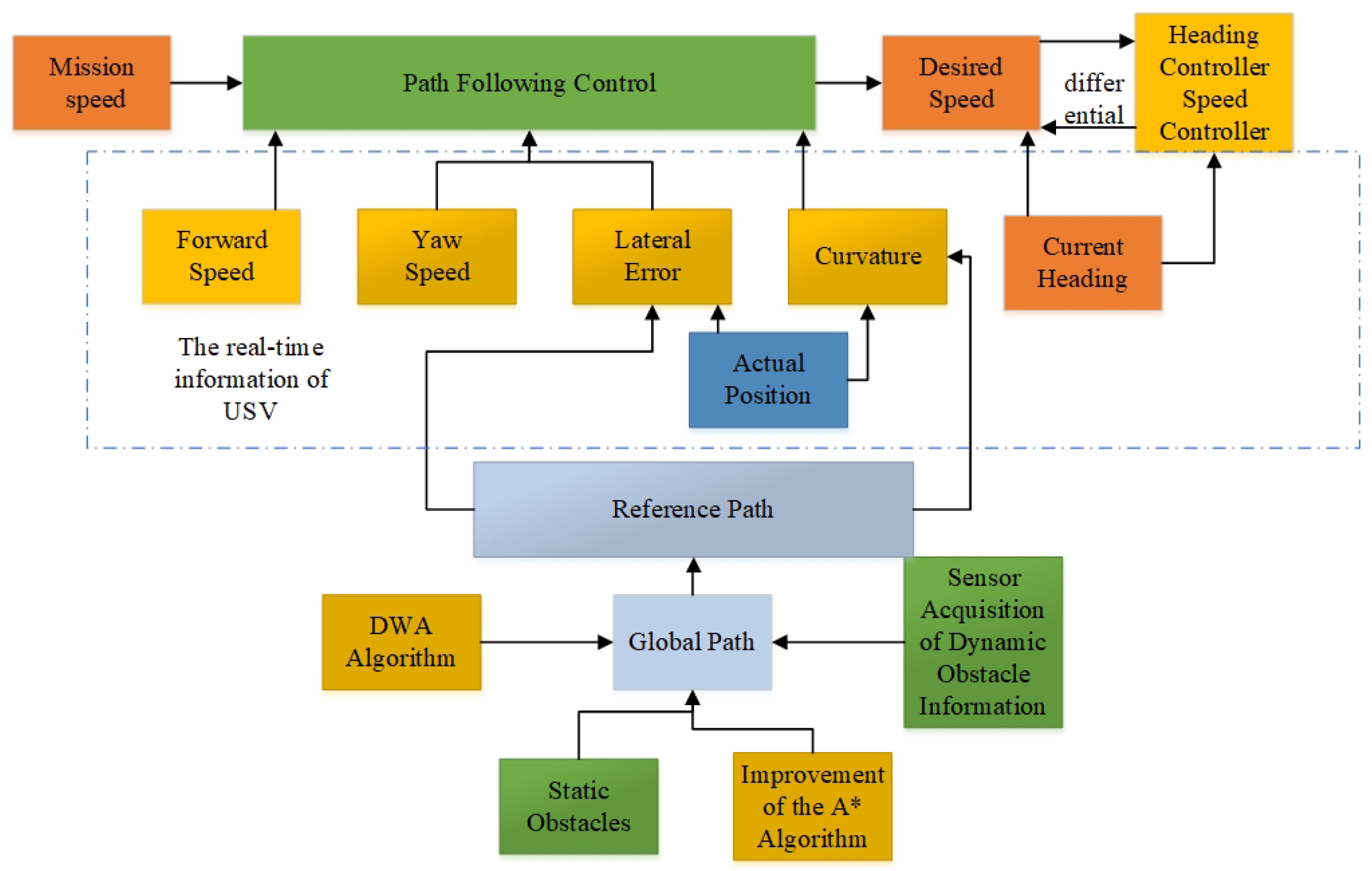
3.3. Control System Design and Architecture
4. Simulation
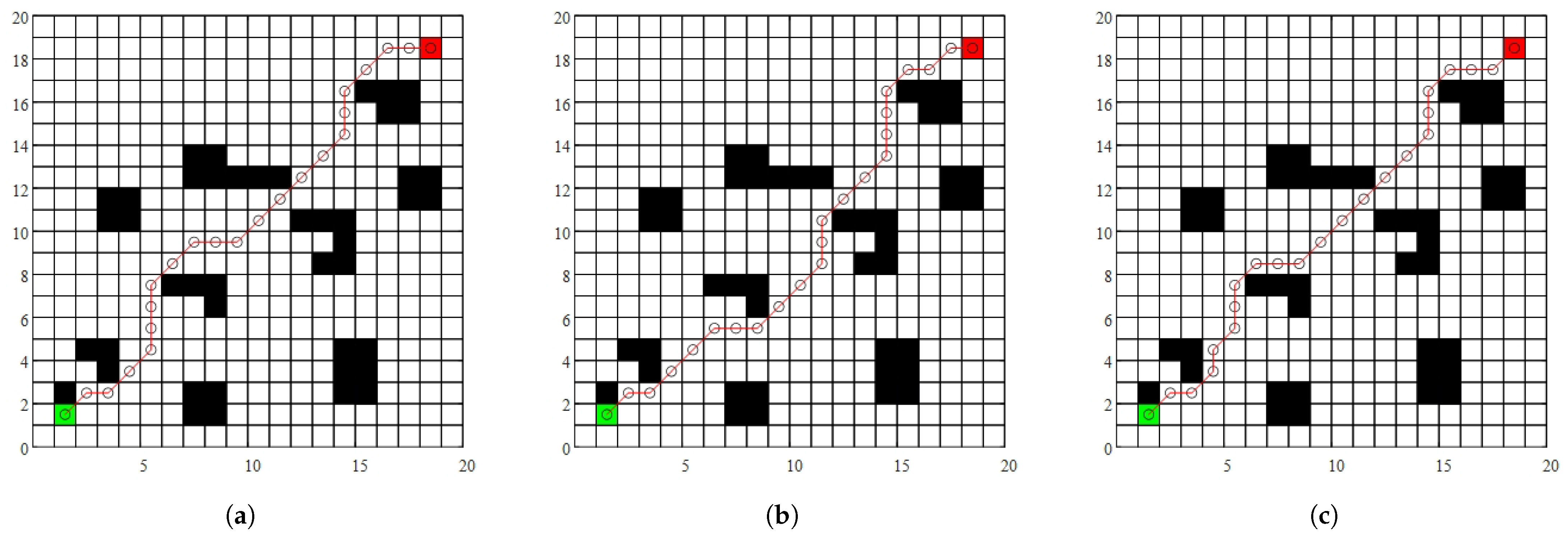
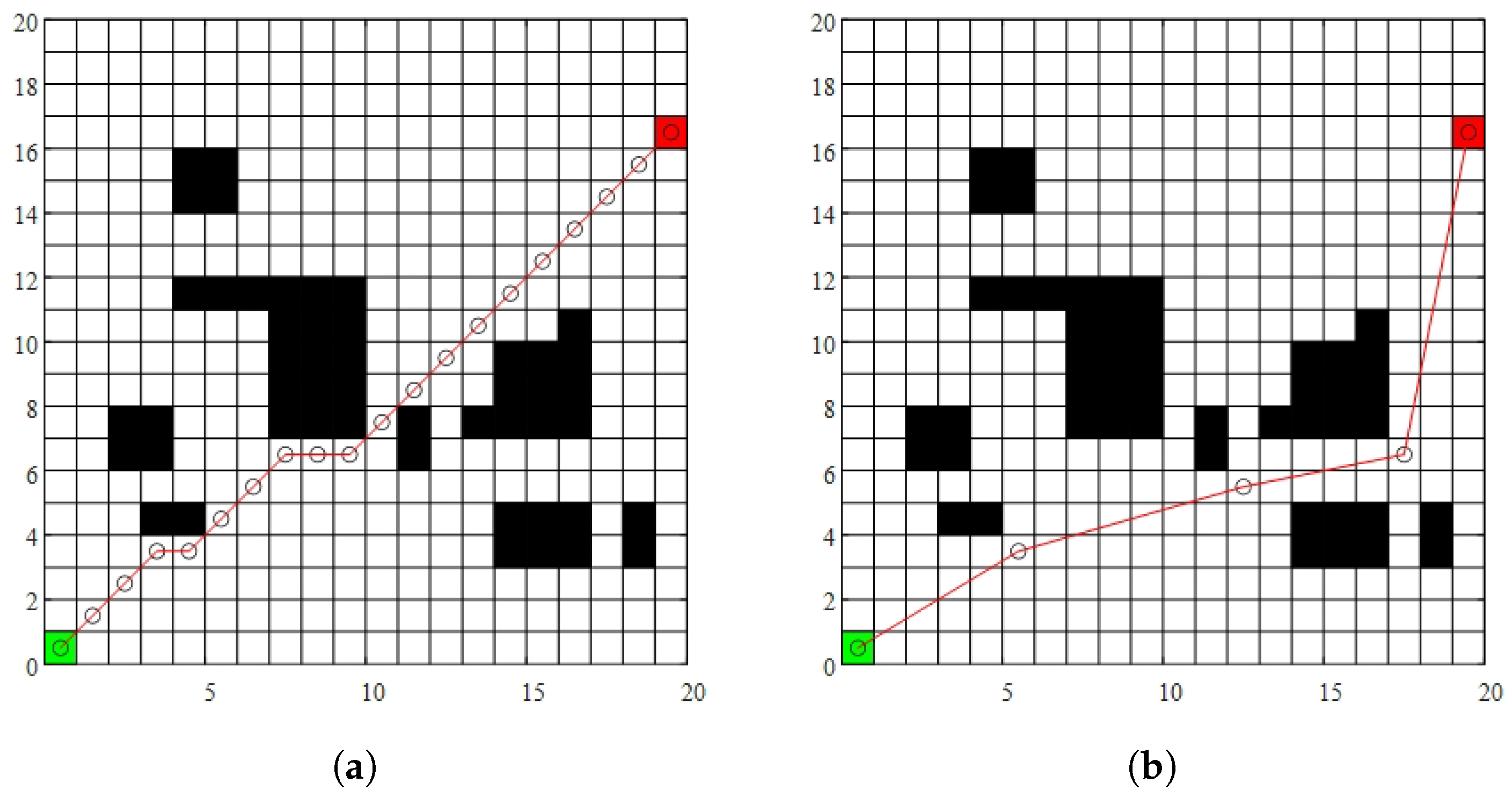
4.1. Simulation Results of Various Improvements in Global Path Planning
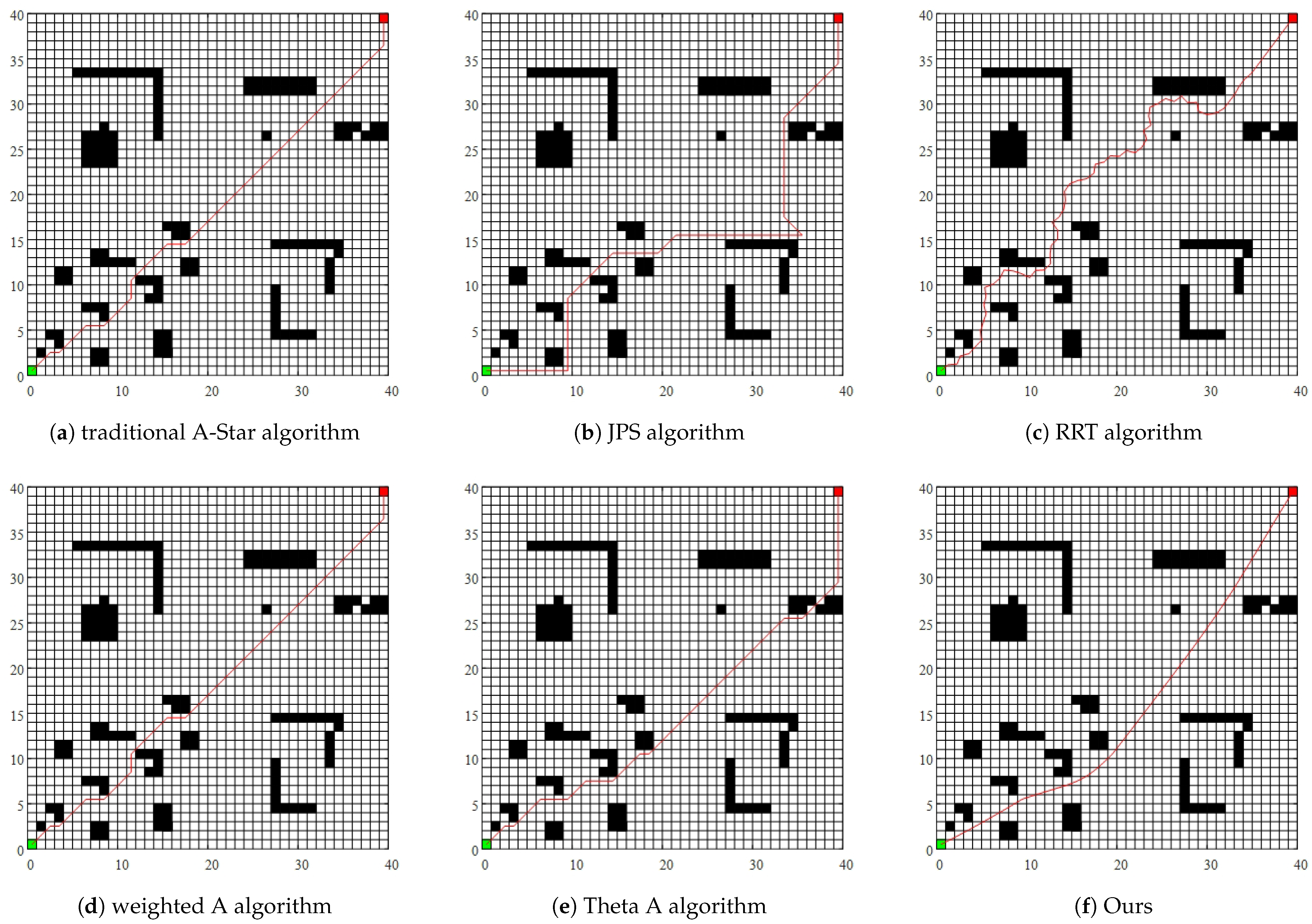
4.2. Comparison with Other Algorithms
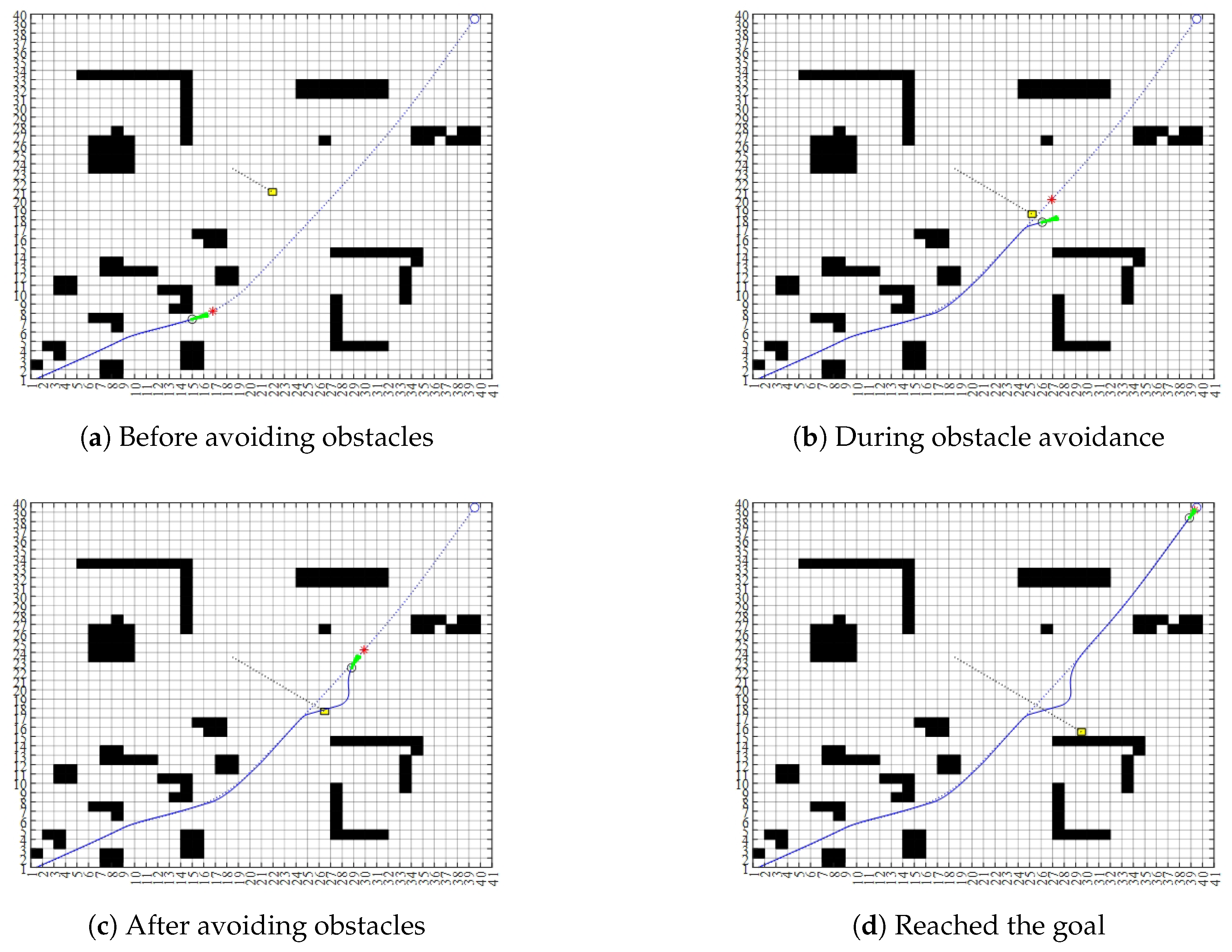
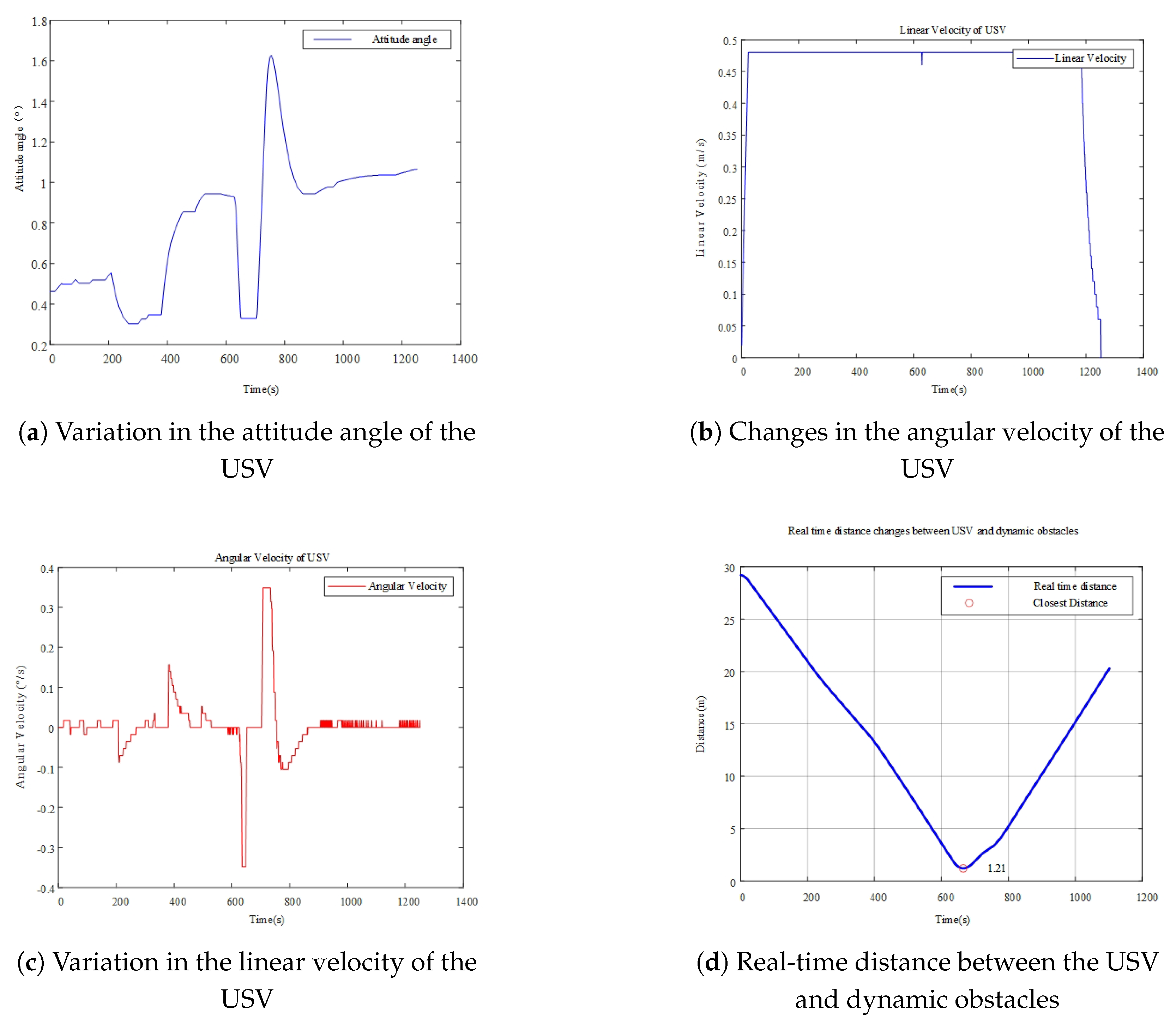
4.3. Dynamic Obstacle Avoidance
5. Results
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A* | A-Star algorithm |
| ACO | Ant Colony Optimization |
| APF | Artificial Potential Field |
| COLREGs | International Regulations for Preventing Collisions at Sea |
| D* | D-Star Algorithm |
| DDPG | Deep Deterministic Policy Gradient |
| DDQN | Double Deep Q-Network |
| DWA | Dynamic Window Approach |
| GA | Genetic Algorithm |
| JPS | Jump Point Search |
| MPC | Model Predictive Control |
| RRT | Rapidly exploring Random Tree |
| VO | Velocity Obstacle |
| USV | Unmanned Surface Vehicle |
References
- Liu, Z.; Zhang, Y.; Yu, X.; Yuan, C. Unmanned surface vehicles: An overview of developments and challenges. Annu. Rev. Control 2016, 41, 71–93. [Google Scholar] [CrossRef]
- Xing, B.; Yu, M.; Liu, Z.; Tan, Y.; Sun, Y.; Li, B. A Review of Path Planning for Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2023, 11, 1556. [Google Scholar] [CrossRef]
- Hu, S.; Tian, S.; Zhao, J.; Shen, R. Path planning of an unmanned surface vessel based on the improved A-Star and dynamic window method. J. Mar. Sci. Eng. 2023, 11, 1060. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connection with Graphs. Numer. Math. 1959, 1, 101–118. [Google Scholar] [CrossRef]
- LaValle, S. Rapidly-Exploring Random Trees: A New Tool for Path Planning. In Research Report 9811; Department of Computer Science, Iowa State University: Ames, IA, USA, 1998. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Dorigo, M.; Di Caro, G.; Gambardella, L.M. Ant algorithms for discrete optimization. Artif. Life 1999, 5, 137–172. [Google Scholar] [CrossRef] [PubMed]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, L.; Bai, Y. Path planning for unmanned surface vehicles based on modified artificial fish swarm algorithm with local optimizer. Math. Probl. Eng. 2022, 2022, 1283374. [Google Scholar] [CrossRef]
- Deng, F.; Jin, L.; Hou, X.; Wang, L.; Li, B.; Yang, H. COLREGs: Compliant dynamic obstacle avoidance of USVs based on the dynamic navigation ship domain. J. Mar. Sci. Eng. 2021, 9, 837. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, P.; Li, B.; Bai, C. A DDPG-Based USV Path-Planning Algorithm. Appl. Sci. 2023, 13, 10567. [Google Scholar] [CrossRef]
- Ren, J.; Zhang, J.; Cui, Y. Autonomous obstacle avoidance algorithm for unmanned surface vehicles based on an improved velocity obstacle method. ISPRS Int. J. Geo-Inf. 2021, 10, 618. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Zhao, S.; Su, P.; Fu, H.; Niu, H. Hybrid path planning for USV with kinematic constraints and COLREGS based on improved APF-RRT and DWA. Ocean Eng. 2025, 318, 120128. [Google Scholar] [CrossRef]
- Liang, J.; Liu, L. Optimal path planning method for unmanned surface vehicles based on improved shark-inspired algorithm. J. Mar. Sci. Eng. 2023, 11, 1386. [Google Scholar] [CrossRef]
- Gu, Y.; Rong, Z.; Tong, H.; Wang, J.; Si, Y.; Yang, S. Unmanned surface vehicle collision avoidance path planning in restricted waters using multi-objective optimisation complying with COLREGs. Sensors 2022, 22, 5796. [Google Scholar] [CrossRef]
- Wang, D.; Chen, H.; Lao, S.; Drew, S. Efficient path planning and dynamic obstacle avoidance in edge for safe navigation of USV. IEEE Internet Things J. 2023, 11, 10084–10094. [Google Scholar] [CrossRef]
- Jaramillo-Martínez, R.; Chavero-Navarrete, E.; Ibarra-Pérez, T. Reinforcement-Learning-Based Path Planning: A Reward Function Strategy. Appl. Sci. 2024, 14, 7654. [Google Scholar] [CrossRef]
- Vashisth, A.; Rückin, J.; Magistri, F.; Stachniss, C.; Popovic, M. Deep Reinforcement Learning with Dynamic Graphs for Adaptive Informative Path Planning. IEEE Robot. Autom. Lett. 2024, 9, 7747–7754. [Google Scholar] [CrossRef]
- Yang, X.; Shi, Y.; Liu, W.; Ye, H.; Zhong, W.; Xiang, Z. Global path planning algorithm based on double DQN for multi-tasks amphibious unmanned surface vehicle. Ocean Eng. 2022, 266, 112809. [Google Scholar]
- Zhou, X.; Wu, P.; Zhang, H.; Guo, W.; Liu, Y. Learn to navigate: Cooperative path planning for unmanned surface vehicles using deep reinforcement learning. IEEE Access 2019, 7, 165262–165278. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhu, B.; Zhou, Y.; Yao, P.; Yu, J. Cooperative path planning of multiple unmanned surface vehicles for search and coverage task. Drones 2022, 7, 21. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, S.R.; Chung, K.S.; Chen, M.L.; Yuan, Z.M. Time-optimal path planning and tracking based on nonlinear model predictive control and its application on automatic berthing. Ocean Eng. 2023, 286, 115228. [Google Scholar] [CrossRef]
- Yang, C.; Pan, J.; Wei, K.; Lu, M.; Jia, S. A novel unmanned surface vehicle path-planning algorithm based on A* and artificial potential field in ocean currents. J. Mar. Sci. Eng. 2024, 12, 285. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Liang, X. Design and Implementation of Global Path Planning System for Unmanned Surface Vehicle among Multiple Task Points. Int. J. Veh. Auton. Syst. 2018, 14, 82–105. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Nadimpalli, S.V. New Fusion Algorithm Provides an Alternative Approach to Robotic Path Planning. arXiv 2020, arXiv:2006.05241. [Google Scholar]
- Kabir, R.; Watanobe, Y.; Islam, M.R.; Naruse, K. Enhanced Robot Motion Block of A-star Algorithm for Robotic Path Planning. Sensors 2024, 24, 1422. [Google Scholar] [CrossRef]
- Hu, Y.; Harabor, D.; Qin, L.; Yin, Q. Regarding goal bounding and jump point search. J. Artif. Intell. Res. 2021, 70, 631–681. [Google Scholar] [CrossRef]
- Zhang, J.; Ling, H.; Tang, Z.; Song, W.; Lu, A. Path planning of USV in confined waters based on improved A* and DWA fusion algorithm. Ocean Eng. 2025, 322, 120475. [Google Scholar] [CrossRef]
- Han, X.; Zhang, X. Multi-scale ThetA* algorithm for the path planning of unmanned surface vehicle. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2022, 236, 427–435. [Google Scholar] [CrossRef]
- Han, S.; Wang, L.; Wang, Y.; He, H. A dynamically hybrid path planning for unmanned surface vehicles based on non-uniform Theta* and improved dynamic windows approach. Ocean Eng. 2022, 257, 111655. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, Y.; Gong, C.; Zhou, Y.; Zeng, C.; Zhu, S. Improved dynamic window approach for Unmanned Surface Vehicles’ local path planning considering the impact of environmental factors. Sensors 2022, 22, 5181. [Google Scholar] [CrossRef]
- Xu, D.; Yang, J.; Zhou, X.; Xu, H. Hybrid path planning method for USV using bidirectional A* and improved DWA considering the manoeuvrability and COLREGs. Ocean Eng. 2024, 298, 117210. [Google Scholar] [CrossRef]
- Yao, M.; Deng, H.; Feng, X.; Li, P.; Li, Y.; Liu, H. Global Path Planning for Differential Drive Mobile Robots Based on Improved BSGA* Algorithm. Appl. Sci. 2023, 13, 11290. [Google Scholar] [CrossRef]
- Liu, L.; Wang, B.; Xu, H. Research on path-planning algorithm integrating optimization A-star algorithm and artificial potential field method. Electronics 2022, 11, 3660. [Google Scholar] [CrossRef]
- Hassani, V.; Lande, S.V. Path planning for marine vehicles using Bézier curves. IFAC-PapersOnLine 2018, 51, 305–310. [Google Scholar] [CrossRef]
- Lai, R.; Wu, Z.; Liu, X.; Zeng, N. Fusion algorithm of the improved A* algorithm and segmented bezier curves for the path planning of mobile robots. Sustainability 2023, 15, 2483. [Google Scholar] [CrossRef]
- Yin, X.; Cai, P.; Zhao, K.; Zhang, Y.; Zhou, Q.; Yao, D. Dynamic path planning of AGV based on kinematical constraint A* algorithm and following DWA fusion algorithms. Sensors 2023, 23, 4102. [Google Scholar] [CrossRef]

| Algorithms | Turning Points | Path Length | Planning Time |
|---|---|---|---|
| Manhattan | 9 | 26.97 | 0.018 |
| Euclidean | 11 | 26.97 | 0.032 |
| Chebyshev | 12 | 26.97 | 0.12 |
| Location of Obstacles | Excluded Path Points |
|---|---|
| Node 1, Node 5 | Node 2 |
| Node 2, Node 8 | Node 5 |
| Node 3, Node 7 | Node 5 |
| Node 5, Node 6 | Node 7 |
| Node 8, Node 4 | Node 7 |
| Node 7, Node 1 | Node 4 |
| Node 6, Node 2 | Node 4 |
| Node 4, Node 3 | Node 2 |
| Algorithms | Turning Points | Path Length | Planning Time | Smoothness |
|---|---|---|---|---|
| A-Star | 9 | 26.97 | 0.325 | Unsmooth |
| Improvement 1 | 11 | 29.31 | 0.078 | Unsmooth |
| Improvement 2 | 5 | 27.64 | 0.068 | Unsmooth |
| Improvement 3 | 5 | 27.17 | 0.071 | smooth |
| Algorithms | Turning Points | Path Length | Planning Time | Smoothness |
|---|---|---|---|---|
| A-Star | 9 | 58.08 | 0.312 | Unsmooth |
| JPS | 9 | 73.21 | 0.075 | Unsmooth |
| RRT | 58 | 68.00 | 0.044 | Unsmooth |
| weight A | 9 | 58.08 | 0.032 | Unsmooth |
| Theta A | 11 | 61.01 | 0.082 | Unsmooth |
| ours | 5 | 56.13 | 0.143 | smooth |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Sun, Z.; Wan, J.; Li, H.; Yang, D.; Li, Y.; Fu, W.; Yu, Z.; Sun, J. Hybrid Path Planning Method for USV Based on Improved A-Star and DWA. J. Mar. Sci. Eng. 2025, 13, 934. https://doi.org/10.3390/jmse13050934
Liu Y, Sun Z, Wan J, Li H, Yang D, Li Y, Fu W, Yu Z, Sun J. Hybrid Path Planning Method for USV Based on Improved A-Star and DWA. Journal of Marine Science and Engineering. 2025; 13(5):934. https://doi.org/10.3390/jmse13050934
Chicago/Turabian StyleLiu, Yan, Zeqiang Sun, Junhe Wan, Hui Li, Delong Yang, Yanping Li, Wei Fu, Zhen Yu, and Jichang Sun. 2025. "Hybrid Path Planning Method for USV Based on Improved A-Star and DWA" Journal of Marine Science and Engineering 13, no. 5: 934. https://doi.org/10.3390/jmse13050934
APA StyleLiu, Y., Sun, Z., Wan, J., Li, H., Yang, D., Li, Y., Fu, W., Yu, Z., & Sun, J. (2025). Hybrid Path Planning Method for USV Based on Improved A-Star and DWA. Journal of Marine Science and Engineering, 13(5), 934. https://doi.org/10.3390/jmse13050934






