Clay Particle Migration and Associated Permeability Damage in Natural Gas Hydrate-Bearing Clayey-Silty Sediments: A Review
Abstract
1. Introduction
2. Clay Particle Migration and Permeability Damage in NGHBS
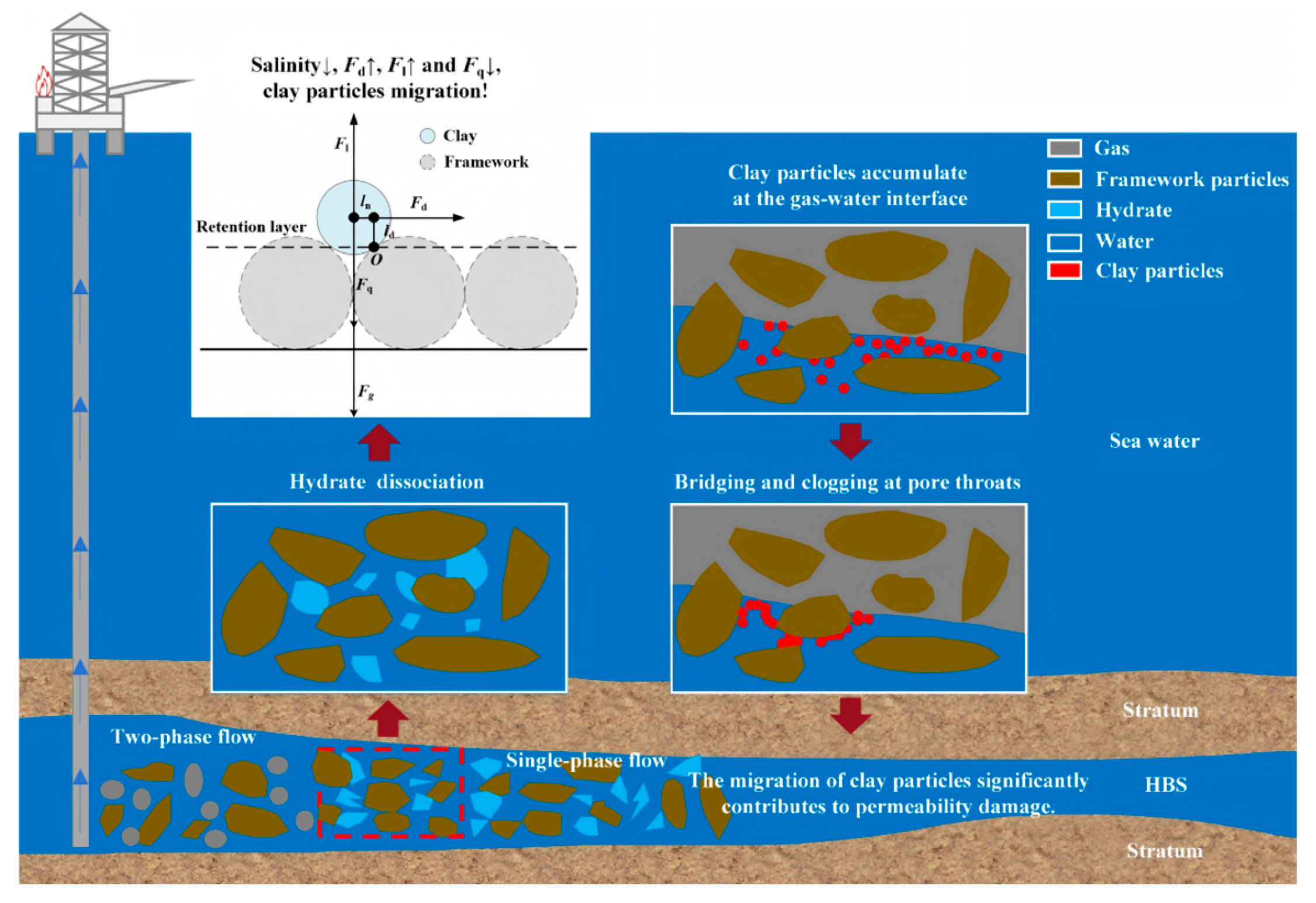
2.1. Permeability Damage During Hydrate Dissociation
2.2. Behavior of Clay Particles During Hydrate Dissociation
3. Mathematical Models of Particle Migration
3.1. Macroscopic Perspective
3.2. Microscopic Perspective
4. Study on Influencing Factors of Particle Migration
4.1. Internal Factors of Particle Migration
4.2. External Conditions for Particle Migration
4.2.1. Fluid Seepage Velocity
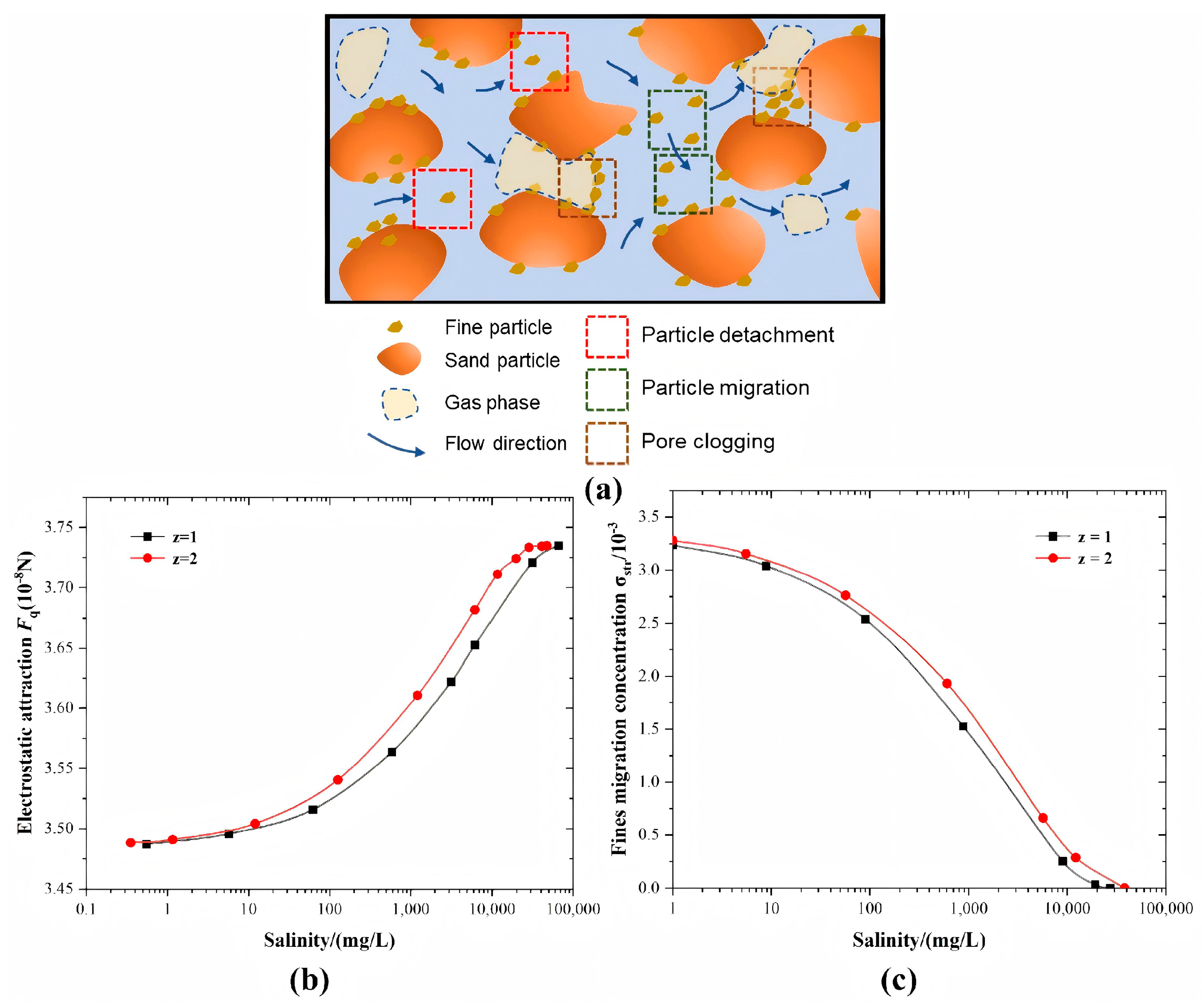
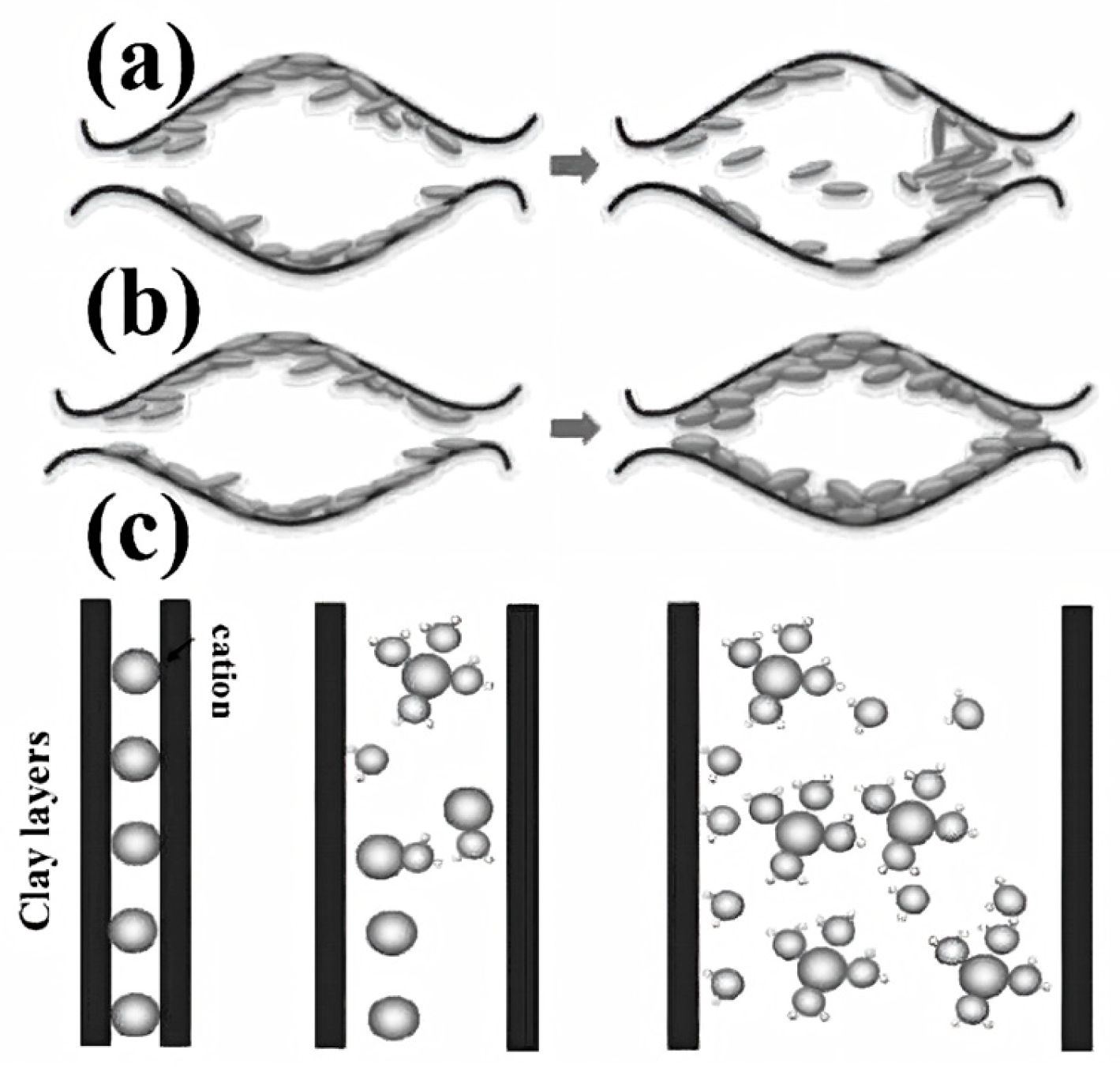
4.2.2. Salinity
4.2.3. pH
4.2.4. Fluid Type
4.2.5. Temperature
4.2.6. Stress Field Mutation
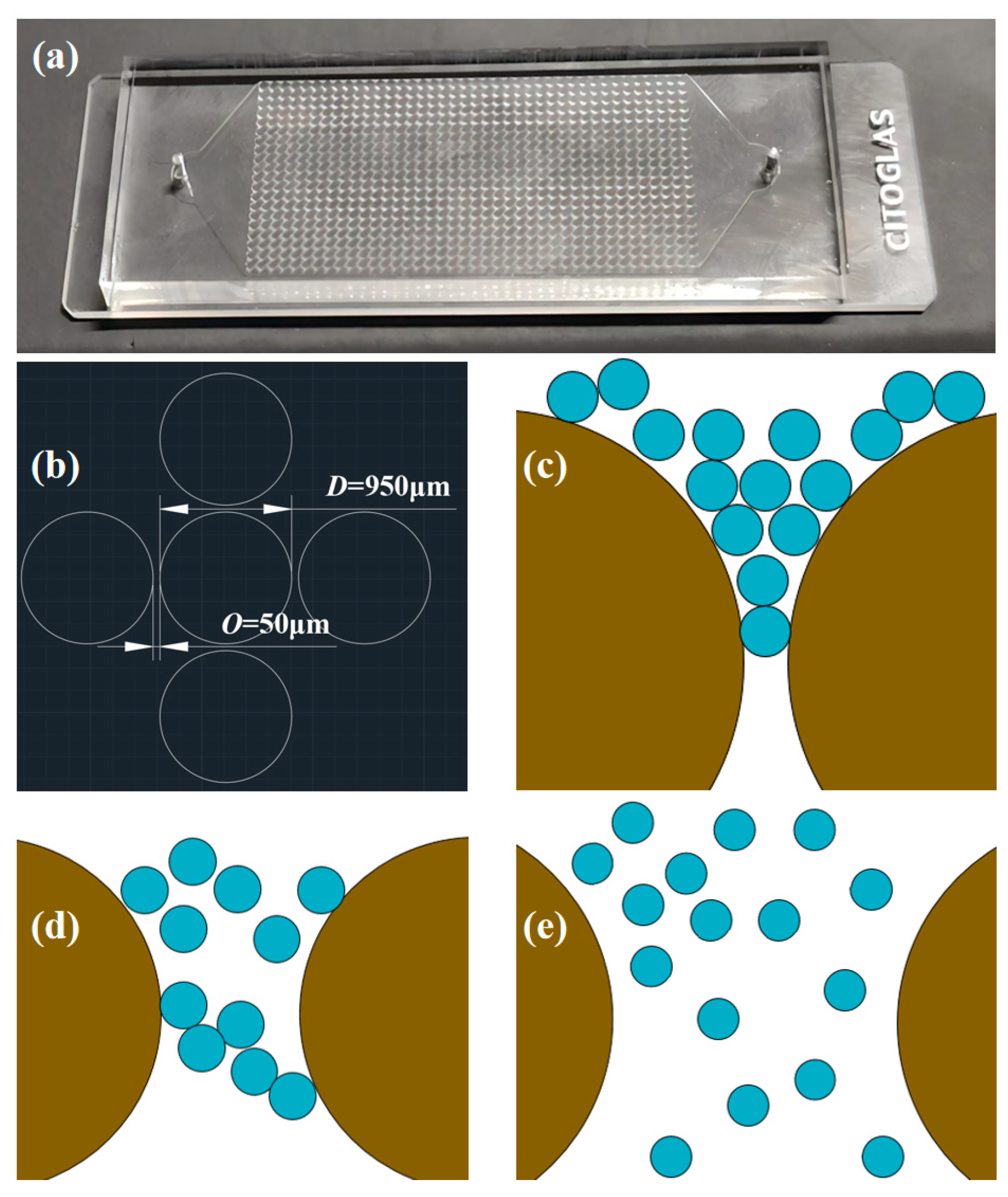
4.3. Visualization Studies on Particle Migration-Clogging
5. Numerical Simulation Studies of Particle Migration
6. Problems and Challenges
- (1)
- Multiphase-multifield coupling. Methane hydrate-bearing clayey-silty sediments involve multiphase systems (free methane (gas), pore water (liquid), and mobile clay particles (solid)), along with coupled physical fields including gas-liquid-solid flow, endothermic dissociation, chemical progress, and stress changes. Clay particle migration is thus governed by complex interactions among multiple physical mechanisms, and influenced jointly by intrinsic reservoir properties and external fluid conditions. Future research should focus on elucidating the dynamics of particle behavior under these coupled environmental conditions.
- (2)
- The complexity of clay particle migration. The behavior of clay particles in porous media involves a series of continuous and complex processes, including detachment, migration, and clogging, which are interconnected and mutually influential. Clay particle migration occurs only after detachment from the pore surfaces, while the subsequent clogging induced during migration directly impacts the permeability of the porous medium. Therefore, future research should adopt a systematic approach to analyze clay particle migration.
- (3)
- Quantitative characterization of permeability damage. It has been demonstrated that the migration-clogging of clay particles is the main cause of permeability damage in clay-silty sediment. However, a clear correlation between the microscopic behavior of clay particles and the macroscopic permeability variation has not yet been established. The permeability damage caused by clay particle migration remains challenging. How to apply the behavior of a clay particle to the permeability damage calculation is the focus for future research.
7. Conclusions
- (1)
- In NGH-bearing clayey-silty sediment, an abnormal phenomenon of "permeability decrease instead of increase" is observed during methane hydrate dissociation. Clay particle migration and the resulting pore clogging are recognized as the primary causes. The dissociation of NGH leads to a reduction of pore-water salinity, which triggers clay particle migration. Meanwhile, the two-phase flow of methane and water further promotes this process. As hydrate saturation increases, the permeability damage degree in clayey-silty sediments first increases and then decreases.
- (2)
- The behaviors of clay particles and other fine particles in sediment include detachment, migration, collision, deposition, and clogging, which are governed by hydrodynamic forces, porous matrix forces, interparticle contact forces, and gravitational forces. Among these, hydrodynamic forces generally facilitate particle migration, while the other forces tend to inhibit particle mobilization and migration. The specific behavior is determined by the torque exerted by these forces on the particle.
- (3)
- The migration and clogging behavior of clay particles are jointly influenced by both intrinsic reservoir properties and external fluid conditions. Among the intrinsic factors, the type and content of clay particles play a dominant role. With respect to external factors, pore-water salinity is particularly critical. Furthermore, the ratio of throat size to particle diameter plays a critical role in determining whether clogging occurs at the throat. When the ratio falls below 10, clay particle clogging becomes highly prone to occur.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sang, S.; Kong, L.; Zeng, Z.; Zhao, Y.; Liu, J.; Zhao, S. Mechanical and deformation behavior of layered hydrate-bearing clayey-silty sediments: Different effective confining pressures and clay content analyses. Acta Geotech. 2025, 20, 861–890. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Y.; Sang, S.; Zeng, Z.; Hua, L.; Kong, L. Triaxial Tests of Hydrate-Bearing Clayey-Silty Sediments Under Different Hydrate Saturations and Effective Confining Pressures. Energy Fuels 2022, 36, 14042–14054. [Google Scholar] [CrossRef]
- Boswell, R.; Collett, T.S. Current perspectives on gas hydrate resources. Energy Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- Yu, Y.-S.; Zhang, X.; Liu, J.-W.; Lee, Y.; Li, X.-S. Natural gas hydrate resources and hydrate technologies: A review and analysis of the associated energy and global warming challenges. Energy Environ. Sci. 2021, 14, 5611–5668. [Google Scholar] [CrossRef]
- Wei, N.; Pei, J.; Li, H.; Zhou, S.; Zhao, J.; Kvamme, B.; Coffin, R.B.; Zhang, L.; Zhang, Y.; Xue, J. Classification of natural gas hydrate resources: Review, application and prospect. Gas Sci. Eng. 2024, 124, 205269. [Google Scholar] [CrossRef]
- Al-Yaseri, A.; Al Mukainah, H.; Lebedev, M.; Barifcani, A.; Iglauer, S. Impact of fines and rock wettability on reservoir formation damage. Geophys. Prospect. 2016, 64, 860–874. [Google Scholar] [CrossRef]
- Han, W.; Wang, Y.; Fan, J.; Li, Y.; Wu, X.; Yu, Y. An experimental study on coal fines migration during single phase water flow. Geofluids 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Yang, D.H.; Wei, C.F.; Yan, R.T.; Tang, Q.; Liu, L. Experimental Study on the Influence of Fine Particle Migration and Fabric Variation on Clay Permeability. Chin. J. Geotech. Eng. 2019, 41, 2009–2017. [Google Scholar]
- Kozhevnikov, E.V.; Turbakov, M.S.; Gladkikh, E.A.; Riabokon, E.P.; Poplygin, V.V.; Guzev, M.A.; Qi, C.; Kunitskikh, A.A. Colloid migration as a reason for porous sandstone permeability degradation during coreflooding. Energies 2022, 15, 2845. [Google Scholar] [CrossRef]
- Kozhevnikov, E.V.; Turbakov, M.S.; Riabokon, E.P.; Gladkikh, E.A. Apparent permeability evolution due to colloid migration under cyclic confining pressure: On the example of porous limestone. Transp. Porous Media 2024, 151, 263–286. [Google Scholar] [CrossRef]
- Wang, L.L. Mechanics of Porous Media; Petroleum Industry Press: Beijing, China, 2022. [Google Scholar]
- Yang, M.P.; Li, Z.P.; Li, Y.; Wang, Z. Deformation Theory and Experimental Study of Porous Media in Oil and Gas Reservoirs. Nat. Gas Ind. 2003, 23, 110–113. [Google Scholar]
- Jing, H.; Zhang, G.D.; Sun, D.L.; Li, B.; Wang, F. Experimental Study on the Effect of Water Injection Multiples on Microscopic Pore Structure of Reservoirs. Pet. Geol. Exp. 2020, 42, 1041–1046. [Google Scholar] [CrossRef]
- Liang, Y.K.; Yu, X.C.; Song, J.F.; Kan, C.; Han, Y.; Xu, Q. Plugging Prevention and Pressure Reduction Effects of Gradient Anti-Clogging Systems During Water Injection in High-Clay Unconsolidated Low-Permeability Sandstone Reservoirs. Oilfield Chem. 2022, 39, 69–75. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Wang, K.; Tao, L.; Liu, J.; Wang, C.; Yao, J.; Zhang, K.; Song, W. Changes in relative permeability curves for natural gas hydrate decomposition due to particle migration. J. Nat. Gas Sci. Eng. 2020, 84, 103634. [Google Scholar] [CrossRef]
- Sbai, M.A.; Azaroual, M. Numerical modeling of formation damage by two-phase particulate transport processes during CO2 injection in deep heterogeneous porous media. Adv. Water Resour. 2011, 34, 62–82. [Google Scholar] [CrossRef]
- Yin, Y.; Cui, Y.; Liu, D.; Lei, M. Study on Microscopic Process of Fine Particle Migration in Loose Soil. Adv. Eng. Sci. 2019, 51, 21–29. [Google Scholar] [CrossRef]
- Ju, B.S.; Ma, M.X.; Qiu, X.Y. Mathematical Modeling Method for Clay Swelling and Particle Migration in Elastic Porous Media. J. Hydrodyn. 2003, 18, 8–15. [Google Scholar]
- Guo, T.K.; Gong, Y.Z.; Liu, X.Q.; Wang, Z.; Xu, J.; Sheng, M.; Luo, Z. Numerical Simulation of Proppant Transport and Placement in Complex Fractures. J. China Univ. Pet. 2022, 46, 89–95. [Google Scholar]
- Pan, L.H.; Wang, H.B.; He, J.Y.; Li, F.X.; Zhou, T.; Li, X.L. Research Progress in Simulation of Proppant Transport and Distribution in Hydraulic Fracturing. Nat. Gas Ind. 2020, 40, 54. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Li, X.; Yuan, Z.; Shao, B.; Liu, L.; Fan, J. Flow behaviors of ellipsoidal suspended particles in porous reservoir rocks using CFD-DEM combined with multi-element particle model. Granul. Matter 2022, 24, 62. [Google Scholar] [CrossRef]
- Li, M.; Kong, D.; Guo, Q.; Liu, X.; Yao, J.; Hu, J.; Chen, L. Investigation of movement and deposition behaviors of solid particles in hydraulic water reservoir via the CFD-DEM coupling method. Chin. J. Mech. Eng. 2022, 35, 118. [Google Scholar] [CrossRef]
- Liu, J.; Parker, E.D.; Camilleri, D. A new particle tracking algorithm for tracer flow simulation. In Proceedings of the SPE Reservoir Simulation Symposium; Society of Petroleum Engineers, Houston, TX, USA, 14–17 February 1999; p. SPE-51905-MS. [Google Scholar]
- Ruckenstein, E.; Prieve, D.C. Adsorption and desorption of particles and their chromatographic separation. AIChE J. 1976, 22, 276–283. [Google Scholar] [CrossRef]
- Al-Abduwani, F.A.H.; Bedrikovetsky, P.; Farajzadeh, R.; Van Den Broek, W.M.G.T.; Currie, P.K. External Filter Cake Erosion: Mathematical Model and Experimental Study. In Proceedings of the SPE European Formation Damage Conference, Sheveningen, The Netherlands, 25–27 May 2005; p. SPE-94635-MS. [Google Scholar]
- Mahmoudi Eshkaftaki, M. New sand control design criteria and evaluation testing for Steam Assisted Gravity Drainage (SAGD) Wellbores. Ph. D. Thesis, University of Alberta, Edmonton, AB, Canada, 2017. [Google Scholar]
- Wang, C.; Montero Pallares, J.D.; Haftani, M.; Nouri, A. Developing a methodology to characterize formation damage (pore plugging) due to fines migration in sand control tests. J. Pet. Sci. Eng. 2020, 186, 106793. [Google Scholar] [CrossRef]
- Guo, Y.; Nouri, A.; Nejadi, S. Effect of slot width and density on slotted liner performance in SAGD operations. Energies 2020, 13, 268. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Liu, C.L.; Liu, L.L.; Chen, P.; Zhang, Z.; Meng, Q. Low-Field Nuclear Magnetic Resonance Observations of Pore Structure and Permeability Changes in Sediments Caused by Hydrate Formation. Mar. Geol. Quat. Geol. 2021, 41, 193–202. [Google Scholar] [CrossRef]
- Zhao, J.; Fan, Z.; Dong, H.; Yang, Z.; Song, Y. Influence of reservoir permeability on methane hydrate dissociation by depressurization. Int. J. Heat Mass Transf. 2016, 103, 265–276. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Z.; Li, Y.; Song, Y.; Ling, Z.; Zhao, J.; Lv, Q. Experimental study on the gas phase permeability of methane hydrate-bearing clayey sediments. J. Nat. Gas Sci. Eng. 2016, 36, 378–384. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Y.; Sun, X.; Li, M.; Jia, R. Experimental study on the gas phase permeability of montmorillonite sediments in the presence of hydrates. Mar. Pet. Geol. 2018, 91, 373–380. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, M.; Mayanna, S.; Schleicher, A.M.; Spangenberg, E.; Schicks, J.M. Reservoir formation damage during hydrate dissociation in sand-clay sediment from Qilian Mountain permafrost, China. Appl. Energy 2020, 263, 114619. [Google Scholar] [CrossRef]
- Shen, P.; Li, G.; Li, B.; Li, X.; Liang, Y.; Lv, Q. Permeability measurement and discovery of dissociation process of hydrate sediments. Journal of Natural Gas Science and Engineering. J. Nat. Gas Sci. Eng. 2020, 75, 103155. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Y.; Sun, X.; Wu, P.; Zheng, J. Experimental study on the effect of methane hydrate decomposition on gas phase permeability of clayey sediments. Appl. Energy 2018, 230, 1304–1310. [Google Scholar] [CrossRef]
- Zhao, Z.K. Experimental Study on Mechanical and Permeability Properties of Fractured Gas Hydrate-Bearing Silty Clay Sediments. Ph.D. Thesis, Yanshan University, Qinhuangdao, China, 2024. [Google Scholar]
- Li, G.; Wu, D.-M.; Li, X.-S.; Lv, Q.-N.; Li, C.; Zhang, Y. Experimental measurement and mathematical model of permeability with methane hydrate in quartz sands. Appl. Energy 2017, 202, 282–292. [Google Scholar] [CrossRef]
- Sun, Z.-F.; Jia, S.; Yuan, Q.; Sun, C.-Y.; Chen, G.-J. One-dimensional study on gas production characteristics of methane hydrate in clayey sediments using depressurization method. Fuel 2020, 262, 116561. [Google Scholar] [CrossRef]
- Han, H.; Wang, Y.; Li, X.-S.; Yu, J.-X.; Feng, J.-C.; Zhang, Y. Experimental study on sediment deformation during methane hydrate decomposition in sandy and silty clay sediments with a novel experimental apparatus. Fuel 2016, 182, 446–453. [Google Scholar] [CrossRef]
- Wang, R.; Liao, B.; Wang, J.; Sun, J.; Wang, Y.; Wang, J.; Wang, Q.; Qu, Y.; Cheng, R. Microscopic molecular insights into methane hydrate growth on the surfaces of clay minerals: Experiments and molecular dynamics simulations. Chem. Eng. J. 2023, 451, 138757. [Google Scholar] [CrossRef]
- Lei, J.; Chen, Z.; Zhao, J.; Wang, Y.; Guo, W. Effect of decrease in pore water salinity induced by hydrate decomposition in clayey silt sediment on the destabilization-migration-clogging characteristics of illite. Energy 2024, 308, 132887. [Google Scholar] [CrossRef]
- Bedrikovetsky, P.; Siqueira, F.D.; Furtado, C.A.; Souza, A.L.S. Modified particle detachment model for colloidal transport in porous media. Transp. Porous Media 2011, 86, 353–383. [Google Scholar] [CrossRef]
- Qi, Y.; Sun, Y.; Li, B.; Shan, H.; Shen, Y.; Zhang, G. Permeability damage and hydrate dissociation barrier caused by invaded fracturing fluid during hydrate reservoir stimulation. Gas Sci. Eng. 2023, 116, 205051. [Google Scholar] [CrossRef]
- Jang, J.; Waite, W.F.; Stern, L.A.; Collett, T.S.; Kumar, P. Physical property characteristics of gas hydrate-bearing reservoir and associated seal sediments collected during NGHP-02 in the Krishna-Godavari Basin, in the offshore of India. Mar. Pet. Geol. 2019, 108, 249–271. [Google Scholar] [CrossRef]
- Feng, Y.; Qu, A.; Han, Y.; Shi, C.; Liu, Y.; Zhang, L.; Zhao, J.; Yang, L.; Song, Y. Effect of gas hydrate formation and dissociation on porous media structure with clay particles. Appl. Energy 2023, 349, 121694. [Google Scholar] [CrossRef]
- Hou, J.; Ji, Y.; Zhou, K.; Liu, Y.; Wei, B. Effect of hydrate on permeability in porous media: Pore-scale micro-simulation: Pore-Scale Micro-Simulation. Int. J. Heat Mass Transf. 2018, 126, 416–424. [Google Scholar] [CrossRef]
- Zhao, J.; Zheng, J.; Li, F.; Yang, M. Gas Gas permeability characteristics of marine sediments with and without methane hydrates in a core holder. J. Nat. Gas Sci. Eng. 2020, 76, 103215. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.; Sang, S.; Hua, L.; Kong, L.; Zeng, Z.; Yuan, Q. Experimental investigation on the permeability characteristics of methane hydrate-bearing clayey-silty sediments considering various factors. Energy 2023, 269, 126811. [Google Scholar] [CrossRef]
- Zhao, Y.; Kong, L.; Liu, J.; Sang, S.; Zeng, Z.; Wang, N.; Yuan, Q. Permeability properties of natural gas hydrate-bearing sediments considering dynamic stress coupling: A comprehensive experimental investigation. Energy 2023, 283, 129214. [Google Scholar] [CrossRef]
- Li, Y.-L.; Ning, F.-L.; Xu, M.; Qi, M.-H.; Sun, J.-X.; Nouri, A.; Gao, D.-L.; Wu, N.-Y. Experimental study on solid particle migration and production behaviors during marine natural gas hydrate dissociation by depressurization. Pet. Sci. 2023, 20, 3610–3623. [Google Scholar] [CrossRef]
- Jung, J.W.; Jang, J.; Santamarina, J.C.; Tsouris, C.; Phelps, T.J.; Rawn, C.J. Gas production from hydrate-bearing sediments: The role of fine particles. Energy Fuels 2012, 26, 480–487. [Google Scholar] [CrossRef]
- Guan, D.; Qu, A.; Wang, Z.; Lv, X.; Li, Q.; Leng, S.; Xiao, B.; Zhang, L.; Zhao, J.; Yang, L.; et al. Fluid flow-induced fine particle migration and its effects on gas and water production behavior from gas hydrate reservoir. Appl. Energy 2023, 331, 120327. [Google Scholar] [CrossRef]
- Miri, R.; Haftani, M.; Nouri, A. A review of fines migration around Steam Assisted Gravity Drainage wellbores. J. Pet. Sci. Eng. 2021, 205, 108868. [Google Scholar] [CrossRef]
- Zhuang, L.; Raoof, A.; Mahmoodlu, M.G.; Biekart, S.; De Witte, R.; Badi, L.; Van Genuchten, M.T.; Lin, K. Unsaturated flow effects on solute transport in porous media. J. Hydrol. 2021, 598, 126301. [Google Scholar] [CrossRef]
- Shapiro, A.A.; Bedrikovetsky, P.G.; Santos, A.; Medvedev, O.O. A stochastic model for filtration of particulate suspensions with incomplete pore plugging. Transp. Porous Media 2007, 67, 135–164. [Google Scholar] [CrossRef]
- Herzig, J.P.; Leclerc, D.M.; Goff, P.L. Flow of suspensions through porous media-application to deep filtration. Ind. Eng. Chem. 1970, 62, 8–35. [Google Scholar] [CrossRef]
- Wang, S.; Shen, Y. Particle-scale study of heat and mass transfer in a bubbling fluidised bed. Chem. Eng. Sci. 2021, 240, 116655. [Google Scholar] [CrossRef]
- Runkel, R.L.; Bencala, K.E.; Broshears, R.E.; Chapra, S.C. Reactive solute transport in streams: 1. Development of an equilibrium-based model. Water Resour. Res. 1996, 32, 409–418. [Google Scholar] [CrossRef]
- Saaltink, M.W.; Carrera, J.; Olivella, S. Mass balance errors when solving the convective form of the transport equation in transient flow problems. Water Resour. Res. 2004, 40, 2003WR002866. [Google Scholar] [CrossRef]
- Chequer, L.; Russell, T.; Behr, A.; Genolet, L.; Kowollik, P.; Badalyan, A.; Zeinijahromi, A.; Bedrikovetsky, P. Non-monotonic permeability variation during colloidal transport: Governing equations and analytical model. J. Hydrol. 2018, 557, 547–560. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Cui, C.Z.; Wei, Z.J.; Liu, L.J.; Li, X.-J.; Pang, L.-L. Mechanism of Fine Particle Migration and Its Impact on Development Efficiency During Low-Salinity Water Flooding. J. Eng. Sci. 2019, 41, 719–730. [Google Scholar]
- Yang, S.; Russell, T.; Badalyan, A.; Schacht, U.; Woolley, M.; Bedrikovetsky, P. Characterisation of fines migration system using laboratory pressure measurements. J. Nat. Gas Sci. Eng. 2019, 65, 108–124. [Google Scholar] [CrossRef]
- Encyclopedia of China Editorial Committee. Encyclopedia of China, 3rd ed.; Encyclopedia of China Publishing House: Beijing, China, 2021. [Google Scholar]
- Hough, D.B.; White, L.R. The calculation of Hamaker constants from Liftshitz theory with applications to wetting phenomena. Adv. Colloid Interface Sci. 1980, 14, 3–41. [Google Scholar] [CrossRef]
- Borukhov, I.; Andelman, D.; Orland, H. Steric effects in electrolytes: A modified Poisson-Boltzmann equation. Phys. Rev. Lett. 1997, 79, 435–438. [Google Scholar] [CrossRef]
- Han, G.; Kwon, T.-H.; Lee, J.Y.; Jung, J. Fines migration and pore clogging induced by single-and two-phase fluid flows in porous media: From the perspectives of particle detachment and particle-level forces. Geomech. Energy Environ. 2020, 23, 100131. [Google Scholar] [CrossRef]
- Russell, T.; Pham, D.; Neishaboor, M.T.; Badalyan, A.; Behr, A.; Genolet, L.; Kowollik, P.; Zeinijahromi, A.; Bedrikovetsky, P. Effects of kaolinite in rocks on fines migration. J. Nat. Gas Sci. Eng. 2017, 45, 243–255. [Google Scholar] [CrossRef]
- Mohan, K.K.; Vaidya, R.N.; Reed, M.G.; Fogler, H.S. Water sensitivity of sandstones containing swelling and non-swelling clays. Colloids Surf. A Physicochem. Eng. Asp. 1993, 73, 237–254. [Google Scholar] [CrossRef]
- Lei, J.; Wang, Y.; Guo, W. Migration Migration characteristics and geohazards risk analysis of swelling clay in clayey silt hydrate sediments. Gas Sci. Eng. 2024, 126, 205347. [Google Scholar] [CrossRef]
- Anderson, R.L.; Ratcliffe, I.; Greenwell, H.C.; Williams, P.A.; Cliffe, S.; Coveney, P.V. Clay swelling—A challenge in the oilfield. Earth-Sci. Rev. 2010, 98, 201–216. [Google Scholar] [CrossRef]
- Low, P.F. The swelling of clay: II. Montmorillonites. Soil Sci. Soc. Am. J. 1980, 44, 667–676. [Google Scholar] [CrossRef]
- Hensen, E.J.M.; Smit, B. Why clays swell. J. Phys. Chem. B 2002, 106, 12664–12667. [Google Scholar] [CrossRef]
- Sameni, A.; Pourafshary, P.; Ghanbarzadeh, M.; Ayatollahi, S. Effect of nanoparticles on clay swelling and migration. Egypt. J. Pet. 2015, 24, 429–437. [Google Scholar] [CrossRef]
- Karpiński, B.; Szkodo, M. Clay minerals–mineralogy and phenomenon of clay swelling in oil & gas industry. Adv. Mater. Sci. 2015, 15, 37–55. [Google Scholar] [CrossRef]
- Yuan, B.; Wood, D.A. A comprehensive review of formation damage during enhanced oil recovery. J. Pet. Sci. Eng. 2018, 167, 287–299. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, W.; Hou, J.; You, Z. Review on physical and chemical factors affecting fines migration in porous media. Water Res. 2022, 214, 118172. [Google Scholar] [CrossRef]
- Bedrikovetsky, P.; Zeinijahromi, A.; Siqueira, F.D.; Furtado, C.A.; De Souza, A.L.S. Particle detachment under velocity alternation during suspension transport in porous media. Transp. Porous Media 2012, 91, 173–197. [Google Scholar] [CrossRef]
- Marquez, M.; Williams, W.; Knobles, M.; Bedrikovetsky, P.; You, Z. Fines Migration in Fractured Wells: Integrating Modeling, Field and Laboratory Data. In Proceedings of the SPE European Formation Damage Conference & Exhibition; Society of Petroleum Engineers, Noordwijk, The Netherlands, 5–7 June 2013; p. SPE-165108-MS. [Google Scholar]
- Mahani, H.; Berg, S.; Ilic, D.; Bartels, W.-B.; Joekar-Niasar, V. Kinetics of low-salinity-flooding effect. SPE J. 2015, 20, 8–20. [Google Scholar] [CrossRef]
- You, Z.; Badalyan, A.; Yang, Y.; Bedrikovetsky, P.; Hand, M. Fines migration in geothermal reservoirs: Laboratory and mathematical modelling. Geothermics 2019, 77, 344–367. [Google Scholar] [CrossRef]
- Vaidya, R.N.; Fogler, H.S. Fines migration and formation damage: Influence of pH and ion exchange. SPE Prod. Eng. 1992, 7, 325–330. [Google Scholar] [CrossRef]
- Tang, Y.; Hu, S.; He, Y.; Wang, Y.; Wan, X.; Cui, S.; Long, K. Experiment on CO2-brine-rock interaction during CO2 injection and storage in gas reservoirs with aquifer. Chem. Eng. J. 2021, 413, 127567. [Google Scholar] [CrossRef]
- Bai, T.; Chen, Z.; Aminossadati, S.M.; Rufford, T.E.; Li, L. Experimental investigation on the impact of coal fines generation and migration on coal permeability. J. Pet. Sci. Eng. 2017, 159, 257–266. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, D.; Ranjith, P.G.; Zhou, Z.; Wu, B.; Kong, L.; Chen, L.; Huang, J. A comprehensive study of fines migration in internally unstable natural gas hydrate reservoirs. Powder Technol. 2024, 433, 119193. [Google Scholar] [CrossRef]
- You, Z.; Bedrikovetsky, P.; Badalyan, A.; Hand, M. Particle mobilization in porous media: Temperature effects on competing electrostatic and drag forces. Geophys. Res. Lett. 2015, 42, 2852–2860. [Google Scholar] [CrossRef]
- Ma, D.; Rezania, M.; Yu, H.-S.; Bai, H.-B. Variations of hydraulic properties of granular sandstones during water inrush: Effect of small particle migration. Engineering Geology. Eng. Geol. 2017, 217, 61–70. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, J.; Bai, H. A state-of-the-art review on rock seepage mechanism of water inrush disaster in coal mines. Int. J. Coal Sci. Technol. 2022, 9, 50. [Google Scholar] [CrossRef]
- Huang, F.; Kang, Y.; You, Z.; You, L.; Xu, C. Critical conditions for massive fines detachment induced by single-phase flow in coalbed methane reservoirs: Modeling and experiments. Energy Fuels 2017, 31, 6782–6793. [Google Scholar] [CrossRef]
- Song, W.; Kovscek, A.R. Direct visualization of pore-scale fines migration and formation damage during low-salinity waterflooding. J. Nat. Gas Sci. Eng. 2016, 34, 1276–1283. [Google Scholar] [CrossRef]
- Zhou, Z.-Q.; Li, L.-P.; Shi, S.-S.; Liu, C. Study on tunnel water inrush mechanism and simulation of seepage failure process. Rock Soil Mech. 2021, 41, 3621–3631. [Google Scholar]
- Kozhevnikov, E.; Turbakov, M.; Riabokon, E.; Gladkikh, E.; Guzev, M.; Qi, C.; Li, X. The mechanism of porous reservoir permeability deterioration due to pore pressure decrease. Adv. Geo-Energy Res. 2024, 13, 96–105. [Google Scholar] [CrossRef]
- Gao, K.X. Research on the Application of Low-Cost Microfluidic Technology in Tertiary Oil Recovery. Ph.D. Thesis, University of Chemical Technology, Beijing, China, 2021. [Google Scholar]
- Peng, Z.L.; Wei, Z.L.; Liu, M.Y.; Li, Y.; Lan, H. Electric-Field-Driven μ-3D Printing of Wax-Based Microfluidic Molds. China Mech. Eng. 2020, 31, 1846–1851. [Google Scholar]
- Ren, L.L. Influencing Factors and Mechanism Analysis of Microplastic Migration in Porous Media Based on Microfluidics. Ph.D. Thesis, China University of Petroleum, Qingdao, China, 2022. [Google Scholar] [CrossRef]
- Pattanayak, P.; Singh, S.K.; Gulati, M.; Vishwas, S.; Kapoor, B.; Chellappan, D.K.; Anand, K.; Gupta, G.; Jha, N.K.; Gupta, P.K.; et al. Microfluidic chips: Recent advances, critical strategies in design, applications and future perspectives. Microfluid. Nanofluid. 2021, 25, 99. [Google Scholar] [CrossRef]
- Fani, M.; Pourafshary, P.; Mostaghimi, P.; Mosavat, N. Application of microfluidics in chemical enhanced oil recovery: A review. Fuel 2022, 315, 123225. [Google Scholar] [CrossRef]
- Khilar, K.C.; Fogler, H.S. Migrations of Fines in Porous Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Khilar, K.C.; Fogler, H.S. Colloidally induced fines migration in porous media. Rev. Chem. Eng. 1987, 4, 41–108. [Google Scholar] [CrossRef]
- Oyeneyin, M.B.; Peden, J.M.; Hosseini, A.; Ren, G. Factors to Consider in the Effective Management and Control of Fines Migration in High Permeability Sands. In Proceedings of the SPE European Formation Damage Conference, The Hague, The Netherlands, 15–16 May 1995; p. SPE-30112-MS. [Google Scholar]
- Bigna, Y.; Oyeneyin, M.S.; Peden, J.M. Investigation of Pore-Blocking Mechanism in Gravel Packs in the Management and Control of Fines Migration. In Proceedings of the SPE Formation Damage Control Symposium, Lafayette, LA, USA, 7–10 February 1994; p. SPE-27342-MS. [Google Scholar]
- Cao, S.C.; Jang, J.; Jung, J.; Waite, W.F.; Collett, T.S.; Kumar, P. 2D micromodel study of clogging behavior of fine-grained particles associated with gas hydrate production in NGHP-02 gas hydrate reservoir sediments. Mar. Pet. Geol. 2019, 108, 714–730. [Google Scholar] [CrossRef]
- Jung, J.; Cao, S.C.; Shin, Y.-H.; Al-Raoush, R.I.; Alshibli, K.; Choi, J.-W. A microfluidic pore model to study the migration of fine particles in single-phase and multi-phase flows in porous media. Microsyst. Technol. 2018, 24, 1071–1080. [Google Scholar] [CrossRef]
- Jung, J.; Kang, H.; Cao, S.C.; Al-Raoush, R.I.; Alshibli, K.; Lee, J.Y. Effects of Fine-Grained Particles’ Migration and Clogging in Porous Media on Gas Production from Hydrate-Bearing Sediments. Geofluids 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Bate, B.; Chen, C.; Liu, P.; Zhou, C.; Chen, X.; Nie, S.; Chen, K.; Chen, Y.; Zhang, S. The migration and deposition behaviors of montmorillonite and kaolinite particles in a two-dimensional micromodel. Materials 2022, 15, 855. [Google Scholar] [CrossRef] [PubMed]
- Jarrar, Z.A.; Al-Raoush, R.I.; Hannun, J.A.; Alshibli, K.A.; Jung, J. 3D synchrotron computed tomography study on the influence of fines on gas driven fractures in Sandy Sediments. Geomech. Energy Environ. 2020, 23, 100105. [Google Scholar] [CrossRef]
- Rao, S.S. The Finite Element Method in Engineering; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Kaliakin, V.N. Introduction to Approximate Solution Techniques, Numerical Modeling, and Finite Element Methods; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Huebner, K.H.; Dewhirst, D.L.; Smith, D.E.; Byrom, T.G. The Finite Element Method for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Szabó, B.; Babuška, I. Finite Element Analysis: Method, Verification and Validation; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Maimaitiming, A.; Rehemaitijiang, Y. Modern numerical simulation methods and their engineering applications. Eng. Mech. 2014, 31, 11–18. [Google Scholar]
- Wang, X.; Gong, L.; Li, Y.; Yao, J. Developments and applications of the CFD-DEM method in particle–fluid numerical simulation in petroleum engineering: A review. Appl. Therm. Eng. 2023, 222, 119865. [Google Scholar] [CrossRef]
- Barboza, B.R.; Chen, B.; Li, C. A review on proppant transport modelling. J. Pet. Sci. Eng. 2021, 204, 108753. [Google Scholar] [CrossRef]
- Civan, F. Reservoir Formation Damage: Fundamentals, Modeling, Assessment, and Mitigation; Gulf Professional Publishing: Houston, TX, USA, 2023. [Google Scholar]
- Xu, H. Design Theory and Methods Based on Numerical Simulation; Beijing Science Press: Beijing, China, 2015. [Google Scholar]
- Mingliang, Z. Numerical Simulation Methods and Applications for Hydrodynamics in Coastal and River Environments; Science Press: Beijing, China, 2015. [Google Scholar]
- Liping, P.; Qiang, W.; Zhu, H. Practical Numerical Simulation of Multiphase Flow: ANSYS Fluent Multiphase Flow Models and Their Engineering Applications; Beijing Science Press: Beijing, China, 2020. [Google Scholar]
- Pengcheng, L. Fundamentals of Reservoir Numerical Simulation; Petroleum Industry Press: Beijing, China, 2014. [Google Scholar]
- Xiaofeng, W.; Dan, L.; Jianping, Z. Numerical Analysis (in the series 21st Century AI Innovation and Applications); Tsinghua University Press: Beijing, China, 2024. [Google Scholar]
- Qingyang, L.; Nengchao, W.; Dayi, Y. Numerical Analysis, 5th ed.; Tsinghua University Press: Beijing, China, 2008. [Google Scholar]
- Fujimoto, R.; Bock, C.; Chen, W.; Page, E.; Panchal, J.H. (Eds.) Research Challenges in Modeling and Simulation for Engineering Complex Systems; Simulation Foundations, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 978-3-319-58543-7. [Google Scholar]
- Wang, J. Continuum theory for dense gas-solid flow: A state-of-the-art review. Chem. Eng. Sci. 2020, 215, 115428. [Google Scholar] [CrossRef]
- Tolk, A. Limitations and usefulness of computer simulations for complex adaptive systems research. In Summer of Simulation: 50 Years of Seminal Computer Simulation Research; Springer International Publishing: Cham, Switzerland, 2019; pp. 77–96. [Google Scholar] [CrossRef]
- Zhong, W.; Yu, A.; Liu, X.; Tong, Z.; Zhang, H. DEM/CFD-DEM modelling of non-spherical particulate systems: Theoretical developments and applications. Powder Technol. 2016, 302, 108–152. [Google Scholar] [CrossRef]
- Fang, J.; Jiao, B.; Zhao, G.; He, L.; Wu, Y.; Dai, C. Study on the channel flow control regulation of particle agents in fractured-vuggy carbonate reservoirs via CFD-DEM coupling method. J. Pet. Sci. Eng. 2019, 180, 495–503. [Google Scholar] [CrossRef]
- Li, Q.; Prigiobbe, V. Numerical simulations of the migration of fine particles through porous media. Transp. Porous Media 2018, 122, 745–759. [Google Scholar] [CrossRef]
- Feng, Q.; Cha, L.; Dai, C.; Zhao, G.; Wang, S. Effect of particle size and concentration on the migration behavior in porous media by coupling computational fluid dynamics and discrete element method. Powder Technol. 2020, 360, 704–714. [Google Scholar] [CrossRef]
- Fan, M.; Chen, C. Numerical simulation of the migration and deposition of fine particles in a proppant-supported fracture. J. Pet. Sci. Eng. 2020, 194, 107484. [Google Scholar] [CrossRef]
- Su, J.; Chai, G.; Wang, L.; Cao, W.; Gu, Z.; Chen, C.; Xu, X.Y. Pore-scale direct numerical simulation of particle transport in porous media. Chem. Eng. Sci. 2019, 199, 613–627. [Google Scholar] [CrossRef]
- Sanematsu, P.C.; Thompson, K.E.; Willson, C.S. Pore-scale modeling of nanoparticle transport and retention in real porous materials. Comput. Geosci. 2019, 127, 65–74. [Google Scholar] [CrossRef]
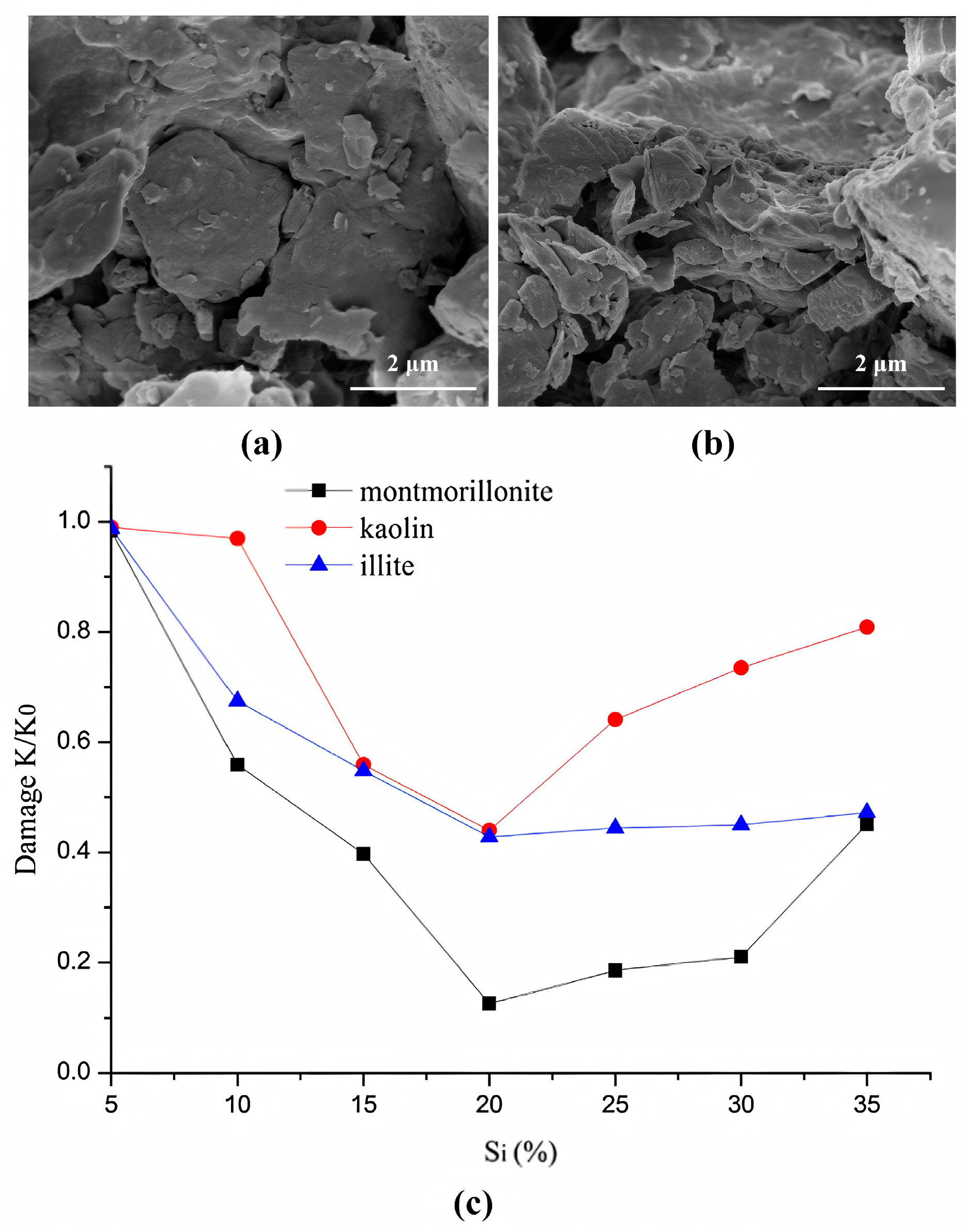
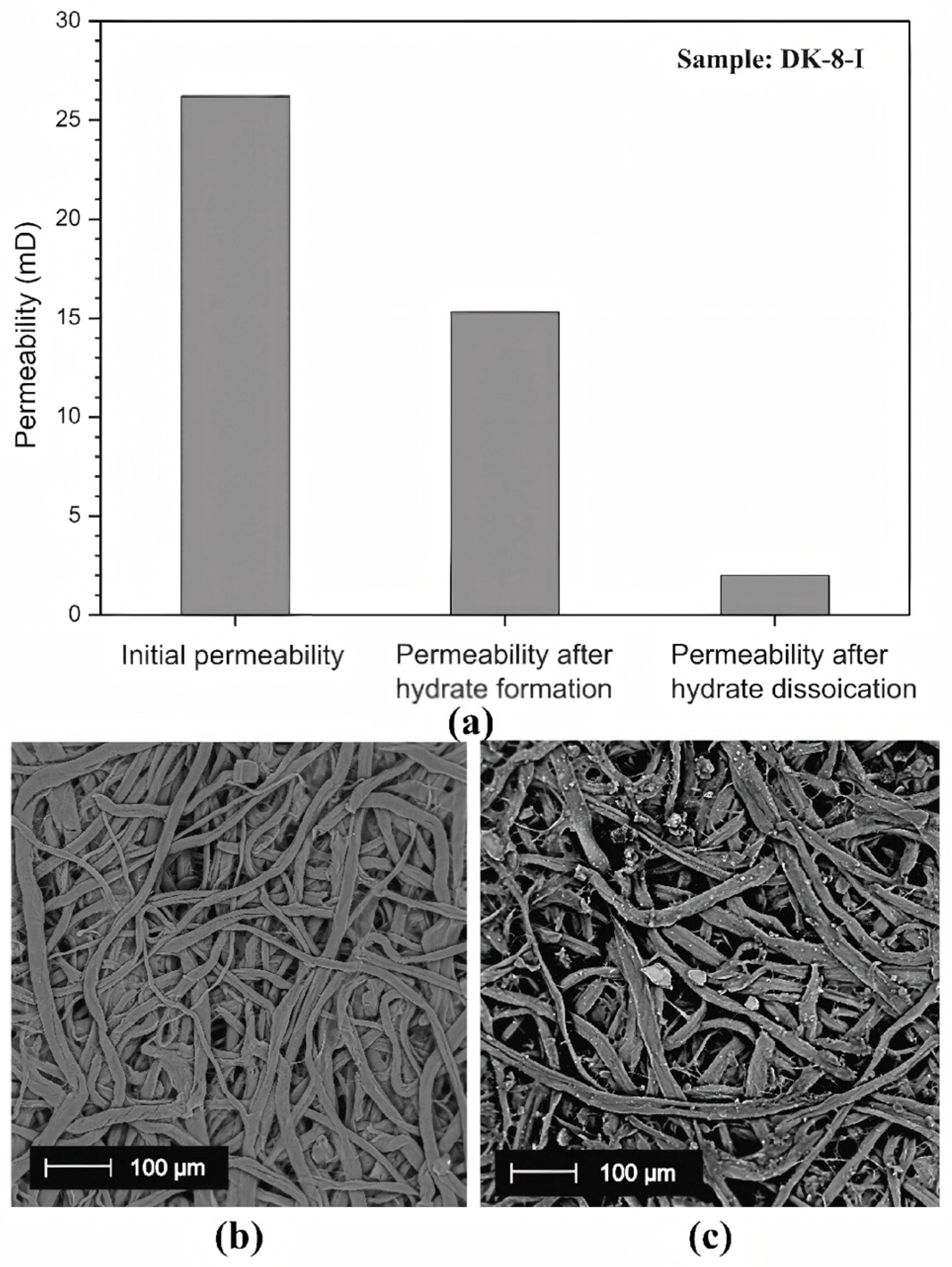



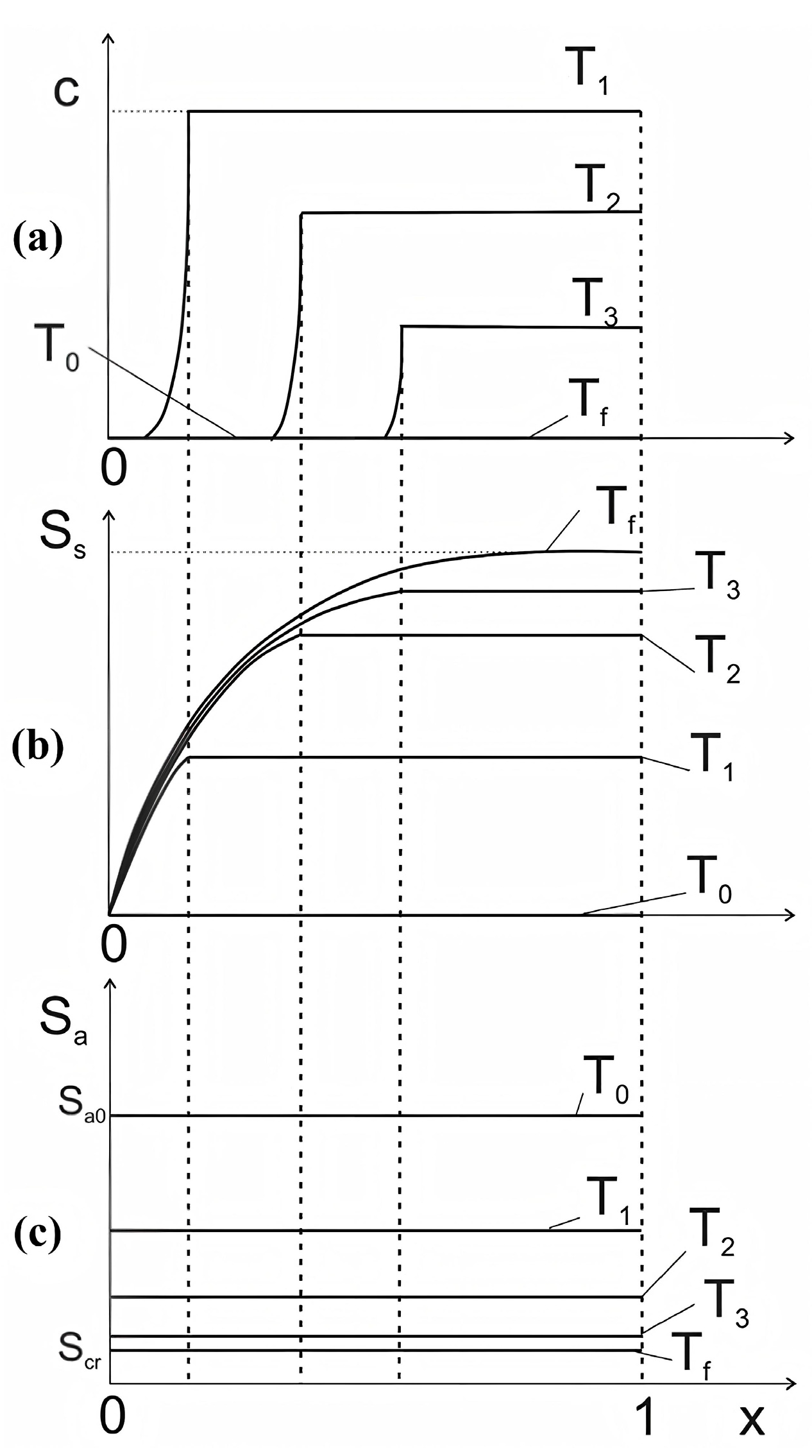
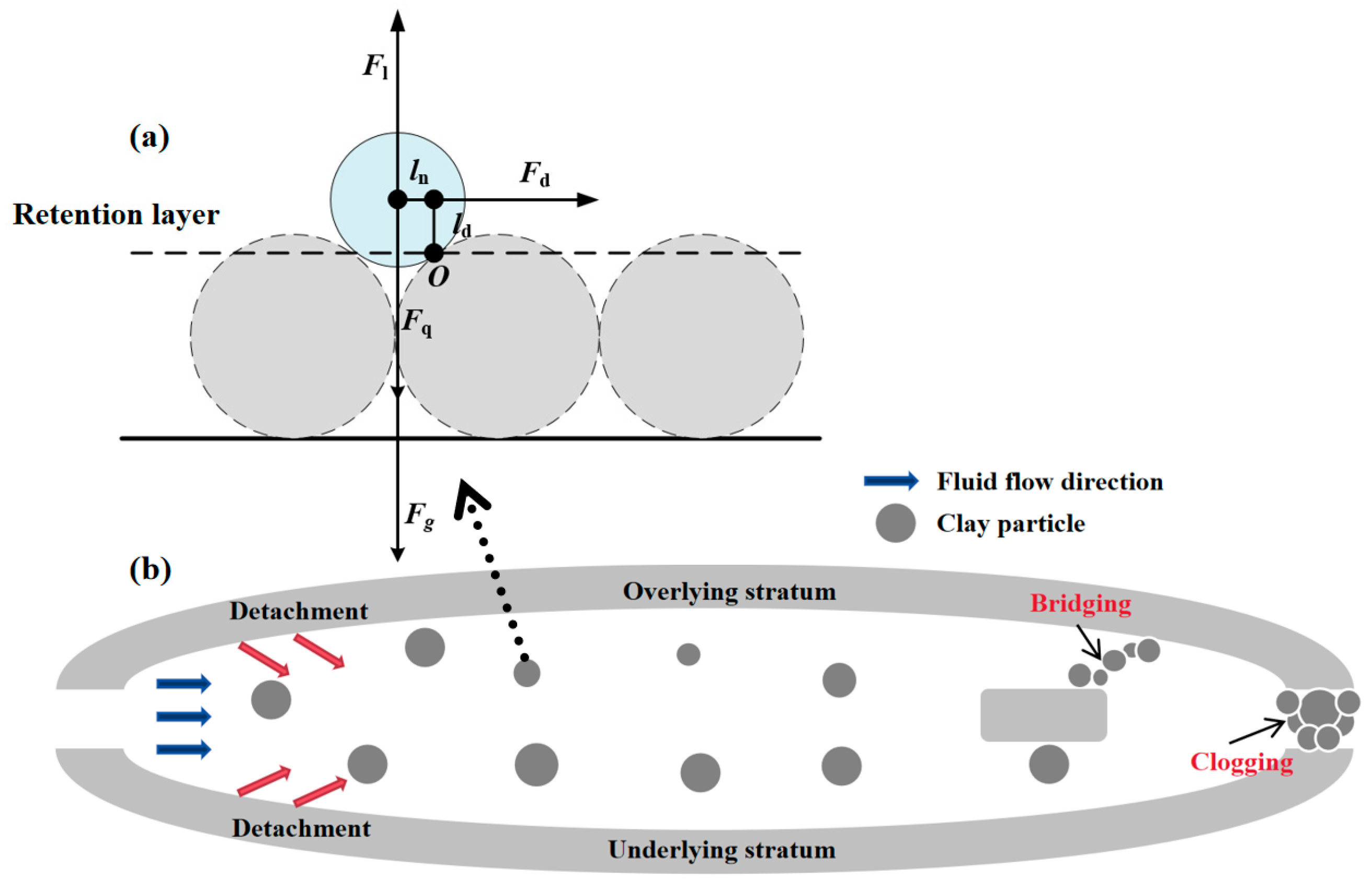


| Experimental Materials | Hydrate Formation Methods and Conditions | Reference |
|---|---|---|
| Kaolinite mixed with ice powder, compacted at −10 °C | Excess gas method at 1 °C and 5.5 MPa | Liu et al. [31] |
| Montmorillonite mixed with ice powder, compacted at −8 °C | Excess gas method at 1 °C and 6 MPa | Wu et al. [32] |
| Core samples from China’s Qilian Mountain hydrate reservoir, saturated with 5% KCl solution | Excess gas method at 0.85 °C and 5 MPa | Wang et al. [33] |
| Quartz sand packing, deionized water saturation | Excess gas method | Shen et al. [34] |
| Kaolinite, montmorillonite, and illite mixed with ice powder, compacted at −10 °C | Excess gas method at 1 °C and 6 MPa | Wu et al. [35] |
| Standard sand and montmorillonite, refrigerated for 24 h | Excess gas method at 1 °C and 5 MPa | Zhao. [36] |
| Unconsolidated quartz sand, compacted and water-saturated | Excess gas method at 8.5 °C and 15 MPa | Li et al. [37] |
| A mixture of quartz sand and sodium bentonite with 3.5% NaCl solution at −1.95 °C, compacted | Excess gas method at −1.95 °C and 10 MPa | Sun et al. [38] |
| Quartz sand and silty clay mixture | Excess gas method at 8.5 °C and 20 MPa | Han et al. [39] |
| Kaolinite and montmorillonite | Excess gas method at 2.8 °C and 7.5 MPa | Wang et al. [40] |
| Quartz sand and illite mixture (wet compaction method) | Excess gas method at 2 °C and 8 MPa | Lei et al. [41] |
| Factors | Reference |
|---|---|
| Clay hydration and swelling lead to pore-throat clogging | Qi et al. [43] |
| Reduced pore water salinity triggers particle migration and subsequent pore-throat clogging | Jang et al. [44] and Feng et al. [45] |
| Flow pathways and hydrate distribution patterns | Hou et al. [46] |
| Stress and confining pressure | Zhao et al. [47]; Zhao et al. [48] and Zhao et al. [49] |
| Factors | Reference |
|---|---|
| Clay particles aggregate due to flocculation effects, while pore water salinity and vertical pressure gradients. | Sun et al. [38] |
| Initial hydrate saturation, depressurization rate and magnitude, and whether the generated gas can continuously exist | Li et al. [50] |
| The generated gas exists in the form of bubbles, which continuously accumulate and expand, while clay particles aggregate at the water-gas interface. | Jung et al. [51] |
| Water content (saturation) and initial hydrate saturation | Guan et al. [52] |
| Categories | Factors | Reference |
|---|---|---|
| Internal Factors | Particle content | (Russell et al. [68] and Mohan et al. [69]) |
| Particle type | (Yang et al. [63] and Lei et al. [70]) | |
| Particle swelling | (Anderson et al. [71]; Low rt al. [72]; Hensen et al. [73]; Sameni et al. [74] and Karpiński et al. [75]) | |
| Particle size | (Yuan et al. [76]) | |
| Reservoir heterogeneity | (Yang et al. [77]) | |
| External Factors | Seepage velocity | (Bedrikovetsky et al. [78] and Marquez et al. [79]) |
| Salinity | (Mahani et al. [80]; You et al. [81]) | |
| pH | (Vaidya. [82] and Tang et al. [83]) | |
| Fluid type | (Bai et al. [84] and Song et al. [85]) | |
| Temperature | (You et al. [86]) | |
| Stress field | (Ma et al. [87,88]) |
| Methods | Main Equations | Core Concept |
|---|---|---|
| CFD–DEM | Fluid phase treated as continuum, solid phase as discrete | |
| LBM–DEM | ||
| TFM | Both fluid and solid phases treated as continuum |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Cui, Z.; Kong, L.; Zhang, Z. Clay Particle Migration and Associated Permeability Damage in Natural Gas Hydrate-Bearing Clayey-Silty Sediments: A Review. J. Mar. Sci. Eng. 2025, 13, 2054. https://doi.org/10.3390/jmse13112054
Wang Z, Cui Z, Kong L, Zhang Z. Clay Particle Migration and Associated Permeability Damage in Natural Gas Hydrate-Bearing Clayey-Silty Sediments: A Review. Journal of Marine Science and Engineering. 2025; 13(11):2054. https://doi.org/10.3390/jmse13112054
Chicago/Turabian StyleWang, Zhuangzhuang, Zhao Cui, Liang Kong, and Zhimin Zhang. 2025. "Clay Particle Migration and Associated Permeability Damage in Natural Gas Hydrate-Bearing Clayey-Silty Sediments: A Review" Journal of Marine Science and Engineering 13, no. 11: 2054. https://doi.org/10.3390/jmse13112054
APA StyleWang, Z., Cui, Z., Kong, L., & Zhang, Z. (2025). Clay Particle Migration and Associated Permeability Damage in Natural Gas Hydrate-Bearing Clayey-Silty Sediments: A Review. Journal of Marine Science and Engineering, 13(11), 2054. https://doi.org/10.3390/jmse13112054







