Multi-Point Seawall Settlement Modeling Using DTW-Based Hierarchical Clustering and AJSO-LSTM Method
Abstract
1. Introduction
2. Methods
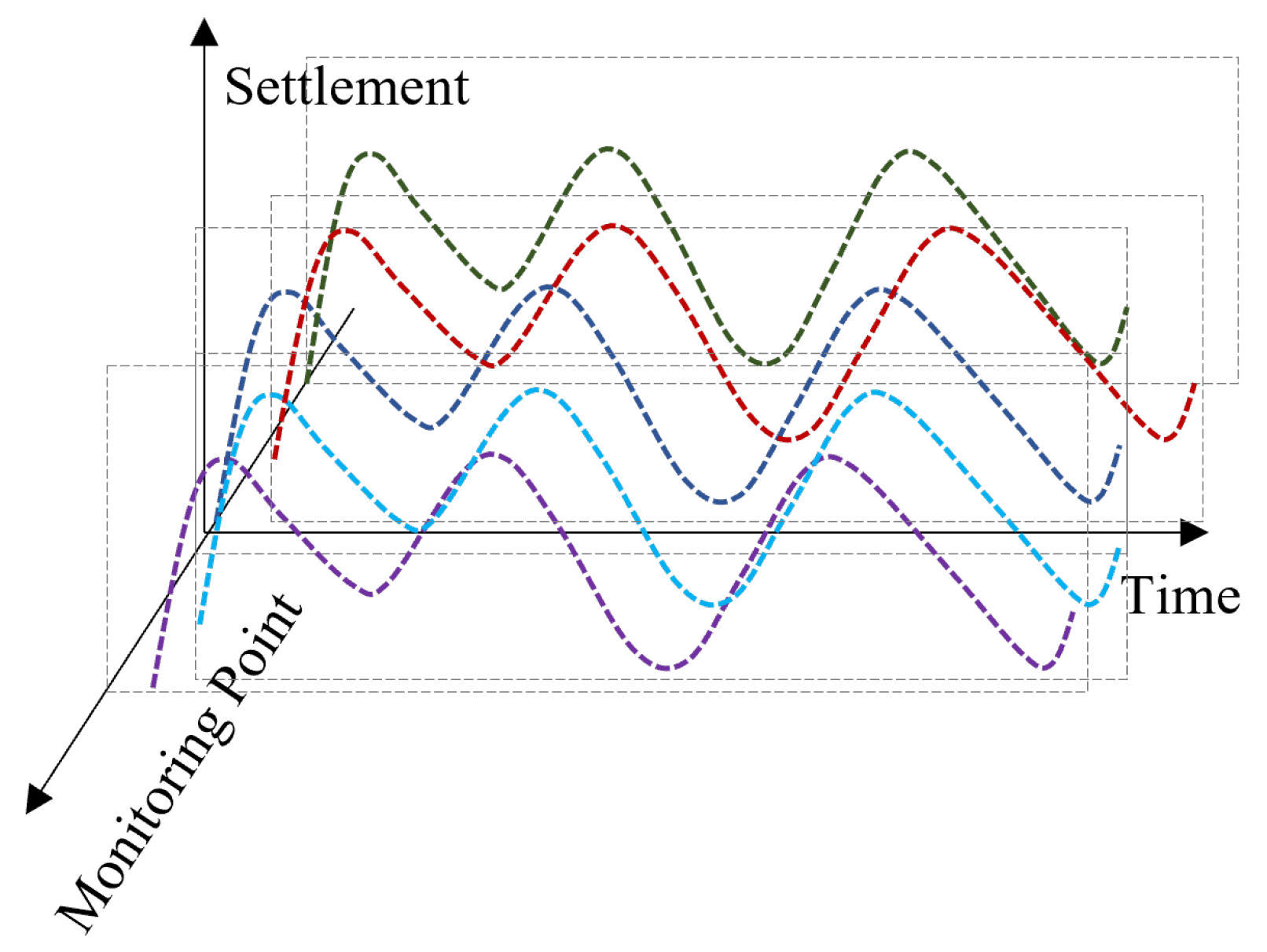
2.1. Spatial Panel Data Structure
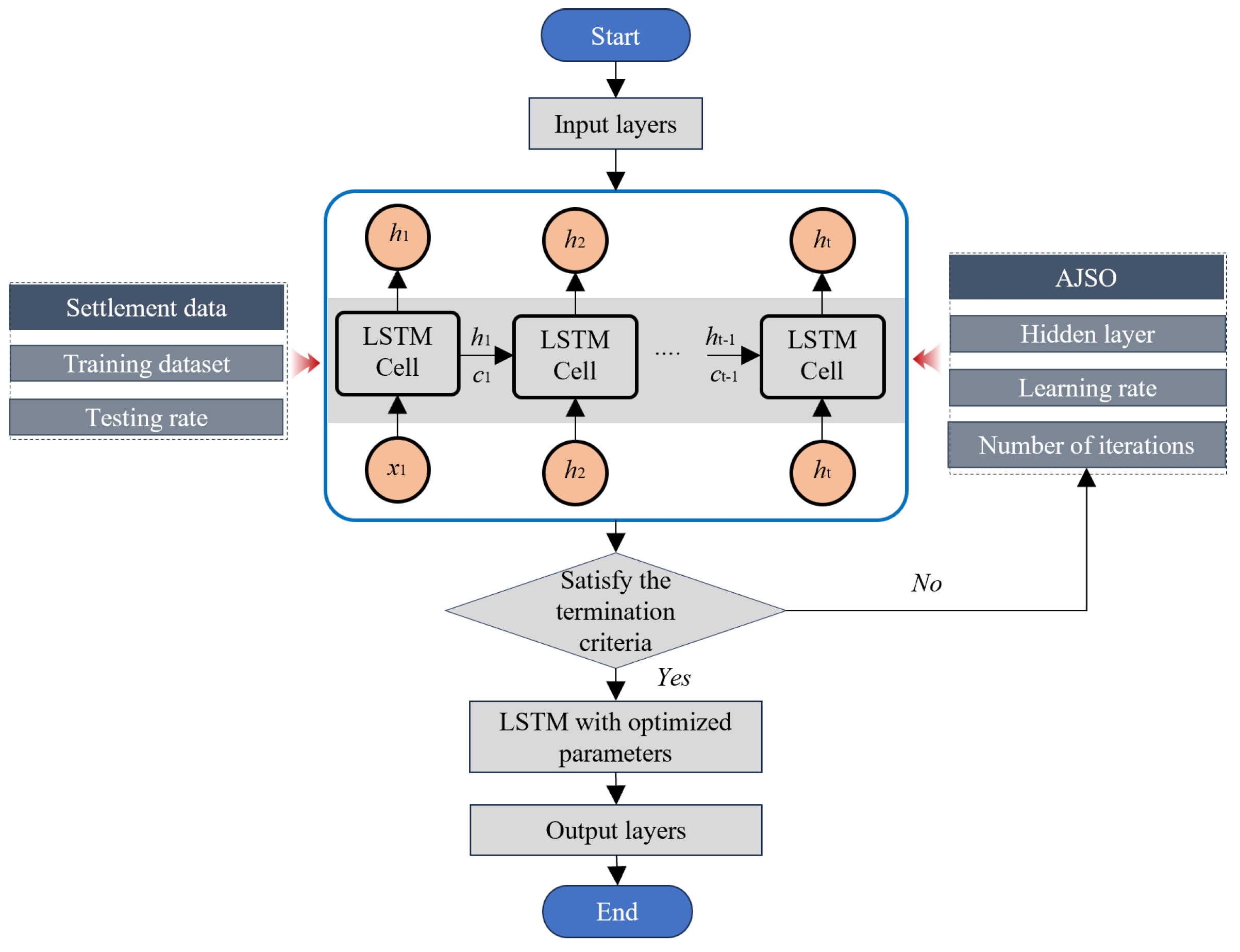
2.2. AJSO-Optimized LSTM Model
- (1)
- Neighborhood scope (cluster-wise masking).
- (2)
- Explicit output mapping of in LSTM (single-step/multi-step).
- (3)
- Multi-point joint (MIMO) output within clusters.
- (4)
- Training loss (explicitly including ) with spatial regularization.
- (5)
- -driven fitness function and AJSO update.
- (6)
- Prediction and evaluation.
2.3. Data Clustering Based on Time-Series Characteristics Using DTW-HC
2.4. Algorithm
| Algorithm 1 DTW-based hierarchical clustering and cluster-wise AJSO–LSTM prediction |
|
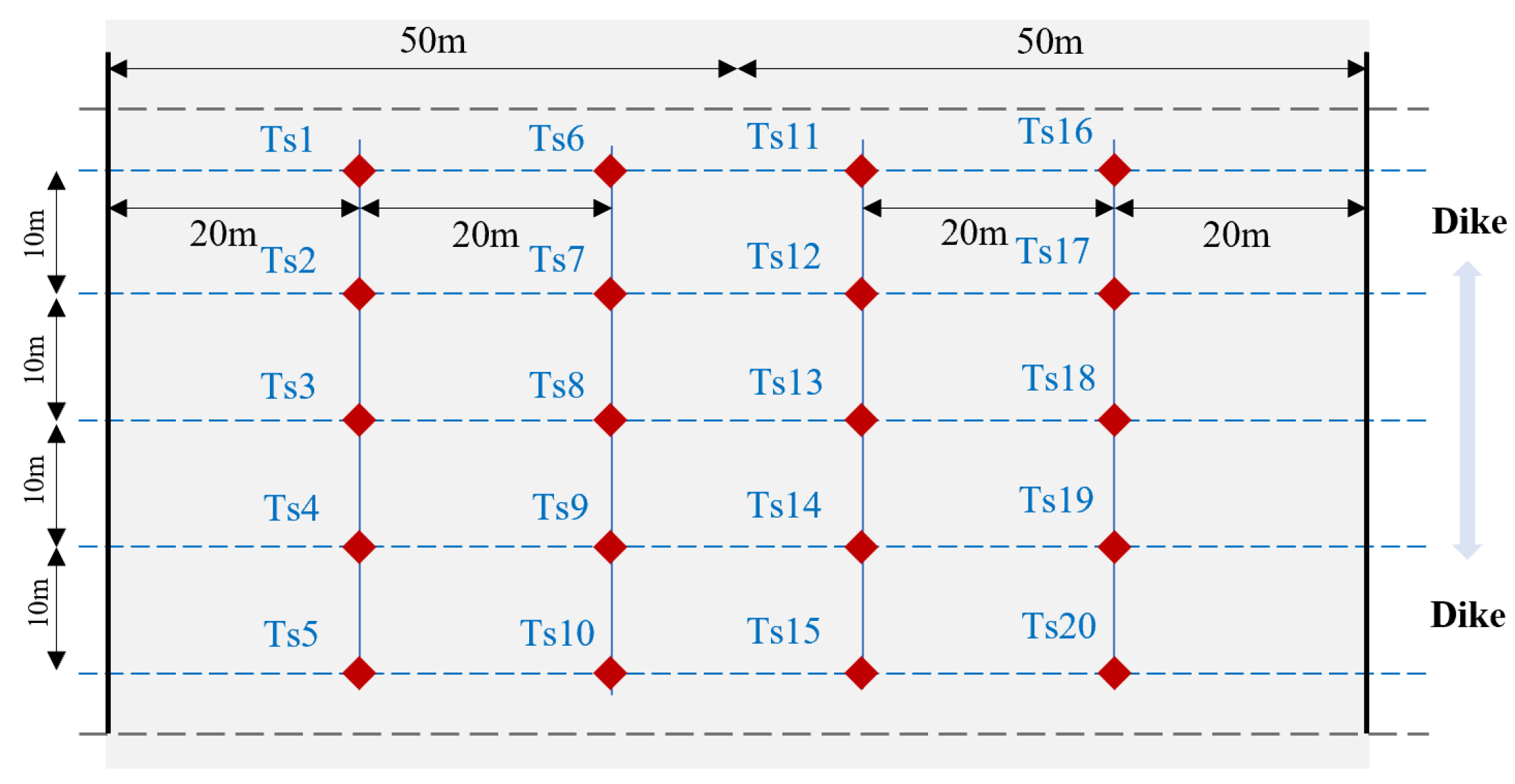
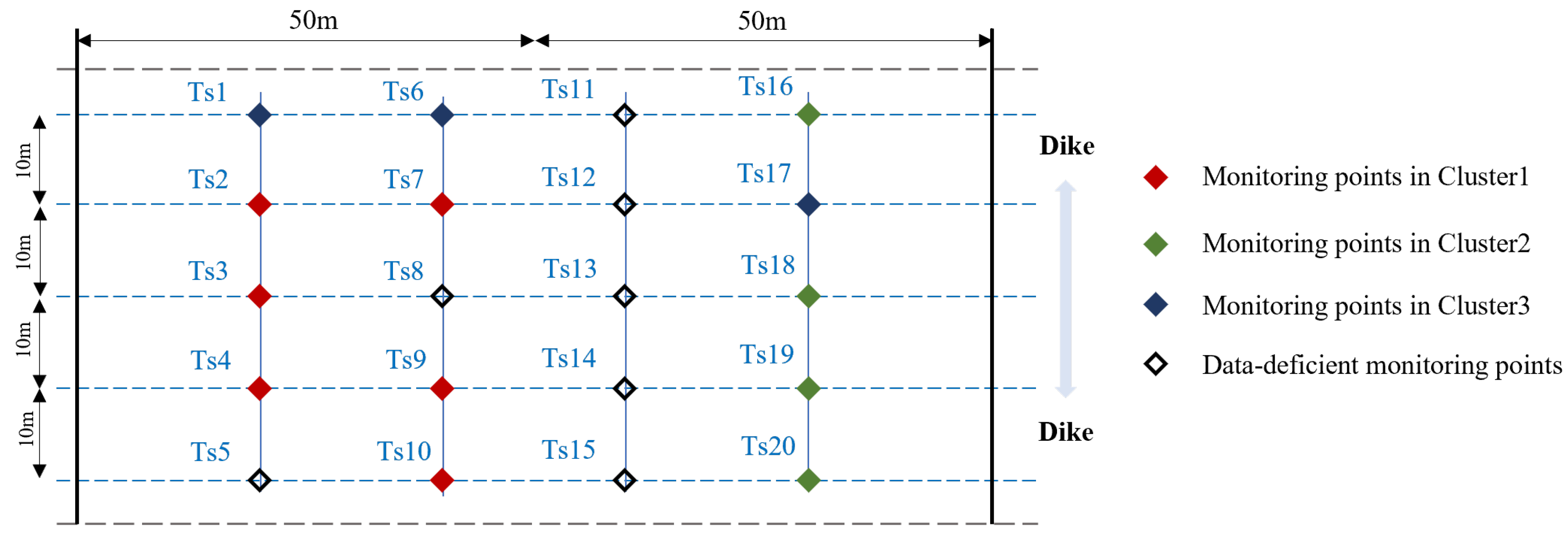
3. Case Study
4. Results
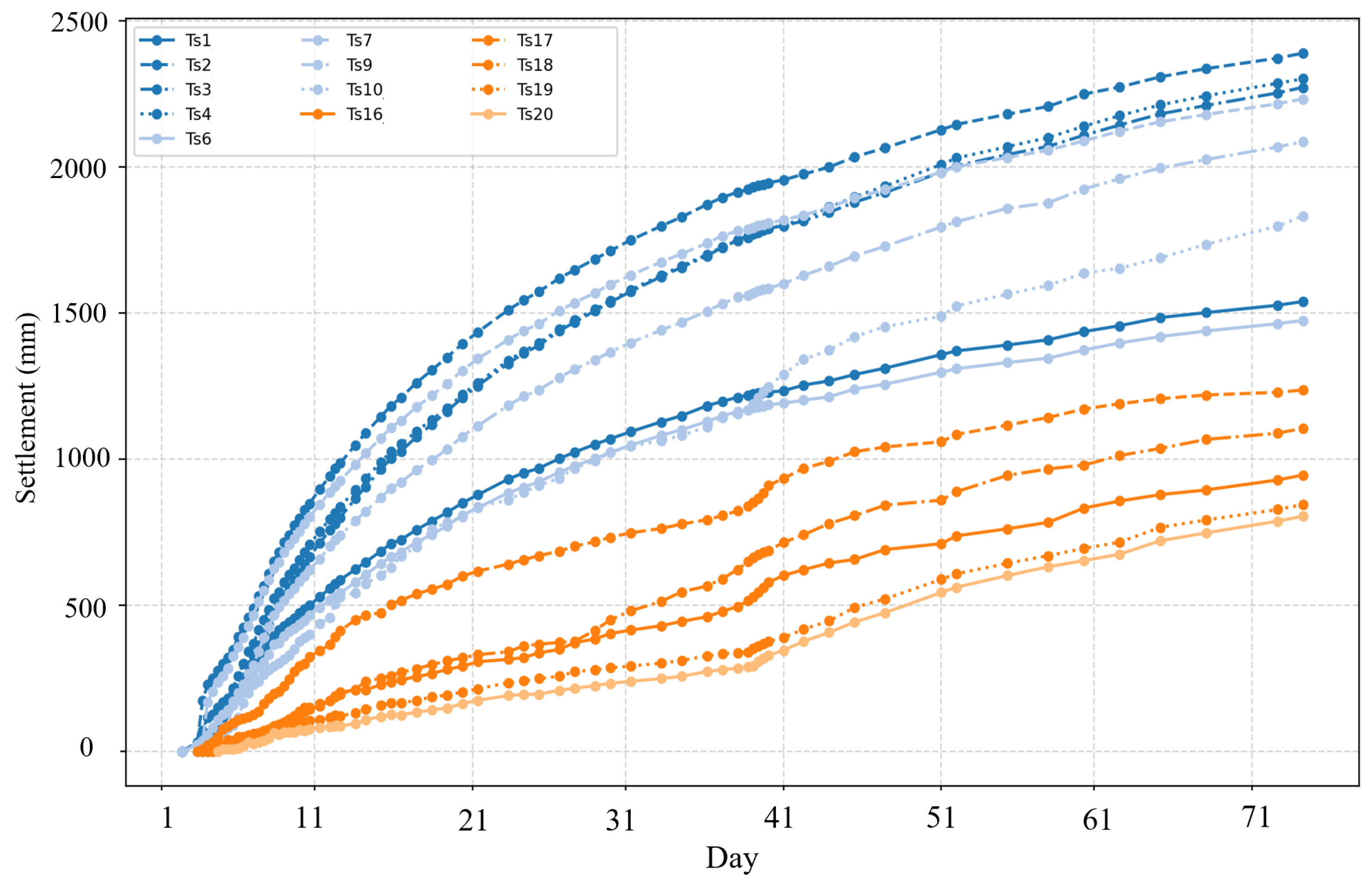
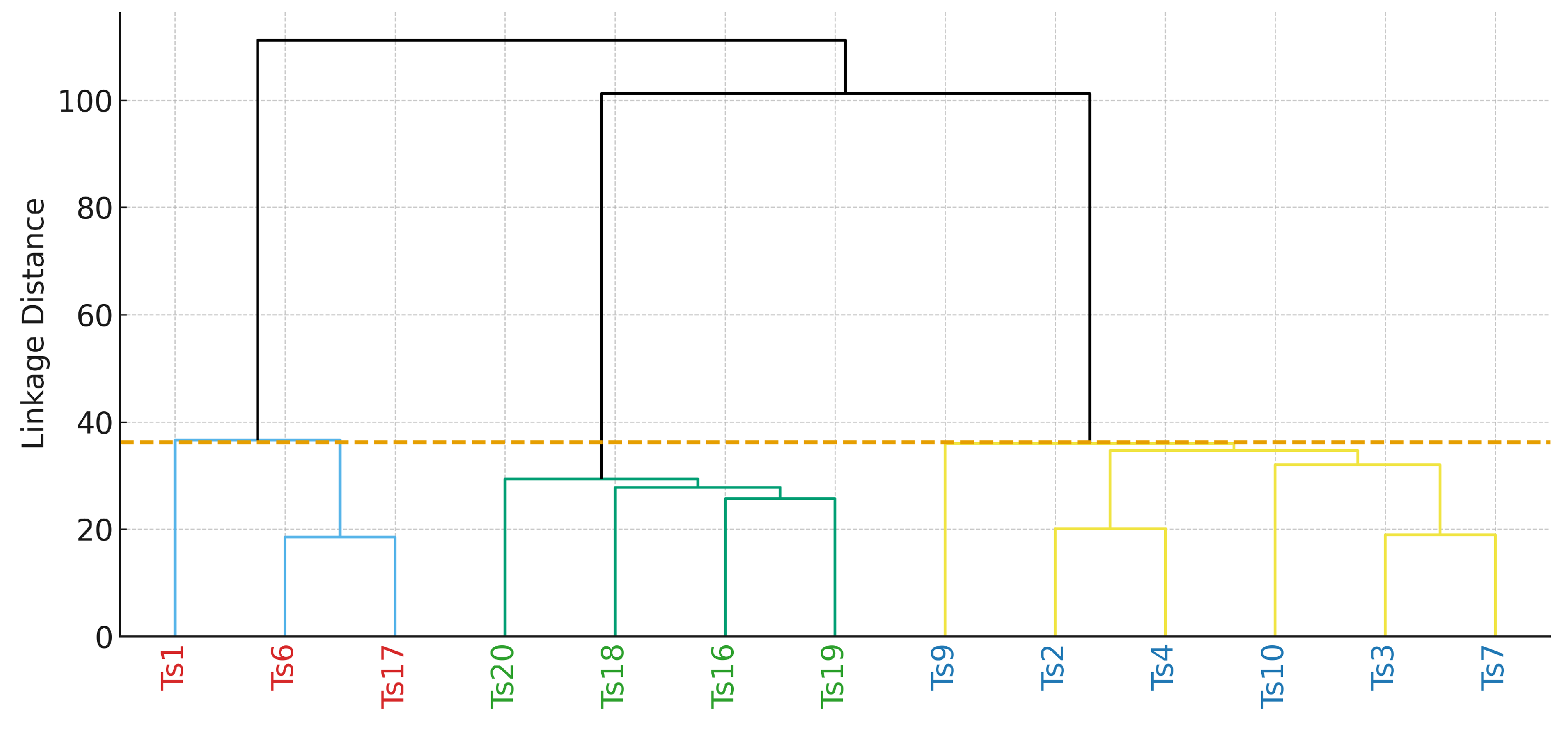
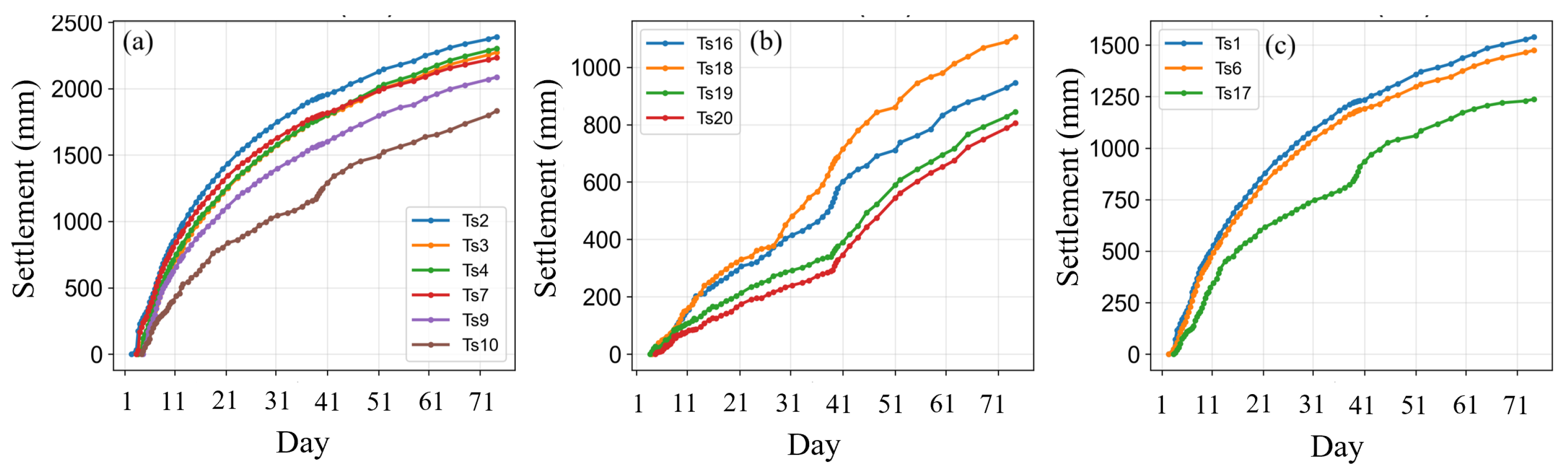
4.1. Clustering Results Based on DTW-HC Method
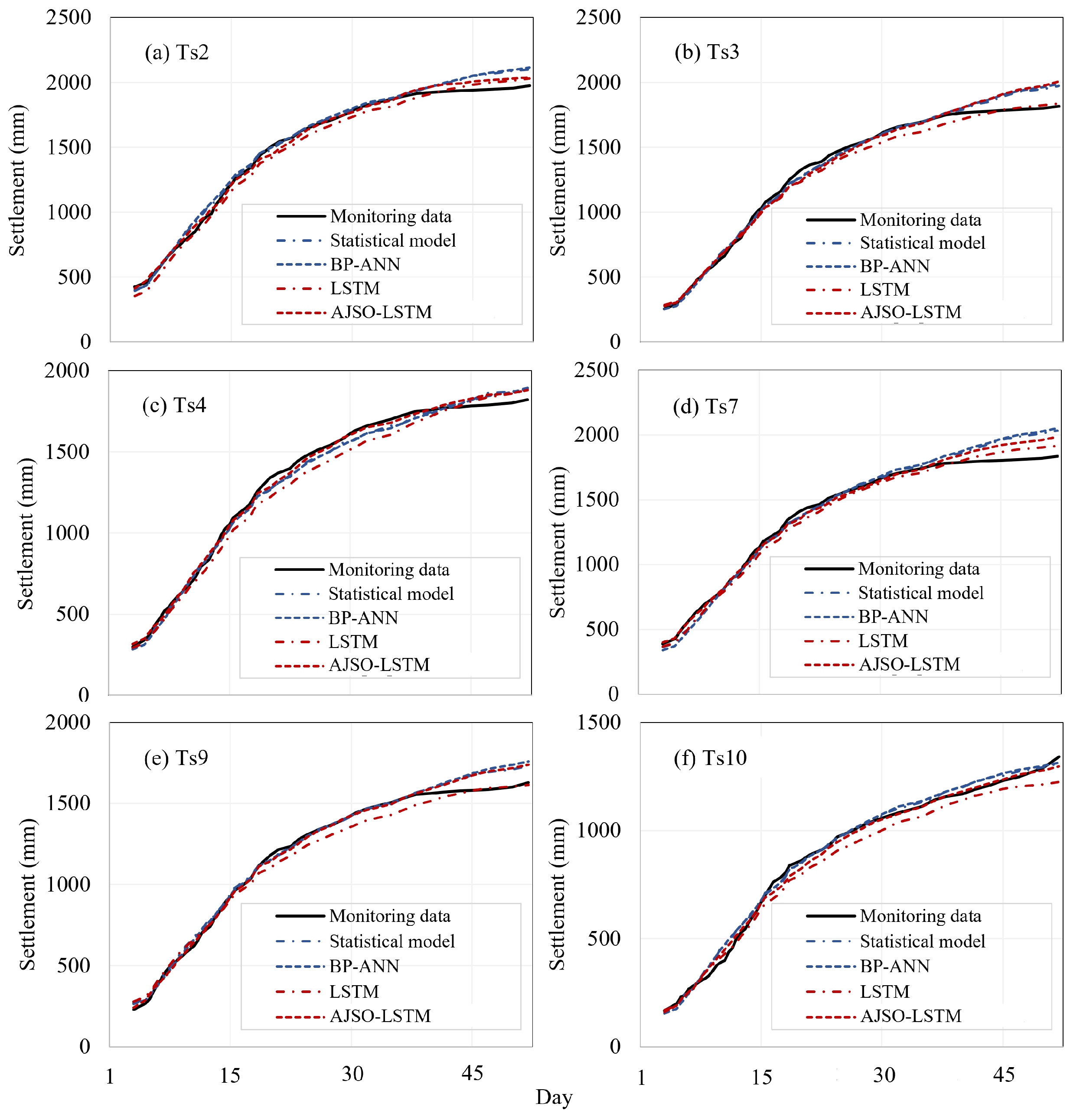
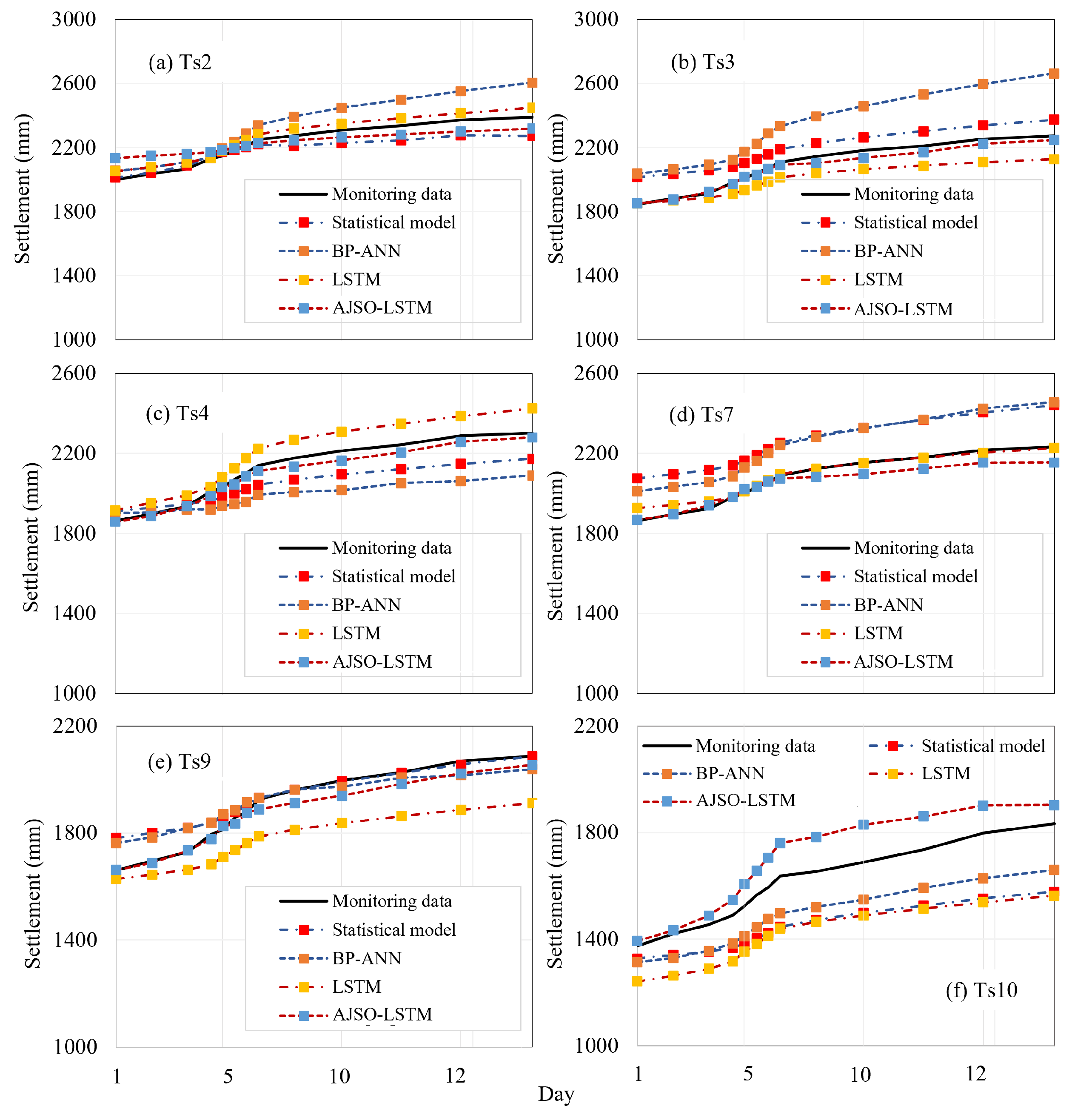
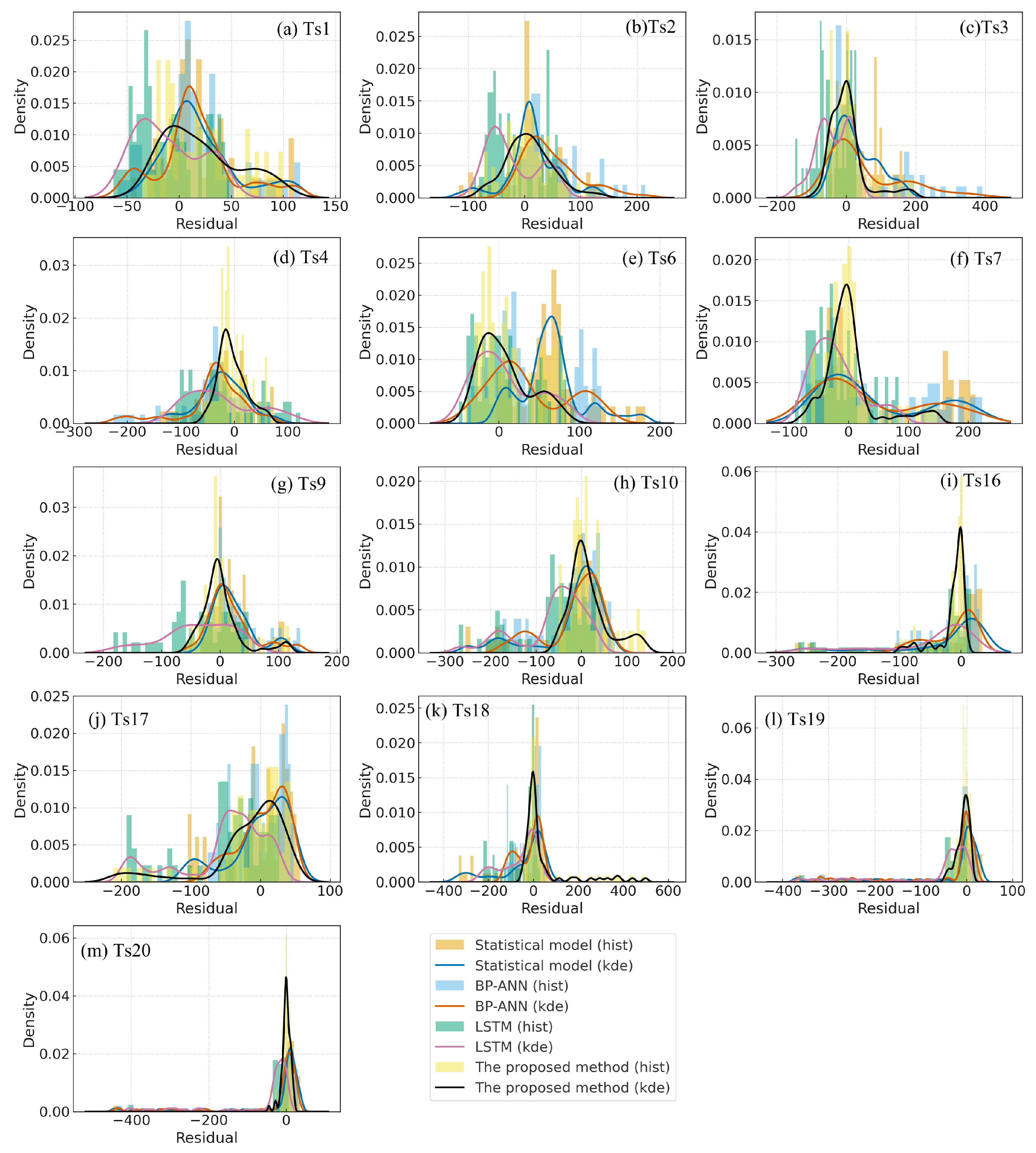
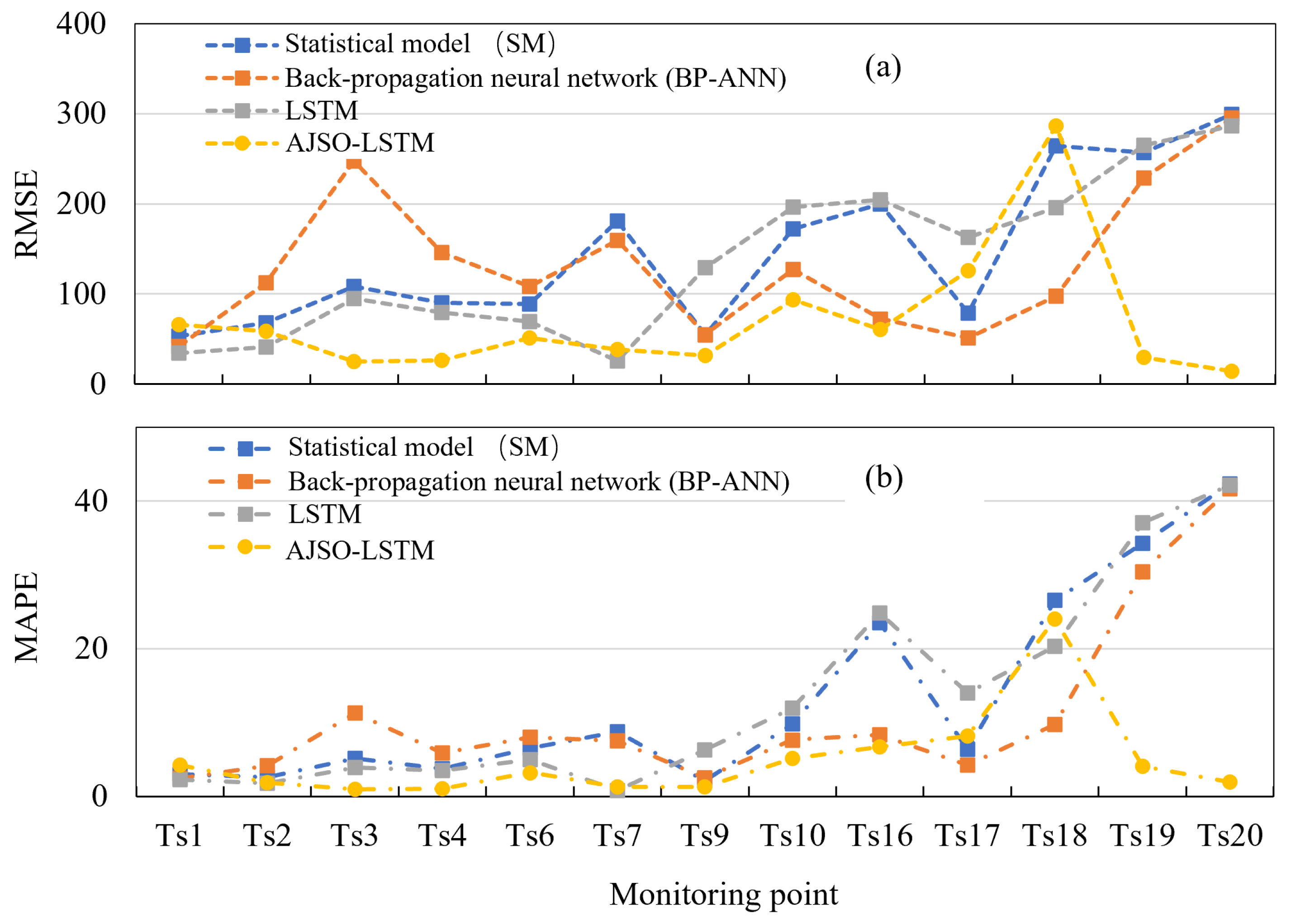
4.2. Prediction Results Based on AJSO-LSTM Method
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AJSO | Adaptive Joint Search Optimization |
| LSTM | Long Short-Term Memory |
| DTW | Dynamic Time Warping |
| HC | Hierarchical Clustering |
| BP-ANN | Backpropagation Artificial Neural Network |
| RBF | Radial Basis Function |
| RMSE | Root Mean Squared Error |
| MAPE | Mean Absolute Percentage Error |
| KDE | Kernel Density Estimation |
| MIMO | Multi-Input Multi-Output |
Appendix A. Fitting Settlements of Cluster 2 and Cluster 3 Points
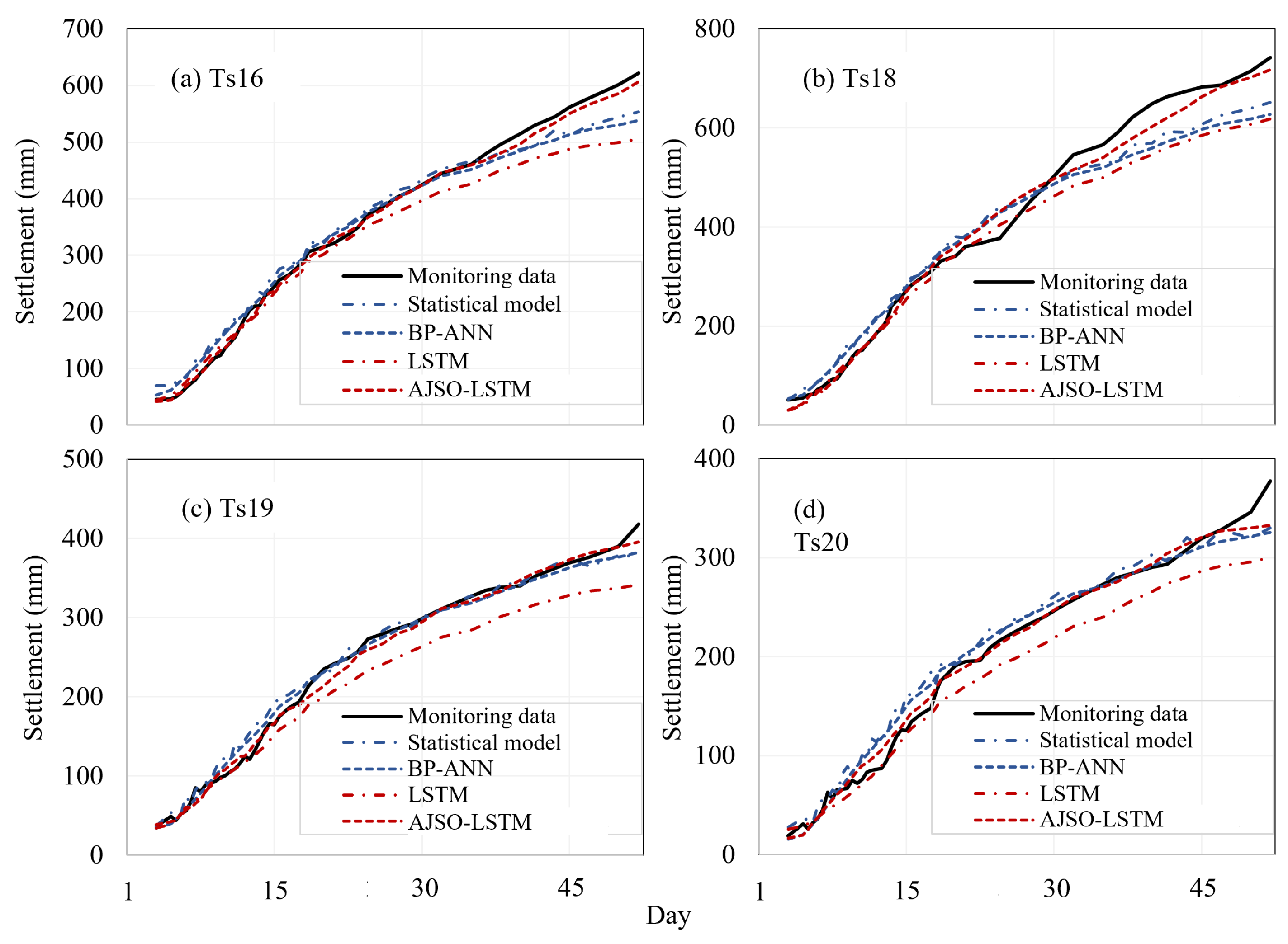

Appendix B. Testing Settlements of Cluster 2 and Cluster 3 Points
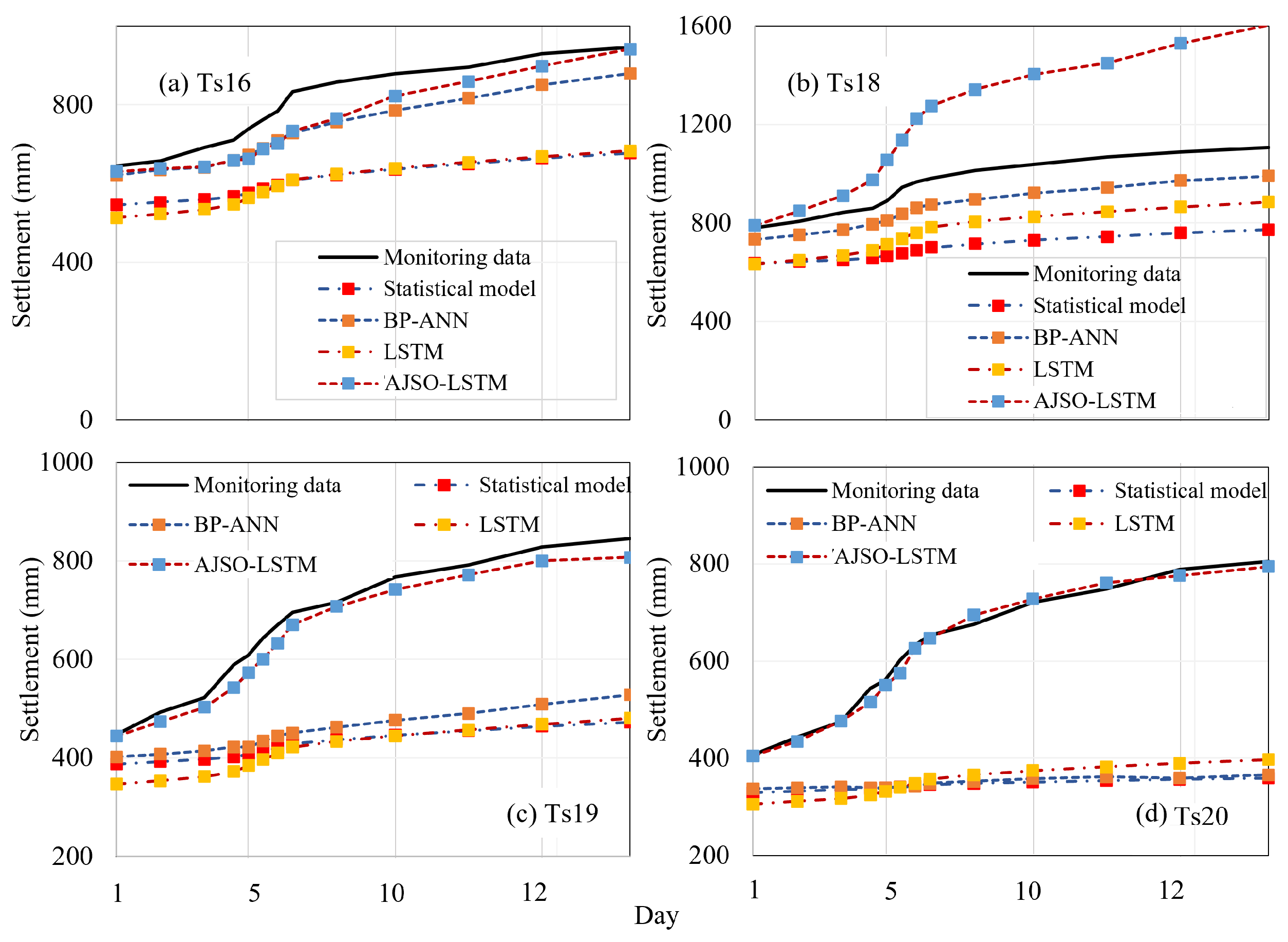
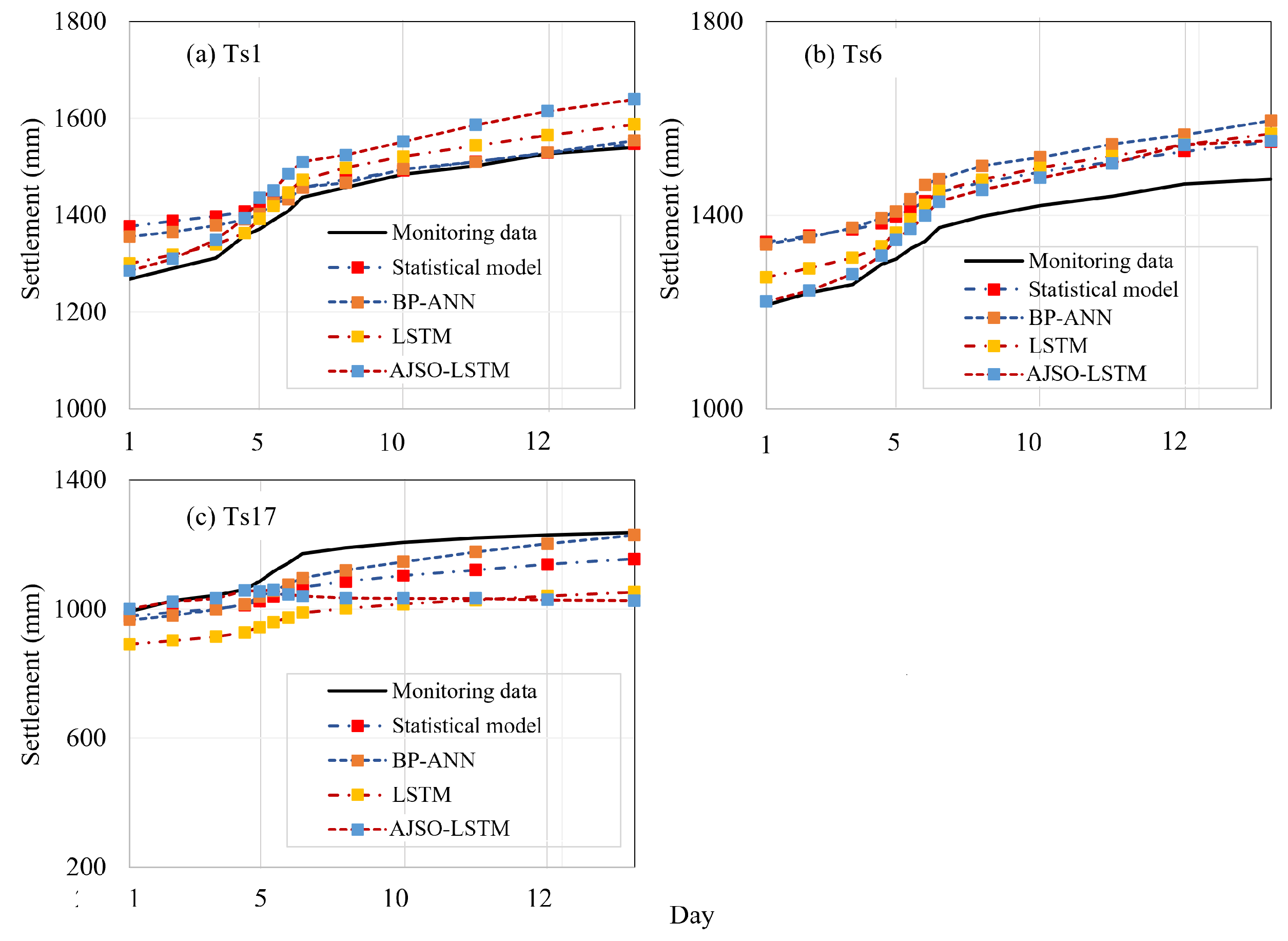
References
- Mi, C.; Gao, J.; Song, Z.; Liu, Y. Hydrodynamic wave forces on two side-by-side barges subjected to nonlinear focused wave groups. Ocean Eng. 2025, 317, 120056. [Google Scholar] [CrossRef]
- Koraim, A.; Heikal, E.; Zaid, A.A. Hydrodynamic characteristics of porous seawall protected by submerged breakwater. Appl. Ocean Res. 2014, 46, 1–14. [Google Scholar] [CrossRef]
- Gong, S.; Gao, J.; Yan, M.; Song, Z.; Shi, H. Effects of floater motion on wave loads during steady-state gap resonance occurring between two non-identical boxes. Ocean Eng. 2025, 323, 120649. [Google Scholar] [CrossRef]
- Galili, E.; Benjamin, J.; Eshed, V.; Rosen, B.; McCarthy, J.; Horwitz, L.K. A submerged 7000-year-old village and seawall demonstrate earliest known coastal defence against sea-level rise. PLoS ONE 2019, 14, e0222560. [Google Scholar] [CrossRef] [PubMed]
- Hazarika, H.; Fukumoto, Y. Sustainable solution for seawall protection against tsunami-induced damage. Int. J. Geomech. 2016, 16, C4016005. [Google Scholar] [CrossRef]
- Li, J.; Meng, Z.; Zhang, J.; Chen, Y.; Yao, J.; Li, X.; Qin, P.; Liu, X.; Cheng, C. Prediction of seawater intrusion run-up distance based on K-means clustering and ANN model. J. Mar. Sci. Eng. 2025, 13, 377. [Google Scholar] [CrossRef]
- Hosseinzadeh, N.; Ghiasian, M.; Andiroglu, E.; Lamere, J.; Rhode-Barbarigos, L.; Sobczak, J.; Sealey, K.S.; Suraneni, P. Concrete seawalls: A review of load considerations, ecological performance, durability, and recent innovations. Ecol. Eng. 2022, 178, 106573. [Google Scholar] [CrossRef]
- Kraus, N.C. The effects of seawalls on the beach: An extended literature review. J. Coast. Res. 1988, SI 4, 1–28. [Google Scholar]
- Zehro, K. Specifications and types of seawall structures needed to protect beaches from sand erosion and storm disasters. Int. J. Adv. Eng. Sci. Appl. 2021, 2, 13–18. [Google Scholar] [CrossRef]
- Hu, Y.; Gu, C.; Meng, Z.; Shao, C. Improve the model stability of Dam’s displacement prediction using a numerical-statistical combined model. Ieee Access 2020, 8, 147482–147493. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.; Oñate, E.; Morán, R. An empirical comparison of machine learning techniques for dam behaviour modelling. Struct. Saf. 2015, 56, 9–17. [Google Scholar] [CrossRef]
- Gao, J.; Hou, L.; Liu, Y.; Shi, H. Influences of bragg reflection on harbor resonance triggered by irregular wave groups. Ocean Eng. 2024, 305, 117941. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Goel, S.; Imielinski, T. Prediction-based monitoring in sensor networks: Taking lessons from MPEG. ACM SIGCOMM Comput. Commun. Rev. 2001, 31, 82–98. [Google Scholar] [CrossRef]
- Yao, K.; Wen, Z.; Yang, L.; Chen, J.; Hou, H.; Su, H. A multipoint prediction model for nonlinear displacement of concrete dam. Comput. Aided Civ. Infrastruct. Eng. 2022, 37, 1932–1952. [Google Scholar] [CrossRef]
- Tatin, M.; Briffaut, M.; Dufour, F.; Simon, A.; Fabre, J.P. Statistical modelling of thermal displacements for concrete dams: Influence of water temperature profile and dam thickness profile. Eng. Struct. 2018, 165, 63–75. [Google Scholar] [CrossRef]
- Goda, K. Statistical modeling of joint probability distribution using copula: Application to peak and permanent displacement seismic demands. Struct. Saf. 2010, 32, 112–123. [Google Scholar] [CrossRef]
- Xi, G.y.; Yue, J.p.; Zhou, B.x.; Tang, P. Application of an artificial immune algorithm on a statistical model of dam displacement. Comput. Math. Appl. 2011, 62, 3980–3986. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, S.H.; Xie, J.; Li, X. Bayesian inverse analysis with field observation for slope failure mechanism and reliability assessment under rainfall accounting for nonstationary characteristics of soil properties. Soils Found. 2025, 65, 101568. [Google Scholar] [CrossRef]
- Chen, H.; Huang, S.; Qiu, H.; Xu, Y.P.; Teegavarapu, R.S.; Guo, Y.; Nie, H.; Xie, H.; Xie, J.; Shao, Y.; et al. Assessment of ecological flow in river basins at a global scale: Insights on baseflow dynamics and hydrological health. Ecol. Indic. 2025, 178, 113868. [Google Scholar] [CrossRef]
- Zhou, J.; Fu, K.; Liang, S.; Li, J.; Liang, J.; An, X.; Liu, Y. Extracting Water Surfaces of the Dike-Pond System from High Spatial Resolution Images Using Deep Learning Methods. Remote Sens. 2024, 17, 111. [Google Scholar] [CrossRef]
- Qin, P.; Cheng, C. Prediction of Seawall Settlement Based on a Combined LS-ARIMA Model. Math. Probl. Eng. 2017, 2017, 7840569. [Google Scholar] [CrossRef]
- Meng, Z.; Hu, Y.; Jiang, S.; Zheng, S.; Zhang, J.; Yuan, Z.; Yao, S. Slope Deformation Prediction Combining Particle Swarm Optimization-Based Fractional-Order Grey Model and K-Means Clustering. Fractal Fract. 2025, 9, 210. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Strauss, A.; Kim, S. Use of monitoring extreme data for the performance prediction of structures: General approach. Eng. Struct. 2008, 30, 3644–3653. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Ma, G.; Rezania, M. Characterization of spatially varying soil properties using an innovative constraint seed method. Comput. Geotech. 2025, 183, 107184. [Google Scholar] [CrossRef]
- Mata, J.; Salazar, F.; Barateiro, J.; Antunes, A. Validation of machine learning models for structural dam behaviour interpretation and prediction. Water 2021, 13, 2717. [Google Scholar] [CrossRef]
- Li, M.; Li, M.; Ren, Q.; Li, H.; Song, L. DRLSTM: A dual-stage deep learning approach driven by raw monitoring data for dam displacement prediction. Adv. Eng. Informatics 2022, 51, 101510. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Li, H.; Fan, Y.; Meng, Z.; Liu, D.; Pan, S. Optimization of Water Quantity Allocation in Multi-Source Urban Water Supply Systems Using Graph Theory. Water 2024, 17, 61. [Google Scholar] [CrossRef]
- Chen, H.; Xu, B.; Qiu, H.; Huang, S.; Teegavarapu, R.S.; Xu, Y.P.; Guo, Y.; Nie, H.; Xie, H. Adaptive assessment of reservoir scheduling to hydrometeorological comprehensive dry and wet condition evolution in a multi-reservoir region of southeastern China. J. Hydrol. 2025, 648, 132392. [Google Scholar] [CrossRef]
- Mugnaini, V.; Fragonara, L.Z.; Civera, M. A machine learning approach for automatic operational modal analysis. Mech. Syst. Signal Process. 2022, 170, 108813. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Xin, J.; Peng, S. TPS-GNN: Predictive model for bridge health monitoring data based on temporal periodicity and global spatial distribution characteristics. Struct. Health Monit. 2025, 14759217251330971. [Google Scholar] [CrossRef]
- Li, Z.H.; Cui, J.X.; Lu, H.P.; Zhou, F.; Diao, Y.L.; Li, Z.X. Prediction model of measurement errors in current transformers based on deep learning. Rev. Sci. Instruments 2024, 95, 044704. [Google Scholar] [CrossRef] [PubMed]
- Bi, J.; Li, J.; Wu, K.; Chen, Z.; Chen, S.; Jiang, L.; Feng, D.; Deng, P. A physics-informed spatial-temporal neural network for reservoir simulation and uncertainty quantification. SPE J. 2024, 29, 2026–2043. [Google Scholar] [CrossRef]
- Qu, X.; Yang, J.; Chang, M. A Deep Learning Model for Concrete Dam Deformation Prediction Based on RS-LSTM. J. Sensors 2019, 2019, 4581672. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Gong, J.; Shu, X.; Zhang, K. The prediction of dam displacement time series using STL, extra-trees, and stacked LSTM neural network. IEEE Access 2020, 8, 94440–94452. [Google Scholar] [CrossRef]
- Madiniyeti, J.; Chao, Y.; Li, T.; Qi, H.; Wang, F. Concrete dam deformation prediction model research based on SSA–LSTM. Appl. Sci. 2023, 13, 7375. [Google Scholar] [CrossRef]
- Zheng, S.; Gu, C.; Shao, C.; Hu, Y.; Xu, Y.; Huang, X. A novel prediction model for seawall deformation based on CPSO-WNN-LSTM. Mathematics 2023, 11, 3752. [Google Scholar] [CrossRef]
- Qin, P.; Cheng, C.; Meng, Z.; Ding, C.; Zheng, S.; Su, H. Multi-Point Seawall Settlement Prediction with Limited Data Volume Using an Improved Fractional-Order Grey Model. Fractal Fract. 2024, 8, 423. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Li, C.Z.; Hu, Z.; Shen, G.Q.; Huang, Z. Foundation pit displacement monitoring and prediction using least squares support vector machines based on multi-point measurement. Struct. Health Monit. 2019, 18, 715–724. [Google Scholar] [CrossRef]
- Li, Y.; Min, K.; Zhang, Y.; Wen, L. Prediction of the failure point settlement in rockfill dams based on spatial-temporal data and multiple-monitoring-point models. Eng. Struct. 2021, 243, 112658. [Google Scholar] [CrossRef]
- Fattahi, H.; Bayatzadehfard, Z. Forecasting surface settlement caused by shield tunneling using ANN-BBO model and ANFIS based on clustering methods. J. Eng. Geol. 2018, 12, 55–84. [Google Scholar]
- Beiranvand, B.; Rajaee, T.; Komasi, M. Presenting the AI models in predicting the settlement of earth dams using the results of spatiotemporal clustering and k-means algorithm. Sci. Rep. 2024, 14, 10207. [Google Scholar] [CrossRef] [PubMed]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Wah, T.Y. Time-series clustering–a decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Liao, T.W. Clustering of time series data—A survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Rani, S.; Sikka, G. Recent techniques of clustering of time series data: A survey. Int. J. Comput. Appl. 2012, 52, 15. [Google Scholar] [CrossRef]
- Sammour, M.; Othman, Z.A.; Rus, A.M.M.; Mohamed, R. Modified dynamic time warping for hierarchical clustering. Int. J. Adv. Sci. Eng. Inf. Technol. 2019, 9, 1481–1487. [Google Scholar] [CrossRef]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Li, H. Time works well: Dynamic time warping based on time weighting for time series data mining. Inf. Sci. 2021, 547, 592–608. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, D.; Xu, X.; Zhang, D. An adaptive joint operating parameters optimization approach for active direct methanol fuel cells. Energies 2023, 16, 2167. [Google Scholar] [CrossRef]
- Zhang, J.; Wan, Z.; Liao, J. Adaptive joint optimization for 3D reconstruction with differentiable rendering. IEEE Trans. Vis. Comput. Graph. 2022, 29, 3039–3051. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]






| Points | 1 | 2 | 3 | … | t |
|---|---|---|---|---|---|
| 1 | … | ||||
| 2 | … | ||||
| 3 | … | ||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋱ | ⋮ |
| n | … |
| Points | 1 | 2 | 3 | … | t |
|---|---|---|---|---|---|
| 1 | … | ||||
| 2 | … | ||||
| 3 | … | ||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋱ | ⋮ |
| n | … |
| Cluster | L | Hidden | Batch | LR | r (m) | h (m) | w | ||
|---|---|---|---|---|---|---|---|---|---|
| C1 | 15 | 16 | 4 | 25 | 15 | 6 | 0.05 | ||
| C2 | 10 | 12 | 4 | 25 | 12 | 6 | 0.02 | ||
| C3 | 12 | 16 | 4 | 25 | 15 | 6 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, C.; Liu, X.; Meng, Z.; Liu, Y. Multi-Point Seawall Settlement Modeling Using DTW-Based Hierarchical Clustering and AJSO-LSTM Method. J. Mar. Sci. Eng. 2025, 13, 2053. https://doi.org/10.3390/jmse13112053
Ding C, Liu X, Meng Z, Liu Y. Multi-Point Seawall Settlement Modeling Using DTW-Based Hierarchical Clustering and AJSO-LSTM Method. Journal of Marine Science and Engineering. 2025; 13(11):2053. https://doi.org/10.3390/jmse13112053
Chicago/Turabian StyleDing, Chunmei, Xian Liu, Zhenzhu Meng, and Yadong Liu. 2025. "Multi-Point Seawall Settlement Modeling Using DTW-Based Hierarchical Clustering and AJSO-LSTM Method" Journal of Marine Science and Engineering 13, no. 11: 2053. https://doi.org/10.3390/jmse13112053
APA StyleDing, C., Liu, X., Meng, Z., & Liu, Y. (2025). Multi-Point Seawall Settlement Modeling Using DTW-Based Hierarchical Clustering and AJSO-LSTM Method. Journal of Marine Science and Engineering, 13(11), 2053. https://doi.org/10.3390/jmse13112053






