Abstract
This paper presents a data-driven model reduction by moment-matching approach to construct control-oriented models for a point absorber device. The methodology chosen and developed generates models which are input-to-state linear, with any nonlinear behaviour confined to the output map. Such a map is the result of a data-driven approximation procedure, where the so-called moment of the point absorber system is estimated via a least-squares procedure. The resulting control-oriented model can inherently preserve steady-state properties of the target WEC system for a user-defined class of input signals of interest, with the computation only dependent upon a suitably defined set of input-output data.
1. Introduction
Wave energy converters (WECs) require control algorithms to enhance their efficiency: It is well-established that suitable control system technology, tailored to maximise energy absorption from ocean waves, has the potential to push WEC systems towards effective commercialisation [1,2,3]. The vast majority of WEC controllers rely upon availability of a suitable control-oriented model, capable of effectively trading accuracy with computational/analytical complexity. The latter can impact both well-posedness of control solutions (i.e., existence of a globally optimal control law for a given operating condition), and real-time capabilities of any specific WEC controller [4]. A pathway towards computation of such parsimonious models is based on model reduction techniques, where a target model is reduced into a ‘simpler’ (yet representative) structure, with a level of complexity suitable for the specific control task.
The relevance behind incorporating nonlinear effects within the WEC control design procedure, i.e., of using nonlinear control-oriented dynamical models, has been extensively demonstrated and stressed in multiple studies, such as those reported in [5,6]. Wave energy systems are, by design, likely to exhibit substantial nonlinear behaviour, given that their principal objective, pursued by the corresponding optimal control law, is to enhance the device motion in order to maximise energy absorption. This, naturally, challenges the assumptions under which linearisation about the WEC equilibrium position is effectively representative (see, e.g., [5,6]). Though rather scarce, we note that attempts at control-oriented model reduction for WEC systems have been presented in, e.g., [7,8,9,10], though simplified models are often computed by selectively ‘ignoring’ specific nonlinear components, based upon a pre-defined set of operating conditions.
Following the central role of systematic model reduction in producing nonliner control-oriented models for WEC control design procedures, we present, in this manuscript, an application of moment-matching-based model reduction wave energy systems. Moment-matching techniques [10,11,12] have the capability of producing reduced models which effectively matches the steady-state response of the target nonlinear system to be reduced.
In particular, we propose a model reduction approach for a point absorber device (whose geometry and corresponding dimensions are adopted from [13]), based upon data-driven moment-matching [14,15]. This device is an offshore, single body, bottom referenced, floating WEC, which extracts energy from the (translational) heave motion (see Figure 1). The main objective pursued in this paper is that of producing accurate and efficient moment-matching-based reduced models for such a WEC system, subject to a variety of input (wave) conditions. Such objective is achieved by first providing a formal proof on existence and uniqueness of the associated family of reduced order models, and by subsequently employing a fully data-driven algorithm for the approximation of the so-called nonlinear moment, based only on input-output data pairs, being this fundamental towards the final computation of the approximating system. Moreover, the proposed strategy is exhaustively illustrated via numerical analysis.
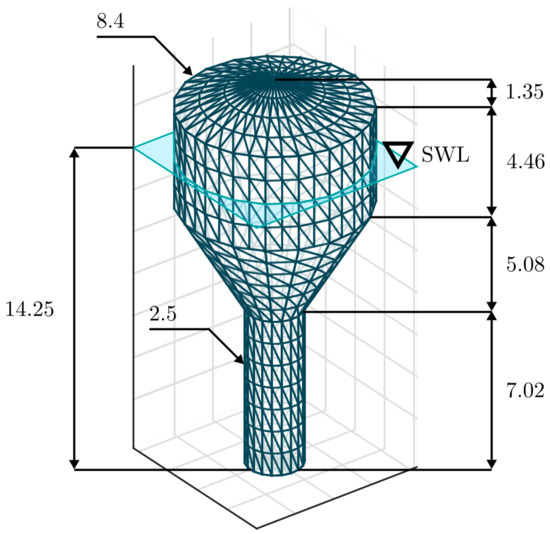
Figure 1.
Schematic of the point absorber device under study. Dimensions are presented in metres. Note that the acronym SWL denotes the still water level.
The reminder of this paper is organised as follows. Section 1.1 presents the notation utilised throughout our study. Section 2 defines the dynamical (target) model of the point absorber system. Section 3 provides a moment-based analysis of the WEC, and proposes a family of reduced models achieving moment-matching from a data-driven perspective. Finally, Section 4 offers a numerical appraisal of the performance of the proposed models, while Section 5 encompasses the main conclusions of our study.
1.1. Notation and Conventions
is the set of non-negative real numbers, the set of pure-imaginary complex numbers, and the set of complex numbers with negative real part. The notation indicates the set of all positive natural numbers up to q, i.e., . The span of the set , where is a vector space over a field , is denoted as . The symbol 0 stands for any zero element, dimensioned according to the context. The spectrum of a matrix , i.e., the set of its eigenvalues, is denoted as . Given two functions, and , the composition , which maps all to , is denoted with . Finally, the Fourier transform of a function f (provided it exists), is denoted as , .
2. Point Absorber Dynamics
The point absorber WEC device adopted in this study, schematically illustrated in Figure 1, whose geometry and corresponding dimensions are adopted from [13]. The system is essentially an offshore WEC (see [16]), where energy is extracted from the heave (translational) mode of motion. The dimensions of such a (full-scale) device are recalled in the schematic presented in Figure 1.
If we constrain the WEC to move in a single degree-of-freedom 1 (DoF), i.e., heave, the equation of motion of such a device can be expressed as a dynamical system , fully characterised in terms of the the so-called nonlinear Cummins’ Equation (see, e.g., [19]), given by 2
where denotes the displacement of the device (selected as the system output 3 y), the radiation force (which accounts for the fluid memory effects), the viscous force, the restoring force, , the wave excitation force (i.e., external uncontrollable input representing the force exerted by waves on the surface of the device), , the control input, and is the inverse of the generalised WEC mass.
The radiation force is modelled based on linear potential theory, and can be hence characterised by a linear, continuous-time, strictly proper, passive 4, system , which directly depends upon the output of system (1). Without any loss of generality, such an output feedback system can be expressed, in state-space representation, as
with , with sufficiently large, , and . The mapping , characterising viscous effects, is written in terms of a smooth approximation of the so-called Morison Equation [22], i.e.,
with sufficiently small, and directly depending on the physical dimensions of the device. The restoring force is expressed in terms of a polynomial mapping in z (see [19]), i.e.,
where is commonly referred to as hydrostatic stiffness, and .
With the specific definitions for the mappings offered above, system in (1) can be expressed in state-space form as
with the total input force, and where the associated state vector is defined as , , with . The triple of matrices , with , , is given by
together with
The mapping , which is exclusively composed of terms characterising the nonlinear behaviour of system (1), can be written as
with defined as
We further note that the maps g and are such that and so that, clearly, and .
3. Moment-Based Analysis of the WEC
We present, in this section, the definition of moments for the point absorber device under study, together with an appropriate structure to achieve model reduction by moment-matching. The concepts recalled in this section are based upon the system-theoretic approach originally proposed in [11], later extended to a large class of systems (and inputs) in, e.g., [14,23,24].
From now on, and for aiming to simplify our exposition, we assume the WEC device is subject to regular input excitation with a given fundamental frequency . Nonetheless, we do note that extension of the following results to irregular sea states can be conducted analogously to [10] (see also the discussion provided in Remark 2).
Remark 1.
The corresponding optimal control input u, which maximises energy absorption (under state-and-input unconstrained conditions) for such an , is a mapping with the same fundamental frequency (see [19,25]).
3.1. Definition of Moment
In view of Remark 1, let the mapping, corresponding to the total external input , be expressed in implicit form, i.e., in terms of a signal generator (often referred to as an exogenous system), described by the set of equations
for , with , and hence , with . From now on, and without any loss of generality, let the output vector of be defined as .
Remark 2.
As discussed previously in this section, and for simplicity of exposition, the signal generator in (10) considers that the corresponding system input is composed of a single fundamental frequency component , i.e., the device is subject to regular (monochromatic) waves. Extension of this strategy for irregular sea states can be performed analogously to the model-based reduction framework in [10], by defining a corresponding signal generator with a sufficiently large set of harmonic multiples of , i.e., with a dynamic matrix given by
with the set of harmonic frequencies , where , and adapting the upcoming results accordingly.
We now introduce the following standing assumption, adopted from [23,23].
Assumption A1.
The pair of matrices is excitable.
Remark 3.
For linear systems, excitability is equivalent to reachability, with playing the role of the input matrix 5.
Remark 4.
If is excitable, i.e., under Assumption A1, one can easily check that , and hence the input mapping ζ is -periodic, where the fundamental period of ζ.
Aiming to provide a formal definition of moment for the point absorber device described in Equation (5), we further introduce an assumption regarding the stability of . Note that, due to the nature of the nonlinear map g, defined in Equation (8), one can check that is an equilibrium (invariant) point of the system defined in Equation (5) straightforwardly, i.e., .
Assumption A2.
The zero equilibrium of the point absorber system is locally exponentially stable.
Note that Assumption A2 is without any loss of generality since, for any set of physically meaningful parameters, system (5) is such that , and hence the zero-equilibrium of is locally exponentially stable (see [13,19]). We are now ready to introduce our first proposition, based upon fundamental results presented in [11].
Proposition 1.
Proof.
See Appendix A for a proof of this statement. □
Definition 1
Remark 5.
The notion of moment in Definition 1, together with the result offered in Proposition 1, imply that the moment of the point absorber WEC system defined in Equation (5) at the signal generator , computed along a particular trajectory , coincides with the (well-defined) steady-state response of the output of the interconnected system (5)–(10), i.e., .
3.2. Model Reduction by Moment-Matching
As briefly discussed throughout Section 1, the theoretical grounds underlying model reduction by moment-matching are rooted in the strong existing connection between moments, as mathematical objects (see Definition 1), and the steady-state output response of the composite system (5)–(10) (see, e.g., [11]). Aiming to keep this paper reasonably self-contained, we recall the definition of a moment-based reduced order model for the nonlinear point absorber WEC system (5), driven by the class of inputs generated by (10).
Definition 2
Though Definition 2 formally introduces the concept of a model reduced by moment-matching, its actual computation is still implicit. Following the result presented in [12], a particularly simple family of reduced models, achieving moment-matching at , of order (dimension) , for the point absorber device defined in equation (5), can be explicitly written in terms of the mapping , with the solution of (12), as
with a free (design) parameter.
Remark 6.
Equation (14) defines a family of reduced order models achieving moment-matching described by an input-to-state linear differential equation with a nonlinear output map. Note that this is highly appealing from a computational perspective: the main ‘cost’ behind solving (14) for a given input signal is merely the cost of solving a linear operator. This is further demonstrated in Section 4 by means of numerical analysis.
Remark 7.
Note that, if , the family of models (14) has the exact same steady-state output response of the nonlinear target point absorber WEC system Σ at the signal generator . Furthermore, given the observability condition on the pair , the complex-valued set can be freely assigned. This, naturally, allows for preservation of particular properties of the target system to be reduced in the computed simplified structure.
Remark 8.
The success of the family of systems (14) in practical scenarios depends entirely upon the availability of the mapping , i.e., the corresponding moment, which solves the partial differential equation (12). Given that, in practice, this is far from trivial (even when in possession of exact knowledge of the system dynamics defined by f and h in (5)), a data-driven formulation is adopted in Section 3.3, to approximate the corresponding moment based upon input-output data.
We now introduce the following result, which is analogous to (Lemma 4, [15]). In particular, we show that the moment for the point absorber device, computed along a specific trajectory of (10), is -periodic, with . This result is instrumental to the data-driven approach presented in Section 3.3.
Proposition 2.
Let and suppose Assumptions A1 and A2 hold. Then, the mapping is -periodic.
Proof.
See Appendix B for a proof of this statement. □
3.3. Approximation of
Motivated by the discussion provided in Remark 8, we follow a data-driven approach to compute an approximation of the corresponding moment. Such a framework was originally introduced in [14], and extended to a specific class of WEC systems in [15]. To achieve a consistent approximation for , we begin by introducing the following assumption.
Assumption A3.
The mapping belongs to the space generated by a family of continuous real-valued functions , with , i.e., there exists a set of constants such that , for every .
Assumption A3 facilitates an almost natural definition for an approximation of , as detailed in the following.
Definition 3.
We call the mapping , with N finite, the approximated moment of the point absorber system (5) at the signal generator .
Remark 9.
When choosing the set of functions , the user can proceed in a ‘trial and error’ procedure, depending on the specific nature of the WEC dynamics. In this paper, we show that a polynomial expansion can be effectively used to approximate the associated moment for the point absorber studied (see Section 4).
Based upon Definition 3, the data-driven approach adopted in our study aims to compute the set of coefficients for the point absorber WEC case, by using information on the steady-state output response of (5). Let us define:
where , and hence the approximated moment can be expressed as
Let be a set of trajectories for the signal generator in (10), computed via a set of corresponding initial conditions , such that each element in the set is excitable, i.e., Assumption A1 holds. Let denote the set of steady-state outputs (computed after a sufficiently large time ) of the point absorber system (5), driven by each generated input .
Based upon the sets defined immediately above, and since the (well-defined) steady-state output response of in (5) coincides with the associated moment evaluated at the corresponding trajectory of the signal generator (10) (see Proposition 1), the approximation can be computed as follows. Let , where each represents a time instant, with . Define and such that
and hence
Before proceeding with the actual computation of , we introduce one last standing assumption.
Assumption A4.
The set of time-instants is chosen such that in (18) is full row rank.
Remark 10.
Finally, note that the coefficient matrix , characterising the approximated moment (see Equation (16)), can be uniquely computed in terms of the least-squares solution of , i.e.,
where the condition is always guaranteed by Assumption A4.
Remark 11.
The least-squares solution proposed in (19) is effectively exploiting the result of Proposition 2. In particular, given that is -periodic, it is sufficient to use the information of the steady-state output response of the point absorber system (5) over a single period, i.e., , to fully characterise .
Remark 12.
Note that, while we explicitly use the (analytical) definition of system (5) throughout our paper, the set of steady-state output data can be generated either with a different numerical model (e.g., solvers based upon computational fluid dynamics), or collected from tailored experiments involving a real WEC prototype.
3.4. Systematic Overview
We provide, in this subsection, a systematic overview of the proposed model reduction procedure, defining a number of fundamental steps () towards the computation of a reduced model by moment-matching for WEC systems, based upon the results presented throughout Section 3. In addition, we provide a companion schematic illustration of the procedure described in this section, in Figure 2.
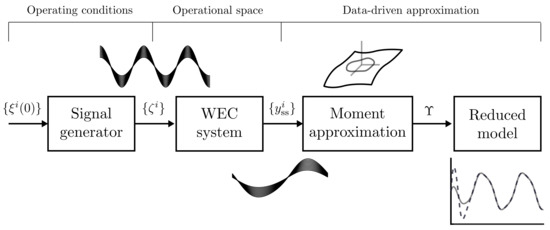
Figure 2.
Schematic representation of the model reduction by moment-matching procedure described throughout Section 3.
- (S1)
- Choose the fundamental frequency associated with the selected wave conditions.
- (S2)
- Compute S as in Equation (10) and set .
- (S3)
- Compute the set of trial trajectories via the set of initial conditions of interest.
- (S4)
- Compute the set of associated input signals .
- (S5)
- For each defined input , with , compute the steady-state output response of the WEC system (collected after a sufficiently large time ).
- (S6)
- Choose the set of time instants , with , such that and Assumption A4 holds.
- (S7)
- Compute the matrices and as in Equation (18).
- (S8)
- Compute as the unique least-square solution expressed in (19).
- (S9)
- Construct the family of reduced order models achieving moment-matching for the WEC system asfor any matrix such that .
4. Numerical Study
For the numerical study presented in this section, we consider the point absorber device described by the dynamical model presented in Section 2, and schematically illustrated in Figure 1. The numerical values for the set of parameters, corresponding with the target system in (5), are as adopted in [19]. The characterisation of the radiation subsystem in (2) is performed here via boundary element methods, using the open-source software NEMOH [27], in combination with a moment-based finite-order parametrisation procedure [28,29], rendering a model with order .
To illustrate the nature of the nonlinear behaviour of the device under scrutiny, i.e., the characteristics of the map g in Equation (8), Figure 3 shows the ‘magnitude’ of the associated nonlinear effects (measured in terms of the 2-norm ), as a function of the first two state variables (displacement, in metres), and (velocity, in metres per second). It can be readily appreciated that, as soon as the device moves away from the physical equilibrium position , grows rapidly, stressing the relevance of the associated nonlinear effects as soon as the WEC system departs from ‘small motion’ conditions.
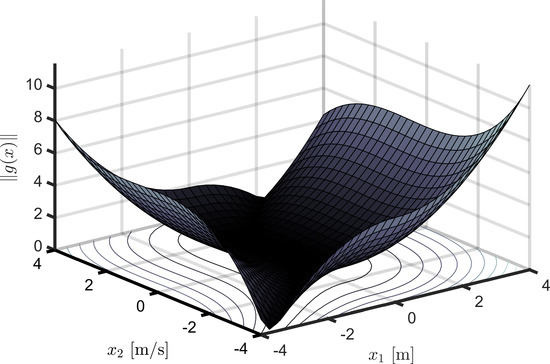
Figure 3.
Indicative measure of the nonlinear behaviour associated with the point absorber system under study.
Recall that, to construct the corresponding reduced order model, a data-driven approximation method is considered in Section 3.3. In particular, such a method explicitly uses input–output data to reconstruct an approximation of moment associated with the point absorber system (5). In line with Section 3.3, Figure 4 presents the set of inputs , , constructed via different initial conditions for the signal generator (10), used to excite system , with a fundamental frequency [rad/s]. Note that such a set of signals corresponds to a controlled WEC operating in regular sea states with period [s], and wave heights in the set [m]. With the set of inputs illustrated in Figure 4, we compute the corresponding set of steady-state outputs for the target system (5). These are presented, using a solid-black line, in Figure 5.
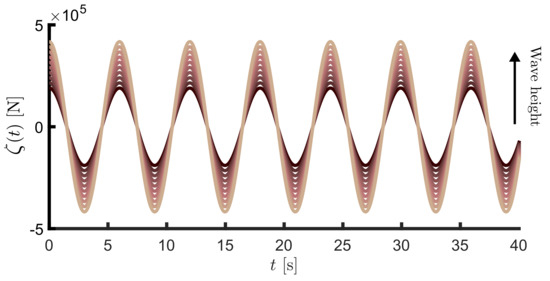
Figure 4.
Set of inputs used to approximate the associated moment.
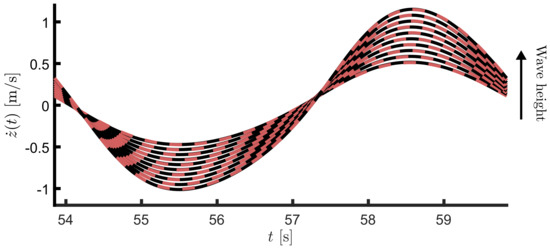
Figure 5.
Target steady-state responses (solid-black), along with the data-driven approximating moment evaluated at each specific trajectory of (dashed-red).
For the selection of the function space generated by the set , used to approximate the corresponding moment (see Definition 3), we select a smooth (polynomial) mapping, defining a manifold, i.e.,
where . Having defined the corresponding input–output set, and the approximation structure of (20), we can directly apply the methodology presented in Section 3.3, and compute the corresponding approximated moment via the well-defined least-squares solution in (19). The optimal coefficients corresponding to the expansion in (20) are presented here in Figure 6, while the outputs resulting from evaluating the approximated moment at each corresponding trajectory of the signal generator (10) are presented in Figure 5, using a dashed-red line, showing a virtually perfect match with each target. Note that, as per the procedure proposed throughout Section 3, a single period [s] is shown in Figure 5, which is sufficient to fully characterise the -periodic steady-state output response of the WEC system.
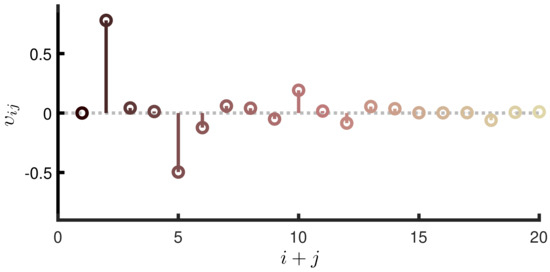
Figure 6.
Computed coefficients for the polynomial expansion (20).
Remark 13.
The approximation results presented in Figure 5 are extended in Figure 7, where the approximated manifold (20) can be effectively appreciated, together with the target moment evaluated at each trajectory corresponding with the set of inputs of Figure 4. Note that we also include the corresponding planar projections for each triple .
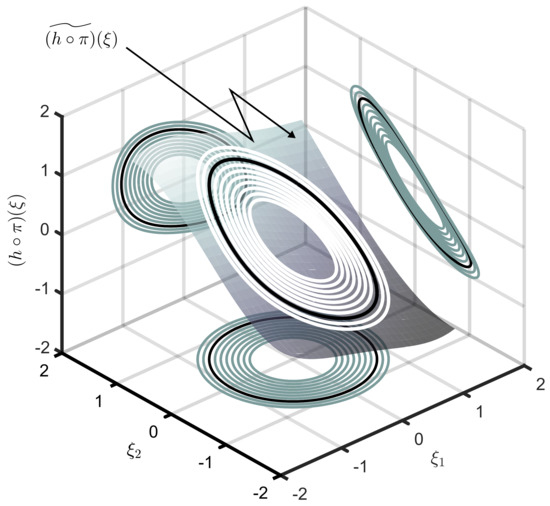
Figure 7.
Approximated moment .
Up until this point, we have presented results concerning the approximation of the moment of the point absorber system. We now use such results to build a reduced model, which is effectively the ultimate objective of this study. Based upon the structure presented in (14), we can construct a 2nd order reduced model for the point absorber system (5) simply as
with a gain matrix chosen such that the set , which coincides with the set of two dominant modes of the Jacobian linearisation of the WEC system about the equilibrium position. Aiming to illustrate the nature of the resulting linear input-to-state dynamics in (21), Figure 8 presents a Bode plot of both the Jacobian linearisation of the point absober model (5) (dotted-blue), and the corresponding linearisation of the reduced model (21) (dashed-red). Note that the latter can be readily defined in terms of (20) as
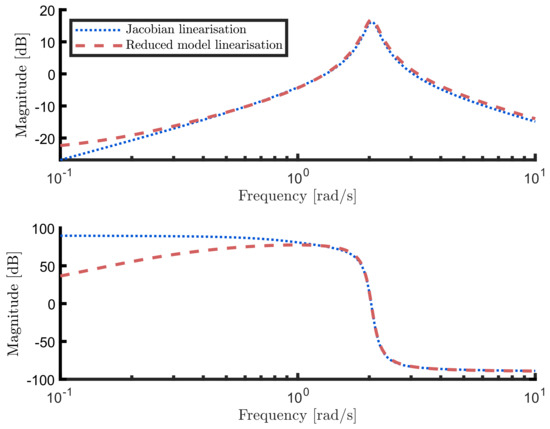
It is clear from Figure 8 that, besides being capable of representing the nonlinear behaviour of the associated WEC system (see also the discussion provided in the following paragraph), the computed reduced model by moment-matching is also able to preserve the dynamics of the WEC system in linear operating conditions. Furthermore, as can be appreciated from Figure 9, the Nyquist plot of system (22) is fully defined on the right-hand-side of the complex plane, i.e., the nonlinear reduced model (21) is locally passive (see, e.g., [30]). Fulfilment of this property not only highlights the consistency of the reduced model with respect to the underlying physical reality of the WEC energy absorption process, but is also fundamental to guarantee existence and uniqueness (i.e., well-possedness) of the solution of a vast family of WEC optimal control algorithms [31].
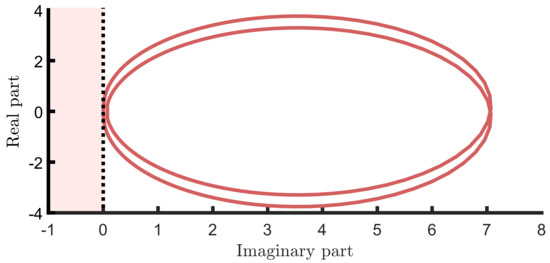
Figure 9.
Nyquist plot of system (22).
Aiming at illustrating the accuracy of the computed reduced model (21) under nonlinear operating conditions, Figure 10 (top) shows output time-traces for both the target nonlinear (solid-black) point absorber system (5), and the moment-based reduced order model (dashed-red) model (21), for an input corresponding to a wave height of [m]. Furthermore, Figure 10 (bottom) offers the evolution of the absolute value of the approximation error, i.e., . It is hence straightforward to appreciate that, once the transient period extinguishes, target and approximating time traces become almost indistinguishable, as expected from the moment-matching-based model reduction procedure proposed in Section 3. Finally, Figure 11 offers a comparison between the normalised run-time 6 required by both target (solved via a Runge–Kutta (4,5) pair), and reduced model by moment-matching. It is clear that the reduced model computes in an order of magnitude faster than the target nonlinear WEC system, both due to its smaller order (dimension), and its linear input-to-state nature.
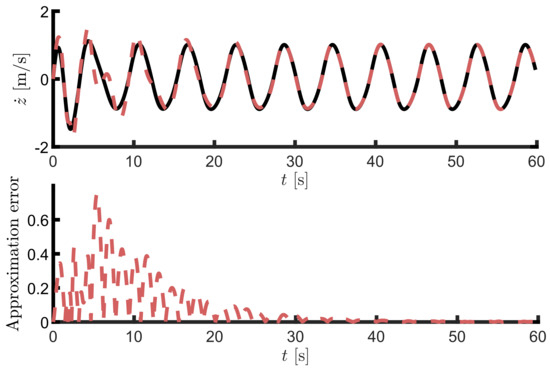
Figure 10.
(Top): Output traces for target point absorber system (solid-black), and the computed approximating model by moment-matching (dashed-red). (Bottom): Error between target and approximating response as a function of time.
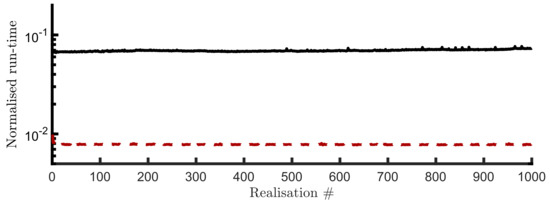
Figure 11.
Normalised run-time required to solve the target nonlinear WEC model (solid black), and the reduced model by moment-matching (dashed red).
5. Conclusions
This paper presents a data-driven approach to construct reduced models for a state-of-the-art wave energy conversion system. The methodology chosen and developed generates models which are input-to-state linear, with any nonlinear behaviour confined to the output map. Such a map is the result of a data-driven approximation procedure, where the so-called moment of the point absorber system is estimated via a least-squares procedure. The user has full control over the complexity of such an approximation, being able to freely select the characteristics of the associated approximation space. The performance of the strategy is illustrated via a numerical case study, showing that the approach is capable of providing parsimonious models with preservation of steady-state response characteristics.
Author Contributions
Conceptualization, G.P., F.J.D.P., N.F. and J.V.R.; methodology, G.P., F.J.D.P. and N.F.; software, G.P., F.J.D.P. and N.F.; formal analysis, G.P., F.J.D.P. and N.F.; resources, J.V.R. and G.M.; writing—original draft preparation, G.P. and N.F.; writing—review and editing, F.J.D.P., J.V.R. and G.M.; visualization, G.P., F.J.D.P. and N.F.; supervision, J.V.R. and G.M.; funding acquisition, G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 101024372. The results of this publication reflect only the author’s view and the European Commission is not responsible for any use that may be made of the information it contains.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A. Proof of Proposition 1
We begin by noting that, under Assumption A1, the triple of matrices is effectively minimal. Furthermore, note that the signal generator (10) is such that with corresponding eigenspaces such that for , i.e., the generator is Poisson stable. Under these conditions, the result of this proposition holds directly via [11], as long as the zero equilibrium of the point absorber system is locally exponentially stable. Since this is the case by Assumption A2, the proof follows.
Appendix B. Proof of Proposition 2
The definition of the autonomous system (10) directly implies that the function is -periodic, with a period (see Remark 4). Furthermore, by Assumption A2, the zero equilibrium of (5) is locally exponentially stable, and its (well-defined) steady-state solution is also -periodic (the reader is referred to [32] for further detail). Taking into account the minimality condition on the triple , i.e., Assumption A1, the following equality holds (see Proposition 1), and it is hence we can conclude that is -periodic.
[custom]
Notes
| 1 | Note that this is performed without any loss of generality, and aiming to simplify the notation used throughout our study. Similar considerations can be made for a multi-DoF WEC system (see, e.g., [17,18].) |
| 2 | From now on, the dependence on t is dropped when clear from the context. |
| 3 | Note that this is performed without any loss of generality, and merely due to the importance of the velocity variable within the WEC optimal control formulation. |
| 4 | See [20,21] for a formal discussion on the dynamical properties associated with . |
| 5 | The interested reader is referred to [26] for a formal treatment of the concept of excitability for a general class of systems. |
| 6 | The normalised run-time is defined as the time required to compute the output corresponding to each analysed model, and the simulation length. |
References
- Ringwood, J.V. Wave energy control: Status and perspectives 2020. IFAC-PapersOnLine 2020, 53, 12271–12282. [Google Scholar] [CrossRef]
- Ringwood, J.V.; Bacelli, G.; Fusco, F. Energy-maximizing control of wave-energy converters: The development of control system technology to optimize their operation. IEEE Control Syst. 2014, 34, 30–55. [Google Scholar]
- García-Violini, D.; Faedo, N.; Jaramillo-Lopez, F.; Ringwood, J.V. Simple Controllers for Wave Energy Devices Compared. J. Mar. Sci. Eng. 2020, 8, 793. [Google Scholar] [CrossRef]
- Faedo, N. Optimal Control and Model Reduction for Wave Energy Systems: A Moment-Based Approach. Ph.D. Thesis, National University of Ireland, Maynooth, Ireland, 2020. [Google Scholar]
- Giorgi, G.; Gomes, R.P.F.; Bracco, G.; Mattiazzo, G. Numerical investigation of parametric resonance due to hydrodynamic coupling in a realistic wave energy converter. Nonlinear Dyn. 2020, 101, 153–170. [Google Scholar] [CrossRef] [PubMed]
- Giorgi, G. Nonlinear Hydrodynamic Modelling of Wave Energy Converters under Controlled Conditions. Ph.D. Thesis, Department of Electronic Engineering, Maynooth University, Maynooth, Ireland, 2018. [Google Scholar]
- Suchithra, R.; Ezhilsabareesh, K.; Samad, A. Development of a reduced order wave to wire model of an OWC wave energy converter for control system analysis. Ocean Eng. 2019, 172, 614–628. [Google Scholar] [CrossRef]
- Penalba Retes, M.; Ringwood, J.V. Systematic complexity reduction of wave-to-wire models for wave energy system design. Ocean Eng. 2020, 217, 107651. [Google Scholar] [CrossRef]
- Penalba, M.; Ringwood, J.V. Linearisation-based nonlinearity measures for wave-to-wire models in wave energy. Ocean Eng. 2019, 171, 496–504. [Google Scholar] [CrossRef]
- Faedo, N.; Piuma, F.J.D.; Giorgi, G.; Ringwood, J.V. Nonlinear model reduction for wave energy systems: A moment-matching-based approach. Nonlinear Dyn. 2020, 102, 1215–1237. [Google Scholar] [CrossRef]
- Astolfi, A. Model reduction by moment matching for linear and nonlinear systems. IEEE Trans. Autom. Control 2010, 55, 2321–2336. [Google Scholar] [CrossRef]
- Scarciotti, G.; Astolfi, A. Nonlinear Model Reduction by Moment Matching. Found. Trends Syst. Control 2017, 4, 224–409. [Google Scholar] [CrossRef]
- Hals, J.; Ásgeirsson, G.S.; Hjálmarsson, E.; Maillet, J.; Möller, P.; Pires, P.; Guérinel, M.; Lopes, M. Tank testing of an inherently phase-controlled wave energy converter. Int. J. Mar. Energy 2016, 15, 68–84. [Google Scholar]
- Scarciotti, G.; Astolfi, A. Data-driven model reduction by moment matching for linear and nonlinear systems. Automatica 2017, 79, 340–351. [Google Scholar] [CrossRef]
- Faedo, N.; Piuma, F.J.D.; Giorgi, G.; Bracco, G.; Ringwood, J.V.; Mattiazzo, G. Data-driven nonlinear model reduction by moment-matching for the ISWEC system. In Proceedings of the 2021 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Mauritius, Mauritius, 7–8 October 2021; pp. 1–6. [Google Scholar]
- Korde, U.A.; Ringwood, J.V. Hydrodynamic Control of Wave Energy Devices; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Folley, M.; Forehand, D. Chapter 8—Conventional Multiple Degree-of-Freedom Array Models. In Numerical Modelling of Wave Energy Converters; Folley, M., Ed.; Academic Press: New York, NY, USA, 2016; pp. 151–164. [Google Scholar]
- Faedo, N.; Scarciotti, G.; Astolfi, A.; Ringwood, J.V. Energy-maximising moment-based constrained optimal control of ocean wave energy farms. IET Renew. Power Gener. 2021, 15, 3395–3408. [Google Scholar] [CrossRef]
- Faedo, N.; Scarciotti, G.; Astolfi, A.; Ringwood, J.V. Nonlinear energy-maximizing optimal control of wave energy systems: A moment-based approach. IEEE Trans. Control Syst. Technol. 2021, 29, 2533–2547. [Google Scholar] [CrossRef]
- Faedo, N.; Peña-Sanchez, Y.; Ringwood, J.V. Parametric representation of arrays of wave energy converters for motion simulation and unknown input estimation: A moment-based approach. Appl. Ocean Res. 2020, 98, 102055. [Google Scholar] [CrossRef]
- Pérez, T.; Fossen, T.I. Time-vs. frequency-domain identification of parametric radiation force models for marine structures at zero speed. Model. Identif. Control 2008, 29, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Morison, J.; Johnson, J.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Astolfi, A.; Scarciotti, G.; Simard, J.; Faedo, N.; Ringwood, J.V. Model Reduction by Moment Matching: Beyond Linearity A Review of the Last 10 Years. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Korea, 14–18 December 2020; pp. 1–16. [Google Scholar]
- Faedo, N.; Scarciotti, G.; Astolfi, A.; Ringwood, J.V. On the Approximation of Moments for Nonlinear Systems. IEEE Trans. Autom. Control 2021, 66, 5538–5545. [Google Scholar] [CrossRef]
- Faedo, N.; Carapellese, F.; Pasta, E.; Mattiazzo, G. On the principle of impedance-matching for underactuated wave energy harvesting systems. Appl. Ocean Res. 2021, 118, 102958. [Google Scholar] [CrossRef]
- Padoan, A.; Scarciotti, G.; Astolfi, A. A Geometric Characterization of the Persistence of Excitation Condition for the Solutions of Autonomous Systems. IEEE Trans. Autom. Control 2017, 62, 5666–5677. [Google Scholar] [CrossRef] [Green Version]
- Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open source BEM solver NEMOH. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Faedo, N.; Peña-Sanchez, Y.; Ringwood, J.V. Finite-order hydrodynamic model determination for wave energy applications using moment-matching. Ocean Eng. 2018, 163, 251–263. [Google Scholar] [CrossRef] [Green Version]
- Pena-Sanchez, Y.; Faedo, N.; Penalba, M.; Giuseppe, G.; Mérigaud, A.; Windt, C.; Violini, D.G.; LiGuo, W.; Ringwood, J. Finite-order hydrodynamic approximation by moment-matching (FOAMM) toolbox for wave energy applications. In Proceedings of the European Tidal and Wave Energy Conference Proceedings (EWTEC), Napoli, Italy, 1–6 September 2019; Volume 2019. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Faedo, N.; Olaya, S.; Ringwood, J.V. Optimal control, MPC and MPC-like algorithms for wave energy systems: An overview. IFAC J. Syst. Control 2017, 1, 37–56. [Google Scholar] [CrossRef] [Green Version]
- Isidori, A.; Astolfi, A. Disturbance attenuation and H∞-control via measurement feedback in nonlinear systems. IEEE Trans. Autom. Control 1992, 37, 1283–1293. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).