Grasping Force Optimization and DDPG Impedance Control for Apple Picking Robot End-Effector
Abstract
1. Introduction
- (1)
- According to the apple contact force model, the gradient flow algorithm is used to optimize the contact force under friction cone, force balance condition, and stability evaluation index constraints. The minimum stable apple grasping force is calculated to provide the desired grasping force for the control strategy.
- (2)
- A deep deterministic policy gradient (DDPG) optimized variable impedance control is designed. The position-based impedance control is improved by using reinforcement learning DDPG algorithm, and the reward function is designed to correct the apple grasping damping coefficient and enhance the control performance during continuous grasping.
- (3)
- An end-effector grasping experimental platform is setup to verify the effectiveness of the proposed method. The simulation and experimental results indicate that the improved impedance control has a smoother grasping force and better dynamic performance for varying sizes apples.
2. Materials and Methods
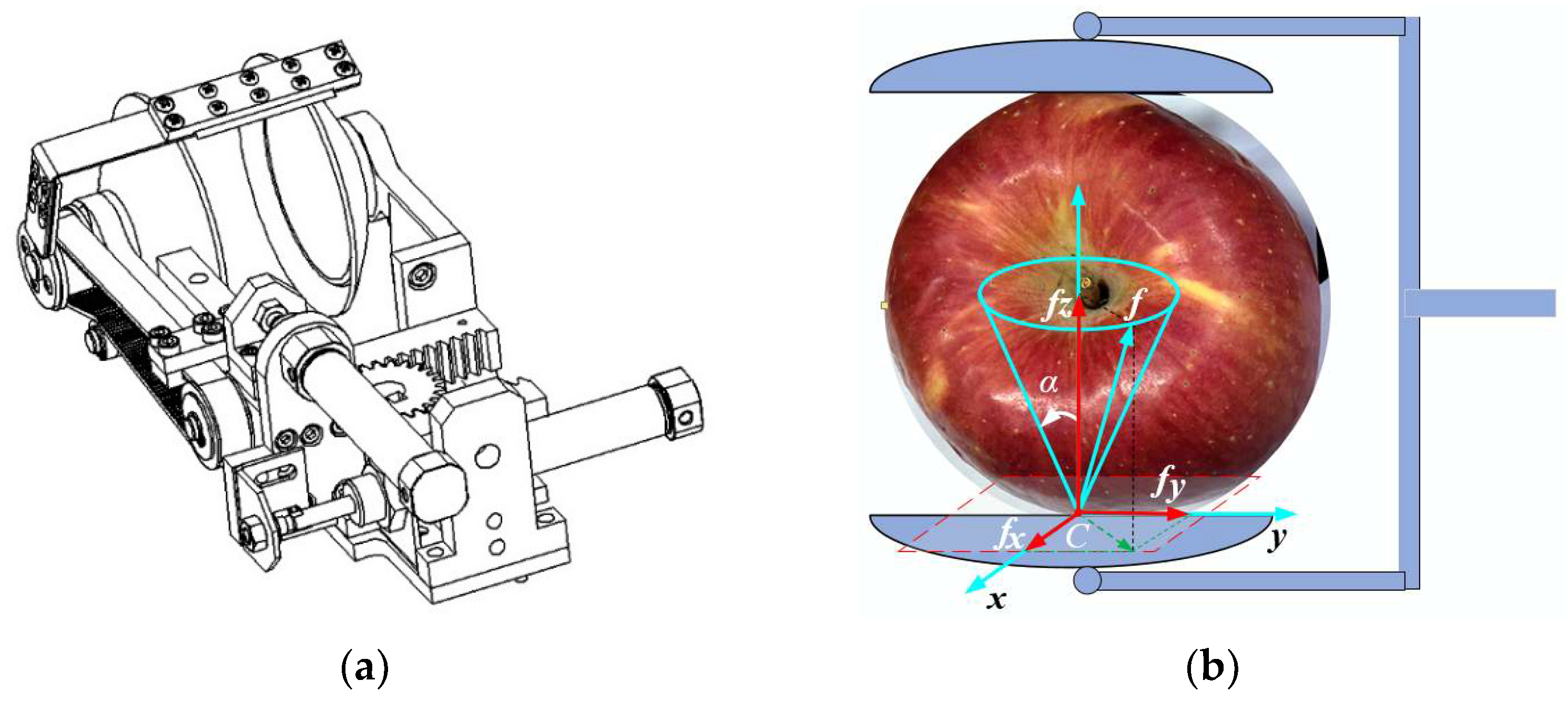
2.1. Apple Grasping Contact Force Optimization
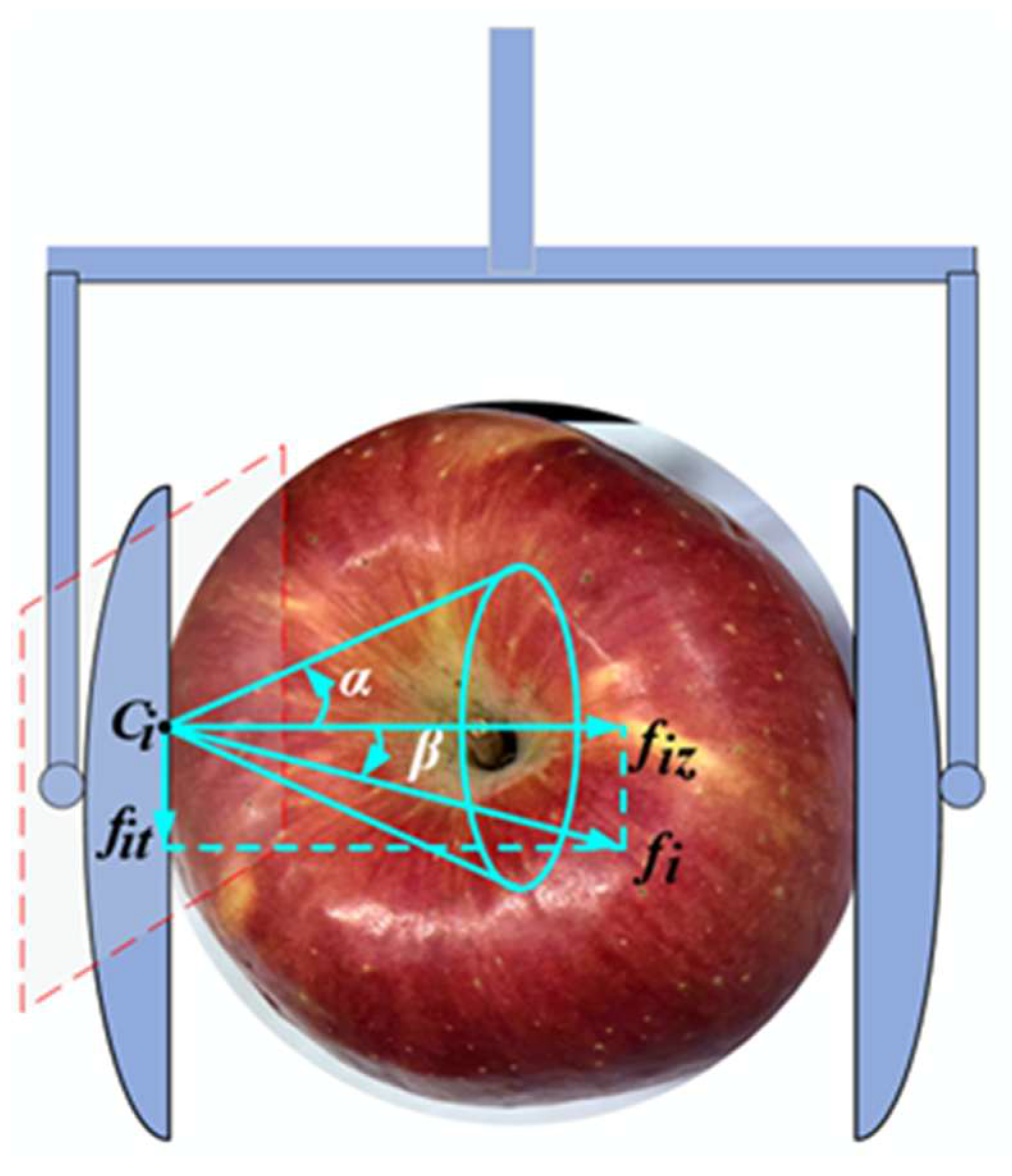
2.1.1. Constraint Conditions
2.1.2. Stability Evaluation Index Grasping Force Optimization Model
2.2. Solution of Contact Force Optimization Model
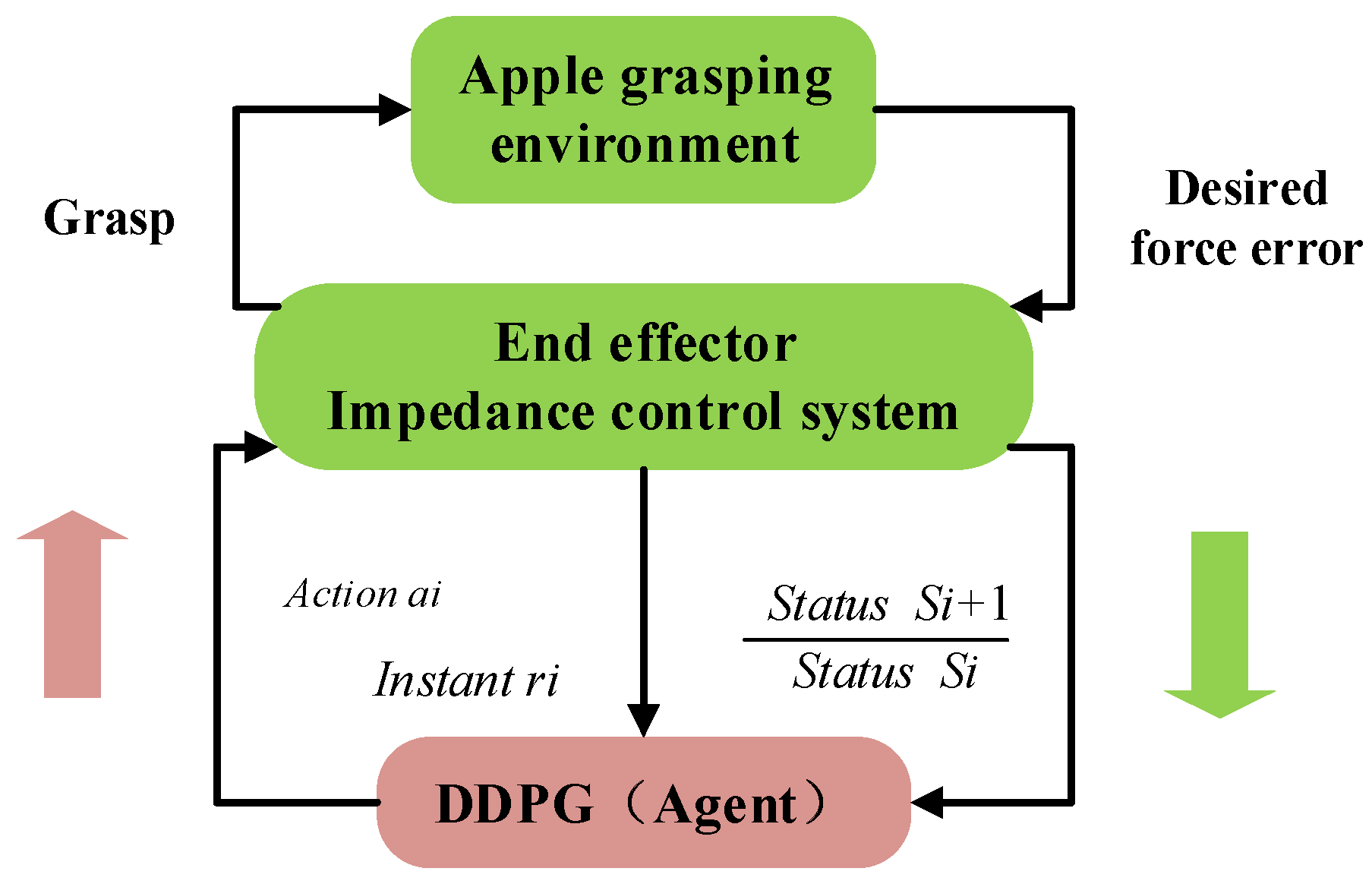
2.3. DDPG-Optimized Variable Impedance Control for Robot End-Effector
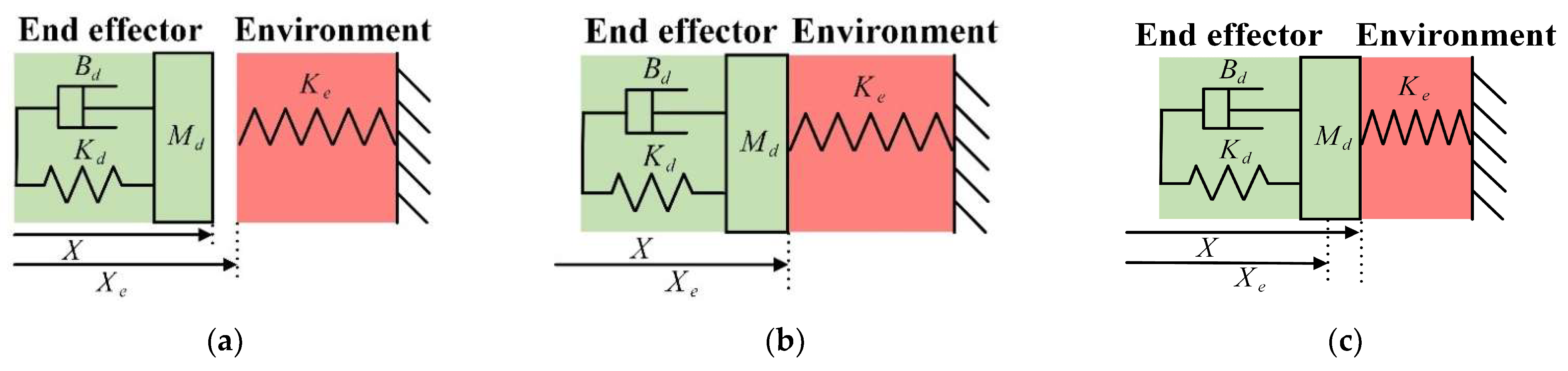
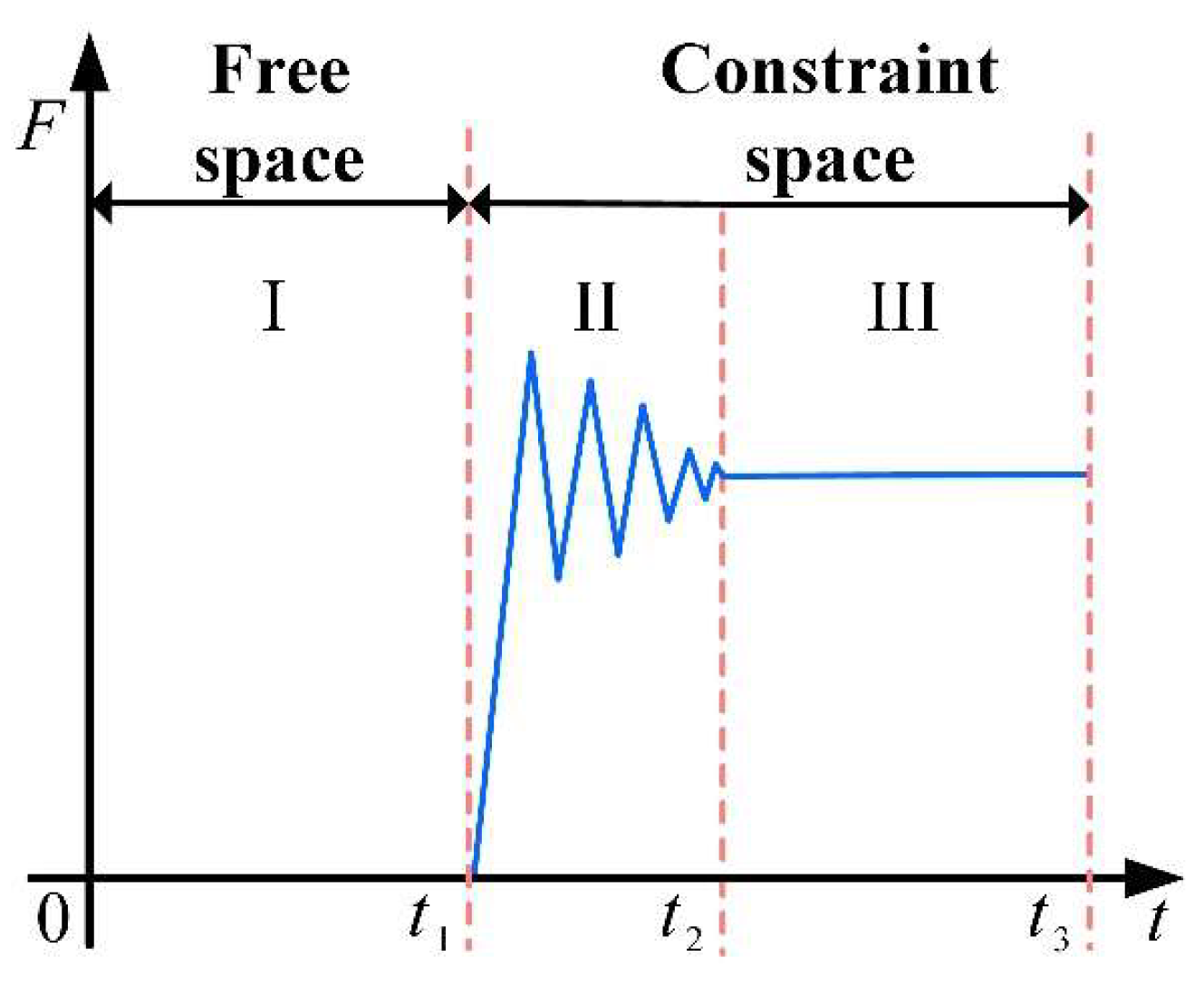
2.3.1. Grasping Contact Process Analysis
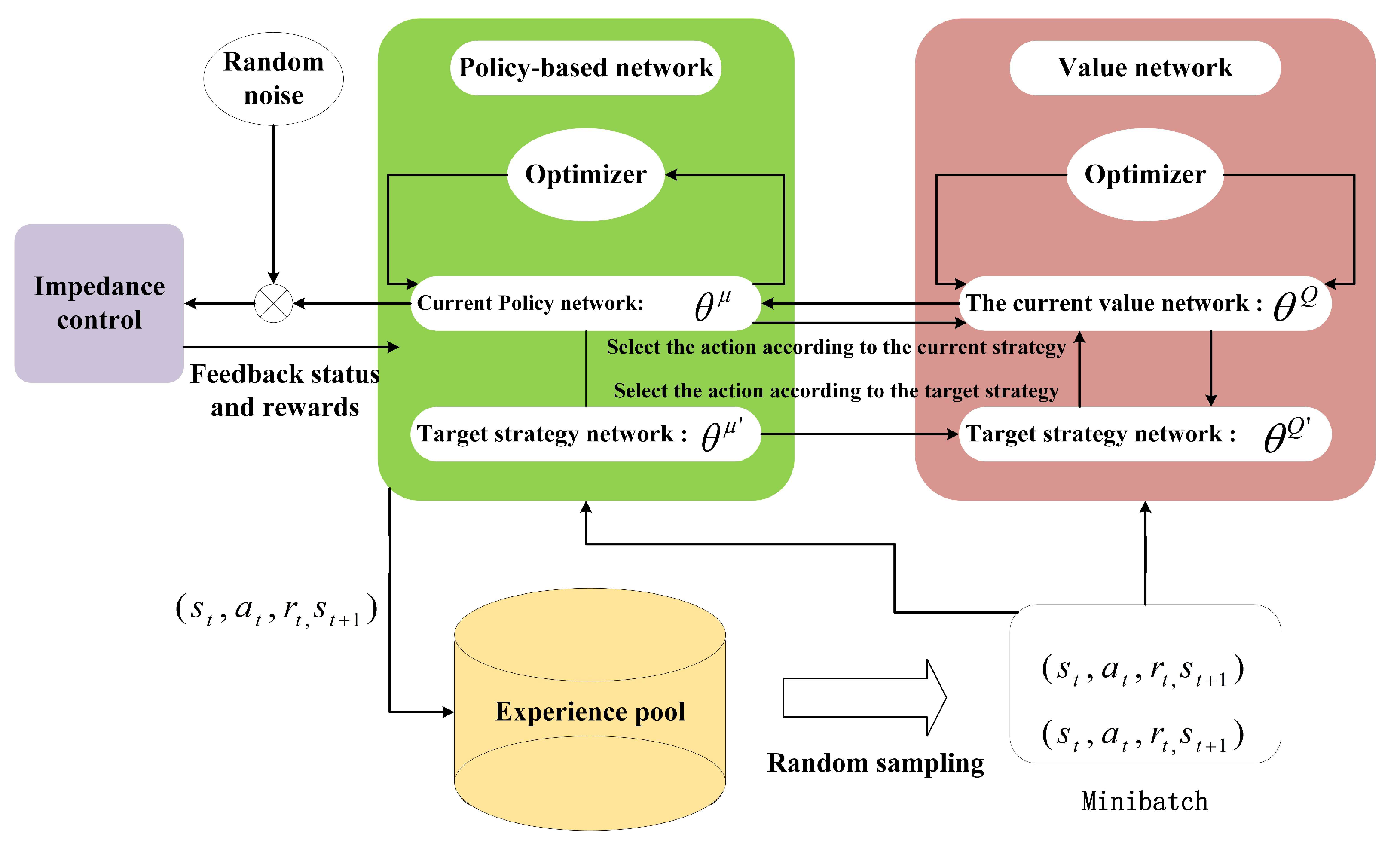
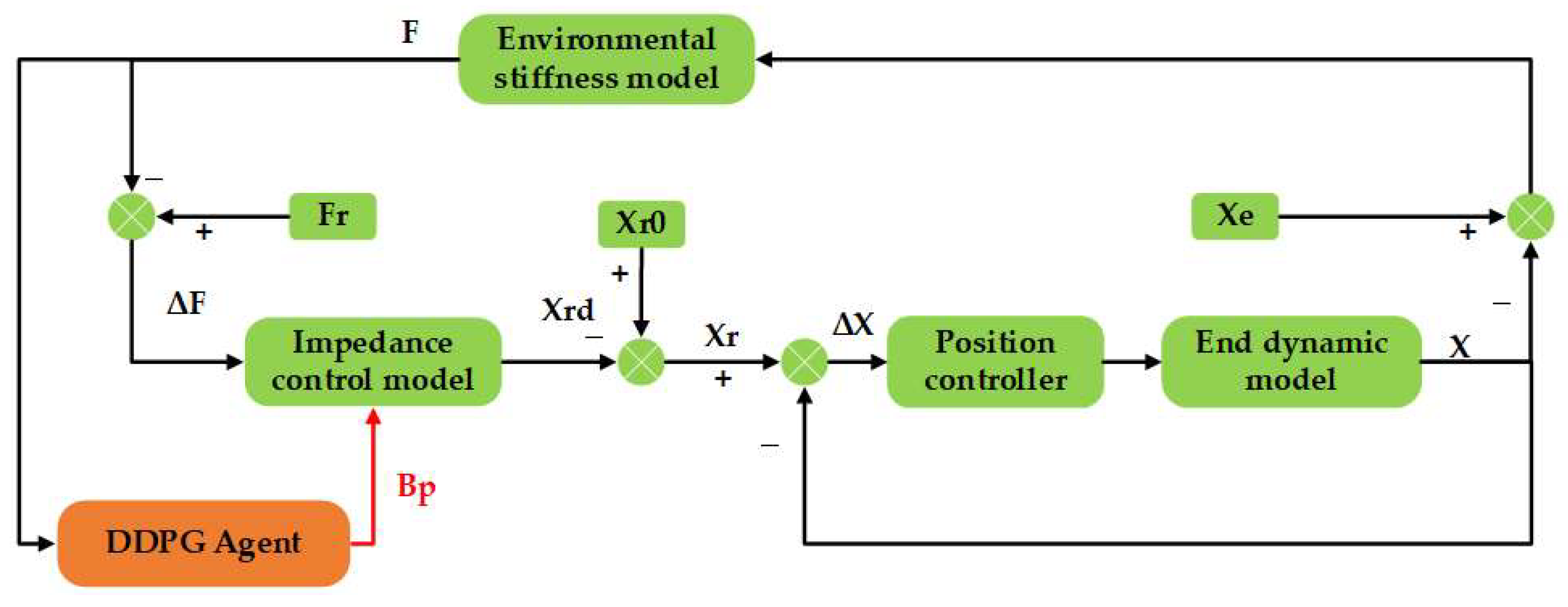
2.3.2. Impedance Control Based on DDPG Algorithm Optimization
DDPG-Optimized Impedance Control
2.3.3. Stability Analysis and Reward Function Design of Control System
3. Results and Discussion
3.1. Optimization Solution of Contact Force of Two-Finger End-Effector
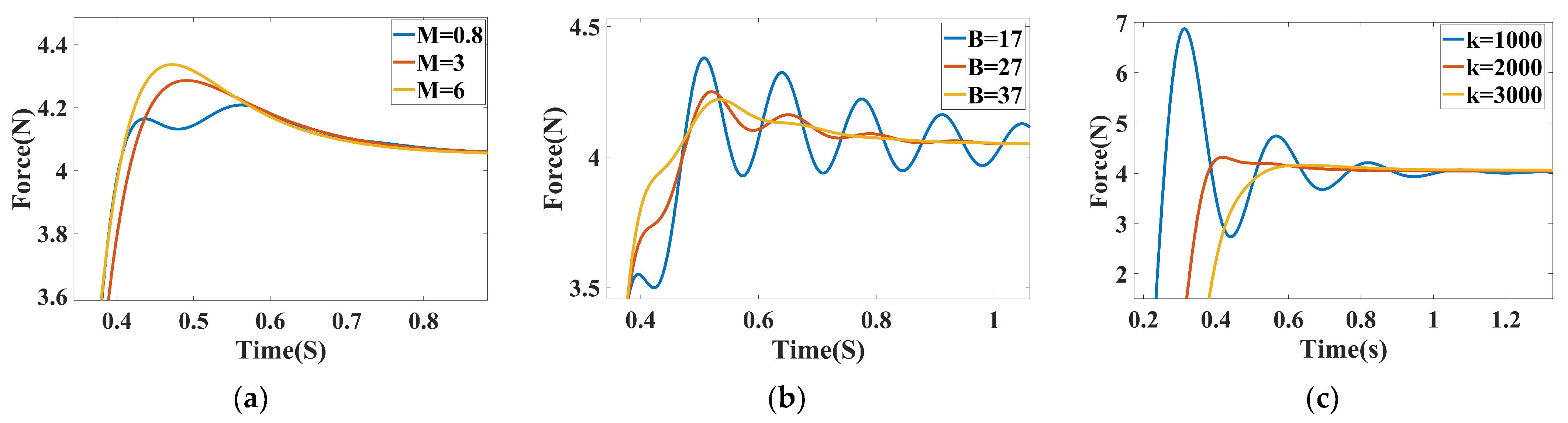
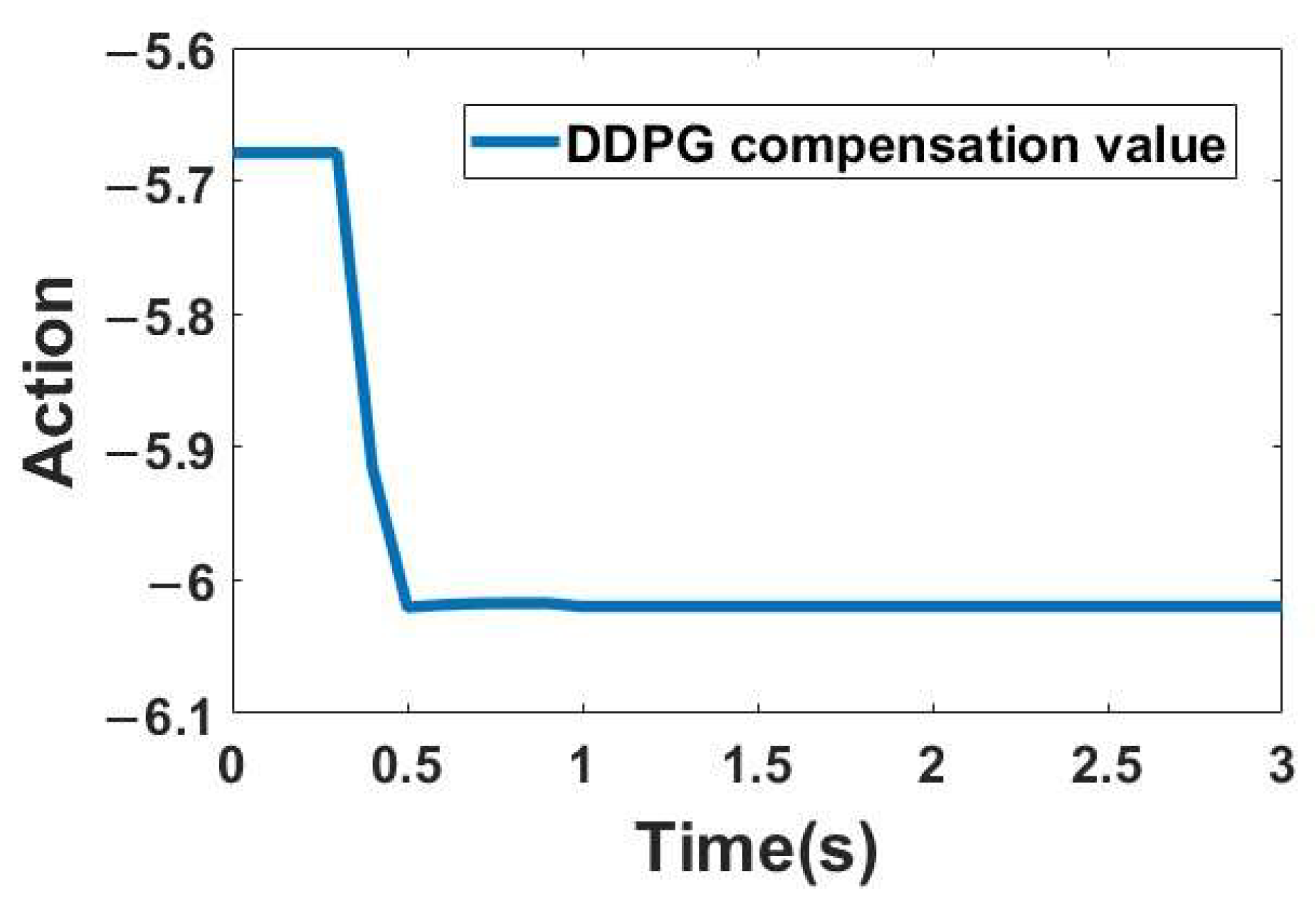
3.2. DDPG-Optimized Impedance Control Simulation
3.2.1. Simulation Under Fixed Environment and Position
3.2.2. Simulation Under Variable Environmental Stiffness Conditions
3.2.3. Simulation Under Variable Environmental Position Conditions
3.3. Actual Grasping Experiment
3.3.1. Experimental Equipment
3.3.2. Verification of Minimum Stable Grasping Force
3.3.3. End-Effector Grasping Force Control Experiment Result
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, H.; Wang, X.; Au, W.; Kang, H.; Chen, C. Intelligent robots for fruit harvesting: Recent developments and future challenges. Precis. Agric. 2022, 23, 1856–1907. [Google Scholar] [CrossRef]
- FAO. World Food and Agriculture: Statistical Yearbook 2024; Food and Agriculture Organization of the United Nations: Rome, Italy, 2024. [Google Scholar]
- Zhang, K.; Lammers, K.; Chu, P.; Li, Z.; Lu, R. System design and control of an apple harvesting robot. Mechatronics 2021, 79, 102644. [Google Scholar] [CrossRef]
- Ji, W.; Zhang, T.; Xu, B.; He, G. Apple recognition and picking sequence planning for harvesting robot in a complex environment. J. Agric. Eng. 2024, 55, 1549. [Google Scholar]
- Xu, B.; Cui, X.; Ji, W.; Yuan, H.; Wang, J. Apple grading method design and implementation for automatic grader based on Improved YOLOv5. Agriculture 2023, 13, 124. [Google Scholar] [CrossRef]
- Chen, K.; Li, T.; Yan, T.; Xie, F.; Feng, Q.; Zhu, Q.; Zhao, C. A soft gripper design for apple harvesting with force feedback and fruit slip detection. Agriculture 2022, 12, 1802. [Google Scholar] [CrossRef]
- Liu, J.; Liang, J.; Zhao, S.; Jiang, Y.; Wang, J.; Jin, Y. Design of a virtual multi-interaction operation system for hand-eye coordination of grape harvesting robots. Agronomy 2023, 13, 829. [Google Scholar] [CrossRef]
- Ji, W.; He, G.; Xu, B.; Zhang, H.; Yu, X. A new picking pattern of a flexible three-fingered end-effector for apple harvesting robot. Agriculture 2024, 14, 102. [Google Scholar] [CrossRef]
- Wang, X.; Kang, H.; Zhou, H.; Au, W.; Wang, M.; Chen, C. Development and evaluation of a robust soft robotic gripper for apple harvesting. Comput. Electron. Agric. 2023, 204, 107552. [Google Scholar] [CrossRef]
- Jia, P.; Wu, L.; Wang, G.; Geng, W.; Yun, F.; Zhang, N. Grasping torque optimization for a dexterous robotic hand using the linearization of constraints. Math. Probl. Eng. 2019, 2019, 5235109. [Google Scholar] [CrossRef]
- Zhang, Y.; Mu, X. An inexact multiblock alternating direction method for grasping-force optimization of multi-fingered robotic hands. J. Inequal. Appl. 2023, 2013, 30. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, W.; Xu, B.; Yu, X. Optimizing contact force on an apple picking robot end-effector. Agriculture 2024, 14, 996. [Google Scholar] [CrossRef]
- Mu, X.; Zhang, Y. Grasping force optimization for multi-fingered robotic hands using projection and contraction methods. J. Optim. Theory Appl. 2019, 183, 592–608. [Google Scholar] [CrossRef]
- Li, Y.; Cong, M.; Liu, D.; Du, Y.; Xu, X. Stable grasp planning based on minimum force for dexterous hands. Intell. Serv. Robot. 2020, 13, 251–262. [Google Scholar] [CrossRef]
- Wang, Q.; Bai, K.; Zhang, L.; Sun, Z.; Jia, T.; Hu, D.; Li, Q.; Zhang, J.; Knoll, A.; Jiang, H.; et al. Towards reliable and damage-less robotic fragile fruit grasping: An enveloping gripper with multimodal strategy inspired by Asian elephant trunk. Comput. Electron. Agric. 2025, 234, 110198. [Google Scholar] [CrossRef]
- Lama, S.; Deemyad, T. Using a rotary spring-driven gripper to manipulate objects of diverse sizes and shapes. Appl. Sci. 2023, 13, 8444. [Google Scholar] [CrossRef]
- Rabenorosoa, K.; Clévy, C.; Lutz, P. Hybrid force/position control applied to automated guiding tasks at the microscale. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010. [Google Scholar]
- Zhang, Z.; Chen, Y.; Wu, Y.; Lin, L.; He, B.; Miao, Z.; Wang, Y. Gliding grasping analysis and hybrid force/position control for unmanned aerial manipulator system. ISA Trans. 2022, 126, 377–387. [Google Scholar] [CrossRef]
- Kumar, N.; Rani, M. Neural network-based hybrid force/position control of constrained reconfigurable manipulators. Neurocomputing 2021, 420, 1–14. [Google Scholar] [CrossRef]
- Neville, H. Impedance control: An approach to manipulation: Part I—Theory. J. Dyn. Syst. Meas. Control 1985, 107, 1–7. [Google Scholar]
- Xie, F.; Chong, Z.; Liu, X.; Zhao, H.; Wang, J. Precise and smooth contact force control for a hybrid mobile robot used in polishing. Robot. Comput.-Integr. Manuf. 2023, 83, 102573. [Google Scholar] [CrossRef]
- Ji, W.; Tang, C.; Xu, B.; He, G. Contact force modeling and variable damping impedance control of apple harvesting robot. Comput. Electron. Agric. 2022, 198, 107026. [Google Scholar] [CrossRef]
- Li, X.; Qian, Y.; Li, R.; Niu, X.; Qiao, H. Robust form-closure grasp planning for 4-pin gripper using learning-based attractive region in environment. Neurocomputing 2020, 384, 268–281. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, L.; Shang, S.; Chung, S. Mechanical properties and microstructure of Fuji apple peel and pulp. Int. J. Food Prop. 2022, 25, 1773–1791. [Google Scholar]
- Bao, X.; Ren, M.; Ma, X.; Gao, S.; Bao, Y.; Li, S. Optimization of contact force for spherical fruit and vegetable picking dexterous hand based on minimum force. J. Agric. Mach. 2025, 56, 333–341. [Google Scholar]
- Liu, Z.; Jiang, L.; Yang, B. Task-oriented real-time optimization method of dynamic force distribution for multi-fingered grasping. Int. J. Humanoid Robot. 2022, 19, 2250013. [Google Scholar] [CrossRef]
- Lei, Q.; Wisse, M. Fast grasping of unknown objects using force balance optimization. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Deng, H.; Luo, H.; Wang, R.; Zhang, Y. Grasping force planning and control for tendon-driven anthropomorphic prosthetic hands. J. Bionic Eng. 2018, 15, 795–804. [Google Scholar] [CrossRef]
- Wen, G.; Yang, T.; Zhou, J.; Fu, J.; Xu, L. Reinforcement learning and adaptive/approximate dynamic programming: A survey from theory to applications in multi-agent systems. J. Control Decis. 2023, 38, 1200–1230. [Google Scholar]
- Chen, G.; Huang, Z.; Jiang, T.; Li, T.; You, H. Force distribution and compliance control strategy for stable grasping of multi-arm space robot. J. Control Decis. 2024, 39, 112–120. [Google Scholar]
- Kitchat, K.; Lin, M.; Chen, H.; Sun, M.; Sakai, K.; Ku, W.; Surasak, T. A deep reinforcement learning system for the allocation of epidemic prevention materials based on DDPG. Expert Syst. Appl. 2024, 242, 122763. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, Y.; Pu, Z.; Hu, J.; Wang, X.; Ke, R. Safe, efficient, and comfortable velocity control based on reinforcement learning for autonomous driving. Transp. Res. Part C Emerg. Technol. 2020, 117, 102662. [Google Scholar] [CrossRef]
- Sutton, R.; Barto, A. Reinforcement learning: An introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Wu, M.; Wang, X.; Jiang, Y.; Zhong, L.; Mo, F. Collaborative temperature control of deep deterministic policy gradient and fuzzy PID. Control Theory Appl. 2022, 39, 2358–2365. [Google Scholar]
- Song, P.; Yu, Y.; Zhang, X. A Tutorial survey and comparison of impedance control on robotic manipulation. Robotica 2019, 37, 801–836. [Google Scholar] [CrossRef]


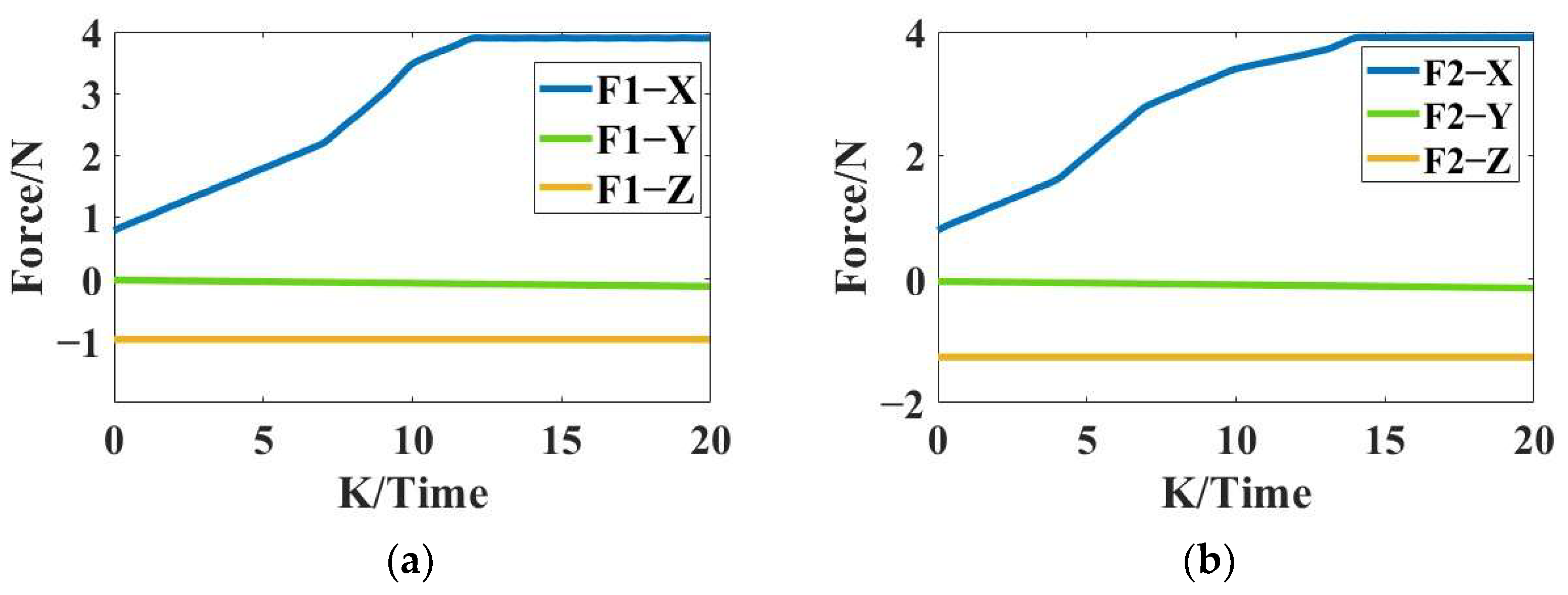


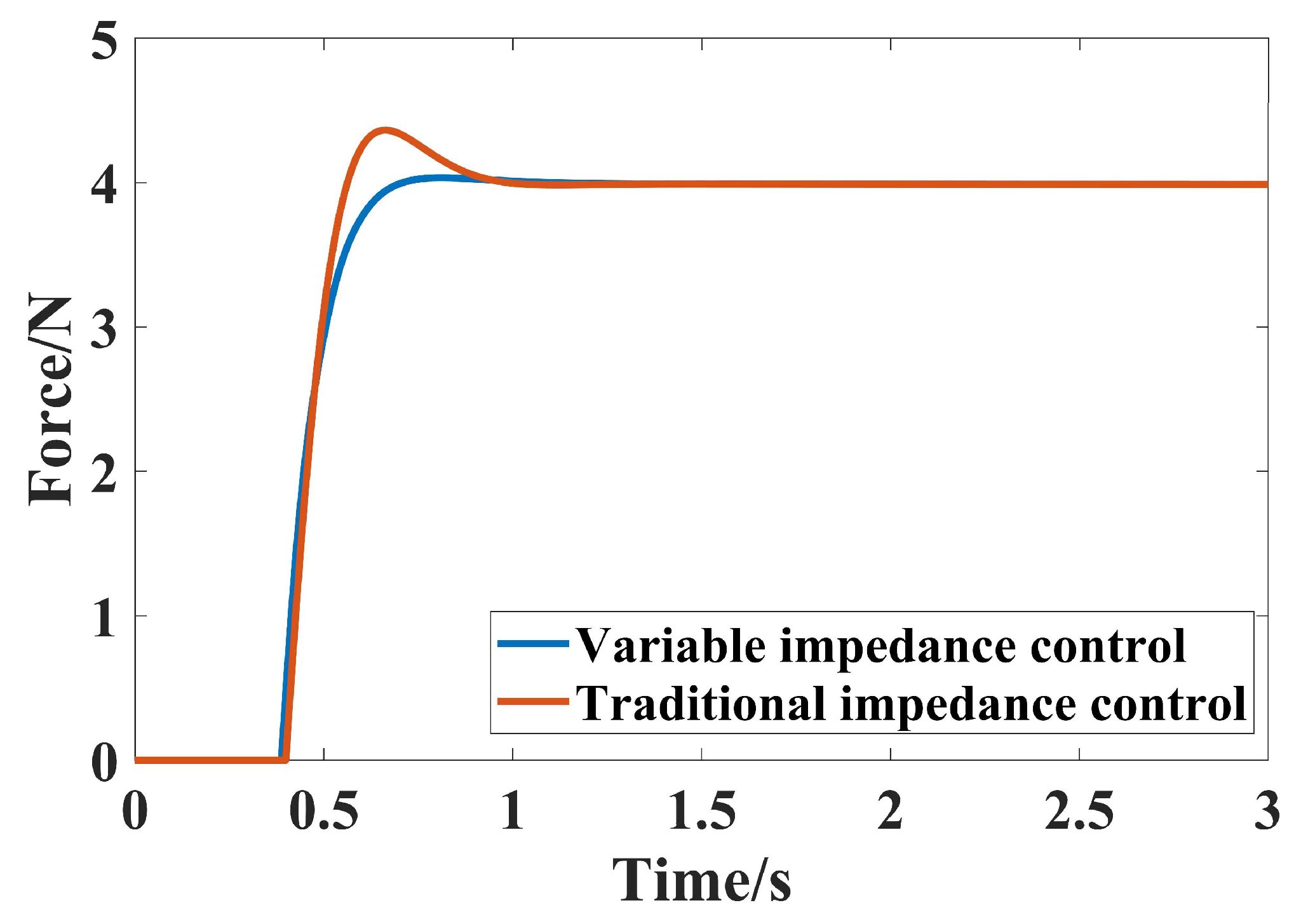


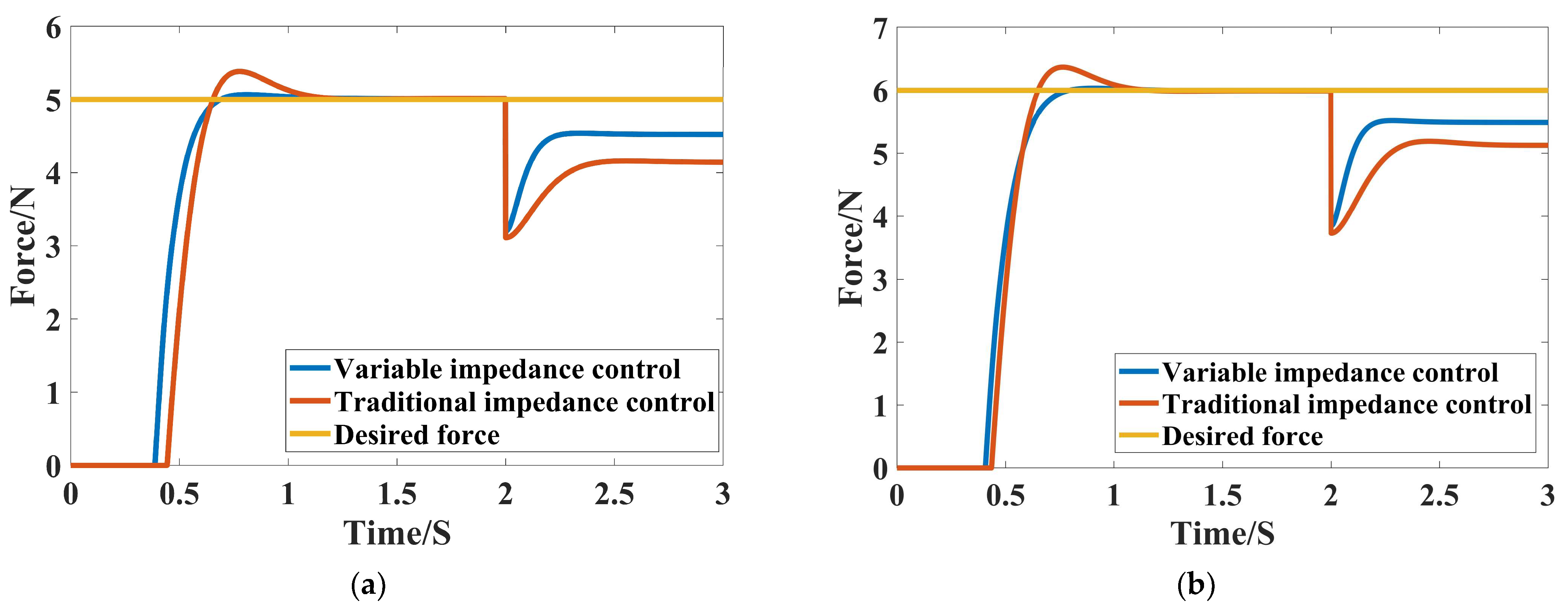

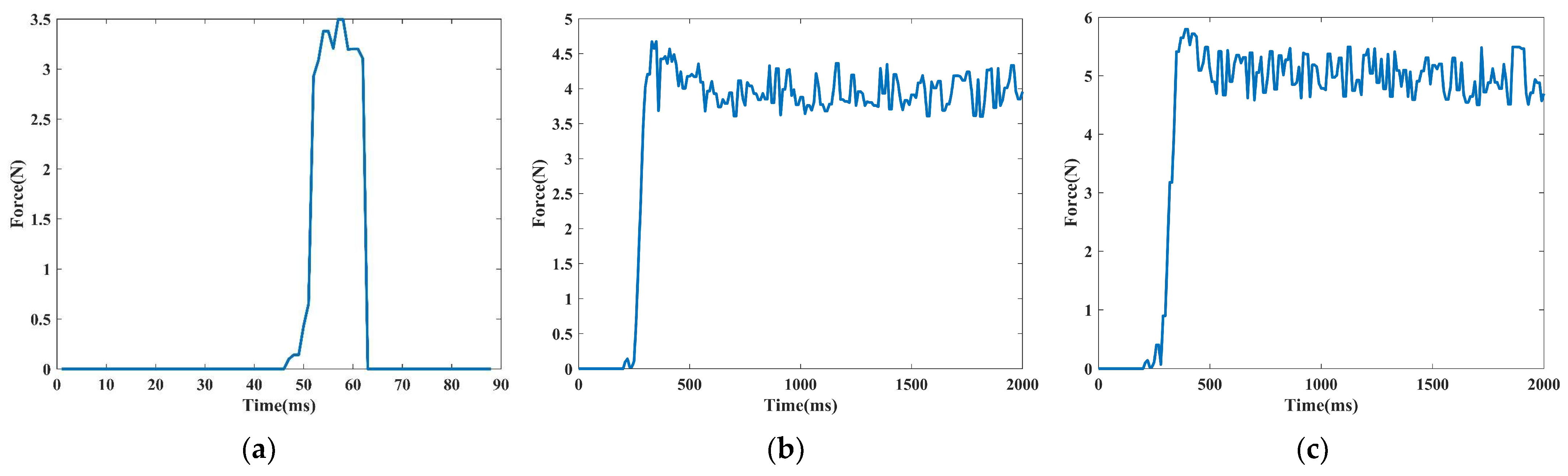

| Contact Point | x (mm) | y (mm) | z (mm) |
|---|---|---|---|
| C1 | 44.98 | −1.17 | 0 |
| C2 | −44.99 | 0.78 | 0 |
| Parameters | M | B0 | K | Fr | Ke | Xe | Xr0 |
|---|---|---|---|---|---|---|---|
| Value | 1 | 70 | 4000 | 4 | 7500 | 0.004 | 0.0045 |
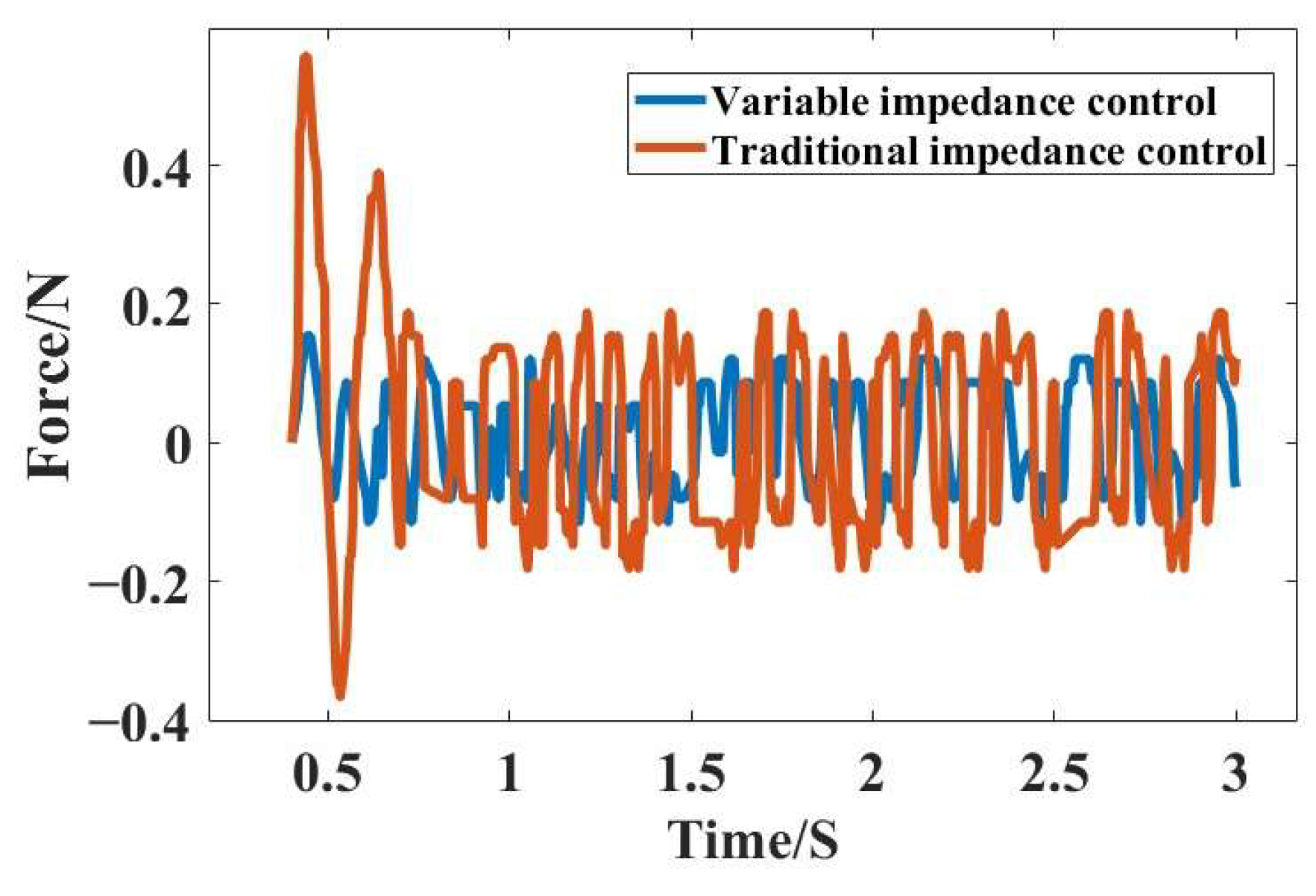
| Number | Variable Impedance Control | Traditional Impedance Control | ||||
|---|---|---|---|---|---|---|
| Peak Value/N | Stable Time/s | Stable Value/N | Peak Value/N | Stable Time/s | Stable Value/N | |
| 5 N | 5.02 | 0.92 | 5.006 | 5.38 | 1.09 | 5.007 |
| 6 N | 6.03 | 0.80 | 6.002 | 6.37 | 1.05 | 6.005 |
| Number | Variable Impedance Control | Traditional Impedance Control | ||||
|---|---|---|---|---|---|---|
| Mutation Force/N | Stable Time/s | Stable Value/N | Mutation Force/N | Stable Time/s | Stable Value/N | |
| 5 N | 5.535 | 2.29 | 5.18 | 5.537 | 2.34 | 5.39 |
| 6 N | 6.518 | 2.38 | 6.16 | 6.520 | 2.43 | 6.33 |
| Number | Variable Impedance Control | Traditional Impedance Control | ||||
|---|---|---|---|---|---|---|
| Mutation Force/N | Stable Time/s | Stable Value/N | Mutation Force/N | Stable Time/s | Stable Value/N | |
| 5 N | 3.201 | 2.26 | 4.63 | 3.181 | 2.76 | 4.14 |
| 6 N | 3.947 | 2.43 | 5.69 | 3.930 | 2.60 | 5.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Ji, W.; Zhang, H.; Ruan, C.; Xu, B.; Wu, K. Grasping Force Optimization and DDPG Impedance Control for Apple Picking Robot End-Effector. Agriculture 2025, 15, 1018. https://doi.org/10.3390/agriculture15101018
Yu X, Ji W, Zhang H, Ruan C, Xu B, Wu K. Grasping Force Optimization and DDPG Impedance Control for Apple Picking Robot End-Effector. Agriculture. 2025; 15(10):1018. https://doi.org/10.3390/agriculture15101018
Chicago/Turabian StyleYu, Xiaowei, Wei Ji, Hongwei Zhang, Chengzhi Ruan, Bo Xu, and Kaiyang Wu. 2025. "Grasping Force Optimization and DDPG Impedance Control for Apple Picking Robot End-Effector" Agriculture 15, no. 10: 1018. https://doi.org/10.3390/agriculture15101018
APA StyleYu, X., Ji, W., Zhang, H., Ruan, C., Xu, B., & Wu, K. (2025). Grasping Force Optimization and DDPG Impedance Control for Apple Picking Robot End-Effector. Agriculture, 15(10), 1018. https://doi.org/10.3390/agriculture15101018








