Optimal Control of Direct Contact Membrane Distillation Operated under Fluctuating Energy Source
Abstract
1. Introduction
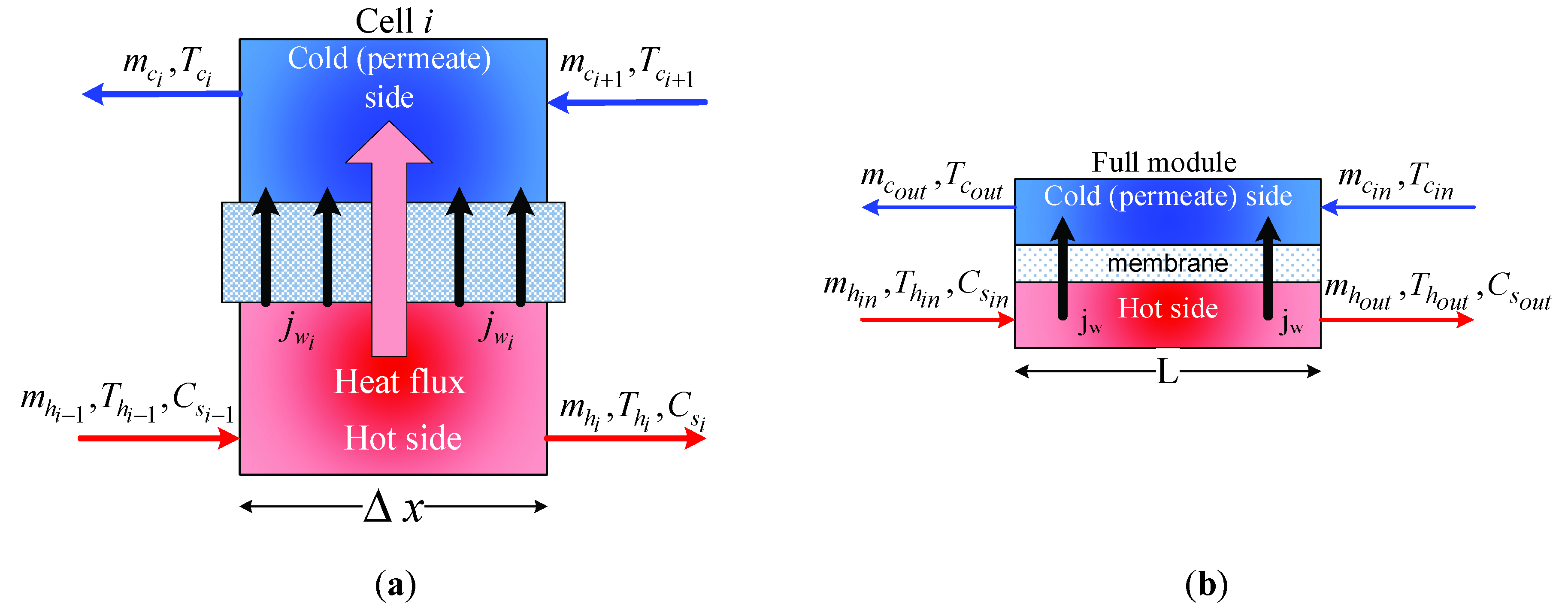
2. Dynamic Model of the MD Process
3. Control Strategy
4. Results and Discussion
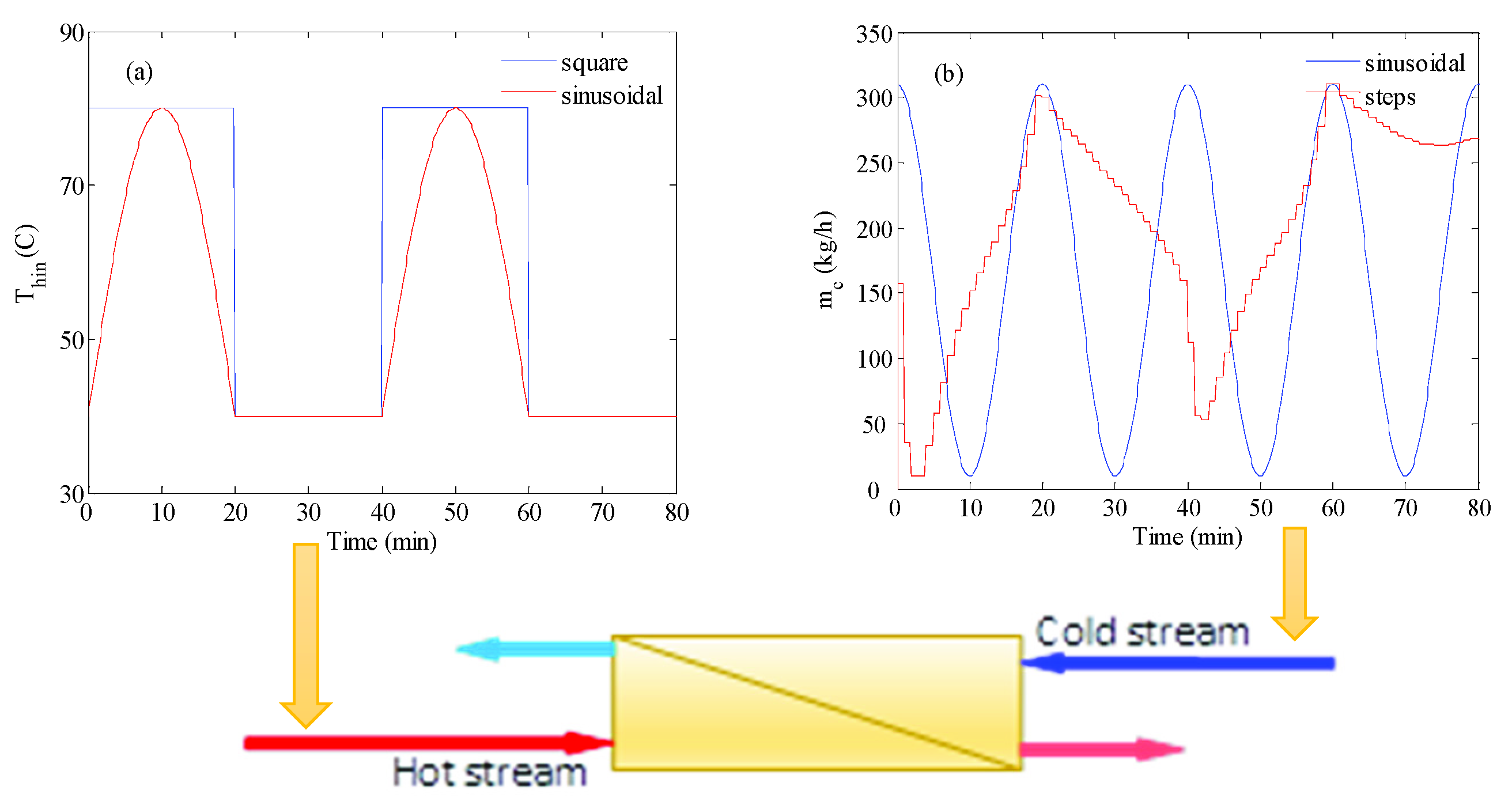
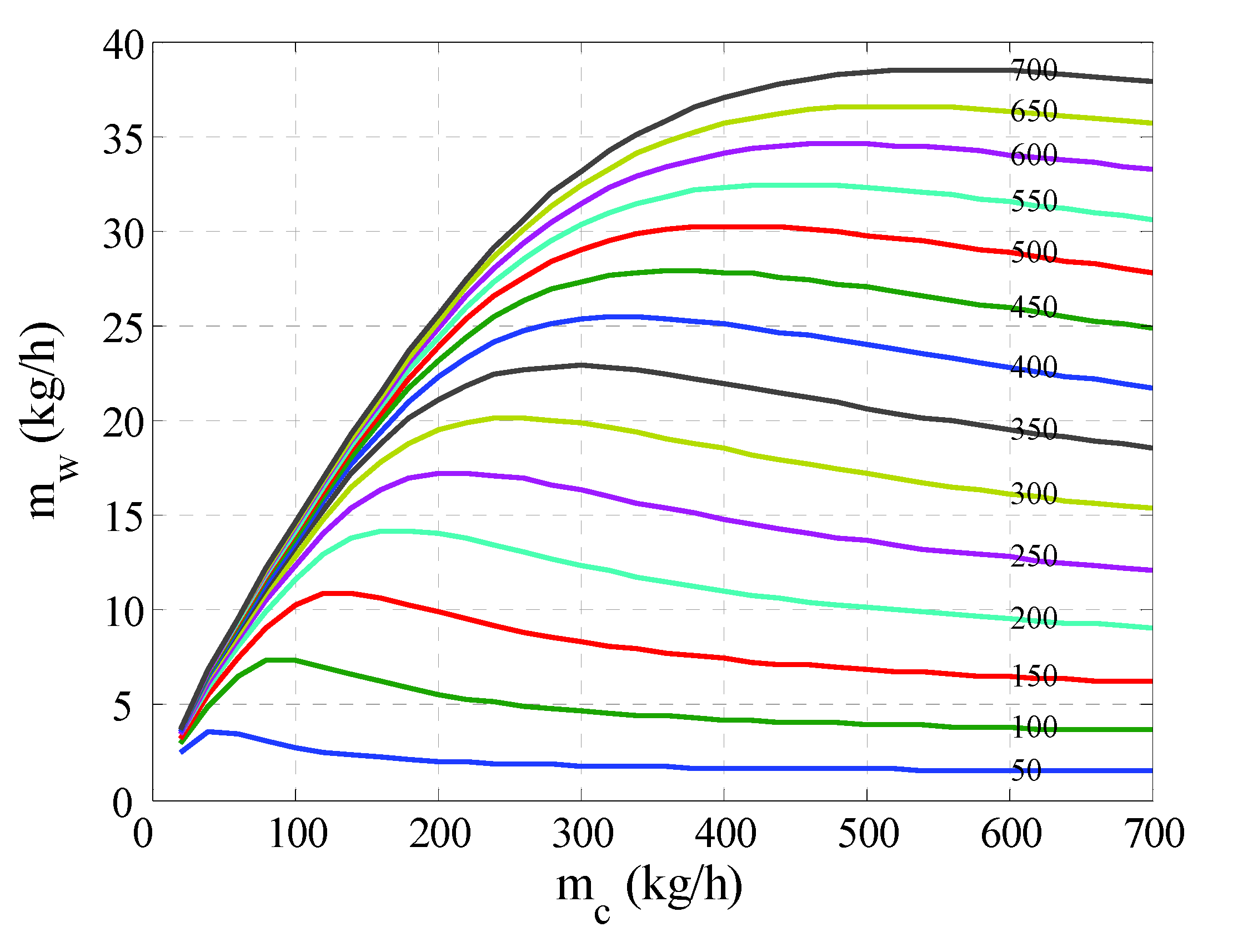
4.1. Process Behavior
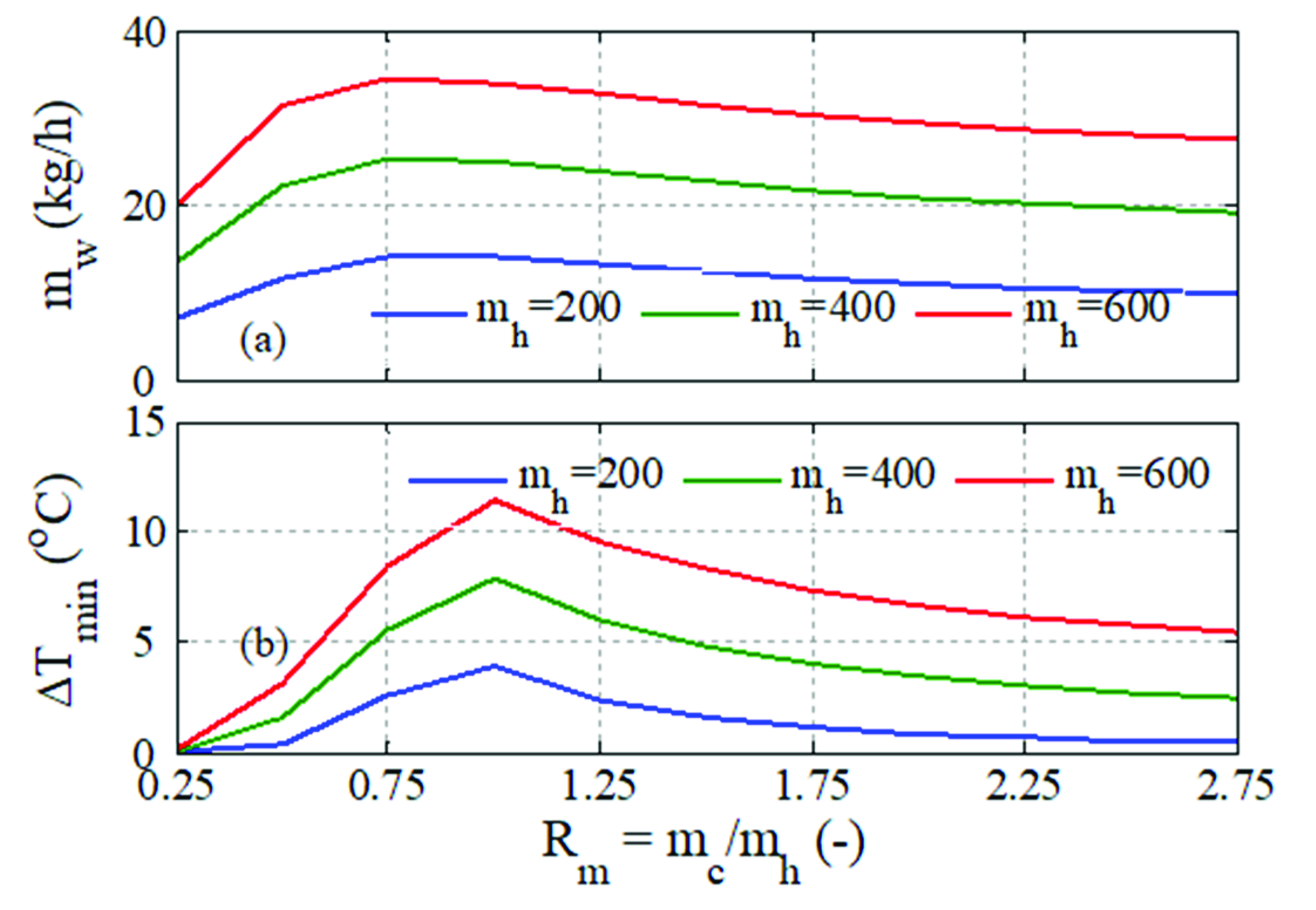
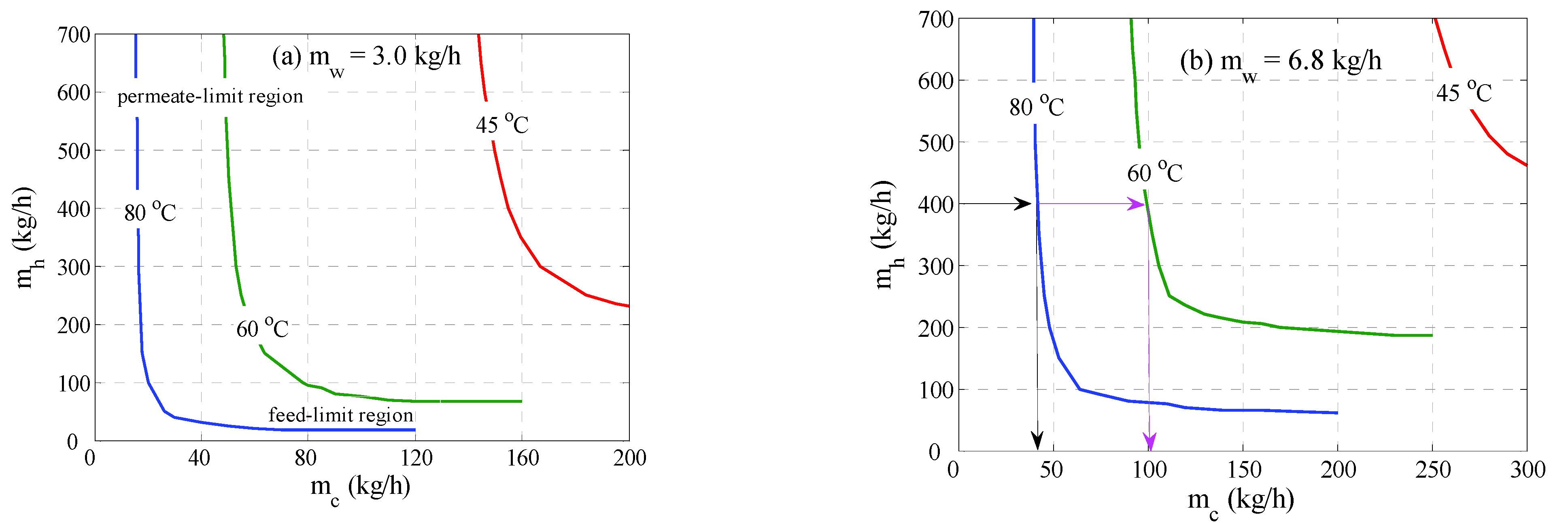
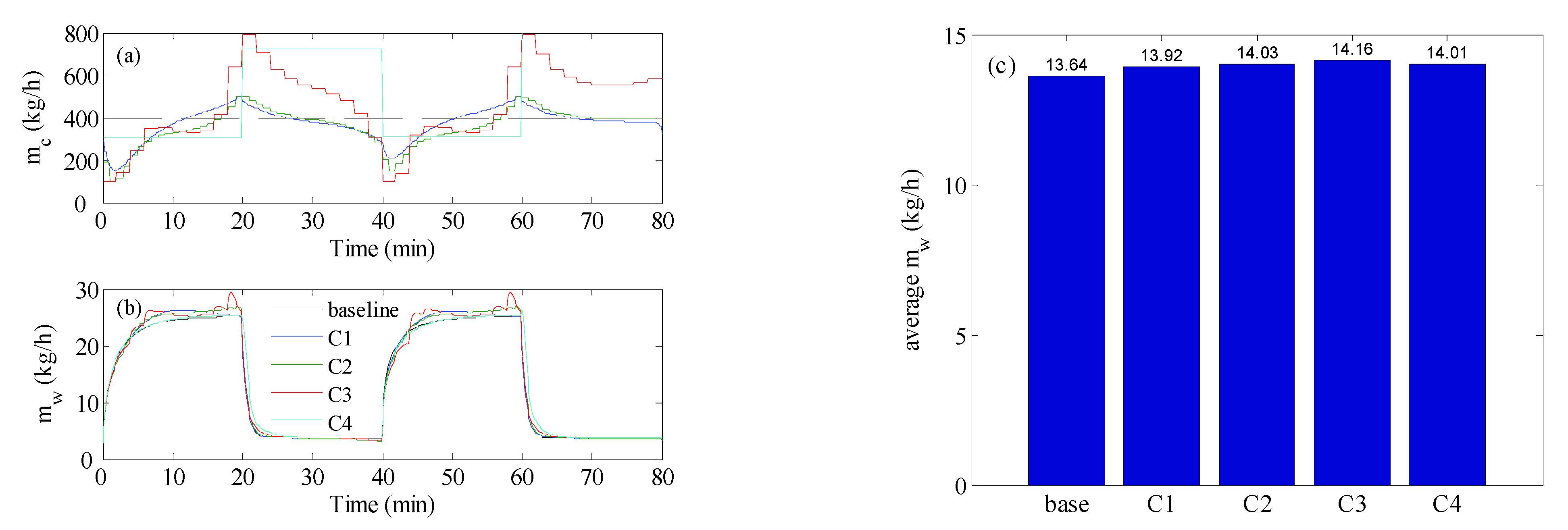
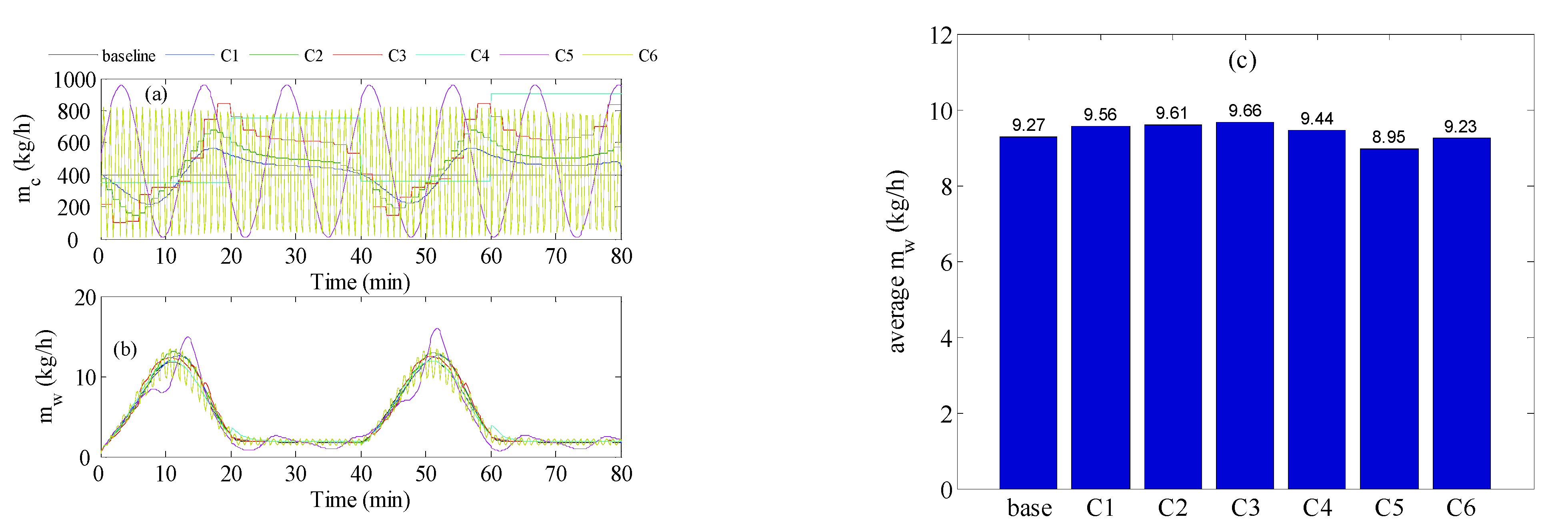
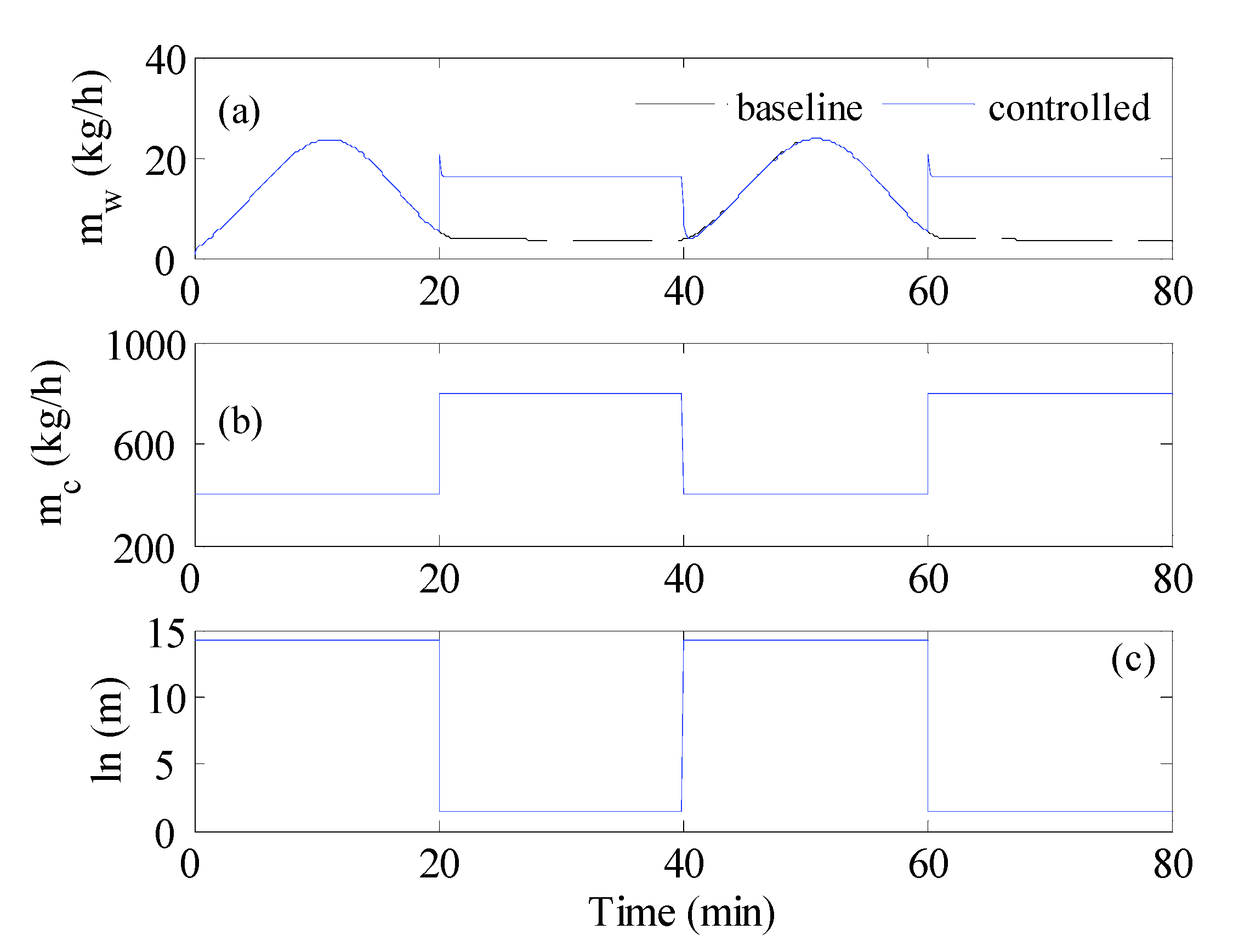
4.2. Optimal Control Analysis
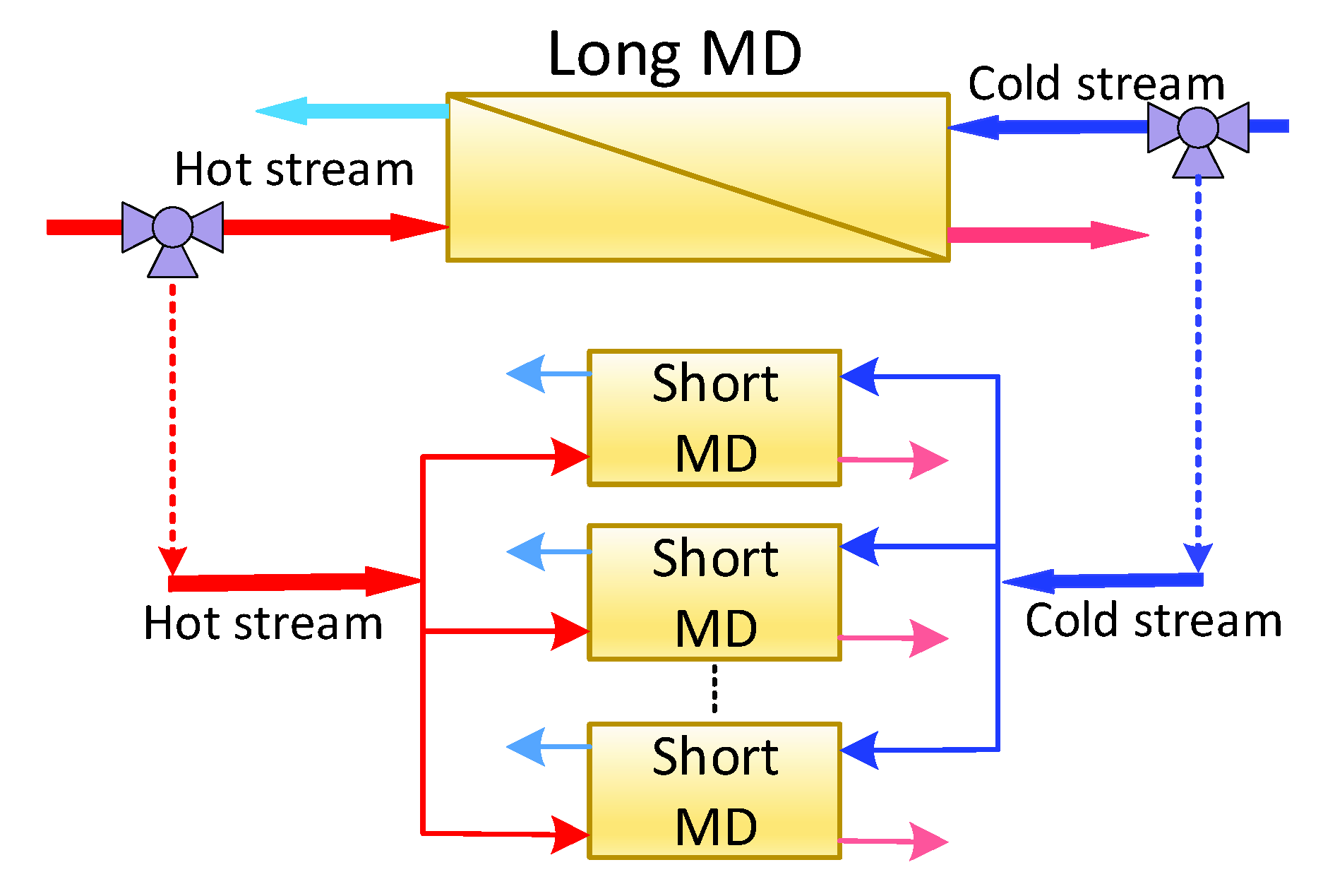
4.3. MD Length Retrofitting
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Cross-sectional area, m2 |
| Cm | Permeability coefficient, kg/m2sPa |
| Knudsen mass flux coefficient, kg/m2sPa | |
| Molecular diffusion mass flux coefficient, kg/m2sPa | |
| Transition mass flux coefficient, kg/m2sPa | |
| Cp | Heat capacity, J/kg.K |
| Cs | Salt concentration, at the bulk, % |
| de | collision diameter of the water vapor and air, m2 |
| dh | Hydraulic diameter, m |
| D | Diffusivity coefficient, m2/s |
| hv | Latent heat of vaporization, J/kg |
| hf, hp, hm | Feed, permeate, and membrane heat-transfer coefficients, W/m2 K |
| Jw | Mass flux, kg/m2h |
| kB | Boltzmann’s constant |
| km | Membrane conductivity, W/m.K |
| ks | Solid-phase thermal conductivity, W/m.K |
| kg | Gas-phase thermal conductivity, W/m.K |
| kn | Knudsen number |
| l | Channel height, m |
| L, ln | Channel length, m |
| Mass flow rate, kg/h | |
| distillate flow rate, kg/h | |
| Mw | Molecular weight |
| Nu | Nusselt Number |
| n | Number of membrane length divisions, i.e., the control elements |
| P1, P2 | Vapor pressure at the feed and permeate membrane surfaces, Pa |
| P | Average membrane interface pressure, Pa |
| Pa | Entrapped air pressure, Pa |
| PD | Membrane pressure multiplied by diffusivity, Pam2/s |
| Pr | Prandtl number |
| r | Membrane pore size, m |
| R | Ideal gas constant also flows rate ratio |
| Re | Reynold Number |
| t | Time |
| Th, Tc | Feed (hot) and permeate (cold) temperatures, K |
| Thb, Tcb | Feed (hot) and permeate (cold) bulk temperatures, K |
| Thm, Tcm | Feed and permeate membrane temperatures, K |
| Outlet and inlet hot feed temperatures, °C | |
| Outlet and inlet cold stream temperatures, °C | |
| T | The average temperature, at the membrane interface; K |
| U | Overall heat-transfer coefficient, W/m2K |
| v | Channel volume, m3 |
| Greek letters | |
| α | Tuning parameter |
| τ | Tortuosity |
| ρ | Water density, kg/m3 |
| δ | Membrane thickness |
| ε | Porosity |
| λ | Mean free path, m |
| μ | Viscosity coefficient, Pa/s |
| Δx | Control volume |
| Subscript | |
| i | Control element, i |
| c | Cold stream |
| h | Hot stream |
Appendix A
References
- UNDESA. International Decade for Action Water for Life 2005–2015; UNDESA: New York, NY, USA, 2022. [Google Scholar]
- Shahzad, M.W.; Burhan, M.; Ng, K.C. A standard primary energy approach for comparing desalination processes. NPJ Clean Water 2019, 2, 1. [Google Scholar] [CrossRef]
- Ghaffour, N.; Soukane, S.; Lee, J.-G.; Kim, Y.; Alpatova, A. Membrane distillation hybrids for water production and energy efficiency enhancement: A critical review. Appl. Energy 2019, 254, 113698. [Google Scholar] [CrossRef]
- González, D.; Amigo, J.; Suárez, F. Membrane distillation: Perspectives for sustainable and improved desalination. Renew. Sustain. Energy Rev. 2017, 80, 238–259. [Google Scholar] [CrossRef]
- Khayet, M. Desalination by membrane distillation. In Encyclopedia of Life Support Systems (EOLSS); EOLSS Publishers Co., Ltd.: Oxford, UK, 2010. [Google Scholar]
- Lu, Y.; Chen, J. Optimal design of multistage membrane distillation systems for water purification. Ind. Eng. Chem. Res. 2011, 50, 7345–7354. [Google Scholar] [CrossRef]
- Minier-Matar, J.; Hussain, A.; Janson, A.; Benyahia, F.; Adham, S. Field evaluation of membrane distillation technologies for desalination of highly saline brines. Desalination 2014, 351, 101–108. [Google Scholar] [CrossRef]
- Ve, Q.L.; Rahaoui, K.; Bawahab, M.; Faqeha, H.; Akbarzadeh, A.; Do, M.C.; Nguyen, Q.L. Experimental investigation of heat transfer correlation for direct contact membrane distillation. J. Heat Transf. 2020, 142, 012001. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R. Direct contact membrane distillation: Effect of mass transfer on heat transfer. J. Membr. Sci. 2001, 188, 137–143. [Google Scholar] [CrossRef]
- Summers, E.K.; Arafat, H.A. Energy efficiency comparison of single-stage membrane distillation (MD) desalination cycles in different configurations. Desalination 2012, 290, 54–66. [Google Scholar] [CrossRef]
- Lawal, D.U.; Khalifa, A.E. Flux prediction in direct contact membrane distillation. Int. J. Mater. Mech. Manuf. 2014, 2, 302–308. [Google Scholar] [CrossRef][Green Version]
- Nakoa, K.; Date, A.; Akbarzadeh, A. A research on water desalination using membrane distillation. Desalin. Water Treat. 2015, 56, 2618–2630. [Google Scholar] [CrossRef]
- Camacho, L.M.; Dumée, L.; Zhang, J.; Li, J.; Duke, M.; Gomez, J.; Gray, S. Advances in membrane distillation for water desalination and purification applications. Water 2013, 5, 94–196. [Google Scholar] [CrossRef]
- Ali, A.; Tsai, J.-H.; Tung, K.-L.; Drioli, E.; Macedonio, F. Designing and optimization of continuous direct contact membrane distillation process. Desalination 2018, 426, 97–107. [Google Scholar] [CrossRef]
- Panagopoulos, A.; Haralambous, K.-J. Minimal Liquid Discharge (MLD) and Zero Liquid Discharge (ZLD) strategies for wastewater management and resource recovery–Analysis, challenges and prospects. J. Environ. Chem. Eng. 2020, 8, 104418. [Google Scholar] [CrossRef]
- Andrjesdóttir, Ó.; Ong, C.L.; Nabavi, M.; Paredes, S.; Khalil, A.; Michel, B.; Poulikakos, D. An experimentally optimized model for heat and mass transfer in direct contact membrane distillation. Int. J. Heat Mass Transf. 2013, 66, 855–867. [Google Scholar] [CrossRef]
- Winter, D.; Koschikowski, J.; Wieghaus, M. Desalination using membrane distillation: Experimental studies on full scale spiral wound modules. J. Membr. Sci. 2011, 375, 104–112. [Google Scholar] [CrossRef]
- Guan, G.; Yang, X.; Wang, R.; Fane, A.G. Evaluation of heat utilization in membrane distillation desalination system integrated with heat recovery. Desalination 2015, 366, 80–93. [Google Scholar] [CrossRef]
- Drioli, E.; Ali, A.; Macedonio, F. Membrane distillation: Recent developments and perspectives. Desalination 2015, 356, 56–84. [Google Scholar] [CrossRef]
- Geng, H.; Wang, J.; Zhang, C.; Li, P.; Chang, H. High water recovery of RO brine using multi-stage air gap membrane distillation. Desalination 2015, 355, 178–185. [Google Scholar] [CrossRef]
- Chen, T.-C.; Ho, C.-D. Immediate assisted solar direct contact membrane distillation in saline water desalination. J. Membr. Sci. 2010, 358, 122–130. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N.; Rommel, M.; Koschikowski, J.; Wieghaus, M. Desalination by a “compact SMADES” autonomous solarpowered membrane distillation unit. Desalination 2007, 217, 29–37. [Google Scholar] [CrossRef]
- Charfi, K.; Khayet, M.; Safi, M.J. Numerical simulation and experimental studies on heat and mass transfer using sweeping gas membrane distillation. Desalination 2010, 259, 84–96. [Google Scholar] [CrossRef]
- Eleiwi, F.; Ghaffour, N.; Alsaadi, A.S.; Francis, L.; Laleg-Kirati, T.M. Dynamic modeling and experimental validation for direct contact membrane distillation (DCMD) process. Desalination 2016, 384, 1–11. [Google Scholar] [CrossRef]
- Karam, A.M.; Alsaadi, A.S.; Ghaffour, N.; Laleg-Kirati, T.M. Analysis of direct contact membrane distillation based on a lumped-parameter dynamic predictive model. Desalination 2017, 402, 50–61. [Google Scholar] [CrossRef]
- Hassan, A.S.; Fath, H.E.; Darwish, M.; Abdulrahim, H. Dynamic performance of vacuum membrane distillation system. Desalin. Water Treat. 2016, 57, 23196–23205. [Google Scholar] [CrossRef]
- Ali, E.; Orfi, J.; Najib, A. Developing and validating a dynamic model of water production by direct-contact membrane distillation. PLoS ONE 2020, 15, e0230207. [Google Scholar] [CrossRef]
- Ali, E.; Saleh, J.; Orfi, J.; Najib, A. Developing and validating linear dynamic models for direct contact membrane distillation during start-up over wide operating conditions. Comput. Chem. Eng. 2020, 134, 106678. [Google Scholar] [CrossRef]
- Kim, J.S.; Chen, J.; Garcia, H.E. Modeling, control, and dynamic performance analysis of a reverse osmosis desalination plant integrated within hybrid energy systems. Energy 2016, 112, 52–66. [Google Scholar] [CrossRef]
- Al-Bastaki, N.; Abbas, A. Use of fluid instabilities to enhance membrane performance: A review. Desalination 2001, 136, 255–262. [Google Scholar] [CrossRef]
- Lai, W.; Ma, Q.; Lu, H.; Weng, S.; Fan, J.; Fang, H. Effects of wind intermittence and fluctuation on reverse osmosis desalination process and solution strategies. Desalination 2016, 395, 17–27. [Google Scholar] [CrossRef]
- Richards, B.S.; Park, G.L.; Pietzsch, T.; Schäfer, A.I. Renewable energy powered membrane technology: Brackish water desalination system operated using real wind fluctuations and energy buffering. J. Membr. Sci. 2014, 468, 224–232. [Google Scholar] [CrossRef]
- Gustafson, R.D.; Hiibel, S.R.; Childress, A.E. Membrane distillation driven by intermittent and variable-temperature waste heat: System arrangements for water production and heat storage. Desalination 2018, 448, 49–59. [Google Scholar] [CrossRef]
- Charrouf, O.; Betka, A.; Abdeddaim, S.; Ghamri, A. Artificial Neural Network power manager for hybrid PV-wind desalination system. Math. Comput. Simul. 2020, 167, 443–460. [Google Scholar] [CrossRef]
- Peng, W.; Maleki, A.; Rosen, M.A.; Azarikhah, P. Optimization of a hybrid system for solar-wind-based water desalination by reverse osmosis: Comparison of approaches. Desalination 2018, 442, 16–31. [Google Scholar] [CrossRef]
- Mohamed, E.S.; Papadakis, G. Design; simulation and economic analysis of a stand-alone reverse osmosis desalination unit powered by wind turbines and photovoltaics. Desalination 2004, 164, 87–97. [Google Scholar] [CrossRef]
- Khiari, W.; Turki, M.; Belhadj, J. Power control strategy for PV/Wind reverse osmosis desalination without battery. Control. Eng. Pract. 2019, 89, 169–179. [Google Scholar] [CrossRef]
- Carta, J.A.; González, J.; Cabrera, P.; Subiela, V.J. Preliminary experimental analysis of a small-scale prototype SWRO desalination plant, designed for continuous adjustment of its energy consumption to the widely varying power generated by a stand-alone wind turbine. Appl. Energy 2015, 137, 222–239. [Google Scholar] [CrossRef]
- Naidu, G.; Jeong, S.; Vigneswaran, S. Influence of feed/permeate velocity on scaling development in a direct contact membrane distillation. Sep. Purif. Technol. 2014, 125, 291–300. [Google Scholar] [CrossRef]
- Ali, E.; Orfi, J.; Najib, A. Nonlinear dynamic modeling and validation of a direct contact membrane distillation for water desalination. Appl. Therm. Eng. 2020, 179, 115719. [Google Scholar] [CrossRef]
- Najib, A.; Orfi, J.; Alansary, H.; Ali, E.; Abdulwahed, Z.; Alzahrani, S.; Chafidz, A. An experimental investigation of a solar-driven desalination system based on multi-effect membrane distillation. Desalin. Water Treat. 2020, 198, 1–18. [Google Scholar] [CrossRef]
- Ali, E.; Orfi, J.; Najib, A. Effects of forced input on the performance of direct contact membrane distillation. Desalin. Water Treat. 2022, 246, 68–81. [Google Scholar] [CrossRef]
- Ali, E.; Orfi, J. An experimentally calibrated model for heat and mass transfer in full-scale direct contact membrane distillation. Desalin. Water Treat. 2018, 116, 1–18. [Google Scholar] [CrossRef]
- Ali, J.O.E.; Najib, A. Thermodynamic analysis of direct contact membrane distillation with/without heat recovery based on experimental data. Desalin. Water Treat. 2019, 466, 52–67. [Google Scholar]
- Najib, E.A.A.; Al-humaizi, K.; Ajbar, A.; Orfi, J.; Boumaza, M. Performance analysis of cascaded membrane distillation arrangement of desalination of brackish water. Desalin. Water Treat. 2017, 76, 19–29. [Google Scholar] [CrossRef]
- Jamel, O.; Abdullah, N.; Emad, A.; Abdulhamid, A.; Maher, A.; Mourad, B.; Khalid, A. Membrane distillation and reverse osmosis-based desalination driven by geothermal energy sources. Desalin. Water Treat. 2017, 76, 40–52. [Google Scholar]
- Fard, Y.M.M.K.; Rhadfi, Y.; Mahmoud, K.A.; Khraisheh, M.; Benyahia, F. Synoptic analysis of direct contact membrane distillation performance in Qatar: A case study. Desalination 2015, 360, 97–107. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, E. Optimal Control of Direct Contact Membrane Distillation Operated under Fluctuating Energy Source. Membranes 2022, 12, 628. https://doi.org/10.3390/membranes12060628
Ali E. Optimal Control of Direct Contact Membrane Distillation Operated under Fluctuating Energy Source. Membranes. 2022; 12(6):628. https://doi.org/10.3390/membranes12060628
Chicago/Turabian StyleAli, Emad. 2022. "Optimal Control of Direct Contact Membrane Distillation Operated under Fluctuating Energy Source" Membranes 12, no. 6: 628. https://doi.org/10.3390/membranes12060628
APA StyleAli, E. (2022). Optimal Control of Direct Contact Membrane Distillation Operated under Fluctuating Energy Source. Membranes, 12(6), 628. https://doi.org/10.3390/membranes12060628




