Thermodynamic Optimization of Ammonia Decomposition Solar Heat Absorption System Based on Membrane Reactor
Abstract
:1. Introduction
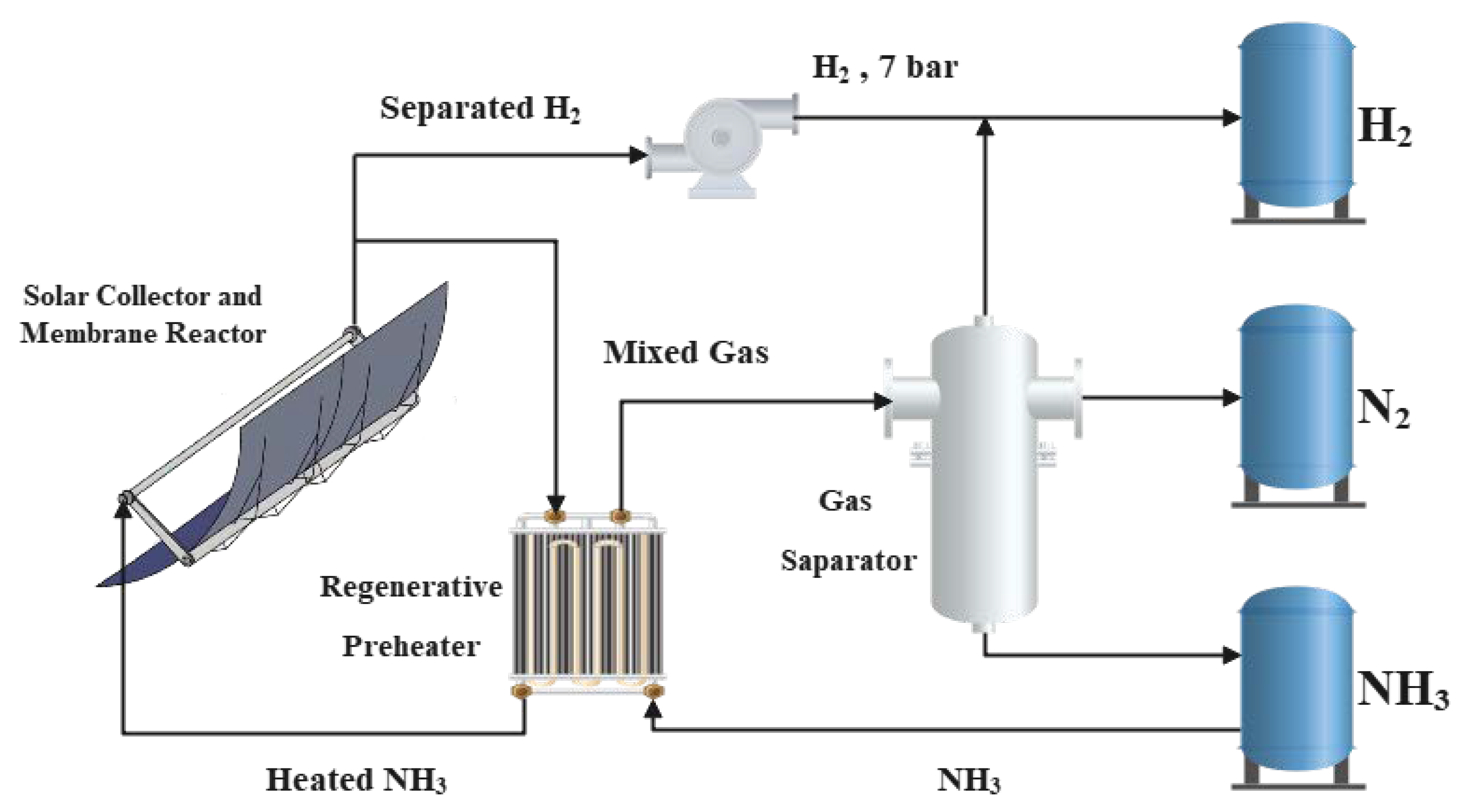
2. Physical Model
2.1. Solar Collector Model
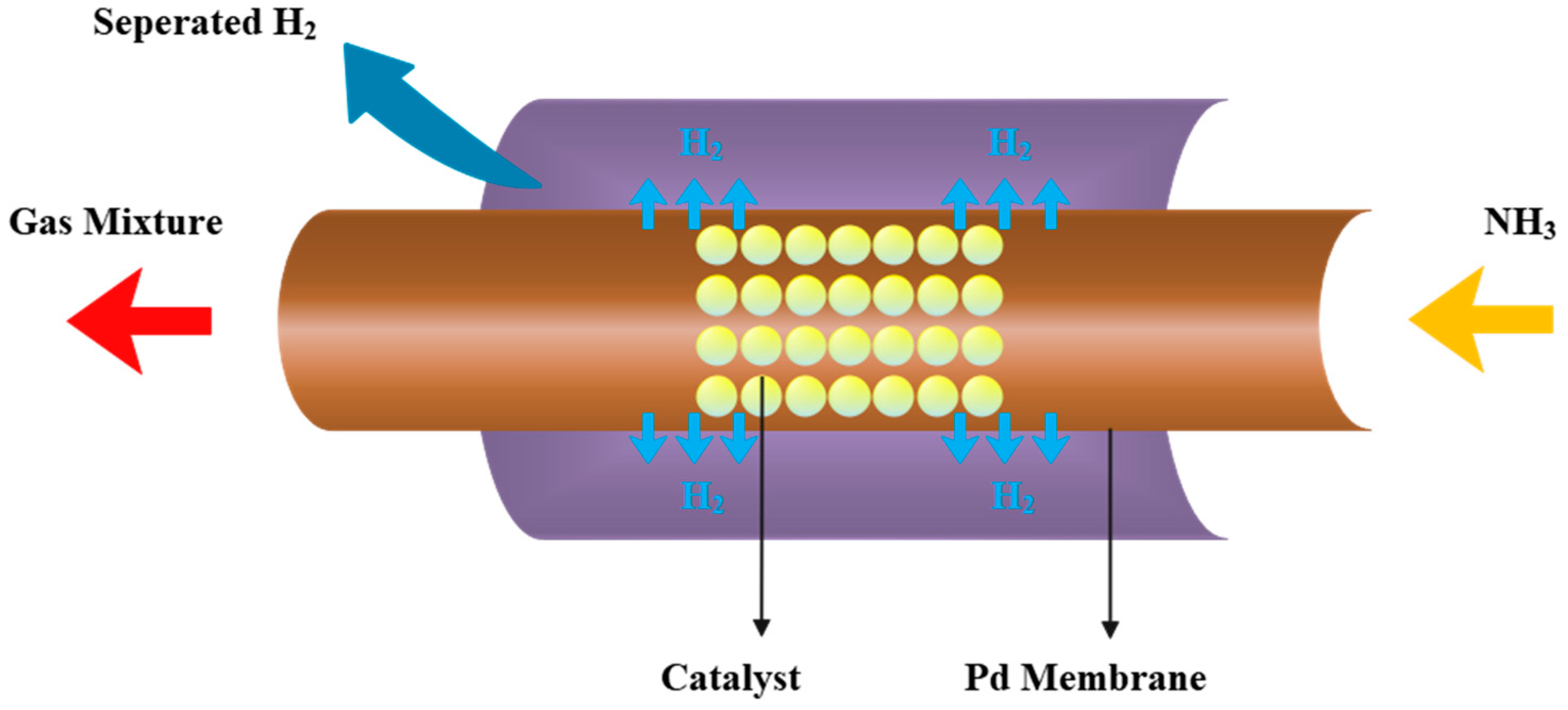
2.2. Ammonia Decomposition Membrane Reactor Model
2.2.1. Reaction Kinetic Equation
2.2.2. Conservation Equations
2.3. Compressor Model
2.4. Performance Index
2.4.1. Heat Absorption Rate
2.4.2. Entropy Generation Rate
2.4.3. Thermal Efficiency
2.4.4. Energy Conversion Rate
3. Optimization Problems
4. Numerical Example and Result Analysis
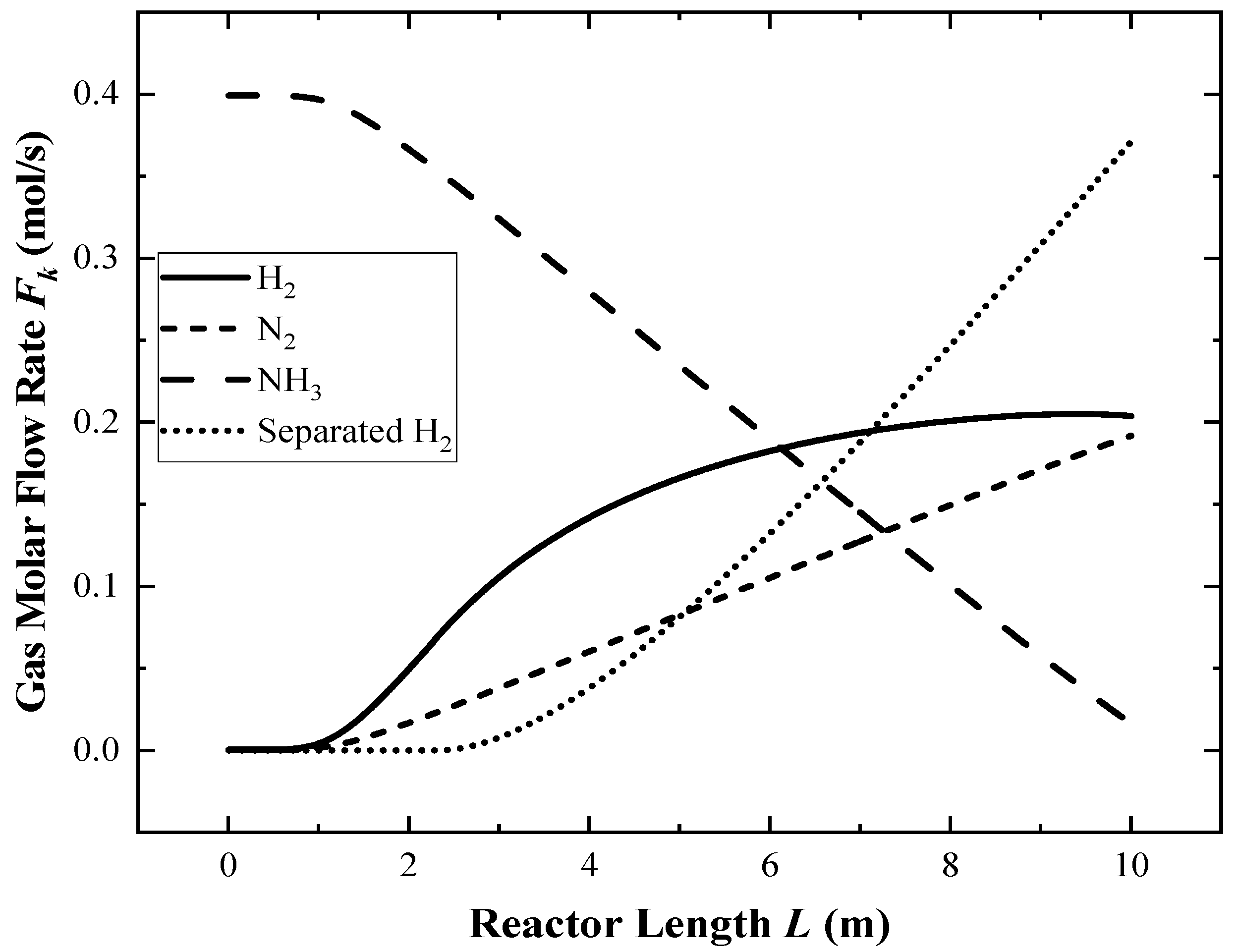
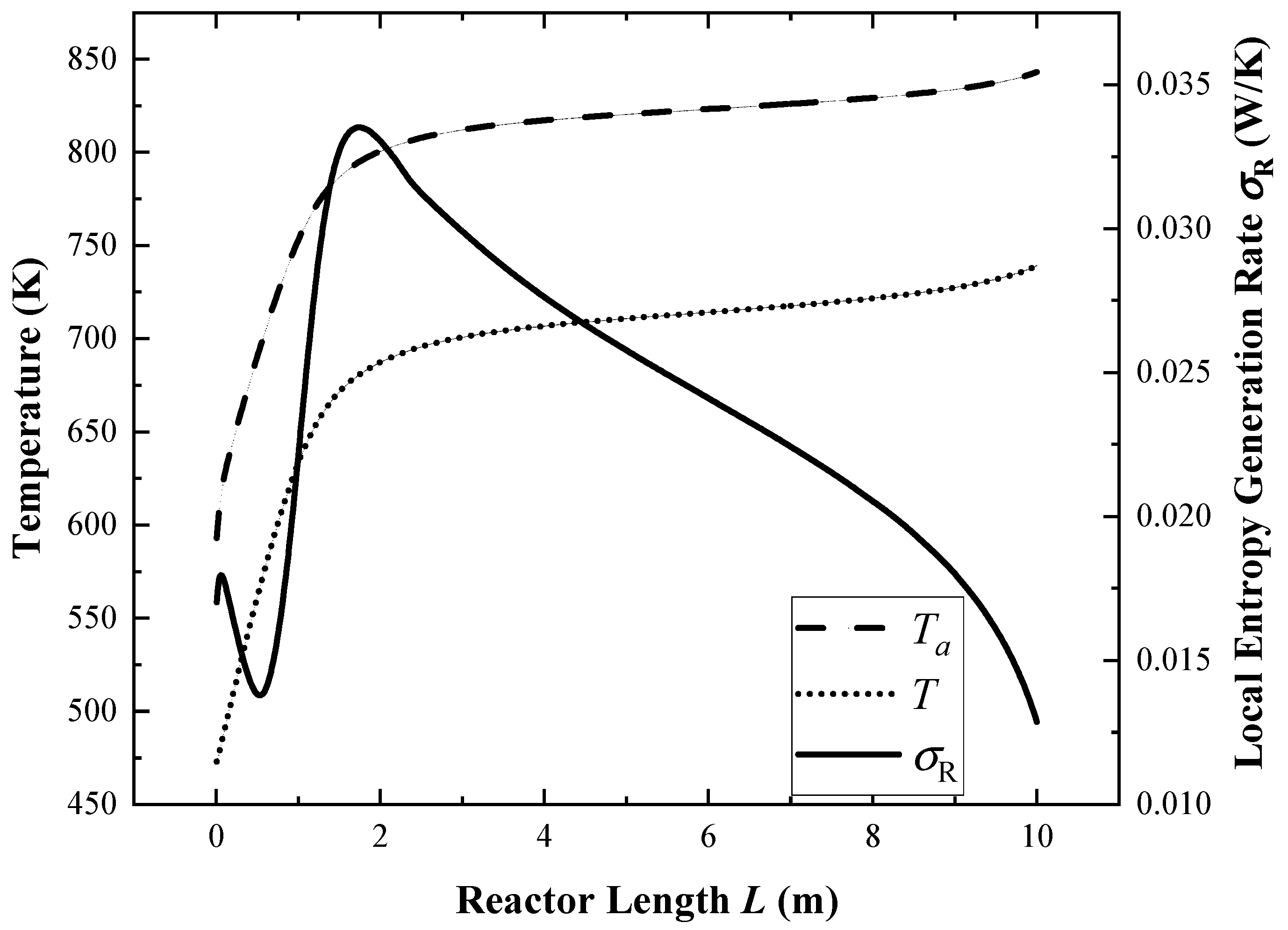
4.1. Performance of the Reference Reactor
4.2. Three-Objective Optimization with the Heat Absorption Rate Constraint
4.3. Four-Objective Optimization Releasing the Heat Absorption Rate Constraint
5. Conclusions
- (1)
- In the four-objective optimization releasing the heat absorption rate constraint, the minimum entropy generation rate and the maximum thermal efficiency have similar optimization directions, while the maximum heat absorption rate and the maximum energy conversion rate have similar optimization directions.
- (2)
- When aiming at the highest energy conversion rate, the system will select the highest ammonia preheat end-state temperature and the lowest permeation zone pressure. When aiming at the highest heat absorption rate, the system will choose the lowest ammonia preheat end-state temperature, the highest ammonia gas flow rate, the smallest reactor radius, the longest reactor length, and the lowest permeation zone pressure.
- (3)
- In the three-objective optimization with the heat absorption rate constraint, the TOPSIS optimal system can reduce the entropy generation rate by 4.8% and increase the thermal efficiency and energy conversion rate by 1.5% and 1.4%, respectively.
- (4)
- In the four-objective optimization releasing the heat absorption rate constraint, the TOPSIS optimal system has a 15.5% reduction in heat absorption rate, a 14% reduction in entropy generation rate, a 15.7% increase in thermal efficiency, and an 8.7% decrease in energy conversion rate.
Author Contributions
Funding
Conflicts of Interest
References
- Wang, D.L.; Zhang, C.; Yang, Y.; Zhang, L.; Bai, W.G.; Li, H.Z.; Yao, M.Y. Research progress of thermochemical energy storage system based on solar thermal power generation. Therm. Power Gener. 2019, 48, 1–9. [Google Scholar]
- Wang, X.H.; Du, X.C.; Wei, J.J. Research progress of different solar thermochemical energy storage systems. Chin. Sci. Bull. 2017, 62, 3631–3642. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Long, X.F. Research progress of solar thermochemical energy storage. Chem. Ind. Eng. Prog. 2014, 33, 3238–3245. [Google Scholar] [CrossRef]
- Lovegrove, K.M. Aspects of Thermochemical Storage and Transfer of Solar Energy Using Ammonia. Ph.D. Thesis, Australian National University, Canberra, Australia, 1992. [Google Scholar]
- Luzzi, A. Solar Thermo-Catalytic Ammonia Dissociation. Ph.D. Thesis, Australian National University, Canberra, Australia, 1996. [Google Scholar]
- Luzzi, A. High temperature solar tests with 1 kW chem ammonia reactor. Fuel Energy Abstr. 1995, 36, 271. [Google Scholar]
- Luzzi, A.; Lovegrove, K.; Filippi, E.; Fricker, H.; Schmitz-Goeb, M.; Chandapillai, M.; Kaneff, S. Techno-economic analysis of a 10 MW solar thermal power plant using ammonia-based thermochemical energy storage. Sol. Energy 1999, 66, 91–101. [Google Scholar] [CrossRef]
- Dunn, R.; Lovegrove, K.; Burgess, G. A review of ammonia-based thermochemical energy storage for concentrating solar power. Proc. IEEE 2012, 100, 391–400. [Google Scholar] [CrossRef]
- Dunn, R.; Lovegrove, K.; Burgess, G.; Pye, J. An experimental study of ammonia receiver geometries for dish concentrators. J. Sol. Energy Eng. 2012, 134, 41007. [Google Scholar] [CrossRef]
- Chuah, C.; Lee, J.; Bae, T. Graphene-based membranes for H2 separation: Recent progress and future perspective. Membranes 2020, 10, 336. [Google Scholar] [CrossRef]
- El-Attar, A.A.; El-Wakil, H.B.; Hassanin, A.H.; Bakr, B.A.; Almutairi, T.M.; Hagar, M.; Elwakil, B.H.; Olama, Z.A. Silver/Snail mucous PVA nanofibers: Electrospun synthesis and antibacterial and wound healing activities. Membranes 2022, 12, 536. [Google Scholar] [CrossRef]
- Dalena, F.; Senatore, A.; Basile, M.; Knani, S.; Basile, A.; Iulianelli, A. Advances in methanol production and utilization, with particular emphasis toward hydrogen generation via membrane reactor technology. Membranes 2018, 8, 98. [Google Scholar] [CrossRef] [Green Version]
- Itoh, N.; Oshima, A.; Suga, E.; Sato, T. Kinetic enhancement of ammonia decomposition as a chemical hydrogen carrier in palladium membrane reactor. Catal. Today 2014, 236, 70–76. [Google Scholar] [CrossRef]
- Abashar, M.E.E.; Al-Sughair, Y.S.; Al-Mutaz, I.S. Investigation of low temperature decomposition of ammonia using spatially patterned catalytic membrane reactors. Appl. Catal. A Gen. 2002, 236, 35–53. [Google Scholar] [CrossRef]
- Abashar, M. The impact of ammonia feed distribution on the performance of a fixed bed membrane reactor for ammonia decomposition to ultra-pure hydrogen. Int. J. Hydrogen Energy 2019, 44, 82–90. [Google Scholar] [CrossRef]
- Wang, B.; Kong, H.; Wang, H.; Wang, Y.; Hu, X. Kinetic and thermodynamic analyses of mid/low-temperature ammonia decomposition in solar-driven hydrogen permeation membrane reactor. Int. J. Hydrogen Energy 2019, 44, 26874–26887. [Google Scholar] [CrossRef]
- Cechetto, V.; Di Felice, L.; Medrano, J.A.; Makhloufi, C.; Zuniga, J.; Gallucci, F. H2 production via ammonia decomposition in a catalytic membrane reactor. Fuel Process. Technol. 2021, 216, 106772. [Google Scholar] [CrossRef]
- Sitar, R.; Shah, J.; Zhang, Z.; Wikoff, H.; Way, J.D.; Wolden, C.A. Compact ammonia reforming at low temperature using catalytic membrane reactors. J. Membr. Sci. 2022, 644, 120147. [Google Scholar] [CrossRef]
- Cerrillo, J.L.; Morlanés, N.; Kulkarni, S.R.; Realpe, N.; Ramírez, A.; Katikaneni, S.P.; Paglieri, S.N.; Lee, K.; Harale, A.; Solami, B.; et al. High purity, self-sustained, pressurized hydrogen production from ammonia in a catalytic membrane reactor. Chem. Eng. J. 2022, 431, 134310. [Google Scholar] [CrossRef]
- Chen, L.G.; Xia, S.J. Progresses in generalized thermodynamic dynamic-optimization of irreversible processes. Sci. Sin. Technol. 2019, 49, 981–1022. [Google Scholar]
- Chen, L.G.; Xia, S.J.; Feng, H.J. Progresses in generalized thermodynamic dynamic-optimization of irreversible cycles. Sci. Sin. Technol. 2019, 49, 1223–1267. [Google Scholar]
- Bejan, A. Notes on the history of the method of entropy generation minimization (finite time thermodynamics). J. Non Equilib. Thermodyn. 1996, 21, 239–242. [Google Scholar]
- Andresen, B.; Berry, R.; Nitzan, A.; Salamon, P. Thermodynamics in finite time. I. The step-Carnot cycle. Phys. Rev. A 1977, 15, 2086–2093. [Google Scholar] [CrossRef]
- Badescu, V. Optimal design and operation of ammonia decomposition reactors. Int. J. Energy Res. 2020, 44, 5360–5384. [Google Scholar] [CrossRef]
- Xie, T.C.; Xia, S.J.; Kong, R.; Li, P.L.; Wang, C. Performance analysis of ammonia decomposition endothermic membrane reactor heated by trough solar collector. Energy Rep. 2022, 8, 526–538. [Google Scholar] [CrossRef]
- Kong, R.; Chen, L.G.; Xia, S.J.; Zhang, L.; Feng, H.J. Minimization of entropy generation rate during hydrogen iodide decomposition reaction process. Sci. Sin. Technol. 2021, 51, 565–579. [Google Scholar] [CrossRef]
- Kong, R.; Chen, L.; Xia, S.; Li, P.; Ge, Y. Minimization of Entropy Generation Rate in Hydrogen Iodide Decomposition Reactor Heated by High-Temperature Helium. Entropy 2021, 23, 82. [Google Scholar] [CrossRef]
- Kong, R.; Chen, L.; Xia, S.; Li, P.; Ge, Y. Performance analysis of hydrogen iodide decomposition membrane reactor under different sweep modes. Energy Convers. Manag. 2021, 244, 114436. [Google Scholar] [CrossRef]
- Xie, T.C.; Xia, S.J.; Wang, C. Multi-objective optimization of Braun-type exothermic reactor for ammonia synthesis. Entropy 2021, 24, 52. [Google Scholar] [CrossRef]
- Wang, C.; Chen, L.G.; Xia, S.J.; Sun, F.R. Maximum production rate optimization for sulphuric acid decomposition process in tubular plug-flow reactor. Energy 2016, 99, 152–158. [Google Scholar] [CrossRef]
- Sun, M.; Xia, S.J.; Chen, L.G.; Wang, C.; Tang, C.Q. Multi-objective optimization of sulfuric acid decomposition process using NSGA-II algorithm. Energy Conserv. 2020, 39, 118–123. [Google Scholar]
- Li, P.L.; Chen, L.G.; Xia, S.J.; Zhang, L.; Kong, R.; Ge, Y.L.; Feng, H.J. Entropy generation rate minimization for steam methane reforming reactor heated by molten salt. Energy Rep. 2020, 6, 685–697. [Google Scholar] [CrossRef]
- Li, P.L.; Chen, L.G.; Xia, S.J.; Zhang, L. Maximum hydrogen production rate optimization for tubular steam methane reforming reactor. Int. J. Chem. React. Eng. 2019, 17, 20180191. [Google Scholar] [CrossRef]
- Li, P.L.; Chen, L.G.; Xia, S.J.; Kong, R.; Ge, Y.L. Total entropy generation rate minimization configuration of a membrane reactor of methanol synthesis via carbon dioxide hydrogenation. Sci. China Technol. Sci. 2022, 65, 657–678. [Google Scholar] [CrossRef]
- Li, P.L.; Chen, L.G.; Xia, S.J.; Zhang, L. Entropy generation rate minimization for methanol synthesis via a CO2 hydrogenation reactor. Entropy 2019, 21, 174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, Y.X.; Modibo, K.T.; Wu, Y.T.; Ma, C.F.; Zhang, Y.Q. Trough solar concentrating heat collection technology. Sol. Energy 2009, 21–26. [Google Scholar]
- Maansson, B.; Andresen, B. Optimal temperature profile for an ammonia reactor. Ind. Eng. Chem. Process Des. Dev. 1986, 25, 59–65. [Google Scholar] [CrossRef]
- Hicks, R.E. Pressure Drop in Packed Beds of Spheres. Ind. Eng. Chem. Fundam. 1970, 9, 500–502. [Google Scholar] [CrossRef]
- Li, Y.; Liao, S.; Gang, L. Thermo-economic multi-objective optimization for a solar-dish Brayton system using NSGA-II and decision making. Int. J. Electr. Power Energy Syst. 2015, 64, 167–175. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [Educational Forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Xu, K.; Lian, J.; Ma, C.; Bin, L. Integrated flood vulnerability assessment approach based on TOPSIS and Shannon entropy methods. Ecol. Indic. 2018, 89, 269–280. [Google Scholar] [CrossRef]
- Shih, H.S.; Shyur, H.J.; Lee, E.S. An extension of TOPSIS for group decision making. Math. Comput. Model. 2007, 45, 801–813. [Google Scholar] [CrossRef]
| Parameter Name | Symbol | Value |
|---|---|---|
| Opening width | Ks | 5.76 m |
| Condenser reflectivity | ηs | 94% |
| Glass outer tube transmittance | δs | 96% |
| Radiation absorption rate of reactor | εs | 95% |
| Reactor surface emissivity | ρs | 14% |
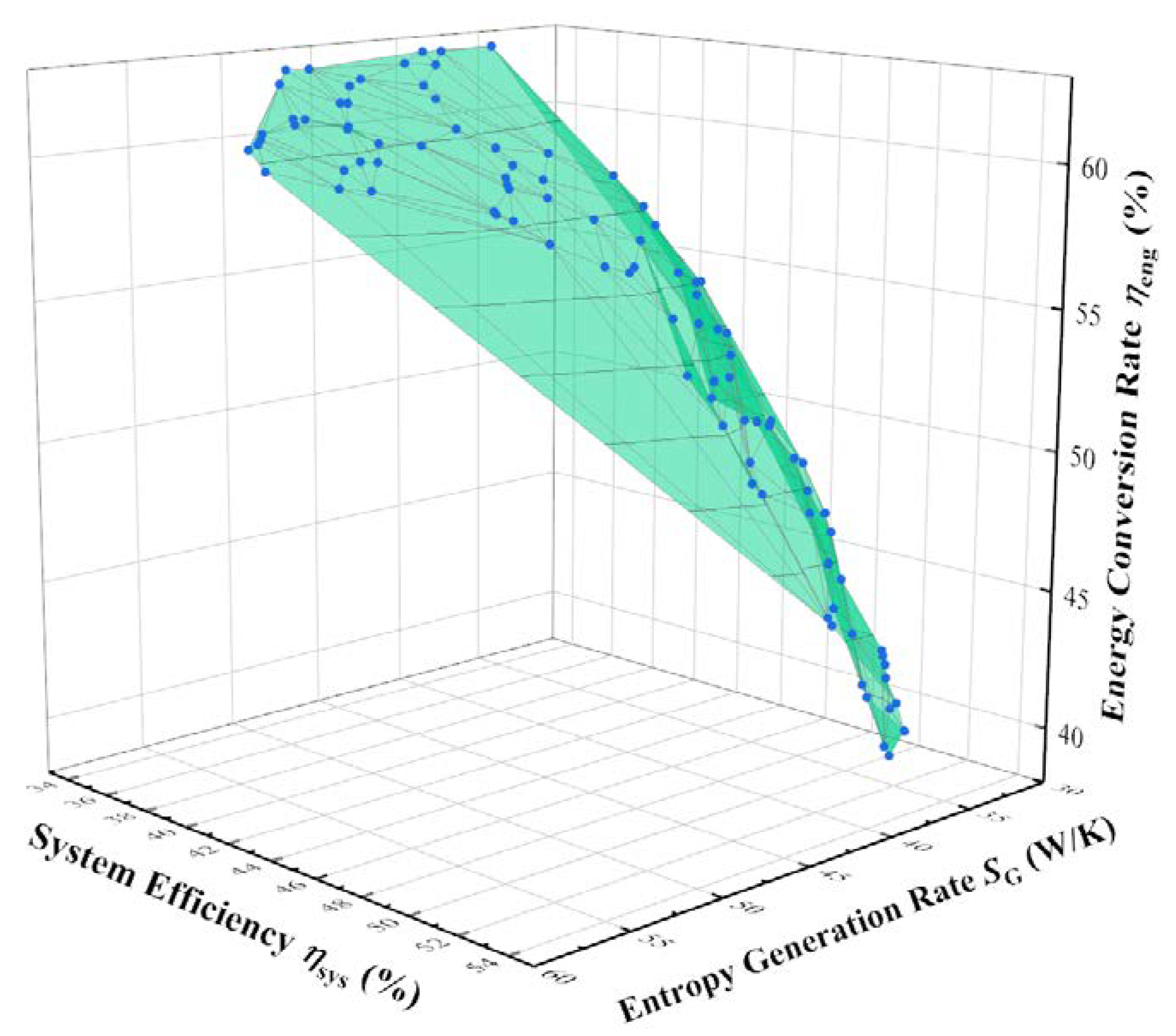
| System Parameters and Performance Indicators | Minimum SG,SUM Point | Maximum ηsys Point | Maximum ηeng Point | TOPSIS Decision Point |
|---|---|---|---|---|
| Ammonia gas preheating final temperature T1 (K) | 400 | 400 | 600 | 400 |
| Ammonia molar flow rate NA (mol/s) | 0.52 | 0.8 | 0.61 | 0.5 |
| Inner radius of membrane reactor R2 (cm) | 3.6 | 2.8 | 3.8 | 3.7 |
| Reactor length L (m) | 10.1 | 9.7 | 10.3 | 10 |
| Osmotic zone pressure pP (kPa) | 54 | 55 | 10 | 45 |
| Entropy generation rate SG (W/K) | 33.1 | 35.4 | 41.0 | 33.2 |
| Thermal efficiency ηsys (%) | 47.7 | 52.6 | 35.1 | 46.8 |
| Energy conversion rate ηeng (%) | 46.7 | 40.2 | 62.8 | 48.5 |
| System Parameters and Performance Indicators | 600 W/m2 | 800 W/m2 | 1000 W/m2 |
|---|---|---|---|
| Ammonia gas preheating final temperature T1 (K) | 400 | 400 | 448 |
| Ammonia molar flow rate NA (mol/s) | 0.31 | 0.5 | 0.6 |
| Inner radius of membrane reactor R2 (cm) | 2.8 | 3.7 | 3.8 |
| Reactor length L (m) | 9.4 | 10 | 10 |
| Osmotic zone pressure pP (kPa) | 35 | 45 | 47 |
| Entropy generation rate SG (W/K) | 23.3 | 33.2 | 44.1 |
| Thermal efficiency ηsys (%) | 44.4 | 46.8 | 47.5 |
| Energy conversion rate ηeng (%) | 49.5 | 48.5 | 51.1 |
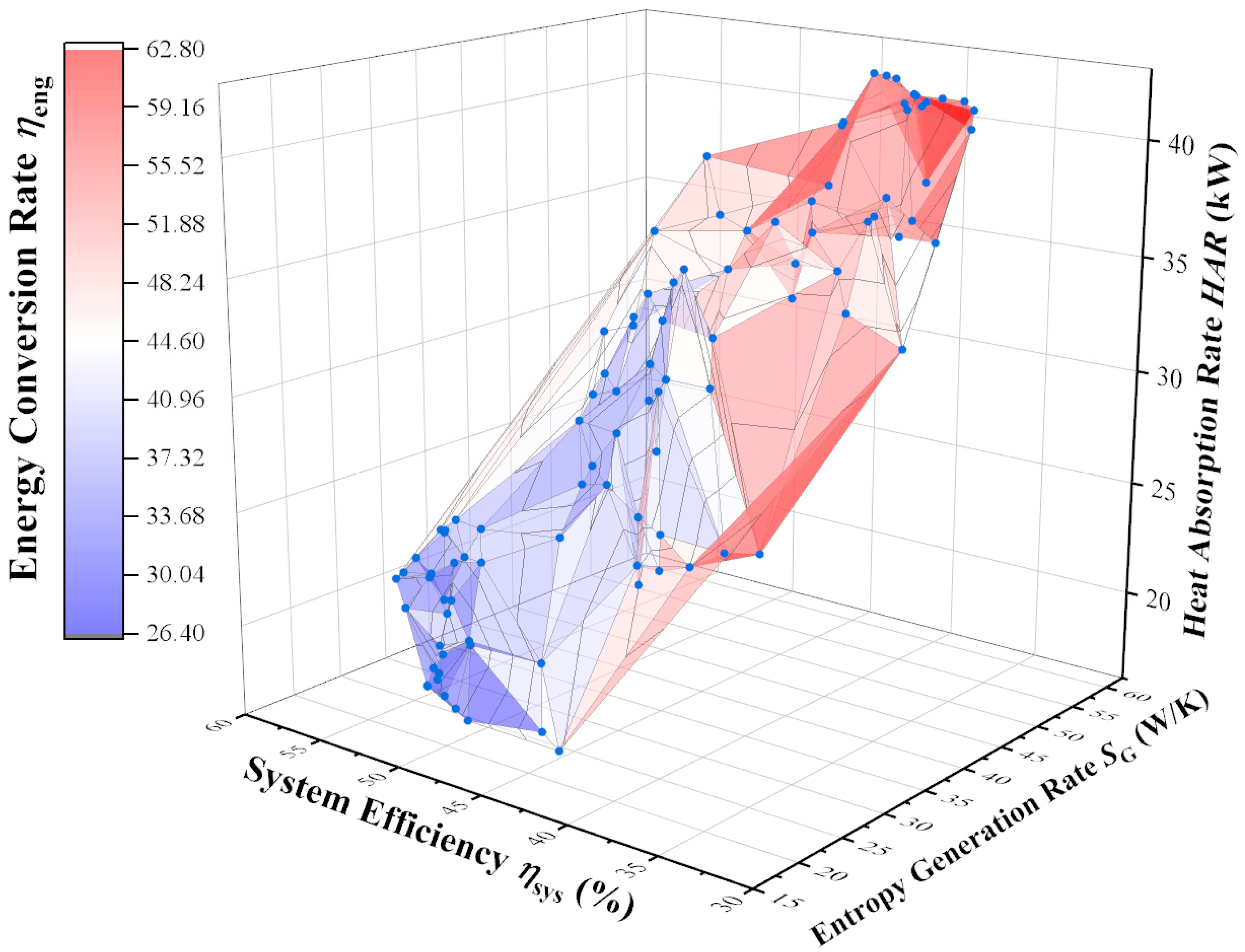
| System Parameters and Performance Indicators | Maximum HAR Point | Minimum SG,SUM Point | Maximum ηsys Point | Maximum ηeng Point | TOPSIS Decision Point |
|---|---|---|---|---|---|
| Ammonia gas preheating final temperature T1 (K) | 400 | 400 | 400 | 600 | 400 |
| Ammonia molar flow rate NA (mol/s) | 0.8 | 0.5 | 0.8 | 0.75 | 0.63 |
| Inner radius of membrane reactor R2 (cm) | 2.8 | 3.8 | 2.8 | 3.8 | 3.8 |
| Reactor length L (m) | 13 | 7 | 7 | 12.8 | 7 |
| Osmotic zone pressure pP (kPa) | 10 | 100 | 53 | 10 | 47 |
| heat absorption rate HAR (kW) | 42.4 | 17.6 | 21.2 | 40.8 | 20.7 |
| Entropy generation rate SG (W/K) | 53.1 | 19.6 | 25.3 | 51.3 | 23.9 |
| Thermal efficiency ηsys (%) | 41.4 | 48.4 | 56.2 | 35.2 | 52.1 |
| Energy conversion rate ηeng (%) | 52.4 | 34.7 | 33.3 | 62.7 | 39.6 |
| System Parameters and Performance Indicators | 600 W/m2 | 800 W/m2 | 1000 W/m2 |
|---|---|---|---|
| Ammonia gas preheating final temperature T1 (K) | 600 | 400 | 400 |
| Ammonia molar flow rate NA (mol/s) | 0.3 | 0.63 | 0.6 |
| Inner radius of membrane reactor R2 (cm) | 3.8 | 3.8 | 3.8 |
| Reactor length L (m) | 7 | 7 | 11.5 |
| Osmotic zone pressure pP (kPa) | 10 | 47 | 76 |
| heat absorption rate HAR (kW) | 16.4 | 20.7 | 39.2 |
| Entropy generation rate SG (W/K) | 19.4 | 23.9 | 43.7 |
| Thermal efficiency ηsys (%) | 33.7 | 52.1 | 48.0 |
| Energy conversion rate ηeng (%) | 62.3 | 39.6 | 46.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, T.; Xia, S.; Jin, Q. Thermodynamic Optimization of Ammonia Decomposition Solar Heat Absorption System Based on Membrane Reactor. Membranes 2022, 12, 627. https://doi.org/10.3390/membranes12060627
Xie T, Xia S, Jin Q. Thermodynamic Optimization of Ammonia Decomposition Solar Heat Absorption System Based on Membrane Reactor. Membranes. 2022; 12(6):627. https://doi.org/10.3390/membranes12060627
Chicago/Turabian StyleXie, Tianchao, Shaojun Xia, and Qinglong Jin. 2022. "Thermodynamic Optimization of Ammonia Decomposition Solar Heat Absorption System Based on Membrane Reactor" Membranes 12, no. 6: 627. https://doi.org/10.3390/membranes12060627
APA StyleXie, T., Xia, S., & Jin, Q. (2022). Thermodynamic Optimization of Ammonia Decomposition Solar Heat Absorption System Based on Membrane Reactor. Membranes, 12(6), 627. https://doi.org/10.3390/membranes12060627






