Robust Backstepping Trajectory Tracking Control of a Quadrotor with Input Saturation via Extended State Observer
Abstract
1. Introduction
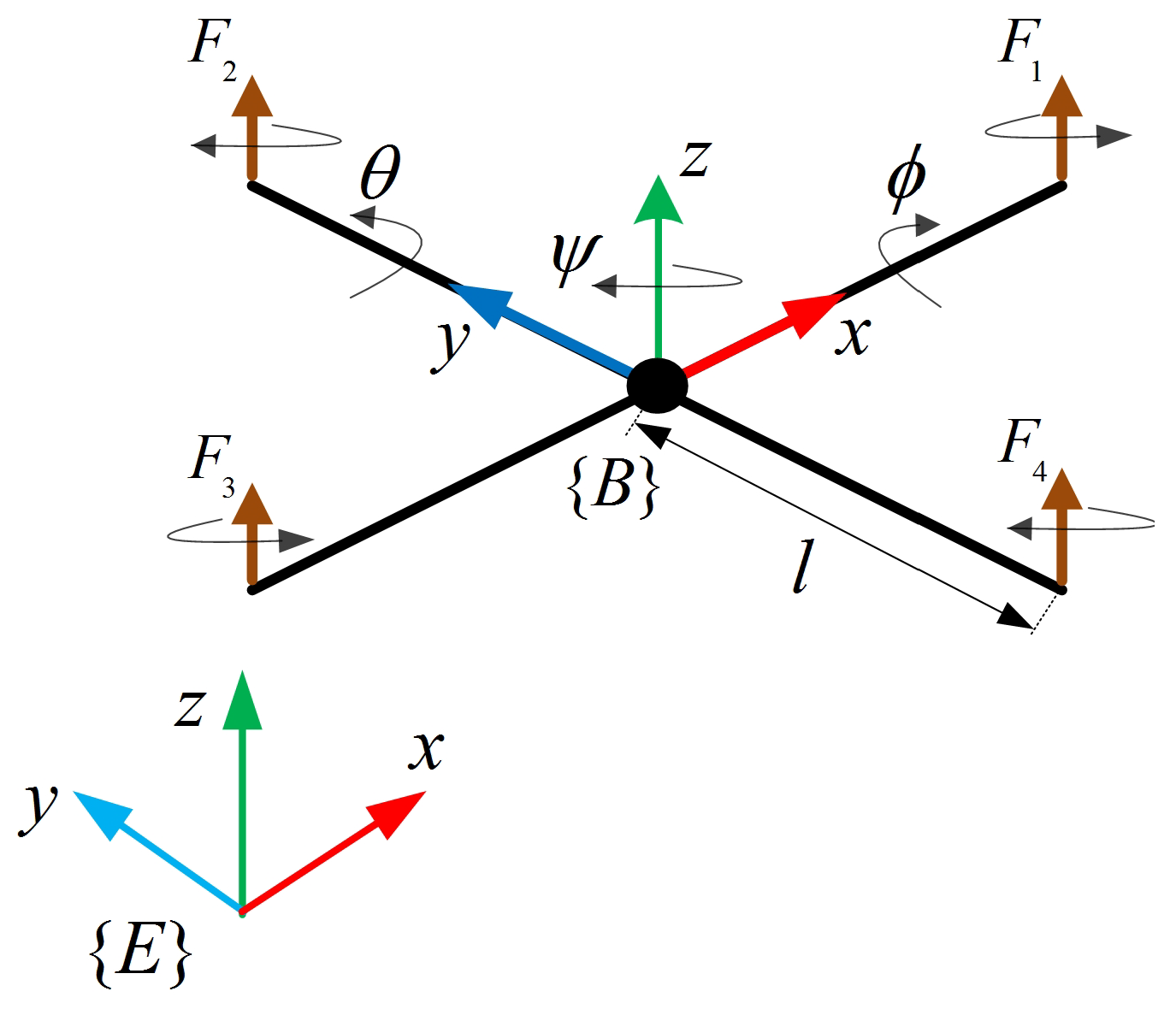
2. Quadrotor Dynamics Model and Problem Formulation
3. Extended State Observer
4. Robust Saturated Backstepping Tracking Controller Design
5. Closed-Loop System’s Stability Analysis
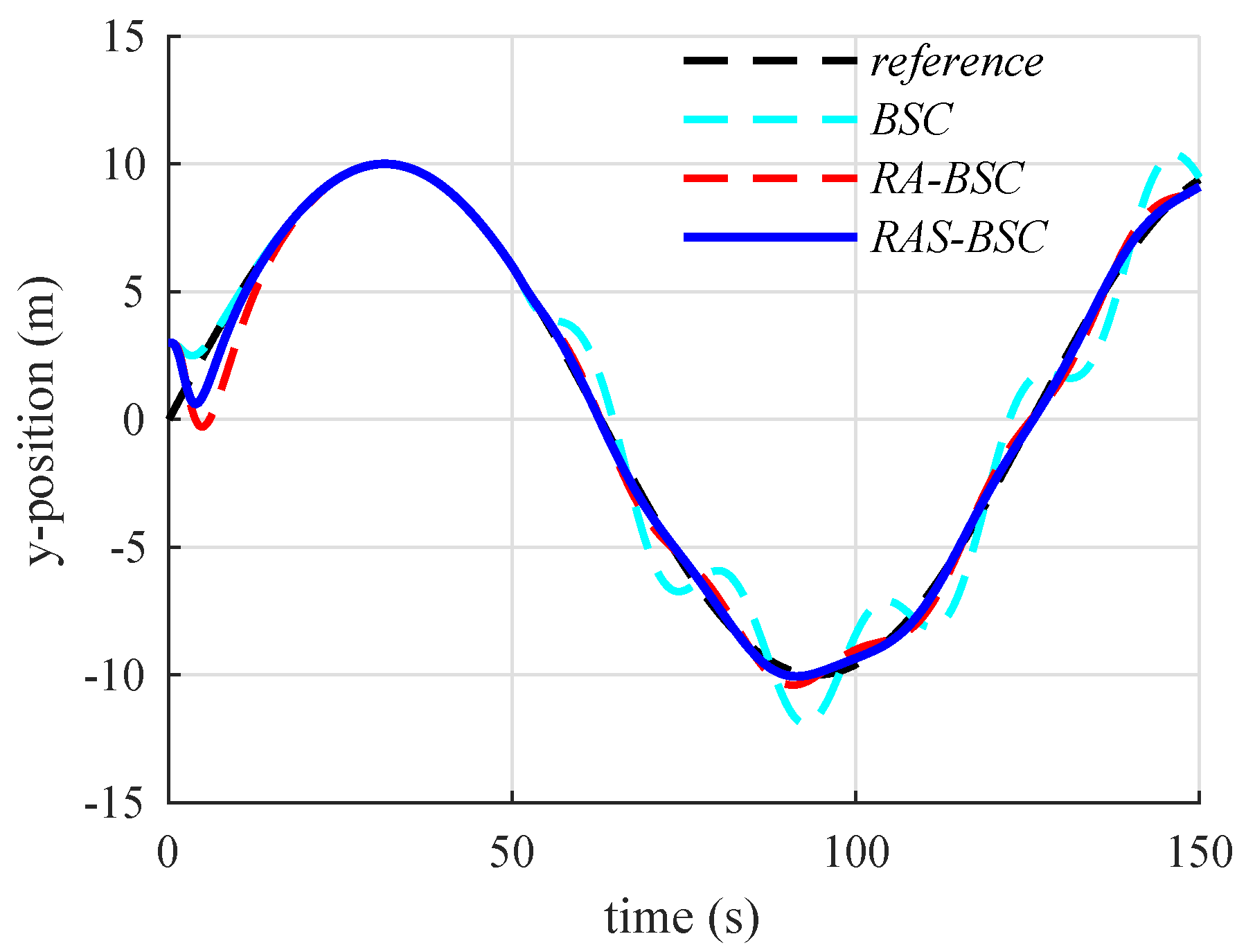
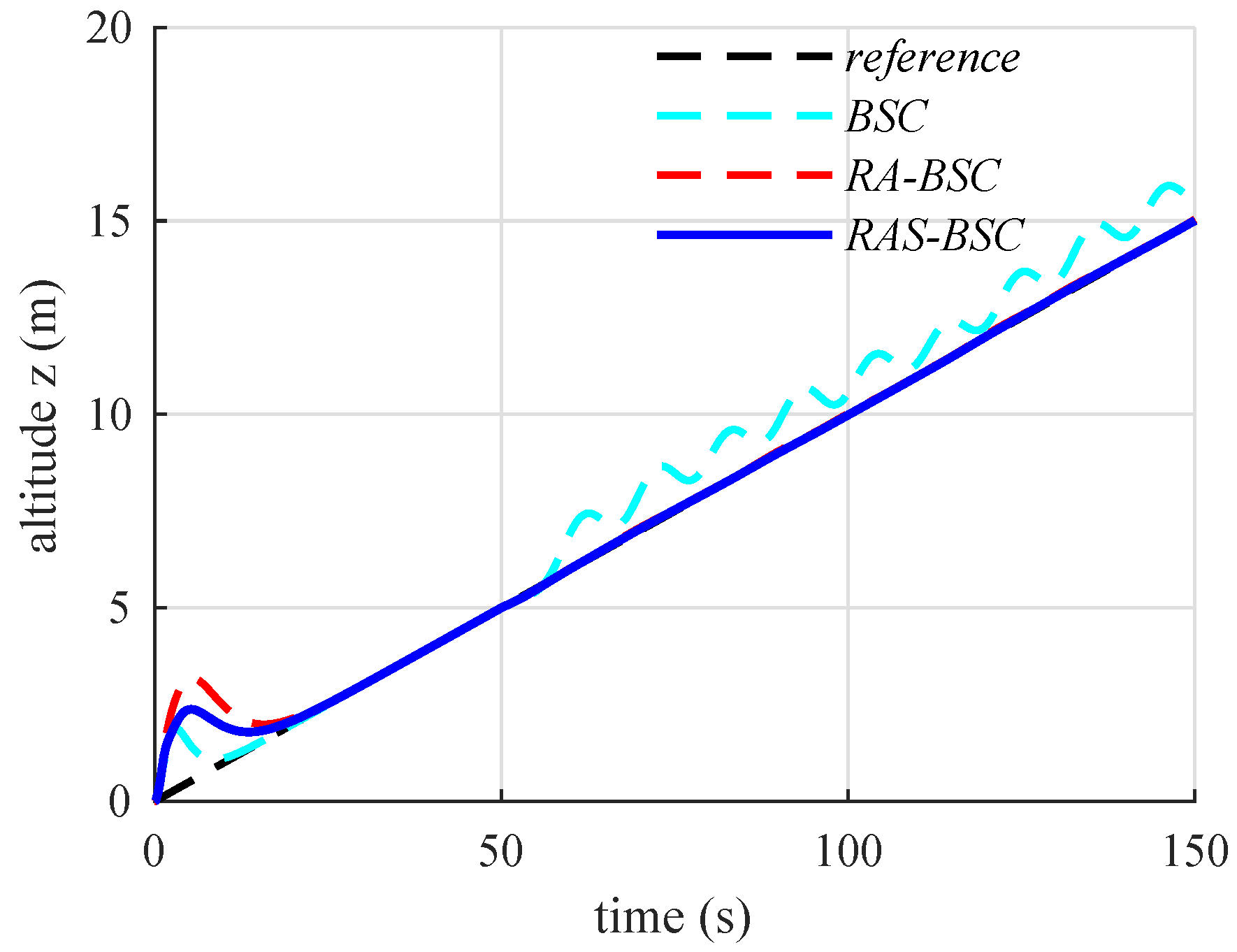
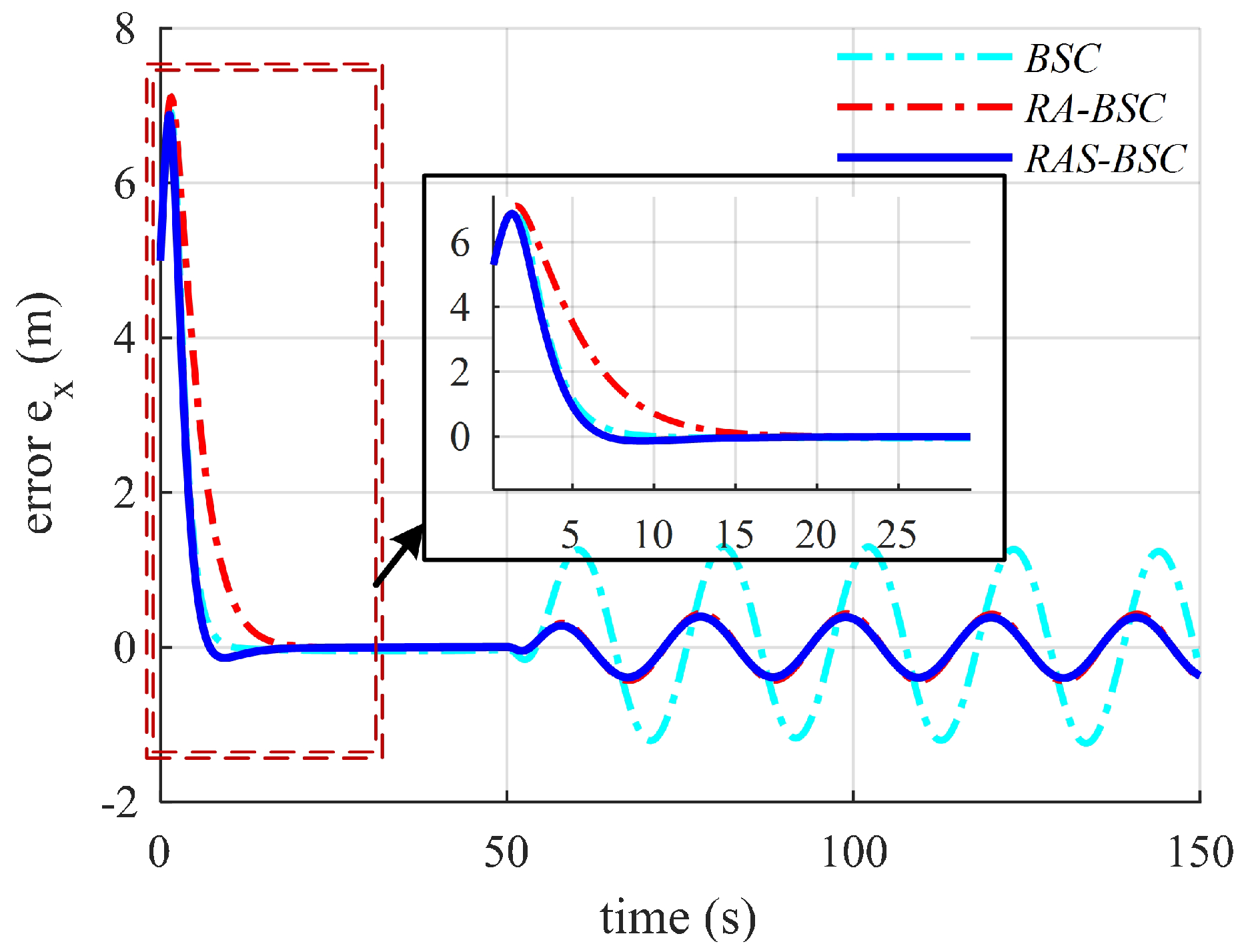
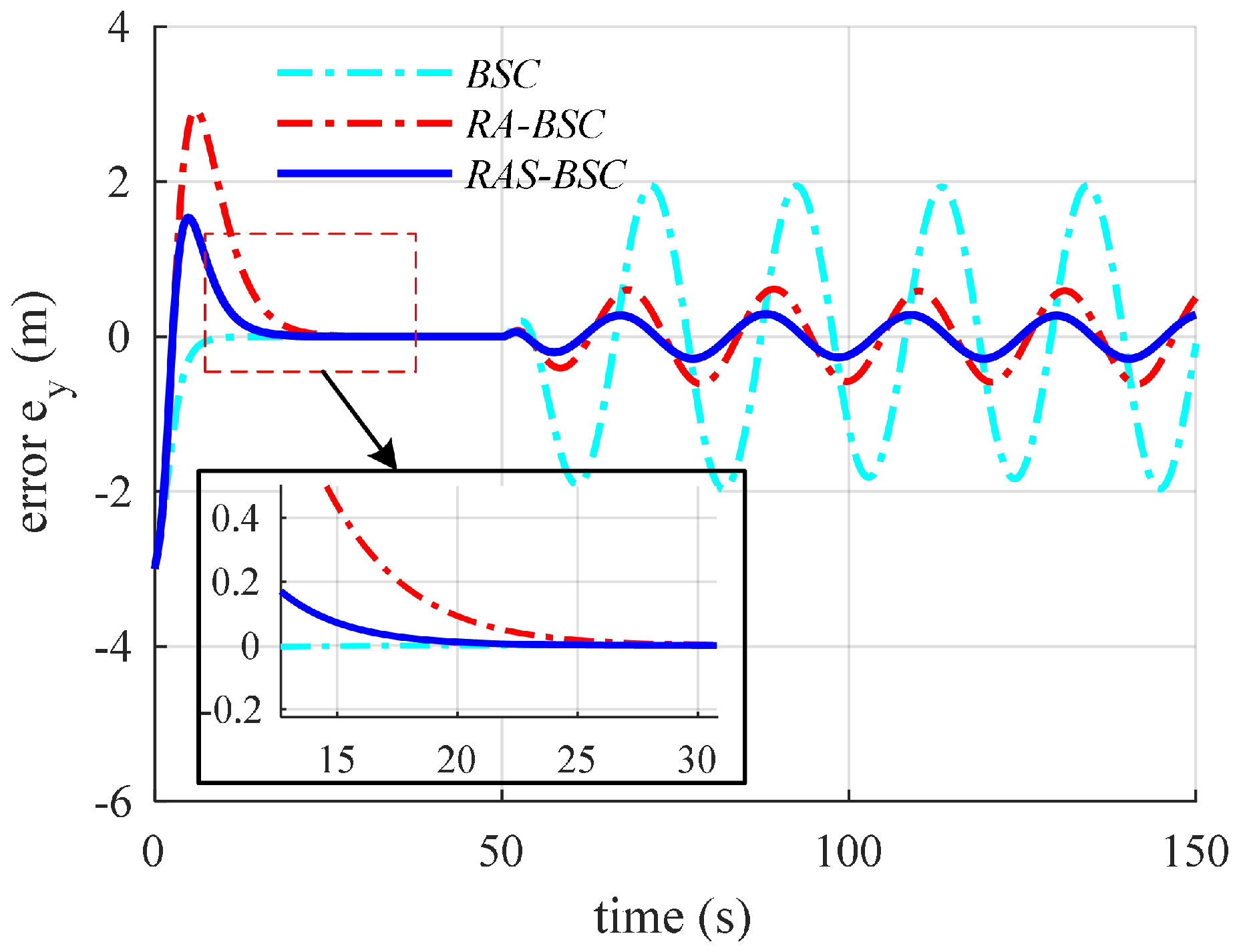
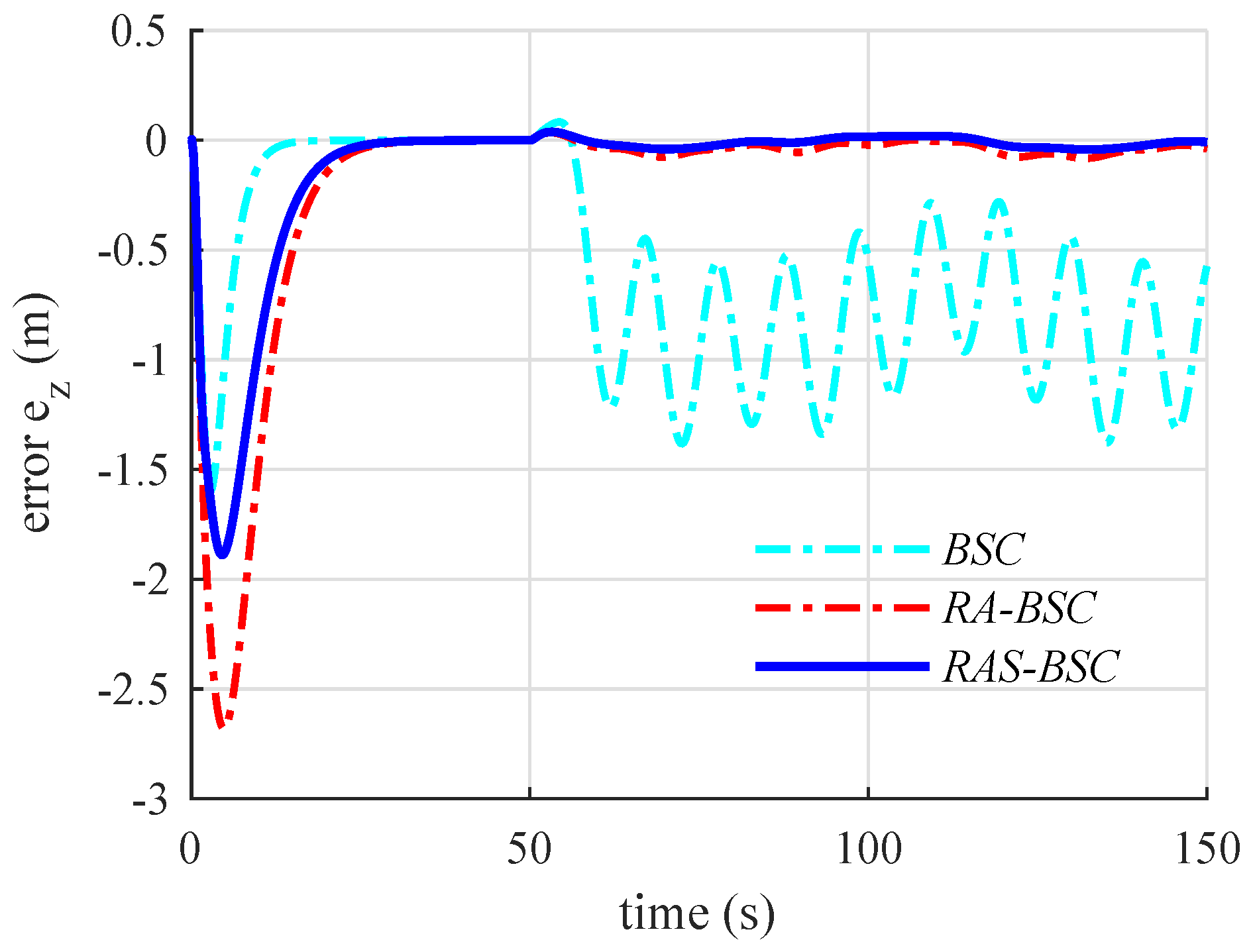
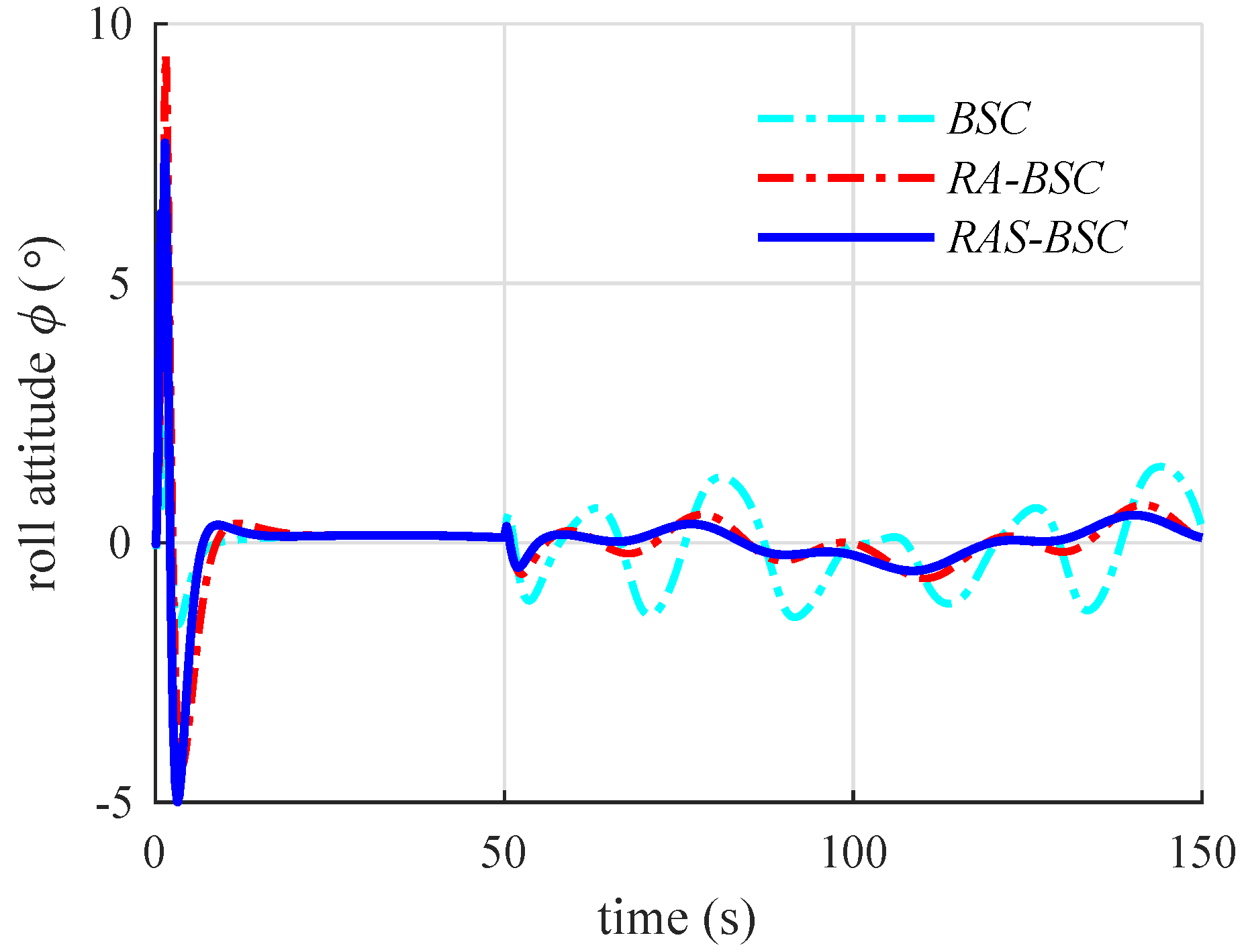
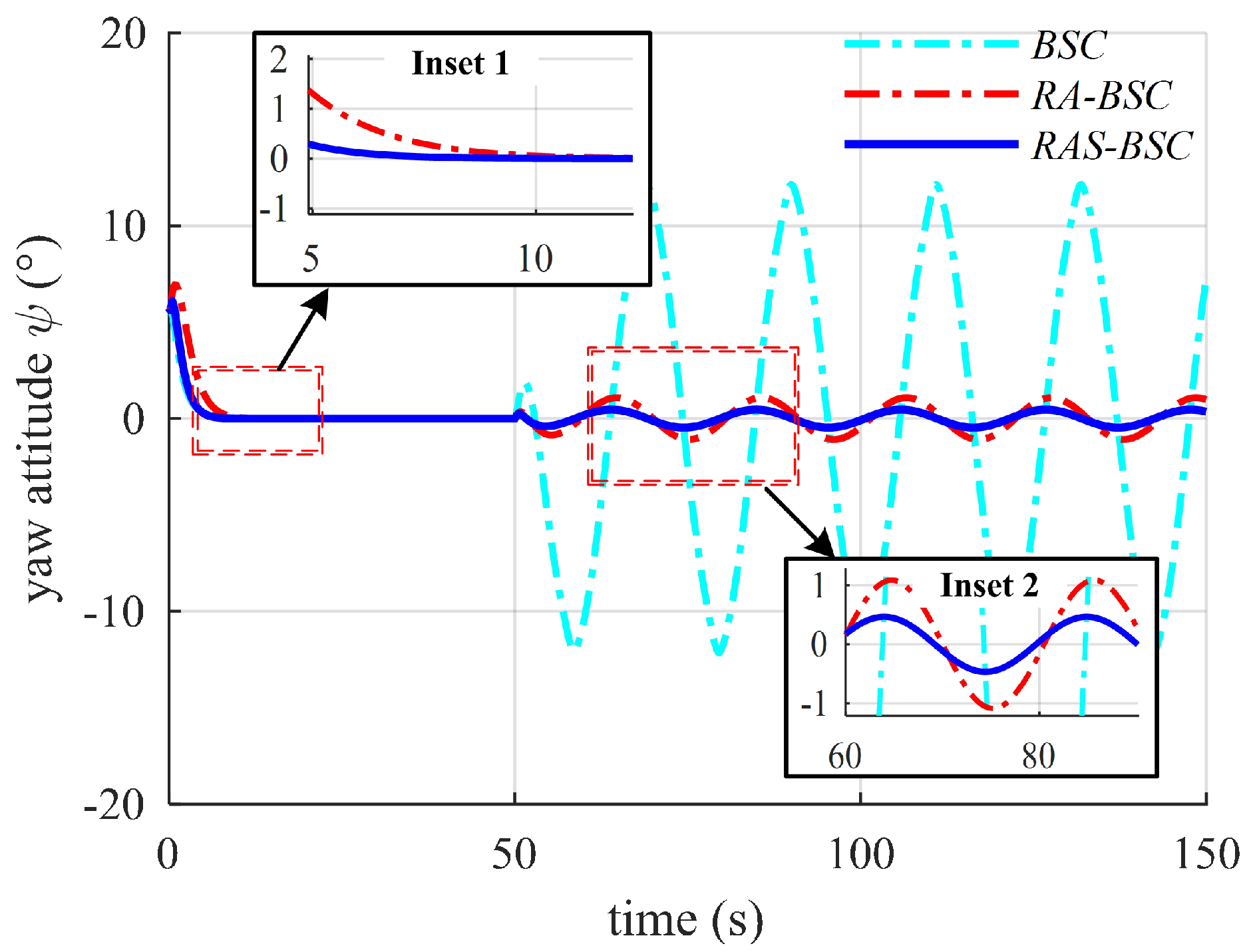
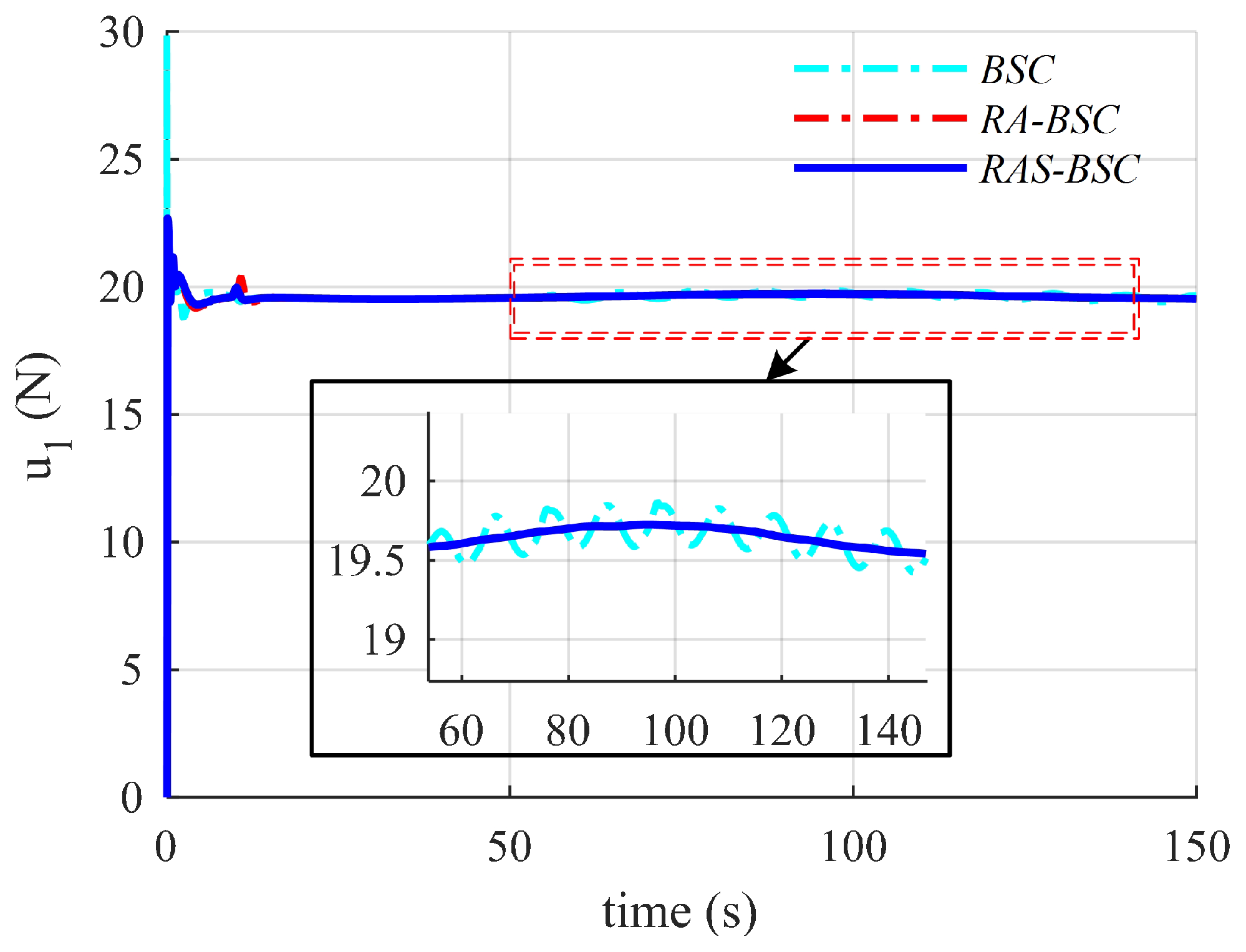
6. Numerical Simulation Results and Discussions
6.1. Simulation Assumptions
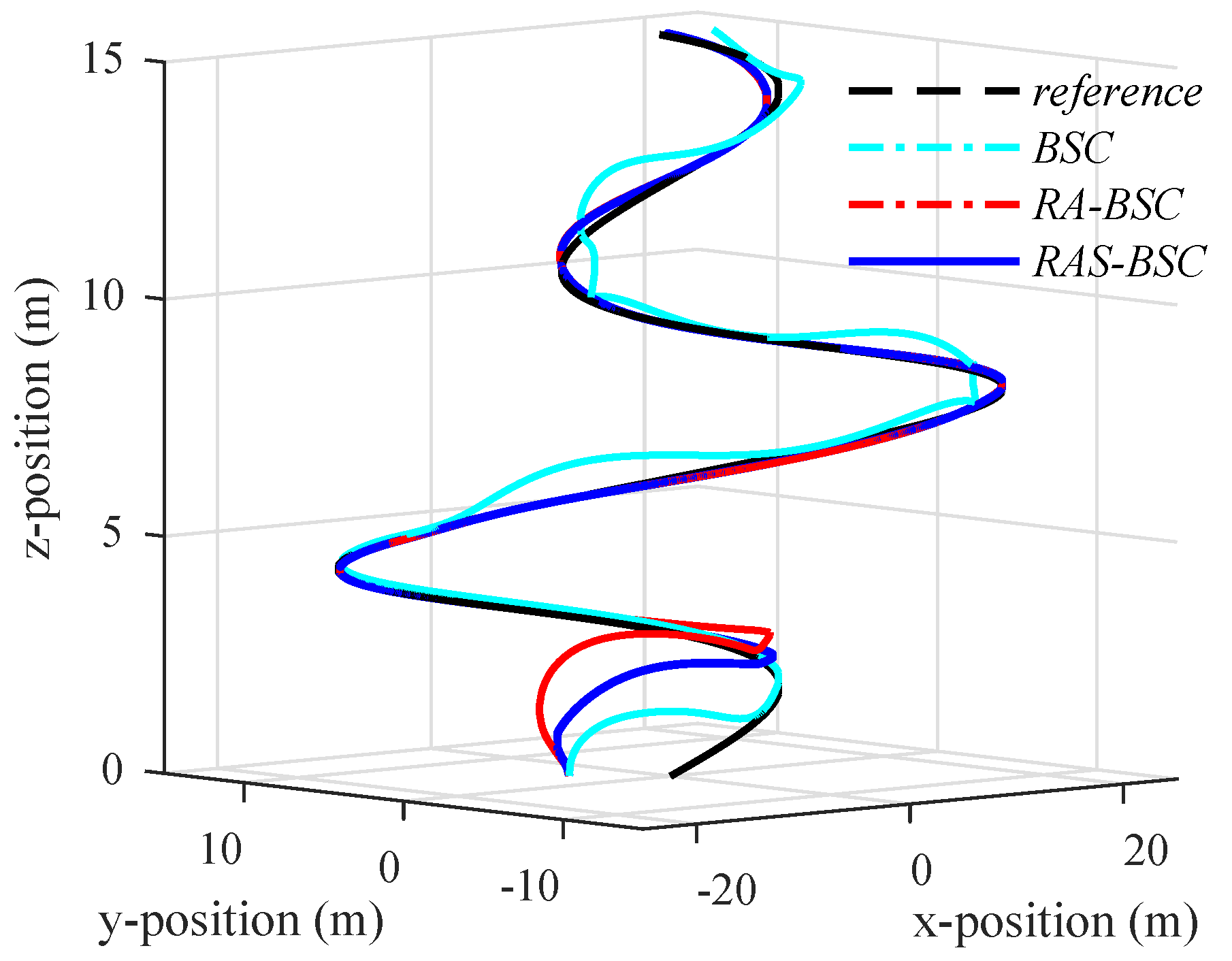
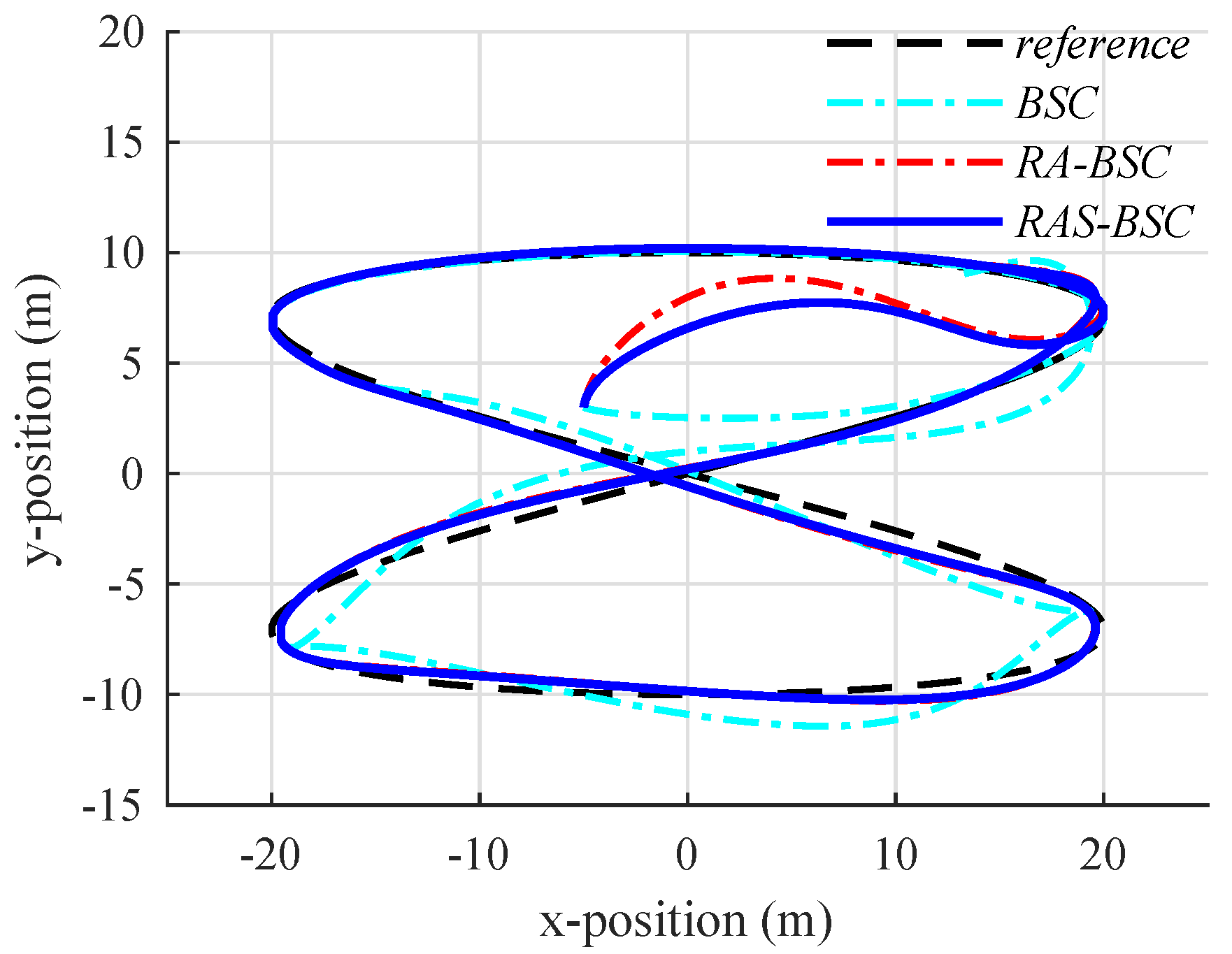
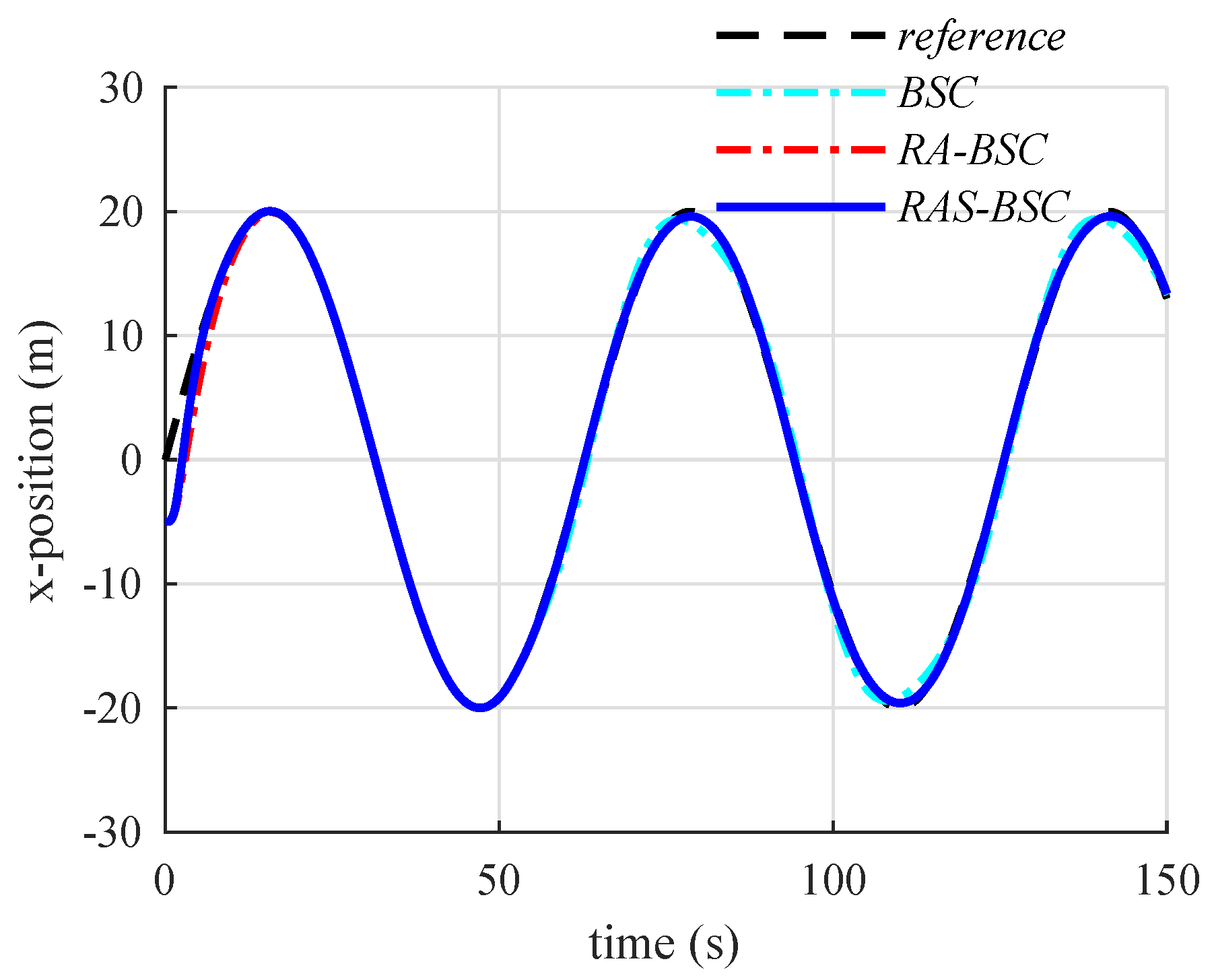
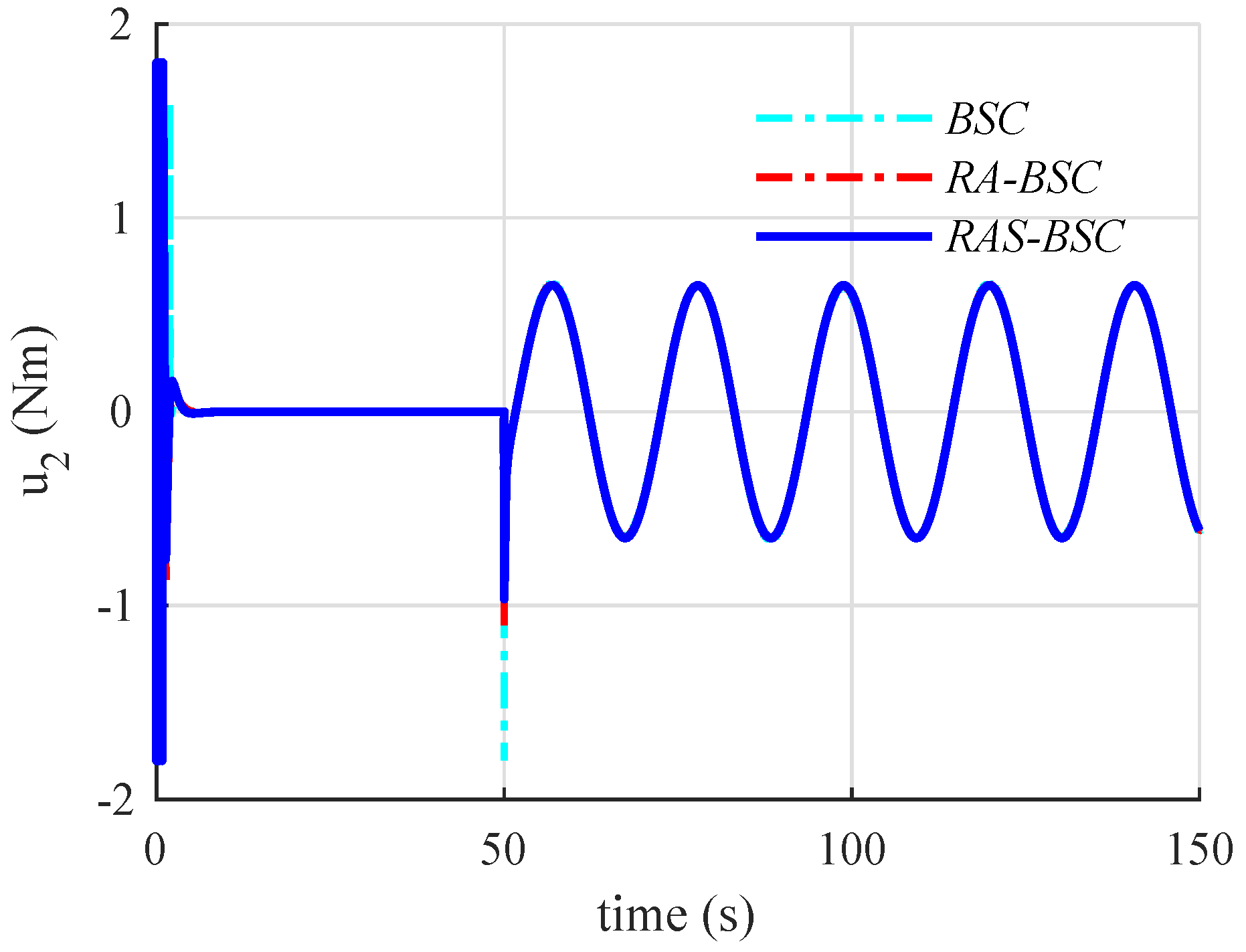
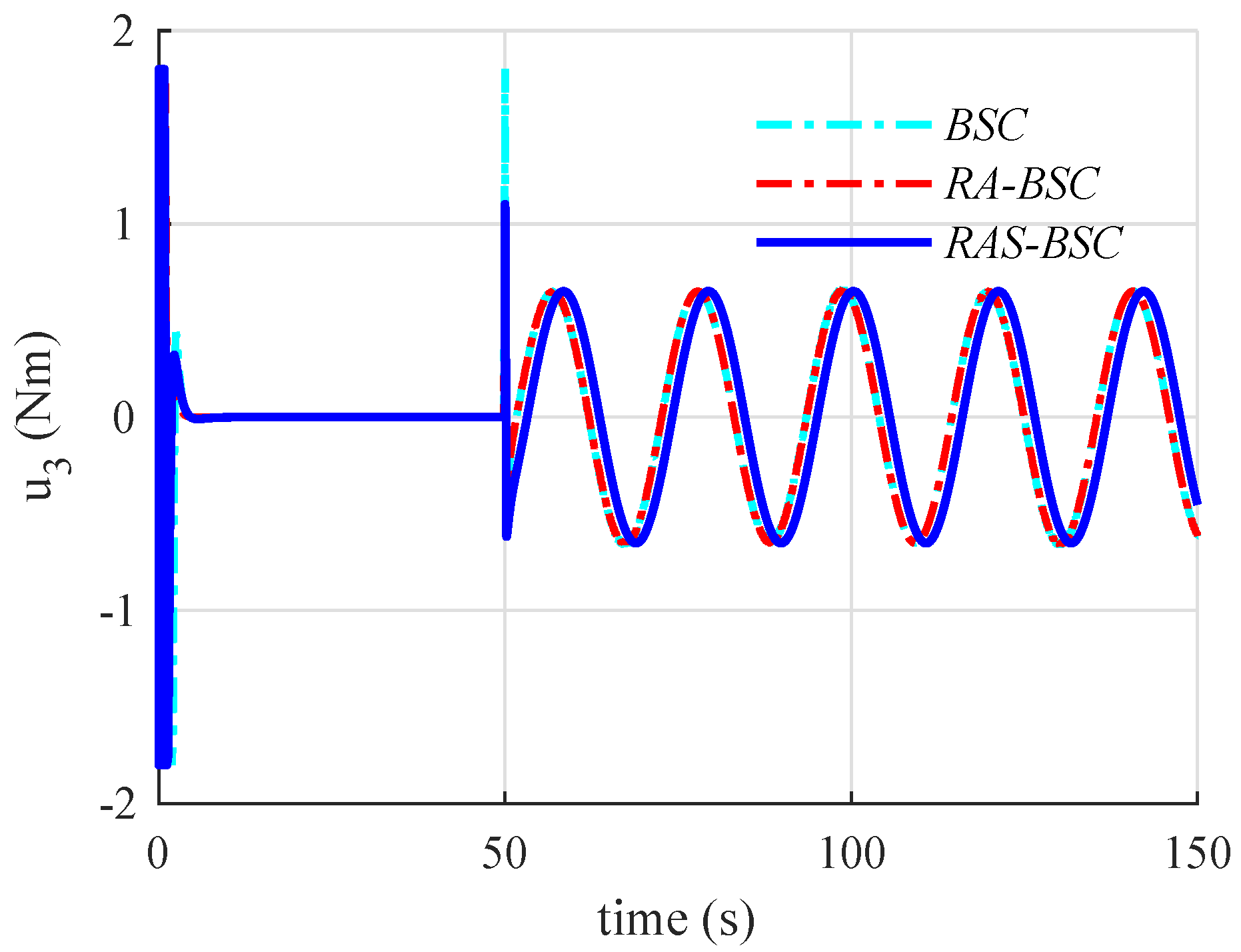
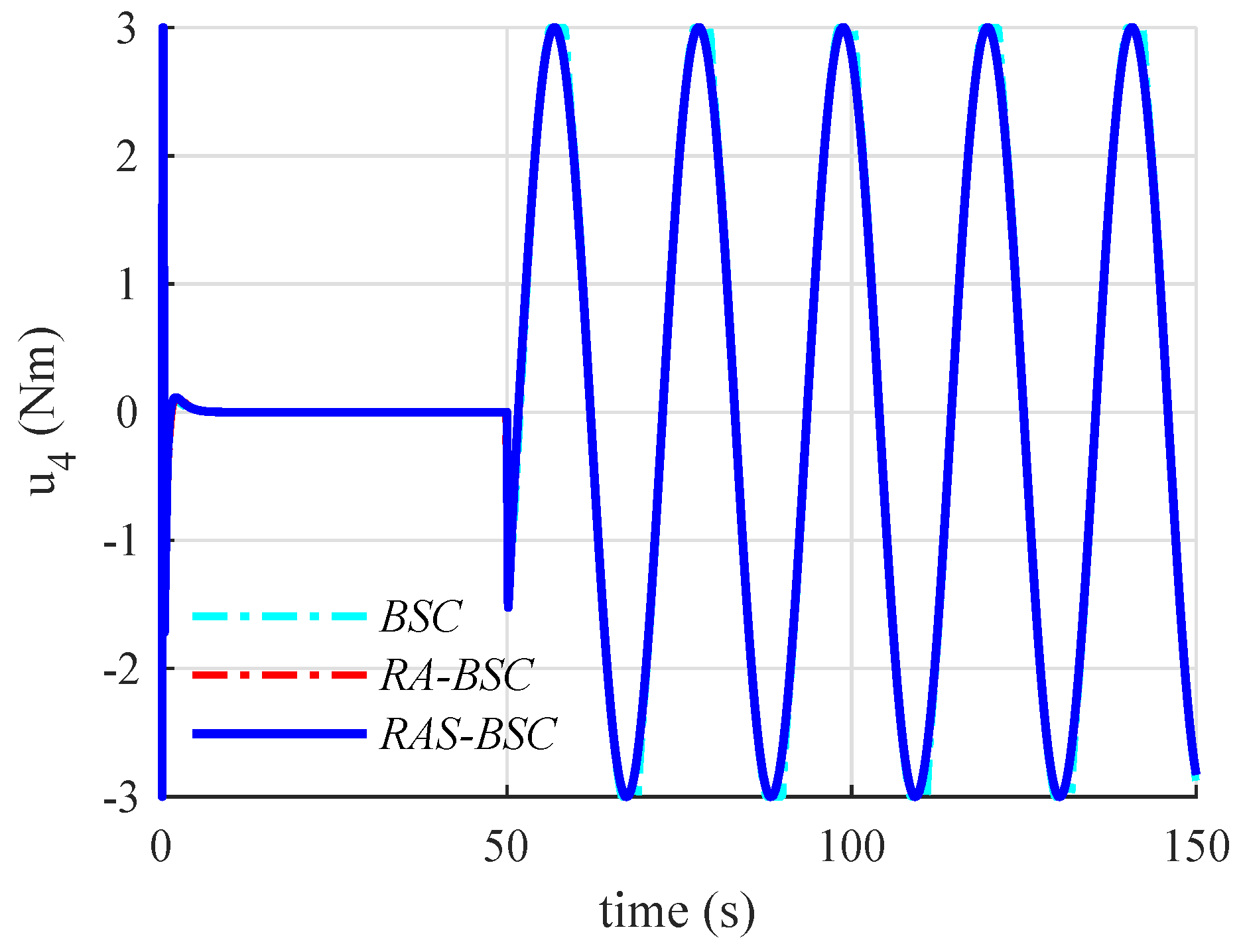
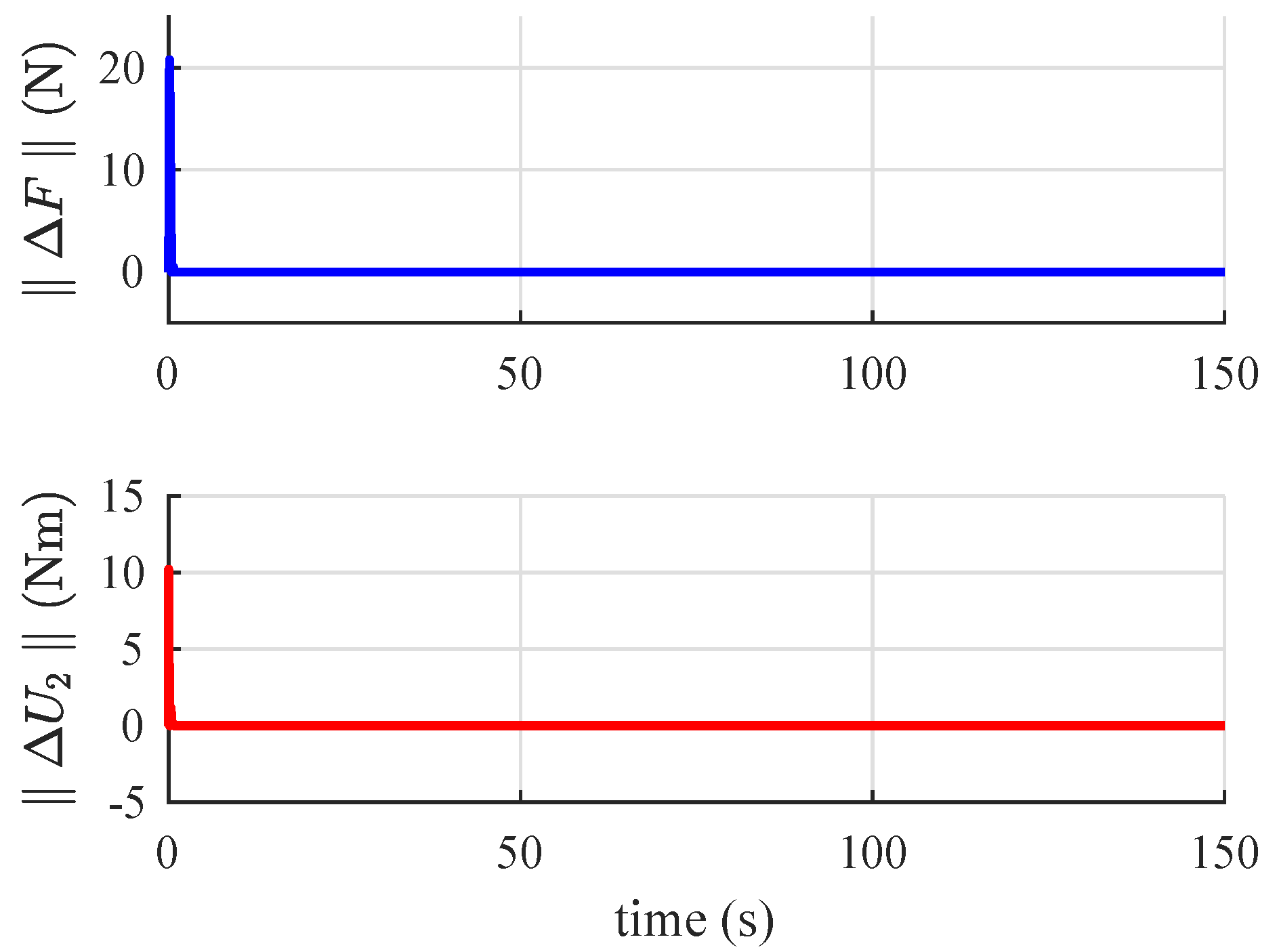
6.2. Simulation Results and Discussions
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bashi, O.I.D.; Hasan, W.Z.W.; Azis, N.; Shafie, S.; Wagatsuma, H. Unmanned aerial vehicle quadcopter: A review. J. Comput. Theor. Nanosci. 2016, 38, 529–554. [Google Scholar] [CrossRef]
- Özbek, N.S.; Önkol, M.; Efe, M.Ö. Feedback control strategies for quadrotor-type aerial robots: A survey. Trans. Inst. Meas. Control 2017, 14, 5663–5675. [Google Scholar] [CrossRef]
- Lee, H.; Kim, H.J. Trajectory tracking control of multirotors from modeling to experiments: A survey. Int. J. Control Autom. Syst. 2017, 15, 281–292. [Google Scholar] [CrossRef]
- Mung, N.X.; Hong, S.K. A Multicopter ground testbed for the evaluation of attitude and position controller. Int. J. Eng. Technol. 2018, 7, 65–73. [Google Scholar]
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-varying formation control for unmanned aerial vehicles with switching interaction topologies. Control Eng. Pract. 2016, 46, 26–36. [Google Scholar] [CrossRef]
- Thanh, H.L.N.N.; Hong, S.K. Quadcopter Robust Adaptive Second Order Sliding Mode Control Based on PID Sliding Surface. IEEE Access 2018, 6, 2169–3536. [Google Scholar]
- Kendoul, F. Nonlinear hierarchical flight controller for unmanned rotorcraft: Design, stability, and experiments. J. Guid. Control Dyn. 2009, 32, 1954–1958. [Google Scholar] [CrossRef]
- Zuo, Z.Y. Trajectory tracking control design with command-filtered compensation for a quadrotor. IET Control Theory Appl. 2010, 4, 2343–2355. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Xuan-Mung, N. Quadcopter Adaptive Trajectory Tracking Control: A New Approach via Backstepping Technique. Appl. Sci. 2019, 9, 3873. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, W.; Hong, S.; Lewis, F.L.; Yu, Y. Robust backstepping-based trajectory tracking control for quadrotors with time delays. IET Control Theory Appl. 2019, 13, 1945–1954. [Google Scholar] [CrossRef]
- Gao, H.; Chen, T. Network-based H∞ output tracking control. IEEE Trans. Autom. Control 2008, 53, 655–670. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/nonlinear H infinity control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Xiong, J.J.; Zheng, E.H. Position and attitude tracking control for a quadrotor UAV. ISA Trans. 2014, 53, 1350–1356. [Google Scholar] [CrossRef] [PubMed]
- Shah, M.Z.; Samar, R.; Bhatti, A.I. Lateral track control of UAVs using the sliding mode approach: From design to flight testing. Trans. Inst. Meas. Control 2015, 37, 457–474. [Google Scholar] [CrossRef]
- Li, Z.; Deng, J.; Lu, R.; Xu, Y.; Bai, J.; Su, C.Y. Trajectory-tracking control of mobile robot systems incorporating neural-dynamic optimized model predictive approach. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 740–749. [Google Scholar] [CrossRef]
- Nascimento, T.P.; Saska, M. Position and attitude control of multi-rotor aerial vehicles: A survey. Annu. Rev. Control 2019, 48, 129–146. [Google Scholar] [CrossRef]
- Tahir, A.; Böling, J.; Haghbayan, M.H.; Toivonen, H.T.; Plosila, J. Swarms of Unmanned Aerial Vehicles—A Survey. IEEE J. Ind. Inf. Integr. 2019, 16, 100106. [Google Scholar] [CrossRef]
- Carrillo, L.R.G.; Vamvoudakis, K.G. Deep-Learning Tracking for Autonomous Flying Systems Under Adversarial Inputs. In IEEE Transactions on Aerospace and Electronic Systems; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Jafari, M.; Xu, H.; Carrillo, L.R.G. A neurobiologically-inspired intelligent trajectory tracking control for unmanned aircraft systems with uncertain system dynamics and disturbance. Trans. Inst. Meas. Control 2019, 41, 417–432. [Google Scholar] [CrossRef]
- Jafari, M.; Xu, H. Intelligent control for unmanned aerial systems with system uncertainties and disturbances using artificial neural network. Drones 2018, 2, 30. [Google Scholar]
- Wang, N.; Su, S.F.; Han, M.; Chen, W.H. Backpropagating constraints-based trajectory tracking control of a quadrotor with constrained actuator dynamics and complex unknowns. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 49, 1322–1337. [Google Scholar] [CrossRef]
- Chen, F.; Lei, W.; Zhang, K.; Tao, G.; Jang, B. A novel nonlinear resilient control for a quadrotor UAV via backstepping control and nonlinear disturbance observer. Nonlinear Dyn. 2016, 85, 1281–1295. [Google Scholar] [CrossRef]
- Yacef, F.; Bouhail, O.; Hamerlain, M.; Rizoug, N. Observer-based adaptive fuzzy backstepping tracking control of quadrotor unmanned aerial vehicle powered by li-ion battery. J. Intell. Robot. Syst. 2016, 84, 179–197. [Google Scholar] [CrossRef]
- Fang, X.; Wu, A.G.; Shang, Y.J.; Dong, N. A novel sliding mode controller for small-scale unmanned helicopters with mismatched disturbance. Nonlinear Dyn. 2016, 83, 1053–1068. [Google Scholar] [CrossRef]
- Yacef, F.; Bouhail, O.; Hamerlain, M.; Rizoug, N. Adaptive RBFNN/integral sliding mode control for a quadrotor aircraft. Neurocomputing 2016, 216, 126–134. [Google Scholar]
- Ahmed, N.; Chen, M. Sliding mode control for quadrotor with disturbance observer. Adv. Mech. Eng. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Rodr-guez-Mata, A.E.; Flores, G.; Mart-nez-Vásquez, A.H.; Mora-Felix, Z.D.; Castro-Linares, R.; Amabilis-Sosa, L.E. Discontinuous High-Gain Observer in a Robust Control UAV Quadrotor: Real-Time Application for Watershed Monitoring. Math. Probl. Eng. 2018, 2018, 4940360. [Google Scholar]
- Chen, M.; Xiong, S.; Wu, Q. Tracking Flight Control of Quadrotor Based on Disturbance Observer. In IEEE Transactions on Systems, Man, and Cybernetics: Systems; IEEE: Piscataway, NJ, USA, 2019; pp. 2168–2216. [Google Scholar]
- Shao, X.; Liu, J.; Cao, H.; Shen, C.; Wang, H. Robust dynamic surface trajectory tracking control for a quadrotor UAV via extended state observer. Int. J. Robust Nonlinear Control 2018, 28, 2700–2719. [Google Scholar] [CrossRef]
- Liu, H.; Li, D.; Yu, Y.; Zhong, Y. Robust trajectory tracking control of uncertain quadrotors without linear velocity measurements. IET Control Theory Appl. 2015, 9, 1746–1754. [Google Scholar] [CrossRef]
- Ma, D.; Xia, Y.; Li, T.; Chang, K. Active disturbance rejection and predictive control strategy for a quadrotor helicopter. IET Control Theory Appl. 2016, 10, 2213–2222. [Google Scholar] [CrossRef]
- Zou, Y. Trajectory tracking controller for quadrotors without velocity and angular velocity measurements. IET Control Theory Appl. 2017, 11, 101–109. [Google Scholar] [CrossRef]
- Tian, B.; Lu, H.; Zuo, Z.; Zong, Q.; Zhang, Y. Multivariable finite-time output feedback trajectory tracking control of quadrotor helicopters. Int. J. Robust Nonlinear Control 2017, 28, 281–295. [Google Scholar] [CrossRef]
- Shao, X.; Liu, J.; Wang, H. Robust backstepping output feedback trajectory tracking for quadrotors via extended state observer and sigmoid tracking differentiator. Mech. Syst. Signal Process. 2018, 104, 631–647. [Google Scholar] [CrossRef]
- He, M.; He, J. Extended State Observer-Based Robust Backstepping Sliding Mode Control for a Small-Size Helicopter. IEEE Access 2018, 6, 33480–33488. [Google Scholar] [CrossRef]
- Zarovy, S.; Costello, M. Extended state observer for helicopter mass and center-of-gravity estimation. J. Aircr. 2015, 52, 1939–1949. [Google Scholar] [CrossRef]
- Koria, D.K.; Kolhe, J.P.; Talole, S.E. Extended state observer based robust control of wing rock motion. Aerosp. Sci. Technol. 2014, 33, 107–117. [Google Scholar] [CrossRef]
- Wang, Q.; Ran, M.; Dong, C. Robust partial integrated guidance and control for missiles via extended state observer. ISA Trans. 2016, 65, 27–36. [Google Scholar] [CrossRef]
- Shao, X.; Wang, H. Back-stepping active disturbance rejection control design for integrated missile guidance and control system via reduced-order ESO. ISA Trans. 2015, 57, 10–22. [Google Scholar]
- Wei, Q.; Chen, M.; Wu, Q. Backstepping-based attitude control for a quadrotor UAV with input saturation and attitude constraints. Control Theory Appl. 2018, 10, 1361–1369. [Google Scholar]
- Cao, N.; Lynch, A.F. Inner—Outer Loop Control for Quadrotor UAVs With Input and State Constraints. IEEE Trans. Control Syst. Technol. 2016, 24, 1797–1804. [Google Scholar] [CrossRef]
- Faessler, M.; Falanga, D.; Scaramuzza, D. Thrust Mixing, Saturation, and Body-Rate Control for Accurate Aggressive Quadrotor Flight. IEEE Robot. Autom. Lett. 2017, 2, 476–482. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Tan, J. Adaptive and robust control of quadrotor aircrafts with input saturation. Nonlinear Dyn. 2017, 89, 255–265. [Google Scholar] [CrossRef]
- Jiang, T.; Lin, D.; Song, T. Finite-Time Backstepping Control for Quadrotors With Disturbances and Input Constraints. IEEE Access 2018, 6, 62037–62049. [Google Scholar] [CrossRef]
- Wang, X.; Su, X.; Sun, L. Disturbance observer-based singularity-free trajectory tracking control of uncertain quadrotors with input saturation. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 5780–5785. [Google Scholar]
- Huang, Y.; Zheng, Z.; Sun, L.; Zhu, M. Saturated adaptive sliding mode control for autonomous vessel landing of a quadrotor. IET Control Theory Appl. 2018, 12, 1830–1842. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, W.; Gong, X.; Wu, J. Simplified Attitude Determination Algorithm Using Accelerometer and Magnetometer with Extremely Low Execution Time. J. Sens. 2018, 2018, 8787236. [Google Scholar] [CrossRef]
- Celis, R.; Cadarso, L. Attitude Determination Algorithms through Accelerometers, GNSS Sensors, and Gravity Vector Estimator. Int. J. Aerosp. Eng. 2018, 2018, 5394057. [Google Scholar] [CrossRef]
- Tan, C.K.; Wang, J.; Paw, Y.C.; Ng, T.Y. Tracking of a moving ground target by a quadrotor using a backstepping approach based on a full state cascaded dynamics. Appl. Soft Comput. 2017, 47, 47–62. [Google Scholar] [CrossRef]
- Mung, N.X.; Hong, S.K. Improved Altitude Control Algorithm for Quadcopter Unmanned Aerial Vehicles. Appl. Sci. 2019, 9, 2122. [Google Scholar] [CrossRef]
- Mung, N.X.; Hong, S.K. Robust Adaptive Formation Control of Quadcopters based on a Leader-Follower Approach. Int. J. Adv. Robot. Syst. 2019, 16. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. Back-stepping control of electro-hydraulic system based on Extended-state-observer with plant dynamics largely unknown. IEEE Trans. Ind. Electron. 2016, 63, 6909–6920. [Google Scholar] [CrossRef]
- Song, B.; Hedrick, J.K. Dynamic Surface Control of Uncertain Nonlinear System; Springer-Verlag London Limited: London, UK, 2011; pp. 19–55. [Google Scholar]
- Flame Wheel ARF Kit. Available online: https://www.dji.com/kr/flame-wheel-arf/spec (accessed on 1 October 2019).
- DJI E305. Available online: http://www.dji.com/product/e305 (accessed on 1 October 2019).

| Symbol | Value | Unit |
|---|---|---|
| m | kg | |
| kg·m | ||
| kg·m | ||
| kg·m | ||
| l | m | |
| g | m/s | |
| diag | ||
| diag | ||
| 30 | N | |
| 1.8 | Nm | |
| 1.8 | Nm | |
| 3 | Nm |
| Symbol | Value and Unit | Description |
|---|---|---|
| [20sin( t), 10sin( t), t] m | Trajectory reference | |
| Desired heading angle | ||
| m | Initial position | |
| m/s | Initial velocity | |
| Initial attitude | ||
| /s | Initial angular velocity | |
| ESO’s bandwidth | ||
| diag[] | Controller gains | |
| diag[] | Controller gains | |
| diag[] | Controller gains | |
| diag[] | Controller gains | |
| diag[] | Controller gains | |
| diag[] | Controller gains | |
| 1 | Controller gains | |
| 0.01 | LPF’s parameters |
| Controller | x-Position | y-Position | z-Position | Heading Angle |
|---|---|---|---|---|
| BSC | 9 s | 14 s | 23 s | 6 s |
| RA-BSC | 15 s | 24 s | 35 s | 9 s |
| RAS-BSC | 9 s | 19 s | 28 s | 6 s |
| Controller | x-Position | y-Position | z-Position | Heading Angle |
|---|---|---|---|---|
| BSC | m | m | m | |
| RA-BSC | m | m | m | |
| RAS-BSC | m | m | m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xuan-Mung, N.; Hong, S.K. Robust Backstepping Trajectory Tracking Control of a Quadrotor with Input Saturation via Extended State Observer. Appl. Sci. 2019, 9, 5184. https://doi.org/10.3390/app9235184
Xuan-Mung N, Hong SK. Robust Backstepping Trajectory Tracking Control of a Quadrotor with Input Saturation via Extended State Observer. Applied Sciences. 2019; 9(23):5184. https://doi.org/10.3390/app9235184
Chicago/Turabian StyleXuan-Mung, Nguyen, and Sung Kyung Hong. 2019. "Robust Backstepping Trajectory Tracking Control of a Quadrotor with Input Saturation via Extended State Observer" Applied Sciences 9, no. 23: 5184. https://doi.org/10.3390/app9235184
APA StyleXuan-Mung, N., & Hong, S. K. (2019). Robust Backstepping Trajectory Tracking Control of a Quadrotor with Input Saturation via Extended State Observer. Applied Sciences, 9(23), 5184. https://doi.org/10.3390/app9235184






