Mechanical Behavior of a Double-Column Self-Centering Pier Fused with Shear Links
Abstract
:Featured Application
Abstract
1. Introduction
2. FE Model and Validation
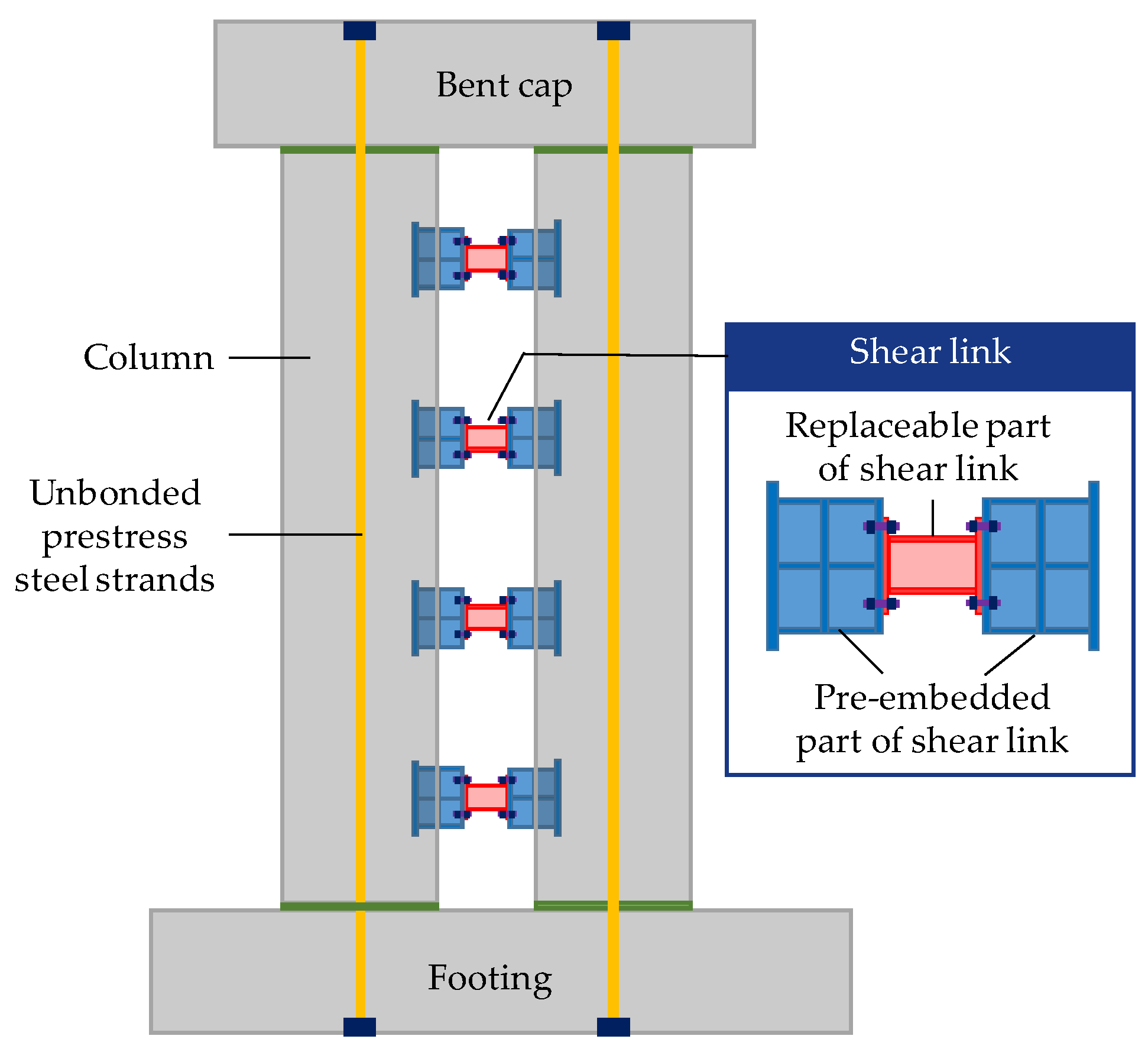
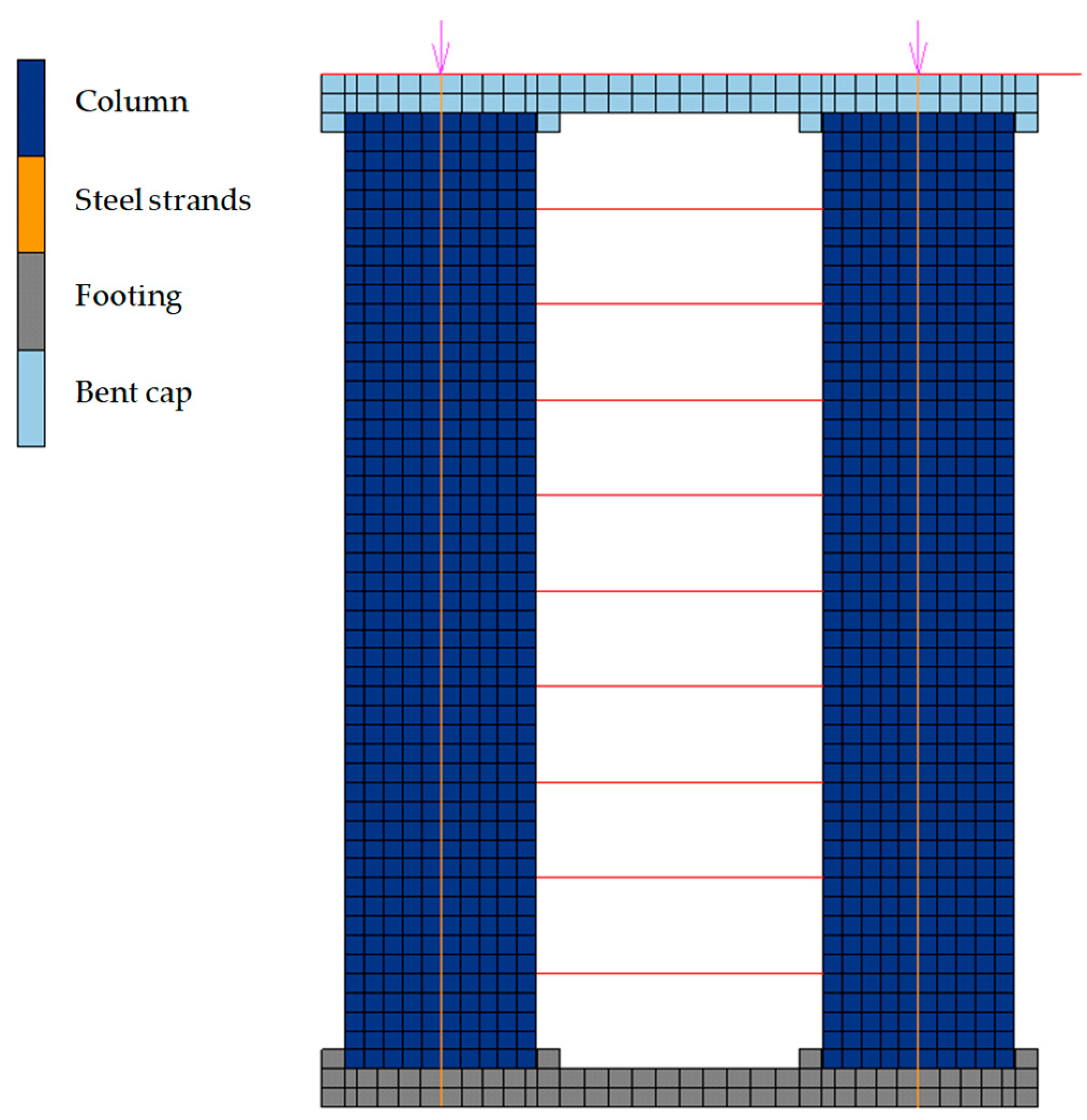
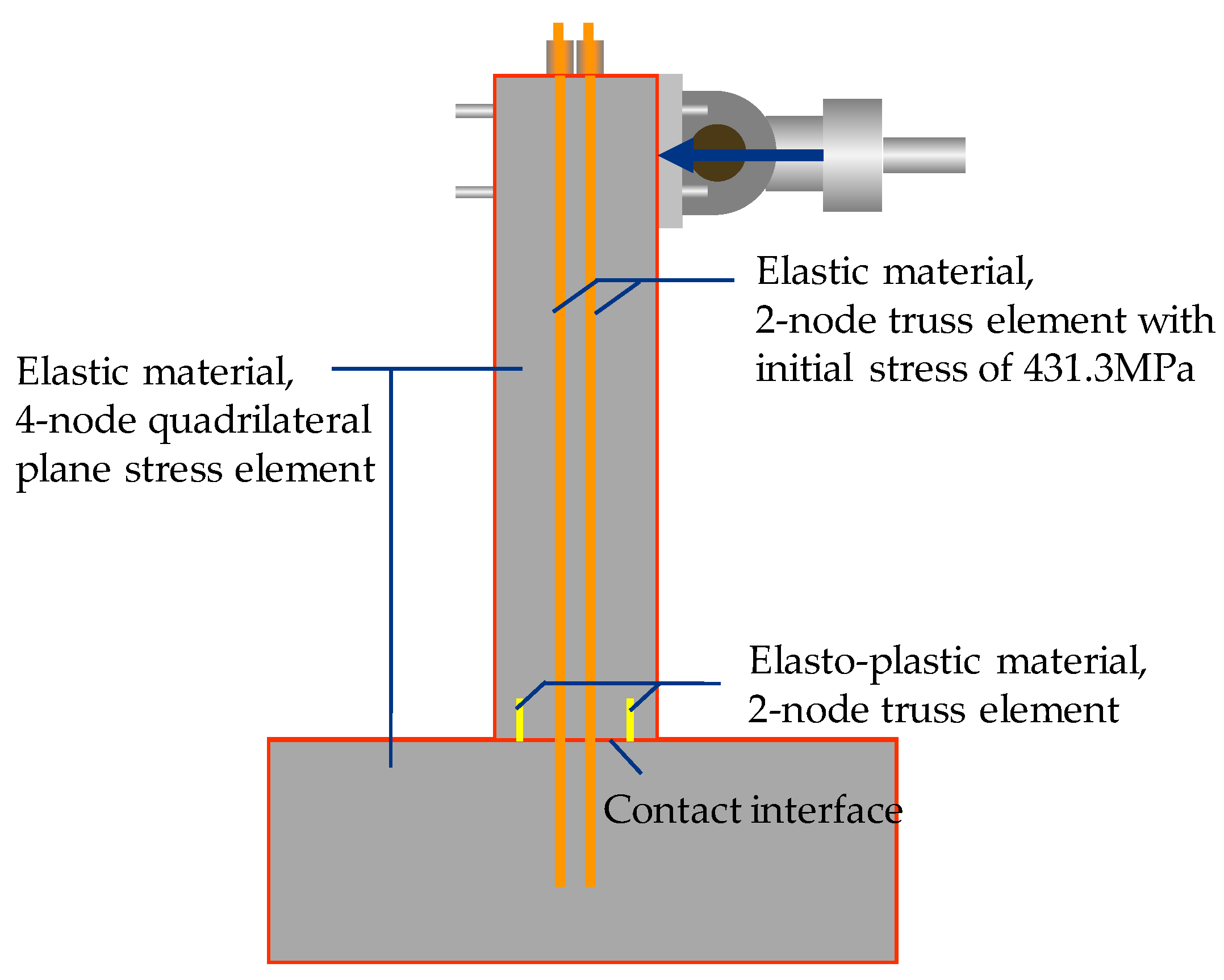
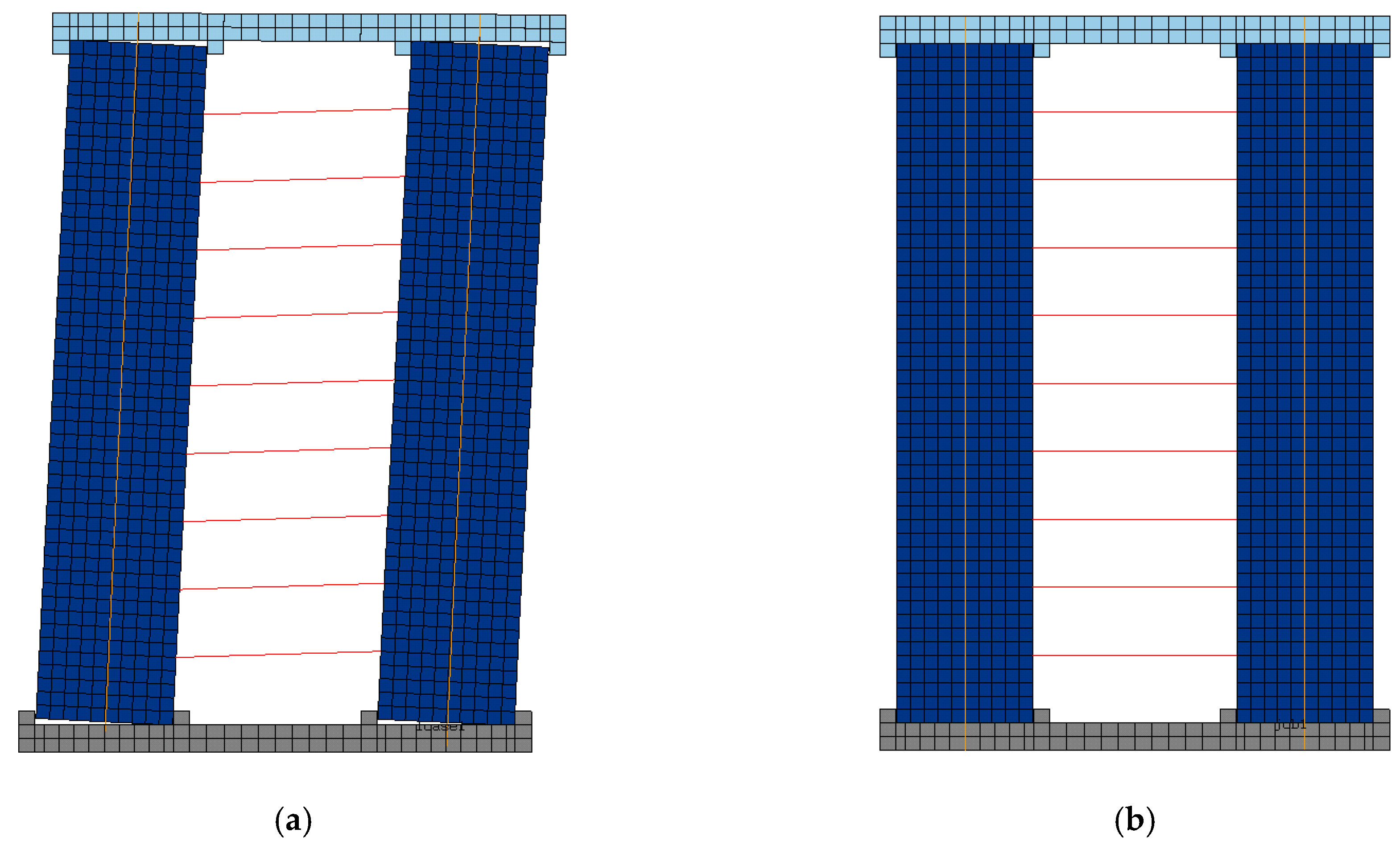
2.1. Modeling Method
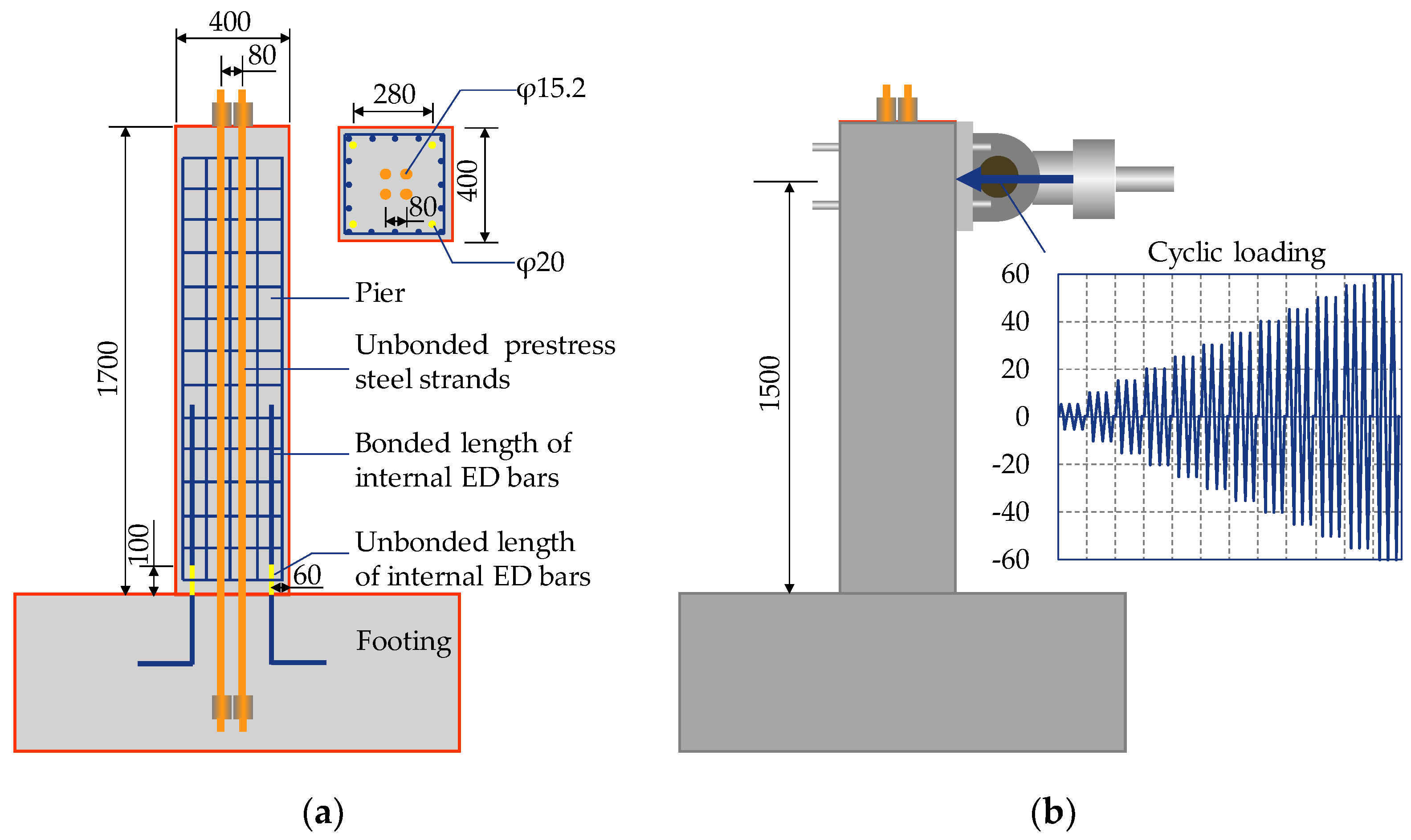
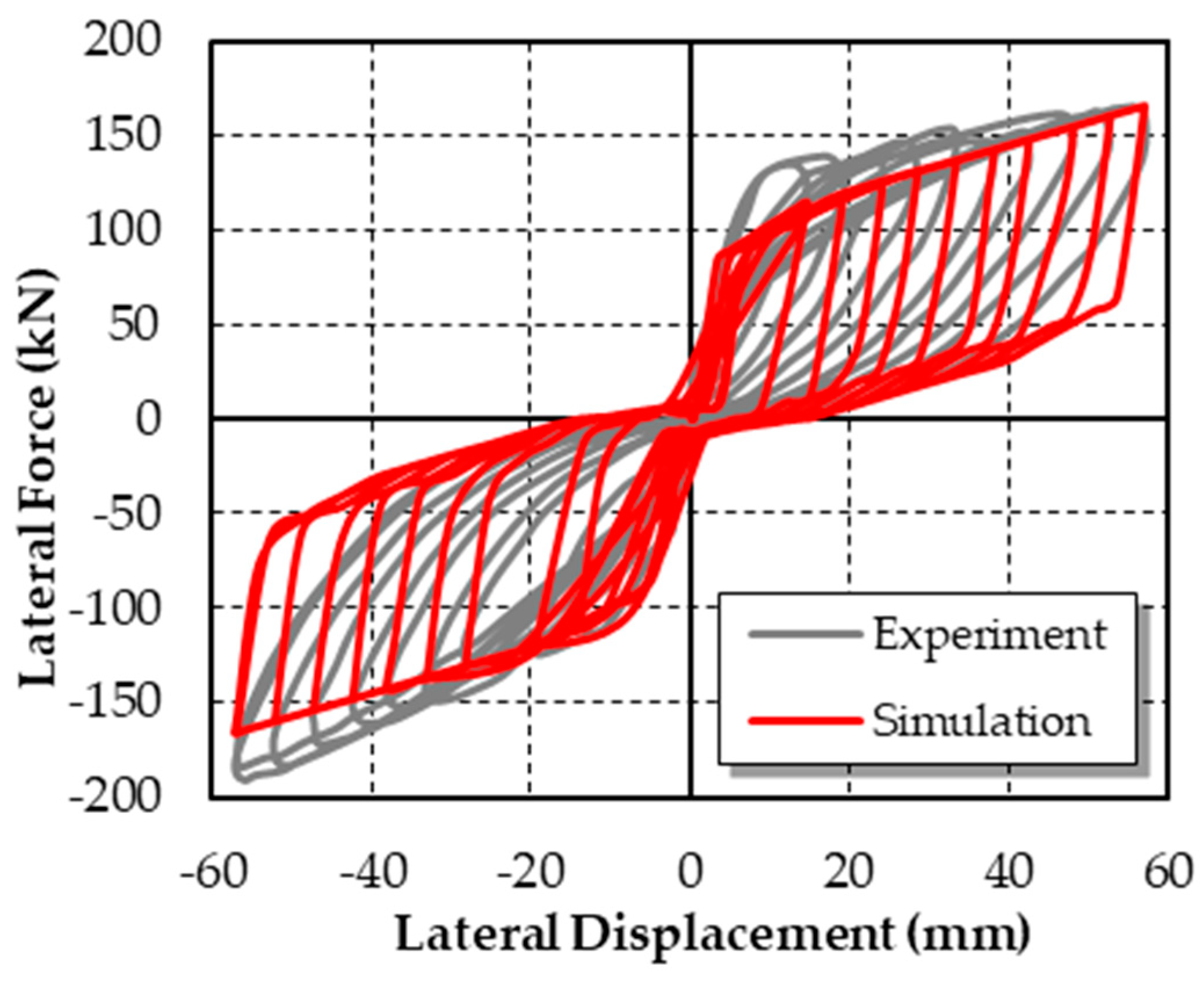
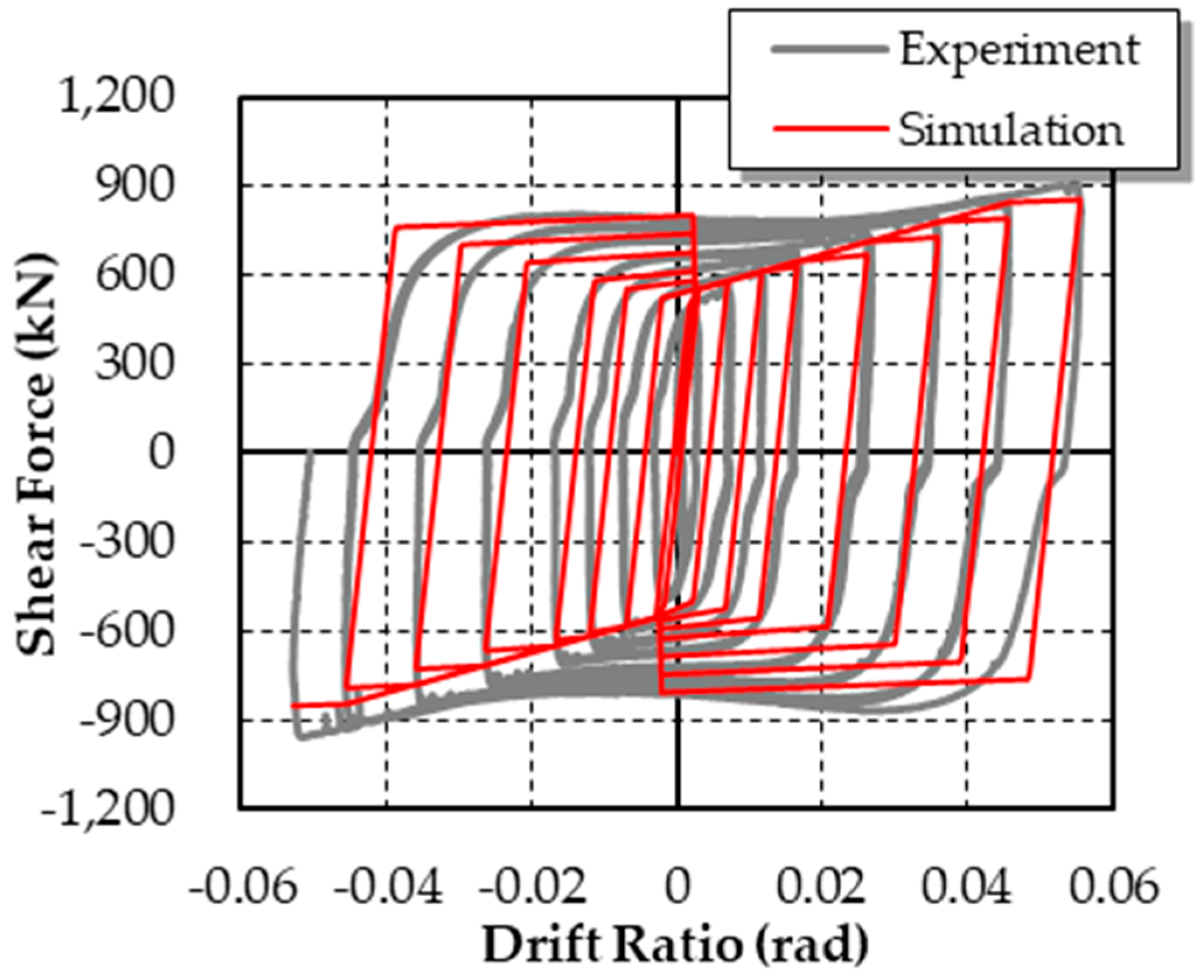
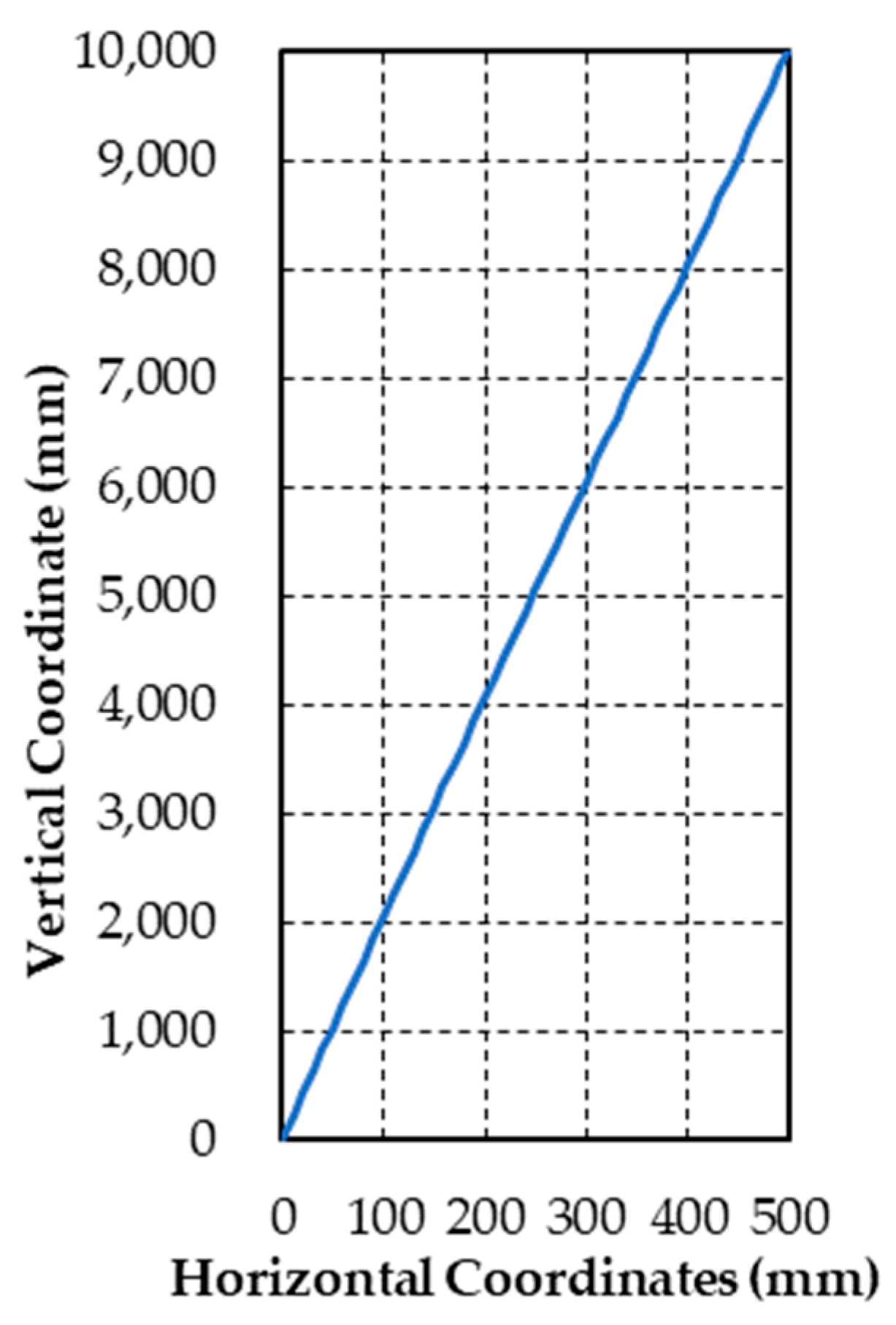
2.2. Validation of Modeling Method
2.2.1. Self-Centering Pier
2.2.2. Shear Links
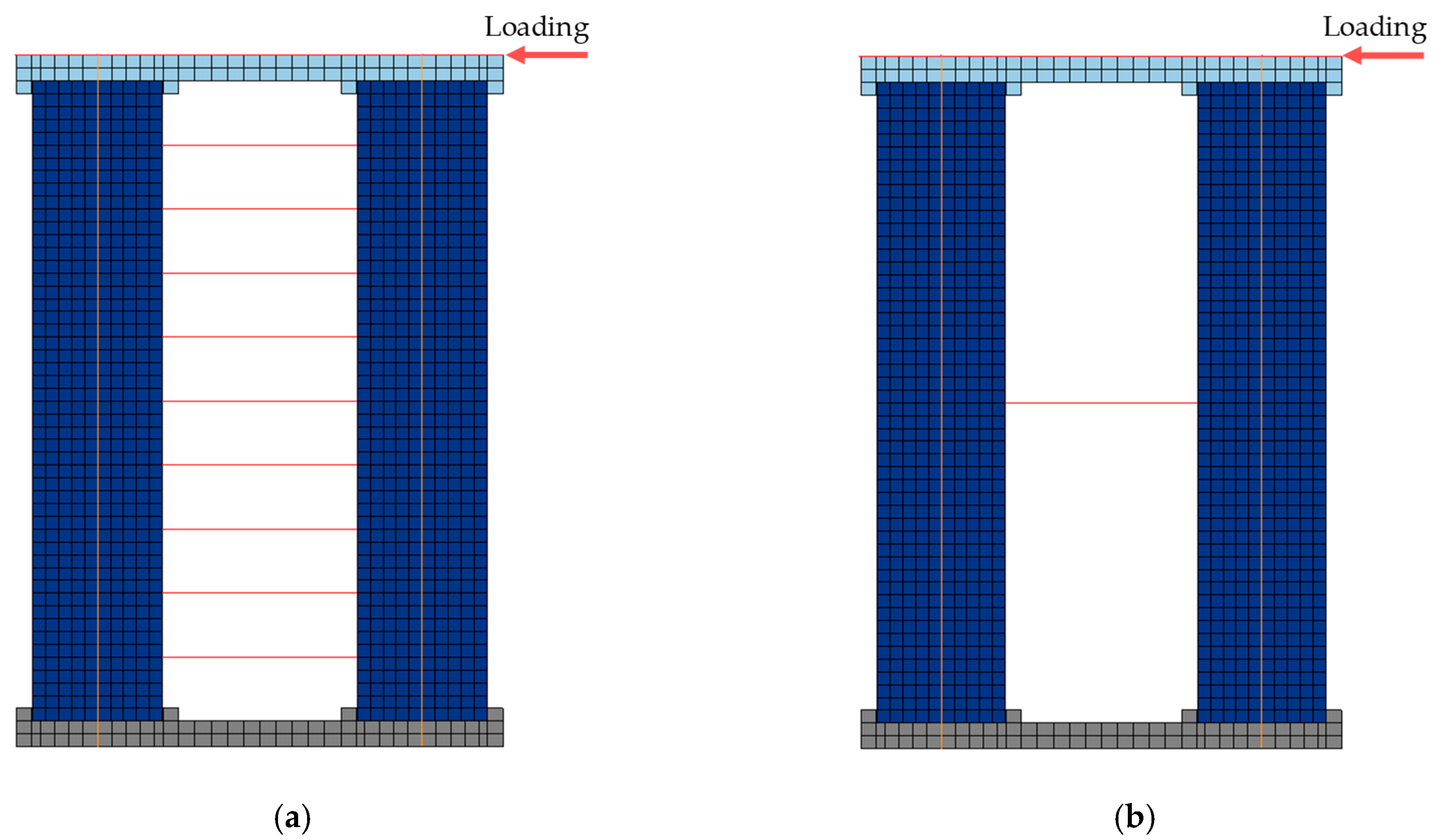
3. Performance of Double-Column Self-Centering Piers with Shear Links under Quasi-Static Cyclic Loading
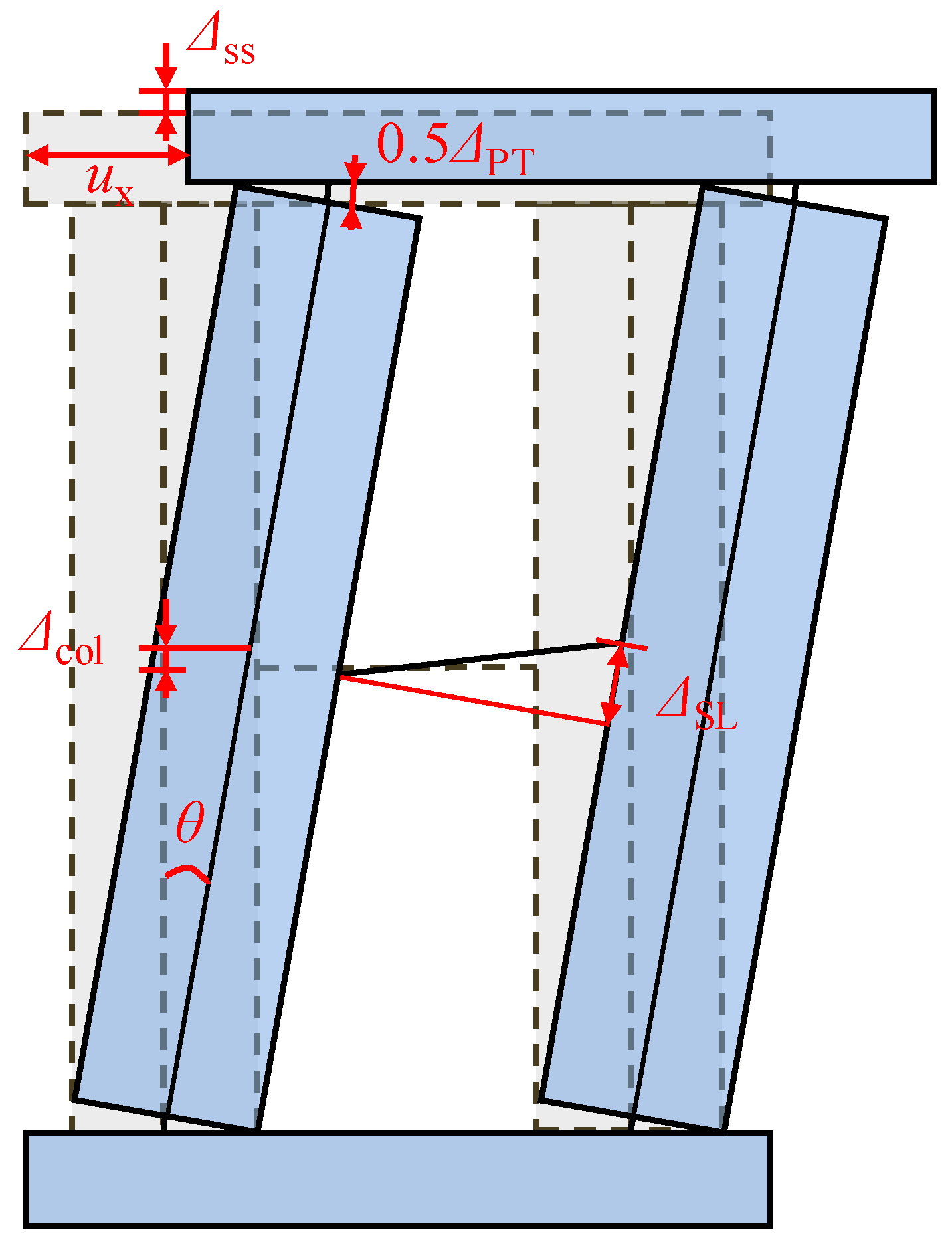
3.1. Rocking Process
3.2. Influence of Shear Link Arrangement
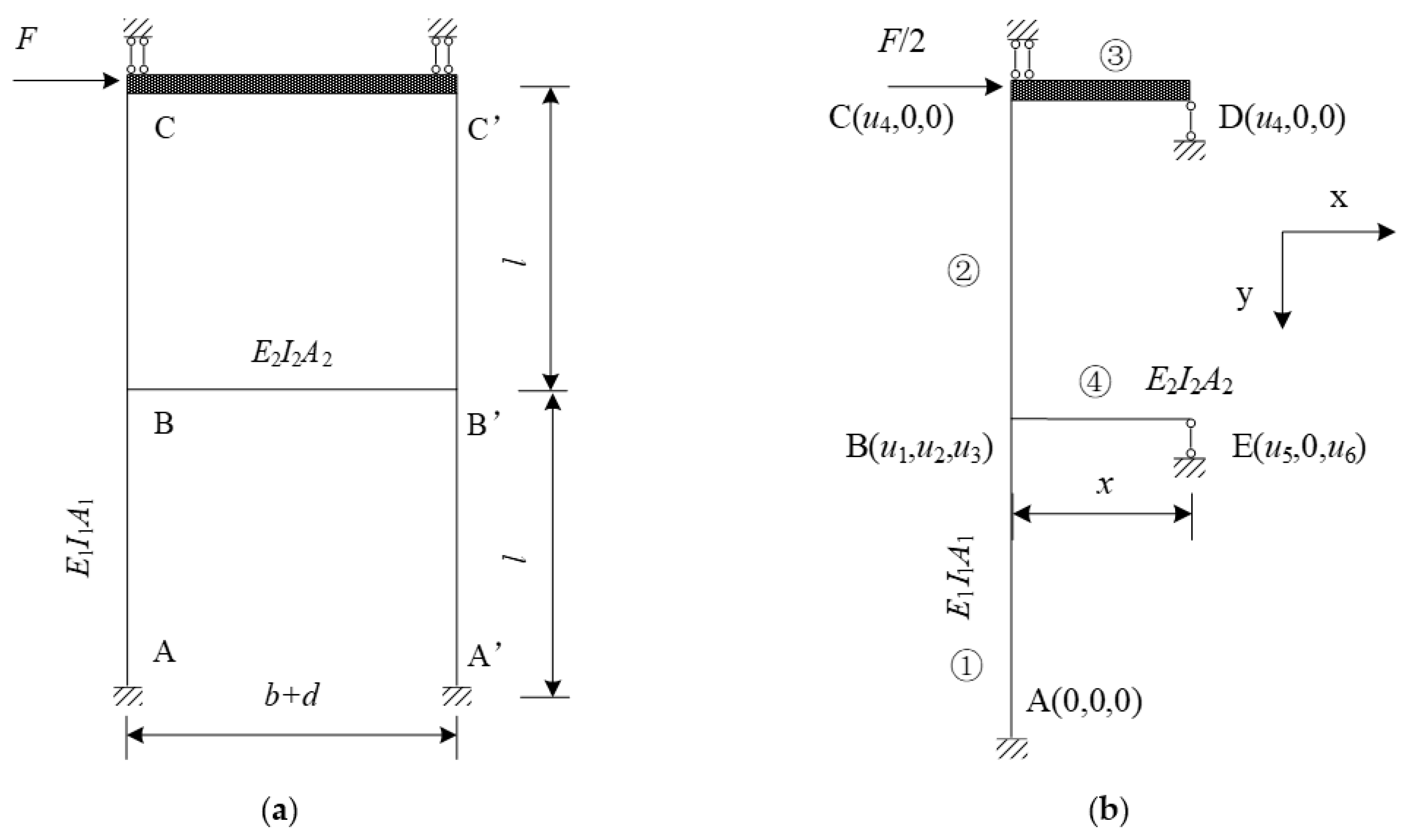
4. Theoretical Analysis of Double-Column Self-Centering Piers with Shear Links
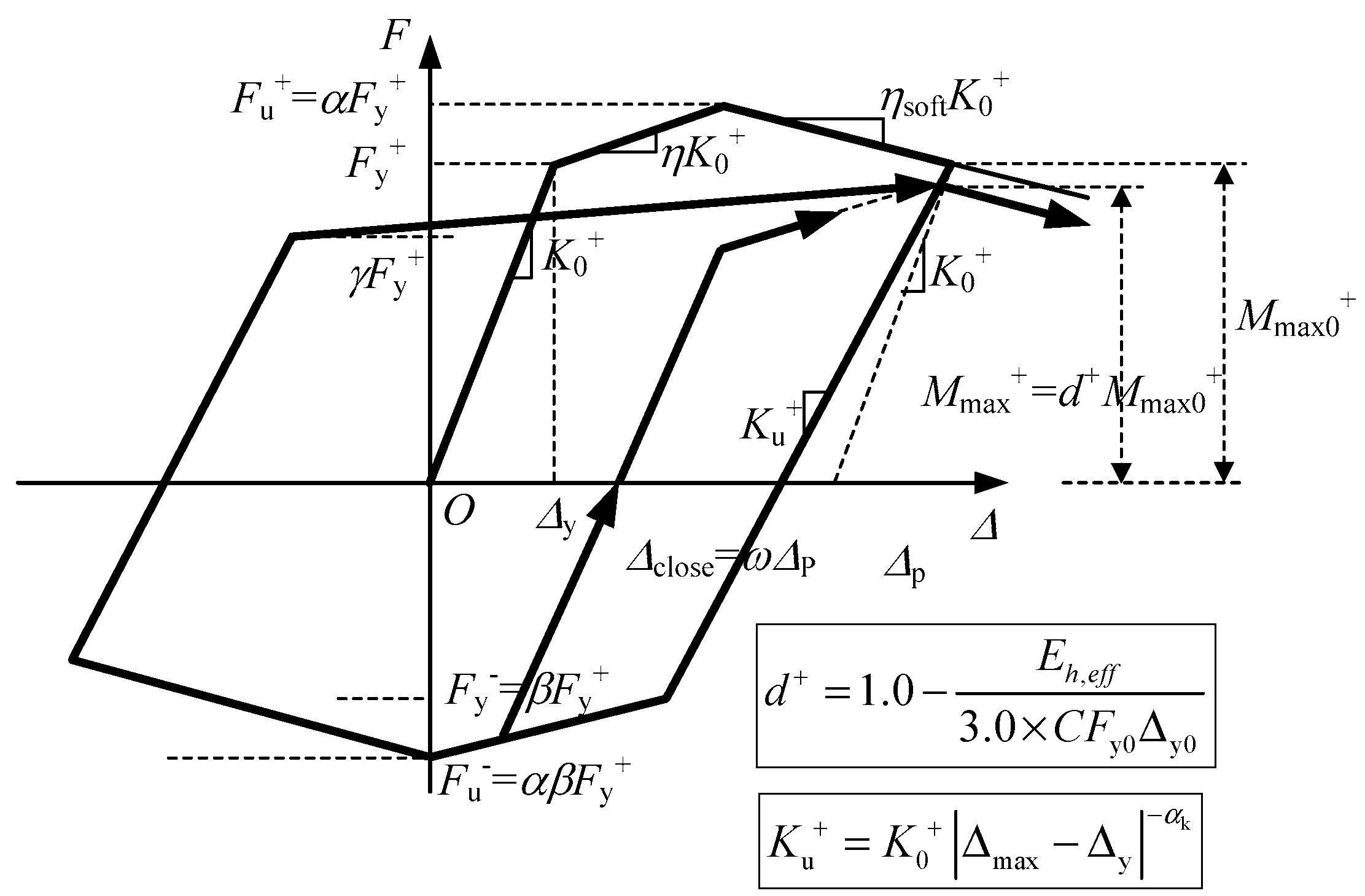
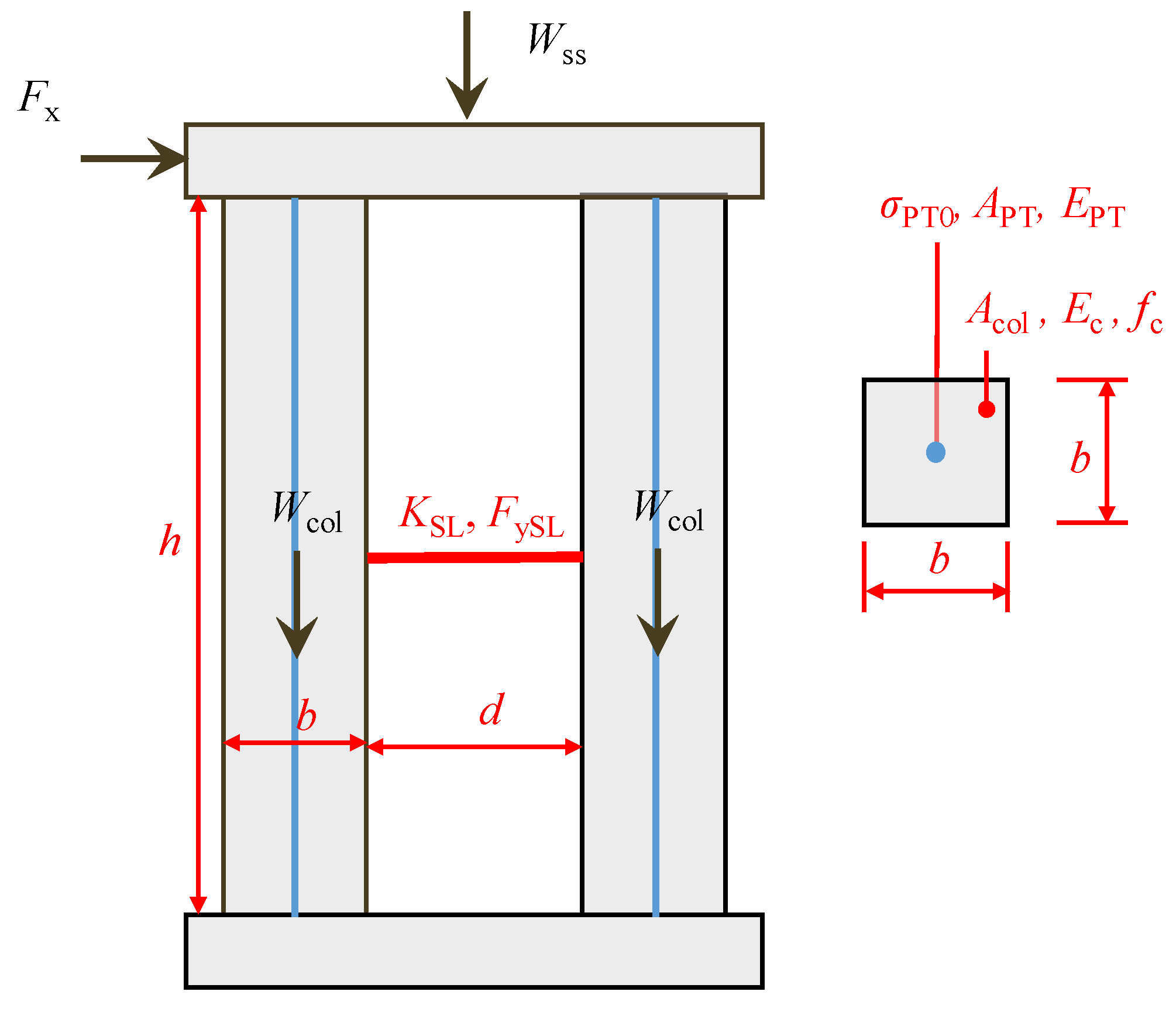
4.1. Theoretical Model Parameters
- Geometrical dimensions: h and Apier are the height and cross section of the columns, respectively; d is the distance between columns and APT is the area of steel strands.
- Material properties: Ec and fc are the elastic modulus and axial compressive strength of concrete, respectively; EPT and fPT are the elastic modulus and the ultimate strength of steel strands, respectively.
- Gravitational forces: Wbeam and Wpier are superstructure gravity and column gravity, respectively.
- Shear link parameters: kSL and FySL are the initial stiffness and yield strength of shear links, respectively.
- Other: FPT0 is the initial prestress of the steel strands. All of these parameters are illustrated in Figure 12.
4.2. Piers with Shear Links
4.2.1. Pre-Rocking State
4.2.2. Rocking State
4.3. Piers without Shear Links
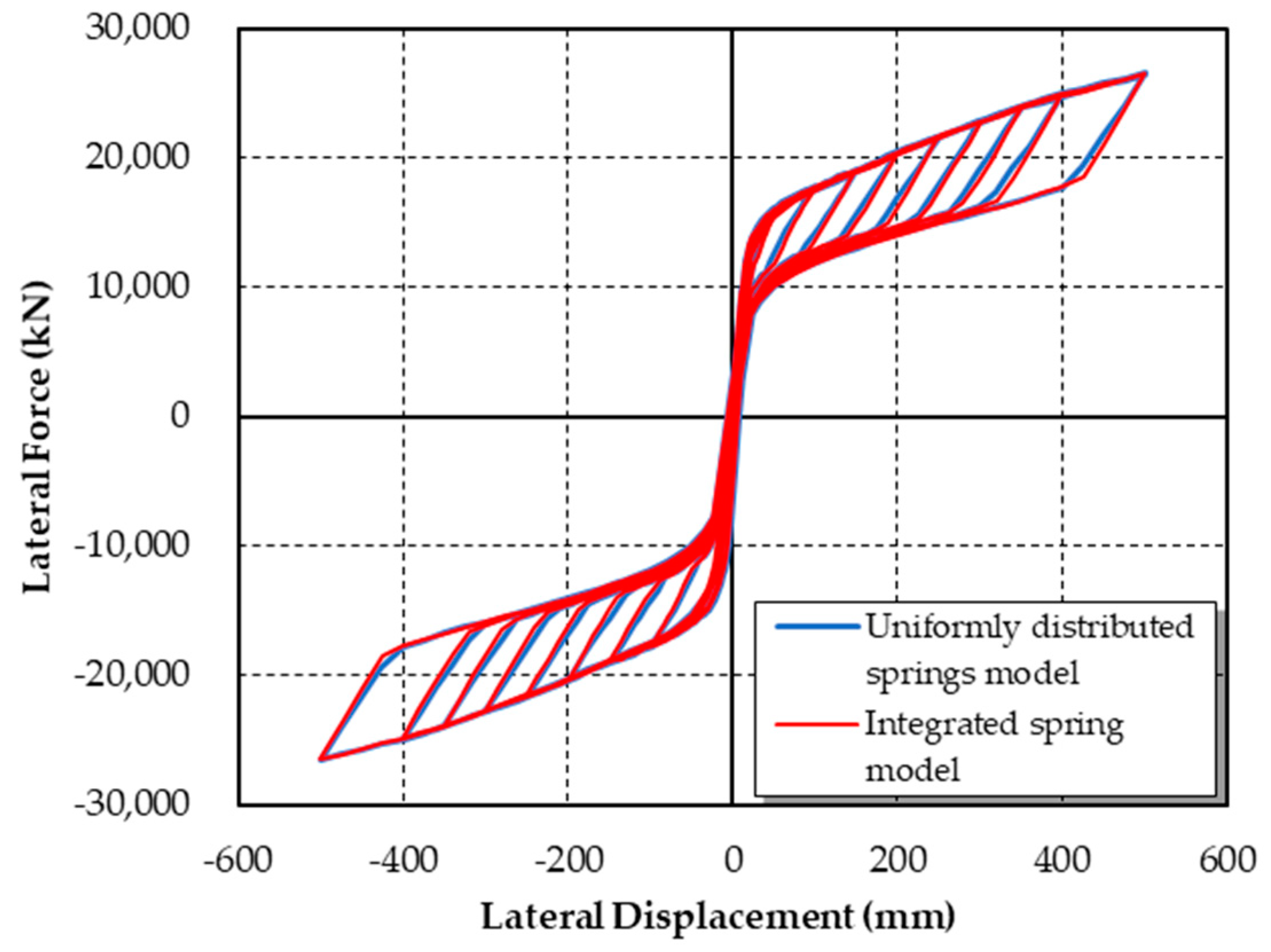
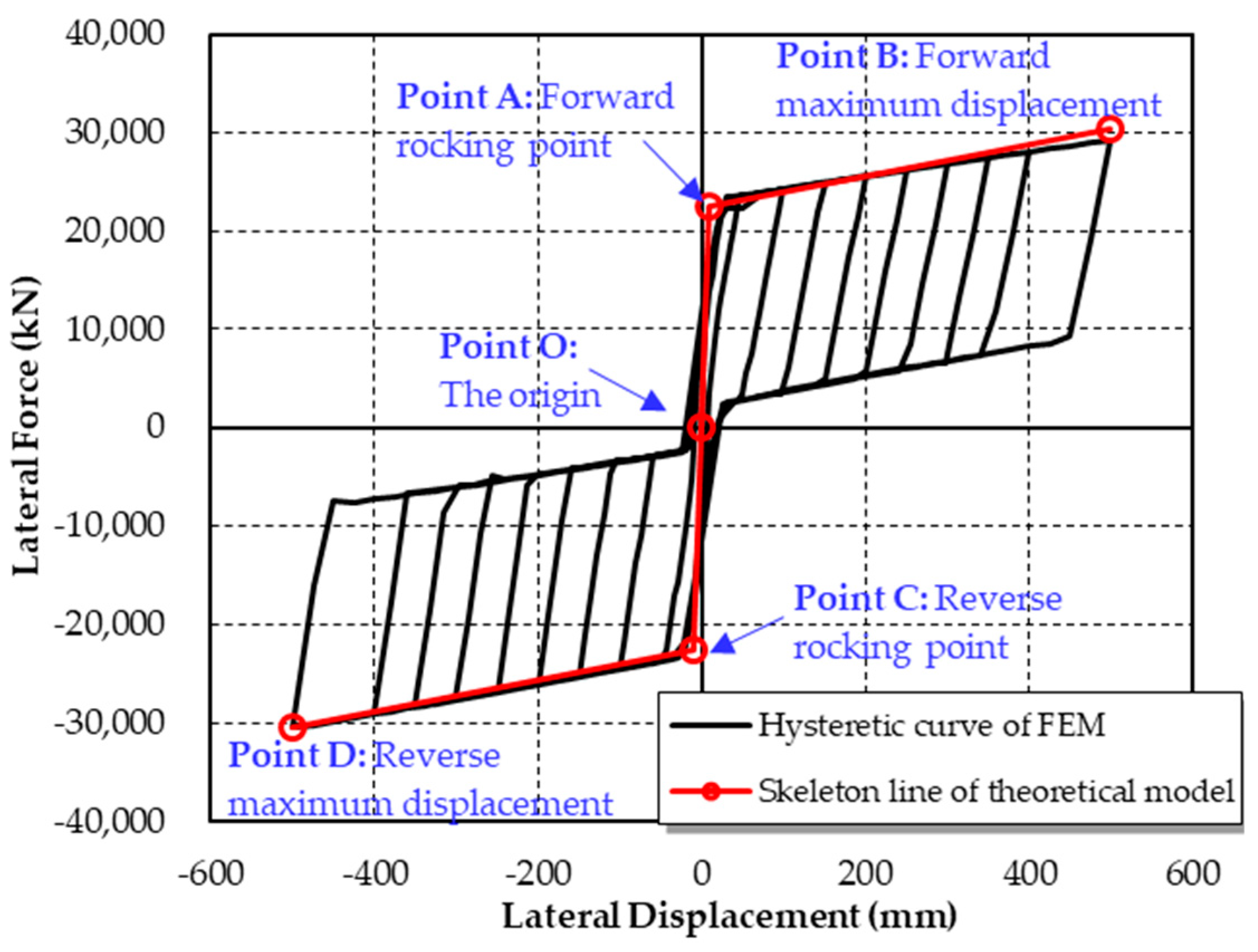
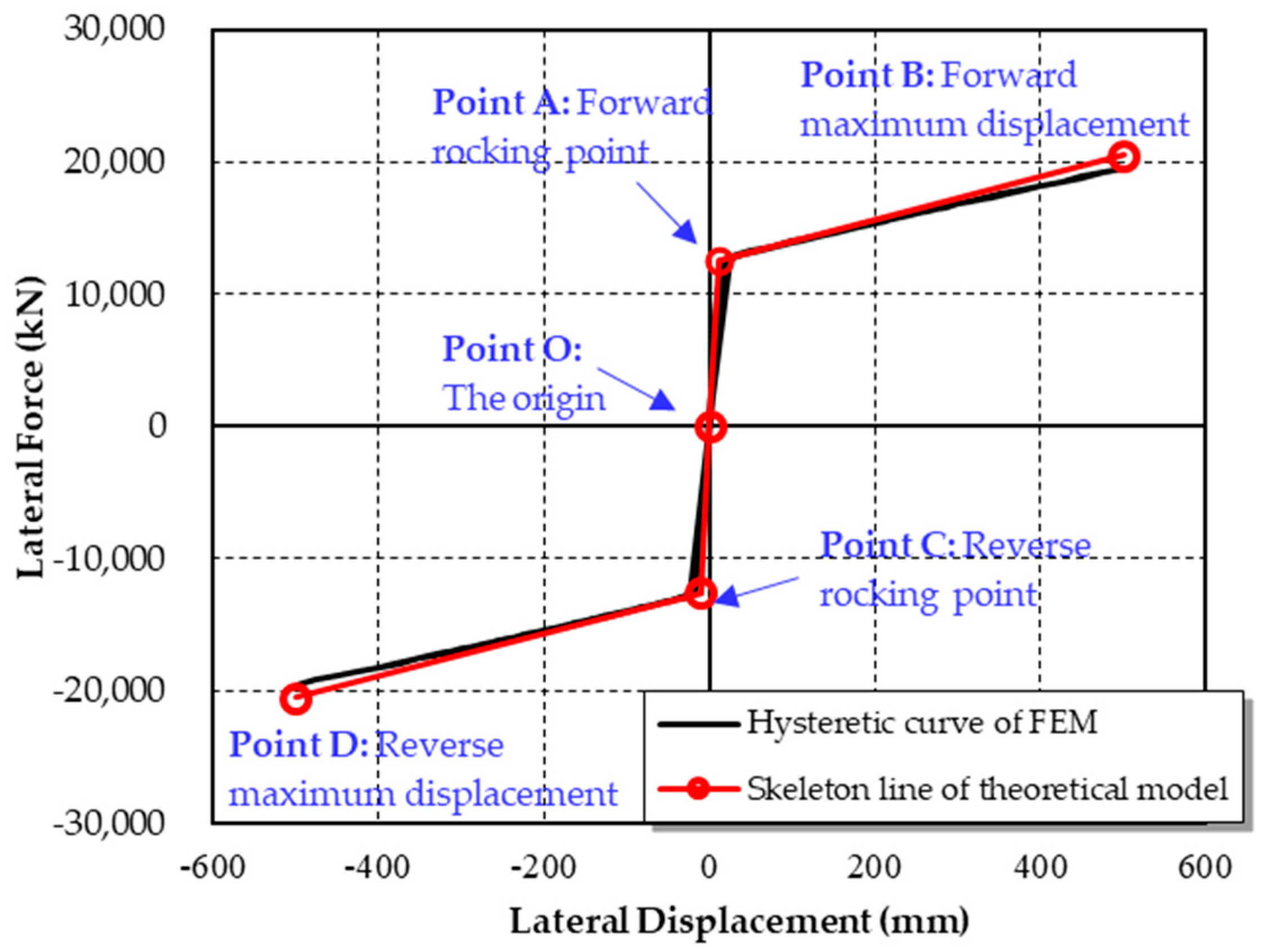
4.4. Model Validation
5. Parametric Analysis
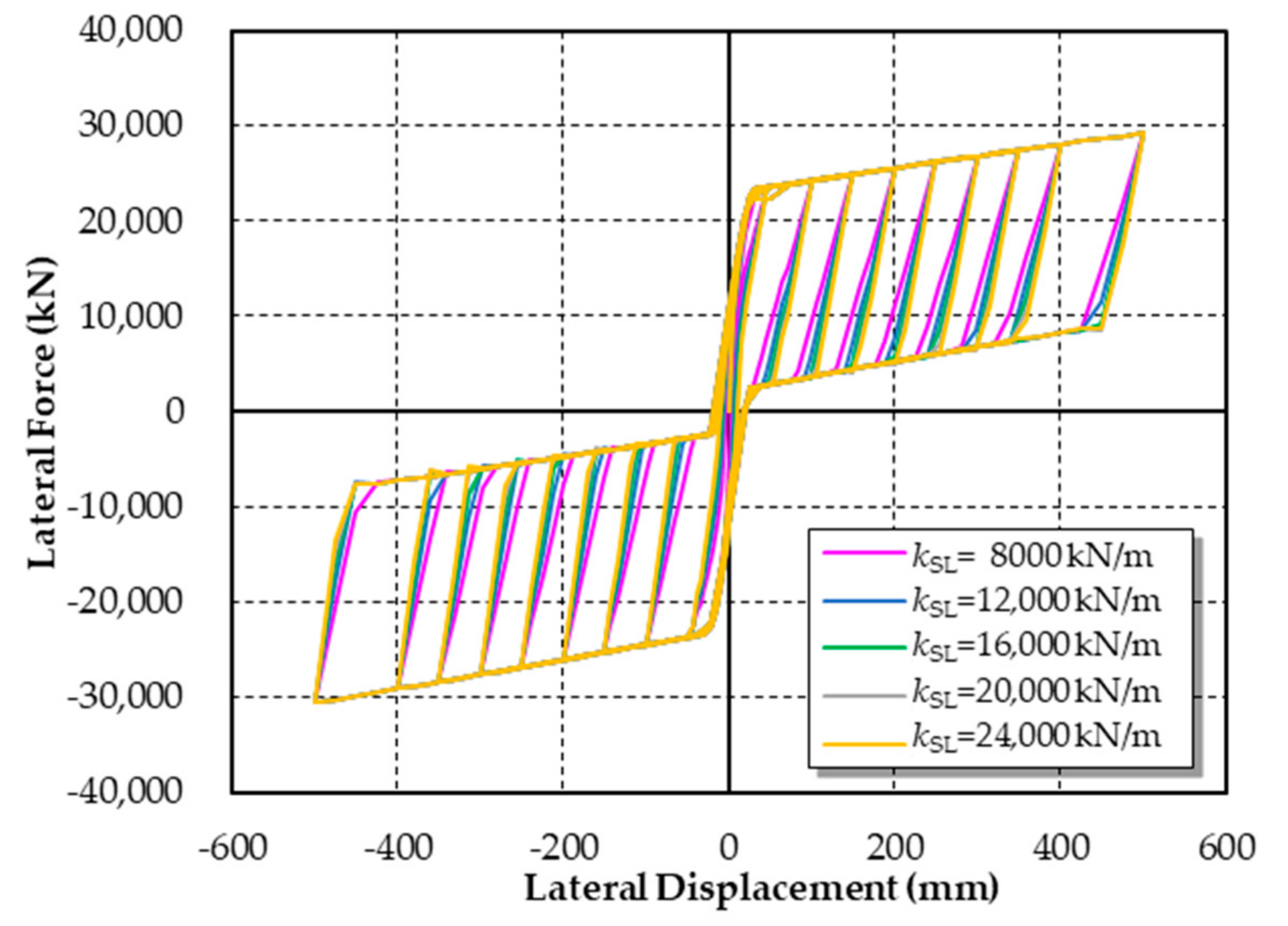
5.1. Influence of Initial Stiffness of Shear Links (kSL)
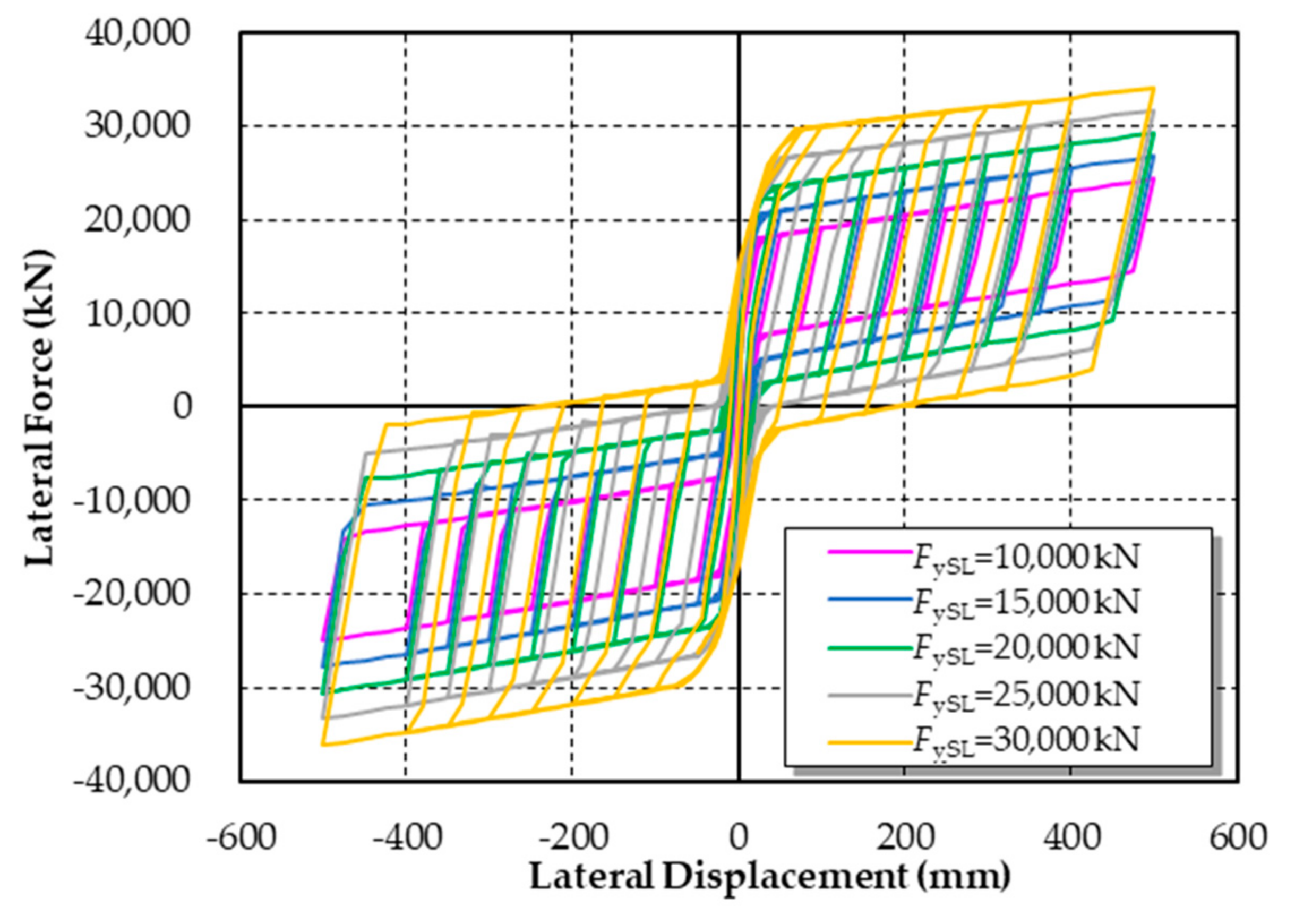
5.2. Influence of Yield Strength of Shear Links (FySL)
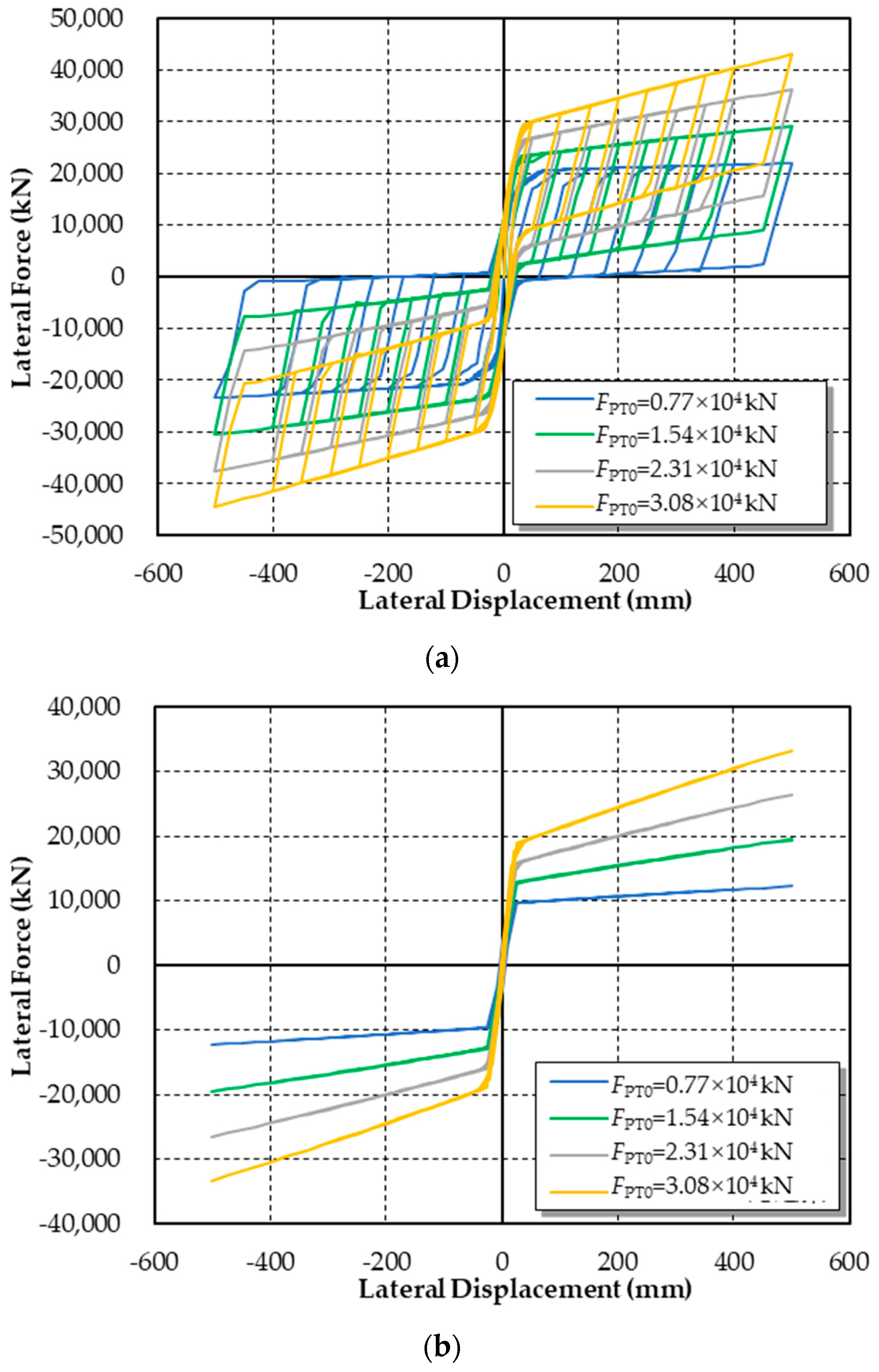
5.3. Influence of Initial Prestress of Steel Strands (FPT0)
6. Conclusions
- The prestressed steel strands provide the proposed pier with a stable self-centering ability, which efficiently reduces the residual displacement. Additionally, the rocking behavior effectively prevents the development of plastic hinges in the columns of conventional reinforced concrete piers. Furthermore, the shear links between columns guarantee the pier has a preferable energy dissipation ability. Therefore, the proposed pier can be used to improve seismic resilience with the remarkable features mentioned above.
- The results of the FE model indicate that, for the short piers, it is reasonable to neglect the deformation of each column when the pier rocks. The integrated spring model and the uniformly distributed spring model show almost the same hysteretic performance. These two observations are the basis of the theoretical model.
- The results derived from the theoretical models show good agreement with the results from the FE models. In this case, the theoretical model based on the matrix displacement method and the virtual work principle can be used for future analysis of the innovated pier.
- According to the parametric analyses, the influence of the initial stiffness of the shear links can be neglected. By enhancing the yield strength of shear links, the energy dissipation capacity of the pier can be improved but the residual displacement will increase. Further, the bigger the initial prestress is, the larger the rocking stiffness of the pier is and the smaller the residual displacement is.
Author Contributions
Funding
Conflicts of Interest
References
- Hyogo Earthquake Engineering Research Center; NIED NEES Consortium, Inc. Report of the Seventh Joint Planning Meeting of NEES/E-Defense Collaborative Research on Earthquake Engineering; Report PEER 109; University of California: Berkeley, CA, USA, 2010. [Google Scholar]
- National Research Council. National Earthquake Resilience: Research, Implementation, and Outreach; National Academies Press: Washington, DC, USA, 2011. [Google Scholar]
- The United Nations Office for Disaster Risk Reduction (UNISDR). 2015. Available online: http://www.unisdr.org/files/43291_sendaiframeworkfordrren.pdf. (accessed on 16 April 2019).
- Kawashima, K.; MacRae, G.A.; Hoshikuma, J.; Nagaya, K. Residual displacement response spectrum. J. Struct. Eng. 1998, 124, 523–530. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2006, 19, 733–738. [Google Scholar] [CrossRef]
- Tremayne, H.; Mahin, S.A. Earthquake Engineering for Resilient Communities: 2012 PEER Internship Program Research Report Collection; Technical Report PEER 07; University of California: Berkeley, CA, USA, 2012. [Google Scholar]
- Mander, J.B.; Cheng, C.T. Seismic Resistance of Bridge Piers Based on Damage Avoidance Design; Technical Report NCEER 97-0014; University of Buffalo: Buffalo, NY, USA, 1997. [Google Scholar]
- Hewes, J.T.; Priestley, M.J.N. Seismic Design and Performance of Precast Concrete Vertebral Bridge Columns; Report No. SSRPe2001/25; Department of Structural Engineering, University of California: San Diego, CA, USA, 2002. [Google Scholar]
- Kwan, W.P.; Billington, S. Unbonded posttensioned concrete bridge piers. i: Monotonic and cyclic analyses. J. Bridge Eng. 2003, 8, 92–101. [Google Scholar] [CrossRef]
- Kwan, W.P.; Billington, S. Unbonded posttensioned concrete bridge piers. ii: Seismic analyses. J. Bridge Eng. 2003, 8, 102–111. [Google Scholar] [CrossRef]
- Sakai, J.; Mahin, S.A. Analytical Investigations of New Methods for Reducing Residual Displacements of Reinforced Concrete Bridge Column; Report No. PEER 2004/02; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2004. [Google Scholar]
- Heiber, D.G.; Wacker, J.M.; Eberhard, M.O.; Stanton, J.F. Precast Concrete Pier Systems for Rapid Construction of Bridges in Seismic Regions; Report No. WA-RD 611.1; Washington Department of Transportation: Olympia, WA, USA, 2005. [Google Scholar]
- Ou, Y.C.; Chiewanichakorn, M.; Ahn, I.S.; Aref, A.J.; Chen, S.S.; Filiatrault, A.; Lee, G.C. Cyclic performance of precast concrete segmental bridge columns: Simplified analytical and finite element studies. Transp. Res. Rec. 2006, 1976, 66–74. [Google Scholar] [CrossRef]
- Palermo, A.; Pampanin, S.; Calvi, G.M. Concept and development of hybrid solutions for seismic resistant bridge systems. J. Earthq. Eng. 2005, 9, 899–921. [Google Scholar] [CrossRef]
- Ou, Y.; Chiewanichakorn, M.; Aref, A.; Lee, G. Seismic performance of segmental precast unbonded posttensioned concrete bridge columns. J. Struct. Eng. 2007, 133, 1636–1647. [Google Scholar] [CrossRef]
- Roh, H.; Reinhorn, A.M. Hysteretic behavior of precast segmental bridge piers with superelastic shape memory alloy bars. Eng. Struct. 2010, 32, 3394–3403. [Google Scholar] [CrossRef]
- Guo, J.; Xin, K.G.; Wu, W.P.; He, M.H. A simplified model and experimental response of self-centring bridge piers with ductile connections. In Proceedings of the 2nd International Conference on Structures and Building Materials, Hangzhou, China, 12–15 August 2012. [Google Scholar]
- Roh, H.; Ou, Y.C.; Kim, J.; Kim, W.S. Effect of yielding level and post-yielding stiffness ratio of ED bars on seismic performance of PT rocking bridge piers. Eng. Struct. 2014, 81, 454–463. [Google Scholar] [CrossRef]
- Nikbakht, E.; Rashid, K.; Hejazi, F.; Osman, S.A. Application of shape memory alloy bars in selfcentring precast segmental columns as seismic resistance. Struct. Infrastruct. Eng. 2015, 11, 297–309. [Google Scholar] [CrossRef]
- Guerrin, G.; Restrepo, J.I.; Massari, M.; Vervelidis, A. Seismic behavior of posttensioned self-centering precast concrete dual-shell steel columns. J. Struct. Eng. 2015, 141, 04014115. [Google Scholar] [CrossRef]
- Li, C.; Hao, H.; Bi, K.M. Numerical study on the seismic performance of precast segmental concrete columns under cyclic loading. Eng. Struct. 2017, 148, 373–386. [Google Scholar] [CrossRef]
- Wang, J.C.; Ou, Y.C.; Chang, K.C.; Lee, G.C. Large-scale seismic tests of tall concrete bridge columns with precast segmental construction. Earthq. Eng. Struct. Dyn. 2008, 37, 1449–1465. [Google Scholar] [CrossRef]
- Marriott, D.; Pampanin, S.; Palermo, A. Quasi-static and pseudo-dynamic testing of unbonded post-tensioned rocking bridge piers with external replaceable dissipaters. Earthq. Eng. Struct. Dyn. 2009, 38, 331–354. [Google Scholar] [CrossRef]
- Guo, T.; Cao, Z.L.; Xu, Z.K.; Lu, S. Cyclic load tests on self-centering concrete pier with external dissipators and enhanced durability. J. Struct. Eng. 2016, 142, 04015088. [Google Scholar] [CrossRef]
- Cao, Z.L.; Wang, H.; Guo, T. Fragility analysis of self-centering prestressed concrete bridge pier with external aluminum dissipators. Adv. Struct. Eng. 2017, 20, 1210–1222. [Google Scholar] [CrossRef]
- Nikoukalam, M.T.; Sideris, P. Resilient bridge rocking columns with polyurethane damage-resistant end segments and replaceable energy-dissipating links. J. Bridge Eng. 2017, 22, 04017064. [Google Scholar] [CrossRef]
- Mashal, M.; Palermo, A.; Keats, G. Innovative metallic dissipaters for earthquake protection of structural and non-structural components. Soil Dyn. Earthq. Eng. 2019, 116, 31–42. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, Z.X.; Liu, X.J.; Chicchi, R.; Shahrooz, B. An innovative resilient rocking column with replaceable steel slit dampers: Experimental program on seismic performance. Eng. Struct. 2019, 183, 830–840. [Google Scholar] [CrossRef]
- Sahoo, D.R.; Rai, D.C. Seismic strengthening of non-ductile reinforced concrete frames using aluminum shear links as energy-dissipation devices. Eng. Struct. 2010, 32, 3548–3557. [Google Scholar] [CrossRef]
- Lu, X.L.; Chen, C.; Jiang, H.J.; Wang, S.S. Shaking table tests and numerical analyses of an RC coupled wall structure with replaceable coupling beams. Earthquake Eng. Struct. Dyn. 2018, 47, 1882–1904. [Google Scholar] [CrossRef]
- Vetr, M.G.; Ghamarib, A.; Bouwkamp, J. Investigating the nonlinear behavior of Eccentrically Braced Frame with vertical shear links (V-EBF). J. Build. Eng. 2017, 10, 47–59. [Google Scholar] [CrossRef]
- Deng, K.L.; Pan, P.; Wang, H.S.; Shen, S.D. Experimental study on slotted RC wall with steel energy dissipation links for seismic protection of buildings. Eng. Struct. 2017, 145, 1–11. [Google Scholar] [CrossRef]
- McDaniel, C.C.; Uang, C.M.; Seible, F. Cyclic testing of built-up steel shear links for the New Bay Bridge. J. Struct. Eng. 2003, 129, 801–809. [Google Scholar] [CrossRef]
- McDaniel, C.C.; Seible, F. Influence of inelastic tower links on cable-supported bridge response. J. Bridge Eng. 2005, 10, 272–280. [Google Scholar] [CrossRef]
- Sun, L.M.; Xie, W. Damage mechanism and damage control of long span cable-stayed bridges under strong earthquake. In Proceedings of the 5th World Conference on Structural Control and Monitoring, Tokyo, Japan, 12–14 July 2010. [Google Scholar]
- Elbahey, S.; Bruneau, M. Structural fuse concept for bridges. Transp. Res. Rec. 2010, 2202, 167–172. [Google Scholar] [CrossRef]
- Elbahey, S.; Bruneau, M. Bridge piers with structural fuses and bi-steel columns I: Experimental testing. J. Bridge Eng. 2012, 17, 25–35. [Google Scholar] [CrossRef]
- Elbahey, S.; Bruneau, M. Bridge piers with structural fuses and bi-steel columns II: Analytical investigation. J. Bridge Eng. 2012, 17, 36–46. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Guidelines for Seismic Design of Highway Bridges (JTGT B02-01-2008); Ministry of Transport of the People’s Republic of China: Beijing, China, 2008. [Google Scholar]
- MSC. Software Corp. MSC. MARC. User’s Manual; MSC Software Corporation: Santa Ana, CA, USA, 2007. [Google Scholar]
- Lu, X.Z.; Guan, H. Earthquake Disaster Simulation of Civil Infrastructures. From Tall Buildings to Urban Areas; Springer Science Press: New York, NY, USA, 2017. [Google Scholar]
- Lu, X.; Lu, X.Z.; Sezen, H.; Ye, L.P. Development of a simplified model and seismic energy dissipation in a super-tall building. Eng. Struct. 2014, 67, 109–122. [Google Scholar] [CrossRef]
- Qu, Z.; Ye, L.P. Strength deterioration model based on effective hysteretic energy dissipation for RC members under cyclic loading. In Proceedings of the 7th International Conference on Urban Earthquake Engineering, Tokyo, Japan, 3–5 March 2010. [Google Scholar]
- Ji, X.D.; Wang, Y.D.; Ma, Q.F.; Okazaki, T. Cyclic behavior of replaceable steel coupling beams. J. Struct. Eng. 2017, 143, 04016169. [Google Scholar] [CrossRef]
| Parameters | Pier with Shear Links | Pier without Shear Links | |
|---|---|---|---|
| Geometrical dimensions | Height of columns, h | 10.0 m | |
| Cross section of columns, Acol | 2.0 m × 2.0 m | ||
| Distance between columns, d | 3.0 m | ||
| Area of steel strands, APT | 12,737.8 mm2 | ||
| Material properties | Elastic modulus of concrete, Ec | 3.6 × 104 MPa | |
| Axial compressive strength of concrete, fc | 38.5 MPa | ||
| Elastic modulus of steel strands, EPT | 1.95 × 105 MPa | ||
| Ultimate strength of steel strands, fPT | 1860 MPa | ||
| Gravitational forces | Gravity of superstructure, Wss | 3.08 × 104 kN | |
| Gravity of columns, Wcol | Ignored | ||
| Shear links | Initial stiffness of shear links, kSL | 1.6 × 104 kN/m | / |
| Yield strength of shear links, FySL | 2.0 × 104 kN | / | |
| Other | Initial prestress of steel strands, FPT0 | 1.54 × 104 kN | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Lu, X.; Zou, Q.; Ye, L.; Di, J. Mechanical Behavior of a Double-Column Self-Centering Pier Fused with Shear Links. Appl. Sci. 2019, 9, 2497. https://doi.org/10.3390/app9122497
Xu L, Lu X, Zou Q, Ye L, Di J. Mechanical Behavior of a Double-Column Self-Centering Pier Fused with Shear Links. Applied Sciences. 2019; 9(12):2497. https://doi.org/10.3390/app9122497
Chicago/Turabian StyleXu, Liangjin, Xinzheng Lu, Qiaoshan Zou, Lieping Ye, and Jin Di. 2019. "Mechanical Behavior of a Double-Column Self-Centering Pier Fused with Shear Links" Applied Sciences 9, no. 12: 2497. https://doi.org/10.3390/app9122497
APA StyleXu, L., Lu, X., Zou, Q., Ye, L., & Di, J. (2019). Mechanical Behavior of a Double-Column Self-Centering Pier Fused with Shear Links. Applied Sciences, 9(12), 2497. https://doi.org/10.3390/app9122497





