Attosecond Pulse Shaping by Multilayer Mirrors
Abstract
1. Introduction
1.1. Attosecond Pulses (Isolated and Pulsed Trains)
1.2. HHG as Major/Only Attosecond Pulse Source
1.3. What Is It Good for? The Applications
2. Simulations of Multilayer Systems: Their Theoretical Optical Performance
- Top layer oxidation. Analysis methods like interface roughness and, additionally, spectral ellipsometry. The thickness loss of the top layer material, as well as the thickness of the native grown oxide layer, should be determined. It is important since those two layers are responsible for a small aperiodicity within the stack, as well as being the first layers the radiation penetrates through—a very important fact in the case of EUV radiation.
- Interlayer formation. Analysis methods similar to interface roughness.
3. Fabrication of Multilayer Coatings
- Electron beam physical vapor deposition (EBPVD) [7,8] is a form of physical vapor deposition in which a target material anode is bombarded with an electron beam. The electron beam arises from a charged tungsten filament under high vacuum. The electron beam causes atoms from the target to transform into the gaseous phase. These atoms then precipitate into solid form, coating everything in the vacuum chamber (within line of sight) with a thin layer of the anode material.
- Magnetron sputtering [9,10,11] is a plasma vapor deposition (PVD) process in which a plasma is created. The positively charged ions from the plasma are accelerated by an electrical field superimposed on the negatively charged electrode or ’target’. The positive ions are accelerated by potentials ranging from a few hundred to a few thousand electron volts and strike the negative electrode with sufficient force to dislodge and eject atoms from the target material. These atoms will be ejected in a typical line-of-sight cosine distribution from the face of the target and will condense on (substrate) surfaces that are placed in proximity to the magnetron sputtering cathode.
- A (dual) ion beam deposition (D-IBD) [12,13,14] apparatus typically consists of an ion source, ion optics, and the deposition target. Optionally, a mass analyzer can be incorporated. In the ion source, materials in the form of a gas, an evaporated solid, or a solution (liquid) are ionized. The ions are then accelerated, focused, or deflected using high voltages or magnetic fields. Optional deceleration at the substrate can be employed to define the deposition energy. This energy usually ranges from a few to a few thousand electron volts. At low energy, molecular ion beams are deposited intact (soft landing), while, at a high deposition energy, molecular ions fragment, and atomic ions penetrate further into the material. This process is known as ion implantation. The ion beam current, which is a quantitative measure for the deposited amount of material, can be monitored during the deposition process.
- Pulsed laser deposition (PLD) [15,16,17] is a physical vapor deposition technique where a high-power pulsed laser beam is focused inside a vacuum chamber to strike the target material that is to be deposited. This material is vaporized from the target in a plasma plume, which deposits the material as a thin film on a substrate. This process can occur in ultrahigh vacuum or in the presence of a background gas, such as oxygen. Oxygen is commonly used when depositing oxides to fully oxygenate the deposited films.
- Metalorganic vapor phase epitaxy (MOVPE), also known as organometallic vapor phase epitaxy (OMVPE) or metalorganic chemical vapor deposition (MOCVD) [46,47], is a chemical vapor deposition method used to produce single or polycrystalline thin films. It is a highly complex process for growing crystalline layers to create complex semiconductor multilayer structures. In contrast to molecular beam epitaxy (MBE), the growth of crystals is by chemical reaction and not by physical deposition. This takes place not in a vacuum but from the gas phase at moderate pressures (10–760 Torr). As such, this technique is preferred for the formation of devices incorporating thermodynamically metastable alloys. It has become a major process in the manufacture of optoelectronics.
4. Achieved Results and Examples of Multilayer Mirrors for Attosecond Pulses
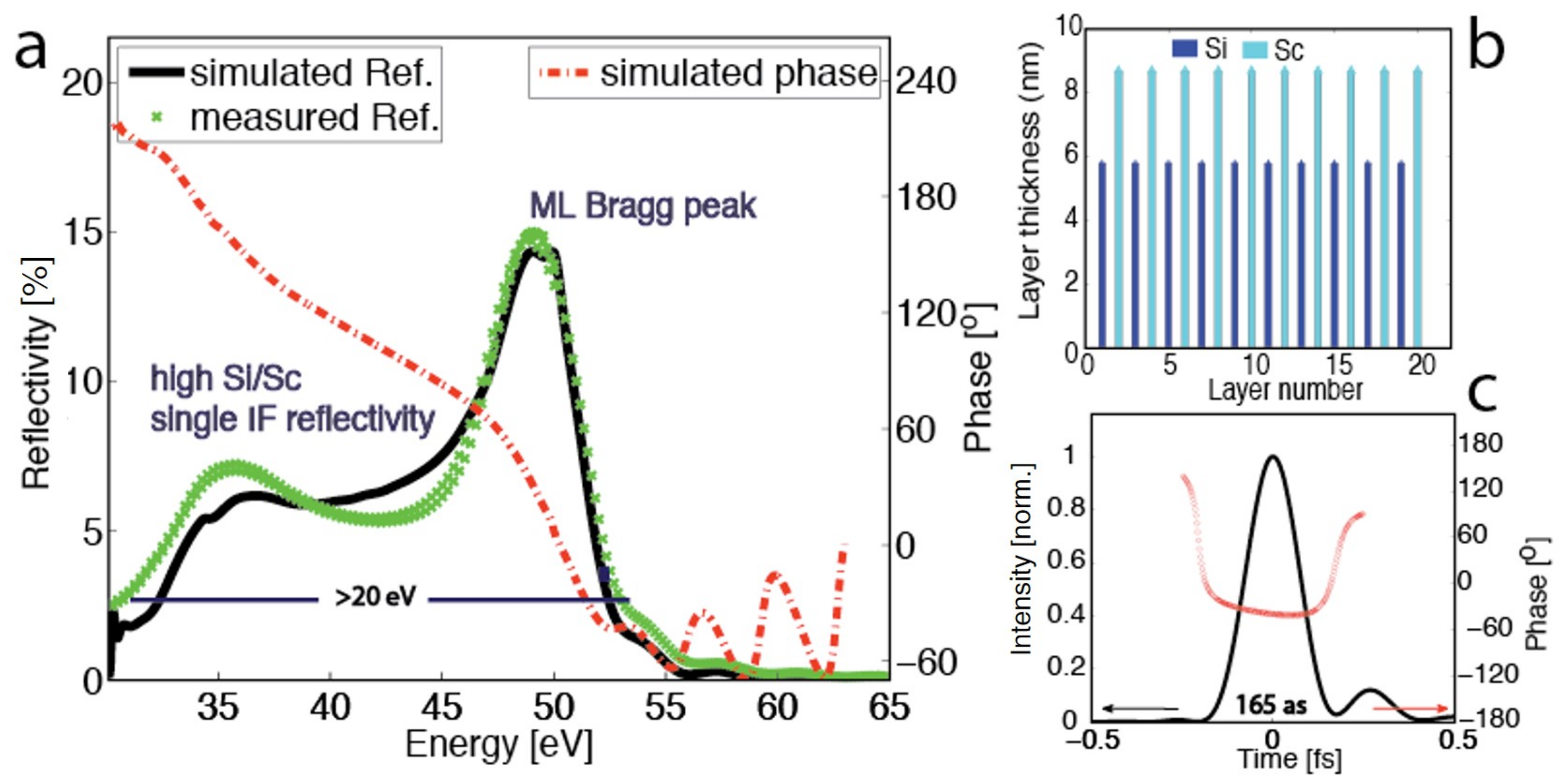
4.1. A Normal Incidence Broadband 30–60 eV Mirror
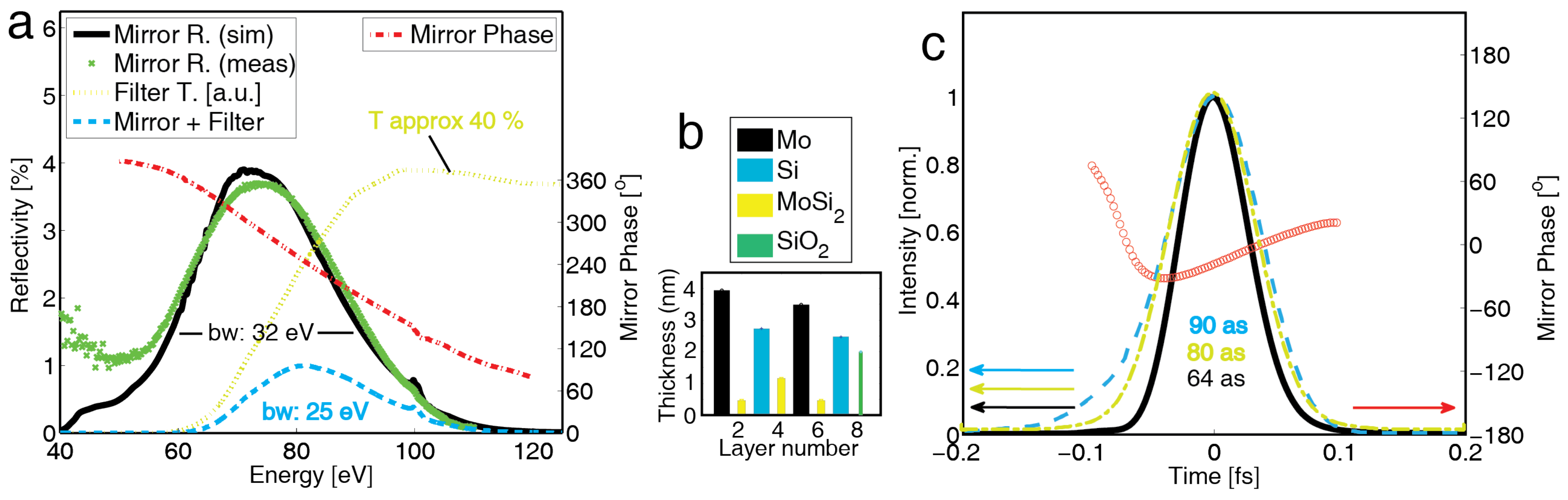
4.2. Short Pulses in the 60–100 eV Range
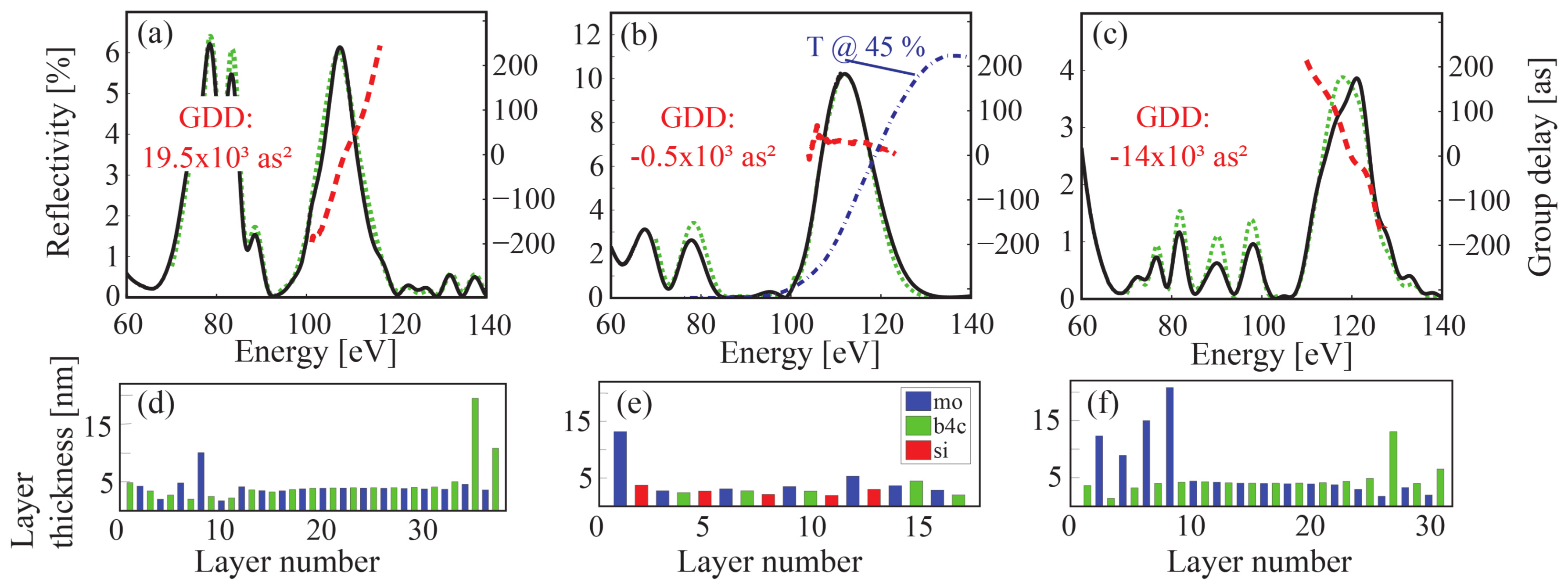
4.3. Above the Silicon L-Edge in the 100–150 eV Photon Range
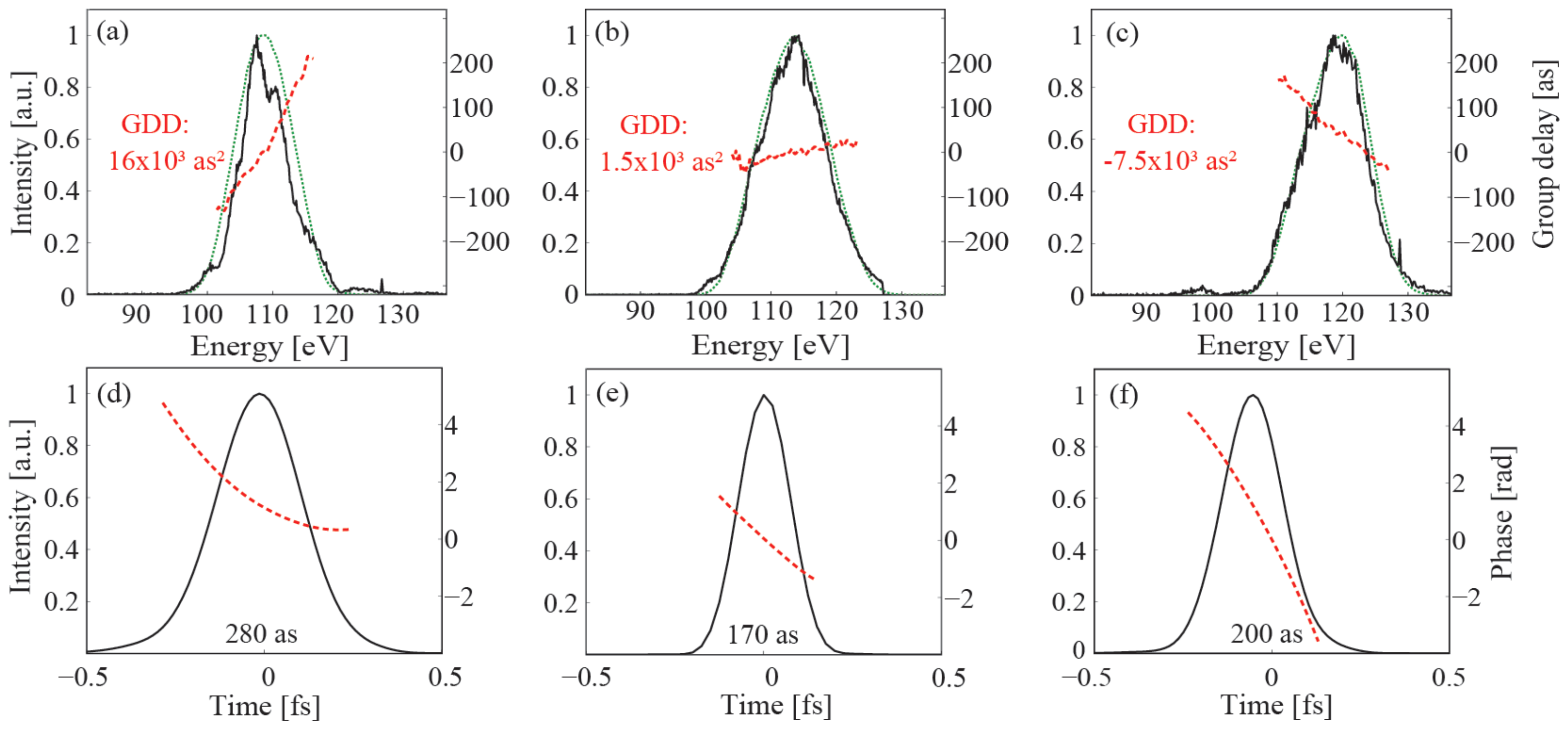
4.3.1. Attosecond Dispersion Control by Multilayer Mirrors above 100 eV
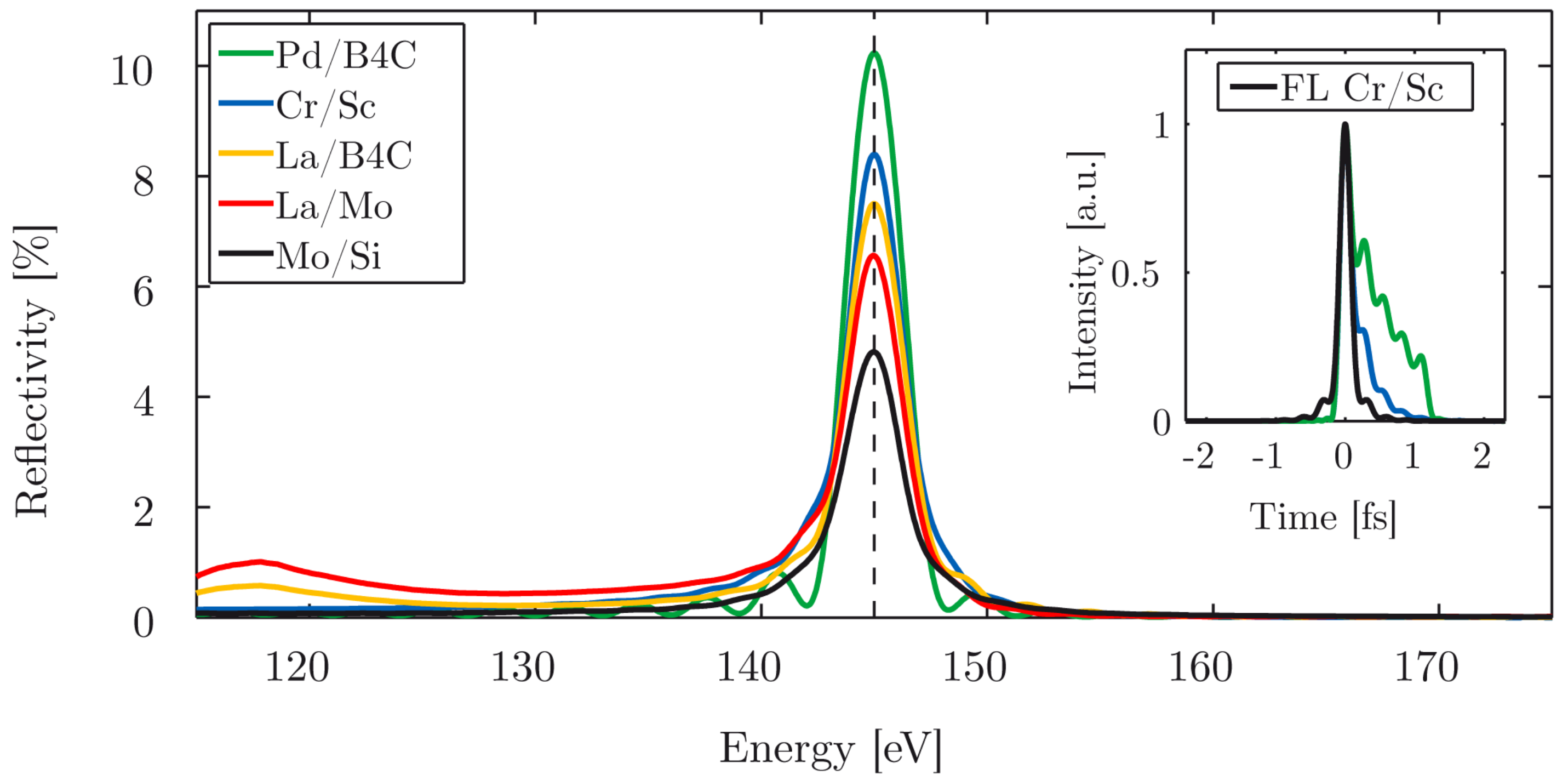
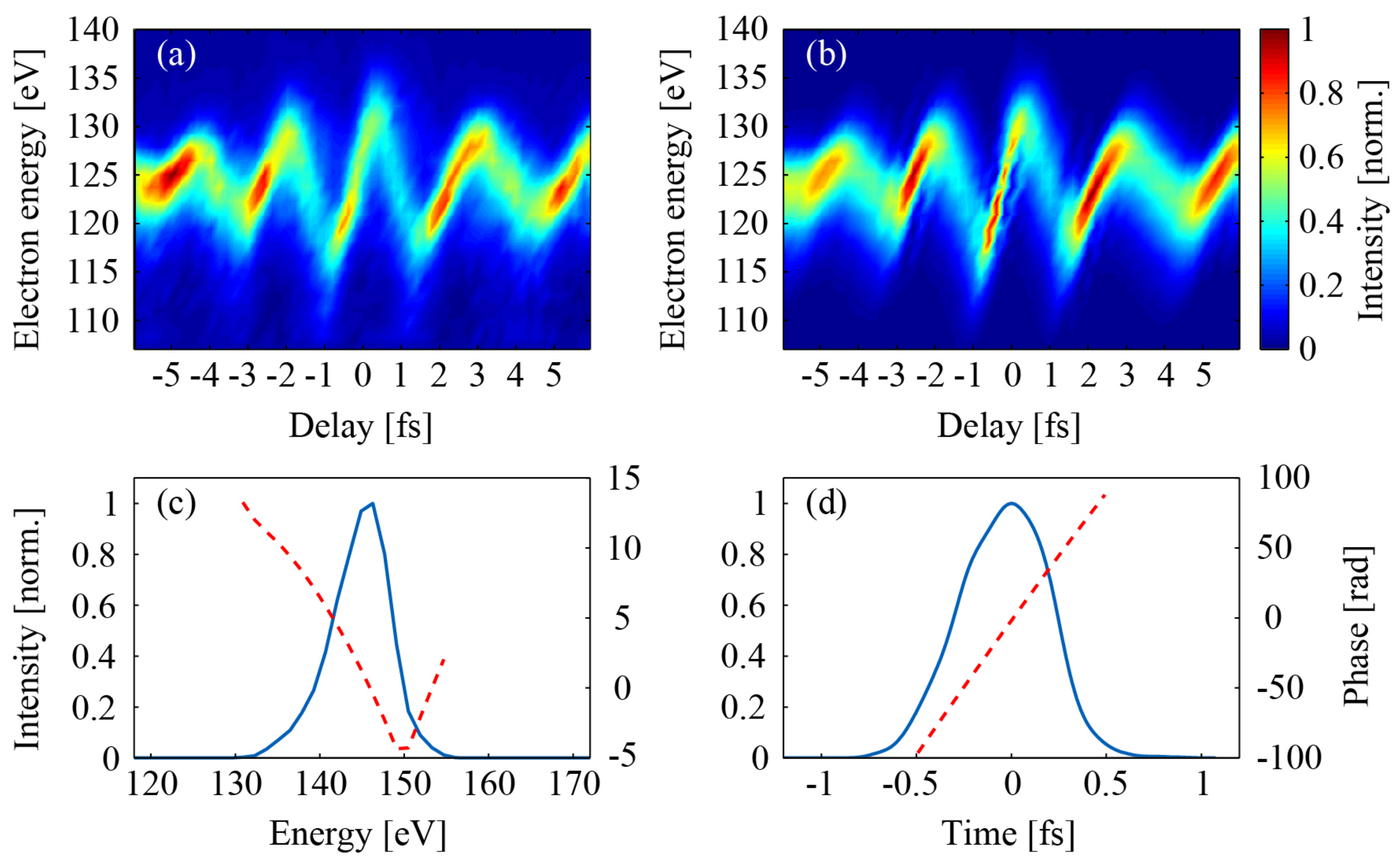
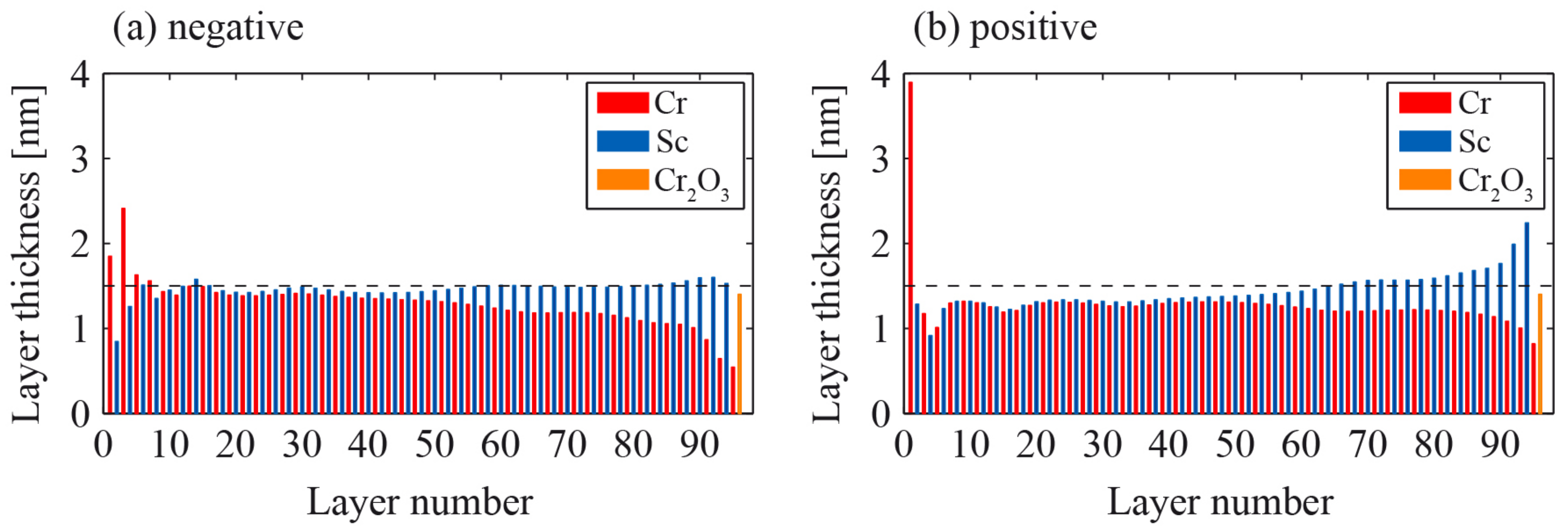
4.3.2. Cr/Sc Multilayer Mirror for Attosecond Pulses at 145 eV
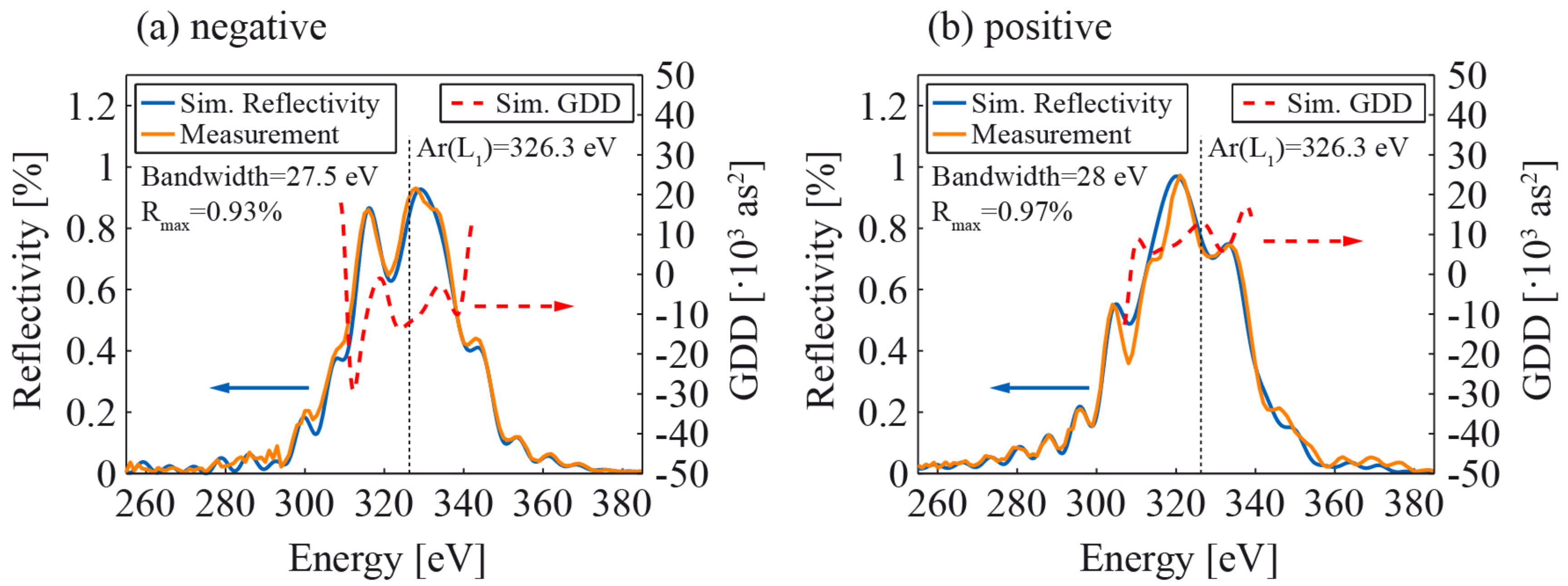
4.4. Multilayer Mirrors for Attosecond Pulses in the Water Window Soft X-Ray Range
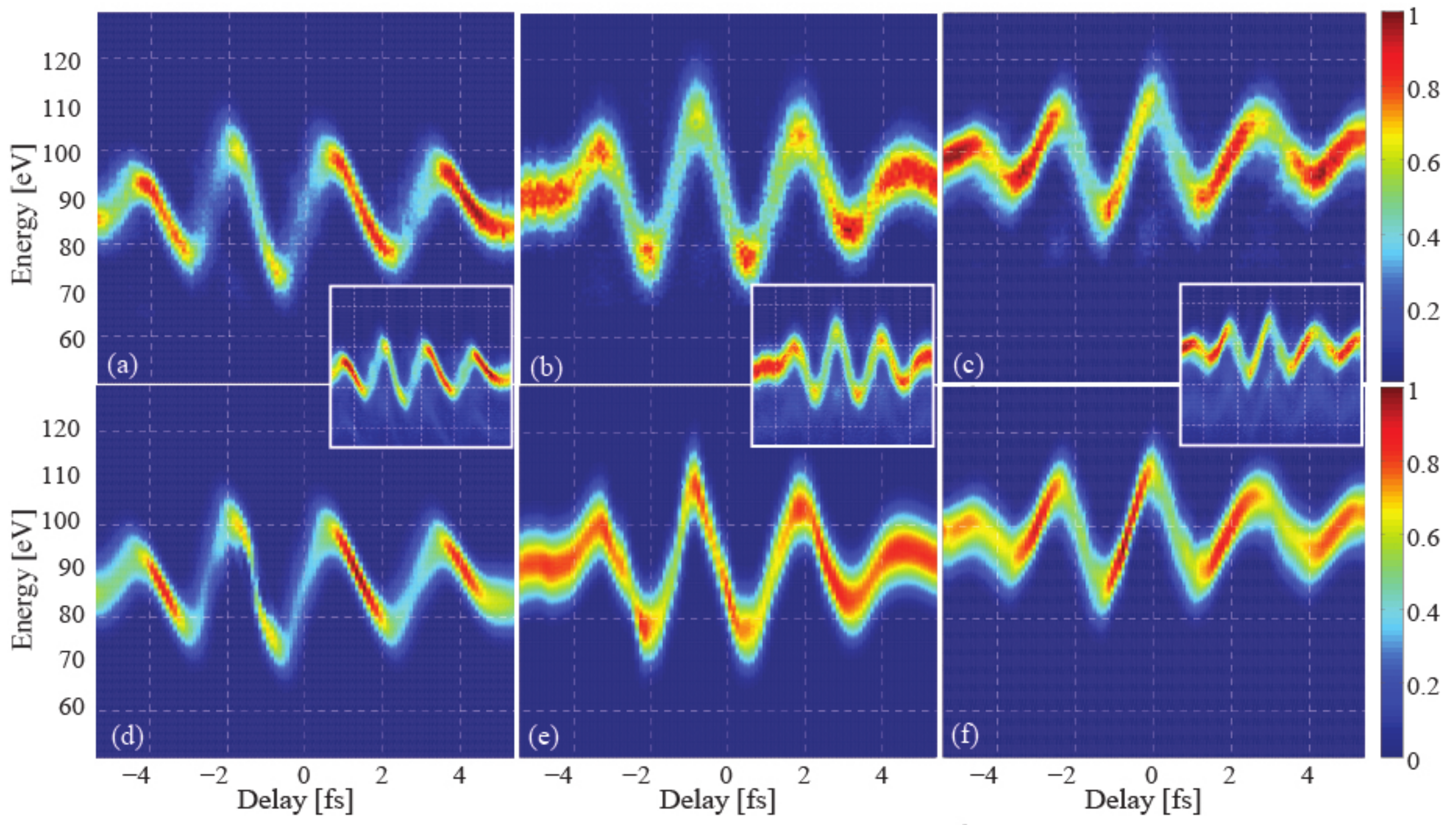
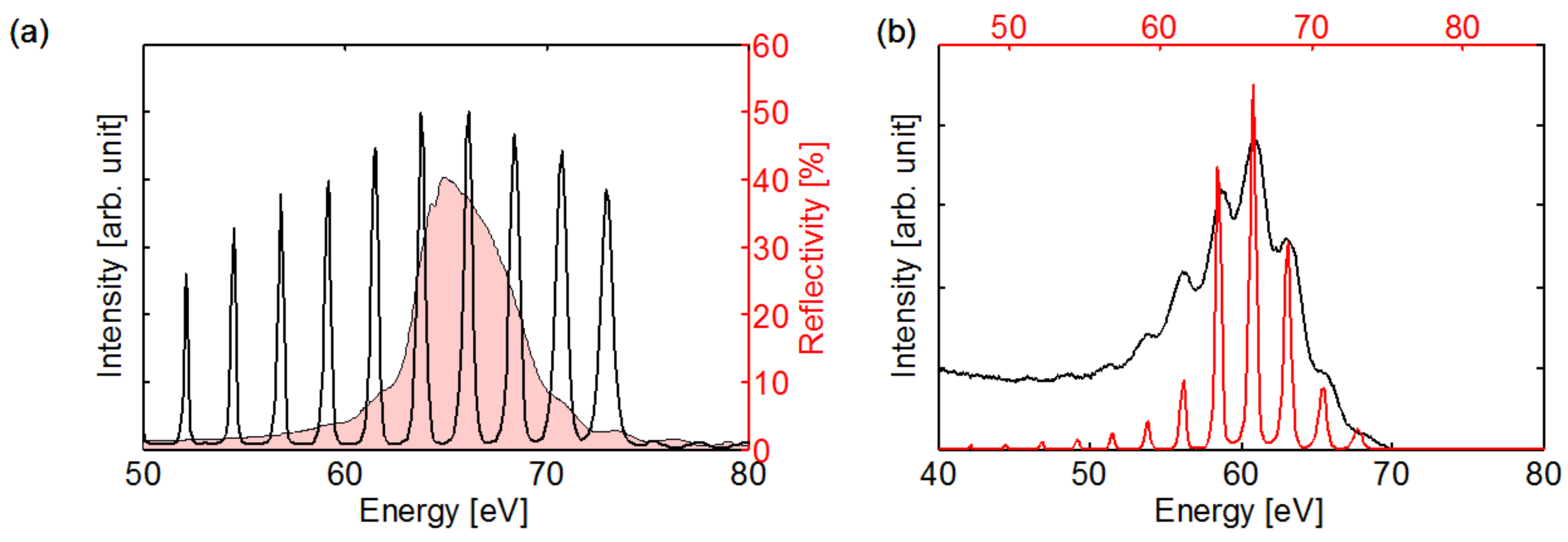
4.5. Attosecond Photoelectron Spectroscopy Utilizing Pulse Trains
5. Outlook
5.1. The Way Toward Ever-Shorter Pulses: Approaching the Atomic Unit of Time
5.2. Multilayer Mirrors for HHG Photon Energies up to the keV Spectral Range
- High single interface reflectivity for grazing incidence.
- For grazing optics, in the case of keV: A photon energy of 1000 eV corresponds to a wavelength of nm. This leads, in the case of normal incidence, to a period in a multilayer mirror. Assuming typical two-material systems, one ends up in a layer with a thickness of ∼ nm, which is close to the limit of technical realization.
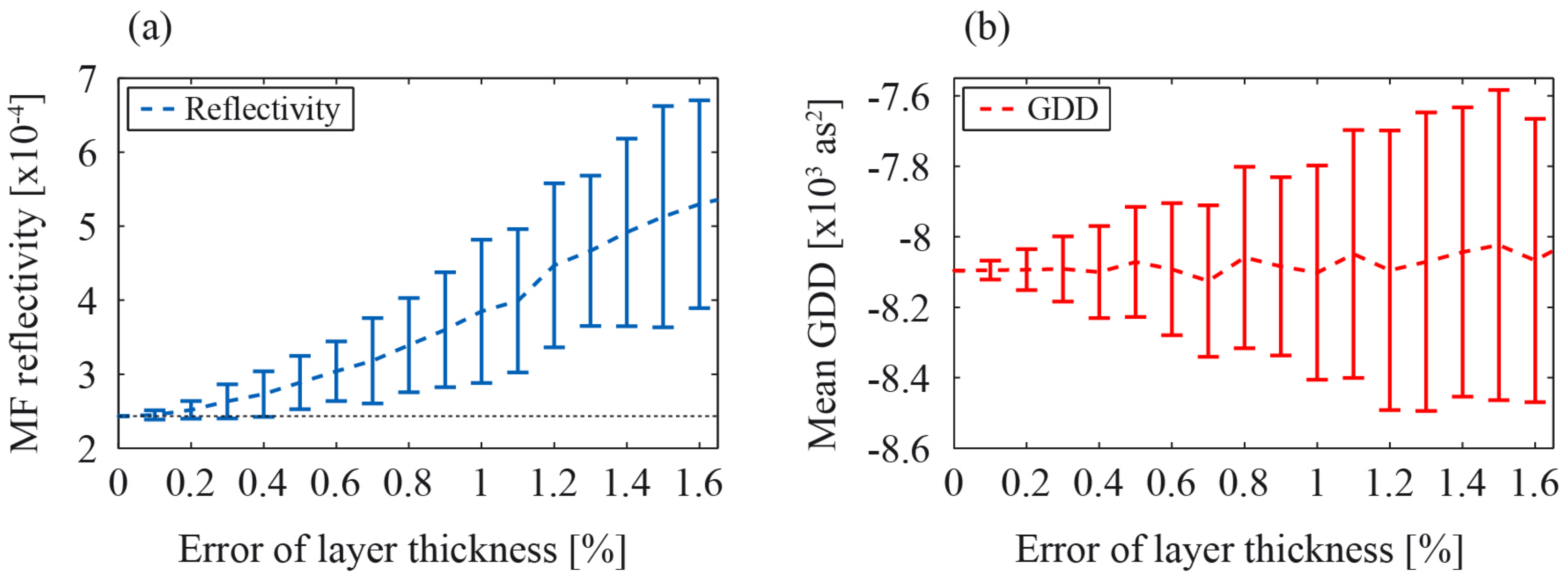
- One can minimize the influence of the roughness on the reflectivity performance: The lower the -ratio, the lower is the reflectivity loss. One thus can minimize the reflectivity loss by reducing the interface roughness or increase the period thickness d. Keeping the central energy from a multilayer mirror constant leads, in the case of a higher period thickness, to a lower grazing incidence angle. This overlaps with the previous statement. Typical roughness values are in the range of 0.4–0.6 nm. Comparable thickness values are strongly discouraged.
- In the case of grazing incidence (compared with multilayer mirrors at normal incidence), only a few layers can contribute to the overall reflectivity, which results in a certain energy in a higher spectral bandwidth support. According to the relation between bandwidth and temporal pulse duration, , this presents the opportunity for shorter pulses.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hentschel, M.; Kienberger, R.; Spielmann, C.; Reider, G.A.; Milosevic, N.; Brabec, T.; Corkum, P.; Heinzmann, U.; Drescher, M.; Krausz, F. Attosecond metrology. Nature 2001, 414, 509–513. [Google Scholar] [CrossRef] [PubMed]
- Morawe, C.; Osterhoff, M. Hard X-ray focusing with curved reflective multilayers. X-Ray Opt. Instrum. 2010, 2010, 479631. [Google Scholar] [CrossRef]
- Schmidt, J.; Guggenmos, A.; Hofstetter, M.; Chew, S.H.; Kleineberg, U. Generation of circularly polarized high harmonic radiation using a transmission multilayer quarter waveplate. Opt. Express 2015, 23, 33564. [Google Scholar] [CrossRef] [PubMed]
- Zürch, M.; Rothhardt, J.; Hädrich, S.; Demmler, S.; Krebs, M.; Limpert, J.; Tünnermann, A.; Guggenmos, A.; Kleineberg, U.; Spielmann, C. Real-time and sub-wavelength ultrafast coherent diffraction imaging in the extreme ultraviolet. Sci. Rep. 2014, 4, 1–5. [Google Scholar] [CrossRef]
- Spiller, E. Reflective multilayer coatings for the far UV region. Appl. Opt. 1976, 15, 2333–2338. [Google Scholar] [CrossRef]
- Bajt, S. Improved reflectance and stability of Mo-Si multilayers. Opt. Eng. 2002, 41, 1797. [Google Scholar] [CrossRef]
- Kozhevnikov, I.V.; Balakireva, L.L.; Fedorenko, A.I.; Kopealets, I.A.; Levashov, V.E.; Stetsenko, A.N.; Struk, I.I.; Vinogradov, A.V. Synthesis and measurement of Os-Si multilayer mirrors optimized for the wavelength 380 Å. Opt. Commun. 1996, 125, 13–17. [Google Scholar] [CrossRef]
- Rajesh, S.; Arivazhagan, V.; Parvathi, M.M. Structural, optical and electrical properties of vacuum evaporated PbSe/ZnSe multilayer thin films. AIP Conf. Proc. 2012, 1451, 197–199. [Google Scholar] [CrossRef]
- Skulina, K.M.; Alford, C.S.; Bionta, R.M.; Makowiecki, D.M.; Gullikson, E.M.; Soufli, R.; Kortright, J.B.; Underwood, J.H. Molybdenum/beryllium multilayer mirrors for normal incidence in the extreme ultraviolet. Appl. Opt. 1995, 34, 3727. [Google Scholar] [CrossRef]
- Bajt, S.; Stearns, D.G.; Kearney, P.A. Investigation of the amorphous-to-crystalline transition in Mo/Si multilayers. J. Appl. Phys. 2001, 90, 1017–1025. [Google Scholar] [CrossRef]
- Rao, P.N.; Nayak, M.; Lodha, G.S.; Rai, S.K.; Srivastava, A.K.; Modi, M.H.; Sagdeo, A. Fabrication and evaluation of large area Mo/Si soft X-ray multilayer mirrors at Indus SR facilities. Adv. Opt. Technol. 2012, 2012, 976868. [Google Scholar] [CrossRef]
- Voronov, D.L.; Gawlitza, P.; Cambie, R.; Dhuey, S.; Gullikson, E.M.; Warwick, T.; Braun, S.; Yashchuk, V.V.; Padmore, H.A. Conformal growth of Mo/Si multilayers on grating substrates using collimated ion beam sputtering. J. Appl. Phys. 2012, 111, 093521. [Google Scholar] [CrossRef]
- El Hajj, A.; Lucas, B.; Chakaroun, M.; Antony, R.; Ratier, B.; Aldissi, M. Optimization of ZnO/Ag/ZnO multilayer electrodes obtained by Ion Beam Sputtering for optoelectronic devices. Thin Solid Films 2012, 520, 4666–4668. [Google Scholar] [CrossRef]
- Grigonis, M.; Émile, J. Knystautas. C/Si multilayer mirrors for the 25–30-nm wavelength region. Appl. Opt. 1997, 36, 2839–2842. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhao, H.; Yao, Q.; Xu, J.; Kimura, H. Structure and magnetism of ZnO/Co multilayers prepared by pulsed laser deposition. Cryst. Res. Technol. 2012, 47, 799–803. [Google Scholar] [CrossRef]
- Siraj, K.; Khaleeq-Ur-Rahman, M.; Rafique, M.S.; Munawar, M.Z.; Naseem, S.; Riaz, S. Pulsed laser deposition and characterization of multilayer metal-carbon thin films. Appl. Surf. Sci. 2011, 257, 6445–6450. [Google Scholar] [CrossRef]
- Chrisey, D.B.; Hubler, G.K. Pulsed Laser Deposition of Thin Films; John Wiley & Sons, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Martínez-Galarce, D.; Soufli, R.; Windt, D.L.; Bruner, M.; Gullikson, E.; Khatri, S.; Spiller, E.; Robinson, J.C.; Baker, S.; Prast, E. Multisegmented, multilayer-coated mirrors for the Solar Ultraviolet Imager. Opt. Eng. 2013, 52, 095102. [Google Scholar] [CrossRef]
- Wagner, C.; Harned, N. EUV lithography: Lithography gets extreme. Nat. Photonics 2010, 4, 24–26. [Google Scholar] [CrossRef]
- Chao, W.; Kim, J.; Rekawa, S.; Fischer, P.; Anderson, E.H. Demonstration of 12 nm Resolution Fresnel Zone Plate Lens based Soft X-ray Microscopy. Opt. Express 2009, 17, 17669. [Google Scholar] [CrossRef]
- Champeaux, J.P.; Troussel, P.; Villier, B.; Vidal, V.; Khachroum, T.; Vidal, B.; Krumrey, M. Development and realization of non-periodic W/Si multilayer mirrors for 5–14 keV X-ray plasma diagnostic. Nucl. Instrum. Methods Phys. Res. Sec. A 2007, 581, 687–694. [Google Scholar] [CrossRef]
- Andronova, N.V.; Kohn, V.G.; Chechin, A.I. Multilayer mirrors as synchrotron radiation monochromators. Nucl. Inst. Methods Phys. Res. A 1995, 359, 131–134. [Google Scholar] [CrossRef]
- Ferray, M.; L’Huillier, A.; Li, X.F.; Lomprk, L.A.; Mainfray, G.; Manus, C. Multiple-harmonic conversion of 1064 nm radiationin rare gases. J. Phys. B Atomic Mol. Opt. Phys. 1988, 21, L31. [Google Scholar] [CrossRef]
- Prasciolu, M.; Leontowich, A.F.G.; Beyerlein, K.R.; Bajt, S. Thermal stability studies of short period Sc/Cr and Sc/B4C/Cr multilayers. Appl. Opt. 2014, 53, 2126. [Google Scholar] [CrossRef] [PubMed]
- Helml, W.; Maier, A.R.; Schweinberger, W.; Grguraš, I.; Radcliffe, P.; Doumy, G.; Roedig, C.; Gagnon, J.; Messerschmidt, M.; Schorb, S.; et al. Measuring the temporal structure of few-femtosecond free-electron laser X-ray pulses directly in the time domain. Nat. Photonics 2014, 8, 950–957. [Google Scholar] [CrossRef]
- Kling, M.F.; Vrakking, M.J. Attosecond Electron Dynamics. Annu. Rev. Phys. Chem. 2008, 59, 463–492. [Google Scholar] [CrossRef] [PubMed]
- Fie, M.; Schultze, M.; Goulielmakis, E.; Dennhardt, B.; Gagnon, J.; Hofstetter, M.; Kienberger, R.; Krausz, F. Versatile apparatus for attosecond metrology and spectroscopy. Rev. Sci. Instrum. 2010, 81, 093103. [Google Scholar] [CrossRef]
- Schweinberger, W.; Sommer, A.; Bothschafter, E.; Li, J.; Krausz, F.; Kienberger, R.; Schultze, M. Waveform-controlled near-single-cycle milli-joule laser pulses generate sub-10 nm extreme ultraviolet continua. Opt. Lett. 2012, 37, 3573. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef]
- Descamps, D.; Lyngå, C.; Norin, J.; L’huillier, A.; Wahlström, C.G.; Hergott, J.F.; Merdji, H.; Salières, P.; Bellini, M.; Hänsch, T.W. Extreme ultraviolet interferometry measurements with high-order harmonics. Opt. Lett. 2000, 25, 135–137. [Google Scholar] [CrossRef]
- Lee, J.; Carlson, D.R.; Jones, R.J. Optimizing intracavity high harmonic generation for XUV fs frequency combs. Opt. Express 2011, 19, 23315–23326. [Google Scholar] [CrossRef]
- Goulielmakis, E.; Loh, Z.H.; Wirth, A.; Santra, R.; Rohringer, N.; Yakovlev, V.S.; Zherebtsov, S.; Pfeifer, T.; Azzeer, A.M.; Kling, M.F.; et al. Real-time observation of valence electron motion. Nature 2010, 466, 739–743. [Google Scholar] [CrossRef] [PubMed]
- Nisoli, M.; Decleva, P.; Calegari, F.; Palacios, A.; Martín, F. Attosecond Electron Dynamics in Molecules. Chem. Rev. 2017, 117, 10760–10825. [Google Scholar] [CrossRef] [PubMed]
- Neppl, S.; Ernstorfer, R.; Cavalieri, A.L.; Lemell, C.; Wachter, G.; Magerl, E.; Bothschafter, E.M.; Jobst, M.; Hofstetter, M.; Kleineberg, U.; et al. Direct observation of electron propagation and dielectric screening on the atomic length scale. Nature 2015, 517, 342–346. [Google Scholar] [CrossRef] [PubMed]
- Chew, S.H.; Sümann, F.; Späth, C.; Wirth, A.; Schmidt, J.; Zherebtsov, S.; Guggenmos, A.; Oelsner, A.; Weber, N.; Kapaldo, J.; et al. Time-of-flight-photoelectron emission microscopy on plasmonic structures using attosecond extreme ultraviolet pulses. Appl. Phys. Lett. 2012, 100, 1–5. [Google Scholar] [CrossRef]
- Tao, Z.; Chen, C.; Szilvási, T.; Keller, M.; Mavrikakis, M.; Kapteyn, H.; Murnane, M. Direct time-domain observation of attosecond final-state lifetimes in photoemission from solids. Science 2016, 353, 62–67. [Google Scholar] [CrossRef] [PubMed]
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-ray interactions: photoabsorption, scattering, transmission, and reflection at E = 50-30000 eV, Z = 1-92. Atomic Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Chi, E.; Shim, J.; Kwak, J.; Baik, H. Silicide formation by solid-state diffusion in Mo/Si multilayer thin films. J. Mater. Sci. 1996, 31, 3567–3572. [Google Scholar] [CrossRef]
- Hofstetter, M.; Aquila, A.; Schultze, M.; Guggenmos, A.; Yang, S.; Gullikson, E.; Huth, M.; Nickel, B.; Gagnon, J.; Yakovlev, V.S.; et al. Lanthanum-molybdenum multilayer mirrors for attosecond pulses between 80 and 130 eV. New J. Phys. 2011, 13, 063038. [Google Scholar] [CrossRef]
- Gerald, E.; Jellison, J. Data Analysis for Spectroscopic Ellipsometry. In Handbook of Ellipsometry; Tompkins, H.G., Irene, E.A., Eds.; William Andrew Publishing: Norwich, NY, USA, 2005; pp. 237–296. [Google Scholar]
- Gullikson, E.M.; Mrowka, S.; Kaufmann, B.B. Recent Developments in EUV Reflectometry at the Advanced Light Source. Proc. SPIE 2001, 4343, 363–373. [Google Scholar] [CrossRef]
- Singh, S.; Basu, S.; Bhatt, P.; Poswal, A.K. Kinetics of alloy formation at the interfaces in a Ni-Ti multilayer: X-ray and neutron reflectometry study. Phys. Rev. B 2009, 79, 1–9. [Google Scholar] [CrossRef]
- Guggenmos, A.; Radünz, S.; Rauhut, R.; Hofstetter, M.; Venkatesan, S.; Wochnik, A.; Gullikson, E.M.; Fischer, S.; Nickel, B.; Scheu, C.; et al. Ion polished Cr/Sc attosecond multilayer mirrors for high water window reflectivity. Opt. Express 2014, 22, 26526–26536. [Google Scholar] [CrossRef]
- Tikhonravov, A.V.; Trubetskov, M.K.; DeBell, G.W. Optical coating design approaches based on the needle optimization technique. Appl. Opt. 2007, 46, 704–710. [Google Scholar] [CrossRef] [PubMed]
- Yakovlev, V.; Tempea, G. Optimization of chirped mirrors. Appl. Opt. 2002, 41, 6514–6520. [Google Scholar] [CrossRef] [PubMed]
- Hamelmann, F.; Haindl, G.; Schmalhorst, J.; Aschentrup, A.; Majkova, E.; Kleineberg, U.; Heinzmann, U.; Klipp, A.; Jutzi, P.; Anopchenko, A.; et al. Metal oxide/silicon oxide multilayer with smooth interfaces produced by in situ controlled plasma-enhanced MOCVD. Thin Solid Films 2000, 358, 90–93. [Google Scholar] [CrossRef]
- Thornton, R.L.; Burnham, R.D.; Streifer, W. High reflectivity GaAs-AlGaAs mirrors fabricated by metalorganic chemical vapor deposition. Appl. Phys. Lett. 1984, 45, 1028–1030. [Google Scholar] [CrossRef]
- Corkum, P.; Krausz, F. Attosecond science. Nat. Phys. 2007, 3, 381–387. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- López-Martens, R.; Varjú, K.; Johnsson, P.; Mauritsson, J.; Mairesse, Y.; Salières, P.; Gaarde, M.B.; Schafer, K.J.; Persson, A.; Svanberg, S.; et al. Amplitude and phase control of attosecond light pulses. Phys. Rev. Lett. 2005, 94, 1–4. [Google Scholar] [CrossRef]
- Sansone, G.; Benedetti, E.; Calegari, F.; Vozzi, C.; Avaldi, L.; Flammini, R.; Poletto, L.; Villoresi, P.; Altucci, C.; Velotta, R.; et al. Isolated Single-Cycle Attosecond Pulses. Science 2006, 314, 443–446. [Google Scholar] [CrossRef]
- Rohwer, T.; Hellmann, S.; Wiesenmayer, M.; Sohrt, C.; Stange, A.; Slomski, B.; Carr, A.; Liu, Y.; Avila, L.M.; Kalläsignne, M.; et al. Collapse of long-range charge order tracked by time-resolved photoemission at high momenta. Nature 2011, 471, 490–494. [Google Scholar] [CrossRef]
- Morlens, A.S.; López-Martens, R.; Boyko, O.; Zeitoun, P.; Balcou, P.; Varjú, K.; Gustafsson, E.; Remetter, T.; L’Huillier, A.; Kazamias, S.; et al. Design and characterization of extreme-ultraviolet broadband mirrors for attosecond science. Opt. Lett. 2006, 31, 1558. [Google Scholar] [CrossRef] [PubMed]
- Uspenskii, Y.A.; Levashov, V.E.; Vinogradov, A.V.; Fedorenko, A.I.; Kondratenko, V.V.; Pershin, Y.P.; Zubarev, E.N.; Mrowka, S.; Schäfers, F. Sc-Si normal incidence mirrors for a VUV interval of 35–50 nm. Nucl. Instrum. Methods Phys. Res. Sec. A 2000, 448, 147–151. [Google Scholar] [CrossRef]
- Goulielmakis, E.; Schultze, M.; Hofstetter, M.; Yakovlev, V.S.; Gagnon, J.; Uiberacker, M.; Aquila, A.L.; Gullikson, E.M.; Attwood, D.T.; Kienberger, R.; et al. Single-Cycle Nonlinear Optics. Science 2008, 320, 1614–1617. [Google Scholar] [CrossRef] [PubMed]
- Guggenmos, A.; Akil, A.; Ossiander, M.; Schäffer, M.; Azzeer, A.M.; Boehm, G.; Amann, M.C.; Kienberger, R.; Schultze, M.; Kleineberg, U. Attosecond photoelectron streaking with enhanced energy resolution for small-bandgap materials. Opt. Lett. 2016, 41, 3714. [Google Scholar] [CrossRef] [PubMed]
- Bourassin-Bouchet, C.; De Rossi, S.; Wang, J.; Meltchakov, E.; Giglia, A.; Mahne, N.; Nannarone, S.; Delmotte, F. Shaping of single-cycle sub-50-attosecond pulses with multilayer mirrors. New J. Phys. 2012, 14, 023040. [Google Scholar] [CrossRef]
- Hofstetter, M.; Schultze, M.; Fieß, M.; Dennhardt, B.; Guggenmos, A.; Gagnon, J.; Yakovlev, V.S.; Goulielmakis, E.; Kienberger, R.; Gullikson, E.M.; et al. Attosecond dispersion control by extreme ultraviolet multilayer mirrors. Opt. Express 2011, 19, 1767. [Google Scholar] [CrossRef] [PubMed]
- Ménesguen, Y.; De Rossi, S.; Meltchakov, E.; Delmotte, F. Aperiodic multilayer mirrors for efficient broadband reflection in the extreme ultraviolet. Appl. Phys. A Mater. Sci. Process. 2010, 98, 305–309. [Google Scholar] [CrossRef]
- Gullikson, E.; Underwood, J.; Batson, P.; Nikitin, V. A soft x-ray/EUV reflectometer based on a laser produced plasma source. J. X-Ray Sci. Technol. 1992, 3, 283–299. [Google Scholar] [CrossRef]
- Kienberger, R.; Goulielmakis, E.; Uiberacker, M.; Baltuska, A.; Yakovlev, V.; Bammer, F.; Scrinzi, A.; Westerwalbesloh, T.; Kleineberg, U.; Heinzmann, U.; et al. Atomic transient recorder. Nature 2004, 427, 817–821. [Google Scholar] [CrossRef]
- Kitzler, M.; Milosevic, N.; Scrinzi, A.; Krausz, F.; Brabec, T. Quantum Theory of Attosecond XUV Pulse Measurement by Laser Dressed Photoionization. Phys. Rev. Lett. 2002, 88, 4. [Google Scholar] [CrossRef]
- Trebino, R.; DeLong, K.W.; Fittinghoff, D.N.; Sweetser, J.N.; Krumbügel, M.A.; Richman, B.A.; Kane, D.J. Measuring ultrashort laser pulses in the time-frequency domain using frequency-resolved optical gating. Rev. Sci. Instrum. 1997, 68, 3277–3295. [Google Scholar] [CrossRef]
- Mairesse, Y.; de Bohan, A.; Frasinski, L.J.; Merdji, H.; Dinu, L.C.; Monchicourt, P.; Breger, P.; Kovačev, M.; Taïeb, R.; Carré, B.; et al. Attosecond Synchronization of High-Harmonic Soft X-rays. Science 2003, 302, 1540–1543. [Google Scholar] [CrossRef]
- Gagnon, J.; Goulielmakis, E.; Yakovlev, V.S. The accurate FROG characterization of attosecond pulses from streaking measurements. Appl. Phys. B Lasers Opt. 2008, 92, 25–32. [Google Scholar] [CrossRef]
- Guggenmos, A.; Jobst, M.; Ossiander, M.; Radünz, S.; Riemensberger, J.; Schäffer, M.; Akil, A.; Jakubeit, C.; Böhm, P.; Noever, S.; et al. Chromium/scandium multilayer mirrors for isolated attosecond pulses at 145 eV. Opt. Lett. 2015, 40, 2846–2849. [Google Scholar] [CrossRef] [PubMed]
- Guggenmos, A.; Rauhut, R.; Hofstetter, M.; Hertrich, S.; Nickel, B.; Schmidt, J.; Gullikson, E.M.; Seibald, M.; Schnick, W.; Kleineberg, U. Aperiodic CrSc multilayer mirrors for attosecond water window pulses. Opt. Express 2013, 21, 21728–21740. [Google Scholar] [CrossRef] [PubMed]
- Schultze, M.; Fieß, M.; Karpowicz, N.; Gagnon, J.; Korbman, M.; Hofstetter, M.; Neppl, S.; Cavalieri, A.L.; Komninos, Y.; Mercouris, T.; et al. Delay in Photoemission. Science 2010, 1658, 1658–1662. [Google Scholar] [CrossRef]
- Montcalm, C.; Sullivan, B.T.; Duguay, S.; Ranger, M.; Steffens, W.; Pépin, H.; Chaker, M. In situ reflectance measurements of soft-x-ray/extreme-ultraviolet Mo/Y multilayer mirrors. Opt. Lett. 1995, 20, 1450–1452. [Google Scholar] [CrossRef]
- Soufli, R.; Spiller, E.; Windt, D.L.; Robinson, J.C.; Gullikson, E.M.; Rodriguez-de Marcos, L.; Fernández-Perea, M.; Baker, S.L.; Aquila, A.L.; Dollar, F.J.; et al. In-band and out-of-band reflectance calibrations of the EUV multilayer mirrors of the Atmospheric Imaging Assembly Instrument aboard the Solar Dynamics Observatory. Proc. SPIE 2012, 8443, 84433C. [Google Scholar] [CrossRef]
- Bajt, S. Molybdenum–ruthenium/beryllium multilayer coatings. J. Vac. Sci. Technol. A 2000, 18, 557–559. [Google Scholar] [CrossRef]
- Sae-Lao, B.; Montcalm, C. Molybdenum-strontium multilayer mirrors for the 8–12 nm extreme-ultraviolet wavelength region. Opt. Lett. 2001, 26, 468–470. [Google Scholar] [CrossRef]
- Montcalm, C.; Kearney, P.A.; Slaughter, J.M.; Sullivan, B.T.; Chaker, M.; Pépin, H.; Falco, C.M. Survey of Ti-, B-, and Y-based soft x-ray-extreme ultraviolet multilayer mirrors for the 2- to 12-nm wavelength region. Appl. Opt. 1996, 35, 5134–5147. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, J.; Yakovlev, V.S. The robustness of attosecond streaking measurements. Opt. Express 2009, 17, 17678. [Google Scholar] [CrossRef] [PubMed]
- Neppl, S.; Ernstorfer, R.; Bothschafter, E.M.; Cavalieri, A.L.; Menzel, D.; Barth, J.V.; Krausz, F.; Kienberger, R.; Feulner, P. Attosecond time-resolved photoemission from core and valence states of magnesium. Phys. Rev. Lett. 2012, 109, 22–26. [Google Scholar] [CrossRef] [PubMed]
- Aquila, A.; Salmassi, F.; Gullikson, E. Metrologies for the phase characterization of attosecond extreme ultraviolet optics. Opt. Lett. 2008, 33, 455–457. [Google Scholar] [CrossRef]
- Muller, H.G. Reconstruction of attosecond harmonic beating by interference of two-photon transitions. Appl. Phys. B Lasers Opt. 2002, 74, 17–21. [Google Scholar] [CrossRef]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a Train of Attosecond Pulses from High Harmonic Generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef] [PubMed]
- Cattaneo, L.; Vos, J.; Lucchini, M.; Gallmann, L.; Cirelli, C.; Keller, U. Comparison of attosecond streaking and RABBITT. Opt. Express 2016, 24, 29060–29076. [Google Scholar] [CrossRef] [PubMed]
- Isinger, M.; Squibb, R.; Busto, D.; Zhong, S.; Harth, A.; Kroon, D.; Nandi, S.; Arnold, C.L.; Miranda, M.; Dahlström, J.M.; et al. Photoionization in the time and frequency domain. Science 2017, 358, 893–896. [Google Scholar] [CrossRef]
- Jain, A.; Gaumnitz, T.; Bray, A.; Kheifets, A.; Wörner, H.J. Photoionization delays in xenon using single-shot referencing in the collinear back-focusing geometry. Opt. Lett. 2018, 43, 4510–4513. [Google Scholar] [CrossRef]
- Heuser, S.; Jiménez Galán, A.; Cirelli, C.; Marante, C.; Sabbar, M.; Boge, R.; Lucchini, M.; Gallmann, L.; Ivanov, I.; Kheifets, A.S.; et al. Angular dependence of photoemission time delay in helium. Phys. Rev. A 2016, 94, 063409. [Google Scholar] [CrossRef]
- Lucchini, M.; Castiglioni, L.; Kasmi, L.; Kliuiev, P.; Ludwig, A.; Greif, M.; Osterwalder, J.; Hengsberger, M.; Gallmann, L.; Keller, U. Light-Matter Interaction at Surfaces in the Spatiotemporal Limit of Macroscopic Models. Phys. Rev. Lett. 2015, 115, 137401. [Google Scholar] [CrossRef] [PubMed]
- Locher, R.; Castiglioni, L.; Lucchini, M.; Greif, M.; Gallmann, L.; Osterwalder, J.; Hengsberger, M.; Keller, U. Energy-dependent photoemission delays from noble metal surfaces by attosecond interferometry. Optica 2015, 2, 405–410. [Google Scholar] [CrossRef]
- Heinrich, S.; Saule, T.; Högner, M.; Cui, Y.; Guggenmos, A.; Pupeza, I.; Kleineberg, U. Energy dependent attosecond photoemission delays from core and valence band states of tungsten. 2018; in press. [Google Scholar]
- Strayer, R.; Mackie, W.; Swanson, L. Work function measurements by the field emission retarding potential method. Surf. Sci. 1973, 34, 225–248. [Google Scholar] [CrossRef]
- Zhao, K.; Zhang, Q.; Chini, M.; Wu, Y.; Wang, X.; Chang, Z. Tailoring a 67 attosecond pulse through advantageous phase-mismatch. Opt. Lett. 2012, 37, 3891. [Google Scholar] [CrossRef] [PubMed]
- Popmintchev, T.; Chen, M.C.; Popmintchev, D.; Arpin, P.; Brown, S.; Ališauskas, S.; Andriukaitis, G.; Balčiunas, T.; Mücke, O.D.; Pugzlys, A.; et al. Bright coherent ultrahigh harmonics in the kev x-ray regime from mid-infrared femtosecond lasers. Science 2012, 336, 1287–1291. [Google Scholar] [CrossRef] [PubMed]
- Bucksbaum, P.H. The future of attosecond spectroscopy. Science 2007, 317, 766–769. [Google Scholar] [CrossRef] [PubMed]
- Haessler, S.; Balčiunas, T.; Fan, G.; Chipperfield, L.E.; Baltuška, A. Enhanced multi-colour gating for the generation of high-power isolated attosecond pulses. Sci. Rep. 2015, 5, 1–15. [Google Scholar] [CrossRef]
- Ossiander, M.; Siegrist, F.; Shirvanyan, V.; Pazourek, R.; Sommer, A.; Latka, T.; Guggenmos, A.; Nagele, S.; Feist, J.; Burgdörfer, J.; et al. Attosecond correlation dynamics. Nat. Phys. 2017, 13, 280–285. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guggenmos, A.; Cui, Y.; Heinrich, S.; Kleineberg, U. Attosecond Pulse Shaping by Multilayer Mirrors. Appl. Sci. 2018, 8, 2503. https://doi.org/10.3390/app8122503
Guggenmos A, Cui Y, Heinrich S, Kleineberg U. Attosecond Pulse Shaping by Multilayer Mirrors. Applied Sciences. 2018; 8(12):2503. https://doi.org/10.3390/app8122503
Chicago/Turabian StyleGuggenmos, Alexander, Yang Cui, Stephan Heinrich, and Ulf Kleineberg. 2018. "Attosecond Pulse Shaping by Multilayer Mirrors" Applied Sciences 8, no. 12: 2503. https://doi.org/10.3390/app8122503
APA StyleGuggenmos, A., Cui, Y., Heinrich, S., & Kleineberg, U. (2018). Attosecond Pulse Shaping by Multilayer Mirrors. Applied Sciences, 8(12), 2503. https://doi.org/10.3390/app8122503




