Featured Application
This work proposes practical image processing to identify main cracks on concrete surfaces by TLS associated with the octree structure.
Abstract
Terrestrial laser scanning (TLS) provides a rapid remote sensing technique to model 3D objects but can also be used to assess the surface condition of structures. In this study, an effective image processing technique is proposed for crack detection on images extracted from the octree structure of TLS data. To efficiently utilize TLS for the surface condition assessment of large structures, a process was constructed to compress the original scanned data based on the octree structure. The point cloud data obtained by TLS was converted into voxel data, and further converted into an octree data structure, which significantly reduced the data size but minimized the loss of resolution to detect cracks on the surface. The compressed data was then used to detect cracks on the surface using a combination of image processing algorithms. The crack detection procedure involved the following main steps: (1) classification of an image into three categories (i.e., background, structural joints and sediments, and surface) using K-means clustering according to color similarity, (2) deletion of non-crack parts on the surface using improved subtraction combined with median filtering and K-means clustering results, (3) detection of major crack objects on the surface based on Otsu’s binarization method, and (4) highlighting crack objects by morphological operations. The proposed technique was validated on a spillway wall of a concrete dam structure in South Korea. The scanned data was compressed up to 50% of the original scanned data, while showing good performance in detecting cracks with various shapes.
1. Introduction
1.1. Background and Purpose of the Study
Terrestrial laser scanning (TLS) is a system that can acquire the three-dimensional (3D) position information of an object remotely with a laser. Terrestrial laser scanning has been increasingly used in the surveys of buildings, bridges, and collapsed rock slopes because it allows easy and rapid surveying, even in the lack of access due to its contactless data collection. Terrestrial laser scanning is mainly developed for the purpose of providing a rapid and accurate remote sensing for 3D objects modeling but can be also used to monitor the structural condition. Moreover, TLS shows an equivalent capacity in damage detection and deformation (or volumetric change) evaluation to conventional photographic methods [1].
For the detection of damages such as crack, spalling, and abrasion, Anil et al. [2] showed the feasibility of TLS by presenting that the measurable width, depth, and orientation of cracks according to the sampling interval of the laser scanner, and the range of the laser beam. Giri and Kharkovsky [3] proved that a laser displacement sensor can measure a cracks’ width up to 0.7 mm on a concrete specimen. Laefer et al. [4] configured the fundamental mathematics to determine the detectable minimum crack width with a terrestrial laser scanner in unit-based masonry by a parametric study using orthogonal offset, interval scan angle, crack orientation, and crack depth. Li et al. [5] proposed a crack detection method based on a second derivative image processing of thermal images from laser heated spots, comparing with the dye penetrant inspection. Kim et al. [6] presented a detection technique that can simultaneously localize and quantify spalling defects on concrete surfaces using TLS. Valenca et al. [7] developed an automatic method based on image processing and laser scanning in assessing cracks in bridges. The captured images were orthorectified by geometric information surveyed by TLS, and then an image processing was performed for crack characterization. Xu et al. [8] suggested an automatic crack detection method through TLS for concrete beam surfaces using a few simple imaging processes techniques such as conversion to gray scale, median filtering, and thresholding.
For the deformation or deflection of structures, Tsakiri et al. [9] took advantage of planes fitted to point clouds extracted from the TLS data when gauging the displacement for monitoring of structural deformation. The plane model is suitable for small areas; thus the section is divided into grid cells. As for monitoring of tunnels, Van Gosliga et al. [10] configured the tunnel model with a cylinder to detect deformations in a bored tunnel. Chang et al. [11] analyzed the deformation of a structure surface by statistical regression such as a polynomial function. Koch [12] proposed the lofting method by estimation of control points and the method showed good accuracy in the 3D non-uniform rational b-splines (NURBS) surface. Jafaru et al. [13] presented a 3D point cloud change analysis approach for tracking small movements over time through a combination of a direct point-wise distance metrics in conjunction with statistical sampling. Khaloo and Lattanzi [14] suggested an algorithm to identify structural anomalies in 3D point clouds of infrastructure systems by linear and non-linear transformations from RGB to non-RGB spaces.
Above these, many researchers have carried out various studies on the damage detection and deformation quantification on various structures by TLS or other equivalent methods, such as photography [15,16,17,18,19,20]. Although these studies have evaluated TLS for the purpose of structural health monitoring, the data capacity, resolution, and accuracy of crack recognition are still pointed out as drawbacks of TLS [21,22].
More specifically for damage detection algorithms, the data from photogrammetry, laser scanners [23], and microwave [24] have been utilized, and the associated imaging processing methods such as edge detection techniques [25], histogram matching, image filtering and change detection [26], and automatic thresholding [27] have been proposed by many researchers. Also, in conjunction with image processing, a logical classification has been applied to find and identify various types of defects for the reduction of inspection time and efforts. Sinha et al. [28] used classification of neuro-fuzzy networks and Khanfar et al. [24] applied the fuzzy logic technique to find concrete structural defects. Moon and Kim [29] used neural networks to detect cracks from images, and Kawamura et al. [30] used genetic algorithms to extract crack patterns from digital images. In many papers, the classification methods show a diversity of algorithms, which means that the operational environment is different from place to place. For example, there are many stains, sediments, joints, efflorescence, and micro-cracks on the surface of structures, and it is not easy to distinguish them from the major structural cracks.
1.2. Scope and Method of Research
In this study, an effective technique is proposed to detect main cracks on a concrete structure by applying imaging processing algorithms appropriate to images extracted from the octree structure of TLS data. The proposed technique aims to overcome the pre-mentioned drawbacks while fully taking advantage of the contactless measurement of TLS. To respond to the drawbacks of the data capacity, resolution, and accuracy of crack recognition, a data compression scheme is proposed based on octree data structure, which has been applied to various research fields such as computer graphics, robotics, etc. [31,32,33,34,35,36] and proved to be a reasonable approach in terms of memory usage and search speed [37,38]. Moreover, an improved algorithm using a 3D significant eigenvector-based shape descriptor allows the octree method to provide a better image recognition [39].
The proposed method is summarized by the following work procedures. First, a shape information model that can maintain the shape change in structure throughout the laser scan data was constructed. The shape information model uses an octree data structure through point-cloud processing and voxelization, and it can efficiently downsample and visualize a large-scale scan data. To respond to the diversity of operation environments in detecting cracks, a combination of image processing algorithms, such as K-means clustering [40], subtraction with median filtering [41], binarization [42], and morphological operations were proposed. The crack detection procedure involved the following steps: (1) segmentation for preprocessing, (2) classification of an image into 3 categories (i.e., background, structural joints, and sediments, and surface) using K-means clustering according to the color similarity, (3) conversion to gray scale and image enhancement using median filtering and improved subtraction, (4) deletion of non-crack parts on the surface by K-means clustering results, (5) detection of major crack objects on the surface based on the Otsu’s binarization method, and (6) highlighting crack objects by morphological operations. The overall workflow is presented in Figure 1.
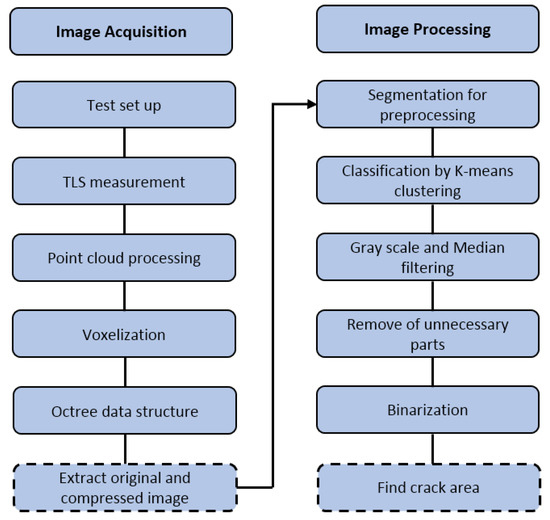
Figure 1.
The workflow of crack detection by terrestrial laser scanning (TLS) measurement.
Then, the proposed technique is validated on a spillway wall of a concrete dam structure in South Korea. The test wall is larger than 100 m2 and has many cracks with various shapes. The wall also has many structural joints and contaminated by serious sediments, which are expected to significantly impede the detection of cracks on the wall surface. The wall is scanned by a Leica ScanStation C5 model at 32 m distance. Along with the original scanned data, the compressed data up to 30%, 50%, and 80% are prepared by the proposed octree data structure. Then, the proposed crack detection procedure is applied to original and compressed images, and the results from the images are compared with the visual inspection result to validate the performance of the proposed technique.
2. TLS Measurement and Data Compression
2.1. 3D Laser Scanning
Terrestrial laser scanning is a technology that helps users easily collect data and generates a 3D virtual model of the physical asset using point clouds as a set of points in 3D space. Laser scanning refers to deflection of the laser beam due to movement of the reflector (mirror), reflection of the laser beam on the object surface, and reception of the reflected laser beam. The laser scanning method includes a triangulation method, a phase difference method, and a time-of-flight method [43]. Laser scanning consists of on-site installation, positioning scan, surface scan, and post-processing of point group coordinate data. The hardware required to operate the laser scanner in the field includes a scanner, a laptop computer, a power supply, and a conveying and a mounting device. When the hardware installation is finished, the scan angle is adjusted to set the scan range on a target object [44].
Since the entire model is achieved by merging the point group coordinate values obtained by each scan, a reference point (reflection target) should be provided to the target point so that at least four reference points are overlapped for each adjacent scanning point. The reference point installed at this time may be absolute coordinates, or relative coordinates around the installation position of the laser scanner. Point coordinate values are accumulated in database (DB) form and can be restored as a 3D image using a post-processing program or numerical analysis of the degree of deformation compared with the original design drawing.
2.2. Voxelization and Octree Data Structure
Voxelization conceptualizes geospatial spaces and express them as volume elements (voxels) using voxel data structures. A voxel is a rectangular parallelepiped block defined in terms of its length (l), width (w), and height (h) and voxel position is indexed by column (i), row (j) and layer (k). The laser scanning point (x, y, z) is transformed to the position of the voxel (i, j, k) [45].
Octree is a data representation method that creates a bounding box for a given shape, and stores it as a visualization object if the shape is contained in the hexahedron equally divided in the x, y, and z coordinates [46]. The octree divides the bisected space in each direction of the x, y, and z axes into eight subspaces and expresses them in a finer area. The eight sub-spaces can be stored in a tree structure as an element called a node, and the depth level of the octree is determined by the number of divided bounding boxes [47]. In this study, the 3D object model (Voxel model) is first generated to easily remove empty nodes by checking empty cells in the sub and left nodes. Thus, it is efficient to implement segmentation and octree in the spatial properties of 3D objects rather than in irregularly distributed point clouds.
Octree has the largest number of leaf nodes corresponding to , and this is equivalent to a 3D grid with a resolution of . Figure 2 shows the number of nodes according to the octree depth level. Here, octree is used to improve processing speed and to save space, and the depth first (DF)-representation proposed by Tamminen [48] is the most popular way to encode octree. This method sequentially stores the information of the nodes encountered in a depth-first search of the octree, and each node is displayed by black, white, and gray, as shown in Figure 2. A black node indicates that the area is full. A white node means it is completely empty, and a gray node means the node is partially black. The gray nodes here indicate that further segmentation may be required. The hexes marked as black or white no longer split. An octree can be set to a level of depth to be divided or can be repeatedly divided by setting the size of the bounding box.
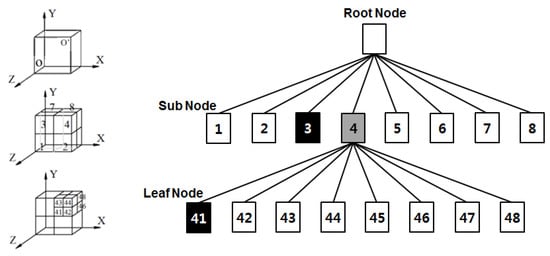
Figure 2.
The depth first (DF)-representation of the octree data structure.
3. Image Processing
The point cloud data obtained by the TLS is compressed by the octree data structure, and it can be converted to an image. To detect cracks from the converted image, a series of image processing techniques are used. Image processing for crack detection on concrete surfaces involves the following seven steps: (1) K-means clustering, (2) conversion into the gray-level image, (3) median filtering and improved subtraction, (4) removal of unnecessary parts using K-means clustering, (5) binarization, (6) morphological closing, and (7) blob removal using area and eccentricity. These seven steps are tabulated in Table 1.

Table 1.
Seven image processing steps for the crack detection.
3.1. K-Means Clustering
K-means clustering is one of the most famous unsupervised learning methods [40]. K-means clustering aims to partition unlabeled data into K clusters using the distance between each pair of data, and the cluster to be included is determined to minimize the mean distance in each cluster. Given a set of data where each data has the dimension, K sets are determined to minimize the within-cluster variance as
where , , denote mean value (i.e., centroid), count, and variance of data in , respectively. Based on the law of total variance [49], the minimizing the within-cluster variance equals to maximizing the out-of-cluster variance.
The basic algorithm of K-means clustering starts from selecting K points as the initial centroids. Then the K clusters are initially formed by assigning all points to the closest centroid and the centroid of each cluster is computed. Then reforming of K clusters and recomputing the centroid of each reformed cluster is repeated until the centroids do not change.
In the image processing, the data corresponds to the color vector in each pixel, and the Euclidean distance of the color vector represents the dissimilarity of the colors of the pixels. By applying K-means clustering, the image can be segmented into K pieces of pixels according to their color similarity corresponding to the concrete surface conditions. Figure 3 shows an example of image segmentation by K-means clustering. The original image in Figure 3a is segmented into three differently colored images in Figure 3b. The blue segment (BS) illustrates the background, and the green segment (GS) illustrates the concrete surface. Notably, the red segment (RS) highlights the sediments and structural joints that are generally dark-colored in the original image, even compared to the cracks on the concrete surface. Since the sediments and structural joints are the biggest impediments in identifying cracks from the images, the third segments obtained at this step will be used in Step 4 to tweeze out the impediment for successful image processing.
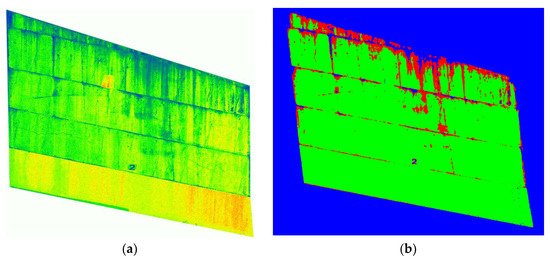
Figure 3.
Image segmentation by K-means clustering (K = 3). (a) Original image; (b) Image segmented by K-means clustering (K = 3).
3.2. Conversion into the Gray-Scale Image
As a next step, the conversion of the true color image (RGB) into a gray-level image by removing hue and saturation information while maintaining luminance is done. In this process, the amount of image data decreases. Specifically, the RGB color of 24-bit ((28)3 = 16,777,216 color) is converted into 8-bit gray-level (28 = 256 level).
3.3. Median Filtering and Improved Subtraction
The obtained gray-level image is processed with improved subtraction processing. Subtraction processing typically eliminates the slight variation such as shadings or irregularly noticeable components. Thus, it is for elimination of the noise as well as the illuminated components from cracks. Figure 4 illustrates how the subtraction finds cracks against the other objects including shading. Illuminance of the original gray-level visualizes objects in the image, and the median filtering removes out sharp illuminance changes that represent small noises or cracks and remains smoothed background image representing concrete surface, large objects, and shading. Then, the subtraction of the original image from the filtered image removes out the background image while remaining objects with sharp illuminance. Since the crack is visualized by very low illuminance profile with shape change, the crack object can be highlighted from the subtracted image, if combined with subsequent image processing to remove out small noises.
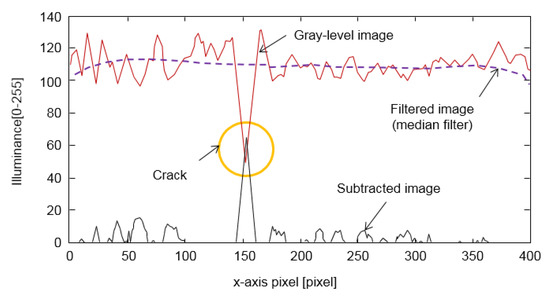
Figure 4.
Crack visualization by subtraction processing [41].
The median filtering converts the gray-level image to a smoothed one. The subtracted image is obtained by the Equation (3).
where Is (xi) is the intensity of the pixel xi, Ri is the neighborhood of that pixel, and I(xj) is the intensity of the pixels in Ri. When the result of the subtraction is a negative number, the result is represented with 0.
In addition, the subtraction result from the Equation (2) was used to get an enhanced image by a manually decided threshold value T. The thresholding operation is processed by the Equation (4).
where IIS(x,y) and Is(x,y) are the results of the improved and the original subtraction method, respectively. The threshold value T is determined manually. By this process, the illuminance difference between cracks and noises is larger and it improves the noise reduction for the next step.
3.4. Removal of Unnecessary Parts Using K-Means Clustering
In Section 3.1, RS data have been separated using the K-means clustering to remove out the parts corresponding to the structural joints and sediments. However, the gradient at the boundary of RS data may still be included at the boundary of the adjacent GS data. Since objects with a linear and thin shape are to be identified during the image processing, the gradient remaining at the boundary of the GS data can be misrecognized as cracks. In this study, the GS data is dilated by 5 pixels and the overlap of the dilated RS data and the GS data is removed from the GS data, resulting in erosion of the GS data at the interface with RS data as shown in Figure 5. This process can significantly minimize the false recognition of cracks.
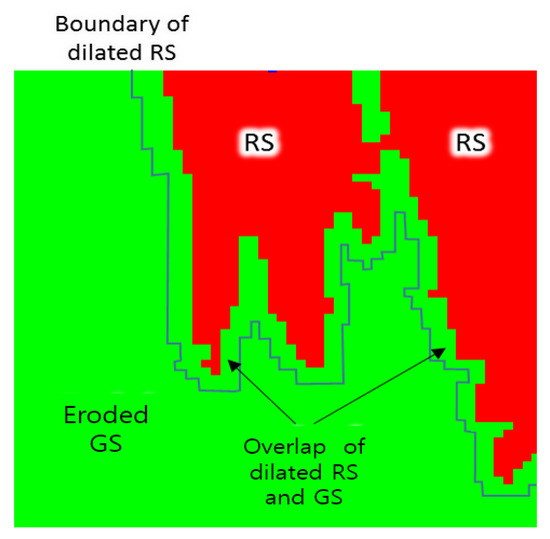
Figure 5.
Dilated red segment (RS) and eroded green segment (GS).
3.5. Binarization
Binarization is the simple and intuitive method in image segmentation. Object pixels can be simply extracted from background by image binarization. This step converts an input gray-level image to a binary image where the values of points are expressed by 0 (black) or 1 (white). The pixel whose intensity is greater than a threshold T is assigned into 1, and the pixel whose intensity is equal to or smaller than T is assigned into 0.
There are various binarization methods according to the method of determining the threshold T, and Otsu’s method [42] is the most widely used binarization method. The Otsu method selects a threshold T by minimizing the within variance of two groups separated by the thresholding operator. The method enables automatic thresholding, but it requires assuming a bimodal distribution of gray-level images. Considering the cracks are a small portion of the image and have high intensity against the background (after removing the dilated RS data) in the subtracted image, the threshold determined by Otsu’s method can be modified to minimize identification of the other objects against cracks. This in this study, 0.2 times T (=0.2 T) is used to binarize crack objects.
3.6. Morphological Operation: Closing and Blob Removal
Morphological operations were pursued to analyze binary images based on the form and structure of the image. Morphological operations included labeling, dilation, erosion, closing, opening, etc. Among various operations, morphological closing aims to fill the holes between the objects in the binarized image (i.e., connected pixel groups), and in this study it was used to connect crack objects by filling the small breaks between the objects and build a large crack object. The maximum filling size as set as 2 pixels not to distort the original crack objects.
After the morphological closing, blobs that had small areas and small eccentricity (ratio between the major and minor axes of an object) as shown in Figure 6 were finally removed out. In this study, the objects with areas smaller than 100 pixels or eccentricity smaller than 0.3 in the original image were removed out.
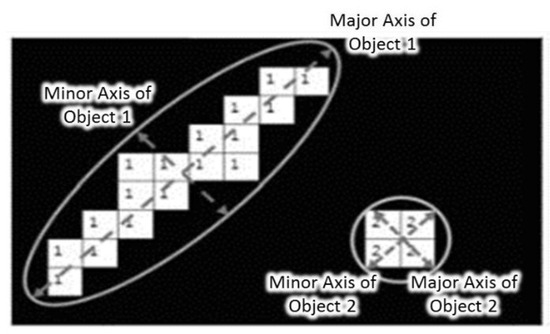
Figure 6.
Major and minor axes of objects.
Figure 7 shows an example showing how the seven image processing steps in Table 1 affected the original image to the end of crack identification. The figure shows that the cross-shape cracks on the original image are highlighted against the structural joints, sediments, and noises by proceeding the steps.
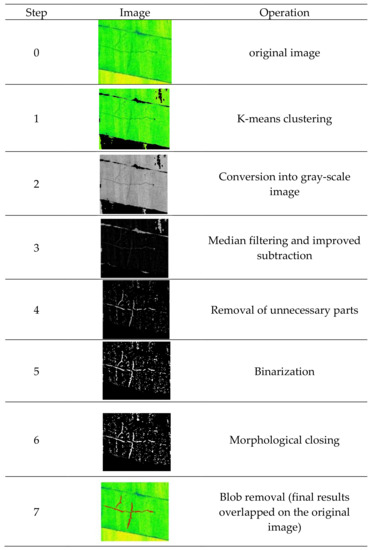
Figure 7.
Example of the proposed image processing.
4. Construction of Octree-Based Shape Information Model
4.1. Test-Bed and Equipment
Laser scanning was performed on the spillway left wall of a concrete dam structure in South Korea. Figure 8 shows the panoramic picture of the TLS measurement setup, and the scan was performed on the second wall surrounded by red lines. The left and right heights of the wall were 11.741 m and 10.118 m, respectively, and the width was 10.00 m. Figure 9 and Table 2 show the enlarged view of the target structure and the information of main crack pattern map through visual inspection. It should be noted that the cracks do not represent the stains, sediments, efflorescence, and microcracks on the surface.

Figure 8.
The panoramic view of TLS measurement set-up.
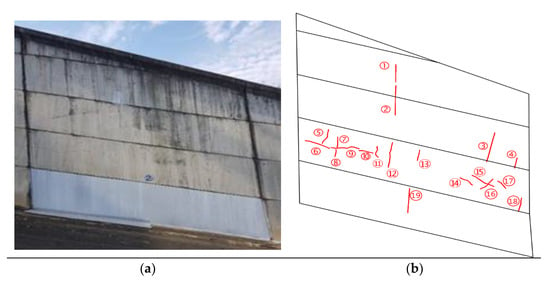
Figure 9.
The enlargement of the target structure and crack pattern map by visual inspection. (a) Target structure; (b) Crack pattern map.

Table 2.
The width and approximate length of cracks.
In this study, we used the Leica ScanStation C5 model as specified in Table 3 to scan the test-bed. The minimum and maximum measurement distance was 31.907 m and 31.918 m, respectively. The left and right angles were 11° and 11.5° and the up and down angles were 90° and −45° as presented in Table 4. The scan mode was set to high-resolution mode, the scanning time was about 28 min and 12 s, and the scan data (PTS format) size was 19.56 MB. The 3D scan data had x, y, and z coordinates at each point. Linux Ubuntu 12.04.2 LTS and C++ were used to configure the octree shape information model and development programming language, respectively.

Table 3.
Specifications of the terrestrial laser scanner.

Table 4.
Setting values of terrestrial laser scanner.
4.2. Construction and Visualization of an Octree-Based Shape Information Model
Figure 10 shows the target image obtained from the 3D laser scan data with 1,367,274 points extracted from the target spillway wall. The octree-based shape information model was constructed according to the flow chart shown in Figure 11. The first step was to convert the scan data from pixels to voxels (in 3D pixels). The second step was to convert the voxel model to the octree data structure, and the last step was the creation of an octree-based shape information model.
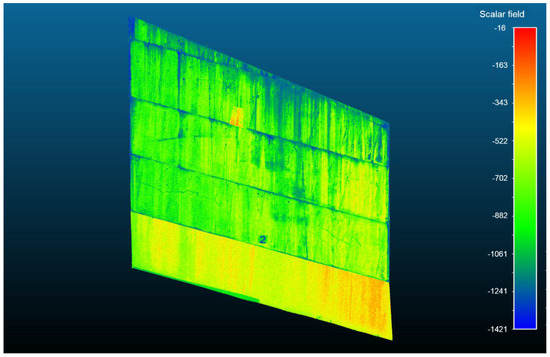
Figure 10.
The scan image extracted from the TLS data.
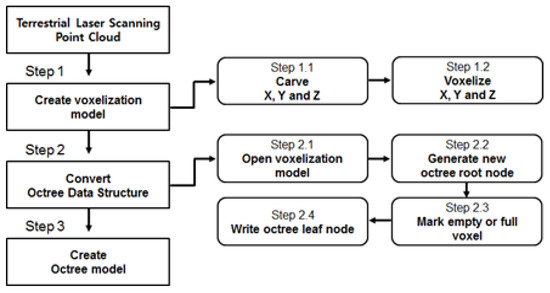
Figure 11.
Process of building the octree information model.
The first step (i.e., the creation of a voxelization model) involved converting the point-cloud data to the voxel type. In this step, the point cloud was read on the basis of each X, Y, and Z direction. The read data was reconstructed as a voxel model and was used to generate the root node in the octree data structure. The voxel model stores the x, y, and z coordinate values and depth, height, and width values of the 3D object model. These were used as input parameters in building the octree information model. The algorithm consists of a numerical code for generating an octree data structure via a voxel model, and it determines the octree resolution by setting a res value. After creating the octree, the inner nodes of the octree were iteratively divided until they reached the res value. After the segmentation was completed, the center point (x, y, z) of the 3D object and the depth, height, and width values were sequentially read and stored in the inner nodes of the octree. If all the point values were stored, the empty areas were removed and the octree file was finally created.
Octovis [50], a viewer program with a 3D tool kit, was used to identify the shape information of the generated octree. The number of points on the target wall was originally 1,367,274, and the file size was 19.56 MB and it was reduced to about 30%, 50%, and 80% as presented in the Table 5 to confirm that cracks could be detected even at a small number of points. Also, the extracted scan images according to the compression ratio is shown in Figure 12.

Table 5.
The number of compressed points and data size by octree structure.
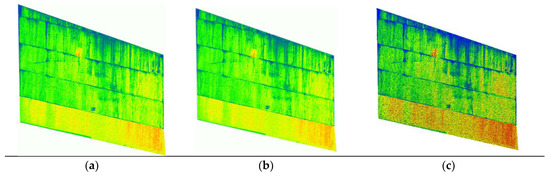
Figure 12.
The TLS scan images by point compression rates. (a) Case 1; (b) Case 2; (c) Case 3.
4.3. Image Processing for Crack Detection
The validity of the proposed algorithm was evaluated for the extracted images from. The original snapshot resolution was 1513 × 810 pixels, but 3026 × 1620 pixels (×2 resolution) was applied for precise crack detection and it was composed of RGB color. First, the original and compressed images were processed using the procedure described in the Table 1. Based on the compression rate, the accuracy of crack detection through the proposed imaging process was evaluated as shown in Figure 13. In case 3, the cracks were hardly recognized due to the poor resolution, so the result was not presented. As a result, most major cracks were identified well even in the Case 2 with compression rate of 50%, and some minor cracks due to drying shrinkage of concrete were recognized as well. The optimum values of the parameters for each case are shown in Table 6 and will be applied generally within the range in the table for other cases.
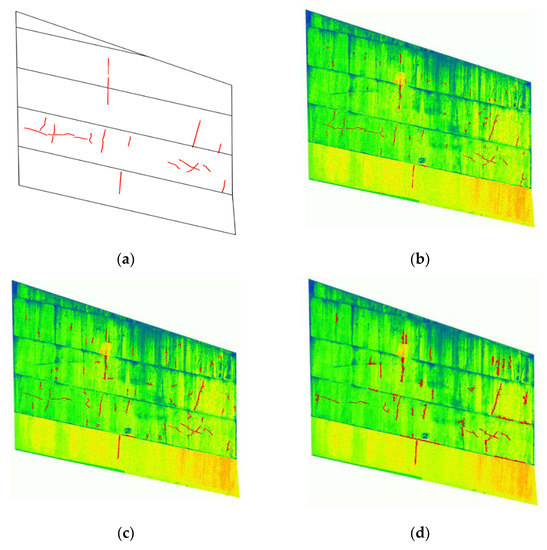
Figure 13.
The image results by the proposed method for three cases. (a) Crack map by visual inspection; (b) Original image; (c) Case 1; (d) Case 2.

Table 6.
The parameter optimization of three cases.
For quantitative comparison of each case, true positive (TP), false negative (FN), and number of false positive (FP) were analyzed and calculated in Figure 14 and Table 7. The quantitative analysis presents the evaluation of accuracy and error in comparison with the crack pattern map detected by visual inspection. For the quantification, two preconditions are assumed: (1) A crack is regarded as a noise and removed if its length was less than 450 mm (the smallest crack length) in the crack pattern map. (2) A crack was considered to be TP if its length was in line with more than 50% of one by visual inspection. As a result, it was confirmed that the accuracy of crack detection in the original image was best among all the cases in terms of TP, FN, and number of FP, and that the accuracy decreased according to the compression rate. However, it should be noted that the accuracy in even case 2 showed 84% in TP. In the original image, all the cracks were identified, but were not fully satisfied with crack lengths by visual inspection. In cases 1 and 2, the identified crack lengths were often exceeded with ones by visual inspection, which can be considered to be overestimated by resolution reduction.
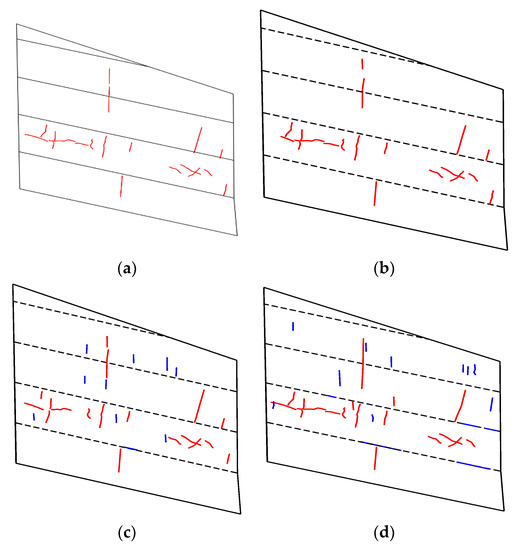
Figure 14.
The cracks identified by the proposed method for three cases. (a) Crack map by visual inspection; (b) Original image; (c) Case 1; (d) Case 2.

Table 7.
Quantitative comparison of the three cases.
In comparison of the number of FP for each case, the errors increased sharply according to the compression rate due to erroneous recognition of the joints and sediments as cracks. Thus, it concludes that the higher the resolution, the higher the probability that the K-means clustering accurately recognizes the crack group.
For comparative evaluation, Talab’s method [51] was applied to the original image as well. Talab’s method was developed to detect cracks in photographic images, and it has the following summarized steps.
- Convert RGB image to grayscale.
- Use the Sobel edge detector to find the edges with masks and get the value of the edge image.
- Use Otsu’s thresholding value to obtain the binary image.
- Find the connected areas in the binary image with the controlled area and put them to the background.
First, Talab’s method for a clear crack case with some stains was applied and compared with the proposed one, as presented in Figure 15. The results in Figure 15 show that Talab’s method detected some undesirable areas such as stains, making it difficult to distinguish them from the major and minor cracks on the concrete surface.

Figure 15.
The comparison of the proposed method with Talab’s method for a clear crack case. (a) Clear crack case; (b) Talab’s method; (c) Proposed method.
Moreover, the filtering by the classification in the proposed method was more effective in our case which had more stains, sediments, and joints, as shown in Figure 16. Thus, the proposed method outperforms in detecting cracks with the help of properly selected image processing algorithms. The K-means clustering significantly helped to remove many parts related to structural joints and sediments while keeping crack objects. Based on the other image processing algorithms, such as improved subtraction and morphological operations, the crack objects were comparably identified while minimizing the noises. Though the quantitative accuracy was not achieved due to the difficulty in assessing the target structure in detail, the visual comparison of Figure 16b,c clarifies the effectiveness of the proposed method in detecting the cracks even by the scanning 30 m distant from the test structure. After detecting the cracks using the proposed method, quantification of cracks can be done by employing existing quantification algorithms mostly based on combination of morphological operations, such as median filtering, morphological opening and closing, skeletonization, edge detection, etc. [52,53,54,55]. Though the lengths and widths of cracks are not quantified in this study, the crack widths obtained by visual inspection in Figure 16a are within 0.2 mm. According to the Korean structural inspection guide, a crack width less than 0.1 mm leads to the grade of the inspected structure as “a”, and width between 0.1 mm and 0.3 mm leads to “b” [56]. Thus, the proposed method can be successfully used as a prospective alternative to the conventional visual inspection of large structures with minimal labor and logistics time.
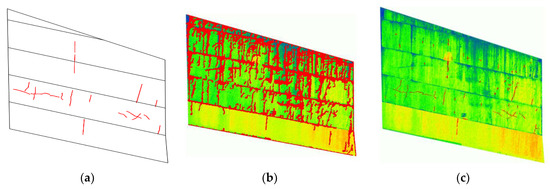
Figure 16.
The comparison of the proposed method with Talab’s method and the crack maps by visual inspection. (a) Crack pattern map; (b) Talab’s method; (c) Proposed method.
5. Conclusions
This study proposed a TLS-based crack detection technique on concrete surfaces using improved image processing associated with data compression. For the data compression, an octree-based shape information model was constructed using laser scanning data. The octree shape information model first transforms the scan data from pixels to voxels in 3D pixels, and the voxel model is converted into an octree data structure to generate an octree-based shape information model. For crack detection using the TLS data, a combination of image processing algorithms is proposed to minimize the false recognition of cracks in diverse operation environments. The proposed algorithm can automatically identify the existence of cracks against stains, sediment, and structural joints with the help of K-means clustering. Furthermore, the concrete crack pattern is visualized through other image processing algorithms such as improved subtraction with median filtering, Ostu’s method, and morphological operations.
A validation test was carried out on a spillway wall in a concrete dam using a Leica ScanStation C10 model located 30 m distance from the wall, and the results are summarized as follows:
- (1)
- The original scan data 19.56 MB was compressed using the octree data structure up to the 31.6%, 50.3%, and 80.2% corresponding to the data size of 13.36 MB, 9.7 MB, and 3.86 MB, respectively.
- (2)
- Most major cracks as well as some minor cracks due to drying shrinkage of concrete could be identified successfully even in the 50% compressed image of the proposed method.
- (3)
- The identified cracks by the proposed method had good agreement with the cracks obtained by visual inspection.
- (4)
- The proposed method could minimize the false recognition of cracks on the structural joints and sediments with the help of K-means clustering, compared to Talab’s method.
For further research, the proposed algorithm needs to be modified and improved with the better accuracy and generality for various cases and other optimization methods can be applied to determine the parameters required in the image processing. The imaging processing associated with the TLS measurement is expected to have an important role in the visualization of cracks and the acquisition of the exact crack information.
Author Contributions
S.C., S.P. and T.O. conceived and designed the experiments; G.C. and T.O. performed the experiments; S.C. and G.C. analyzed the data; S.P. contributed device/analysis tools; S.C. and T.O. wrote the paper.
Funding
This research was funded by the Incheon National University.
Acknowledgments
This work was supported by the Incheon National University Research Grant in 2015.
Conflicts of Interest
The authors declare no conflict of interest
References
- Olsen, M.J.; Kuester, F.; Chang, B.J.; Hutchinson, T.C. Terrestrial laser scanning-based structural damage assessment. J. Comput. Civ. Eng. 2009, 24, 264–272. [Google Scholar] [CrossRef]
- Anil, E.B.; Akinci, B.; Garrett, J.H.; Kurc, O. Characterization of laser scanners for detecting cracks for post-earthquake damage inspection. In Proceedings of the International Symposium on Automation and Robotics in Construction and Mining (ISARC), Montreal, QC, Canada, 11–15 August 2013. [Google Scholar]
- Giri, P.; Kharkovsky, S. Detection of surface crack in concrete using measurement technique with laser displacement sensor. IEEE Trans. Instrum. Meas. 2016, 65, 1951–1953. [Google Scholar] [CrossRef]
- Laefer, D.F.; Truong-Hong, L.; Carr, H.; Singh, M. Crack detection limits in unit based masonry with terrestrial laser scanning. NDT & E Int. 2014, 62, 66–76. [Google Scholar]
- Li, T.; Almond, D.P.; Rees, D.A.S. Crack imaging by scanning pulsed laser spot thermography. NDT & E Int. 2011, 44, 216–225. [Google Scholar]
- Kim, M.K.; Sohn, H.; Chang, C.C. Localization and quantification of concrete spalling defects using terrestrial laser scanning. J. Comput. Civ. Eng. 2014, 29, 04014086. [Google Scholar] [CrossRef]
- Valença, J.; Puente, I.; Júlio, E.; González-Jorge, H.; Arias-Sánchez, P. Assessment of cracks on concrete bridges using image processing supported by laser scanning survey. Constr. Build. Mater. 2017, 146, 668–678. [Google Scholar] [CrossRef]
- Xu, X.; Yang, H.; Neumann, I. Concrete crack measurement and analysis based on terrestrial laser scanning technology. Sens. Transducers 2015, 186, 168–172. [Google Scholar]
- Tsakiri, M.; Lichti, D.; Pfeifer, N. Terrestrial Laser Scanning for Deformation Monitoring. In Proceedings of the 3rd IAG/12th FIG Symposium, Baden, Austria, 22–24 May 2006; pp. 22–24. [Google Scholar]
- Van Gosliga, R.; Lindenbergh, R.; Pfeifer, N. Deformation analysis of a bored tunnel by means of terrestrial laser scanning. In Proceedings of the International Archives of the Photogrammetry, Dresden, Germany, 25–27 September 2006; pp. 25–27. [Google Scholar]
- Chang, Y.; LAI, S.; Peng, S.; Chang, K. Non-Contact Bridge Deflection Measurement: Application of Laser Technology. In Proceedings of the Integrating Generations FIG Working Week, Stockholm, Sweden, 14–19 June 2008; pp. 14–19. [Google Scholar]
- Koch, K. Three-dimensional NURBS surface estimated by lofting method. J. Adv. Manuf. Technol. 2010, 49, 1059–1068. [Google Scholar] [CrossRef]
- Jafari, B.; Khaloo, A.; Lattanzi, D. Deformation tracking in 3D point clouds via statistical sampling of direct cloud-to-cloud distances. J. Nondestruct. Eval. 2017, 36, 65. [Google Scholar] [CrossRef]
- Khaloo, A.; Lattanzi, D. Automatic Detection of Structural Deficiencies Using 4D Hue-Assisted Analysis of Color Point Clouds. Conf. Proc. Soc. Exp. Mech. 2019, 2, 197–205. [Google Scholar]
- Dai, K.; Li, A.; Zhang, H.; Chen, S.E.; Pan, Y. Surface damage quantification of the post-earthquake building based on terrestrial laser scan data. Struct. Control Health 2018, 25, e2210. [Google Scholar] [CrossRef]
- Dawood, T.; Zhu, Z.; Zayed, T. Computer vision–based model for moisture marks detection and recognition in subway networks. J. Comput. Civ. Eng. 2017, 32, 04017079. [Google Scholar] [CrossRef]
- Law, D.W.; Silcock, D.; Holden, L. Terrestrial laser scanner assessment of deteriorating concrete structures. Struct. Control Health 2018, 25, e2156. [Google Scholar] [CrossRef]
- Song, M.; Yousefianmoghadam, S.; Mohammadi, M.E.; Moaveni, B.; Stavridis, A.; Wood, R.L. An application of finite element model updating for damage assessment of a two-story reinforced concrete building and comparison with lidar. Struct. Health Monit. 2018, 17, 1129–1150. [Google Scholar] [CrossRef]
- Lõhmus, H.; Ellmann, A.; Märdla, S.; Idnurm, S. Terrestrial laser scanning for the monitoring of bridge load tests–two case studies. Surv. Rev. 2018, 50, 270–284. [Google Scholar] [CrossRef]
- Baeza, F.J.; Ivorra, S.; Bru, D.; Varona, F.B. Structural health monitoring systems for smart heritage and infrastructures in Spain. In Mechatronics for Cultural Heritage and Civil Engineering; Springer: New York, NY, USA, 2018; pp. 271–294. [Google Scholar]
- Laefer, D.F.; Gannon, J.; Deely, E. Reliability of crack detection methods for baseline condition assessments. J. Infrastruct. Syst. 2010, 16, 129–137. [Google Scholar] [CrossRef]
- Koch, C.; Georgieva, K.; Kasireddy, V.; Akinci, B.; Fieguth, P. A review on computer vision based defect detection and condition assessment of concrete and asphalt civil infrastructure. Adv. Eng. Inform. 2015, 29, 196–210. [Google Scholar] [CrossRef]
- Chae, M.; Abraham, D. Neuro-fuzzy approaches for sanitary sewer pipeline condition assessment. J. Comput. Civ. Eng. 2001, 15, 4. [Google Scholar] [CrossRef]
- Khanfar, A.; Abu-Khousa, M.; Qaddoumi, N. Microwave near-field nondestructive detection and characterization of disbonds in concrete structures using fuzzy logic techniques. Compos. Struct. 2003, 62, 335–339. [Google Scholar] [CrossRef]
- Adbel-Qader, I.; Abudayyeh, O.; Kelly, M. Analysis of edge-detection techniques for crack identification in bridges. J. Comput. Civ. Eng. 2003, 17, 255. [Google Scholar] [CrossRef]
- Guo, W.; Soibelman, L.; Garrett, J., Jr. Automated defect detection for sewer pipeline inspection and condition assessment. Autom. Constr. 2009, 18, 587–596. [Google Scholar] [CrossRef]
- Ng, H. Automatic thresholding for defect detection. Pattern Recogn. Lett. 2006, 27, 1644–1649. [Google Scholar] [CrossRef]
- Sinha, S.; Fieguth, P. Neuro-fuzzy network for the classification of buried pipe defects. Autom. Constr. 2006, 15, 73–83. [Google Scholar] [CrossRef]
- Moon, H.; Kim, J. Intelligent crack detecting algorithm on the concrete crack image using neural network. In Proceedings of the 28th ISARC, Seoul, Korea, 29 June–2 July 2011; pp. 1461–1467. [Google Scholar]
- Kawamura, K.; Miyamoto, A.; Nakamura, H.; Sato, R. Proposal of a crack pattern extraction method from digital images using an interactive genetic algorithm. JSCE 2003, 742, 115–131. [Google Scholar]
- Goswami, P.; Zhang, Y.; Pajarola, R.; Gobbetti, E. High Quality Interactive Rendering of Massive Point Models using Multi-way kd-Trees. In Proceedings of the 18th Pacific Conference on Computer Graphics and Applications 2010, Hangzhou, China, 25–27 September 2010; pp. 93–100. [Google Scholar]
- Saxena, M.; Finnigan, P.M.; Graichen, C.M.; Hathaway, A.F.; Parthasarathy, V.N. Octree-based automatic mesh generation for non-manifold domains. Eng. Comput. 1995, 11, 1–14. [Google Scholar] [CrossRef]
- Woo, H.; Kang, E.; Wang, S.; Lee, K.H. A new segmentation method for point cloud data. Int. J. Mach Tools Manuf. 2002, 42, 167–178. [Google Scholar] [CrossRef]
- Wang, M.; Tseng, Y.H. Lidar data segmentation and classification based on octree structure. In Proceedings of the XXth ISPRS Congress, Istanbul, Turkey, 12–23 July 2004. [Google Scholar]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Gr. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Cho, H.; Cho, W.; Park, J.; Song, N. 3D building modeling using aerial LiDAR data. Korean J. Remote Sens. 2008, 24, 141–152. [Google Scholar]
- Marechal, L. Advances in octree-based all hexahedral mesh generation: Handling sharp features. In Proceedings of the 18th International Meshing Roundtable, Salt Lake City, UT, USA, 25–28 October 2009; pp. 65–84. [Google Scholar]
- Han, S.; Lee, S.; Kim, S.P.; Kim, C.; Heo, J.; Lee, H.A. Comparison of 3D R-tree and octree to index large point clouds from a 3D terrestrial laser scanner. Korean J. Geomat. 2011, 29, 531–537. [Google Scholar] [CrossRef]
- Wang, J.; Lindenbergh, R.; Menenti, M. SigVox—A 3D feature matching algorithm for automatic street object recognition in mobile laser scanning point clouds. ISPRS J Photogramm. 2017, 128, 111–129. [Google Scholar] [CrossRef]
- Richard, O.D.; Peter, E.H. Pattern Classification and Scene Analysis; John Wiley and Sons: New York, NY, USA, 1973. [Google Scholar]
- Fujita, Y.; Hamamoto, Y. A robust automatic crack detection method from noisy concrete surfaces. Mach. Vis. Appl. 2010, 22, 1–10. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE. Trans. Syst. Man Cybern. C 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Fukuchi, T.; Shiina, T. Industrial Applications of Laser Remote Sensing; Bentham Science Publishers: Oak Par, IL, USA, 2012. [Google Scholar]
- Hocken, R.J.; Pereira, P.H. Coordinate Measuring Machines and Systems; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Wu, B.; Yu, B.; Yue, W.; Shu, S.; Tan, W.; Hu, C.; Huang, Y.; Wu, J.; Liu, H. A Voxel-Based Method for Automated Identification and Morphological Parameters Estimation of Individual Street Trees from Mobile Laser Scanning Data. Remote. Sens 2013, 5, 584–611. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, J.J. Compression of Normal Vectors using Octree Encoding. Soc. CAD/CAM Eng. 2007, 12, 109–117. [Google Scholar]
- Ryu, J.H. Efficient Octree Encoding for Real Time Transmission of 3D Geometry Data Through Internet. Soc. CAD/CAM Eng. 2002, 7, 262–268. [Google Scholar]
- Tamminen, M. Efficient Octree Conversion by Connectivity Labeling. In Proceedings of the 11th Annual Conference on Computer Graphics and Interactive Techniques, Minneapolis, MN, USA, 23–27 July 1984. [Google Scholar]
- Weiss, N.A. A Course in Probability; Addison–Wesley: Singapore, 2005; pp. 385–386. [Google Scholar]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robots 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Ahmed, M.T.; Huanga, Z.; Fan, X.; Liu, H.M. Detection crack in image using Otsu method and multiple filtering in image processing techniques. Optik 2015, 127, 1–4. [Google Scholar] [CrossRef]
- Liu, C.; Tang, C.S.; Shi, B.; Suo, W.B. Automatic quantification of crack patterns by image processing. Comput. Geosci. 2013, 57, 77–80. [Google Scholar] [CrossRef]
- Adhikari, R.S.; Moselhi, O.; Bagchi, A. Image-based retrieval of concrete crack properties for bridge inspection. Autom. Constr. 2014, 39, 180–194. [Google Scholar] [CrossRef]
- Liu, Y.; Cho, S.; Spencer, B.F., Jr.; Fan, J. Automated assessment of cracks on concrete surfaces using adaptive digital image processing. Smart Struct. Syst. 2014, 14, 719–741. [Google Scholar] [CrossRef]
- Liu, Y.F.; Cho, S.; Spencer, B.F., Jr.; Fan, J.S. Concrete crack assessment using digital image processing and 3D scene reconstruction. J. Comput. Civ. Eng. 2014, 30, 04014124. [Google Scholar] [CrossRef]
- Korea Ministry of Land, Infrastructure, and Transport (MLIT) and Korea. Guideline for Regular and Detailed Inspection; Korea Infrastructure Safety and Technology Corporation (KISTeC): Jinju, Korea, 2017; pp. 6–23. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).