Thermal and Performance Analysis of a Photovoltaic Module with an Integrated Energy Storage System
Abstract
:1. Introduction
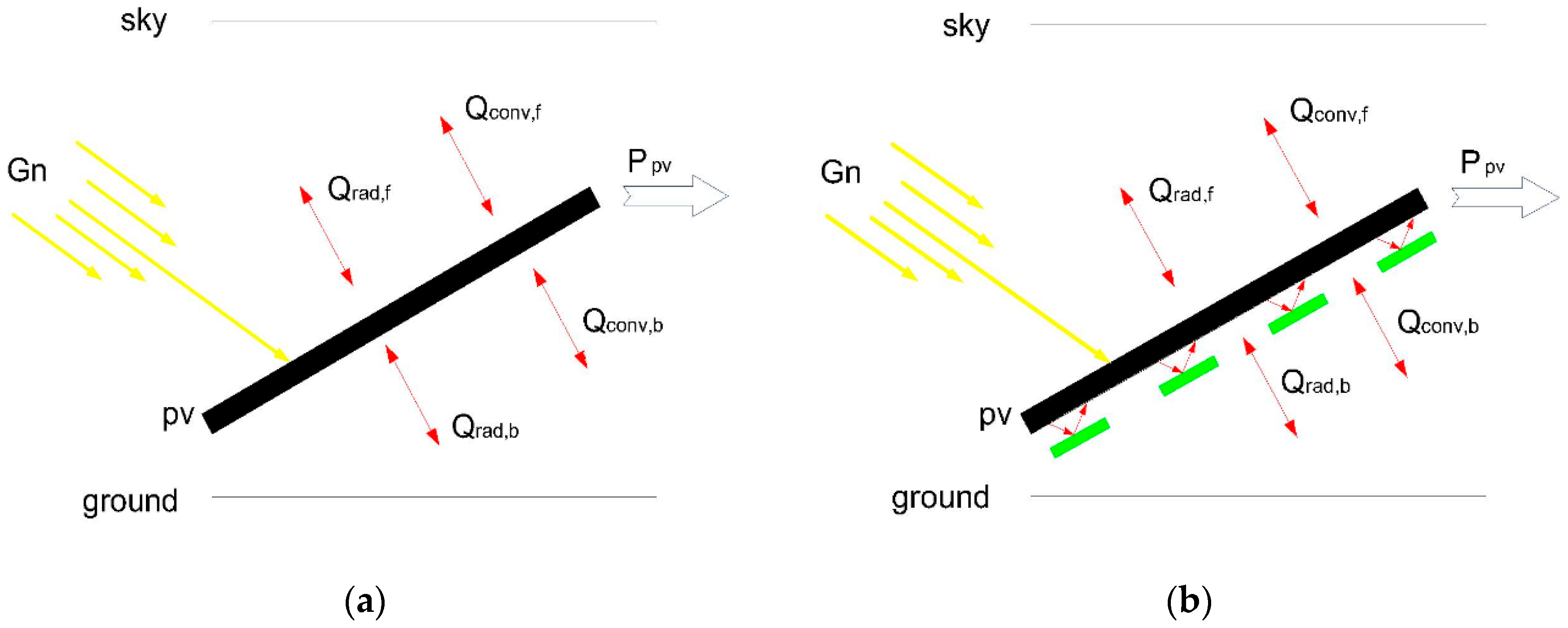
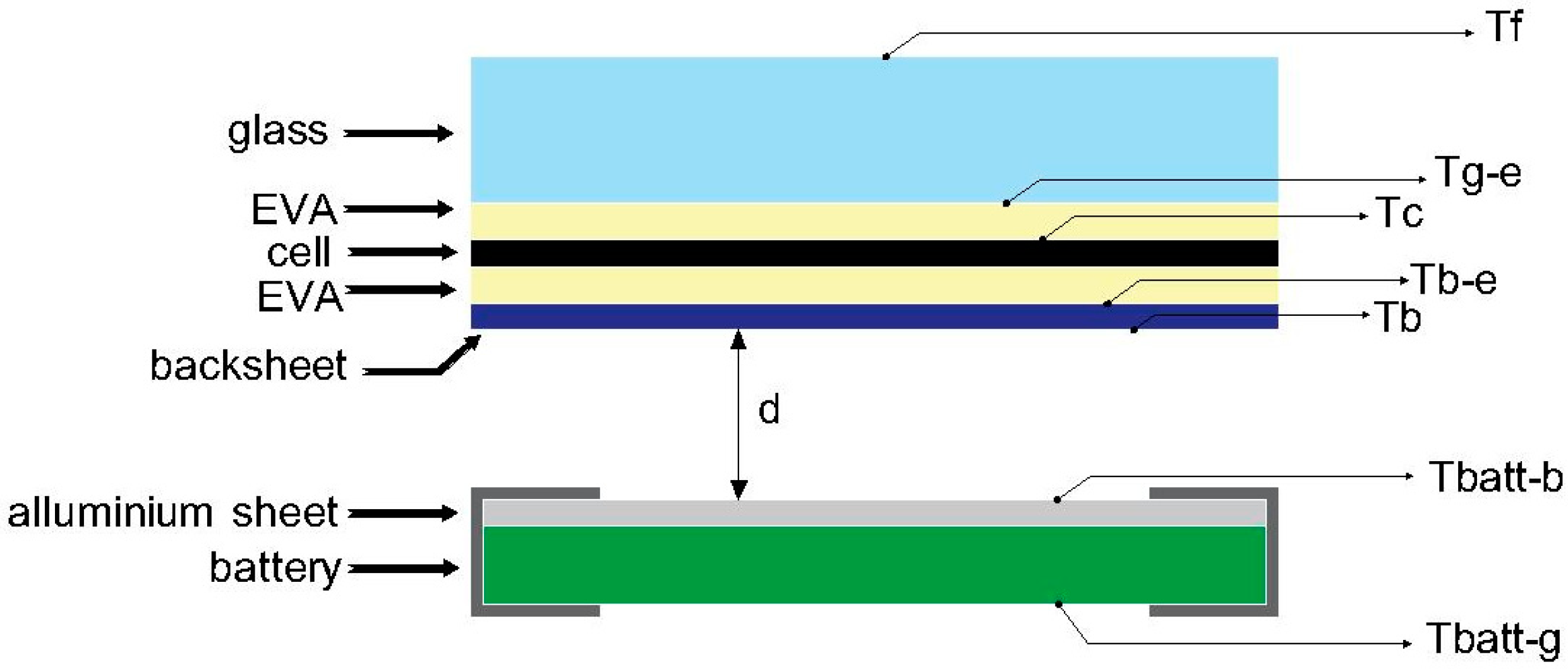
2. Thermal Model of a Single PV Module
2.1. Models
- One-dimensional (1D) thermal models.
- Isothermal surface was approximated as a flux node, so edge effects were neglected.
- Negligible thermal capacitances [10].
- Material properties of PV module layers were constant, as shown in Table 1.
- PV cell temperature was considered uniform due to the higher value of its thermal conductivity (k) compared to any of the other layers.
- Apparent sky temperature Ts was calculated according to [11]:where Ta is the air temperature and δT is the variation depending on atmospheric conditions.
- Ground temperature (on the back side of the PV module) was equal to air temperature (Tg = Ta).
- Convective heat exchange coefficients were evaluated with empirical formulations and it was assumed that wind flowed around the module, both front and back sides [12].
- Reflection (ρ), transmission (τ), and absorption (α) coefficients were independent from temperature.
- Internal reflection phenomena between the layers of PV module were neglected.
- Emissivity of surfaces were independent from temperature and wavelength, values are given in Table 2.
- According to the radiative heat transfer, the view factor was assumed to be unity. With this approximation, the front surface of PV module saw only the sky, whereas the back surface saw only the ground. Radiative heat exchange coefficients were simplified by this assumption.
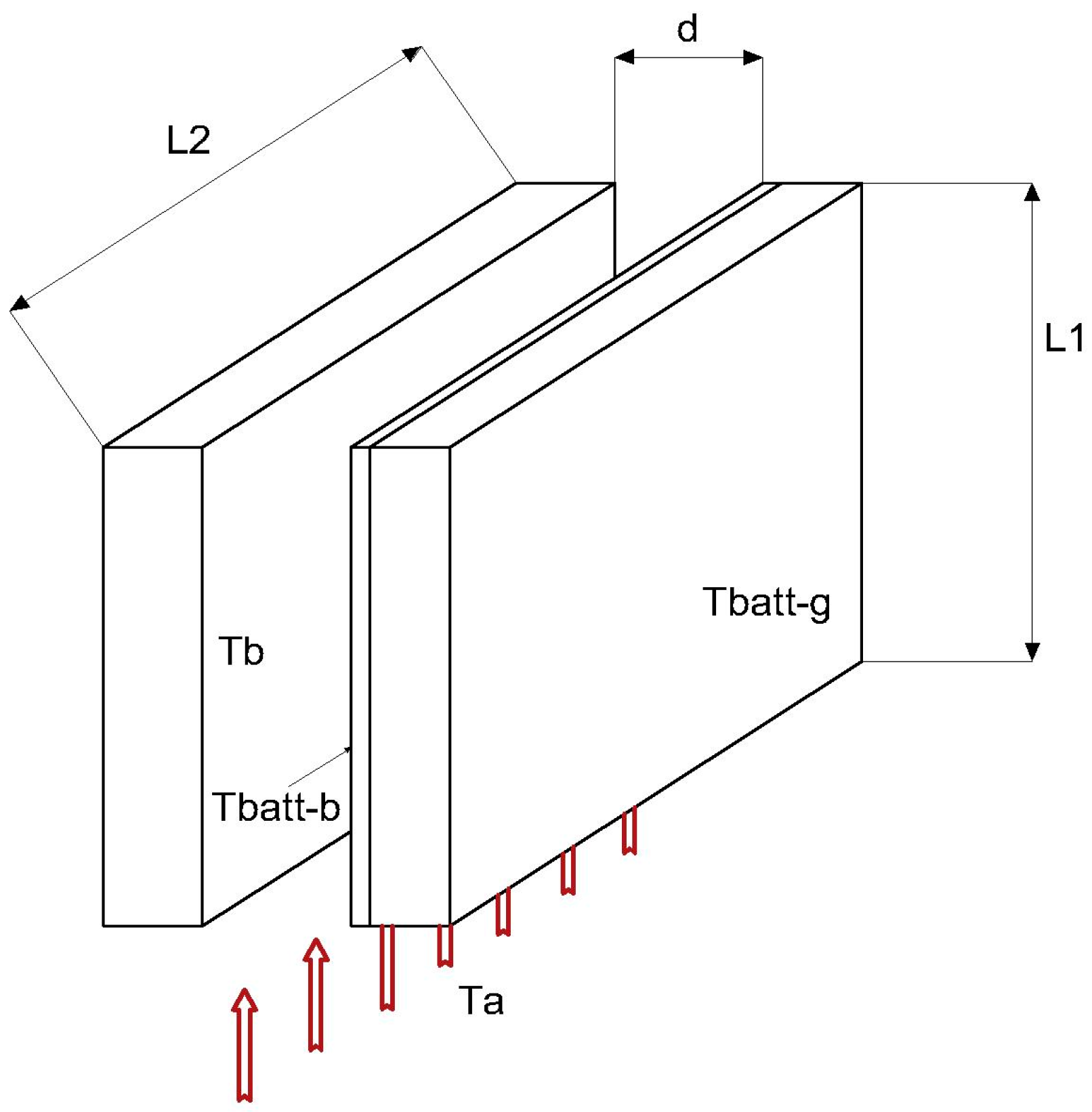
- All surfaces had the same area A of the PV module: A = 1.31 m2 in the case study.
- Batteries did not produce any heat flow while charging or discharging (battery losses were neglected).
2.2. Thermal Balance Equations
2.3. Convective and Radiative Coefficients
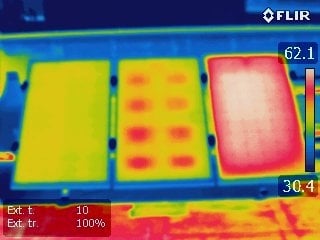
3. Models Results and Measurements
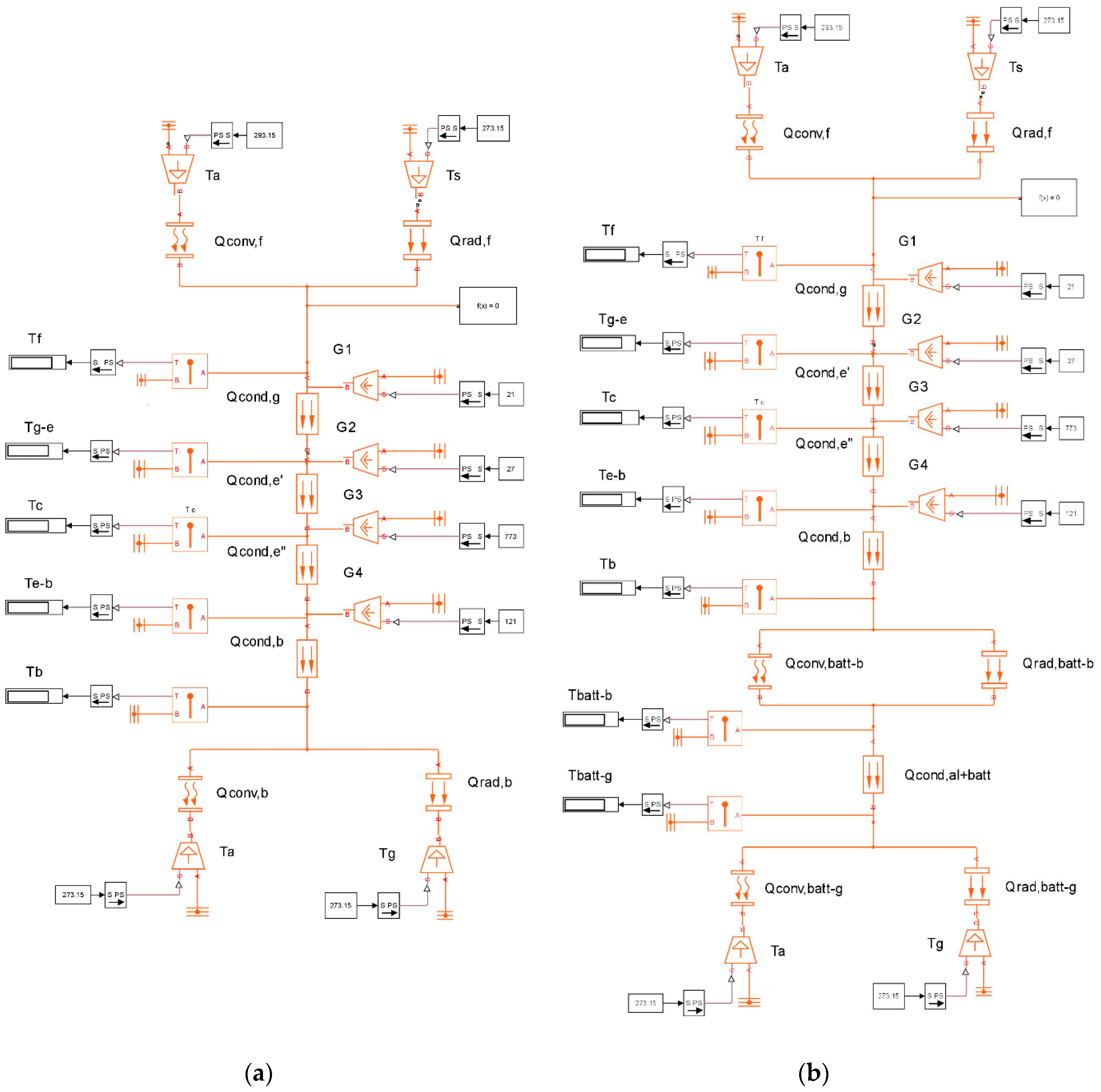
3.1. Simulink Thermal Models
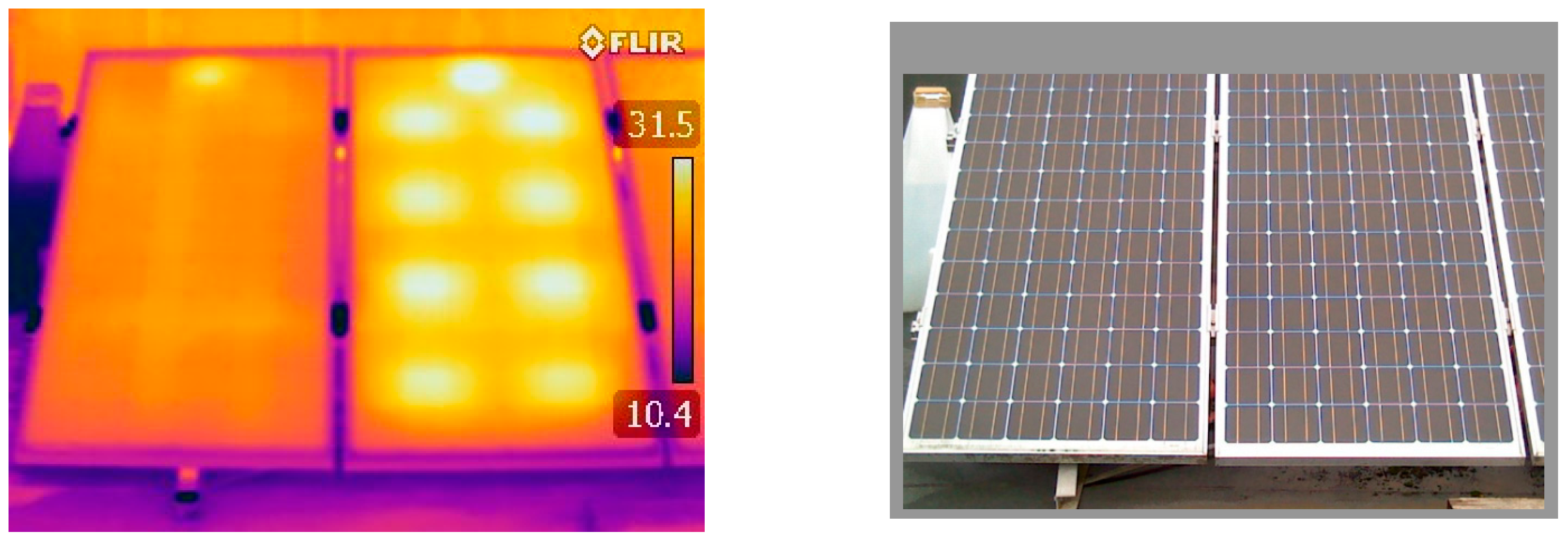
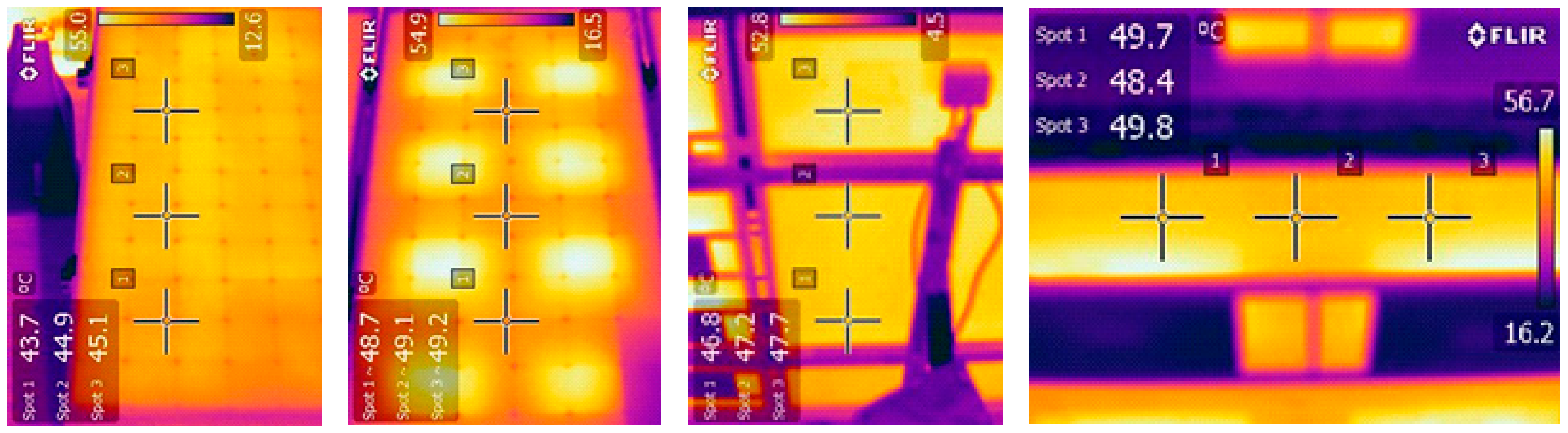
3.2. Thermal Model Validation
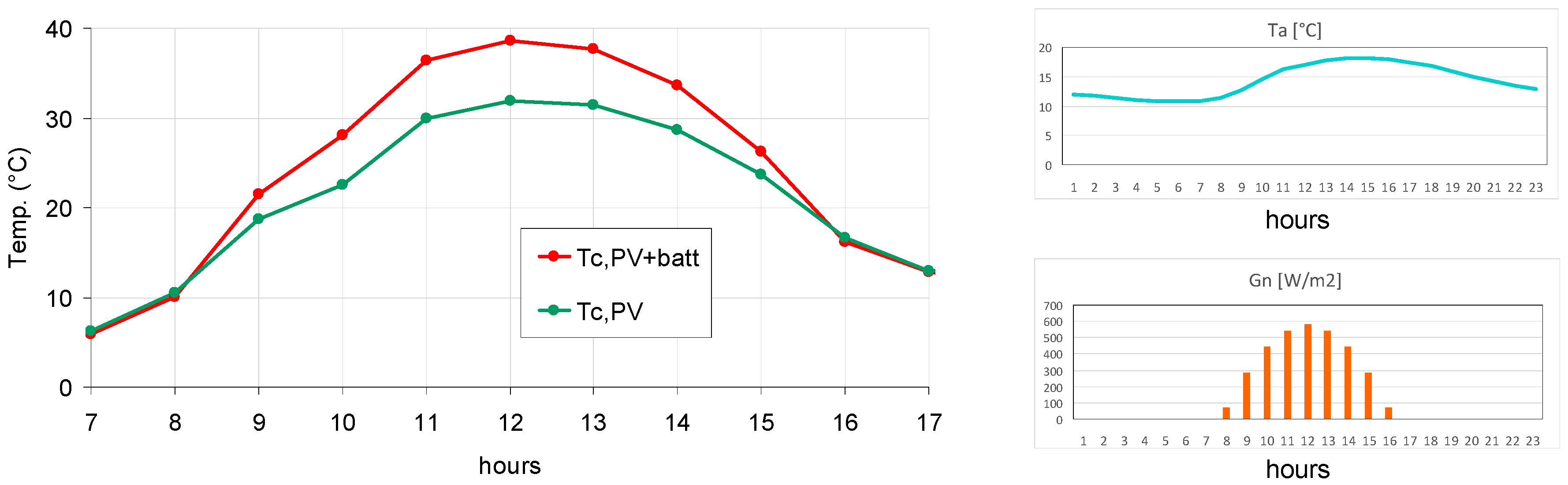
4. Temperature Extrapolation
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Thang, T.V.; Ahmed, A.; Kim, C.; Park, J. Flexible System Architecture of Stand-Alone PV Power Generation with Energy Storage Device. IEEE Trans. Energy Convers. 2015, 30, 1386–1396. [Google Scholar] [CrossRef]
- Li, P.; Dargaville, R.; Cao, Y.; Li, D.-Y. Storage Aided System Property Enhancing and Hybrid Robust Smoothing for Large-Scale PV Systems. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Reddy, S.S.; Momoh, J.A. Realistic and Transparent Optimum Scheduling Strategy for Hybrid Power System. IEEE Trans. Smart Grid 2015, 6, 3114–3125. [Google Scholar] [CrossRef]
- Fath, H.; Al Tarabsheh, A.; Ghazal, A.; Asad, M.; Morci, Y.; Etier, I.; El Haj, A. Performance of Photovoltaic Cells in Photovoltaic Thermal (PVT) Modules. IET Renew. Power Gener. 2016, 10, 1–7. [Google Scholar]
- Khelifa, A.; Touafek, K.; Ben Moussa, H. Approach for the Modelling of Hybrid Photovoltaic–thermal Solar Collector. IET Renew. Power Gener. 2015, 9, 207–217. [Google Scholar] [CrossRef]
- Xu, X.; Meyers, M.M.; Sammakia, B.G.; Murray, B.T.; Chen, C. Performance and Reliability Analysis of Hybrid Concentrating Photovoltaic/thermal Collectors with Tree-Shaped Channel Nets’ Cooling System. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 967–977. [Google Scholar] [CrossRef]
- Grandi, G.; Rossi, C.; Hammami, M. Modulo Fotovoltaico con Sistema di Accumulo Integrato (PV Module with Integrated Energy Storage); Patent Deposit Number A28517 LCA.gf; Alma Mater Studiorum, University of Bologna: Bologna, Italy, 2016. [Google Scholar]
- Hu, Y.; Cao, W.; Ma, J.; Finney, S.J.; Li, D. Identifying PV Module Mismatch Faults by a Distribution Analysis. IEEE Trans. Device Mater. Reliab. 2014, 14, 951–960. [Google Scholar] [CrossRef]
- Bardhi, M.; Grandi, G.; Tina, G.M. Comparison of PV Cell Temperature Estimation by Different Thermal Power Exchange Calculation Methods. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’12), Santiago de Compostela, Spain, 28–30 March 2012. [Google Scholar]
- Tina, G.M.; Scrofani, S. Electrical and Thermal Model for PV Module Temperature Evaluation. In Proceedings of the Mediterranean Electrotechnical Conference, MELECON, Ajaccio, France, 5–7 May 2008; pp. 585–590. [Google Scholar]
- Bardhi, M.; Grandi, G.; Premuda, M. Steady State Global Power Balance for Ground- Mounted Photovoltaic Modules Ground-Mounted Photovoltaic Modules. In Proceedings of the Third International Renewable Energy Congress, Hammamet, Tunisia, 20–22 December 2011; pp. 359–365. [Google Scholar]
- Hemenway, D.; Sakurai, H.; Sampath, W.; Barth, K. Thermal Modeling of PV Modules Using Computational Simulation. In Proceedings of the IEEE 40th Photovoltaic Specialist Conference, Denver, CO, USA, 8–13 June 2014; pp. 1344–1347. [Google Scholar]
- Chen, Y.; Zhuo, F.; Liu, X.; Xiong, L. Thermal Modelling and Performance Assessment of PV Modules Based on Climatic Parameters. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3282–3286. [Google Scholar]
- Guyer, E.C. Handbook of Applied Thermal Design; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Adrian, B. Convective Heat Transfer, 4th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hu, Y.; Cao, W.; Wu, J.; Ji, B.; Holliday, D. Thermography-Based Virtual MPPT Scheme for Improving PV Energy Efficiency under Partial Shading Conditions. IEEE Trans. Power Electron. 2014, 29, 5667–5672. [Google Scholar] [CrossRef]
- Romary, F.; Caldeira, A.; Jacques, S.; Schellmanns, A. Thermal Modelling to Analyze the Effect of Cell Temperature on PV Modules Energy Efficiency. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications (EPE 2011), Birmingham, UK, 30 August–1 September 2011; pp. 1–9. [Google Scholar]




| Layer’s Material | s [mm] | k [W/(m·K)] | ρ | τ | α |
|---|---|---|---|---|---|
| Glass | 4.0 | 1.8 | 0.1 | 0.88 | 0.02 |
| Ethylene Vinyl Acetate (EVA) | 0.4 | 0.35 | - | 0.97 | 0.03 |
| Silicon PV cell | 0.4 | 150 | - | - | 1 |
| Backsheet | 0.3 | 0.3 | - | - | 1 |
| ε | |
|---|---|
| PV module front surface (glass) (f) | 0.91 |
| PV module back surface (backsheet) (b) | 0.85 |
| Sky | 0.91 |
| Ground | 0.94 |
| Polished aluminum plates | 0.04 |
| Commercial PV Module | Modified PV Module with Integrated Energy Sotrage | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| °C | W/m2 | Without Batteries (°C) | Area Covered by Batteries (°C) | Area Not Covered by Batt. (°C) | avg (°C) | (°C) | |||||||||
| Ta | Gn | Tf | Tc,pv | Tb | Tf | Tc | Tb | Tbatt-b | Tbatt-g | Tf | Tc | Tb | Tc,pv+batt | ΔT | |
| January | 2.9 | 741 | 26.6 | 27.7 | 27.2 | 42.6 | 44.6 | 44.5 | 9.3 | 9.3 | 33.9 | 35.4 | 35.1 | 38.9 | 11.2 |
| February | 5.8 | 869 | 33.4 | 34.8 | 34.1 | 52.0 | 54.3 | 54.2 | 13.3 | 13.3 | 41.7 | 43.4 | 43.0 | 47.5 | 12.8 |
| March | 12.1 | 994 | 42.7 | 44.3 | 43.6 | 63.6 | 66.2 | 66.1 | 20.3 | 20.3 | 51.5 | 53.5 | 53.0 | 58.3 | 14.0 |
| April | 17.0 | 1079 | 49.6 | 51.3 | 50.5 | 71.6 | 74.4 | 74.3 | 26.0 | 26.0 | 58.6 | 60.7 | 60.2 | 65.9 | 14.6 |
| May | 21.5 | 1106 | 54.2 | 55.9 | 55.6 | 76.4 | 79.3 | 79.2 | 30.3 | 30.2 | 63.0 | 65.2 | 64.6 | 70.5 | 14.6 |
| June | 26.3 | 1107 | 58.5 | 60.2 | 59.4 | 80.0 | 82.9 | 82.8 | 34.8 | 34.8 | 66.9 | 69.1 | 68.5 | 74.3 | 14.1 |
| July | 28.9 | 1107 | 60.7 | 62.4 | 61.6 | 82.0 | 84.9 | 84.8 | 37.3 | 37.3 | 68.9 | 71.1 | 70.5 | 76.3 | 13.9 |
| August | 28.3 | 1095 | 59.8 | 61.6 | 60.7 | 81.0 | 83.8 | 83.8 | 36.6 | 36.6 | 68.0 | 70.2 | 69.7 | 75.4 | 13.8 |
| September | 24.1 | 1034 | 54.4 | 56.1 | 55.3 | 74.8 | 77.5 | 77.4 | 32.2 | 32.1 | 62.5 | 64.6 | 64.1 | 69.5 | 13.4 |
| October | 17.0 | 914 | 44.5 | 45.9 | 45.6 | 63.2 | 65.6 | 65.5 | 24.6 | 24.6 | 52.3 | 54.1 | 53.7 | 58.5 | 12.5 |
| November | 10.0 | 777 | 33.9 | 35.2 | 34.7 | 50.4 | 52.4 | 52.3 | 16.5 | 16.4 | 41.2 | 42.8 | 42.4 | 46.4 | 11.2 |
| December | 4.8 | 701 | 26.9 | 28.0 | 27.5 | 41.8 | 43.6 | 43.6 | 10.5 | 10.4 | 33.8 | 35.2 | 34.9 | 38.4 | 10.4 |
| Temperatures (°C) | Power | |||
|---|---|---|---|---|
| Tc,pv | Tc,pv+batt | ΔT | ΔP% | |
| January | 24.3 | 34.1 | 9.8 | −5.1 |
| February | 30.9 | 42.1 | 11.2 | −5.8 |
| March | 40.0 | 52.3 | 12.3 | −6.4 |
| April | 46.7 | 59.6 | 12.9 | −6.7 |
| May | 51.4 | 64.3 | 12.9 | −6.7 |
| June | 55.7 | 68.2 | 12.4 | −6.5 |
| July | 58.0 | 70.2 | 12.3 | −6.4 |
| August | 57.1 | 69.3 | 12.2 | −6.3 |
| September | 51.8 | 63.6 | 11.8 | −6.1 |
| October | 42.0 | 53.0 | 11.0 | −5.7 |
| November | 31.8 | 41.5 | 9.8 | −5.1 |
| December | 24.8 | 33.8 | 9.1 | −4.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammami, M.; Torretti, S.; Grimaccia, F.; Grandi, G. Thermal and Performance Analysis of a Photovoltaic Module with an Integrated Energy Storage System. Appl. Sci. 2017, 7, 1107. https://doi.org/10.3390/app7111107
Hammami M, Torretti S, Grimaccia F, Grandi G. Thermal and Performance Analysis of a Photovoltaic Module with an Integrated Energy Storage System. Applied Sciences. 2017; 7(11):1107. https://doi.org/10.3390/app7111107
Chicago/Turabian StyleHammami, Manel, Simone Torretti, Francesco Grimaccia, and Gabriele Grandi. 2017. "Thermal and Performance Analysis of a Photovoltaic Module with an Integrated Energy Storage System" Applied Sciences 7, no. 11: 1107. https://doi.org/10.3390/app7111107
APA StyleHammami, M., Torretti, S., Grimaccia, F., & Grandi, G. (2017). Thermal and Performance Analysis of a Photovoltaic Module with an Integrated Energy Storage System. Applied Sciences, 7(11), 1107. https://doi.org/10.3390/app7111107