Abstract
As serious traffic problems have increased throughout the world, various types of studies, especially traffic simulations, have been conducted to investigate this issue. Activity-based traffic simulation models, such as MATSim (Multi-Agent Transport Simulation), are intended to identify optimal combinations of activities in time and space. It is also necessary to examine commuting-based traffic simulations. Such simulations focus on optimizing travel times by adjusting departure times, travel modes or travel routes to present travel suggestions to the public. This paper examines the optimal departure times of metro users during rush hour using a newly developed simulation tool. A strategy for identifying relatively optimal departure times is identified. This study examines 103,637 person agents (passengers) in Shenzhen, China, and reports their average departure time, travel time and travel utility, as well as the numbers of person agents who are late and miss metro trips in every iteration. The results demonstrate that as the number of iterations increases, the average travel time of these person agents decreases by approximately 4 min. Moreover, the latest average departure time with no risk of being late when going to work is approximately 8:04, and the earliest average departure time with no risk of missing metro trips when getting off work is approximately 17:50.
1. Introduction
With the development of national economies and the acceleration of urbanization, traffic congestion has become a common problem around the world [1,2]. Traffic congestion produces broad social and environmental costs, such as delays in the delivery of goods, air pollution, changes in microclimates, increases in the urban heat island effect, increases in respiratory problems and lost productivity [3]. To address this severe challenge, intelligent transportation system (ITS)-based studies have become increasingly prevalent, especially in the field of traffic simulation. Traffic simulations, which represent an important component of ITSs and differ from traditional mathematical modelling, can simulate traffic-related phenomena, including the flow of traffic and traffic accidents. They can also reproduce the spatial and temporal variations in traffic flow and help to analyze the characteristics of vehicles, drivers, pedestrians, roads and traffic [4,5]. Moreover, using virtual reality technology, traffic simulations can intuitively show the status of traffic in real time, including whether roads are smooth, whether traffic accidents are present and what kind of solutions can be used to address traffic problems, without risk.
Traffic simulations can be divided into macroscopic, microscopic and mesoscopic scales [6]. The macroscopic traffic simulation model was proposed by Whitham and Richards and is mainly used to study the characteristics of traffic flow globally [7,8]. Microscopic traffic simulations, such as the car-following model (Reuschel, Pipes) and the lane-changing model (Gipps, 1986), can describe the conditions of traffic networks and the detailed behaviors of traffic participants to a high degree [9,10,11]. The description of traffic systems provided by the mesoscopic traffic simulation model proposed by Prigogine and Andrews lies between those of the macroscopic and microscopic models. The mesoscopic model describes the inflow and outflow behaviors of vehicles at links and intersections or at links and stops, but it does not include car-following or lane-changing models [12]. In terms of application, macroscopic and mesoscopic traffic simulations are both used for traffic planning and management; mesoscopic traffic simulations can also be used to present travel suggestions to the public, whereas microscopic traffic simulations can be used for traffic accident analysis and automated driving.
Despite the different scales at which traffic simulation research is conducted, most traffic simulation tools are based on multi-agent models, which are a powerful tool for the simulation of complex systems. Such a model is dynamic and captures nonlinear interactions, and its components exhibit unpredictable reactions that result in realistic behavior patterns [13,14,15]. Agent technology originated at MIT in the 1970s. Agents are typically defined as independent and autonomous entities that can coordinate with each other according to the different states of other entities and systems and determine their own actions and states [16]. Various kinds of elements, such as people, vehicles, links, and traffic lights, have been viewed as agents. These elements communicate and collaborate to simulate complex traffic conditions in simulation tools. Among the many simulation tools that exist today, our research focuses on those that are concerned with resident trips. MATSim (Multi-Agent Transport Simulation), Albatross and ADAPTS (Agent-based Dynamic Activity Planning and Travel Scheduling) are typical examples of these simulation tools [17,18,19]. Most traffic simulation tools that are concerned with resident trips use activity-based models to identify optimal combinations of activities in time and space [20]. However, it is also necessary to carry out commuting-based traffic simulations, especially for public transit.
The key element of the simulation tools mentioned above is the replanning module, which employs the scores and plans of the agents and determines whether these travel plans must be modified. Most optimization algorithms for travel planning focus on four dimensions, specifically the departure time, travel route, travel mode and the combinations of activities represented by the activity chain [21]. The optimization of the departure time contains two steps. The first of these steps involves setting a range of time adjustments based on the current departure time. The second step involves drawing an adjustment value at random from within the range and adding this adjustment to the previous departure time (Balmer et al., 2005; Gao, 2013) [2,22]. The optimization of the travel route is based on static traffic assignment using the user equilibrium (UE) or the stochastic user equilibrium (SUE) models (Raney et al., 2003) [23]. The multinomial logit model and the probit model are often used to optimize the mode of travel, and the optimization of the combinations of activities represented by the activity chain is based on heuristic solution algorithms, such as hill-climbing algorithms or the tabu search algorithm (Balmer and Axhausen, 2009; Nagel and Axhausen, 2016) [20,21,24,25].
Of the four types of optimization algorithms, research on the optimization of departure time is still insufficient. The challenges involved in such studies are as follows. First, it is difficult to define the direction of adjustment of the departure time, i.e., whether the optimal departure time is earlier or later than the current departure time. Second, it is also difficult to know when the iteration can be stopped. In this study, iteration refers to the replanning process in our simulation tool. Person agents must replan their travel strategies—i.e., perform departure time adjustment—to avoid late arrival or missing their desired metro trips. If there are no person agents who are late when going to work or who become caught in congestion at metro stops when getting off work, the iteration will end.
In view of the two challenges identified above, this paper aims to explore a strategy for adjusting departure times to obtain relatively optimal travel utility values, using metro travel as an example. To address the first problem, the two concepts of “obligatory arrival times” and “empirical travel times” are introduced to determine the direction of departure time adjustment. For the second problem, an explicit condition is proposed for the termination of iteration. With these adjustments, shorter travel times can be achieved. Moreover, we find the latest average departure time with no risk of being late when going to work and the earliest average departure time with no risk of missing metro trips when getting off work. This research on the optimization of departure times will broaden the horizons in this field and can be used to provide the public with suggestions regarding their travel plans.
2. Methodology
This section first presents a brief overview of the general simulation approach used in MATSim and then introduces our self-developed multi-agent simulation tool. Here, we focus on the core of our simulation tool and how it differs from MATSim.
2.1. Overview of MATSim
This section first gives a brief overview of the general simulation approach used in MATSim and then introduces our self-developed multi-agent simulation tool. Here, we focus on the core of our simulation tool and how it differs from MATSim.
MATSim is an activity-based, extendable, multi-agent simulation framework implemented in Java. It is a widely-used simulation tool that is designed to model a single day, the common unit for activity-based models. Because MATSim is activity based, every agent optimizes its daily activity chain in competition for space and time with all other agents. A MATSim run contains a configurable number of iterations, represented by the loop and detailed below [21]. A MATSim run starts with initial demand from the activity chain, road network, places of work and residences of a population within a study area. Every person that is considered an agent in MATSim possesses a fixed number of one-day plans, and each plan is composed of a daily activity chain. The plan of each agent is executed by mobsim and is given a score based on its performance by a scoring function. Based on the score that an agent’s plan receives, the replanning module decides whether the plan must be modified in terms of its departure time, route, mode and/or destination [21]. The simulation output data can be used to analyze the results and to monitor the progress of the current simulation setup. Some of the files summarize a complete run, whereas others are created for a specific iteration only.
The selection of the replanning fraction represents a related issue; 10% is a frequently-used heuristic value that works well in practice [23]. This fraction of person agents both improves the average population score and causes the system to relax as soon as possible by adjusting the travel plans. The iterative process is repeated until the average population score stabilizes. Note that there is no quantitative measure of when the system has “relaxed”. Thus, it is difficult to determine the number of iterations needed for specific simulation scenarios; this number depends on the number of agents and the replanning strategy used.
2.2. Overview of the New Simulation System CCTSim
MATSim is an activity-based transport simulation system that performs whole-day simulations. It focuses on the optimization of the schedules of agents over an entire day and produces optimal combinations of a schedule’s activity chain, such as the number, type and sequence of activities [20]. However, there are two main reasons why MATSim is not suitable for simulating commuting behavior. First, the plan for each agent in MATSim consists of that person’s behavior throughout the entire day, including activities and travel alternately. It does not provide a way to focus solely on commuting, which is merely the process of travelling between home and the workplace. Second, the adjustment of departure times in MATSim is random, and there is no way to consider an obligatory arrival time. Thus, it does not permit the determination of the departure time adjustment direction.
The new simulation tool, which is called the Citizen Commuting Transportation Simulation tool (CCTSim), is mainly concerned with the optimization of the commutes of citizens during rush hour. It simulates three traffic modes, specifically metro, buses and private cars, which include most travel patterns. The CCTSim loop shown as Figure 1 is similar to the MATSim loop, and the differences between the modules in the two models are as follows.
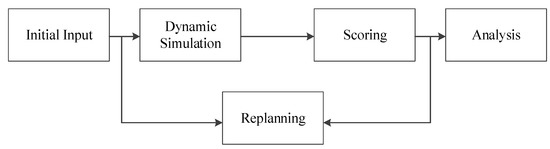
Figure 1.
CCTSim (Citizen Commuting Transportation Simulation) loop.
2.2.1. Initial Input
The initial input of CCTSim includes road networks, workplaces and residences within the study area and the plans of individual person agents, as well as metro stops and routes and bus stops and routes. More elements are considered as agents in CCTSim than in MATSim. These additional agent types include people, metro trains, buses and cars, and they are considered because these elements change during the simulation process. Note that, because CCTSim focuses on travel, the plan of each person agent is made up of travel chains, rather than activity chains.
2.2.2. Dynamic Simulation
CCTSim is motivated by an event queue, which contains a sequence of events in chronological order. In the process of our simulation, each agent, such as a person or vehicle, will generate various events. For example, when a person agent sets out, it generates an event called “PersonSetOutEvent”. Each event has two attributes, “StartTime” and “FinishTime”. When an event is performed, the simulation tool calculates the finish time of the event. The finish time is assigned to the start time of the next event associated with the person agent, such as a “PersonGetInMetroStopEvent”, a “PersonGetInBusStopEvent” or a “PersonGetInCarStopEvent”. Finally, the event in question is posted to the event queue. Figure 2 shows a sketch of the event queue in CCTSim.
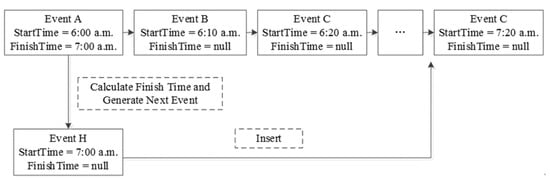
Figure 2.
Sketch of the event queue in the Citizen Commuting Transportation Simulation tool (CCTSim).
2.2.3. Scoring
The scores of travel plans are used to measure the actual performance of the plans, and they represent the basis of the replanning module. The CCTSim scoring function is loosely based on the MATSim utility function. However, it does not contain activity components, and some changes are made to the travel-related components.
The utility of a travel plan is divided into two parts, which represent going to work () and getting off work ().
- The going to work travel plan is computed as the travel utility plus the arrival utility :where is the empirical travel time; is the real travel time; is the arrival time; and is the obligatory arrival time, which is set to 9:00 a.m. are three parameters, for which the default values are 4, 5/3 and −12 in the simulations described here.
- Because there is no obligatory arrival time when getting off work, the getting-off-work travel plan is computed as the travel utility :where the variables have the same meanings as in Equation (1), above.
Note that the travel utility takes the absolute and relative differences between both the empirical and real travel times into account. In addition, the performance of a given plan is better if the arrival time is close to the obligatory arrival time, rather than the earlier the better. However, the arrival time cannot be later than the obligatory arrival time. A severe late arrival penalty is assigned to travel plans that do not satisfy this constraint.
2.2.4. Replanning
Replanning strategies are the basic innovation modules available in CCTSim. The travel plan of each person agent is adjusted according to its actual performance. The performances of the travel plans improve as these plans are successively adjusted in the iterations of the simulation. In this version, the replanning module includes two main parts.
1. Replanning of departure times using public transit
Since work has an arrival time constraint, somewhat different strategies are used when adjusting the departure times for going to work and getting off work.
- (1)
- Adjusting the departure time for going to workThe objective of replanning when to leave for work is to identify a relatively optimal departure time such that the travel time of a person agent is as short as possible, and the person agent arrives as close as possible to the obligatory arrival time, without being late.
- (2)
- Adjusting the departure time for getting off workThe objective of replanning when to leave from work is simply to make the travel times of the person agents as short as possible.
2. Replanning of travel routes when using private cars
The simulation tool applies the SUE model to transportation and makes some changes to identify optimal travel routes from the point of view of person agents.
Notably, this paper focuses only on the replanning of departure times for the case of metro travel.
2.2.5. Analysis
CCTSim creates output data that can be used to analyze the results of the simulation, as well as to monitor the progress of the current simulation. The simulation results created in every iteration can be visualized to reflect the spatio-temporal variations in traffic pressure. The typical output data are interpreted as follows.
1. Score statistics
The scores of the travel plans of all of the person agents in every iteration are recorded in a text file. These scores are plotted to show the individual and average performance of the travel plans in every iteration.
2. Events
Every action in the simulation is recorded as an event, and each event has one or more attributes. By default, data such as the time when an event occurred, the agent ID that triggered the event, the position where the event occurred, the type of event and other relevant information are included.
3. Commuting pressure
The commuting pressure refers to the pressure exerted by passengers on public transit and the pressure exerted by road traffic at every link. The pressure exerted by passengers (i.e., the number of person agents occupying a metro train or bus) is output for each iteration, and the pressure exerted by road traffic on every link is recorded at intervals to monitor dynamic vehicle counts.
3. Scenario
3.1. The Study Area and Its Metro Network
Shenzhen is a coastal city located in the south of China, northeast of the Pearl River Estuary. This city is located south of the Tropic of Cancer, between 113°46′ and 114°37′ east in longitude and between 22°27′ and 22°52′ north in latitude, and the total area of Shenzhen is approximately 1952.84 km2.
Before 2016, the metro network in Shenzhen, which was developed by the Shenzhen Metro Group, originally had five lines. It was extended by an additional three lines in 2016. Our simulation applies to 199 metro stops on all eight of these lines, as well as the departure timetable for the metro trains. Figure 3 shows the location of Shenzhen in China and the metro network in Shenzhen. The specific values of the major attributes of the metro trains, such as capacity, speed, numbers of carriages and door counts, are shown in Section 4. Notably, the results (the person agents’ average departure time, travel time and travel utility, as well as the numbers of person agents who are late and miss metro trips in every iteration) are reported as sums over all eight metro lines.
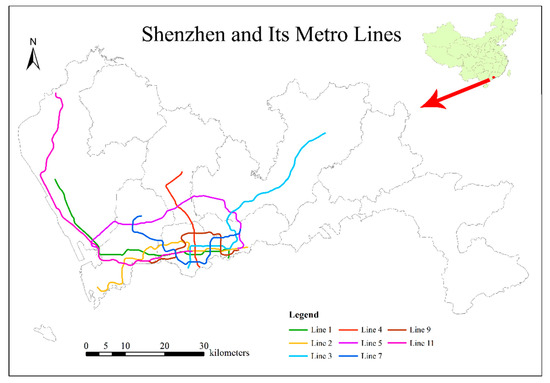
Figure 3.
Study area and its metro lines.
3.2. The Travel Plans of Person Agents
The travel plans of person agents represent the most important initial input data in CCTSim. Specifically, the generation of metro travel plans includes two steps.
1. Selecting the person agents who employ the metro
It is assumed that, if the distances from both the workplaces and the residences of the person agents to the nearest metro stop are less than 500 m, they will travel using the metro. Through the use of ArcGIS (ArcGIS 10.3, Esri, Redlands, CA, USA, 2014), 124,910 person agents are selected, and they are assigned corresponding travel plans in the next step.
2. Identifying the metro travel plans of the person agents
We apply the Baidu Map API (application program interface) to obtain the travel plans of the person agents who use the metro in as much detail as possible. The results show that some of the agents can reach their destinations directly, whereas others need to transfer. Table 1 shows sample metro travel routes used by the agents. After excluding error messages returned by the Baidu Map API and person agents with metro travel plans having empirical travel times of more than two and a half hours (because they spend too much time in travelling and might choose a faster mode of travel), 103,637 person agents remain. These remaining person agents are simulated in this paper.

Table 1.
Information on the metro travel routes of person agents.
3.3. The Simulation and Replanning Process
Using these input data, CCTSim can simulate the travel of person agents during rush hour. More importantly, in the following, we present detailed strategies for optimizing the departure time of each person agent in every iteration.
1. The determination of the initial departure time
The attribute of empirical travel time is listed in the second column of Table 2. This quantity represents the time spent in travel and is returned together with the corresponding travel route. Using the empirical travel time, the initial departure time of each person agent is set to the difference between the obligatory arrival time and the empirical travel time when going to work. This procedure is more practical than a stochastic departure time and helps to determine the specific direction of replanning. The initial departure time for getting off work is set stochastically to a time between 17:30 and 18:30.

Table 2.
The values of metro attributes in reality.
2. The risk of being late
When going to work, each person agent employing a particular initial departure time confronts the risk of being late. Two factors drive lateness; the real travel time may be longer than the empirical travel time, and each person agent has the possibility of missing metro trips due to limited capacity and being forced to wait for the next metro train. This phenomenon can be described as congestion. When a person agent is late for work, the performance of the travel plan is bad because the plan receives a severe penalty in scoring. Congestion also extends travel time, which also decreases the utility of the corresponding travel plan. Thus, person agents tend to set out earlier to avoid the risk of missing their planned trip. However, an early departure time typically results in an increased travel time and premature arrival, which leads to the travel plan receiving a low score. This system resembles a game in which each person agent attempts to optimize his/her departure time.
3. The strategies used to optimize the departure time of each person agent
The objectives of adjusting travel plans are mentioned in Section 2.2.4. The specific procedures followed in going to work and getting off work are shown in Figure 4a,b.
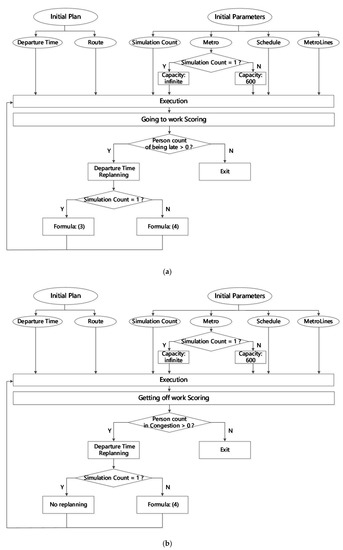
Figure 4.
(a) The procedure used in replanning going to work strategies; (b) The procedure used in replanning getting off work strategies.
(1) Going to work
- ①
- In the first iteration, in order to avoid congestion, the metro capacity is set to an infinite number. Thus, all of the person agents can execute their initial travel plan without congestion. The simulation tool counts person agents as being late if their real travel time is longer than the corresponding empirical time and notes how late they arrive. Subsequently, the initial departure times of these person agents are adjusted forward so that they will not be late again using the same travel routes. The following formula is used to adjust the initial departure time:where is the amount of time by which a person agent is late, measured in minutes; is the hour of the arrival time; is the hour of the obligatory time; is the minutes of the arrival time; is the minutes of the obligatory time, is the seconds of the arrival time; is the new departure time in the next iteration; is the departure time in this iteration; is the departure time interval of the metro; and is the floor function.
- ②
- In the subsequent iterations, the metro capacity is set to a suitable value, and each person agent faces the possibility of being late due to missing a metro trip. Note that the passage flow simulation in our simulation tool is implemented as a queue simulation, in which each metro stop is represented as a first-in first-out queue. Thus, person agents who were late in the last iteration can beat other competitors and board a given metro train by setting out just a few minutes, even one minute, early. The following formula gives the departure time adjustment:where the is the departure time in iteration (x + 1), is the departure time in iteration x and is the step length (minutes) of the departure time adjustment for person agents who were late when going to work or missed metro trips when getting off work in the previous iteration. Specifically, has a negative value for the forward adjustment of the departure time when going to work and a positive value for the backward adjustment of the departure time when getting off work.
- ③
- As this iterative adjustment is performed, the departure time becomes increasingly early for those who are late, and the congestion is progressively reduced. The iterative process is stopped when none of the person actors are late. At that point, all of the metro trains that previously experienced congestion are full when leaving their stops.
(2) Getting off work
The strategies used in optimizing the departure time of each person agent when getting off work are similar to those employed when going to work. Since there is no arrival time constraint, the optimization simply shortens the travel time of each person agent. The departure times of the person agents are deferred when congestion occurs, and the iteration is stopped when no stops display congestion.
4. Results and Discussion
The simulations are undertaken assuming different values for , the step length of the departure time adjustment shown in Formula 3. In this section, is set to 1 min, 2 min and 4 min, and the corresponding numbers of iterations are 201, 92 and 81. We present the departure time adjustments that result in every iteration, as well as the number of person agents who arrive late, the occurrence of congestion at metro stops and the average travel time, travel score and departure times for going to work and getting off work for the person agents. The specific results for every iteration are shown in the Supplementary Materials.
Because only 103,637 person agents are included in the simulation, whereas more than 500 thousand people take the metro during rush hour, the values of the metro attributes require appropriate adjustment [26]. Table 2 and Table 3 show the specific values of the metro attributes in reality and in the simulation test.

Table 3.
The values of metro attributes in the simulation test.
4.1. The Number of Person Agents Who Are Late and the Occurrence of Congestion at Metro Stops
This section examines the number of person agents who arrive late when going to work and the level of congestion at metro stops when getting off work. Figure 5 shows the results in every iteration for different step lengths of departure time adjustment. Note that “HToW” (home to work) hereinafter means going to work, whereas “WToH” (work to home) means getting off work. In addition, blue, green and red lines indicate that the step lengths of departure time adjustment are 1 min, 2 min and 4 min, respectively. Overall, as the number of iterations increases, the number of person agents who arrive late to work and the congestion at metro stops getting off work decreases to zero. The rate at which congestion decreases is much faster than that of person agents who arrive late. In addition, as the step length of departure time adjustment increases, the convergence speed also becomes faster. The decreasing trend of the three results began in the second iteration because the metro capacity is set to infinite in the first iteration, but is set to plausible values in the other iterations. Furthermore, the number of person agents who arrive late displays small fluctuations as this quantity decreases to lower values. At that time, a certain departure time adjustment may cause some person agents who arrived at their workplace before the obligatory arrival time in the previous iteration to be late again. This phenomenon results from the finite capacity of the metro system and competition among the person agents; however, it is temporary and does not change the main decreasing trend.
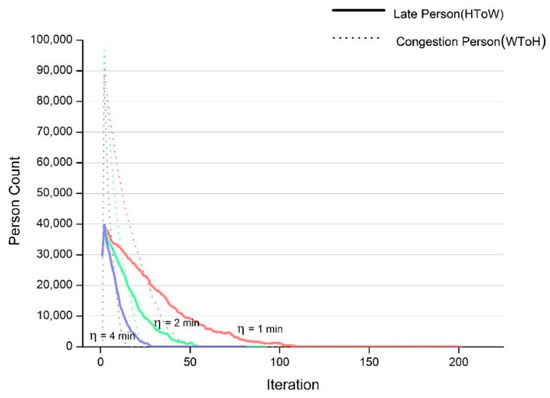
Figure 5.
The numbers of person agents who are late or encounter congestion in each iteration. HToW: home to work; WToH: work to home.
4.2. Average Travel Score
This section examines the average travel score of person agents going to work and getting off work. Figure 6 shows the results in every iteration for the different step lengths of departure time adjustment. Overall, as the number of iterations increases, the average travel score of the person agents increases. The average travel scores when getting off work is much better than that when going to work because there is an obligatory arrival time when going to work; person agents who are late for work will incur a severe penalty for this travel, whereas there is no such rule when getting off work. In addition, as the step length of departure time adjustment increases, the convergence speed also increases. The increasing trend of the three results begins in the second iteration, and there are slight fluctuations in the average travel score of going to work as it increases to a higher value, but these fluctuations do not change the main rising trend. The reason for these fluctuations is similar to that mentioned in Section 4.1.
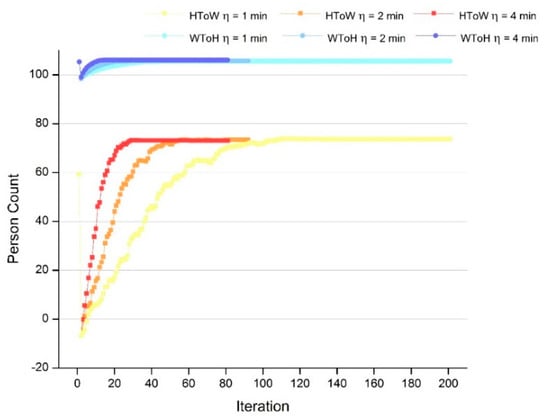
Figure 6.
The average travel scores of the person agents in each iteration. HToW, home to work; WToH, work to home.
4.3. Average Departure Time and Travel Time
This section examines the average departure times and travel times of the person agents when going to work and getting off work. Figure 7a–c show the results in every iteration for the different step lengths of departure time adjustment. Overall, as the number of iterations increases, the average travel time of the person agents decreases by approximately 3–5 min. It decreases from 45 min down to 40 min when going to work and from 40 min down to 37 min when getting off work. The average departure times of the person agents become earlier by approximately 15 min when going to work and later by approximately 5 min when getting off work. Moreover, when the iteration ends, the latest average departure time with no risk of being late when going to work is approximately 8:04, and the earliest average departure time with no risk of missing metro trips when getting off work is approximately 17:50. Interestingly, the average travel time of the person agents initially increases and then decreases. Although the average travel time displays the same trend for person agents going to work and getting off work, these trends result from different underlying causes. When getting off work, the increase in travel time is caused by the differences in metro capacity among the iterations. Therefore, the incidence of congestion at metro stops is so high that the travel time of the person agents in the second iteration is obviously longer than that in the first iteration. In the remainder of the iterations, since the person agents that experience adjusted departure times experienced congestion in the previous iteration and the direction of adjustment of the departure time is backward, their travel time must decrease as the number of iterations increases. On the other hand, when going to work, travel time rises in the second iteration for reasons that are similar to those that drive the increase in travel time when getting off work, but a different and somewhat complex cause drives the increase in travel time in the other iterations. Note that the person agents with adjusted departure times arrived late in the previous iteration, and the adjustment direction of the departure time is forward. At the beginning of the iteration, there are so many person agents who arrive late that an adjustment causes only a fraction of the person agents to arrive at their workplaces before the obligatory time. However, the arrival times of most of the person agents do not change, and their travel time is extended by the step length. As the number of iterations increases, the number of person agents who arrive late gradually decreases, resulting in reductions in the number of person agents that receive adjustments, and the travel times of greater numbers of person agents are shortened, due to the decrease in congestion at the metro stops. Thus, the average travel time begins to decrease, due to the objectives we employ in the dynamic optimization of departure time.
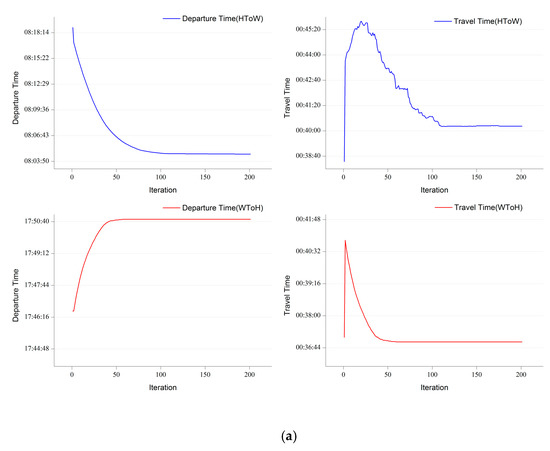
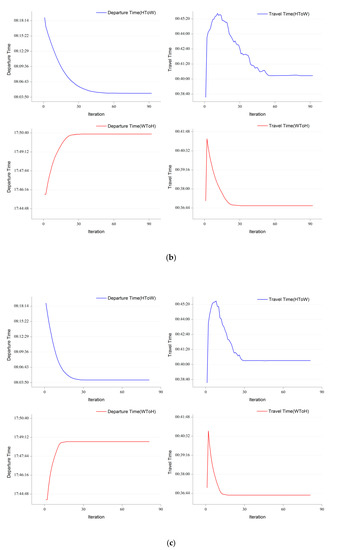
Figure 7.
(a) The average departure times and travel times of the person agents when going to work and getting off work in each iteration for a 1-min step length ( = 1 min); (b) The average departure times and travel times of the person agents when going to work and getting off work in each iteration for a 2-min step length ( = 2 min); (c) The average departure times and travel times of the person agents when going to work and getting off work in each iteration for a 4-min step length ( = 4 min).
4.4. Verification of Our Simulation Results
To verify our simulation results, we compare the differences in the average travel times and average departure times when going to work and getting off work between simulation and reality. Table 4 and Table 5 show these differences between simulation and reality. The real data on the times at which people board at and depart from metro stops were obtained from the Shenzhen Metro Group. Moreover, we have calculated the average walking times from home to the origin metro stop and from the destination metro stop to the workplace. These times are helpful for calculating the average travel times without including walking time and the average times of boarding at and departing from metro stops in the simulation. Table 6 presents these results. The abbreviations “HToS” and “SToW” stand for “home to metro stop” and “metro stop to workplace”.

Table 4.
The differences between simulation and reality when going to work.

Table 5.
The differences between simulation and reality when getting off work.

Table 6.
The walking time results from our simulation. HToS, home to metro stop; SToW, metro stop to workplace.
The experiments reported in Section 4.1 and Section 4.3 demonstrate the core heuristics of the replanning strategy, namely that the average departure times of person agents when going to work should be as late as possible with no risk of being late and the average departure times of person agents when getting off work should be as early as possible with no risk of missing metro trips. With this strategy, the average travel time also becomes shorter.
However, there are some implicit flaws in our optimization strategy; some person agents who are represented as going to work are still caught in congestion when the iteration has ended. In addition, this paper does not consider bus and car trips because of a lack of relevant data. Furthermore, the computational efficiency of the simulation process is relatively low and should be improved by means of parallel computing.
5. Conclusions
- The method presented here represents a research method that is appropriate for the study of urban resident trips using multi-agent technology. This method illustrates the flow of people in any transportation facility at any time and can overcome the flaws of traditional mathematical and statistical models, such as difficulties in describing complex traffic and trip environments.
- A strategy for performing dynamic optimization of the departure times of metro users has been proposed to solve the two problems mentioned at the end of the Introduction. With this strategy, the average travel time becomes shorter, and there is no premature arrival when going to work and no late departure when getting off work. These results can provide the public with suggestions regarding their travel plans and allow commuters more time to do other things, such as sleeping, eating breakfast and shopping.
- Furthermore, the severe congestion at some metro stops leads to long wait times during rush hour. Thus, the existing metro resources are still having difficulties in meeting the actual travel demand. These findings can provide suggestions to public transport management departments, such as to shorten the departure intervals and accelerate the speeds of train operation. The different parameter values of departure intervals and train speeds must be tested in our simulation tool to find better results.
- There are several aspects of the problem that should be investigated in future research. First, large-scale simulations of other modes of travel, such as car or bus travel, should be tested in our simulation tools to better optimize commuters’ departure times and travel routes. Second, the optimal departure interval for each metro line during rush hour should be found to assist in transport planning. It will increase the transportation capacity of metro system without wasting transportation resources. Finally, the person agents’ travel strategies could be modified by introducing game theory to attempt to explore the Nash equilibrium of commuters’ travel strategies. It will be the best travel strategies for any commuter in theory when taking metro during rush hour.
Acknowledgments
We thank Tianqi Qiu, Yumiao Wang, Yanjun Qiao, Miss Shanshan Han and Yuan Wei for their help. In addition, this study is supported by the National Key Research and Development Programme of China (2016 YFC 0803106) and the National Natural Science Foundation of China (Project No. 41371427).
Author Contributions
All the authors contributed to this study. Specifically, Yuliang Xi and Yu Zhang developed the simulation tool, pre-processed the data and conducted the primary experiments, cartography and analysis of the results. Qingyun Du and Fu Ren organized the content and obtained research funding for the study. Biao He introduced the research idea, directed the development of the simulation tool and provided research data collected in Shenzhen. Yuliang Xi wrote the manuscript. Xinyue Ye helped to revise the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, J.W. Study on Agent-Based Intelligent Traffic Control Strategy and Visual Dynamic Simulation; China Agricultural University: Beijing, China, 2001. [Google Scholar]
- Gao, J. Space-Time Coordinating Optimization Theory and Method of Urban Multilevel Transit Network Based on the Travel Behavior of Residents; Beijing Jiao Tong University: Beijing, China, 2013. [Google Scholar]
- Enock, T.; Ren, M.; Eren, E.O. An Alternative Approach to Network Demand Estimation: Implementation and Application in Multi-Agent Transport Simulation (MATSim). Procedia Comput. Sci. 2014, 37, 382–389. [Google Scholar]
- Shanghai Municipal Engineering Administration Department, Tongji University. Study on Shanghai Expressway Transportation Management System; Shanghai Municipal Engineering Administration Department: Shanghai, China, 2000.
- Papageorgiou, M.; Blosseville, J.M.; Haj-Salem, H. Modelling and Real-Time Control of Traffic Flow on the Southern Part of Boulevard Peripherique in Paris: Part I: Modelling. Transp. Res. Part A 1990, 24, 345–359. [Google Scholar] [CrossRef]
- Wang, Y.L. Agent-Based Design and Implementation of Microscopic Traffic Simulation System; University of Electronic Science and Technology of China: Chengdu, China, 2012. [Google Scholar]
- Lighthill, M.J.; Whitham, G.B. A Theory of Traffic Flow on Long Crowded Roads. Proc. R. Soc. Lond. 1955, 1178, 317–345. [Google Scholar] [CrossRef]
- Richards, P.I. Shock Waves on the Highway. Oper. Res. 1956, 4, 42–51. [Google Scholar] [CrossRef]
- Reuschel, A. Vehicle Movements in a Platoon with Uniform Acceleration or Deceleration of Lead Vehicle. Z. Oesterreichisch. Ing. Archit. Ver. 2003, 95, 50–62. [Google Scholar]
- Pipes, L.A. An Operational Analysis of Traffic Dynamics. J. Appl. Phys. 1953, 4, 274–281. [Google Scholar] [CrossRef]
- Gipps, P.G. A Model for the Structure of Lane Changing Decisions. Transp. Res. B 1986, 20, 403–414. [Google Scholar] [CrossRef]
- Prigogine, I.; Andrews, F.C. A Boltzmann Like Approach for Traffic flow. Oper. Res. 2003, 8, 789–797. [Google Scholar] [CrossRef]
- Karina, R.; Carelia, G.; Manuel, C. Agent-Based Model for Automaticity Management of Traffic Flows across the Network. Appl. Sci. 2017, 7, 928–945. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press, Inc.: New York, NY, USA, 2009. [Google Scholar]
- Toroczkai, Z. Complex networks the challenge of interaction topology. Los Alamos Sci. 2005, 29, 94–109. [Google Scholar]
- Lian, J. Intelligent Traffic Control System Based on Agent; Shandong University of Science and Technology: Qingdao, China, 2007. [Google Scholar]
- MATSim. Available online: http://www.matsim.org/ (accessed on 1 July 2017).
- Arentze, T.A.; Timmermans, H.J. A Learning-Based Transportation Oriented Simulation System. Transp. Res. Part B 2004, 38, 613–633. [Google Scholar] [CrossRef]
- Auld, J.A.; Mohammadian, A. Planning Constrained Destination Choice Modeling in the Adapts Activity-Based Model. In Proceedings of the Transportation Research Board 90th Annual Meeting, Washington, DC, USA, 23–27 January 2011. [Google Scholar]
- Feil, M.; Balmer, M.; Axhausen, K.W. New Approaches to Generating Comprehensive All-Day Activity-Travel Schedules. In Proceedings of the Transportation Research Board Annual Meeting, Washington, DC, USA, 10–14 January 2010. [Google Scholar]
- Horni, A.; Nagel, K.; Axhausen, K.W. The Multi-Agent Transport Simulation MATSim; Swiss Fed Inst Tech—Zurich Switzerland: Zurich, Switzerland, 2016. [Google Scholar]
- Balmer, M.; Raney, B.; Nagel, K. Adjustment of Activity Timing and Duration in an Agent-Based Traffic Flow Simulation. In Progress in Activity-Based Analysis; Elsevier: Amsterdam, The Netherlands, 2005; pp. 91–114. [Google Scholar]
- Raney, B.; Cetin, N.; Völlmy, A.; Vrtic, M.; Axhausen, K.; Nagel, K. An Agent-Based Microsimulation Model of Swiss Travel: First Results. Netw. Spat. Econ. 2003, 3, 23–41. [Google Scholar] [CrossRef]
- Cetin, N.; Burri, A.; Nagel, K. A Large-Scale Agent-Based Traffic Microsimulation Based on Queue Model. In Proceedings of the Swiss Transport Research Conference (STRC), Monte Verita, Switzerland, 19–21 March 2003. [Google Scholar]
- Kaddoura, I.; Kickhöfer, B.; Neumann, A.; Tirachini, A. Public Transport Supply Optimization in an Activity-Based Model: Impacts of Activity Scheduling Decisions and Dynamic Congestion. In Proceedings of the Latsis Symposium, Zurich, Switzerland, 11–14 September 2012; pp. 12–38. [Google Scholar]
- Huang, L.; Tang, X.L.; Lin, Y.L. Spatio-Temporal Analysis of Public Transport Passenger Flow Based on Public Transport Card Data—A Case Study of Shenzhen. China High-Tech Enterp. 2016, 17, 87–89. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).