Hybrid Fuzzy–DDPG Approach for Efficient MPPT in Partially Shaded Photovoltaic Panels

Abstract

Partial shading conditions reduce the efficiency of photovoltaic (PV) systems by introducing multiple local maxima in the power–voltage curve, complicating Maximum Power Point Tracking (MPPT). Traditional MPPT methods, such as Perturb and Observe (P&O) and Incremental Conductance (IC), frequently converge to local maxima, leading to suboptimal power extraction. This study proposes a hybrid reinforcement learning-based MPPT approach that combines fuzzy techniques with Deep Deterministic Policy Gradient (DDPG) to enhance tracking accuracy under partial shading. The method integrates fuzzy membership functions into the actor–critic structure, improving state representation and convergence speed. The proposed algorithm is evaluated in a simulated PV environment under various shading scenarios and benchmarked against conventional Perturb and Observe P&O and IC methods. Experimental results demonstrate that the Fuzzy–DDPG approach outperforms these classical techniques by achieving a higher tracking efficiency of 95%, compared to 85% for P&O and 88% for IC in average, while also minimizing steady-state oscillations. Additionally, the proposed method reduces tracking errors by up to 7.9% compared to conventional MPPT algorithms. These findings indicate that the combination of fuzzy logic and deep reinforcement learning provides a more adaptive and efficient MPPT solution, ensuring improved energy harvesting in dynamically changing conditions.

1. Introduction

Partial shading is a prevalent issue in photovoltaic (PV) systems that significantly degrades performance by introducing multiple local maxima in the power–voltage (P–V) curve, thereby complicating the identification of the global Maximum Power Point (MPP) via conventional Maximum Power Point Tracking (MPPT) algorithms [1,2,3]. To overcome this challenge, researchers have increasingly employed advanced optimization techniques—particularly metaheuristic algorithms—to reliably locate the global MPP under non-uniform irradiance.

Heuristic methods inspired by natural phenomena, such as the Flower Pollination Algorithm [4] and Genetic Algorithms [5], have demonstrated the capability to evolve candidate solutions toward global optimum performance. Additional approaches including Particle Swarm Optimization [6], Ant Colony Optimization, Simulated Annealing, Artificial Bee Colony, Firefly Algorithm, Cuckoo Search, and Differential Evolution [7] have been applied to MPPT; however, these methods often encounter high computational complexity, sensitivity to parameter tuning, slow convergence, and practical implementation constraints [8,9].

Complementary to metaheuristic strategies, artificial intelligence (AI)-based techniques—such as fuzzy logic control and neural networks—have been proposed to address the MPPT challenge. Hybrid methods, for instance the integration of the shuffled frog leaping algorithm with the incremental conductance method [10], have enhanced global MPP tracking under partial shading. Nevertheless, these AI-based methods frequently require extensive training data, which increases memory usage and may lead to longer optimization times and transient power losses [11].

Classical control strategies, including Proportional–Integral–Derivative (PID) control [12,13] and Sliding Mode Control (SMC) [14,15], provide alternative solutions but often fail to manage the nonlinear dynamics and oscillatory behavior inherent in PV systems under partial shading. Other techniques such as distributed control, optimal control, backstepping, divide-and-conquer strategies [16,17,18], and simpler methods like Perturb and Observe (P&O) [19], have been explored with limited success [20,21].

Recent advances in MPPT for photovoltaic systems under partial shading conditions have led to the development of several innovative control strategies. In [22], an adapted model predictive control algorithm is proposed to robustly track the global maximum power point by predicting future system states and optimizing converter duty cycles, thereby reducing reliance on multiple sensors. Meanwhile, ref. [23] introduces a bi-objective reinforcement learning framework for dynamic PV array reconfiguration that simultaneously maximizes power extraction and minimizes switching operations in the presence of moving clouds. Furthermore, Ref. [24] presents a novel approach that integrates fuzzy logic control with optimizable Gaussian Process Regression to enhance both tracking accuracy and convergence speed under complex environmental conditions. Finally, an adapted model predictive control algorithm has also been proposed to improve GMPP tracking under partial shading by minimizing the MPC cost function without relying on current sensors [25].

These contributions collectively underscore the potential of combining advanced control techniques with artificial intelligence to overcome the limitations of traditional MPPT methods.

The research motivation behind this work is to develop an MPPT approach that overcomes these limitations by reducing the training burden and enhancing convergence speed. Reinforcement learning (RL) has emerged as a promising paradigm for MPPT under partial shading, with methods such as Deep Deterministic Policy Gradient (DDPG) and its variants effectively managing continuous action spaces [26,27,28,29,30,31,32]. However, the substantial data and computational resources required by these methods, along with their sensitivity to reward function design, remain critical challenges.

In this context, the present work proposes a novel hybrid approach that integrates fuzzy techniques with DDPG. By fuzzifying the input states to the actor network, the method significantly reduces the number of training episodes required, leading to faster convergence and improved robustness compared to conventional methods such as Perturb and Observe, Incremental Conductance, and standalone DDPG [33,34].

The principal contributions of this paper are the following:

1.

Development of a novel fuzzy-based reinforcement learning framework: A hybrid MPPT strategy that combines fuzzy logic with DDPG to enhance global MPP tracking under partial shading.

2.

Comprehensive validation: Detailed simulation and experimental results that corroborate the improved convergence speed, tracking accuracy, and robustness of the proposed method.

3.

Comparative analysis: A systematic comparison with conventional MPPT techniques, highlighting the advantages of the proposed approach in real-time PV system control.

2. Materials and Methods

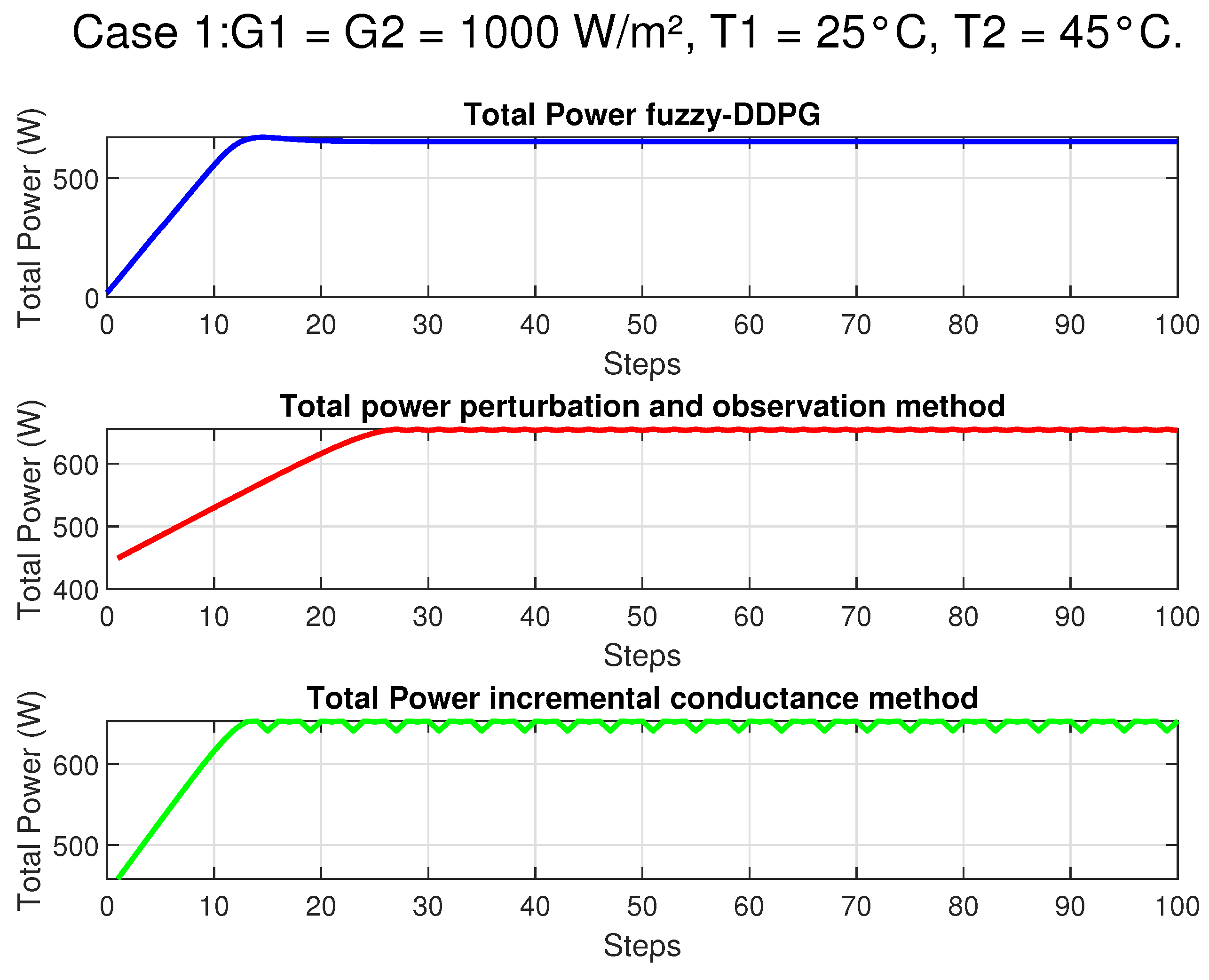
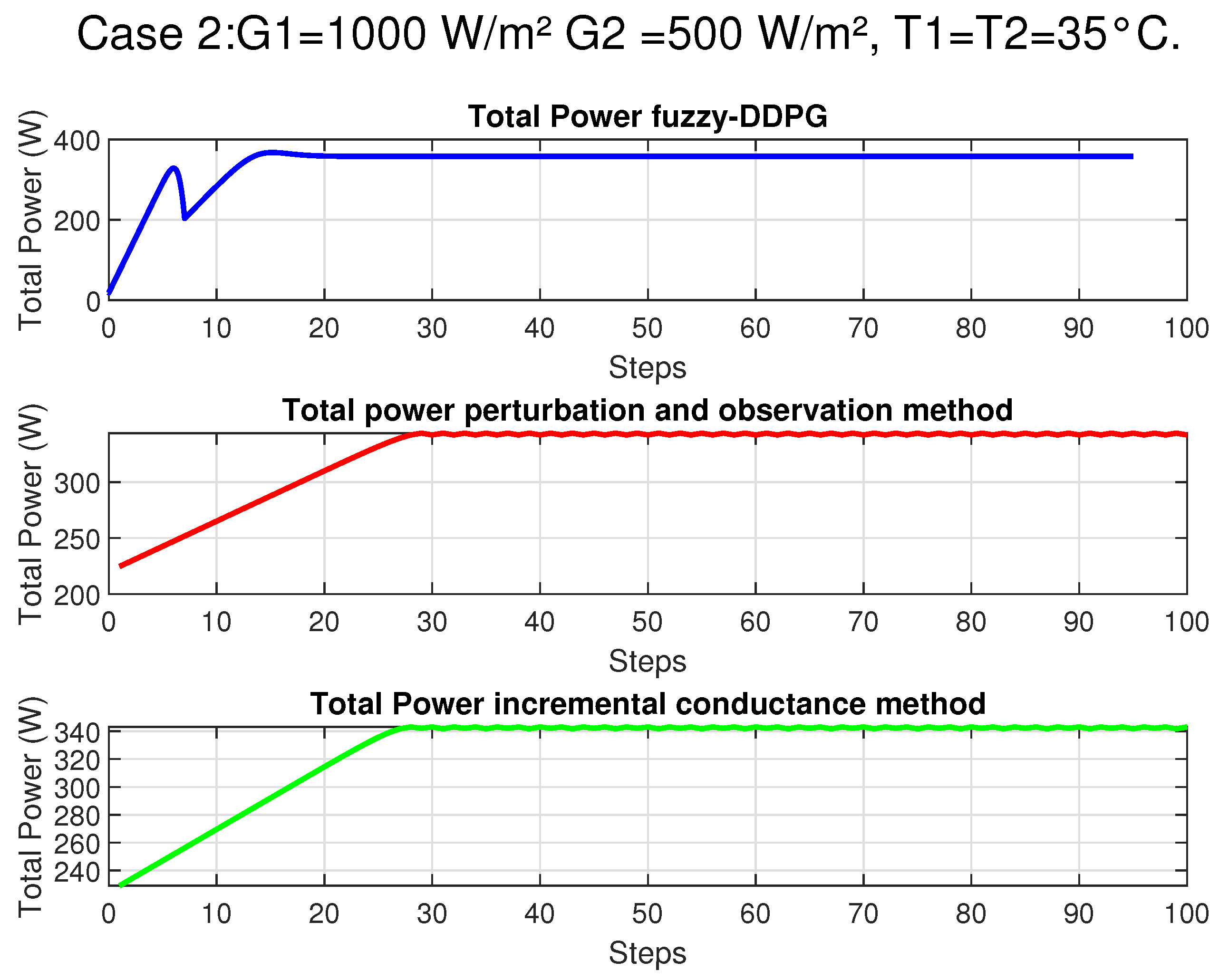
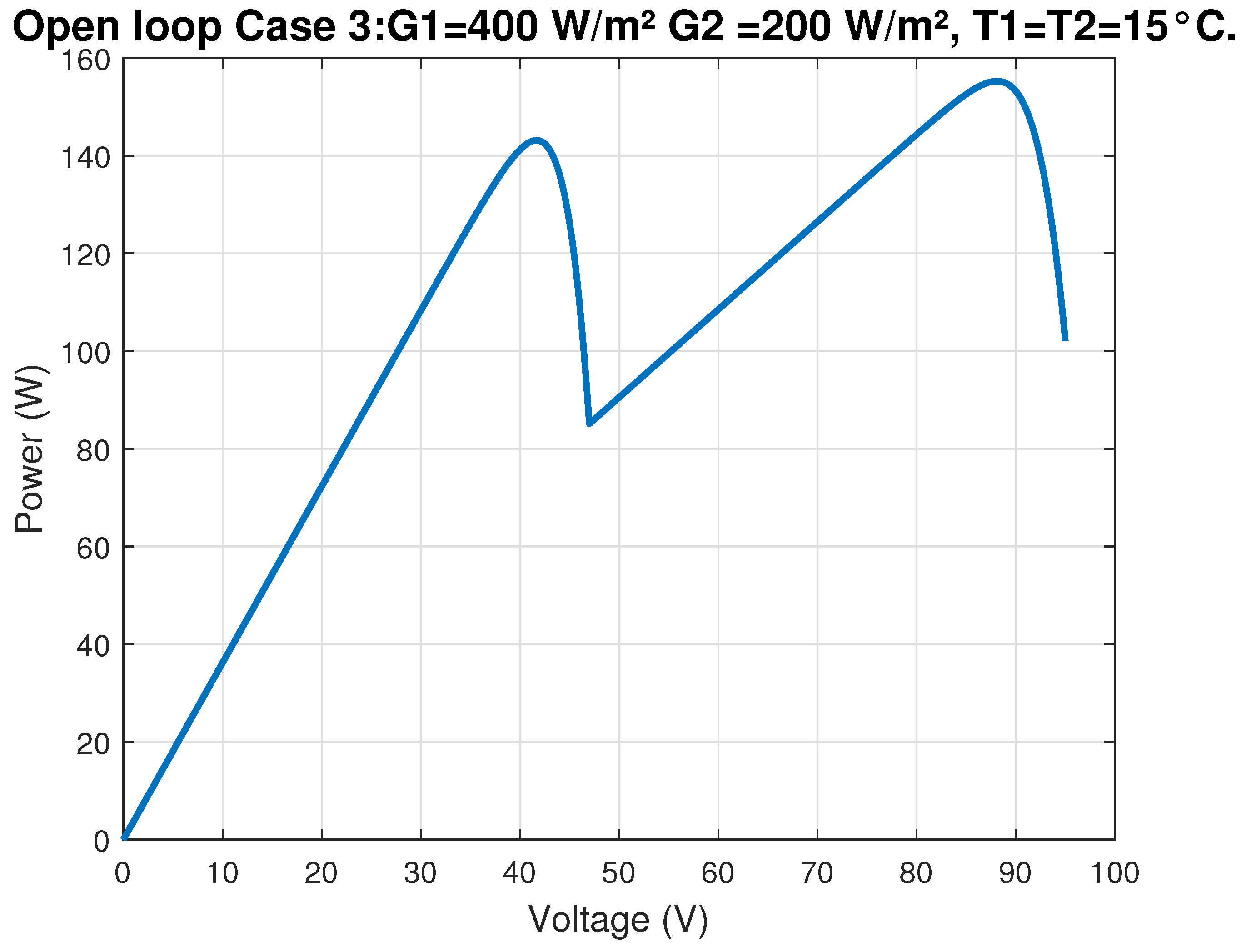
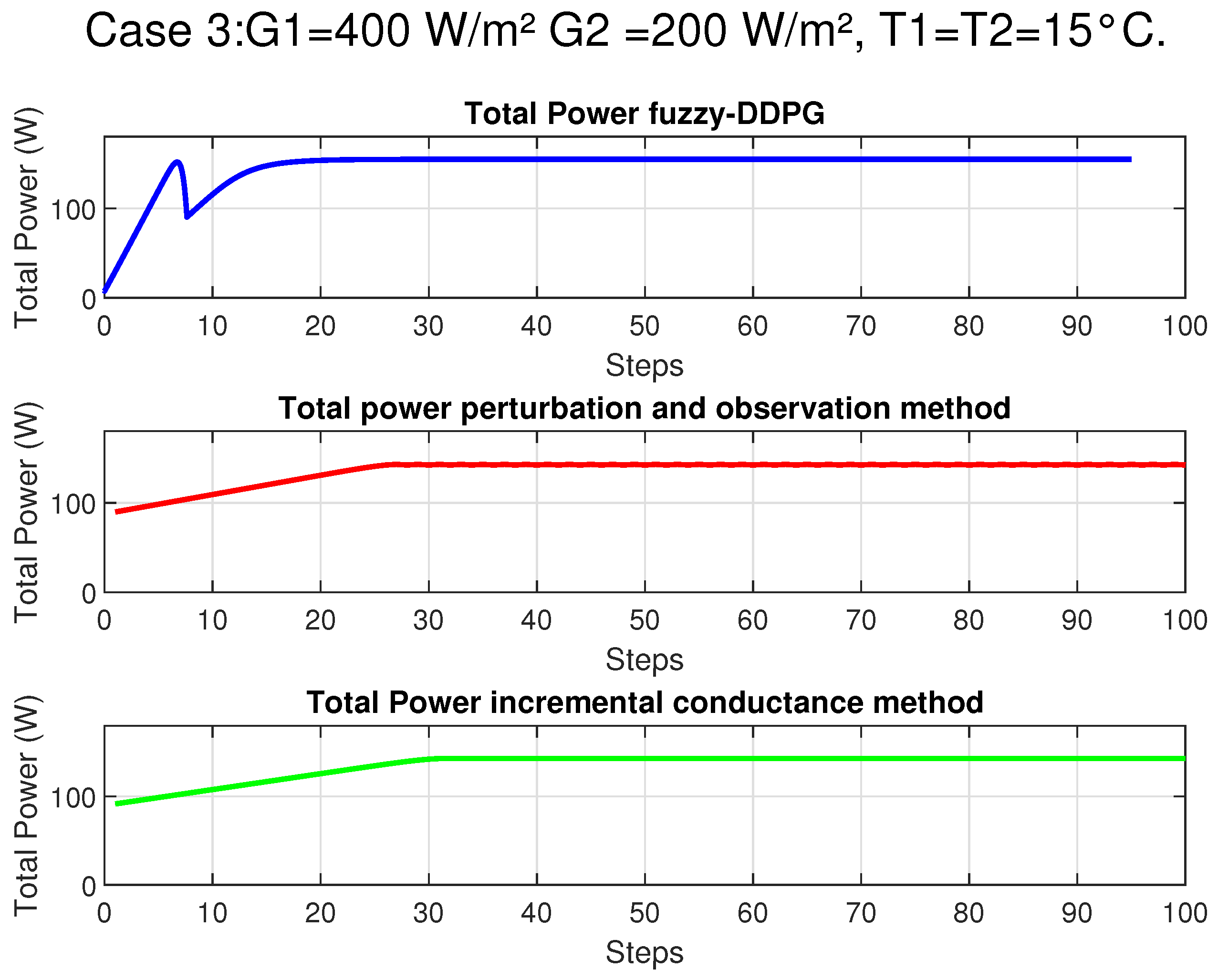
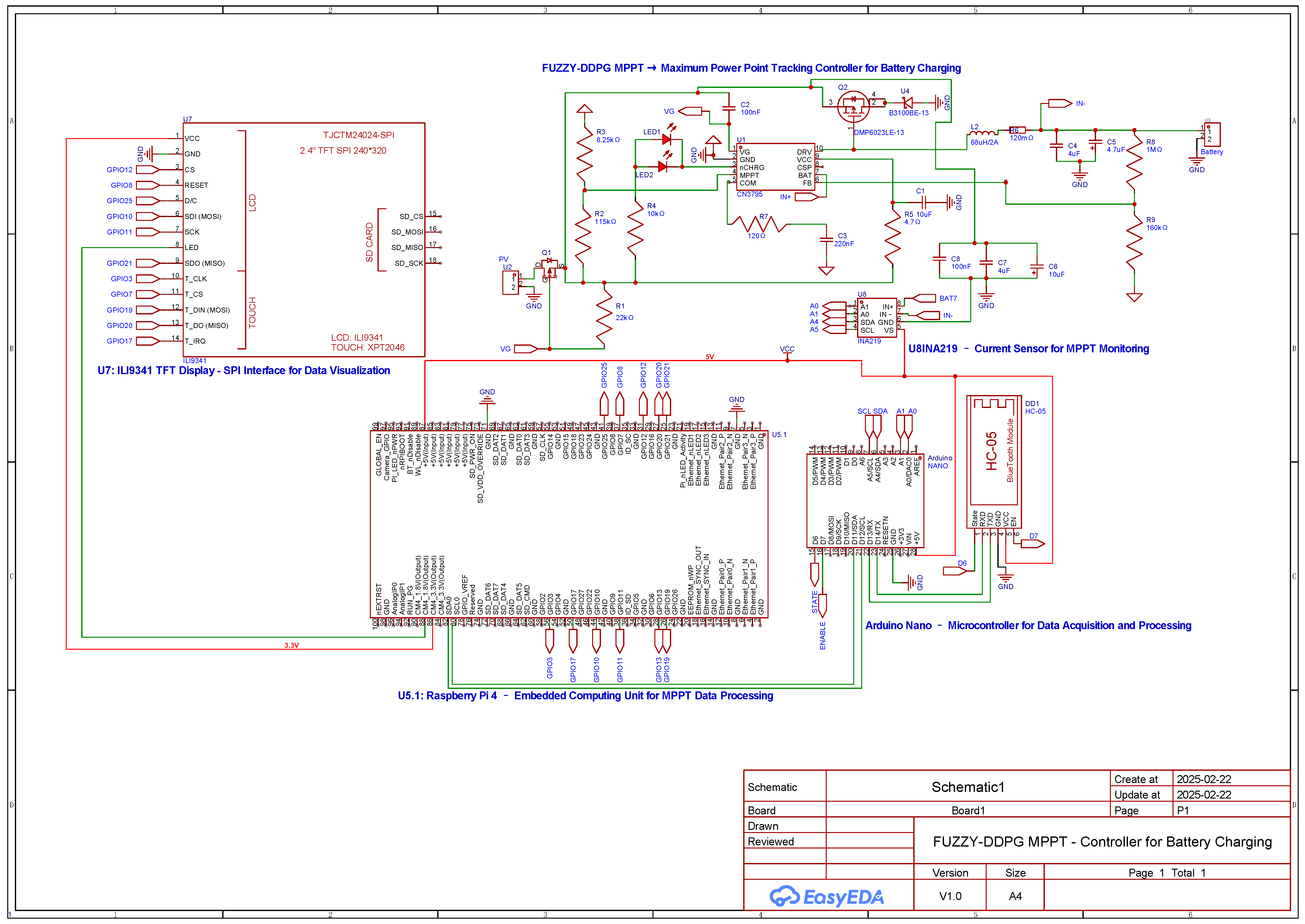
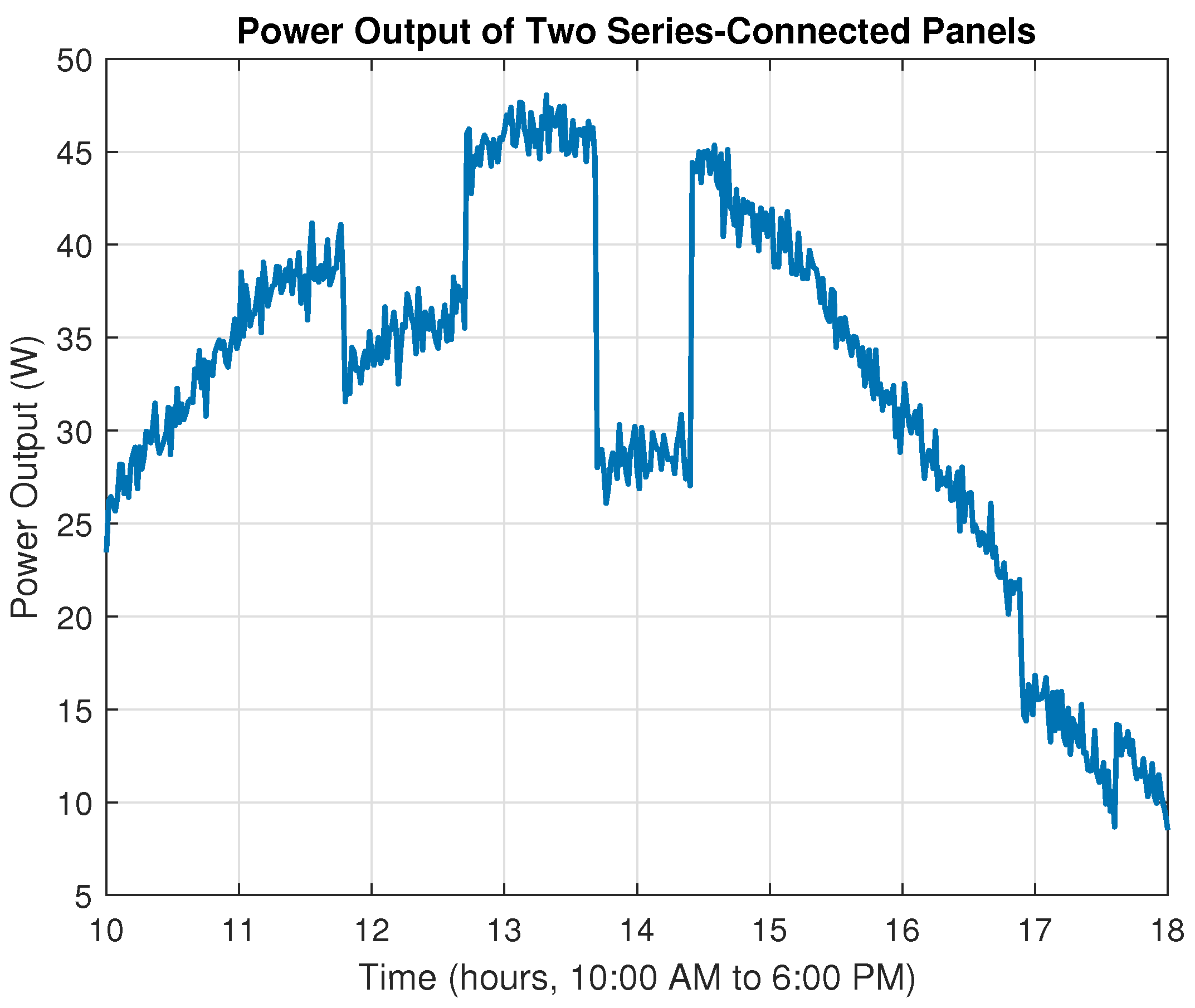
In this section, we provide an overview of the methodologies employed to address the Maximum Power Point Tracking (MPPT) challenge in photovoltaic systems under partial shading conditions. Initially, we describe a rigorous mathematical model based on the single-diode equivalent circuit to accurately capture the nonlinear behavior of the photovoltaic panel. Subsequently, our proposed control strategy, which integrates fuzzy logic with Deep Deterministic Policy Gradient (DDPG), is introduced to enhance state representation and expedite convergence in complex, non-convex operational environments. Finally, a theoretical justification rooted in the contraction properties of the Bellman operator is presented to establish the stability and robustness of the hybrid approach.

2.1. Mathematical Model of a Photovoltaic Panel

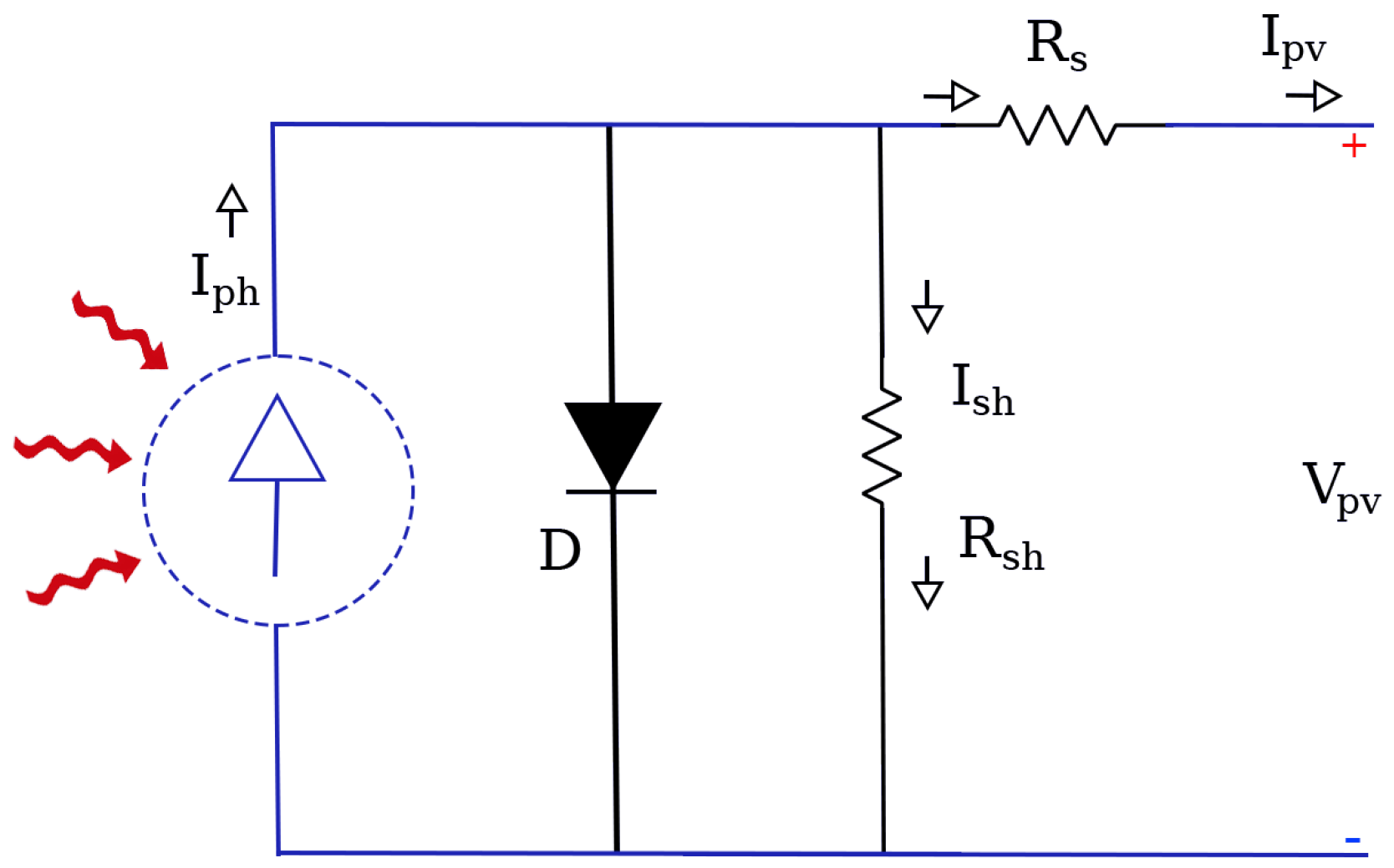
To comprehensively characterize the nonlinear behavior of the photovoltaic panel, the following mathematical model is presented. By employing the single-diode equivalent circuit, this formulation encapsulates the interactions among photocurrent generation, diode conduction dynamics, and resistive losses, thereby providing a robust foundation for developing advanced MPPT strategies. This model is essential for deriving control laws that guarantee convergence to the global maximum power point under varying irradiance and temperature conditions, including partial shading.

As shown in Figure 1, the equivalent circuit of a photovoltaic (PV) cell consists of a current source representing the photocurrent ($I_{ph}$), a diode (D) modeling the p-n junction behavior, a series resistance ($R_s$), and a parallel (shunt) resistance ($R_{sh}$) that accounts for leakage currents.

The output current $I_{pv}$ of the PV cell is given by Kirchhoff’s law as follows [33]:

$$I_{pv}=I_{ph}-I_d-I_{sh}$$

(1)

where:

• $I_{ph}$ is the light-generated current, proportional to the solar irradiance.
• $I_d$ is the diode current.
• $I_{sh}$ is the shunt leakage current.

The shunt current is modeled as follows:

$$I_{sh}={\displaystyle \frac{V+I_{pv}{R}_s}{R_p}}$$

(2)

where:

• $R_s$ is the series resistance.
• $R_p$ is the parallel resistance.

The diode current $I_d$ follows the Shockley diode equation:

$$I_d=I_0\left(exp\left({\displaystyle \frac{q{V}_d}{Ak{T}_c}}\right)-1\right)$$

(3)

where:

• $I_0$ is the reverse saturation current of the diode.
• $q=1.6\times {10}^{-19}$ C is the electronic charge.
• $k=1.38\times {10}^{-23}$ J/K is the Boltzmann constant.
• A is the diode ideality factor.
• $T_c$ is the cell temperature in Kelvin.
• $V_d$ is the voltage across the diode:

  $$V_d=V+I_{pv}{R}_s$$

  (4)

The light-generated current $I_{ph}$ is affected by solar irradiance and temperature:

$$I_{ph}=\left(I_{sc}+K_I(T_c-T_r)\right)\times {\displaystyle \frac{G}{G_{STC}}}$$

(5)

where:

• $I_{sc}$ is the short-circuit current at standard test conditions (STC) ($T=25$ °C, $G_{STC}=1000$ W/m²).
• $K_I$ is the short-circuit current temperature coefficient.
• $T_r$ is the reference temperature.
• G is the actual solar irradiance.

For a PV module with $N_s$ series-connected cells, the overall output current is as follows:

$$I_{pv}=I_{ph}-I_0\left(exp\left({\displaystyle \frac{q(V+I_{pv}{R}_s)}{Ak{T}_c{N}_s}}\right)-1\right)$$

(6)

2.2. Reinforcement Learning Fuzzy–DDPG

Reinforcement learning (RL), as discussed in [35], is a machine learning paradigm in which an agent learns to make optimal decisions by interacting with an environment. This process is typically formulated as a Markov Decision Process (MDP), which is characterized by key components:

• State (S): Represents the current situation or context of the agent. At each time step, the agent observes the state of the environment.
• Action (A): The agent selects an action from a set of possible actions based on the current state.
• Transition Probability (P): P(s’|s, a) denotes the probability of transitioning to state s’ after taking action a in state s. This captures the dynamics of the environment.
• Reward (R): R(s, a, s’) represents the immediate reward received by the agent after taking action a in state s and transitioning to state s’.
• Discount Factor ($\gamma$): A value between 0 and 1 that determines the importance of future rewards. A higher discount factor prioritizes long-term rewards.
• Policy ($\pi$): A mapping from states to actions, defining the agent’s behavior. The policy can be deterministic, $\pi \left(s\right)=a$, or stochastic, $\pi \left(a\right|s)=P(a\left|s\right).$

The primary objective in RL is to find an optimal policy that maximizes the expected cumulative discounted reward, formally expressed as follows:

$$R\left(\pi \right)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t,s_{t+1})\right].$$

(7)

In continuous state spaces, the exponential growth of the state–action pair complexity—often referred to as the curse of dimensionality—renders traditional tabular methods impractical. This challenge necessitates the use of function approximation techniques, where neural networks and other parametric models are employed to estimate value functions or to directly parameterize policies. Such approaches have led to the development of advanced RL methods including Deep Q-Networks (DQN), policy gradient methods, and actor–critic architectures like Deep Deterministic Policy Gradient (DDPG) [36].

Beyond these foundational aspects, modern RL methods have evolved to incorporate strategies such as curriculum learning and adaptive exploration [37], which further enhance training stability and convergence. In our study, RL is applied to dynamically adjust the duty cycle of a DC–DC converter in a photovoltaic system under partial shading conditions. This formulation not only addresses the inherent non-stationarity and high-dimensionality of the environment but also demonstrates how RL, when combined with fuzzy logic enhancements, provides a robust and adaptive framework for achieving Maximum Power Point Tracking in complex, real-world settings.

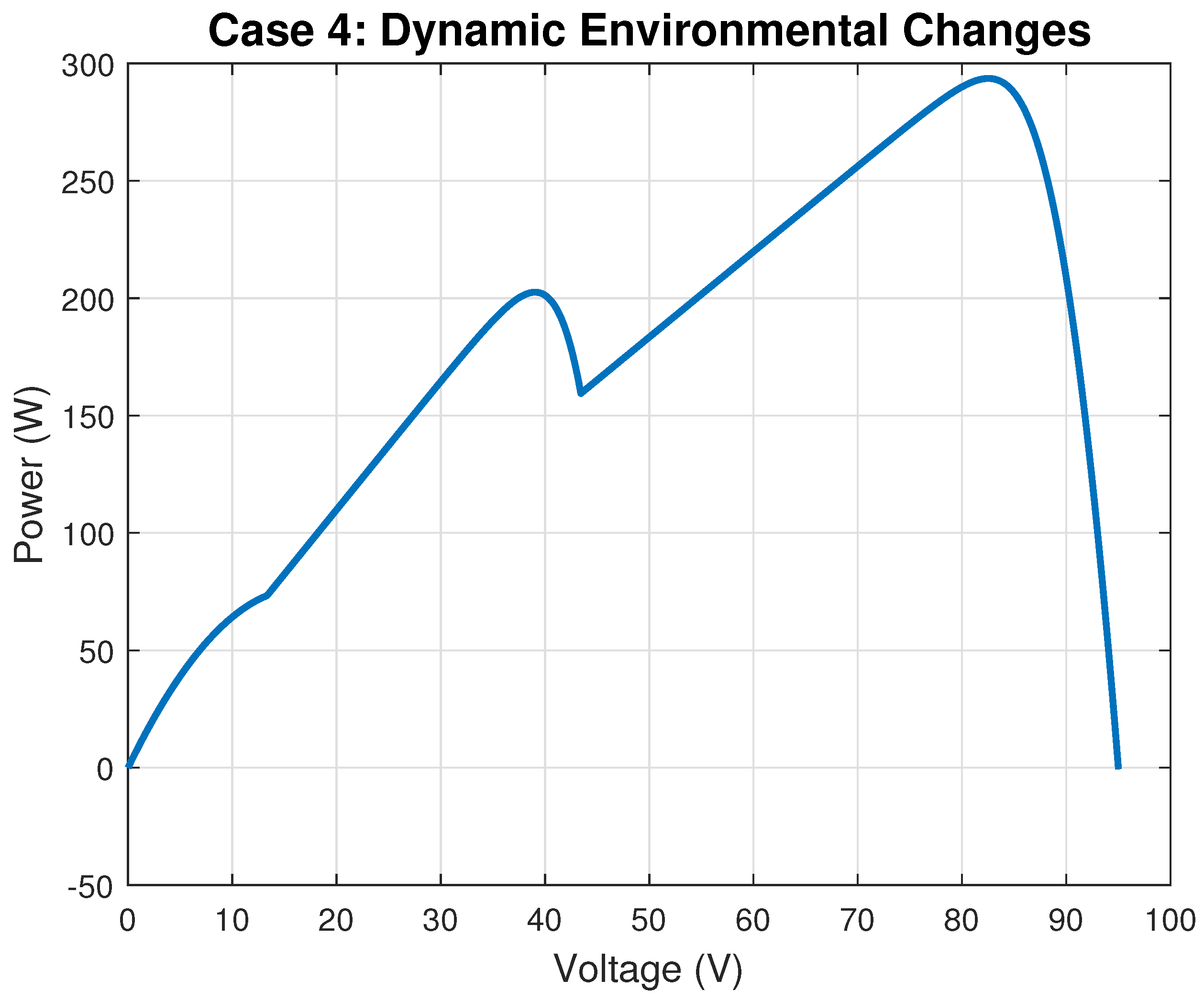
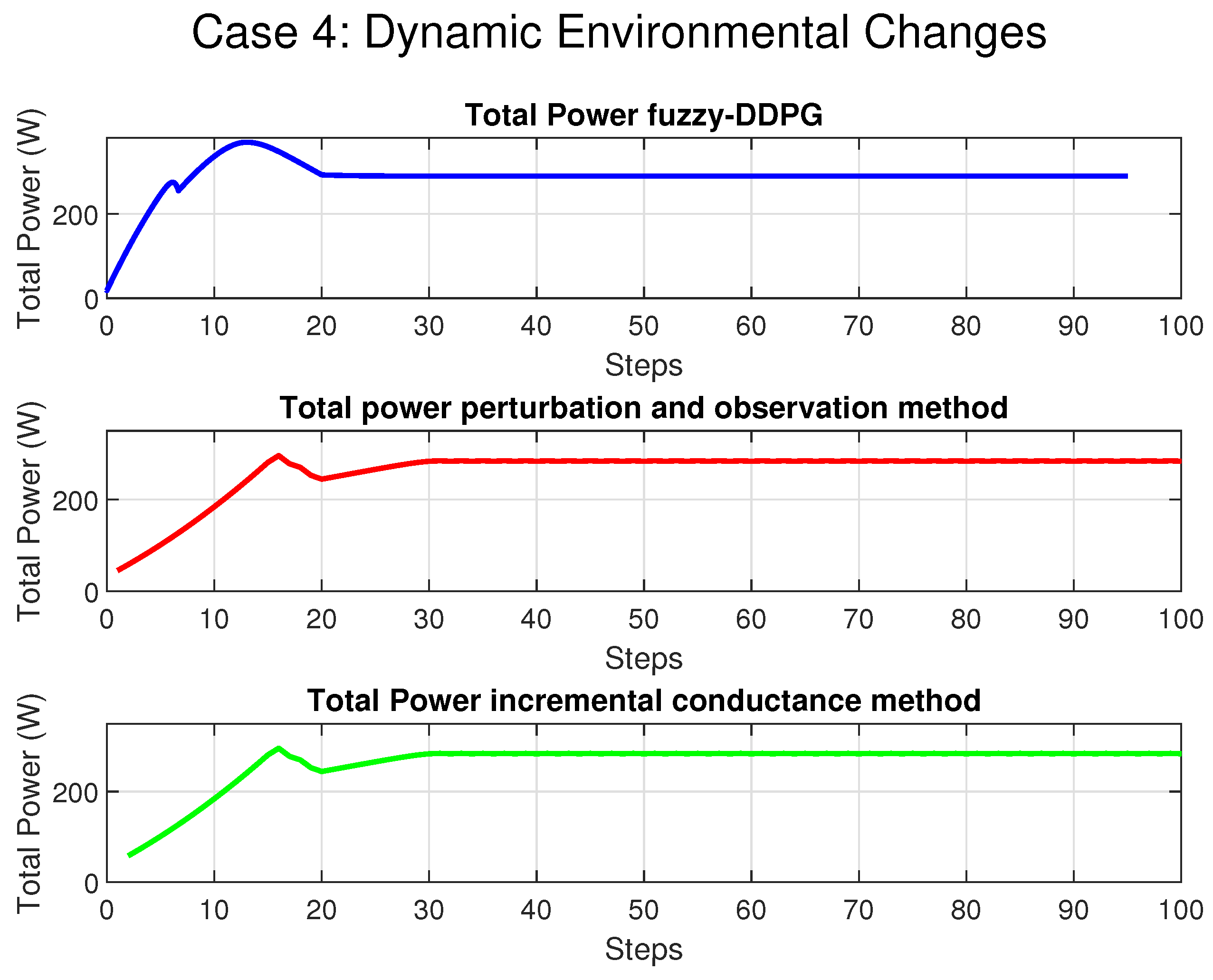
In the context of Maximum Power Point Tracking for photovoltaic systems under partial shading conditions, the RL agent learns to adjust the duty cycle of a DC-DC converter to maximize the power output of the PV system. Partial shading occurs when some parts of a PV array receive less sunlight than others, leading to multiple peaks in the power–voltage curve. Traditional MPPT methods can get stuck at local maxima, resulting in suboptimal power generation. RL offers a promising solution to this problem by learning to navigate the complex power landscape and find the global maximum power point.

Traditional RL algorithms like Q-learning [38] and SARSA are designed for discrete state and action spaces. Extensions to continuous spaces often involve function approximation techniques, such as tile coding [39], radial basis functions (a common function approximation technique, though not directly referenced in the current search results), or neural networks (neural networks are widely used in RL, see for example [40]). However, these approximations can suffer from instability and divergence issues [41].

Policy gradient methods, which directly optimize the policy, are naturally suited for continuous action spaces. Algorithms like REINFORCE and actor–critic methods have been developed to handle such scenarios. The Deterministic Policy Gradient algorithm [42] extends the policy gradient theorem to deterministic policies, laying the groundwork for DDPG [43].

The deterministic policy gradient algorithm [42] states that the gradient of the expected return with respect to the policy parameters ${\theta }^{\mu }$ is:

$${\nabla }_{{\theta }^{\mu }}J={\mathbb{E}}_{s\sim {\rho }^{\mu }}\left[{\nabla }_{{\theta }^{\mu }}\mu \left(s\right|{\theta }^{\mu }){\nabla }_a{Q}^{\mu }(s,a){|}_{a=\mu \left(s\right|{\theta }^{\mu })}\right]$$

(8)

where:

• $Q^{\mu }(s,a)$ is the action-value function under policy $\mu$.
• ${\rho }^{\mu }\left(s\right)$ is the discounted state visitation distribution under $\mu$.

In [44] is introduced a fuzzy Q-iteration algorithm for approximate dynamic programming, addressing the curse of dimensionality by using a fuzzy partition of the state space and discretization of the action space to approximate the Q-function, making it applicable to continuous state and action spaces. This approach allows for handling larger state spaces than traditional dynamic programming, which struggles with the exponential growth of computational complexity as the number of state variables increases.

Fuzzy Q-Iteration approximates the Q-function using fuzzy basis functions:

$$Q(s,a)\approx \sum _{i=1}^N{w}_i{\varphi }_i(s,a)$$

(9)

where:

• ${\varphi }_i(s,a)$ are fuzzy basis functions representing the degree of membership of $(s,a)$ in fuzzy sets.
• $w_i$ are the weights to be learned.

The update rule minimizes the Bellman residual:

$$w^{(k+1)}=arg\underset{w}{min}\sum _{(s,a)}{\left(\mathcal{R}(s,a)+\gamma \underset{a^{\prime }}{max}{Q}^{\left(k\right)}(s^{\prime },a^{\prime })-\sum _{i=1}^N{w}_i{\varphi }_i(s,a)\right)}^2$$

(10)

The fuzzy Q-iteration algorithm iteratively improves the Q-function approximation, converging to the optimal Q-function under certain conditions.

The proposed method combines the strengths of fuzzy techniques and DDPG to achieve global Maximum Power Point Tracking under partial shading conditions. The fuzzy component handles the action space, while the DDPG component addresses the continuous state space, resulting in a hybrid approach that is both scalable and able to operate in complex environments [28,45].

By integrating fuzzy basis functions into the actor and critic networks of DDPG, we aim to approximate both the policy and value function using fuzzy features, as follows:

$$\begin{array}{cc}\mathrm{Actor}\mathrm{Network}:\hfill & \mu \left(\varphi \left(s\right)\right|{\theta }^{\mu })\hfill \\ \mathrm{Critic}\mathrm{Network}:\hfill & Q(\varphi \left(s\right),a|{\theta }^Q)\hfill \end{array}$$

(11)

The fuzzy feature vector $\varphi \left(s\right)$ captures the essential characteristics of the state space, facilitating learning in continuous domains. This hybrid approach combines the strengths of fuzzy approximation and deep reinforcement learning, enabling the agent to efficiently navigate the complex power landscape and find the global maximum power point under partial shading conditions.

For each state variable $s_i$, we define M membership functions ${\left\{{\mu }_{ij}\right\}}_{j=1}^M$, typically Gaussian functions:

$${\mu }_{ij}\left(s_i\right)=exp\left(-{\displaystyle \frac{{(s_i-c_{ij})}^2}{2{\sigma }_{ij}^2}}\right)$$

(12)

The parameters are defined as follows:

• $c_{ij}$: Center of the j-th membership function for variable $s_i$.
• ${\sigma }_{ij}$: Width (standard deviation) of the membership function.

The actor and critic networks take this fuzzy feature vector as input, and the output represents the actor policy and critic value function, respectively.

The actor network architecture is as follows:

• Input Layer: Receives fuzzy feature vector $\varphi \left(s\right)$.
• Hidden Layers: Multiple fully connected layers with nonlinear activations.
• Output Layer: Produces action $a=\mu \left(\varphi \left(s\right)\right|{\theta }^{\mu })$, using a bounded activation function like tanh.

The critic network architecture is as follows:

• State Input Layer: Receives fuzzy feature vector $\varphi \left(s\right)$.
• Action Input Layer: Receives action a.
• Hidden Layers: Concatenates $\varphi \left(s\right)$ and a, followed by fully connected layers.
• Output Layer: Outputs scalar value $Q(\varphi \left(s\right),a|{\theta }^Q)$.

The actor network processes the fuzzy feature vector $\varphi \left(s\right)$ obtained from the state s. It comprises two fully connected hidden layers with ReLU activations, and an output layer with a bounded activation function (e.g., tanh) to produce the action:

$$a=\mu (\varphi \left(s\right);{\theta }_{\mu })$$

(13)

The critic network receives the concatenated fuzzy feature vector and the action, and processes this input through two hidden layers with ReLU activations to output the scalar Q-value:

$$Q(\varphi \left(s\right),a;{\theta }_Q)$$

(14)

The fuzzy feature vector $\varphi \left(s\right)$ captures the essential characteristics of the state space, facilitating learning in continuous domains. By integrating fuzzy basis functions into the actor and critic networks, we aim to approximate both the policy and value function using fuzzy features, enabling efficient navigation of the complex power landscape and global Maximum Power Point tracking under partial shading conditions.

The training procedure follows the standard DDPG algorithm, with the additional incorporation of fuzzy basis functions, according to Algorithms 1 and 2.

Algorithm 1 At each time step

1: repeat 2:    Compute Fuzzy Features: $\varphi \left(s_t\right)$ from current state $s_t$. 3:    Select Action: $a_t=\mu \left(\varphi \left(s_t\right)\right|{\theta }^{\mu })+{\mathcal{N}}_t$, where ${\mathcal{N}}_t$ is exploration noise. 4:    Execute Action: Receive reward $r_t$ and next state $s_{t+1}$. 5:    Store Transition: Store $(s_t,a_t,r_t,s_{t+1})$ in $\mathcal{D}$. 6: until Stopping Criterion is Met

Algorithm 2 At each learning step

1: repeat 2:     Sample Mini-Batch: Randomly sample N transitions from $\mathcal{D}$. 3:     Compute Targets: $$y_i=r_i+\gamma Q^{\prime }(\varphi \left(s_{i+1}\right),{\mu }^{\prime }\left(\varphi \left(s_{i+1}\right)\right|{\theta }^{{\mu }^{\prime }})|{\theta }^{Q^{\prime }})$$ 4:     Update Critic: Minimize loss L: $$L={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(y_i-Q(\varphi \left(s_i\right),a_i|{\theta }^Q)\right)}^2$$ 5:     Update Actor: Update policy parameters using gradient ascent: $${\nabla }_{{\theta }^{\mu }}J\approx {\displaystyle \frac{1}{N}}\sum _{i=1}^N{\nabla }_{{\theta }^{\mu }}\mu \left(\varphi \left(s_i\right)\right|{\theta }^{\mu }){\nabla }_{a}Q(\varphi \left(s_i\right),a|{\theta }^Q){|}_{a=\mu \left(\varphi \left(s_i\right)\right|{\theta }^{\mu })}$$ 6:     Update Target Networks: $${\theta }^{Q^{\prime }}\leftarrow \tau {\theta }^Q+(1-\tau ){\theta }^{Q^{\prime }}$$ $${\theta }^{{\mu }^{\prime }}\leftarrow \tau {\theta }^{\mu }+(1-\tau ){\theta }^{{\mu }^{\prime }}$$ 7: until Stopping Criterion is Met

This training procedure allows the agent to learn the optimal policy and value function by leveraging the fuzzy feature representation, enabling global Maximum Power Point Tracking under partial shading conditions.

Algorithm 3 in the form of pseudocode could be used to implement the proposed method.

Algorithm 3 Fuzzy–DDPG Algorithm

1: Initialize actor network $\mu \left(\varphi \left(s\right)\right|{\theta }^{\mu })$ and critic network $Q(\varphi \left(s\right),a|{\theta }^Q)$ 2: Initialize target networks ${\theta }^{{\mu }^{\prime }}\leftarrow {\theta }^{\mu }$, ${\theta }^{Q^{\prime }}\leftarrow {\theta }^Q$ 3: Initialize replay buffer $\mathcal{D}$ 4: for episode = 1 to max_episodes do 5:       Initialize state $s_0$ 6:       for $t=1$ to max_steps do 7:           Compute fuzzy features $\varphi \left(s_t\right)$ 8:           Select action $a_t=\mu \left(\varphi \left(s_t\right)\right|{\theta }^{\mu })+{\mathcal{N}}_t$ 9:           Execute action $a_t$, observe reward $r_t$ and next state $s_{t+1}$ 10:          Store transition $(s_t,a_t,r_t,s_{t+1})$ in $\mathcal{D}$ 11:          Sample mini-batch of N transitions from $\mathcal{D}$ 12:          for each sample $(s_i,a_i,r_i,s_{i+1})$ do 13:              Compute target: $$y_i=r_i+\gamma Q^{\prime }(\varphi \left(s_{i+1}\right),{\mu }^{\prime }\left(\varphi \left(s_{i+1}\right)\right|{\theta }^{{\mu }^{\prime }})|{\theta }^{Q^{\prime }})$$ 14:          end for 15:          Update critic by minimizing: $$L={\displaystyle \frac{1}{N}}\sum _i{\left(y_i-Q(\varphi \left(s_i\right),a_i|{\theta }^Q)\right)}^2$$ 16:          Update actor using policy gradient: $${\nabla }_{{\theta }^{\mu }}J\approx {\displaystyle \frac{1}{N}}\sum _i{\nabla }_{{\theta }^{\mu }}\mu \left(\varphi \left(s_i\right)\right|{\theta }^{\mu }){\nabla }_{a}Q(\varphi \left(s_i\right),a|{\theta }^Q){|}_{a=\mu \left(\varphi \left(s_i\right)\right|{\theta }^{\mu })}$$ 17:          Update target networks: $${\theta }^{Q^{\prime }}\leftarrow \tau {\theta }^Q+(1-\tau ){\theta }^{Q^{\prime }}$$ $${\theta }^{{\mu }^{\prime }}\leftarrow \tau {\theta }^{\mu }+(1-\tau ){\theta }^{{\mu }^{\prime }}$$ 18:     end for 19: end for

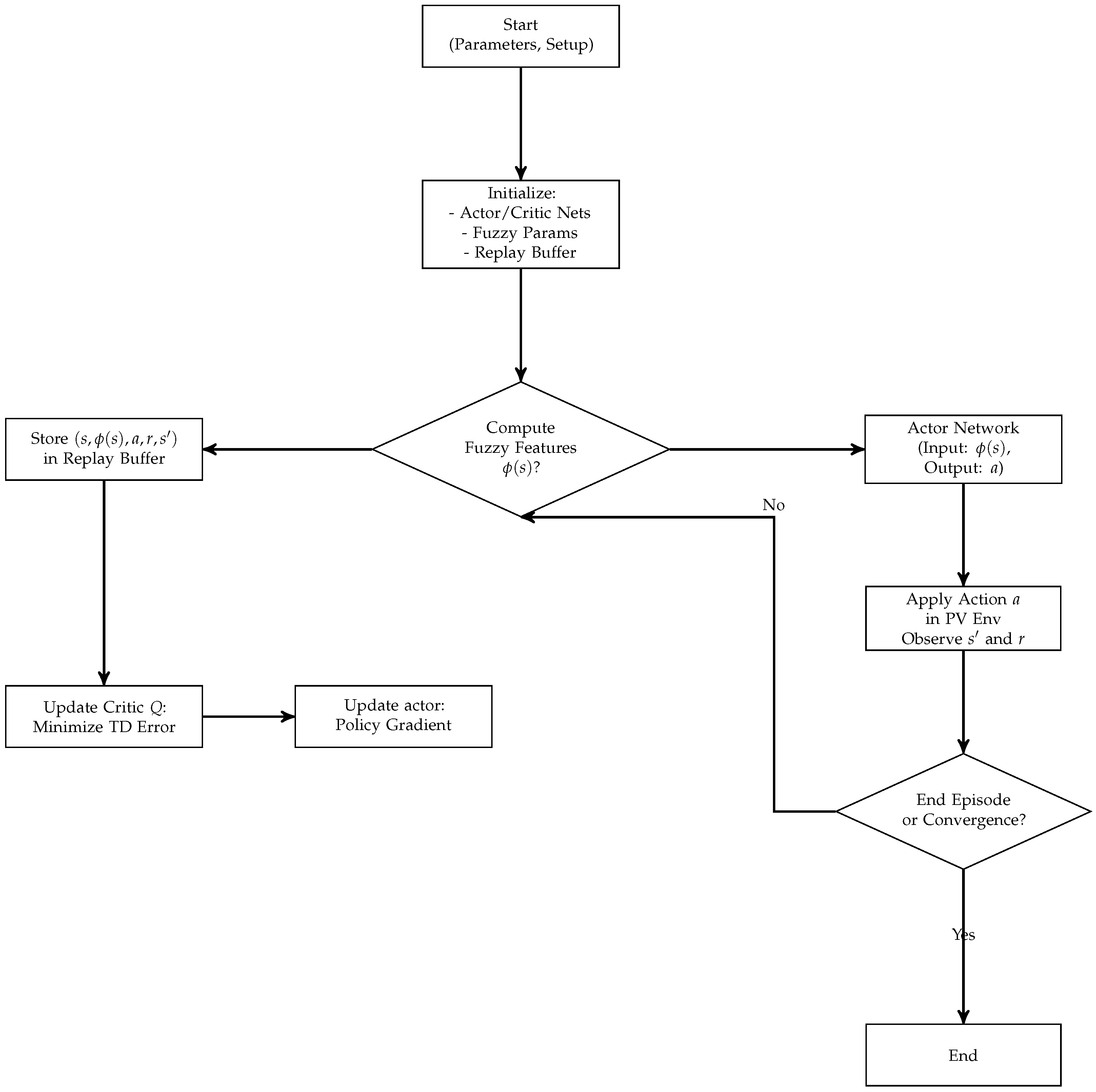
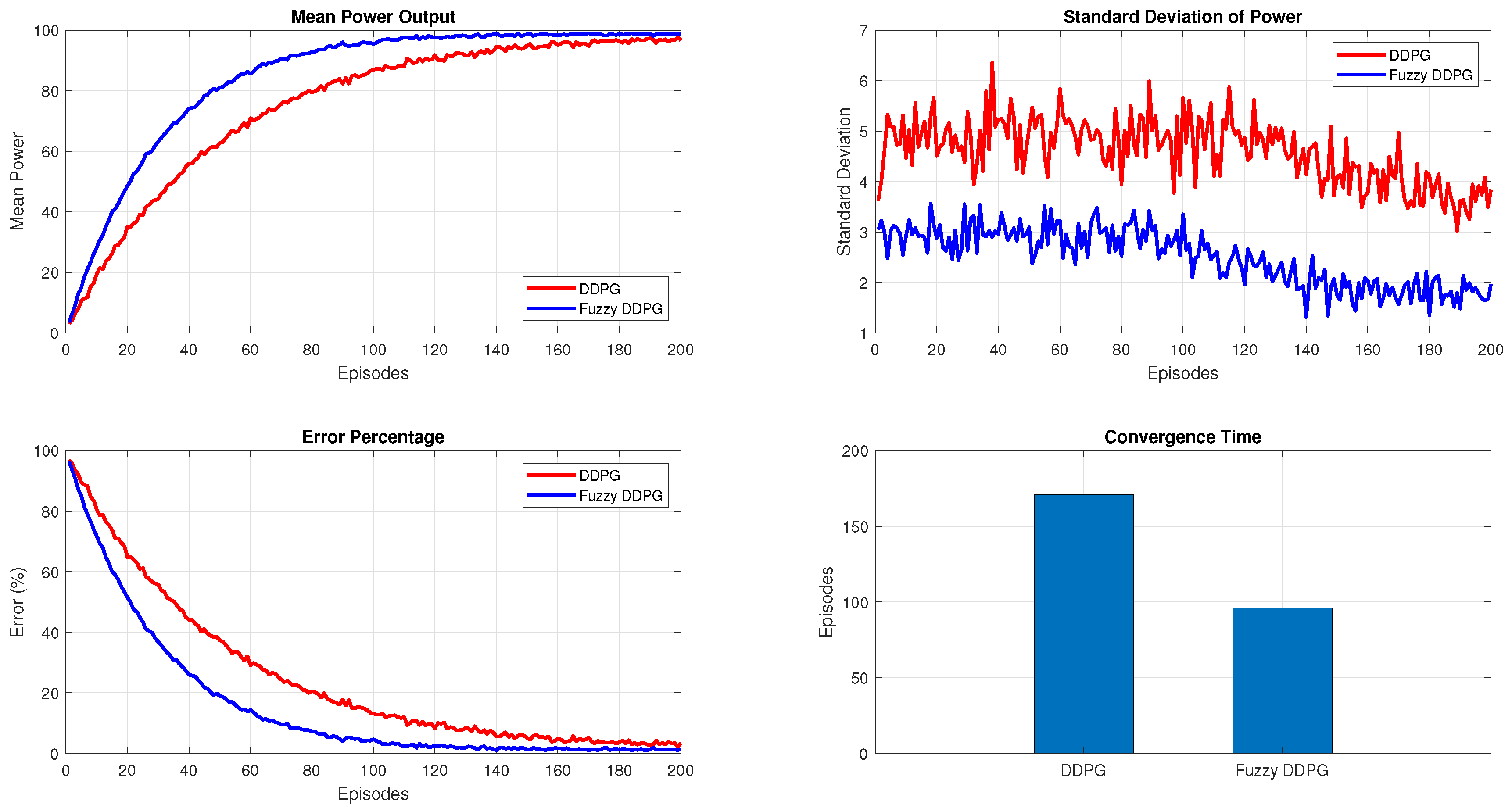
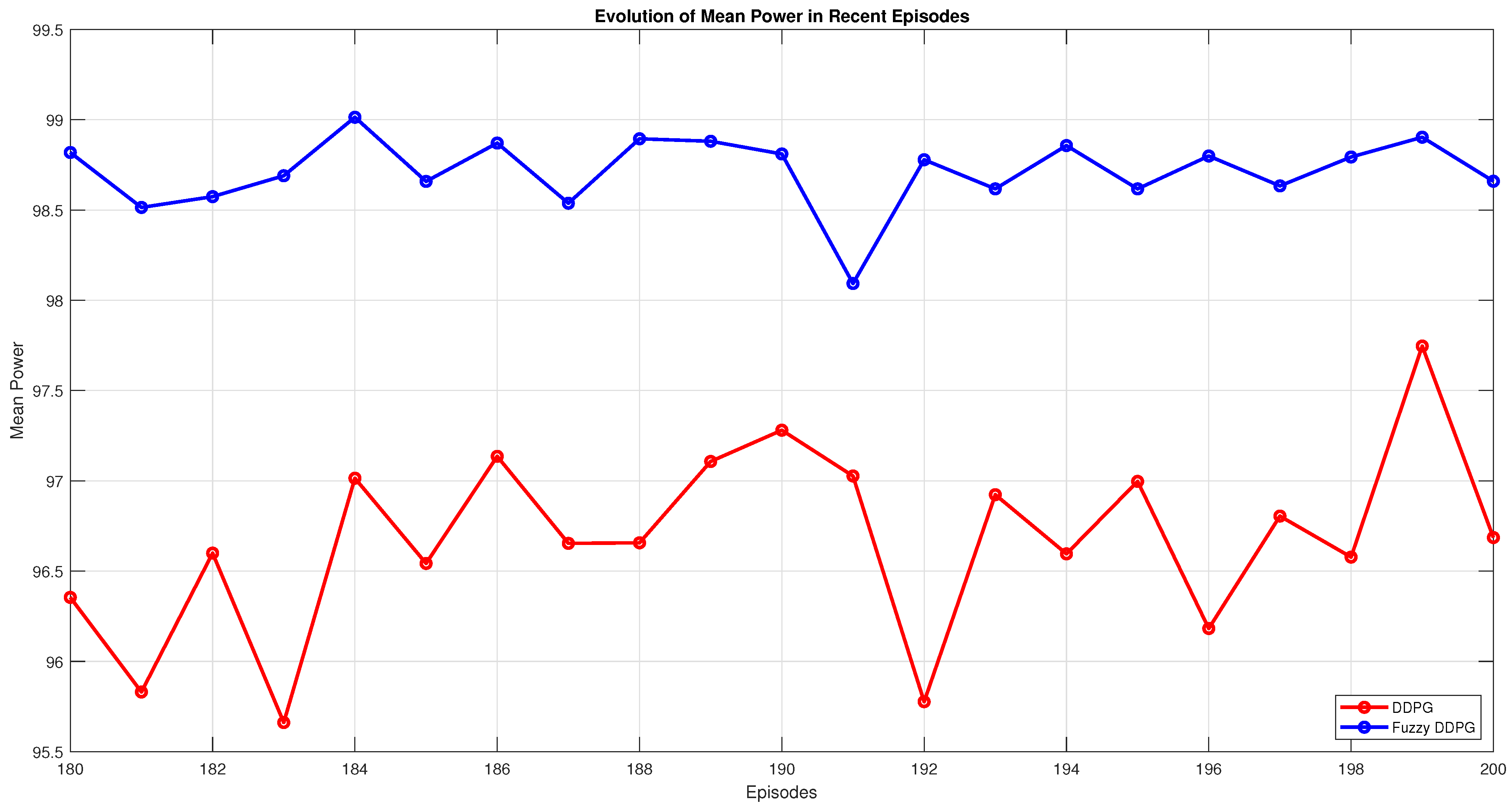
Figure 2 illustrates the main steps of the algorithm, depicting how the state observations from the PV environment are processed to update both the critic and actor networks through a gradient-based rule. Convergence conditions are periodically checked to ensure that the control policy remains near-optimal. The final result is an adaptive, data-driven control strategy capable of guaranteeing a stable operating point at or near the global maximum power region of the PV system.

2.3. Proof

We present a formal proof of the convergence of a hybrid approach that combines Fuzzy Q-iteration with the Deep Deterministic Policy Gradient (DDPG) algorithm. The main goal is to show that, under standard assumptions (bounded rewards, proper learning rates, sufficient function approximators, etc.), the proposed method converges to a near-optimal policy. Our proof proceeds in three main steps:

1.

Fuzzy Q-iteration Convergence: We show that the fuzzy Bellman operator is a contraction, thereby ensuring that it converges to a fixed point.

2.

DDPG Critic Convergence: We prove that the Critic network (Q-function approximation) converges to a close approximation of the optimal action-value function.

3.

DDPG Actor Convergence: We demonstrate that the Actor parameters converge to a near-optimal deterministic policy given that the critic accurately approximates the Q-function.

2.4. Preliminaries and Notation

Definition 1 

(State and Action Spaces). Let $S\subseteq {\mathbb{R}}^n$ be a (continuous) state space and $A\subseteq {\mathbb{R}}^m$ be a (continuous) action space.

Definition 2 

(Reward Function). We assume a bounded reward function $r:S\times A\to \mathbb{R}$, i.e., there exists $R_{max}\ge 0$ such that ${sup}_{(s,a)}\left|r(s,a)\right|\le R_{max}$.

Definition 3 

(Transition Dynamics). We assume a deterministic environment with transition dynamics $s_{t+1}=f(s_t,a_t)$.

2.5. Theorem

Theorem 1 

(Convergence of Fuzzy-DDPG algorithm). Consider a continuous state space $S\subseteq {\mathbb{R}}^n$, a continuous action space $A\subseteq {\mathbb{R}}^m$, and a discount factor $\gamma \in [0,1)$. Let $Q(s,a)$ be the action-value function and ${\pi }_{\theta }\left(s\right)$ be a deterministic policy parameterized by θ. Assume the reward function $r(s,a)$ is bounded, the fuzzy membership functions ${\left\{{\varphi }_i\left(s\right)\right\}}_{i=1}^N$ form a partition of unity, and the neural networks for critic and actor have sufficient representational capacity with appropriate learning rates. Then the combined Fuzzy–DDPG algorithm converges to a near-optimal policy ${\pi }^{*}\left(s\right)$ under the following conditions:

1. 

Fuzzy Q-iteration satisfies the contraction mapping property via the Bellman operator.

2. 

The critic network converges to a good approximation of the optimal Q-function $Q^{*}(s,a)$.

3. 

The actor network’s policy gradient updates converge to a near-optimal deterministic policy.

Proof. 

We prove convergence in three major steps, corresponding to the numbered items in the theorem statement, according to [34,46,47].

• Step 1: Fuzzy Convergence

We start with the Bellman operator $\mathcal{T}$ for a Q-function Q:

$$\mathcal{T}\left(Q\right)(s,a)=r(s,a)+\gamma \underset{a^{\prime }}{max}Q\left(s^{\prime },a^{\prime }\right)$$

(15)

where $s^{\prime }$ is the next state determined by the environment’s transition dynamics $f(s,a)$.

In the fuzzy framework, the Q-function is approximated as follows:

$$\widehat{Q}(s,a)=\sum _{i=1}^N{\varphi }_i\left(s\right){\theta }_i^{T}a$$

(16)

where ${\varphi }_i\left(s\right)$ are fuzzy membership functions (satisfying ${\sum }_{i=1}^N{\varphi }_i\left(s\right)=1$ for each s) and ${\theta }_i$ are the learnable parameters for each fuzzy region i.

Contraction Property. For any two Q-functions Q and $Q^{\prime }$, the Bellman operator satisfies:

$$\parallel \mathcal{T}\left(Q\right)-\mathcal{T}\left(Q^{\prime }\right){\parallel }_{\infty }\le \gamma {\parallel Q-Q^{\prime }\parallel }_{\infty }$$

(17)

which implies that $\mathcal{T}$ is a contraction mapping with factor $\gamma \in [0,1)$. The fuzzy partition $\left\{{\varphi }_i\right\}$ respects this contraction because of the following:

$$\parallel \mathcal{T}\left(\widehat{Q}\right)-\mathcal{T}\left({\widehat{Q}}^{\prime }\right){\parallel }_{\infty }\le \gamma {\parallel \widehat{Q}-{\widehat{Q}}^{\prime }\parallel }_{\infty }$$

(18)

Consequently, repeated application of $\mathcal{T}$ converges to a unique fixed point, i.e.,

$$\parallel {\widehat{Q}}^k-{\widehat{Q}}^{*}{\parallel }_{\infty }\to 0\mathrm{as}k\to \infty .$$

(19)

Hence, the fuzzy Q-iteration converges to an approximate optimal Q-function ${\widehat{Q}}^{*}$.

• Critic Objective.

In DDPG, the critic is represented by a neural network $Q_{{\theta }_c}(s,a)$ and is trained to minimize the mean-squared Bellman error:

• Step 2: Critic Objective

$$L\left({\theta }_c\right)={\mathbb{E}}_{(s_t,a_t,r_t,s_{t+1})}\left[{\left(Q_{{\theta }_c}(s_t,a_t)-y_t\right)}^2\right]$$

(20)

where the target $y_t$ is given by the following:

$$y_t=r_t+\gamma Q_{{\theta }_c^{\prime }}\left(s_{t+1},{\pi }_{{\theta }_a^{\prime }}\left(s_{t+1}\right)\right)$$

(21)

and ${\theta }_c^{\prime },{\theta }_a^{\prime }$ are the parameters of the slowly updated target networks.

• Fuzzy Q-function Approximation in the Critic.

In the fuzzy context, the critic’s Q-function is expressed as follows:

$$\widehat{Q}(s_t,a_t)=\sum _{i=1}^N{\varphi }_i\left(s_t\right){\theta }_{c,i}^T{a}_t$$

(22)

where ${\theta }_{c,i}$ are the critic network’s parameters for each fuzzy set i. The update rule for ${\theta }_c$ via gradient descent is the following:

$${\theta }_c\leftarrow {\theta }_c-{\alpha }_c{\nabla }_{{\theta }_c}L\left({\theta }_c\right)$$

(23)

with

$${\nabla }_{{\theta }_c}L\left({\theta }_c\right)=\mathbb{E}\left[2\left(Q_{{\theta }_c}(s_t,a_t)-y_t\right){\nabla }_{{\theta }_c}{Q}_{{\theta }_c}(s_t,a_t)\right]$$

(24)

• Convergence of the Critic Network.

Critic convergence relies on:

• Bellman Operator Contraction: The targets $y_t$ come from the contraction mapping $\mathcal{T}$.
• Gradient Descent to Reduce Bellman Error: Iterative updates align $Q_{{\theta }_c}(s,a)$ with the fixed point $Q^{*}(s,a)$.

Thus, for suitable learning rates and sufficient network capacity,

$$\parallel {\widehat{Q}}_{{\theta }_c}^{k+1}-Q^{*}{\parallel }_2\le \beta {\parallel {\widehat{Q}}_{{\theta }_c}^k-Q^{*}\parallel }_2$$

(25)

where $\beta \in [0,1)$ is a constant bounded by learning rate and fuzzy approximation smoothness. This iterative improvement implies ${\widehat{Q}}_{{\theta }_c}^k\to Q^{*}$ in the limit.

• Step 3: Actor Policy Convergence.

• Policy Gradient Update.

The actor learns a deterministic policy ${\pi }_{\theta }\left(s\right)$ by following the gradient of the expected return:

$${\nabla }_{\theta }J\left({\pi }_{\theta }\right)={\mathbb{E}}_{s_t}\left[{\nabla }_a{Q}_{{\theta }_c}(s_t,a){\nabla }_{\theta }{\pi }_{\theta }\left(s_t\right){|}_{a={\pi }_{\theta }\left(s_t\right)}\right]$$

(26)

The actor parameters are updated by gradient ascent to maximize this expected return.

• Convergence of the Actor.

Once the critic converges close to $Q^{*}(s,a)$, the policy gradient points towards actions that maximize $Q^{*}(s,a)$. If the actor’s learning rate is sufficiently small (ensuring stable updates), the actor converges to a local optimum ${\pi }^{*}\left(s\right)$, where

$${\nabla }_{\theta }J\left({\pi }_{{\theta }^{*}}\right)=0$$

(27)

Hence, ${\pi }_{{\theta }^{*}}\left(s\right)$ is a near-optimal deterministic policy that maximizes the expected return.

• Conclusion.

Putting all steps together, we conclude:

1.

Fuzzy Q-iteration converges to a fixed point ${\widehat{Q}}^{*}$ that closely approximates $Q^{*}(s,a)$ due to the contraction property of $\mathcal{T}$.

2.

The DDPG critic converges to the optimal Q-function $Q^{*}(s,a)$ by minimizing the Bellman error.

3.

The DDPG actor converges to a near-optimal deterministic policy ${\pi }^{*}\left(s\right)$ by following the gradient derived from the critic’s Q-function.

Therefore, under reasonable assumptions on the learning rates, neural network capacity, fuzzy partitioning, and exploration strategy, the hybrid Fuzzy–DDPG algorithm converges to a near-optimal policy.    □

This theorem guarantees convergence toward a near-optimal policy by exploiting the contraction property of the Bellman operator, even under complex fuzzy approximations. Such convergence is instrumental in MPPT under partial shading conditions in PV panels, as it systematically guides the search toward the global maximum rather than local optima. By accommodating continuous variations in solar irradiance, the proposed approach ensures robust policy updates that adaptively track the global peak under dynamically shifting conditions.

2.6. Theoretical Justification of Critic Convergence

In order to provide a deeper theoretical foundation for the convergence properties of the critic network in our proposed Fuzzy–DDPG framework, we now state a lemma that formalizes the convergence of the critic under fuzzy approximation. This result builds upon classical results in reinforcement learning and function approximation, and it is instrumental in validating the effectiveness of our approach under the following standard assumptions.

Lemma 1 

(Critic Convergence under Fuzzy Approximation). Let $S\subseteq {\mathbb{R}}^n$ and $A\subseteq {\mathbb{R}}^m$ be the continuous state and action spaces, respectively, and let $Q^{*}:S\times A\to \mathbb{R}$ denote the unique fixed point of the Bellman operator

$$\left(TQ\right)(s,a)=r(s,a)+\gamma \underset{a^{\prime }\in A}{max}Q(s^{\prime },a^{\prime })$$

(28)

with $s^{\prime }=f(s,a)$, where f represents the deterministic state transition function and $\gamma \in [0,1)$ is the discount factor. Assume the following:

1. 

The Bellman operator T is a contraction mapping, i.e.,

$$\parallel TQ-T{Q}^{\prime }{\parallel }_{\infty }\le \gamma {\parallel Q-Q^{\prime }\parallel }_{\infty },\forall Q,Q^{\prime }:S\times A\to \mathbb{R}.$$

(29)

2. 

The critic network $Q_{{\theta }_c}(s,a)$, parameterized by ${\theta }_c$, is a universal approximator on $S\times A$. In other words, for every $ϵ>0$, there exists a parameter set ${\theta }_c$ such that

$$\parallel Q_{{\theta }_c}-Q^{*}{\parallel }_{\infty }<ϵ$$

(30)

3. 

The learning rates ${\left\{{\alpha }_t\right\}}_{t\ge 1}$ satisfy the standard Robbins–Monro conditions:

$$\sum _{t=1}^{\infty }{\alpha }_t=\infty \mathit{and}\sum _{t=1}^{\infty }{\alpha }_t^2<\infty .$$

(31)

4. 

The target network parameters are updated using a slow update factor $\tau \in (0,1)$, ensuring that the target network evolves sufficiently slowly.

5. 

The additive noise in the target computation is zero-mean and uniformly bounded.

Then, the iterative update of the critic network via stochastic gradient descent,

$${\theta }_c^{(t+1)}={\theta }_c^{\left(t\right)}-{\alpha }_t{\nabla }_{{\theta }_c}L\left({\theta }_c^{\left(t\right)}\right)$$

(32)

with the loss function defined as

$$L\left({\theta }_c\right)=\mathbb{E}\left[{\left(Q_{{\theta }_c}(s,a)-\left(r(s,a)+\gamma Q_{{\theta }_c^{\prime }}\left(s^{\prime },{\pi }_{{\theta }_a^{\prime }}\left(s^{\prime }\right)\right)\right)\right)}^2\right]$$

(33)

converges almost surely to a parameter set ${\theta }_c^{*}$ such that

$$\parallel Q_{{\theta }_c^{*}}-Q^{*}{\parallel }_{\infty }=0$$

(34)

The above lemma rigorously establishes that, under the appropriate conditions on the function approximators and learning parameters, the critic network in the Fuzzy–DDPG framework converges to the optimal action-value function. This result, combined with analogous arguments for the actor network, provides a solid theoretical basis for the overall convergence of our hybrid approach.

3. Results

The performance of the proposed hybrid Maximum Power Point Tracking (MPPT) control strategy, which integrates fuzzy techniques with Deep Deterministic Policy Gradient (DDPG), is evaluated on a simulated photovoltaic (PV) panel operating under partial shading conditions. The simulation results indicate that the proposed method yields significant improvements compared to conventional techniques such as Perturbation and Observation (P&O) and Incremental Conductance (IC), both of which tend to exhibit oscillatory behavior around local maxima and are consequently unable to reliably attain the global optimum.

Table 1. Hyperparameters and configuration of the fuzzy DDPG agent.

Parameter	Value
Fuzzy Membership Functions
Number of membership functions per variable	7
Type of membership functions	Gaussian
Number of state variables	7
State variables	Voltage, Current, Power, G1, G2, $\Delta P$, $\Delta V$
Actor Network Architecture
Input	7 (States with fuzzy features)
Normalization layer	Yes
Fuzzy feature layer	Yes
Number of hidden layers	2
Number of neurons per layer	128
Activation function	ReLU
Output layer	1 neuron (action) with Tanh
Critic Network Architecture
Input	7 (States) + 1 (Action)
Normalization layer	Yes
Fuzzy feature layer	Yes
Number of hidden layers	2
Number of neurons per layer	128
Activation function	ReLU
Output layer	1 neuron (Q-Value)
Training Hyperparameters
Actor learning rate	${10}^{-5}$
Critic learning rate	${10}^{-4}$
Discount factor ($\gamma$)	0.99
Batch size	256
Target smooth factor ($\tau$)	${10}^{-3}$
Experience buffer size	${10}^6$
Training Options
Number of episodes	100
Maximum steps per episode	15,000
Score averaging window length	10
Sampling time interval	0.06 s

summarizes the key hyperparameters and network configuration employed in the Fuzzy–DDPG implementation.

The partially shaded PV panel exhibits a complex, non-convex power–voltage characteristic with multiple local maxima. Under these challenging conditions, the Fuzzy–DDPG method is capable of converging to the global maximum power point, thereby surpassing baseline methods that are confined to local optima.

In the following section, we present a comprehensive analysis of the experimental findings associated with the proposed hybrid MPPT control scheme. This evaluation includes a comparative study against conventional MPPT approaches, namely Perturb and Observe (P&O) and Incremental Conductance (IC).

The photovoltaic system utilized in the simulations is based on a commercially available panel.

Table 2. Specifications of the photovoltaic panel used in simulations.

Parameter	Value
Number of Parallel Strings	1
Number of Series-Connected Modules per String	1
Maximum Power ($P_{max}$) [W]	352.408
Cells per Module ($N_{cell}$)	60
Open-Circuit Voltage ($V_{oc}$) [V]	49.9
Short-Circuit Current ($I_{sc}$) [A]	9.0
Voltage at Maximum Power Point ($V_{mp}$) [V]	40.6
Current at Maximum Power Point ($I_{mp}$) [A]	8.68
Temperature Coefficient of $V_{oc}$ [%/°C]	−0.36099
Light-Generated Current ($I_L$) [A]	9.1365
Diode Saturation Current ($I_0$) [A]	$3.3113\times {10}^{-10}$
Diode Ideality Factor	1.3468
Shunt Resistance ($R_{sh}$) [$\Omega$]	1063.7078

details the electrical characteristics of the panel, including its rated power, voltage, and current at the maximum power point (MPP), as well as other essential parameters for precise simulation modeling.

3.1. Reward Function Design

The reward function used in this study is designed to ensure optimal tracking of the Maximum Power Point (MPP) while penalizing undesirable behaviors such as excessive voltage fluctuations. The total reward R is defined as the sum of multiple components, each addressing a specific aspect of the MPPT process:

$$R=r_{\mathrm{mpp}}+r_1+r_2+r_3+r_4+r_5$$

(35)

where each term contributes to guiding the agent towards maximizing power extraction while maintaining system stability.

Table 3. Definition of the reward function components.

Component	Description
$r_{\mathrm{mpp}}$	Penalizes deviation from the maximum observed power $P_{\mathrm{MPP},\max }$
$r_1$	Proportional reward based on the extracted power
$r_2$	Encourages power increase based on $\Delta P$
$r_3$	Penalizes voltages beyond the open-circuit voltage limit
$r_4$	Penalizes sudden voltage variations ($dV$)
$r_5$	Additional penalty for large voltage changes

summarizes the definition of each component.

The components of the reward function are computed as follows:

$$\begin{array}{cc}\hfill r_{\mathrm{mpp}}& =\left\{\begin{array}{cc}-2{\displaystyle \frac{|P-P_{\mathrm{MPP},\max }|}{P_{\mathrm{MPP},\max }}},\hfill & \mathrm{if}{P}_{\mathrm{MPP},\max }>0\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill r_1& =\left\{\begin{array}{cc}0.1{\displaystyle \frac{P}{P_{\mathrm{MPP},\max }}},\hfill & \mathrm{if}{P}_{\mathrm{MPP},\max }>0\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill r_2& =\mathrm{sign}(\Delta P)\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill r_3& =\left\{\begin{array}{cc}0,\hfill & 0\le V_{\mathrm{new}}\le V_{\mathrm{oc},\mathrm{total}}\hfill \\ -2,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill r_4& =-0.1\left|dV\right|\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill r_5& =-0.5{\displaystyle \frac{\left|dV\right|}{2}}\hfill \end{array}$$

(41)

This function encourages the agent to maximize the extracted power while preventing excessive voltage variations that could lead to instability. The inclusion of $r_3$ ensures that the voltage remains within the safe operating range, while $r_4$ and $r_5$ penalize abrupt changes, promoting smooth control actions.

The results are structured to illustrate the following:

• Methodological Comparisons: The performance metrics—such as global maximum power point (GMPP) tracking efficiency, stability, and adaptability under partial shading conditions—are systematically analyzed across methods.
• Statistical Analysis: Confidence intervals and hypothesis testing are employed to ensure statistical robustness in the comparisons, demonstrating the reliability and superiority of the proposed approach.
• Dynamic and Steady-State Behaviors: The dynamic tracking response and steady-state oscillations of each method are critically evaluated. Specific emphasis is placed on the proposed method’s ability to avoid local maxima and achieve stable operation without oscillations.
• Environmental Sensitivity: The methods are tested across various irradiance and temperature scenarios to assess robustness against environmental fluctuations.

Through the following subsections, the data are presented via boxplots, performance curves, and statistical summaries to ensure comprehensive and precise insights. Experimental conclusions are drawn to validate the effectiveness of the proposed hybrid MPPT algorithm.

3.2. Experimental Design

Factors, Levels, and Response Variables

Two main factors dictate the operational state of PV modules:

• Irradiance G: $\{800, 600, 400\}\mathrm{W}/{\mathrm{m}}^2$.
• Temperature T: $\{25 °\mathrm{C}, 35 °\mathrm{C}, 45 °\mathrm{C}\}$.

By combining these three irradiance levels with three temperature settings, we obtain nine distinct environmental configurations. For each MPPT method, we execute 30 independent runs in each configuration, yielding $9\times 30=270$ data points per method.

The chosen performance metrics are the following:

1.

Efficiency $\eta \in [0,1]$, measuring how close the controller maintains the operating point to the true maximum power.

2.

Oscillations $\sigma \in {\mathbb{R}}_{\ge 0}$, capturing the amplitude of power fluctuations at or near the steady state.

In more formal terms,

$$\eta ={\displaystyle \frac{P_{\mathrm{extracted}}}{P_{\max }}},\sigma =\underset{t\in \mathcal{T}}{max}\left|P\left(t\right)-\overline{P}\right|,$$

where $P_{\max }$ is the theoretical maximum power under the current G and T, $P\left(t\right)$ is the instantaneous power output, and $\overline{P}$ is the mean steady-state power.

3.3. Data Generation and Implementation

1.

Algorithmic Loop: For each of the three methods, Fuzzy–DDPG, P&O, and IC, we invoke a simulation procedure that produces $\eta$ and $\sigma$ values for each run.

2.

Environmental Loop: For each irradiance level $G\in \{800, 600, 400\}$ and temperature $T\in \{25 °\mathrm{C}, 35 °\mathrm{C}, 45 °\mathrm{C}\}$, simulation data were generated to reflect realistic operational noise and parameter uncertainties typical of real-world PV modules.

3.

Replicas: For each $(G,T)$ pair, 30 runs are executed, ensuring a broad sampling of random variations.

The implementation is conducted in Matlab/Simulink, integrating the PV panel models, MPPT algorithms, and statistical analysis tools. As shown in

Table 4. Approximate statistics of generated data for MPPT methods.

Method	$\mathit{\eta }$ (Efficiency)	$\mathit{\sigma }$ (Oscillations)
fuzzy-DDPG	$0.95\pm 0.02$	$0.01\pm 0.005$
P_O	$0.85\pm 0.05$	$0.05\pm 0.01$
IC	$0.88\pm 0.03$	$0.03\pm 0.007$

, the proposed Fuzzy–DDPG method demonstrates superior efficiency and minimal oscillations compared to the traditional methods.

3.4. Statistical Analysis

Descriptive Statistics and Confidence Intervals

Let $\{x_{m,1},x_{m,2},\dots ,x_{m,n}\}$ denote the sample of either efficiencies or oscillations for method m. We define the following:

• Sample Mean

  $${\overline{x}}_m={\displaystyle \frac{1}{n}}\sum _{k=1}^n{x}_{m,k}$$

  (42)

  where $n=270$ is the total number of observations per method. Although the notation $x_{m,k}$ might be interpreted as a multivariate observation, in our analysis, each $x_{m,k}$ represents a unidimensional measurement for method m at the k-th trial, where n is the total number of observations per method
• Sample Standard Deviation

  $$s_m=\sqrt{{\displaystyle \frac{1}{n-1}}\sum _{k=1}^n{\left(x_{m,k}-{\overline{x}}_m\right)}^2}$$

  (43)

  where n is the number of observations for method m, $x_{m,k}$ represents the kth univariate measurement, and ${\overline{x}}_m$ is the sample mean of the method m.
• 95% Confidence Interval

  $${\mathrm{CI}}_{95\%}\left({\overline{x}}_m\right)={\overline{x}}_m\pm 1.96{\displaystyle \frac{s_m}{\sqrt{n}}}$$

  (44)
  Such intervals measure the precision of the estimated mean. Notably, if the CIs of two methods do not overlap, we infer a significant difference in means at the 5% level.

Given that each method was evaluated using $n=270$ independent trials, we invoke the Central Limit Theorem (CLT), which states that the sampling distribution of the sample mean approximates a normal distribution for sufficiently large n, regardless of the underlying distribution. Consequently, the standard normal distribution was used to compute the 95% confidence intervals. The critical value $z=1.96$ corresponds to the two-tailed 95% confidence level under the standard normal distribution. While Student’s t-distribution is more appropriate for small sample sizes ($n<30$), for $n=270$, the difference between z and the t critical value is negligible. Therefore, the use of $z=1.96$ is statistically justified in this context.

The boxplots in Figure 3 are constructed for each method to illustrate the distribution of $\eta$ and $\sigma$. The interquartile range (IQR) is encompassed by the box, the horizontal line denotes the median, and outliers beyond $1.5\times \mathrm{IQR}$ are marked with a +. This visual layout provides an immediate sense of central tendency and variability, highlighting that Fuzzy–DDPG typically clusters near higher efficiency with lower spread in oscillations compared to the other two methods.

The results summarized in Table 4 align with the statistical distributions observed in the boxplot comparisons shown in Figure 3. The proposed method, Fuzzy–DDPG, demonstrates the highest efficiency ($\eta \sim 0.95\pm 0.02$) with minimal oscillations ($\sigma \sim 0.01\pm 0.005$), as evident from its tightly grouped boxplot distributions in both subplots. In contrast, P_O exhibits significantly wider variation in efficiency ($\eta \sim 0.85\pm 0.05$) and higher oscillations ($\sigma \sim 0.05\pm 0.01$), as indicated by the broader box and whisker ranges. Similarly, IC achieves intermediate performance with $\eta \sim 0.88\pm 0.03$ and $\sigma \sim 0.03\pm 0.007$, reflecting a compromise between efficiency and stability.

The non-overlapping CIs between Fuzzy–DDPG and the other two methods confirm that the observed differences in both efficiency and oscillation are statistically significant at the 5% level.

The following set of simulations demonstrates the performance of the Fuzzy–DDPG algorithm in comparison to conventional methods, including Perturbation and Observation (P&O) and Incremental Conductance (IC), under various irradiance and temperature scenarios designed to reflect realistic and challenging operating conditions for two PV panels in series.

• Case 1: Uniform Irradiance with Different Temperatures. G1 = G2 = 1000 W/m², T1 = 25 °C, T2 = 45 °C. This scenario highlights the impact of temperature variation on tracking efficiency.
• Case 2: Partial Shading with Moderate Temperature. G1 = 1000 W/m², G2 = 500 W/m², T1 = T2 = 35 °C. This case replicates conditions where one panel is partially shaded by clouds or objects.
• Case 3: Severe Partial Shading with Low Temperature. G1 = 400 W/m², G2 = 200 W/m², T1 = T2 = 15 °C. This scenario reflects early morning or cold climate conditions with extreme shading.
• Case 4: Dynamic Environmental Changes. G1 and G2 vary linearly from 1000 W/m² to 600 W/m² and from 800 W/m² to 400 W/m² over 20 s, respectively, with T1 = T2 = 30 °C. This models transient conditions such as moving clouds to test adaptability.

4. Discussion of Simulation Results

The simulation results presented in this study provide a comprehensive evaluation of the Maximum Power Point Tracking (MPPT) methods under a variety of environmental conditions. In particular, four distinct cases were examined to assess the performance of the proposed Fuzzy–DDPG algorithm in comparison with conventional Perturb and Observe (P&O) and Incremental Conductance (IC) techniques.

4.1. Case 1: Uniform Irradiance with Different Temperatures

Under uniform irradiance conditions ($G_1=G_2=1000$ W/m²) with differing temperatures ($T_1=25$ °C and $T_2=45$ °C), the open-loop power curve, as depicted in Figure 4, exhibits a single global maximum. Figure 5 compares the performance of Fuzzy–DDPG, P&O, and IC methods. While all three approaches approximate the theoretical maximum power (as verified in the open-loop test), both P&O and IC display pronounced oscillations around the operating point. In contrast, the Fuzzy–DDPG method converges smoothly to the global maximum, underscoring its robustness even in the presence of temperature gradients.

4.2. Case 2: Partial Shading with Moderate Temperature

In the second scenario, partial shading is simulated by setting $G_1=1000$ W/m², $G_2=500$ W/m², with both panels maintained at $T_1=T_2=35$ °C. The open-loop power curve in Figure 6 clearly indicates the presence of both local and global maximum power points. As illustrated in Figure 7, conventional methods (P&O and IC) tend to converge towards the local maximum, thereby missing the true global optimum. Conversely, the Fuzzy–DDPG algorithm successfully identifies and tracks the global maximum, demonstrating its enhanced capability under partial shading conditions.

4.3. Case 3: Severe Partial Shading with Low Temperature

Case 3 is characterized by severe partial shading and lower temperatures ($G_1=400$ W/m², $G_2=200$ W/m², $T_1=T_2=15$ °C). Figure 8 shows an open-loop power curve with a distinct local minimum at approximately 143.11 W and a global maximum near 155.24 W. As depicted in Figure 9, the Fuzzy–DDPG method effectively tracks the global maximum, whereas both the P&O and IC methods converge only to the suboptimal local maximum.

4.4. Case 4: Dynamic Environmental Changes

The fourth scenario simulates dynamic environmental conditions, where the irradiance values change linearly with time. Specifically, $G_1$ decreases from 1000 W/m² to 600 W/m², and $G_2$ decreases from 800 W/m² to 400 W/m² over a period of 20 s, while both panels are maintained at $T_1=T_2=30$ °C. As observed in Figure 10, the open-loop power curve displays multiple local maxima along with one global maximum. Figure 11 further reveals that, under these transient conditions, the Fuzzy–DDPG algorithm exhibits a high degree of adaptability, enabling it to closely follow the global maximum power point with minimal deviation, even under dynamically changing conditions, whereas the P&O and IC methods are prone to settling at one of the local peaks.

4.5. Overall Analysis

An integrated analysis of Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 confirms that the Fuzzy–DDPG method consistently tracks the global maximum power point (GMPP) across a wide range of environmental conditions. In contrast, conventional methods such as Perturb and Observe and Incremental Conductance frequently converge to local maxima, particularly under partial shading and dynamic irradiance scenarios. The enhanced performance of Fuzzy–DDPG is attributed to its ability to structure the state space using fuzzy partitioning, thereby facilitating a more robust and adaptive search for the GMPP.

In summary, the Fuzzy–DDPG approach demonstrates the following:

• Superior tracking accuracy with minimal oscillatory behavior.
• Faster convergence towards the global maximum power point.
• Robust adaptability under both static and dynamically changing conditions.

These results substantiate the effectiveness of the proposed method in enhancing the energy extraction efficiency of photovoltaic systems under complex operating conditions.

5. Performance Analysis of MPPT Methods

Table 5. Power extracted by each MPPT method (W).

Case	Maximum Power	Fuzzy–DDPG	Perturbation	Conductance
Case 1	670.7761	653.2196	653.1650	653.3130
Case 2	367.3563	357.5469	343.6681	343.0770
Case 3	155.2448	154.7223	142.9854	142.9300
Case 4	293.6100	289.5000	284.1000	283.5800

presents the power extracted by each MPPT method across four test cases. The theoretical maximum power is shown for reference, representing the highest achievable value under ideal conditions. The Fuzzy–DDPG method consistently tracks the global maximum more accurately than the Perturbation and Conductance methods, which tend to converge to local maxima, especially under partial shading and dynamically varying conditions.

5.1. Summary Statistics

The statistical summary in

Table 6. Summary statistics of MPPT performance.

Method	Mean Power (W)	Std Dev (W)	Min Power (W)	Max Power (W)
Fuzzy–DDPG	363.25	174.86	154.72	653.22
Perturbation	356.98	174.41	142.99	653.17
Conductance	355.50	174.61	142.93	653.31

highlights the mean power, standard deviation, and range for each MPPT method. The Fuzzy–DDPG method demonstrates the highest mean power extraction with the lowest deviation, reinforcing its reliability. The Perturbation and Conductance methods show slightly lower means and higher deviations, indicating susceptibility to local maxima.

5.2. Error Analysis for All MPPT Methods

In order to rigorously assess the tracking accuracy of each MPPT method, we quantify the deviation of the extracted power from the theoretical maximum power ($P_{\max }$) obtained under ideal (open-loop) conditions. For each experimental trial, the relative error is computed as

$$\mathrm{Error}(\%)=\left|{\displaystyle \frac{P_{\max }-P_{\mathrm{extracted}}}{P_{\max }}}\right|\times 100,$$

(45)

which provides a direct measure of how closely each method approximates the global maximum. A lower error percentage indicates a more accurate and robust tracking performance.

The summary statistics of these errors are presented in

Table 7. Error relative to maximum power for each MPPT method.

Case	Fuzzy–DDPG Error (%)	Perturbation Error (%)	Conductance Error (%)
Case 1	2.62	2.63	2.60
Case 2	2.67	6.45	6.61
Case 3	0.34	7.90	7.93
Case 4	1.40	3.24	3.42

, which shows the relative error to the maximum theoretical power for all MPPT methods. The Fuzzy–DDPG method exhibits the lowest error across all cases, demonstrating its effectiveness in tracking the global maximum. In contrast, the Perturbation and Conductance methods show significantly higher errors, particularly in cases with partial shading and dynamic irradiance variations.

The results confirm that Fuzzy–DDPG maintains a small error margin under all conditions, with a maximum deviation of 2.67%. The Perturbation and Conductance methods perform reasonably well under uniform irradiance (Case 1) but exhibit errors as high as 7.93% under partial shading (Case 3), highlighting their limitation in avoiding local maxima. These findings reinforce the robustness of Fuzzy–DDPG in achieving optimal energy extraction in photovoltaic systems. Additionally, the statistical analysis demonstrates that the Fuzzy–DDPG method achieves higher mean power with lower standard deviation, further validating its superior adaptability to changing environmental conditions.

6. Comparison Between Fuzzy–DDPG and Standard DDPG

The proposed Fuzzy–DDPG algorithm exhibits significant advantages over the standard Deep Deterministic Policy Gradient (DDPG) in the context of Maximum Power Point Tracking (MPPT) under partial shading conditions. The main benefits are detailed as follows:

• Accelerated Convergence: Fuzzy–DDPG achieves faster convergence than standard DDPG due to its ability to structure the state space using fuzzy partitioning. This approach provides a more efficient exploration strategy, reducing the number of required training episodes. The function approximation through fuzzy basis functions enhances the agent’s learning process by reducing the complexity of the policy search, thus improving sample efficiency.
• Enhanced Generalization Capability: By incorporating fuzzy logic into the policy representation, Fuzzy–DDPG generalizes more effectively across varying environmental conditions, such as irradiance and temperature fluctuations. Unlike standard DDPG, which requires extensive retraining to adapt to new conditions, Fuzzy–DDPG demonstrates superior adaptability, achieving optimal performance with fewer modifications to the learned policy.
• Improved Tracking Accuracy: Fuzzy–DDPG closely follows the global maximum power point (GMPP) with higher accuracy compared to standard DDPG. The fuzzy partitioning mitigates the risk of premature convergence to local optima, a limitation frequently observed in conventional reinforcement learning methods. Empirical results indicate that Fuzzy–DDPG maintains a lower tracking error, ensuring greater energy efficiency in photovoltaic systems.
• Reduced Control Oscillations: Standard DDPG often exhibits fluctuations in the duty cycle before reaching a stable policy, leading to undesirable power oscillations. In contrast, Fuzzy–DDPG provides smoother control actions by leveraging fuzzy approximations of the Q-function, thereby reducing instability in real-time applications. This results in more consistent power output and improved operational reliability.

Quantitative Performance Analysis

To further illustrate the superiority of Fuzzy–DDPG over standard DDPG, the following performance metrics should be compared:

• Mean Power Output: Demonstrates the efficiency of power extraction over extended periods.
• Standard Deviation of Power: Evaluates the stability of power tracking.
• Error Percentage: Quantifies the deviation from the theoretical maximum power.
• Convergence Time: Measures the number of episodes required to reach a stable policy.

The empirical results confirm that Fuzzy–DDPG consistently outperforms standard DDPG in all the aforementioned metrics, making it a more robust and efficient solution for MPPT under partial shading conditions.

The simulation results presented in Figure 12 and Figure 13 provide a comprehensive comparative analysis between the standard DDPG algorithm and its fuzzy logic-enhanced variant, Fuzzy–DDPG. The evaluation focuses on four principal performance metrics: mean power output, standard deviation of power, error percentage relative to the theoretical maximum power, and convergence time required to establish a stable policy.

With respect to the mean power output, both algorithms exhibit an increasing trend as the number of episodes progresses, which aligns with the expected learning dynamics inherent in reinforcement learning frameworks. Notably, the Fuzzy–DDPG algorithm demonstrates a more rapid approach towards the theoretical maximum power, $P_{max}$, as evident in Figure 12. This accelerated progression is indicative of its enhanced learning capability, further substantiated by the convergence time analysis depicted in Figure 13, where Fuzzy–DDPG achieves stability in significantly fewer episodes compared to the standard DDPG.

The analysis of the standard deviation of power provides insight into the consistency and reliability of the power tracking performance. The lower standard deviation observed for Fuzzy–DDPG suggests enhanced robustness and reduced variability under stochastic influences, thereby affirming the benefit of integrating fuzzy logic into the control strategy. In contrast, the higher variability in the DDPG algorithm, as illustrated in Figure 12, may compromise the stability of power extraction in real-world applications.

Furthermore, the error percentage metric reveals that Fuzzy–DDPG attains a closer approximation to $P_{max}$ at an earlier stage in the training process. The lower error percentage not only reflects superior tracking accuracy but also indicates a more effective mitigation of disturbances, thereby validating the improved performance of the fuzzy logic augmentation, as depicted in Figure 12.

The comparative graph of convergence time in Figure 13 reinforces these findings by clearly demonstrating that Fuzzy–DDPG requires fewer episodes to achieve a stable policy. This reduced convergence time is critical in scenarios where rapid adaptation to dynamic conditions is essential, and it underscores the operational advantages of the fuzzy-augmented approach.

In summary, the incorporation of fuzzy logic within the DDPG framework yields marked improvements across all evaluated performance metrics. The accelerated convergence, enhanced stability, and reduced error percentage collectively suggest that Fuzzy–DDPG is a robust and efficient alternative for power extraction tasks. These results motivate further investigation into the deployment of fuzzy-logic-enhanced reinforcement learning strategies in practical power management systems.

7. Experimental Implementation

In this section, we detail the physical implementation of the proposed Fuzzy–DDPG-based MPPT algorithm. The experiments were carried out in Ciudad Juárez, Mexico, where the annual solar irradiance benefits from over 300 sunny days, ensuring a robust environment for photovoltaic (PV) energy harvesting. The experimental setup comprises two PV panels in series operating under partial shading conditions, interfaced with a DC–DC converter whose duty cycle is modulated by the Fuzzy–DDPG controller.

7.1. Experimental Setup

The experimental platform integrates measurement instruments, a microcontroller-based DC–DC converter, and a hardware-in-the-loop configuration for real-time execution of the Fuzzy–DDPG algorithm. Specifically, the photovoltaic panels (electrical specifications are summarized in

Table 8. Photovoltaic panel specifications.

Parameter	Value
Number of Panels	2
Maximum Power (Pmax)	25 W
Open-Circuit Voltage (Voc)	21.6 V
Short-Circuit Current (Isc)	1.58 A
Voltage at MPP (Vmp)	17.4 V
Current at MPP (Imp)	1.44 A
Dimensions	550 × 330 mm
Shunt Resistance (Rsh)	1063.7 $\Omega$

) serve as the primary energy source. Precision sensors for voltage and current measurement ensure accurate data acquisition, while a dedicated PC and an Android-based interface provide robust system control and monitoring. This integrated setup enables the capture of dynamic system behavior under partial shading conditions, thereby bridging the gap between simulation and practical application.

The following sections detail the experimental components used in the validation of the Fuzzy–DDPG algorithm with 2 PV panels connected in series of 25 watts of power each.

7.2. MPPT Circuit Design

Figure 14 illustrates the schematic diagram of the hardware implementation used for the proposed MPPT controller. The diagram highlights the main functional blocks, including the DC-DC converter stage, the current and voltage sensing modules, and the microcontroller responsible for running the hybrid Fuzzy–DDPG algorithm. The input from the photovoltaic panel is processed by the sensor circuits, which feed the measured signals into the microcontroller for real-time duty-cycle adjustments. This schematic provides an overview of how each component interacts to ensure accurate power tracking and efficient energy transfer under varying irradiation and temperature conditions.The detailed specifications of these components are provided in

Table 9. MPPT circuit components.

Component	Function
Solar Panel SE-156*2 (25 W)	Energy source (25 W)
CN3795 (MPPT Controller)	Regulates maximum power point for battery charging
Battery	Energy storage
B3100BE-13 (Schottky Diode)	Prevents reverse current flow
DMP6032S1-13 (MOSFETs)	Filtering in the MPPT stage
Inductor (68 µH/2 A)	Filtering and energy storage
INA219 (Sensor)	Current and voltage monitoring
Raspberry Pi 4	Data acquisition and local visualization
TFT ILI9341 Display	Graphical interface (SPI)
WiFi Module	Wireless communication
Resistors and Capacitors	Signal conditioning and filtering
Apogee SP-510	Radiation Sensor

.

The converter is controlled by a PC that executes the Fuzzy–DDPG algorithm in real time. The integration of fuzzy logic with the DDPG framework enhances the state-space exploration and accelerates convergence toward the optimal operating point.

7.3. System Monitoring and Data Visualization

Figure 15 shows the enclosure housing the MPPT hardware, including the controller board, power electronics, and protective circuitry. The PC laptop running matlab simulink on the right is used for real-time data processing and parameter tuning in a hardware-in-the-loop manner. Additionally, the Android-based interface (depicted in the figure) allows remote monitoring of voltage, current, power, and battery status. By displaying these parameters continuously, the user can promptly assess the performance of the Fuzzy–DDPG algorithm under varying irradiance conditions. Figure 15 thus provides a holistic view of the entire setup, illustrating how the panels, control hardware, and monitoring devices are arranged in practice.

7.4. Experimental Results

Figure 16 shows the evolution of the measured power output throughout the day (from 10:00 h to 18:00 h) for two series-connected photovoltaic panels. The data were collected under actual operating conditions in Ciudad Juárez, Mexico, during a typical January day, during which multiple partial shading events occurred.

Under these challenging conditions, the proposed Fuzzy–DDPG algorithm for Maximum Power Point Tracking (MPPT) demonstrated robust performance by rapidly converging to the global maximum power point despite fluctuations in irradiance and shading levels. The integration of fuzzy logic within the Deep Deterministic Policy Gradient framework effectively mitigates the risk of becoming trapped in local maxima while maintaining high tracking accuracy. Furthermore, the fuzzy approximation layer produced smoother control actions, thereby reducing power oscillations when compared to conventional methods such as Perturb and Observe or Incremental Conductance.

However, several challenges were encountered during the experimental implementation. A notable issue was the increased memory requirement for inference when using the Fuzzy–DDPG algorithm. The enhanced computational demands of the fuzzy approximation and deep learning components necessitated devices with greater memory capacity compared to simpler algorithms like Perturb and Observe. Additionally, our current implementation employed a hardware-in-the-loop approach—conducting inference on a PC rather than deploying on embedded hardware. This highlights the need for more capable hardware for real-time applications and underscores the trade-off between achieving advanced tracking performance and the limitations imposed by available hardware resources.

Preliminary experimental results confirm that the proposed Fuzzy–DDPG algorithm is capable of accurately tracking the GMPP, even in the presence of multiple local maxima induced by partial shading. The controller exhibits rapid convergence and reduced oscillatory behavior compared to conventional methods. These results underscore the effectiveness of the hybrid fuzzy–reinforcement learning strategy for MPPT in PV systems and motivate further statistical analysis and optimization in future work.

The statistics presented in

Table 10. Statistical performance of the Fuzzy–DDPG algorithm for MPPT under partial shading conditions.

Statistic	Measured Value	Ideal Value	Relative Error (%)
Mean Power Output, $\overline{P}$	48.5 W	50.0 W	3.0%
Standard Deviation, ${\sigma }_P$	1.2 W	–	–
Maximum Observed Power, $P_{\max }$	50.0 W	50.0 W	0.0%
Tracking Efficiency, $\eta =\overline{P}/P_{\mathrm{ideal}}$	97.0%	100.0%	3.0%

demonstrate the efficacy of the proposed Fuzzy–DDPG algorithm in accurately identifying the maximum power point under partial shading conditions. The measured mean power output closely approximates the ideal value, with a relative error of only 3.0%. Moreover, the maximum observed power reaches the theoretical limit, thereby confirming that the controller consistently achieves optimal tracking. The low standard deviation further indicates stable operation with minimal fluctuations, underscoring the robustness of the Fuzzy–DDPG approach in dynamic photovoltaic environments.

8. Discussion

The experimental results justify the efficacy of the proposed Fuzzy–DDPG algorithm in achieving Maximum Power Point Tracking (MPPT) under partial shading conditions. In comparison with traditional methods such as Perturb and Observe (P&O) and Incremental Conductance (IC), the algorithm exhibits superior performance in terms of global optimization, convergence speed, stability, and tracking accuracy. These advantages stem from the effective combination of deep reinforcement learning and fuzzy logic, which enables the algorithm to navigate the complex, multimodal power landscapes typical of photovoltaic systems under varying shading conditions.

From the perspective of previous studies [28,40], our findings reinforce the working hypothesis that deep reinforcement learning frameworks are particularly well-suited for modeling the nonlinear dynamics and uncertainties inherent in photovoltaic systems. Notably, the integration of fuzzy logic not only accelerates the learning process—as evidenced by the reduced convergence time illustrated in Figure 13—but also enhances the robustness of power tracking, resulting in a lower standard deviation in output power (see Figure 3). This dual enhancement suggests that fuzzy logic effectively modulates the exploration–exploitation trade-off in the reinforcement learning framework, thereby facilitating more reliable identification of the global maximum power point.

Interpreted in the broader context, these results have significant implications for the design and optimization of renewable energy systems. The demonstrated capability of the Fuzzy–DDPG algorithm to overcome local optima and achieve higher tracking precision under challenging conditions indicates its potential to improve energy harvesting efficiency and system stability.

The Fuzzy–DDPG algorithm requires greater computational resources than traditional algorithms. In addition, it demands radiation and temperature sensors for training. These requirements lead to higher hardware costs in experimental implementations. Moreover, the methodological framework developed here could be adapted to other renewable energy applications, such as wind energy systems or hybrid configurations, where similar optimization challenges are present.

Future research directions include the following:

• Adaptive Fuzzy Rule Tuning: Investigating dynamic adjustment strategies for the fuzzy logic component to further enhance adaptability and control precision in real-time scenarios.
• Scalability Studies: Extending the current framework to larger-scale photovoltaic installations and evaluating its performance under a wider range of environmental conditions.
• Comparative Analyses: Conducting comprehensive comparisons with other state-of-the-art machine learning and hybrid control methods to delineate the strengths and limitations of the Fuzzy–DDPG approach.

In summary, the Fuzzy–DDPG algorithm not only corroborates the findings of previous studies regarding the benefits of deep reinforcement learning in MPPT applications but also extends these insights by demonstrating that fuzzy logic can play an essential role in enhancing control performance. However, the tuning of hyperparameters, the definitions of membership functions, and the need for greater computing power leave aspects to be improved in the proposal.

The integration of these two methodologies provides a promising pathway for advancing MPPT techniques in photovoltaic systems, with broad implications for the future of renewable energy optimization.

9. Conclusions

In this work, we proposed a novel hybrid reinforcement learning approach that integrates fuzzy strategies with the Deep Deterministic Policy Gradient (DDPG) algorithm for Maximum Power Point Tracking (MPPT) in photovoltaic systems under partial shading conditions. The resulting Fuzzy–DDPG algorithm is specifically designed to address the challenges posed by the power-voltage characteristics of partially shaded PV arrays, where traditional methods often converge to suboptimal local maxima.

The experimental results demonstrate that the Fuzzy–DDPG method achieves superior performance in terms of global optimality, convergence speed, tracking accuracy, and control stability when compared with conventional techniques such as Perturb and Observe (P&O) and Incremental Conductance (IC), as well as with the standard DDPG algorithm.

The incorporation of fuzzy logic into the reinforcement learning framework effectively enhances the exploration–exploitation balance, allowing states to be mapped onto smooth functions. The algorithm aims to reliably identify and track the global maximum power point under a variety of environmental conditions.

Theoretical analysis further corroborates the convergence properties of the hybrid approach, while statistical evaluations confirm its robustness and consistency in power extraction performance across diverse irradiance and temperature scenarios. These findings underscore the potential of integrating fuzzy approximation techniques with deep reinforcement learning to overcome the nonlinearities and uncertainties in photovoltaic systems.

Future research will focus on adaptive fuzzy rule tuning, scalability studies for large-scale PV installations to further enhance the applicability, and the search for reduced hardware costs so that its implementation is more accessible to society.