Are Ionospheric Disturbances Spatiotemporally Invariant Earthquake Precursors? A Multi-Decadal 100-Station Study

Abstract

Earthquake prediction remains one of the central unsolved problems in geophysics, and ionospheric variability offers a promising yet debated window into the earthquake preparation process through lithosphere–atmosphere–ionosphere coupling. Progress has been hindered by methodological limitations in prior studies, including the use of inappropriate performance metrics for highly imbalanced seismic data, the reliance on geographically and temporally narrow data, and inclusion of inherent spatial or temporal features that artificially inflate model performance while preventing the discovery of genuine ionospheric precursors. To address these challenges, we introduce a global, temporally validated machine learning framework grounded in thirty-eight years of ionospheric observations from more than a hundred ionosonde stations. We eliminate lookahead bias through strict temporal partitioning, prevent overlapping precursor windows across samples to eliminate autocorrelation artifacts and apply sophisticated feature selection to exclude spatial and temporal identifiers, enabling prevention of data leakage and coincidence effects. We investigate whether spatiotemporally invariant ionospheric precursors exist across diverse seismic regions, addressing the field’s reliance on geographically isolated case studies. Cross-regional validation shows that our models yield modest classification skill above chance levels, with our best-performing model achieving a weighted F1 score of 71% though performance exhibits pronounced sensitivity to temporal validation configuration, suggesting these results represent an upper bound on operational accuracy. While multimodal fusion with complementary precursor channels could possibly improve performance, our focus remains on establishing whether ionospheric observations alone contain learnable, region-independent seismic signatures. These findings suggest that ionospheric precursors, if they exist as universal phenomena, exhibit weaker cross-regional consistency than previously reported in case studies, raising questions about their standalone utility for earthquake prediction while indicating potential value as one component within multimodal observation systems.

1. Introduction

Earthquakes represent one of the most destructive natural phenomena, posing a persistent threat to human life due to their unpredictable nature. The lithosphere-atmosphere-ionosphere coupling (LAIC) hypothesis proposes that pre-earthquake crustal stress releases electromagnetic radiation and modifies atmospheric chemistry, producing detectable ionospheric anomalies days to weeks before seismic rupture [1]. Despite decades of research reporting ionospheric perturbations before major earthquakes [2,3,4], the field remains mired in controversy. Critics argue that reported correlations reflect coincidental alignment between periodic ionospheric variability and earthquake occurrence rather than genuine physical coupling [5,6], while proponents counter that methodological limitations in statistical analysis obscure real precursor signals [7]. The search for reliable earthquake precursors has motivated diverse monitoring approaches spanning seismological, geodetic, geochemical, electromagnetic, and ionospheric domains. Recent machine learning approaches for structural damage detection [8,9] offer relevant methodological frameworks for precursor identification.

Three interrelated methodological problems in experimental design have limited the validity of ionospheric precursor research, resulting in the current uncertainty. First, studies predominantly rely on case study approaches analyzing individual earthquakes or single monitoring stations [10,11], where limited sample sizes permit neither robust statistical inference nor separation of genuine precursors from random fluctuations in naturally variable ionospheric parameters. Second, inappropriate performance metrics have systematically inflated reported predictive skill. Accuracy metrics applied to highly imbalanced datasets where earthquakes constitute rare events produce misleadingly high values even for models with minimal true predictive power, while the absence of proper train-test temporal partitioning allows models to exploit retrospective labeling artifacts unavailable in prospective deployment [12]. Third, and most critically, feature sets incorporating explicit temporal or spatial information enable models to learn earthquake occurrence patterns rather than ionospheric precursors, achieving high performance through data leakage while providing no insight into physical LAIC mechanisms.

Our previous work on earthquake forecasting techniques [13] and Schumann resonance signals in the Greek region [14] attempted to move beyond isolated electromagnetic case studies toward systematic analysis. Subsequently, we investigated ionospheric precursors at Athens station (AT138) using statistical correlation and machine learning, obtaining marginally significant correlations but poor predictive performance. This weak performance may stem from fundamental limitations inherent to single-station analysis, including regional ionospheric peculiarities, contamination from Athens’ exceptionally high seismic frequency producing overlapping precursor windows, and insufficient sample diversity to distinguish genuine coupling from coincidental correlation [15,16].

Single-station studies face a fundamental identification problem where local meteorological disturbances, space weather effects, and instrumental artifacts can all produce ionospheric anomalies indistinguishable from putative seismic precursors when analyzed in isolation. By analyzing observations from over a hundred globally distributed ionosonde stations spanning thirty-eight years, we reframe the question from “do ionospheric anomalies precede individual earthquakes?" to “do spatiotemporally invariant precursor patterns exist across diverse seismic regions?" If LAIC represents a genuine physical phenomenon, ionospheric signatures should appear systematically before earthquakes across different tectonic settings, independent of regional ionospheric climatology or local space weather conditions. Conversely, if single-region correlations reflect coincidence or regional artifacts, these patterns will not replicate consistently across a globally heterogeneous station network. This transformation from anomaly detection to universality testing provides a definitive empirical test of whether ionospheric observations contain learnable, location-independent seismic signatures or whether reported precursors represent statistical artifacts of geographically constrained analysis.

2. Theoretical Foundation: Lithosphere–Atmosphere–Ionosphere Coupling

The Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) framework [1,17] provides a proposed physical basis for seismo-ionospheric interactions, describing how pre-seismic processes in the crust may produce measurable ionospheric responses. While individual case studies have reported apparent precursory signatures, the physical mechanisms remain debated, the evidence base is inconsistent, and alternative explanations involving space weather, meteorology, and statistical artifacts have not been systematically excluded [5,6]. Nonetheless, the model identifies three principal coupling pathways operating on distinct temporal and physical scales.

Chemical channel: Progressive crustal stress is hypothesized to enhance microfracturing and radon release [18,19]. Radon decay would increase ion production in the boundary layer, potentially modifying atmospheric conductivity, and perturbing the global electric circuit [20]. These electric field disturbances could map to ionospheric heights and alter plasma density hours to days before an earthquake. However, radon emanation exhibits strong meteorological and hydrological controls, including barometric pumping, soil moisture, temperature gradients, and precipitation, which can dominate over tectonic signals [21,22]. The literature presents a mixture of positive case studies [23,24] alongside null results or very low detection rates [22,25] and inconsistent temporal patterns that complicate seismogenic attribution [21]. Site-specific geological factors, measurement techniques, and  data quality issues further limit the generalizability of radon-based precursor claims.

Acoustic channel: Crustal deformation can excite acoustic–gravity waves (AGWs) that propagate upward and amplify in the rarefied atmosphere [26,27]. Upon reaching the ionosphere, AGWs modulate neutral dynamics, ion–neutral collisions, and vertical plasma transport, producing periodic electron density variations. This channel primarily governs short-timescale (minutes to hours) co-seismic and post-seismic disturbances [28,29], though pre-seismic AGW signatures have also been reported [30]. The acoustic channel is the most physically plausible LAIC pathway for co-seismic and post-seismic ionospheric disturbances, though clear pre-seismic AGW signatures remain controversial.

Electromagnetic channel: Stressed rocks may generate electromagnetic emissions through piezoelectric, electrokinetic, and defect-activated charge mechanisms [31,32]. These ULF–VLF fields may propagate to or interact with the ionosphere, where they could heat electrons, modify temperature anisotropy, and trigger plasma instabilities [33,34]. This pathway is the most speculative, with disputed laboratory evidence, unclear propagation mechanisms, and limited observational validation [6,35]. This hypothetical pathway may operate throughout the preparation stage and thus provide some of the earliest signals.

In summary, LAIC theory provides a conceptual framework for seismo-ionospheric coupling, but the physical mechanisms remain insufficiently validated, the evidence base is heterogeneous and often contradictory, and systematic studies controlling for confounding factors are scarce. Whether ionospheric anomalies reflect genuine lithospheric coupling or arise from space weather variability, atmospheric dynamics, and statistical coincidences remains an open question that motivates the large-scale, rigorously controlled investigation presented in this work. In practice, these channels likely act concurrently, with their relative strengths depending on earthquake parameters, geological context, and ionospheric conditions [4]. Because our dataset includes both bottomside (foE, foF1) and topside (foF2, TEC) parameters, it is well suited to investigating the layer-specific signatures expected from the chemical, acoustic, and electromagnetic coupling mechanisms.

3. Data

Figure 1 shows the spatial distribution of our ionospheric monitoring stations. Several stations are positioned in seismically active regions (like Athens), while others occupy low-seismicity or aseismic areas (like Fortaleza). These station types contribute complementary data. Seismically active regions provide positive samples of ionospheric conditions preceding earthquakes but offer limited quiet periods for negative sampling. Conversely, low-seismicity stations yield abundant negative samples, ensuring a balanced class ratio.

Data Acquisition and Station Network

We firstly downloaded ionospheric data from 129 globally distributed monitoring stations spanning 1987–2025, yielding 13,932 station-months of observations and 57.8 million raw ionospheric measurements. The network encompasses diverse geographic and tectonic environments, covering latitudes from −74.6° to 81.4° (Figure 1). Data availability varies substantially across stations, with 25 stations providing long-term coverage exceeding 200 months, 30 stations contributing medium-duration records between 100 and 199 months, and 75 stations offering shorter observational periods below 100 months, reflecting the heterogeneous nature of global ionospheric monitoring infrastructure. Ionospheric measurements were retrieved from the Lowell GIRO Data Center [36], including critical plasma frequencies (foF2, foF1, foE, foEs), peak heights (hmF2, hmF1, hmE), virtual reflection heights (hF2, hF, hE, hEs), bottomside and topside thickness parameters (B0, B1), propagation factors (MUFD, MD), scale heights (hmF2, scaleF2), M(3000)F2 propagation factor, and total electron content (TEC). Raw measurements were quality-controlled, retaining 34.3 million high-confidence observations (59.4% of raw data) and yielding 106 final stations with cleaned data suitable for analysis.

Because ionospheric anomalies can arise from both lithospheric processes and space weather disturbances, we integrate space weather indices to distinguish genuine seismo-ionospheric coupling from solar-driven ionospheric variability that could otherwise generate false precursor signals. Space weather parameters were obtained from NASA’s OMNIWeb service [37], including solar flux indices (F10.7), geomagnetic activity indices (Kp, Dst), and additional solar wind parameters. This auxiliary dataset comprises approximately 150,000 co-temporal hourly observations, mirroring the time span of our ionospheric measurements.

Figure 2 illustrates temporal data availability across a representative sample of stations overlaid with earthquake events within each station’s monitoring range. Ionospheric measurements are recorded at 5 min intervals yielding 288 potential observations per day. We calculate availability as monthly averaged percentages by normalizing daily measurement counts to 144 as our expected baseline/quality threshold and then aggregating by month. Blue shading intensity reflects the mean monthly availability percentage. The visualization reveals substantial variability in both data coverage and earthquake occurrence across stations and time periods.

Seismic catalogs were obtained from the United States Geological Survey (USGS) Earthquake Hazards Program [38], encompassing 855,075 deduplicated global events with magnitude $M\ge 2.0$ across the same 38-year timespan, of which 60,707 events exceeded our prediction target threshold of $M\ge 5.0$.

We employ a two-threshold approach following extensive empirical investigation to optimize the trade-off between sufficient training samples, generalisation and unambiguous class separation. Earthquake-positive samples are defined exclusively by events with $M\ge 5.0$–the threshold where earthquakes begin causing moderate damage and constitute operationally relevant prediction targets. Seismically quiet periods (negative samples) are defined as intervals with no events $M\ge 2.5$ within the monitoring radius, ensuring true background ionospheric conditions. This creates a magnitude buffer zone ($2.5\le M<5.0$) deliberately excluded from both classes to eliminate ambiguous cases where moderate seismicity might produce subtle ionospheric perturbations that would confound the classification boundary, ensuring our model learns to distinguish genuine precursors of damaging earthquakes from truly quiescent ionospheric states.

4. Preprocessing Pipeline

Transformation of raw ionospheric measurements and earthquake catalogs into machine learning-ready features requires a systematic preprocessing pipeline addressing spatial-temporal alignment, class balance, and feature extraction while preventing data leakage. Our approach comprises four sequential stages designed to maximize signal extraction while maintaining methodological rigor.

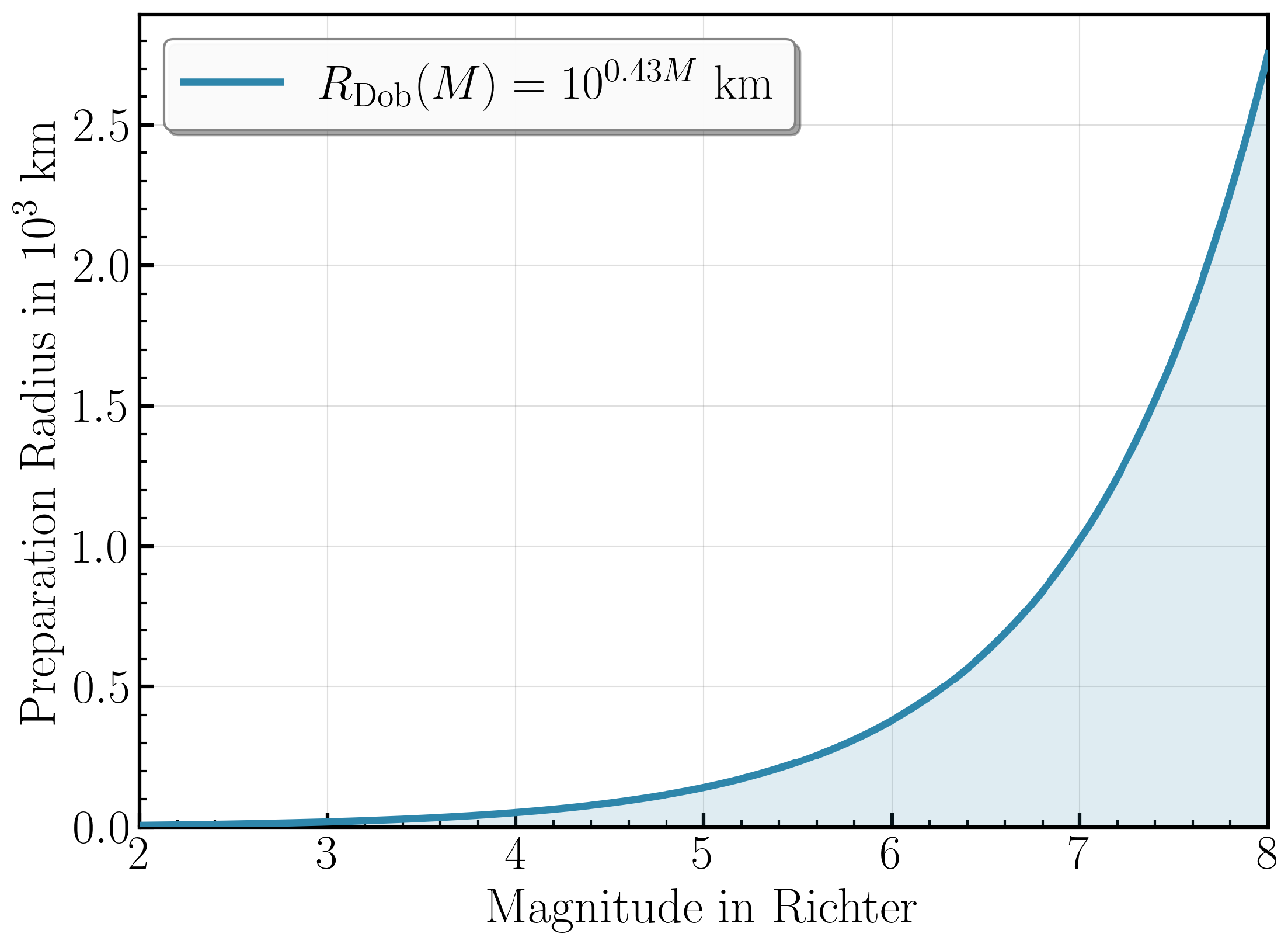
4.1. Spatial Filtering via Dobrovolsky Radius

For each ionosonde station and earthquake event, we apply spatial filtering based on the Dobrovolsky radius [39], an empirical formula estimating the earthquake preparation zone:

$$R_{\mathrm{Dob}}\left(M\right)={10}^{0.43M}\mathrm{km}$$

(1)

where M denotes earthquake magnitude. This relation, derived from crustal strain observations, provides a physically-motivated threshold for identifying potentially coupled ionosphere-lithosphere interactions. Following extensive investigation of relaxation factors ranging from $\alpha =0.1$ to $\alpha =3.0$, we adopt the baseline configuration $\alpha =1.0$ (i.e., $R_{\mathrm{eff}}\left(M\right)=R_{\mathrm{Dob}}\left(M\right)$). This conservative and pragmatic choice preserves the original Dobrovolsky formulation without arbitrary scaling, minimizing the risk of spurious correlations from overly permissive spatial filtering while maintaining sufficient spatial coverage for physically plausible coupling interactions. Only earthquakes with epicenter-station distance $d\le R_{\mathrm{eff}}\left(M\right)$ and magnitude $M\ge 2.5$ are retained, filtering approximately 856,000 events into station-specific candidate sets.

Figure 3 shows the exponential scaling of preparation zone radius with magnitude under baseline configuration ($\alpha =1.0$). At our minimum threshold of M5.0, the 141 km radius restricts samples to nearby events within plausible coupling distance, while M8.0 events with 2754 km radii can potentially influence multiple geographically distant stations, providing rare multi-station observations that test spatiotemporal invariance in precursor patterns.

4.2. Temporal Window Construction

After thorough experimentation on the window size, we choose to construct 30-day observation windows preceding each earthquake, selected to capture the characteristic timescale of ionospheric precursors reported in the literature (1–30 days before events) [1]. Each earthquake $M\ge 5.0$ generates one positive sample with its associated 30-day ionospheric time series ending immediately before the event. To establish class balance and enable supervised learning, we generate an equal number of control (negative) samples by randomly selecting 30-day windows during seismically quiet periods at each station, defined as intervals with no earthquakes above $M\ge 2.5$ within $R_{\mathrm{eff}}$ during or immediately following the window. This balanced sampling strategy ensures a 1:1 positive-negative ratio, which enables effective supervised training by mitigating the severe class imbalance inherent to rare-event prediction, while the chronological sampling ensures the preservation of the natural temporal dynamics of the ionospheric features.

4.3. Feature Extraction via Multi-Scale Statistical Aggregation

From each 30-day window, we extract statistical moments across multiple temporal scales (1, 3, 7, 14, and 30 days) for our ionospheric parameters (foF2, TEC, hmF2, etc.) and space weather indices (Kp, Dst, F10.7, solar wind parameters). For each parameter p and timescale t, we compute mean, standard deviation, minimum, maximum, median, skewness, and kurtosis, yielding hundreds of candidate features per sample. This multi-scale representation captures both short-term fluctuations and longer-term trends potentially indicative of LAIC processes, enabling the learning algorithm to discover optimal temporal integration patterns.

4.4. Quality Assurance and Temporal Integrity

We impose strict quality thresholds to ensure data completeness and reliability. Ionospheric parameters from GIRO are confidence-graded on a 0–100 scale reflecting measurement reliability based on ionogram autoscaling quality, signal-to-noise ratio, and validation against manual scaling. Following systematic investigation across multiple threshold configurations (CS ≥ 60, 70, 80, 90), we adopt CS ≥ 70 as the optimal trade-off between data retention (59.4% of raw measurements) and measurement quality. We retain only measurements meeting this confidence criterion, filtering out uncertain or poorly-constrained values that could introduce noise into the learning process. Similarly, after evaluating temporal completeness thresholds ranging from 60% to 90%, we require that temporal windows contain at least 70% valid high-confidence measurements after accounting for ionosonde outages and data gaps, as this threshold balances robust statistical aggregation against excessive sample loss from overly stringent requirements, yielding 850 final samples with superior model performance compared to stricter thresholds.

To ensure statistical rigor, we enforce a strict temporal non-overlapping constraint per station, preventing autocorrelation artifacts where sliding windows violate sample independence. In contrast, we allow temporally overlapping windows from geographically distant stations. While simultaneous observations of a single event are empirically rare–due to the sparse global distribution of ionosondes relative to typical earthquake preparation zones–they are retained when they occur. Because local ionospheric conditions are uncorrelated across large distances, these rare multi-station events provide critical independent samples that enable the model to distinguish localized seismic precursors from global solar-driven disturbances. Furthermore, as our network spans diverse geomagnetic latitudes, analyzing these events against contrasting background dynamics forces the learning algorithm to identify spatiotemporally invariant precursor features that persist across regimes, rather than overfitting to regional peculiarities.

After applying spatial filtering (Dobrovolsky radius with $\alpha =1.0$), temporal window construction (30-day precursor windows), quality assurance criteria (confidence $\ge 70\%$, data completeness $\ge 70\%$), and strict temporal non-overlapping constraints per station, our final dataset comprises 850 samples across 106 stations. This includes 428 earthquake-positive samples (events with $M\ge 5.0$) and 422 seismically-quiet negative samples, yielding a balanced 1:1 class ratio suitable for supervised binary classification.

5. Feature Selection and Data Leakage Mitigation

High-dimensional feature spaces extracted from ionospheric time series risk violating the requirement that sample size substantially exceeds feature dimensionality ($n\gg p$). When $n\lesssim p$, the curse of dimensionality arises, whereby models overfit noise and exploit spurious correlations rather than genuine signal. Additionally, periodic solar-driven variability introduces coincidence bias–a form of data leakage where models exploit temporal patterns unrelated to physical lithosphere-atmosphere-ionosphere coupling (LAIC).

5.1. Exclusion of Spurious Spatiotemporal Features

We first exclude all inherent spatiotemporal features (date, season, latitude, etc.) that encode no physical information about LAIC processes.

Beyond this standard practice, we also come across a subtler issue. Space weather indices such as F10.7, Kp, and Dst exhibit strong 27-day and annual periodicities driven by solar rotation and Earth’s orbital motion. When these solar periodicities coincidentally align with the quasi-periodic temporal distribution of earthquakes over the 11-year solar cycle, models can exploit this spurious correlation as an indirect temporal marker of earthquake occurrence—a form of data leakage unrelated to physical LAIC coupling.

To identify and exclude such spurious predictors, we conduct a two-dimensional correlation analysis. For each space weather feature, we compute both its absolute correlation with earthquake occurrence periodicity, which quantifies potential for temporal leakage, and its absolute correlation with ionospheric parameters, which measures genuine physical coupling to the ionosphere. Features exhibiting strong correlation with earthquake periodicity serve as potential temporal proxies for seismic occurrence and are therefore excluded to prevent data leakage. Features exhibiting strong correlation with ionospheric parameters reflect genuine solar-ionospheric coupling and are retained to account for space weather-driven ionospheric variability.

Figure 4 reveals that certain space weather indices correlate strongly with seismic event periodicity, marking them as spurious predictors requiring systematic exclusion. F10.7 solar flux indices, however, exhibit minimal correlation with earthquakes but strong correlation with ionospheric parameters, aligning with LAIC’s physical premise that solar activity modulates ionospheric background conditions. We therefore retain F10.7 features while excluding periodicity-correlated indices, ensuring our feature set captures ionosphere-earthquake coupling rather than coincidental temporal patterns.

5.2. Ensemble-Based Feature Ranking

For the remaining ionospheric features, we employ multiple feature importance methods to avoid relying on any single approach. Tree-based models evaluate features based on how well they split the data, while permutation importance measures how much prediction quality degrades when each feature is shuffled. Mutual information captures arbitrary non-linear dependencies between features and earthquake occurrence, and ANOVA F-statistics test for differences in feature distributions between earthquake and non-earthquake cases.

Critically, feature selection is performed exclusively on training data with validation and test sets completely held out. This temporal separation ensures that features cannot be selected based on spurious correlations with future data, as any random patterns that appear informative in training will fail to generalize to unseen years. The consensus ensemble approach across four independent statistical methods further guards against selecting features that correlate by chance with seismic activity in the training period.

We normalize the importance scores from each method and average them to create a consensus ranking. Features are selected based on their consistency across methods–those that rank highly in multiple approaches and show stable importance scores. This multi-method validation reduces the risk of overfitting to algorithm-specific artifacts, as genuine precursory signals should manifest across diverse statistical perspectives while spurious correlations typically appear only under specific analytical assumptions.

The final 25-feature set (see Appendix A) emphasizes short-term variability measures and temporal dynamics, indicating that earthquake preparation may manifest through transient ionospheric disturbances. The features selected show a clear preference for profile thickness parameters (B0, B1) and TEC trends. This finding suggests that the model primarily exploits structural variations in the electron density profile. Features spanning timescales up to 30 days are present, and the retention of solar F10.7 indices provides the necessary context to separate these structural anomalies from solar-driven variability.

6. Temporal Data Splitting and Distribution Balance

6.1. The Critical Importance of Temporal Validation

Temporal validation is fundamental to earthquake precursor research, yet frequently violated in the literature, leading to severe data leakage and unrealistic performance estimates. Random cross-validation—the standard approach in machine learning—is fundamentally inappropriate for time series prediction tasks because it allows models to train on future information and test on past events, directly contradicting operational deployment scenarios where only historical data informs future predictions [12]. This temporal leakage enables models to exploit artifacts of the data collection process and retrospective labeling, producing artificially inflated metrics that collapse when deployed prospectively. Only strict temporal splitting—where all training data precedes validation and test data—provides honest estimates of real-world predictive capability.

6.2. The Distribution Shift Problem

As shown in Figure 5, our dataset exhibits pronounced temporal clustering, with certain years (highlighted in red) experiencing substantially elevated seismic activity while others remain relatively quiet.

Years with disproportionately high seismic activity demonstrate pronounced temporal clustering. Naive temporal splitting—partitioning data by chronological cutoffs without regard to class distributions—introduces distribution shift when earthquake frequency varies significantly over time. This temporal variability creates a fundamental statistical problem. When high-activity years fall disproportionately in the test partition, models can achieve spurious predictive performance by learning the temporal density pattern of earthquake occurrence rather than genuine ionospheric precursors. Our temporal split maintains balanced earthquake occurrence rates across partitions but inevitably introduces feature distribution shift due to natural geophysical variation. While the target label distribution remains constant at 50% positive samples across splits, ionospheric and solar parameters exhibit significant temporal evolution driven by solar cycles, long-term ionospheric trends, and  atmospheric variability. This feature shift represents the realistic challenge our models face. Predicting earthquakes under different geophysical conditions than encountered during training, testing whether learned precursor patterns generalize across varying solar activity regimes rather than memorizing epoch-specific correlations. Therefore, this variability mandates the use of a stratified approach to ensure a consistent balance of seismic activity levels across all partitions, preventing the model from exploiting this global temporal clustering as an artifactual prediction signal.

Figure 6 further illustrates that seismic activity clustering is spatially heterogeneous, with different regions experiencing peak seismicity in distinct years. This regional variability confirms that a simple chronological cut-off, applied without considering activity levels, would lead to regional class imbalance and violate the required uniform positive-negative ratio across the temporally separated partitions. This challenge, combined with the global temporal clustering shown in Figure 5, mandates a stratified temporal splitting strategy to ensure robust generalization of learned precursor patterns.

6.3. Stratified Temporal Splitting

We implement a stratified temporal split with training (80%), validation (10%), and test (10%) partitions that maintain chronological order while balancing seismic activity levels. Years are categorized by global earthquake frequency into low, medium, and high activity strata, then allocated proportionally to each split to ensure consistent positive-negative ratios. This prevents models from exploiting temporal density patterns rather than learning genuine ionospheric precursors, while strict temporal partitioning (training precedes validation precedes test) eliminates lookahead bias and provides performance estimates generalizable to prospective deployment.

7. Methodology

Our methodology employs a systematic machine learning pipeline to investigate seismo-ionospheric coupling through spatiotemporally invariant feature learning, comparing state-of-the-art classification algorithms on rigorously preprocessed ionospheric data.

7.1. Model Selection and Hyperparameter Tuning

We compare machine learning architectures with fundamentally different learning strategies for spatiotemporal feature patterns. Tree-based ensembles (Random Forest, Extra Trees, Histogram Gradient Boosting) excel at capturing non-linear feature interactions through recursive partitioning without requiring feature scaling or parametric assumptions. Sequential boosting methods (XGBoost, LightGBM, CatBoost, AdaBoost, Gradient Boosting) iteratively refine predictions by fitting residual errors, often achieving superior generalization through adaptive regularization [40]. Kernel methods (SVM) and neural networks (MLP) offer complementary strengths in handling high-dimensional feature spaces through explicit kernel transformations and learned hierarchical representations, respectively. Simple baselines (Logistic Regression, Gaussian Naive Bayes, K-Nearest Neighbors, Decision Tree) provide essential reference points for evaluating whether model complexity yields genuine predictive gains.

For our hyperparameter optimization, we employ RandomizedSearchCV to efficiently explore algorithm-specific parameter distributions [41]. Cross-validation is implemented through GroupTimeSeriesSplit with fixed-size folds, which partitions data into chronologically ordered splits where training sets strictly precede validation sets. This fixed-size approach ensures consistent evaluation conditions across folds while maintaining strict temporal ordering. With this design, we ensure that hyperparameters are selected based on genuine temporal generalization rather than artificial patterns arising from random splits or spatial leakage. In our optimization we target the weighted F1-score to maximize the harmonic mean of precision and recall across both classes, ensuring the model prioritizes both the detection of seismic precursors (sensitivity) and the correct identification of quiet periods (specificity) with equal weight.

7.2. Evaluation Protocol

Model assessment employs a comprehensive multi-metric framework designed for imbalanced classification. Area Under the ROC Curve (AUC) quantifies discrimination capacity independent of threshold selection [42], Matthews Correlation Coefficient (MCC) measures prediction quality accounting for class imbalance [43], weighted F1-score balances precision and recall weighted by class support [44], and Cohen’s Kappa assesses agreement beyond chance expectation [45]. Additionally, we compute balanced accuracy to equalize class contributions, geometric mean (G-mean) of sensitivity and specificity for joint class-wise performance, and average precision for recall-oriented evaluation. Our protocol guards against over-optimization on any single criterion, a pervasive pitfall in imbalanced learning [46]. Our evaluation proceeds on the temporally held-out test set, with balanced undersampling ensuring metric stability, while validation splits guide hyperparameter selection.

8. Experimental Results

We evaluate binary classification performance using temporal validation on 3 years of held-out data from 2022 to 2025 after implementing strict spatiotemporal filtering across 106 global stations, yielding a final dataset of 850 samples.

Table 1. Classification performance on balanced temporal test set (2022–2025, CS ≥ 70). Bold indicates the best performance for each metric.

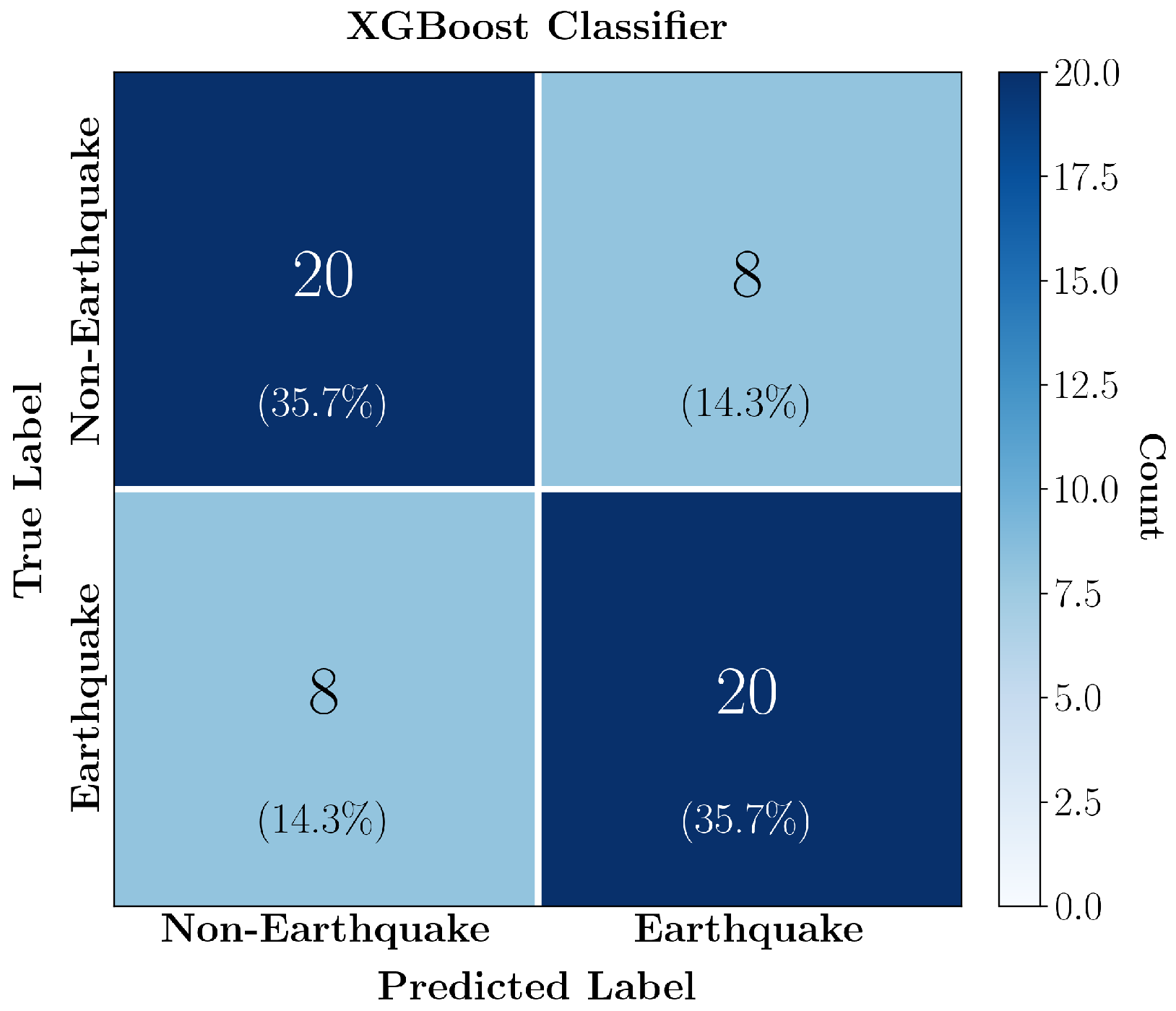
Model	F1-W	MCC	AUC	Bal-Acc	Kappa	G-Mean
XGBoost	0.714	0.429	0.774	0.714	0.429	0.714
Extra Trees	0.714	0.429	0.773	0.714	0.429	0.714
Neural Network	0.713	0.433	0.730	0.714	0.429	0.711
Random Forest	0.696	0.393	0.742	0.696	0.393	0.696
Histogram Gradient Boosting	0.696	0.393	0.781	0.696	0.393	0.696
LightGBM	0.679	0.357	0.736	0.679	0.357	0.679
Gradient Boosting	0.678	0.358	0.719	0.679	0.357	0.678
Deep NN	0.625	0.250	0.714	0.625	0.250	0.625
AdaBoost	0.571	0.143	0.615	0.571	0.143	0.571
Logistic Regression	0.571	0.143	0.619	0.571	0.143	0.571
KNN	0.571	0.143	0.606	0.571	0.143	0.570

summarizes results on the balanced temporal test set. While diverse algorithms achieve consistent above-random performance, the moderate improvement demonstrates weaker cross-regional generalization than reported in geographically constrained case studies, suggesting that spatiotemporal autocorrelation artifacts, inadequate temporal validation, data leakage, and selection bias may have inflated prior results.

While all architectures mentioned in Section 7.1 were trained and evaluated through rigorous hyperparameter optimization, we present results only for models demonstrating substantive predictive skill, as lower-performing algorithms provide limited insight into our specific task of ionospheric precursor detection.

Performance spans from tree-based ensembles and neural networks to baseline algorithms such as Logistic Regression and KNN. The consistent above-random performance across diverse algorithms suggests that learnable signal may exist in ionospheric observations, albeit weak, though the limited magnitude of improvement indicates that ionospheric precursors exhibit only moderate cross-regional consistency or represent weak precursory phenomena. Figure 7 presents the confusion matrix for XGBoost on the held-out test set.

Impact of Test Set Size on Model Performance

Our experimental design employed a strict temporal train-test split to prevent data leakage. We evaluated model sensitivity to test set size by varying the split ratio from 10% to 50%, observing a general downward trend in weighted F1-score from approximately $0.71$ (10% test) to $0.56$ (50% test), though with noticeable fluctuations at intermediate ratios. This decline reflects multiple compounding factors including reduced training data availability, which limits the model’s capacity to learn rare precursor patterns, increased temporal variability in larger test windows, and temporal distribution shift in both feature space (evolving geophysical conditions) and target space (varying class balance across different seismic activity periods, as we mentioned earlier).

We adopted a 10% test split for final evaluation as a pragmatic response to data scarcity in our precursor dataset and we report results at this split ratio. However, standard statistical learning theory indicates that performance estimates from small test sets exhibit high variance and limited coverage of the true data distribution. Combined with the non-stationarity inherent to geophysical time series, our estimates likely represent an upper bound on operational performance. While performance remains above chance across all split ratios, the modest gains and pronounced sensitivity to validation configuration indicate that exploitable precursor signals, if present, are weak. These findings should be interpreted with appropriate caution.

9. Conclusions and Next Steps

We investigate whether spatiotemporally invariant ionospheric earthquake precursors exist across diverse seismic regions, analyzing multiple decades of data from globally distributed stations with strict spatiotemporal protocols to eliminate data leakage, spurious correlations and autocorrelation artifacts. Temporal validation on held-out data from 2022 to 2025 enables assessment of cross-regional generalization beyond the geographically isolated case studies that dominate the existing literature.

Our best-performing classifier achieves a weighted F1 score of 70% on a 10% temporal test split, demonstrating that learnable patterns exist in ionospheric observations. However, performance degrades systematically to 56% on larger test windows (50% split), indicating that exploitable precursor signals, while statistically detectable, are weak and our reported metrics likely represent an upper bound that should be interpreted cautiously.

These findings raise fundamental questions about universality. The limited cross-regional generalization indicates that ionospheric signals may be weaker and more variable than case studies suggest, highly dependent on local geological and atmospheric conditions, or contaminated by confounding factors not fully controlled in our analysis.

Future work should investigate whether multimodal fusion of complementary LAIC-coupled observations can improve cross-regional performance, and whether regional specialization training separate models for distinct tectonic regimes yields stronger results than our global approach.

Our study demonstrates that ionospheric measurements encode modest but learnable precursory information when evaluated under strict spatiotemporal controls. While ionospheric monitoring alone cannot support operational earthquake warning systems, the consistent above-chance performance across diverse algorithms suggests potential value as one component within multimodal sensor fusion frameworks, though the weak signal strength and validation sensitivity underscore the preliminary nature of these findings.