Thermal Behavior and Operation Characteristic of the Planetary Gear for Cutting Reducers

Abstract

Bolter miners have been widely used in coal mining or excavation industries. Its efficiency is closely related to the performance of its cutting reducer, which is literally determined by the thermal behavior of the planetary gear set. Thus, this study conducts experimental investigation on the thermal behavior of a cutting reducer (produced by Zhengzhou Machinery Research Institute Transmission Technology Co., Ltd., rated input power 170 kW, transmission ratio 3.06), where the results show the high temperature rise around the intermediate shaft for unloaded condition and significant influence of the torque for loaded conditions. Then, the Finite Element Method (FEM) is used to analyze the temperature field and thermal–structural coupling of the planetary gear set. The thermal stress and deformation increase by 11.5% and 38.4%, respectively, indicating high risk of gear damage. Moreover, the load spectrum imitating the actual industrial condition is added to the KISSsoft to evaluate the reliability and contact of the planetary gear set. The findings including low safety factors of the sun gear tooth surface and planetary gear root, slipping during the sun gear and planetary gear meshing, and uneven contact fluctuations can benefit planetary gear set optimization.

1. Introduction

Bolter miners are the most important equipment in the process of coal mine automatic mining or tunnel excavation. Due to the harsh working conditions, heavy load and complex operation parameters during coal mining, frequent vibrations and shocks are exerted on a bolter miner, leading to a relatively high failure rate of its key component, namely, a cutting reducer. Thus, the cutting reducer has a significant impact on the cutting rate and the overall production efficiency of the bolter miner [1,2]. Further research has stated that 80% failure is due to the friction thermal wear, pitting and gear tooth fracture of a series of planetary gear sets installed in a cutting reducer [3,4,5,6]. It is necessary to analyze the thermal behavior of planetary gear sets to provide theoretical support for the design, optimization and maintenance of cutting reducers.

The cutting reducer of the bolter miner adopts a three-stage planetary gear set transmission. The large torque load borne by the low-speed planetary gear and the impact load transmitted by the cutting head result in significant changes in the failure rate and temperature rise at a low-speed stage. The theories and thermal simulations for solving the thermal boundary conditions of gears are reliable. Zhou [7] established a thermal network model based on the heat transfer theory to predict the contact temperature of spur gears. Hu [8] established a herringbone gear pair single tooth model and predicted the steady state temperature field distribution of the gears which was consistent with that measured experimentally. Roda-Casanova and Gonzalez-Perez [9] carried out steady state thermal analysis of gears by the FEM and obtained the temperature field on the gear geometry. Li [10] derived the theoretical calculation formula of gear thermal boundary and analyzed the influence of different parameters on gear temperature rise by the FEM, from which the distribution law of the three-dimensional temperature field of spur/helical gear transmission under different working conditions was revealed. Lan [11] discussed the influence of gear structure parameters on the unsteady temperature field and root thermal stress of large transmission ratio gears.

Despite these contributions, most theoretical approaches are confined to single tooth or gear pair analyses. They fail to capture the complex thermal behavior of planetary gear sets under ultimate loads. While these basic models provide foundational insights, recent research has focused on the complex thermal–structural coupling dynamics of planetary systems under heavy loads. Unlike single gear pairs, planetary sets exhibit unique heat dissipation challenges due to their compact structures and multi-mesh interactions. Zhang [12] developed an analytical thermal–fluid iterative coupling method for oil-jet lubricated planetary gears, revealing that high-speed airflow significantly hindered lubricant penetration and escalated the thermal risk. Similarly, Bi [13] established a nonlinear dynamic model for wind power planetary gears, demonstrating that tooth surface temperature rise was a critical bifurcation parameter affecting system stability. In terms of structural response, Yu [14] conducted a coupled thermal–structural resonance reliability analysis, confirming that thermal deformation altered the natural frequency of the gear-rotor system, which accelerated wear. Yao [15] further quantified this effect, showing that optimized 3D topology modification can reduce thermal deformation by 46.5% and significantly improve transmission accuracy.

Furthermore, the impact of thermal behavior on reliability has become a focal point of modern research. Zivkovic [16] proposed a “bottom-up” reliability evaluation model for planetary transmissions, emphasizing the competitive risk of component failure modes under operational stress. Li [17] introduced a hierarchical Finite Element Method to predict fatigue reliability, highlighting that the traditional methods tend to underestimate the dangerous tooth load histories. Experimental investigations by Alkarkhi [18] and Muratovic [19] have also verified that ambient temperature and friction heat accumulation were the primary drivers of tribological failure and thermo-elastic instability. Additionally, recent advancements in physical model-driven approaches by Cao [20] and electric–thermal coupling simulations by Capelli [21] suggested that multi-physics modeling was essential for accurately predicting the performance degradation of complex gearboxes.

In parallel with finite element modeling, specialized gear calculation software has proven indispensable for fatigue and contact analysis. For instance, Rogkas [22] utilized KISSsoft simulations to perform multi-objective optimization analysis on a micro-gearbox system, effectively revealing durability and performance metrics relevant to complex transmission designs. Bergsted [23] calculated the gear contact stress and specific film thickness of the corresponding load stage by the KISSsoft and obtained the gear surface roughness influence on the pitting and micro corrosion life. Irsel [24] used the KISSsoft to calculate the strength of bevel gears with the ISO, AGMA, and DIN calculation methods and compared the results to those computed by the Ansys FEM. The difference between the two results was less than 7%.

At present, limited analysis of thermal behavior as well as the related strength and contact analysis has been reported for planetary gears under actual working conditions. Scant practical data is available for the design or optimization of planetary gear sets. Therefore, this study experimentally investigates the thermal behavior of a cutting reducer under low speeds. Furthermore, to gain deeper insights into the mechanisms driving the thermal behavior, the FEM is used to analyze the heat transfer and thermal–structural coupling of the planetary gear set, from which the temperature field, the heating position, the thermal stress and strain of the gears under heavy load are explored. Finally, the key factors contributing to the gear fatigue strength and contact under actual working conditions are analyzed by the KISSsoft modeling. It is expected that the analysis on the performance of a bolter miner will provide theoretical support for cutting reducer design. The findings including changing the lubrication method, implementing addendum modification and crowning modification on the gears will help improve the durability of the cutting reducer.

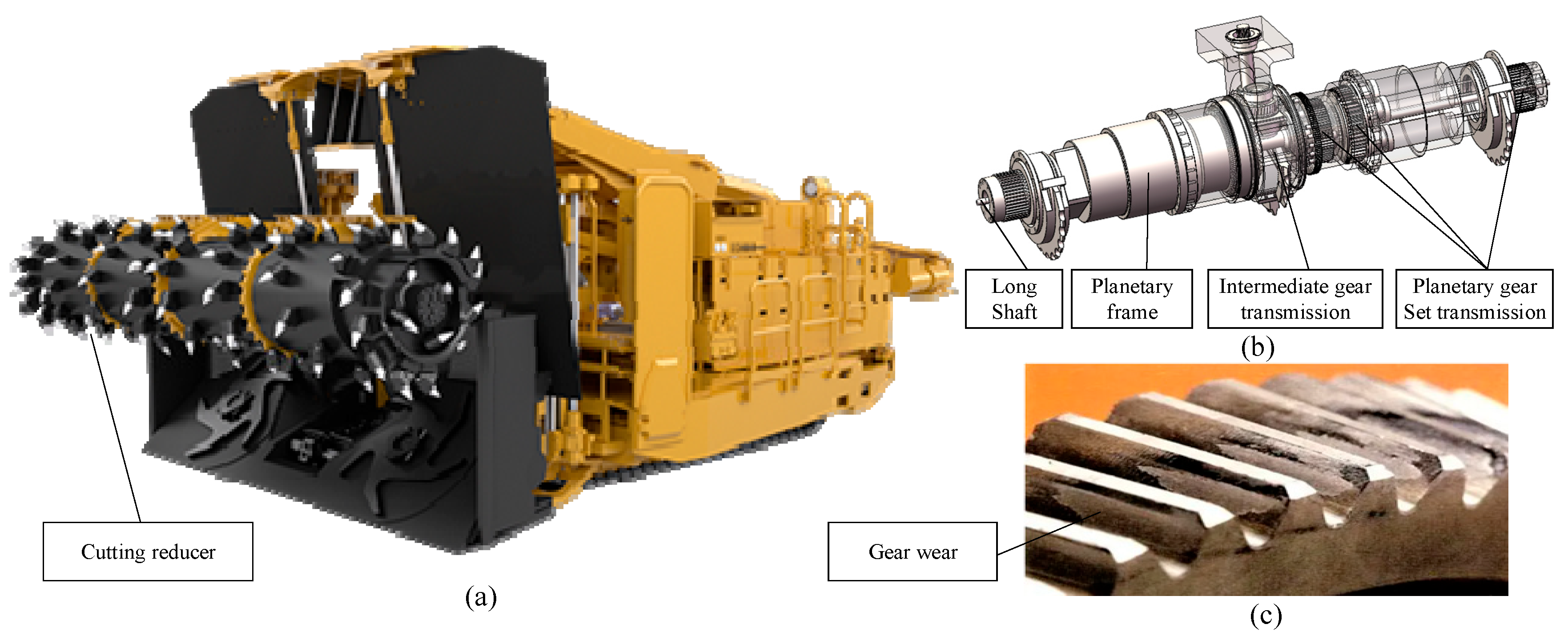
2. Experimental Analysis of Cutting Reducer

The performance of the cutting reducer is investigated via a series of tests with different operation conditions according to Chinese Standard JB/T5558-2015 [25] that is proposed for testing reducers or increasers. The structural configuration of the bolter miner and its cutting reducer, along with failure modes of planetary gears, are illustrated in Figure 1.

The working efficiency of the cutting reducer is regarded as the proportion of the input energy that is effectively used in the energy conversion during transmission. It affects the service life, economic benefits, reliability and stability of the gearbox. A performance test platform is established for the cutting reducer based on which the working efficiency and temperature field of the planetary gear set inside the cutting reducer are measured. As shown in Figure 2a, the cutting reducer is driven by the motor at the back, and the power is transmitted through the input shaft, the immediate shaft, the planetary gear set and the output shaft. The output shaft is connected to a loading motor via a coupling to imitate actual working conditions. The driving motor and loading motor are controlled by a control system via a control system, as shown in Figure 2b. Furthermore, the temperatures at different locations of the cutting reducer, including the input shaft temperature, the left end output temperature, the left middle rack temperature, the right intermediate rack temperature, the right end output temperature and the oil temperature, are measured, as shown in Figure 2c.

In terms of instruments, a TI-3 efficiency instrument is calibrated before use. The working efficiency test is carried out at a room temperature of 27 °C, and the input end is set to run clockwise with an input speed of 1478 r/min. The rated power of the test is 170 kW, and 25%, 50%, 75%, 100% and 110% of the rated power are applied individually in series. Each test is performed longer than 30 min. Furthermore, JZ2000 and JZ60000 torque speed sensors are connected to detect the efficiency of the gear under the loading condition, and DS18B20 and MLX90614 sensors are used to measure the temperature. The DS18B20 sensor can measure temperatures from −55 °C to +125 °C with an accuracy of ±0.5 °C from −10 °C to +85 °C. It has a programmable resolution from 9 Bits to 12 Bits. The MLX90614 is an Infra-Red thermometer for non-contact temperature measurements in the range of −20…120 °C with a resolution of 0.14 °C. The oil temperature is measured at the surface closest to the bearing on the reducer outer surface. During the test, the drive and load torques are provided with the input speed or torque controlled through a control system.

2.1. Cutting Reducer Performance

The performance of the cutting reducer including the working efficiency and temperature of each component is shown in Figure 3. It can be observed that with the gradual increase in power, the working efficiency increases from 70% approximately until it reaches a stable output. Accordingly, the temperatures at different locations increase with a slightly concave trend from 40.2 °C to 95.6 °C in the power range of 42.5 kW to170 kW. The maximum temperature difference at different locations under each power case is about 8.3 °C. For power larger than 170 kW, the temperature rise is minimal. On the other hand, the oil temperature remains from 30 to 50 °C, which is within a normal working temperature range.

2.2. Running Temperature Analysis

To explore the thermal stability and reliability of the cutting reducer under a rated condition, the temperature rise test is carried out at 33 °C room temperature, with the heavy load industrial gear oil used for oil immersion lubrication. The input end is set to run clockwise with an input speed of 1478 r/min and an input torque of 1099 N·m. The input power is 170 kW. In addition, the temperature rise for a non-loaded condition is carried out to evaluate the performance stability, the working efficiency and the heat load of the reducer. Figure 4 shows the temperature rise in each component that is defined in Figure 1. It can be found that the temperatures of the input part, middle part and the oil rise linearly and gradually with time. The increasing trend is more obvious than the temperature rise in the output part. The maximum surface temperature reaches 94 °C, and the maximum oil temperature reaches 91.5 °C. It is clear that the high load operation accelerates the temperature rise. Thus, appropriate cooling treatment is required to avoid the damage and extend the working life of the reducer gear set. Figure 4b shows that the temperature of the secondary planetary gear set at the output end gradually tends to 55.4 °C under a long-term constant speed and no load, and the maximum oil temperature is 58.6 °C, which is within the normal operating temperature of 40–60 °C. The maximum temperatures of the planetary frame and intermediate office stand are 67.8 °C and 42.7 °C, respectively, after 420 min running. It can also be observed that the thermal capacity and thermal conductivity of the secondary planetary gear set are decent, and the operation is relatively stable, effectively ensuring the stable output of the reducer. During the test, the reducer operates normally without abnormal sound or oil leakage, and the overall temperature rise is within the normal working range.

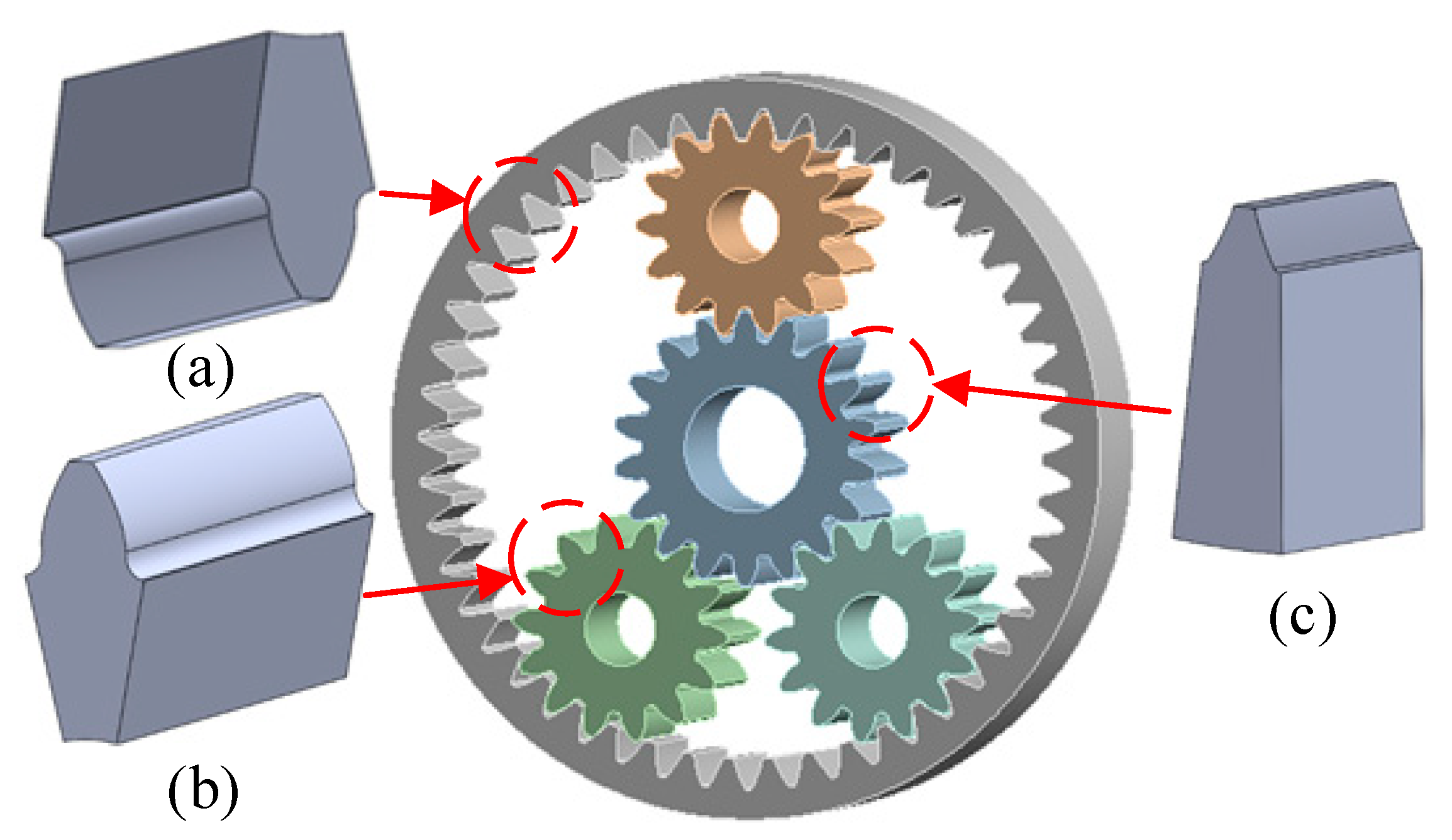
3. Thermal Behavior Analysis of Planetary Gear

The temperature field of the cutting reducer is closely associated with the thermal behavior of the planetary gears during meshing. However, the lab test fails to gain insight of the temperature, the contact stress and the thermal–structural coupling of the planetary gear set. Thus, simulations using the FEM are employed. The planetary gear set is commonly, omposed of a sun gear, a series of planetary gears and an inner ring gear. The planetary gears play a role of supporting and load-sharing during transmission, and each gear has a relatively large number of meshing teeth. Considering the calculation time and the symmetry of the planetary gear set, three planetary gears are considered to ensure that each tooth surface obtains good mesh quality and accurate load. The SolidWorks(2022) software is used to build up the gear models, based on which the planetary gear set is assembled with correct constraints and clearance, as shown in Figure 5. The basic parameters of the planetary gear set of the cutting reducer are listed in

Table 1. Basic parameters of the planetary gear set.

Nominal Power (kw)	170
Nominal torque (N·m)	42,513.36
Tooth number Z1, Z2, Z3 (-)	18, 14, 47
Displacement factor x1, x2, x3 (-)	0.28, 0.39, 0.48
Tooth addendum coefficient ha/hf (-)	1.0
Tooth width (mm)	102
Material density ρ1, ρ2, ρ3 (kg/m3)	7830, 7830, 7850
Elastic modulus (Pa)	2.06 × 1011
Center distance (mm)	182.5
Poisson’s Ratio (-)	0.3
Specific heat c1, c2, c3 (J/(kg·K))	485, 485, 460
Coefficient of linear expansion (m/°C)	1.15 × 10−5
Pressure angle (rad)	20
Thermal conductivity λ1, λ2, λ3 (W/(m·°C))	50/50/44

. The material of the sun gear and planet gear is 18CrNiMo7-6, and the material of the internal gear is 42CrMo.

3.1. Thermal Boundary Conditions

Before studying the thermal behavior of the gears, it is necessary to clarify the heat transfer mode and related solution methods. Heat transfer occurs via three distinct mechanisms, namely, conduction, convection and radiation [26]. This investigation focuses on the convective heat transfer and heat flux. The convective heat transfer of the gear mainly considers the convective heat transfer coefficient of the gear end face, meshing surface and gear tip circumferential surface, which is generally calculated by the empirical formula [27]. The planetary gear set is lubricated by heavy-duty N320 industrial gear oil. Through the laboratory test, the gear oil temperature is 92 °C when the reducer reaches heat balance. At this temperature, the density of gear oil is 853 kg/m³; the kinematic viscosity is 7.557 × 10⁻⁶ m²/s; the specific heat capacity is 2088 J/(kg·°C); and the thermal conductivity is 0.1238 W/(m·K). Convective heat transfer from the spur gear face is simplified to a rotating disk model for analysis. After calculation, the Reynolds number Re is less than 1.95 × 105. Thus, the liquid flow on the gear surface is laminar, and the formula for calculating the convection heat transfer coefficient of the gear end face is

$$h_s=0.308{\lambda }_c{(m+2)}^{0.5}{P_r}^{0.5}{(w_1/v)}^{0.5}$$

(1)

Similarly, the convective heat transfer coefficient of the gear meshing surface is given by

$$h_c=0.228{R_e}^{0.731}{P_r}^{0.333}{l}_c/d$$

(2)

There is also heat exchange between other surfaces such as the addendum surface, the root curve, the non-intermeshing surface of the gear tooth and the contact medium. These surfaces are approximately regarded as the Reynolds number of the cylindrical surface rotating around the center of rotation. The convective heat transfer coefficient can be expressed as

$$h_d={\displaystyle \frac{0.133{\mathrm{Re}}^{\frac{2}{3}}P{r}^{\frac{1}{3}}{\lambda }_f}{d}}$$

(3)

where m is an exponential constant, which indicates the temperature distribution trend of the radial direction of the end face, m = 2; Pr is the Prandtl number of lubricating oil; R_e is the Reynolds number of gear oil; λ_c is the thermal conductivity of gear oil, W/(m·K)⁻¹; w₁ is the rotation speed of the sun gear, rad/s; v is the kinematic viscosity of gear oil, m²/s. r_c is the radius of rotation of the gear surface, m; and d is the pitch circle diameter of the gear, m.

For the planetary gear set, the sliding friction of gears is the main factor affecting the gear friction heat flux. The magnitude of the friction heat flux is mainly determined by the contact stress between the tooth meshing surfaces, the relative sliding speed, the friction factor and the heat flux distribution coefficient. The calculation formula of gear meshing friction heat is

$$q=Pf{v}_c$$

(4)

During the meshing process, the frictional heat flux of the sun gear and the planetary gear surface at any meshing point C is

$$\begin{array}{l}{q}_{1c}=\beta \gamma fP{v}_c\\ q_{2c}=(1-\beta )\gamma fP{v}_c\\ \beta ={\displaystyle \frac{\sqrt{{\upsilon }_{c1}}}{\sqrt{{\upsilon }_{c1}}+\sqrt{{\upsilon }_{c2}}}}\end{array}$$

(5)

When the gear system reaches steady state thermal equilibrium, the heat flux generated by the two gears in the actual contact period on the meshing surface is equivalent to the average of one meshing period. Therefore, the average heat flux of the two gears is

$$\left\{\begin{array}{l}\overline{q_{1c}}={\displaystyle \frac{a{\omega }_1}{v_{c1}\pi }}{q}_{c1}\\ \overline{q_{2c}}={\displaystyle \frac{a{\omega }_2}{v_{c2}\pi }}{q}_{c2}\end{array}\right.$$

(6)

where q is the frictional heat flux of gear meshing, W/m²; β is the heat flux distribution coefficient; γ is the thermal energy conversion coefficient, γ = 0.9~0.95; f is the relative sliding friction coefficient of the tooth surface meshing point; P is the average contact stress of the gear meshing surface, Pa; a is the half-width of the contact area, m; ω₁ and ω₂ are the angular velocities of the driving wheel and the driven wheel, respectively, rad/s; v_c is the relative sliding speed of the gear meshing surface, m/s; and v_c1 and v_c2 are the relative sliding speeds of the driving wheel and the driven wheel, respectively, m/s.

The thermal boundary conditions of the planetary gear set are determined to ensure the accuracy and reliability of the gear thermal simulations. The thermal boundary conditions and loading area of the gear obtained by the above theoretical formula are shown in Figure 6.

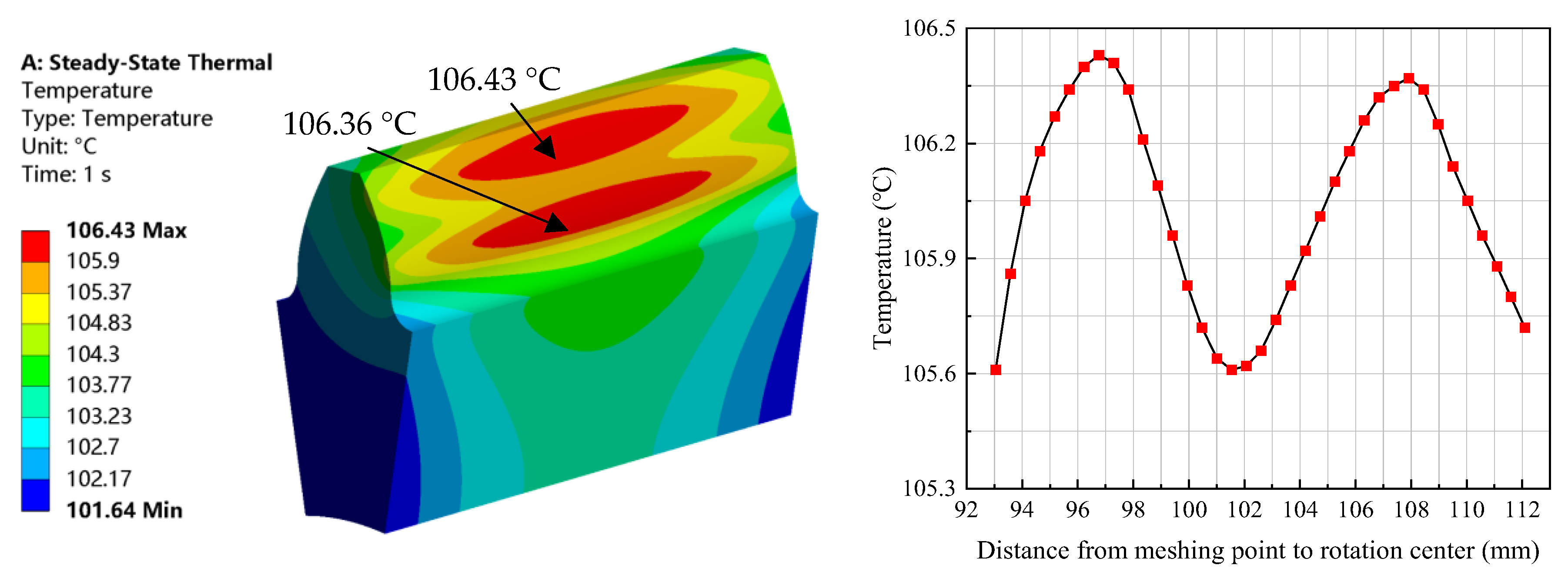
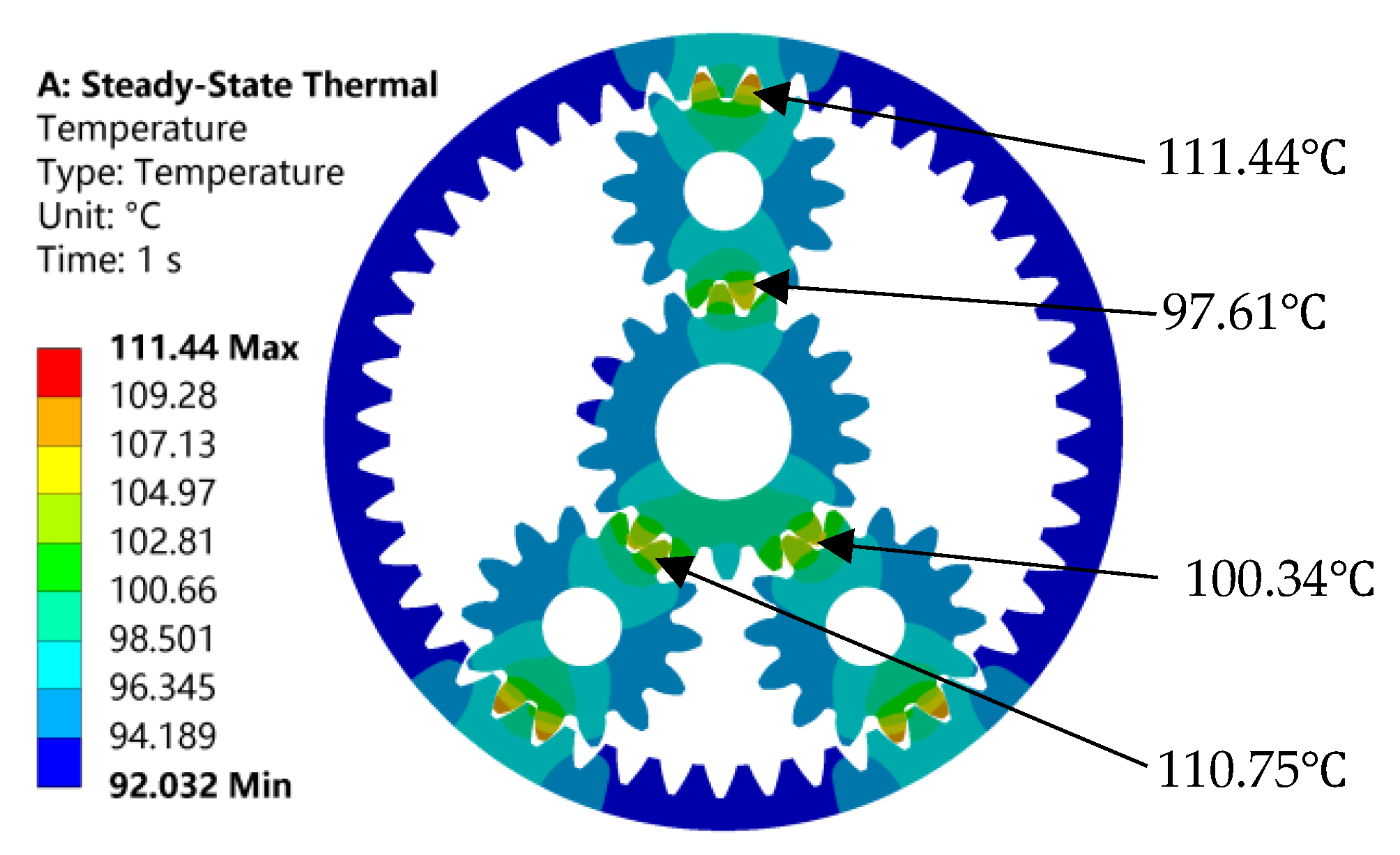
3.2. Planet Gear Temperature Field

After the boundary conditions of each gear tooth are loaded, the steady-state thermal solution is carried out. As shown in Figure 7, the temperature gradient of the planetary gear is large and nearly elliptical. The highest temperature of the tooth surface is 111.21 °C and is located at the top of the tooth meshing with the inner gear ring. The lowest temperature is 103.48 °C, located on the tooth’s end face. In the external meshing transmission, the friction heat flow increases due to the sharp increase in the tooth root meshing load, so that the meshing temperature gradually decreases from the tooth root position to the tooth top while in the internal meshing transmission. The heat generation of the tooth root/tooth top of the planetary gear is prominent, and the risk of scuffing and wear is high.

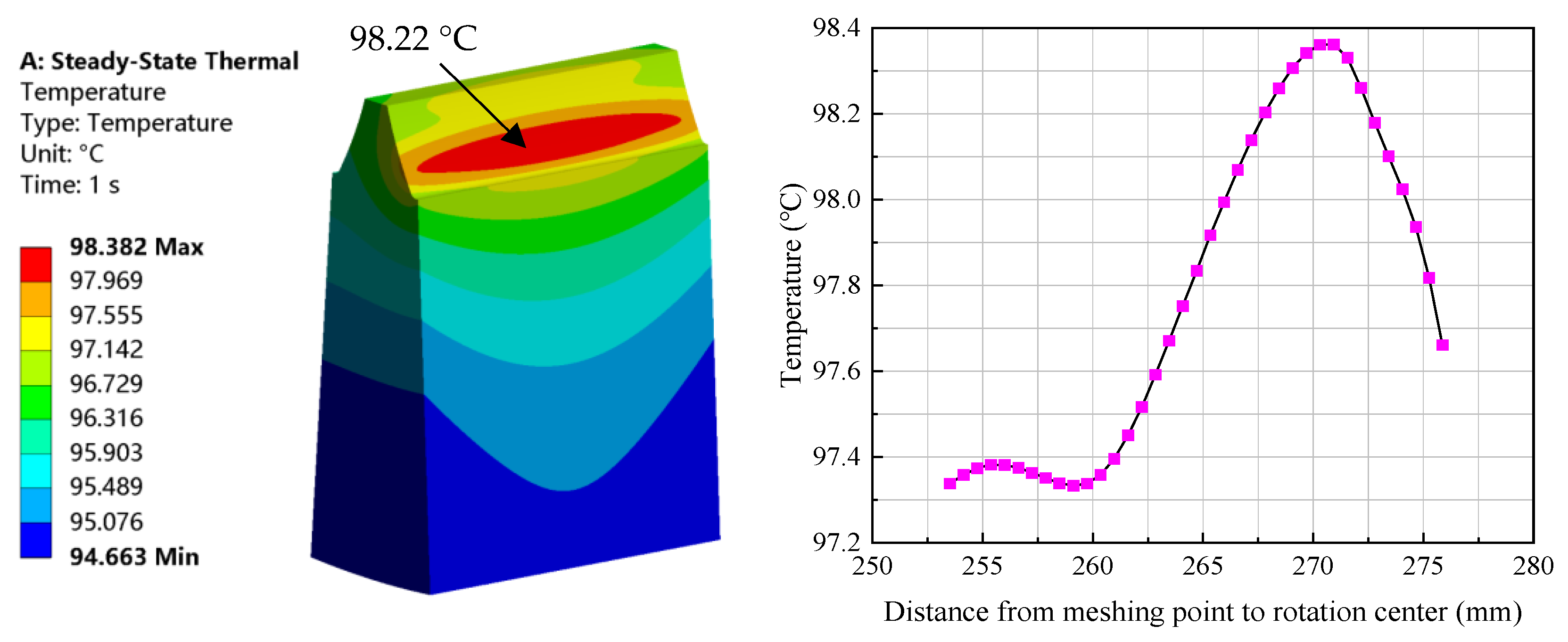
3.3. Sun Gear Temperature Field

As shown in Figure 8, the temperature field of the sun gear is distributed in an ‘8’ oval shape. The maximum contact temperature of the gear teeth reaches 106.43 °C, which is mainly located at the tip and root of the tooth. The minimum temperature is 101.64 °C, which is mainly located at both ends of the tooth. The central temperature of the sun gear tooth surface is along the tooth profile direction, and the temperature decreases from the tooth root to the pitch circle to the tooth top. The highest temperature of the gear tooth is distributed between the pitch circle and the tooth root circle, and the valley value is near the pitch circle. The tooth root/tooth top is subjected to more heat production during the meshing in/out, which easily causes scuffing and wear.

3.4. Internal Gear Temperature Field

As shown in Figure 9, the temperature distribution of the gear ring is nearly elliptical, and the tooth root position is seriously overheated. The temperature is as high as 98.36 °C, and the lowest temperature is 94.66 °C, which is located at the end face of the gear tooth. The temperature distribution along the tooth profile direction at the center of the tooth width is opposite to that of the planetary gear, and the overall temperature distribution is almost a linear gradient distribution. The load and lubrication at the tooth root of the gear tooth are poor.

4. Thermal–Structural Coupling of Planetary Gear Set

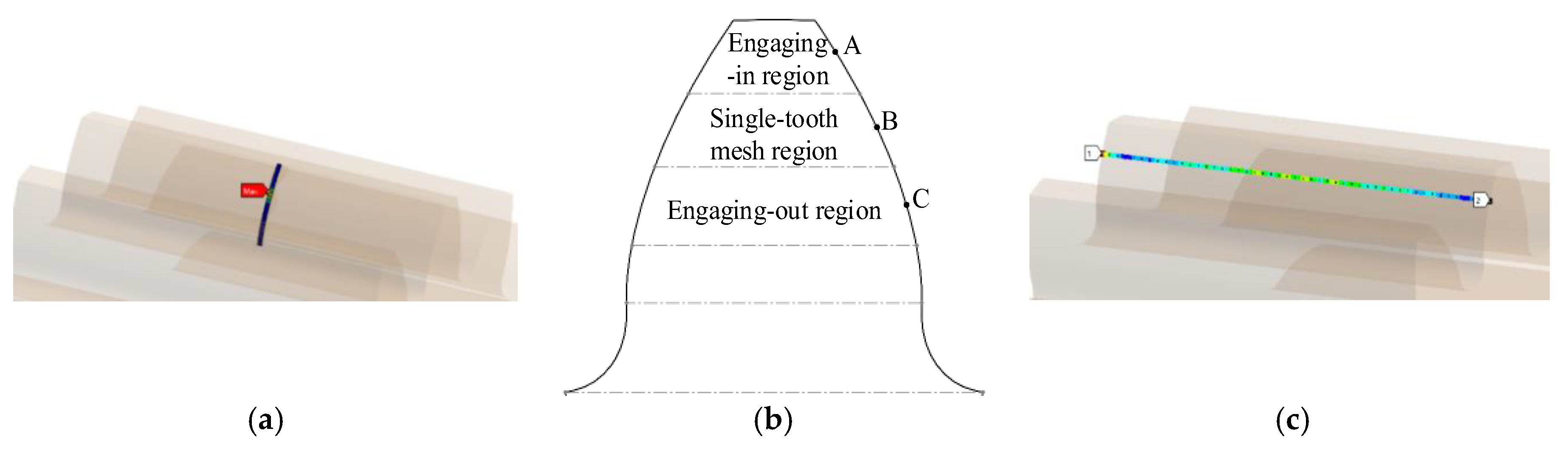
4.1. Meshing and Contact Constraints

Considering the structural complexity and meshing accuracy requirements of the gear set, the Sweep method to mesh the gear set as a whole is used, with a size of 5 mm. The Element Sizing method is employed to refine the mesh of each gear meshing surface, with a size of 1.2 mm. The overall quality of the mesh is medium, and the total number of finite element meshes is 797,240. The number of element nodes is 3,587,034, and the mesh division is shown in Figure 10a. In the static module setting, a cylindrical support constraint is applied to the inner hole surface of the sun gear and the planetary gear to simulate the support of the bearing. The tangential direction is set to be ‘free’, and the other directions are fixed. The sun gear is used as the input of the entire gear system, and the rated working condition is applied to the inner hole surface of 42,513.355 N·m. In the static module analysis setting option, the ‘Large Deflection’ is set to ‘on’, and the ambient temperature is set to be 30 °C, as shown in Figure 10b.

4.2. Thermal Analysis

To better simulate the gear thermal working environment, the average heat flux obtained from the above solution onto a pair of gear surfaces separately is loaded after completing the grid division, and the ambient temperature is set to be 30 °C. From Figure 11, it can be visually observed that the high-temperature regions (indicated in red) are clearly concentrated at the multiple meshing interfaces. Consequently, the maximum temperature distribution of the gear set is found on the meshing surface of the inner ring gear and the planetary gear. The highest temperatures of the planetary gear and the inner ring gear are 111.44 °C and 104.48 °C, respectively, which are slightly higher than the previous single tooth temperatures of 111.21 °C and 98.363 °C, giving the differences of 0.21% and 6.22%, respectively. It shows the temperature performance and complexity of the gear set under assembly constraints. It is necessary to perform additional cooling treatment on the internal gear pair. In addition, the highest temperature of the sun gear reaches 107.19 °C, which is 0.76 °C higher than its single tooth temperature. The load distribution and assembly constraints of the gear set have a great influence on the temperature field distribution of the gear, and it is necessary to optimize the system lubrication, design and manufacturing, and assembly constraints.

4.3. Contact Stress and Strain Analysis

To better explore the thermal contact performance of the output gear system under rated working conditions, static structure and thermal–structure coupling analysis are carried out. The thermal deformation of the prominent parts is accurately located to predict and prevent the loss of thermal deformation, based on which reference basis and direction for the modification optimization and manufacturing assembly of the gear set are provided.

Under the rated working condition, the maximum stress and strain of the gear set are concentrated on the meshing working surface of the sun gear and the planetary gear, and the gear ring generates an ‘annular stress concentration zone’ due to the assembly constraints, as shown in Figure 12. The maximum stress and strain of the static structure are 1026.9 MPa and 0.0050925 mm, while the maximum stress and strain under thermal load are 1144.7 MPa and 0.0070479 mm, showing nearly 11.5% and 38.4% higher than those of the static structure, respectively. The gear set is significantly affected by the assembly constraints and thermal effects. As its contact transmission stability is reduced, there is a risk of fatigue damage in its service life. The simulation results reasonably reflect the complexity and uncertainty of the thermal–structural coupling of the gear set under thermal load and assembly constraints.

4.4. Comparative Analysis Between Static and Coupling

An external meshing gear pair in the maximum stress–strain zone of the gear set is selected for comparison analysis. Especially, the key meshing contact characteristics of the planetary gear in the high-temperature zone is investigated. The node processing method is used to process the meshing tooth surface and tooth width center of the planetary gear to obtain the node coordinates and stress values. The contact stress curves at different meshing points and the strain values at key points (A, B, C) are drawn for comparative analysis, as shown in Figure 13 and Figure 14.

As shown in Figure 14, the static and coupled contact stress distribution of the gear is roughly identical, and the maximum contact stress is obtained in the single-tooth meshing area. The maximum stress of the static and thermal coupling contact is 982.49 MPa and 1101.29 MPa, respectively, which are close to the maximum stress calculated by the Hertz theory (1107.47 MPa). The stress distribution of the thermal coupling single-tooth meshing area is higher than that of the Hertz theory, and the thermal stress expansion reaches 12.1%. In addition, the maximum thermal deformation of the gear increases by 0.85 μm, with an increase of nearly 17.1%. The middle area of the tooth width is a significant mutation compared with its two ends, and the risk of tooth surface wear and fatigue failure is high.

5. Actual Performance Analysis of Planetary Gear Set

The KISSsoft is a professional gear transmission design and analysis software, which is able to analyze the contact and meshing performance of gear teeth and provide the optimization schemes for gear parameters under different working conditions. Thus, the temperature rise and the contact characteristics of the planetary gear set are simulated via the KISSsoft. The workflow is illustrated in Figure 15.

The gear parameters and lubrication data obtained by the planetary gear lab test are imported into the KISSsoft software package. The methods proposed by Standard ISO/TS 6336-20/21 [28], ISO6336: 2019 [29] and the Bertsche calculation are used for analysis. The load spectrum is designed according to the actual loading condition of the planetary gear set. The power and frequency are listed in

Table 2. Load spectrum of planetary gear set.

Number	Power (kw)	Frequency
1	85	15%
2	170	30%
3	255	35%
4	340	15%
5	374	5%

.

5.1. Strength Check and Life Analysis

According to the requirements of Standard ISO/TR 13989-2:2000 [30], the safety standard of the gear contact ratio is [ε] = 1.2~1.4. The root safety factor is greater than or equal to 1.5, whereas the tooth surface safety factor is greater than or equal to 1. Also, the gluing safety factor standard is greater than or equal to 1.5, and the minimum bending and contact safety factor standards are SFmin ≥ 1.3, SHmin ≥ 1, respectively.

As shown in

Table 3. Strength check of gear set.

Input Items (Calculation with Load Spectrum)	Factor
Contact ratios (Sun—Planets) εαm, εβ, εγm	1.221, 0.000, 1.227
Contact ratios (Planets—Internal gear) εαm, εβ, εγm	1.466, 0.000, 1.466
Actual tip circle (mm) of Sun, Planets, Internal gear	224.449, 182.936, 506.661
Root safety of Sun, Planets, Internal gear	1.982, 1.579, 1.911
Flank safety of Sun, Planets, Internal gear	0.905, 1.001, 1.190
Safety against scuffing (integral temperature) of Sun, Planets, Internal gear	1.616, 1.616, 3.229
Safety against scuffing (flash temperature) of Sun, Planets, Internal gear	1.634, 1.634, 6.261
Required safety for tooth root—SFmin	1.400
Required safety for tooth flank—SHmin	1.000
Required service life (h)	10,000.000
Service life—Hatt (h)	8783.500

, through the calculation of load spectrum, the meshing contact ratio of the outer and inner gear pairs is 1.227 and 1.466, respectively, which are within the standard range. The safety factor of the tooth root of the three gears meets the requirements of the gear meshing transmission standard. However, the safety factor of the tooth root of the planetary gear is the lowest, which proves that the tooth root is under a breaking risk. The safety factors of the sun gear, planet gear and internal gear are 0.905, 1.001 and 1.190, respectively. The sun gear is slightly lower than the standard, and the risk of gluing and wear is high. It is necessary to carry out tooth profile modification. The temperature gluing safety factor of the gear set is much larger than the standard temperature factor of 1.5. Meanwhile, the service life of the gear system does not meet the predetermined requirements. Thus, the material upgrade and tooth modification, lubrication optimization and other treatments should be considered to improve the service life.

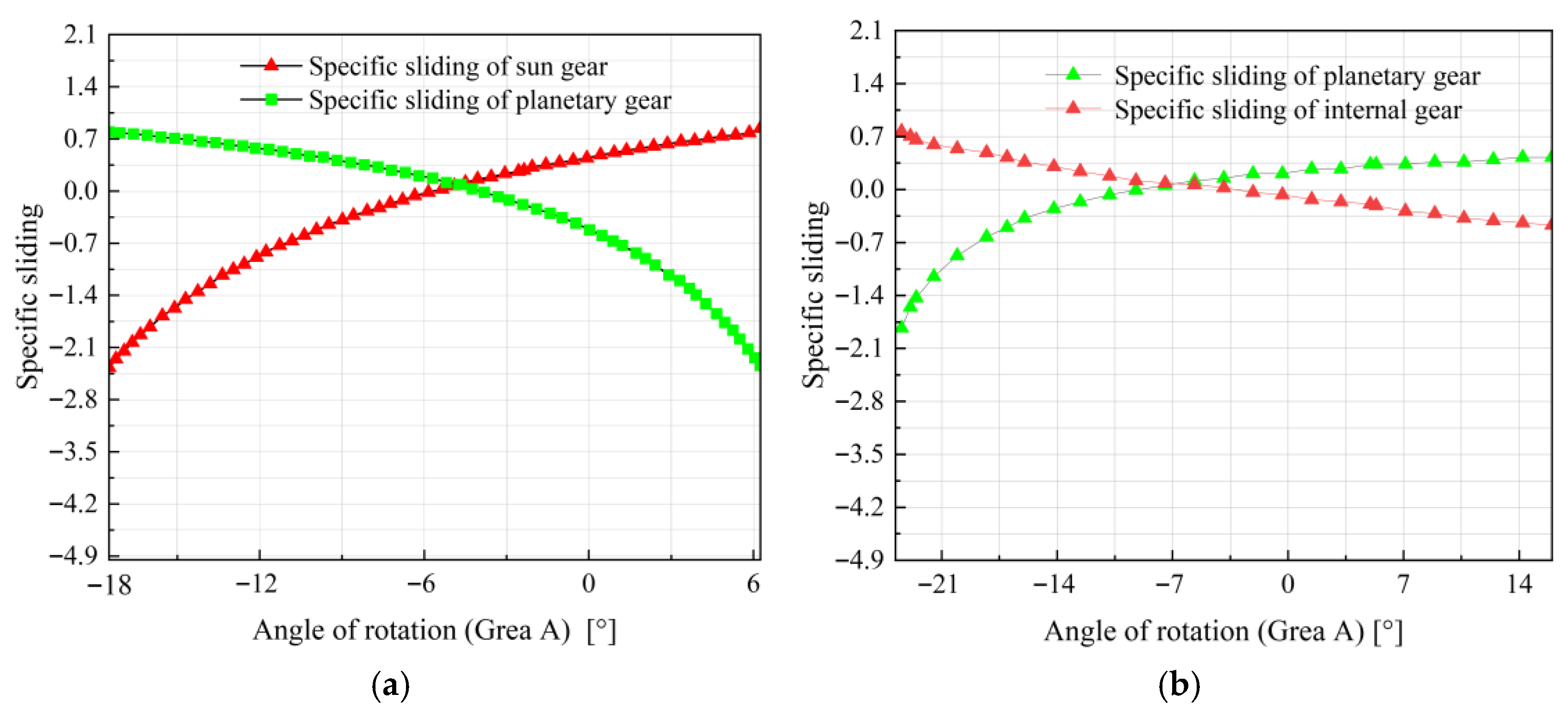
5.2. Slip Rate Analysis

Slip rate affects the unsteady effect of gear elastohydrodynamic lubrication, which is an important criterion for evaluating the wear degree and scuffing of gear transmission [31]. The sliding ratio standard shows perfect meshing in (−1, 1), good meshing in (−3, 3) and very poor meshing in (−∞, −3) and (3, ∞). Figure 16 shows that under the load spectrum, the sliding rate intervals of the driving wheels of the external and internal meshing gears are (−2.371, 0.841) and (−0.866, 0.468), respectively, which meet the working requirements. However, the specific sliding difference in the planetary gear is more obvious than that of the other two gears. Thus, the temperature rise and wear risk of the planetary gear may be much greater than the other gears.

5.3. Transmission Error

To evaluate the dynamic performance of the planetary gear system, the transmission error of the gear system under actual working conditions is analyzed according to the load spectrum calculation. The transmission error stands for the deformation of the sun gear in the direction of the gear meshing line. From Figure 17, it can be found that the transmission error of the planetary gear system fluctuates periodically from −155.982 μm to −146.294 μm from the meshing in to the meshing out. The fluctuation of the absolute peak is more frequent, even in some meshing points. The mutation indicates that some vibration or noise is generated during the transmission process. It is necessary to adjust the frequency to avoid vibration and design a reasonable meshing angle to improve the stability of the system.

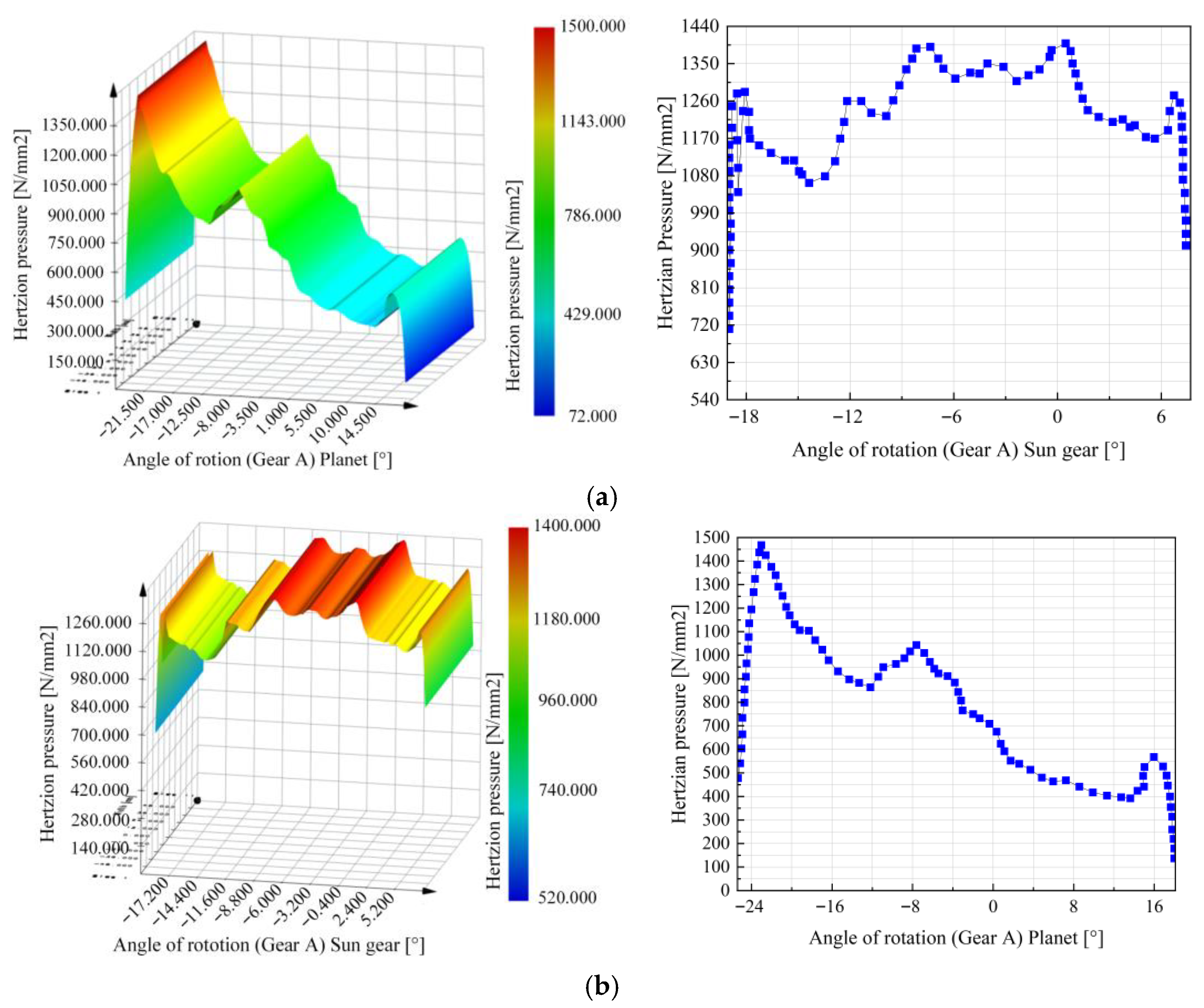
5.4. Stress Analysis

Gear stress is an important index to measure the performance of gear transmissions. Excessive gear stress causes tooth fracture, tooth surface pitting, etc., which further affects the fatigue life of the entire gear set. The stress of the planetary gear set is considered by the influence factors such as the use coefficient, installation factor, dynamic factor, end face load factor and actual load spectrum in practical engineering applications based on the KISSsoft.

From Figure 18, the maximum stress values generated by the external meshing and internal meshing are 1367.554 MPa and 1464.047 MPa, respectively. The contact stress fluctuates frequently with step changes. Due to the influence of the transmission error, uneven output and excessive meshing transmission angle, the load of the external meshing gear pair is relatively concentrated in the middle of the meshing, whereas the internal meshing gear pair is almost linearly reduced from the tooth root meshing to the tooth tip meshing. With the risk of local wear, overheating and sliding, it is necessary to modify the gears, optimize the lubrication and operate the gear set under reasonable load.

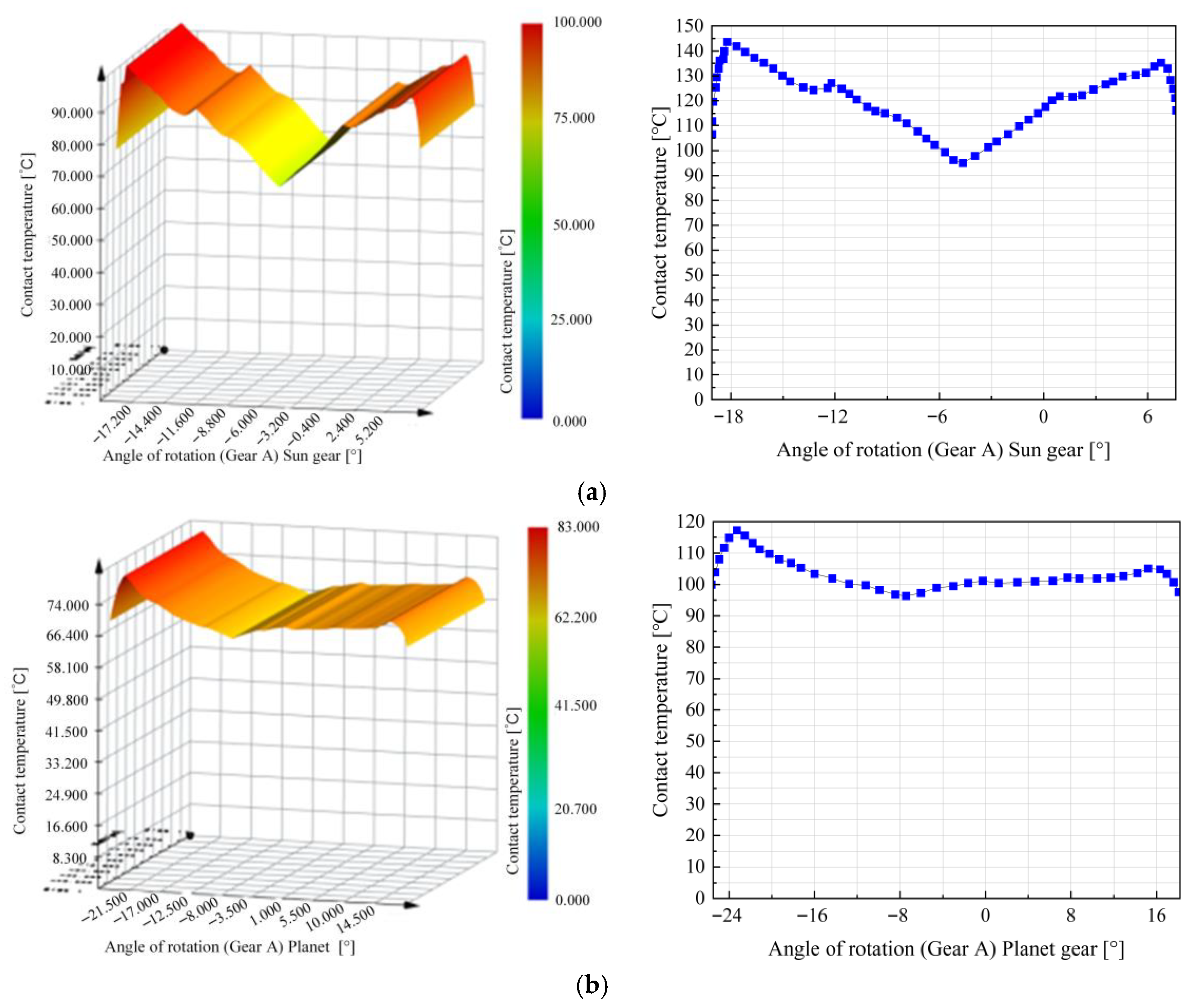
5.5. Contact Temperature

In the process of gear transmission, the friction between the gear teeth produces more friction heat, which increases the surface temperature of the contact tooth surface. Especially in the case of heavy load, the gear teeth are more likely to produce tooth surface wear, pitting, gluing, and affect the gear transmission efficiency. Figure 19 shows the external and internal gear pairs obtain high temperature in the area with large meshing angle (addendum/dedendum), and the contact temperature is as high as 144.8 °C and 117.9 °C, respectively. These values are within the safe range of scuffing, and are in good agreement with the risk warning of temperature field simulations. This verifies the model is capable of capturing the key thermal load area. Additionally, the maximum distribution of contact temperature is biased towards one end of the gear tooth rather than evenly distributed on the tooth surface.

6. Conclusions

Focusing on improving the performance of a bolter miner, the temperature field, the thermal–structural coupling, the thermal stress and strain of the cutting reducer as well as its key component, that is, the planetary gear set are analyzed experimentally and numerically. The main findings are summarized as follows.

(1)

The experiment confirmed that the cutting reducer has a high transmission efficiency of 91.3%. The temperature rise is more obvious under high loading conditions where the maximum temperature can reach 94 °C. The planetary gear set is thermally stable and functions well at low speeds without load. However, the highest temperature measurement of 70.8 °C at the intermediate shaft of the planetary gear set may indicate the risk of localized overheating. It is recommended to upgrade the lubrication method from splash lubrication to targeted forced circulation, with fixed high-pressure nozzles arranged at the exit of the meshing zone to utilize high-speed oil flow for removing accumulated heat.

(2)

A FEM model for thermal analysis of the planetary gear set is developed with the thermal boundary conditions including the heat transfer coefficient and heat flux being obtained theoretically. The greatest temperature is observed to occur at the planetary gear with a magnitude of 111.21 °C, and the maximum deformation of 0.11413 mm is located at the internal gear, showing the potential of lubrication failure and excessive wear. In engineering practice, synthetic lubricating oils with a high viscosity index should be selected to maintain sufficient oil-film thickness and strength under high temperatures, thereby protecting the high-temperature meshing regions of the planetary gears and internal ring gear.

(3)

A thermal–structural coupling model of the planetary gear set is developed. It is found that the temperature of the planetary gear is the highest, followed by the sun gear and the internal gear. Moreover, the thermal load and deformation are more distinct. The thermal stress of the planetary gear set is 11.5% higher than that of the pure static simulation, and the deformation is increased by 38.4%. This quantitative result provides a direct basis for structural design. To counteract the influence of thermal deformation, pre-compensation modification techniques can be adopted to implement tip relief and crowning on the sun gear and planetary gears.

(4)

The strength calculation and dynamic contact analysis of the planetary gear set are carried out using the KISSsoft (2022) software. Through analysis, the slip rate of the external meshing gear pair is large, and the transmission error fluctuates frequently, indicating the likelihood of the gear transmission instability and wear resistance. Thus, appropriate meshing angles and modifications should be adopted. Additionally, the contact temperature of the planetary gear set is obvious with load; therefore, it is necessary to use better lubrication and gear oil for heat dissipation. Therefore, to ensure reliability under extreme operating conditions, greater thermal backlash should be reserved in the tolerance design to accommodate tooth-thickness expansion at high temperatures and prevent gear jamming and shaft-locking failures.

This study employs FEM and KISSsoft to reveal key thermodynamic characteristics, yet it still has several limitations in light of the increasing intelligence requirements of bolter miners. Current research primarily focuses on steady-state temperature fields. However, during operation, the load of bolter miners exhibits severe transient fluctuations. Steady-state models cannot capture the thermal shock effect during instantaneous load mutations. Future work should establish a transient thermal–structural coupled dynamic model to study the dynamic response of flash temperature on tooth surfaces and its impact on the metallographic structure of the material surface within milliseconds of load step changes, thereby explaining the causes of early gear failure.