Short-Term Wind Power Forecasting Based on Adaptive LSTM and BP Neural Network

Abstract

To enhance power dispatching and mitigate grid connection fluctuations, this paper proposes a wind power prediction model based on Long Short-Term Memory-Back Propagation Neural Network (LSTM-BP) optimized by an adaptive Particle Swarm Optimization algorithm (aPSO). Initially, anomalies and missing values in raw wind farm data are addressed using the quartile method and filled via cubic spline interpolation. The data is then denoised using the Autoregressive Integrated Moving Average (ARIMA) model. Statistical and combined features are extracted, and Bayesian optimization is applied for optimal feature selection. To overcome the limitations of single models, a hybrid approach is adopted where a BP neural network is used in conjunction with LSTM. The optimal features are first input into the BP neural network to learn the current relationship between features and wind power. Then, historical data of both the features and wind power are fed into the LSTM to generate preliminary predictions. These LSTM outputs are subsequently passed into the trained BP neural network, and the final wind power prediction result is obtained through network integration. This combined model leverages the temporal learning capabilities of LSTM and the fitting strengths of BP, while aPSO ensures optimal parameter tuning, ultimately enhancing prediction accuracy and robustness in wind power forecasting. The experimental results show that the proposed model achieves a MAE of 0.54 MW and a MAPE of 10.5% in one-step prediction, reducing the error by over 35% compared to benchmark models such as ARIMA-LSTM and LSTM-BP. Multi-step prediction validation on 2000 sets of real wind farm data demonstrates the robustness and generalization capabilities of the proposed model.

1. Introduction

1.1. Background Knowledge

As the most mature renewable energy with huge potential for scale, wind energy accounts for a rising proportion of the global power mix. In the face of the growing energy demand and the depletion of fossil energy reserves, coupled with the international situation highlighting energy security, governments around the world are actively supporting the development of clean energy, including wind energy. Thanks to resource endowment and technological maturity, wind power has received widespread support, and 2023 was a record year for new installations, with 117 GW of new grid-connected wind capacity globally [1].

However, the inherent variability in wind speed and direction causes instability in the power generation frequency and voltage of wind systems, leading to the intermittent operation of turbines. This results in highly stochastic output from wind farms [2]. Consequently, the reliability and stability of both the farms and the integrated grid are severely constrained by the unpredictable nature of wind resources, which is also critical for the stable operation of the broader power system [3].

In this context, achieving accurate forecasts for wind power generation has become the key to resolving the impasse. Accurate predictions allow grid scheduling departments to optimize the power mix and reserve capacity arrangements, effectively mitigating the influence of wind power fluctuations on grid balance and significantly enhancing grid stability and the capacity to accommodate wind power. In recent years, countries around the world have gradually realized the huge potential of wind energy, followed by the rapid construction of wind farms around the world. Additionally, centralized dispatch and control centers for wind power forecasting have already been operational with the establishment of wind farms, significantly reducing operating costs [4,5]. However, considering the differences in meteorological conditions and wind turbine factors of each wind farm, it is very important to propose a prediction method with high reliability and high accuracy that is applicable to a variety of wind farm environments.

1.2. Literature Review

Wind power prediction has always been a key problem in smart grid dispatching due to its nonlinearity, volatility and strong randomness. Especially in actual operation, the frequent changes in wind speed, limited accuracy of measurement equipment and variable environmental factors lead to a large number of abnormal points and noise data in wind power data, which further aggravates the complexity of wind power prediction. Therefore, in order to improve the accuracy and stability of prediction, domestic and foreign scholars have carried out extensive and in-depth research on wind power prediction technology and gradually formed a research system represented by statistical modeling methods, physical mechanism models, artificial intelligence methods and hybrid optimization algorithms.

To address outlier data and forecast uncertainty, Quan et al. [6] proposed a neural network-based prediction interval method for short-term load and wind power forecasting. Unlike traditional point forecasting, they modeled the distribution of forecast errors and constructed confidence intervals to capture forecast uncertainty. This method effectively improves forecast reliability, ensuring good coverage of the prediction interval encompassing the majority of true values while also avoiding interference from extreme points, enhancing the model’s robustness and practicality. Liu et al. [7] proposed a series of short-term wind speed forecasting methods based on wavelet decomposition and hybrid models, comparing the performance of models such as Fast Ensemble Empirical Mode Decomposition-Multi-Layer Perceptron (FEEMD-MLP) and Fast Ensemble Empirical Mode Decomposition-adaptive neuro fuzzy inference system (FEEMD-ANFIS). Genetic algorithms (GA) were also used to optimize parameters to enhance model performance. Wavelet decomposition can separate wind speed fluctuations of varying scales. Combined with intelligent algorithms, the model can better handle outliers and noise, significantly reducing forecast error. The results indicate that, compared to traditional methods, the new hybrid model significantly improves stability and accuracy

For the wind power prediction type, the methods mainly include physical modeling and statistical modeling. The former relies on information such as wind speed field simulation, terrain parameters, and wind turbine structural characteristics. Although it has theoretical rigor and physical interpretation capabilities, it relies on a large amount of meteorological and environmental data, which is difficult and costly to obtain, making it unsuitable for real-time scheduling. In contrast, statistical modeling is based on historical data-driven modeling and has the advantages of high modeling efficiency and low cost. In particular, direct modeling methods such as Markov chain Monte Carlo [8] and Auto-Regressive Moving Average (ARMA) [9] do not rely on external meteorological data, but they have high data requirements and tend to ignore external environmental variables, limiting their application in newly built wind farms or when data is missing.

In artificial intelligence prediction technology, Back Propagation (BP) Neural Networks and support vector machines (SVM) [10] are the earliest representative models introduced into the field of wind power prediction. Traditional BP have the advantages of strong nonlinear mapping capabilities and simple structure, but they generally have defects such as falling into local extreme values and slow convergence. To this end, researchers have tried to introduce intelligent optimization strategies such as GA and Particle Swarm Optimization algorithms (PSO) to initialize and adjust their weight parameters, significantly improving their global optimal search capabilities and model generalization performance. For example, Zheng [11] integrated GA, PSO and ANFIS models, ran two algorithms separately in each round of iteration, and determined the current global solution by comparing their respective optimal solutions. The experiments on multiple seasonal datasets were significantly better than traditional neural networks, and the error reduction rate was between 3.75% and 9.73%.

In most recent years, least squares support vector machines (LS-SVM) [12] have attracted attention in wind power prediction. Compared with traditional SVM, LS-SVM replaces convex quadratic programming with a system of linear equations, simplifies the solution process, and improves the computational efficiency of the model under large datasets.

Deep learning technology has also demonstrated strong modeling capabilities in processing complex time series information in recent years. LSTM has become the core technology in wind power time series modeling due to its advantage in handling long-term dependency problems [13,14,15]. Compared with traditional neural networks, LSTM effectively avoids the gradient vanishing and explosion problems through the gating mechanism and can more comprehensively extract deep features in time series. At the same time, convolutional neural network (CNN) has gradually been introduced into wind power prediction tasks due to its successful application in image and local feature extraction [16] and is particularly suitable for extracting spatiotemporal correlation structures in multidimensional meteorological data. Chen et al. [17] proposed a hybrid prediction model that optimizes the BP neural network, combining Long Short-Term Memory (LSTM) with an improved sparrow search algorithm. This model significantly improves prediction accuracy and stability by using SSA denoising, CEEMDAN decomposition, and fuzzy entropy to assess component complexity and employs Spearman correlation for component reorganization. However, this model primarily targets wind speed prediction and does not consider the nonlinear conversion relationship between wind power and wind speed.

In addition, in terms of network structure design and hyperparameters tuning, scholars have also proposed a variety of optimization strategies in recent years. The joint reasoning LSTM network designed by Alahi et al. [18] has shown better results than traditional LSTM in multiple prediction scenarios; An Attention Enhanced Graph Convolutional-LSTM (AGC-LSTM) network proposed by Si et al. [19] has improved the ability to extract spatiotemporal features by introducing graph convolution and attention mechanisms. In terms of parameter optimization, the introduction of intelligent optimization methods such as Ant Clony Optimization-BP (ACO-BP) [20] and Gravitational Search Algorithm-BP (GSA-BP) [21] has improved the performance of the model on learning efficiency and robustness of prediction.

In order to overcome the problems of insufficient feature extraction capability, high computational complexity, and insufficient utilization of multi-dimensional feature fusion in existing models, this paper proposes a LSTM-BP combined prediction model optimized by an adaptive Particle Swarm Optimization (aPSO). Based on data cleaning and feature construction, the model uses the interquartile method (IQR) to remove abnormal data, uses the Autoregressive Integrated Moving Average (ARIMA) to preprocess data noise to remove noise, and then extracts statistical features such as standard deviation, maximum value, and mean to construct a representative combination feature set. In order to avoid the training burden caused by redundant dimensions, Bayesian optimization is further used for dimensionality reduction screening. In the design of the prediction structure, BP is used to model nonlinear relationships, and LSTM is used to capture the laws of time series. The outputs of the two are fused, and finally the aPSO is used to globally optimize the network hyperparameters to avoid falling into the local optimum, thereby improving the prediction accuracy of the model.

1.3. Main Contribution and Chapter Arrangement

In conclusion, a novel hybrid framework incorporating IQR, ARIMA, Bayesian optimization, aPSO, and LSTM-BP techniques is proposed to advance the accuracy and applicability of wind power forecasting. The principal contributions stemming from this research are detailed in

Table 1. Main contributions of this study.

Research Area	Limitations of Existing Methods	Improvements and Contributions
Data preprocessing	Simple interpolation or deletion	Quartile method to identify outliers + cubic spline interpolation filling + ARIMA noise removal
Feature Engineering	Statistical feature	Statistical features + combined features + Bayesian optimization feature selection
Model Architecture	Simple concatenation	LSTM-BP hybrid + aPSO parameter optimization
Optimization methods	Traditional PSO	Adaptive PSO + dynamic subgroup division + anti-local optimal mechanism
Validation Framework	Single-step prediction verification	Multi-step prediction verification

.

The remainder of this paper is organized as follows: Section 2 details the methodologies for data preprocessing and feature engineering; Section 3 provides a systematic explanation of the core algorithms, including LSTM, BP, and aPSO, along with their integration framework; Section 4 covers the experimental setup, results analysis, and comparative validation; and Section 5 concludes this paper with a summary and prospects for future research directions.

2. Methodology

The models and analyses in this study were implemented in Python 3.8.12 (Python Software Foundation, Wilmington, DE, USA). The LSTM and BP neural networks were constructed using the TensorFlow framework (v2.7.0; https://www.tensorflow.org/, accessed on 4 November 2024). Key data processing and feature engineering steps utilized the Scikit-learn library (v1.0.2; https://scikit-learn.org/, accessed on 4 November 2024). Effective model predictions hinge on three key stages: data preprocessing, feature extraction, and the construction of a memory-based prediction model. The workflow of the proposed hybrid model is depicted in Figure 1. This section begins by detailing the algorithms employed in the data processing phase.

2.1. Data Preprocessing

All data preprocessing steps in this study strictly adhered to the principle of forward validation to prevent information leakage. First, the division of the training and test sets was performed in strict chronological order, ensuring that all test data points occurred after the training set time points. This partitioning method prevented any test data from influencing the training process, thereby maintaining the authenticity and reliability of the model. Furthermore, the calculation of all preprocessing parameters was strictly confined to the training set. For example, the IQR ranges, ARIMA model coefficients, and feature statistics were extracted only from the training set data, preventing the influence of test set information on model parameters. Finally, the data processing followed the principle of forward filling, meaning that the test set data was processed using only parameters determined from the training set, ensuring that the model was free of future information, thus preventing information leakage and potential data bias. These measures together constitute the strict data leakage prevention protocol of this study, which aims to ensure the fairness and credibility of the model evaluation and prevent any form of future information leakage from affecting the final results.

2.1.1. Abnormal Data Processing

This article utilizes the IQR algorithm to distinguish between normal sample data and anomalous sample data. As shown in Figure 2, the IQR refers to sorting any set of wind power data by size and dividing them into four equal parts. When a specific piece of wind power data lies at the boundary of the sorted wind power dataset, it is referred to as a quartile. The spacing between the quartiles can be used to represent a data sequence or a skewed distribution. Therefore, the IQR is considered to be accurate and stable.

The first quartile, second quartile, and third quartile are the wind power data located at the boundary points. From the upper limit to the lower limit, the wind power data decreases. The IQR range represents the difference in the size of the data.

By arranging the wind power data in ascending order, the sample can be obtained by $P=\left\{P_1,P_2,P_3,\cdots P_n\right\}$. The calculation formula for the quartiles is as follows [22]:

Calculation of the median value $P_2$:

$$P_2=\left\{\begin{array}{c}{P}_{{\displaystyle \frac{n+1}{2}}},n=2k+1, \\ 0.5P_{{\displaystyle \frac{n}{2}}}+0.5P_{{\displaystyle \frac{n+2}{2}}},n=2k\end{array}\right.$$

(1)

In the formula, $P_{{\displaystyle \frac{n}{2}}}$ is the characteristic data sample of the wind power for the nth instance, k is a natural number.

If the total number of feature data n is even, the $P$ of the ascending sample is split into two datasets with the median $P_2$ as the limit ($P_2$ is independent and not included in the two datasets). Calculate the medians and $P_2^{″}$ of the split data, respectively. Therefore, according to the definition of quartiles, the first quartile can be described as $P_1=P_2^{\prime }$ and the third quartile cab be described as $P_3=P_2^{″}$. When the total number of wind power data n = 4k + 3:

$$\left\{\begin{array}{c}{P}_1=0.75P_{k+1}+0.25P_{k+2}\\ P_3=0.25P_{3k+2}+0.75P_{3k+3}\end{array}\right.$$

(2)

When the total number of wind power data n = 4k + 1:

$$\left\{\begin{array}{c}{P}_1=0.25P_k+0.75P_{k+1}\\ P_3=0.75P_{3k+1}+0.25P_{3k+2}\end{array}\right.$$

(3)

By calculating $P_1$ and $P_3$ through the aforementioned process, the IQR range can be obtained as:

$$I_{QR}=P_3-P_1$$

(4)

According to the IQR range, the limits of the abnormal data values within the sample can be determined:

$$\left[F_1,F_2\right]=\left[Q_1-1.5I_{QR},Q_3+1.5I_{QR}\right]$$

(5)

In the Equation (5), $F_1$ represents the lower limit of the sequence; $F_2$ represents the upper limit of the sequence. Any data that falls outside the range from the lower limit to the upper limit is considered abnormal data.

After removing the outlier data points, the meteorological time series and power time series exhibited gaps. To ensure the continuity and validity of the series, this paper employs the method of cubic spline interpolation to correct and fill in the missing sequences, the calculation formula is as shown by Equation (6) [23].

$$S\left(x\right)={\displaystyle \frac{{\left(x_{j+1}-x\right)}^3}{6h_j}}{M}_j+{\displaystyle \frac{{\left(x-x_j\right)}^3}{6h_j^3}}{M}_{j+1}+\left({\displaystyle \frac{x_{j+1}-x}{h_j}}\right)\left(f_j-{\displaystyle \frac{h_j^2}{6}}{M}_j\right)+\left({\displaystyle \frac{x-x_j}{h_j}}\right)\left(f_{j+1}-{\displaystyle \frac{h_j^2}{6}}{M}_{j+1}\right)$$

(6)

where $x\in \left[x_j,x_{j+1}\right]{, h}_j=x_{j+1}-x_j,M_i=S^{″}\left(x_i\right)\left(i=1,2,\cdots ,n\right)$.

The effect of removing and filling outliers in the air pressure data is shown in Figure 3.

2.1.2. Autoregressive Integrated Moving Average

Upon refining the initial dataset through outlier removal and missing data imputation, the ARIMA model is employed to improve data stability and forecast stability by modeling and transforming the processed time series. As a classical statistical approach, ARIMA is extensively used in analyzing non-stationary time series. Its core principle involves applying differencing to remove trends and seasonal components, thus stabilizing the series, followed by modeling the linear dependency structure using autoregressive (AR) and moving average (MA) terms.

Specifically, while the data processed through three iterations of spline interpolation exhibits continuity and smoothness at the data points, it may still retain certain local fluctuations and trend drifts, which could impact the efficiency of deep neural networks in recognizing temporal structures. The ARIMA model, as a linear time series modeling tool, is capable of extracting structural information from the sequence from a statistical perspective, thereby allowing the subsequent input features to align more closely with the dynamic pattern perception requirements of the following LSTM network, based on the premise of approximate stationarity. Thus, ARIMA processing not only serves as a means of noise reduction but also plays a role in dimensionality reduction and structural reorganization in the feature space, providing a more expressive foundation of input data for modeling wind power forecasting.

The ARIMA model is a statistical methodology that uses historical time series data to identify underlying patterns and forecast future values [24]. It is denoted as ARIMA (p, d, q), where its parameters are defined as follows: p signifies the order of the autoregressive component, q represents the order of the moving average component, and d is the number of differencing operations required to achieve stationarity in the time series. Its mathematical expression is depicted as Equation (7) [23]:

$$\begin{gathered} Y_t=\alpha +{\beta }_1+{\beta }_2{Y}_{t-1},\cdots ,{\beta }_p{Y}_{t-\mathrm{p\hspace{1em}\hspace{1em}\hspace{1em}}} \\ \hspace{1em}\hspace{1em}\hspace{1em}+\in t+{\varnothing }_1\in t-1+{\varnothing }_2\in t-2,\cdots {\varnothing }_q\in t-q \end{gathered}$$

(7)

where $Y_t$ is the forecasted value, $\alpha$ is the constant term, $Y_{t-1}$, $Y_{t-2},\cdots$, $Y_{t-p}$ are the lags of $Y$ up to $p$ lags, ${\in }_{t-1},{\in }_{t-2},\cdots {\in }_{t-q}$ are the lagged predicted errors up to $q$ lags and ${\beta }_1,{\beta }_2,\cdots ,{\beta }_p$ are the lag coefficients, while ${\varnothing }_1,{\varnothing }_2,\cdots {\varnothing }_q$ are error coefficients.

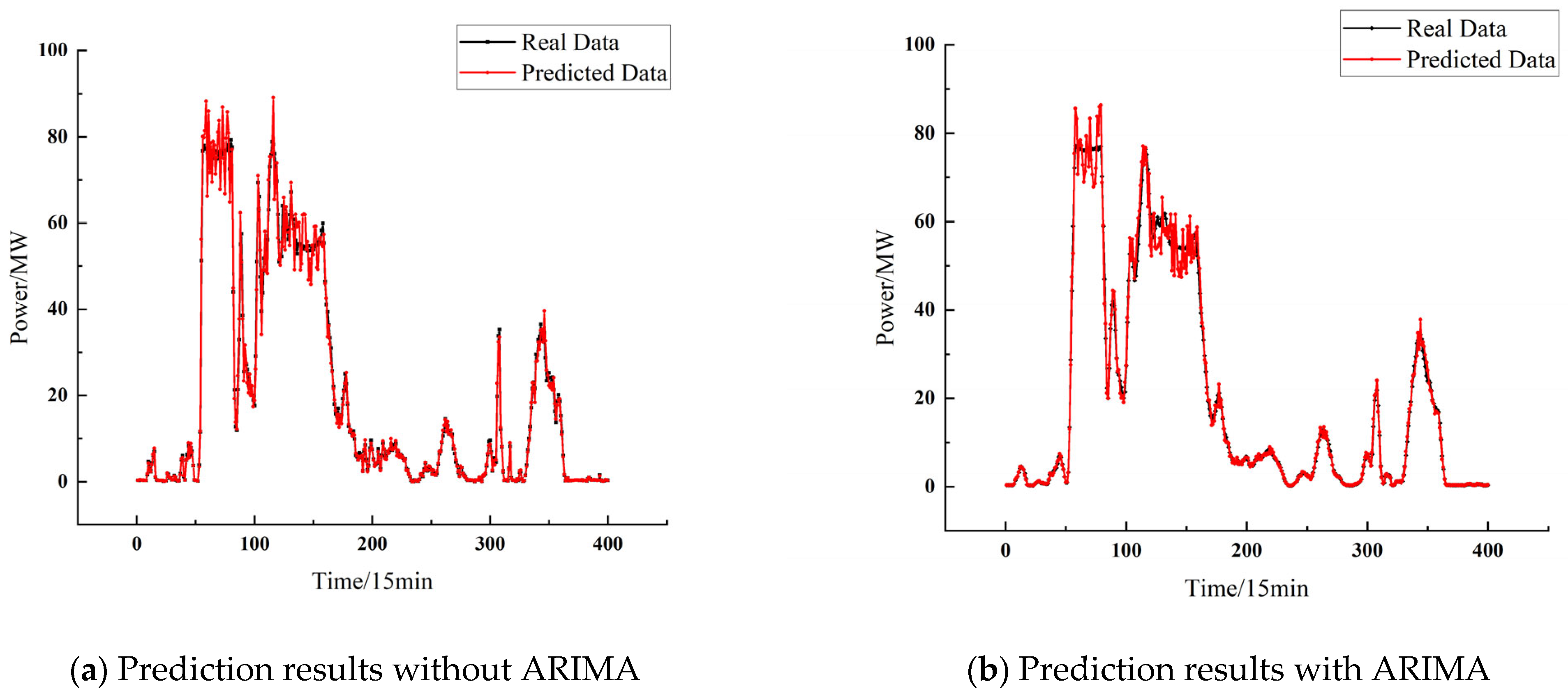
The introduction of this model during the preprocessing stage not only effectively reduces the potential random fluctuations in the data that could interfere with subsequent model training, but also enhances the stability and generalization capability of the neural network when learning temporal dependencies. The power prediction comparison chart before and after ARIMA noise reduction processing of the data is shown in Figure 4 below.

This study employed the ARIMA model as a key data preprocessing step to improve the stationarity and predictability of wind power series. Through systematic model identification and parameter estimation, the optimal ARIMA (2,1,0) model structure was determined [25]. Stationarity was tested by the Augmented Dickey–Fuller method (ADF). The ADF statistic of the original series was −2.34 (p = 0.16), indicating nonstationary characteristics. After first-order differencing, the series reached stationarity, with the ADF statistic improving to −6.78 (p = 0.0001). Based on this, the differencing order d = 1 was determined.

The selection of model order was guided by the analysis of the Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF). The original series’ ACF displayed a slow decay, while its PACF showed a significant cut-off after the second lag, suggesting an appropriate autoregressive order of p = 2. The ARIMA (2,1,0) configuration was further validated through model comparison using the Akaike Information Criterion (AIC), achieving a superior AIC value of 1245.2.

The application of ARIMA preprocessing substantially optimized the wind power series, reducing its standard deviation from 6.61 MW to 1.24 MW—an 81.2% decrease that effectively suppressed random fluctuations. This noise reduction is also evidenced by the Ljung–Box test, where the Q statistic dropped from 245.6 (p < 0.001) to 18.3 (p = 0.108), indicating the effective elimination of autocorrelation [26]. The resulting restructured series provides a more regularized input feature space for the subsequent LSTM-BP model.

To quantitatively evaluate the actual contribution of ARIMA preprocessing to forecasting performance, a rigorous ablation experiment was designed, and the results are shown in

Table 2. ARIMA ablation experiments.

	MAE (MW)	RMSE (MW)	MAPE (%)	MSE (MW2)
Proposed Model	0.54	0.90	10.5	0.81
None-ARIMA	0.72	1.25	13.8	1.56
Improvement	−25%	−28%	−23.9%	−48.1%

. The full model (including ARIMA) and the ablation model (excluding ARIMA) were compared and validated under the same experimental conditions. The experimental results show that ARIMA preprocessing reduces the model’s mean absolute error (MAE) from 0.72 MW to 0.54 MW in one-step forecasts, a relative improvement of 25.0%, and the root mean square error (RMSE) from 1.25 MW to 0.90 MW, a relative improvement of 28.0%. In multi-step forecasting scenarios, the complete model demonstrates superior error control capabilities.

2.2. Features Construction and Extraction

The characteristics are the dominant factors determining the accuracy of the predictive model. Therefore, it is essential to conduct an in-depth exploration of the meteorological features that are highly correlated with wind power generation, in order to construct more effective features. The relevant meteorological features are represented as ${Y=\left[Y_1,Y_2,\cdots ,Y_n\right]}^T$, where $Y_i=\left[y_{i1},y_{i2},\cdots ,y_{im}\right]$ (i = 1, 2, ⋯, n) represents the feature at the i-th moment, $y_{ik}$ (k = 1, 2, ⋯, M) denotes the k-th feature among $Y$, n is the sample size, and M is the number of meteorological features. The feature construction is as follows:

The predictive accuracy of a model is largely determined by the quality of its input features. A thorough investigation into the meteorological factors strongly correlated with wind power output is therefore crucial for constructing more powerful predictive features. These relevant meteorological features are represented by a matrix ${Y=\left[Y_1,Y_2,\cdots ,Y_n\right]}^T$, where each $Y_i=\left[y_{i1},y_{i2},\cdots ,y_{im}\right](\mathrm{f}\mathrm{o}\mathrm{r} i =1, 2, \cdots ,n)$, corresponds to the feature vector at the i-th time step. Here, $y_{ik}$ (with k = 1, 2, …, M) denotes the k-th meteorological variable within $Y_i$, n is the total sample size, and M is the number of features. The feature construction process is described as follows:

• Original features, Y = [Y₁, Y₂,⋯, Y_n]^T
• Temporal characteristics. That is, the time corresponding to the feature, the year, month, day, day of the week, as well as the hour, minute and other characteristics.
• Combined features. The constructed combination features comprise both linear and nonlinear types, designed to elucidate the respective linear and nonlinear interdependencies among the input variables. The corresponding computational formulas are detailed in Equation (8).

$$\left\{\begin{array}{c}{f}_{ia}=y_{ij}+y_{ik}\\ f_{is}=y_{ij}-y_{ik}\\ f_{im}=y_{ij}{y}_{ik}\\ f_{id}={\displaystyle \frac{y_{ij}}{y_{ik}}}\end{array}\right.$$

(8)

In the equation: j, k = 1, 2, …, M; $f_{ia}, f_{is}, f_{im}, f_{id}$ represent the additive, subtractive, multiplicative, and divisive characteristics of the sample at the i-th moment.

4.

Statistical Characteristics. The data fluctuation within the time window can be represented as follows:

$$\left\{\begin{array}{c}{\overline{y}}_{ik{t}_w}={\displaystyle \frac{1}{2t_w+1}}{\sum }_{v=-t_w}^{t_w}{y}_{\left(i+v\right)k}\\ S_{ik{t}_w}={\left[{\displaystyle \frac{1}{2t_{w+1}}}{\sum }_{v=-t_w}^{t_w}{\left(y_{\left(i+v\right)k}-{\overline{y}}_{ik{t}_w}\right)}^2\right]}^{{\displaystyle \frac{1}{2}}}\\ y_{max k{t}_w}=max\left\{y_{\left(v-t_w\right)k},y_{\left(v-t_w+1\right)k},\cdots ,y_{\left(v+t_w\right)k}\right\}\end{array}\right.$$

(9)

In Equation (9), the terms ${\overline{y}}_{ik{t}_w},$ $S_{ik{t}_w}$ and $y_{max k{t}_w}$ on the left-hand side represent the average, standard deviation, and maximum value of the k-th feature within the time window $\left[i-t_w,i+t_w\right]$, respectively. The parameter $t_w$ defines the size of this window.

According to the correlation analysis shown in Figure 5, it can be inferred that in the original features, wind speed at various heights will be a critical factor in predicting actual power generation.

Bayesian optimization is commonly used in machine learning to select optimal parameters. To reduce model computational complexity and find the optimal feature combination, this paper applies Bayesian optimization to the number of features (num1) used to extract statistical features and the number of features (num2) used for feature combination. This is used to constrain feature dimensions and optimize model parameters, constructing a sample parameter combination $\left[p_1,p_2,\cdots ,p_q\right]$, where $p_s (s=1,2,\cdots ,q)$ is the s-th feature combination and q is the number of feature combinations. The steps for Bayesian optimization parameter tuning are as follows.

• Gaussian process estimation. The Gaussian process estimation begins by selecting a set of r feature combinations [p₁, p₂,⋯,p_r] from the constructed pool and evaluating their corresponding loss functions [L(p₁), L(p₂,⋯,L(p_r)], where L(p_s) (for s = 1, 2,⋯,r) denotes the loss associated with the s-th combination. The sample set D_r, is then formed by pairing these parameters with their losses, as defined in Equation (10).

$$D_r=\left\{\left(p_s,L\left(p_s\right)\right),s=1,2,\cdots r\right\}$$

(10)

The estimated loss function follows a Gaussian distribution. The joint distribution of the loss values $\left[{L(p}_1),L(p_2),\cdots ,L(p_r)\right]$ is given by Equation (11):

$$\left\{\begin{array}{c}\left[L\left(p_1\right),L\left(p_2\right),\cdots ,L\left(p_r\right)\right]~N(0,K)\\ K=\left[\begin{array}{ccc}k(p_1,p_1)& \cdots & k(p_1,p_r)\\ ⋮& \ddots & ⋮\\ k(p_r,p_1)& \cdots & k(p_r,p_r)\end{array}\right]\end{array}\right.$$

(11)

where k (·,·) is the kernel function and represents the covariance.

2.

Selecting sampling points. The Expected Improvement (EI) function is introduced as an acquisition function to identify new sampling points by comparing the expected loss of a candidate point against the current best. This study employs the Tree-structured Parzen Estimator (TPE) to construct the EI function. Let p⁺ represent the current optimal parameter set, and y^* be a threshold value greater than the corresponding loss L(p⁺). The mathematical expectation for this process is given by Equation (12).

$$\left\{\begin{array}{c}E(p_s)={\int }_{-\infty }^{y^{*}}(y^{*}-y)P\left(y\right|p_s)dy={\displaystyle \frac{\gamma y^{*}\mathcal{l}(p_s)-\mathcal{l}(p_s){\int }_{-\infty }^{y^{*}}P\left(p_s\right)dy}{\gamma \mathcal{l}\left(p_s\right)+(1-\gamma )g\left(p_s\right)}}\\ P(p_s|y)=\left\{\begin{array}{c}\mathcal{l}\left(p_s\right),y\le y^{*}\\ g\left(p_s\right),y>y^{*}\end{array}\right.\end{array}\right.$$

(12)

where $P(·)$ is the probability of density function, $P\left(y\right|p_s)$ is the probability of y occurring when $p_s$ occurs, $P\left(p_s\right|y)$ is the probability of $p_s$ occurring when y occurs, and $P\left(p_s\right)$ is the probability of $p_s$ occurring; $\gamma$ is the distribution weight; $\mathcal{l}\left(p_s\right)$ is the distribution function when $y\le y^{*}$; and $g\left(p_s\right)$ is the probability density function when $y>y^{*}$.

The point where the function $E(·)$ takes its maximum value is used as the sampling point to obtain the new optimal parameter combination $p_{new}$, as is shown in Equation (13).

$$p_{new}=argmax E\left(p_s\right)$$

(13)

where $argmax E\left(p_s\right)$ represents the parameter that maximizes the mathematical expectation function.

3.

Update the Gaussian distribution of L(p_s).

Since the new sample is added, the Gaussian distribution has been updated by Equation (14):

$$\left\{\begin{array}{c}\left[L\left(p_1\right),L\left(p_2\right),\cdots ,L\left(p_r\right),L\left(p_{new}\right)\right]~N(0,\left[\begin{array}{cc}K& k^{\prime }\\ {\left(k^{\prime }\right)}^T& k(p_{new},p_{new})\end{array}\right])\\ k^{\prime }={\left[k(p_{new},p_1),k(p_{new},p_2),\cdots ,k(p_{new},p_r)\right]}^T\end{array}\right.$$

(14)

According to Formula (13), the new distribution of L($p_{new}$) is calculated by Equation (15):

$$\left\{\begin{array}{c}P\left(L\right(p_{new}|D_r,p_{new}))~N(\mu ,{\sigma }^2)\\ \mu ={(k\prime )}^T{K}^{-1}{\left[L\right(p_1),L(p_2),\cdots ,L(p_r\left)\right]}^T\\ {\sigma }^2=k(p_{new},p_{new})-{\left(k^{\prime }\right)}^T{K}^{-1}{k}^{\prime }\end{array}\right.$$

(15)

where $\mu$ and $\sigma$ are the mean and standard deviation, respectively.

4.

Repeat steps 2, 3, and 4 until the maximum number of iterations is reached and the optimal output point is calculated.

Following the aforementioned feature construction methodology, the initial dataset incorporates air temperature, humidity, air pressure, wind speed, and wind direction measured at four different heights. From each of these base variables, three statistical characteristics were derived, yielding a total of 33 statistical features. For combined features, the commutativity of addition and multiplication operations resulted in $2C_{44}^2=1892$ new features. In contrast, as subtraction and division are non-commutative, they contributed $2\times 2C_{44}^2=3784$ additional features. Furthermore, five time-related features were included, bringing the total feature set to 5725. The substantial dimensionality of this set considerably prolongs model training time. To address this, a Bayesian hyperparameter tuning approach was employed to identify the most predictive features and reduce their number, with the parameter search space detailed in

Table 3. Parameter search space.

Parameter	Range	Sampling Method
$n_{um1}$	[1, 11]	Discrete random sampling
$n_{um2}$	[2, 33]	Discrete random sampling

.

A Bayesian optimization method was used to select features. This method determines the degree of influence of a feature on wind power based on the magnitude of its effect on the model fitting error. Meteorological features that minimize the model fitting error were selected, as shown in

Table 4. Selected features used in prediction.

	Combined Features	Statistical Features
Selected features	WS_30	WS_10
	WS_CEN	WS_30
	WS_30_SD	WS_50
	WS_CEN_mean	WS_CEN
	WD_CEN_mean	WD_10
	Air_P	WD_30
	Air_T_mean	WD_50
	Air_P_mean	WD_CEN
	Air_P_max	Air_P
	Air_T
	Air_H_mean
	Air_P_SD

.

3. Algorithms and Models

3.1. Adaptive Particle Swarm Optimization Algorithm

The classic PSO has limitations in certain complex optimization problems. In the classic PSO, the flight of particles is influenced by both the global optimum and the individual optimum, which makes the algorithm prone to becoming stuck in local optima when handling complex multimodal functions. Furthermore, while the classic PSO converges quickly in the early stages, it tends to take a longer time to converge in later stages, making it difficult to rapidly find the global optimum. The performance of the PSO is also heavily reliant on the setting of parameters such as inertia weight and learning factors, necessitating extensive debugging and experience accumulation.

To address these issues, aPSO has been introduced. The adaptive inertia weight strategy dynamically adjusts the inertia weight during the iteration process, improving the algorithm’s global search and local convergence capabilities, while the adaptive learning factor allows for dynamic adjustment of the learning factor based on the iteration process, enhancing the exploration and exploitation capacities. The adaptive population structure utilizes dynamic population structures such as virtual populations and hierarchical populations to increase the diversity and robustness of the algorithm. To enhance the global search ability and avoid becoming trapped in local optima, adaptive mutation operations have also been introduced. By incorporating these adaptive strategies, the performance of the PSO algorithm for complex optimization problems can be effectively improved, leading to enhanced convergence speed and robustness, as well as greater adaptability of the algorithm.

Due to the significant differences in the distribution of various particles, the entire population can be adaptively divided into several subgroups by utilizing the concept of clustering [27]. In order to enhance population diversity, different learning strategies can be employed for the various subgroups to update particles of different types.

In order to classify subgroups, this study adopts an algorithm known as the Fast Search and Cluster Method. This method demonstrates exceptional clustering performance, automatically identifying cluster centers within the dataset and efficiently clustering samples of arbitrary shape. The fundamental principles of the Fast Search and Cluster Method can be summarized in two characteristics: firstly, the distance between cluster centers and points of high local density is significant; secondly, cluster centers are surrounded by points of low local density. Through this method, the subgroups within the datasets can be effectively delineated and the corresponding cluster centers can be identified. This algorithm not only handles datasets of arbitrary shapes but also achieves efficient clustering while identifying cluster centers.

In D-dimensional search space, there is a population $S=\left\{x_1,x_2,\cdots ,x_h\right\}$, consisting of h particles, where $x_i=\left[x_{i1},x_{i2},\cdots ,x_{iD}\right]$, where ${\delta }_{id}$ is the spacing between itself and particles of higher density, the variable ${\rho }_{id}$ given by the d-th dimension of the i-th particle represents the local density of the particle.

$${\rho }_{id}={\sum }_{j\ne i}\mathit{exp}\left(-{\displaystyle \frac{d_{ij}^2}{d_c}}\right)$$

(16)

In the above formula: $d_{ij}$ is the Euclidean distance between ${ x}_{id}$ and $x_{jd}$; $d_c$ is the truncated distance.

$${\delta }_{id}={min}_{j:{\rho }_{jd}>{\rho }_{id}}\left(d_{ij}\right)$$

(17)

The sample with the highest local density satisfies the conditions:

$${\delta }_{id}={max}_j\left(d_{ij}\right)$$

(18)

A maximum in the local density, as described by Equation (16), results in a ${\delta }_{id}$ value substantially exceeding the distance $\delta$ to the nearest neighbors. Subgroup centers are thus characterized by a high particle density $\rho$ coupled with a large $\delta$, making them the preferred choices for cluster centers. The classification of other particles is determined by assigning them to the nearest sample whose density exceeds their own.

Based on the classification results mentioned above, particles in each subgroup can be categorized as either general or locally optimal particles. Under the guidance of the optimal particles within the subgroup, ordinary particles will autonomously explore and expand in space, with the updating formula being:

$$x_{id}=w{x}_{id}+c_1{r}_1\left({pbest}_{id}-x_{id}\right)+c_2{r}_2\left({cgbest}_{cd}-x_{id}\right)$$

(19)

In the Equation (19), ${pbest}_{id}$ denotes the best positional information of the i-th particle in the d-th dimension; ${cgbest}_{cd}$ indicates the best positional information within the c-th sub-group.

By integrating the information of each subgroup for updating, the local optimal particle can enhance the information exchange between subgroups. The particle update formula is:

$$x_{id}=w{x}_{id}+c_1{r}_1\left({pbest}_{id}-x_{id}\right)+c_2{r}_2\left({\displaystyle \frac{1}{C}}{\sum }_{c=1}^C{cgbest}_{cd}-x_{id}\right)$$

(20)

A nonlinear decreasing strategy is used for inertia weight design, expressed mathematically as:

$$w(t)=w_{end}+(w_{start}-w_{end})\times e^{-\alpha {\left({\displaystyle \frac{t}{T_{max}}}\right)}^{\beta }}$$

(21)

where $w_{start}$ = 0.9, $w_{end}$ = 0.4, $\alpha$ = 4, and $\beta$ = 2. This strategy maintains a high inertia weight in the early stages of iteration to enhance global exploration capabilities, and automatically reduces the weight in the later stages of iteration to improve local development accuracy.

The adaptive adjustment of the learning factor is based on population diversity feedback, which is specifically expressed as:

$$\left\{\begin{array}{c}{c}_1(t)=c_{1,min}+(c_{1,max}-c_{1,min})\times {\displaystyle \frac{D\left(t\right)}{D_{max}}}\\ c_2(t)=c_{2,min}+(c_{2,max}-c_{2,min})\times {\displaystyle \frac{1-D\left(t\right)}{D_{max}}}\end{array}\right.$$

(22)

The population diversity $D\left(t\right)$ is calculated by the Euclidean distance between particles. This design enables the algorithm to dynamically adjust the balance between individual cognition and social learning according to the search status.

The mutation operation uses a Cauchy-Gaussian mixture strategy. When the population is detected to be stuck in a local optimum, mutation is performed according to the Equation (23).

$$x_{mut}=x_{best}+{\eta }_1\times Cauchy\left(\mathrm{0,1}\right)+{\eta }_2\times N\left(\mathrm{0,1}\right)$$

(23)

where ${\eta }_1$ and ${\eta }_2$ are adaptive step lengths, effectively enhancing the algorithm’s ability to escape from local optima.

Within a subpopulation, the locally optimal particle not only guides the search direction of its members but also facilitates information exchange between different subpopulations. However, reliance solely on this single particle, as in Equation (19), carries a significant risk. Even a minor deviation of this guiding particle can lead the entire subswarm to stagnate in a local optimum. To mitigate this, it is crucial for subswarms to incorporate information from others. Equation (20) addresses this by using the average information of locally optimal particles from all subswarms to guide updates. This mechanism enhances inter-subswarm knowledge transfer and effectively prevents premature convergence.

To validate the effectiveness of the aPSO algorithm, this study conducted a systematic performance evaluation on six standard test functions, as detailed in

Table 5. Performance comparison on standard test functions.

Test Function	Algorithm	Optimum Average	Standard Deviation
Sphere	Traditional PSO	3.24 × 1015	2.16 × 10−15
	LDW-PSO	1.87 × 10−16	9.43 × 10−17
	aPSO	5.32 × 10−18	3.28 × 10−18
Rastrigin	Traditional PSO	24.36	8.74
	LDW-PSO	18.52	6.93
	aPSO	12.47	4.25
Ackley	Traditional PSO	0.084	0.032
	LDW-PSO	0.056	0.021
	aPSO	0.023	0.008

. Compared with mainstream variants such as the classic PSO, linearly decreasing weight PSO, compression factor PSO, and genetic mutation-based PSO, aPSO demonstrated superior convergence characteristics on all test functions. On the Sphere function, aPSO achieved an optimal solution of $5.32\times {10}^{-18}$, significantly outperforming the classic PSO’s $3.24\times {10}^{-15}$ and the linearly decreasing weight PSO’s $1.87\times {10}^{-16}$. On the multimodal Rastrigin function, aPSO achieved an optimal value of 12.47, while the classic PSO and compression factor PSO only reached 24.36 and 18.52, respectively. In terms of convergence speed, aPSO achieved an average of 124 generations on the test functions, an improvement of approximately 25–40% over the comparison algorithms.

Compared with existing PSO variants, the innovation of aPSO is mainly reflected in the construction of a multi-mechanism collaborative adaptive framework. For the first time, the algorithm integrates the adaptive mechanisms of inertia weight, learning factor, population structure and mutation operation into a unified framework, forming a synergistic effect among various mechanisms. The parameter adjustment strategy is based on real-time feedback of population distribution characteristics, abandoning the traditional time-driven or rule-driven mode. The hybrid mutation strategy combines the large step-size jump characteristics of Cauchy mutation and the small step-size fine search characteristics of Gaussian mutation to achieve an effective balance between exploration and development. In terms of computational complexity, through the optimization design of cluster analysis, the algorithm controls the time complexity at the O (N log N) level while maintaining excellent performance. These improvements make aPSO particularly suitable for high-dimensional, nonlinear and complex optimization problems such as wind power forecasting, providing a new technical approach for the application of intelligent optimization algorithms in the energy field.

3.2. Back Propagation Neural Network

As a foundational deep learning technique, BP neural network employs a gradient-based supervised learning framework that originated in the 1980s. Its application to wind power forecasting began in the early 1990s, at which time research empirically confirmed its effectiveness in capturing the complex nonlinear interdependencies among factors such as wind speed, direction, and generated power.

Due to its strong nonlinear modeling capabilities, the BP excels at capturing complex nonlinear relationships and is able to effectively describe the nonlinear mapping. The self-learning characteristics of BP neural network enable it to automatically learn from historical data, significantly enhancing the adaptability of the model. Its strong generalization ability allows a well-trained BP neural network model to make accurate predictions for new input data, showcasing its robust generalization capabilities. Additionally, its built-in parallel computing structure allows for rapid processing of large volumes of data, meeting the demands for real-time predictions.

A BP neural network is structured with input, hidden, and output layers, each containing numerous interconnected neurons. Its central tenet is error backpropagation for supervised learning. During training, input data is processed through forward propagation, undergoing nonlinear transformations across layers to produce an output. The resulting error is then propagated backward from the output layer to the input layer. This backward-passed error serves as the basis for calculating gradients, which guide the systematic modification of all synaptic weights and neuronal biases. This cyclical process of forward inference and backward learning allows the network to progressively approximate complex functions, making it a universal and adaptable tool for tasks ranging from classification to regression.

The training mechanism of the BP neural network is conceptually divided into two distinct phases. The first phase involves the forward propagation of input signals, which are progressively transformed by nonlinear activation functions in the hidden and output layers to generate a computed output. The second phase consists of error backpropagation, where the discrepancy between the computed and desired outputs is allocated backward across the network’s layers. This is followed by a systematic adjustment of all synaptic weights and neuronal thresholds, guided by this error distribution. The ultimate aim of this process is parameter optimization, converging the network toward a state of minimal error.

The BP neural network possesses excellent data fitting capabilities by combining the learning mechanisms of forward propagation and backward propagation. By continuously optimizing network parameters, the BP neural network can approximate any continuous function, thereby enabling the modeling and prediction of complex relationships. The network gradually optimizes itself by continuously iterating and updating weights and thresholds, in order to achieve a more accurate fitting and prediction of the input data.

3.3. Long Short-Term Memory

LSTM, improved from the recurrent neural network (RNN), has become one of the widely used neural network models for handling time-series data and sequence modeling tasks after years of development and optimization. The core idea of the LSTM is to effectively retain and transmit long-term memory information through carefully designed structural units, thereby learning and capturing temporal dependencies in the data. These structural units include input gates, forget gates, and output gates. Through these gating mechanisms, LSTM networks can automatically learn and adapt to the long-term dependencies present in time-series data without being affected by issues such as vanishing or exploding gradients.

As illustrated in Figure 6, these gates allow the network to selectively remember, ignore, or output information, granting it resilience against the vanishing/exploding gradient problem and a superior ability to model long-term relationships in sequential data.

The input gate determines the content from the current input data that should be passed to the cell state. It is composed of a sigmoid activation function and the multiplication operation with the relevant elements, calculated as follows:

$$i_t=\sigma \left(W_{xi}{x}_t+W_{hi}{h}_{t-1}+b_i\right)$$

(24)

In the Equation (24), $x_t$ is the input at the current time step, $h_{t-1}$ is the hidden state from the previous time step, $W_{xi}$ and $W_{hi}$ are the weight matrices for the input and hidden state, respectively, and $b_i$ is the bias, $i_t$ is the output of the input gate at the current time step, which determines the extent to which the current input updates the cell state.

The forget gate determines what should be forgotten in the cell state, and the calculation method is as follows:

$$f_t=\sigma \left(W_{xf}{x}_t+W_{hf}{h}_{t-1}+b_f\right)$$

(25)

Among them, $W_{xf}$ and $W_{hf}$ are the weight matrices for the input and hidden states, respectively, while $b_f$ is the bias. The output of the forget gate, $f_t$ determines the information that should be forgotten from the cell state.

The update of the cell state is achieved through the combination of the input gate, the forget gate, and a Tanh activation function, as described by the following formula:

$${\tilde{C}}_t=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(W_{xc}{x}_t+W_{hc}{h}_{t-1}+b_c)$$

(26)

Among them, ${\tilde{C}}_t$ is the candidate cell state, $W_{xc}$ and $W_{hc}$are the weights for the input and hidden states, respectively, and $b_c$ is the bias.

The update of the cell state is determined by the input gate and the candidate cell state, as expressed by the following equation:

$$C_t=f_t{C}_{t-1}+i_t{\tilde{C}}_t$$

(27)

Among them, $C_{t-1}$ is the cell state from the previous time step. Controlled by the forget gate and the input gate, LSTM can selectively retain historical information and update new information, thereby achieving the modeling of long-term dependencies.

The output gate determines the information from the cell state that is passed to the hidden state and inputs it into the next time step. The calculation formula is as follows:

$$O_t=\sigma \left(W_{xo}{x}_t+W_{ho}{h}_{t-1}+b_o\right)$$

(28)

Among them, $O_t$ is the output gate, which determines the extent to which information from the cell state is output to the hidden state.

By combining the cell state and the output gate, the hidden state at the current time step is obtained, as described by the Equation (29):

$$h_t=O_t·\mathit{tanh}\left(C_t\right)$$

(29)

Finally, the hidden state $h_t$ of LSTM will be used as the input of the next time step and continue to participate in the subsequent learning and prediction process.

The forget gate in the LSTM network can control which information the network forgets to adapt to the changes in data features at different time points, thus enhancing the adaptability and generalization ability of the network. Due to the gating mechanism of the LSTM network, the calculations in the network can be highly parallelized, which is conducive to efficient training and reasoning on hardware such as GPUs.

Since the LSTM network is good at processing time-series information and can capture long-term dependent relationships in the data, it is more suitable for predicting future wind power output. And because it can retain long-term memory, it helps to process slowly changing data features such as wind speed and can more accurately predict wind power. The ability to learn different time scale patterns determines that when the LSTM neural network is utilized to wind power prediction, it has the ability to adapt to changes in data of different frequencies and trends.

3.4. Long Short-Term Memory-Back Propagation Neural Network

In terms of model selection, this paper uses a BP neural network as a complementary component to the LSTM, primarily due to its unique advantages in nonlinear mapping. Compared to machine learning algorithms like SVM and Random forests, the BP neural network exhibits stronger nonlinear fitting capabilities and can effectively learn the complex mapping relationship between LSTM outputs and wind power. Furthermore, the BP network’s structural design offers high flexibility, which makes it easily integrates with the LSTM network to build an end-to-end hybrid architecture. On the aspect of computational efficiency, compared to deeply stacked LSTM structures, the BP network significantly reduces the complexity of parameters and significantly improves training speed. Furthermore, the BP neural network has been extensively validated in engineering applications and demonstrates high reliability and stability, providing strong support for the deployment of practical wind power forecasting systems.

The LSTM-BP hybrid model achieves significant improvements in forecasting accuracy through a multi-layered mechanism. First, the LSTM network focuses on extracting long-term dependencies in time-series, effectively capturing the temporal dynamics of wind power. Second, the BP neural network strengthens the learning of nonlinear associations between current-time features and outputs, enhancing the model’s responsiveness to transient changes. Furthermore, the BP network also has the ability to learn the LSTM prediction residuals, further optimizing forecast results through an error correction mechanism. Ultimately, this architecture effectively integrates deep temporal features with shallow statistical features, constructing a hierarchical feature representation system that comprehensively improves the model’s predictive performance.

During the feature space partitioning process, the input feature space is divided into a temporal feature subset and an instantaneous feature subset. The model utilizes a dual-path parallel processing structure, with the LSTM temporal path processing historical temporal information and the BP instantaneous path processing current-time features.

3.5. Long Short-Term Memory-Back Propagation Neural Network Optimized by Adaptive Particle Swarm Optimization Algorithm

When constructing the LSTM-BP network model, parameters such as the number of batches and the number of hidden layer units need to be set. These parameters directly affect the structure of the network. The setting of parameters will have a significant influence on the performance of the model, so it is very important to choose appropriate parameters.

This study proposes an LSTM-BP prediction model based on aPSO for wind power prediction. The model comprehensively improves the PSO algorithm and combines it with adaptive learning strategy to match wind power characteristic data which include wind speed, temperature, humidity, wind turbine model and other data with the topology of the LSTM-BP network to achieve higher prediction performance and smaller errors. By utilizing the aPSO to optimize the hyperparameter selection of the LSTM-BP neural network, the optimal network topology can be more effectively determined, thereby improving the prediction performance of wind power characteristic data. Compared with traditional empirical methods and experimental methods, this method based on aPSO has higher efficiency and accuracy.

The structure of the LSTM-BP is controlled by the size of the hyperparameters. This study combines aPSO algorithm with the LSTM-BP model to match the network structure of the model with the wind power characteristic data.

The parameter optimization process proceeds as follows: First, the LSTM-BP network is trained on the training dataset. The validation set is then fed into this pre-trained network to generate wind power predictions. The Root Mean Square Error (RMSE) between these predictions and the actual values serves as the particle fitness function. Each particle’s position, representing a set of hyperparameters, is iteratively updated based on its own historical best position and the swarm’s global best. This cycle of evaluation and update continues until either a predefined number of iterations is reached or accuracy criteria are satisfied. The final global best solution is subsequently assigned as the optimized hyperparameter set for the LSTM-BP model.

The parameter optimization for the LSTM-BP model is achieved through aPSO algorithm. While the standard PSO algorithm, known for its simple design and rapid convergence, is prone to local optima, the aPSO variant mitigates this by dynamically partitioning the population into subgroups and updating particles based on the swarm’s distribution. This enhancement is crucial for optimizing the BP neural network, a foundational architecture renowned for its operational stability and straightforward hardware implementation. A key characteristic of BP is its forward signal propagation and backward error transmission. However, its performance is highly sensitive to initial weights and thresholds, often resulting in suboptimal convergence. The aPSO algorithm addresses this by using the fitness of each particle as a candidate solution to identify superior initial parameters for the LSTM-BP network, thereby improving its predictive accuracy. The overall architecture of the aPSO-LSTM-BP model is depicted in Figure 7.

The aPSO used in this paper effectively avoids falling into local optimal solutions through a variety of collaborative mechanisms. The algorithm adopts a dynamic inertia weight strategy and adaptively adjusts parameters according to the iterative process, thereby achieving an effective balance between global exploration and local development. The subgroup clustering mechanism based on the fast search clustering method can dynamically divide the population structure and significantly enhance the diversity of the population. In terms of information sharing, the local optimal particles effectively break the local convergence state by receiving information from other subgroups. At the same time, the adaptive learning factor can dynamically adjust parameters to further improve the algorithm’s adaptability to complex optimization problems. Compared with traditional optimization methods such as particle swarm optimization and genetic algorithm, aPSO demonstrates superior global search capabilities and convergence stability in high-dimensional, nonlinear problems such as wind power forecasting, providing an effective solution to complex optimization problems. The search range and optimal value used in different algorithms of the model are recorded in

Table 6. Hyper parameters of proposed model.

Optimization Stage	Parameters	Search Range	Optimal Value
aPSO	Number of particles	$[20, 50]$	30
	Maximum iterations	$[50, 200]$	100
	Inertia weight	[0.4, 0.9]	adaptive
LSTM	Hidden unit	[32, 128]	64
	Learning rate	[1 × 10−4, 1 × 10−2]	0.005
BP	Number of hidden units	[1, 3]	2
	Number of cells	$[16, 64]$	32

.

4. Experiments and Results

4.1. Data Description

The data used in this study comes from the China State Grid Renewable Energy Generation Forecasting Competition [28]. This article uses the actual power and meteorological data of a domestic wind farm, where each piece of data is obtained every fifteen minutes, including six columns of external meteorological characteristic data such as wind speed at the wind turbine hub, wind direction at the wind turbine hub, temperature, air pressure, and relative humidity, as well as one column of wind power data at the corresponding time. There is some missing and abnormal data in the dataset.

Table 7. Specific information of the wind turbines.

Nominal Generation Output Capacity (MW)	Wind Turbine Model	Detailed Turbine Information	Number of Turbines
75	GW1500/85	Capacity: 1500 kW	50
		Hub height: 85.0 m
		Rotor diameter: 87.0 m
		Website: https://en.wind-turbine-models.com/turbines/1201-goldwind-gw-87-1500 (accessed on 14 October 2024)

below shows the specific information of the wind turbines used in the wind farm, and the total output capacity is 75 MW.

As shown in the one-step prediction in Figure 8, each group of data contains five input values and one output value. The original dataset was partitioned into 1995 samples, derived from an initial pool of 2000 data constructions. From these, a training set of 1595 samples and a test set of 200 samples were created. Each sample, regardless of its assignment to the training or test set, comprises five input variables and a single output value. The foundational statistics characterizing the dataset are detailed in

Table 8. Basic statistics of the data.

Statistics	Power (MW)	WS_CEN (m/s)	WD_CEN (°)	Air_T (°C)	Air_H (%)	Air_P (Pa)
Mean	5.60	3.83	180.38	6.77	18.26	889.53
Minimum	0.12	0	20.47	−3.98	8.97	888.73
Maximum	27.94	7.72	338.17	14.62	34.30	890.2
Standard deviation	6.61	1.83	91.99	5.42	7.19	0.2872

below.

4.2. Evaluation Metrics

In order to measure the prediction performance of the prediction model, much literature has proposed a variety of performance evaluation indicators. Similarly, four evaluation indicators, Mean Square Error (MSE), MAE, RMSE and Mean Absolute Percentage Error (MAPE), were selected to verify the prediction accuracy of the model. Their meanings and specific calculations are shown in

Table 9. Performance evaluation index.

Index	Formula	Units
MSE	${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_i-\widehat{y_i})}^2$	${\mathrm{MW}}^2$
MAE	${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|y_i-\widehat{y_i}\right|$	$\mathrm{MW}$
RMSE	$\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_i-\widehat{y_i})}^2}$	$\mathrm{MW}$
MAPE	${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{\widehat{y_i}-y_i}{y_i}}\right|\times 100\%$	$\%$

.

In the formulation, $y_i$ denotes the actual value, $\widehat{y_i}$ is the predicted value, and n stands for the total number of predictions. MSE measures the expected squared difference between actual and predicted values. MAE, which avoids cancellation of positive and negative errors, indicates the magnitude of the prediction error. RMSE represents the dispersion degree of the prediction error. Finally, MAPE quantifies the overall average performance of the prediction error, where a smaller value indicates that the prediction is closer to the actual value.

4.3. Prediction Results and Comparative Analysis

A comparative analysis was conducted to further evaluate the robustness and predictive accuracy of the proposed model against existing ARIMA-LSTM, ARIMA-aPSOBP, and LSTM-BP models. The respective performance of each model for one-step, two-step, and three-step ahead predictions is visually compared in the line charts provided in Figure 9, Figure 10 and Figure 11.

The four evaluation index values obtained by the above four prediction models are listed in

Table 10. Forecasting error of different models.

		MAE (MW)	RMSE (MW)	MAPE (%)	MSE (MW2)
Proposed Method	Step-1	0.54	0.90	10.5	0.81
	Step-2	0.69	1.21	12.3	1.45
	Step-3	0.81	1.47	14.0	2.15
ARIMA-aPSOBP	Step-1	0.65	1.13	11.3	1.28
	Step-2	0.91	1.60	15.1	2.56
	Step-3	0.96	1.75	17.5	3.05
ARIMA-LSTM	Step-1	0.79	1.43	14.7	2.03
	Step-2	1.16	2.18	19.6	4.74
	Step-3	1.46	2.70	25.3	7.29
LSTM-BP	Step-1	0.85	1.44	15.4	2.07
	Step-2	1.02	1.81	18.4	3.28
	Step-3	1.30	2.22	23.6	4.92

, which compares the performance of our method with the three forecasting models at different forecasting step sizes. It clearly shows that, overall, the error metrics of all methods increase with increasing forecasting step size, indicating that the model’s ability to withstand uncertainty gradually weakens as the forecast horizon extends. However, there are significant differences between the different methods in terms of error accumulation rate and stability.

First, the performance of our method for one-step forecasting shows that it outperforms the comparison models in both mean error and relative error. For example, its MAE and MAPE levels are both at their lowest values, demonstrating that this method accurately captures local variations in wind power. Furthermore, its RMSE is significantly lower than that of the other models, demonstrating that, in the short term, this method effectively mitigates the impact of individual large deviations on overall accuracy.

Further examining the two-step forecasting phase, while all methods experience an increase in error, the increase in error for our method is relatively moderate. The RMSE and MSE metrics are particularly noticeable, with the gap compared to the comparison models being even more pronounced. This demonstrates that this method exhibits greater stability during error accumulation and is able to maintain reasonable accuracy over longer forecast windows.

In three-step forecasting, differences between models are further amplified. The ARIMA-LSTM model’s error rises rapidly, with its MAPE exceeding 25%, indicating insufficient robustness for long-term time series forecasting. The LSTM-BP performs second best, also exhibiting a significant trend of error accumulation. In contrast, our proposed method exhibits more stable error control, with its MAE and RMSE consistently remaining relatively low, demonstrating its ability to effectively mitigate the adverse effects of increasing the forecast step size.

To comprehensively evaluate the predictive performance of the proposed model, residual analysis was used to further examine the distribution characteristics of the model’s prediction errors. Figure 12 show the residual distribution of the proposed method. It can be observed that when the wind power is non-zero, the residual points are evenly distributed on both sides of the zero baseline, with no obvious systematic deviation pattern, indicating that the model has good unbiasedness. The fluctuation range of the residual values is mainly concentrated in the range of ±1.5 MW, and its distribution shows a random dispersion characteristic, indicating that the model successfully captures the main regular components in the data and effectively controls unexplained random fluctuations.

In the horizontal comparative analysis, a variety of representative prediction methods were supplemented as benchmark models for systematic comparison, as shown in

Table 11. Prediction errors of proposed model with traditional model.

	Step	MAE (MW)	RMSE (MW)	MAPE (%)
GRU	1	0.78	1.35	14.2
LSTM	1	1.02	1.81	18.4
Linear regression	1	1.89	2.45	32.7
Random forest	1	1.23	1.76	21.3
XGBoost	1	1.15	1.62	19.8
Proposed Method	1	0.54	0.90	10.5

.

In order to objectively evaluate the rationality of the prediction errors reported in this study, it is crucial to examine them in a broader academic context. Admittedly, the MAPE error reported in this paper is higher than the MAPE of less than 5% reported in some literature on standard benchmark datasets [29]. This difference is mainly due to the inherent characteristics and quality of the datasets used in different studies. For example, Michalakopoulos et al. [29] constructed a high-quality dataset with low volatility and high signal-to-noise ratio by integrating physical information theory power curves with high-precision numerical weather forecast data, enabling their TFT model to achieve a MAPE close to 5%. In contrast, the dataset processed in this study faces higher practical challenges, including significant noise, a certain proportion of missing data, and inconsistency. These factors together constitute a more challenging prediction environment, objectively limiting the upper limit of accuracy that any model can achieve. However, it is under such challenging conditions that the model proposed in this study demonstrates its core value. Compared with a series of baseline models including LSTM, GRU, XGBoost, it achieves the most significant performance improvement, as shown in Table 11, which fully demonstrates the effectiveness and robustness of the method in complex real-world scenarios.

Ablation experiment results shown in

Table 12. Results of ablation experiments.

Model	Step	MAE (MW)	RMSE (MW)	MAPE (%)
LSTM	1	1.02	1.81	18.4
BP	1	1.30	2.22	23.6
LSTM-BP	1	0.85	1.44	15.4
Proposed Method	1	0.54	0.90	10.5

reveal the unique contributions and complementary properties of each model component. When using the LSTM network alone, the model demonstrates excellent performance in time series modeling, effectively capturing long-term dependencies in wind power data. However, it is relatively insensitive to transient changes in features. In contrast, while the BP neural network alone possesses strong nonlinear mapping capabilities and can accurately fit complex relationships between input and output, it struggles to effectively learn long-term dependency patterns when processing time series data. A hybrid model combining the LSTM and BP networks leverages the synergistic advantages of both architectures, significantly reducing prediction error by approximately 30% compared to a single model, demonstrating the rationality and effectiveness of the hybrid architecture design. Furthermore, the aPSO algorithm is introduced for parameter tuning, further improving model performance and reducing prediction error by approximately 35%. This result highlights the critical role of intelligent optimization algorithms in model parameter optimization. In summary, the complementary functions and collaborative optimization of each component contribute to the final model’s outstanding performance in wind power forecasting.

4.4. Statistical Significance Test Analysis

To verify the statistically significant superiority of the proposed method over the baseline model, this study employed paired t-tests and Wilcoxon signed-rank tests for dual validation. The paired t-test is used to detect systematic differences in mean error values between models, while the Wilcoxon test, as a nonparametric method, makes more relaxed assumptions about the error distribution, providing complementary validation.

Forecast error samples for each model were collected from the test set, and paired differences were calculated:

$$d_i = {errors}_{{baseline}_i}-{errors}_{{proposed}_i}, i = 1, 2, \cdots , n$$

(30)

where n = 200 is the test sample size, ${errors}_{{baseline}_i}$ and ${errors}_{{proposed}_i}$ are the baseline error and the error of the proposed method, respectively. The statistical test is performed as follows:

The paired t-test statistic is:

$$t = {\displaystyle \frac{mean\left(d\right)}{\frac{std\left(d\right)}{\sqrt{n}}}}, df = n-1$$

(31)

The Wilcoxon test calculates a statistic based on the ranks of the absolute values of the differences. The results of the are summarized in

Table 13. Significance test.

Comparison Model	Inspection Methods	Statistics	p-Value
ARIMA-LSTM	Paired t-test	$\mathrm{t}=8.45$	$<0.001$
	Wilcoxon rank-sum test	$\mathrm{W}=18560$	$<0.001$
ARIMA-aPSOBP	Paired t-test	$\mathrm{t}=6.23$	$<0.001$
	Wilcoxon rank-sum test	$\mathrm{W}=17230$	$<0.001$
LSTM-BP	Paired t-test	$\mathrm{t}=4.87$	$<0.001$
	Wilcoxon rank-sum test	$\mathrm{W}=15890$	$0.002$

.

Comprehensive statistical test results show that all comparisons reached the statistically significant level (p < 0.01), thus rejecting the null hypothesis. These statistical evidences support the significant superiority of the proposed method over the benchmark model.

4.5. Full-Year Error Analysis and Seasonal Performance Evaluation

To comprehensively evaluate the model’s generalization and robustness across different seasons and months, we conducted supplementary testing over eleven months on the one-year dataset. 2000 experimental samples were selected for each month to ensure independence of the evaluation. The model used the same hyperparameters in each test month to verify its inherent adaptability without seasonal adjustment. The distribution of the full-year forecast error (MAE) is shown in the in

Table 14. Twelve-month one-step forecast error statistics.

Month	MAE (MW)	RMSE (MW)	MAPE (%)
January	$0.54$	$0.90$	10.5
February	$0.58$	$0.95$	11.2
March	$0.65$	$1.05$	12.8
April	$0.78$	$1.22$	15.1
May	$0.82$	$1.28$	16.0
June	$0.88$	$1.38$	17.5
July	0.86	1.35	16.9
August	0.84	1.32	16.3
September	0.75	1.18	14.5
October	0.63	1.02	12.1
November	0.57	0.96	11.5
December	0.55	0.92	10.8

in detail.

Table 14 reveals a clear seasonal pattern. The model’s forecast error is lowest from late autumn through winter (October to February), begins to rise during the spring transition period (March to May), and peaks in summer (June to August). This “low in winter, high in summer” pattern is consistent with the seasonal variation in atmospheric boundary layer stability: in winter, the atmosphere is stable and wind conditions are smooth; in summer, thermally driven turbulence and gusty winds lead to highly intermittent and stochastic wind resources, increasing the difficulty of forecasting. Even in the most challenging summer months, the model’s MAPE remains below 18%, with an MAE below 0.9 MW, demonstrating the model’s reliable baseline forecasting capabilities under complex meteorological conditions.

In order to evaluate the forecast accuracy of the proposed model and place it within the current research context, the result has been compared with the work of Al-Duais and Al-Sharpi [8]. This study also addresses time series wind power forecasting and employs the classic seasonal autoregressive integrated moving average model. Their reported short-term forecast average absolute percentage error ranges from 13.09% to 14.66%.

The aPSO-LSTM-BP hybrid model proposed in this study performs at 10.5% to 12.8% on the same metrics. This comparison demonstrates that the MAPE of this proposed model surpasses both the best and worst reported values at 13.09% and 14.66%, respectively. This result clearly demonstrates that the proposed method significantly improves forecast accuracy compared to the classic SARIMA model, effectively reducing forecast error. This comparison validates the advantages of our model in addressing the nonlinearity and instability of wind power series, further demonstrating its scientific contribution and potential for application.

5. Conclusions and Future Work

To tackle the challenges in wind power forecasting—such as prevalent abnormal data, significant noise interference, and limited model accuracy—this paper introduces a hybrid LSTM-BP model enhanced by the aPSO algorithm. The proposed methodology begins by cleansing the data with the quartile method for anomaly detection and cubic spline interpolation for imputation. The ARIMA model is then applied to suppress noise and enhance the stationarity of the time series. Subsequently, a high-dimensional input space incorporating statistical and combined features is constructed, with Bayesian optimization employed to select the most relevant features and reduce dimensionality. In the modeling phase, a BP neural network fits nonlinear relationships, while a LSTM network captures temporal dependencies. Finally, the aPSO algorithm globally optimizes the network’s hyperparameters, substantially boosting the model’s generalization capability and forecasting precision.

The experimental results show that compared with baseline models such as ARIMA-aPSOBP, ARIMA-LSTM, and LSTM-BP, the proposed model achieves lower MAE, RMSE, MAPE, and MSE values at different forecast step sizes, demonstrating higher forecasting accuracy and robustness. Especially in multi-step forecasting, this model effectively suppresses error accumulation, significantly outperforming traditional single or simple combination models. Furthermore, validation across multiple months throughout the year further demonstrates the model’s adaptability and stability across different seasons and meteorological conditions.

For grid operators and system planners, this model can provide more reliable wind power output forecasts for short-term grid power balance and reserve capacity allocation, reducing scheduling errors caused by wind power fluctuations. Furthermore, high-precision forecasts help mitigate the impact of wind power integration on frequency and voltage, improving the power system’s interference resistance and operational reliability. Accurate wind power output forecasts enable more rational scheduling of conventional unit startups and shutdowns and inter-regional transmission plans, enhancing wind power absorption. Long-term, reliable power forecasts provide data support for grid expansion, energy storage deployment, and power market bidding strategies, promoting energy mix optimization and improving market efficiency.

In summary, the hybrid forecasting model proposed in this paper is not only methodologically advanced and effective but also demonstrates significant engineering value in practical applications. It is suitable for the operational and planning needs of modern power systems with high renewable energy penetration. Future research can be carried out from the following three aspects: first, limited by the noise level and feature completeness of the current data, the prediction error still has room for further optimization. Therefore, a pressing future work is first to apply this model to more publicly available wind power datasets with high-quality annotations and rich features, second, to further introduce more meteorological and operating environment characteristics to explore the potential of multimodal data fusion to improve model performance, and third, to combine probabilistic prediction and uncertainty quantification methods to construct interval or distribution prediction models to better serve power grid dispatching decisions and new energy consumption needs. In addition, in order to further verify and highlight the superiority of this framework within a wider range of advanced models, subsequent work can introduce more cutting-edge baseline models such as Transformer and Attention LSTM for systematic comparison.