Intelligent System for Student Performance Prediction: An Educational Data Mining Approach Using Metaheuristic-Optimized LightGBM with SHAP-Based Learning Analytics
Abstract
1. Introduction
- Development of hybrid predictive models that integrate LightGBM with FOX, GTO, PSO, SCSO, and SSA for optimized hyperparameter tuning.
- Application of SHAP for interpretability, enabling detailed analysis of feature importance and its influence on prediction outcomes.
- Empirical comparison of five swarm-based optimizers on student performance data, highlighting their relative strengths and weaknesses.
- Provision of a reliable and transparent framework that combines high predictive accuracy with interpretability, thereby supporting learners, educators, and policymakers.
2. Literature Review
3. Methodology
3.1. Fox Optimization Algorithm (FOX)
3.2. Giant Trevally Optimizer (GTO)
3.3. Particle Swarm Optimization (PSO)
3.4. Sand Cat Swarm Optimization (SCSO)
3.5. Salp Swarm Algorithm (SSA)
3.6. Light Gradient Boosting Machine (LightGBM)
3.7. Proposed Model Optimization Framework
- max_depth: Controls the maximum depth of individual decision trees. A well-tuned depth prevents overfitting by limiting model complexity. The search range is set to .
- learning_rate: Regulates the contribution of each tree during boosting. A value too low results in slow convergence, while a value too high may lead to overshooting the optimum. The range () is explored.
- no_estimators determines the number of boosting rounds in LightGBM. It directly influences model performance, generalization, and training. The range is explored.
- Step 1: Preprocess the educational dataset by normalizing input features, encoding categorical variables.
- Step 2: Partition the dataset into training and testing.
- Step 3: Initialize the LightGBM model with default hyperparameters and define the search bounds for each tunable parameter as specified above.
- Step 4: Employ each metaheuristic algorithm (FOX, GTO, PSO, SCSO, SSA) to optimize the hyperparameter configuration. Optimizers apply different population update mechanisms as defined in Section 3.1, Section 3.2, Section 3.3, Section 3.4, Section 3.5; steps of each optimizer are iterated in their original literature. The algorithm iteratively updates candidate solutions based on fitness evaluation using the MSE score as the objective function. In this study, the objective function is defined as the mean of the MSE over a 2-fold cross-validation, computed on the training dataset for each candidate hyperparameter set. This approach ensures a robust assessment of model performance while maintaining computational efficiency during the search process.
- Step 5: At each iteration, compute the fitness of the current hyperparameter set, update the global best and individual best positions, and assess convergence criteria. The process continues until the maximum number of iterations is reached or convergence is achieved.
- Step 6: Retrieve the optimal hyperparameter set identified by each optimizer. Evaluate the final model on the test set using multiple performance metrics.
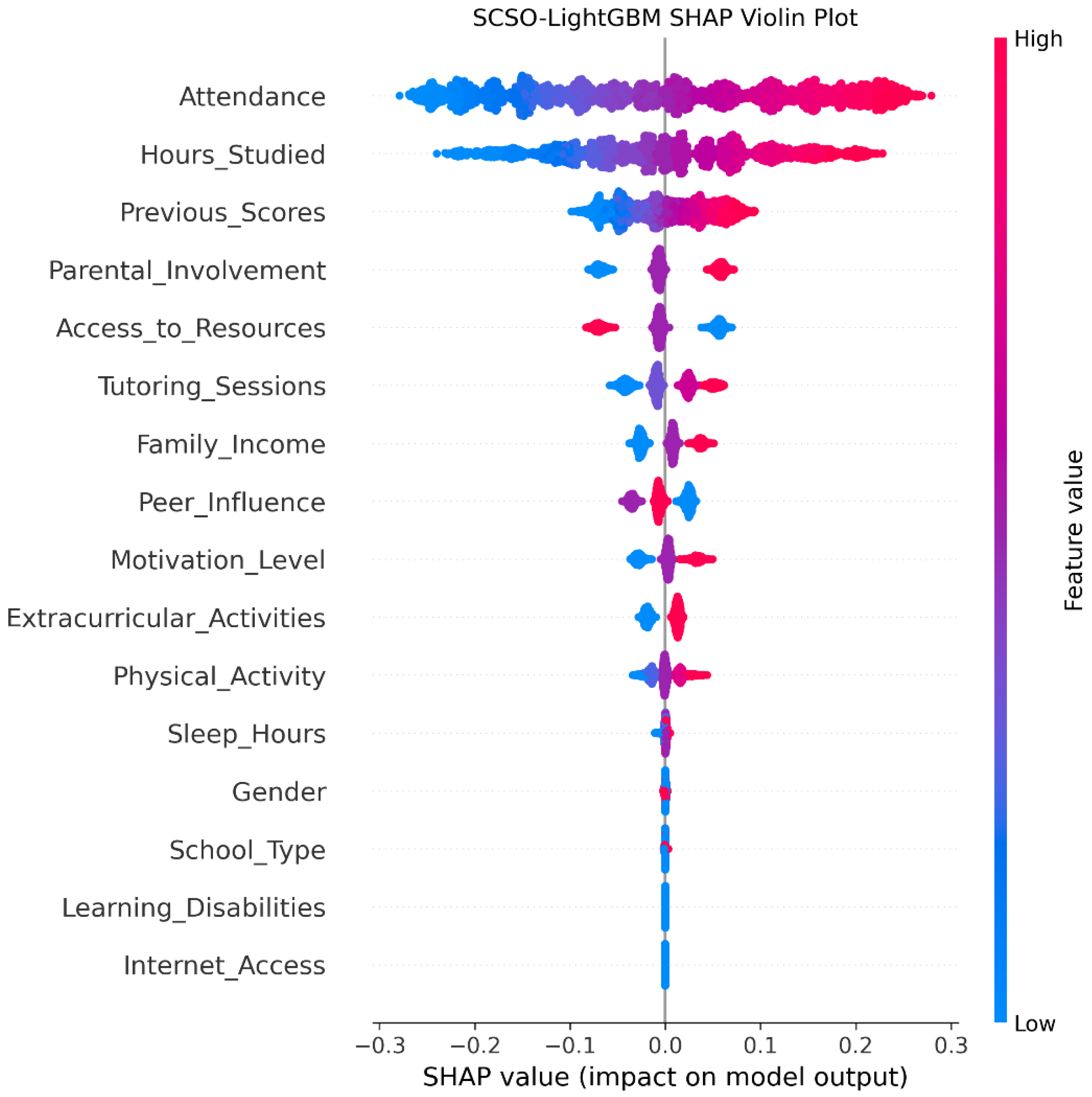
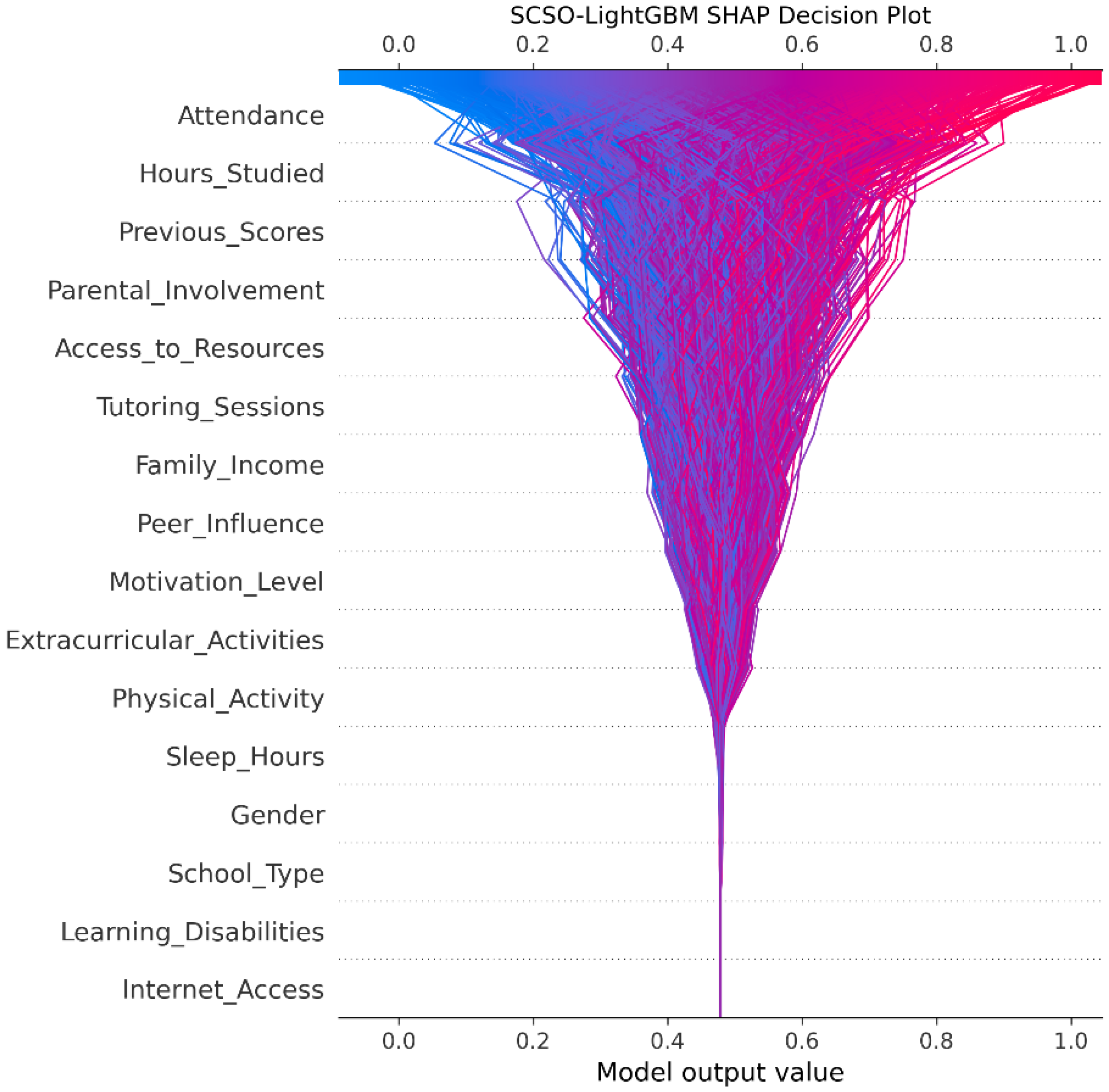
- Step 7: Perform SHAP analysis to interpret model predictions, identify key influencing features, and validate the results against pedagogical insights.
3.8. Data
3.9. Model Evaluation Metrics
3.10. Proposed Comparative Optimization Framework
4. Experiment and Discussion
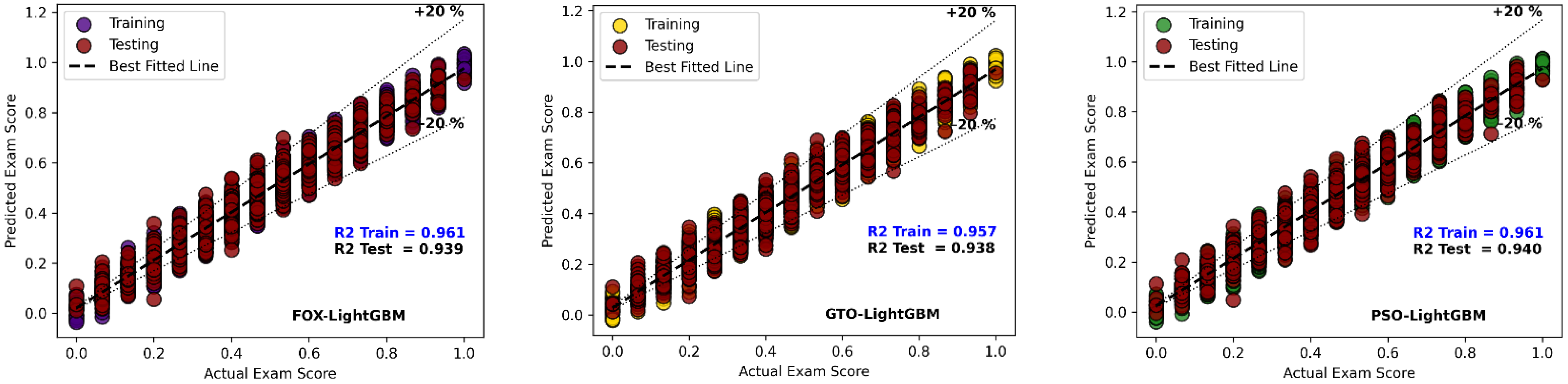
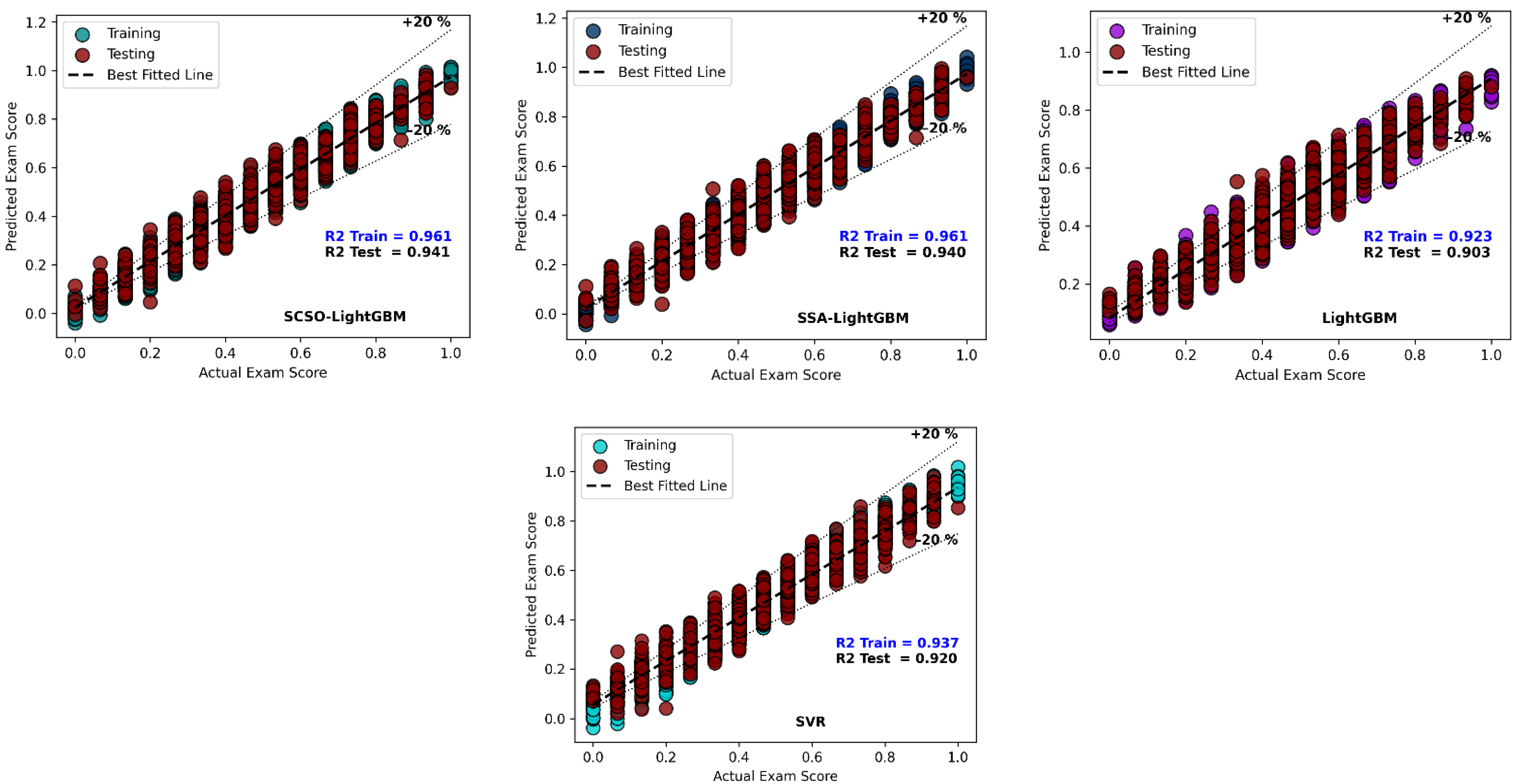
4.1. Student Performance Prediction
4.1.1. Cross-Validation Analysis
4.1.2. Independent Run Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saksiriruthai, S. Human Capital as a Determinant of Long-Term Economic Growth. In Research Anthology on Preparing School Administrators to Lead Quality Education Programs; IGI Global Scientific Publishing: Hershey, PA, USA, 2021; pp. 1518–1533. [Google Scholar] [CrossRef]
- Baumann, C.; Hamin. The role of culture, competitiveness and economic performance in explaining academic performance: A global market analysis for international student segmentation. J. Mark. High. Educ. 2011, 21, 181–201. [Google Scholar] [CrossRef]
- Barro, R.J.; McCleary, R.M. Religion and Economic Growth across Countries. Am. Sociol. Rev. 2003, 68, 760–781. [Google Scholar] [CrossRef]
- Barro, R.J. Determinants of Economic Growth: A Cross-Country Empirical Study; National Bureau of Economic Research: Cambridge, MA, USA, 1996; p. 5698. [Google Scholar] [CrossRef]
- Sultana, T.; Dey, S.R.; Tareque, M. Exploring the linkage between human capital and economic growth: A look at 141 developing and developed countries. Econ. Syst. 2022, 46, 101017. [Google Scholar] [CrossRef]
- Ahmed, W.; Wani, M.A.; Plawiak, P.; Meshoul, S.; Mahmoud, A.; Hammad, M. Machine learning-based academic performance prediction with explainability for enhanced decision-making in educational institutions. Sci. Rep. 2025, 15, 26879. [Google Scholar] [CrossRef]
- Vaarma, M.; Li, H. Predicting student dropouts with machine learning: An empirical study in Finnish higher education. Technol. Soc. 2024, 76, 102474. [Google Scholar] [CrossRef]
- Dwivedi, D.N.; Mahanty, G.; Dwivedi, V.N. The Role of Predictive Analytics in Personalizing Education: Tailoring Learning Paths for Individual Student Success. In Enhancing Education with Intelligent Systems and Data-Driven Instruction; IGI Global Scientific Publishing: Hershey, PA, USA, 2024; pp. 44–59. [Google Scholar] [CrossRef]
- Pelima, L.R.; Sukmana, Y.; Rosmansyah, Y. Predicting University Student Graduation Using Academic Performance and Machine Learning: A Systematic Literature Review. IEEE Access 2024, 12, 23451–23465. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Sayed, S.; Abdoulhalik, A.; Moutari, S.; Oyedele, L. Applications of machine learning to water resources management: A review of present status and future opportunities. J. Clean. Prod. 2024, 441, 140715. [Google Scholar] [CrossRef]
- Ke, W.; Chan, K.-H. A Multilayer CARU Framework to Obtain Probability Distribution for Paragraph-Based Sentiment Analysis. Appl. Sci. 2021, 11, 11344. [Google Scholar] [CrossRef]
- Xing, Z.; Lam, C.-T.; Yuan, X.; Im, S.-K.; Machado, P. MMQW: Multi-Modal Quantum Watermarking Scheme. IEEE Trans. Inf. Forensics Secur. 2024, 19, 5181–5195. [Google Scholar] [CrossRef]
- Alnasyan, B.; Basheri, M.; Alassafi, M. The power of Deep Learning techniques for predicting student performance in Virtual Learning Environments: A systematic literature review. Comput. Educ. Artif. Intell. 2024, 6, 100231. [Google Scholar] [CrossRef]
- Hasan, R.; Palaniappan, S.; Raziff, A.R.A.; Mahmood, S.; Sarker, K.U. Student Academic Performance Prediction by using Decision Tree Algorithm. In Proceedings of the 2018 4th International Conference on Computer and Information Sciences (ICCOINS), Kuala Lumpur, Malaysia, 13–14 August 2018; pp. 1–5. [Google Scholar]
- Alamri, H.L.; S. Almuslim, R.; S. Alotibi, M.; K. Alkadi, D.; Ullah Khan, I.; Aslam, N. Predicting Student Academic Performance using Support Vector Machine and Random Forest. In Proceedings of the 2020 3rd International Conference on Education Technology Management, London, UK, 17–19 December 2020; Association for Computing Machinery: New York, NY, USA, 2021; pp. 100–107. [Google Scholar]
- Salah Hashim, A.; Akeel Awadh, W.; Khalaf Hamoud, A. Student Performance Prediction Model based on Supervised Machine Learning Algorithms. IOP Conf. Ser. Mater. Sci. Eng. 2020, 928, 032019. [Google Scholar] [CrossRef]
- Sravani, B.; Bala, M.M. Prediction of Student Performance Using Linear Regression. In Proceedings of the 2020 International Conference for Emerging Technology (INCET), Belgaum, India, 5–7 June 2020; pp. 1–5. [Google Scholar]
- Tripathi, A.; Yadav, S.; Rajan, R. Naive Bayes Classification Model for the Student Performance Prediction. In Proceedings of the 2019 2nd International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, India, 5–6 July 2019; Volume 1, pp. 1548–1553. [Google Scholar]
- Huang, C.; Zhou, J.; Chen, J.; Yang, J.; Clawson, K.; Peng, Y. A feature weighted support vector machine and artificial neural network algorithm for academic course performance prediction. Neural Comput. Appl. 2023, 35, 11517–11529. [Google Scholar] [CrossRef]
- Ahmed, S.T.; Al-Hamdani, R.; Croock, M.S. Enhancement of student performance prediction using modified K-nearest neighbor. TELKOMNIKA (Telecommun. Comput. Electron. Control) 2020, 18, 1777–1783. [Google Scholar] [CrossRef]
- Baashar, Y.; Alkawsi, G.; Mustafa, A.; Alkahtani, A.A.; Alsariera, Y.A.; Ali, A.Q.; Hashim, W.; Tiong, S.K. Toward Predicting Student’s Academic Performance Using Artificial Neural Networks (ANNs). Appl. Sci. 2022, 12, 1289. [Google Scholar] [CrossRef]
- Parrales-Bravo, F.; Caicedo-Quiroz, R.; Barzola-Monteses, J.; Cevallos-Torres, L. Applying Bayesian Networks to Predict and Understand the Student Academic Performance. In Proceedings of the 2024 Second International Conference on Advanced Computing & Communication Technologies (ICACCTech), Sonipat, India, 16–17 November 2024; pp. 738–743. [Google Scholar]
- Yang, S.J.H.; Lu, O.H.T.; Huang, A.Y.Q.; Huang, J.C.H.; Ogata, H.; Lin, A.J.Q. Predicting Students’ Academic Performance Using Multiple Linear Regression and Principal Component Analysis. J. Inf. Process. 2018, 26, 170–176. [Google Scholar] [CrossRef]
- Wilson, A.; Anwar, M.R. The Future of Adaptive Machine Learning Algorithms in High-Dimensional Data Processing. Int. Trans. Artif. Intell. 2024, 3, 97–107. [Google Scholar] [CrossRef]
- Yaqoob, A.; Verma, N.K.; Aziz, R.M. Metaheuristic Algorithms and Their Applications in Different Fields. In Metaheuristics for Machine Learning; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2024; pp. 1–35. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf (accessed on 29 August 2025).
- Xu, H.; Kim, M. Combination prediction method of students’ performance based on ant colony algorithm. PLoS ONE 2024, 19, e0300010. [Google Scholar] [CrossRef] [PubMed]
- Fang, R.; Zhou, T.; Yu, B.; Li, Z.; Ma, L.; Luo, T.; Zhang, Y.; Liu, X. Prediction model of middle school student performance based on MBSO and MDBO-BP-Adaboost method. Front. Big Data 2025, 7, 1518939. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.; Liu, Y.; Jia, Y. Evaluation of students’ performance during the academic period using the XG-Boost Classifier-Enhanced AEO hybrid model. Expert Syst. Appl. 2024, 238, 122136. [Google Scholar] [CrossRef]
- Lowast, A.E.; Amalarethinam, D.I.G. A Hybrid Model of Enhanced Teacher Learner Based Optimization (ETLBO) with Particle Swarm Optimization (PSO) Algorithm for Predicting Academic Student Performance. INDJST 2025, 18, 772–783. [Google Scholar] [CrossRef]
- Li, G.; Cui, J.; Fu, H.; Sun, Y. Light GBM and GA Based Algorithm for Predicting and Improving Students’ Performance in Higher Education in the Context of Big Data. In Proceedings of the 2024 7th International Conference on Education, Network and Information Technology (ICENIT), Dalian, China, 16–18 August 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Apriyadi, M.R.; Ermatita; Rini, D.P. Hyperparameter Optimization of Support Vector Regression Algorithm using Metaheuristic Algorithm for Student Performance Prediction. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 144–150. [Google Scholar] [CrossRef]
- Kamal, M.; Chakrabarti, S.; Ramirez-Asis, E.; Asís-López, M.; Allauca-Castillo, W.; Kumar, T.; Sanchez, D.T.; Rahmani, A.W. Metaheuristics Method for Classification and Prediction of Student Performance Using Machine Learning Predictors. Math. Probl. Eng. 2022, 2022, 2581951. [Google Scholar] [CrossRef]
- Xu, H. Prediction of Students’ Performance Based on the Hybrid IDA-SVR Model. Complexity 2022, 2022, 1845571. [Google Scholar] [CrossRef]
- Song, X. Student performance prediction employing k-Nearest Neighbor Classification model and meta-heuristic algorithms. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 4397–4412. [Google Scholar] [CrossRef]
- Ma, C. Improving the Prediction of Student Performance by Integrating a Random Forest Classifier with Meta-Heuristic Optimization Algorithms. | EBSCOhost. Available online: https://openurl.ebsco.com/contentitem/doi:10.14569%2Fijacsa.2024.01506106?sid=ebsco:plink:crawler&id=ebsco:doi:10.14569%2Fijacsa.2024.01506106 (accessed on 30 August 2025).
- Ali, M.; Liaquat, M.D.; Atta, M.N.; Khan, A.; Lashari, S.A.; Ramli, D.A. Improving Student Performance Prediction Using a PCA-based Cuckoo Search Neural Network Algorithm. Procedia Comput. Sci. 2023, 225, 4598–4610. [Google Scholar] [CrossRef]
- Punitha, S.; Devaki, K. A high ranking-based ensemble network for student’s performance prediction using improved meta-heuristic-aided feature selection and adaptive GAN for recommender system. Kybernetes 2024. [Google Scholar] [CrossRef]
- Hai, Q.; Wang, C. Optimizing Student Performance Prediction: A Data Mining Approach with MLPC Model and Metaheuristic Algorithm. | EBSCOhost. Available online: https://openurl.ebsco.com/contentitem/doi:10.14569%2Fijacsa.2024.0150407?sid=ebsco:plink:crawler&id=ebsco:doi:10.14569%2Fijacsa.2024.0150407 (accessed on 30 August 2025).
- Mohammed, H.; Rashid, T. FOX: A FOX-inspired optimization algorithm. Appl. Intell. 2023, 53, 1030–1050. [Google Scholar] [CrossRef]
- Sadeeq, H.T.; Abdulazeez, A.M. Giant Trevally Optimizer (GTO): A Novel Metaheuristic Algorithm for Global Optimization and Challenging Engineering Problems. IEEE Access 2022, 10, 121615–121640. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Proceedings of ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 36, 2627–2651. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Wang, J.; Chi, J.; Ding, Y.; Yao, H.; Guo, Q. Based on PCA and SSA-LightGBM oil-immersed transformer fault diagnosis method. PLoS ONE 2025, 20, e0314481. [Google Scholar] [CrossRef] [PubMed]
- Florek, P.; Zagdański, A. Benchmarking state-of-the-art gradient boosting algorithms for classification. arXiv 2023, arXiv:2305.17094. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Z.; Yang, H.; Tian, M. Predicting Coronary Heart Disease Using an Improved LightGBM Model: Performance Analysis and Comparison. IEEE Access 2023, 11, 23366–23380. [Google Scholar] [CrossRef]
- Alshari, H.; Saleh, A.; Odabas, A. Comparison of Gradient Boosting Decision Tree Algorithms for CPU Performance. Erciyes Tip Derg. 2021, 157–168. [Google Scholar]
- Farhan, M.; Chen, T.; Rao, A.; Shahid, M.I.; Xiao, Q.; Salam, H.A.; Ma, F. An experimental study of knock analysis of HCNG fueled SI engine by different methods and prediction of knock intensity by particle swarm optimization-support vector machine. Energy 2024, 309, 133165. [Google Scholar] [CrossRef]
- Sun, C.; Qin, W.; Yun, Z. A State-of-Health Estimation Method for Lithium Batteries Based on Fennec Fox Optimization Algorithm–Mixed Extreme Learning Machine. Batteries 2024, 10, 87. [Google Scholar] [CrossRef]
- Tan, C.; Sun, M.; Liu, W.; Tan, W.; Zhang, X.; Zhu, C.; Li, D. An Adaptive Layering Dual-Parameter Regularization Inversion Method for an Improved Giant Trevally Optimizer Algorithm. IEEE Access 2024, 12, 160761–160775. [Google Scholar] [CrossRef]
- Punitha, A.; Ramani, P.; Ezhilarasi, P.; Sridhar, S. Dynamically stabilized recurrent neural network optimized with intensified sand cat swarm optimization for intrusion detection in wireless sensor network. Comput. Secur. 2025, 148, 104094. [Google Scholar] [CrossRef]
- Yang, Z.; Jiang, Y.; Yeh, W.-C. Self-learning salp swarm algorithm for global optimization and its application in multi-layer perceptron model training. Sci. Rep. 2024, 14, 27401. [Google Scholar] [CrossRef]
- Student Performance Factors. Available online: https://www.kaggle.com/datasets/lainguyn123/student-performance-factors (accessed on 17 August 2025).
- Wang, T.; Zhang, M.; Li, Z. Explainable machine learning links erosion damage to environmental factors on Gansu rammed earth Great Wall. npj Herit. Sci. 2025, 13, 366. [Google Scholar] [CrossRef]
- Ahmed, A.H.A.; Jin, W.; Ali, M.A.H. Prediction of compressive strength of recycled concrete using gradient boosting models. Ain Shams Eng. J. 2024, 15, 102975. [Google Scholar] [CrossRef]
- Haryadi, D.; Hakim, A.R.; Atmaja, D.M.U.; Yutia, S.N. Implementation of Support Vector Regression for Polkadot Cryptocurrency Price Prediction. JOIV Int. J. Inform. Vis. 2022, 6, 201–207. [Google Scholar] [CrossRef]


| Hours_Studied | Attendance | Parental_Involvement | Access_to_Resources | Extracurricular_Activities | Sleep_Hours | Previous_Scores | Motivation_Level | ||
| count | 4313 | 4313 | 4313 | 4313 | 4313 | 4313 | 4313 | 4313 | |
| mean | 19.94 | 79.96 | 1.09 | 0.9 | 0.6 | 7.02 | 75.01 | 0.91 | |
| std | 5.24 | 11.45 | 0.69 | 0.7 | 0.49 | 1.2 | 14.34 | 0.69 | |
| min | 8 | 60 | 0 | 0 | 0 | 5 | 50 | 0 | |
| 25% | 16 | 70 | 1 | 0 | 0 | 6 | 63 | 0 | |
| 50% | 20 | 80 | 1 | 1 | 1 | 7 | 75 | 1 | |
| 75% | 24 | 90 | 2 | 1 | 1 | 8 | 87 | 1 | |
| max | 31 | 100 | 2 | 2 | 1 | 9 | 100 | 2 | |
| Internet_Access | Tutoring_Sessions | Family_Income | School_Type | Peer_Influence | Physical_Activity | Learning_Disabilities | Gender | Exam_Score | |
| count | 4313 | 4313 | 4313 | 4313 | 4313 | 4313 | 4313 | 4313 | 4313 |
| mean | 0 | 1.29 | 0.79 | 0.3 | 1 | 2.96 | 0 | 0.42 | 67.14 |
| std | 0 | 0.97 | 0.74 | 0.46 | 0.89 | 0.98 | 0 | 0.49 | 3.11 |
| min | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 60 |
| 25% | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 65 |
| 50% | 0 | 1 | 1 | 0 | 1 | 3 | 0 | 0 | 67 |
| 75% | 0 | 2 | 1 | 1 | 2 | 4 | 0 | 1 | 69 |
| max | 0 | 3 | 2 | 1 | 2 | 5 | 0 | 1 | 75 |
| Optimizer | Parameter Settings |
|---|---|
| FOX | |
| GTO | , |
| PSO | = 0.9, 0.4 |
| SCSO | = [0, ], |
| SSA |
| FOX-LightGBM | GTO-LightGBM | PSO-LightGBM | SCSO-LightGBM | SSA-LightGBM | LightGBM | SVR | ||
|---|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.9693 | 0.9581 | 0.9598 | 0.9609 | 0.9606 | 0.9224 | 0.9363 |
| STD | 7.212 × 10−3 | 5.647 × 10−3 | 1.114 × 10−3 | 5.173 × 10−4 | 8.283 × 10−4 | 8.680 × 10−4 | 4.054 × 10−4 | |
| RMSE | AVG | 3.606 × 10−2 | 4.234 × 10−2 | 4.155 × 10−2 | 4.100 × 10−2 | 4.113 × 10−2 | 5.775 × 10−2 | 5.231 × 10−2 |
| STD | 4.198 × 10−3 | 2.884 × 10−3 | 4.934 × 10−4 | 3.221 × 10−4 | 4.349 × 10−4 | 3.102 × 10−4 | 2.069 × 10−4 | |
| MSE | AVG | 1.318 × 10−3 | 1.801 × 10−3 | 1.727 × 10−3 | 1.681 × 10−3 | 1.692 × 10−3 | 3.335 × 10−3 | 2.737 × 10−3 |
| STD | 3.073 × 10−4 | 2.392 × 10−4 | 4.124 × 10−5 | 2.650 × 10−5 | 3.595 × 10−5 | 3.581 × 10−5 | 2.145 × 10−5 | |
| ME | AVG | 1.365 × 10−1 | 1.467 × 10−1 | 1.436 × 10−1 | 1.396 × 10−1 | 1.440 × 10−1 | 1.943 × 10−1 | 1.008 × 10−1 |
| STD | 1.515 × 10−2 | 7.976 × 10−3 | 8.224 × 10−3 | 7.349 × 10−3 | 7.337 × 10−3 | 1.046 × 10−2 | 5.541 × 10−4 | |
| RAE | AVG | 6.947 × 10−2 | 8.156 × 10−2 | 8.005 × 10−2 | 7.900 × 10−2 | 7.925 × 10−2 | 1.113 × 10−1 | 1.008 × 10−1 |
| STD | 8.158 × 10−3 | 5.286 × 10−3 | 7.716 × 10−4 | 7.940 × 10−4 | 1.060 × 10−3 | 8.750 × 10−4 | 6.880 × 10−4 |
| FOX-LightGBM | GTO-LightGBM | PSO-LightGBM | SCSO-LightGBM | SSA-LightGBM | LightGBM | SVR | ||
|---|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.9331 | 0.9343 | 0.9406 | 0.9412 | 0.9409 | 0.9074 | 0.9257 |
| STD | 4.131 × 10−3 | 4.544 × 10−3 | 1.238 × 10−3 | 2.060 × 10−3 | 1.963 × 10−3 | 1.672 × 10−3 | 2.589 × 10−3 | |
| RMSE | AVG | 5.354 × 10−2 | 5.306 × 10−2 | 5.049 × 10−2 | 5.021 × 10−2 | 5.034 × 10−2 | 6.303 × 10−2 | 5.647 × 10−2 |
| STD | 1.549 × 10−3 | 2.054 × 10−3 | 6.341 × 10−4 | 1.011 × 10−3 | 5.022 × 10−4 | 9.757 × 10−4 | 1.193 × 10−3 | |
| MSE | AVG | 2.869 × 10−3 | 2.820 × 10−3 | 2.550 × 10−3 | 2.522 × 10−3 | 2.534 × 10−3 | 3.974 × 10−3 | 3.190 × 10−3 |
| STD | 1.679 × 10−4 | 2.177 × 10−4 | 6.447 × 10−5 | 1.031 × 10−4 | 5.030 × 10−5 | 1.236 × 10−4 | 1.353 × 10−4 | |
| ME | AVG | 1.755 × 10−1 | 1.694 × 10−1 | 1.620 × 10−1 | 1.637 × 10−1 | 1.638 × 10−1 | 2.071 × 10−1 | 2.117 × 10−1 |
| STD | 1.543 × 10−2 | 1.391 × 10−2 | 6.862 × 10−3 | 8.939 × 10−3 | 1.586 × 10−2 | 2.015 × 10−2 | 2.909 × 10−2 | |
| RAE | AVG | 1.032 × 10−1 | 1.022 × 10−1 | 9.731 × 10−2 | 9.677 × 10−2 | 9.701 × 10−2 | 1.215 × 10−1 | 1.088 × 10−1 |
| STD | 3.456 × 10−3 | 3.861 × 10−3 | 2.182 × 10−3 | 2.745 × 10−3 | 1.314 × 10−3 | 3.084 × 10−3 | 3.314 × 10−3 |
| FOX-LightGBM | GTO-LightGBM | PSO-LightGBM | SCSO-LightGBM | SSA-LightGBM | LightGBM | SVR | ||
|---|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.9682 | 0.9610 | 0.9590 | 0.9609 | 0.9608 | 0.9229 | 0.9371 |
| STD | 8.981 × 10−3 | 8.017 × 10−3 | 2.782 × 10−3 | 5.743 × 10−4 | 8.170 × 10−4 | 2.220 × 10−16 | 0 | |
| Best | 0.9828 | 0.9732 | 0.9633 | 0.9618 | 0.9622 | 0.9229 | 0.9371 | |
| RMSE | AVG | 3.667 × 10−2 | 4.085 × 10−2 | 4.210 × 10−2 | 4.111 × 10−2 | 4.111 × 10−2 | 5.772 × 10−2 | 5.217 × 10−2 |
| STD | 5.348 × 10−3 | 4.342 × 10−3 | 1.398 × 10−3 | 3.012 × 10−4 | 3.012 × 10−4 | 6.939 × 10−18 | 2.776 × 10−17 | |
| Best | 2.730 × 10−2 | 3.402 × 10−2 | 3.986 × 10−2 | 4.065 × 10−2 | 4.065 × 10−2 | 5.772 × 10−2 | 5.217 × 10−2 | |
| MSE | AVG | 1.373 × 10−3 | 1.688 × 10−3 | 1.774 × 10−3 | 1.690 × 10−3 | 1.697 × 10−3 | 3.332 × 10−3 | 2.722 × 10−3 |
| STD | 3.884 × 10−4 | 3.467 × 10−4 | 1.203 × 10−4 | 2.472 × 10−5 | 3.530 × 10−5 | 8.674 × 10−19 | 4.337 × 10−19 | |
| Best | 7.450 × 10−4 | 1.158 × 10−3 | 1.589 × 10−3 | 1.653 × 10−3 | 1.636 × 10−3 | 3.332 × 10−3 | 2.722 × 10−3 | |
| ME | AVG | 1.340 × 10−1 | 1.483 × 10−1 | 1.521 × 10−1 | 1.444 × 10−1 | 1.432 × 10−1 | 1.980 × 10−1 | 1.005 × 10−1 |
| STD | 1.588 × 10−2 | 1.516 × 10−2 | 1.253 × 10−2 | 7.535 × 10−3 | 8.347 × 10−3 | 0 | 4.163 × 10−17 | |
| Best | 1.006 × 10−1 | 1.248 × 10−1 | 1.323 × 10−1 | 1.343 × 10−1 | 1.331 × 10−1 | 1.980 × 10−1 | 1.005 × 10−1 | |
| RAE | AVG | 7.028 × 10−2 | 7.829 × 10−2 | 8.069 × 10−2 | 7.880 × 10−2 | 7.895 × 10−2 | 1.106 × 10−1 | 9.999 × 10−2 |
| STD | 1.025 × 10−2 | 8.323 × 10−3 | 2.679 × 10−3 | 5.773 × 10−4 | 8.205 × 10−4 | 2.776 × 10−17 | 4.163 × 10−17 | |
| Best | 5.233 × 10−2 | 6.521 × 10−2 | 7.640 × 10−2 | 7.791 × 10−2 | 7.751 × 10−2 | 1.106 × 10−1 | 9.999 × 10−2 |
| FOX-LightGBM | GTO-LightGBM | PSO-LightGBM | SCSO-LightGBM | SSA-LightGBM | LightGBM | SVR | ||
|---|---|---|---|---|---|---|---|---|
| R2 | AVG | 0.9332 | 0.9316 | 0.9364 | 0.9386 | 0.9388 | 0.9032 | 0.9196 |
| STD | 3.275 × 10−3 | 3.517 × 10−3 | 2.868 × 10−3 | 1.296 × 10−3 | 6.900 × 10−4 | 4.441 × 10−16 | 2.220 × 10−16 | |
| Best | 0.9391 | 0.9382 | 0.9404 | 0.9406 | 0.9399 | 0.9032 | 0.9196 | |
| RMSE | AVG | 5.283 × 10−2 | 5.348 × 10−2 | 5.156 × 10−2 | 5.069 × 10−2 | 5.058 × 10−2 | 6.363 × 10−2 | 5.799 × 10−2 |
| STD | 1.294 × 10−3 | 1.366 × 10−3 | 1.152 × 10−3 | 5.344 × 10−4 | 2.851 × 10−4 | 1.388 × 10−17 | 0 | |
| Best | 5.048 × 10−2 | 5.086 × 10−2 | 4.995 × 10−2 | 4.986 × 10−2 | 5.015 × 10−2 | 6.363 × 10−2 | 5.799 × 10−2 | |
| MSE | AVG | 2.793 × 10−3 | 2.862 × 10−3 | 2.660 × 10−3 | 2.570 × 10−3 | 2.559 × 10−3 | 4.048 × 10−3 | 3.363 × 10−3 |
| STD | 1.370 × 10−4 | 1.471 × 10−4 | 1.199 × 10−4 | 5.428 × 10−5 | 2.898 × 10−5 | 0 | 0 | |
| Best | 2.548 × 10−3 | 2.586 × 10−3 | 2.495 × 10−3 | 2.486 × 10−3 | 2.515 × 10−3 | 4.048 × 10−3 | 3.363 × 10−3 | |
| ME | AVG | 1.743 × 10−1 | 1.816 × 10−1 | 1.758 × 10−1 | 1.610 × 10−1 | 1.657 × 10−1 | 2.201 × 10−1 | 2.037 × 10−1 |
| STD | 9.157 × 10−3 | 1.867 × 10−2 | 1.419 × 10−2 | 1.162 × 10−2 | 1.029 × 10−2 | 2.776 × 10−17 | 5.551 × 10−17 | |
| Best | 1.502 × 10−1 | 1.608 × 10−1 | 1.510 × 10−1 | 1.508 × 10−1 | 1.476 × 10−1 | 2.201 × 10−1 | 2.037 × 10−1 | |
| RAE | AVG | 1.040 × 10−1 | 1.053 × 10−1 | 1.015 × 10−1 | 9.976 × 10−2 | 9.955 × 10−2 | 1.252 × 10−1 | 1.141 × 10−1 |
| STD | 2.546 × 10−3 | 2.688 × 10−3 | 2.268 × 10−3 | 1.052 × 10−3 | 5.610 × 10−4 | 0 | 6.939 × 10−17 | |
| Best | 9.935 × 10−2 | 1.001 × 10−1 | 9.831 × 10−2 | 9.814 × 10−2 | 9.870 × 10−2 | 1.252 × 10−1 | 1.141 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abukader, A.; Alzubi, A.; Adegboye, O.R. Intelligent System for Student Performance Prediction: An Educational Data Mining Approach Using Metaheuristic-Optimized LightGBM with SHAP-Based Learning Analytics. Appl. Sci. 2025, 15, 10875. https://doi.org/10.3390/app152010875
Abukader A, Alzubi A, Adegboye OR. Intelligent System for Student Performance Prediction: An Educational Data Mining Approach Using Metaheuristic-Optimized LightGBM with SHAP-Based Learning Analytics. Applied Sciences. 2025; 15(20):10875. https://doi.org/10.3390/app152010875
Chicago/Turabian StyleAbukader, Abdalhmid, Ahmad Alzubi, and Oluwatayomi Rereloluwa Adegboye. 2025. "Intelligent System for Student Performance Prediction: An Educational Data Mining Approach Using Metaheuristic-Optimized LightGBM with SHAP-Based Learning Analytics" Applied Sciences 15, no. 20: 10875. https://doi.org/10.3390/app152010875
APA StyleAbukader, A., Alzubi, A., & Adegboye, O. R. (2025). Intelligent System for Student Performance Prediction: An Educational Data Mining Approach Using Metaheuristic-Optimized LightGBM with SHAP-Based Learning Analytics. Applied Sciences, 15(20), 10875. https://doi.org/10.3390/app152010875






