MH-WMG: A Multi-Head Wavelet-Based MobileNet with Gated Linear Attention for Power Grid Fault Diagnosis

Abstract

Artificial intelligence is increasingly embedded in power systems to boost efficiency, reliability, and automation. This study introduces an end-to-end, AI-driven fault-diagnosis pipeline built around a Multi-Head Wavelet-based MobileNet with Gated Linear Attention (MH-WMG). The network takes time-series signals converted into images as input and branches into three heads that, respectively, localize the fault area, classify the fault type, and predict the distance bin for all short-circuit faults. Evaluation employs the canonical Kundur two-area four-machine system, partitioned into six regions, twelve fault scenarios (including normal operation), and twelve predefined distance bins. MH-WMG achieves high performance: perfect accuracy, precision, recall, and F1 (1.00) for fault-area detection; strong fault-type identification (accuracy = 0.9604, precision = 0.9625, recall = 0.9604, and F1 = 0.9601); and robust distance-bin prediction (accuracy = 0.8679, precision = 0.8725, recall = 0.8679, and F1 = 0.8690). The model is compact and fast (2.33 M parameters, 44.14 ms latency, 22.66 images/s) and outperforms baselines in both accuracy and efficiency. The pipeline decisively outperforms conventional time-series methods. By rapidly pinpointing and classifying faults with high fidelity, it enhances grid resilience, reduces operational risk, and enables more stable, intelligent operation, demonstrating the value of AI-driven fault detection for future power-system reliability.

1. Introduction

Growing population, industrial expansion, and technological advances are driving wider deployment of electrical power systems to meet rising demand [1]. Concurrently, surging interest in AI especially the rapid proliferation of models and LLMs such as Chat-GPT—adds substantial electricity use from processor-intensive training and inference [2,3]. This demand, illustrated by Google’s nuclear-power deal for AI training and Bitcoin’s load (≈168.77 TWh/year) [4,5], magnifies stress on the grid. Amid these rising loads, grid reliability depends on core assets—especially transmission lines, which carry power over short and long distances. Ensuring high-quality, fault-free transmission is therefore essential, as failures on these lines propagate quickly and undermine the performance of the entire system. However, as this component is complex, it may suffer from different faults, abnormal conditions, caused by several factors such as environmental (such as lightning strikes, rain, ice buildup, and high winds), natural (animals and vegetation) [6], insulation contamination (salt spray or pollution) [7], structural flaws, and other operational issues. Consequently, two major faults can occur in transmission lines, namely, open and short circuit faults. Due to the fact that, short-circuit faults contribute to a much higher fault current comparing to open-circuit faults, then, they have become more popular and focused on. The short-circuit faults are classified under five main categories which are single line to ground, double line, double line to ground, triple line faults, triple line to ground faults [8,9]. The first type is the most popular fault among them [10]. Detecting the first occurrence of these faults and clearing them as quickly as possible is vital. Therefore, various studies aim to detect, classify, and localize these faults to enhance system stability, increase durability, maximize efficiency, improve fault resilience, and ensure the reliable and high-quality operation of the electrical network [11,12]. Recently, AI-driven methods, including deep learning architectures such as Deep Residual Networks (DRNs), Recurrent Neural Networks (RNN), Convolutional Neural Networks (CNNs), and hybrid models that combine multiple techniques, have been widely used. Recent advances in deep learning for fault diagnosis also include spiking neural networks (SNNs), which enable low-power, event-driven inference on time–frequency data; see, for example, biologically inspired compound defect detection using an SNN with continuous time–frequency gradients [13]. Other techniques, such as specific thresholds, statistical methods, various transforms, and machine learning algorithms have also been implemented for the same purpose. Recent progress in data-driven fault diagnosis spans adaptive thresholding with coordinate attention in tree-inspired networks for aero-engine bearings under strong noise and multi-branch parallel perception with feature-fusion strategies for multi-sensor bearing health monitoring [14,15]. While these advances demonstrate robust representation learning in noisy, rotating-machinery settings, our problem targets high-voltage transmission-line short-circuit events captured by PMUs, where time–frequency transients and grid topology call for a different design.

In pursuit of this goal, we present a unified framework for short-circuit fault diagnosis that treats time-series waveforms as images. Raw PMU signals from the Kundur two-area four-machine benchmark are conditioned and converted into 224 × 224 × 3 Morlet wavelet scalograms, producing time–frequency heatmaps that capture transient features. These scalograms are analyzed by our Multi-Head Wavelet-based MobileNet with Gated Linear Attention (MH-WMG), which in a five-second window identifies the faulted area (six regions), classifies the fault type (11 modes plus normal), and estimates the fault distance (12 bins). MH-WMG achieves perfect fault-area detection (accuracy, precision, recall, F1 = 1.00), strong fault-type classification (accuracy 0.9604, precision 0.9625, recall 0.9604, F1 0.9601), and robust distance-bin prediction (accuracy 0.8679, precision 0.8725, recall 0.8679, F1 0.8690). The model is compact and fast, with 2.33 M parameters, 44.14 ms latency, and 22.66 images/s throughput, and it outperforms the compared baselines in both accuracy and efficiency.

It is crucial to note that this study is scoped to overhead high-voltage (HV) transmission networks modeled by the standard Kundur two-area four-machine benchmark. In this setting, transmission lines operate at HV levels (nominal ≈ 230 kV) and the system is effectively (solidly) grounded via transformer neutrals. In addition, we restrict the scope to two-terminal, untapped lines (no intermediate taps/solders); multi-terminal or tapped corridors are excluded because a fault on a tap can be dual to a main-line fault, hindering unique localization. Because isolated or high-resistance grounded medium-voltage feeders exhibit low-current earth faults rather than high-current short-circuits, their detection principles differ; these regimes are therefore out of scope for the present work.

The article is organized as follows. Section 2 introduces the foundational concepts and summarizes related work. Section 3 describes the data acquisition setup and raw signal characteristics, and details the overall system architecture and the internal design of the proposed MH–WMG network. Section 4 presents the implementation procedure and reports comprehensive experimental results. Section 5 highlights the main findings and implications, and discusses limitations and directions for future research. Finally, Section 6 summarizes the contributions and key results.

2. Background and Related Work

This section first outlines the foundational concepts used throughout—electrical faults in HV networks; conventional line-mounted damage-detection devices; phasors; the Pearson correlation coefficient; wavelet transforms; MobileNet; and Gated Linear Attention—and then reviews related work to situate MH–WMG within classical and modern fault-diagnosis approaches.

2.1. Background

This section surveys the core concepts that support our study: the characteristics of electrical faults especially short-circuit events, phasor-measurement techniques, Pearson correlation coefficient, the fundamentals of the wavelet transform, and the design principles of the MobileNet-V3 architecture, and Gated Linear Attention (GLA). Understanding these topics gives the technical foundation needed for the next analyses and model development.

2.1.1. Electrical Faults

In general, electrical fields including power systems, power transmission lines, electrical machines, and electrical circuits can exhibit unusal conditions called faults. In short, a fault in electrical system can occur due to a failure in one or more of its components which lead to unusual operation of that equipment. The most popular faults are open and short-circuit faults [16]. Their terms can define these faults as the first occurs as the current path is broken (opened), such as a broken cable joint and the second occurs as the current passes through an unintended low resistance path (shortened), such as a fallen tree on transmission lines. For short-circuit faults, according to Ohm’s law ($V=IR$), a huge amount of electrical current will be present, as the current has an inverse relationship with the resistance, which is low in that path. Both of these faults contribute to severe consequences such as reduction of system reliability, power quality disturbances, equipment damage, under-utilization of protective devices, service interruption, thermal and mechanical stress, and safety concerns [17,18], thereby jeopardizing the power system.

Nevertheless, in power system analysis and design, short-circuit faults generally receive more attention than open-circuit faults as they lead to high fault currents. Moreover, short-circuit faults do not occur in just one regular type; instead, there are two main types of short-circuits: symmetrical and unsymmetrical faults [19]. Refer to Figure 1 for the types of each one.

These types of faults are called symmetrical since, even though they bring a huge amount of current to the system, they do not disturb its symmetry, equal magnitudes, and 120° phase separation of the three phases. As the magnitude and the separation stay the same, these types of faults can be either Line-to-Line-to-Line (LLL) or Line-to-Line-to-Line-to-Ground (LLLG). In contrast to symmetrical faults, when an unsymmetrical fault occurs, the system’s symmetry is disturbed, resulting in each phase current having a different magnitude and the separation angle between phases deviating from 120°. These types of faults can occur in three forms: Line-to-Ground (LG), Line-to-Line (LL), and Line-to-Line-to-Ground (LLG).

2.1.2. Conventional Line-Mounted Damage Detection Devices

Many overhead lines use devices on the line to find faults with either one-ended or two-ended measurements (modal/mode-parameter signals), including impedance and traveling-wave approaches [20,21]. In practice, modern units can point repair crews to about one span of accuracy, which is very useful [22]. Still, these devices have known limits: they often need very accurate time sync and reliable communications (especially for two-ended setups); they can be affected by noise, CT/PT saturation, and lightning; they struggle with high-resistance or evolving faults and with multi-terminal/tapped lines; they are harder to use on series-compensated corridors or grids rich in power electronics; wide coverage can be costly to install and maintain; and they rarely provide well-calibrated confidence for operators. These gaps motivate complementary, system-level methods that use richer waveform information, give unified detection–type–distance outputs, and report calibrated probabilities to support decisions—goals addressed by the proposed MH-WMG framework.

2.1.3. Phasor

A Phasor is a complex number used to represent a sinusoidal quantity such as voltage or current in Alternating Current (AC) systems. It is basically a mathematical trick to turn the problem of adding/subtracting sinusoids from a messy trigonometric task into a simpler problem of complex-number arithmetic. Eventually, it can be converted back to the time domain if needed. A time-domain sinusoidal signal like $v\left(t\right)=V_{m}sin(\omega t+\theta )$ can be expressed in the phasor form using the following Equation (1).

$$\overrightarrow{V}=V_m\angle \theta ;\overrightarrow{V}=V_m{e}^{j\theta },$$

(1)

where $V_m$ is the amplitude, $\omega$ is the angular frequency, and $\theta$ is the phase angle. Suppose a phasor representing voltage is ${\displaystyle \tilde{V}=100\angle {30}^{\circ }}$ volts (peak). The magnitude of 100 V indicates that the sinusoidal voltage swings from $+100$ V to $-100$ V. If we use RMS values instead, it would be approximately $70.7$ V RMS (since $V_{RMS}=\frac{V_{peak}}{\sqrt{2}}$). The angle of ${30}^{\circ }$ compared to a reference wave—a chosen sinusoidal signal (often at zero phase) used as the baseline against which all other sinusoidal signals’ phases are measured—at $0^{\circ }$, this waveform starts its cycle ${30}^{\circ }$ earlier than the reference one. Concretely, if the reference wave is at zero phase when $t=0$, this wave is already ${30}^{\circ }$ into its sine cycle at that instant.

2.1.4. Pearson Correlation Coefficient

In short, it is a statistics approach that measures the strength and direction of a linear association between two quantitative variables. It computes a correlation matrix across all columns, extracting and sorting the correlations of each feature with respect to the target feature [23]. Its output ranges between $-1$ and $+1$, that is, $-1\le r_{XY}\le +1$. A value of $+1$ indicates a perfect positive linear relationship, $-1$ a perfect negative linear relationship, and 0 implies no linear correlation between the variables. So that, the features whose correlation with the target variable exceeds a predetermined threshold can be identified. It can be calculated using Equation (2).

$$r_{XY}={\displaystyle \frac{{\sum }_{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{{\sum }_{i=1}^n{\left(x_i-\overline{x}\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}},$$

(2)

where n is the total number of data points, $x_i$ is the i-th observed value of feature X, $y_i$ is the i-th observed value of feature Y, $\overline{x}$ is the mean (average) of all $x_i$, $\overline{y}$ is the mean of all $y_i$, $r_{XY}$ is the correlation coefficient between X and Y.

2.1.5. Wavelet Transform

The wavelet word in wavelet transform refers to small wave [24] mean in French language which actually reflects the core of it. The wavelet transform was initially introduced in 1980 as a powerful tool for analyzing the local differentiability of functions—meaning how smoothly the function behaves around specific points— and for precisely detecting and characterizing singularities, which are abrupt changes or irregularities within a signal [25]. Unlike other transforms, such as the Fourier transform—which lacks time localization—the wavelet transform provides a joint representation of both time and frequency, converting a signal from the time domain into the time-frequency domain [26]. The Fourier transform is still useful for time-series analysis, as shown in [27]. However, the wavelet transform introduces a trade-off between time and frequency resolution, resulting in a lower frequency resolution compared to that of the Fourier transform [28]. The wavelet transform can be calculated using Equation (3).

$$W(a,b)={\displaystyle \frac{1}{\sqrt{\left|a\right|}}}{\int }_{-\infty }^{+\infty }x\left(t\right){\psi }^{*}\left({\displaystyle \frac{t-b}{a}}\right)\mathrm{d}t,$$

(3)

where $W(a,b)$ is wavelet coefficient (result of transform), $x\left(t\right)$ is signal or function to be analyzed, $\psi \left(t\right)$ is mother wavelet function, a is scale parameter dilation/compression factor), b is translation (shift) parameter, ${\psi }^{*}\left(t\right)$ is complex conjugate of the mother wavelet, and t is time or spatial variable. Any signal with all the following three conditions can be considered as a mother Wavelet, first, zero mean condition, which means the average value of the wavelet function should be exactly zero, meaning its positive and negative areas balance each other out. Second, finite energy (limited duration) which refers to the wavelet function should exist only for a limited duration or interval, with its energy concentrated within this period. It should not extend infinitely or keep going indefinitely. In signal processing, signal energy describes how strong or concentrated the signal is within a certain period. Specifically, it can be mathematically calculated as the integral (sum) of the square of its amplitude over time, refer to Equation (4).

$$E={\int }_{-\infty }^{+\infty }{\left|f\left(t\right)\right|}^{2}dt,$$

(4)

where E is energy of the signal, $f\left(t\right)$ is signal function, t is time variable, and $\left|f\right(t\left)\right|$ is magnitude (amplitude) of the function $f\left(t\right)$. Third is the admissibility condition so that the mother wavelet can be mathematically transformed back and forth without losing important information. It is crucial to note that if any of the stated constraints is violated then the signal can not be used as a mother wavelet.

2.1.6. MobileNet

Lately, interest in building small and efficient Neural Networks (NNs) has grown due to the widespread use of resource-constrained devices such as mobile phones. The goal of these NNs is to fit onto such devices, thereby improving performance by reducing both memory usage and inference time [29]. One example is MobileNet, a small CNN pre-trained model that uses depthwise separable convolutions to significantly reduce the number of parameters. As its name suggests, MobileNet is well-suited for mobile and embedded vision applications [30]. There are three main versions of MobileNet: v1, v2, and v3 (the latter includes v3-large and v3-small). MobileNet-v2 offers higher efficiency in terms of parameter count, Central Process Unit (CPU) and memory usage, accuracy, running time, number of feature map channels, and overall operations [31]. Meanwhile, MobileNet-V3 is even more accurate compared to MobileNet-v2. Specifically, MobileNet-V3 small is approximately 6.6% more accurate and has similar latency when compared to MobileNet-v2 [32]. MobileNet-V3 introduced squeeze-and-excitation modules and replaced the sigmoid part of the Swish activation function (Equation (5)) with ReLU6, resulting in the hard-Swish (h-swish) non-linearity (Equation (6)), which can produce negative values. Consequently, models using ReLU6 are lighter than those using Sigmoid. ReLU6 (Equation (7)) is a variant of ReLU capped at 6—an experimentally determined threshold that helps models extract sparse features more quickly. Additionally, h-swish reduces the number of memory accesses, leading to lower latency overall.

$$swish\left(x\right)=x·\sigma \left(x\right).$$

(5)

$$h-swish\left(x\right)=x·{\displaystyle \frac{ReLU6(x+3)}{6}}.$$

(6)

$$ReLU6\left(x\right)=min\left(max(0,x),6\right).$$

(7)

The typical inverted-residual bottleneck block in MobileNet-V3 can be summarised as follows. Let the input tensor have spatial resolution $h\times w$ and k channels. First, a $1\times 1$ expansion convolution widens the channel dimension to $tk$ (where t is the expansion ratio) and applies the block’s non-linearity—ReLU or the lighter hard-swish (h-swish) used throughout MobileNet-V3. Next, a $3\times 3$ depth-wise convolution with stride s processes each channel independently, producing feature maps of size $(h/s)\times (w/s)\times tk$. When the block is equipped with a squeeze-and-excitation (SE) module, global average pooling is followed by two fully-connected layers with ReLU and a hard-sigmoid gating function, thereby re-weighting channels adaptively. A final linear $1\times 1$ projection convolution then reduces the channel count to $k^{\prime }$. When $s=1$ and $k=k^{\prime }$ a residual shortcut is added, completing the inverted-residual structure. For the case $s=1$ the approximate floating-point-operation (FLOP) cost of a block is stated in Equation (8).

$$FLOP=\underset{\mathrm{expansion}}{\underbrace{hwkt}}+\underset{\mathrm{depth}-\mathrm{wise}}{\underbrace{9hwtk}}+\underset{\mathrm{projection}}{\underbrace{hwtk{k}^{\prime }}},$$

(8)

where the middle and last terms scale by $1/s^2$ when $s>1$.

2.1.7. Gated Linear Attention

GLA is a lightweight yet effective mechanism designed to enrich token representations by introducing content-dependent interactions without adding trainable parameters. In GLA, the input $\mathbf{X}\in {\mathbb{R}}^{S\times D}$ is shared across the query, key, and value matrices: $\mathbf{Q}=\mathbf{K}=\mathbf{V}=\mathbf{X}$. The affinity matrix $\mathbf{A}\in {\mathbb{R}}^{S\times S}$ is computed as $\mathbf{A}=ELU\left(\mathbf{Q}{\mathbf{K}}^{\top }\right)$, where the exponential linear unit (ELU) introduces smooth sparsity to the attention scores. A gating vector $\mathbf{g}\in {\mathbb{R}}^S$ is then derived by applying a sigmoid function to the row-wise sums of $\mathbf{A}$, i.e., $\mathbf{g}=\sigma \left({\sum }_{i=1}^S{\mathbf{A}}_{i:}\right)$. The intermediate output $\mathbf{Z}$ is obtained via element-wise gating: $\mathbf{Z}=\left(\mathbf{A}\mathbf{V}\right)\odot \mathbf{g}[:,\mathbf{1}]$, where ⊙ denotes the Hadamard product. Finally, a residual connection $\mathbf{Y}=\mathbf{Z}+\mathbf{X}$ facilitates gradient flow and model stability [33]. Because GLA relies solely on algebraic operations (matrix multiplication, summation, and element-wise activations), it retains computational efficiency while enriching the expressiveness of token-wise representations. Benefits provided by GLA can be summarized as follows:

1.

Global contextualization—every token is updated with information from all other tokens via the affinity matrix $\mathbf{A}$.

2.

Adaptive gating—the sigmoid vector $\mathbf{g}$ selectively filters the aggregated context so that only the most salient information is retained.

3.

Low model cost—GLA adds no trainable weights and keeps the computational complexity at $\mathcal{O}\left(S^{2}d\right)$, leaving the overall parameter count of the distance-bin head unchanged.

Hence, GLA enhances representational power and regularizes the model without inflating the model size.

2.2. Related Works

Short-circuit fault identification, classification, and localization in power transmission lines have been areas of active research, with scientists achieving high levels of efficiency using a variety of methods. Over the years, a wide range of topologies and algorithms have been employed for fault diagnosis, including traditional threshold-based techniques, machine learning algorithms, various artificial intelligence approaches, and other techniques. Time-series signals and their image-based representations (e.g., scalograms) are the key data sources for fault analysis. Forecasting models such as those compared in [34] reveal subtle deviations before a fault occurs, while the scalograms can also help detect and classify the events.

A hybrid Fault Detection and Diagnosis (FDD) approach, which mainly uses Principal Component Analysis (PCA) along with sliding windows of the Discrete Fourier Transform (DFT) and Discrete Hilbert Transform (DHT), is presented in [35]. The data used consist of 619 Comma-Separated Values (CSV) files containing seven different short-circuit faults generated by the HyperSim simulator. Their model was employed for two purposes: fault detection and identification, achieving accuracies of 100% and approximately 98%, respectively. However, the work classifies only 7 out of 12 short-circuit faults, inculding normal operation. It also lacks details regarding the training procedure and information on the importance of each method within the proposed hybrid approach.

In [36], a method based on Mallat decomposition algorithm is used to detect short-circuit faults. Other methods, such as the Wavelet Detection Method (WDM), Current Rate of Change Method (CRCM), and Current Waveform Area Method (CWAM), are implemented as well. Their purpose was millisecond-level detection of short-circuit faults before they occur. The system’s hardware includes current converters and a chip connected via Serial Peripheral Interface (SPI) to two Microcontroller Units (MCUs) responsible for data gathering and fault detection. The sampling frequency is set to 10 kHz exceeding twice the typical 3 kHz fault transient frequency, to ensure timely data collection. Their algorithm is implemented in C using Keil 5.0 software. The proposed WDM was tested in 42 experiments and was able to detect faults within 2 ms, while two other methods achieved 0.5 ms. They stated that also the threshold setting in CRCM and CWAM methods is challenging; thresholds set too low can decrease algorithm reliability by causing false detections, whereas thresholds set too high delay fault detection, reducing algorithm responsiveness.

The study [37] utilized the Capsule Network with Sparse Filtering (CNSF) for the detection and classification of transmission line faults. The model encodes the time series signal into a Gramian Angular Field (GAF) image, which undergoes a discrete wavelet transform, resulting in a single feature representing the fault condition. Four transmission line models (TL-1 to TL-4) were simulated in MATLAB/Simulink R2022b to benchmark the CNSF-based Fault Detection and Classification (FDC) system. The generated data contains 3465 distinct fault cases for each of the ten short-circuit faults and the non-fault case, leading to a total of 38,115 samples. The model achieved an accuracy between 99.47% and 99.72%. When noise was added to the data, the accuracy decreased to 97%. As a limitation, this study also does not provide any information about the training procedure and lacks the validation part, leaving the model performance ambiguous and suggesting potential overfitting issues.

The Transfer Function (TF) method is used in [38] for detecting single-phase-to-ground short-circuit faults. However, based on the obtained results, the TF method is considered inadequate; therefore, a CNN and a hybrid Deep Reinforcement Learning (DRL) approach are examined. To assess the performance of the models, the system described in [39] is simulated using the ATP/EMTP environment. This study investigates single-phase-to-ground faults applied at six equally divided segments of a transmission line, with fault impedances ranging from 1 to 5000 Ohms. The research uses the correlation coefficient (R), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE) as evaluation metrics. The CNN model achieved (0.9521, 0.2963, 0.5443), while the DRL model achieved (0.9661, 0.2222, 0.4713) for (R, MSE, RMSE), respectively. However, this study does not provide details about the tuning process or the final values of the hyperparameters. As a result, reproducing the used models is nearly impossible.

Random Forest (RF), K-Nearest Neighbors (KNN), Long Short-Term Memory (LSTM) networks, and hybrid RF-LSTM-tuned KNN techniques are explored in terms of detecting and classifying faults in power transmission lines in [40]. These models are applied to two different data: a Kaggle data and a real-time simulation data. The first is obtained from a system that contains four 11 kV generators and transformers. The data itself has two parts—binary and multiclass with 12,001 rows and 9 columns, and 7861 rows and 10 columns, respectively. The other data has 11,701 rows and 10 columns. It is related to current and voltage signals. Six cases, including a no-fault situation, are investigated. As a data preprocessing step, PCA was utilized. Eventually, for the binary problem, the obtained accuracies are 99.75% for KNN and 99.72% for RF. For the multiclass problem, RF-LSTM was able to achieve 99.93% accuracy. While there can be 11 classes, preparing a model to detect only 6 of them may, in some cases, be insufficient.

The study by [41] evaluates various types of CNNs such as ResNet-152v2, Inception-v3, EfficientNet-B2, DenseNet, Xception, etc., and proposes a new model. This study introduces an innovative deep learning model that combines 1-D CNNs and a transformer encoder to automatically identify fault type, phase, and location. The CNNs are used to extract key features, while the transformer encoder applies attention mechanisms to capture important time-based patterns and understand long-term dependencies in the current signals. They are all evaluated using F1-score, Matthews Correlation Coefficient (MCC), and accuracy metrics over the IEEE 14-bus distribution system. The training data contain 2355 samples, and the test data contain 785 samples, with a ratio of 75:25. The included faults are symmetrical faults, unsymmetrical faults, and High-Impedance Faults (HIFs). DenseNet achieved the best performance for fault bus location with an MCC of 97.8%, and the Xception transformer was best for phase classification with an MCC of 97.53%. In addition, the proposed Xception transformer achieved (accuracy, F1-score, MCC) of (0.9860, 0.9858, 0.9753) for type and phase classification, and (0.9809, 0.9806, 0.9614) for bus location. The study did not mention the importance of each layer in their proposed model in terms of an ablation study. The feature importance of each layer and data leakage tests are also not stated.

The research carried out in [42] leverages the Continuous Wavelet Transform (CWT) and a CNN optimized using Bayesian optimization. The proposed model is designed to classify eleven types of short-circuit faults and determine their locations. The data used is synthetic, generated by simulating faults with resistance values ranging from 50 ohms to 2 kilo-ohms and durations between 20 ms and 2 s over a radial distribution network. The data consist of 26,754 samples. The model achieved an accuracy of 91.4% for fault detection, 93.77% for correct branch identification, and 94.93% for fault type classification. For fault location, it attained a RMSE of 2.45%. As the proposed model relies heavily on synthetic data, this limits its realism and requires detailed grid knowledge. Additionally, the model struggles with unseen fault types, changes in grid topology, and has limited performance in mesh network configurations.

Another study that investigates short-circuit fault region, type, and location in power transmission lines is presented in [43]. The authors employed an LSTM model for this task. The data used is based on the Kundur two-area four-machine system and includes both current and voltage signal magnitudes and angles. The system is divided into six regions. The training set consists of 1081 samples, while the test set includes 1481 samples. These were collected separately over 10 s simulations, with faults applied at varying distances along the transmission lines. The model achieved an average accuracy of 87.41% in identifying the faulted region, including all six areas and the no-fault case. For fault type classification, the reported metric pertains to only one region, with an average accuracy of 96.75%. Regarding fault distance estimation, the model yielded a mean absolute error of 0.213, with a standard deviation of 0.196, a minimum of 0.004, and a maximum of 0.632. However, there are notable issues in the study. There appears to be data leakage between the training and test sets, as they were collected separately and may share overlapping fault distances. Additionally, the model achieves 100% accuracy on the training set, while significantly lower performance is observed on the test set—indicating a clear case of overfitting. Furthermore, critical aspects such as hyperparameter tuning and layer-wise feature importance analysis were not discussed.

This study [44] introduces a novel approach for estimating single phase-to-ground faults in high voltage DC transmission lines using Discrete Wavelet Transform (DWT) and Extreme Learning Machine (ELM). Fault data are simulated in MATLAB based on a monopolar High Voltage Direct Current (HVDC) system, and wavelet coefficients are used to extract features such as Shannon entropy and signal energy. These features are then normalized and fed into the ELM for fault location estimation. The Daubechies (db4) wavelet is used to analyze the first 20 ms of simulated fault signals. DWT yields 13 features, but the 12th-level approximate coefficient is discarded due to its low-frequency content. As a result, 22 feature vectors are extracted from current and voltage signals per fault location. The proposed method achieved R of 0.99443. Nevertheless, the model lacks further detailed evaluation and has only been applied to a single data.

The goal of [45]’s study is to develop an efficient fault detection and identification method for power systems by enhancing the detection of small defects in transmission lines. The proposed hybrid approach combines Stationary Wavelet Transform (SWT), undecimated reconstruction using the Algebraic Summation Operation (ASO), and Continuous Wavelet Transform (CWT) to improve signal redundancy and feature extraction. This technique aims to support early fault detection for predictive maintenance, thereby improving the reliability and stability of power system operations. The system used is related to the Djibouti power grid model, and the obtained data has a 0.2 s simulation time and 4000 data points. The model used different mother wavelets for different fault types and was able to detect five different types of faults at an approximate average time of 0.1167s. However, the research lacks detailed information about the used data, such as the number of generated samples per fault, which in turn does not ensure the actual performance of the model.

3. Materials and Methods

This section provides the necessary foundations for this study, including data aquision system, data description, general pipeline of the proposed system, and the internal structure of MH-WMG model.

3.1. Data Overview

This part of the study provides a comprehensive overview of the test system and data sources utilized throughout the study. First, the Kundur two-area four-machine Test System is introduced as the simulation environment used to generate diverse fault scenarios and evaluate the proposed model. Then, the data acquisition system is detailed, outlining the methods and tools employed to collect different signals.

3.1.1. Kundur Two-Area Four-Machine Test System

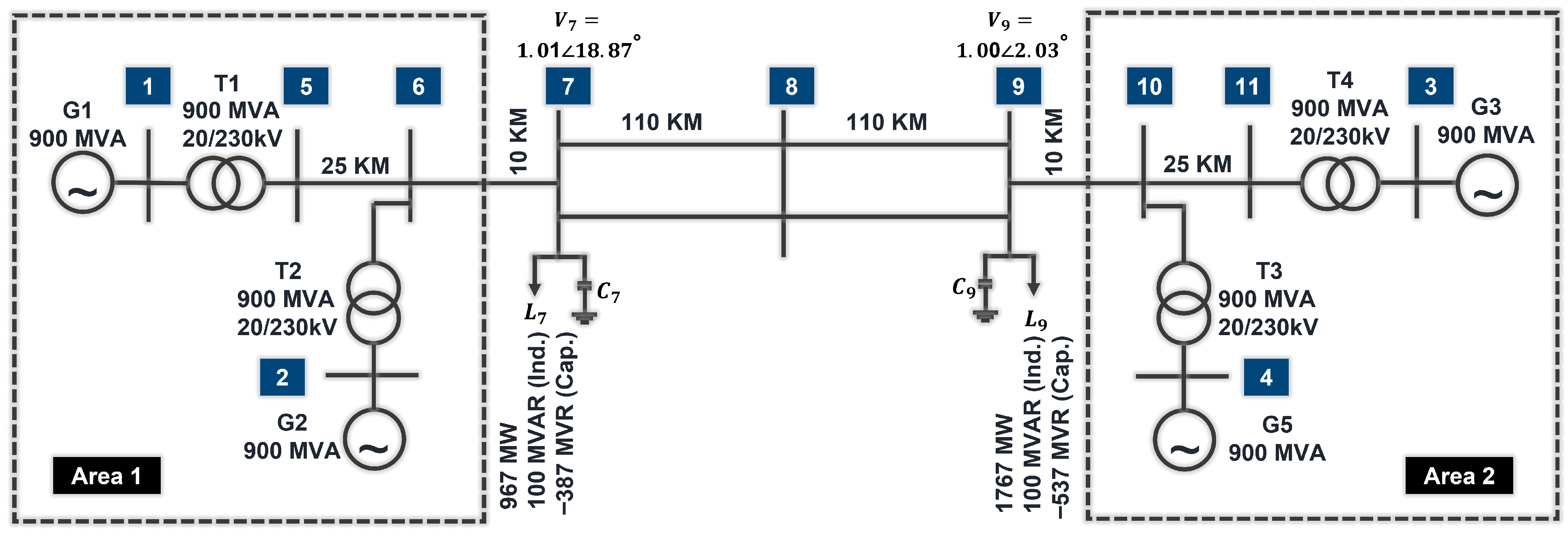
Since it includes almost the most important electrical equipments, The Kundur two-area four-machine system, introduced by Prabha Kundur [46], is a well-known system that researchers use to conduct studies related to the power system stability. It is used extensively in several fields such as analyzing small-signal, transient, and voltage stabilities. In addition, this system is widely used for small-signal stability analysis using eigenvalue analysis, transient stability studies for fault conditions, Load-Frequency Control (LFC) studies, Voltage stability and reactive power management, wide-area damping controller design, etc.

The system itself is prepared and publicly available, including a Phasor Measurement Unit (PMU) implemented in MATLAB/Simulink R2022b [47], which can be easily deployed. Data from scopes related to voltage, current, power, and other electrical quantities can be readily obtained. Specifically, the system consists of two symmetrical areas, each containing one load and two synchronous generators, with a transformer connected to each generator, as illustrated in Figure 2. It is important to note that all experiments are conducted on the Kundur two-area system, comprising two generator areas coupled by long overhead tie-lines at HV (approximately 230 kV) with solid/effective neutral grounding. The analysis and thresholds are developed for this grounding practice; isolated, resonant (Petersen-coil), and high-resistance grounded networks are not considered here and represent applicability limits of the proposed method.

The system includes 10 transmission lines, which interconnect the buses, including the 220 km tie-line between the two areas. The key parameters of the system are presented in

Table 1. Kundur two-area four-machine system parameters.

Parameter	Value	Notes
Number of Generators	4 (G1, G2, G3, G4)	–
Number of Areas	2 (Area 1 and Area 2)	–
Generator Ratings	900 MVA each	Identical ratings
Transmission Voltage Level	230 kV	–
Transmission Line Impedance	$j0.001$ p.u. per km	Per unit values
Tie-Line Power Transfer	∼400 MW	Inter-area transfer
Excitation System	IEEE Type-1	Standard model
Governor System	IEEE Type-G1	Standard model
Load Type	Constant-Power load	–
Load in Each Area	∼967 MW	Steady-state load

– Values are based on the standard Kundur benchmark system.

.

Table 2. Scope of applicability.

Voltage Class	Grounding	Dominant Fault Current	In Scope
HV (≈230 kV)	Solid/effective	High short-circuit current	Yes
MV (10–36 kV)	Isolated/high-R	Low earth-fault current	No
MV/HV	Resonant (Petersen coil)	Limited earth-fault current	No

summarizes the applicability of this study across network regimes. The scope is limited to high-voltage (≈230 kV) transmission lines with solid/effective grounding, where high short-circuit currents prevail. Medium-voltage systems with isolated, high-resistance, or resonant grounding are excluded because they exhibit low or limited earth-fault currents and follow different protection principles. The benchmark simulations consider metallic and low-resistance short circuits (effective fault resistance $\approx 0\mathrm{\Omega }$); evolving arc/resistive faults were not included in the training distribution.

3.1.2. Data Acquisition System

The data acquisition system uses the Kundur two-area four-machine system as a source. The system, as shown in Figure 2, has 11 buses. Six different regions are defined, each starting with one bus and ending at the next. Specifically, the following local regions are defined: Region 1 between buses 5 and 6, Region 2 between buses 6 and 7, Region 3 between buses 10 and 11, Region 4 between buses 9 and 10, Region 5 between buses 7 and 8, and Region 6 between buses 8 and 9. In the publicly available MATLAB R2022b built-in model, Regions 1, 2, 3, and 4 use one three-phase $\pi$-section line per region, while Regions 5 and 6 use one distributed-parameter line per region.

The three-phase $\pi$ section line has three parameters which are positive and zero sequence resistance, inductance, and capacitance per unit length. On the other hand, the distributed parameter line has also three parameters which are resistance, reactance, and capacitance per unit length. The initial values of these parameters for each one are the same and they are as follows:

• $[0.0001\times 529,1.61]\mathrm{\Omega }/\mathrm{km}$
• $\left[{\displaystyle \frac{0.001\times 529}{377}},0.0061\right]\mathrm{H}/\mathrm{km}$
• $\left[{\displaystyle \frac{0.00175}{529\times 377}},5.2489\times {10}^{-9}\right]\mathrm{F}/\mathrm{km}$

respectively. Here, 529 is the line’s reactance given in ohms per kilometer. Multiplying by 0.001 converts this reactance into ohms per meter. Dividing by 377 (which is $\pi$ × 60) converts the reactance (in ohms per meter) to inductance (in henries per meter).

As a part of the whole approach is presented in Figure 3 which compares the original part, (a), versus the modified part, (b), related to previously defined regions 1 and 2. To enable the application of short-circuit faults along the entire length of a line, an additional device is installed in each region, shown in Figure 3(I). In every region, both the three-phase $\pi$ section line and the distributed parameter line are divided into two identical parts. Splitting the three-phase $\pi$ section line yields identical results because it is defined as a section with lumped parameters [48]. However, when applied to the distributed parameter line, this approach produces only approximate results, as it employs distributed resistance, inductance, and capacitance parameters. Additionally, a three-phase voltage–current (VI) measurement device is integrated between the two devices and connected to a two-port oscilloscope to accurately record voltage and current during fault conditions, exhibited in Figure 3(II). To apply short-circuit faults, a three phase fault block is included as it is in Figure 3(III). Finally to measure the voltages, currents, and their angels scopes are included and the measurement devices output s directed as inputs for them, as shown in Figure 3(IV, V, and VI).

Because a segment cannot be of zero length, we start by assigning the first segment, lets call it s1, a length equal to the predetermined increment and segment, s2, the remainder of the total length. At each iteration, segment (s1) is increased by the predetermined increment, while segment (s2) is reduced by the same amount—thus preserving the overall length. This process is repeated until segment (s2) becomes equal in length to the initial length of segment (s1).

On the other hand, because resistance, inductance, and capacitance are specified per unit length, there is no need to adjust these parameters when the segment length changes. They inherently represent the amount per kilometer. Similarly, because frequency is a system-level parameter, it remains constant regardless of segment length. Immediately after adjusting the segment lengths, the fault type is applied at the connection between segments (s1) and (s2).

Since there are three phases and a ground (A, B, C, and G), there are 16 possible on/off combinations ($2^4=16$). However, only 12 of these represent valid fault conditions. Single-line faults without ground and the case of ground-only faults are excluded. For instance, the combination (on, on, off, off) represents a double-line fault between phases A and B, while phases C and G remain unaffected. This methodology is applied consistently across all areas and faults.

To make it more obvious, an example is given in

Table 3. Parameter calculation technique applied at each data-acquisition iteration.

Iter.	S	L (km)	F (Hz)	R ($\mathbf{\Omega }$/km)	I (H/km)	C (F/km)
1	s1	0.5	U	U	U	U
1	s2	24.5	U	U	U	U
2	s1	1.0	U	U	U	U
2	s2	24.0	U	U	U	U
⋮	⋮	⋮	⋮	⋮	⋮	⋮
$x^{\left(N\right)}$	s1	24.5	U	U	U	U
$x^{\left(N\right)}$	s2	0.5	U	U	U	U

U indicates values unchanged during each iteration.

which illustrates the iteration process for (on, on, off, off) fault type applied at region 1.

Where Iter denotes the iteration number, S is the segment name, L represents the length at which the fault is applied, F is the frequency, R is the resistance, I is the inductance, C is the capacitance, and $x^{\left(N\right)}$ denotes the value at the final iteration. Finally, U means Unchanged during the iteration.

3.1.3. Data Collection

Using the methodology outlined in the previous subsection and utilizing MATLAB R2022b and Simscape 6.1 toolboxes within Simulink, the system is subjected to both normal operation and various fault conditions. These faults are applied at different incremental length rates. A summary of the predefined regions, their corresponding buses, lengths, and incremental lengths is presented in

Table 4. Predefined region summary.

Region	Bus	L (km)	$\mathbf{\Delta }\mathit{L}$ (km)
A1	5–6	25	0.5
A2	6–7	10	0.2
A3	10–11	25	0.5
A4	9–10	10	0.2
A5	7–8	110	2.2
A6	8–9	110	2.2

Regions are predefined based on bus connections and line segment lengths.

.

This was intentionally ensured to address the issue of imbalance. The total number of samples is calculated using Equation (9), below.

$$T_s=\left({\displaystyle \frac{L}{\mathrm{\Delta }L}}-1\right)\times N_f,$$

(9)

where $T_s$ is the total number of samples, L is the total length (km), $\mathrm{\Delta }L$ is the incremental length (km), and $N_f$ is the number of fault scenarios. The subtraction of one accounts for the fact that the iteration does not begin at zero length for segment (s1), as explained in the previous section. When sampling over a simulation time of 5 s at a rate of ${\displaystyle \frac{1}{60}}$, the data consist of 300 data points, calculated using Equation (10).

$$N_i={\displaystyle \frac{T_{\mathrm{sim}}}{f_s}},$$

(10)

where $N_i$ is the number of intervals, $T_{s}im$ is the simulation time, and $f_s$ is the sampling rate. Including the initial time point at $t=0$ adds an extra row, resulting in a total of 301 data entries.

During this research, a total of 9,557,352 data points which make 31,752 individual CSV data files were generated, comprising 5292 files per faulted area and 588 files per scope. In total, nine different scopes were considered, including B1 (the output from the Area 1 generator bus onto the tie-line toward Area 2), B2 (the output from the Area 2 generator bus onto the tie-line toward Area 1), generator 1 current, generator 1 voltage, generator 1 power, four machines, faulted PMU current, faulted PMU voltage, and faulted voltage and current. For each fault, 42 distinct features were extracted, and the symbols and corresponding descriptions for these features are provided below

• vabc_g1_magnitude vabc_g1_angle,
  vabc_g1_f: Voltage phasor quantities (magnitude, angle, frequency) from the PMUs.
• iabc_g1_magnitude, iabc_g1_angle,
  iabc_g1_f: Current phasor quantities (magnitude, angle, frequency) from the PMUs.
• p_g1_magnitude_1, p_g1_magnitude_2: The per-unit real power going out to the final display block of generators 1 and 2, respectively.
• b1_v_1, b1_v_2, b1_v_3: Instantaneous phase-to-neutral voltages (phases A, B, C) at Bus B1; output of Area 1 generator bus sent onto the tie-line toward Area 2.
• b1_i_1, b1_i_2, b1_i_3: Instantaneous phase-to-neutral currents at Bus B1.
• b2_v_1, b2_v_2, b2_v_3: Instantaneous phase-to-neutral voltages at Bus B2; output of Area 2 generator bus sent onto the tie-line toward Area 1.
• b2_i_1, b2_i_2, b2_i_3: Instantaneous phase-to-neutral currents at Bus B2.
• machines_pa_1–machines_pa_4: Air-gap or accelerating power in per-unit; electrical (net) power coming from Generators M1–M4.
• machines_w_1–machines_w_4: Rotor speed in per-unit of nominal (1 pu = synchronous speed).
• machines_dtheta_1, machines_dtheta_2: Rotor-angle deviation (degrees) of each generator relative to the reference machine (Machine 1).
• faulted_pmu_v_m, faulted_pmu_v_a,
  faulted_pmu_v_f: Voltage phasor quantities (magnitude, angle, frequency) from PMUs for the faulted area.
• faulted_pmu_i_m, faulted_pmu_i_a,
  faulted_pmu_i_f: Current phasor quantities (magnitude, angle, frequency) from PMUs for the faulted area.
• faulted_v_1, faulted_v_2, faulted_v_3: Three-phase voltage waveforms related to the faulted area.
• faulted_i_1, faulted_i_2, faulted_i_3: Three-phase current waveforms related to the faulted area.

3.2. System Main Architecture

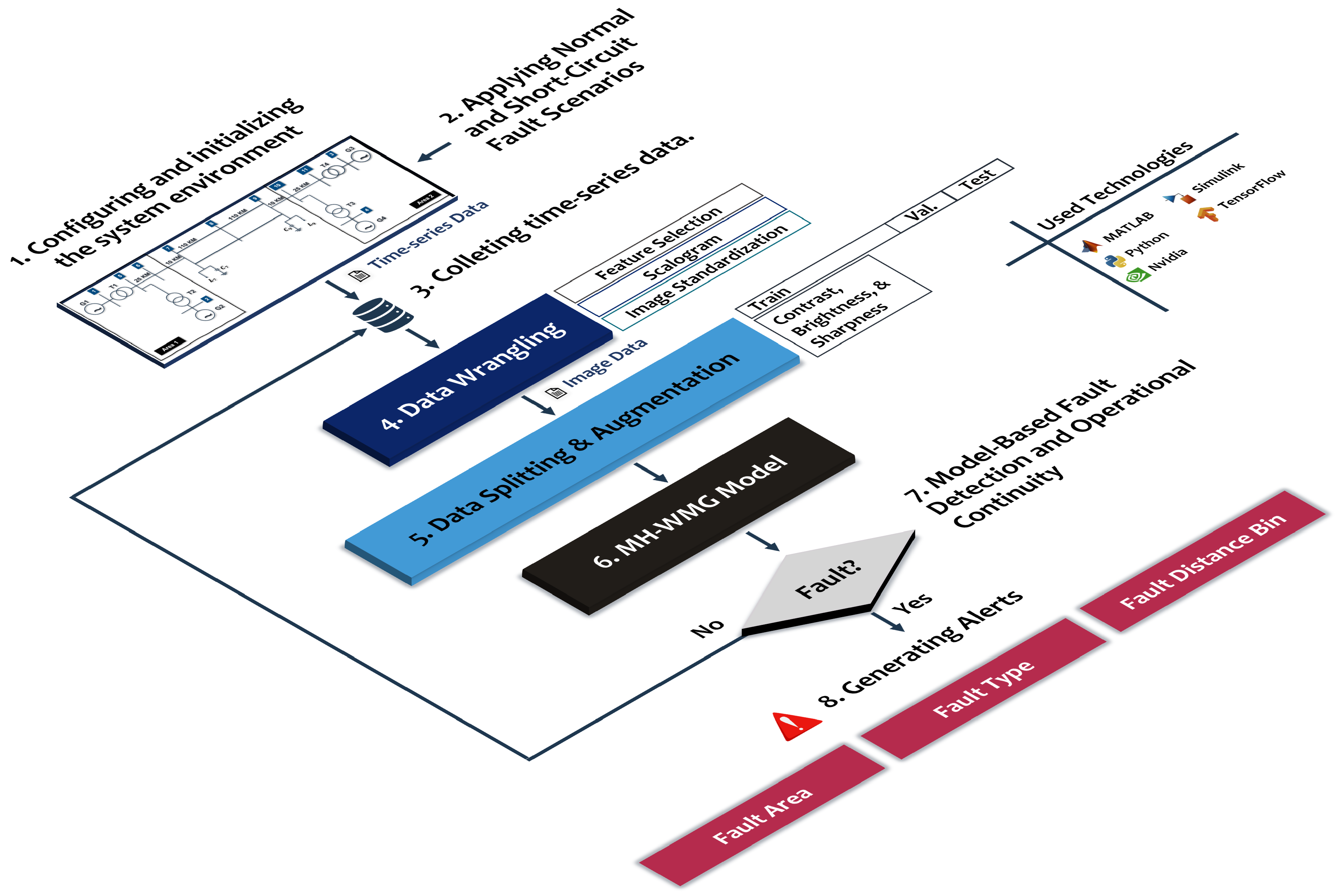
In the current section, only the general information about the system main architecture is supposed to be given. However, the detailed explanation of each stage is provided within the research. The main architecture of this study follows the general standard of AI pipelines. It mainly consists of seven distinct stages that are obviously can be seen in Figure 4.

The first two stages include both applying the normal and fault situations on the prepared system. After that, the data are collected from different scopes, then, saved as CSV files in tabular format. These three steps are significantly explained in the Data Overview Section. Next, a data wrangling process is applied on the collected data. Specifically, this stage has three substages which are feature selection, scalogram, and image standardization. Feature selection is performed using the Pearson correlation coefficient, where the mean of each feature is calculated, and the features most strongly correlated with the target variable are selected. On the other hand, scalogram is applied using Wavelet Transform with Morlet mother wavelet in order to obtain the image related to the time series data. As a last step of data wrangling, the image is standardized using zero mean normalization. Then, the data is split into training, validation, and test with the ration of 70%, 15%, and 15%, respectively. After that, the training data are augmented using random contrast adjustment, brightness increase, and sharpening filter techniques. Subsequently, the training data are used to train the proposed MH-WMG model, while the validation data support a robust training process by promoting generalization rather than memorization. Finally, the performance of the trained model is evaluated using the test data. The workflow’s next phase is governed by the MH-WMG model’s output. If no fault is detected, the pipeline simply reiterates the previous steps on newly arriving data. When a fault is recognized, the faulted region is flagged and the system proceeds to determine both the fault type and the corresponding fault-distance bin. System preparation is carried out in MATLAB/Simulink R2022b, whereas data manipulation and model training are performed in Python 3.12.9 with TensorFlow, accelerated on NVIDIA Graphics Processing Units (GPUs).

3.3. MH-WMG Internal Structure

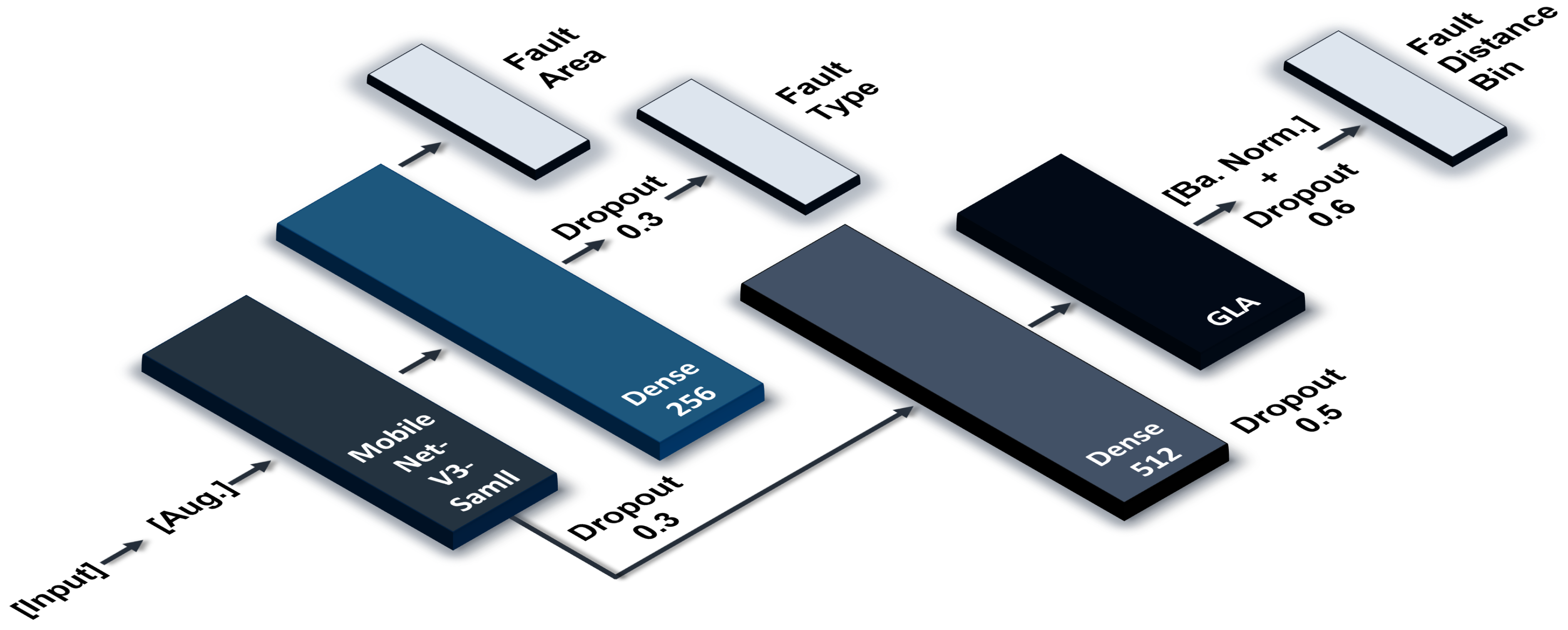
The proposed model simultaneously addresses three classification tasks, which are localizing the faulted area, identifying the fault type, and estimating the fault-distance bin. It mainly consists of one input, augmentation, a shared MobileNet-V3-Small backbone, fully connected layers, L1 and L2 regularizations, batch normalization, and GLA mechanism. The internal structure of the proposed model MH-WMG is seen in Figure 5.

From this shared representation, three task-specific heads, each with its own lightweight sub-network, independently refine the features required for their respective predictions. The complete structure and components of each head are as follows:

3.3.1. Input and Augmentation

Before any learnable layers, each $224\times 224\times 3$ RGB frame passes through a lightweight, fully differentiable pipeline: Random contrast with range ± 30% to enforce contrast invariance, additive brightness shift of $+0.1$ (after normalizing pixels to $[0,1]$) to decorrelate class labels from ambient light, and Depth-wise sharpening using the fixed $3\times 3$ kernel $\left[\begin{array}{ccc}0& -1& 0\\ -1& 5& -1\\ 0& -1& 0\end{array}\right]$, which boosts high-frequency edges—helpful for the downstream fault-localization tasks.

The augmentation is done online or on-the-fly because each transformation is computed just in time while the batch is flowing through the network. As soon as a batch reaches the augmentation layer during training, the layer instantly applies its random contrast, brightness, and sharpening operations. The altered images exist only for that single forward/back-prop pass; they are never written to disk or reused as fixed files.

The batch (B) keeps the same size, but every time the batch visits the model the pictures look slightly different which enhances the model generalization process and prevents overfitting. Based on that, it adds zero trainable parameters while boosting robustness and produces (B, 224, 224, 3) image output. The information related to the input and augmentation stages, the shape of the image at each stage, and the value used are clearly stated in

Table 5. Key tensor statistics after each augmentation stage.

Stage	Shape	Value Range
Input image	$B\times 224\times 224\times 3$	$[0,255]$
RandomContrast $\left(0.3\right)$	Same	$\left[(1-0.3)x,(1+0.3)x\right]$
Brightness $+0.1$	Same	$x+0.1$ (after scaling)
SharpenLayer	Same	≈$[0,1]$ (clipped later)

.

3.3.2. MobileNet V3-Small Backbone Layer

MobileNet-V3-Small layer is used as a backbone. Its main job is to take a raw RGB image of size 224 × 224 × 3 pixels and squeeze it down into a much smaller, information-rich vector often called a compact semantic signature. Therefore, instead of passing all 150,528 pixel values to the rest of the model, this layer extracts the most meaningful visual patterns (edges, textures, shapes, etc.) and hands the downstream layers a concise feature vector that captures the essence of the image. It has 1,529,968 trainable parameters and produces a per-image 1024-element feature vector with shape (B, 1024). In short, MobileNet-V3-Small offers the sweet spot between compute-budget, accuracy, and a ready-made 1024-D feature vector that our dense and attention branches can exploit immediately.

The previous two layers are mutual between all the three heads, however, the rest of each head is different.

3.3.3. First Head

The head transforms the 1024-dimensional feature vector into a six-class probability distribution that roughly localizes the faulted area in each input image. Its architecture consists of (i) a dropout layer (rate = 0.3); (ii) a fully connected layer with 256 units, ReLU activation function, and L2 regularization ($\lambda$ = 0.2); and (iii) a six-unit soft-max output layer with L2 of $\lambda$ = 0.1. This configuration offers sufficient representational capacity while keeping the parameter budget modest: the first dense layer contributes 524,800 trainable parameters, the dropout layer adds none, and the final dense layer adds 1542. The six output probabilities correspond to the candidate fault zones, and the zone with the highest probability is taken as the model’s prediction.

The droupout layer main role is adding regularization. It randomly sets 30% of activations to zero during training, forcing the downstream dense layer to rely on multiple complementary feature pathways. This noticeably reduces over-fitting without adding parameters. The FC layer increases the non-linear projection & feature synthesis. It compresses/expands the 1024-D backbone descriptor into a 512-D latent space, enabling the model to learn higher-order interactions among the original features. ReLU injects non-linearity, while the relatively strong L2 penalty keeps the weight magnitudes small, encouraging smoother decision boundaries and improving generalization. Eventually, the output layer is for making probabilistic classification. Maps the 512-D latent vector to six logits, then converts them into a valid probability simplex via soft-max.

3.3.4. Second Head

It is responsible for the classification of fault types across 12 distinct fault categories. It shares the 512-D hidden representation from the first head; however, it only adds a new dropout layer with 0.3 rate. In addition, the output layer has 12 neurons and also a L2 of 0.2. It adds 3084 trainable parameters to the model architecture. Since the semantic distance between adjacent fault types is smaller, the network benefits from the same representation but with a separate dropout mask and its own logits.

3.3.5. Third Head

This head predicts one of 12 fault distance bins. After input, augmentation, and MobileNet-V3-Small, a seperate 512-unit FC layer with ReLU activation function and L1 of 0.1 rate, and a dropout layer with rate of 0.5 are added. After the Reshape layer, the feature tensor is viewed as a token matrix $\mathbf{X}\in {\mathbb{R}}^{S\times d}$ with sequence length $S=32$ and token dimension $d=16$. Then, after flattening, a batch normalization and 60% dropout layers are added.

Gated Linear Attention (GLA). Given token features $\mathbf{X}\in {\mathbb{R}}^{T\times D}$, we set $\mathbf{Q}=\mathbf{K}=\mathbf{V}=\mathbf{X}$. The affinity is $\mathbf{A}=ELU\left(\mathbf{Q}{\mathbf{K}}^{\top }\right)\in {\mathbb{R}}^{T\times T}$. A gate vector is $\mathbf{g}=\sigma \left(\mathbf{A}\mathbf{1}\right)\in {\mathbb{R}}^T$, with $\mathbf{1}$ the all-ones vector. The gated output is $\mathbf{Z}=\left(\mathbf{A}\mathbf{V}\right)\odot \left(\mathbf{g}{\mathbf{1}}_D^{\top }\right)\in {\mathbb{R}}^{T\times D}$, and the residual $\mathbf{Y}=\mathbf{Z}+\mathbf{X}$. This uses only matrix multiplications, element-wise activations, and a residual path.

We explicitly use ELU for $\mathbf{A}$ to induce smooth sparsity and a logistic gate $\sigma (·)$ over row-sums of $\mathbf{A}$, yielding token-wise gates $\mathbf{g}$. Broadcasting $\mathbf{g}$ across feature dimensions ($\mathbf{g}{\mathbf{1}}_D^{\top }$) produces element-wise modulation before the residual addition.

Tokenization for the distance head can be summarized as the following: the shared feature vector $\mathbf{h}\in {\mathbb{R}}^{512}$ is linearly projected and reshaped to $\mathbf{T}\in {\mathbb{R}}^{32\times 16}$ (32 tokens, 16-D each), i.e., $\mathbf{T}=reshape(\mathbf{W}\mathbf{h}+\mathbf{b},32,16)$. GLA operates over $\mathbf{T}$ to model local interactions across pseudo-temporal/image patches. The output is flattened and passed to a softmax classifier over 12 distance bins.

Eventually, the output layer has 12 neurons with softmax activation function and L1 of 0.1. Specifically, the first fully connected (FC) layer introduces 262,400 trainable parameters, the batch-normalization layer adds 2048 more, and the final output layer brings in an additional 6156 parameters. The trainable parameters related to this head are summerized in

Table 6. Fault distance bin head output shape and trainable parameters.

Layer	Output Shape	Trainable Params
Dense 512, ReLU, L1	$B\times 512$	262,400
Dropout $p=0.5$	$B\times 512$	0
Reshape	$B\times 32\times 16$	0
GLA ($d=16$)	$B\times 32\times 16$	0
Flatten	$B\times 512$	0
BatchNorm + Dropout $p=0.6$	$B\times 512$	2048
Dense 12, softmax, L1	$B\times 11$	6156
Total	—	270,604

Dense layers contribute the majority of trainable parameters, while reshaping, GLA, and dropout layers add none.

.

While the first two heads require only a single soft-max layer to map these shared features to six and twelve categories, respectively, the distance-bin head must infer continuous fault-location information that is inherently harder to localize. Consequently, it adds a deeper pathway before its 12-way softmax. These extra stages inject non-linear context modeling and regularization, giving the network enough capacity to resolve subtle patterns needed to predict fault distance bin.

The training objective and loss weights of the model are as follows: the network is trained with a multi-task cross-entropy objective, using Equation (11).

$$\mathcal{L}=\alpha {\mathcal{L}}_{\mathrm{area}}+\beta {\mathcal{L}}_{\mathrm{type}}+\gamma {\mathcal{L}}_{\mathrm{distance}},$$

(11)

with $\alpha =1.0$, $\beta =3.0$, $\gamma =6.0$. These weights reflect the higher operational value and relative difficulty of distance localization, while maintaining strong performance on area and type. We validated these weights on the development split; they yielded the best trade-off without destabilizing training. The configuration helps the backbone focus on spatial features for estimating distance, while also learning to classify fault area and fault type.

3.3.6. MH-WMG Hyperparameters Recap

The full model contains 2,316,862 trainable parameters and 13,136 non-trainable parameters, total of 2,329,998, which is small enough for real-time inference on a single RTX 4070, yet large enough to learn all three tasks jointly. Adam is used with a base step size of $4.5\times {10}^{-5}$; mini-batches of 16 images keep GPU’s Random Access Memory (RAM) usage below 8 GB. Dropout, L2 weight decay ($0.10$ and $0.20$), and L1 regularization ($0.10$) are applied to dense layers to help prevent overfitting. The loss-weight tuple $(1:3:6)$ biases learning toward accurate range prediction without sacrificing class accuracy. Refer to

Table 7. MH-WMG hyperparameters.

Parameter	Value
Backbone	MobileNet-V3-Small
Input resolution	${224}^2$ RGB
Batch size	16
Base learning rate	$4.5\times {10}^{-5}$ (Adam)
Epochs	100
Loss function	Weighted SCCE
Loss weights	$(1,3,6)$
$L_2$ weight decay	0.2, 0.1
$L_1$ (distance head)	0.1
Dropout p	0.3/0.5/0.6
Augmentation	Contrast ±30%, $\mathrm{\Delta }$bright $+0.1$, sharpen

for a summary of the model’s hyperparameters.

4. Results

In the subsections that follow, we trace the proposed pipeline from data collection to model output results. We begin by detailing the train–validation–test partition and the leakage-detection protocol that guarantees statistical independence. Next, we explain how we made correlation-based feature selection. Then, we show how wavelet transform converts raw 1-D time series data into compact 2-D inputs, and we summarize the class balancing, normalization, and augmentation steps that shape the model final training entity. We then present the core performance metrics on the validation and test sets, followed by an ablation study that isolates the impact of the GLA layer, augmentation, dense bottleneck, and dropout. Eventually, this section is closed with a clear discussion of current limitations.

4.1. Data Split and Data Leakage Check

In this research, the data are divided into three subsets —training, validation, and test— in what is commonly referred to as a data split. The training set is used to train the model, the validation set helps monitor performance improvements during training, and the test set evaluates the final model on unseen data. Here, the data are split in a 70%–15%–15% ratio (2468, 530, 530 samples).

A critical concern when splitting data are ensuring that no sample appears in more than one subset, a situation known as data leakage. Data leakage makes performance metrics unreliable because the model is inadvertently trained on data that also appear in validation or test sets. To avoid this issue, we verified that all samples in the training, validation, and test sets are distinct by comparing each pair of subsets. Figure 6 illustrates a representative sample from each subset, as well as their differences, clearly showing no overlap among them. Consequently, we can confidently state that there is no data leakage in the prepared data, ensuring the reliability of our results.

4.2. Data Preprocessing and Image Generation

For each CSV file, the data are read and a descriptive statistics, mean, is calculated for each column. Then, they are complied along with the fault type label, into a single feature dictionary. A sample of the original time series data is shown in Figure 7a.

To isolate the most influential features, the Pearson correlation coefficient approach is used. In general, there is no universal scientific rule or widely accepted fixed threshold for this approach; however, some sources such as [49] classify the thresholds into three categories: 0.10 as a small effect, 0.30 as a medium effect, and 0.50 as a large effect. In this study, a value between small and medium, 0.15, is selected. Therefore, those with an absolute correlation below the 0.15 threshold are filtered out. Consequently, as shown in Figure 7b, 20 features exceeding this threshold are selected and listed below, sorted in alphabetical order: b1_i_1, b1_v_1, b1_v_3, b2_v_3, faulted_i_3, faulted_pmu_i_a, faulted_pmu_i_m, faulted_pmu_v_a, faulted_v_1, faulted_v_2, faulted_v_3, machines_dtheta_1, machines_dtheta_2, machines_pa_1, machines_pa_2, machines_w_1, machines_w_2, vabc_g1_angle, vabc_g1_f, and vabc_g1_mag-

nitude.

Then, the previously stated 20 important features are selected and Min-Max Scaler is applied to scale all values between 0 and 1, see Figure 7c. The obtained time series data are used to generate 2-D image data. All files related to the same fault are concatenated horizontally so that all the 20 features are as one data. Then, the Continuous Wavelet Transform (CWT) is applied with Morlet wavelet over 59 different scales. These 59 scales are obtained by dividing the rows number by 5, which is totally based on trial-and-error method. Each scale corresponds to a different level of resolution: smaller scales are sensitive to high-frequency, short-duration patterns, while larger scales detect lower-frequency, longer-duration trends. The result is a two-dimensional array of wavelet coefficients, with shape $(59,301)$, as the input signal contains 301 time points. In this output, each row represents the wavelet coefficients computed at a specific scale across all time steps, and each column corresponds to a specific point in time for all scales. Therefore, rather than producing 59 separate outputs, the CWT returns a unified matrix that captures how strongly each scaled wavelet matches different portions of the signal. This output is visualized as a scalogram, see Figure 7d, where the x-axis represents time, the y-axis represents scale, and the color intensity indicates the magnitude of the wavelet coefficients. Eventually, the resulting coefficients are visualized as 2-D images on a $5\times 4$ subplot grid where each subplot represent a feature of the selected 20 features. Tick marks and axes are removed for clarity, and the final image is saved at a resolution of $4650\times 3234$ pixels and 300 Dots per Inch (DPI). As a result, a total of 3528 images were generated. These image representations encode the signals’ joint time-frequency structure; before entering the model, their pixel intensities are standardized to zero mean and rescaled to lie within the range [−1, 1].

4.3. Fault Distance Bins Preparation

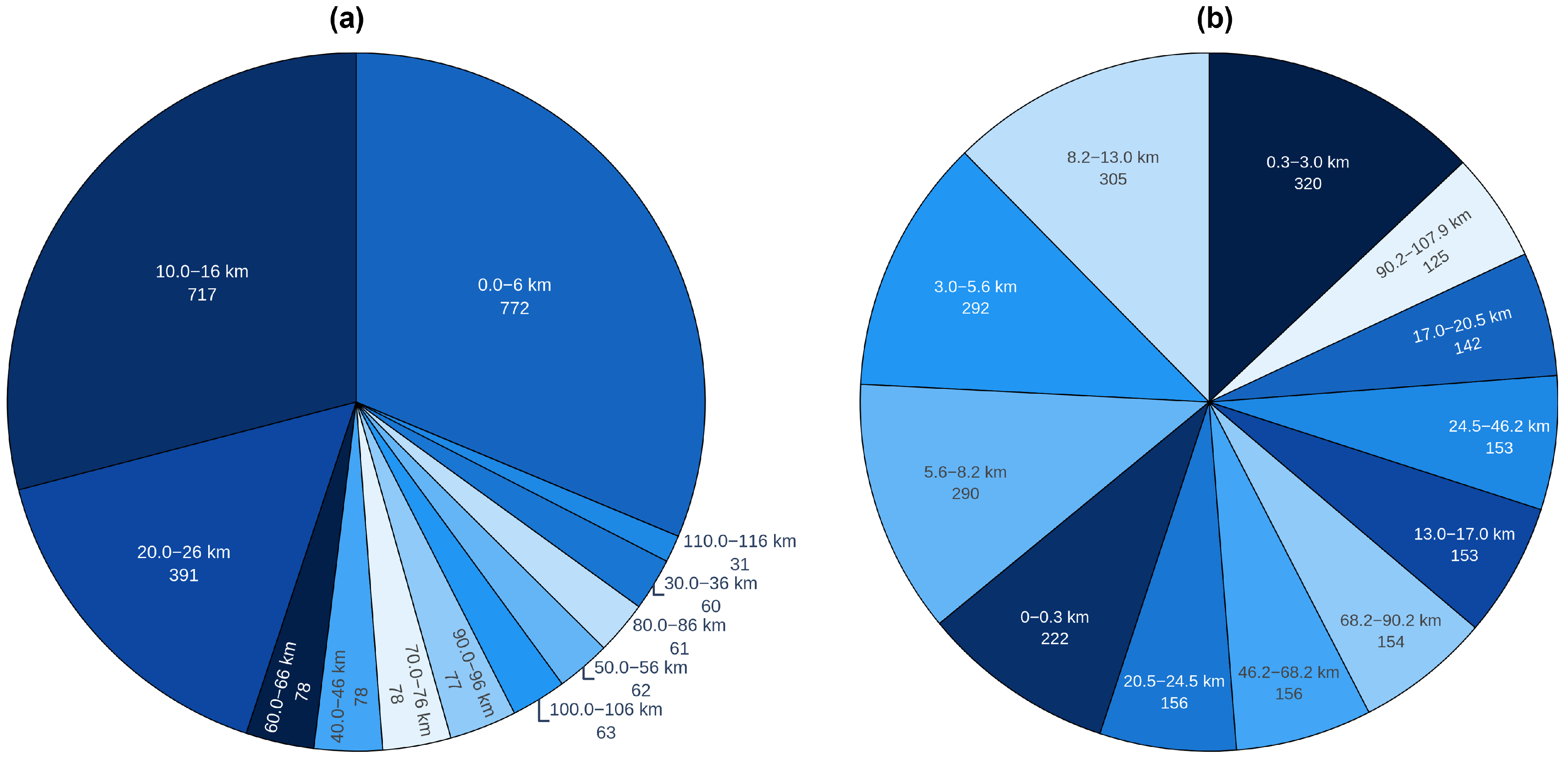
For fault area and fault type the images are generated and ready to be given to the model. On the other hand, the fault distance bins use the same images, nevertheless, their labels are not ready yet. If a fixed length such as 6-km bin approach is used for all lines globally, you will inevitably have some bins with many samples (because that 6-km interval covers multiple lines) and some bins with fewer samples, as shown in Figure 8a, which leads to imbalance problems. To ensure a balanced data for the fault distance classification task, each transmission region was segmented into predefined distance bins. This stratified binning strategy allowed for more equitable representation of fault events across the entire transmission line. For instance, the bins were defined with varying distance ranges such as (0–0.3 km), (0.3–3.0 km), (3.0–5.6 km), up to (90.2–107.9 km), with the number of samples per bin ranging from 216 to 480. This variation was carefully chosen to reflect the underlying structure of the network while maintaining a reasonable class balance as seen in Figure 8b.

Such a design was critical for mitigating class imbalance, which can negatively impact the learning dynamics of classification models. Consequently, this approach contributed to improving both the robustness and generalization capacity of the proposed fault distance prediction system.

4.4. Model Training

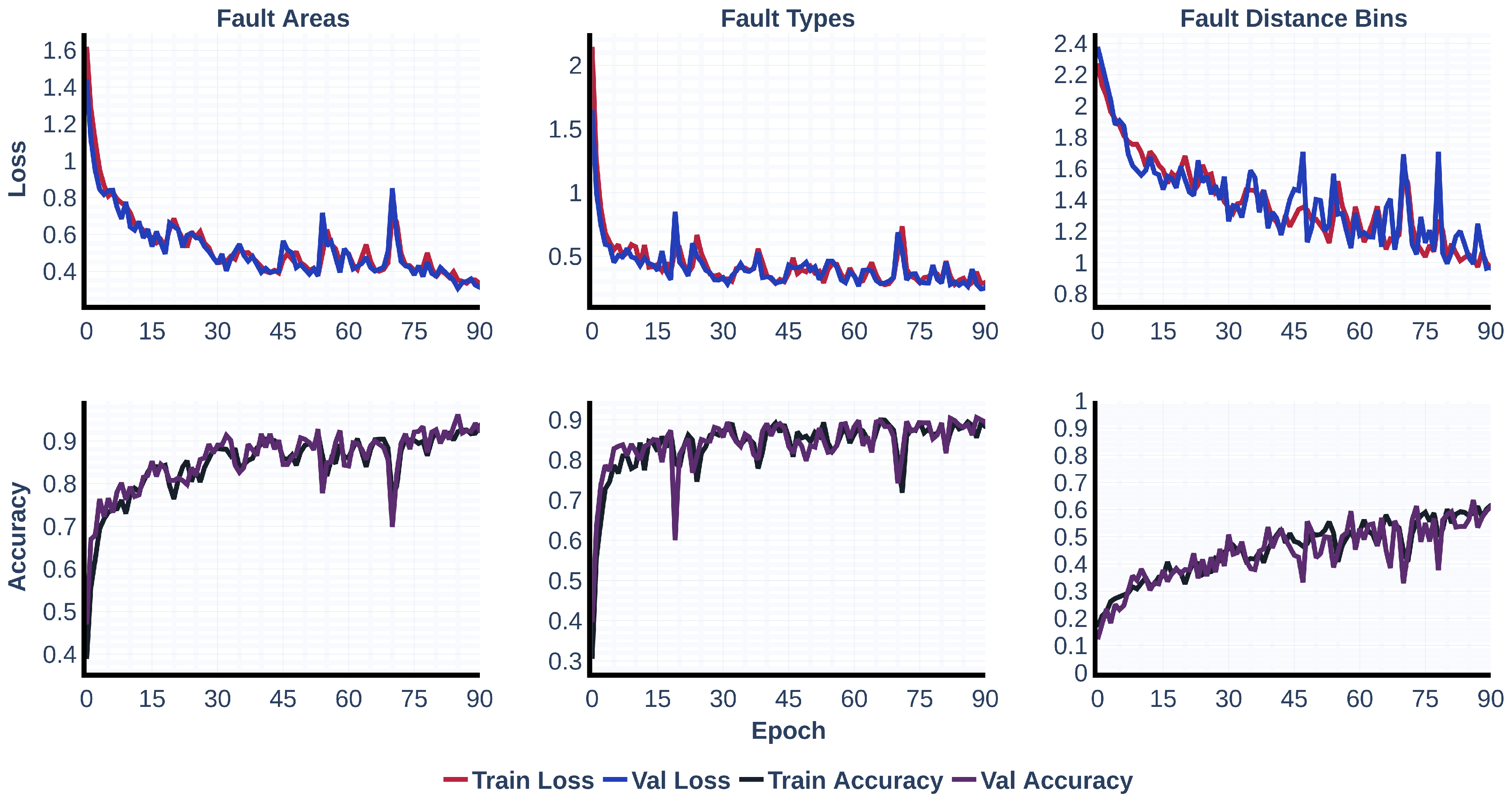
To demonstrate the effectiveness of the proposed model, its performance is compared against a baseline time-series model employing an LSTM backbone. The training procedures, including loss and accuracy trends per epoch, for both the time-series baseline and the proposed model are illustrated in Figure 9 and Figure 10, respectively. In Figure 9, the first subplot, depicting the primary loss curve of fault areas, exhibits a sharp decline during the initial ten epochs, followed by a slower descent punctuated by small oscillations, eventually stabilizing around 0.35. This trend indicates that the recurrent architecture initially captures coarse location patterns but later encounters challenges due to unstable gradients that hinder convergence. The adjacent plot to the right, depicting the “Fault Type Loss” follows a similar trajectory but plateaus at a higher value, around 0.5. This suggests that distinguishing between fault types—such as single-line-to-ground and double-line faults—is more complex when only raw waveforms are available. The rightmost subplot, associated with fault distance estimation, accentuates these limitations: starting above 2.4, it descends erratically to about 1.1, exhibiting pronounced oscillations. This behavior highlights the difficulty of extracting spatial fault information when the model processes data solely along the temporal axis. The accuracy plots directly beneath those losses confirm this narrative. “Fault Areas Accuracy” jumps beyond 0.80 by epoch 15 and edges towards 0.91, but the sawtooth pattern can tell that the optimizer is still struggling with inconsistent batches. “Fault Type Accuracy” increases more rapidaly, plateauing near 0.85. Finally, “Fault Distance Accuracy” struggles upward from 0.19 to just over 0.65, mirroring the noisy loss above and revealing that the model still misplaces a fault more than forty percent of the time.

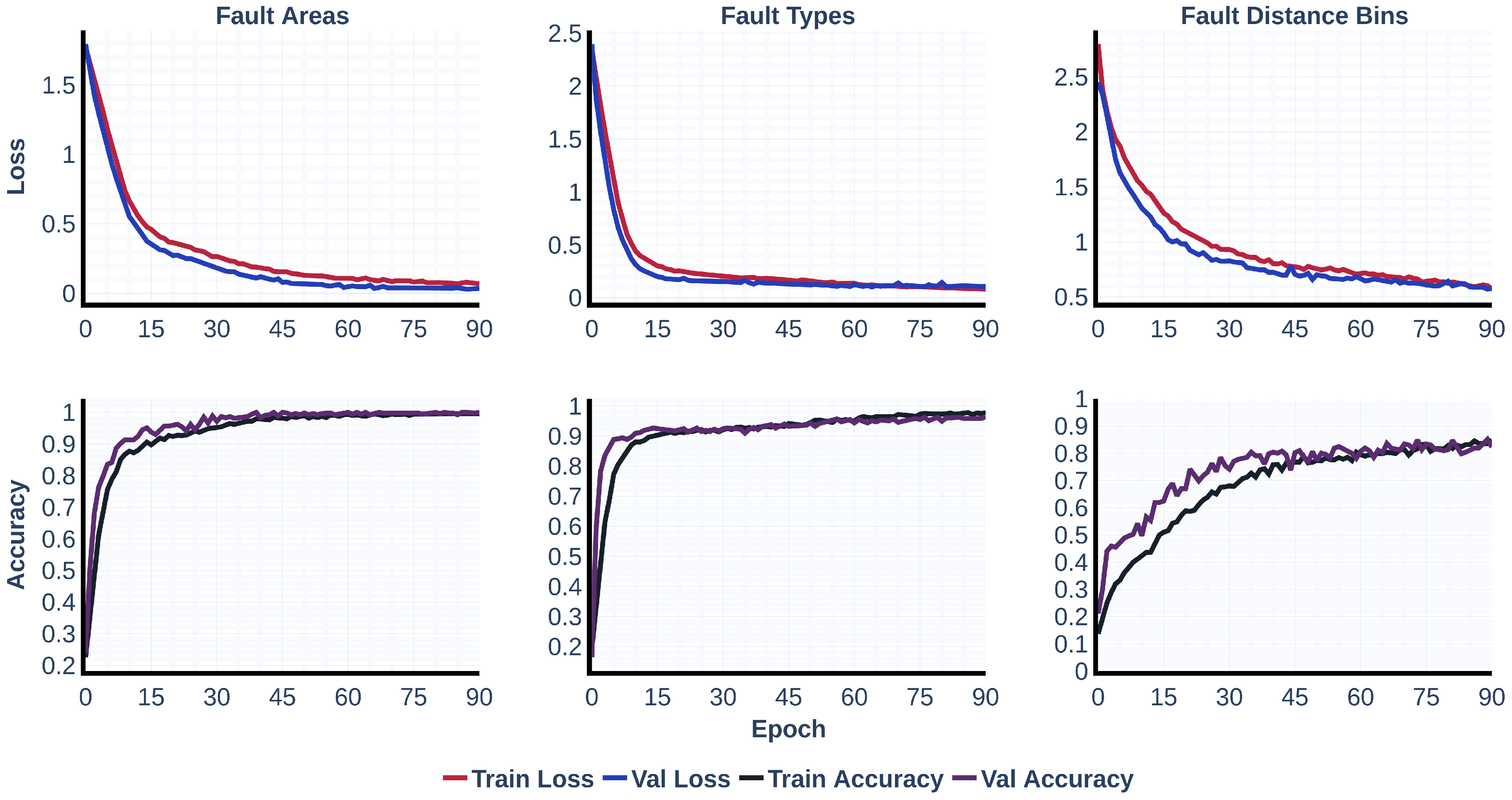
Nevertheless, the proposed approach that is provided during this reaserch is shown in Figure 10 reflecting the richer representation. The “Faulted Area Loss” falls in a smooth exponential arc to below 0.15, with the training line staying just slightly below the validation line which is a clear sign of stable training and almost zero overfitting. The “Fault Type Loss” mirrors that grace, gliding to roughly 0.2 without the earlier jitter, while the “Fault Distance Loss” goes down from 2.5 to about 0.55 almost as smoothly, demonstrating that depth wise convolutions can tease distance information out of spatial gradients much more effectively than an LSTM can from raw sequence samples. Accuracy gains are equally striking. “Faulted Area Accuracy” past 0.95 by epoch 20, finishing just at about 1.0. In the center, “Fault Type Accuracy” keeps rising well into training, cresting around 0.96 without a train-over-val gap which confirms good generalization. The most dramatic improvement lies in “Fault Distance Accuracy,” which climbs steadily to roughly 0.86, wiping out the erratic swings seen in the time series model and turning a once unreliable head into a dependable predictor.

Taken together, the two figures show a clear picture: the proposed pipeline converges more smoothly, reaches substantially lower losses, and delivers much higher accuracies—especially for the distance task because the two-dimensional representation exposes spatial–temporal patterns that convolutional filters can isolate and share across all three heads, whereas the LSTM is constrained to sequential dependencies and struggles to capture the same richness from raw waveforms.

4.5. Performance Metrics

All the following results are obtained from the test data. The confusion-matrix blocks at the top of Figure 11 starkly contrast the two fault-area classifiers. In the time-series baseline (left), dark cells hug the diagonal yet several red-boxed errors persist, notably five A2 samples mis-labelled as A1 and fifteen A3 cases leaking into A6. These slips drive the macro F1 down to 0.94 (refer to

Table 8. Time series approach fault area classification performance.

Class	Precision	Recall	F1-Score	Support
A1	0.9457	1.0000	0.9721	87
A2	1.0000	0.9444	0.9714	90
A3	0.8969	1.0000	0.9457	87
A4	1.0000	0.8989	0.9467	89
A5	0.9881	0.8384	0.9071	99
A6	0.8370	0.9872	0.9059	78
Accuracy	—	—	0.9415	530
Macro avg	0.9446	0.9448	0.9415	530
Weighted avg	0.9479	0.9415	0.9415	530

). Conversely, the proposed model (right) shows a perfectly saturated diagonal with every off-diagonal entry at zero, mirroring the flawless precision, recall, and F1 = 1.00 reported in

Table 9. Proposed model fault area classification performance.

Class	Precision	Recall	F1-Score	Support
A1	1.0000	1.0000	1.0000	82
A2	1.0000	1.0000	1.0000	90
A3	1.0000	1.0000	1.0000	96
A4	1.0000	1.0000	1.0000	94
A5	1.0000	1.0000	1.0000	84
A6	1.0000	1.0000	1.0000	84
Accuracy	—	—	1.0000	530
Macro avg	1.0000	1.0000	1.0000	530
Weighted avg	1.0000	1.0000	1.0000	530

. The visual and numerical evidence together confirm that spatial cues mined from scalograms eliminate the residual ambiguity that an LSTM sees only in the temporal axis.

A similar pattern emerges in the fault type layer. The baseline matrix (center-left) still captures the main diagonal but red frames reveal systematic confusion—most strikingly for ‘on_on_on_off’, where 15 of 40 cases are mis-classified, dragging its F1 to 0.57 and the overall accuracy to 0.88 (see

Table 10. Time series approach fault type classification performance.

Subclass Pattern	Precision	Recall	F1-Score	Support
off_off_on_on	1.0000	0.9762	0.9880	42
off_on_off_on	0.9286	0.9750	0.9512	40
off_on_on_off	0.7843	0.9302	0.8511	43
off_on_on_on	0.9608	0.8305	0.8909	59
on_off_off_on	1.0000	1.0000	1.0000	37
on_off_on_off	0.9811	1.0000	0.9905	52
on_off_on_on	1.0000	0.9130	0.9545	46
on_on_off_off	1.0000	1.0000	1.0000	35
on_on_off_on	0.9630	1.0000	0.9811	52
on_on_on_off	0.4286	0.2308	0.3000	39
off_off_off_off	1.0000	1.0000	1.0000	45
on_on_on_on	0.4828	0.7000	0.5714	40
Accuracy	—	—	0.8849	530
Macro avg	0.8774	0.8796	0.8732	530
Weighted avg	0.8862	0.8849	0.8806	530

). The proposed head (center-right) tightens nearly every subclass to a single-cell diagonal; only the same difficult pattern shows minor leakage, yet its F1 climbs to 0.77, lifting the global accuracy to 0.96 (see

Table 11. Proposed model fault type classification performance.

Subclass Pattern	Precision	Recall	F1-Score	Support
off_off_on_on	1.0000	1.0000	1.0000	38
off_on_off_on	1.0000	1.0000	1.0000	42
off_on_on_off	1.0000	1.0000	1.0000	42
off_on_on_on	1.0000	1.0000	1.0000	41
on_off_off_on	1.0000	1.0000	1.0000	48
on_off_on_off	1.0000	1.0000	1.0000	50
on_off_on_on	1.0000	1.0000	1.0000	38
on_on_off_off	1.0000	1.0000	1.0000	53
on_on_off_on	1.0000	1.0000	1.0000	47
on_on_on_off	0.7059	0.8571	0.7742	42
off_off_off_off	1.0000	1.0000	1.0000	44
on_on_on_on	0.8333	0.6667	0.7407	45
Accuracy	—	—	0.9604	530
Macro avg	0.9616	0.9603	0.9596	530
Weighted avg	0.9625	0.9604	0.9601	530

). The gain stems from dropout-augmented dense features that retain phase relationships lost in raw waveforms, enabling the attention mechanism to spotlight subtle switching signatures.

Improvements are most pronounced in fault distance bins estimation. The baseline distance matrix (bottom-left) displays a broad diagonal blur with many red mis-bins and an overall accuracy of 0.66; entire extreme ranges (0–0.2 km) receive no correct hits (refer to

Table 12. Time series approach fault distance bin classification performance.

Distance Bin	Precision	Recall	F1-Score	Support
0–0.2 km	0.0000	0.0000	0.0000	4
0.3–2.8 km	0.7297	0.8060	0.7660	67
3.0–5.5 km	0.5366	0.6377	0.5828	69
5.6–8.0 km	0.6786	0.5588	0.6129	68
8.2–12.5 km	0.6286	0.6027	0.6154	73
13.0–16.5 km	0.6452	0.5263	0.5797	38
17.0–20.0 km	0.6429	0.5806	0.6102	31
20.5–24.2 km	0.7143	0.8108	0.7595	37
24.5–44.0 km	0.6923	0.7105	0.7013	38
46.2–66.0 km	0.5957	0.7568	0.6667	37
68.2–88.0 km	0.6875	0.6286	0.6567	35
90.2–107.8 km	0.8621	0.7576	0.8065	33
Accuracy	—	—	0.6604	530
Macro avg	0.6178	0.6147	0.6131	530
Weighted avg	0.6598	0.6604	0.6568	530

). After Dense–GLA–BatchNorm-Dropout processing, the proposed model (bottom-right) sharpens the diagonal, markedly raising per-bin recalls—e.g., 0–0.2 km jumps from 0% to 94%—and boosts global accuracy to 0.87 (refer to

Table 13. Proposed model fault distance bin classification performance.

Distance Bin	Precision	Recall	F1-Score	Support
0–0.2 km	1.0000	0.9362	0.9670	47
0.3–2.8 km	0.9016	0.8462	0.8730	65
3.0–5.5 km	0.8194	0.8939	0.8551	66
5.6–8.0 km	0.8154	0.8413	0.8281	63
8.2–12.5 km	0.9231	0.8571	0.8889	70
13.0–16.5 km	0.8056	0.8788	0.8406	33
17.0–20.0 km	0.7500	0.7500	0.7500	28
20.5–24.2 km	0.7105	0.8438	0.7714	32
24.5–44.0 km	0.8333	0.7576	0.7937	33
46.2–66.0 km	0.9355	0.8788	0.9062	33
68.2–88.0 km	0.9394	0.9688	0.9538	32
90.2–107.8 km	1.0000	0.9643	0.9818	28
Accuracy	—	—	0.8679	530
Macro avg	0.8695	0.8681	0.8675	530
Weighted avg	0.8725	0.8679	0.8690	530

). This 21-point surge underscores how attending over 2-D token maps recovers faint spatial harmonics that one-dimensional recurrent filters miss, decisively validating the superiority of the image-driven architecture across all three diagnostic tasks.

4.6. Layer-Wise MH-WMG Model Outputs

Figure 12 begins from the middle row, which illustrates the fault-area head. It starts with the original and augmented waveform images; MobileNet-V3 extracts a 32 × 32 feature grid, which the Dense-256 bottleneck compresses into 32 × 8 activations. This leads to the fault-area head’s bar chart, showing a dominant (>90%) spike at the correct region. The top row presents the fault-type head: the same MobileNet features are passed through an additional dropout layer that introduces variability before classification. Its bar plot peaks at the correct subclass while showing a minor shoulder for a visually similar fault. The bottom row displays the fault-distance bin head: a Dense-512 layer expands the features to 32 × 16, and Gated Linear Attention enhances the distance-relevant tokens. However, the effects of batch normalization and dropout are not visualized here. The output probabilities accurately highlight the correct fault-distance bin. Together, the three stacked rows demonstrate how shared features diverge into task-specific pathways—compression for area, dropout for type, and attention for distance—enabling the model to disentangle multiple fault attributes within a unified architecture.

Figure 13 illustrates the effect of the GLA block on feature activations within the MH-WMG network. Each point along the horizontal axis corresponds to one of the 512 neurons in the last FC layer; the vertical axis shows that neuron’s raw activation value for a representative fault sample.

Before GLA (blue curve), activations span an extremely wide range (−2000 to >7000), with many large positive spikes. These high-magnitude values indicate that numerous neurons respond strongly even when their contribution may be redundant or noisy. After GLA (black curve), the same neurons exhibit a much narrower dynamic range (−500 to +1800). GLA suppresses most of the extreme peaks while allowing a smaller subset of salient responses to remain.

The marked reduction in amplitude and variance confirms that GLA acts as a soft gating mechanism: it filters out less informative channels, sharpens class-relevant signals, and thereby delivers a more compact, noise-robust representation to the fault distance bins classifier head. This attenuation helps stabilize gradients during training and ultimately contributes to the model’s superior accuracy for classifying fault distance bins.

4.7. Ablation Study

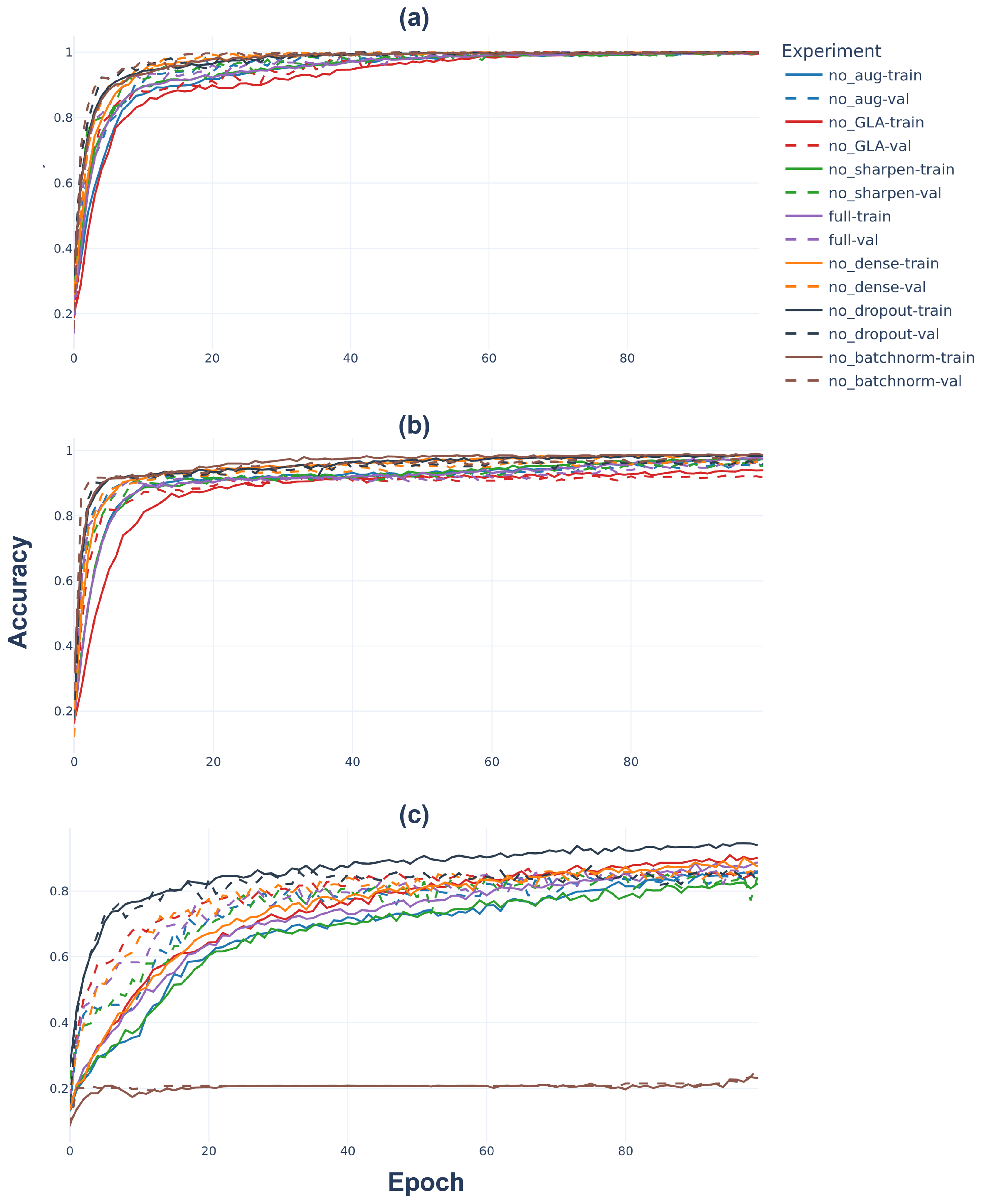
The conducted ablation study consists of seven variants, including full approach. Figure 14 presents the epoch–accuracy trajectories for the fault area, fault type, and fault distance bin heads in parts (a), (b), and (c), respectively. For the first two easier heads (a) and (b) every configuration, including the most aggressive removals, converges rapidly to $\approx 0.96–1.00$ accuracy within the first twenty epochs, and the train/validation gaps remain negligible thereafter. This indicates that the shared MobileNet-V3-Small backbone already provides highly separable representations; neither the GLA block, the sharpening kernel, nor the Dense/Dropout stack is strictly required for those tasks. However, the (c) part paints a different picture. All variants except (No Batchnorm) climb steadily from random chance to the $0.80–0.88$ band, but they do so at different speeds. The full model (blue) and the No Dropout run (black) reach their final plateau earliest, suggesting that Dropout acts mainly as a regularizer rather than a performance booster. Removing the GLA layer (No GLA) in red slows learning during the first thirty epochs and never fully catches up, highlighting GLA’s value for sequence aware localization. The brown curves (No Batchnorm.) collapse after an initial climb and level off near $0.24$ implying that the single Batch-Norm layer before the distance head is critical for stabilizing that branch’s gradient flow.

Table 14. Ablation study results over test data.

Experiment	Test Main Acc	Test Sub Acc	Test Dist Acc
MH-WMG	1.000000	0.960402	0.867900
No GLA	0.998113	0.932076	0.845283
No Aug.	1.000000	0.975472	0.837736
No Dense	1.000000	0.975472	0.835849
No Dropout	1.000000	0.986792	0.826415
No Sharpen	1.000000	0.984906	0.803774
No Batchnorm.	1.000000	0.984906	0.239623

confirms the visual trends on a held-out test set. Fault area accuracy stays at or near $100\%$ for every model, while fault Type accuracy fluctuates within a tight 0.93–0.99 band. The strongest discriminator among variants is again the distance head: the full model tops the leaderboard at $0.86$, followed closely by (No GLA) and (No Aug.) ablating the Dense or Dropout layers incurs a marginal drop ($\mathrm{\Delta }\approx 0.03–0.04$), whereas turning off Batch-Norm is catastrophic, slashing accuracy to $0.24$. Taken together, the figure and table underline two main conclusions: (i) The backbone alone is almost sufficient for the first two heads; however, the other layers increase the accuracy, but (ii) for distance estimation, the GLA mechanism, the stabilizing effect of Batch Normalization, and the regularizing effect of Dropout are essential components, each contributing measurable performance gains.

4.8. Computational Efficiency

To substantiate our claim that MH-WMG is lightweight and suitable for real-time use, we compared parameter counts and measured inference speed on a single NVIDIA RTX 4070 with batch size 1 (

Table 15. Parameter efficiency and inference speed: MH-WMG vs. other models.

Model	Params (M)	Latency (ms)	Throughput (img/s)
MH-WMG	2.33	44.14	22.66
ResNet50	25.64	73.44	13.62
EfficientNetB0	5.33	62.01	16.13
EfficientNetB3	12.32	74.68	13.39

). For clarity, Table 15 reports Model (the architecture under evaluation), Params (M) (total trainable parameters in millions, a proxy for capacity and memory footprint), Latency (ms) (mean wall-clock time to process one image; lower is faster), and Throughput (img/s) (images processed per second; higher is better). MH-WMG has 2.33 M parameters, which is smaller than EfficientNet-B0 (5.33 M), EfficientNet-B3 (12.32 M), and ResNet-50 (25.64 M). It also achieves the lowest latency (44.14 ms per image) and the highest throughput (22.66 images/s), outperforming all baselines. These results show that MH-WMG is both compact and fast, supporting real-time inference on commodity GPUs while maintaining a transparent and reproducible design.

4.9. Baseline CNNs on Wavelet Scalograms

To contextualize MH–WMG, we trained standard image backbones on the same prepared inputs scalograms. The baselines included ResNet50, EfficientNet-B0, EfficientNet-B3, MobileNetV2, and DenseNet121. Despite using the same image representations, these models failed to learn effective decision boundaries and produced near–chance performance across all tasks (area, type, and distance), see

Table 16. Performance of baseline CNNs on wavelet scalograms.

Model	area_acc	type_acc	dist_acc	area_F1	type_F1	dist_F1
ResNet50	0.2321	0.0887	0.1302	0.1133	0.0147	0.0273
EfficientNet-B0	0.1642	0.0623	0.0849	0.1106	0.0376	0.0631
EfficientNet-B3	0.1792	0.0679	0.0679	0.0929	0.0471	0.0492
MobileNetV2	0.1679	0.0906	0.1226	0.0613	0.0476	0.0182
DenseNet121	0.1736	0.0604	0.0547	0.0493	0.0095	0.0086

, where acc is the accuracy. This outcome is consistent with a domain–shift gap: features learned from natural images transfer poorly to PMU–derived time–frequency scalograms without task–specific adaptation.

These results reinforce the need for an image pipeline and architecture tailored to PMU time–frequency data. In contrast to the baselines, MH–WMG learns discriminative representations for all three tasks while remaining compact and fast.

4.10. Confidence Calibration and Interpretability

Table 17. Calibration metrics before and after temperature scaling.

Head	Temperature T	NLL	Brier	ECE	MCE
		B/A	B/A	B/A	B/A
Fault Areas	0.429	0.032/0.004	0.005/0.003	0.030/0.003	0.594/0.721
Fault Types	0.937	0.106/0.106	0.061/0.061	0.020/0.018	0.527/0.673
Fault Distance Bins	0.615	0.571/0.487	0.269/0.235	0.162/0.069	0.340/0.287

reports negative log-likelihood (NLL), Brier score, expected calibration error (ECE), and maximum calibration error (MCE) before/after (B/A) temperature scaling for all heads, together with the learned temperature T. Temperature scaling yields the largest gains for fault Areas: ($T=0.429$) improves on NLL/Brier/ECE (NLL $0.032\to 0.004$, Brier $0.005\to 0.003$, ECE $0.030\to 0.003$), while MCE increases ($0.594\to 0.721$), suggesting slightly heavier tails despite overall better calibration. Fault types: ($T=0.937$) is effectively well calibrated pre-scaling (NLL and Brier unchanged at $0.106$ and $0.061$), with a small ECE reduction ($0.020\to 0.018$) and a higher MCE ($0.527\to 0.673$), reflecting limited headroom and some increase in worst-case miscalibration. Eventually, for fault distance bins: ($T=0.615$): NLL $0.571\to 0.487$, Brier $0.269\to 0.235$, ECE $0.162\to 0.069$, and MCE $0.340\to 0.287$, indicating substantially improved calibration.

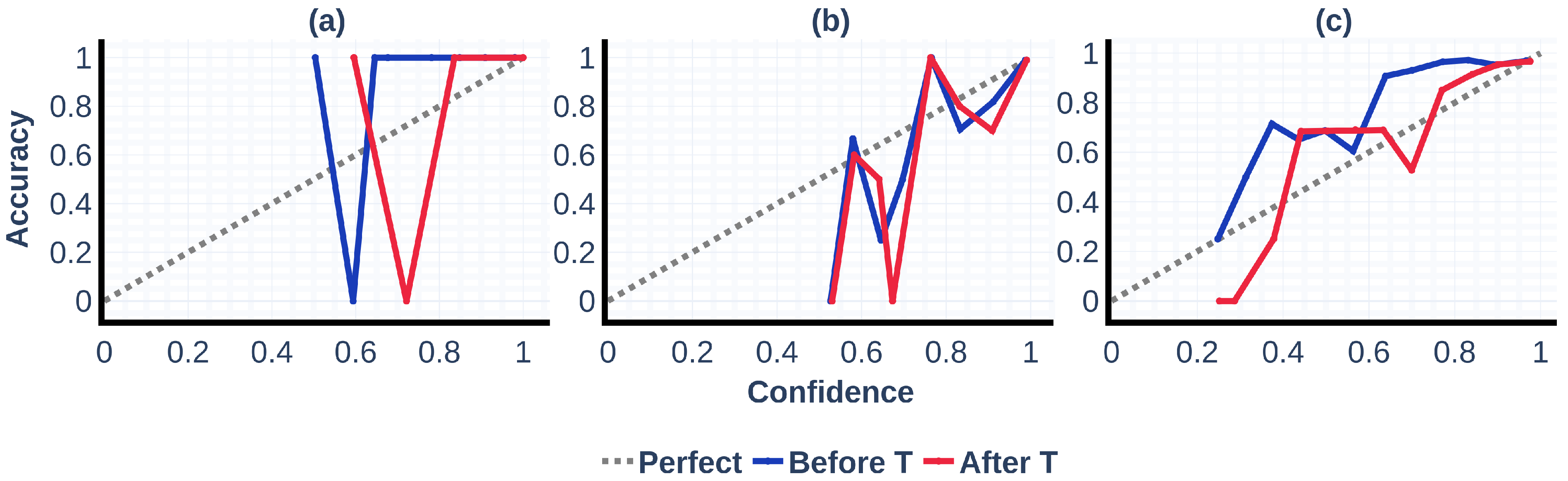
Figure 15 presents reliability diagrams for the fault area, type, and distance heads, respectively, where the dashed line denotes perfect calibration (predicted confidence equals empirical accuracy). Each curve reports bin-averaged accuracy as a function of confidence before (blue) and after (red) temperature scaling. The main head (a) is already well calibrated at high confidence, with negligible change after scaling. The subclass head (b) shows moderate miscalibration at mid-confidence bins that is partially corrected by scaling, bringing the curve closer to the identity. The distance head (c) exhibits the largest improvement: post-scaling accuracy aligns more closely with confidence across bins, indicating substantially better-calibrated probabilities without altering prediction accuracy. Collectively, these results confirm that temperature scaling enhances the reliability of reported probabilities, especially for the distance head.

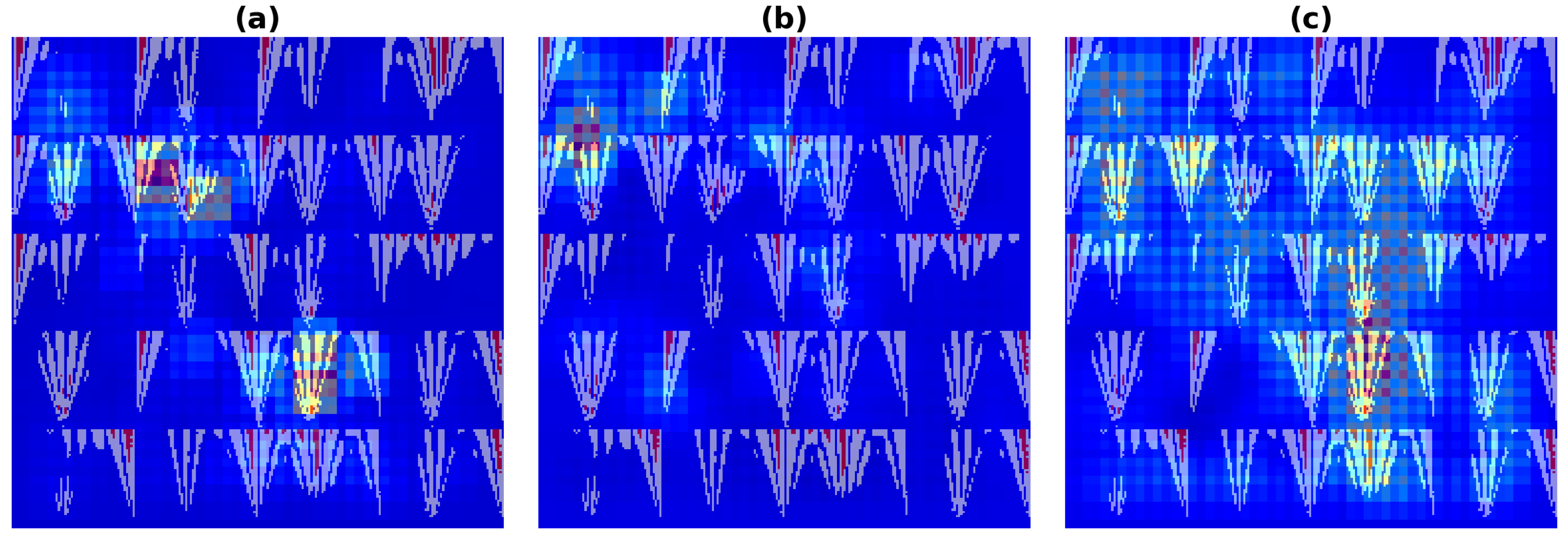
We additionally include Occlusion analysis, see Figure 16, which shows a sample from the validation data. Each panel visualizes the change in predicted confidence when small image patches are occluded (warm colors = larger confidence drop → higher attribution). The fault area head exhibits localized hotspots around salient structures, indicating that global fault/no-fault decisions depend on a few discriminative regions. The fault type head shows weaker, more diffuse responses, consistent with the finer granularity of subclass labels and greater reliance on distributed cues. The fault distance bin head presents a vertically elongated high-attribution band that aligns with the visible fault trajectory/arc region, suggesting that spatially contiguous evidence is most informative for estimating distance. Checkerboard artifacts reflect the occlusion stride/patch size and do not affect the qualitative conclusion that all heads focus on fault-relevant structures, with the distance head exhibiting the most coherent spatial attention.

5. Discussion

This work presents a fully documented, AI-driven model MH-WMG for comprehensive power-grid fault diagnosis. Using a MATLAB/Simulink R2022b acquisition platform, we record a high-resolution set of 42 distinct signals for every symmetrical and unsymmetrical short-circuit fault in the Kundur two-area four-machine benchmark. The raw waveforms are expanded through data augmentation (time shifts, amplitude jitter, band-limited noise) and rigorously partitioned to prevent leakage. After correlation-based feature selection, each trace is rendered as a wavelet scalogram, preserving the fleeting, non-stationary fault signatures more effectively than a purely time series representation.

At the modelling stage, a single-input, wavelet-based MobileNet-V3-Small backbone and FC layer feed three parallel heads that incorporate fully connected layers, dropout, batch normalization, regularizers, and GLA. These heads jointly classify (i) the faulted region (six classes), (ii) the fault type (eleven classes plus normal), and (iii) the fault distance bin, framed as a 12-class problem with region-specific, variable-length bins. Aligning distance bins with the physical layout of each line preserves class balance and improves performance. The multi-head configuration also outperforms a three-stage cascade, simplifying control and training.

The proposed MH–WMG model demonstrates strong performance across all tasks. On the Kundur two–area four–machine system, it achieves perfect fault–area localization (accuracy, precision, recall, and F1 equal to 1.00), high fault–type classification (accuracy 0.9604, precision 0.9625, recall 0.9604, F1 0.9601), and robust distance–bin estimation (accuracy 0.8679, precision 0.8725, recall 0.8679, F1 0.8690). These findings support the working hypothesis that time–frequency imaging of PMU waveforms, paired with a compact convolutional backbone and Gated Linear Attention, is more effective for short–circuit diagnosis than conventional time–series pipelines.

Consistent with prior work, our results also reveal the limits of generic CNN/RNN baselines on PMU wavelet images. Trained on the same 224 × 224 Morlet scalograms, ResNet50, EfficientNet-B0/B3, MobileNetV2, and DenseNet121 perform near chance (area 0.16–0.23; type 0.06–0.09; distance 0.05–0.13). This reflects a domain shift from natural images to PMU time–frequency data; by design, MH-WMG bridges this gap and achieves consistent gains across all heads.

Probabilistic calibration improves with simple post–hoc scaling. For the Distance–Bins head, expected calibration error decreases from 0.162 to 0.069, alongside reductions in negative log–likelihood (0.571 to 0.487) and Brier score (0.269 to 0.235). The Fault–Areas head also shows lower NLL, Brier, and ECE after scaling, although maximum calibration error increases from 0.594 to 0.721, suggesting heavier tails rather than systematic miscalibration. The Fault–Types head is already well calibrated, with unchanged NLL and Brier and a small ECE improvement (0.020 to 0.018). Reliability curves move closer to the identity line, and attribution maps consistently highlight fault–relevant regions, which is conducive to operator trust and triage.

The approach is efficient and deployable. The model contains 2.33 million parameters, achieves a per–image latency of 44.14 ms, and processes 22.66 images per second at batch size one. The full pipeline—scalogram preprocessing followed by MobileNetV3–Small with Gated Linear Attention—runs on commodity CPU servers; a GPU is optional when lower latency is required at fleet scale.

The costs can be grouped into three parts: hardware, training, and inference. Hardware: a single 8 GB, 80 W GPU (≈$200–$\$500$) with a standard workstation (CPU/RAM/SSD/PSU, ≈$600–$\$1200$) totals ≈ $800–$\$1700$. Training: this is a one-time cost; on our 8 GB, 80 W GPU, MH-WMG converges in about 45 min, consuming $\approx 0.06\mathrm{kWh}$ $(0.08\mathrm{kW}\times 0.75\mathrm{h})$, which is ≈$0.007–$\$0.015$ at $0.12–$0.25/kWh (dataset and settings may vary). Inference: after training, inference is simple and fast—batched forward passes are sub-second per sample on the same GPU and about 1–3 s on a modern CPU; the per-sample energy for a 1 s pass at 80 W is ≈$2\times {10}^{-5}\mathrm{kWh}$, i.e., $\$2\times {10}^{-6}$–$\$6\times {10}^{-6}$ at typical electricity prices. Amortized over three years at 50 k samples/month, hardware adds only ≈$$3\times {10}^{-4}$–$\${10}^{-3}$ per sample, and the <8 GB memory need makes on-premise or edge deployment straightforward.

Several limitations merit attention. First, rendering 224 × 224 × 3 wavelet scalograms introduces preprocessing overhead and a potential failure point before inference. Second, representing distance with 12 discrete bins simplifies learning and preserves class balance but limits spatial resolution. Third, training on a fixed 20-cycle window and a specific sampling rate complicates transfer to PMUs with different configurations, which may require padding, resampling, or retraining. Finally, the current validation focuses on metallic or low–resistance faults; evolving resistive faults and certain medium-voltage grounding schemes remain outside scope.

Future work should reduce preprocessing cost, evaluate continuous or hybrid regression for distance to improve spatial precision, and validate the method on larger and evolving networks. Adaptive windows and sampling–aware training may ease cross–PMU transfer. Under strict energy constraints, spiking architectures are a complementary direction for low–power inference on time–frequency inputs. A techno-economic analysis is also warranted to quantify end-to-end benefits at utility scale.

6. Conclusions

This study presents an end-to-end, image-based pipeline for short-circuit fault diagnosis that converts PMU waveforms into Morlet wavelet scalograms and jointly predicts fault area, fault type, and fault distance bin. On the canonical Kundur system, the model attains perfect area localization, strong type classification, and robust distance estimation while remaining compact and fast (2.33 million parameters, 44.14 ms per image, 22.66 images per second). The method improves calibration with simple temperature scaling, requires no additional field instrumentation beyond existing PMUs, and consistently outperforms conventional time-series baselines. By enabling rapid, accurate, and interpretable fault triage, MH–WMG offers a practical path toward more resilient and intelligent grid operation and provides a transparent, reproducible benchmark for future extensions.