Hybrid ML/DL Approach to Optimize Mid-Term Electrical Load Forecasting for Smart Buildings
Abstract
1. Introduction
- The capability to model building energy consumption based on grid power.
- Integration of high-resolution energy and meteorological data.
2. Literature Review
| Ref. | Dataset | Frequency | Features | Models | Key Findings | Limitations |
|---|---|---|---|---|---|---|
| [21] | Educational buildings | Hourly | Energy usage behavior | RF, RT, SVR | ML methods provide accurate hourly forecasts in educational buildings. | Restricted to two buildings; no DL/hybrid comparison. |
| [22] | Residential smart grid | Daily | Usage patterns | ANN, SVR, CART, LR, SARIMA | Comparative daily forecasting shows ML superiority over statistical models. | Daily horizon only; potential over-fitting issues. |
| [26] | University campus | Hourly | Operations, HVAC | DNN, RF, SVM, GBT | DNN with engineered HVAC features improves accuracy. | Relies on engineered HVAC variables; no hybrid approaches. |
| [28] | Commercial buildings | Hourly, Monthly | Cooling load factors | RF, IPWOA, ELM | Hybrid RF–IPWOA–ELM enhances cooling load prediction. | Focused only on cooling load; limited generalization. |
| [29] | UCI Repository | Hourly | Voltage, occupancy, power | CNN–LSTM | CNN–LSTM outperforms classical baselines in smart meter data. | Based on a single household; no weather variables. |
| [30] | Residential buildings | Yearly | Weather, occupancy, design | ANN, DNN, RF, KNN, SVM | DNN provides robust performance for annual load forecasting. | Annual horizon; lacks short/medium-term forecasting detail. |
| [37] | Utility data | Hourly | Weather + power demand | RF | RF achieves low day-ahead forecast errors. | System-level forecasting; not building-specific. |
| [36] | Cooling load data | Hourly | Env. factors, occupancy | SVR | SVR with environmental variables enhances prediction accuracy. | Limited to summer season; one office building only. |
| [38] | Hospital energy data | Daily | Load consumption | XGBoost, RF | Ensemble methods outperform individual learners for hospital load. | No DL or hybrid models tested. |
| [39] | Mixed datasets | Hourly | Usage and weather | SVR, LSTM | SVR achieves comparable or better results than LSTM. | Narrow scope of hybrid testing; dataset heterogeneity challenges. |
| [40] | Commercial building | 15-min | Timestamp + load | KCNN–LSTM | Combining clustering with DL improves short-term forecasts. | Limited exogenous features; scalability uncertain. |
| [33] | Multiple building types (Japan) | Hourly | Historical load, weather | LSTM + Multi-source Transfer Learning (MK-MMD) | Multi-source domain adaptation improves performance vs. single-source transfer. | Requires domain similarity; complex setup. |
| [34] | Green buildings (China) | Daily | Historical consumption, temp., humidity | Seq2Seq + Attention + Transfer Learning | Attention-guided TL model forecasts accurately across climate zones. | Model needs careful tuning; limited to similar use cases. |
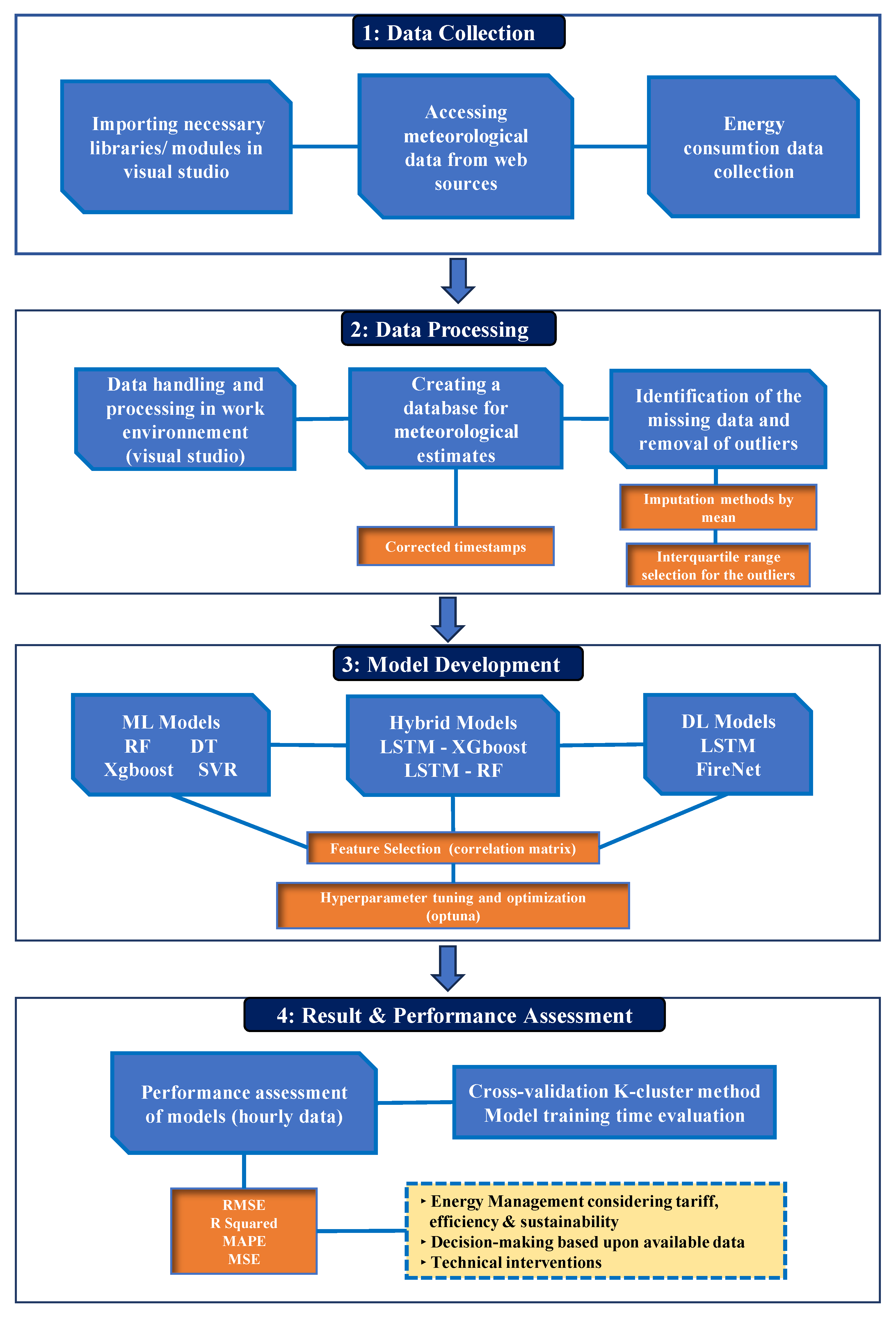
3. Methodology
3.1. Data Description and Analysis
3.2. Feature Selection
3.3. Machine Learning Models
3.4. Deep Learning Models
3.5. Hybrid Models
3.6. Hyper-Parameter Optimization
3.7. Implementation Details
4. Experimental Results and Discussion
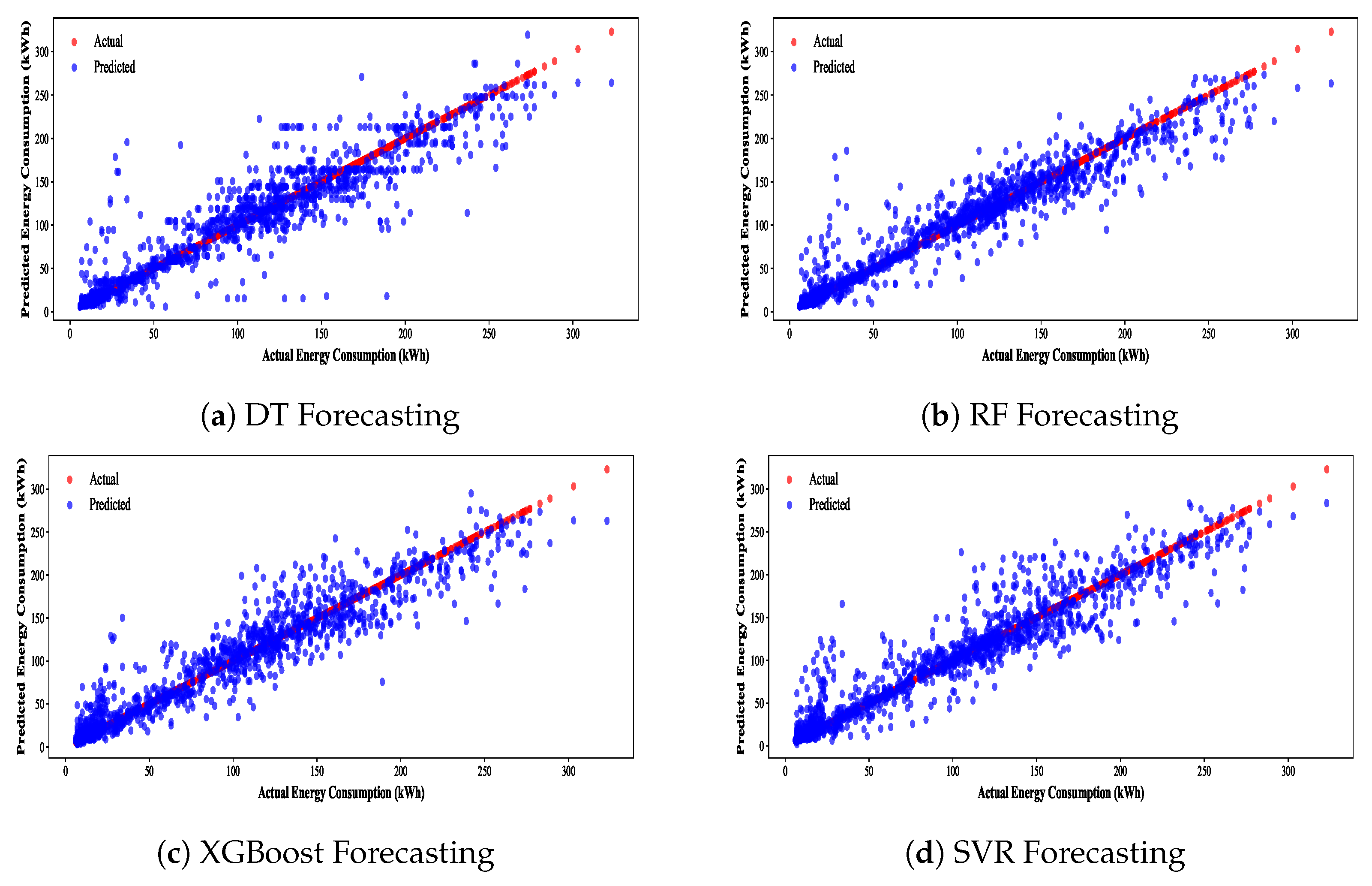
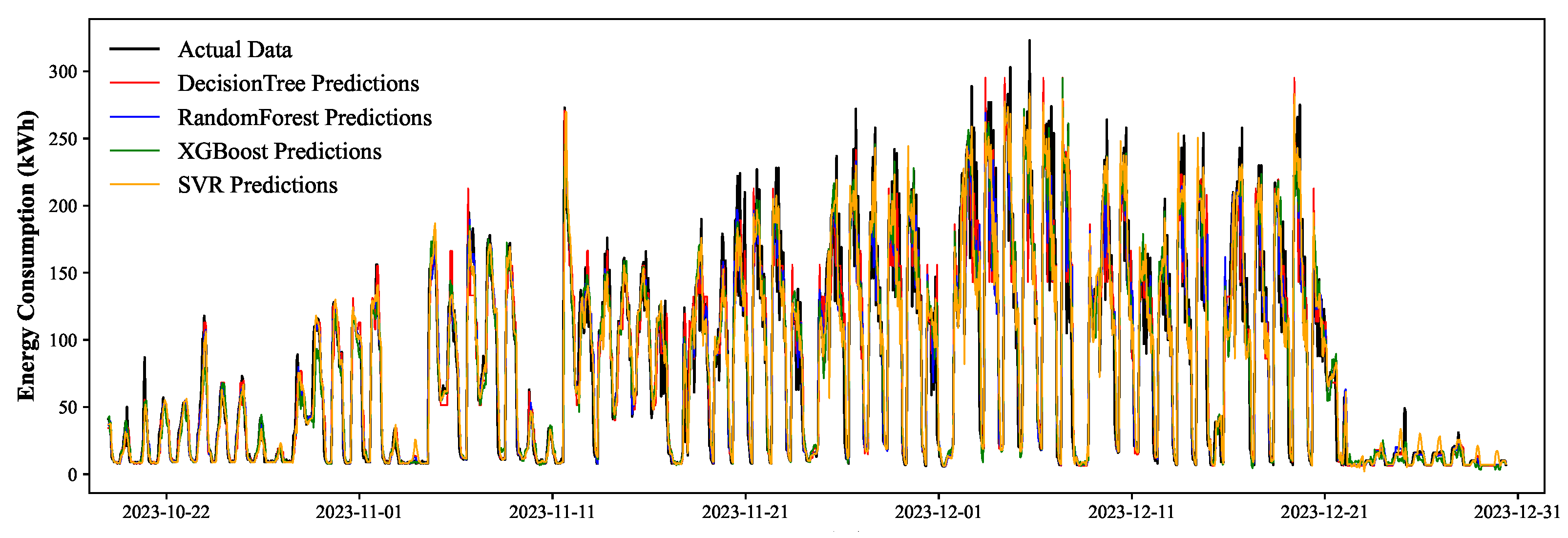
4.1. Machine Learning-Based Forecasting Results
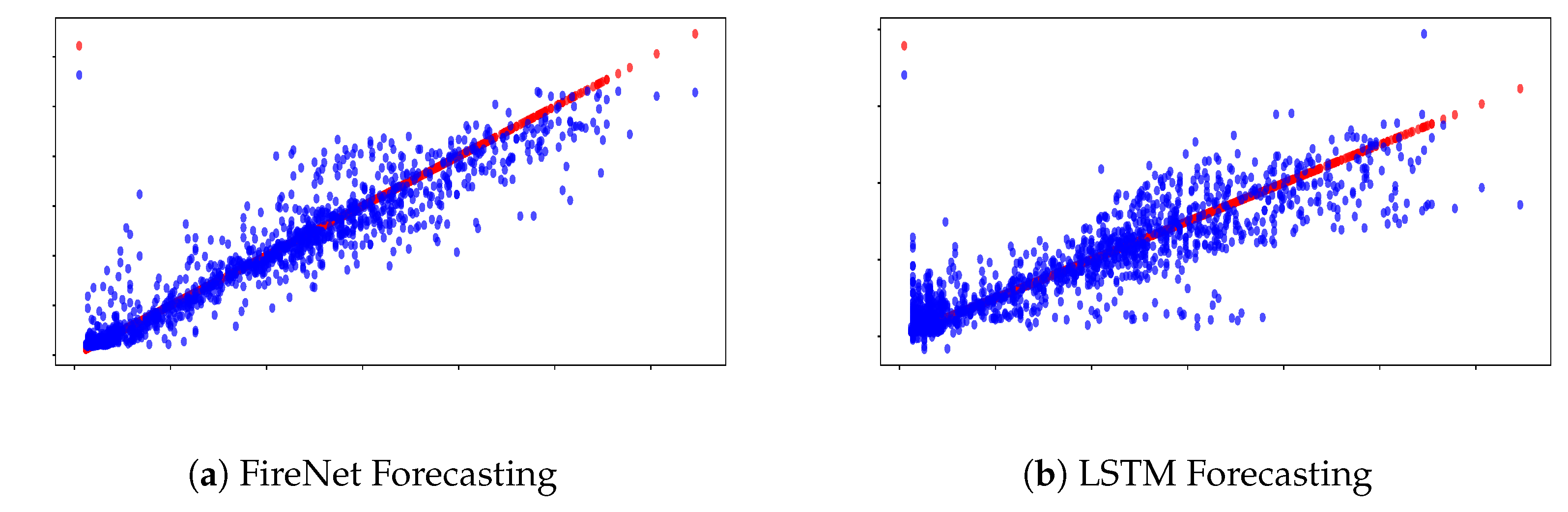
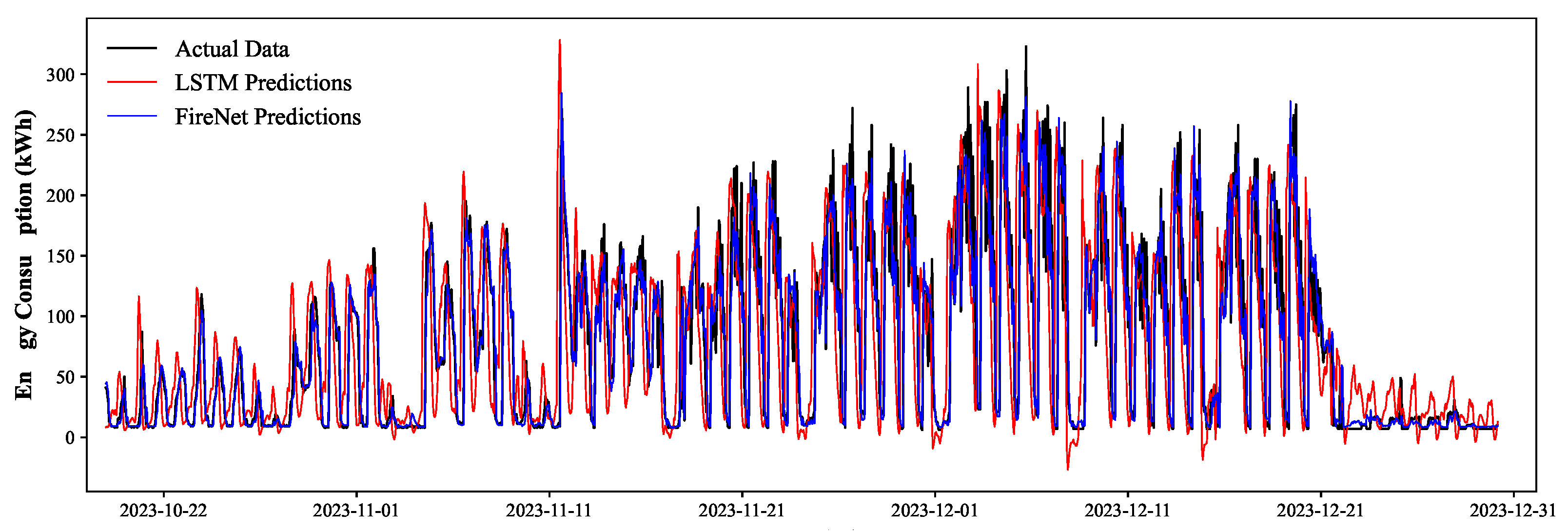
4.2. Deep Learning-Based Forecasting Results
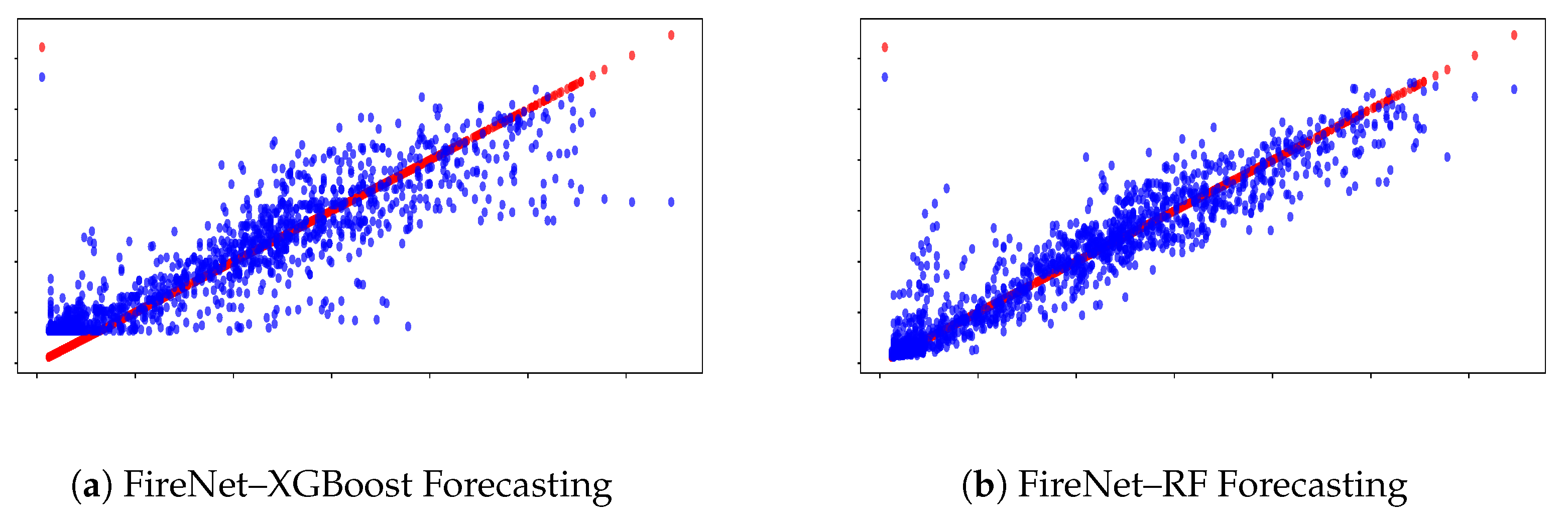
4.3. Hybrid Model Performance
5. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Oliveira, G.M.; Vidal, D.G.; Ferraz, M.P. Urban Lifestyles and Consumption Patterns. In Encyclopedia of the UN Sustainable Development Goals; Springer: Cham, Switzerland, 2020; pp. 851–860. [Google Scholar] [CrossRef]
- Bilgen, S. Structure and environmental impact of global energy consumption. Renew. Sustain. Energy Rev. 2014, 38, 890–902. [Google Scholar] [CrossRef]
- González-Torres, M.; Pérez-Lombard, L.; Coronel, J.F.; Maestre, I.R.; Yan, D. A review on buildings energy information: Trends, end-uses, fuels and drivers. Energy Rep. 2022, 8, 626–637. [Google Scholar] [CrossRef]
- Afshan, S.; Ozturk, I.; Yaqoob, T. Facilitating renewable energy transition, ecological innovations and stringent environmental policies to improve ecological sustainability. Renew. Energy 2022, 196, 151–160. [Google Scholar] [CrossRef]
- Salkuti, S.R. Emerging and Advanced Green Energy Technologies for Sustainable and Resilient Future Grid. Energies 2022, 15, 6667. [Google Scholar] [CrossRef]
- Zhao, J.; Patwary, A.K.; Qayyum, A.; Alharthi, M.; Bashir, F.; Mohsin, M.; Hanif, I.; Abbas, Q. The determinants of renewable energy sources for the fueling of green and sustainable economy. Energy 2022, 238, 122029. [Google Scholar] [CrossRef]
- Giovanni, G.D.; Rotilio, M.; Giusti, L.; Ehtsham, M. Exploiting building information modeling and machine learning for optimizing rooftop photovoltaic systems. Energy Build. 2024, 313, 114250. [Google Scholar] [CrossRef]
- Ehtsham, M.; Rotilio, M.; Cucchiella, F. Deep learning augmented medium-term photovoltaic energy forecasting. Energy Rep. 2025, 13, 4299–4317. [Google Scholar] [CrossRef]
- El-Afifi, M.I.; Sedhom, B.E.; Eladl, A.A.; Elgamal, M.; Siano, P. Demand side management strategy for smart building using multi-objective hybrid optimization technique. Results Eng. 2024, 22, 102265. [Google Scholar] [CrossRef]
- Raza, A.; Jingzhao, L.; Adnan, M.; Ahmad, I. Optimal load forecasting and scheduling strategies for smart homes peer-to-peer energy networks. Results Eng. 2024, 22, 102188. [Google Scholar] [CrossRef]
- Ehtsham, M.; Rotilio, M.; Cucchiella, F.; Giovanni, G.D.; Schettini, D. Investigating the effects of hyperparameter sensitivity on machine learning algorithms for PV forecasting. In Proceedings of the E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2025; Volume 612, p. 01002. [Google Scholar] [CrossRef]
- Lazos, D.; Sproul, A.B.; Kay, M. Optimisation of energy management in commercial buildings with weather forecasting inputs: A review. Renew. Sustain. Energy Rev. 2014, 39, 587–603. [Google Scholar] [CrossRef]
- Iqbal, N.; Kim, D.H. IoT task management mechanism based on predictive optimization for efficient energy consumption in smart residential buildings. Energy Build. 2022, 257, 111762. [Google Scholar] [CrossRef]
- Pawar, P.; TarunKumar, M. An IoT based Intelligent Smart Energy Management System. Measurement 2020, 152, 107187. [Google Scholar] [CrossRef]
- Khan, S.U.; Khan, N.; Ullah, F.U.M.; Kim, M.J.; Lee, M.Y.; Baik, S.W. Towards intelligent building energy management: AI-based framework for power consumption and generation forecasting. Energy Build. 2023, 279, 112705. [Google Scholar] [CrossRef]
- Mathumitha, R.; Rathika, P.; Manimala, K. Intelligent deep learning techniques for energy consumption forecasting in smart buildings: A review. Artif. Intell. Rev. 2024, 57, 35. [Google Scholar] [CrossRef]
- Santos, M.L.; García, S.D.; García-Santiago, X.; Ogando-Martínez, A.; Camarero, F.E.; Gil, G.B.; Ortega, P.C. Deep learning and transfer learning techniques applied to short-term load forecasting of data-poor buildings in local energy communities. Energy Build. 2023, 292, 113164. [Google Scholar] [CrossRef]
- Wahid, F.; Ghazali, R.; Shah, A.S.; Fayaz, M. Prediction of energy consumption in the buildings using multi-layer perceptron and random forest. Int. J. Adv. Sci. Technol. 2017, 101, 13–22. [Google Scholar] [CrossRef]
- NASA Power Data Access Viewer: Prediction of Worldwide Energy Resource. Available online: https://power.larc.nasa.gov/data-access-viewer/ (accessed on 1 February 2025).
- International Energy Agency. World Energy Outlook 2024; IEA: Paris, France, 2024. [Google Scholar]
- Wang, Z.; Wang, Y.; Zeng, R.; Srinivasan, R.S.; Ahrentzen, S. Random Forest based hourly building energy prediction. Energy Build. 2018, 171, 11–25. [Google Scholar] [CrossRef]
- Chou, J.S.; Tran, D.S. Forecasting energy consumption time series using machine learning techniques based on usage patterns of residential householders. Energy 2018, 165, 709–726. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Wang, J.Q.; Du, Y.; Wang, J. LSTM based long-term energy consumption prediction with periodicity. Energy 2020, 197, 117197. [Google Scholar] [CrossRef]
- Alam, G.M.I.; Tasnia, N.; Biswas, T.; Hossen, M.J.; Tanim, S.A.; Miah, M.S.U. Real-Time Detection of Forest Fires Using FireNet-CNN and Explainable AI Techniques. IEEE Access 2025, 13, 51150–51181. [Google Scholar] [CrossRef]
- Yesilyurt, H.; Dokuz, Y.; Dokuz, A.S. Data-driven energy consumption prediction of a university office building using machine learning algorithms. Energy 2024, 310, 133242. [Google Scholar] [CrossRef]
- Alotaibi, B.S.; Abuhussain, M.A.; Dodo, Y.A.; Al-Tamimi, N.; Maghrabi, A.; Ojobo, H.; Naibi, A.U.; Benti, N.E. A novel approach to estimate building electric power consumption based on machine learning method: Toward net-zero energy, low carbon and smart buildings. Int. J. Low-Carbon Technol. 2024, 19, 2335–2345. [Google Scholar] [CrossRef]
- Gao, Z.; Yu, J.; Zhao, A.; Hu, Q.; Yang, S. A hybrid method of cooling load forecasting for large commercial building based on extreme learning machine. Energy 2022, 238, 122073. [Google Scholar] [CrossRef]
- Kim, T.Y.; Cho, S.B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Sulaimon, I.; Sunmola, F.; Ajayi, S. Building energy consumption prediction for residential buildings using deep learning and other machine learning techniques. J. Build. Eng. 2022, 45, 103406. [Google Scholar] [CrossRef]
- Sunder, R.; R, S.; Paul, V.; Punia, S.K.; Konduri, B.; Nabilal, K.V.; Lilhore, U.K.; Lohani, T.K.; Ghith, E.; Tlija, M. An advanced hybrid deep learning model for accurate energy load prediction in smart building. Energy Explor. Exploit. 2024, 42, 2241–2269. [Google Scholar] [CrossRef]
- Yenagimath, M. Electrical Load Forecasting using Improved Feature Selection and Hybrid Deep Learning Algorithms for Power System Situational Awareness. Deleted J. 2024, 20, 2825–2836. [Google Scholar] [CrossRef]
- Lu, H.; Wu, J.; Ruan, Y.; Qian, F.; Meng, H.; Gao, Y.; Xu, T. A multi-source transfer learning model based on LSTM and domain adaptation for building energy prediction. Int. J. Electr. Power Energy Syst. 2023, 149, 109024. [Google Scholar] [CrossRef]
- Peng, X.; Li, Y.; Zhou, H. Transfer Learning and Attention-Enhanced Seq2Seq Model for Green Building Load Forecasting. Sci. Rep. 2025, 15, 16953. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Lu, S.; Zhou, S.; Tian, Z.; Kim, M.; Liu, J.; Liu, X. A Systematic Review of Building Energy Consumption Prediction: From Perspectives of Load Classification, Data-Driven Frameworks, and Future Directions. Appl. Sci. 2025, 15, 3086. [Google Scholar] [CrossRef]
- Zhong, H.; Wang, J.; Jia, H.; Mu, Y.; Lv, S. Vector field-based support vector regression for building energy consumption prediction. Appl. Energy 2019, 242, 403–414. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Cao, L.; Li, Y.; Zhang, J.; Jiang, Y.; Han, Y.; Wei, J. Electrical load prediction of healthcare buildings through single and ensemble learning. Energy Rep. 2020, 6, 2751–2767. [Google Scholar] [CrossRef]
- Ismail, L.; Materwala, H.; Dankar, F.K. Machine Learning Data-Driven Residential Load Multi-Level Forecasting with Univariate and Multivariate Time Series Models Toward Sustainable Smart Homes. IEEE Access 2024, 12, 55632–55668. [Google Scholar] [CrossRef]
- Somu, N.; R, G.R.M.; Ramamritham, K. A deep learning framework for building energy consumption forecast. Renew. Sustain. Energy Rev. 2021, 137, 110591. [Google Scholar] [CrossRef]
- Hussain, A.; Franchini, G.; Giangrande, P.; Mandelli, G.; Fenili, L. A Comparative Analysis of Machine Learning Models for Medium-Term Load Forecasting in Smart Commercial Building. In Proceedings of the 2024 IEEE 12th International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 18–20 August 2024; pp. 228–232. [Google Scholar] [CrossRef]
- Chandler, W.S.; Hoell, J.M.; Westberg, D.; Zhang, T.; Stackhouse, P.W. NASA Prediction of Worldwide Energy Resource High Resolution Meteorology Data For Sustainable Building Design; Technical Report; NASA: Washington, DC, USA, 2013. [Google Scholar]
- Zhang, J.; Xu, Z.; Wei, Z. Absolute Logarithmic Calibration for Correlation Coefficient with Multiplicative Distortion. Commun. Stat.-Simul. Comput. 2023, 52, 482–505. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Mallala, B.; Azeez Khan, P.; Pattepu, B.; Eega, P.R. Integrated Energy Management and Load Forecasting Using Machine Learning. In Proceedings of the 2024 2nd International Conference on Sustainable Computing and Smart Systems (ICSCSS), Coimbatore, India, 10–12 July 2024; pp. 1004–1009. [Google Scholar] [CrossRef]
- Zhu, J.; Dong, H.; Zheng, W.; Li, S.; Huang, Y.; Xi, L. Review and prospect of data-driven techniques for load forecasting in integrated energy systems. Appl. Energy 2022, 321, 119269. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, R.; Wu, Z.; Liu, T. Short-Term Power Load Forecasting Model Based on Fuzzy Neural Network using Improved Decision Tree. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 482–486. [Google Scholar] [CrossRef]
- Alrobaie, A.; Krarti, M. A Review of Data-Driven Approaches for Measurement and Verification Analysis of Building Energy Retrofits. Energies 2022, 15, 7824. [Google Scholar] [CrossRef]
- Olawuyi, A.; Ajewole, T.; Oladepo, O.; Awofolaju, T.T.; Agboola, M.; Hasan, K. Development of an Optimized Support Vector Regression Model Using Hyper-Parameters Optimization for Electrical Load Prediction. UNIOSUN J. Eng. Environ. Sci. 2024, 6. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Lazzari, F.; Mor, G.; Cipriano, J.; Gabaldon, E.; Grillone, B.; Chemisana, D.; Solsona, F. User behavior models to forecast electricity consumption of residential customers based on smart metering data. Energy Rep. 2022, 8, 3680–3691. [Google Scholar] [CrossRef]
- Dabrowski, J.J.; Zhang, Y.; Rahman, A. ForecastNet: A Time-Variant Deep Feed-Forward Neural Network Architecture for Multi-step-Ahead Time-Series Forecasting. In Neural Information Processing. ICONIP 2020; Yang, H., Pasupa, K., Leung, A.C.S., Kwok, J.T., Chan, J.H., King, I., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12534. [Google Scholar] [CrossRef]
- Forootan, M.M.; Larki, I.; Zahedi, R.; Ahmadi, A. Machine Learning and Deep Learning in Energy Systems: A Review. Sustainability 2022, 14, 4832. [Google Scholar] [CrossRef]
- Rafi, S.H.; Nahid-Al-Masood; Deeba, S.R.; Hossain, E. A Short-Term Load Forecasting Method Using Integrated CNN and LSTM Network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
- Hussain, A.; Giangrande, P.; Franchini, G.; Fenili, L.; Messi, S. Analyzing the Effect of Error Estimation on Random Missing Data Patterns in Mid-Term Electrical Forecasting. Electronics 2025, 14, 1383. [Google Scholar] [CrossRef]
- Hakyemez, T.C.; Adar, O. Testing the Efficacy of Hyperparameter Optimization Algorithms in Short-Term Load Forecasting. arXiv 2024, arXiv:2410.15047. [Google Scholar] [CrossRef]
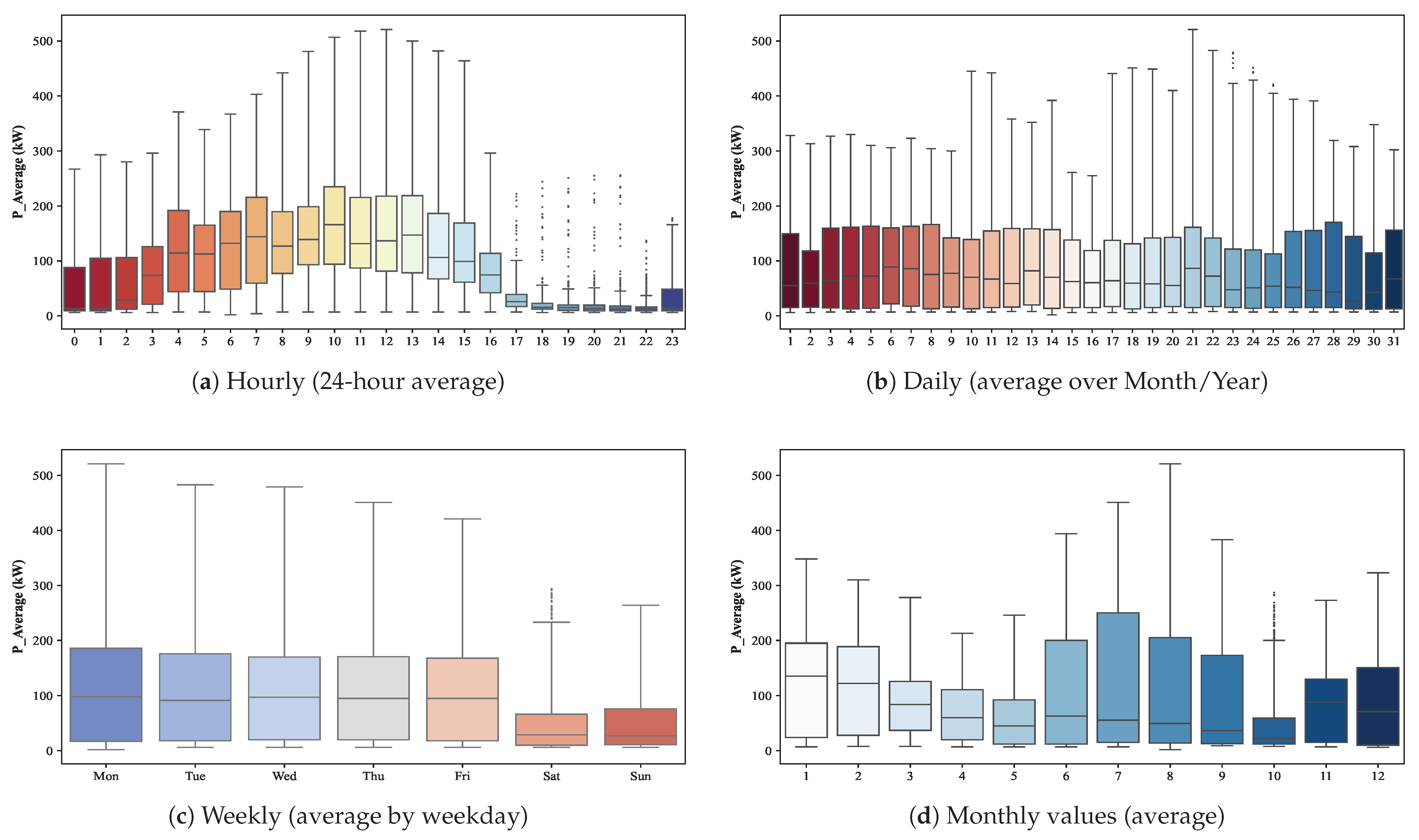

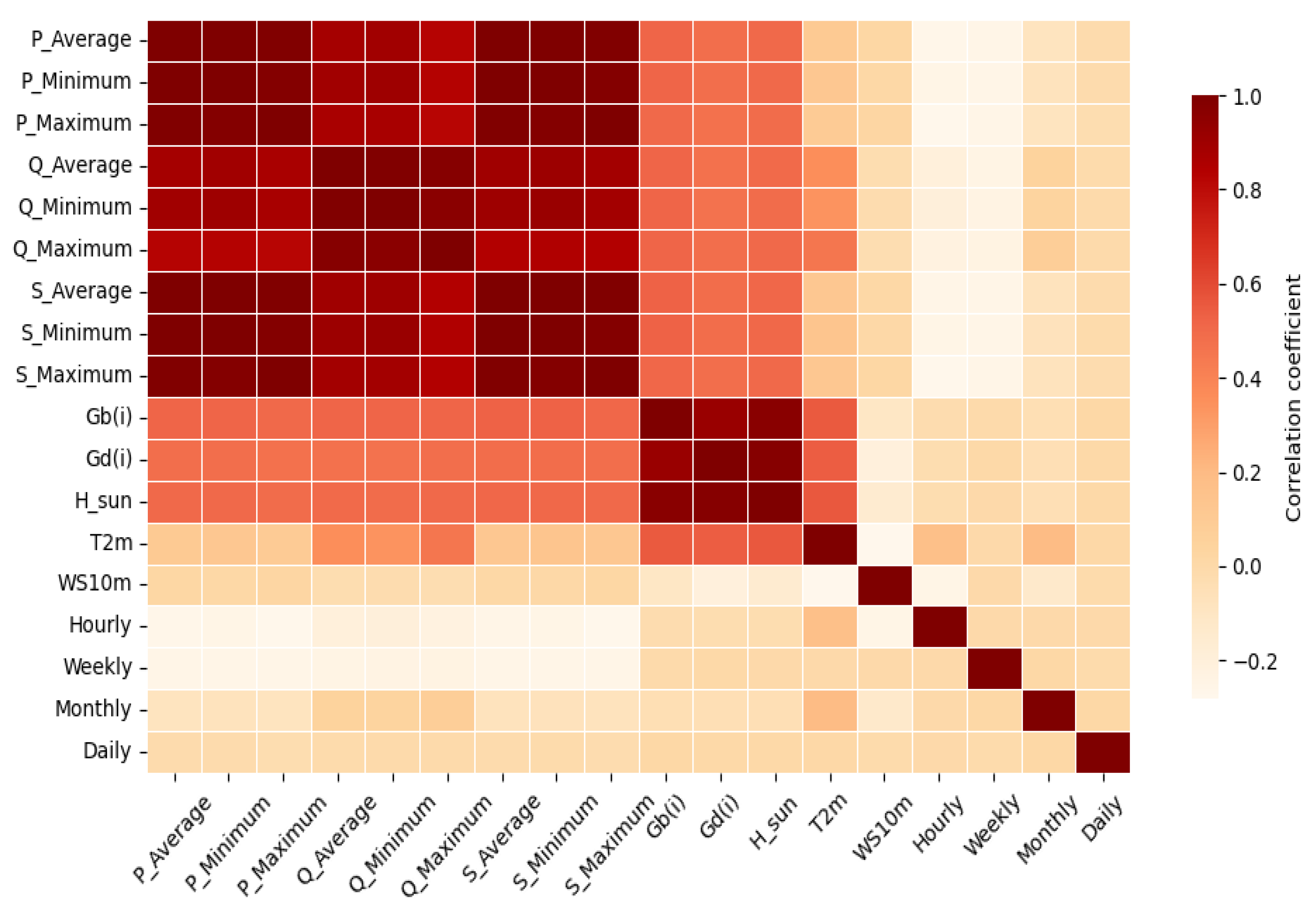

| Date | Time | (kW) | (kW) | (kW) | (kvar) | (kvar) | (kvar) | (kVA) | (kVA) | (kVA) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 January 2021 | 08:00:00 | 356 | 336 | 376 | 32 | 29 | 36 | 311 | 291 | 331 |
| 1 January 2021 | 09:00:00 | 345 | 324 | 373 | 30 | 26 | 33 | 300 | 279 | 328 |
| 1 January 2021 | 10:00:00 | 351 | 329 | 380 | 31 | 28 | 37 | 306 | 284 | 336 |
| 1 January 2021 | 11:00:00 | 357 | 334 | 387 | 33 | 29 | 37 | 312 | 289 | 343 |
| 1 January 2021 | 12:00:00 | 361 | 331 | 389 | 33 | 28 | 36 | 316 | 287 | 345 |
| Date | Time | Gb(i) (W/m2) | Gd(i) (W/m2) | H_sun (h) | T2m (°C) | WS10m (m/s) |
|---|---|---|---|---|---|---|
| 1 January 2021 | 08:00:00 | 56.005 | 43.800 | 8.39 | −1.440 | 1.585 |
| 1 January 2021 | 09:00:00 | 103.139 | 75.933 | 14.83 | 1.100 | 0.997 |
| 1 January 2021 | 10:00:00 | 142.206 | 96.400 | 19.25 | 3.866 | 0.483 |
| 1 January 2021 | 11:00:00 | 186.007 | 93.733 | 21.20 | 4.933 | 0.593 |
| 1 January 2021 | 11:00:00 | 165.273 | 97.200 | 20.49 | 5.143 | 0.745 |
| Index | Electrical Load Classification |
|---|---|
| 1 | Original time-series data (unmodified raw observations). |
| 2 | Weekdays (Monday to Friday), excluding Holidays. |
| 3 | Weekend (Saturday and Sunday) and Holidays. |
| 4 | Statistical aggregation features: Daily, Weekly, and Monthly Averages. |
| 5 | Seasonal categorization into Winter, Spring, Summer, and Autumn. |
| Block | Filters | Kernel Size | Pool Size | Output Shape |
|---|---|---|---|---|
| 1 | 32 | 5 | 2 | |
| 2 | 64 | 5 | 2 | |
| 3 | 128 | 3 | 2 | |
| 4 | 256 | 3 | 2 | |
| 5 | 512 | 3 | – |
| Model | Parameter | Range | Optuna Value |
|---|---|---|---|
| Decision Tree | max_depth | [10, 20, 30, 50, 100] | 7 |
| min_samples_split | [2, 3, 5, 10] | 10 | |
| min_samples_leaf | [1, 5, 10] | 8 | |
| criterion | [mse, mae] | mse | |
| split_strategy | [best, random] | best | |
| Random Forest | n_estimators | [50, 100, 150, 200, 300] | 80 |
| max_depth | [10, 30, 50, 70, 100, None] | 13 | |
| min_samples_split | [2, 3, 5, 10] | 7 | |
| min_samples_leaf | [1, 2, 3, 4, 5] | 5 | |
| max_features | [auto, sqrt, log2] | sqrt | |
| bootstrap | [True, False] | True | |
| XGBoost | n_estimators | [50, 300] | 261 |
| max_depth | [3, 20] | 4 | |
| learning_rate | [0.01, 0.3] | 0.051 | |
| subsample | [0.5, 1.0] | 0.949 | |
| colsample_bytree | [0.5, 1.0] | 0.813 | |
| gamma | [0, 5] | 3.704 | |
| reg_alpha | [0, 5] | 3.083 | |
| reg_lambda | [0, 5] | 3.442 | |
| SVR | C | [0.1, 100] (log) | 34.95 |
| epsilon | [0.001, 1.0] (log) | 0.244 | |
| kernel | [rbf, linear] | rbf | |
| gamma | [scale, auto] | auto | |
| FireNet | filters | [32, 64, 128] | 64 |
| dropout_rate | [0.2, 0.5] (uniform) | 0.2132 | |
| learning_rate | [0.0005, 0.01] (log) | 0.000507 | |
| batch_size | [16, 32, 64] | 64 | |
| LSTM | units | [32, 50, 64] | 32 |
| dropout_rate | [0.1, 0.5] (uniform) | 0.285 | |
| learning_rate | [0.0005, 0.01] (log) | 0.007215 | |
| batch_size | [16, 32, 64] | 16 |
| Model | Training Time (s) | MSE | RMSE | R2 Score | MAPE (%) |
|---|---|---|---|---|---|
| DT | 0.01620 | 778.2 | 27.90 | 0.8514 | 35.68 |
| RF | 1.101 | 527.7 | 22.97 | 0.8992 | 33.63 |
| XGBoost | 0.05100 | 518.5 | 22.77 | 0.9010 | 37.17 |
| SVR | 41.13 | 2111 | 45.95 | 0.7460 | 44.79 |
| Model | Training Time (s) | MSE | RMSE | R2 Score | MAPE (%) |
|---|---|---|---|---|---|
| FireNet | 22.61 | 923.5 | 30.39 | 0.8237 | 39.90 |
| LSTM | 46.97 | 1280 | 35.78 | 0.7558 | 96.21 |
| Model | Training Time (s) | MSE | RMSE | R2 | MAPE (%) |
|---|---|---|---|---|---|
| FireNet-XGBoost | 33.69 | 350.2 | 18.71 | 0.9334 | 27.00 |
| FireNet-RF | 21.11 | 418.4 | 20.45 | 0.9205 | 29.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, A.; Franchini, G.; Akram, M.; Ehtsham, M.; Hashim, M.; Fenili, L.; Messi, S.; Giangrande, P. Hybrid ML/DL Approach to Optimize Mid-Term Electrical Load Forecasting for Smart Buildings. Appl. Sci. 2025, 15, 10066. https://doi.org/10.3390/app151810066
Hussain A, Franchini G, Akram M, Ehtsham M, Hashim M, Fenili L, Messi S, Giangrande P. Hybrid ML/DL Approach to Optimize Mid-Term Electrical Load Forecasting for Smart Buildings. Applied Sciences. 2025; 15(18):10066. https://doi.org/10.3390/app151810066
Chicago/Turabian StyleHussain, Ayaz, Giuseppe Franchini, Muhammad Akram, Muhammad Ehtsham, Muhammad Hashim, Lorenzo Fenili, Silvio Messi, and Paolo Giangrande. 2025. "Hybrid ML/DL Approach to Optimize Mid-Term Electrical Load Forecasting for Smart Buildings" Applied Sciences 15, no. 18: 10066. https://doi.org/10.3390/app151810066
APA StyleHussain, A., Franchini, G., Akram, M., Ehtsham, M., Hashim, M., Fenili, L., Messi, S., & Giangrande, P. (2025). Hybrid ML/DL Approach to Optimize Mid-Term Electrical Load Forecasting for Smart Buildings. Applied Sciences, 15(18), 10066. https://doi.org/10.3390/app151810066








