Next Article in Journal
Comparative Analysis of Natural Language Processing Techniques in the Classification of Press Articles
Previous Article in Journal
Lifting-Line Predictions for Optimal Dihedral Distributions in Ground Effect
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 17
10.3390/app15179554
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Acoustic Emission and Infrared Radiation Temperature Characteristics of Coal with Varying Bedding Planes Under Uniaxial Compression

by
Yang Wu
1,
Bin Liu
1,2,*,
Shirui Wang
3 and
Bo Pang
3
1
State Key Laboratory of Water Resource Protection and Utilization in Coal Mining, National Institute of Clean and Low Carbon Energy, Beijing 102211, China
2
State Key Laboratory of Digital Intelligent Technology for Unmanned Coal Mining, Anhui University of Science and Technology, Huainan 232001, China
3
Information Institute of the Ministry of Emergency Management of the People’s Republic of China, Beijing 100029, China
*
Author to whom correspondence should be addressed.
Appl. Sci. 2025, 15(17), 9554; https://doi.org/10.3390/app15179554
Submission received: 11 August 2025 / Revised: 29 August 2025 / Accepted: 29 August 2025 / Published: 30 August 2025
(This article belongs to the Section Acoustics and Vibrations)
Browse Figures
Versions Notes

Abstract

As a core structure in coal mine underground reservoirs, the coal pillar dams’ stability is susceptible to the orientation of coal bedding planes. This study examines the deformation characteristics, acoustic emission (AE) evolution, and infrared radiation temperature (IRT) response of coal specimens with varying bedding angles (0°, 30°, 60°, 90°), investigating microscopic failure mechanisms and AE-IRT correlations. The results show that compressive strength and elastic modulus follow a V-shaped trend with increasing bedding angle, initially decreasing before rising. The proportion of low-amplitude events (40–60 dB) increases, while the higher-amplitude (>60 dB) AE signals decrease with the bedding angle. The AE b-values increase with the bedding angles. Mean IRT temperatures exhibit an overall increasing trend with significant fluctuations, and fluctuation amplitudes display an N-shaped pattern. Microscopically, all specimens undergo tensile–shear composite failure, but shear failure contribution varies markedly: 30° specimens show the highest shear proportion, while 60° specimens show the lowest. There is a positive correlation between AE and IRT. The correlation coefficient (γ) is relatively low at 0°, but it is higher at 30°, 60°, and 90°. This research provides a theoretical underpinning for optimizing the design and stability evaluation of coal mine underground reservoirs.

1. Introduction

Coal mine underground reservoir technology serves as a crucial approach for achieving water resource conservation and efficient utilization in mines. Its core structure—the dam body composed of abandoned coal pillars in goaf areas—primarily fulfills the essential functions of sealing water storage spaces and maintaining reservoir stability [1,2,3]. However, as a typical sedimentary rock mass, coal possesses a widely developed internal bedding structure that confers significant mechanical anisotropy [4,5,6]. This anisotropy profoundly influences the strength performance, failure behaviors, and deformation mechanisms of the coal pillar dam. Consequently, it is imperative to conduct an in-depth investigation into how different bedding orientations predominantly influence the mechanical response and failure mechanisms of coal pillar dams.
As the most prominent structural features in coal–rock masses, bedding planes exert a decisive influence on their strength properties, deformation behavior, and failure mechanisms. As a critical research focus in rock mechanics, mining engineering, and energy geology, significant progress has recently been driven by extensive experimental and theoretical studies on the bedding plane effect. Zhao et al. [7] investigated the dynamic indirect tensile properties of bedding coal based on the impact tests. Viljoen et al. [8] analyzed the bedding plane effect on the degradation characteristics of coal based on the microfocus x-ray computed tomography. Wang et al. [9] conducted a comparative analysis of the permeability of coal in the vertical direction and the parallel direction. Liu et al. [10] obtained the deformation and permeability properties of bedding coal. Ju et al. [11] investigated the loading rate and bedding plane effects on the dynamic deformation behavior and crack propagation characteristics. Maruvanchery et al. [12] analyzed the bedding orientations effect on KIC and the energy consumed for rock. Wang et al. [13] obtained the bedding plane effects on dynamic crack propagation characteristics and fracture toughness of bedding coal. Zhou et al. [14] investigated the influence of bedding planes and loading rates on acoustic emission (AE) evolution and energy conversion of bedding coal. Shi et al. [15] obtained the bedding angle and loading rate effects on the dynamic tensile failure pattern of coal and shale. Khalili et al. [16] analyzed the bending strength and crack propagation mechanism of rock-like material at varying bedding planes. Wang et al. [17,18] investigated the energy evolution and mechanical properties of coal with varying bedding planes under high confining pressure. Mashhadiali et al. [19] established a shear strength prediction model for anisotropic rocks through theoretical and experimental analysis. Sun et al. [20] analyzed the fracture properties and fracture process of coal with varying bedding angles and sizes. Huang et al. [21] discussed the extension mechanism and formation process under hydraulic fractures for bedding coal. Zhang et al. [22] obtained the influence of bedding angles on the infrared radiation temperature (IRT) characteristics and energy evolution of bedding coal. Huang et al. [23] studied the damage evolution and energy dissipation mechanism of coal with varying bedding planes under uniaxial compressive conditions. Tang et al. [24] analyzed the influence of bedding angle on the mechanical response and permeability properties of gas-bearing coal. Ma et al. [25] obtained the effect of bedding angle on the fracture behaviors of bedding coal. Sun et al. [26] investigated the crack propagation behaviors of coal with varying bedding angles during a mode II loading test.
During the damage and failure process of coal–rock mass, accumulated elastic strain energy is released as acoustic, thermal, electrical, and magnetic energy [27,28]. AE and IRT techniques—capable of monitoring internal crack initiation, propagation, and coalescence, as well as surface temperature variations during deformation failure—are widely used to study coal–rock failure processes [28,29,30]. In recent years, the AE and IRT technologies have been combined to characterize the failure process. Rankin et al. [31] analyzed the AE and IRT characteristics during the combustion process of turbulent premixed flames. Pieczyska et al. [32] obtained the martensitic transformation pattern for TiNi shape-memory alloy (SMA) based on the AE and IRT technologies. Xu et al. [33] investigated the AE and IRT evolution and precursors of sandstone under the cyclic loading and unloading conditions. Yin et al. [34] studied the damage evolution and failure precursors of coal with various burst tendencies by the comprehensive monitoring of AE and IRT. Chang et al. [35] analyzed the AE, IRT, and crack propagation evolution for fissured rock under uniaxial compression conditions.
The influence of bedding planes on the mechanical properties (such as compressive strength, tensile strength, and fracture toughness), deformation behavior, and failure mechanisms has been extensively studied, and some scholars have combined AE and IRT techniques to investigate deformation behavior. However, research on the bedding effect characteristics of coal specimens combining AE and IRT remains relatively scarce. Thus, Uniaxial compression tests were performed on coal specimens featuring bedding orientations of 0°, 30°, 60°, and 90°, and the deformation and failure processes were monitored using AE and IRT techniques. The deformation behavior, AE evolution, and IRT response were systematically analyzed to elucidate micro-failure mechanisms and the interrelationship between AE and IRT signals. This finding provides a solid theoretical foundation and technical support for improving stability assessment models and securing the efficient and safe operation of coal mine underground reservoirs.

2. Materials and Methods

2.1. Coal Specimen

The coal was sourced from the 3−1 coal seam at Hongqinghe Coal Mine, Ordos, China. The coal seam occurs at a depth ranging from 583.55 to 861.90 m, averaging 718.60 m. The seam thickness ranges from 0.50 to 10.05 m, averaging 6.23 m. Seam dip angles range from 1° to 3°, averaging 2°. The immediate roof lithology is primarily sandy mudstone, while the immediate floor consists mainly of sandy mudstone and mudstone. The coal is black with a streak of dark brown to brownish-black. Bright coal and vitrain exhibit endogenous fissures, and the seam contains minor pyrite nodules. From a macroscopic perspective, the coal type is predominantly semi-dull coal, followed by semi-bright coal, with only a minor proportion being dull coal. Analysis results from relevant literature indicate that coal specimens from this seam possess a strong bursting liability. According to the requirements of the experimental design, the drilling direction was respectively aligned at 0°, 30°, 60°, and 90° with the bedding plane, and the coal specimens were then machined into standard cylindrical specimens (Φ 50 mm × H 100 mm) (Figure 1). The coal specimen grouping and density are illustrated in Table 1.

2.2. Testing System

As shown in Figure 1, the testing machine system employs an MTS E45.305 electronic (MTS, Eden Prairie, MN, USA) universal testing machine, featuring a rated maximum axial load capacity of 300 kN. This system offers a loading rate range of 0.001–250 mm/min with an accuracy of ±0.3%. The AE monitoring system utilizes a PCI Express 8 multi-channel AE instrument manufactured by the American company PAC (Marion, IA, USA). This instrument is paired with miniature AE sensors (Model: Nano30), with a frequency range of 125–750 kHz. The IRT monitoring system utilizes a FAST-M200 cooled infrared camera manufactured by Canada-based TOLOPS (Montreal, PQ, Canada). This camera provides a maximum resolution of 640 × 512 pixels and a temperature range of 0–100 °C. Its resolution is adjustable based on experimental requirements, supporting a maximum acquisition frame rate of 5600 Hz.

2.3. Experimental Methods

The AE monitoring system was set to a 40 dB signal threshold and 1 MHz sampling frequency, contrasting with the IRT monitoring system’s 40 Hz sampling rate. The testing machine system utilized a displacement rate of 0.06 mm/min under constant loading conditions. Six miniature AE sensors were mounted on the coal specimen surface using the same layout as in previous research [36]. During the test, the testing machine system, AE monitoring system, and IRT monitoring system were synchronously triggered to ensure data acquisition synchronization. Personnel were required to remain stationary throughout experiments to minimize interference with IRT measurements.

3. Results and Analysis

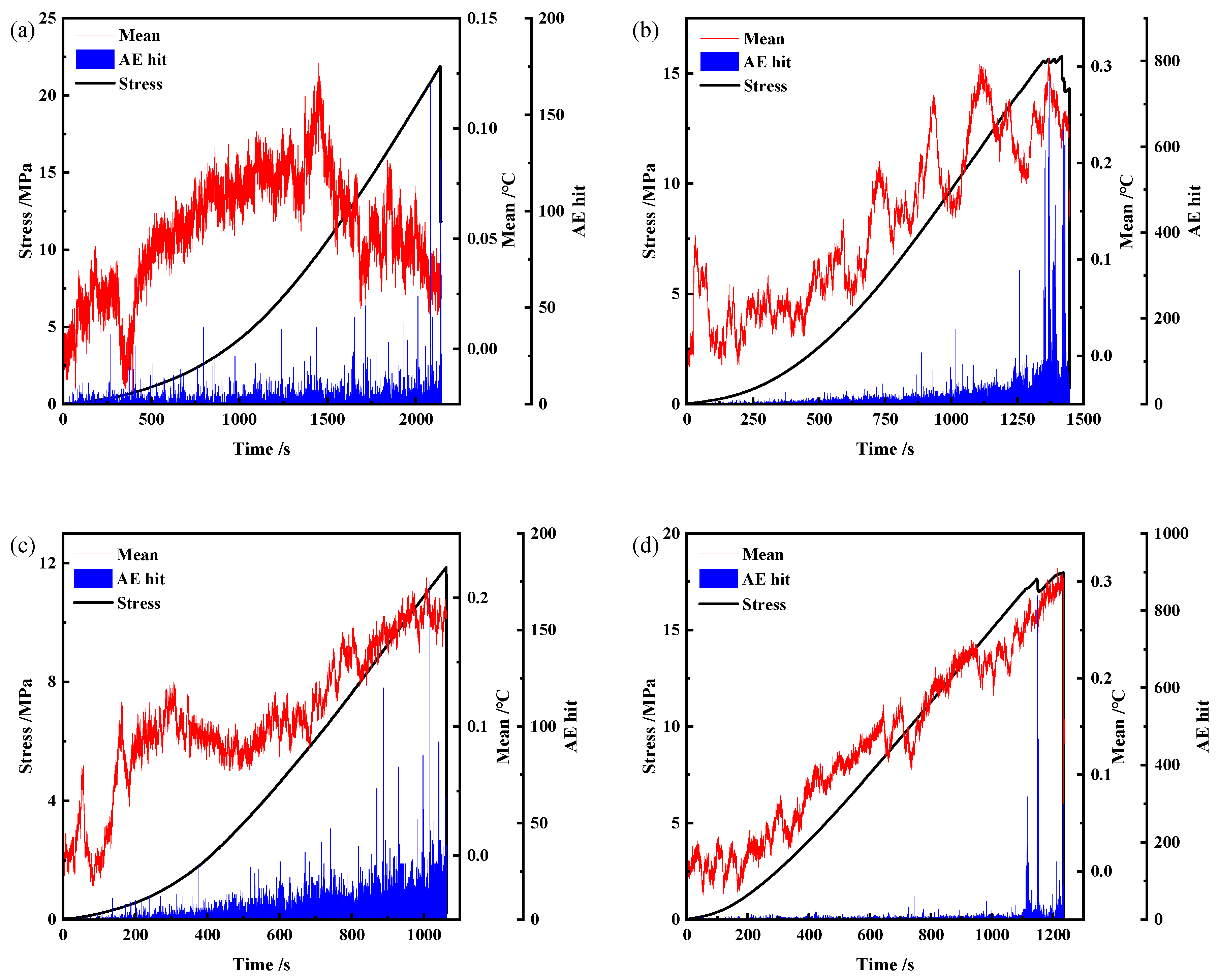
3.1. Deformation Characteristics

According to the uniaxial compressive strength (UCS) calculation formula, the mechanical parameters of coal specimens with varying bedding planes are presented in Table 1. The UCS ranges from 11.70 to 34.35 MPa, and the mean UCS of coal specimens at bedding angles of 0°, 30°, 60°, and 90° is 25.50, 18.41, 12.38, and 16.81 MPa, respectively. As illustrated in Figure 2, the UCS displays a V-shaped variation trend—initially decreasing and subsequently increasing when the bedding angle increases [22]. At a bedding angle of 0°, the mean UCS reaches its maximum value of 25.50 MPa. When the bedding angle increases to 60°, the UCS decreases to 12.38 MPa, representing a reduction rate of 51.45%. Acting as inherent potential weak planes within the coal mass, bedding planes readily become the stress concentration zones and preferential paths for crack initiation and propagation, which may induce disaster modes such as asymmetric deformation, progressive spalling, and even overall instability. Thus, considering the stability and safety of the coal pillar dam, it is necessary to ensure that the loading direction is perpendicular to the bedding plane.
The uniaxial compressive stress–strain curves at varying bedding angles are plotted in Figure 3. The failure process of coal specimens consists of four phases: primary crack compaction phase, elastic deformation phase, plastic deformation phase, and post-peak failure phase. As axial stress increases, the coal specimen first enters the primary crack compaction phase, where primary fissures or pores are compacted and closed, resulting in an upward concave stress–strain curve. At the elastic deformation phase, the curve shows an approximately linear increase. For coal specimens at bedding angles of 0°, 60°, and 90°, instantaneous brittle failure occurs upon reaching peak stress, accompanied by a rapid stress drop. In contrast, the 30° coal specimen retains certain load-bearing capacity after the peak stress until final failure is triggered by further crack propagation.
According to the definition of elastic modulus, the elastic modulus results of each coal specimen are presented in Table 1. The elastic modulus of coal specimens with varying bedding angles ranges from 1.15 to 1.87 GPa. The mean elastic modulus reaches its minimum value of 1.45 GPa at a bedding angle of 30°, while peaking at 1.70 GPa at 90°. As the bedding angle increases, the elastic modulus of coal specimens shows a V-shaped trend characterized by an initial decrease followed by an increase (Figure 4).

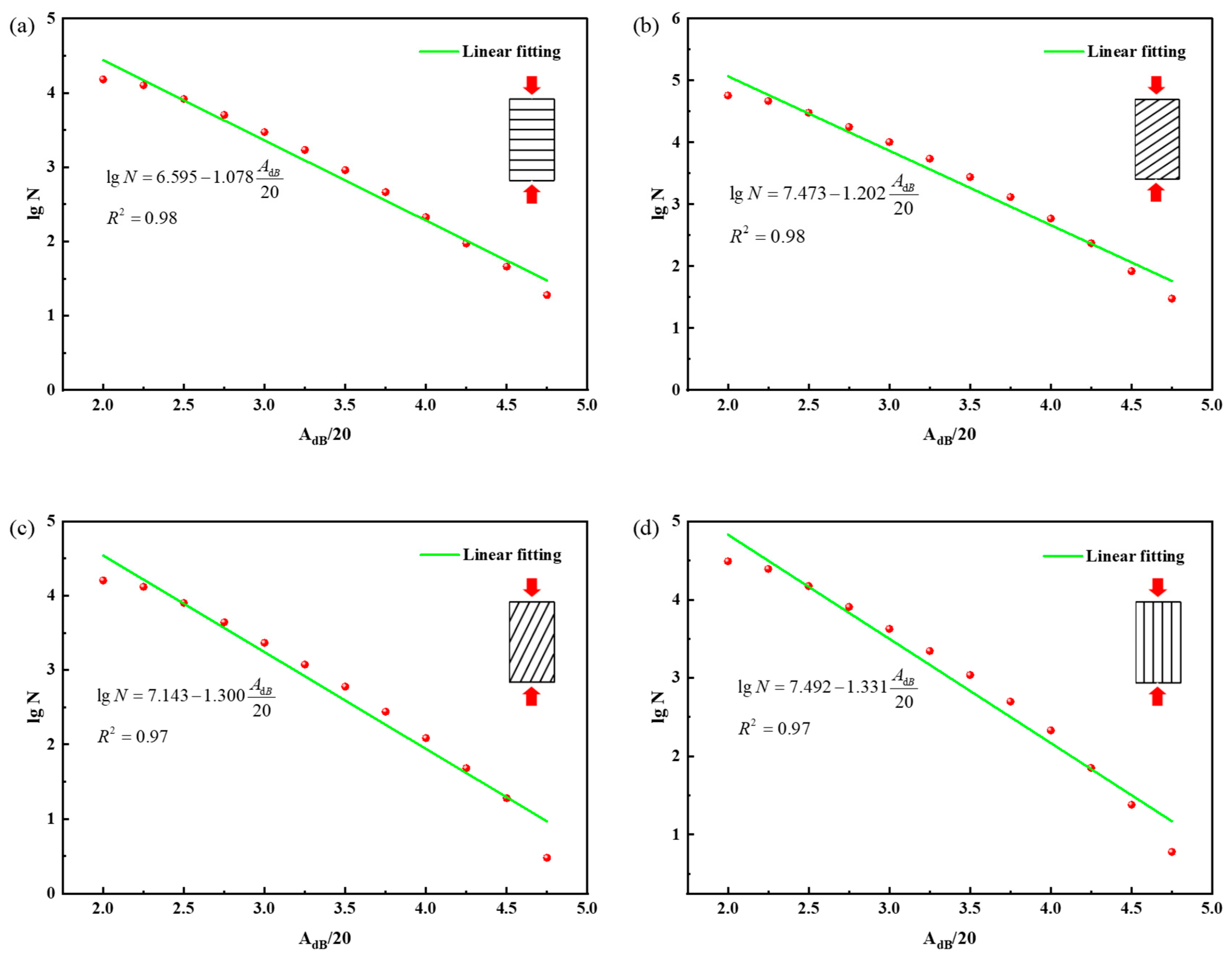
3.2. AE Evolution

The AE absolute energy evolution in coal specimens with varying bedding angles exhibits broadly similar patterns (Figure 5). The compression test process under varying bedding angles can encompass four distinct stages: fissure compaction stage (I), crack initiation stage (II), stable crack propagation stage (III), and unstable crack propagation stage (IV). During the initial loading phase, coal specimens enter the fissure compaction stage, where primary fissures and pores are compressed and closed under external force. This stage generates only weak AE signals with a slight increase in absolute energy. As the load increases, the process transitions to the crack initiation stage, where microcracks begin to form, accompanied by a gradual rise in absolute energy. With further load increment, coal specimens enter the stable crack propagation stage. Microcracks accelerate in initiation and propagation, leading to a sharp increase in AE signals and a significant acceleration in absolute energy growth rate. Ultimately, coal specimens reach the unstable crack propagation stage where massive microcrack propagation and coalescence occur, with absolute energy reaching its maximum before instantaneous failure of the specimen. Notably, the absolute energy reaches its maximum (23.4 × 108 aJ) at 30° bedding angle, while the minimum (2.54 × 108 aJ) occurs at 60°—approximately 10.85% of the 30° bedding angle. Consequently, as the bedding angle increases, the absolute energy exhibits an N-shaped trend: rising initially, then falling, and rising again. This phenomenon arises because bedding angle variation fundamentally alters the failure mechanisms and mechanical properties (such as compressive strength), thereby influencing energy absorption.
Figure 6 illustrates the distribution of AE amplitudes in coal specimens with various bedding angles. The proportional distribution across various amplitude ranges remains generally consistent at various bedding orientations. The low-amplitude range (40–60 dB) consistently dominates, constituting over 80% of AE events. Conversely, high amplitudes (>60 dB) exhibit lower proportions, which progressively fall as amplitude increases. Notably, the low-amplitude AE signals proportion (40–60 dB) rises with bedding angle, with values of 80.46%, 82.21%, 85.51%, and 86.34% observed. Correspondingly, the proportions of higher-amplitude AE events (>60 dB) decrease with increasing bedding angle. Generally, the AE events with higher amplitudes represent large-scale cracks, while those with lower amplitudes correspond to small-scale cracks. Consequently, the large-scale cracks proportion decreases, while small-scale cracks proportion increases, with increasing bedding angle.
Based on the principle that earthquake frequency decreases exponentially with increasing magnitude, Gutenberg established an empirical formula for calculating the b-value. Thus, the AE b-value can be obtained as follows [37,38,39]:
lg N = a − b A d B 20
where N represents the cumulative number exceeding a certain threshold, AdB represents the AE amplitude, and a and b are constants.
The AE b-value characterizes the scale of amplitude distribution in AE events. A higher b-value implies a greater ratio of small-scale cracks within the coal–rock masses, signifying that the internal development is dominated by the small-scale crack initiation and propagation. Conversely, a lower b-value suggests the opposite trend. As shown in Figure 7, the AE b-values of coal specimens with varying bedding angles are 1.078, 1.202, 1.300, and 1.331, respectively, and their R-squared values are higher than 0.97. The AE b-values of coal specimens increase with the increasing bedding angles, indicating that the proportion of small-scale cracks increases.

3.3. IRT Evolution

Generally, temperatures in shear crack zones rise while decreasing in tensile crack zones during the failure process [40,41]. Due to anisotropic properties arising from the internal structure of coal specimens, localized failure modes exhibit variations. This consequently leads to differential thermal changes in shear and tensile crack zones, resulting in heterogeneous variations across the temperature field.
During the IRT field calculations, a rectangular region is selected along the contour of the coal specimen to compute temperature information within this area, which is stored in matrix form. The IRT field matrix at any time (t), denoted as Tt(x,y), is given as follows:
T t ( x , y ) = T t ( 1 , 1 ) T t ( 1 , 2 ) ⋯ T t ( 1 , p y ) T t ( 2 , 1 ) T t ( 2 , 2 ) ⋯ T t ( 2 , p y ) ⋮ ⋮ ⋱ ⋮ T t ( p x , 1 ) T t ( p x , 2 ) ⋯ T t ( p x , p y )
where px and py represent the maximum pixels in rows and columns of the IRT field matrix.
To minimize the influence of ambient noise and specimen variability, the initial IRT field serves as a reference baseline. The pixel-wise temperature differentials between the IRT field acquired during loading and this reference IRT field are defined as the differential temperature field ΔTt(x,y).
Δ T t ( x , y ) = T t ( x , y ) − T 0 ( x , y )
According to previous research [41], the mean IRT of the differential temperature field is obtained. As illustrated in Figure 8, the mean IRT shows an overall increasing trend, but there are also many fluctuations during the loading process. During the fissure compaction stage, the mean IRT exhibits a fluctuating upward trend, attributable to the compression and closure of initial pores and fissures under external loading. As the load increases, the mean IRT continues to climb with fluctuations, driven by the gradual initiation of microcracks. In the stable crack propagation stage, the mean IRT rises with continued fluctuation as microcracks accelerate in both initiation and propagation. Finally, during the unstable crack propagation stage, the mean IRT decreases at 0°, 30°, and 60°, whereas it increases at 90°. For coal specimens at 0°, 30°, 60°, and 90°, the mean IRT fluctuation amplitudes measure 0.15 °C, 0.31 °C, 0.22 °C, and 0.30 °C, respectively. This N-shaped pattern corresponds to the variation trend of the AE absolute energy. This phenomenon demonstrates that changes in bedding angle alter the coal specimens’ failure mechanism and mechanical properties, thus affecting the IRT trend. As illustrated in Figure 8, the mean IRT values during failure time for coal specimens at varying bedding angles (0°, 30°, 60°, and 90°) are 0.03 °C, 0.17 °C, 0.19 °C, and −0.03 °C, respectively. The primary reason is that specimens with 0° and 30° bedding angles predominantly exhibit tensile–shear failure, while the 60° specimen is mainly characterized by shear failure, and the 90° specimen primarily undergoes tensile failure. Typically, temperatures rise in shear crack zones but decrease in tensile crack zones, thus accounting for the observed trend.

4. Discussions

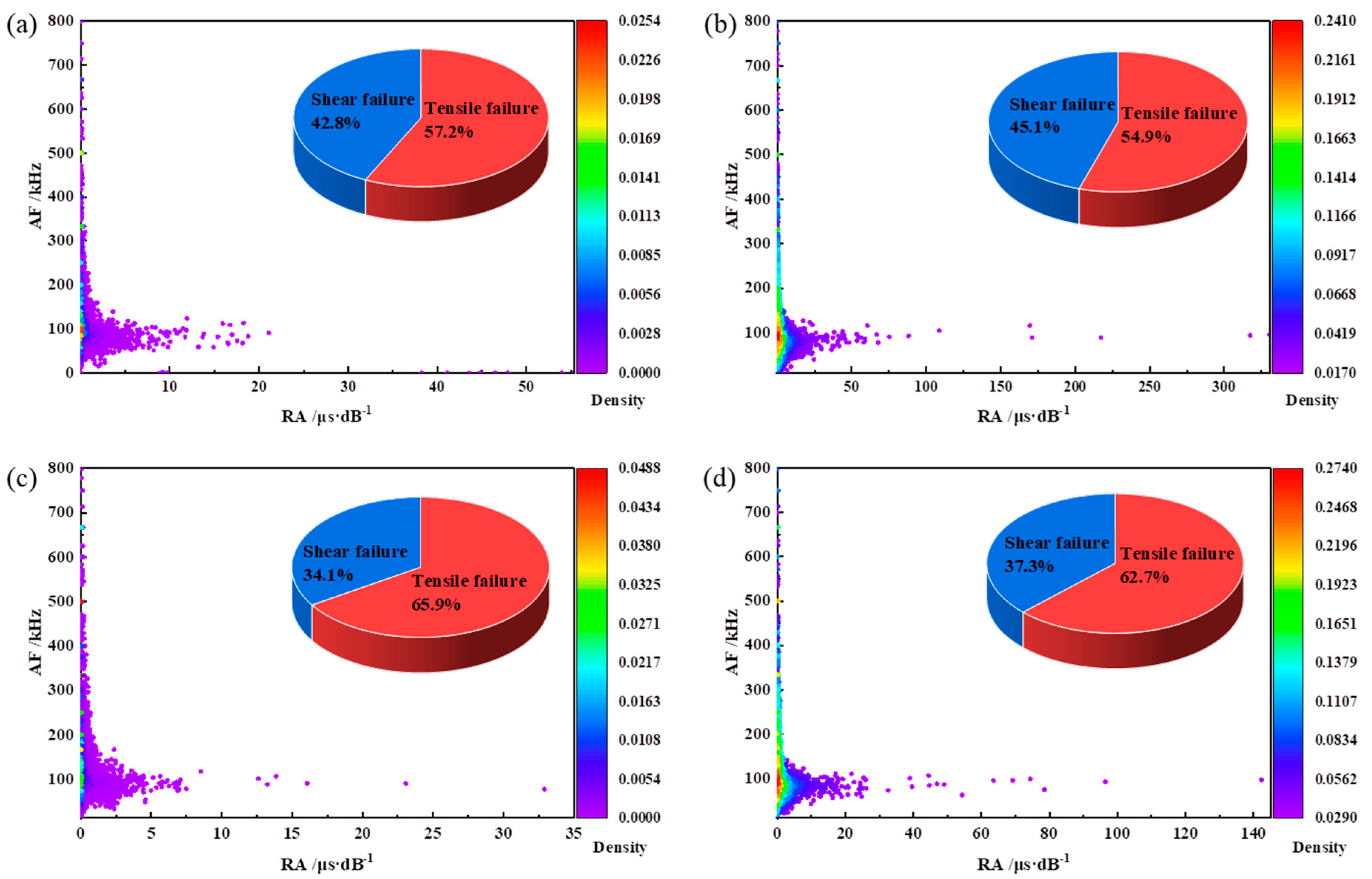
4.1. Microfailure Mechanism

Previous research has revealed that the microfailure mechanism can be identified through the AF value (count/duration) and RA value (rise time/amplitude) of the AE signals [36,42,43]. As illustrated in Figure 9, the AF values for coal specimens with varying bedding angles range from 0 to 800 kHz. In contrast, the RA values exhibit considerable variation, with ranges of 0–56 μs/dB, 0–330 μs/dB, 0–33 μs/dB, and 0–145 μs/dB observed at 0°, 30°, 60°, and 90°, respectively. The AE signals are predominantly clustered near the low AF axial, indicating that tensile failure constitutes the primary microfailure mechanism. The ratio of AF to RA is used to identify the micro-failure mechanism: a value higher than 1000 indicates tensile failure, while a value less than 1000 indicates shear failure. Figure 9 reveals that the microfailure mechanism of coal specimens at varying bedding angles is tensile–shear composite failure, with distinct proportions of shear failure contribution. The 30° specimens exhibit the highest shear failure proportion, while the 60° specimens show the lowest. It should be noted that the shear failure referred to here pertains specifically to the microscopic failure mechanism, which differs from the macroscopic failure mode.

4.2. Correlation Between AE and IRT

AE essentially originates from the elastic wave release caused by microcrack initiation, propagation, and frictional sliding, representing a sudden release of strain energy. Meanwhile, IRT monitoring captures changes in infrared radiation on or near the surface of the coal–rock mass due to variations in thermal energy (frictional heat, heat converted from fracture energy, stress-induced heating, etc.). Both AE and IRT can be used to identify the damage and failure process of coal and rock [33,35,44]. The evolution pattern of stress, mean IRT, and AE hit for coal specimens with varying bedding planes is shown in Figure 10. During the fissure compaction stage, the mean IRT exhibits a fluctuating upward trend with low AE hit counts, attributed to the compression and closure of primary fissures and pores. As the load increases, the mean IRT continues to rise with fluctuations, accompanied by occasional AE signals, driven by the gradual initiation of microcracks. In the stable crack propagation stage, the mean IRT continues its fluctuating ascent as microcrack initiation and propagation accelerate, while AE hits remain at a high level. Finally, during the unstable crack propagation stage, the mean IRT decreases at bedding angles of 0°, 30°, and 60°, while it increases at 90°. Concurrently, AE hits increase rapidly. Approaching peak stress, the mean IRT either increases or decreases rapidly, while AE hit counts simultaneously rise to their maximum. The analysis reveals a correlation between AE and IRT. To quantitatively investigate the correlation between AE and IRT, the Pearson correlation coefficient (γ) was obtained according to the formula [41].
γ x y = ∑ i = 1 n ( x i − x ¯ ) ( y i − y ¯ ) ∑ i = 1 n ( x i − x ¯ ) 2 ∑ i = 1 n ( y i − y ¯ ) 2
where xi represents the sequence of mean IRT, and yi represents the sequence of absolute energy (i = 1, 2, 3…n).
The Pearson correlation coefficient (γ) ranges from −1 to 1. A value greater than 0 indicates a positive correlation, while a value less than 0 indicates a negative correlation. According to the above calculation, the correlation coefficients (γ) between AE and IRT for coal specimens at varying bedding angles (0°, 30°, 60°, and 90°) are 0.17, 0.68, 0.76, and 0.52, respectively. The phenomenon indicates that there is a positive correlation between AE and IRT. The correlation coefficient (γ) is relatively low at 0°, but it is higher at 30°, 60°, and 90°.
Both AE and IRT represent forms of release for accumulated internal strain energy, but they exhibit distinct differences: AE enables real-time monitoring of internal material failure, while IRT primarily detects changes in surface temperature, resulting in a time delay [34,35,45]. In field applications, IRT technology is susceptible to environmental interference. However, as a non-contact monitoring method, IRT technology also offers distinct advantages in areas where sensor deployment is difficult. Thus, integrating IRT with techniques such as AE and microseismic monitoring (MS) becomes necessary to achieve effective monitoring and early warning.

5. Conclusions

This study analyzed the deformation pattern, AE characteristics, and IRT evolution, exploring the microscopic failure mechanisms and the correlation between AE and IRT parameters. The principal conclusions are as follows:
(1) The UCS ranges from 11.70 to 34.35 MPa, while the elastic modulus ranges from 1.15 to 1.87 GPa. Both UCS and elastic modulus exhibit a consistent V-shaped variation trend, characterized by an initial decrease followed by an increase.
(2) As the bedding angle increases, the proportion of low-amplitude (40–60 dB) AE signals increases, while the proportion of higher-amplitude (>60 dB) AE signals decreases. The AE b-values increase with the bedding angles, indicating that the small-scale cracks proportion increases.
(3) The mean IRT shows an overall increasing trend with many fluctuations. The mean IRT fluctuation amplitudes show an N-shaped pattern, and the mean IRT values at failure time for coal specimens at 0°, 30°, 60°, and 90° are 0.03 °C, 0.17 °C, 0.19 °C, and −0.03 °C, respectively.
(4) The microfailure mechanism of coal specimens at varying bedding angles is tensile–shear composite failure, with distinct proportions of shear failure contribution. The 30° specimens exhibit the highest shear failure proportion, while the 60° specimens show the lowest.
(5) There is a positive correlation between AE and IRT. In field applications, integrating IRT with techniques such as AE and microseismic monitoring (MS) becomes necessary to achieve effective monitoring and early warning.

Author Contributions

Conceptualization, Y.W. and B.L.; methodology, Y.W. and B.L.; investigation, S.W. and B.L.; resources, B.L. and S.W.; data curation, B.L. and S.W.; writing—original draft preparation, Y.W. and B.L.; writing—review and editing, S.W. and B.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (grant no. 52204121), the Open Fund of the State Key Laboratory of Water Resource Protection and Utilization in Coal Mining (grant no. WPUKFJJ2022-04), the S&T Innovation and Development Project of the Information Institution of the Ministry of Emergency Management (grant nos. 2025507, 2024504), the Youth Fund Program of Humanities and Social Sciences Research of the Ministry of Education (grant no. 23YJC740058), and the National Science and Technology Major Project (2024ZD1700104).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

This research was supported by the State Key Laboratory for Fine Exploration and Intelligent Development of Coal Resources, China University of Mining and Technology-Beijing.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Gu, D.Z.; Yan, Y.G.; Zhang, Y.; Wang, E.Z.; Cao, Z.G. Experimental Study and Numerical Simulation for Dynamic Response of Coal Pillars in Coal Mine Underground Reservoir. Meitan Xuebao/J. China Coal Soc. 2016, 41, 1589–1597. [Google Scholar] [CrossRef]
  2. Gu, D.Z. Theory Framework and Technological System of Coal Mine Underground Reservoir. Meitan Xuebao/J. China Coal Soc. 2015, 40, 239–246. [Google Scholar] [CrossRef]
  3. Gu, D.; Cao, Z.; Li, J.; Wu, B.; Zhang, Y.; Jiang, B.; Guo, Q.; Wang, H.; Wu, Y.; Shi, X.; et al. Original Experimental Platform System and Application of Underground Coal Mine Reservoirs. Meitan Xuebao/J. China Coal Soc. 2024, 49, 100–113. [Google Scholar] [CrossRef]
  4. Zhao, Y.; Zhao, G.F.; Jiang, Y.; Elsworth, D.; Huang, Y. Effects of Bedding on the Dynamic Indirect Tensile Strength of Coal: Laboratory Experiments and Numerical Simulation. Int. J. Coal Geol. 2014, 132, 81–93. [Google Scholar] [CrossRef]
  5. Kim, H.; Cho, J.W.; Song, I.; Min, K.B. Anisotropy of Elastic Moduli, P-Wave Velocities, and Thermal Conductivities of Asan Gneiss, Boryeong Shale, and Yeoncheon Schist in Korea. Eng. Geol. 2012, 147–148, 68–77. [Google Scholar] [CrossRef]
  6. Kim, K.Y.; Zhuang, L.; Yang, H.; Kim, H.; Min, K.B. Strength Anisotropy of Berea Sandstone: Results of X-Ray Computed Tomography, Compression Tests, and Discrete Modeling. Rock Mech. Rock Eng. 2016, 49, 1201–1210. [Google Scholar] [CrossRef]
  7. Zhao, Y.; Liu, S.; Jiang, Y.; Wang, K.; Huang, Y. Dynamic Tensile Strength of Coal under Dry and Saturated Conditions. Rock Mech. Rock Eng. 2016, 49, 1709–1720. [Google Scholar] [CrossRef]
  8. Viljoen, J.; Campbell, Q.P.; le Roux, M.; Hoffman, J.W. The Influence of Bedding-Plane Orientation on the Degradation Characteristics of a South African Waterberg Coal. Int. J. Coal Prep. Util. 2017, 37, 179–194. [Google Scholar] [CrossRef]
  9. Wang, Z.; Pan, J.; Hou, Q.; Yu, B.; Li, M.; Niu, Q. Anisotropic Characteristics of Low-Rank Coal Fractures in the Fukang Mining Area, China. Fuel 2018, 211, 182–193. [Google Scholar] [CrossRef]
  10. Liu, C.; Yin, G.; Li, M.; Shang, D.; Deng, B.; Song, Z. Deformation and Permeability Evolution of Coals Considering the Effect of Beddings. Int. J. Rock Mech. Min. Sci. 2019, 117, 49–62. [Google Scholar] [CrossRef]
  11. Ju, M.; Li, J.; Li, J.; Zhao, J. Loading Rate Effects on Anisotropy and Crack Propagation of Weak Bedding Plane-Rich Rocks. Eng. Fract. Mech. 2020, 230, 106983. [Google Scholar] [CrossRef]
  12. Maruvanchery, V.; Kim, E. Effects of a High Temperature (500 °C) on the Fracture Processes in Calcite-Cemented Sandstone Along Bedding-Plane Orientations. Rock Mech. Rock Eng. 2020, 53, 955–966. [Google Scholar] [CrossRef]
  13. Wang, W.; Zhao, Y.; Sun, Z.; Lu, C. Effects of Bedding Planes on the Fracture Characteristics of Coal under Dynamic Loading. Eng. Fract. Mech. 2021, 250, 107761. [Google Scholar] [CrossRef]
  14. Zhou, J.; Zhao, Y.; Paneiro, G.; Liu, W.; Wang, X.; Wang, H.; Gao, Y.; Han, C.; Zhang, X. Loading Rate and Bedding Plane Coupled Effect Study on Coal Failure under Uniaxial Compression: Acoustic Emissions and Energy Dissipation Analysis. Geofluids 2022, 2022, 9028178. [Google Scholar] [CrossRef]
  15. Shi, X.; Zhao, Y.; Yao, W.; Gong, S.; Danesh, N.N. Dynamic Tensile Failure of Layered Sorptive Rocks: Shale and Coal. Eng. Fail. Anal. 2022, 138, 106346. [Google Scholar] [CrossRef]
  16. Khalili, M.; Fahimifar, A.; Shobeiri, H. The Effect of Bedding Planes on the Bending Strength of Rock-like Material and Evaluation of the Crack Propagation Mechanism. Theor. Appl. Fract. Mech. 2023, 127, 104061. [Google Scholar] [CrossRef]
  17. Wang, X.; Zhao, Y.; Zhang, X.; Sun, Z.; Gao, Y.; Jiang, Y. Effects of Anisotropy on Strength and Deformability of Anthracite Under High Confinement. Rock Mech. Rock Eng. 2023, 56, 2157–2183. [Google Scholar] [CrossRef]
  18. Wang, X.; Zhao, Y.; Gao, Y.; Sun, Z.; Liu, B.; Jiang, Y. Energy Evolution of Anthracite Considering Anisotropy Under High Confining Pressure: An Experimental Investigation. Rock Mech. Rock Eng. 2023, 56, 6735–6759. [Google Scholar] [CrossRef]
  19. Mashhadiali, N.; Molaei, F. Theoretical and Experimental Investigation of a Shear Failure Model for Anisotropic Rocks Using Direct Shear Test. Int. J. Rock Mech. Min. Sci. 2023, 170, 105561. [Google Scholar] [CrossRef]
  20. Sun, Z.; Zhao, Y.; Gao, Y.; Elmo, D.; Gao, S.; Wang, X. Effect of Size and Anisotropy on Fracture Process Zone of Coal: An Experiment and Numerical Simulation. Eng. Fract. Mech. 2024, 306, 110227. [Google Scholar] [CrossRef]
  21. Huang, L.; Li, B.; Wu, B.; Li, C.; Wang, J.; Cai, H. Study on the Extension Mechanism of Hydraulic Fractures in Bedding Coal. Theor. Appl. Fract. Mech. 2024, 131, 104431. [Google Scholar] [CrossRef]
  22. Zhang, G.; Zhao, Y.; Sun, Y.; Gong, Z. Energy Evolution and Infrared Radiation Characteristics of Different Bedded Coal under Uniaxial Compression. Meitan Kexue Jishu/Coal Sci. Technol. 2024, 52, 48–59. [Google Scholar] [CrossRef]
  23. Huang, L.; Li, B.; Li, C.; Wu, B.; Wang, J. Research on Anisotropic Characteristics and Energy Damage Evolution Mechanism of Bedding Coal under Uniaxial Compression. Energy 2024, 301, 131659. [Google Scholar] [CrossRef]
  24. Tang, X.; Xu, F.; Bi, Y.; Bi, R.; Guo, Y.; Huo, N. Mechanical and Permeability Characteristics of Gas-Bearing Coal Under Various Bedding Angles. Processes 2025, 13, 176. [Google Scholar] [CrossRef]
  25. Ma, S.; He, J.; Xiong, D.; Zhu, R.; Qu, Z.; Fang, D. Fracture Evolution Behavior of Deep Coal with Bedding Planes: An in-Situ ΜCT Study Based on Deep Learning. Opt. Laser Technol. 2025, 189, 113149. [Google Scholar] [CrossRef]
  26. Sun, Z.; Zhao, Y.; Gao, Y.; Wang, X.; Wang, H.; Liu, B.; Jiang, Y. Effects of Bedding Characteristics on Crack Propagation of Coal under Mode II Loading: Laboratory Experiment and Numerical Simulation. J. Rock Mech. Geotech. Eng. 2025, 17, 1037–1052. [Google Scholar] [CrossRef]
  27. Seredin, V.V.; Khrulev, A.S. Variations of Temperature in Specimens of Rocks and Geomaterials under Failure. J. Min. Sci. 2016, 52, 683–688. [Google Scholar] [CrossRef]
  28. Jiang, Y.; Lu, Y.; Zhao, Y.; Song, Y.; Tao, L. Multiparameter Monitoring Experiments for Instability Destruction of Coal Samples. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2012, 31, 667–674. [Google Scholar]
  29. Gao, Y.; Zhao, Y.; Wang, H.; Liu, B.; Hartlieb, P.; Gao, S. Loaded Failure Characteristics of Anthracite Derived from Microwave Irradiation: Acoustic Emission Evaluation. Rock Mech. Rock Eng. 2023, 56, 8809–8831. [Google Scholar] [CrossRef]
  30. Wu, L.; Wang, J. Infrared Radiation Features of Coal and Rocks under Loading. Int. J. Rock Mech. Min. Sci. 1998, 35, 969–976. [Google Scholar] [CrossRef]
  31. Rankin, B.A.; Blunck, D.L.; Monfort, J.; Kiel, B.V.; Gore, J.P. Infrared Radiation and Acoustic Characteristics of Combustion Instabilities in Turbulent Premixed Flames. J. Propuls. Power 2012, 28, 862–865. [Google Scholar] [CrossRef]
  32. Pieczyska, E.A.; Tobushi, H.; Takeda, K.; Stróz, D.; Ranachowski, Z.; Kulasiński, K.; Kúdela, S.; Luckner, J. Martensite Transformation Bands Studied in TiNi Shape Memory Alloy by Infrared and Acoustic Emission Techniques. Kov. Mater. 2012, 50, 309–318. [Google Scholar] [CrossRef]
  33. Xu, H.; Ma, L.; Cao, K.; Khan, N.M.; Hussain, S.; Niu, D.; Alarifi, S.S.; Bacha, S. Precursors of Cyclic Loading and Unloading Sandstone Failure Based on “Acoustic-Thermal” Loading–Unloading Response Ratio. Sustainability 2023, 15, 10158. [Google Scholar] [CrossRef]
  34. Yin, S.; Li, Z.; Wang, E.; Liu, Y.; Niu, Y.; Yang, H. Damage Status and Failure Precursors of Different Coal Impact Types Based on Comprehensive Monitoring of Infrared Radiation and Acoustic Emission. Appl. Sci. 2024, 14, 8792. [Google Scholar] [CrossRef]
  35. Chang, L.; Chen, L.; Zhang, M.; Li, D.; Li, Y. Experimental Study on Infrared Radiation and Crack Evolution Characteristics during the Failure Process of Rocks with Pre-Set Crack. Infrared Phys. Technol. 2024, 138, 105236. [Google Scholar] [CrossRef]
  36. Liu, B.; Zhao, Y.; Hua, X.; Ling, C.; Wang, X. Failure Characteristic and Acoustic Emission Spatio-Temporal Evolution of Coal under Different Cyclic Loading Rates. Energy Sci. Eng. 2023, 11, 2039–2051. [Google Scholar] [CrossRef]
  37. Shang, D.; Zhang, S.; Jiang, Y.; Wang, X.; Zhang, J.; Liu, J.; Wang, Y. Elucidating the Rate-Dependent Shear Failure Mechanism in Cement Fractures Based on Multi-Parameter Acoustic Emission Analysis. J. Build. Eng. 2025, 111, 113161. [Google Scholar] [CrossRef]
  38. Burud, N.B.; Chandra Kishen, J.M. Application of Generalized Logistic Equation for B-Value Analysis in Fracture of Plain Concrete Beams under Flexure. Eng. Fract. Mech. 2019, 210, 228–246. [Google Scholar] [CrossRef]
  39. Liang, Y.; Yang, Y.; Xin, G.; Zou, Q.; Ran, Q.; Qin, D. Mechanical Properties and Crack Propagation Characteristics of Mudstone under Different Loading Frequencies. Eng. Fract. Mech. 2025, 316, 110863. [Google Scholar] [CrossRef]
  40. Ma, L.; Sun, H. Spatial-Temporal Infrared Radiation Precursors of Coal Failure under Uniaxial Compressive Loading. Infrared Phys. Technol. 2018, 93, 144–153. [Google Scholar] [CrossRef]
  41. Lou, Q.; He, X. Experimental Study on Infrared Radiation Temperature Field of Concrete under Uniaxial Compression. Infrared Phys. Technol. 2018, 90, 20–30. [Google Scholar] [CrossRef]
  42. Zhang, G.; Yu, Y.; Zhang, W. Experimental Investigation of the Acoustic Emission and Energy Evolution of Bedded Coal under Uniaxial Compression. Sci. Rep. 2025, 15, 12578. [Google Scholar] [CrossRef]
  43. De Smedt, M.; Andreev, K.; Shetty, N.; Verstrynge, E. Effectiveness of Acoustic Emission Parameters to Monitor the Crack Formation in Refractories—Case Study on Castables of Different Brittleness. J. Eur. Ceram. Soc. 2019, 39, 5423–5432. [Google Scholar] [CrossRef]
  44. Botvina, L.R.; Bolotnikov, A.I.; Sinev, I.O.; Beletsky, E.N. Acoustic Emission, Damage and Fracture Mechanisms of Structural Steel under Mixed-Mode Loading. Eng. Fract. Mech. 2023, 292, 109635. [Google Scholar] [CrossRef]
  45. Zhao, Y.; Jiang, Y. Acoustic Emission and Thermal Infrared Precursors Associated with Bump-Prone Coal Failure. Int. J. Coal Geol. 2010, 83, 11–20. [Google Scholar] [CrossRef]
Applsci 15 09554 g001
Figure 1. The layout of the testing system.
Figure 1. The layout of the testing system.
Applsci 15 09554 g001
Applsci 15 09554 g002
Figure 2. Variation in compressive strength for coal specimens with varying bedding planes.
Figure 2. Variation in compressive strength for coal specimens with varying bedding planes.
Applsci 15 09554 g002
Applsci 15 09554 g003
Figure 3. Relation between the stress and strain of typical coal specimens with varying bedding planes.
Figure 3. Relation between the stress and strain of typical coal specimens with varying bedding planes.
Applsci 15 09554 g003
Applsci 15 09554 g004
Figure 4. Variation in elastic modulus for coal specimens with varying bedding planes.
Figure 4. Variation in elastic modulus for coal specimens with varying bedding planes.
Applsci 15 09554 g004
Applsci 15 09554 g005
Figure 5. Evolution of stress, absolute energy, and AE hit for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°. Fissure compaction stage (I), crack initiation stage (II), stable crack propagation stage (III), and unstable crack propagation stage (IV).
Figure 5. Evolution of stress, absolute energy, and AE hit for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°. Fissure compaction stage (I), crack initiation stage (II), stable crack propagation stage (III), and unstable crack propagation stage (IV).
Applsci 15 09554 g005
Applsci 15 09554 g006
Figure 6. Distribution of AE amplitude for coal specimens with varying bedding planes.
Figure 6. Distribution of AE amplitude for coal specimens with varying bedding planes.
Applsci 15 09554 g006
Applsci 15 09554 g007
Figure 7. Fitting results of AE b-values for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°.
Figure 7. Fitting results of AE b-values for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°.
Applsci 15 09554 g007
Applsci 15 09554 g008
Figure 8. Evolution of stress and mean IRT for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°. Fissure compaction stage (I), crack initiation stage (II), stable crack propagation stage (III), and unstable crack propagation stage (IV).
Figure 8. Evolution of stress and mean IRT for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°. Fissure compaction stage (I), crack initiation stage (II), stable crack propagation stage (III), and unstable crack propagation stage (IV).
Applsci 15 09554 g008
Applsci 15 09554 g009
Figure 9. Distribution of AF and RA for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°.
Figure 9. Distribution of AF and RA for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°.
Applsci 15 09554 g009
Applsci 15 09554 g010
Figure 10. Evolution of stress, mean IRT, and AE hit for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°.
Figure 10. Evolution of stress, mean IRT, and AE hit for coal specimens with varying bedding planes: (a) 0°, (b) 30°, (c) 60°, and (d) 90°.
Applsci 15 09554 g010
Table 1. Physical and mechanical information of the coal specimens.
Table 1. Physical and mechanical information of the coal specimens.
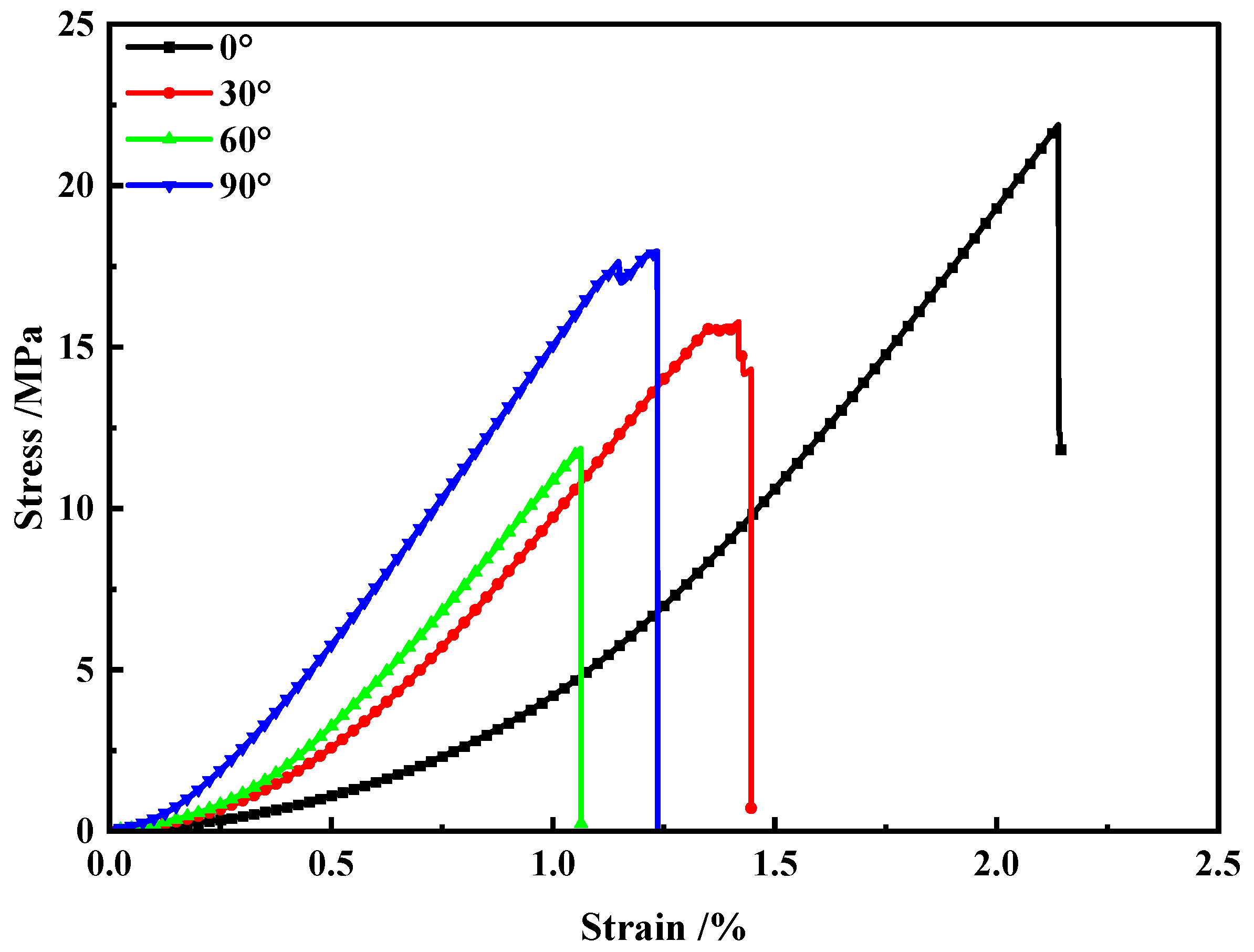
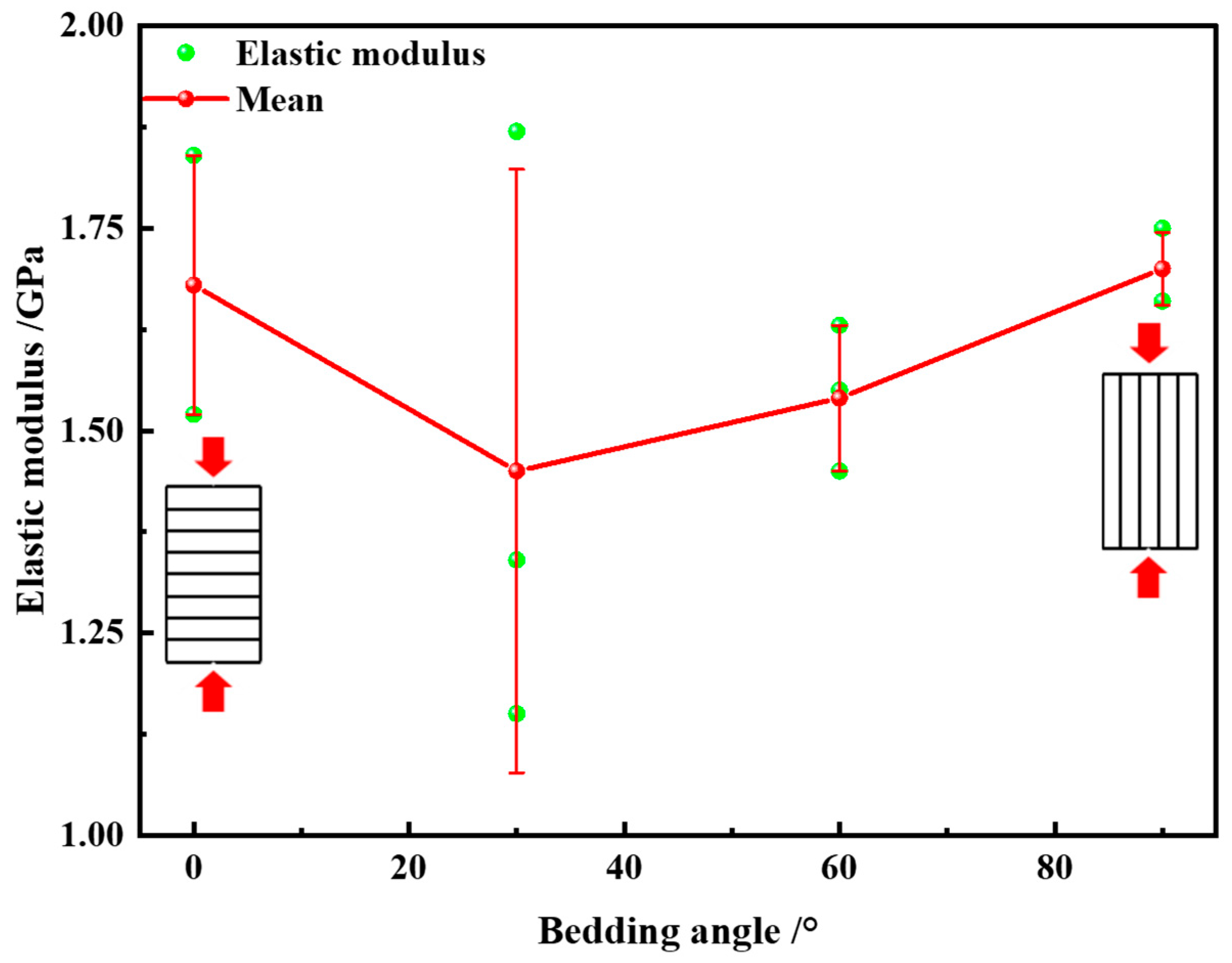
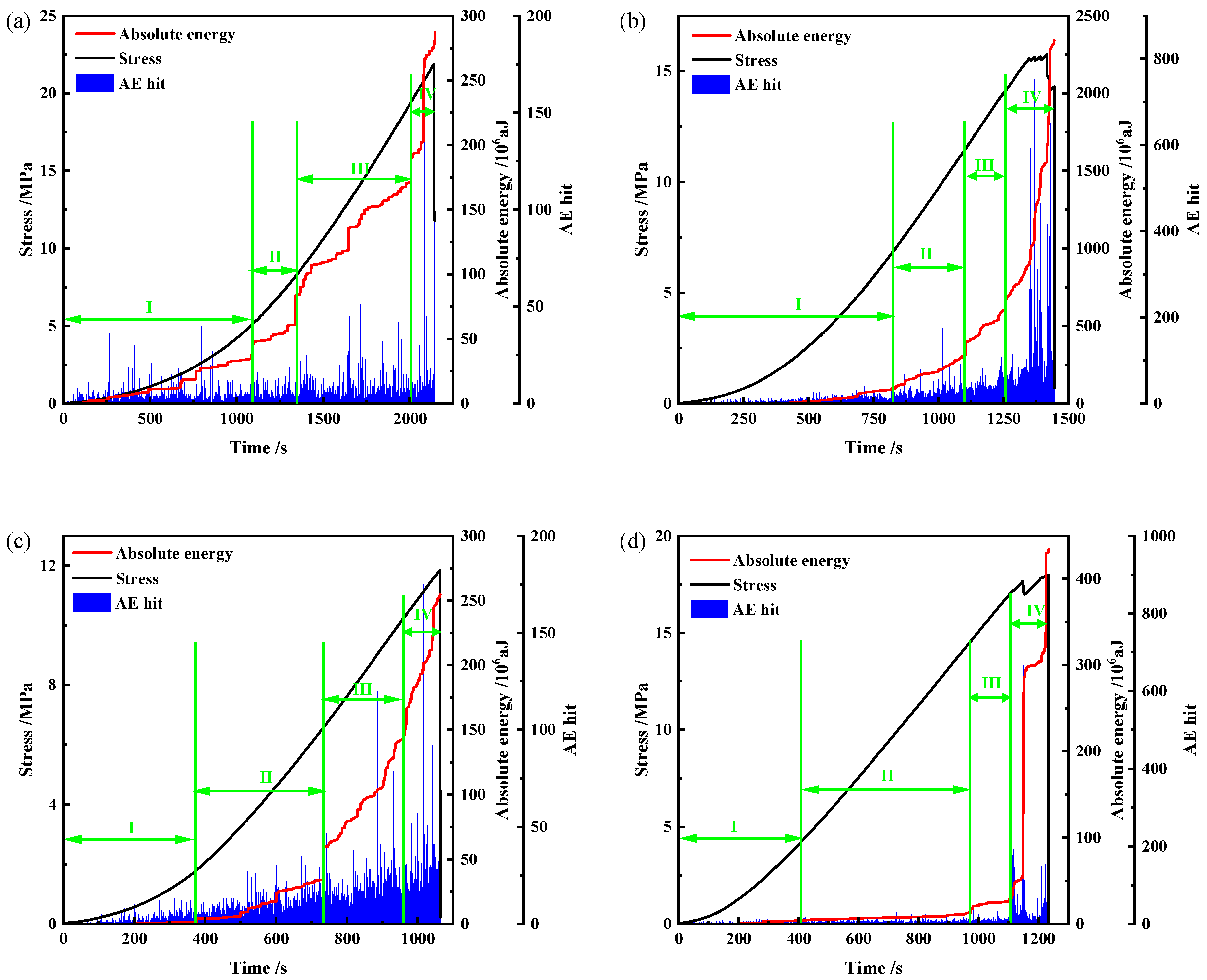
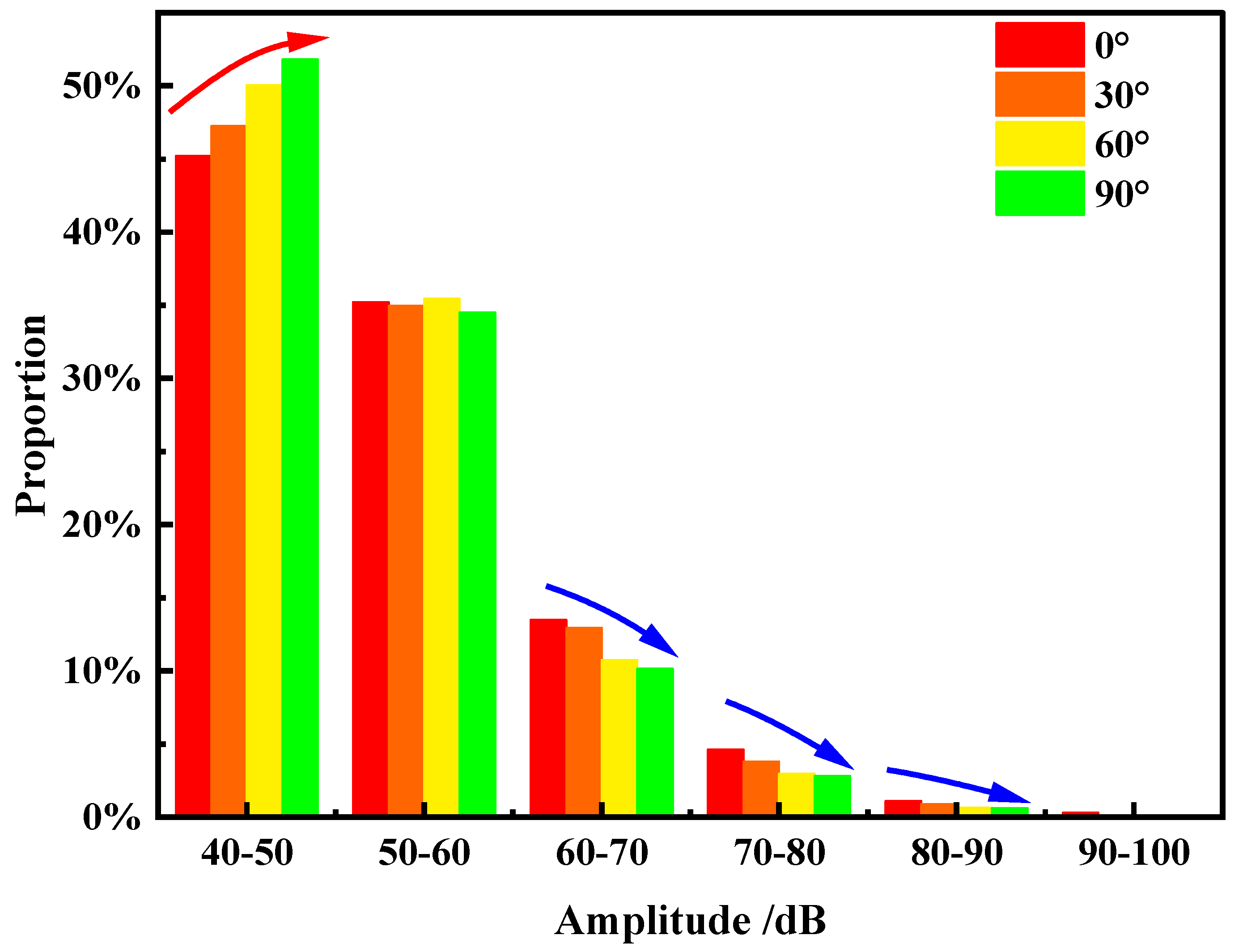
Specimen No.Density
g/cm3		Compressive Strength
MPa		Mean
MPa		Elastic Modulus
GPa		Mean
GPa
S-0-11.2522.2325.501.841.68
S-0-21.2634.351.68
S-0-31.2419.771.52
S-30-11.2615.9218.411.871.45
S-30-21.2319.291.15
S-30-31.2620.031.34
S-60-11.3213.3512.381.451.54
S-60-21.2211.701.55
S-60-31.3012.071.63
S-90-11.2617.9016.811.661.70
S-90-21.2714.671.75
S-90-31.2217.851.70
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wu, Y.; Liu, B.; Wang, S.; Pang, B. Acoustic Emission and Infrared Radiation Temperature Characteristics of Coal with Varying Bedding Planes Under Uniaxial Compression. Appl. Sci. 2025, 15, 9554. https://doi.org/10.3390/app15179554

AMA Style

Wu Y, Liu B, Wang S, Pang B. Acoustic Emission and Infrared Radiation Temperature Characteristics of Coal with Varying Bedding Planes Under Uniaxial Compression. Applied Sciences. 2025; 15(17):9554. https://doi.org/10.3390/app15179554

Chicago/Turabian Style

Wu, Yang, Bin Liu, Shirui Wang, and Bo Pang. 2025. "Acoustic Emission and Infrared Radiation Temperature Characteristics of Coal with Varying Bedding Planes Under Uniaxial Compression" Applied Sciences 15, no. 17: 9554. https://doi.org/10.3390/app15179554

APA Style

Wu, Y., Liu, B., Wang, S., & Pang, B. (2025). Acoustic Emission and Infrared Radiation Temperature Characteristics of Coal with Varying Bedding Planes Under Uniaxial Compression. Applied Sciences, 15(17), 9554. https://doi.org/10.3390/app15179554

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop