Generalized Frequency Division Multiplexing—Based Direct Mapping—Multiple-Input Multiple-Output Mobile Electroencephalography Communication Technique
Abstract
Featured Application
Abstract
1. Introduction
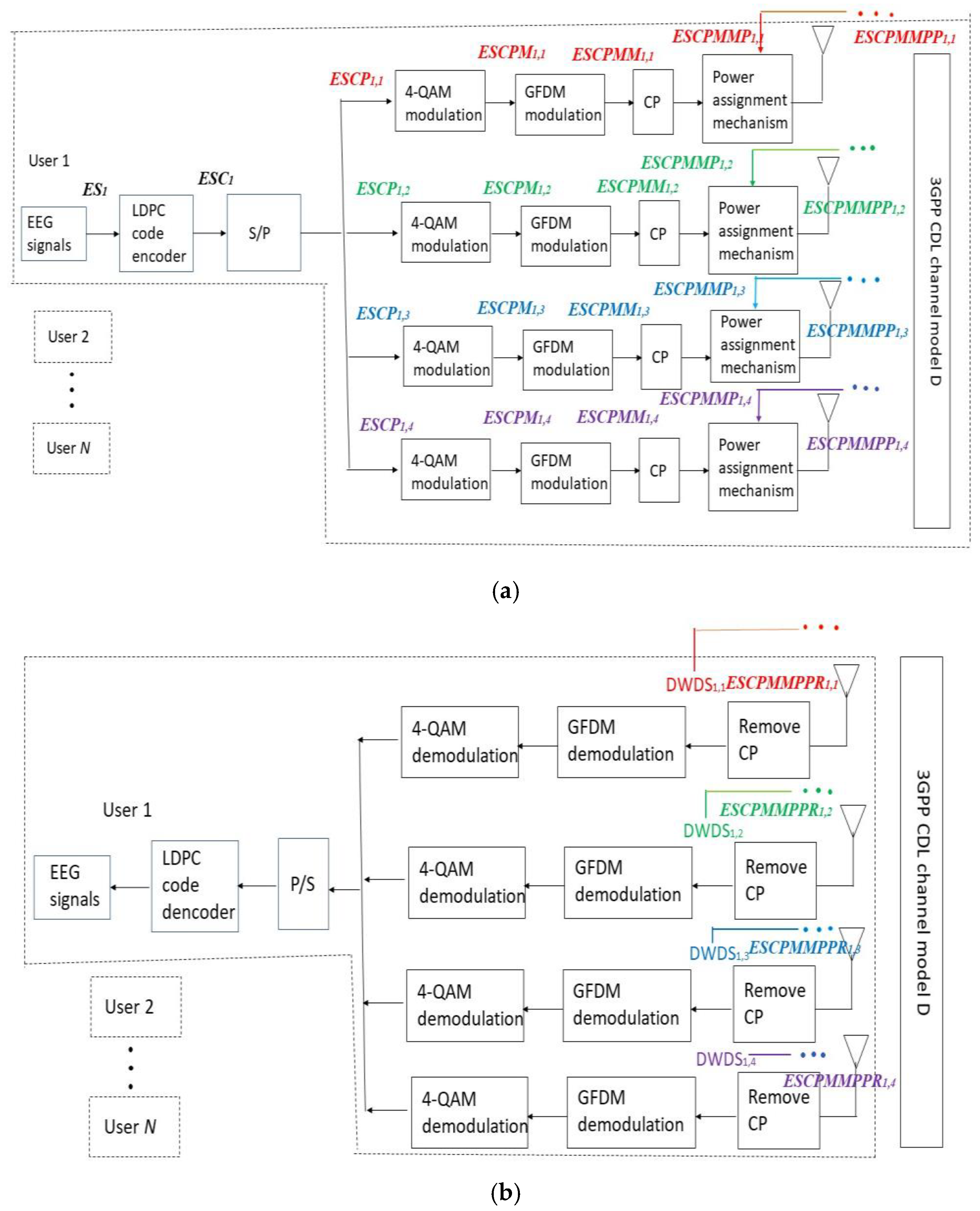
2. Methods
- Step 1: Use 4-QAM, and the (2000, 1000) LDPC code encoder to meet the quality-of-service requirements for mobile EEG transmission.
- Step 2: Set the initial transmission power weighting of for EEG signals.
- Step 3: Measure the received .
- Step 4: If the measured exceeds the mobile EEG transmission threshold at the required EEG BER of , then update to , where is equal to 1/30.
- If , go to Step 3; otherwise, go to Step 5.
- Step 5: If the measured is less than the mobile EEG transmission threshold at the required EEG BER of , then update to , where is equal to 1/30.
- If , go to Step 3; otherwise, go to Step 4.
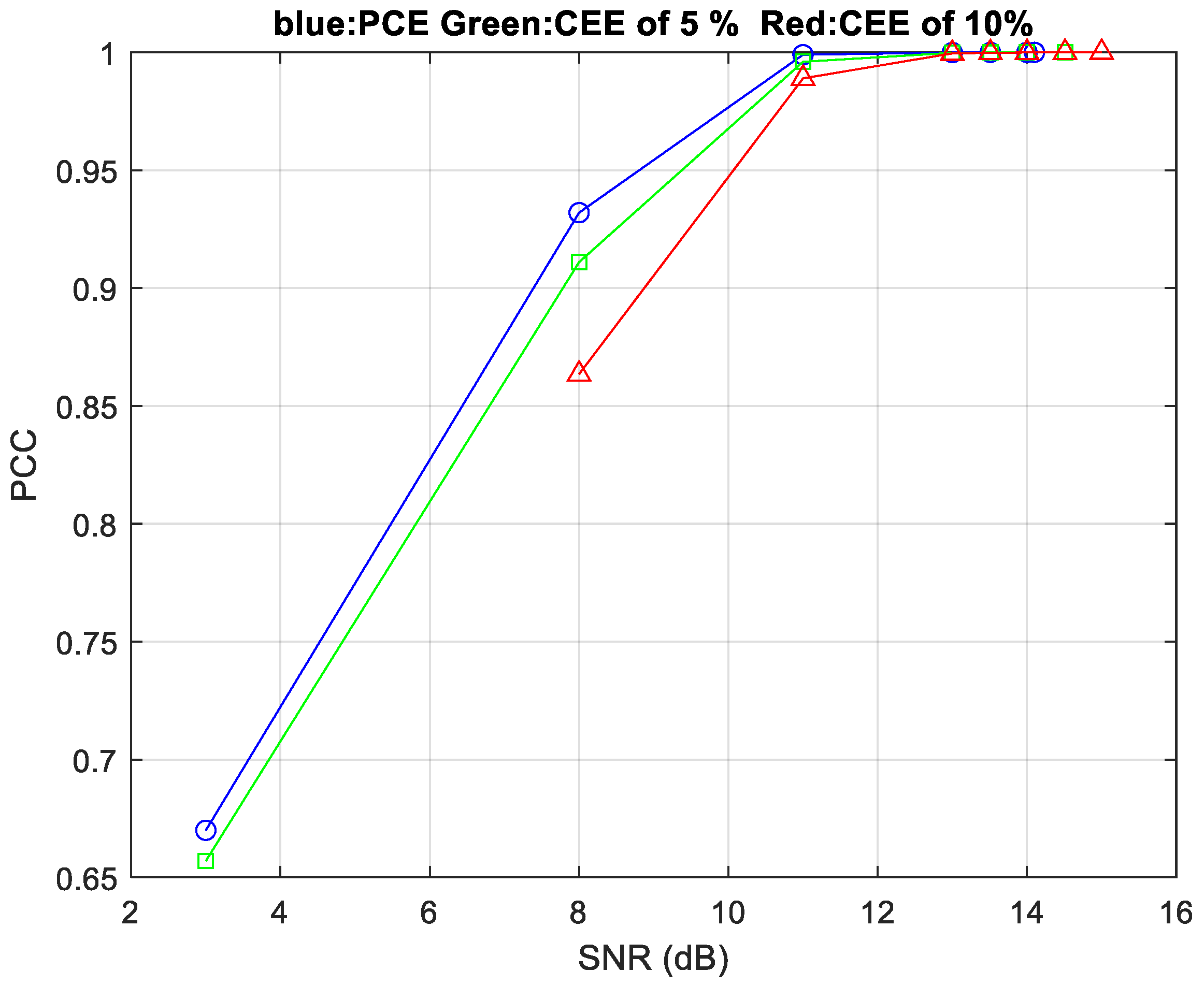
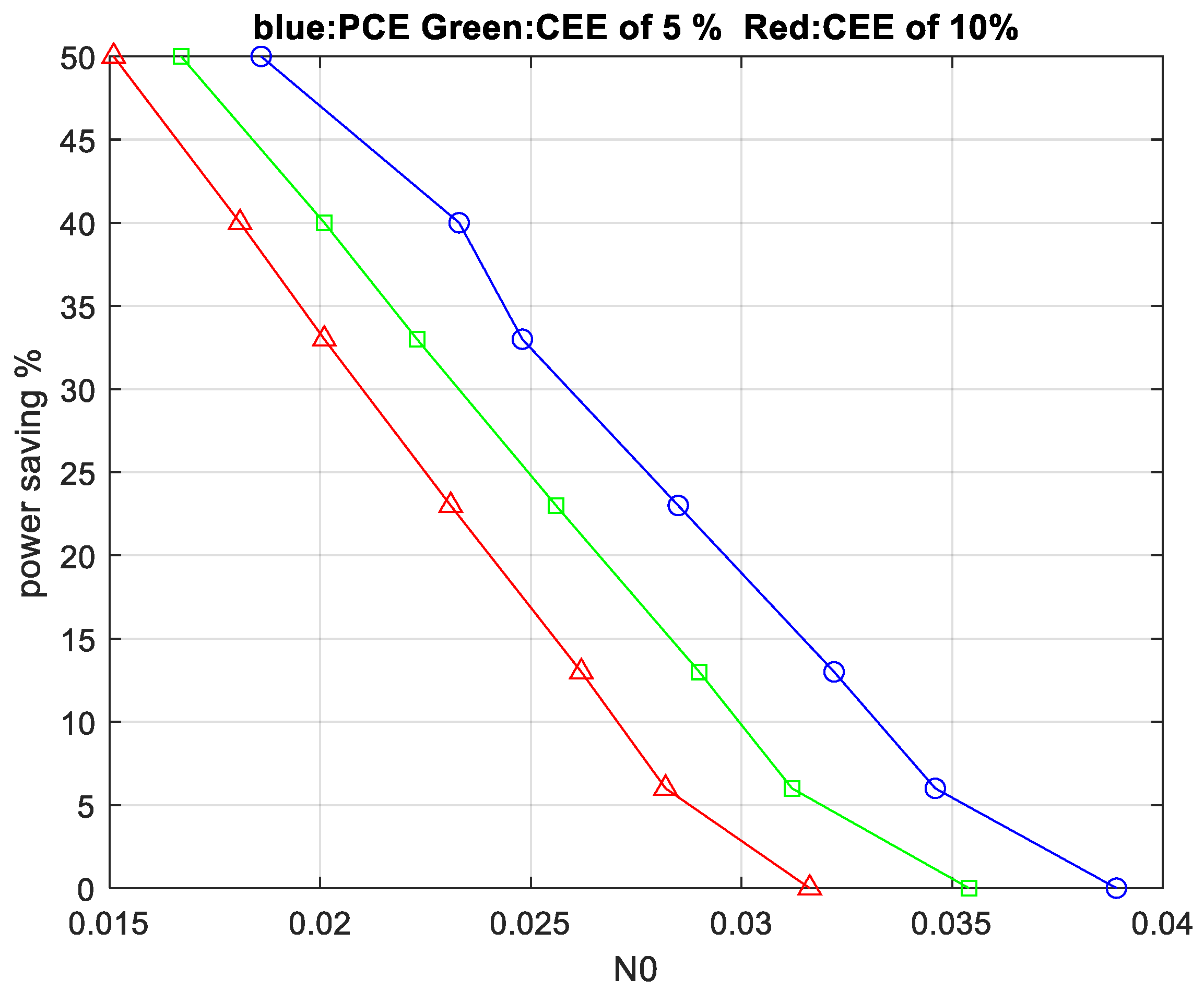
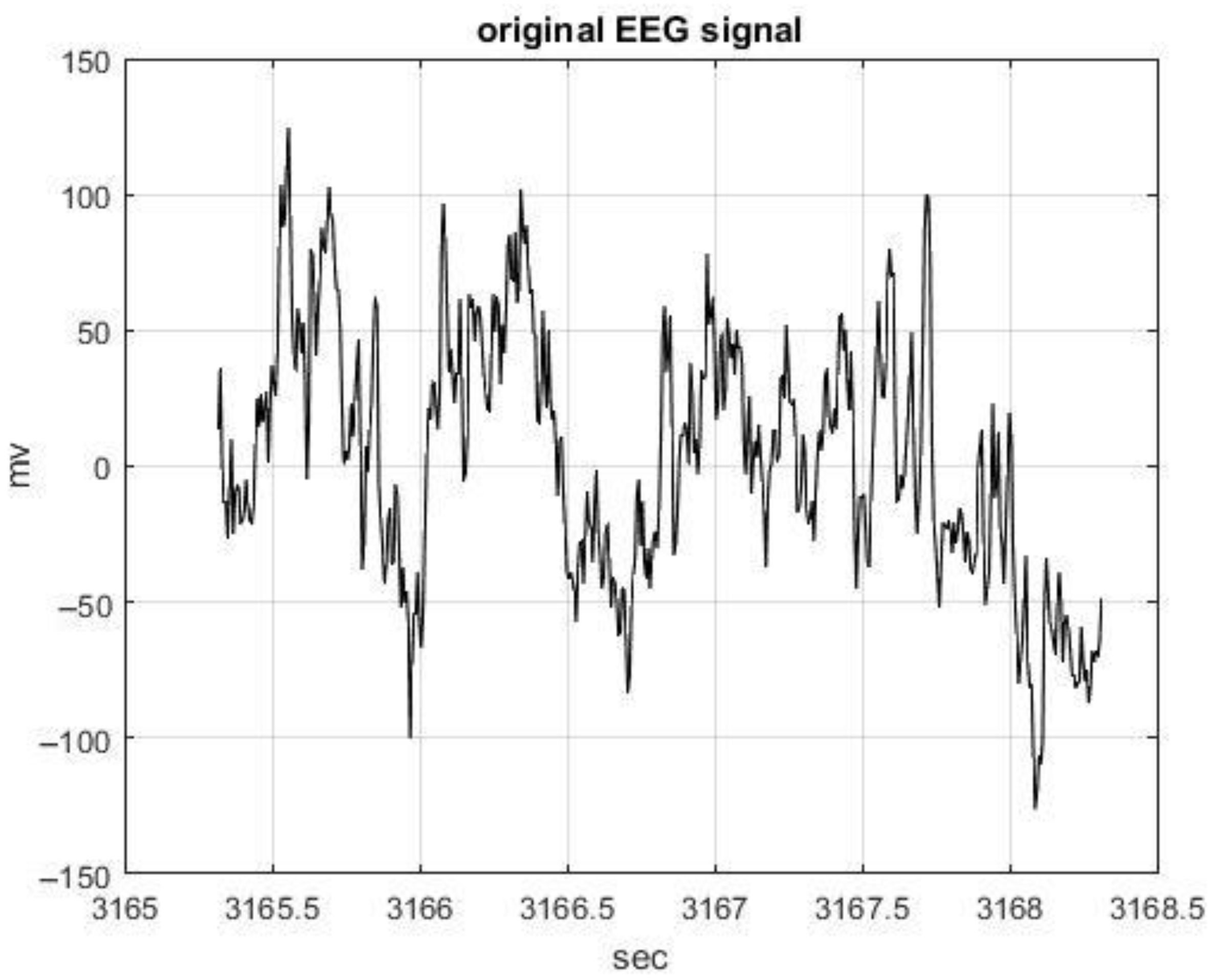
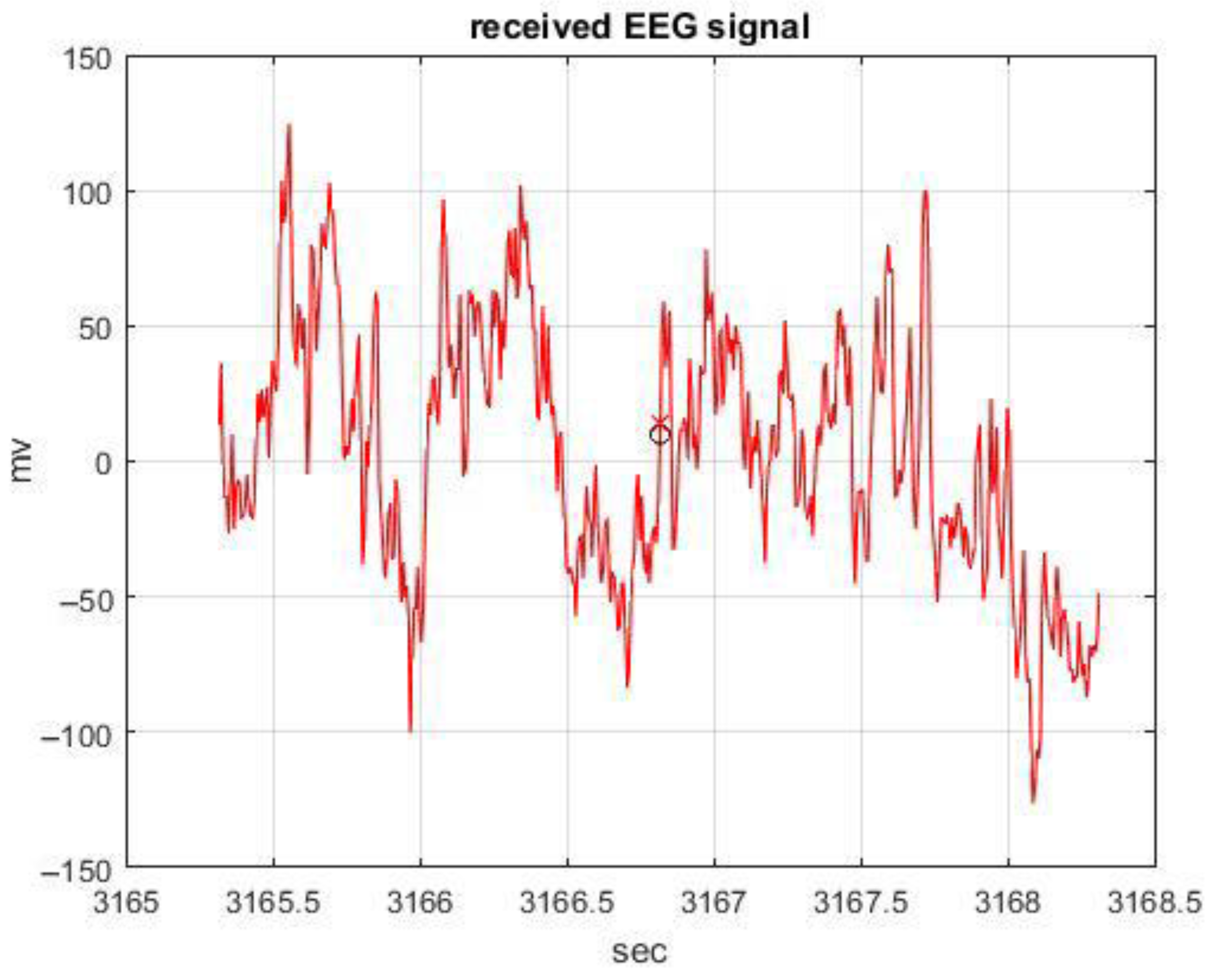
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| Symbols | |
| EEG signal bit stream for the nth user | |
| LDPC encoded EEG signal bit stream for the nth user | |
| S/P LDPC encoded EEG signal bit stream of the lth transmission antenna for the nth user | |
| 4-QAM S/P LDPC encoded EEG signal symbol stream of the lth transmission antenna for the nth user | |
| GFDM-based 4-QAM S/P LDPC encoded EEG signal symbol stream of the lth transmission antenna for the nth user | |
| GFDM-based 4-QAM S/P LDPC encoded EEG signal symbol stream of the lth transmission antenna for the nth user with the CP | |
| GFDM-based 4-QAM S/P LDPC encoded EEG signal symbol stream of the lth transmission antenna for the nth user with the CP and PAM | |
| 3GPP CDL channel impulse response of the lth transmission antenna and the pth receiver antenna, for the nth user | |
| ignal-to-noise ratio of EEG packets received by the pth receiver antenna for the nth user | |
| Original EEG signal in the MECT | |
| Received EEG signal in the MECT | |
| W | Length of EEG signal. |
| Pearson correlation coefficient | |
| PS | Power saving |
| Variance of additive white Gaussian noise of the l-th transmission antenna, and the p-th receiver antenna for the nth user. | |
| Transmission power weighting factor of the lth transmission antenna for the nth user | |
| Abbreviations | |
| 3GPP | 3rd Generation Partnership Project |
| 5G | 5th generation |
| 6G | 6th generation |
| AWGN | Additive white Gaussian noise |
| BCI | Brain-computer interface |
| BER | Bit error rate |
| BPSK | Binary phase-shift keying |
| CDL | Cluster delay line |
| CEE | Channel estimation error |
| CP | Cyclic prefix |
| CPM | Continuous phase modulation |
| DM | Direct mapping |
| DWDS | Double-window detection scheme |
| EEG | Electroencephalography |
| FBMC | Filter bank multicarrier |
| FER | Frame error rate |
| FPGA | Field-programmable gate array |
| GFDM | Generalized frequency division multiplexing |
| IM | Index modulation |
| IoT | Internet of Things |
| IoMT | Internet of Medical Things |
| JPEG | Joint Photographic Experts Group |
| LDPC | Low-density parity-check |
| LOS | Line-of-sight |
| MECT | Mobile EEG communication technology |
| MIMO | Multi-input-multi-output |
| MSE | Mean square error |
| NLOS | Non-line-of-sight |
| OFDM | Orthogonal frequency division multiplexing |
| OOB | Out-of-band |
| OQAM | Offset QAM |
| OTFS | Orthogonal time frequency space |
| OVSF | Orthogonal variable spreading factor |
| PAM | Power assignment mechanism |
| PCC | Pearson-correlation coefficients |
| PCE | Perfect channel estimation |
| P/S | Parallel-to-serial |
| PSNR | Peak signal-to-noise ratio |
| QAM | Quadrature amplitude modulation |
| RC | Rate-compatible |
| ResNET | Residual deep neural network |
| RRC | Root-raised cosine |
| RMSE | Root mean square error |
| SE | Spectral efficiency |
| SNR | Signal-to-noise ratio |
| STC | Space time code |
| S/P | Serial-to-parallel |
| STBC | Space time block code |
| SER | Symbol error rate |
| UAMCS | Underwater acoustic multimedia communication system |
References
- Lin, X.; Zhang, J.; Lin, Y.; Kim, J. Fundamentals of 6G Communications and Networking; Springer Nature Switzerland AG: Cham, Switzerland, 2024; pp. 1–754. [Google Scholar]
- Meena, P.; Pal, M.B.; Jain, P.K.; Pamula, R. 6G Communication Networks: Introduction, Vision, Challenges, and Future Directions. Wirel. Pers. Commun. 2022, 125, 1097–1112. [Google Scholar] [CrossRef]
- Beyrouthy, T.; Mostafa, N.; Roshdy, A.; Karar, A.S.; Alkork, S. Review of EEG-Based Biometrics in 5G-IoT: Current Trends and Future Prospects. Appl. Sci. 2024, 14, 534. [Google Scholar] [CrossRef]
- Kumar, K.B.S.; Sujatha, B.R. FPGA Design of an Efficient EEG Signal Transmission Through 5G Wireless Network Using Optimized Pilot Based Channel Estimation: A Telemedicine Application. Wirel. Pers. Commun. 2022, 123, 3597–3621. [Google Scholar] [CrossRef]
- Lin, C.F.; Chang, S.H. Advanced Mobile Communication Techniques in the Fight Against the COVID-19 Pandemic Era and Beyond: An Overview of 5G/B5G/6G. Sensors 2023, 23, 7817. [Google Scholar] [CrossRef]
- Michailow, N.; Matthé, M.; Gaspar, I.S.; Caldevilla, A.N.; Mendes, L.L.; Festag, A.; Fettweis, G. Generalized Frequency Division Multiplexing for 5th Generation Cellular Networks. IEEE Trans. Commun. 2014, 62, 3045–3061. [Google Scholar] [CrossRef]
- Wang, Y.; Fortier, P. Performance Analysis of LDPC Coded GFDM Systems. IET Commun. 2022, 16, 1663–1673. [Google Scholar] [CrossRef]
- Li, Y.; Niu, K.; Dong, C. Polar-Coded GFDM Systems. IEEE Access 2019, 7, 149299–149307. [Google Scholar] [CrossRef]
- Ssimbwa, J.; Lim, B.; Ko, Y.C. GFDM Frame Design for Low-latency Industrial Networks. Journa Commun. Netw. 2022, 24, 336–346. [Google Scholar] [CrossRef]
- Wang, H.F.; Ueng, F.B.; Chiang, C.T. High Spectral Efficiency and Low Error Rate MIMO–GFDM for Next-Generation Communication Systems. IEEE Trans. Veh. Technol. 2022, 71, 503–517. [Google Scholar] [CrossRef]
- Juajinoy, J.L.C.; Cal-Braz, J.; Neto, R.S. Detection Strategies for MIMO-GFDM-IM System. IET Commun. 2025, 19, e70016. [Google Scholar] [CrossRef]
- Tasadduq, I.A. CPM-GFDM: A Novel Combination of Continuous Phase Modulation and Generalized Frequency Division Multiplexing for Wireless Communication. Appl. Sci. 2023, 13, 854. [Google Scholar] [CrossRef]
- Kalsotra, S.; Singh, A.K.; Joshi, H.D. Performance analysis of space time coded generalized frequency division multiplexing system over generalized fading channels. Trans. Emerg. Telecommun. Technol. 2022, 13, e4423. [Google Scholar] [CrossRef]
- Choa, H.; Ahnb, J.M.; Nohc, J.H.; Song, H.Y. Some new LDPC-coded orthogonal modulation schemes for high data rate transmissions in navigation satellite systems. ICT Express 2024, 10, 588–593. [Google Scholar] [CrossRef]
- Kwak, W.S.; Kim, J.W. Design of LDPC code for uncorrelated Rayleigh fading channel using modified outage probability. ICT Express 2025, 11, 442–447. [Google Scholar] [CrossRef]
- Hyla, J.; Sułek, W.; Zydorczyk, W.; Dziczkowski, L.; Filipowski, W. Efficient LDPC Encoder Design for IoT-Type Devices. Appl. Sci. 2021, 12, 2558. [Google Scholar] [CrossRef]
- Liu, J.; Hao, Z.; Zhao, L.; Lian, J.; Jun Tao, J.; Fan, Y.; Feng, Q. A Low Valid Throughput Loss LDPC Codec Architecture with Variable Code Rate. IEEE Trans. Circuits Syst.—II Express Briefs 2024, 71, 2644–2648. [Google Scholar] [CrossRef]
- Cummins, A.D.; Mitchell, D.G.M.; Perrins, E. Rate-Compatible, Bandwidth-Efficient, Low-Density Parity-Check (LDPC) Codes for Aeronautical Telemetry. Entropy 2024, 26, 1045. [Google Scholar] [CrossRef] [PubMed]
- Gunturu, A.; Godala, A.R.; Sahoo, A.K.; Chavva, A.K.R. Performance Analysis of OTFS Waveform for 5G NR mmWave Communication System. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021. [Google Scholar]
- Usatyuk, V.S.; Egorov, S.I. 2D/3D ResNet Deep Neural Network for 4G and 5G NR Wireless Channel Estimation. In Proceedings of the IEEE 25th International Conference on Digital Signal Processing and its Applications (DSPA), Moscow, Russia, 29–31 March 2023. [Google Scholar]
- Earlea, B.; Al-Habashna, A.; Wainera, G.; Lic, X.; Xuec, G. Machine Learning-Based Small-Scale Parameter Extraction for Improved Wireless Channel Model Fidelity. In Proceedings of the IEEE Annual Modeling and Simulation Conference (ANNSIM), Washington, DC, USA, 20–23 May 2024. [Google Scholar]
- Jiang, T.; Zhang, J.; Pan Tang, P.; Tian, L.; Zheng, Y.; Dou, J.; Asplund, H.; Raschkowski, L.; Errico, R.; Tommi Jämsä, T. 3GPP Standardized 5G Channel Model for IIoT Scenarios: A Survey. IEEE Internet Things J. 2021, 8, 8799–8815. [Google Scholar] [CrossRef]
- Lin, C.F.; Wu, C.F.; Hsieh, C.L.; Chang, S.H.; Parinov, I.A.; Shevtsov, S. Generalized Frequency Division Multiplexing-Based Low-Power Underwater Acoustic Image Transceiver. Sensors 2022, 22, 313. [Google Scholar] [CrossRef]
- 5G Study on Channel Model for Frequencies from 0.5 to 100 GHz; 3GPP TR 38.901; Hanoi University of Technology: Hanoi, Vietnam, 2020.
- EEG Motor Movement/Imagery Dataset. Available online: https://physionet.org/content/eegmmidb/1.0.0/ (accessed on 26 August 2025).
- Lin, C.T.; Wang, Y.; Chen, S.F.; Huang, K.C.; Liao, L.D. Design and Verification of a Wearable Wireless 64-Channel High-Resolution EEG Acquisition System with Wi-Fi Transmission. Med. Biol. Eng. Comput. 2023, 61, 3003–3019. [Google Scholar] [CrossRef]
- Santhosh Kumar, K.B.; Sujatha, B.R.; Sushma, N. Machine Learning-based Channel Estimation for EEG Signal Transmission in MIMO-OFDM System. In Proceedings of the IEEE International Conference on Recent Advances in Information Technology for Sustainable Development (ICRAIS), Manipal, India, 6–7 November 2024. [Google Scholar]
- Revanna, B.R.; Akhila, S.; Santhosh Kumar, K.B.; Sushma, N.; Radhika, K.A.; Ghouse Ahamed, Z. EEG Transmission over 6G Optimized Pilot-Based Channel Estimation. In Proceedings of the IEEE International Conference on Circuits, Control, Communication and Computing (I4C), Bangalore, India, 4–5 October 2024. [Google Scholar]
- Kanemoto, D.; Takimoto, E.; Hirose, T. Development of Low-power and High-accuracy Wireless EEG Transmission System Using Compressed Sensing with an EEG Basis. In Proceedings of the IEEE International Conference on Circuits, and Systems (ISCAS), London, UK, 25–28 May 2025. [Google Scholar]
- Lin, C.F.; Chang, K.T. A Power Assignment Mechanism in Ka-band OFDM-based Multi-satellites Mobile Telemedicine. J. Med. Biol. Eng. 2008, 28, 17–22. [Google Scholar]
- Lin, C.F.; Hung, S.I.; Chiang, I.H. An 802.11n wireless local area network transmission scheme for wireless telemedicine application. Proc. IMechE Part H J. Eng. Med. 2010, 224, 1201–1208. [Google Scholar] [CrossRef] [PubMed]




| Technology | Technological Characteristics |
|---|---|
| GFDM modulation | Michailow et al. [6] |
| Channel model | 3GPP CDL channel model D (LOS) |
| Carrier central frequency | 28 GHz |
| Mobile speed | 400 km/h |
| MIMO | 4 × 4 DM |
| Number of subcarriers (B) | 128 |
| Number of subsymbols (C) | 9 |
| Filter method | RRC |
| Roll-off factor | 0.1 |
| Modulation | 4-QAM |
| Channel coding | (2000, 1000) LDPC code |
| Transmission media | ECG signals |
| Power weighting factors | 15/30, 16/30, …, 30/30 |
| BER limits for EEG transmission | |
| EEG test transmission signals | EEG Motor Movement/Imagery Dataset [25] |
| CEEs (%) | SNR (dB) | BER | MSE | PCC |
|---|---|---|---|---|
| 0 | 11.00 | 3.36 | 0.99944 | |
| 5 | 11.00 | 24.25 | 0.99600 | |
| 10 | 11.00 | 68.04 | 0.98898 | |
| 0 | 13.51 | 0.999989228 | ||
| 5 | 13.51 | 0.999935264 | ||
| 10 | 13.51 | 1.15 | 0.999810395 | |
| 0 | 14.10 | 0.999999999762218 | ||
| 5 | 14.51 | 0.999999998 | ||
| 10 | 15.00 | 0.999999997622151 |
| References | Technological Notes |
|---|---|
| Lin et al. [26] |
|
| Santhosh Kumar et al. [27] |
|
| Revanna et al. [28] |
|
| Kanemotoet al. [29] |
|
| Kumaret al. [4] |
|
| Lin et al. [30] |
|
| Lin et al. [31] |
|
| The proposed method |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-F.; Chen, K.-Y. Generalized Frequency Division Multiplexing—Based Direct Mapping—Multiple-Input Multiple-Output Mobile Electroencephalography Communication Technique. Appl. Sci. 2025, 15, 9451. https://doi.org/10.3390/app15179451
Lin C-F, Chen K-Y. Generalized Frequency Division Multiplexing—Based Direct Mapping—Multiple-Input Multiple-Output Mobile Electroencephalography Communication Technique. Applied Sciences. 2025; 15(17):9451. https://doi.org/10.3390/app15179451
Chicago/Turabian StyleLin, Chin-Feng, and Kun-Yu Chen. 2025. "Generalized Frequency Division Multiplexing—Based Direct Mapping—Multiple-Input Multiple-Output Mobile Electroencephalography Communication Technique" Applied Sciences 15, no. 17: 9451. https://doi.org/10.3390/app15179451
APA StyleLin, C.-F., & Chen, K.-Y. (2025). Generalized Frequency Division Multiplexing—Based Direct Mapping—Multiple-Input Multiple-Output Mobile Electroencephalography Communication Technique. Applied Sciences, 15(17), 9451. https://doi.org/10.3390/app15179451





