Next Article in Journal
Improvement and Radiation-Resistance Study of an Optical Displacement Sensing System Based on a Position Sensitive Detector
Next Article in Special Issue
Pain Neuroscience Education to Reduce Catastrophizing: A Parallel Randomized Trial in Youth Athletes
Previous Article in Journal
Induction Motor Fault Diagnosis Using Low-Cost MEMS Acoustic Sensors and Multilayer Neural Networks
Previous Article in Special Issue
Retrospective Observational Cohort Study of Mid-Term Outcomes Following Ponseti Method for Idiopathic Clubfoot
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 17
10.3390/app15179382
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Sex Differences in the High Jump Kinematics of U18 Adolescent Athletes

by
Vassilios Panoutsakopoulos
Biomechanics Laboratory, School of Physical Education and Sport Science at Thessaloniki, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
Appl. Sci. 2025, 15(17), 9382; https://doi.org/10.3390/app15179382
Submission received: 11 July 2025 / Revised: 18 August 2025 / Accepted: 22 August 2025 / Published: 26 August 2025
(This article belongs to the Special Issue Advances in Sports Science and Biomechanics)
Browse Figures
Versions Notes

Abstract

Biomechanical analyses of technique are essential for performance improvement in athletic jumps, but scarce evidence exists for adolescent athletes in the literature. The purpose of this study was to examine the sex differences in the high jump biomechanics of U18 athletes. Twenty-one women (15.2 ± 1.0 yrs) and twenty-one men (15.2 ± 1.2 yrs) Greek U18 high jumpers were recorded in regional competitions using two cameras (sampling frequency: 60 fps). The kinematic parameters of the last step, the take-off, and the crossbar clearance were calculated using 3D-DLT analysis. The independent samples t-test was used to detect significant (p < 0.05) differences between groups. Results revealed that men had significantly (p < 0.05) better performance, with larger last step angle and length, body center of mass (BCM) height at the final touchdown and take-off, approach and vertical BCM take-off velocity, touchdown lateral inclination of the take-off leg, and swing leg knee angle at take-off. Women had significantly (p < 0.05) higher vertical BCM velocity at touchdown. No differences (p > 0.05) were observed for take-off angle, the support leg knee angle, the inclination of the torso at touchdown, or the vertical BCM displacement during the take-off phase. The anthropometric and physical conditioning differences between sexes contributed to the findings of the study. Coaches should consider the age and sex differences of adolescent athletes when designing training programs to optimize high jump performance.

1. Introduction

The high jump is a track and field event that has significantly evolved during the last century in terms of its technique [1]. Furthermore, additional factors contributing to the enhancement of high jump performance include improvements in sporting equipment such as footwear, jumping surface, and landing mat, as well as the implication of specialized training programs aimed at optimizing performance [2,3]. Currently, the technique with which the high jump is predominantly performed is the “Fosbury Flop”. The elements of the Fosbury Flop technique, which differentiate it from previous techniques, are the curved approach run, the take-off from the “far” foot with regard to the crossbar, and the crossbar clearance from the back [4]. At the beginning of this century, further improvement was observed in the average men’s high jump performance as a result of the introduction of a new regulation regarding the overall allowed fault attempts at some major European Athletics events, since fewer failed attempts were observed and higher average official performance was documented [5].
The basic methodological approach to interpret and evaluate athletics technique is kinematic analysis, which is categorized into qualitative and quantitative analyses [6]. Most of the contemporary knowledge regarding the high jump technique is derived from the quantitative evaluation of the technique, as examined with the use of three-dimensional kinematic analyses of the athletes’ efforts in Olympic Games [7,8] and World Athletics Championships [9,10,11,12,13,14,15,16]. In addition to kinematics, quantitative data have also been reported on the kinetic parameters (e.g., impulse, angular momentum) that determine jump height [17,18,19,20,21,22].
The critical kinematic parameters of the body center of mass (BCM), which characterize the support phase of the last steps of the approach, are its horizontal velocity [12,23], the lateral inclination of the trunk towards the center of the trajectory curve [9,19,24], and the reduction in its height in the last stride [9,25]. Accordingly, the backward tilt of the torso and the position of the swinging leg during positioning are considered essential for the effective application of the jumper’s abilities during the landing-take-off phase [9,23,24,25,26], the jumper’s initial mechanical energy at the start of the jump push [17], the conversion of the horizontal to vertical BCM velocity [8], the push along the vertical axis [18], the participation of the swinging members to create angular momentum around the body’s rotation axes [19,20,21,22], as well as the height and vertical BCM take-off velocity [8,12,14,18,26]. In conclusion, the optimization of performance in the crossbar clearance phase depends on the management of the acquired rotational momentum, as well as on the amplitude of the trunk hyperextension and the synchronization of the movements to achieve it [21].
Significant sex differences were noted in the comparison of elite high jumpers, including variables that represent physical condition parameters (e.g., speed and explosive power), namely the BCM velocities [16,27]. The results of the study by Frutos et al. [28] showed that sex differences in high jump biomechanics increase during adolescence and into adulthood. It is suggested that the differences in take-off and performance are due to anthropometric, motoric, and maturational variables rather than the kinematic parameters that interpret technique [29,30]. In general, it has been observed in past research that sex differences exist in adolescent track and field jumpers regarding kinematic parameters related to physical fitness abilities, but not kinematic parameters that interpret the technical execution of the take-off technique, such as joint angles and body segment inclination [31,32]. In the case of the high jump, limited performance-related sport biomechanics research has been conducted in the U18 category of high jumpers. The information provided in the respective literature does not explicitly report the recorded values for men and women U18 jumpers [28], or it concerns only a limited number of examined biomechanical parameters [29]. Furthermore, the possible sex difference regarding the relationship between kinematic parameters and high jump performance in U18 athletes has not yet been investigated. The present study aims to fill this gap in the literature by providing evidence for the sex differences in a variety of kinematic parameters that interpret the high jump technique in U18 jumpers.
Due to the limited information regarding the sex differences in the high jump technique of adolescent athletes, the purpose of this study was to examine the biomechanical differences in the high jump technique of U18 athletes. It was hypothesized that differences would be observed in the parameters expressing physical conditioning (i.e., horizontal and vertical BCM velocity) but not in the parameters that interpret the high jump technique (i.e., knee joint angle at take-off, BCM take-off angle, and orientation of the body segments). The findings of the present study could assist coaches in designing more efficient age- and sex-specific training programs to optimize jump height performance in U18 athletes.

2. Materials and Methods

2.1. Participants

A convenient sample of 42 athletes who competed in the men’s (n = 21) and women’s (n = 21) U18 high jump event during the 2022, 2023, and 2024 editions of a local athletics meeting served as participants in the study. The mean (± standard deviation) age, height, body mass, body mass index, and best performance for the men were 15.2 ± 1.2 years, 1.84 ± 0.04 m, 66.2 ± 2.3 kg, 19.7 ± 1.4 kg/m2, and 1.69 ± 0.14 m, respectively, and for the women were 15.2 ± 1.0 years, 1.72 ± 0.04 m, 58.1 ± 4.1 kg, 19.6 ± 1.0 kg/m2, and 1.51 ± 0.12 m, respectively. Participation in the study was granted after fulfilling the inclusion criteria, namely an absence of injury for 3 months before the measurements, an absence of any disability (musculoskeletal or neurological), a record of systematic participation in the training program, and participation in track and field competitions for at least 3 years. The study was conducted after obtaining signed parental consent and was in accordance with the provisions of the Declaration of Helsinki and the Ethics Code of the Research Committee of the Aristotle University of Thessaloniki. The research was approved by the Ethics Committee of the Aristotle University of Thessaloniki, Greece (approval number: 260574/2022).

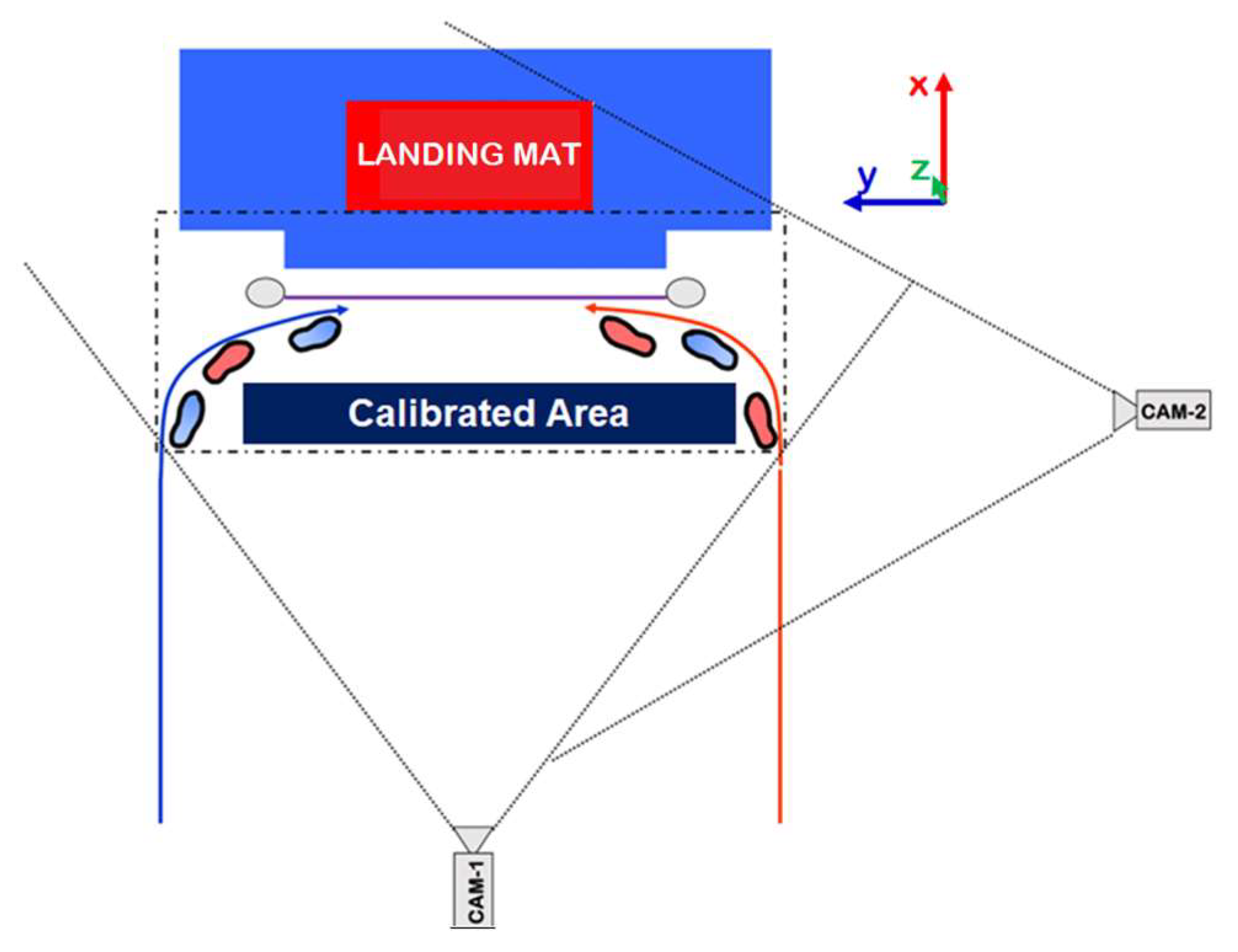
2.2. Data Acquisition

The jumpers’ attempts were recorded using two fixed digital cameras (Samsung Galaxy S6 and Samsung Galaxy S7 Edge smartphones, Samsung, Incheon, Republic of Korea), which operated in full high definition mode (resolution: 1920 × 1080 px) at a recording frequency of 60 fps and a shutter speed of 1/2000. The selected sampling frequency is in agreement with past research on similar examinees [29]. The cameras were placed on fixed tripods according to the arrangement shown in Figure 1 and at a height of 1.47 m from the ground. The distance of the cameras from the base of the right upright post was 28.0 m. The cameras were zoomed in to have a recording view adequate to capture the following phases of the high jump technique: the last step of the approach, the take-off, the crossbar clearance, and the landing on the mat. The synchronization of the videos was performed using the recorded audio signals via the corresponding function of the analysis software (A.P.A.S. v.14.1.0.5, Ariel Dynamics Inc., Trabuco Canyon, CA, USA) as a reference.
The area included in the field of view of the cameras was calibrated with a 1.6 m × 1.6 m × 1.8 m calibration frame with reference points (diameter: 5 cm) every 40 cm. The calibration frame was placed at predetermined points on the ground, which included the area where the last two steps of the approach and the take-off were executed. Reference points were also taken on the upright posts, the crossbar, and the mat. The above reference points were used to extract three-dimensional coordinates through three-dimensional direct linear transformation (3D-DLT) kinematic analysis [33]. The Y-axis was parallel to the crossbar, with positive values being from the right upright post to the left upright post (Figure 1). The X-axis was perpendicular to the Y-axis, with positive values being from the crossbar to the landing mat, while the Z-axis was vertical and perpendicular to the X- and Y-axes, with positive values being from the ground to the sky. The base of the right upright post was adopted as the reference point (X, Y, Z) = (0, 0, 0) of the three-dimensional Cartesian system, and the Y-axis was the reference axis. The setup of the experimental procedure was conducted by the same experienced researcher in all examined editions of the athletics meeting.

2.3. Data Analysis

Eighteen anatomical points of the body (tip of the toe, ankle, knee, hip, shoulder, elbow, wrist, and fingers on both sides of the body, the neck, and the head) and selected points in the filming view were manually digitized in each field. To calculate BCM 3D coordinates and the segmental inertia properties for the link segment model, the proportional subject-specific height and weight characteristic formulas recommended by Plagenhoef [34] were used.
Cut-off frequency for smoothing was set at 6 Hz [29,35]. Digitization, smoothing, and analyses were performed with the A.P.A.S. v.14.1.0.5 software (Ariel Dynamics Inc., Trabuco Canyon, CA, USA). The accuracy of the 3D reconstruction was determined by the root mean square (RMS) error after randomly re-digitizing 10% of the captured frames. An RMS error of 3.5 cm, 1.0 cm, and 1.1 cm was found for the X-, Y-, and Z-axes, respectively.
Based on the XYZ coordinates of the digitized anatomical points, the experimental parameters were as follows:
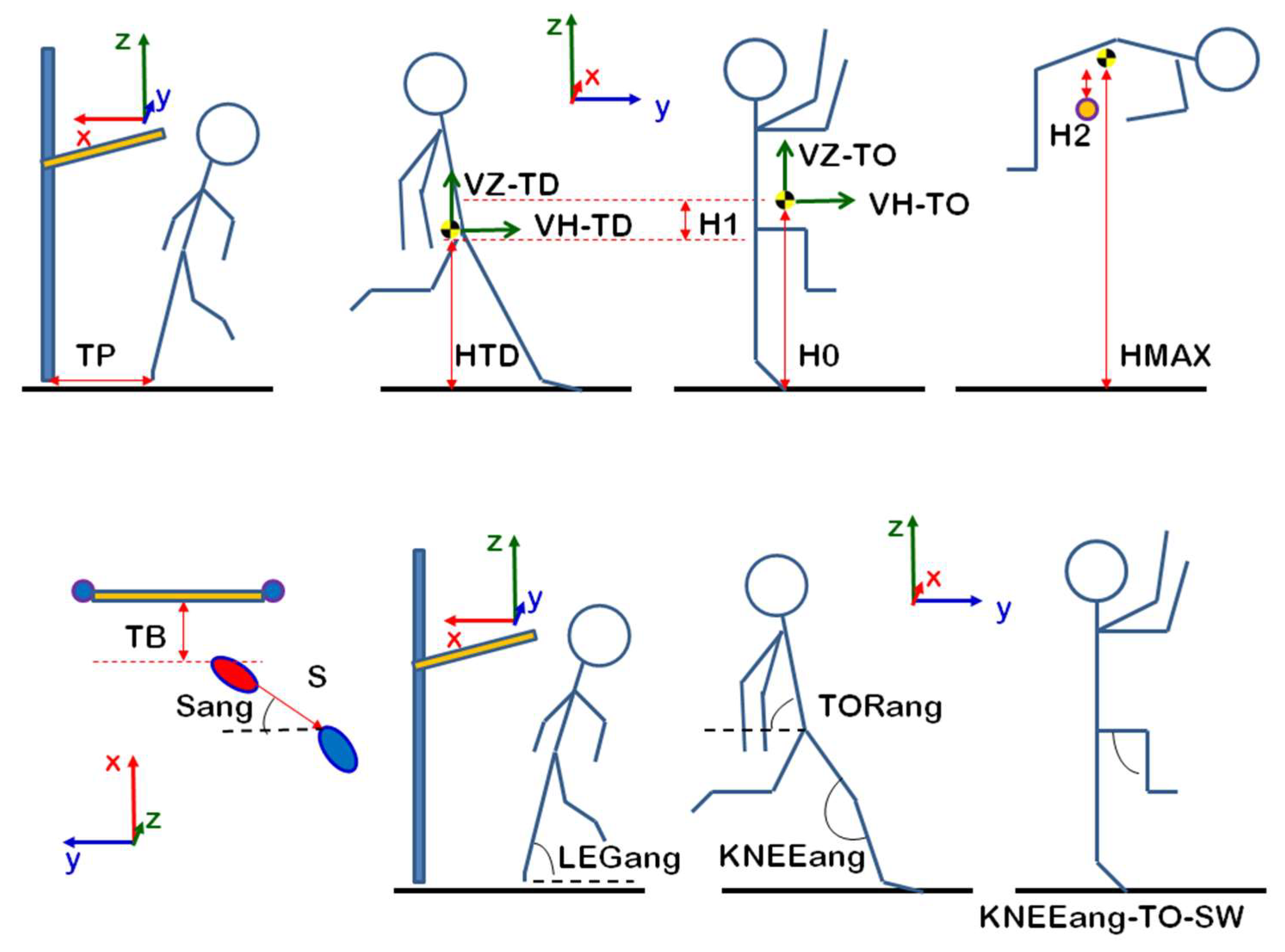
  • the maximum height of the BCM trajectory (HMAX), as well as the height of the BCM at the instant of the final touchdown (HTD) and take-off (H0),
  • the vertical displacement of the BCM from the time of take-off to the highest point of its trajectory (H1), as the difference in the vertical axis of the BCM position at these instances,
  • the vertical distance between the crossbar and the highest point of the BCM trajectory (H2), as the difference in the vertical axis of the highest point of the BCM trajectory and the position of the center of the crossbar at the instant of HMAX,
  • the distance between the toes of the take-off leg and the respective upright post (TP), as the horizontal distance on the Y-axis between the two points at the time of foot placement,
  • the distance between the toes of the take-off leg and the center of the crossbar (TB), as the horizontal distance on the X-axis between the two points at the time of foot placement,
  • the last step (1L) length (S), as the distance in the XY plane of the toes of the supporting leg between the take-off from the last step and the full foot contact at the take-off phase,
  • the direction of the step with respect to the longitudinal axis of the crossbar (Sang), as the angle formed in the XY plane between the Y-axis and the line connecting the position of the toes of the supporting leg in the last step and the take-off phase,
  • the horizontal velocity (VH) as the resultant velocity of the BCM in the X- and Y-axes at the instants of foot placement (TD) and take-off (TO), as well as the take-off at the last step (VH-TO-1L),
  • the vertical velocity (VZ), as the velocity of the BMS in the Z-axis at the instants of TD and TO,
  • the take-off angle of the BCM (AngPr), as the value of the arctangent of the ratio of the vertical to the horizontal take-off velocity of the BCM,
  • the inclination of the take-off leg (LEGang), as the angle formed by the line connecting the lateral malleolus and the hip with the XY plane at the instant of foot placement for the take-off phase,
  • the inclination of the torso (TORang), as the angle formed by the line connecting the hip of the take-off leg and the neck with the Z-axis at the instant of foot placement for the take-off phase,
  • the angle of the knee (KNEEang) joint for both the support and the swing (SW) leg, as the angle formed between the thigh and the shank,
  • the knee joint range of motion (ROM) from TD to its maximum flexion (MKF) and from MKF to the instant of take-off,
The duration of the take-off phase (TIME), namely the time from TD to TO, was also examined. Figure 2 provides a visualization of the examined kinematic parameters.

2.4. Statistical Analysis

The normality of distribution was examined using the Shapiro–Wilk test (p > 0.05). The equality of variance was examined with Levene’s test (p > 0.05). The results of these tests showed that the assumptions for the use of parametric statistics were met. Thus, an independent samples t-test was conducted to examine possible sex differences between men and women U18 high jumpers. The results of the t-test are reported as tdf, where df = n1 + n2 − 2. The effect sizes were checked using Cohen’s d, where the magnitude of d < 0.2, d ≥ 0.2, d ≥ 0.5, and d ≥ 0.8 was interpreted as trivial, small, medium, and large effect sizes, respectively [36].
The possible linear relationship between the official result and the examined kinematic parameters was examined using the Pearson correlation coefficient (r). This examination was conducted separately for the men and women groups. Values of r within the range of 0.00–0.09, 0.10–0.39, 0.40–0.69, 0.70–0.89, and 0.90–1.00 were interpreted as negligible, weak, moderate, strong, and very strong relationships, respectively [37]. Significant correlations were followed up for the comparison of r between men and women U18 high jumpers by implementing Fisher’s r-to-Z transformation. This check was conducted using the Psychometrica freeware calculator [38].
The IBM SPSS Statistics v.28.0 software (International Business Machines Corp., Armonk, NY, USA) was used for the statistical analyses. For all analyses, an a = 0.05 level of significance was set.

3. Results

3.1. Spatio-Temporal Parameters

The official result was 1.74 ± 0.16 m for men and 1.55 ± 0.11 m for women, revealing significantly (t40 = 4.493, p < 0.001, d = 1.39, large effect size) higher performance for men. Table 1 presents the spatio-temporal parameters for the last step and the take-off phase. Men had significantly (p < 0.05) larger S, Sang, TB, HTD, H0, and HMAX compared to women. In the men’s group, the official result was significantly (p < 0.05) positively moderately correlated with TB, H0, and H1. Regarding the women’s group, a significant (p < 0.05) positive strong correlation between the official result and S was found. The Fisher’s r-to-Z transformation revealed a significant (p < 0.05) sex difference regarding the correlation between S and the official result (Z = −2.808, p = 0.002).
Figure 3 depicts H0, H1, and H2 as percentages of HMAX. Significant sex differences were found for H0 (t40 = 2.750, p = 0.009, d = 0.85, large effect size) and H1 (t40 = 2.750, p = 0.009, d = 0.85, large effect size), but not for H2 (t40 = 0.499, p = 0.620, d = 0.15, trivial effect size).

3.2. Body Center of Mass Velocity Parameters

Regarding the BCM velocity parameters, significant (p < 0.05) sex differences were observed for VH-TO-1L, VH-TD, and VZ-TO, as larger values were recorded for men than women (Table 2). On the other hand, women had significantly (p < 0.05) higher VZ-TD compared to men. The official result in men was significantly (p < 0.05) positively strongly correlated with VZ-TO and AngPr, as well as negatively moderately correlated with VH-TO. A significant (p < 0.05) positive moderate correlation between the official result with VH-TD and VZ-TD, as well as a positive strong correlation between the official result with VZ-TO, was evident in the women’s group. The Fisher’s r-to-Z transformation revealed a significant (p < 0.05) sex difference regarding the correlations between VH-TD, VH-TO, VZ-TD, and AngPr and the official result (Z = −1.331, p = 0.002, Z = −2.637, p = 0.004, Z = −3.118, p = 0.001, and Z = 2.905, p = 0.002, respectively).

3.3. Angular Kinematic Parameters

Table 3 depicts the results for the examined angular kinematics. Significant (p < 0.05) sex differences were observed for KNEEang-TO-SW, as larger values were recorded for men, and LEGang, since women performed the last touchdown with a more upright support leg. Only LEGang and KNEEang-TO-SW were significantly (p < 0.05) moderately correlated with the official result in the women’s group. The Fisher’s r-to-Z transformation showed that the correlation for LEGang was significantly (p < 0.05) different (Z = −2.878, p = 0.002) between men and women.

4. Discussion

The hypothesis of this study was partially confirmed, as sex differences were observed in the parameters expressing physical conditioning, such as the horizontal and vertical components of the BCM velocity at the take-off for the last step and the jump. However, the hypothesis that no sex differences would exist in the rotational kinematic parameters that interpret technique (i.e., joint angles, segment inclination) was not supported by the present findings, since men U18 high jumpers placed the support leg more laterally inclined at the touchdown for the take-off phase and had a more extended swing leg knee angle at take-off compared to the women.
The effort of the participants in the examined jumps was of a high level, as the average official height was higher than the average stated personal bests before the analyzed competitions. However, the official result was lower than the performances in previous studies with age-matched athletes [28]. Nevertheless, as found in previous studies [16,28], a sex difference was evident. The average vertical distance between the crossbar and the highest point of the BCM trajectory in the present study was, on average, 0.11 m. Although this clearance height could be acceptable for developing high jumpers, criteria established in the relevant literature indicate that this clearance height represents an ineffective technique for clearing the crossbar [21]. This finding can be interpreted as an inferior clearing technique of the crossbar displayed by the participants compared to adult Greek [39], international, women [40] World Championship- and Olympic-level [9,10,11,12,13,14,15,16] high jumpers, for whom an average value of ≈0.07 m has been observed.
The above result can be attributed to the combination of the proximity of the take-off point to the crossbar, the lower AngPr, and the reduced VZ-TO in the examined jumpers, specifically the women high jumpers. The examined women U18 high jumpers had a lower TB and VZ-TO than the men jumpers, which was in agreement with past research [16]. It is suggested that the combination of the above factors could create difficulties for an efficient clearance of the bar [21,41]. In addition, the proximity of the take-off point compared to the crossbar is considered a contributing factor for the occurrence of injuries to the ankle and/or the knee joint of the take-off leg [42]. Due to this fact, it is believed that jumpers fail to effectively utilize the speed acquired in the approach, which consequently leads to lower performance [42].
From a biomechanical point of view, the parameters related to BCM energy at the instants of touchdown and take-off are considered essential indicators for high jump performance [43]. Specifically, VZ-TO is considered the most important factor for determining high jump performance [18]. Thus, the reduced performance of the women U18 jumpers can be attributed to the lower values recorded for this parameter compared to the men U18 jumpers. The vertical velocity of the swing segments during the take-off phase contributes to the vertical velocity of the swing members [8,11,20]. Optimizing the use of the swing limbs for maximum performance requires synchronization and inter-limb coordination of the movements during the take-off phase. This is because, during this phase, the swing limbs should be driven sharply upwards and should terminate their movement just before the instant of take-off [22]. The possible causes of the inefficient swing of the upper limbs during the push-off can be attributed to their ineffective body posture and segment movements during the last step [8]. Thus, it is preferable to increase the HTD at touchdown by displaying a low backward torso inclination that is considered an essential body posture adjustment for an efficient take-off [26].
In the present study, the above-mentioned technical element was displayed by the participants with no apparent sex difference. The backward tilt of the torso at the instant of the touchdown for the take-off phase facilitates the exploitation of the horizontal velocity of the BCM acquired in the approach, the greater vertical displacement of the BCM during this phase, and the integration of the movements of the swing segments in the generated impulse [26]. It is desirable that the vertical velocity of the BCM have a positive value at the instant of the touchdown for the take-off phase. The importance of this fact is the presence of favorable conditions where the conversion of the horizontal to vertical BCM velocity will be effective [13]. This was observed in the men U18 high jumpers examined, and it was found in almost half of the women jumpers, where the average value was slightly positively and moderately positively correlated with the official result, respectively, indicating a sex difference. However, the lower horizontal and vertical BCM take-off velocity values recorded in the present study compared to top international jumpers indicate the unfavorable utilization of the horizontal to vertical conversion by the examined U18 Greek high jumpers.
A sex difference was observed for HTD, which agrees with past findings [16] and can be attributed to the body height differences between the examined men and women athletes. This difference should be noted with caution, as HTD is not a performance-related factor [11,40]. On the other hand, H0 was higher in men than in women U18 jumpers, which was also found in past research [16,28]. However, the recorded values were lower than those reported in the past for adult athletes [7,10,11,12,14,39,40]. This sex difference indicates lower force, work, and power output capabilities in the examined women compared to the men U18 high jumpers, which is corroborated by other studies [20,44,45]. The lower H0 is also related to the elevation and the speed of execution of the swing segments movement [46].
In addition to sex differences in anthropometric parameters, the more extended knee of the swing leg of the men U18 athletes might have influenced this result, despite the KNEEang-TO-SW values displayed by the women U18 high jumpers being in agreement with past findings [16]. The more extended KNEEang-TO-SW is believed to be demonstrated by power floppers, namely the high jumpers who depend on strength parameters to optimize HMAX [47]. On the other hand, the flexed KNEEang-TO-SW was found to be correlated with the height achieved [48]. It is proposed to be an indication of speed floppers, namely, the high jumpers who depend on velocity parameters to achieve HMAX. This sex difference between the assumed dependency on power and speed by men and women U18 high jumpers, respectively, is in line with findings regarding the strength application capabilities between sexes in adolescent athletes [44].
The AngPr (by approximately 8 deg) and VZ-TO in the present study were considerably lower than those reported in previous studies for elite adult high jumpers [7,8,10,11,12,13,14,15,49]. As mentioned above, VZ-TO is an essential factor for the maximization of high jump performance. An increase in H0 and VZ-TO can be accomplished by an effective stretch–shortening cycle function of the take-off leg extensor muscles [20,25,50]. It is suggested that good performers in the high jump achieve better scores in performance-related parameters in the vertical jump [51] and ankle plantar flexion torque [52] tests. During the execution of the high jump technique, this can be effectively monitored by the take-off leg joint angles during the take-off phase [23].
Regarding the knee joint angle, the participants had a KNEEang-TD within the range of values recorded in the top international jumpers [7,10,12,13,14,16,40,53], with no sex differences as reported in past research [16,27]. The effectiveness of the stretch–shortening cycle is related to the minimum possible flexion of the knee joint during the take-off phase [23], which depicts the strength and power abilities of a high jumper [40]. Past research suggested that the best performers present a faster transition from the stretching to the shortening phase of take-off, with the effectiveness of this transition being indicated by smaller knee flexion and higher vertical BCM velocity [40]. In the present study, the average angle KNEEang-MKF was approximately 8 deg more flexed than found in other studies [7,10,12,13,14,52], while it was similar to that of adult men Greek high jumpers [38]. The magnitude of the ROM-TD-MKF was found to be related to factors such as strength and leg stiffness [13,20,53,54]. These factors have been associated with power jumpers, as they seem to present less leg stiffness compared to speed floppers [55].
Considering the developmental aspect of KNEEang-MKF, it is important to consider that in prepubertal children, where the scissors technique is suggested as the preferred high jump technique, the duration of the take-off phase is negatively correlated with KNEEang-MKF. This indicates a poor ability to effectively convert kinetic to potential energy [56]. Thus, it seems logical that the lack of physical ability for U18 high jumpers to handle the power production requirements in the take-off phase in a time-constrained ROM-MKF-TO is reflecting the low capability of the knee extensors for accelerating the body upwards in the late take-off phase [57]. This is because the knee angle is strongly related to peak power output [58,59]. In the present study, no sex difference in the knee joint during this phase was observed, but the results were suggestive of an excessive KNEEang-MKF. On the other hand, the angles of the take-off leg confirmed past research [16,27,29].
A sex difference was evident for the length and the direction of the last stride, with the former being in agreement with past findings in age-matched jumpers [28] but not for adult [60] high jumpers. In younger, novice jumpers, S is a predictor of the official result [56]. In the present study, the official results for women U18 high jumpers seemed to be related to S more than for the men athletes. On the other hand, despite the observed sex difference, the values recorded for the Sang of the examined athletes were within the suggested range (20–40 deg) according to previous researchers [8,18,26,39]. Sang is associated with the height of the BCM during the touchdown at the take-off phase [8,14,19].
In addition to anthropometry [28,29], another parameter that contributed to the observed sex difference regarding the BCM height at the positioning for the jump was probably the sex difference in the inclination of the take-off leg at the touchdown for the take-off phase. The average observed value for men was in reasonable agreement with the values indicated as optimum (56 deg) take-off leg inclination in simulation studies [23]. The inclination of the body towards the center of the curve is suggested to be related to the decrease in the BCM height [9,19]. The increased inclination of the body contributes to running the curved approach without reducing the BCM speed and thus being a factor in the creation of angular momentum and increased VZ-TO [8,24,25].
In general, a more curved approach facilitates higher BCM height without the requirement for enhanced joint kinetic exertions during the take-off phase since the curved approach optimizes the initial condition to increase H1. This is favorable for an effective take-off [61] and aids in the transformation of horizontal kinetic energy into vertical dynamic energy [62]. The latter can be accomplished by increasing energy at touchdown via a faster approach or increasing the rate of energy conversion [20,52]. Nevertheless, a stable body posture is required to effectively execute the take-off technique, and the hip joint plays an important role [52]. Furthermore, it is proposed that the hip abductors and the lumbar lateral flexors also function as energy generators and not only as stabilizers [63]. Thus, the more inclined positioning of the take-off leg exhibited by the men U18 high jumpers compared to the women provided a more advantageous initial condition for higher performance [47]. The importance of this factor is also supported by the finding that a negative moderate correlation between LEGang and the official result was revealed in the women’s group, indicating that the inclined positioning for the take-off is an essential performance parameter.
Previous studies in high-level high jumpers have shown that VH-TO is correlated with VZ-TO [8,20], which in turn is correlated with HMAX [14]. The latter relationship was also found in the present study. Furthermore, it seems that VZ-TO and the parameters directly or indirectly related to approach speed, along with the height of the BCM flight, the AngPr, the height of the hip above the crossbar, and TIME, are important for a successful high jump since they were correlated with high jump performance for elite women athletes in a longitudinal case study [64]. In this study, larger correlation coefficients between the BCM speed parameters and official performance were revealed in the examined women than in the wen U18 high jumpers. This can be an indication that adolescent women with higher physical conditioning can reach higher performance levels compared to age-matched women athletes with less strength/power production capabilities.
In addition to the comparison between the biomechanics of men and women U18 high jumpers, another strength of this study is the provision of quantitative data regarding the kinematics of the high jump and the sex difference regarding their relationship with performance. In addition, coaches can obtain essential information regarding the values of kinematic parameters (e.g., BCM velocity and height, joint angles, body segment orientation) of adolescent high jumpers of both sexes, especially those competing in the U18 category. Furthermore, based on these values, coaches can acknowledge which aspects of the jump are subject to differences due to sex, thus designing more effective training programs. However, a possible limitation of this study could be the low sampling rate of the cameras, as this could pose errors regarding the synchronization of the cameras and the exact estimation of the BCM-related parameters. Nevertheless, biomechanical studies have been conducted with similar [65] or even lower sampling frequencies (e.g., 50 fps [29,60,66]). Another possible limitation that might prevent the generalization of the present findings is that the analysis was only conducted on each athlete’s highest successful attempt in the competition. However, this approach is suggested to be of increased ecological validity, as it is suggested that athletes reach their maximum capabilities in an official competition [67]. In addition, the interpretation of the differences in the take-off point and take-off leg planting parameters should be treated with caution due to the relatively high RMS error found in the X-axis. Finally, the fact that the participants comprised a convenience sample, added to their low level of performance, further lessens the generalization of the findings of the present study.
In conclusion, success in a high jump, namely the performance of successful crossbar clearances, is determined by technical (e.g., backward lean, positioning of the trail leg) and physical fitness parameters, namely the high approach velocity and the optimum take-off phase duration [68]. The results showed that sex differences were revealed in the examined U18 Greek high jumpers, not only regarding the kinematic parameters related to physical fitness capabilities (e.g., BCM speed) but also in the kinematic parameters that interpret technique (e.g., positioning angle of the take-off leg, the knee joint of the swing leg). It appeared that the examined groups differed in the percentage proportions of individual heights for the trajectory of the BCM, implying sex-related alterations regarding the conversion of the horizontal to vertical velocity of the BCM during the take-off phase. As an athlete’s technique is not something predetermined, common, or stable, but rather something that constantly changes depending on the phase of their athletic development [6], adjustments in jumping technique should be accompanied by a corresponding improvement in physical fitness abilities. Thus, coaches should design sex- and age-specific training programs to optimize high jump performance.
Future research should focus on examining sex differences in adolescent high jumpers from the perspective of technical execution of the curved approach running gait and the swing of the free limbs in the take-off phase, in addition to measuring the strength/power capabilities of the muscles acting at the hip in this population. Furthermore, a deeper understanding of the biomechanics of the high jump technique as performed by adolescent athletes should be explored by utilizing high-speed and high-resolution motion capture systems combined with examination of take-off kinetics. It is recommended that these studies be cross-sectional to evaluate the progression across development and to examine larger populations of athletes from different countries.

Funding

This research was funded by “Kostas Chimonides’ Athletes and Friends Club”, grant number 264953/11.10.2022 under the No 74975 Research Project of the Research Committee of the Aristotle University of Thessaloniki, Greece.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of the Aristotle University of Thessaloniki, Greece (protocol code 260574/2022 and date of approval: 6 October 2022).

Informed Consent Statement

Informed parental consent was obtained from all subjects involved in the study.

Data Availability Statement

The data presented in this study are available upon reasonable request from the corresponding author due to ethical reasons.

Conflicts of Interest

The author declares no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
1Llast step
3Dthree-dimensional
3D-DLTthree-dimensional direct linear transformation
AngPrtake-off angle
BCMbody center of mass
H0BCM height at the instant of take-off
H1vertical BCM displacement from H0 to HMAX
H2vertical distance of the BCM from the middle of the crossbar at the instant of HMAX
HMAXmaximum height of the BCM trajectory
HTDBCM height at the instant of final touchdown
KNEEangangle of the knee joint
LEGangthe inclination of the take-off leg
MKFmaximum knee flexion
RMSroot mean square
ROMknee joint range of motion
Slast step length
Sangthe direction of the step with respect to the longitudinal axis of the crossbar
TBhorizontal distance in the X-axis between the crossbar and the toes of the take-off leg
TDinstant of touchdown
TIMEduration of the take-off phase
TOinstant of take-off
TORangthe inclination of the torso
TPhorizontal distance in the Y-axis between the respective upright post and the toes of the take-off leg
VHhorizontal BCM velocity
VZvertical BCM velocity

References

  1. Dapena, J. The evolution of high jumping technique: Biomechanical analysis. In Scientific Proceedings of the XX International Symposium on Biomechanics in Sports; Gianikellis, K.E., Ed.; Universidad de Extremadura: Extremadura, Spain, 2002; pp. 3–7. [Google Scholar]
  2. Lippi, G.; Banfi, G.; Favaloro, E.J.; Rittweger, J.; Maffulli, N. Updates on improvement of human athletic performance: Focus on world records in athletics. Br. Med. Bull. 2008, 87, 7–15. [Google Scholar] [CrossRef] [PubMed]
  3. Balmer, N.; Pleasence, P.; Nevill, A. Evolution and revolution: Gauging the impact of technological and technical innovation on Olympic performance. J. Sports Sci. 2012, 30, 1075–1083. [Google Scholar] [CrossRef]
  4. Schiffer, J. The high jump. New Stud. Athl. 2009, 24, 9–22. [Google Scholar]
  5. Theodorou, A.; Skordilis, E. Consequences of the new competition rules for the high jump at the European Team Championships. New Stud. Athl. 2009, 24, 23–30. [Google Scholar]
  6. Kollias, I.A. Biomechanics of Sport Movement; Kyriakidis Bros Publishers: Thessaloniki, Greece, 2019. [Google Scholar]
  7. Conrad, A.; Ritzdorf, W. Biomechanical analysis of the high jump. In Scientific Research Project at the Games of the XXIVth Olympiad, Seoul 1988; Brüggemann, G.P., Glad, B., Eds.; International Amateur Athletic Federation: London, UK, 1990; pp. 177–217. [Google Scholar]
  8. Dapena, J. The high jump. In Biomechanics in Sport; Zatsiorsky, V., Ed.; Blackwell Publishing: Oxford, UK, 2000; pp. 284–311. [Google Scholar]
  9. Ae, M.; Sakatani, M.; Yokoi, T.; Hashihara, Y.; Shibukawa, K. Biomechanical analysis of the preparatory motion for takeoff in the Fosbury Flop. Int. J. Sport Biomech. 1986, 2, 66–77. [Google Scholar] [CrossRef]
  10. Brüggemann, G.P.; Conrad, T. High Jump. In Biomechanical Research in Track and Field: 1st World Junior Championships, Athens 1986; Susanka, P., Brüggemann, G.P., Tsarouchas, E., Eds.; S.E.G.A.S.-Ε.Κ.A.Ε.: Athens, Greece, 1986; pp. 121–148. [Google Scholar]
  11. Brüggemann, G.P.; Loch, M. The high jump. New Stud. Athl. 1992, 7, 67–72. [Google Scholar]
  12. Brüggemann, G.P.; Arampatzis, A. Men’s high jump. New Stud. Athl. 1997, 12, 66–69. [Google Scholar]
  13. Iiboshi, A.; Ae, M.; Tkamatsu, J.; Nagasawa, M.; Tang, H.P.; Yuuki, M. Techniques of elite high jumpers at the 3rd IAAF World Championships in Athletics. In Abstracts of the XIV ISB Congress; I.S.B.: Paris, France, 1993; pp. 608–609. [Google Scholar]
  14. Isoletho, J.; Virmavirta, M.; Kyröläinen, H.; Komi, P. Biomechanical analysis of the high jump at the 2005 IAAF World Championships in Athletics. New Stud. Athl. 2007, 22, 17–27. [Google Scholar]
  15. Killing, W. Zweimal bronze für Deutschlands Höhenjäger. Leichtathlet. Train. 2009, 20, 26–35. [Google Scholar]
  16. Nicholson, G.; Jongerius, N.; Tucker, C.B.; Thomas, A.; Merlino, S.; Bissas, A. The association between hip-shoulder separation angles and technique characteristics in world-class high jumpers. Front. Sports Act. Living 2022, 4, 873526. [Google Scholar] [CrossRef]
  17. Brüggemann, G.P.; Arampatzis, A. Sport Performance Limits: Long jump and high jump. Kινησιολογία 1997, 2, 103–114. [Google Scholar]
  18. Coh, M.; Supej, M. Biomechanical model of the take-off action in the high jump—A case study. New Stud. Athl. 2008, 23, 63–73. [Google Scholar]
  19. Dapena, J. Mechanics of translation in the Fosbury-flop. Med. Sci. Sports Exerc. 1980, 12, 37–44. [Google Scholar] [CrossRef]
  20. Dapena, J.; Mcdonald, C.; Cappaert, J. A regression analysis of high jumping technique. Int. J. Sport Biomech. 1990, 6, 246–261. [Google Scholar] [CrossRef]
  21. Dapena, J. Biomechanical studies in the high jump and the implications to coaching. Track Field Q Rev. 1992, 92, 34–38. [Google Scholar]
  22. Lees, A.; Rojas, J.; Cepero, M.; Soto, V.; Gutierrez, M. How the free limbs are used by elite high jumpers in generating vertical velocity. Ergonomics 2000, 43, 1622–1636. [Google Scholar] [CrossRef] [PubMed]
  23. Greig, M.P.; Yeadon, M.R. The influence of touchdown parameters on the performance of a high jumper. J. Appl. Biomech. 2000, 16, 367–378. [Google Scholar] [CrossRef]
  24. Tan, J.C.C.; Yeadon, M.R. Why do high jumpers use a curved approach? J. Sports Sci. 2005, 23, 775–780. [Google Scholar] [CrossRef]
  25. Dapena, J.; Chung, C.S. Vertical and radial motions of the body during the take-off phase of high jumping. Med. Sci. Sports Exerc. 1988, 20, 290–302. [Google Scholar] [CrossRef]
  26. Hay, J.G. The Biomechanics of Sports Techniques, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
  27. Pavlovic, R. The differences of kinematic parameters high jump between male and female finalists World Championship Daegu, 2011. Turk. J. Kinesiol. 2017, 3, 60–69. [Google Scholar]
  28. Frutos, J.B.; Elvira, J.L.L.; Andrés, J.M.P. Diferencias de género en salto de altura según categorías de edad. Apunt. Educ. Fís. Deporte. 2013, 111, 62–69. [Google Scholar] [CrossRef]
  29. Bermejo, J.; Palao, J.M.; Elvira, J.L.L. Effect of age on high jump take-off biomechanics. Port. J. Sport Sci. 2011, 11 (Suppl. 2), 155–158. [Google Scholar]
  30. Laffaye, G. Fosbury flop: Predicting performance with a three-variable model. J. Strength Cond. Res. 2011, 25, 2143–2150. [Google Scholar] [CrossRef] [PubMed]
  31. Panoutsakopoulos, V. Junior triple jumpers: Kinematic differences between male and female. Mod. Athl. Coach 2009, 47, 7–13. [Google Scholar]
  32. Panoutsakopoulos, V.; Papaiakovou, G.; Kollias, I.A. A biomechanical analysis and assessment of the technique elements of the last strides, the touchdown and the takeoff of junior male and female long jumpers. Inq. Sport Phys. Edu. 2009, 7, 333–343. [Google Scholar]
  33. Kollias, I.A. Sources of error and their elimination in the use of DLT with the basic recording tools for the analysis of human body in motion. Exerc. Societ. J. Sport Sci. 1997, 18, 9–26. [Google Scholar]
  34. Plagenhoef, S. Patterns of Human Motion: A Cinematographic Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
  35. Winter, D.A.; Sidwall, H.D.; Hobson, D.A. Measurement and reduction of noise in kinematics of locomotion. J. Biomech. 1974, 7, 157–159. [Google Scholar] [CrossRef]
  36. Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates Publishers: Hillsdale, NJ, USA, 1988. [Google Scholar]
  37. Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
  38. Lenhard, W.; Lenhard, A. Hypothesis Tests for Comparing Correlations. Psychometrica 2014. Available online: https://www.psychometrica.de/correlation.html (accessed on 29 June 2025).
  39. Panoutsakopoulos, V.; Theodorou, A.; Kollias, I. Three-dimensional kinematic analysis of the technique of top Greek male high jumpers. Κινησιολογία-Βιολογική Κατεύθυνση 2014, 5, 71–84. [Google Scholar]
  40. Panoutsakopoulos, V.; Kollias, I. 3-D biomechanical analysis of women’s high jump. New Stud. Athl. 2012, 27, 31–48. [Google Scholar]
  41. Ritzdorf, W.; Conrad, A.; Loch, M. Intraindividual comparison of the jumps of Stefka Kostadinova at the II World Championships in Athletics Rome 1987 and the Games of the XXIV Olympiad Seoul 1988. New Stud. Athl. 1989, 4, 35–41. [Google Scholar]
  42. Watanabe, T. New methodological approach for distancing the takeoff point further from the bar when high jumping using the flop technique. Jpn. J. Phys. Educ. Hlth. Sport Sci. 2014, 59, 297–314. [Google Scholar] [CrossRef]
  43. Atta, I.I.; Bursais, A.K.; Alibrahim, M.S.; Alhumaid, M.M.; Hassan, A.K.; Frikha, M.; Al-Nuaim, A. Biomechanical determinants of elite high jump performance in Egypt: Part 2, the percentage contributions of biomechanical indicators and special factors to achievement level. J. Phys. Edu. Sport 2025, 25, 764–772. [Google Scholar] [CrossRef]
  44. Panoutsakopoulos, V.; Kotzamanidou, M.C.; Manou, V. Sex differences exist in the relationship between vertical jump performance biomechanical parameters and hamstring/quadriceps ratio in adolescent U18 track and field athletes. Sports 2024, 12, 295. [Google Scholar] [CrossRef] [PubMed]
  45. Malina, R.M.; Sławinska, T.; Ignasiak, Z.; Rożek, K.; Kochan, K.; Domaradzki, J.; Fugiel, J. Sex differences in growth and performance of track and field athletes 11–15 years. J. Hum. Kinet. 2010, 24, 79–85. [Google Scholar] [CrossRef]
  46. Rao, C.R.; Kishore, Y.; Rao, J.R. Biomechanical analysis of centre of mass height during the takeoff phase in fosbury flop high jump of national level participants. Int. J. Mod. Commun. Technol. Res. 2014, 2, 265758. [Google Scholar]
  47. Mateos-Padorno, C.; García-Manso, J.M.; Martínez-Patiño, M.J.; Valverde-Esteve, T. Analysis of effectiveness of free segment actions and antero-posterior and lateral body displacements during the take-off phase of high jump (flop style). Int. J. Perform. Anal. Sport 2019, 19, 14–27. [Google Scholar] [CrossRef]
  48. Atta, I.I.; Bursais, A.K.; Alibrahim, M.S.; Al-Nuaim, A. Biomechanical determinants of elite high jump performance in Egypt: Part 1-analysis of kinematic variables and performance. J. Phys. Edu. Sport 2024, 24, 1936–1944. [Google Scholar] [CrossRef]
  49. Adashevskiy, V.M.; Iermakov, S.S.; Marchenko, A.A. Biomechanics aspects of technique of high jump. Phys. Edu. Stud. 2013, 2, 11–18. [Google Scholar] [CrossRef]
  50. Tobe, N.; Kariyama, Y.; Hayashi, R.; Kigoshi, K.; Ogata, M. Characteristics of joint kinetics of the lower limb during take-off motion in high jump. Jpn. J. Phys. Educ. Health Sport Sci. 2019, 64, 625–635. [Google Scholar] [CrossRef]
  51. Zushi, A.; Tobe, N.; Zushi, K.; Yoshida, T. Assessment of takeoff execution ability in high jumpers by rebound jump. Jpn. J. Phys. Educ. Health Sport Sci. 2023, 68, 117–130. [Google Scholar] [CrossRef]
  52. Fujimori, T.; Sado, N. Mechanical properties of the gastrocnemius muscle-tendon unit in male athletic high jumpers. Physiol. Rep. 2025, 13, e70370. [Google Scholar] [CrossRef] [PubMed]
  53. Ae, M.; Nagahara, R.; Ohshima, Y.; Koyama, H.; Takamoto, M.; Shibayama, K. Biomechanical analysis of the top three male high jumpers at the 2007 World Championships in Athletics. New Stud. Athl. 2008, 23, 45–52. [Google Scholar]
  54. Laffaye, G. Le saut en hauteur en Fosbury et les facteurs de performance. Sci. Motr. 2001, 42, 3–15. [Google Scholar]
  55. Boden, E.; Braunstein, B.; Heinrich, K.; Sanno, M.; Stäudle, B.; Ritzdorf, W.; Brüggemann, G.-P.; Albracht, K.; Goldmann, J.-P. Leg- and joint stiffness in male elite high jump: The influence of stiffness on sports performance. ISBS Proc. Arch. 2017, 35, 748–750. [Google Scholar]
  56. Ljubičić, S. Kinematic analysis of high jump using the scissors technique. Stud. Sport 2024, 18, 173–182. [Google Scholar] [CrossRef]
  57. Sado, N.; Yoshioka, S.; Fukashiro, S. Non-extension movements inducing over half the mechanical energy directly contributing to jumping height in human running single-leg jump. J. Biomech. 2020, 113, 110082. [Google Scholar] [CrossRef] [PubMed]
  58. Fujimori, T.; Tobe, N.; Sado, N. Inter-joint differences exist in kinetic demand for performance in high jump. ISBS Proc. Arch. 2023, 41, 37. [Google Scholar]
  59. Toshihide, F.; Naoto, T.; Natsuki, S. Joint kinetic demand for performance in high jump. Sports Biomech. 2024, in press. [Google Scholar] [CrossRef] [PubMed]
  60. Mateos-Padorno, C.; García-Manso, J.M.; Fuentes García, J.P.; Martínez-Patiño, M.J. Kinematic analysis of the final stride approach in Spanish elite high jumpers. Int. J. Perform. Anal. Sport 2021, 21, 421–434. [Google Scholar] [CrossRef]
  61. Dapena, J. Mechanics of rotation in the Fosbury-flop. Med. Sci. Sports Exerc. 1980, 12, 45–53. [Google Scholar] [CrossRef] [PubMed]
  62. Sado, N.; Yoshioka, S.; Fukashiro, S. Curved approach in high jump induces greater jumping height without greater joint kinetic exertions than straight approach. Med. Sci. Sports Exerc. 2022, 54, 120–128. [Google Scholar] [CrossRef]
  63. Sado, N.; Yoshioka, S.; Fukashiro, S. Hip abductors and lumbar lateral flexors act as energy generators in running single-leg jumps. Int. J. Sports Med. 2018, 39, 1001–1008. [Google Scholar] [CrossRef]
  64. Blažević, I.; Antekolović, L.; Mejovšek, M. Variability of high jump kinematic parameters in longitudinal follow-up. Kinesiology 2006, 38, 63–71. [Google Scholar]
  65. Becker, J.; Wu, W.F. Integrating biomechanical and motor control principles in elite high jumpers: A transdisciplinary approach to enhancing sport performance. J. Sport Health Sci. 2015, 4, 341–346. [Google Scholar] [CrossRef]
  66. Goldacre, M.; Born, Z.; Mundt, M.; Millett, E.; Phillips, E.; Alderson, J. Pose estimation or manual digitising: Can automating technologies change the current in-field assessment of high jump? ISBS Proc. Arch. 2023, 41, 42. [Google Scholar]
  67. Christensen, B.; Zebas, C. A comparison of practice and competition approach velocities and the position of the top handhold at the pole plant in pole vaulters. In Proceedings of the 18th International Conference of Biomechanics in Sports, Hong Kong, China, 25–30 June 2000; Hong, Y., Johns, D.P., Sanders, R., Eds.; I.S.B.S: Hong Kong, China, 2000. [Google Scholar]
  68. Nicholson, G.; Epro, G.; Merlino, S.; Walker, J.; Bissas, A. Differences in run-up, take-off, and flight characteristics: Successful vs. unsuccessful high jump attempts at the IAAF World Championships. Front. Sports Act. Living 2024, 6, 1352725. [Google Scholar] [CrossRef]
Applsci 15 09382 g001
Figure 1. Schematic representation of the experimental setup.
Figure 1. Schematic representation of the experimental setup.
Applsci 15 09382 g001
Applsci 15 09382 g002
Figure 2. Schematic representation of the examined parameters. TP: the distance between the toes of the take-off leg and the respective upright post; VZ-TD: the vertical body center of mass (BCM) velocity at touchdown; VH-TD: the horizontal BCM velocity at touchdown; HTD: the BCM height at touchdown; VZ-TO: the vertical BCM velocity at take-off; VH-TO: the horizontal BCM velocity at take-off; H0: BCM take-off height; H1: the vertical BCM displacement from the time of take-off to the highest point of its trajectory; H2: the vertical distance between the crossbar and the highest point of the BCM trajectory; HMAX: the maximum height of the BCM trajectory; TB: the distance between the toes of the take-off leg and the center of the crossbar; S: the length of the last step; Sang: the direction of the step with respect to the longitudinal axis of the crossbar; LEGang: the inclination of the take-off leg at touchdown; TORang: the inclination of the torso at touchdown; KNEEang: the angle of the knee joint of the take-off leg; KNEEang-TO-SW: the angle of the knee joint of the swing leg at take-off.
Figure 2. Schematic representation of the examined parameters. TP: the distance between the toes of the take-off leg and the respective upright post; VZ-TD: the vertical body center of mass (BCM) velocity at touchdown; VH-TD: the horizontal BCM velocity at touchdown; HTD: the BCM height at touchdown; VZ-TO: the vertical BCM velocity at take-off; VH-TO: the horizontal BCM velocity at take-off; H0: BCM take-off height; H1: the vertical BCM displacement from the time of take-off to the highest point of its trajectory; H2: the vertical distance between the crossbar and the highest point of the BCM trajectory; HMAX: the maximum height of the BCM trajectory; TB: the distance between the toes of the take-off leg and the center of the crossbar; S: the length of the last step; Sang: the direction of the step with respect to the longitudinal axis of the crossbar; LEGang: the inclination of the take-off leg at touchdown; TORang: the inclination of the torso at touchdown; KNEEang: the angle of the knee joint of the take-off leg; KNEEang-TO-SW: the angle of the knee joint of the swing leg at take-off.
Applsci 15 09382 g002
Applsci 15 09382 g003
Figure 3. The components of the maximum height of the BCM trajectory (HMAX) as BCM height at the instant of take-off (H0), vertical BCM displacement from H0 to HMAX (H1), and vertical distance of the BCM from the middle of the crossbar at the instant of HMAX (H2); *: p < 0.05.
Figure 3. The components of the maximum height of the BCM trajectory (HMAX) as BCM height at the instant of take-off (H0), vertical BCM displacement from H0 to HMAX (H1), and vertical distance of the BCM from the middle of the crossbar at the instant of HMAX (H2); *: p < 0.05.
Applsci 15 09382 g003
Table 1. Results (mean ± standard deviation) for the spatio-temporal parameters of the last step and the take-off phase and their correlation with the official result.
Table 1. Results (mean ± standard deviation) for the spatio-temporal parameters of the last step and the take-off phase and their correlation with the official result.
ParameterMen (n = 21)r (p)-MenWomen (n = 21)r (p)-Womentpd [95% Confidence Interval]
S (m)1.72 ± 0.200.06 (0.800)1.58 ± 0.18 *0.76 (<0.001) ‡2.3950.0210.74 medium [0.11, 1.36]
Sang (deg)29.33 ± 5.270.51 (0.108)21.91 ± 7.63 *0.16 (0.623)2.6870.0141.12 large [0.23, 2.00]
TP (m)0.51 ± 0.400.29 (0.207)0.49 ± 0.20−0.27 (0.232)0.1160.9080.36 small [−0.57, 0.64]
TB (m)0.77 ± 0.160.59 (0.011) ‡0.67 ± 0.15 *0.29 (0.210)2.0540.0470.66 medium [0.01, 1.30]
HTD (m)0.92 ± 0.05−0.13 (0.564)0.88 ± 0.05 *−0.07 (0.759)2.0640.0460.64 medium [0.01, 1.25]
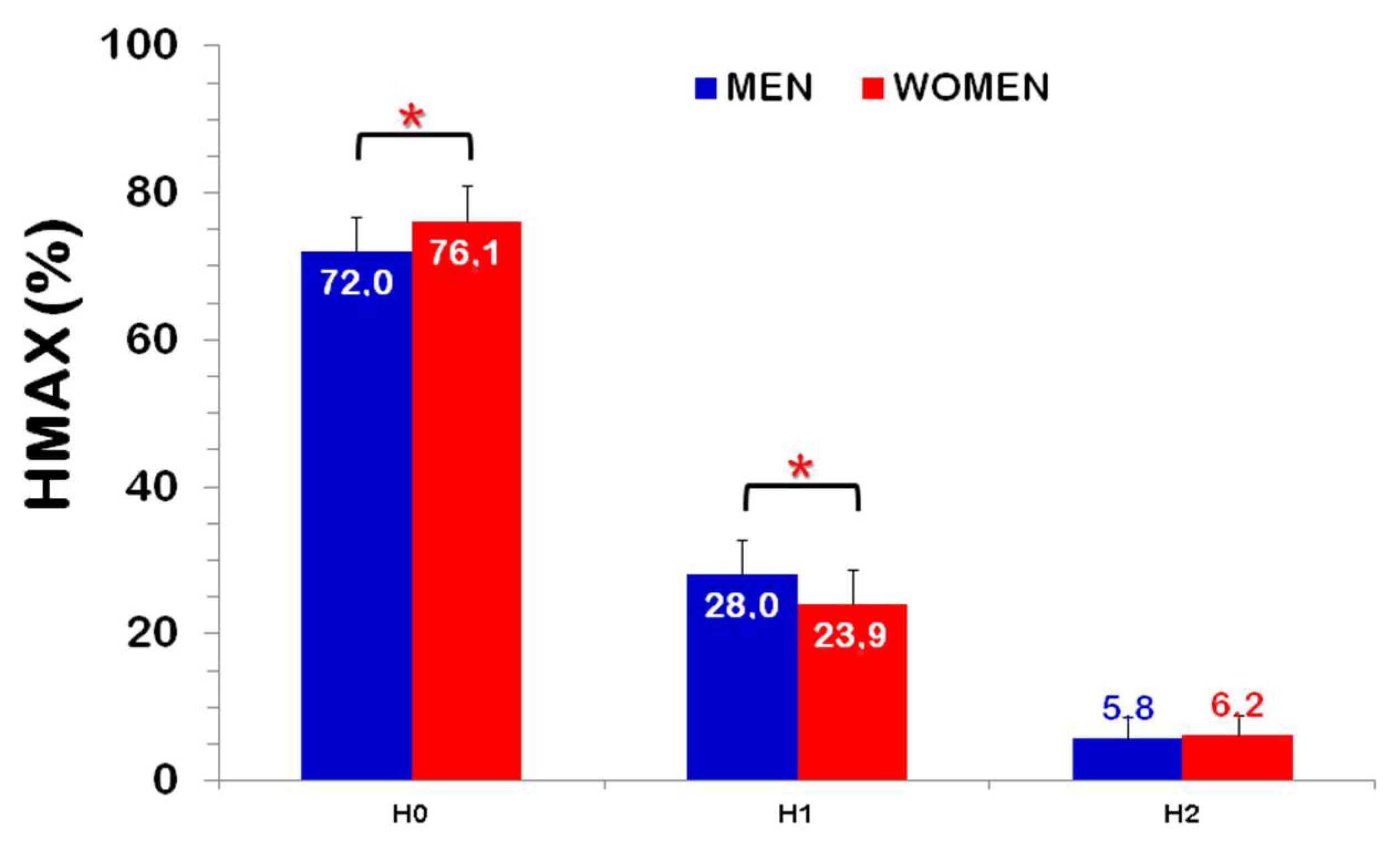
H0 (m)1.32 ± 0.070.49 (0.025) ‡1.25 ± 0.06 *0.33 (0.149)3.3340.0021.03 large [0.38, 1.67]
HMAX (m)1.84 ± 0.140.96 (<0.001) ‡1.65 ± 0.10 *0.91 (<0.001) ‡5.241<0.0011.62 large [0.91, 2.31]
H1 (m)0.41 ± 0.070.61 (0.004) ‡0.37 ± 0.070.34 (0.130)1.7750.0840.55 medium [−0.07, 1.66]
H2 (m)0.11 ± 0.05−0.63 (0.002) ‡0.10 ± 0.04−0.39 (0.085)0.1670.8680.05 trivial [−0.55, 0.66]
TIME (s)0.180 ± 0.0220.30 (0.180)0.172 ± 0.016−0.28 (0.220)1.3440.1870.42 small [−0.20, 1.02]
*: significant (p < 0.05) sex difference; ‡: significant (p < 0.05) correlation with the official result.
Table 2. Results (mean ± standard deviation) for the body center of mass velocity and the take-off angle and their correlation with the official result.
Table 2. Results (mean ± standard deviation) for the body center of mass velocity and the take-off angle and their correlation with the official result.
ParameterMen (n = 21)r (p)-MenWomen (n = 21)r (p)-Womentpd [95% Confidence Interval]
VH-TO-1L (m/s)6.73 ± 0.510.33 (0.319)5.98 ± 0.58 *0.55 (0.062)3.2700.0041.37 large [0.44, 2.27]
VH-TD (m/s)6.46 ± 0.600.32 (0.343)5.70 ± 0.71 *0.65 (0.021) ‡2.7420.0061.15 large [0.25, 2.02]
VH-TO (m/s)3.98 ± 0.31−0.68 (0.021) ‡3.71 ± 0.420.05 (0.869)1.7930.0870.73 medium [−0.11, 1.56]
VZ-TD (m/s)−0.24 ± 0.20−0.38 (0.252)0.01 ± 0.24 *0.58 (0.048) ‡2.7460.0121.15 large [0.25, 2.02]
VZ-TO (m/s)3.57 ± 0.290.71 (0.015) ‡3.06 ± 0.43 *0.75 (0.003) ‡3.3870.0031.39 large [0.48, 2.28]
AngPr (deg)41.83 ± 3.570.85 (<0.001) ‡41.28 ± 6.120.28 (0.348)0.2620.7960.11 trivial [−0.70, 0.91]
*: significant (p < 0.05) sex difference; ‡: significant (p < 0.05) correlation with the official result.
Table 3. Results (mean ± standard deviation) for the angular kinematic parameters and their correlation with the official result.
Table 3. Results (mean ± standard deviation) for the angular kinematic parameters and their correlation with the official result.
ParameterMen (n = 21)r (p)-MenWomen (n = 21)r (p)-Womentpd [95% Confidence Interval]
KNEEang-TD (deg)157.19 ± 9.380.33 (0.146)157.86 ± 8.760.04 (0.881)0.2420.8100.08 trivial [−0.68, 0.53]
KNEEang-MKF (deg)135.48 ± 9.08−0.25 (0.344)134.70 ± 6.520.16 (0.508)0.2880.7750.10 trivial [−0.57, 0.77]
KNEEang-TO (deg)171.39 ± 5.180.05 (0.819)171.72 ± 4.29−0.15 (0.518)0.2300.8190.07 trivial [−0.68, 0.53]
KNEEang-TO-SW (deg)98.95 ± 22.160.19 (0.807)77.08 ± 13.66 *0.62 (0.003) ‡2.6640.0141.45 large [0.29, 2.59]
ROM-TD-MKF (deg)−23.44 ± 11.02−0.26 (0.323)−23.52 ± 6.810.21 (0.383)0.0220.9820.08 trivial [−0.66, 0.67]
ROM-MKF-TO (deg)36.01 ± 8.83−0.33 (0.209)36.32 ± 7.010.58 (0.048)0.1150.9090.04 trivial [−0.70, 0.63]
TORSOang-TD (deg)86.16 ± 7.10−0.18 (0.434)85.14 ± 5.750.22 (0.250)0.5090.6140.16 trivial [−0.45, 0.64]
LEGang-TD (deg)58.73 ± 4.05−0.26 (0.317)62.62 ± 4.74 *−0.60 (0.007) ‡2.6300.0130.88 large [0.19, 1.56]
*: significant (p < 0.05) sex difference; ‡: significant (p < 0.05) correlation with official result.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Panoutsakopoulos, V. Sex Differences in the High Jump Kinematics of U18 Adolescent Athletes. Appl. Sci. 2025, 15, 9382. https://doi.org/10.3390/app15179382

AMA Style

Panoutsakopoulos V. Sex Differences in the High Jump Kinematics of U18 Adolescent Athletes. Applied Sciences. 2025; 15(17):9382. https://doi.org/10.3390/app15179382

Chicago/Turabian Style

Panoutsakopoulos, Vassilios. 2025. "Sex Differences in the High Jump Kinematics of U18 Adolescent Athletes" Applied Sciences 15, no. 17: 9382. https://doi.org/10.3390/app15179382

APA Style

Panoutsakopoulos, V. (2025). Sex Differences in the High Jump Kinematics of U18 Adolescent Athletes. Applied Sciences, 15(17), 9382. https://doi.org/10.3390/app15179382

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop