Structural Optimization of a Pipeline Savonius Hydro Turbine Based on Broad Learning
Abstract
1. Introduction
2. Numerical Simulation Methodology
2.1. Design Parameters
2.2. Computational Domain
2.3. Turbulence Model and Boundary Conditions
2.4. Mesh and Independence Verification
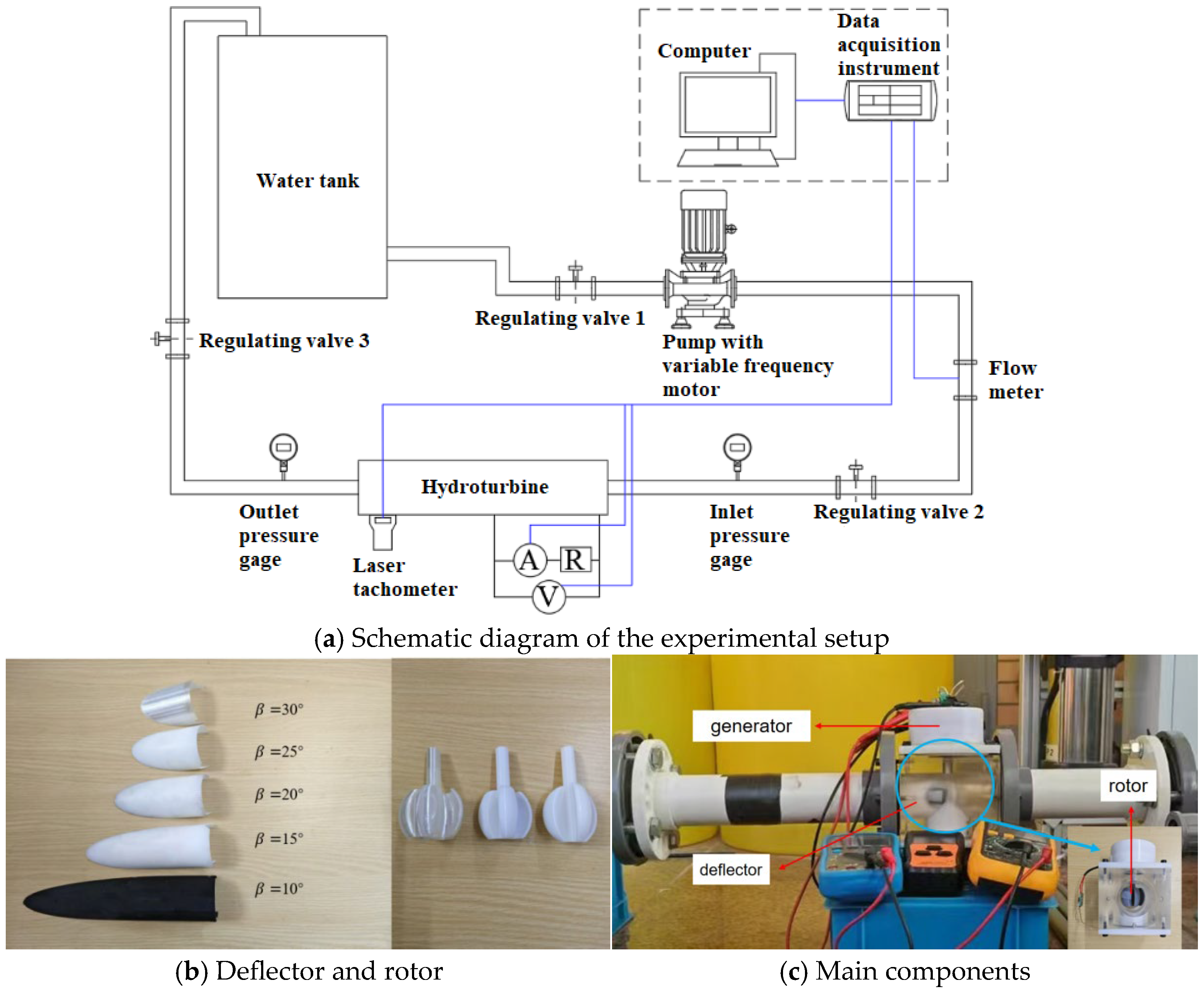
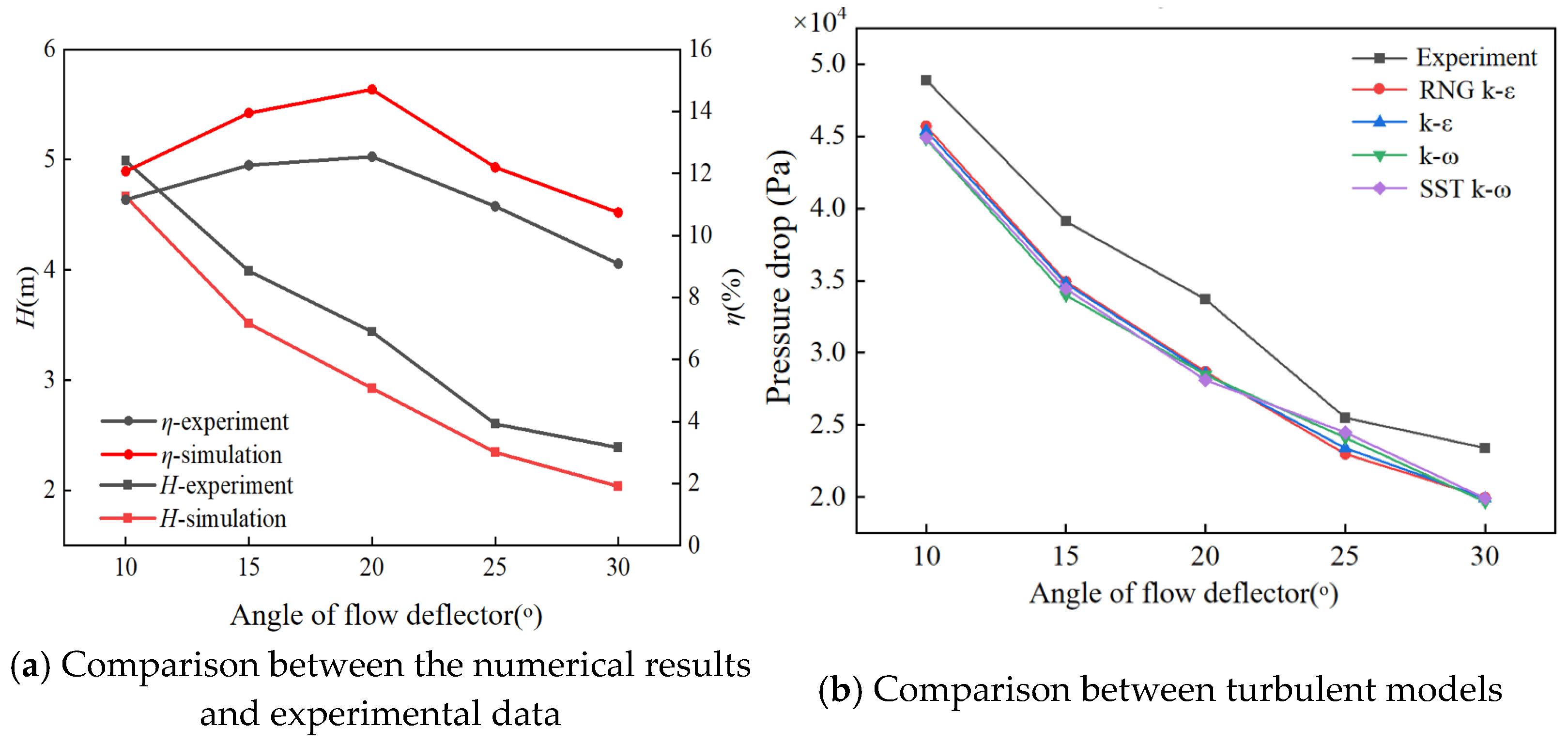
2.5. Experiment and Numerical Model Reliability
3. Results
3.1. Single-Factor Analysis
3.1.1. Effects of Deflector Angle
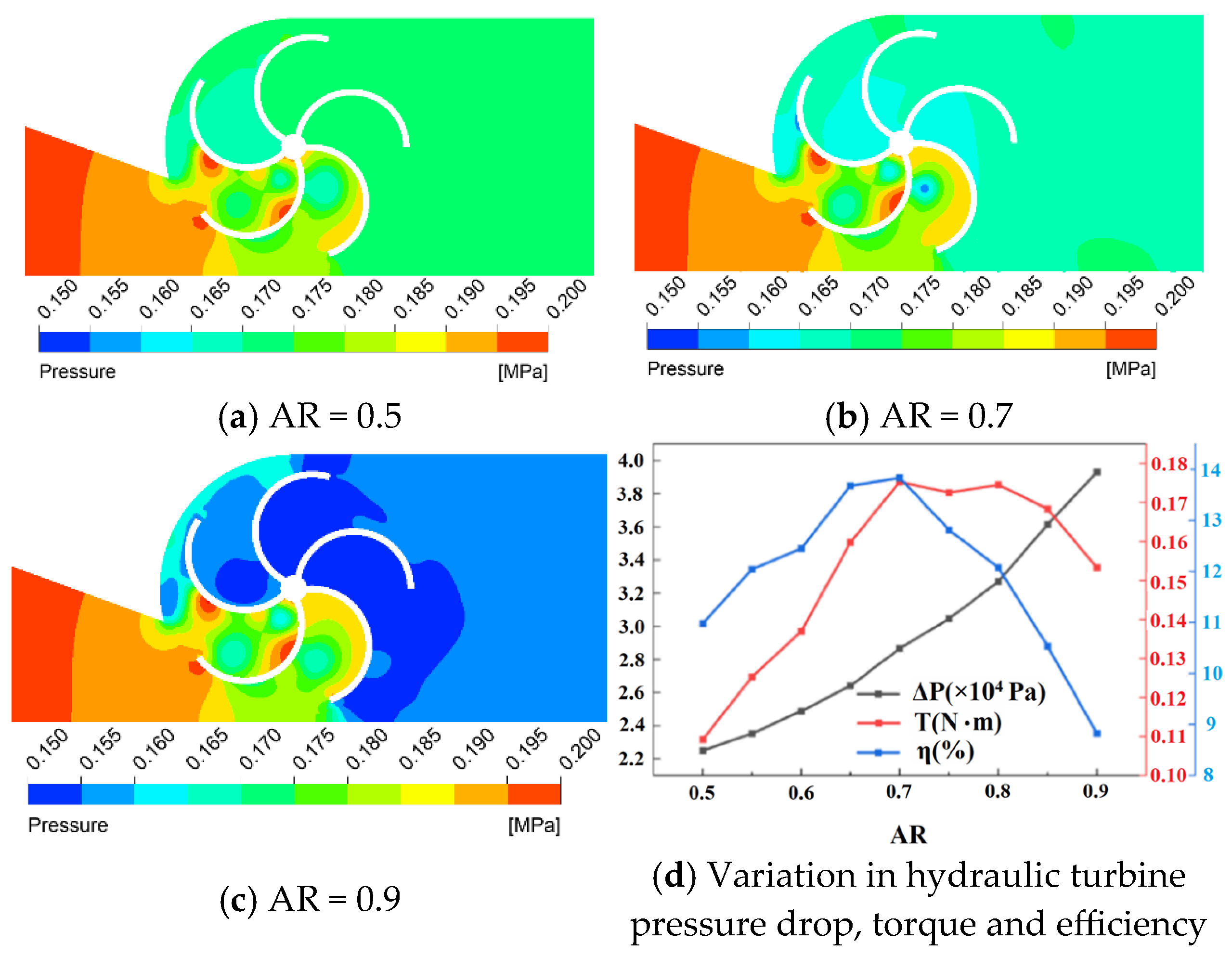
3.1.2. Effects of Aspect Ratio
3.1.3. Effects of Blade Number
3.2. Optimization of Structure Parameters
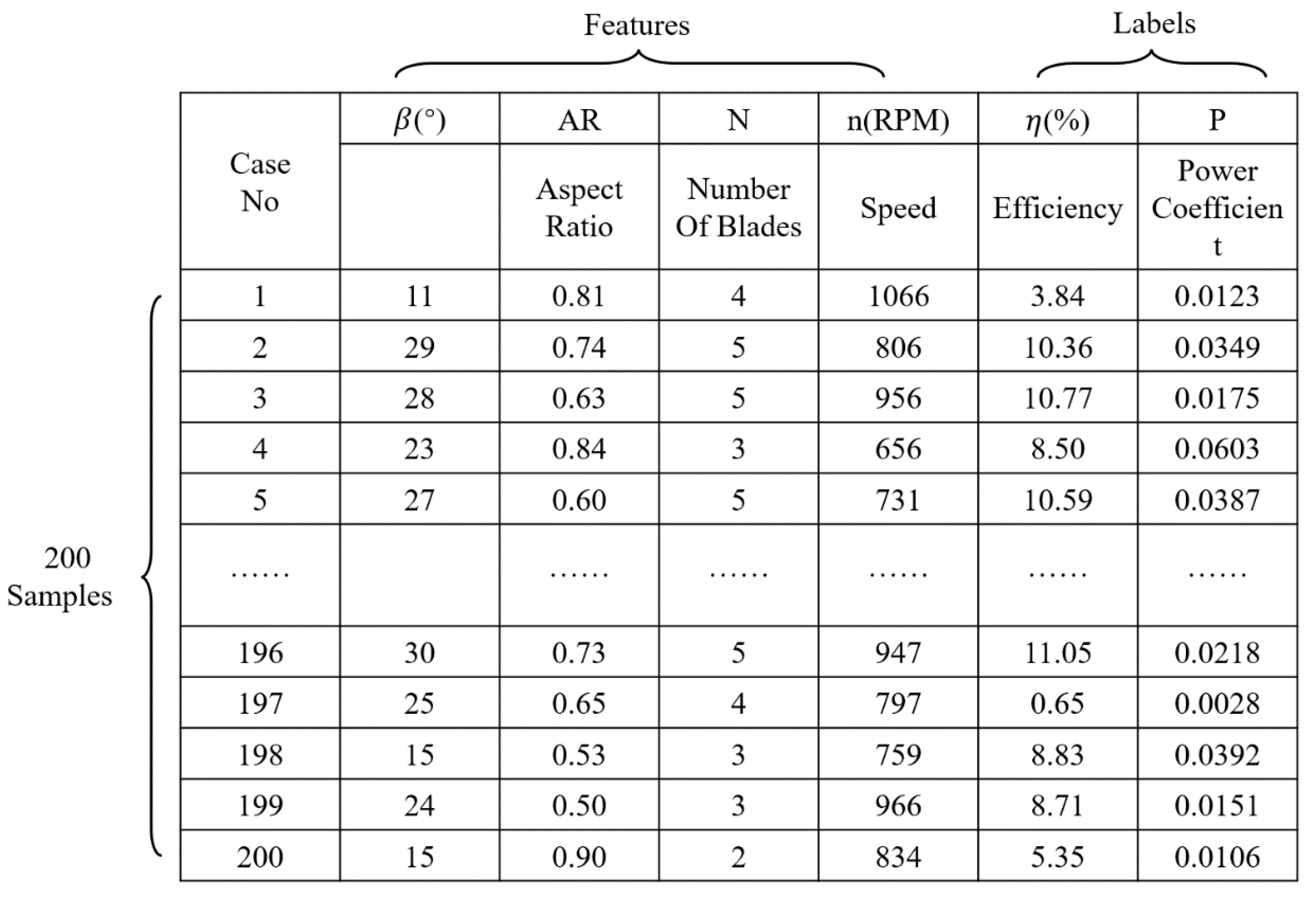
3.2.1. Database Establishment
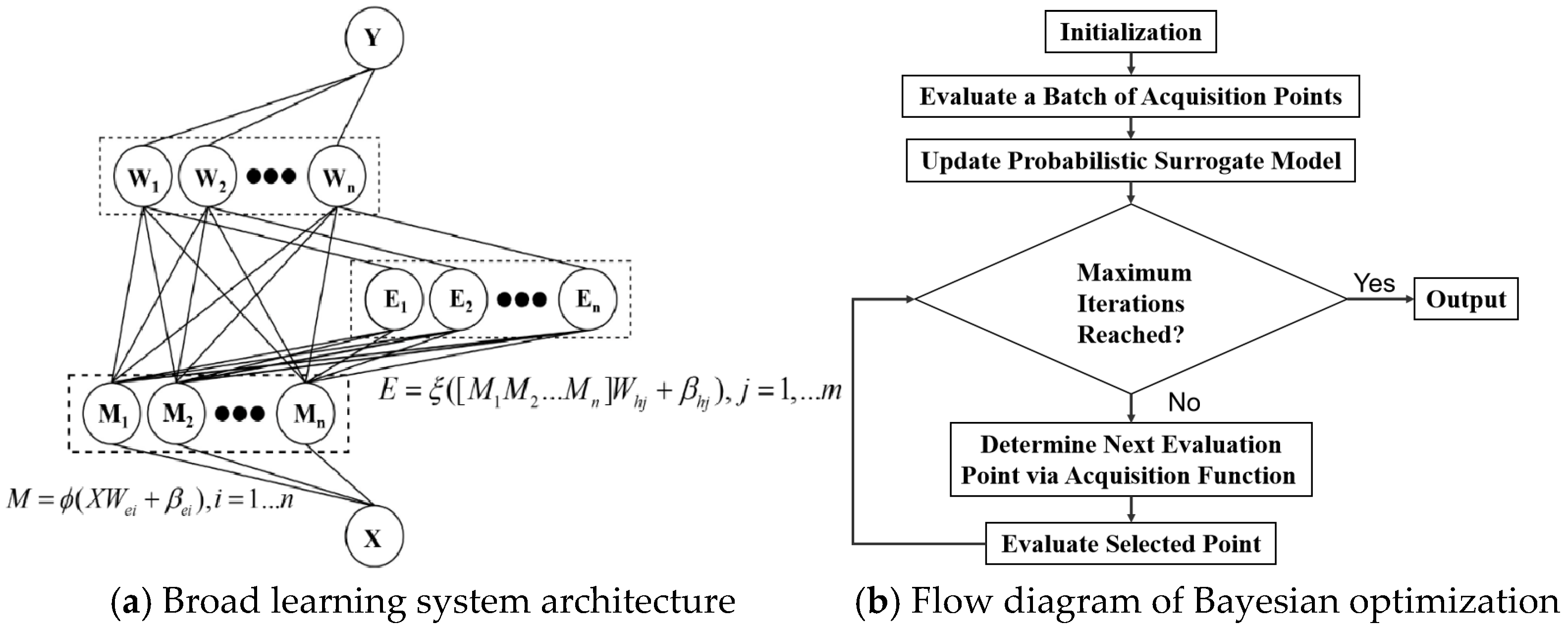
3.2.2. Model Training and Evaluation
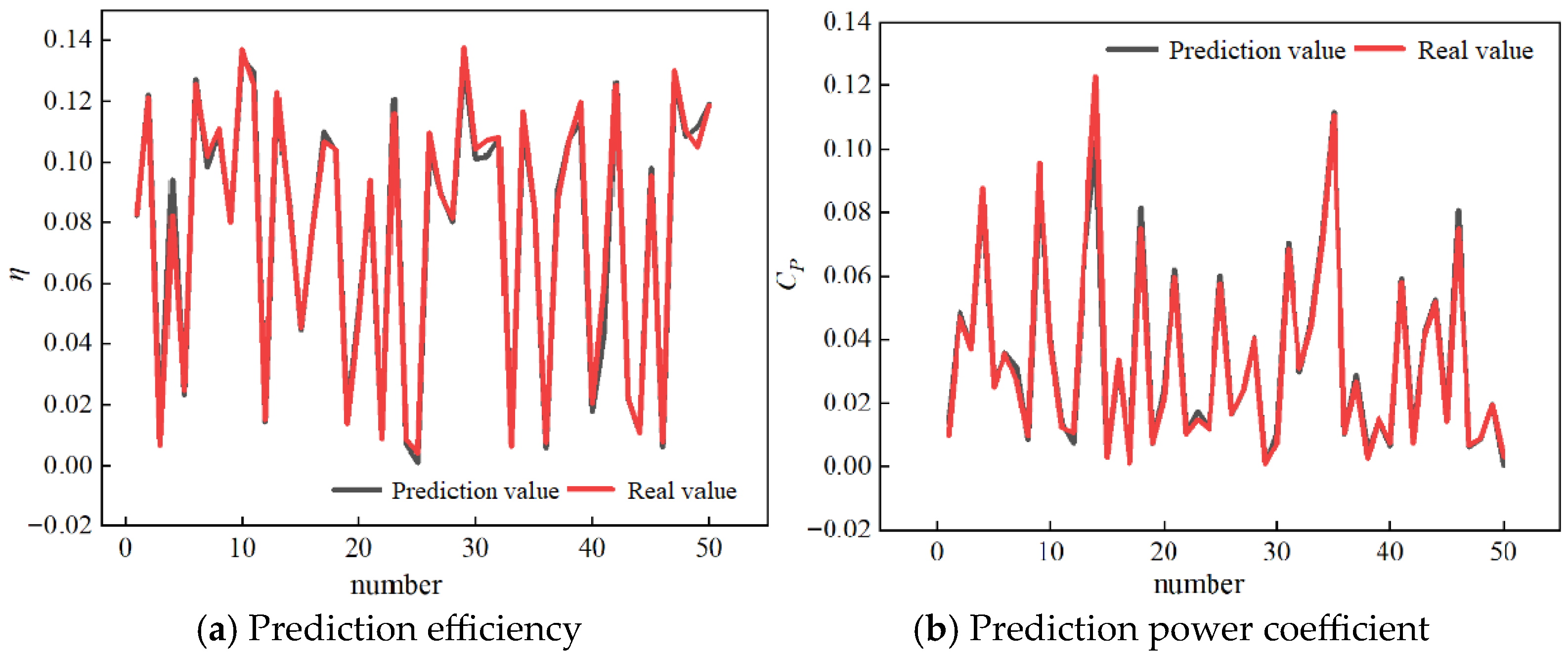
3.2.3. Analysis and Validation of Optimization Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jamil, F.; Ibrahim, M.; Ullah, I.; Kim, S.; Kahng, H.K.; Kim, D.H. Optimal smart contract for autonomous greenhouse environment based on IoT blockchain network in agriculture. Comput. Electron. Agric. 2022, 192, 106573. [Google Scholar] [CrossRef]
- Darko, R.O.; Yuan, S.; Hong, L.; Liu, J.; Yan, H. Irrigation, a productive tool for food security—A Review. Acta Agric. Scand. Sect. B—Soil Plant Sci. 2016, 66, 191–206. [Google Scholar] [CrossRef]
- Zhang, C.Z.; Yan, H.; Ni, Y.X.; Akhlaq, M.; Zhou, J.N.; Xue, R. Effect of micro-spray on plant growth and chlorophyll fluorescence parameter of tomato under high temperature condition in a greenhouse. Sci. Hortic. 2022, 306, 111441. [Google Scholar] [CrossRef]
- Tang, L.Y.; Tang, S.Q.; Tang, Y.; Yan, H.F. Performance experiment and numerical prediction on the optimization design of the micro-sized water turbine for the hose reel irrigator. Int. J. Agric. Biol. Eng. 2018, 11, 108–115. [Google Scholar] [CrossRef]
- Penzotti, G.; Lodi Rizzini, D.; Caselli, S. A planning strategy for sprinkler-based variable rate irrigation. Comput. Electron. Agric. 2023, 212, 108126. [Google Scholar] [CrossRef]
- Chen, R.; Li, H.; Wang, J.; Guo, X.; Xiang, Y. Evaluating soil water movement and soil water content uniformity under sprinkler irrigation with different soil texture and irrigation uniformity using numerical simulation. J. Hydrol. 2023, 626, 130356. [Google Scholar] [CrossRef]
- Lakhiar, I.A.Z.; Wang, C.G.; He, B.; Hao, B.B.; Han, Y.J.; Wang, B.Y.; Bao, R.X.; Syed, T.N.; Chauhdary, J.N.; Rakibuzzaman, M. A review of precision irrigation water-saving technology under changing climate for enhancing water use efficiency, crop yield, and environmental footprints. Agriculture 2024, 14, 1141. [Google Scholar] [CrossRef]
- Azevedo, J.A.R.; Santos, F.E.S. Energy harvesting from wind and water for autonomous wireless sensor nodes. IET Circuits Devices Syst. 2012, 6, 413–420. [Google Scholar] [CrossRef]
- Mysorewala, M.F.; Cheded, L.; Aliyu, A. Review of energy harvesting techniques in wireless sensor-based pipeline monitoring networks. Renew. Sustain. Energy Rev. 2022, 157, 112012. [Google Scholar] [CrossRef]
- Karray, F.; Garcia-Ortiz, A.; Jmal, M.W.; Obeid, A.M.; Abid, M. EARNPIPE: A testbed for smart water pipeline monitoring using wireless sensor network. Procedia Comput. Sci. 2016, 96, 285–294. [Google Scholar] [CrossRef]
- Fassahat, A.M.; Qureshi, U.; Tuncay, K. A method to integrate energy harvesters into wireless sensor nodes for embedded in pipe monitoring applications. In Proceedings of the 5th International Conference on Energy Aware Computing Systems & Applications, Cairo, Egypt, 24–26 March 2015. [Google Scholar]
- Tian, W.L.; Song, B.W.; Mao, Z.Y. Conceptual design and numerical simulations of a vertical axis water turbine used for underwater mooring platforms. Int. J. Nav. Archit. Ocean. 2013, 5, 625–634. [Google Scholar]
- Abdollahzadeh, M.; Zhu, Y.; Bayatsarmadi, B.; Vepsäläinen, M.; Razmjou, A.; Murugappan, K.; Rodopoulos, T.; Asadnia, M. Portable multiplexed ion-selective sensor for long-term and continuous irrigation water quality monitoring. Comput. Electron. Agric. 2024, 227, 109455. [Google Scholar] [CrossRef]
- Innocenti, A.; Pazzi, V.; Napoli, M.; Ciampalini, R.; Orlandini, S.; Fanti, R. Electrical resistivity tomography: A reliable tool to monitor the efficiency of different irrigation systems in horticulture field. J. Appl. Geophys. 2024, 230, 105527. [Google Scholar] [CrossRef]
- Vandôme, P.; Leauthaud, C.; Moinard, S.; Sainlez, O.; Mekki, I.; Zairi, A.; Belaud, G. Making Technological innovations accessible to agricultural water management: Design of a low-cost wireless sensor network for drip irrigation monitoring in Tunisia. Smart Agric. Technol. 2023, 4, 100227. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.X.; Liu, C.P.; Lau, C.H.; Lo, M. A novel vertical axis water turbine for power generation from water pipelines. Energy 2013, 54, 184–193. [Google Scholar] [CrossRef]
- Menet, J.L. A double-step Savonius rotor for local production of electricity: A design study. Renew. Energy 2004, 29, 1843–1862. [Google Scholar] [CrossRef]
- Paraschivoiu, I. Wind Turbine Design: With Emphasis on Darrieus Concept; Presses inter Polytechnique: Montréal, QC, Canada, 2002. [Google Scholar]
- Khan, M.N.I.; Iqbal, T.; Hinchey, M.; Masek, V. Performance of Savonius rotor as a water current turbine. J. Ocean. Technol. 2009, 4, 71–83. [Google Scholar]
- Kumar, A.; Saini, R.P. Performance parameters of Savonius type hydrokinetic turbine: A review. Renew. Sustain. Energy Rev. 2016, 64, 289–310. [Google Scholar] [CrossRef]
- Kamoji, M.A.; Kedare, S.B.; Prabhu, S.V. Experimental investigations on single stage, two stage and three stage conventional Savonius rotor. Int. J. Energy Res. 2008, 32, 877–895. [Google Scholar] [CrossRef]
- Golecha, K.; Eldho, T.I.; Prabhu, S.V. Influence of the deflector plate on the performance of modified Savonius water turbine. Appl. Energy 2011, 88, 3207–3217. [Google Scholar] [CrossRef]
- Rehman, M.U.; Ali, Z. Performance improvement of Savonius hydrokinetic turbine using upstream crescent shape deflector. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 3. [Google Scholar] [CrossRef]
- Payambarpour, S.A.; Najafi, A.F.; Magagnato, F. Investigation of deflector geometry and turbine aspect ratio effect on 3D modified in-pipe hydro Savonius turbine: Parametric study. Renew. Energy 2020, 148, 44–59. [Google Scholar] [CrossRef]
- Lv, K.; Xie, Y.; Zhang, X.; Wang, Y. Development of Savonius rotors integrated into control valves for energy harvesting. Sustainability 2020, 12, 8579. [Google Scholar] [CrossRef]
- Thiyagaraj, J.; Rahamathullah, I.; Anbuchezhiyan, G.; Barathiraja, R.; Ponshanmugakumar, A. Influence of blade numbers, overlap ratio and modified blades on performance characteristics of the Savonius hydro-kinetic turbine. Mater. Today Proc. 2021, 46, 4047–4053. [Google Scholar] [CrossRef]
- Talukdar, P.K.; Sardar, A.; Kulkarni, V.; Saha, U.K. Parametric analysis of model Savonius hydrokinetic turbines through experimental and computational investigations. Energy Convers. Manag. 2018, 158, 36–49. [Google Scholar] [CrossRef]
- Sobczak, K. Numerical investigations of an influence of the aspect ratio on the Savonius rotor performance. J. Phys. Conf. Ser. 2018, 1101, 012034. [Google Scholar] [CrossRef]
- Saad, A.S.; El-Sharkawy, I.I.; Ookawara, S.; Ahmed, M. Performance enhancement of twisted-bladed Savonius vertical axis wind turbines. Energy Convers. Manag. 2020, 209, 112673. [Google Scholar] [CrossRef]
- Payambarpour, S.A.; Najafi, A.F.; Magagnato, F. Investigation of blade number effect on hydraulic performance of in-pipe hydro Savonius turbine. Int. J. Rotating Mach. 2019, 2019, 8394191. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Guo, X.; Lou, C.; Shen, Z.; Chen, J.; Du, J. Development of inline hydroelectric generation system from municipal water pipelines. Energy 2018, 144, 535–548. [Google Scholar] [CrossRef]
- Abdelaziz, K.R.; Nawar, M.A.; Ramadan, A.; Attai, Y.A.; Mohamed, M.H. Performance assessment of a modified of Savonius rotor: Impact of sine and conical blade profiles. Energy 2023, 272, 127172. [Google Scholar] [CrossRef]
- Salleh, M.B.; Kamaruddin, N.M. Power Performance and flow structure analysis of a deflector-augmented Savonius hydrokinetic turbine under variable flow speeds. Ocean. Eng. 2025, 325, 120789. [Google Scholar] [CrossRef]
- Ismail, M.A.; Othman, A.K.; Zen, H. Numerical investigation of rotational speed on pump as turbine for microhydro applications. Appl. Mech. Mater. 2016, 833, 11–18. [Google Scholar] [CrossRef]
- Hasanzadeh, N.; Payambarpour, S.A.; Najafi, A.F.; Magagnato, F. Investigation of in-pipe drag-based turbine for distributed hydropower harvesting: Modeling and optimization. J. Clean. Prod. 2021, 298, 126710. [Google Scholar] [CrossRef]
- Zuo, K.; Ye, Z.; Bu, S.; Yuan, X.; Zhang, W. Fast simulation of airfoil flow field via deep neural network. Aerosp. Sci. Technol. 2024, 150, 109207. [Google Scholar] [CrossRef]
- Huang, Z.; Li, T.; Huang, K.; Ke, H.; Lin, M.; Wang, Q. Predictions of flow and temperature fields in a T-Junction based on dynamic mode decomposition and deep learning. Energy 2022, 261, 125228. [Google Scholar] [CrossRef]
- Xu, M.; Fan, B.; Lin, R.; Lin, R.; Wu, X.; Zheng, S.; Gu, Y.; Mou, J. Advances in the application of intelligent algorithms to the optimization and control of hydrodynamic noise: Improve energy efficiency and system optimization. Appl. Sci. 2025, 15, 2084. [Google Scholar] [CrossRef]
- Li, Q.; Wan, R.; Wu, Z.; Yan, Y.; Zhang, X. Intelligent analysis of flow field in cleaning chamber for combine harvester based on YOLOv8 and reasoning mechanism. Appl. Sci. 2025, 15, 2200. [Google Scholar] [CrossRef]
- Gong, L.; Chen, Y. Machine learning-enhanced IoT and wireless sensor networks for predictive analysis and maintenance in wind turbine systems. Int. J. Intell. Netw. 2024, 5, 133–144. [Google Scholar]
- Jin, J.; Liu, Z.; Chen, C.L.P. Discriminative graph regularized broad learning system for image recognition. Sci. China Inform. Sci. 2018, 61, 112209. [Google Scholar] [CrossRef]
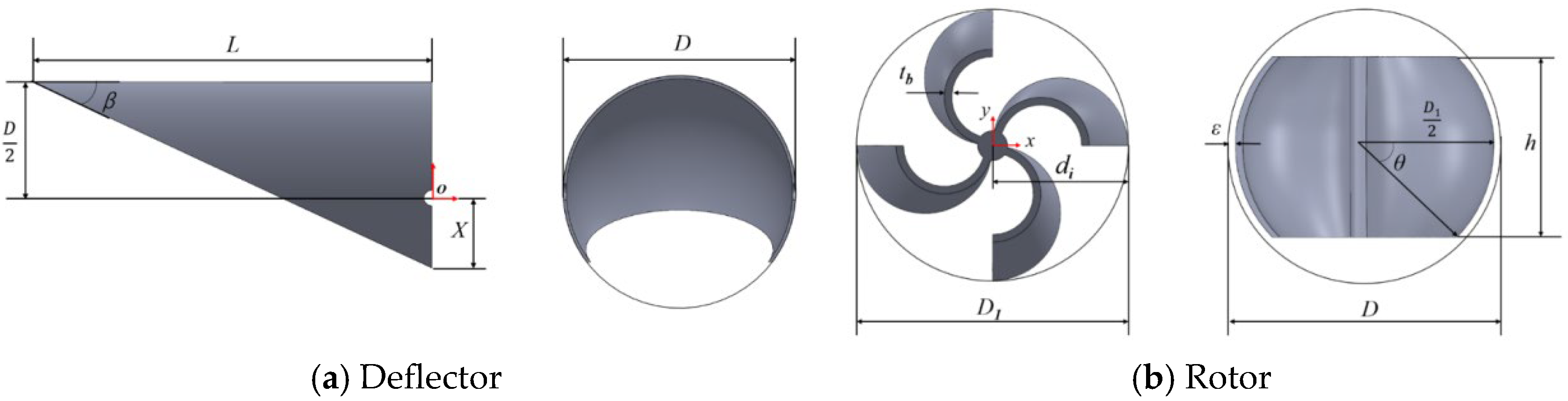


| Factor | Ref. | Value Range | Optimal Value | Pipe Diameter | Working Condition | η/Cp |
|---|---|---|---|---|---|---|
| Leading Component | [16] | Vertical and slanted block | Slanted block with eye-shaped opening | = 100 mm | = 50 kPa | = 15.8% |
| [23] | Crescent shape | 30° | Water speed 0.48 m/s | |||
| [24] | 10–40 | 20° | = 100 mm | = 20 kPa, n = 50 rad/s | = 16.2% | |
| Aspect Ratio | [24] | 0.4–0.9 | 0.9 | = 100 mm | = 30 kPa, n = 50 rad/s | = 10.3% |
| [25] | 0.8–0.9 | 0.8 | = 100 mm | Water speed 2 m/s | = 8.65% | |
| Blade Number | [16] | 3–24 | 12 | = 100 mm | = 50 kPa | = 15.8% |
| [30] | 2–10 | 5 | = 100 mm | = 20 kPa, n = 50 rad/s | = 28.2% | |
| [26] | 2–6 | 2 | 0.3 m × 0.3 m | Water speed 0.8 m/s | = 0.105 | |
| [31] | 3, 6, 9, 12 | 12 | = 250 mm | Water speed 1.5 m/s | = 6.5% | |
| Blade Shape | [27] | Oval semicircle | Semicircle | 2.5 m × 1.5 m | Water speed 0.8 m/s | |
| [32] | Sine semicircle cone | Cone | \ | Wind speed 9 m/s |
| Parameter | Symbol | Value |
|---|---|---|
| Rotor OD (mm) | D1 | 54 |
| Pipe ID (mm) | D | 60 |
| Clearance of rotor blade and pipe inner wall (mm) | ε | 3 |
| Rotor height (mm) | h | 27/29.7/32.4/35.1/37.8/ 40.5/43.2/45.9/48.6 |
| The angle between the upper and lower end faces of the rotor and the middle section at the center of the rotor (°) | θ | - |
| Blade thickness (mm) | tb | 3 |
| Blade diameter at any section of rotor blade axial direction | di | - |
| Deflector length | L | 272.4/179.2/132.0/103.0/83.2 |
| Distance of the deflector across the center plane | X | 18 |
| Deflector angle (°) | β | 10/15/20/25/30 |
| Blockage coefficient | 0.8 |
| Parameter | (°) | AR | N | N (rpm) |
|---|---|---|---|---|
| Range of value | 10–30 | 0.5–0.9 | 2–5 | 600–1200 |
| Search Target | Value | Angle of Diversion (°) | Aspect Ratio | Blade Number | Rotational Speed (rpm) |
|---|---|---|---|---|---|
| 0.2138 | 10 | 0.775 | 3 | 1098 | |
| 0.1859 | 10 | 0.9 | 3 | 600 |
| Optimum Parameter | (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Angle of Diversion (°) | Aspect Ratio | Blade Number | Rotational Speed (rpm) | ||||||
| 10 | 0.775 | 3 | 1098 | 0.2138 | 0.2168 | 1.383 | / | / | / |
| 10 | 0.9 | 3 | 600 | / | / | / | 0.1859 | 0.1843 | 0.868 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Hu, J.; Zhang, Y.; Yu, H.; Shen, W.; Xu, Y.; Zheng, J. Structural Optimization of a Pipeline Savonius Hydro Turbine Based on Broad Learning. Appl. Sci. 2025, 15, 9181. https://doi.org/10.3390/app15169181
Liu X, Hu J, Zhang Y, Yu H, Shen W, Xu Y, Zheng J. Structural Optimization of a Pipeline Savonius Hydro Turbine Based on Broad Learning. Applied Sciences. 2025; 15(16):9181. https://doi.org/10.3390/app15169181
Chicago/Turabian StyleLiu, Xingxiang, Jing Hu, Yao Zhang, He Yu, Wenfeng Shen, Yiming Xu, and Jieqing Zheng. 2025. "Structural Optimization of a Pipeline Savonius Hydro Turbine Based on Broad Learning" Applied Sciences 15, no. 16: 9181. https://doi.org/10.3390/app15169181
APA StyleLiu, X., Hu, J., Zhang, Y., Yu, H., Shen, W., Xu, Y., & Zheng, J. (2025). Structural Optimization of a Pipeline Savonius Hydro Turbine Based on Broad Learning. Applied Sciences, 15(16), 9181. https://doi.org/10.3390/app15169181






