Numerical Study on Tree Belt Impact on Wind Shear on Agricultural Land
Abstract
1. Introduction
2. Methods
2.1. Experimental Setup
2.2. Numerical Method
2.2.1. Computational Domain and Grid
2.2.2. Turbulence Modeling
2.2.3. Boundary Conditions
- u* = friction velocity (m/s),
- z0 = aerodynamic terrain roughness (m).
2.2.4. Modeling the Momentum Sink
2.2.5. Discretization Schemes
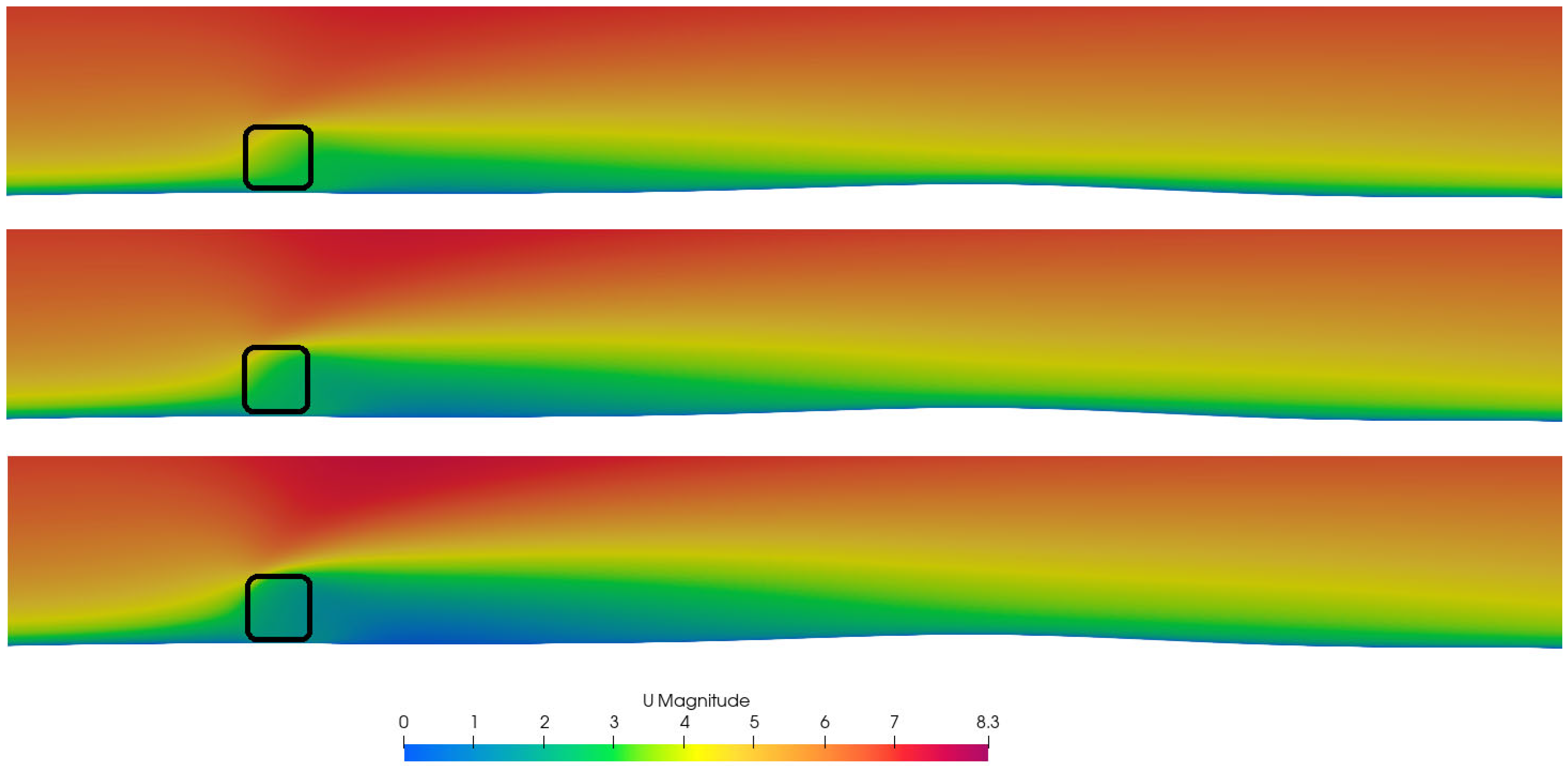
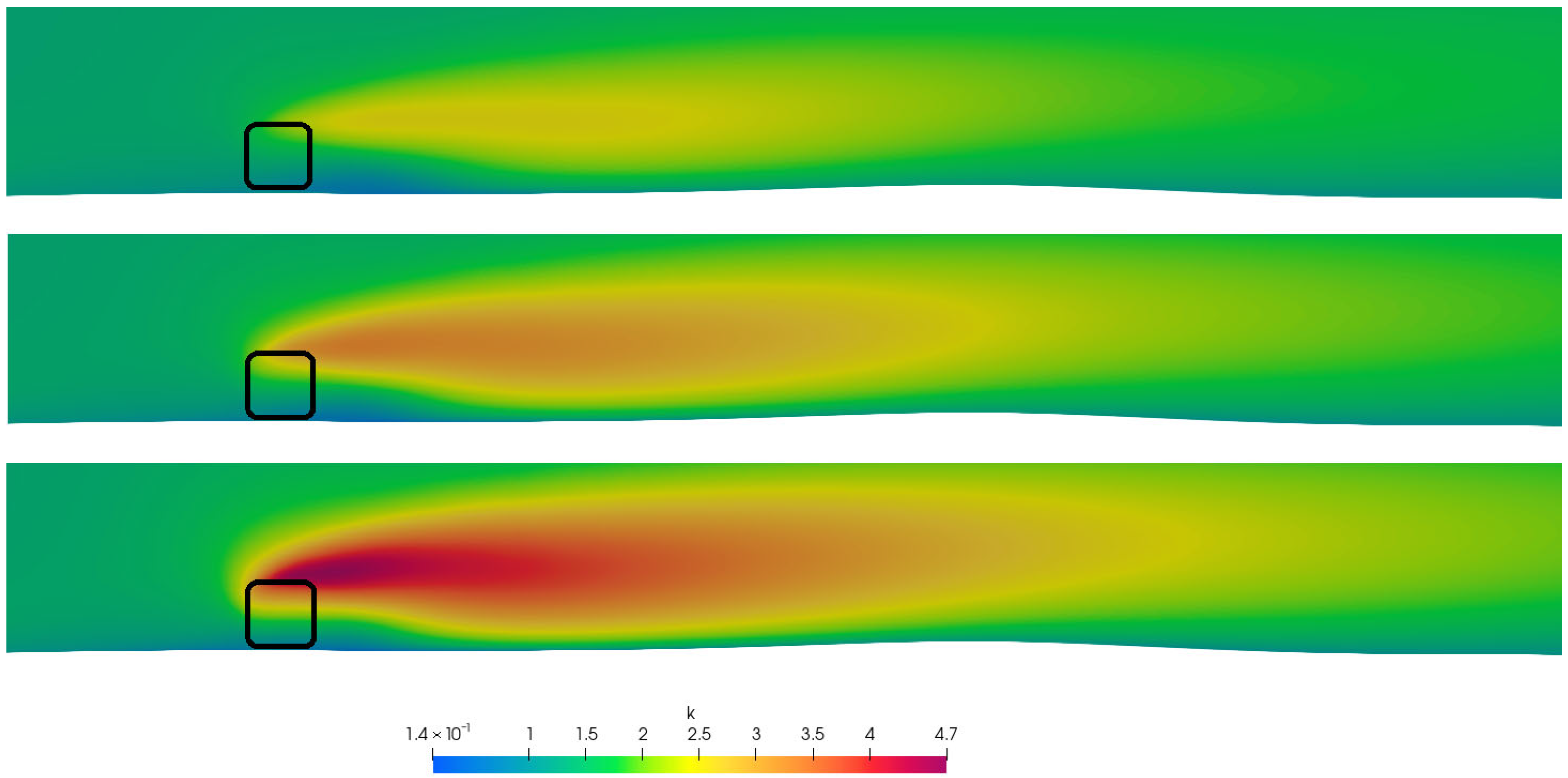
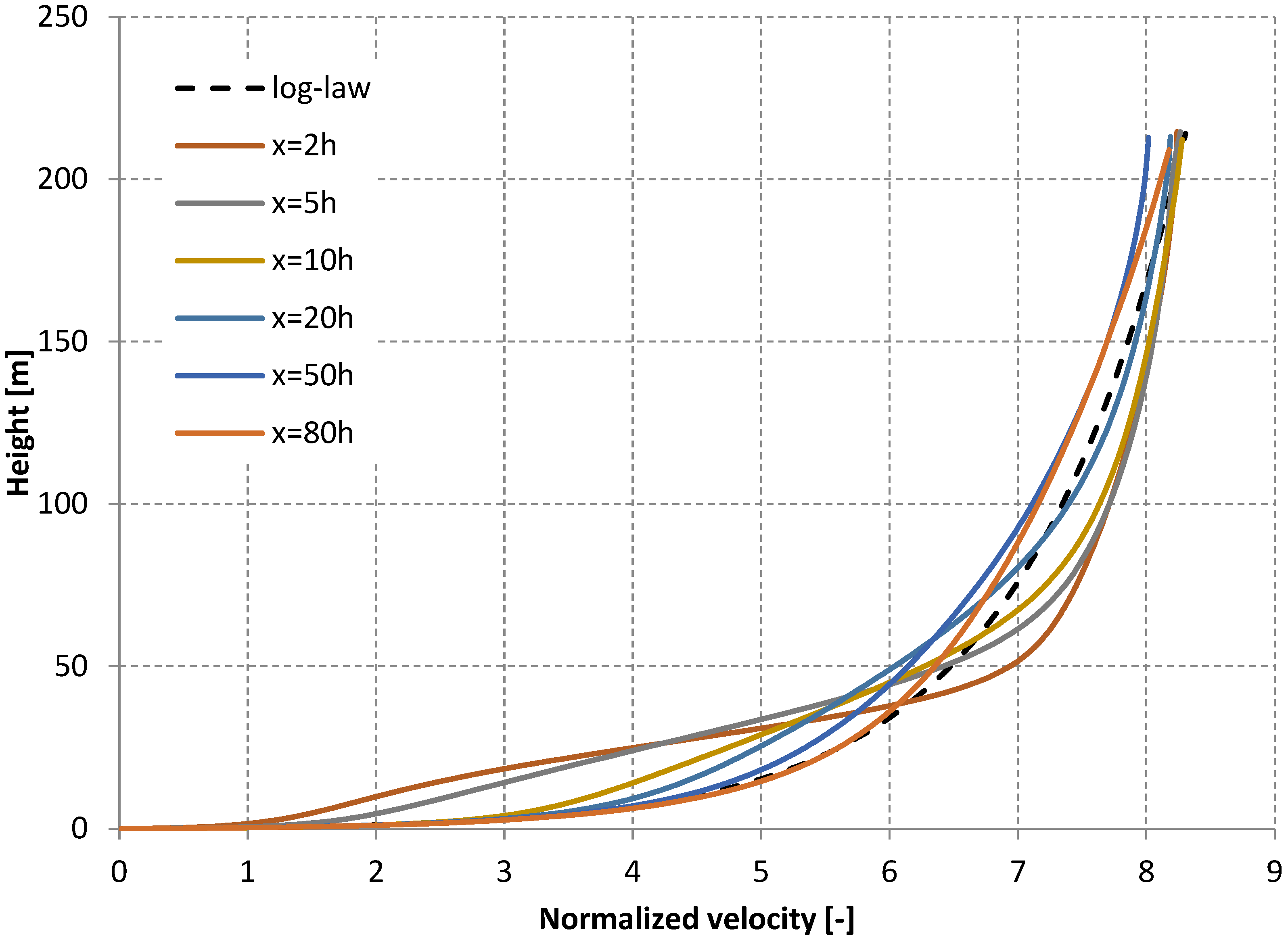
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuntzman, J.; Brom, J. From Fields to Microclimate: Assessing the Influence of Agricultural Landscape Structure on Vegetation Cover and Local Climate in Central Europe. Remote Sens. 2025, 17, 6. [Google Scholar] [CrossRef]
- Ntawuruhunga, D.; Ngowi, E.E.; Mangi, H.O.; Salanga, R.J.; Shikuku, K.M. Climate-smart agroforestry systems and practices: A systematic review of what works, what doesn’t work, and why. For. Policy Econ. 2023, 150, 102937. [Google Scholar] [CrossRef]
- Mume, I.D.; Workalemahu, S. Review on Windbreaks Agroforestry as a Climate Smart Agriculture Practices. Am. J. Agric. For. 2021, 9, 342–347. [Google Scholar]
- Ali, M.M.; Pal, A.C.; Bari, M.S.; Rahman, M.L.; Sarmin, I.J. Agroforestry as a Climate-Smart Strategy: Examining the Factors Affecting Farmers’ Adoption. Biol. Life Sci. Forum 2024, 30, 29. [Google Scholar]
- Kanianska, R.; Kizeková, M.; Jančová, Ľ.; Čunderlík, J.; Dugátová, Z. Effect of Soil Erosion on Soil and Plant Properties with a Consequence on Related Ecosystem Services. Sustainability 2024, 16, 7037. [Google Scholar] [CrossRef]
- Majaura, M.; Böhm, C.; Freese, D. The Influence of Trees on Crop Yields in Temperate Zone Alley Cropping Systems: A Review. Sustainability 2024, 16, 3301. [Google Scholar] [CrossRef]
- Sadorsky, P. Wind energy for sustainable development: Driving factors and future outlook. J. Clean. Prod. 2021, 289, 125779. [Google Scholar] [CrossRef]
- Kuczyński, W.; Wolniewicz, K.; Charun, H. Analysis of the wind turbine selection for the given wind conditions. Energies 2021, 14, 7740. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Du, S.; Li, C.; Siu, Y.L.; Rong, Y. The impact of onshore wind power pro-jects on ecological corridors and landscape connectivity in Shanxi, China. J. Clean. Prod. 2020, 254, 120075. [Google Scholar] [CrossRef]
- Ali, S.; Taweekun, J.; Techato, K.; Waewsak, J.; Gyawali, S. GIS based site suitability assessment for wind and solar farms in Songkhla, Thailand. Renew. Energy 2019, 132, 1360–1372. [Google Scholar] [CrossRef]
- Duranay, Z.B.; Güldemir, H.; Coşkun, B. The Role of Wind Turbine Siting in Achieving Sustainable Energy Goals. Processes 2024, 12, 2900. [Google Scholar] [CrossRef]
- Cleugh, H.A. Field measurements of windbreak effects on airflow, turbulent exchanges and microclimates. Aust. J. Exp. Agric. 2002, 42, 665–677. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, T.; Pan, Y. Porous Barriers and Agricultural Wind Flow. Environ. Fluid Mech. 2020, 45, 34–56. [Google Scholar]
- Zhou, Q.; Hu, T. Numerical Simulations of Wind Flow around Forest Belts. Environ. Fluid Mech. 2020, 45, 456–478. [Google Scholar]
- Xie, S.; Martinez-Vazquez, P.; Baniotopoulos, C. Experimental Measurements of Wind Flow Characteristics on an Ellipsoidal Vertical Farm. Buildings 2024, 14, 3646. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, X.; Hu, T. LES Simulations for Wind Energy. J. Environ. Model. 2018, 56, 890–906. [Google Scholar]
- Wang, J.; Patruno, L.; Zhao, G.; Tamura, Y. Windbreak effectiveness of shelterbelts with different characteristic parameters and arrangements by means of CFD simulation. Agric. For. Meteorol. 2024, 344, 109813. [Google Scholar] [CrossRef]
- Hu, T.; Liu, X.; Zhao, P. Advanced Simulation Methods for Wind Shear Analysis. J. Fluid Dyn. 2021, 67, 245–260. [Google Scholar]
- Wang, J.; Patruno, L.; Chen, Z.; Yang, Q.; Tamura, Y. Windbreak Effectiveness of Single and Double-Arranged Shelterbelts: A Parametric Study Using Large Eddy Simulation. Forests 2024, 15, 1760. [Google Scholar] [CrossRef]
- Poulain, P.; Craig, K.J.; Meyer, J.P. Transient simulation of an atmospheric boundary layer flow past a heliostat using the Scale-Adaptive Simulation turbulence model. J. Wind. Eng. Ind. Aerodyn. 2021, 218, 104740. [Google Scholar] [CrossRef]
- Szigeti, N.; Frank, N.; Vityi, A. The Multifunctional Role of Shelterbelts in Intensively Managed Agricultural Land—Silvoarable Agroforestry in Hungary. Acta Silv. Lignaria Hung. 2020, 16, 19–38. [Google Scholar] [CrossRef]
- Abdalla, Y.Y.; Fangama, I.M. Effect of Shelterbelts on Crop Yield in the Agricultural Scheme of Al-Rahad, Sudan. Int. J. Curr. Microbiol. Appl. Sci. 2015, 4, 1–4. [Google Scholar]
- Carnovale, D.; Bissett, A.; Thrall, P.H.; Baker, G. Plant genus (Acacia and Eucalyptus) alters soil microbial community structure and relative abundance in shelterbelts with regenerated vegetation. Appl. Soil Ecol. 2019, 133, 1–11. [Google Scholar] [CrossRef]
- Zaady, E.; Katra, I.; Shuker, S.; Knoll, Y.; Shlomo, S. Tree Belts for Decreasing Aeolian Dust-Carried Pesticides from Cultivated Areas. Geosciences 2018, 8, 286. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Yu, C. Impact of Windbreaks on Airflow Dynamics. J. Renew. Energy Stud. 2019, 32, 123–136. [Google Scholar]
- Siriri, D.; Wilson, J.; Coe, R.; Tenywa, M.M.; Bekunda, M.A.; Ong, C.K.; Black, C.R. Trees improve water storage and reduce soil evaporation in agroforestry systems on bench terraces in SW Uganda. Agrofor. Syst. 2013, 87, 45–58. [Google Scholar] [CrossRef]
- Lin, B.B. The role of agroforestry in reducing water loss through soil evaporation and crop transpiration in coffee agroecosystems. Agric. For. Meteorol. 2010, 150, 510–518. [Google Scholar] [CrossRef]
- Alharbi, S.; Felemban, A.; Abdelrahim, A.; Al-Dakhil, M. Agricultural and Technology-Based Strategies to Improve Water-Use Efficiency in Arid and Semiarid Areas. Water 2024, 16, 1842. [Google Scholar] [CrossRef]
- Zhu, J.; Luo, X.; Zhai, Y.; Zhang, G.; Zhou, C.; Chen, Z. Study on the Impact of Tree Species on the Wind Environment in Tree Arrays Based on Fluid–Structure Interaction: A Case Study of Hangzhou Urban Area. Buildings 2024, 14, 1409. [Google Scholar] [CrossRef]
- Zhang, L.; Zhan, Q.; Lan, Y. Effects of the tree distribution and species on outdoor environment conditions in a hot summer and cold winter zone: A case study in Wuhan residential quarters. Build. Environ. 2018, 130, 27–39. [Google Scholar] [CrossRef]
- Manickathan, L.; Defraeye, T.; Allegrini, J.; Derome, D.; Carmeliet, J. Comparative study of flow field and drag coefficient of model and small natural trees in a wind tunnel. Urban For. Urban Green. 2018, 35, 230–239. [Google Scholar] [CrossRef]
- Sun, Q.; Zheng, B.; Liu, T.; Zhu, L.; Hao, X.; Han, Z. The optimal spacing interval between principal shelterbelts of the farm-shelter forest network. Environ. Sci. Pollut. Res. 2022, 29, 12680–12693. [Google Scholar] [CrossRef]
- Gualtieri, G.; Secci, S. Methods to extrapolate wind resource to the turbine hub height based on power law: A 1-h wind speed vs. Weibull distribution extrapolation comparison. Renew. Energy 2012, 43, 183–200. [Google Scholar] [CrossRef]
- Wan, J.; Liu, J.; Ren, G.; Guo, Y.; Hao, W.; Yu, J.; Yu, D. A universal power-law model for wind speed uncertainty. Clust. Comput. 2019, 22, 10347–10359. [Google Scholar] [CrossRef]
- Liu, H.; Chen, G.; Hua, Z.; Zhang, J.; Wang, Q. Wind Shear Model Considering Atmospheric Stability to Improve Accuracy of Wind Resource Assessment. Processes 2024, 12, 954. [Google Scholar] [CrossRef]
- Zhou, L.; Wu, H.; Li, Z.N. Review of research on trees’ wind resistance and effects on wind environment. J. Nat. Disasters 2015, 24, 199–206. [Google Scholar]
- Wu, X.; Zou, X.; Zhou, N.; Zhang, C.; Shi, S. Deceleration efficiencies of shrub windbreaks in a wind tunnel. Aeolian Res. 2015, 16, 11–23. [Google Scholar] [CrossRef]
- Zeng, F.; Simeja, D.; Ren, X.; Chen, Z.; Zhao, H. Influence of Urban Road Green Belts on Pedestrian-Level Wind in Height-Asymmetric Street Canyons. Atmosphere 2022, 13, 1285. [Google Scholar] [CrossRef]
- Chan, P.W.; Lai, K.K. Evidence of Terrain-Induced Windshear Due to Lantau Island over the Third Runway of the Hong Kong International Airport—Examples and Numerical Simulations. Appl. Sci. 2025, 15, 83. [Google Scholar] [CrossRef]
- Zhou, X.H.; Brandle, J.R.; Mize, C.W.; Takle, E.S. Three-dimensional aerodynamic structure of a tree shelterbelt: Definition, characterization and working models. Agrofor. Syst. 2005, 63, 133–147. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, G.; Chen, Z.; Zhu, J. The Influence of Wind-Induced Response in Urban Trees on the Surrounding Flow Field. Atmosphere 2023, 14, 1010. [Google Scholar] [CrossRef]
- Lee, S.-H.; Kim, H.; Moon, H.; Kim, H.-S.; Han, S.-S.; Jeong, S. Effects of Wind Barrier Porosity and Inclination on Wind Speed Reduction. Appl. Sci. 2023, 13, 8310. [Google Scholar] [CrossRef]
- Wu, X.; Guo, Z.; Wang, R.; Fan, P.; Xiang, H.; Zuo, X.; Yin, J.; Fang, H. Optimal design for wind fence based on 3D numerical simulation. Agric. For. Meteorol. 2022, 323, 109072. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, L.; Xiao, Y. Simulation of the Neutral Atmospheric Flow Using Multiscale Modeling: Comparative Studies for SimpleFoam and Fluent Solver. Atmosphere 2024, 15, 1259. [Google Scholar] [CrossRef]
- Sharma, A.; Brazell, M.J.; Vijayakumar, G.; Ananthan, S.; Cheung, L.; deVelder, N.; Henry de Frahan, M.T.; Matula, N.; Mullowney, P.; Rood, J.; et al. ExaWind: Open-source CFD for hybrid-RANS/LES geometry-resolved wind turbine simulations in atmospheric flows. Wind Energy 2024, 27, 225–257. [Google Scholar] [CrossRef]
- Misar, A.S.; Uddin, M. Effects of Solver Parameters and Boundary Conditions on RANS CFD Flow Predictions over a Gen-6 NASCAR Racecar; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2022. [Google Scholar]
- Siddiqui, M.S.; Khalid, M.H.; Zahoor, R.; Butt, F.S.; Saeed, M.; Badar, A.W. A numerical investigation to analyze effect of turbulence and ground clearance on the performance of a roof top vertical–axis wind turbine. Renew. Energy 2021, 164, 978–989. [Google Scholar] [CrossRef]
- Lu, S.; Liu, J.; Hekkenberg, R. Mesh properties for RANS simulations of airfoil-shaped profiles: A case study of rudder hydrodynamics. J. Mar. Sci. Eng. 2021, 9, 1062. [Google Scholar] [CrossRef]
- Ma, G.; Tian, L.; Song, Y.; Zhao, N. Effects of Turbulence Modeling on the Simulation of Wind Flow over Typical Complex Terrains. Appl. Sci. 2024, 14, 11438. [Google Scholar] [CrossRef]
- Drame, A.S.; Wang, L.; Zhang, Y. Granular Stack Density’s Influence on Homogeneous Fluidization Regime: Numerical Study Based on EDEM-CFD Coupling. Appl. Sci. 2021, 11, 8696. [Google Scholar] [CrossRef]
- Tan, X.; Liu, Y.; Sha, B.; Zhang, N.; Chen, J.; Wang, H.; Mao, J. Study on Wind Resistance Performance of Transmission Tower Using Fixture-Type Reinforcement Device. Appl. Sci. 2025, 15, 747. [Google Scholar] [CrossRef]
- Chougule, A.; Mann, J.; Segalini, A.; Dellwik, E. Spectral tensor parameters for wind turbine load modeling from forested and agricultural landscapes. Wind Energy 2015, 18, 469–481. [Google Scholar] [CrossRef]
- He, C.; Shao, W. Numerical simulation of shelter effect assessment for single-row windbreaks on the periphery of oasis farmland. J. Arid. Environ. 2024, 222, 105165. [Google Scholar] [CrossRef]
- Aili, A.; Xu, H.; Waheed, A.; Bakayisire, F.; Xie, Y. Synergistic windbreak efficiency of desert vegetation and oasis shelter forests. PLoS ONE 2024, 19, e0312876. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, X.; Wu, X.; Zou, X.; Zhang, C.; Fang, H.; Xiang, H. Optimal design for vegetative windbreaks using 3D numerical simulations. Agric. For. Meteorol. 2021, 298–299, 108290. [Google Scholar] [CrossRef]
- Dimitrov, N.; Natarajan, A.; Kelly, M.C. Model of wind shear conditional on turbulence and its impact on wind turbine loads. Wind Energy 2015, 18, 1917–1931. [Google Scholar] [CrossRef]
- Ren, G.; Liu, J.; Wan, J.; Li, F.; Guo, Y.; Yu, D. The analysis of turbulence intensity based on wind speed data in onshore wind farms. Renew. Energy 2018, 123, 756–766. [Google Scholar] [CrossRef]
- Zhao, X.; Jiang, N.; Liu, J.; Yu, D.; Chang, J. Short-term average wind speed and turbulent standard deviation forecasts based on one-dimensional convolutional neural network and the integrate method for probabilistic framework. Energy Convers. Manag. 2020, 203, 112239. [Google Scholar] [CrossRef]
- Zhu, C.; Yang, Q.; Wang, D.; Huang, G.; Liang, S. Fragility Analysis of Transmission Towers Subjected to Downburst Winds. Appl. Sci. 2023, 13, 9167. [Google Scholar] [CrossRef]
- Dimitrov, N.; Natarajan, A.; Mann, J. Effects of normal and extreme turbulence spectral parameters on wind turbine loads. Renew. Energy 2017, 101, 1180–1193. [Google Scholar] [CrossRef]
- Cheng, S.; Elgendi, M.; Lu, F.; Chamorro, L.P. On the Wind Turbine Wake and Forest Terrain Interaction. Energies 2021, 14, 7204. [Google Scholar] [CrossRef]
- Badrkhani Ajaei, B.; El Naggar, M.H. Consideration of Rocking Wind Turbine Foundations on Undrained Clay with an Efficient Constitutive Model. Appl. Sci. 2025, 15, 457. [Google Scholar] [CrossRef]
- Shen, S.; Zhang, H.; Li, F.; Chen, W. Optimizing wind turbine placement in agricultural areas with tree belts: A study on flow acceleration and maintenance cost reduction. Renew. Energy 2021, 175, 920–930. [Google Scholar]
- Hernandez-Ramirez, G.; Hatfield, J.L.; Prueger, J.H.; Sauer, T.J. Energy balance and turbulent flux partitioning in a corn-soybean rotation in the Midwest US. Theor. Appl. Climatol. 2010, 100, 79–92. [Google Scholar] [CrossRef]
- Vanderwende, B.; Lundquist, J.K. Could crop height affect the wind resource at agriculturally productive wind farm sites? Bound.-Layer Meteorol. 2016, 158, 409–428. [Google Scholar] [CrossRef]
- Li, L.; Ma, W.; Duan, X.; Wang, S.; Wang, Q.; Gu, H.; Wang, J. Effects of Wind Farm Construction on Soil Nutrients and Vegetation: A Case Study of Linxiang Wind Farm in Hunan Province. Sustainability 2024, 16, 6350. [Google Scholar] [CrossRef]
- Han, X.; Lu, C.; Wang, J. Long-Term Impacts of 250 Wind Farms on Surface Temperature and Vegetation in China: A Remote Sensing Analysis. Remote Sens. 2025, 17, 10. [Google Scholar] [CrossRef]
- Chen, X.; Ye, X.; Zhang, Y.; Xiong, X. Analysis of Wind Speed Characteristics Along a High-Speed Railway. Appl. Sci. 2025, 15, 138. [Google Scholar] [CrossRef]
- Bošnjaković, M.; Hrkać, F.; Stoić, M.; Hradovi, I. Environmental Impact of Wind Farms. Environments 2024, 11, 257. [Google Scholar] [CrossRef]
- Jia, Z.; Yang, X.; Chen, A.; Yang, D.; Zhang, M.; Wei, L. Localized Eco-Climatic Impacts of Onshore Wind Farms: A Review. J. Resour. Ecol. 2024, 15, 151–160. [Google Scholar]
- Miri, A.; Webb, N.P. Characterizing the spatial variations of wind velocity and turbulence intensity around a single Tamarix tree. Geomorphology 2022, 414, 108382. [Google Scholar] [CrossRef]
- Cleugh, H.A. Effects of windbreaks on airflow, microclimates and crop yields. Agrofor. Syst. 1998, 41, 55–84. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Chang, S.X.; Cui, S.; Jagadamma, S.; Zhang, Q.; Cai, Y. Residue retention promotes soil carbon accumulation in minimum tillage systems: Implications for conservation agriculture. Sci. Total. Environ. 2020, 740, 140147. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Canadell, J.G.; Yu, L.; Yu, L.; Zhang, W.; Smith, P.; Fischer, T.; Huang, Y. Climate drives global soil carbon sequestration and crop yield changes under conservation agriculture. Glob. Change Biol. 2020, 26, 3325–3335. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zeng, X.; Decker, J.; Dawson, L. A GPU-Implemented Lattice Boltzmann Model for Large Eddy Simulation of Turbulent Flows in and around Forest Shelterbelts. Atmosphere 2024, 15, 735. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, M.; Li, T.; Xiao, F.; Zheng, X. An Integrated Framework for Landscape Indices’ Calculation with Raster–Vector Integration and Its Application Based on QGIS. ISPRS Int. J. Geo-Inf. 2024, 13, 242. [Google Scholar] [CrossRef]
- Shin, S.S.; Park, S.D.; Kim, G. Applicability Comparison of GIS-Based RUSLE and SEMMA for Risk Assessment of Soil Erosion in Wildfire Watersheds. Remote Sens. 2024, 16, 932. [Google Scholar] [CrossRef]
- Li, H.; Yan, Z.; Zhang, Z.; Lang, J.; Wang, X. A Numerical Study of the Effect of Vegetative Windbreak on Wind Erosion over Complex Terrain. Forests 2022, 13, 1072. [Google Scholar] [CrossRef]
- Kong, T.; Liu, B.; Henderson, M.; Zhou, W.; Su, Y.; Wang, S.; Wang, L.; Wang, G. Effects of Shelterbelt Transformation on Soil Aggregates Characterization and Erodibility in China Black Soil Farmland. Agriculture 2022, 12, 1917. [Google Scholar] [CrossRef]
- Terziev, A.; Panteleev, Y.; Iliev, I.; Beloev, H. Evaluation of the influence of the windbreak trees on the change of wind shear in weakly complex terrains. E3S Web Conf. 2021, 286, 02015. [Google Scholar] [CrossRef]
- Available online: https://www.vde-verlag.de/iec-normen/251347/iec-61400-50-1-2022.html (accessed on 6 January 2025).
- Available online: http://www.dataforwind.com/ (accessed on 6 January 2025).
- Cressie, N.A.C. The Origins of Kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Gromke, C.; Blocken, B. Influence of avenue-trees on air quality at the urban neighborhood scale. Part I: Quality assurance studies and turbulent Schmidt number analysis for RANS CFD simulations. Environ. Pollut. 2015, 196, 214–223. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Hargreaves, D.M.; Wright, N.G. On the use of the k–ε model in commercial cfd software to model the neutral atmospheric boundary layer. J. Wind Eng. Ind. Aerodyn. 2007, 95, 355–369. [Google Scholar] [CrossRef]
- Hellman, G. Über die Bewegung der Luft in den untersten Schichten der Atmosphäre. Meteorol. Z. 1915, 32, 273–285. [Google Scholar]
- Greenshields, C.J.; Weller, H.G. Weller Notes on Computational Fluid Dynamics: General Principles ISBN-10 1399920782. Available online: https://doc.cfd.direct/notes/cfd-general-principles/numerical-method (accessed on 6 January 2025).
- Bergstrom, D.J.; Kotey, N.A.; Tachie, M.F. The Effects of Surface Roughness on the Mean Velocity Profile in a Turbulent Boundary Layer. J. Fluids Eng. 2002, 124, 664–670. [Google Scholar] [CrossRef]
- Carlo, O.S.; Fellini, S.; Palusci, O.; Marro, M.; Salizzoni, P.; Buccolieri, R. Influence of Obstacles on Urban Canyon Ventilation and Air Pollutant Concentration: An Experimental Assessment. Build. Environ. 2024, 250, 111143. [Google Scholar] [CrossRef]
- Arunvinthan, S.; Gouri, P.; Divysha, S.; Devadharshini, R.; Nithya Sree, R. Effect of Trough Incidence Angle on the Aerodynamic Characteristics of a Biomimetic Leading-Edge Protuberanced (LEP) Wing at Various Turbulence Intensities. Biomimetics 2024, 9, 354. [Google Scholar] [CrossRef]
- Tucker, P.G. Trends in Turbomachinery Turbulence Treatments. Progress. Aerosp. Sci. 2013, 63, 1–32. [Google Scholar] [CrossRef]
- Schwarz, C.M.; Ehrich, S.; Peinke, J. Wind turbine load dynamics in the context of turbulence intermittency. Wind Energy Sci. 2019, 4, 581–594. [Google Scholar] [CrossRef]
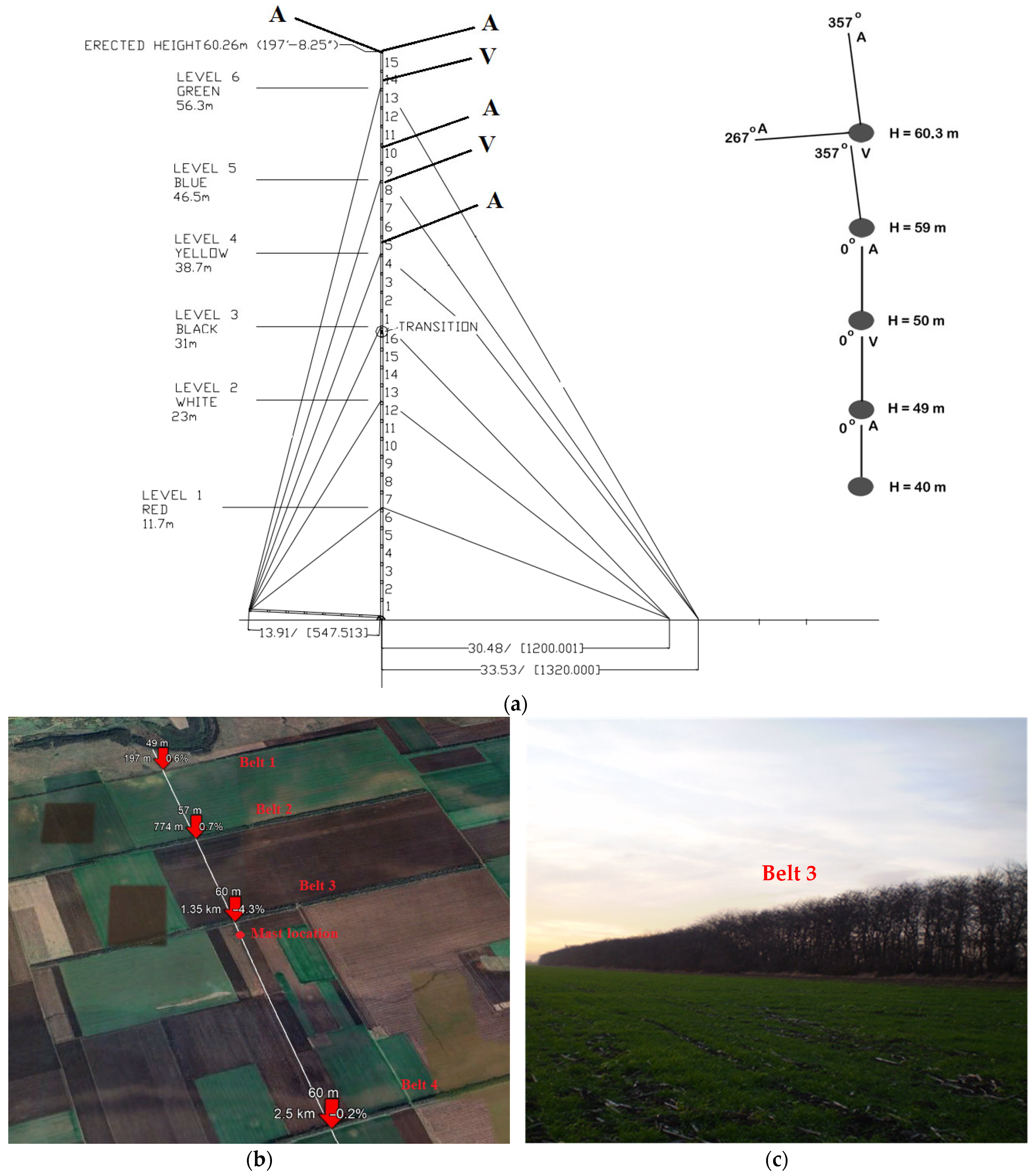
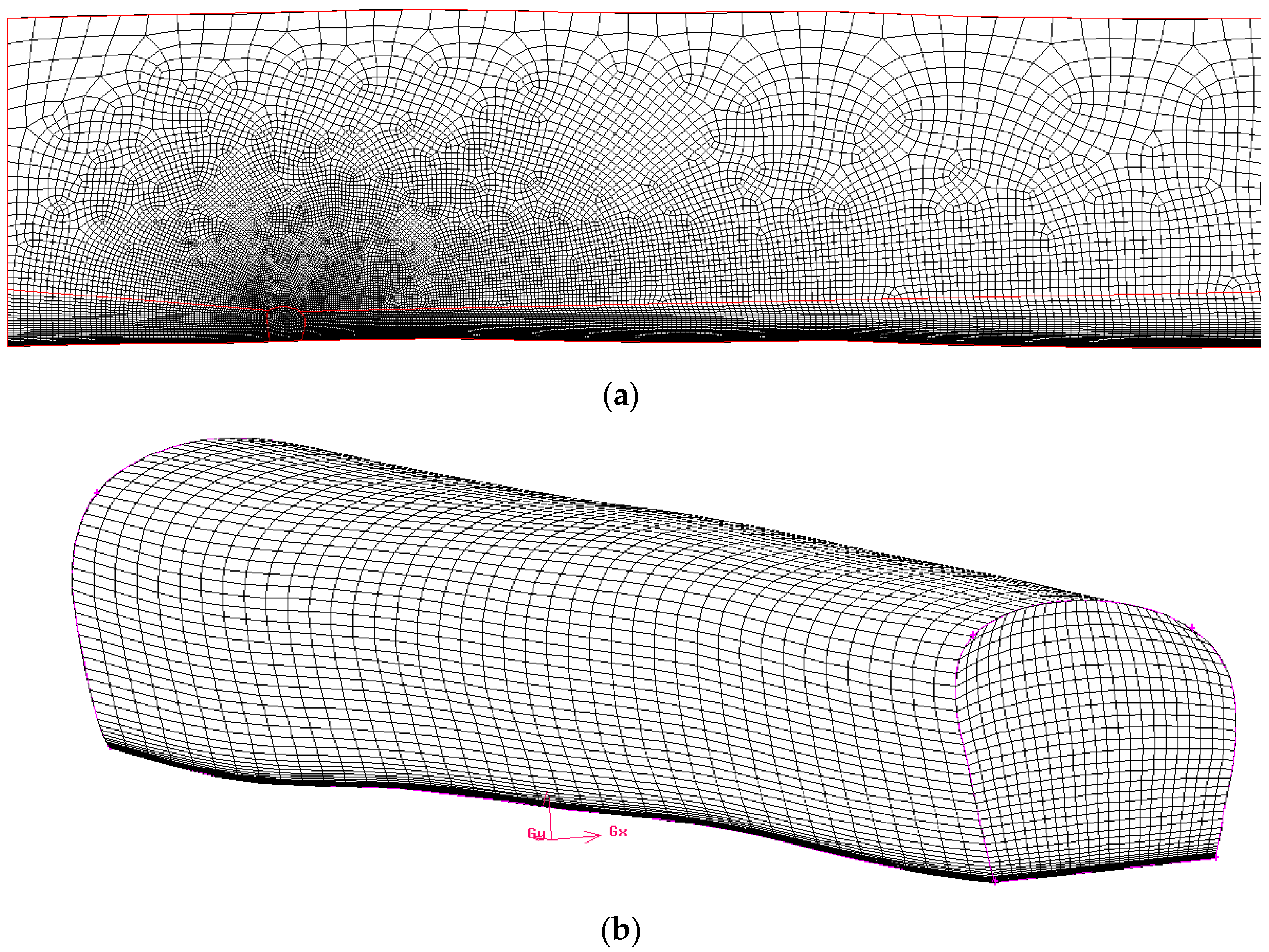
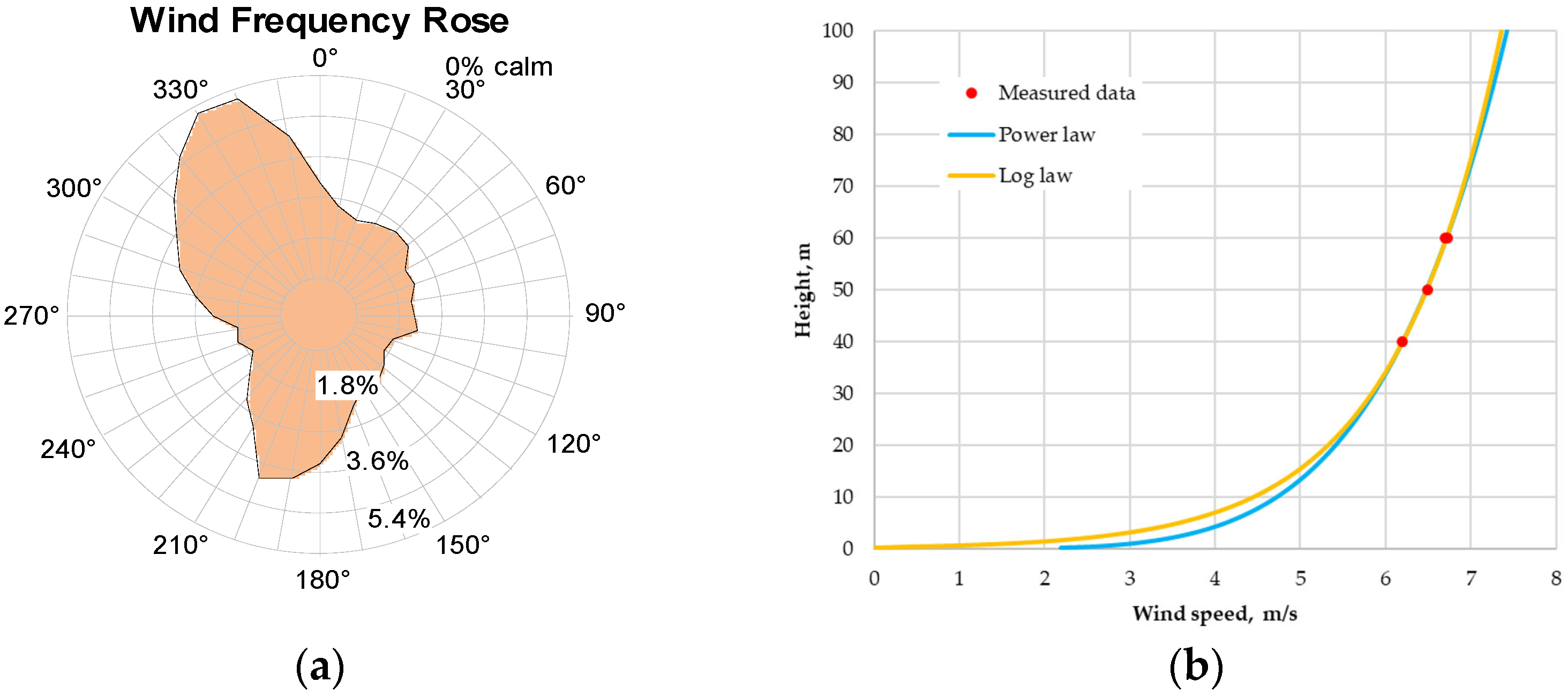



| Sensor | Type | Range | Precision |
|---|---|---|---|
| Anemometer | A100R | 0.2 up to 75 m/s | 1% of reading between 10 and 50 m/s, 2% above 50 m/s |
| Wind vane | 200P | 0 up to 360o | ±3° steady winds over 5 m/s |
| Temperature | Vaisala HMP50 | −40 up to 60 °C | ±1.6 °C at −40 °C; up to ±0.4 °C at 0 °C; ±0.6 °C at 40 °C outdoor temperature |
| Humidity | Vaisala HMP50 | 0 to 100% | ±3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terziev, A.; Bode, F.; Zlateva, P.; Pichurov, G.; Ivanov, M.; Denev, J.; Stankov, B. Numerical Study on Tree Belt Impact on Wind Shear on Agricultural Land. Appl. Sci. 2025, 15, 7450. https://doi.org/10.3390/app15137450
Terziev A, Bode F, Zlateva P, Pichurov G, Ivanov M, Denev J, Stankov B. Numerical Study on Tree Belt Impact on Wind Shear on Agricultural Land. Applied Sciences. 2025; 15(13):7450. https://doi.org/10.3390/app15137450
Chicago/Turabian StyleTerziev, Angel, Florin Bode, Penka Zlateva, George Pichurov, Martin Ivanov, Jordan Denev, and Borislav Stankov. 2025. "Numerical Study on Tree Belt Impact on Wind Shear on Agricultural Land" Applied Sciences 15, no. 13: 7450. https://doi.org/10.3390/app15137450
APA StyleTerziev, A., Bode, F., Zlateva, P., Pichurov, G., Ivanov, M., Denev, J., & Stankov, B. (2025). Numerical Study on Tree Belt Impact on Wind Shear on Agricultural Land. Applied Sciences, 15(13), 7450. https://doi.org/10.3390/app15137450









