A Seven-Parameter Spectral/hp Finite Element Model for the Linear Vibration Analysis of Functionally Graded Shells with Nonuniform Thickness

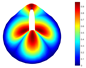
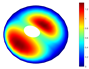
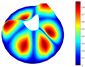
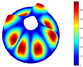
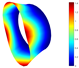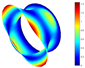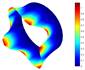Abstract

This contribution presents a finite element shell model capable of performing linear vibration analyses of shell-type structures made of functionally graded material (FGM). The model is based on the seven-parameter spectral/hp finite element formulation, which allows the analysis ofFG shells of either uniform or nonuniform thickness. Equations of motion are derived using the Hamilton’s principle and the material properties of the constituents are considered to follow a power-law volume distribution through the thickness direction. The verification of the present model is carried out by comparing with numerical results available in the literature, and with numerical simulations performed in a commercial software. To demonstrate the capabilities of the present formulation, the free vibration response of different shell structures, with nonuniform thickness, to the variation of the geometrical parameters (e.g., radius-to-thickness ratio) and the mechanical properties is reported.

1. Introduction

The extensive field of engineering applications in diverse industries (e.g., automotive, nautical, aeronautics, aerospace) in conjunction with the continuously more demanding design requirements has led to the development of advanced materials capable of addressing their needs, improving their performance, or eliminating deficiencies of conventional materials. For instance, composite materials allow a weight reduction in structural members or machine components without compromising the design requirements. Among these advanced materials, an interesting material known as functionally graded material (FGM) is found, which is basically a material with a variation of mechanical properties along one direction or more. In the literature, it is well known that FGMs were introduced to overcome the limitations of composites, such as delamination at high temperatures due to stress concentrations at interfaces of the composite [1,2]. The concept of FGM was introduced in the 1980s by a group of scientists in Japan [1,3,4]. The available computational resources nowadays, which are very powerful tools for engineers, and the complexities involved in the modeling of new materials have motivated the development of numerical models to predict their mechanical behavior. In the last three decades, researchers have shown increasing interest in the area of FGMs.

As mentioned earlier, the functionally graded materials present—in the most general case—a variation of properties through various directions (e.g., along thickness coordinate), and they are usually composed of a mixture of two materials. Therefore, this variation made the FGM a heterogeneous material; due to this fact, different mathematical models, also known as homogenization schemes [5], have been used to evaluate the effective properties of the FGMs, and the gradation of the volume fraction. Several analytic approaches have been proposed, like self-consistent estimates, Mori–Tanaka scheme, Vegard’s rule, composite sphere assemblage model, composite cylindrical assemblage model, the simplified strength of materials method, the method of cells, and micromechanical models [5,6,7]. Some models that have attracted more attention are Voigt’s mixture rule, Mori–Tanaka scheme, and self-consistent models [8]. Generally, the rule of mixture and Mori–Tanaka schemes are used by researchers [3].

The present literature review is limited to those works reporting the free vibration analysis of functionally graded (FG) shell structures, specially those considering a variation of the material properties through the thickness and using a power-law volume distribution of the constituents. Despite this, during the review, free vibration analyses of FG plates with uniform thickness were also found in the works [9,10,11,12,13,14,15,16,17], while vibration analyses of FG plates with variable thickness can be found in [18,19,20].

Studies related to shells of uniform thickness were presented by Matsunaga [21], Tornabene, Viola and Inman [22], Tornabene and Viola [23], Iqbal, Naeem and Sultana [24], Neves et al. [25], Su et al. [26,27], Su, Jin and Ye [28], Torabi and Ansari [29], Ersoy, Mercan and Civalek [30], Brischetto [31], Pham et al. [32], Moita et al. [33], Zannon et al. [34], and Bagheri et al. [35]. In the aforementioned works, the formulations are based on different theories such as first-order shear deformation theory (FSDT), third-order shear deformation theory (TSDT), higher-order shear deformation theory (HSDT), wave propagation approach, Carrera’s unified formulation, and three-dimensional elasticity theory.

Analysis of the free vibration of stepped FG shells was reported by Li et al. [36] and Gong et al. [37]. Formulations considering the variation of the shell thickness were presented by Tornabene, Fantuzzi, and Bacciocchi [38] for the analysis of FG laminated free-form doubly-curved shells and panels, and by Tornabene et al. [39] for FG sandwich shell structures. However, they used different schemes to model the variation of the mechanical properties, such as four-parameter power-law, Weibull, and exponential distributions.

Furthermore, in the literature, the modeling of FG shell type structures or FG plates by means of commercial finite element codes is also reported. Examples of models using ANSYS are the works of Rao, Blessington, and Tarapada [40], Mouli et al. [41], and Marzavan and Nastasescu [42]. In this regard, Burlayenko et al. [43] used a three-dimensional brick finite element available in ABAQUS to model the free vibration of FG sandwich plates.

In the literature, several works related to the seven-parameter finite element formulation can be found [44,45,46,47,48]. However, to date, the implementations of this formulation were devoted to performing different analyses than the modal analysis of FG shell structures with nonuniform thickness.

The main aim of this work is to extend the finite element analysis previously presented in [49] for the modeling of shell-type structures made of FGMs; that is, to take into account the FGM behavior in the seven-parameter finite element formulation in order to determine the natural frequencies and vibration modes of arbitrary FG shell structures with uniform and nonuniform thicknesses. Moreover, due to the few results available in the literature for FG shell-like structures with variable thickness, a user-defined routine to model these type of structures by means of the commercial code ANSYS mechanical APDL is developed and used to compare the results of the present finite element model. In addition, the routine performance is verified using natural frequencies of FG structures with constant thickness reported in the literature.

2. Theoretical Formulation

Since the present work is an extension of the finite element model presented in [49], the most relevant aspects related to the formulation are given below, and a more detailed explanation can be found in the previously mentioned work. In Figure 1, the three-dimensional (3D) geometry of the shell element $\mathbf{\Phi }$ and the discretization of the mid-surface $\mathbf{\Omega }$ are shown; the main idea to model the 3D domain is to represent it by means of its mid-surface. In this case, Figure 1 illustrates the discretization of the shell’s mid-surface using spectral nodes for an element with polynomial order $p=4$.

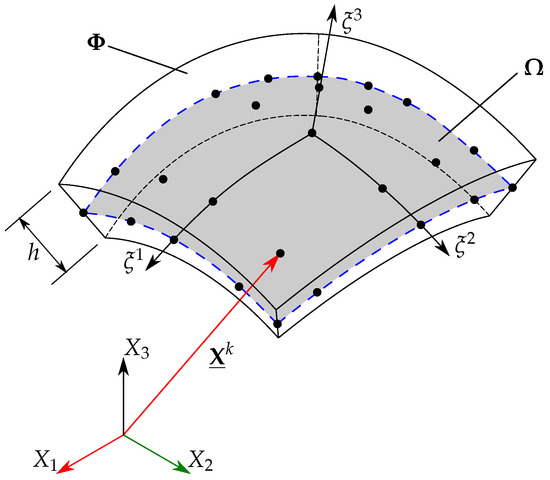
Figure 1. Mid-surface and spectral nodes of a shell element.

2.1. Geometrical Parameters

The position vector of a typical point in the element $\mathbf{\Phi }$ can be approximated as

$$\mathbf{X}=\sum _{k=1}^q{\psi }_k\left({\xi }_1,{\xi }_2\right)\left({\underline{\mathbf{X}}}^k+{\xi }^3\frac{h}{2}{\underline{\mathbf{n}}}^k\right),$$

(1)

where ${\psi }_k\left({\xi }^1,{\xi }^2\right)$ is the k-th two-dimensional (2D) Lagrange interpolation function of order p, ${\underline{\mathbf{X}}}^k$ is the position vector, ${\underline{\mathbf{n}}}^k$ is the unit normal vector of the k-th spectral node, and h denotes the thickness in the k-th spectral node position, so the thickness variation can be easily considered. The total number of nodes per element is $q=\left(p+1\right)\left(p+1\right)$.

Additionally, a set of covariant basis vectors for each point in the element must be defined:  

$${\mathbf{g}}_i=\frac{\partial \mathbf{X}}{\partial {\xi }^i}\equiv {\mathbf{X}}_{,i}i=1,2,3.$$

(2)

A differential line element in the typical shell element, in terms of the curvilinear coordinates, can be expressed as

$${\left\{\begin{array}{c}d{X}_1\\ d{X}_2\\ d{X}_3\end{array}\right\}}^T={\left\{\begin{array}{c}d{\xi }^1\\ d{\xi }^2\\ d{\xi }^3\end{array}\right\}}^T\left[\begin{array}{ccc}{\displaystyle \frac{\partial X_1}{\partial {\xi }^1}}& {\displaystyle \frac{\partial X_2}{\partial {\xi }^1}}& {\displaystyle \frac{\partial X_3}{\partial {\xi }^1}}\\ {\displaystyle \frac{\partial X_1}{\partial {\xi }^2}}& {\displaystyle \frac{\partial X_2}{\partial {\xi }^2}}& {\displaystyle \frac{\partial X_3}{\partial {\xi }^2}}\\ {\displaystyle \frac{\partial X_1}{\partial {\xi }^3}}& {\displaystyle \frac{\partial X_2}{\partial {\xi }^3}}& {\displaystyle \frac{\partial X_3}{\partial {\xi }^3}}\end{array}\right]={\left\{d\xi \right\}}^T\left[\mathbf{J}\right],$$

(3)

where $\left[\mathbf{J}\right]$ is the Jacobian matrix with determinant J. In conjunction with the covariant basis vectors, a contravariant set of basis vectors ${\mathbf{g}}^i$ is defined, as follows:

$$\begin{array}{ccc}{\mathbf{g}}^1={\displaystyle \frac{{\mathbf{g}}_2\times {\mathbf{g}}_3}{J}},& {\mathbf{g}}^2={\displaystyle \frac{{\mathbf{g}}_3\times {\mathbf{g}}_1}{J}},& {\mathbf{g}}^3={\displaystyle \frac{{\mathbf{g}}_1\times {\mathbf{g}}_2}{J}}.\end{array}$$

2.2. Displacement Field

The displacement field of the seven-parameter formulation considered in this work is given by [46,47]

$$\mathbf{u}\left(\mathbf{X},t\right)=\underline{\mathbf{u}}\left({\xi }^{\alpha },t\right)+{\xi }^3{\displaystyle \frac{h}{2}}\mathit{\phi }\left({\xi }^{\alpha },t\right)+{\left({\xi }^3\right)}^2{\displaystyle \frac{h}{2}}\mathbf{\Psi }\left({\xi }^{\alpha },t\right),$$

(4)

where

$$\underline{\mathbf{u}}\left({\xi }^{\alpha },t\right)={\underline{u}}_i\left({\xi }^{\alpha },t\right){\widehat{\mathbf{E}}}_i,\mathit{\phi }\left({\xi }^{\alpha },t\right)={\mathit{\phi }}_i\left({\xi }^{\alpha },t\right){\widehat{\mathbf{E}}}_i,\mathbf{\Psi }\left({\xi }^{\alpha },t\right)=\mathsf{\Psi }\left({\xi }^{\alpha },t\right)\underline{\mathbf{n}}\left({\xi }^{\alpha }\right),$$

Here, ${\widehat{\mathbf{E}}}_i$ is a unit vector in direction i of the Cartesian coordinate system $X_1{X}_2{X}_3$; therefore, the subindex i takes the values of 1, 2, and 3.

In Equation (4), the vector $\underline{\mathbf{u}}\left({\xi }^{\alpha },t\right)$ is associated with the mid-surface displacements in the three directions, $\mathit{\phi }\left({\xi }^{\alpha },t\right)$ is the difference vector which gives the change in the mid-surface director, and the vector $\mathbf{\Psi }\left({\xi }^{\alpha },t\right)$ is defined by scaling the normal vector $\underline{\mathbf{n}}$ with the seventh parameter $\mathsf{\Psi }$, which denotes the thickness stretch and mitigates the Poisson’s locking phenomena that appear in the six-parameter formulation [47,48].

2.3. Strains

The strains in the element are obtained by considering only the linear part of the Green–Lagrange strain tensor, and are given by

$$\mathbf{E}={\displaystyle \frac{1}{2}}\left({\mathbf{u}}_{,i}·{\mathbf{g}}_j+{\mathbf{g}}_i·{\mathbf{u}}_{,j}\right){\mathbf{g}}^i\otimes {\mathbf{g}}^j,$$

(5)

which can be expressed in their covariant components as [50]

$$\mathbf{E}=E_{\alpha \beta }{\mathbf{g}}^{\alpha }\otimes {\mathbf{g}}^{\beta }+E_{\alpha 3}{\mathbf{g}}^{\alpha }\otimes {\mathbf{g}}^3+E_{3\alpha }{\mathbf{g}}^3\otimes {\mathbf{g}}^{\alpha }+E_{33}{\mathbf{g}}^3\otimes {\mathbf{g}}^3,$$

(6)

where, considering only the linear terms associated with the thickness coordinate, the covariant components are

$$\begin{array}{ccc}\hfill E_{\alpha \beta }& =& {\epsilon }_{\alpha \beta }^{\left(0\right)}\left({\xi }^{\alpha },t\right)+{\xi }^3{\epsilon }_{\alpha \beta }^{\left(1\right)}\left({\xi }^{\alpha },t\right),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill E_{\alpha 3}& =& {\epsilon }_{\alpha 3}^{\left(0\right)}\left({\xi }^{\alpha },t\right)+{\xi }^3{\epsilon }_{\alpha 3}^{\left(1\right)}\left({\xi }^{\alpha },t\right),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill E_{3\alpha }& =& E_{\alpha 3},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill E_{33}& =& {\epsilon }_{33}^{\left(0\right)}\left({\xi }^{\alpha },t\right)+{\xi }^3{\epsilon }_{33}^{\left(1\right)}\left({\xi }^{\alpha },t\right).\hfill \end{array}$$

(10)

3. Constitutive Equations

In this work, the FGM constituents are considered to behave as isotropic linear elastic materials. It is worth pointing out that despite this assumption, the FGM analyzed here remains heterogeneous along the thickness direction, and the simple rule of mixtures is used as a homogenization scheme to evaluate the effective material properties of the FGM, which is written as [47,51]

$$P\left({\xi }^3\right)=\left(P_{top}-P_{bot}\right)V_{top}^i\left({\xi }^3\right)+P_{bot},$$

(11)

where $P\left({\xi }^3\right)$ denotes the effective material property (e.g., Young’s modulus, mass density, Poisson’s ratio) along the thickness coordinate, $P_{top}$ and $P_{bot}$ are the material properties of the top and bottom constituents, respectively, while $V_{top}^i\left({\xi }^3\right)$ is the volume distribution of the top constituent—through thickness—corresponding to the following forms of the power-law [22]:

$$V_{top}^I\left({\xi }^3\right)={\left({\displaystyle \frac{1+{\xi }^3}{2}}\right)}^n,$$

(12)

$$V_{top}^{II}\left({\xi }^3\right)={\left({\displaystyle \frac{1-{\xi }^3}{2}}\right)}^n,$$

(13)

where n is the volume fraction exponent or power-law index, and its value may be greater or equal to zero. In order to adequately compare with numerical results reported in the literature, the volume distribution $V_{top}^{II}\left({\xi }^3\right)$ is also considered in this work.

From now on, to distinguish the aforementioned volume distributions, the volume distribution given by Equation (12) is referred to as FG-I and the volume distribution described by Equation (13) is referred to as FG-II.

Now, for the assumed constituent materials, the fourth-order elasticity tensor, in terms of contravariant vectors, is given by

$$\mathbf{C}=C^{ijkl}{\mathbf{g}}_i\otimes {\mathbf{g}}_j\otimes {\mathbf{g}}_k\otimes {\mathbf{g}}_l,$$

(14)

where the contravariant components are determined by

$$C^{ijkl}=\lambda \left({\xi }^3\right)g^{ij}{g}^{kl}+\mu \left({\xi }^3\right)\left(g^{ik}{g}^{jl}+g^{il}{g}^{jk}\right).$$

(15)

In Equation (15), $\lambda \left({\xi }^3\right)$ and $\mu \left({\xi }^3\right)$ are the Lamé parameters defined in terms of Young’s modulus, $E\left({\xi }^3\right)$, and Poisson’s ratio, $\nu \left({\xi }^3\right)$, as

$$\lambda \left({\xi }^3\right)={\displaystyle \frac{\nu \left({\xi }^3\right)E\left({\xi }^3\right)}{\left[1+\nu \left({\xi }^3\right)\right]\left[1-2\nu \left({\xi }^3\right)\right]}},\mu \left({\xi }^3\right)={\displaystyle \frac{E\left({\xi }^3\right)}{2\left[1+\nu \left({\xi }^3\right)\right]}}.$$

Also, in Equation (15), $g^{ij}$ denotes the contravariant components of the Riemannian metric tensor in the reference configuration, given as ${\displaystyle g^{ij}={\mathbf{g}}^i·{\mathbf{g}}^j}$.

Recalling the considerations of the constituents behavior previously mentioned in this section, the mechanical behavior is assumed to follow Hooke’s law. Then, the relation between the second Piola–Kirchhoff stress tensor and the Green–Lagrange strain tensor is given by   

$$\mathbf{S}=\mathbf{C}\mathbf{E},$$

(16)

And the contravariant components of $\mathbf{S}$ are determined by $S^{ij}=C^{ijkl}{E}_{kl}$.

4. Equations of Motion

The equations of motion associated with the present finite element model are derived using the Hamilton’s principle, which is defined as [52]

$${\int }_0^T\left[\delta K-\left(\delta U+\delta V\right)\right]dt=0,$$

(17)

where $\delta K$ represents the virtual kinetic energy, $\delta U$ is the virtual strain energy, and $\delta V$ is the virtual potential energy due to external loads.

From Hamilton’s principle, the mass matrix, the stiffness matrix, and the load vector can be obtained straightforwardly using the virtual kinetic energy, the virtual strain energy, and the virtual potential energy, respectively. However, for the present study, it is sufficient to compute the stiffness and mass matrices to define the finite element model.

For the displacement field considered here, the virtual kinetic energy is given by

$$\begin{array}{ccc}\hfill {\displaystyle \delta K}& =& {\int }_A\left\{I_0\left(\delta \dot{\underline{\mathbf{u}}}·\dot{\underline{\mathbf{u}}}\right)+I_1\left[{\displaystyle \frac{h}{2}}\left(\dot{\underline{\mathbf{u}}}·\delta \dot{\mathit{\phi }}+\dot{\mathit{\phi }}·\delta \dot{\underline{\mathbf{u}}}\right)\right]+I_2\left[{\displaystyle \frac{h}{2}}\left(\dot{\underline{\mathbf{u}}}·\delta \dot{\mathsf{\Psi }}\mathbf{n}+{\displaystyle \frac{h}{2}}\dot{\mathit{\phi }}·\delta \dot{\mathit{\phi }}+\dot{\mathsf{\Psi }}\mathbf{n}·\delta \dot{\underline{\mathbf{u}}}\right)\right]+\right.\hfill \\ & & \left.+I_3\left[{\displaystyle \frac{h^2}{4}}\left(\dot{\mathit{\phi }}·\delta \dot{\mathsf{\Psi }}\mathbf{n}+\dot{\mathsf{\Psi }}\mathbf{n}·\delta \dot{\mathit{\phi }}\right)\right]+I_4\left[{\displaystyle \frac{h^2}{4}}\left(\dot{\mathsf{\Psi }}\delta \dot{\mathsf{\Psi }}{\left|\right|\mathbf{n}\left|\right|}^2\right)\right]\right\}dA,\hfill \end{array}$$

(18)

And the virtual strain energy is given by

$$\delta U={\int }_A\left[A^{ijkl}\delta {\epsilon }_{ij}^{\left(0\right)}{\epsilon }_{kl}^{\left(0\right)}+B^{ijkl}\left(\delta {\epsilon }_{ij}^{\left(1\right)}{\epsilon }_{kl}^{\left(0\right)}+\delta {\epsilon }_{ij}^{\left(0\right)}{\epsilon }_{kl}^{\left(1\right)}\right)+D^{ijkl}\delta {\epsilon }_{ij}^{\left(1\right)}{\epsilon }_{kl}^{\left(1\right)}\right]dA.$$

(19)

In Equation (18), $\left|\right|\mathbf{n}\left|\right|$ is the norm of the normal vector $\underline{\mathbf{n}}$, the dot indicates the partial derivative with respect time, and the mass inertias are defined as

$${\displaystyle \left\{I_0,I_1,I_2,I_3,I_4\right\}={\int }_{-1}^1\left\{1,{\xi }^3,{\left({\xi }^3\right)}^2,{\left({\xi }^3\right)}^3,{\left({\xi }^3\right)}^4\right\}\rho \left({\xi }^3\right)Jd{\xi }^3,}$$

where $\rho \left({\xi }^3\right)$ is the mass density.

In Equation (19), the contravariant components $A^{ijkl},B^{ijkl},D^{ijkl}$ are the effective extensional, extensional–bending coupling, and bending fourth-order stiffness tensor components [47]. Such components are calculated using the following definitions:

$$\begin{array}{ccc}{\displaystyle A^{ijkl}={\int }_{-1}^1{C}^{ijkl}Jd{\xi }^3,}\hfill & {\displaystyle B^{ijkl}={\int }_{-1}^1{\xi }^3{C}^{ijkl}Jd{\xi }^3,}\hfill & {\displaystyle D^{ijkl}={\int }_{-1}^1{\left({\xi }^3\right)}^2{C}^{ijkl}Jd{\xi }^3.}\hfill \end{array}$$

The expressions of Equations (18) and (19) are used to determine the mass and stiffness matrices, respectively.

5. Finite Element Model

The present vibration analysis assumes harmonic motion; therefore, the generalized displacements $\underline{\mathbf{u}}\left({\xi }^{\alpha },t\right)$, $\mathit{\phi }\left({\xi }^{\alpha },t\right)$ and the seventh parameter $\mathsf{\Psi }$ can be expressed as [53]

$$\begin{array}{ccc}\hfill \underline{\mathbf{u}}\left({\xi }^{\alpha },t\right)& =& \underline{\mathbf{u}}\left({\xi }^{\alpha }\right)e^{-i\omega t},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill \mathit{\phi }\left({\xi }^{\alpha },t\right)& =& \mathit{\phi }\left({\xi }^{\alpha }\right)e^{-i\omega t},\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill \mathsf{\Psi }\left({\xi }^{\alpha },t\right)& =& \mathsf{\Psi }\left({\xi }^{\alpha }\right)e^{-i\omega t},\hfill \end{array}$$

(22)

Note that $\omega$ represents the frequency of natural vibration and $i=\sqrt{-1}$. For the finite element approximation, the displacements and the seventh parameter are approximated as

$$\begin{array}{ccc}{\displaystyle \underline{\mathbf{u}}\left({\xi }^{\alpha }\right)=\sum _{j=1}^q{\psi }_j\left({\xi }^{\alpha }\right)\underline{\mathbf{u}},}& {\displaystyle \mathit{\phi }\left({\xi }^{\alpha }\right)=\sum _{j=1}^q{\psi }_j\left({\xi }^{\alpha }\right)\mathit{\phi },}& {\displaystyle \mathsf{\Psi }\left({\xi }^{\alpha }\right)=\sum _{j=1}^q{\psi }_j\left({\xi }^{\alpha }\right)\mathsf{\Psi }.}\end{array}$$

(23)

To obtain the mass matrix $\left[{\mathbf{M}}^e\right]$ and the stiffness matrix $\left[{\mathbf{K}}^e\right]$ of the element e, the generalized displacements and the seventh parameter must be replaced by their approximations in the virtual kinetic energy of Equation (18) and in the virtual strain energy of Equation (19), respectively.

Therefore, the finite element model (i.e., the eigenvalue problem) governing the free vibration analysis can be written as

$$\left(\left[\mathbf{K}\right]-{\omega }^2\left[\mathbf{M}\right]\right)\left\{\mathbf{\Delta }\right\}=\left\{0\right\},$$

(24)

where $\left\{\mathbf{\Delta }\right\}$ is the vibration mode vector associated with $\omega$, and $\left[\mathbf{K}\right]$ and $\left[\mathbf{M}\right]$ are the global stiffness and mass matrices, respectively, which result from assembling the local stiffness and mass matrices of each element. Note that, if it is the case, boundary conditions must be applied to the global matrices. In this work, the eigenvalue problem is solved using a C++ template library for linear algebra called Eigen [54].

Finally, to illustrate the general process for the present finite element analysis, a flowchart is depicted in Figure 2. The dashed rectangle represents the processes executed for each seven-parameter element in the model mesh.

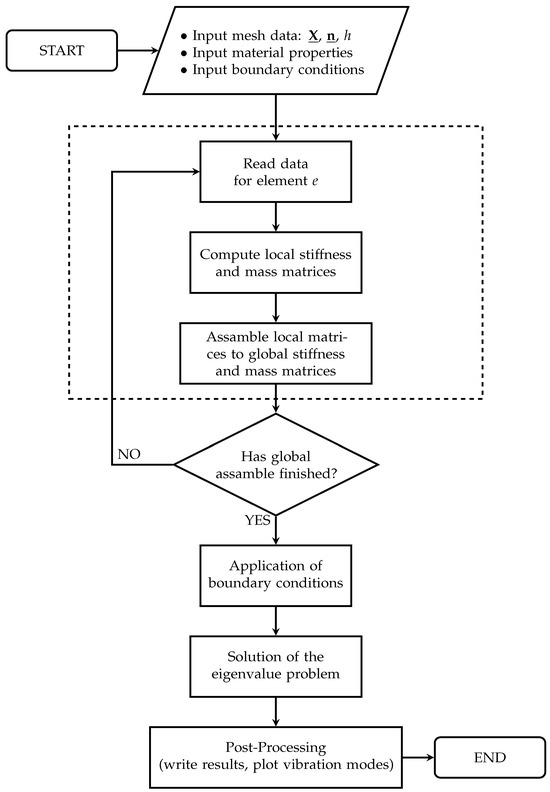
Figure 2. Flowchart for the overall finite element analysis process.

6. Solid Model

This section presents a brief description about the solid model made in ANSYS, which is used to compare results with the ones obtained by means of the present finite element model.

The solid model is meshed using linear solid elements, i.e., SOLID185 elements. To emulate the mechanical property variations of the FGM, several layers were defined through thickness direction. An isotropic material was assigned to each layer, where its mechanical properties were evaluated according to its position along the thickness direction and using Equation (11). For instance, in Figure 3, a close-up image of the materials through the thickness direction is depicted.

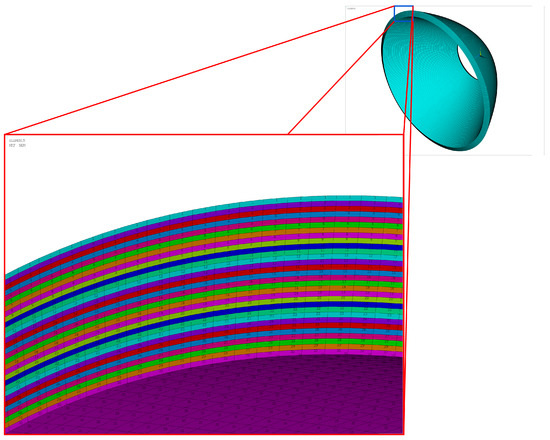
Figure 3. Solid model for a parabolic shell and a close-up image showing the materials through thickness direction.

Regarding the boundary conditions used in this study, clamped edge and simply supported edge, these are defined as follows:

• Clamped edge: all the degrees of freedom of the nodes associated with the corresponding edge are constrained.
• Simply supported edge: all the degrees of freedom for the nodes located at the mid-surface of the solid model are constrained, and the remaining nodes are constrained in the tangential and the thickness directions.

Note that, in order to obtain nodes at the mid-surface, an even number of layers must be defined, since linear solid elements are used.

7. Results

In this section, the geometrical parameters of the shell structures analyzed here are introduced. In addition, the convergence studies and numerical comparisons are included. At the end, the influence of the geometrical parameters and material properties on the natural frequencies is presented to illustrate the performance of the present model. All natural frequencies are reported in Hertz.

7.1. Geometrical Parameters

For the shells studied here, the position vector used to describe the mid-surface of the shell and the functions for variation of the thickness are listed below. In addition, the geometrical parameters are depicted in Figure 4, Figure 5 and Figure 6. Note that the thickness variation is linear for all the shells, and the conical, parabolic, and hemispherical shells are truncated.

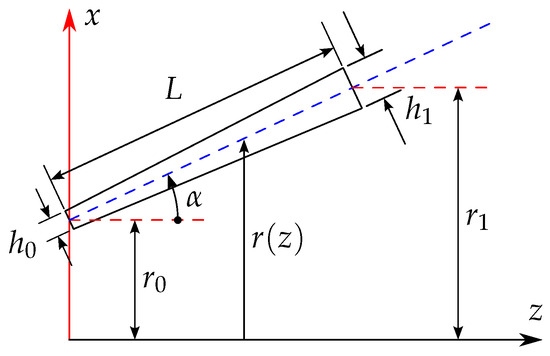
Figure 4. Geometrical parameters and revolution profile for a conical shell.

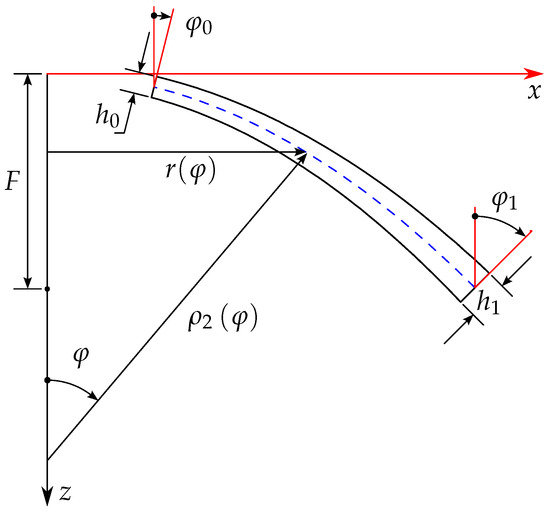
Figure 5. Geometrical parameters and revolution profile for a parabolic shell.

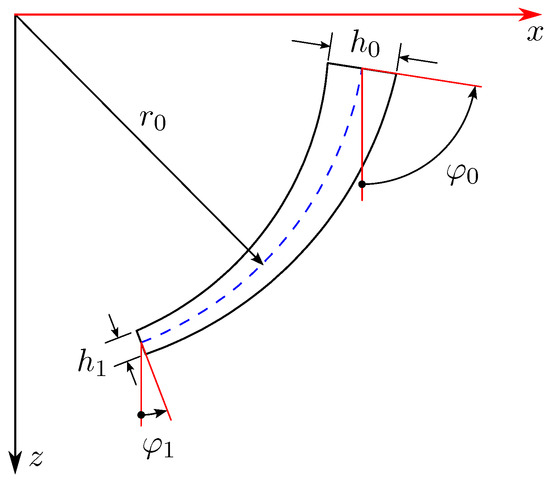
Figure 6. Geometrical parameters and revolution profile for a hemispherical shell.

1.

Conical shell

• Mid-surface:

  $$\mathbf{r}(\theta ,z)=r\left(z\right)cos\theta \widehat{\mathbf{i}}+r\left(z\right)sin\theta \widehat{\mathbf{j}}+z\widehat{\mathbf{k}},\begin{array}{c}0\le z\le Lcos\alpha \\ 0\le \alpha <\pi /2\\ 0\le \theta \le 2\pi \end{array}$$

  (25)

  where $r\left(z\right)=r_0+{\displaystyle \frac{r_1-r_0}{Lcos\alpha }}z$.
• Thickness variation:

  $$h\left(z\right)=h_0+\left(h_1-h_0\right){\displaystyle \frac{z}{Lcos\alpha }},\begin{array}{c}0\le z\le Lcos\alpha \\ 0\le \alpha <\pi /2\end{array}$$

  (26)

2.

Cylindrical shell $\left(\alpha =0\right)$

• Mid-surface:

  $$\mathbf{r}(\theta ,z)=r_{0}cos\theta \widehat{\mathbf{i}}+r_{0}sin\theta \widehat{\mathbf{j}}+z\widehat{\mathbf{k}},\begin{array}{c}0\le z\le L\\ 0\le \theta \le 2\pi \end{array}$$

  (27)
• Thickness variation:

  $$h\left(z\right)=h_0\left[1+{\displaystyle \frac{h_1-h_0}{h_0}}{\displaystyle \frac{z}{L}}\right],0\le z\le L$$

  (28)

3.

Parabolic shell

• Mid-surface:

  $$\mathbf{r}(\phi ,\theta )=r\left(\phi \right)cos\theta \widehat{\mathbf{i}}+r\left(\phi \right)sin\theta \widehat{\mathbf{j}}+{\displaystyle \frac{r{\left(\phi \right)}^2}{4F}}\widehat{\mathbf{k}},\begin{array}{c}{\phi }_0\le \phi \le {\phi }_1\\ 0\le \theta \le 2\pi \end{array}$$

  (29)

  where $r\left(\phi \right)=2Ftan\phi$, with F being the focal distance [55].
• Thickness variation:

  $$h\left(\phi \right)=h_0\left[1+\beta \left({\displaystyle \frac{\phi -{\phi }_0}{{\phi }_1-{\phi }_0}}\right)\right],{\phi }_0\le \phi \le {\phi }_1$$

  (30)

4.

Hemispherical shell

• Mid-surface:

  $$\mathbf{r}(\phi ,\theta )=r_{0}sin\phi cos\theta \widehat{\mathbf{i}}+r_{0}sin\phi sin\theta \widehat{\mathbf{j}}+r_{0}cos\phi \widehat{\mathbf{k}},\begin{array}{c}{\phi }_0\le \phi \le {\phi }_1\\ 0\le \theta \le 2\pi \end{array}$$

  (31)
• Thickness variation:

  $$h\left(\phi \right)=h_0\left[1-\beta \left({\displaystyle \frac{\phi -{\phi }_0}{{\phi }_1-{\phi }_0}}\right)\right],{\phi }_0\ge \phi \ge {\phi }_1$$

  (32)

An additional parameter, used in the following sections when reporting natural frequencies of shells with variable thickness, is the average thickness, $h_m$, which is defined as

$$h_m={\displaystyle \frac{h_0+h_1}{2}}.$$

(33)

7.2. Boundary Conditions

For convenience, a nomenclature based on capital letters is used to describe the boundary conditions applied in each case of study. The letters C, F, and S denote a clamped edge, a free edge, and a simply supported edge, respectively.

The clamped edge (C) restricts all the degrees of freedom associated with the nodes at the end that represent the maximum thickness, while the nodes located at a free edge (F) are unrestricted.

Furthermore, the parabolic shell structure analyzed here is subjected to SF boundary conditions (i.e., simply-supported-free). Therefore, the degrees of freedom of the nodes at the simply supported edge (S) are restricted as follows:

$$\underline{\mathbf{u}}=\mathsf{\Psi }=0.$$

(34)

7.3. Material Properties

The mechanical properties used in this work, for the bottom and top constituents, are listed below [23]:

• Aluminum: $E_{bot}=70$ GPa, ${\rho }_{bot}=2707$ kg/m${}^3$, ${\nu }_{bot}=0.3$;
• Zirconia: $E_{top}=168$ GPa, ${\rho }_{top}=5700$ kg/m${}^3$, ${\nu }_{top}=0.3$.

where $E_i$ is the modulus of elasticity, ${\rho }_i$ denotes the mass density, and ${\nu }_i$ the Poisson’s ratio. Note that subindex i indicates the surface position.

7.4. Convergence Study

To achieve mesh independence, convergence studies were performed for each shell geometry analyzed in this work. The results of these studies are presented and discussed in Appendix A. It is worth mentioning that for all cases analyzed with the present finite element model, seven-parameter elements of order $p=8$ were used to mesh the domains.

In general, for the shells with uniform thickness (UT) and linear variable thickness (LVT) studied in this work, it is observed that convergence is obtained with a mesh size of 25 elements—within the first ten frequencies. The only case where a good convergence is achieved with a mesh size of 16 elements is the parabolic shell with UT.

7.5. Numerical Verification

To verify the performance of the present model, the natural frequencies obtained were compared with those results reported in the literature. It must be noted that the numerical comparisons correspond to shells with uniform thickness. In addition, a comparison is included with results obtained by using linear solid elements (SOLID185). The latter allows us to verify the behavior of the present model for shells with thickness variation.

In the following comparisons, the natural frequencies obtained by means of the present model are indicated by the label 7-PL. On the other hand, the label 3D represents the results obtained using solid elements in the commercial code ANSYS.

Table 1, Table 2 and Table 3 present a comparison for conical, cylindrical, and parabolic shells, respectively. The natural frequencies obtained using the present formulation show very good agreement with the ones reported in the literature and the ones computed by means of solid elements in ANSYS.

Table 1. Comparison for a conical shell with UT and CF boundary conditions (FG-II).

		Natural Frequency
$\mathit{n}$	Model	${\mathit{f}}_{\mathbf{1}}$–${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$–${\mathit{f}}_{\mathbf{4}}$	${\mathit{f}}_{\mathbf{5}}$–${\mathit{f}}_{\mathbf{6}}$	${\mathit{f}}_{\mathbf{7}}$–${\mathit{f}}_{\mathbf{8}}$	${\mathit{f}}_{\mathbf{9}}$–${\mathit{f}}_{\mathbf{10}}$	${\mathit{f}}_{\mathbf{11}}$–${\mathit{f}}_{\mathbf{12}}$	${\mathit{f}}_{\mathbf{13}}$–${\mathit{f}}_{\mathbf{14}}$	${\mathit{f}}_{\mathbf{15}}$
0.6	7-PL	206.20	225.98	279.08	318.23	348.99	355.98	398.53	444.36
	3D *	205.93	226.02	279.55	318.32	348.57	356.80	397.36	444.55
	FSDT [22]	205.96	225.52	277.93	318.18	349.48	-	-	-
1	7-PL	205.12	224.88	277.82	316.39	347.13	354.42	396.71	441.88
	3D *	204.79	224.81	278.08	316.47	346.59	354.94	395.26	442.02
	FSDT [22]	204.91	224.44	276.66	316.32	347.66	-	-	-
5	7-PL	204.19	228.16	285.59	309.64	346.64	366.47	404.55	434.38
	3D *	203.69	227.75	285.14	309.65	345.64	365.74	402.10	434.30
	FSDT [22]	203.93	227.67	284.26	309.57	347.08	-	-	-

* 1,188,000 SOLID185 elements.

Table 2. Comparison for a cylindrical shell with UT and CF boundary conditions (FG-II).

		Natural Frequency
$\mathit{n}$	Model	${\mathit{f}}_{\mathbf{1}}$–${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$–${\mathit{f}}_{\mathbf{4}}$	${\mathit{f}}_{\mathbf{5}}$–${\mathit{f}}_{\mathbf{6}}$	${\mathit{f}}_{\mathbf{7}}$–${\mathit{f}}_{\mathbf{8}}$	${\mathit{f}}_{\mathbf{9}}$	${\mathit{f}}_{\mathbf{10}}$–${\mathit{f}}_{\mathbf{11}}$	${\mathit{f}}_{\mathbf{12}}$–${\mathit{f}}_{\mathbf{13}}$	${\mathit{f}}_{\mathbf{14}}$–${\mathit{f}}_{\mathbf{15}}$
0.6	7-PL	148.95	213.76	250.23	375.14	414.34	418.82	454.43	523.52
	3D *	148.68	212.79	250.17	372.70	414.69	417.01	453.73	519.60
	FSDT [22]	150.03	212.94	250.74	370.63	415.47	420.39	-	-
1	7-PL	148.07	213.04	248.56	374.04	411.54	416.78	451.68	521.55
	3D *	147.74	211.83	248.49	371.09	411.89	414.67	450.87	517.02
	FSDT [22]	149.29	212.22	249.31	369.46	412.97	418.46	-	-
5	7-PL	147.51	220.44	242.75	388.72	401.19	422.08	446.11	537.48
	3D *	147.04	218.65	242.64	384.31	401.56	418.91	444.89	530.75
	FSDT [22]	148.75	219.49	243.43	383.71	402.56	423.57	-	-

* 990,000 SOLID185 elements.

Table 3. Comparison for a parabolic shell with UT and SF boundary conditions (FG-I).

		Natural Frequency
$\mathit{n}$	Model	${\mathit{f}}_{\mathbf{1}}$–${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$–${\mathit{f}}_{\mathbf{4}}$	${\mathit{f}}_{\mathbf{5}}$–${\mathit{f}}_{\mathbf{6}}$	${\mathit{f}}_{\mathbf{7}}$	${\mathit{f}}_{\mathbf{8}}$	${\mathit{f}}_{\mathbf{9}}$	${\mathit{f}}_{\mathbf{10}}$–${\mathit{f}}_{\mathbf{11}}$	${\mathit{f}}_{\mathbf{12}}$–${\mathit{f}}_{\mathbf{13}}$
0.6	7-PL	115.04	162.58	162.67	190.60	194.75	194.75	205.35	218.29
	3D *	115.01	162.54	162.88	190.60	195.42	195.42	205.37	217.36
	FSDT [23]	115.40	162.85	165.07	193.28	193.28	196.66	210.82	-
1	7-PL	114.15	161.55	161.83	189.18	193.88	193.88	203.94	217.37
	3D *	114.10	161.52	161.98	189.16	194.43	194.43	203.95	216.39
	FSDT [23]	114.49	161.95	164.01	192.32	192.32	195.22	209.38	-
5	7-PL	114.15	157.94	161.82	186.26	195.78	195.78	202.13	218.63
	3D *	113.98	157.87	161.79	186.15	196.02	196.02	201.99	217.16
	FSDT [23]	114.44	160.33	161.78	194.04	194.04	194.05	207.19	-

* 840,000 SOLID185 elements.

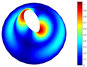
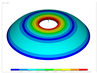
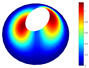
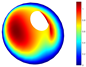
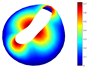
In addition, Table 4 shows a comparison of the vibration modes for a parabolic shell with uniform thickness and with a volume distribution of the type FG-I. A very good coincidence is observed in the depicted modes. Moreover, similar modes were reported in [23].

Table 4. Vibration mode comparison for a parabolic shell with UT and SF boundary conditions, $n=5$ (FG-I).

Model	Vibration Mode
	${\mathit{f}}_{\mathbf{1}}$–${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$–${\mathit{f}}_{\mathbf{4}}$	${\mathit{f}}_{\mathbf{5}}$–${\mathit{f}}_{\mathbf{6}}$	${\mathit{f}}_{\mathbf{7}}$	${\mathit{f}}_{\mathbf{8}}$–${\mathit{f}}_{\mathbf{9}}$	${\mathit{f}}_{\mathbf{10}}$–${\mathit{f}}_{\mathbf{11}}$
7-PL	$114.15$ Hz	$157.94$ Hz	$161.82$ Hz	$186.26$ Hz	$195.78$ Hz	$202.13$ Hz
3D	$113.98$ Hz	$157.87$ Hz	$161.79$ Hz	$186.15$ Hz	$196.02$ Hz	$201.99$ Hz

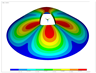
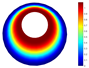
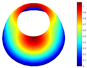
Finally, a comparison of the natural frequencies for a hemispherical shell with constant thickness and CF boundary conditions is shown in Table 5. The results of the present model and the 3D model are in accordance with those reported in [23].

Table 5. Comparison for a hemispherical shell with UT and CF boundary conditions (FG-I).

		Natural Frequency
$\mathit{n}$	Model	${\mathit{f}}_{\mathbf{1}}$–${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$–${\mathit{f}}_{\mathbf{4}}$	${\mathit{f}}_{\mathbf{5}}$–${\mathit{f}}_{\mathbf{6}}$	${\mathit{f}}_{\mathbf{7}}$–${\mathit{f}}_{\mathbf{8}}$	${\mathit{f}}_{\mathbf{9}}$	${\mathit{f}}_{\mathbf{10}}$–${\mathit{f}}_{\mathbf{11}}$	${\mathit{f}}_{\mathbf{12}}$–${\mathit{f}}_{\mathbf{13}}$	${\mathit{f}}_{\mathbf{14}}$–${\mathit{f}}_{\mathbf{15}}$
0.6	7-PL	142.75	204.61	286.86	335.28	379.76	411.97	450.15	457.29
	3D *	143.01	205.53	286.90	336.75	379.75	411.97	450.15	459.24
	FSDT [23]	142.56	204.01	286.77	334.14	379.53	411.83	-	-
1	7-PL	141.76	203.20	284.87	332.97	377.05	409.05	446.97	454.12
	3D *	142.01	204.09	284.89	334.38	377.04	409.05	446.96	456.00
	FSDT [23]	141.59	202.64	284.78	331.87	376.84	408.93	-	-
5	7-PL	141.34	207.57	278.77	338.35	369.92	401.34	440.98	456.69
	3D *	141.43	207.98	278.72	338.95	369.76	401.19	440.70	457.67
	FSDT [23]	141.14	206.90	278.68	337.12	369.68	401.19	-	-

* 1,017,000 SOLID185 elements.

7.6. Numerical Results

The main aim of this section is to present the natural frequencies for several type of shells with LVT, such as conical, cylindrical, parabolic, and hemispherical. Along with the present results (7-PL), the natural frequencies obtained by means of solid elements in ANSYS are included for comparison purposes. For all study cases and listed frequencies, the maximum relative errors of the present model with respect to 3D result are reported for each power-law index.

The natural frequencies for conical shells with LVT under CF boundary conditions are presented in Table 6, Table 7 and Table 8 for different values of the ratio $r_0/h_m$ and angle $\alpha$. The volume distribution of the top constituent follows the expression of Equation (13), i.e., FG-II.

Table 6. Natural frequencies for conical shells with LVT and CF boundary conditions (FG-II, $r_0/h_m=2.5$, $h_m=3/4$, $L/h_m=10$, $h_1/h_0=2$).

	$\mathit{\alpha }={30}^{\circ }$						$\mathit{\alpha }={60}^{\circ }$
	$\mathit{n}$						$\mathit{n}$
	$\mathbf{0}.\mathbf{6}$		1		5		$\mathbf{0}.\mathbf{6}$		1		5
	7PL	3D	7PL	3D	7PL	3D	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	101.96	99.10	101.58	98.62	103.00	99.57	88.96	86.55	88.61	86.12	90.34	87.46
$f_3$–$f_4$	125.12	124.75	124.38	124.02	121.97	121.50	93.71	92.40	93.41	91.98	92.86	91.27
$f_5$	160.29	155.02	159.92	154.34	164.31	157.48	106.33	105.18	106.04	104.73	104.82	103.43
$f_6$	160.29	155.02	159.92	154.34	164.31	157.48	120.96	117.73	120.49	117.11	124.14	119.97
$f_7$	181.57	177.36	180.78	176.37	182.29	176.86	120.96	117.73	120.49	117.11	124.14	119.97
$f_8$	181.57	177.36	180.78	176.37	182.29	176.86	154.15	151.57	153.71	150.91	153.15	149.78
$f_9$	205.72	204.42	204.22	203.21	198.99	199.79	159.58	156.52	159.04	155.78	159.71	155.72
$f_{10}$	205.91	204.42	204.77	203.21	201.79	199.86	159.58	156.52	159.04	155.78	159.71	155.72
$f_{11}$	205.91	206.41	204.77	205.02	201.79	199.87	164.50	160.34	163.86	159.44	168.87	163.06
$f_{12}$	207.73	206.85	207.01	205.99	202.72	201.65	164.50	160.34	163.86	159.44	168.87	163.06
Max. Error	$3.40\%$	-	$3.61\%$	-	$4.34\%$	-	$2.77\%$	-	$2.89\%$	-	$3.56\%$	-

Table 7. Natural frequencies for conical shells with LVT and CF boundary conditions (FG-II, $r_0/h_m=5$, $h_m=3/4$, $L/h_m=10$, $h_1/h_0=2$).

	$\mathit{\alpha }={30}^{\circ }$						$\mathit{\alpha }={60}^{\circ }$
	$\mathit{n}$						$\mathit{n}$
	$\mathbf{0}.\mathbf{6}$		1		5		$\mathbf{0}.\mathbf{6}$		1		5
	7PL	3D	7PL	3D	7PL	3D	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	73.76	72.43	73.38	72.01	73.23	71.65	64.23	62.47	63.98	62.16	64.69	62.64
$f_3$–$f_4$	84.73	82.08	84.41	81.68	86.67	83.55	72.78	71.76	72.55	71.44	71.84	70.62
$f_5$–$f_6$	104.14	103.72	103.58	103.14	101.67	101.15	77.18	74.79	76.86	74.40	79.19	76.38
$f_7$	124.04	120.57	123.65	120.00	127.76	123.35	82.39	81.54	82.17	81.20	80.96	79.93
$f_8$	124.04	120.57	123.65	120.00	127.76	123.35	105.15	102.48	104.71	101.93	108.29	104.89
$f_9$	151.23	147.91	150.50	147.07	149.20	147.02	105.15	102.48	104.71	101.93	108.29	104.89
$f_{10}$	151.23	147.91	150.50	147.07	151.13	147.02	119.33	115.18	118.91	114.62	119.88	114.99
$f_{11}$	152.28	151.27	151.73	150.61	151.13	148.02	121.86	117.67	121.40	117.08	122.83	117.87
$f_{12}$	156.70	152.27	156.02	151.42	158.92	153.33	121.86	117.67	121.40	117.08	122.83	117.87
Max. Error	$3.22\%$	-	$3.34\%$	-	$3.74\%$	-	$3.61\%$	-	$3.74\%$	-	$4.25\%$	-

Table 8. Natural frequencies for conical shells with LVT and CF boundary conditions (FG-II, $r_0/h_m=10$, $h_m=3/4$, $L/h_m=10$, $h_1/h_0=2$).

	$\mathit{\alpha }={30}^{\circ }$						$\mathit{\alpha }={60}^{\circ }$
	$\mathit{n}$						$\mathit{n}$
	$\mathbf{0}.\mathbf{6}$		1		5		$\mathbf{0}.\mathbf{6}$		1		5
	7PL	3D	7PL	3D	7PL	3D	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	52.69	51.04	52.43	50.75	52.89	51.00	45.53	43.84	45.36	43.63	45.57	43.66
$f_3$–$f_4$	58.04	55.90	57.78	55.60	58.52	56.87	46.64	44.56	46.44	44.33	47.45	45.13
$f_5$–$f_6$	59.39	58.42	59.08	58.08	59.31	57.38	50.32	48.99	50.15	48.77	49.73	48.21
$f_7$	72.78	70.51	72.48	70.14	74.97	72.28	54.03	52.76	53.87	52.48	53.19	51.78
$f_8$	72.78	70.51	72.48	70.14	74.98	72.28	54.96	52.76	54.71	52.48	56.50	54.00
$f_9$	77.08	76.52	76.69	76.11	75.30	74.63	54.96	52.81	54.71	52.58	56.50	54.00
$f_{10}$	77.08	76.52	76.69	76.11	75.30	74.63	68.97	66.86	68.65	66.49	71.16	68.65
$f_{11}$	92.91	91.54	92.51	91.07	90.61	89.98	68.97	66.86	68.65	66.49	71.16	68.65
$f_{12}$	93.83	91.54	93.45	91.07	96.85	93.97	87.13	85.17	86.73	84.70	89.95	87.44
Max. Error	$3.84\%$	-	$3.92\%$	-	$3.73\%$	-	$4.66\%$	-	$4.76\%$	-	$5.14\%$	-

From the comparisons presented in Table 6, Table 7 and Table 8, the maximum values of relative error ranges from $3.22\%$ to $4.34\%$ for conical shells with an angle $\alpha ={30}^{\circ }$, and the maximum value is obtained when $n=5$. Regarding the conical shells with $\alpha ={60}^{\circ }$, the maximum errors are found in a range from $2.77\%$ to $5.14\%$, with the maximum value occurring when $n=5$. Considering fixed values of the power-law exponent, the natural frequencies decrease as the value of ratio $r_0/h_m$ increases, which is an expected behavior since the ratio values reported are related to thick and thin shells. In addition, the angle $\alpha$ also has an influence on the natural frequencies as it can be seen for fixed ratios of $r_0/h_m$, that is, lower values are obtained as the angle $\alpha$ increases.

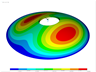
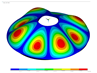
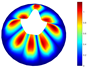
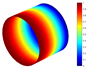
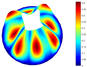
In Table 9, several vibration modes for a conical shell with LVT, CF boundary conditions, and $n=0.6$ are compared with those obtained by means of the solid elements (3D model). For both models, the vibration modes are very similar.

Table 9. Vibration modes for a conical shell with LVT, CF boundary conditions and $\alpha ={60}^{\circ }$, $n=0.6$ (FG-II, $r_0/h_m=5$, $h_m=3/4$, $L/h_m=10$, $h_1/h_0=2$).

Model	Vibration Mode
	${\mathit{f}}_{\mathbf{1}}$–${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$–${\mathit{f}}_{\mathbf{4}}$	${\mathit{f}}_{\mathbf{5}}$–${\mathit{f}}_{\mathbf{6}}$	${\mathit{f}}_{\mathbf{7}}$	${\mathit{f}}_{\mathbf{8}}$–${\mathit{f}}_{\mathbf{9}}$	${\mathit{f}}_{\mathbf{10}}$	${\mathit{f}}_{\mathbf{11}}$–${\mathit{f}}_{\mathbf{12}}$
7-PL	$64.23$ Hz	$72.78$ Hz	$77.18$ Hz	$82.39$ Hz	$105.15$ Hz	$119.33$ Hz	$121.86$ Hz
3D	$62.47$ Hz	$71.76$ Hz	$74.79$ Hz	$81.54$ Hz	$102.48$ Hz	$115.18$ Hz	$117.67$ Hz

In Table 10, Table 11 and Table 12, the natural frequencies for several ratios $r_0/h_m$ of a cylindrical shell with LVT subjected to CF boundary conditions are reported.

Table 10. Natural frequencies for a cylindrical shell with LVT and CF boundary conditions (FG-II, $r_0/h_m=2.5$, $h_m=3/4$, $L/h_m=10$, $h_1/h_0=2$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	64.07	63.72	63.28	62.98	62.17	61.75
$f_3$	123.97	121.23	122.50	120.98	119.37	121.87
$f_4$	129.65	121.23	129.78	120.98	134.06	124.17
$f_5$	129.65	126.14	129.78	124.89	134.06	124.17
$f_6$–$f_7$	191.89	191.01	190.34	189.49	186.81	185.65
$f_8$	203.99	203.77	202.46	202.23	197.49	197.18
$f_9$–$f_{10}$	217.19	204.85	217.00	204.04	220.95	205.82
$f_{11}$	313.85	294.01	314.23	293.37	320.46	299.19
$f_{12}$	313.85	294.01	314.23	293.37	323.41	299.19
Max. Error	$6.95\%$	-	$7.28\%$	-	$8.10\%$	-

Table 11. Natural frequencies for a cylindrical shell with LVT and CF boundary conditions (FG-II, $r_0/h_m=5$, $h_m=3/4$, $L/h_m=10$, $h_1/h_0=2$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	58.50	56.58	58.17	56.21	58.80	56.58
$f_3$–$f_4$	79.10	78.91	78.44	78.29	76.87	76.63
$f_5$–$f_6$	96.15	92.18	95.92	91.81	99.21	94.57
$f_7$	125.24	125.97	124.11	124.94	120.98	121.83
$f_8$–$f_9$	157.38	153.83	156.55	152.89	156.72	152.33
$f_{10}$–$f_{11}$	162.94	156.82	162.61	156.20	168.25	160.75
$f_{12}$–$f_{13}$	179.49	173.24	178.90	172.36	182.66	174.78
Max. Error	$4.31\%$	-	$4.48\%$	-	$4.91\%$	-

Table 12. Natural frequencies for a cylindrical shell with LVT and CF boundary conditions (FG-II, $r_0/h_m=10$, $h_m=3/4$, $L/h_m=10$, $h_1/h_0=2$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	48.37	46.58	48.11	46.30	48.72	46.67
$f_3$–$f_4$	54.00	53.11	53.65	52.75	53.14	52.09
$f_5$–$f_6$	58.00	55.57	57.75	55.28	59.51	56.76
$f_7$–$f_8$	76.64	75.27	76.13	74.90	74.61	74.25
$f_9$–$f_{10}$	78.00	76.34	77.70	75.84	80.52	77.33
$f_{11}$–$f_{12}$	104.59	101.58	104.20	101.09	108.05	104.37
Max. Error	$4.36\%$	-	$4.46\%$	-	$4.84\%$	-

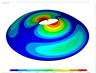
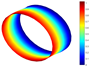
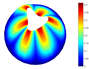
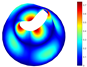
For the natural frequencies presented in Table 10, Table 11 and Table 12, corresponding to cylindrical shells, the range for the maximum errors is between $4.31\%$ and $8.10\%$, with the maximum value occurring in the case when $r_0/h_m=2.5$ and $n=5$. Note that the aforementioned radius-to-thickness ratio describes a very thick shell. However, for greater values of the ratio, the value of errors are below $4.91\%$. For illustration purposes, a comparison of several vibration modes of a cylindrical shell with LVT, CF boundary conditions, and $n=5$ is presented in Table 13.

Table 13. Vibration modes for a cylindrical shell with LVT and CF boundary conditions, $n=5$ (FG-II, $r_0/h_m=5$, $h_m=3/4$, $L/h_m=10$, $h_1/h_0=2$).

Model	Vibration Mode
	${\mathit{f}}_{\mathbf{1}}$–${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$–${\mathit{f}}_{\mathbf{4}}$	${\mathit{f}}_{\mathbf{5}}$–${\mathit{f}}_{\mathbf{6}}$	${\mathit{f}}_{\mathbf{7}}$	${\mathit{f}}_{\mathbf{8}}$–${\mathit{f}}_{\mathbf{9}}$	${\mathit{f}}_{\mathbf{10}}$
7-PL	$58.80$ Hz	$76.87$ Hz	$99.21$ Hz	$120.98$ Hz	$156.72$ Hz	$168.25$ Hz
3D	$56.58$ Hz	$76.63$ Hz	$94.57$ Hz	$121.83$ Hz	$152.33$ Hz	$160.75$ Hz

Natural frequencies for parabolic shells with LVT and under SF boundary conditions are presented in Table 14, Table 15 and Table 16. The volume distribution of the top constituent follows the expression of Equation (12), i.e., FG-I.

Table 14. Natural frequencies for a parabolic shell with LVT and SF boundary conditions (FG-I, $F/h_m=5$, $F=0.875$ m, $\beta =1.5$, ${\phi }_0=\pi /6$, ${\phi }_1=\pi /3$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	138.98	133.61	137.35	132.00	136.85	130.85
$f_3$–$f_4$	181.80	177.58	180.53	176.21	183.46	179.06
$f_5$–$f_6$	232.68	232.88	230.73	230.96	225.53	225.64
$f_7$–$f_8$	252.57	252.06	251.06	250.34	255.86	254.68
$f_9$–$f_{10}$	302.11	298.29	300.57	296.72	299.31	294.62
$f_{11}$–$f_{12}$	306.54	300.91	305.01	299.20	309.83	303.04
Max. Error	$4.02\%$	-	$4.05\%$	-	$4.59\%$	-

Table 15. Natural frequencies for a parabolic shell with LVT and SF boundary conditions (FG-I, $F/h_m=10$, $F=0.875$ m, $\beta =1.5$, ${\phi }_0=\pi /6$, ${\phi }_1=\pi /3$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	119.48	115.77	118.64	114.89	118.94	116.41
$f_3$–$f_4$	122.05	119.91	120.77	118.66	120.81	116.84
$f_5$–$f_6$	172.76	172.33	171.76	171.22	173.29	172.75
$f_7$–$f_8$	208.23	210.71	207.04	209.37	209.48	211.53
$f_9$–$f_{10}$	228.63	227.59	227.39	226.31	223.38	223.67
$f_{11}$–$f_{12}$	230.51	230.82	228.80	229.13	225.88	224.48
Max. Error	$3.21\%$	-	$3.26\%$	-	$3.40\%$	-

Table 16. Natural frequencies for a parabolic shell with LVT and SF boundary conditions (FG-I, $F/h_m=20$, $F=0.875$ m, $\beta =1.5$, ${\phi }_0=\pi /6$, ${\phi }_1=\pi /3$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	78.31	78.03	77.70	77.41	78.79	78.05
$f_3$–$f_4$	112.95	114.96	112.32	114.26	112.91	112.39
$f_5$–$f_6$	116.41	116.08	115.36	115.04	115.13	116.39
$f_7$–$f_8$	155.52	159.99	154.62	158.99	154.93	158.71
$f_9$–$f_{10}$	170.88	176.93	169.87	175.80	170.10	175.69
$f_{11}$–$f_{12}$	182.82	184.09	181.73	182.96	179.73	180.76
Max. Error	$3.42\%$	-	$3.38\%$	-	$3.18\%$	-

From the comparisons presented for parabolic shells in Table 14, Table 15 and Table 16, the maximum values of relative error are within the range of $3.18\%$ to $4.59\%$. In these comparisons, note that for a thin shell (e.g., $F/h_m=20$), the maximum error occurs when $n=0.6$, conversely to minor values of the ratio. For a fixed value of the volume fraction exponent, a decrease in values of the natural frequencies is observed as the ratio $F/h_m$ increases.

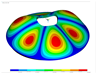
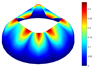
To complement the comparisons presented for parabolic shells, the vibration modes corresponding to a parabolic shell with LVT, SF boundary conditions, and $n=0.6$ are shown in Table 17. It can be noted that similar contours are obtained using both models.

Table 17. Vibration modes for a parabolic shell with LVT and SF boundary conditions, $n=0.6$ (FG-I, $F/h_m=5$, $F=0.875$ m, $\beta =1.5$, ${\phi }_0=\pi /6$, ${\phi }_1=\pi /3$).

Model	Vibration Mode
	${\mathit{f}}_{\mathbf{1}}$–${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$–${\mathit{f}}_{\mathbf{4}}$	${\mathit{f}}_{\mathbf{5}}$–${\mathit{f}}_{\mathbf{6}}$	${\mathit{f}}_{\mathbf{7}}$–${\mathit{f}}_{\mathbf{8}}$	${\mathit{f}}_{\mathbf{9}}$–${\mathit{f}}_{\mathbf{10}}$	${\mathit{f}}_{\mathbf{11}}$–${\mathit{f}}_{\mathbf{12}}$
7-PL	$138.98$ Hz	$181.80$ Hz	$232.68$ Hz	$252.57$ Hz	$302.11$ Hz	$306.54$ Hz
3D	$133.61$ Hz	$177.58$ Hz	$232.88$ Hz	$252.06$ Hz	$298.29$ Hz	$300.91$ Hz

For the hemispherical shell, the natural frequencies for several values of the ratio $r_0/h_m$ are presented in Table 18, Table 19, Table 20 and Table 21.

Table 18. Natural frequencies for a hemispherical shell with LVT and CF boundary conditions (FG-I, $r_0/h_m=2.5$, $r_0=2$ m, $\beta =2$, ${\phi }_0=\pi /2$, ${\phi }_1=\pi /6$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	442.59	423.35	437.86	418.65	434.18	413.44
$f_3$–$f_4$	458.16	425.35	453.14	420.03	456.14	419.90
$f_5$	619.59	598.02	615.52	589.93	598.59	583.48
$f_6$	634.79	626.47	625.45	621.43	620.69	605.34
$f_7$–$f_8$	687.08	643.50	679.83	635.00	683.42	632.22
$f_9$	756.26	718.08	747.01	708.77	738.23	693.93
$f_{10}$–$f_{11}$	774.88	721.68	763.24	711.05	757.58	699.82
$f_{12}$	906.26	881.70	899.18	868.81	874.43	854.77
Max. Error	$7.16\%$	-	$7.31\%$	-	$7.95\%$	-

Table 19. Natural frequencies for a hemispherical shell with LVT and CF boundary conditions (FG-I, $r_0/h_m=5$, $r_0=2$ m, $\beta =2$, ${\phi }_0=\pi /2$, ${\phi }_1=\pi /6$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	312.90	292.48	310.07	289.79	315.58	293.36
$f_3$–$f_4$	382.61	375.14	379.14	371.83	375.03	366.38
$f_5$–$f_6$	461.50	433.85	457.54	429.81	467.90	437.24
$f_7$	563.95	542.00	556.87	536.10	550.30	528.42
$f_8$	632.93	598.01	625.57	591.51	619.64	588.23
$f_9$	632.93	598.02	625.57	591.51	626.45	588.23
$f_{10}$	634.47	614.37	628.57	608.52	626.45	602.37
$f_{11}$	639.65	642.00	635.46	637.34	626.63	621.72
$f_{12}$	687.48	654.55	681.40	648.09	694.55	655.38
Max. Error	$6.53\%$	-	$6.54\%$	-	$7.04\%$	-

Table 20. Natural frequencies for a hemispherical shell with LVT and CF boundary conditions (FG-I, $r_0/h_m=10$, $r_0=2$ m, $\beta =2$, ${\phi }_0=\pi /2$, ${\phi }_1=\pi /6$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	213.69	204.60	212.06	203.05	213.72	203.73
$f_3$–$f_4$	278.82	261.85	276.89	259.97	284.29	266.47
$f_5$–$f_6$	348.85	347.55	346.21	344.94	340.23	338.50
$f_7$–$f_8$	428.30	410.50	425.27	407.47	435.41	416.22
$f_9$	478.89	465.83	474.40	461.85	471.54	457.11
$f_{10}$–$f_{11}$	496.81	482.31	492.13	478.18	490.25	474.15
$f_{12}$	541.01	522.79	536.21	518.42	538.24	517.91
Max. Error	$6.08\%$	-	$6.11\%$	-	$6.27\%$	-

Table 21. Natural frequencies for a hemispherical shell with LVT and CF boundary conditions (FG-I, $r_0/h_m=20$, $r_0=2$ m, $\beta =2$, ${\phi }_0=\pi /2$, ${\phi }_1=\pi /6$).

	n
	$\mathbf{0.6}$		1		5
	7PL	3D	7PL	3D	7PL	3D
$f_1$–$f_2$	166.08	156.34	165.07	155.34	165.93	159.11
$f_3$–$f_4$	168.36	165.52	167.19	164.37	169.40	162.67
$f_5$–$f_6$	258.15	247.58	256.59	246.01	263.57	252.32
$f_7$–$f_8$	330.83	331.02	328.56	328.75	321.87	321.89
$f_9$–$f_{10}$	368.54	359.67	366.25	357.34	375.09	365.31
$f_{11}$	422.31	419.84	419.00	416.72	412.14	409.15
$f_{12}$–$f_{13}$	437.11	434.21	433.59	430.96	426.26	422.88
Max. Error	$5.87\%$	-	$5.89\%$	-	$4.27\%$	-

Lastly, from the natural frequencies of hemispherical shells presented in Table 18, Table 19, Table 20 and Table 21, it is noted that the maximum relative errors are above the values obtained in the previous comparisons reported here; they are found in a range between $4.27\%$ and $7.95\%$. The higher values of maximum relative errors occur when a very thick shell is analyzed, i.e., $r/h_m=2.5$. It must be mentioned that the majority of the maximum relative errors are above $5\%$.

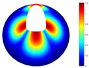
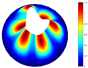
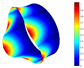
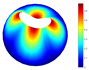
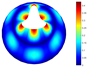
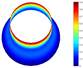
In addition, Table 22 presents comparisons of the vibration modes obtained using both models (7-PL and 3D) for a hemispherical shell with LVT, CF boundary conditions, and $n=5$. The similarities between models for vibration modes and natural frequencies are noted in these comparisons.

Table 22. Vibration modes for a hemispherical shell with LVT and CF boundary conditions, $n=5$ (FG-I, $r_0/h_m=10$, $r_0=2$ m, $\beta =2$, ${\phi }_0=\pi /2$, ${\phi }_1=\pi /6$).

Model	Vibration Mode
	${\mathit{f}}_{\mathbf{1}}$–${\mathit{f}}_{\mathbf{2}}$	${\mathit{f}}_{\mathbf{3}}$–${\mathit{f}}_{\mathbf{4}}$	${\mathit{f}}_{\mathbf{5}}$–${\mathit{f}}_{\mathbf{6}}$	${\mathit{f}}_{\mathbf{7}}$–${\mathit{f}}_{\mathbf{8}}$	${\mathit{f}}_{\mathbf{9}}$	${\mathit{f}}_{\mathbf{10}}$–${\mathit{f}}_{\mathbf{11}}$
7-PL	$213.72$ Hz	$284.29$ Hz	$340.23$ Hz	$435.41$ Hz	$471.54$ Hz	$490.25$ Hz
3D	$203.73$ Hz	$266.47$ Hz	$338.50$ Hz	$416.22$ Hz	$457.11$ Hz	$474.15$ Hz

In general, the behavior of natural frequencies is similar to that observed when analyzing thin and thick shells, that is, an increase in the frequencies value is observed when the shells become thicker. In addition, the study cases analyzed in this section demonstrate the behavior of the present model.

8. Conclusions

From the present work, the following conclusions can be drawn:

• A finite element model for the linear vibration analysis, using spectral/hp elements based on a seven-parameter shell formulation, is extended to study functionally graded shells.
• Comparisons with the numerical results of a simulation using solid elements verify the performance of the present formulation. In addition, the comparisons suggest that the present formulation shows a better behavior for the modeling of conical, cylindrical, and parabolic shells subjected to the boundary conditions considered herein.
• In general, although the relative errors are between $6\%$ and $8\%$ obtained in the study of hemispherical shells, the present formulation has a good behavior for moderately thick to thin shells. It must be recalled that mechanical properties through the thickness of the 3D model are approximated using several layers in this direction. On the other hand, in the studies reported using the present formulation, the variation of the mechanical properties is evaluated using several Gauss-points while numerical integration through thickness is made, resulting in a closer approximation of them. For the aforementioned reasons, some differences between results, but a similar behavior, can be expected.
• Studying the effect of the power-law index on the free vibration response is relevant since, for a given thick or thin shell and boundary conditions, its response may be stiffer or not as the power-law index increases.
• Finally, the spectral/hp seven-parameter formulation used in the present finite element model allows a straightforward implementation of the FGM behavior and the use of three-dimensional constitutive equations. These features allow the use of considerably fewer elements, and therefore computational time, to model FG shell structures, when compared with models made of solid elements.