Nonlinear Vibration Characteristics and Bifurcations of a Rotor System Subjected to Brush Seal Forces
Abstract
:1. Introduction
2. The Nonlinear Rotor System
3. Nonlinear Motions of the Brush Seal Rotor System
3.1. Bifurcation Characteristics
3.2. Numerical Simulation
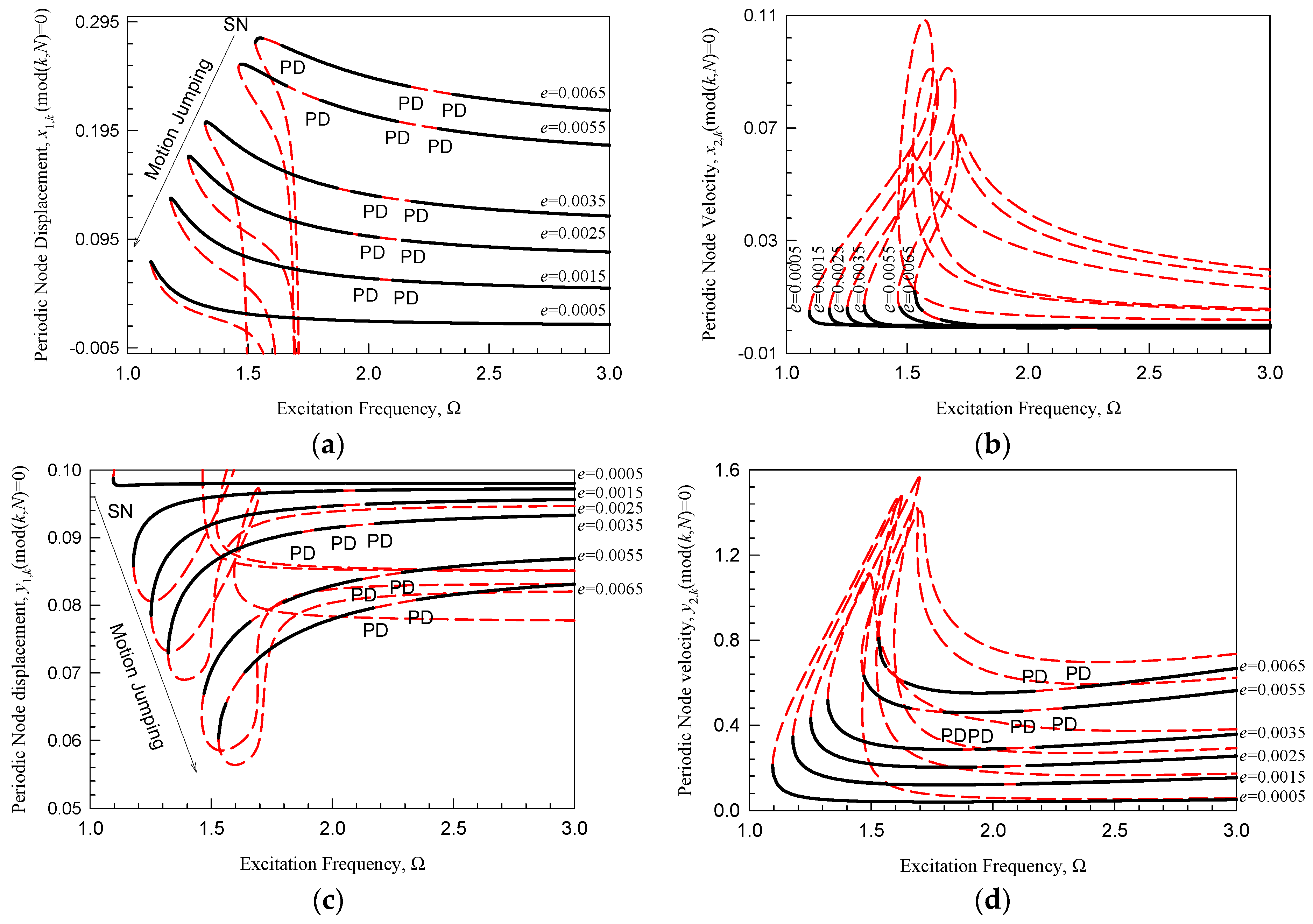
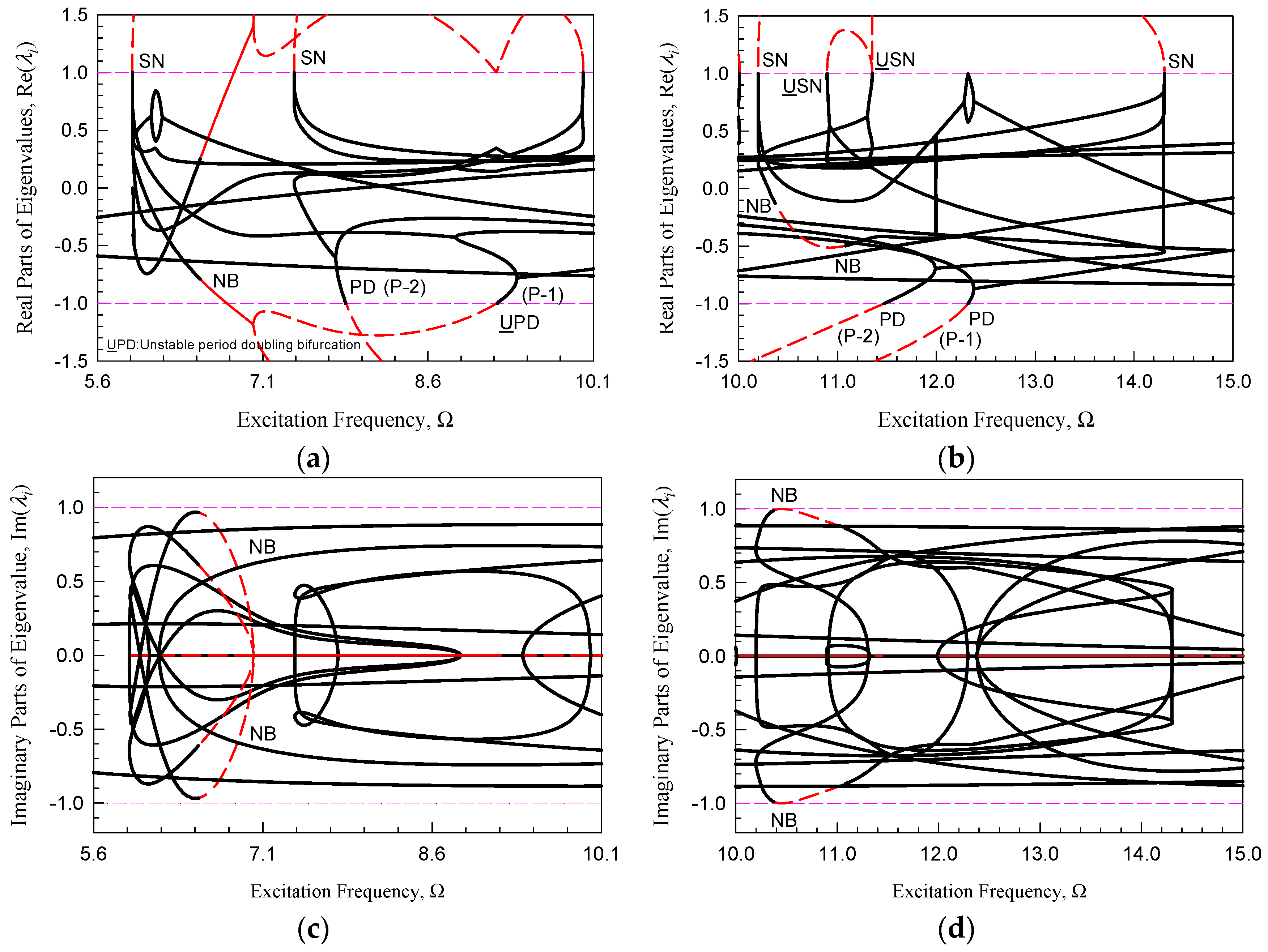
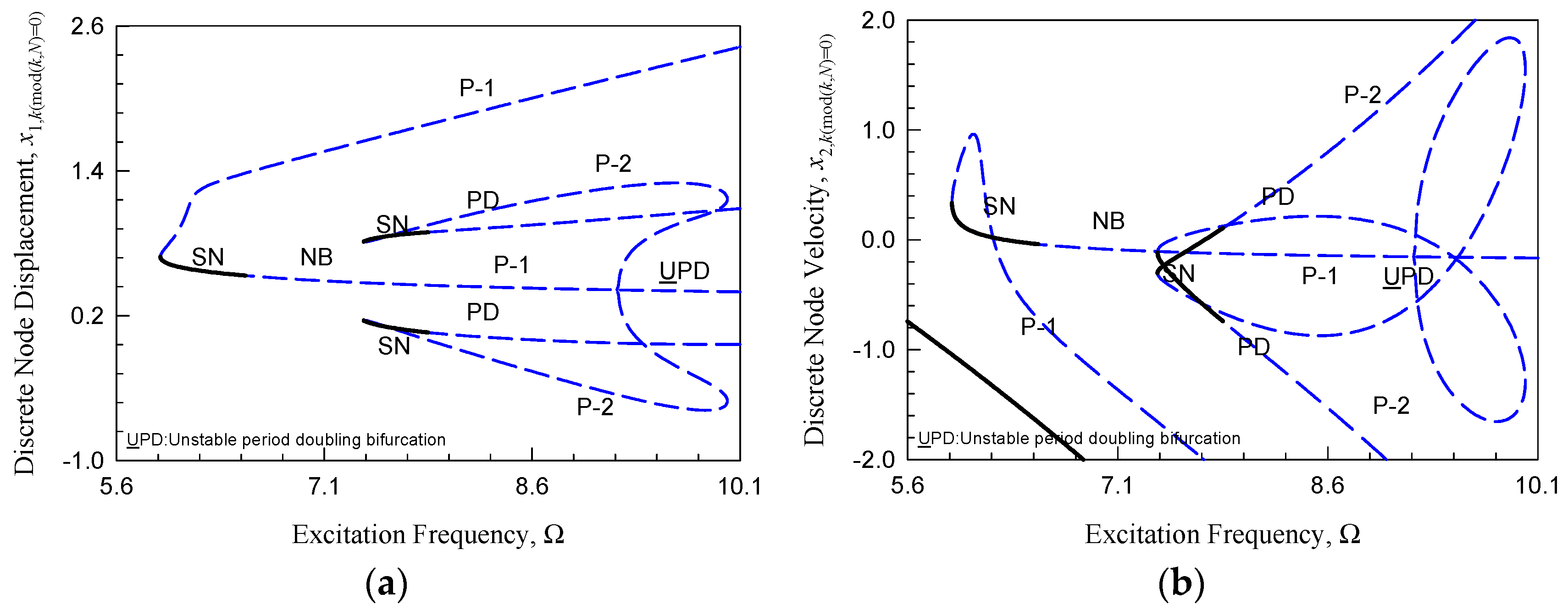
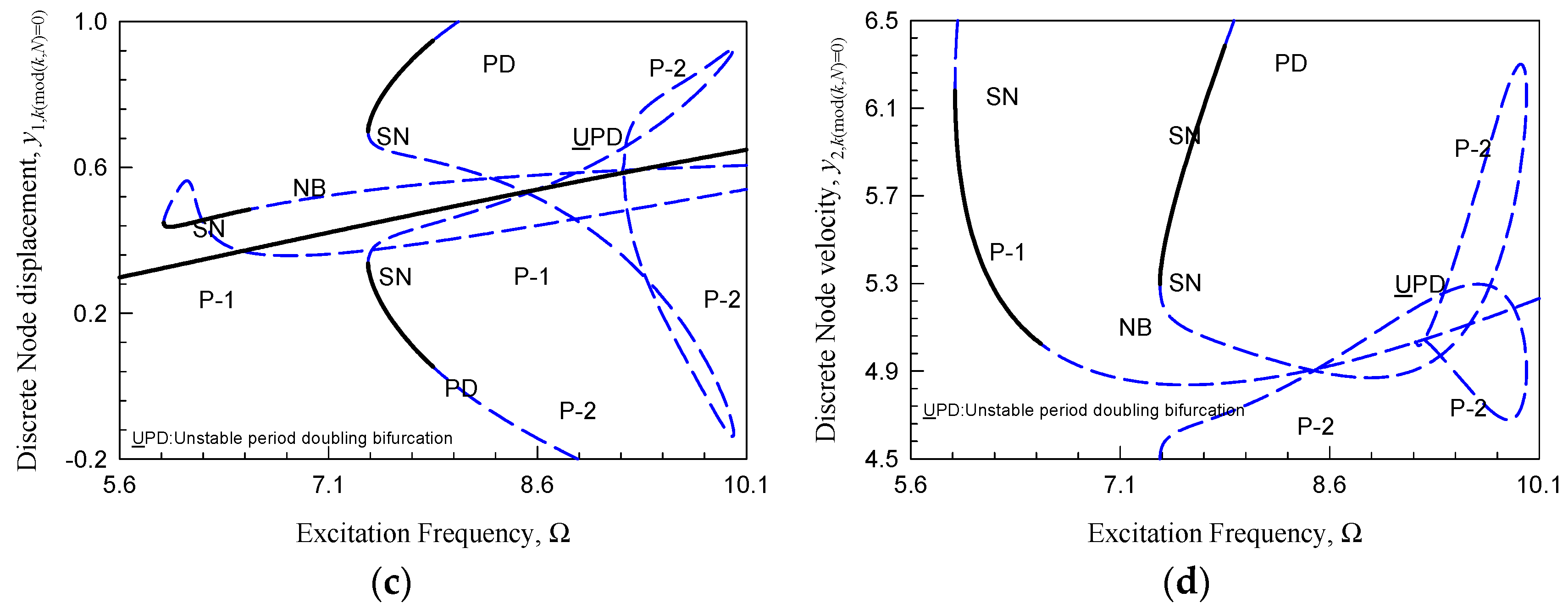
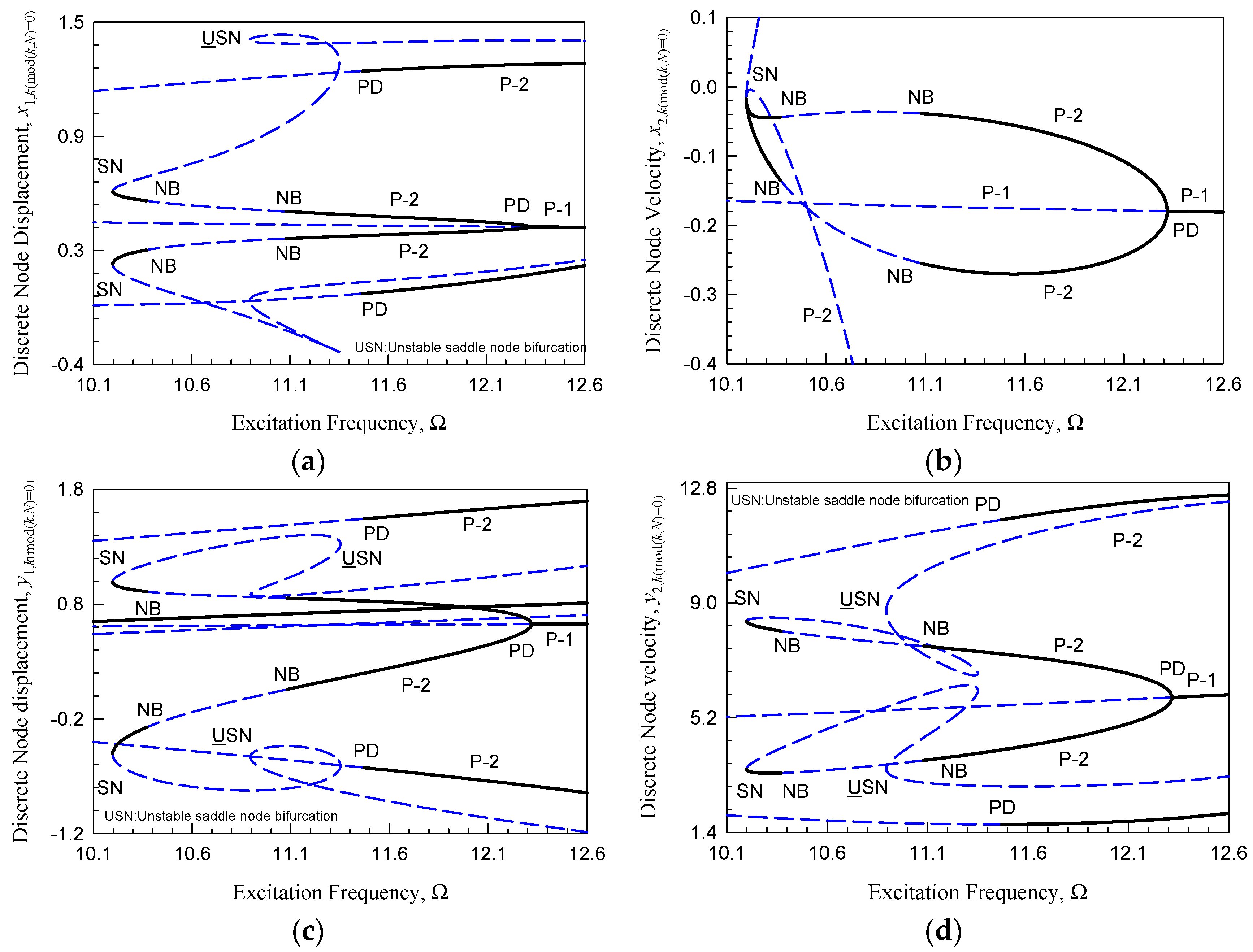
3.3. Bifurcation Diagrams
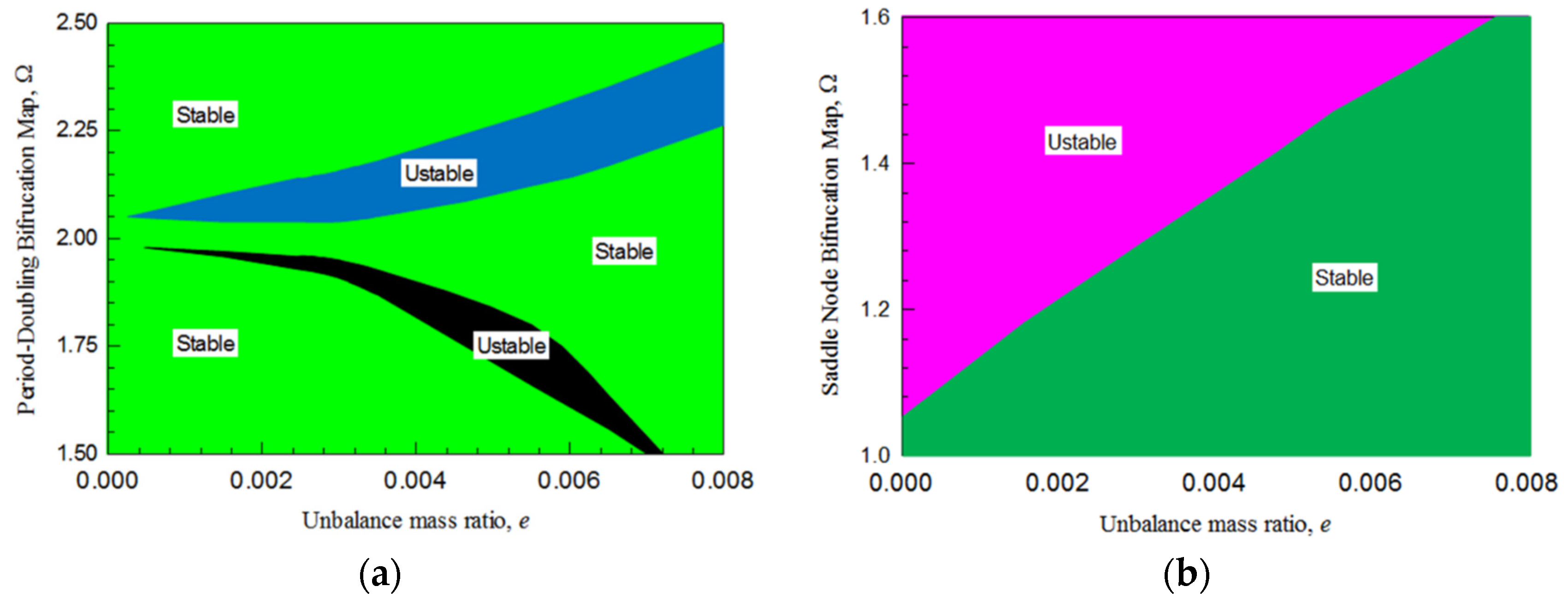
3.4. Parameter Maps of SN and PD
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Holle, G.F.; Krishnan, M.R. Gas turbine engine brush seal applications. In Proceedings of the 26th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Orlando, FL, USA, 16–18 July 1990. Paper no. AIAA 90-2142. [Google Scholar]
- Menendez, R.P.; Xia, J. Recent developments in brush seals for large industrial gas turbines. In Proceedings of the 36th AIAA/ASME/SAE/ASEE/Joint Propulsion Conference and Exhibit, Huntsville, AL, USA, 16–19 July 2000. Paper no. AIAA 00-3374. [Google Scholar]
- Aslan-Zada, F.E.; Mammadov, V.A.; Dohnal, F. Brush seals and labyrinth seals in gas turbine applications. Proc. Inst. Mech. Eng. Part A J. Power Energy 2013, 227, 216–230. [Google Scholar] [CrossRef]
- Chupp, R.E.; Hendricks, R.C.; Lattime, S.B.; Steinetz, B.M. Sealing in turbomachinery. J. Propuls. Power 2006, 22, 313–349. [Google Scholar] [CrossRef]
- Sun, D.; Du, C.; Liu, Y.; Zhan, P.; Xin, Q. Experiment on bristle deflection and oscillation characteristics of brush seals. Acta Aeronaut. Astronaut. Sin. 2020, 41, 123364. (In Chinese) [Google Scholar] [CrossRef]
- Sun, D.; Li, G.; Ai, Y.; Liu, Y.; Zhan, P.; Xin, Q. Numerical study on heat transfer mechanism of brush seal based on three-dimensional solid modeling. J. Aerosp. Power 2019, 34, 1633–1643. [Google Scholar]
- Sun, D.; Ding, H.; Li, G.; Liu, C.; Liu, B.; Zhi, Q. Theory and experiment on the leakage characteristics of brush seals based on fluid-structure interaction. J. Aerosp. Power 2019, 34, 1519–1529. [Google Scholar]
- Lv, B.; Li, W.; Ouyang, H. Moving force-induced motion of a rotating beam with elastic boundary conditions. Int. J. Struct. Stab. Dyn. 2015, 15, 1450035. [Google Scholar] [CrossRef]
- Sharatchandra, M.C.; Rhode, D.L. Computed effects of rotor-induced swirl on brush seal performance-part 2: Bristle force analysis. J. Tribol. 1996, 118, 920–926. [Google Scholar] [CrossRef]
- Stango, R.J.; Zhao, H.; Shia, C.Y. Analysis of contact mechanics for rotor-bristle interference of brush seal. J. Tribol. 2003, 125, 414–421. [Google Scholar] [CrossRef]
- Zhao, H.; Stango, R.J. Effect of flow-induced radial load on brush/rotor contact mechanics. J. Tribol. 2004, 126, 208–215. [Google Scholar] [CrossRef]
- Huang, S.; Suo, S.; Li, Y.; Wang, Y. Theoretical and experimental investigation on tip forces and temperature distributions of the brush seal coupled aerodynamic force. J. Eng. Gas Turbines Power 2014, 136, 052502. [Google Scholar] [CrossRef]
- Chai, B.; Fu, X. Numerical Simulation on Flow and Temperature Distributions of Brush Seals. Lubr. Eng. 2016, 41, 121–125+131. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Z.; Jiao, Y.; Liu, S. Computational analysis of nonlinear dynamics of a multi-disk rotor-bearing-brush seal system. In Mechanisms and Machine Science, Proceedings of the 10th International Conference on Rotor Dynamics—IFToMM, Rio de Janeiro, Brazil, 23–27 September 2018; Springer: Cham, Switzerland, 2018; pp. 350–362. [Google Scholar]
- Wei, Y.; Chen, Z.; Dowell, E.H. Nonlinear characteristics analysis of a rotor-bearing-brush seal system. Int. J. Struct. Stab. Dyn. 2018, 18, 1850063. [Google Scholar] [CrossRef]
- Amer, T.S.; Moatimid, G.M.; Amer, W.S. Dynamical Stability of a 3-DOF Auto-Parametric Vibrating System. J. Vib. Eng. Technol. 2022. [Google Scholar] [CrossRef]
- Ha, Y.; Ha, T.; Byun, J.; Lee, Y. Leakage effects due to bristle deflection and wear in hybrid brush seal of high-pressure steam turbine. Tribol. Int. 2020, 150, 106325. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Li, J.; Yan, X. Numerical Investigation on the Leakage Flow and Rotordynamic Characteristics of Brush-Labyrinth Seal. J. Xi’an Jiao Tong Univ. 2019, 53, 28–35. [Google Scholar] [CrossRef]
- Luo, A.C.J. Periodic flows to chaos based on discrete implicit mappings of continuous nonlinear systems. Int. J. Bifurc. Chaos 2015, 25, 1550044. [Google Scholar] [CrossRef]
- Luo, A.C.J. Discretization and Implicit Mapping Dynamics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Xu, Y.; Zhao, R.; Jiao, Y.; Chen, Z. Stability and bifurcations of complex motions of brush-seal rotor system. Chaos 2023, 30, 103114. [Google Scholar]



| Name | Symbols |
|---|---|
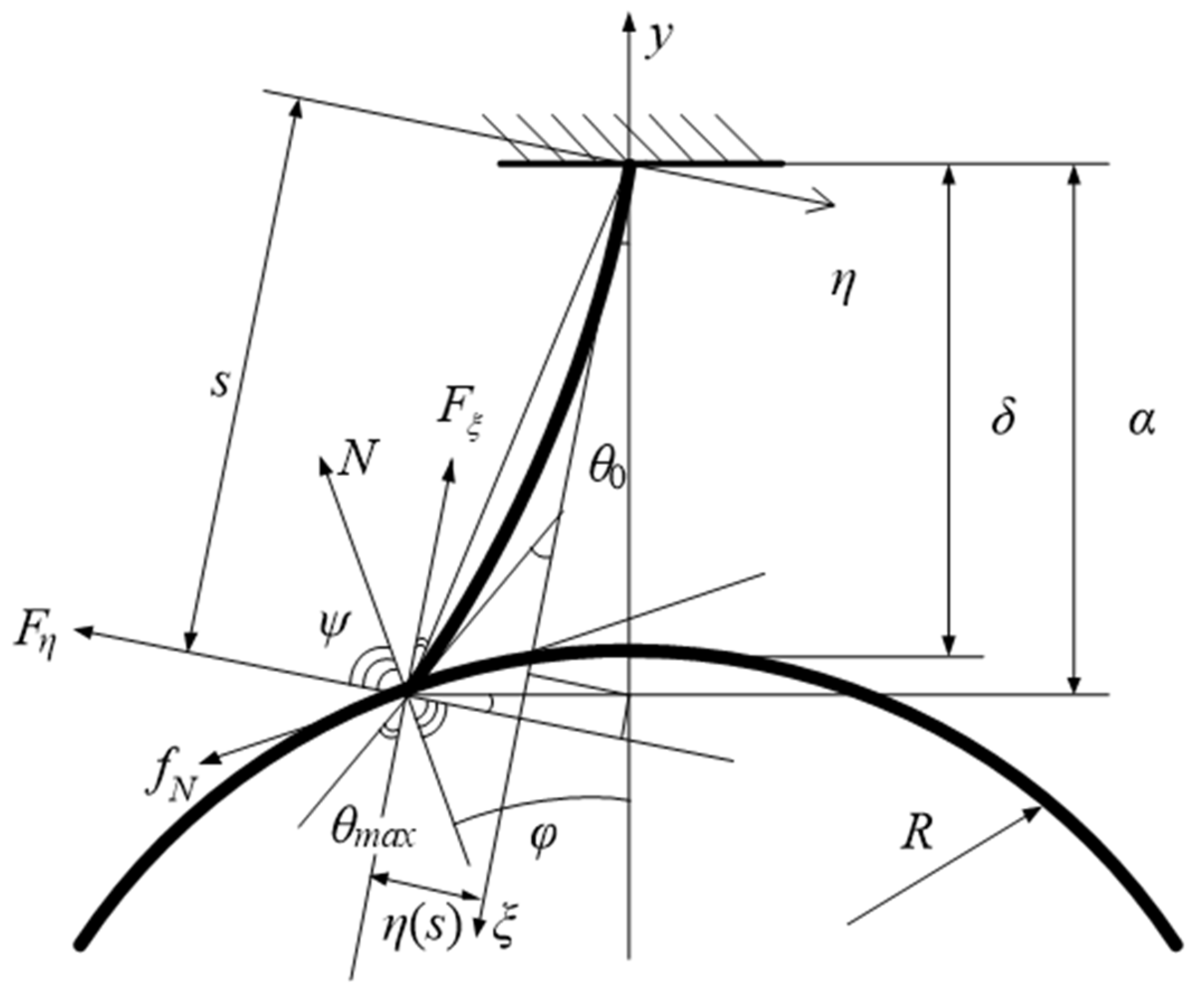
| Brush bristle deformation coordinate system | (η, ξ) |
| Brush seal coordinate system | (x, y) |
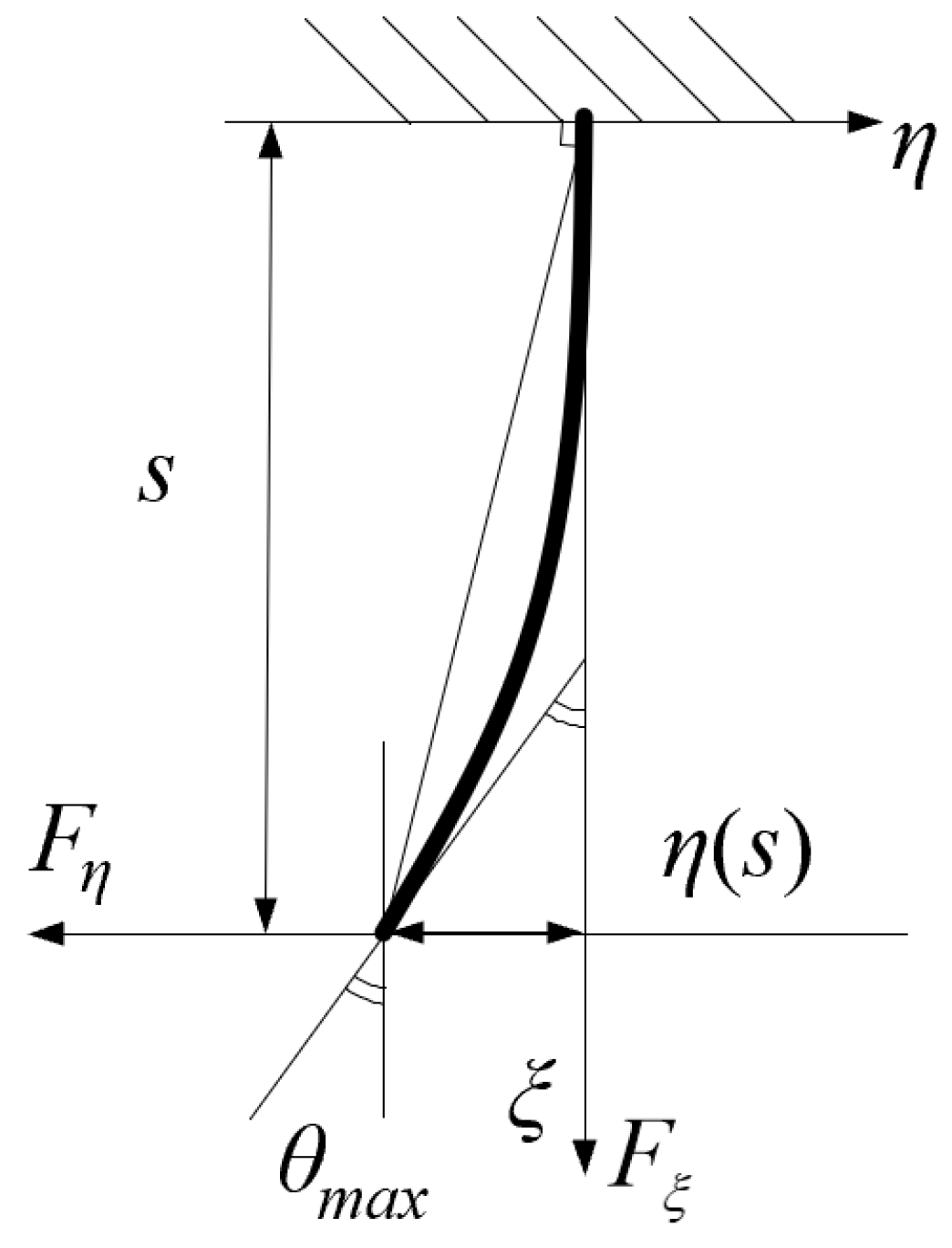
| Bristle length after deformation | s |
| Actual radius clearance | δ |
| Bristle contact deflection angle | φ |
| The η-directional force of the bristle | Fη |
| The ξ-directional force of the bristle | Fξ |
| Maximum turning angle of the bristle | θmax |
| Sliding friction | fN |
| The projection of s on the radius direction | α |
| Shaft radius | R |
| Bristle pre-rotation angle | θ0 |
| Maximum deflection | η(s) |
| Normal force on shaft journal | N |
| Normal force of a single brush bristle on the shaft journal | N1 |
| Friction coefficient of the rotor | μ |
| Angle between normal force and sealing force | ψ |
| Eccentricity | e |
| Declination angle | γ |
| Minimum gap | δmax |
| The angle between the circumferential direction and the negative direction of the y-axis | ρ |
| Brush bristle diameter | R0 |
| Moment of inertia of the bristle cross section | I |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Wang, M.; Lu, D.; Zhang, Y.; Xu, Z.; Xu, Y. Nonlinear Vibration Characteristics and Bifurcations of a Rotor System Subjected to Brush Seal Forces. Appl. Sci. 2023, 13, 11539. https://doi.org/10.3390/app132011539
Zou Y, Wang M, Lu D, Zhang Y, Xu Z, Xu Y. Nonlinear Vibration Characteristics and Bifurcations of a Rotor System Subjected to Brush Seal Forces. Applied Sciences. 2023; 13(20):11539. https://doi.org/10.3390/app132011539
Chicago/Turabian StyleZou, Yingyong, Mukai Wang, Duhui Lu, Yongde Zhang, Zili Xu, and Yeyin Xu. 2023. "Nonlinear Vibration Characteristics and Bifurcations of a Rotor System Subjected to Brush Seal Forces" Applied Sciences 13, no. 20: 11539. https://doi.org/10.3390/app132011539
APA StyleZou, Y., Wang, M., Lu, D., Zhang, Y., Xu, Z., & Xu, Y. (2023). Nonlinear Vibration Characteristics and Bifurcations of a Rotor System Subjected to Brush Seal Forces. Applied Sciences, 13(20), 11539. https://doi.org/10.3390/app132011539






