Multi-Modal 3D Shape Clustering with Dual Contrastive Learning
Abstract
:1. Introduction
- (1)
- A dual contrastive learning network for multi-modal 3D shape clustering is proposed to discover the underlying clustering partitions of unlabeled 3D shapes. To the best of our knowledge, this is the first deep multi-modal 3D shape clustering method;
- (2)
- By simultaneously ensuring the representation consistency within multi-view modality and between point cloud and multi-view modalities, a representation-level dual contrastive learning module is proposed to capture discriminative 3D shape features for clustering;
- (3)
- To further boost the compactness of clustering partitions, an assignment-level dual contrastive learning module is proposed to simultaneously capture consistent clustering assignments within multi-view modality and between point cloud and multi-view modalities;
- (4)
- Experimental results on two widely used 3D shape benchmark datasets are presented to demonstrate the superior clustering performance of the proposed DCL-Net.
2. Related Works
2.1. Unsupervised 3D Shape Feature Learning
2.2. Deep Multi-Modal Clustering
2.3. Contrastive Learning
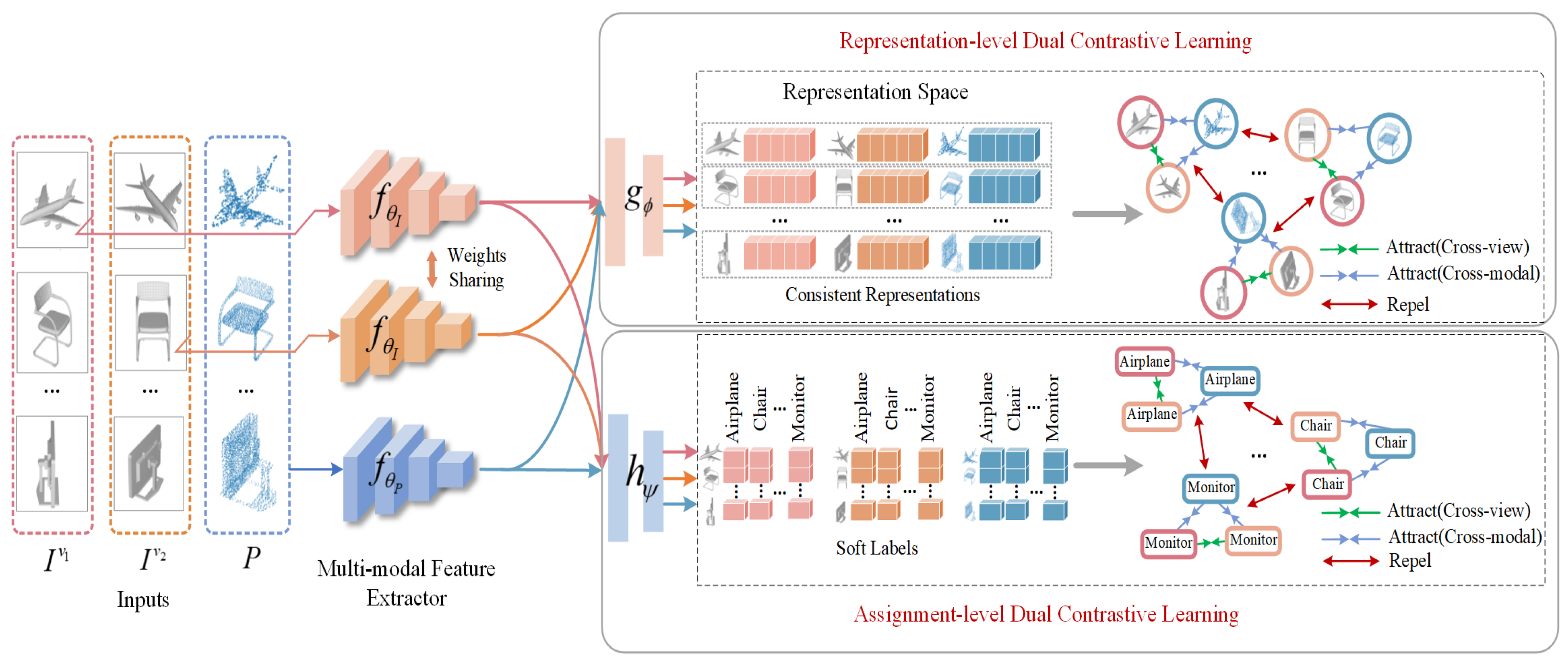
3. The Proposed Method
3.1. Architecture of DCL-Net
3.2. Representation-Level Dual Contrastive Learning
3.3. Assignment-Level Dual Contrastive Learning
3.4. Implementation Details
4. Experimental Results
4.1. Experimental Setup
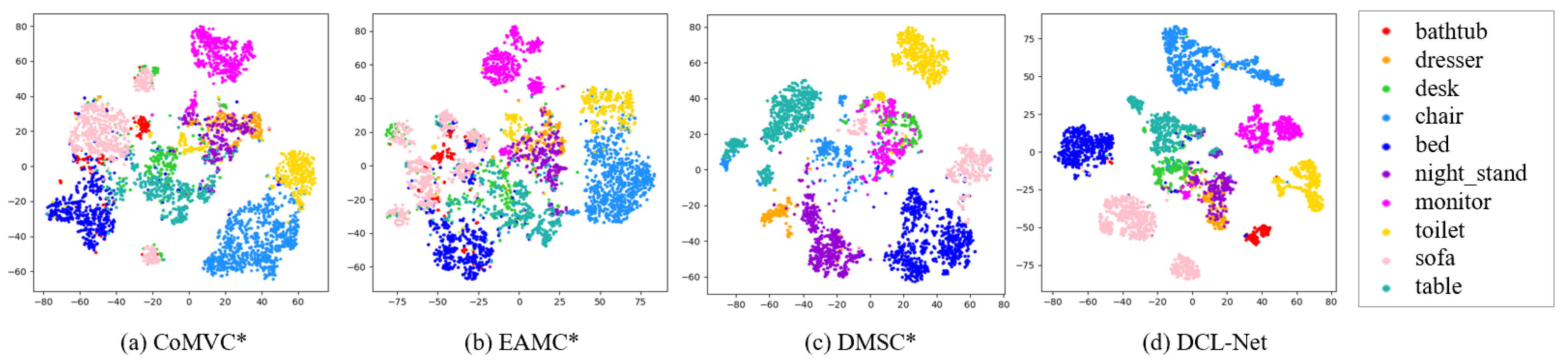
4.2. Comparison Results
4.3. Evaluation of Key Components
4.3.1. Evaluation of the Proposed RDCL Module and ADCL Module
4.3.2. Evaluation of the Cross-View and Cross-Modal Contrastive Learning
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, C.; Guo, Y.; Yang, J.; An, W. Learning multi-view representation with LSTM for 3D shape recognition and retrieval. IEEE Trans. Multimed. 2018, 21, 1169–1182. [Google Scholar] [CrossRef]
- Dai, G.; Xie, J.; Fang, Y. Deep correlated holistic metric learning for sketch-based 3D shape retrieval. IEEE Trans. Image Process. 2018, 27, 3374–3386. [Google Scholar] [CrossRef] [PubMed]
- Bu, S.; Wang, L.; Han, P.; Liu, Z.; Li, K. 3D shape recognition and retrieval based on multi-modality deep learning. Neurocomputing 2017, 259, 183–193. [Google Scholar] [CrossRef]
- Qiu, S.; Anwar, S.; Barnes, N. Geometric back-projection network for point cloud classification. IEEE Trans. Multimed. 2021, 24, 1943–1955. [Google Scholar] [CrossRef]
- Han, Z.; Lu, H.; Liu, Z.; Vong, C.; Liu, Y.; Zwicker, M.; Han, J.; Chen, C. 3D2SeqViews: Aggregating sequential views for 3D global feature learning by CNN with hierarchical attention aggregation. IEEE Trans. Image Process. 2019, 28, 3986–3999. [Google Scholar] [CrossRef]
- Chen, S.; Zheng, L.; Zhang, Y.; Sun, Z.; Xu, K. VERAM: View-enhanced recurrent attention model for 3D shape classification. IEEE Trans. Vis. Comput. Graph. 2018, 25, 3244–3257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, B.; Lei, J.; Fu, H.; Zhang, C.; Chua, T.; Li, X. Unsupervised video action clustering via motion-scene interaction constraint. IEEE Trans. Circuits Syst. Video Technol. 2018, 30, 131–144. [Google Scholar] [CrossRef]
- Kumar, K.; Shrimankar, D. Deep event learning boost-up approach: DELTA. Multimed. Tools. Appl. 2018, 77, 26635–26655. [Google Scholar] [CrossRef]
- Lei, J.; Li, X.; Peng, B.; Fang, L.; Ling, N.; Huang, Q. Deep spatial-spectral subspace clustering for hyperspectral image. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 2686–2697. [Google Scholar] [CrossRef]
- Kumar, K.; Shrimankar, D.; Sing, N. Equal partition based clustering approach for event summarization in videos. In Proceedings of the International Conference on Signal-Image Technology & Internet-Based Systems, Naples, Italy, 28 November–1 December 2016. [Google Scholar]
- Peng, B.; Lei, J.; Fu, H.; Shao, L.; Huang, Q. A recursive constrained framework for unsupervised video action clustering. IEEE Trans. Industr. Inform. 2020, 16, 555–565. [Google Scholar] [CrossRef]
- You, H.; Feng, Y.; Zhao, X.; Zou, C.; Ji, R.; Gao, Y. PVRNet: Point-view relation neural network for 3D shape recognition. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Yu, C.; Lei, J.; Peng, B.; Shen, H.; Huang, Q. SIEV-Net: A structure-information enhanced voxel network for 3D object detection from LiDAR point clouds. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5703711. [Google Scholar] [CrossRef]
- Kumar, K.; Shrimankar, D.; Singh, N. Event BAGGING: A novel event summarization approach in multiview surveillance video. In Proceedings of the International Conference on Innovations in Electronics, Signal Processing and Communication, Shillong, India, 6–7 April 2017. [Google Scholar]
- Kumar, K.; Shrimankar, D. F-DES: Fast and deep event summarization. IEEE Trans. Multimed. 2017, 20, 323–334. [Google Scholar] [CrossRef]
- Pan, Z.; Yu, W.; Lei, J.; Ling, N.; Kwong, S. TSAN: Synthesized view quality enhancement via two-stream attention network for 3D-HEVC. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 345–358. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–18283. [Google Scholar] [CrossRef] [PubMed]
- Afham, M.; Dissanayake, I.; Dissanayake, D.; Dharmasiri, A.; Thilakarathna, K.; Rodrigo, R. CrossPoint: Self-supervised cross-modal contrastive learning for 3D point cloud understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022. [Google Scholar]
- Jing, L.; Zhang, L.; Tian, Y. Self-supervised feature learning by cross-modality and cross-view correspondences. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021. [Google Scholar]
- Xu, J.; Tang, H.; Ren, Y.; Zhu, X.; He, L. Contrastive multi-modal clustering. arXiv 2021, arXiv:2106.11193. [Google Scholar]
- Trosten, D.; Lokse, S.; Jenssen, R.; Kampffmeyer, M. Reconsidering representation alignment for multi-view clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021. [Google Scholar]
- Achlioptas, P.; Diamanti, O.; Mitliagkas, I.; Guibas, L. Learning representations and generative models for 3D point clouds. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Zhao, Y.; Birdal, T.; Deng, H.; Tombari, F. 3D point capsule networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Los Angeles, CA, USA, 15–21 June 2019. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. FoldingNet: Point cloud auto-encoder via deep grid deformation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake, UT, USA, 18–22 June 2018. [Google Scholar]
- Sanghi, A. Info3D: Representation learning on 3D objects using mutual information maximization and contrastive learning. In Proceedings of the European Conference on Computer Vision, Virtual, 23–28 August 2020. [Google Scholar]
- Han, Z.; Liu, Z.; Han, J.; Vong, C.; Bu, S.; Chen, C. Mesh convolutional restricted Boltzmann machines for unsupervised learning of features with structure preservation on 3-D meshes. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2268–2281. [Google Scholar] [CrossRef]
- Park, J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. DeepSDF: Learning continuous signed distance functions for shape representation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Los Angeles, CA, USA, 15–21 June 2019. [Google Scholar]
- Han, Z.; Shang, M.; Liu, Y.; Zwicker, M. View Inter-Prediction GAN: Unsupervised representation learning for 3D shapes by learning global shape memories to support local view predictions. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Wu, J.; Zhang, C.; Xue, T.; Freeman, B.; Tenenbaum, J. Learning a probabilistic latent space of object shapes via 3D generative-adversarial modeling. In Proceedings of the Conference and Workshop on Neural Information Processing System, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Girdhar, R.; Fouhey, D.F.; Rodriguez, M.; Gupta, A. Learning a predictable and generative vector representation for objects. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Kumar, K. Text query based summarized event searching interface system using deep learning over cloud. Multimed. Tools. Appl. 2021, 80, 11079–11094. [Google Scholar] [CrossRef]
- Chang, J.; Wang, L.; Meng, G.; Xiang, S.; Pan, C. Deep adaptive image clustering. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Kumar, K.; Shrimankar, D.; Singh, N. Eratosthenes sieve based key-frame extraction technique for event summarization in videos. Multimed. Tools. Appl. 2018, 77, 7383–7404. [Google Scholar] [CrossRef]
- Kumar, K. Event video skimming using deep keyframe. J. Vis. Commun. Image Represent. 2019, 58, 345–352. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, X.; Lei, J.; Zhang, Z.; Ling, N.; Huang, Q. LVE-S2D: Low-light video enhancement from static to dynamic. IEEE Trans. Circuits Syst. Video Technol. 2022. [Google Scholar] [CrossRef]
- Pan, Z.; Yuan, F.; Lei, J.; Fang, Y.; Shao, X.; Kwong, S. VCRNet: Visual Compensation Restoration Network for No-Reference Image Quality Assessment. IEEE Trans. Image Process. 2022, 31, 1613–1627. [Google Scholar] [CrossRef]
- Pan, Z.; Yuan, F.; Yu, W.; Lei, J.; Ling, N.; Kwong, S. RDEN: Residual distillation enhanced network-guided lightweight synthesized view quality enhancement for 3D-HEVC. IEEE Trans. Circuits Syst. Video Technol. 2022; Early Access. [Google Scholar] [CrossRef]
- Ngiam, J.; Khosla, A.; Kim, M.; Nam, J.; Lee, H.; Ng, A. Multi-modal deep learning. In Proceedings of the International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Andrew, G.; Arora, R.; Bilmes, J.; Livescu, K. Deep canonical correlation analysis. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Abavisani, M.; Patel, V. Deep multimodal subspace clustering networks. IEEE J. Sel. Top. Sign. Process. 2018, 12, 1601–1614. [Google Scholar] [CrossRef] [Green Version]
- Peng, B.; Lei, J.; Fu, H.; Jia, Y.; Zhang, Z.; Li, Y. Deep video action clustering via spatio-temporal feature learning. Neurocomputing 2021, 456, 519–527. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Q.; Tao, Z.; Gao, Q.; Yang, Z. Deep adversarial multi-view clustering network. In Proceedings of the International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019. [Google Scholar]
- Zhou, R.; Shen, Y. End-to-end adversarial-attention network for multi-modal clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Virtual, 14–19 June 2020. [Google Scholar]
- Zhuang, C.; Zhai, A.; Yamins, D. Local aggregation for unsupervised learning of visual embeddings. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Virtual, 16–18 June 2020. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, Virtual, 12–18 July 2020. [Google Scholar]
- Chen, X.; He, K. Exploring simple siamese representation learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021. [Google Scholar]
- Grill, J.B.; Strub, F.; Altché, F.; Tallec, C.; Richemond, P.; Buchatskaya, E.; Doersch, C.; Pires, B.A.; Guo, Z.; Azar, M.G.; et al. Bootstrap your own latent-a new approach to self-supervised learning. In Proceedings of the Conference and Workshop on Neural Information Processing System, Virtual, 6–12 December 2020. [Google Scholar]
- Tian, Y.; Krishnan, D.; Isola, P. Contrastive multi-view coding. In Proceedings of the European Conference on Computer Vision, Virtual, 23–28 August 2020. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Qi, C.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 22–25 July 2017. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2015. [Google Scholar]
- Zhang, C.; Liu, Y.; Fu, H. AE2-Nets: Autoencoder in autoencoder networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Los Angeles, CA, USA, 15–21 June 2019. [Google Scholar]
- Rand, W. Objective criteria for the evaluation of clustering methods. J. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef]
- Maaten, L.V.D.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm as 136: A k-means clustering algorithm. J. R. Stat. Soc. 1979, 28, 100–108. [Google Scholar] [CrossRef]
| Method | ModelNet10 | ModelNet40 | ||||||
|---|---|---|---|---|---|---|---|---|
| ACC | NMI | ARI | F-score | ACC | NMI | ARI | F-score | |
| CoMVC* | 0.6703 | 0.6520 | 0.5920 | 0.6408 | 0.4191 | 0.5769 | 0.3608 | 0.3841 |
| EAMC* | 0.7040 | 0.6583 | 0.5890 | 0.6455 | 0.4563 | 0.5403 | 0.3259 | 0.3685 |
| DMSC* | 0.7638 | 0.7291 | 0.7426 | 0.7766 | 0.5516 | 0.6847 | 0.5236 | 0.5556 |
| DCL-Net | 0.7932 | 0.8218 | 0.7646 | 0.7934 | 0.6120 | 0.7246 | 0.5761 | 0.6022 |
| Method | ModelNet10 | ModelNet40 | ||||||
|---|---|---|---|---|---|---|---|---|
| ACC | NMI | ARI | F-score | ACC | NMI | ARI | F-Score | |
| w/o ADCL | 0.6901 | 0.7437 | 0.6538 | 0.6958 | 0.5572 | 0.7241 | 0.4573 | 0.4779 |
| w/o RDCL | 0.7921 | 0.7872 | 0.7476 | 0.7782 | 0.4966 | 0.6581 | 0.4321 | 0.4641 |
| DCL-Net | 0.7932 | 0.8218 | 0.7646 | 0.7934 | 0.6120 | 0.7246 | 0.5761 | 0.6022 |
| Method | ModelNet10 | ModelNet40 | ||||||
|---|---|---|---|---|---|---|---|---|
| ACC | NMI | ARI | F-score | ACC | NMI | ARI | F-score | |
| w/o cross-modal contrastive learning | 0.7644 | 0.7881 | 0.7214 | 0.7557 | 0.5666 | 0.7080 | 0.5204 | 0.5400 |
| w/o cross-view contrastive learning | 0.7791 | 0.8142 | 0.7526 | 0.7828 | 0.5566 | 0.6926 | 0.4940 | 0.5315 |
| DCL-Net | 0.7932 | 0.8218 | 0.7646 | 0.7934 | 0.6120 | 0.7246 | 0.5761 | 0.6022 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, G.; Zheng, Z.; Chen, L.; Qin, T.; Song, J. Multi-Modal 3D Shape Clustering with Dual Contrastive Learning. Appl. Sci. 2022, 12, 7384. https://doi.org/10.3390/app12157384
Lin G, Zheng Z, Chen L, Qin T, Song J. Multi-Modal 3D Shape Clustering with Dual Contrastive Learning. Applied Sciences. 2022; 12(15):7384. https://doi.org/10.3390/app12157384
Chicago/Turabian StyleLin, Guoting, Zexun Zheng, Lin Chen, Tianyi Qin, and Jiahui Song. 2022. "Multi-Modal 3D Shape Clustering with Dual Contrastive Learning" Applied Sciences 12, no. 15: 7384. https://doi.org/10.3390/app12157384
APA StyleLin, G., Zheng, Z., Chen, L., Qin, T., & Song, J. (2022). Multi-Modal 3D Shape Clustering with Dual Contrastive Learning. Applied Sciences, 12(15), 7384. https://doi.org/10.3390/app12157384






