Adaptive Salp Swarm Algorithm for Optimization of Geotechnical Structures

Abstract

Based on the salp swarm algorithm (SSA), this paper proposes an efficient metaheuristic algorithm for solving global optimization problems and optimizing two commonly encountered geotechnical engineering structures: reinforced concrete cantilever retaining walls and shallow spread foundations. Two new equations for the leader- and followers-position-updating procedures were introduced in the proposed adaptive salp swarm optimization (ASSA). This change improved the algorithm’s exploration capabilities while preventing it from converging prematurely. Benchmark test functions were used to confirm the proposed algorithm’s performance, and the results were compared to the SSA and other effective optimization algorithms. A Wilcoxon’s rank sum test was performed to evaluate the pairwise statistical performances of the algorithms, and it indicated the significant superiority of the ASSA. The new algorithm can also be used to optimize low-cost retaining walls and foundations. In the analysis and design procedures, both geotechnical and structural limit states were used. Two case studies of retaining walls and spread foundations were solved using the proposed methodology. According to the simulation results, ASSA outperforms alternative models and demonstrates the ability to produce better optimal solutions.

1. Introduction

The objective function in most engineering problems is non-convex and discontinuous, with a large number of design variables. As a result, traditional deterministic optimization techniques based on mathematical principles may struggle to find a global optimum solution due to local optima trapping. The use of powerful metaheuristic optimization algorithms for obtaining a global optimum to overcome this limitation is of interest, and metaheuristic algorithms have proven to be an excellent alternative for solving complex problems in recent decades [1,2,3,4,5,6].

The most common geo-structures in practical application are reinforced concrete retaining walls and spread footings, which have received considerable attention in recent studies [7,8]. These structures are commonly used and typically involve a large volume of material. In the past, the initial anticipated dimensions of retaining structures were tested for stability and other building code requirements. If the dimensions were insufficient to meet the constraints, they were adjusted until all the requirements were met. During this time-consuming, iterative process, the cost of construction was not taken into account. In the optimum design of these structures, the dimensions that provide the lowest cost and weight of construction while meeting all the design requirements are automatically determined.

Several metaheuristic algorithms for geotechnical engineering problems have recently been developed and are widely used. Despite the fact that metaheuristic methods can produce acceptable results, no algorithm outperforms another in solving all the optimization problems. Furthermore, the objective function in most geotechnical engineering optimization problems, such as shallow foundations, retaining structures, and pile optimization, is discontinuous and has a large number of design variables. As a result, several research projects have been launched in order to improve the performance and efficiency of the existing metaheuristics. Some of these are modified particle swarm optimizations [9,10], modified harmony search algorithms [11], modified gravitational search algorithms [12], modified sine cosine algorithms [13], improved salp swarm algorithms [14], modified ant colony optimizations [15], modified teaching–learning-based optimizations [16], improved tunicate swarm algorithms [17], and modified wild horse optimizations [18]. According to the effectiveness of the metaheuristics and their modified versions, these methods have been widely used to solve several geotechnical engineering problems, as presented in Table 1.

Table 1. Application of metaheuristic algorithms for geotechnical engineering problems.

Author, Year	Reference	Optimization Method	Application
Goh, 2000	[19]	Genetic algorithm	Locate the critical circular slip surface in slope stability analysis
Zolfaghari, Heath, and McCombie, 2005	[20]	Genetic algorithm	Search for critical noncircular failure surface in slope stability analysis
Cheng et al., 2007	[1]	Particle swarm optimization	Analyze two-dimensional slope stability
Cheng et al., 2008	[11]	Improved harmony search algorithm	Analyze slope stability
Chan, Zhang, and Ng, 2009	[21]	Hybrid genetic algorithms	Optimize pile groups
Kahatadeniya, Nanakorn, and Neaupane, 2009	[22]	Ant colony optimization	Determine the critical failure surface of earth slope
Khajehzadeh et al., 2011	[23]	Modified particle swarm optimization	Optimize design of spread footing and retaining wall
Camp and Akin, 2012	[24]	Big bang–big crunch optimization	Optimize design of retaining wall
Camp and Assadollahi, 2013	[25]	Hybrid big bang–big crunch algorithm	Optimize CO2 and cost of reinforced concrete footings
Khajehzadeh et al., 2013	[26]	Hybrid firefly algorithm	Multi-objective optimization of foundations
Kang, Li, and Ma, 2013	[27]	Artificial bee colony algorithm	Locate the critical slip surface in slope stability analysis
Khajehzadeh, Taha, and Eslami, 2014	[12]	Hybrid adaptive gravitational search algorithm	Multi-objective optimization of retaining walls
Kashani, Gandomi, and Mousavi, 2016	[28]	Imperialistic competitive algorithm	Locate the critical slip surface of earth slope
Gordan et al., 2016	[29]	Particle swarm optimization and neural network	Predict seismic slope stability
Gandomi and Kashani, 2017	[7]	Accelerated particle swarm optimization, firefly algorithm, Levy-flight krill herd, whale optimization algorithm, ant lion optimizer, grey wolf optimizer, moth–flame optimization algorithm, and teaching–learning-based optimization algorithm	Minimize construction cost of shallow foundation
Aydogdu, 2017	[30]	Biogeography-based optimization algorithm	Optimize cost of retaining wall
Gandomi et al., 2017	[31]	Genetic algorithm, differential evolution, evolutionary strategy, and biogeography-based optimization	Analyze slope stability
Mahdiyar et al., 2017	[32]	Monte Carlo simulation technique	Assess safety of slope
Gandomi, Kashani, and Zeighami, 2017	[2]	Interior search algorithm	Optimize retaining wall
Chen et al., 2019	[33]	Hybrid imperialist competitive algorithm and artificial neural network	Predict safety factor values of retaining walls
Koopialipoor et al., 2019	[34]	Imperialist competitive algorithm, genetic algorithm, particle swarm optimization, and artificial bee colony combined with artificial neural network	Predict slope stability under static and dynamic conditions
Yang et al., 2019	[35]	Neural network system	Design retaining wall structures based on smart and optimal systems
Xu et al., 2019	[36]	Hybrid artificial neural network and ant colony optimization	Assess dynamic conditions of retaining wall structures
Himanshu and Burman, 2019	[37]	Particle swarm optimization	Determine critical failure surface considering seepage and seismic loading
Kalemci et al., 2020	[38]	Grey wolf optimization algorithm	Optimize retaining walls
Kaveh, Hamedani, and Bakhshpoori, 2020	[39]	Eleven metaheuristic algorithms	Optimize design of cantilever retaining walls
Kashani et al., 2020	[4]	Differential algorithm, evolution strategy, and biogeography-based optimization algorithm	Optimize design of shallow foundation
Sharma, Saha, and Lohar, 2021	[40]	Hybrid butterfly and symbiosis organism search algorithm	Optimize retaining wall
Kaveh and Seddighian, 2021	[41]	Black hole mechanics optimization, firefly algorithm, evolution strategy, and sine cosine algorithm	Optimize slope critical surfaces considering seepage and seismic effects
Temur, 2021	[42]	Teaching–learning-based optimization	Optimize retaining wall
Li and Wu, 2021	[43]	Improved salp swarm algorithm	Locate critical slip surface of slopes
Khajehzadeh, Keawsawasvong, et al., 2022	[44]	Hybrid tunicate swarm algorithm and pattern search	Seismic analysis of earth slope
Arabali et al., 2022	[45]	Adaptive tunicate swarm algorithm	Optimize construction cost and CO2 emissions of shallow foundation
Khajehzadeh, Keawsawasvong, and Nehdi, 2022	[46]	Artificial neural network combined with rat swarm optimization	Predict the ultimate bearing capacity of shallow foundations and their optimum design
Khajehzadeh, Kalhor, et al., 2022	[47]	Adaptive sperm swarm optimization	Optimize design of retaining structures under seismic load
Kashani et al., 2022	[48]	Multi-objective particle swarm optimization, multi-objective multiverse optimization and Pareto envelope-based selection algorithm	Multi-objective optimization of mechanically stabilized earth retaining wall

A new meta-heuristic algorithm called the salp swarm algorithm (SSA) simulates salp fish swarming in deep waters [49]. Section 2 contains more information on the SSA’s motivation and mathematical modelling. The SSA in its basic model can be extended or hybridized with another algorithm to produce better answers for future problems, similar to other metaheuristic approaches [14,43,50].

This paper presents an adaptive salp swarm algorithm (ASSA) for optimization by introducing new position-updating equations for leader and follower salps. This change significantly improves the algorithm’s performance and convergence speed. A set of well-known standard benchmark functions from the literature is used to validate the effectiveness of the proposed approach. Furthermore, numerical geotechnical structure optimization tests are used to investigate the proposed method’s performance and efficiency.

2. Salp Swarm Algorithm

A salp is a type of marine animal in the Salpidae family. It has a cylindrical structure with apertures at the ends similar to those of a jellyfish, which move and eat by pumping water through internal feeding filters in their gelatinous bodies. The salp swarm algorithm (SSA), a population-based optimization technique, was developed by Mirjalili et al. [49]. The salp chain can be used to calculate the SSA’s behavior while hunting for optimal feeding sources (i.e., the target of this swarm is a food position in the search space called FP). To mathematically model salp chains, they are sampled into two groups: followers and leaders. The salp at the head of the chain is known as the leader, while the others are known as followers. The swarm is led by the leader of these salps, and the followers follow in his footsteps. The chain begins with a leader, who is followed by the followers to guide their movements.

Similar to other swarm-based algorithms, the salp location is specified in a n-dimensional search space, where n is the number of variables in a given problem. As a result, the positions of all the salps are recorded in a two-dimensional matrix known as X, as shown in Equation (1):

$$X_i=\left[\begin{array}{cccc}{x}_1^1& x_2^1& \dots & x_d^1\\ x_1^2& x_2^2& \dots & x_d^2\\ ⋮& ⋮& \dots & ⋮\\ x_1^n& x_2^n& \dots & x_d^n\end{array}\right]$$

(1)

The fitness of each salp is then determined in order to define which salp has the best fitness. It is also supposed that the swarm’s goal is a food position called FP in the search area.

The following equation can be used by the leader salp to change positions:

$$x_i^1=\{\begin{array}{cc}F{P}_i+r_1\left(\left(u{b}_i-l{b}_i\right)r_2+l{b}_i\right)& r_3\ge 0\\ F{P}_i-r_1\left(\left(u{b}_i-l{b}_i\right)r_2+l{b}_i\right)& r_3<0\end{array}$$

(2)

where $x_i^1$ denotes the first salp’s position in the ith dimension, and FP_i denotes the food position in the ith dimension. The lower and upper bounds of the ith dimension are represented by $l{b}_i$ and $u{b}_i$, respectively, and the coefficient r₁ is calculated with Equation (3):

$$r_1=2e^{-{\left(\frac{4t}{t_{max}}\right)}^2}$$

(3)

In addition, the random numbers r₂ and r₃ are between 0 and 1. The maximum number of iterations is t_max, and the current iteration is t. It is worth noting that the r₁ coefficient is critical in a SSA because it balances exploration and exploitation throughout the search. The following equations are used to change the positions of the followers:

$$x_i^j=\frac{1}{2}\left(x_i^j+x_i^{j-1}\right)$$

(4)

where j ≥ 2. In case some agents transfer outside of the search area, Equation (6) shows how to move salps back into the search area if they leave it:

$$x_i^j=\{\begin{array}{cc}l{b}_i& if x_i^j\le l{b}_i\\ u{b}_i& if x_i^j\ge u{b}_i\\ x_i^j& otherwise\end{array}$$

(5)

The pseudocode of the SSA is shown in Algorithm 1.

Algorithm 1. Salp swarm algorithm

Initialize the salp population xi (i = 1, 2, …, n) considering $l{b}_i$ and $u{b}_i$ while t ≤ tmax    Calculate the fitness of each search agent (salp)   Put the best search agent as FP (Food position)   Update r1 by Equation (3)     for each salp (xi)       if i = 1         Update the position of the leading salp by Equation (2)       else         Update the position of the follower salp by Equation (4)       end     end   Amend the salps based on the upper and lower bounds of variables  Calculate the fitness of each search agent FP Update the food position t = t + 1  end return the food position FP and its best fitness

3. Adaptive Salp Swarm Algorithm

Even though the SSA has the capability to generate acceptable results in comparison to other well-known techniques [49], the obtained results of the SSA are prone to becoming stuck in a local optimum, making it unsuitable for very complex problems with multiple local optima [43].

The leading salp adjusts its location in the SSA in response to the food situation (i.e., the position of the best salp in the whole population), as observed in Equation (2). The SSA algorithm updates the location of the leader salp around a single point at each incarnation pass, and other salps (followers) follow the leader. If the algorithm fails to recover because it lacks knowledge of the food position (FP), the algorithm fails. In other words, once an algorithm converges, it loses its ability to explore and then becomes inactive. As a result of this mechanism, the SSA algorithm becomes locked at local minimum points. In light of these circumstances, an adaptive version of the SSA (ASSA) is proposed to address the aforementioned flaw, while also increasing the algorithm’s search capability and flexibility.

In the proposed ASSA, half of the population is considered as leaders, and the remaining salps are followers, which improves the algorithm’s performance and exploring capabilities. The following equation is then used to update the position of the leader salps:

$$x_i^j=\{\begin{array}{cc}{x}_i^j+r_1\left(F{P}_i-x_i^j\right)& r_3\ge 0.5\\ x_i^j-r_1\left(F{P}_i-x_i^j\right)& r_3<0.5\end{array}$$

(6)

The leaders adjust their positions in response to the state of the food source, as well as their previous position, as shown in Equation (6).

This process increases exploration while also allowing the SSA to conduct a more powerful global search across the entire search space. To improve the proposed ASSA’s search efficiency, the followers update their positions according to the following equation:

$$x_i^j=ran{d}^2\left(x_i^j+x_i^{j-1}\right)$$

(7)

In addition, in the suggested ASSA, at each iterative process, the worst salp with the highest objective function value is replaced with a completely random salp. The flowchart of the proposed ASSA is shown in Figure 1.

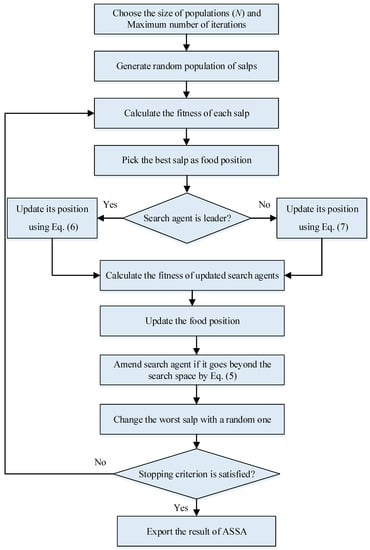
Figure 1. Flowchart of ASSA.

4. Model Verification

A set of numerical reference test functions was used in this section to compare and confirm the achievement and effectiveness of the proposed adaptive salp swarm algorithm (ASSA). In the empirical evidence literature, these functions have commonly been used to determine the performance of optimizers [51,52].

The mathematical models and characteristics of these test functions are shown in Table 2 and Table 3. This standard set was divided into two categories: (1) unimodal functions with a single global best for testing the algorithm convergence pace and enslavement ability and (2) multimodal functions with multiple local minimums and a global ideal for testing an algorithm’s local optima avoidance and exploratory capacity. MATLAB R2020b was used to create the suggested algorithms. All these functions should be minimized. Furthermore, all the functions had dimensions of 30. Three-dimensional drawings of these benchmark functions are illustrated in Figure 2 and Figure 3.

Table 2. Description of unimodal benchmark functions.

Function	Range	${\mathit{f}}_{\mathit{m}\mathit{i}\mathit{n}}$	n (Dim)
$F_1\left(X\right)={\displaystyle \sum }_{i=1}^n{x}_i^2$	${\left[-100, 100\right]}^n$	0	30
$F_2\left(X\right)={\displaystyle \sum }_{i=1}^n\left|x_i\right|+{\displaystyle \prod }_{i=1}^n\left|x_i\right|$	${\left[-10, 10\right]}^n$	0	30
$F_3\left(X\right)={\displaystyle \sum }_{i=1}^n{\left({\displaystyle \sum }_{j=1}^i{x}_j\right)}^2$	${\left[-100, 100\right]}^n$	0	30
$F_4\left(X\right)=\underset{i}{\max } \left\{\left|x_i\right|, 1\le i\le n \right\}$	${\left[-100, 100\right]}^n$	0	30
$F_5\left(X\right)={\displaystyle \sum }_{i=1}^{n-1}\left[100{\left(x_{i+1}-x_i^2\right)}^2+{\left(x_i-1\right)}^2\right]$	${\left[-30, 30\right]}^n$	0	30
$F_6\left(X\right)={\displaystyle \sum }_{i=1}^n{\left(\left[x_i+0.5\right]\right)}^2$	${\left[-100, 100\right]}^n$	0	30
$F_7\left(X\right)={\displaystyle \sum }_{i=1}^{n}i{x}_i^4+random\left[0,1\right)$	${\left[-1.28, 1.28\right]}^n$	0	30

Table 3. Description of multimodal benchmark functions.

Function	Range	${\mathit{f}}_{\mathit{m}\mathit{i}\mathit{n}}$	n (Dim)
$F_8\left(X\right)={\displaystyle \sum }_{i=1}^n-x_i\sin \left(\sqrt{\left|x_i\right|}\right)$	${\left[-500, 500\right]}^n$	428.9829 × n	30
$F_9\left(X\right)={\displaystyle \sum }_{i=1}^n\left[x_i^2-10\cos \left(2\pi x_i\right)+10\right]$	${\left[-5.12, 5.12\right]}^n$	0	30
$\begin{array}{cc}\hfill F_{10}\left(X\right)=& -20 \exp \left(-0.2\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{x}_i^2}\right)\hfill \\ & -\exp \left(\frac{1}{n}{\displaystyle \sum }_{i=1}^n\cos \left(2\pi x_i\right)\right)+20+e\hfill \end{array}$	${\left[-32, 32\right]}^n$	0	30
$F_{11}\left(X\right)=\frac{1}{4000}{\displaystyle \sum }_{i=1}^n{x}_i^2-{\displaystyle \prod }_{i=1}^n\cos \left(\frac{x_i}{\sqrt{i}}\right)+1$	${\left[-600, 600\right]}^n$	0	30
$\begin{array}{cc}\hfill F_{12}\left(X\right)=& \frac{\pi }{n}\left\{10\sin \left(\pi y_1\right)+{\displaystyle \sum }_{i=1}^{n-1}{\left(y_i-1\right)}^2\left[1+10{\sin }^2\left(\pi y_{i+1}\right)\right]+{\left(y_n-1\right)}^2\right\}\hfill \\ & +{\displaystyle \sum }_{i=1}^{n}u\left(x_i,10, 100, 4\right)\hfill \\ \hfill y_i=& 1+\frac{x_{i+4}}{4} u\left(x_i,a, k, m\right)=\{\begin{array}{cc}k{\left(x_i-a\right)}^m\hfill & x_i>a\\ 0\hfill & a<x_i<a\\ k{\left(-x_i-a\right)}^m\hfill & x_i<-a\end{array}\hfill \end{array}$	${\left[-50, 50\right]}^n$	0	30
$\begin{array}{cc}\hfill F_{13}\left(X\right)=& 0.1\{{\sin }^2\left(3\pi x_1\right)\hfill \\ & +{\displaystyle \sum }_{i=1}^n{\left(x_i-1\right)}^2\left[1+{\sin }^2\left(3\pi x_i+1\right)\right]\hfill \\ & +{\left(x_n-1\right)}^2\left[1+{\sin }^2\left(2\pi x_n\right)\right]\}\hfill \\ & +{\displaystyle \sum }_{i=1}^{n}u\left(x_i,5, 100, 4\right)\hfill \end{array}$	${\left[-50, 50\right]}^n$	0	30

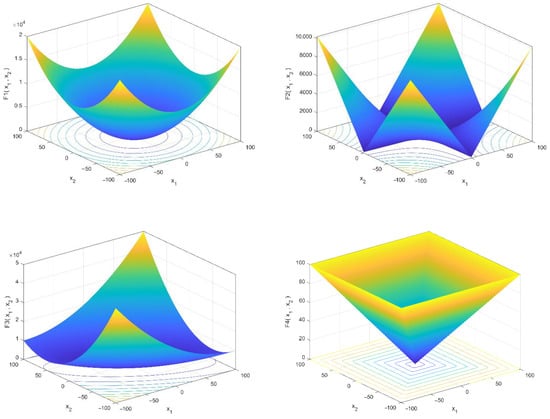
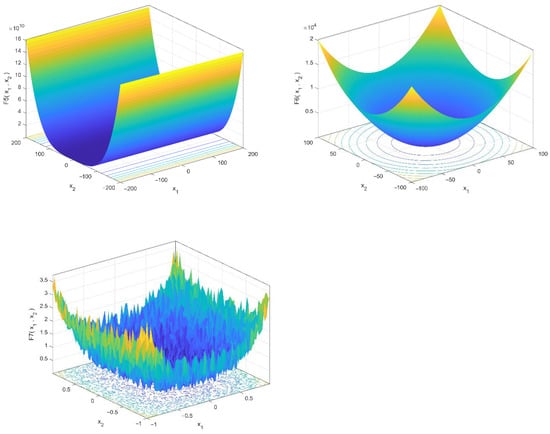
Figure 2. 3-D versions of unimodal benchmark functions.

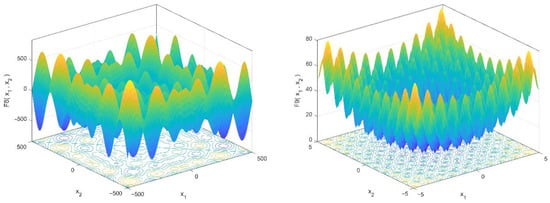
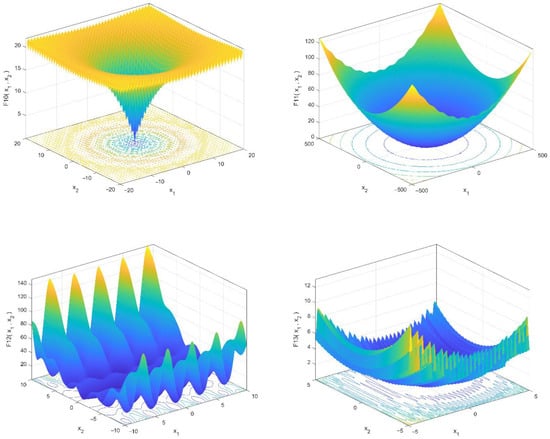
Figure 3. 3-D versions of multimodal benchmark functions.

The proposed ASSA was compared to the original SSA, as well as to some well-known optimization methods, such as the genetic algorithm developed by [53], the particle swarm optimization (PSO) proposed by [54], the firefly algorithm (FA) introduced by [55], the multiverse optimizer (MVO) developed by [56], and the tunicate swarm algorithm (TSA) introduced by [52]. For all methodologies, the sizes of the solutions (N) and the maximum number of iterations (t_max) were set to 30 and 1000, respectively, in order to make fair comparisons between them.

Because the results of a single run of a metaheuristic method are stochastic, they may be incorrect. As a result, statistical analysis should be performed in order to provide a fair comparison and evaluate an algorithm’s efficacy. To address this issue, 30 runs for the mentioned methods were performed, with the results presented in Table 4 and Table 5.

Table 4. Comparison of different methods in solving unimodal test functions.

F	Index	ASSA	SSA	GA	PSO	FA	MVO	TSA
F1	Mean	2.23 × 10−227	3.29 × 10−7	1.95 × 10−12	4.98 × 10−9	7.11 × 10−3	2.81 × 10−1	8.31 × 10−56
	Std.	0.00	5.92 × 10−7	2.01 × 10−11	1.40 × 10−8	3.21 × 10−3	1.11 × 10−1	1.02 × 10−58
F2	Mean	5.96 × 10−105	1.911	6.53 × 10−18	7.29 × 10−4	4.34 × 10−1	3.96 × 10−1	8.36 × 10−35
	Std.	1.91 × 10−104	1.614	5.10 × 10−17	1.84 × 10−3	1.84 × 10−1	1.41 × 10−1	9.86 × 10−35
F3	Mean	3.27 × 10−180	1.50 × 103	7.70 × 10−10	14.0	1.66 × 103	43.1	1.51 × 10−14
	Std.	0.00	7.07 × 102	7.36 × 10−9	7.13	6.72 × 102	8.97	6.55 × 10−14
F4	Mean	1.56 × 10−104	2.44 × 10−5	91.7	6.00 × 10−1	1.11 × 10−1	8.80 × 10−1	1.95 × 10−5
	Std.	3.47 × 10−105	1.89 × 10−5	56.7	1.72 × 10−1	4.75 × 10−2	2.50 × 10−1	4.49 × 10−4
F5	Mean	2.56 × 10−1	1.36 × 102	5.57 × 102	49.3	79.7	1.18 × 102	28.4
	Std.	4.78 × 10−1	1.54 × 102	41.6	38.9	73.9	1.43 × 102	8.40 × 10−1
F6	Mean	3.76 × 10−7	5.72 × 10−7	3.15 × 10−1	6.92 × 10−2	6.94 × 10−3	2.02 × 10−2	3.67
	Std.	1.23 × 10−7	2.44 × 10−7	9.98 × 10−2	2.87 × 10−2	3.61 × 10−3	7.43 × 10−3	3.35 × 10−1
F7	Mean	2.71 × 10−6	8.82 × 10−5	6.79 × 10−4	8.94 × 10−2	6.62 × 10−2	5.24 × 10−2	1.80 × 10−3
	Std.	2.33 × 10−6	6.94 × 10−5	3.29 × 10−3	2.06 × 10−2	4.23 × 10−2	1.37 × 10−2	4.62 × 10−4

Table 5. Comparison of different methods in solving multimodal test functions.

F	Index	ASSA	SSA	GA	PSO	FA	MVO	TSA
F8	Mean	–1.21 × 104	–7.46 × 103	–5.11 × 103	–6.01 × 103	–5.85 × 103	–6.92 × 103	–7.89 × 103
	Std.	4.89 × 102	6.34 × 102	4.37 × 102	1.30 × 103	1.61 × 103	9.19 × 102	599.2
F9	Mean	0.00	55.45	1.23 × 10−1	47.2	15.1	1.01× 102	151.4
	Std.	0.00	18.27	41.1	10.3	12.5	18.9	35.87
F10	Mean	8.88 × 10−16	2.84	5.31 × 10−11	3.86 × 10−2	4.58 × 10−2	1.15	2.409
	Std.	0.00	6.58 × 10−1	1.11 × 10−10	2.11 × 10−1	1.20 × 10−2	7.87 × 10−1	1.392
F11	Mean	0.00	2.29 × 10−1	3.31 × 10−6	5.50 × 10−3	4.23 × 10−3	5.74 × 10−1	7.7 × 10−3
	Std.	0.00	1.29 × 10−1	4.23 × 10−5	7.39 × 10−3	1.29 × 10−3	1.12 × 10−1	5.7 × 10−3
F12	Mean	2.31 × 10−5	6.82	9.16 × 10−8	1.05 × 10−2	3.13 × 10−4	1.27	6.373
	Std.	2.46 × 10−5	2.72	4.88 × 10−7	2.06 × 10−2	1.76 × 10−4	1.02	3.458
F13	Mean	1.44 × 10−4	21.31	6.39 × 10−2	4.03 × 10−1	2.08 × 10−3	6.60 × 10−2	2.897
	Std.	1.95 × 10−4	16.99	4.49 × 10−2	5.39 × 10−1	9.62 × 10−4	4.33 × 10−2	6.43 × 10−1

Table 4 and Table 5 show that, for all the functions, the ASSA could provide better solutions in terms of mean value of the objective functions than the conventional SSA, as well as the other optimization techniques. The results also showed that the mean and standard deviation of the ASSA were significantly lower than those of the other strategies, indicating that the algorithm was stable. The ASSA outperformed both the standard method and alternative optimization approaches, according to the findings.

In order to obtain significant effectiveness between two or more algorithms, a nonparametric Wilcoxon’s rank sum test is often used [57]. In this study, a pairwise comparison was performed using the best results from 30 runs of each algorithm. The Wilcoxon’s rank sum test returned the p-value, the sum of the positive ranks (R+), and the sum of the negative ranks (R−). Table 6 shows the results of the Wilcoxon’s rank sum test for all the benchmark functions. The p-value is the smallest level of significance for detecting differences. In this study, the level of significance was set at 0.05 (α = 0.05). If the p-value was smaller than 0.05, it meant that the better result achieved by the best method in each pairwise comparison was statistically significant and was not obtained by chance. However, there was no significant difference between the two examined methods if the p-value was greater than 0.05. Such a result is indicated with “NA” in the “win” rows of Table 6. In addition, if the R+ was greater than the R−, the ASSA had a better performance than the alternative technique. Otherwise, the ASSA had a poor performance, and the other approach had a better performance [58].

Table 6. Results of Wilcoxon’s rank sum test for benchmark functions.

Fun.	Index	ASSA vs. SSA	ASSA vs. GA	ASSA vs. PSO	ASSA vs. FA	ASSA vs. MVO	ASSA vs. TSA
F1	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F2	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F3	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F4	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F5	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F6	p-val.	6.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	453	465	465	465	465	465
	R−	12	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F7	p-val.	6.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	453	465	465	465	465	465
	R−	12	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F8	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F9	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F10	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F11	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
F12	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	0.0	465	465	465	465
	R−	0.0	465	0.0	0.0	0.0	0.0
	Win	ASSA	GA	ASSA	ASSA	ASSA	ASSA
F13	p-val.	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6	2.0 × 10−6
	R+	465	465	465	465	465	465
	R−	0.0	0.0	0.0	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA	ASSA	ASSA	ASSA
	Superior /Inferior/NA	13/0/0	12/1/0	13/0/0	13/0/0	13/0/0	13/0/0

According to the findings of the Wilcoxon’s rank sum test in Table 6, the pairwise comparison of the ASSA and the SSA in the optimization of thirteen test functions demonstrated that the new approach outperformed the original method in all thirteen cases. Similarly, in the other pairwise comparisons, the ASSA provided better results for the majority of the test suite. As a result of the nonparametric statistical analysis, the ASSA created much better answers and performed significantly better than the other techniques.

5. Foundation Optimization

A shallow spread foundation, as an essential geotechnical structure, must safely and reliably support the superstructure, guarantee stability against soil-bearing capacity failings and excessive settlement, and reduce concrete stresses. Aside from these design criteria, spread footings must meet a number of other criteria: they must have enough shear and moment capacities in both the long and short dimensions; the load-carrying capacity of the foundation must not be surpassed; and the reinforcing steel configuration must meet all building code criteria [59]. The foundation optimization problem requires determining the objective function, layout constraint, and design variables, which are discussed in the following subsections.

5.1. Objective Function

The total cost of the spread footing was the study’s objective function, which can be expressed mathematically as follows:

$$f\left(X\right)=C_c{V}_c+C_e{V}_e+C_b{V}_b+C_f{A}_f+C_s{W}_s$$

(8)

In Equation (8), C_c, C_e, C_b, C_f, and C_s are the unit costs of concrete, excavation, backfill, formwork, and reinforcement, respectively. The unit costs considered here are listed in Table 7 [60].

Table 7. Spread footing assembly unit cost [60].

Item	Symbol	Unit	Unit Cost (USD)
Excavation	Ce	m3	25.16
Formwork	Cf	m2	51.97
Reinforcement	Cs	kg	2.16
Concrete	Cc	m3	173.96
Backfill	Cb	m3	3.97

5.2. Design Variables

Figure 4 depicts the design features for the given model. The design variables were divided into two categories: those that described geometric dimensions and those that described steel reinforcement. As shown in Figure 4, there were four spatial design variables that reflected the foundation dimensions: the foundation’s length (Y₁), the width (Y₂), the thickness (Y₃), and the embedment’s depth (Y₄). The steel reinforcement also had two design variables: the longitudinal reinforcement (Y₅) and the transverse reinforcement (Y₆).

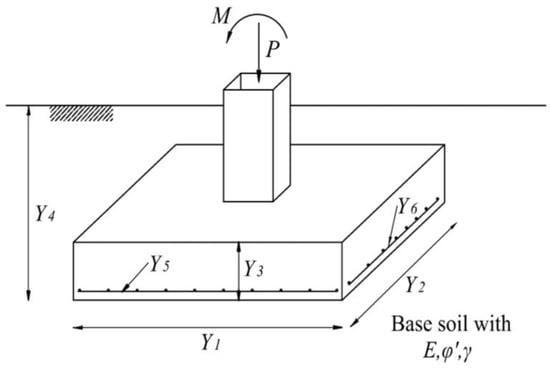
Figure 4. Design variables of the footing.

5.3. Design Constraints

While optimizing and designing a reinforced concrete footing, both structural and geotechnical limit states should be considered. Two different geotechnical limit states are the bearing capacity of the surrounding geo-material and the permitted settlement of the footing. The shear capacity of the footing (one- and two-way shear), flexural capacity, and reinforcement limitation are all structural limit states. The structural limit states are investigated using ACI 318-11 specifications [59]. Service loads are commonly used to satisfy geotechnical limit states. Even so, factored loads can be used for structural limit states. Table 8 provides a list of both structural and geotechnical limit states.

Table 8. Design constraints of spread footing.

Failure Mode	Constraint
Bearing capacity	$q_{max}\le \frac{q_{all}}{FS}$
Settlement of foundation	$\delta \le {\delta }_{all}$ $\delta =\frac{P\left(1-{\mu }^2\right)}{k_{z}E\sqrt{Y_1{Y}_2}}$ $k_z=-0.0017{\left(\frac{Y_2}{Y_1}\right)}^2+0.0597\left(\frac{Y_2}{Y_1}\right)+0.9843$
Eccentricity	e ≤ Y1/6
One-way (wide beam) shear	$V_u\le \frac{1}{6}{\varnothing }_v\sqrt{f{\prime }_c}bd$
Two-way (punching) shear	$V_u\le min\left\{\left(1+\frac{2}{{\beta }_c}\right)/6,\left(\frac{{\alpha }_{s}d}{b_0}+2\right)/12,\frac{1}{3}\right\}{\varnothing }_v\sqrt{f{\prime }_c}bd$
Bending moment	$M_u\le {\varnothing }_M{A}_s{f}_y\left(d-\frac{a}{2}\right)$
Minimum and maximum reinforcements	${\rho }_{min}bd\le A_s\le {\rho }_{max}bd$
Limitation of depth of embedment	0.5 ≤ Y4 ≤ 2

All the parameters presented in Table 8 are defined in Table 9.

Table 9. Definition of parameters of Table 7.

Parameter	Definition
qult	ultimate bearing capacity of the foundation soil
qmax	maximum contact pressure at the interface between the bottom of a foundation and the underlying soil
δall	allowable settlement of foundation
δ	immediate settlement of foundation
ϕV	shear strength reduction factor equal to 0.75
f′c	compression strength of concrete
b0	perimeter of critical section taken at d/2 from face of column
b	width of the section
βc	ratio of long side to short side of column section
αs	is equal to 40 for interior columns
Mu	bending moment
ϕM	flexure strength reduction factor equal to 0.9
As	cross-sectional area of steel reinforcement
fy	yield strength of steel
ρmin	minimum reinforcement ratio
ρmax	maximum reinforcement ratio

6. Retaining Structure Optimization

Reinforced concrete retaining walls are structures that are built to withstand lateral soil pressure as the land elevation changes. The retaining structure design process necessitates several considerations, such as structural dimensions, material characteristics, and needed reinforcement. Generally, the designer’s experience plays a critical role in the cost-effective and safe design of these structures. However, the optimum design of retaining walls is independent of user experience, and the results satisfy both safety and economy.

6.1. Objective Functions

In the case of retaining structure optimization, the total construction cost of the retaining wall was considered as an objective function that incorporated the cost of materials, as well as labor and installation costs, that could be represented as follows:

$$f\left(X\right)=C_c{V}_c+C_e{V}_e+C_b{V}_b+C_f{A}_f+C_s{W}_s$$

(9)

In Equation (9), C_c, C_e, C_b, C_f, and C_s are the unit costs of concrete, excavation, backfill, formwork, and reinforcement, respectively. Table 10 presents the unit construction of a retaining structure [61].

Table 10. Basic prices considered in the analysis.

Item	Unit	Unit Cost (USD/m)
Excavation	m3	11.41
Foundation formwork	m2	36.82
Stem formwork	m2	37.08
Reinforcement	kg	1.51
Concrete in foundations	m3	104.51
Concrete in stem	m3	118.05
Backfill	m3	38.10

6.2. Design Variables

Figure 5 depicts the retaining wall model’s cross-section, design variables, and external load. As shown in this diagram, the dimensions of the retaining wall are represented by five geometric design variables: the heel width, represented by X₁; the top stem thickness, represented by X₂; the bottom stem thickness, represented by X₃; the toe width, represented by X₄; and the base slab thickness, represented by X₅. Three additional design features are included in the steel reinforcement of the various sections of the retaining wall. The vertical steel reinforcement in the stem is designated as X₆, the horizontal steel reinforcement in the toe is designated as X₇, and the horizontal steel reinforcement in the heel is designated as X₈. B is the foundation’s base width, H is the wall’s total height, and H′ is the stem’s height.

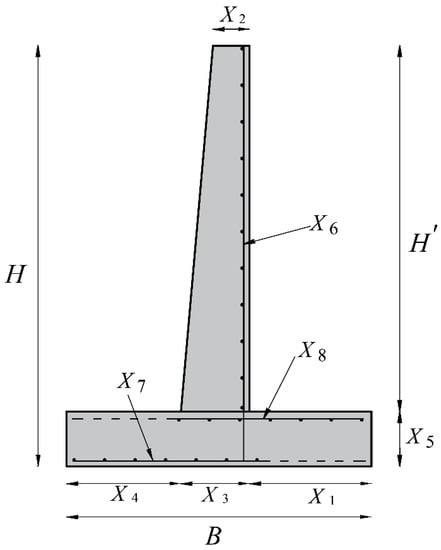
Figure 5. Design variables of the retaining structure.

6.3. Design Constraints

Figure 6 depicts the general forces acting on the retaining wall. Table 11 summarizes and presents the various design constraints that were taken into account when optimizing the concrete retaining wall.

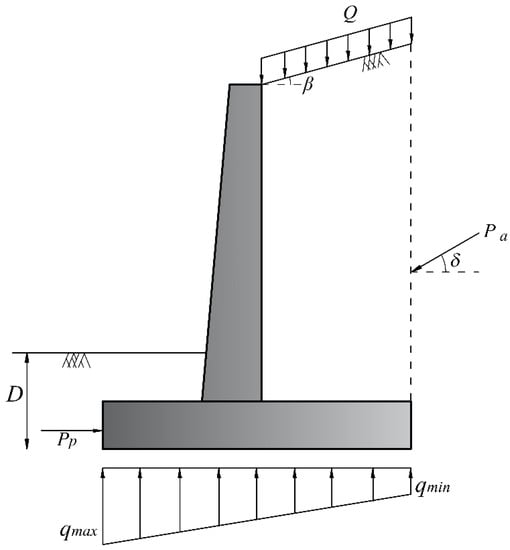
Figure 6. Forces acting on the retaining wall.

Table 11. Failure modes of retaining wall.

Failure Mode	Constraints
Sliding stability	FSS ≤ (ΣFR/ΣFd)
Overturning stability	FSO ≤ (ΣMR/ΣMO)
Bearing capacity	FSb ≤ (qult/qmax)
Eccentricity failure	e ≤ (B/6) $e=\frac{b}{2}-\frac{{{\displaystyle \sum }}^{}{M}_R-{{\displaystyle \sum }}^{}{M}_O}{{{\displaystyle \sum }}^{}V}$
Toe shear	Vut ≤ Vnt
Toe moment	Mut ≤ Mnt
Heel shear	Vuh ≤ Vnh
Heel moment	Muh ≤ Mnh
Shear at bottom of stem	Vus ≤ Vns
Moment at bottom of stem	Mus ≤ Mns
Deflection at top of stem	(1/150) × H′ ≤ δmax

All the parameters presented in Figure 6 and Table 11 are defined in Table 12.

Table 12. Definition of parameters of Figure 6 and Table 10.

Parameter	Definition
β	backfill slop angle
D	depth of soil in front of the wall
Q	distributed surcharge load
Pa	active earth pressure
Pp	passive earth pressure
FSS	required factor of safety against sliding
FSO	required factor of safety against overturning
FSb	required factor of safety against bearing capacity
∑FR	sum of the horizontal resisting forces
∑Fd	sum of the horizontal driving forces
∑MR	sum of the moments of forces that tends to resist overturning about the toe
∑MO	sum of the moments of forces that tends to overturn the structure about the toe
∑V	sum of the vertical forces due to the weight of wall
Vut	ultimate shearing force of toe
Vuh	ultimate shearing force of heel
Vus	ultimate shearing force of stem
Vn	nominal shear strength of concrete
Mut	ultimate bending moment of toe
Muh	ultimate bending moment of heel
Mus	ultimate bending moment of toe stem
Mn	nominal flexural strength of concrete
δmax	maximum deflection at the top of the stem

In addition to the constraints mentioned above, the design variables had practical lower and upper values [62]. Table 13 summarizes the lower and upper boundaries of the design variables.

Table 13. Upper bound and lower bound for design variables of retaining wall.

Description	Lower Bound	Upper Bound
Width of footing	Bmin= 0.4 H	Bmax = 0.7 H
Thickness of base slab	X5min= H/12	X5max= H/10
Width of toe	X4min= 0.4 H/3	X4max= 0.7 H/3
Stem thickness at top	X2min= 20 cm	-
Steel reinforcement ratio	${\rho }_{min}=max\left\{\frac{1.4}{f_y},0.25\frac{\sqrt{f{\prime }_c}}{f_y}\right\}$	${\rho }_{max}=0.85{\beta }_1\frac{{f^{\prime }}_c}{f_y}\left(\frac{600}{600+f_y}\right)$

7. Design Examples

This section investigates numerical problems of geotechnical structures in order to evaluate the ASSA performance. To address the current inquiry, a MATLAB code was developed to computerize the design approach based on the ACI 318-11 specifications, as stated earlier [59].

In order to consider the constraints and transform a constrained optimization to an unconstrained problem, a penalty function method was used in this paper:

$$F\left(X\right)=f\left(X\right)+r{\displaystyle \sum }_{i=1}^{p}max{\left\{0,g_i\left(X\right)\right\}}^l$$

(10)

where F(X) is the penalized objective function, f(X) is the problem’s original objective function presented in (8) and (9), and g(X) is the problem’s constraints presented in Table 7 and Table 10 for the spread footing and retaining wall, respectively. r is a penalty factor considered equal to 1000, l is the power of the penalty function considered equal to 2, and p is the total number of constraints.

To demonstrate the efficacy of the proposed technique, the findings were compared to state-of-the-art algorithms such as particle swarm optimization (PSO) and the firefly algorithm (FA) in the following cases. The maximum number of iterations in any algorithm was assumed to be 1000. Because of the stochastic behavior of the metaheuristics in the following experiments, all the algorithms were run 30 times, and the best results of the analyses for the minimum cost obtained by each method are reported.

7.1. Spread Footing Optimization

The first two design examples were concerned with the best design for a dry sand inner surface spread footing. Table 14 lists the other input parameters for such case studies.

Table 14. Input parameters for design examples 1 and 2.

Parameter	Unit	Value for Example 1	Value for Example 2
Effective friction angle of base soil	degree	35	30
Unit weight of base soil	kN/m3	18.5	18.5
Young’s modulus	MPa	50	35
Poisson’s ratio	−	0.3	0.3
Vertical dead load (D)	kN	2000	4200
Vertical live load (L)	kN	1000	2100
Moment (M)	kN-m	0.0	850
Concrete cover	cm	7.0	7.0
Yield strength of reinforcing steel	MPa	400	400
Compressive strength of concrete	MPa	30	28
Factor of safety for bearing capacity	−	3.0	3.0
Allowable settlement of footing	m	0.04	0.04

The presented procedure solved the problem by combining all the previously mentioned algorithms. Table 15 and Table 16 show the best results of the analyses for the lowest cost.

Table 15. Optimization results for design example 1.

Design Variable	Unit	Optimum Values ASSA	Optimum Values SSA	Optimum Values FA	Optimum Values PSO
(Y1)	cm	169.5	158.3	155.3	169.4
(Y2)	cm	218.8	248.5	253.1	219.2
(Y3)	cm	57.5	58.1	58.2	60
(Y4)	cm	200	158.2	200	200
(Y5)	cm2	39.58	48.2	49.65	37.75
(Y6)	cm2	25.13	21.74	20.94	23.91
Objective function	USD	1091	1098	1162	1108

Table 16. Optimization result for design example 2.

Design Variable	Unit	Optimum Values ASSA	Optimum Values SSA	Optimum Values FA	Optimum Values PSO
(Y1)	cm	153	153.1	159.3	153.2
(Y2)	cm	833.4	833.2	819.1	837.6
(Y3)	cm	80.6	80.6	82.4	80.8
(Y4)	cm	200	200	200	200
(Y5)	cm2	277.1	277.2	256.8	278.1
(Y6)	cm2	20.54	21.1	24.7	20.6
Objective function	USD	4512	4520	4650	4544

Table 15 and Table 16 show that the optimization findings computed by the proposed ASSA were lower than those calculated by the conventional SSA and other approaches, indicating that the new method was effective. Table 15 shows that, contrary to popular belief that the best shape for a footing under vertical load is square, a rectangular footing provided a more cost-effective design.

7.2. Retaining Structure Optimization

The optimal design of two retaining walls with heights of 4 and 6 m was the subject of this section. Table 17 lists the other parameters that were required for this example.

Table 17. Input parameters for design examples 3 and 4.

Parameter	Unit	Value for Example 3	Value for Example 4
Height of stem	m	4.0	6
Internal friction angle of retained soil	degree	36	36
Internal friction angle of base soil	degree	0.0	34
Unit weight of retained soil	kN/m3	17.5	17.5
Unit weight of base soil	kN/m3	18.5	18.5
Unit weight of concrete	kN/m3	23.5	24
Cohesion of base soil	kPa	125	100
Depth of soil in front of wall	m	0.5	0.75
Surcharge load	kPa	20	30
Backfill slop	degree	10	15
Concrete cover	cm	7.0	7.0
Yield strength of reinforcing steel	MPa	400	400
Compressive strength of concrete	MPa	21	28
Shrinkage and temporary reinforcement percent	-	0.002	0.002
Factor of safety for overturning stability	-	1.5	1.5
Factor of safety against sliding	-	1.5	1.5
Factor of safety for bearing capacity	-	3.0	3.0

Table 18 and Table 19 show the results of the assessments for the examples with the lowest cost.

Table 18. Optimization results for design example 3.

Design Variable	Unit	Optimum Values ASSA	Optimum Values SSA	Optimum Values FA	Optimum Values PSO
(X1)	m	0.7233	0.6947	0.6948	0.6436
(X2)	m	0.2	0.2	0.2	0.25
(X3)	m	0.4674	0.5	0.5	0.55
(X4)	m	0.7778	0.7778	0.7778	0.7778
(X5)	m	0.2727	0.2727	0.2723	0.2727
(X6)	cm2/m	6.67	6.66	6.66	6.66
(X7)	cm2/m	6.75	6.75	6.75	6.75
(X8)	cm2/m	6.75	6.75	6.75	6.75
Objective function	USD/m	822.73	827.02	860.42	848.17

Table 19. Optimization results for design example 4.

Design Variable	Unit	Optimum Values ASSA	Optimum Values SSA	Optimum Values FA	Optimum Values PSO
(X1)	m	1.423	1.391	1.459	1.444
(X2)	m	0.25	0.25	0.246	0.249
(X3)	m	0.531	0.532	0.466	0.517
(X4)	m	0.755	0.772	0.773	0.774
(X5)	m	0.331	0.374	0.352	0.339
(X6)	cm2/m	25.38	25.64	32.21	27.52
(X7)	cm2/m	6.78	6.75	6.75	7.02
(X8)	cm2/m	7.94	7.47	7.57	8.39
Objective function	USD/m	1631.2	1643.1	1668.4	1653.9

Table 18 and Table 19 show that, when compared to the traditional SSA and other methods, the ASSA may be able to provide a better solution by calculating lower values of the objective functions. It can be observed that the ASSA’s best price was relatively lower than that of the SSA and significantly lower than that of the PSO and FA. However, additional experiments revealed that increasing the maximum number of iterations reduced the distinctions between the algorithm results. The fact that the best solution was found in the first iteration was due to the effective modification of the algorithm proposed in this study. The modified algorithm demonstrated a much-enhanced efficacy.

In order to determine the statistical significance of the comparative results between the considered algorithms in all the design examples, a nonparametric Wilcoxon’s rank sum test was performed between the results. In this regard, utilizing the results obtained from 30 runs of each method, a pairwise comparison was conducted. According to the results of the Wilcoxon’s rank sum test in Table 20, the pairwise comparison between the ASSA and the SSA revealed that, in the optimization of four design examples, the new method had superior performances in three cases. In addition, for design example 3, both methods were statistically equivalent. Similarly, in the other pairwise comparisons, the ASSA provided better results. Therefore, the nonparametric statistical analysis proved that the ASSA generated significantly better solutions and, comparatively, had a superior performance over the other algorithms.

Table 20. Results of Wilcoxon’s rank sum test for design examples.

Example No.	Index	ASSA vs. SSA	ASSA vs. FA	ASSA vs. PSO
Ex. 1	p-val.	6.0 × 10−6	1.73 × 10−6	1.73 × 10−6
	R+	453	465	465
	R−	12	0.0	0.0
	Win	ASSA	ASSA	ASSA
Ex. 2	p-val.	0.012	1.73 × 10−6	1.73 × 10−6
	R+	354	465	465
	R−	111	0.0	0.0
	Win	ASSA	ASSA	ASSA
Ex. 3	p-val.	0.106	1.73 × 10−6	1.73 × 10−6
	R+	311	465	465
	R−	154	0.0	0.0
	Win	NA	ASSA	ASSA
Ex. 4	p-val.	1.73 × 10−6	1.73 × 10−6	1.73 × 10−6
	R+	465	465	465
	R−	0.0	0.0	0.0
	Win	ASSA	ASSA	ASSA
	Superior /Inferior/NA	3/0/1	4/0/0	4/0/0

8. Conclusions

The primary objective of this study was to introduce an adaptive version of the salp swarm algorithm (ASSA). Two new equations for the leader- and follower-updating positions were introduced to improve the proposed ASSA’s search and discovery abilities. In the standard SSA, the leading salp modifies its position based on a single point, which is the food location. However, due to a lack of knowledge about the real position of the food location, the algorithm may be locked at the local optimum. To overcome this weakness and to improve the exploration ability of the algorithm, in the proposed ASSA, half of the population was considered as leaders, which adjusted their positions not only based on the food location but also based on their previous positions. In addition, instead of the constant value considered in an SSA for follower-position-updating, in the ASSA, a random value was proposed. In addition, at each iteration of the optimization process, the ASSA replaced the worst salp, yielding the highest fitness value with a randomly generated salp. A statistical analysis was carried out in order to make an accurate assessment of the new algorithm’s performance. The proposed method was shown to perform admirably in terms of accuracy, stability, and robustness when tested on some well-known unimodal and multimodal test functions. The paper’s second goal was to automate a cost-effective design process for spread foundations and retaining walls. A computer program in Matlab was developed to reduce the cost of retaining structures and spread footings. On four case studies of these structures, the proposed method was compared to a classical SSA and some state-of-the-art metaheuristic algorithms. Given the final results, it was demonstrated that the ASSA outperformed the other techniques and should be able to provide better optimal results. The new method concurrently satisfied geotechnical and structural limit states while simultaneously providing a cost-effective design.