Predicting Rock Brittleness Using a Robust Evolutionary Programming Paradigm and Regression-Based Feature Selection Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Field Investigation
2.1.2. Feature Selection Process
2.2. Methods
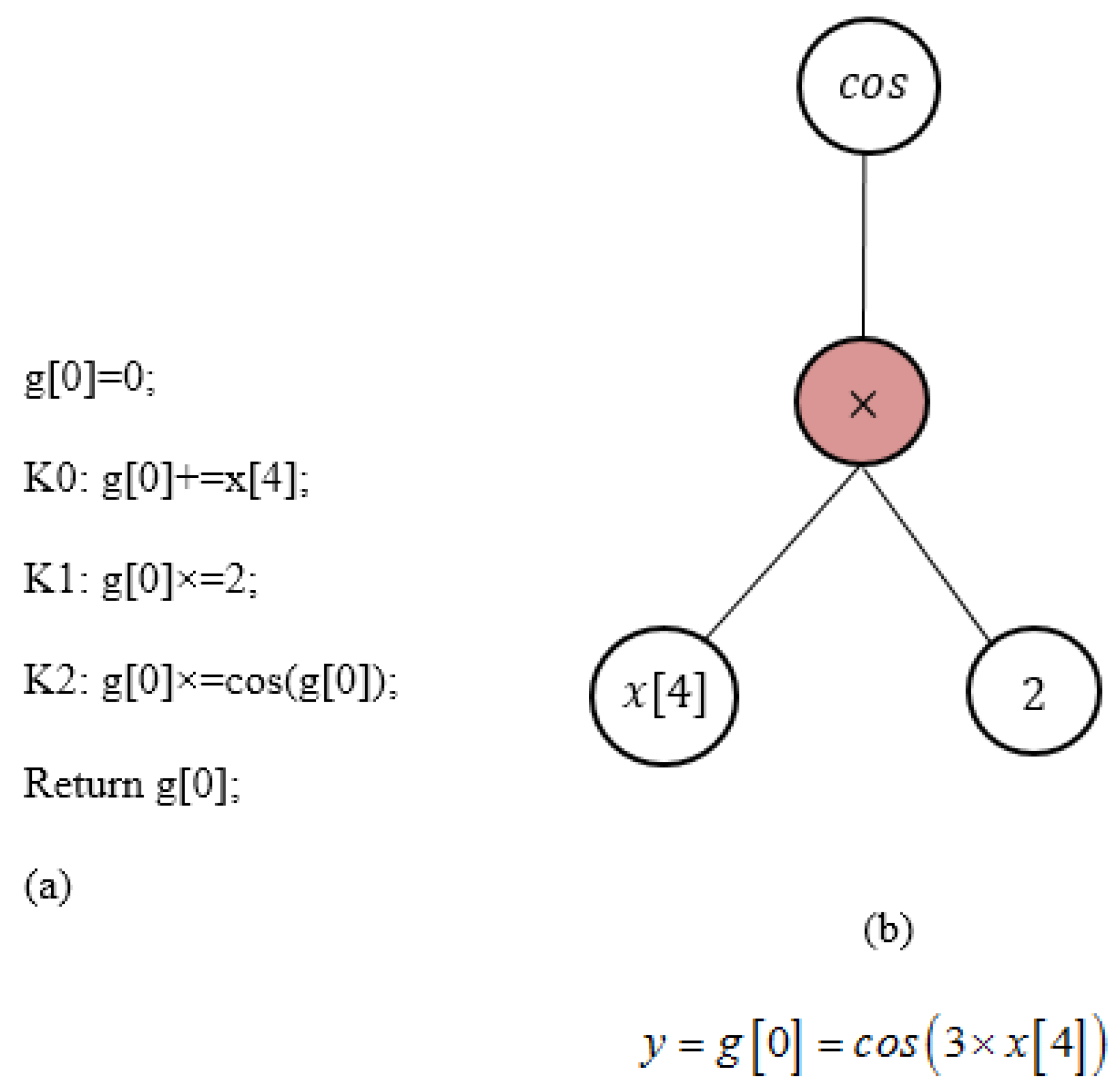
2.2.1. Linear Genetic Programming (LGP)
- Initialization: Creating the initial population randomly (programs), and then calculating the fitness function of each program.
- Main operators:
- (1)
- Tournament selection: This operator randomly selects several individuals from the population. Two individuals with the best fitness functions are chosen from these individuals, and two others as the worst solutions [43].
- (2)
- Crossover operator: This operator is applied to combine some elements of the best solutions with each other to create two new solutions (individuals).
- (3)
- Mutation operator: Mutation is used to create two new individuals by transforming each of the best solutions.
- Elitist mechanism: The worst solutions are replaced with transformed solutions based on this mechanism.
2.2.2. Local Weighted Linear Regression (LWLR)
2.2.3. KStar Model
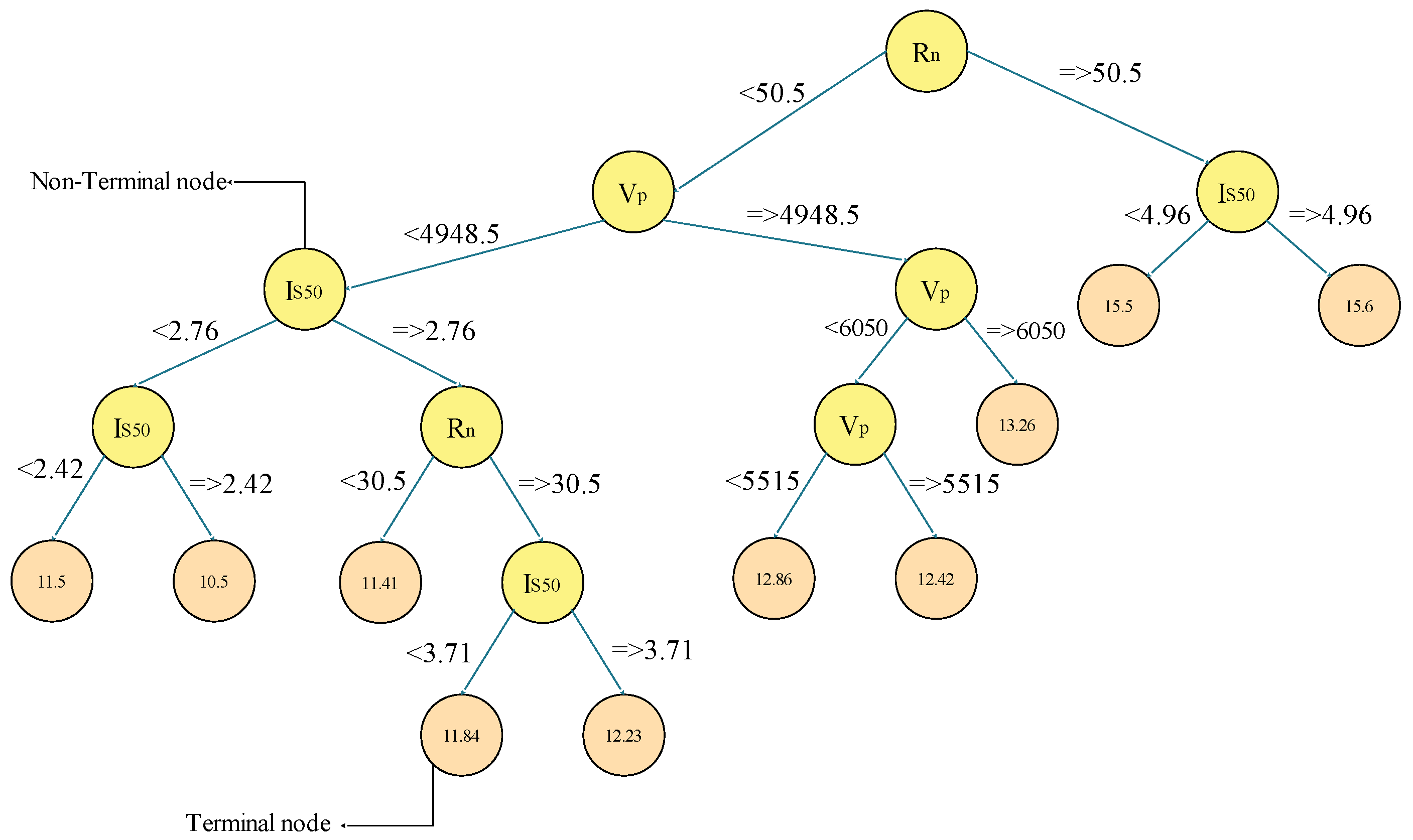
2.2.4. Bootstrap Aggregate (Bagged) Regression Tree (BRT)
3. Statistical Criteria for Evaluation of Models
- Correlation coefficient (R) can be expressed as
- 2.
- Root mean square error (RMSE) can be expressed as
- 3.
- Mean absolute percentage error is defined as
- 4.
- Scatter Index can be expressed as
- 5.
- Willmott’s agreement Index [49] can be expressed as
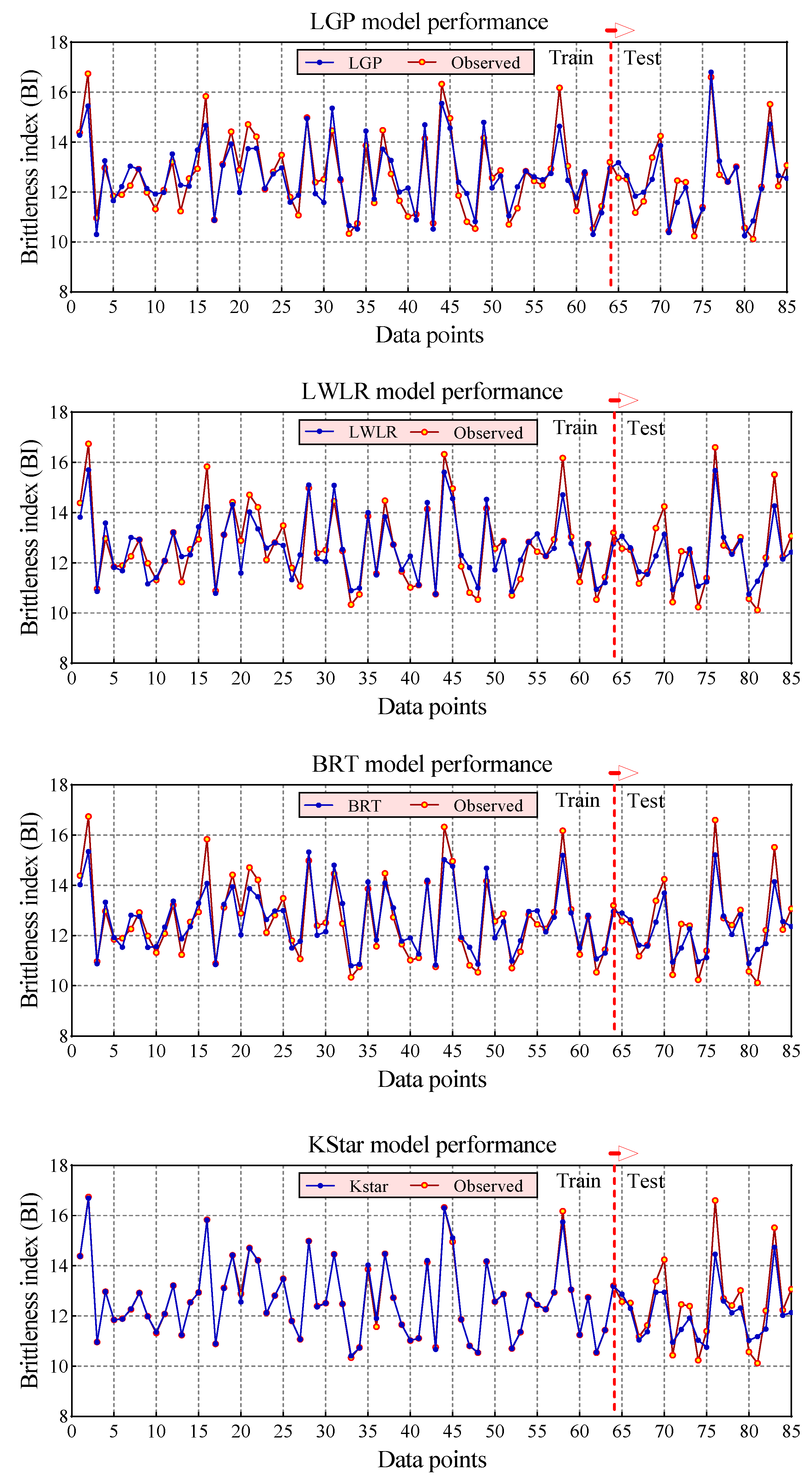
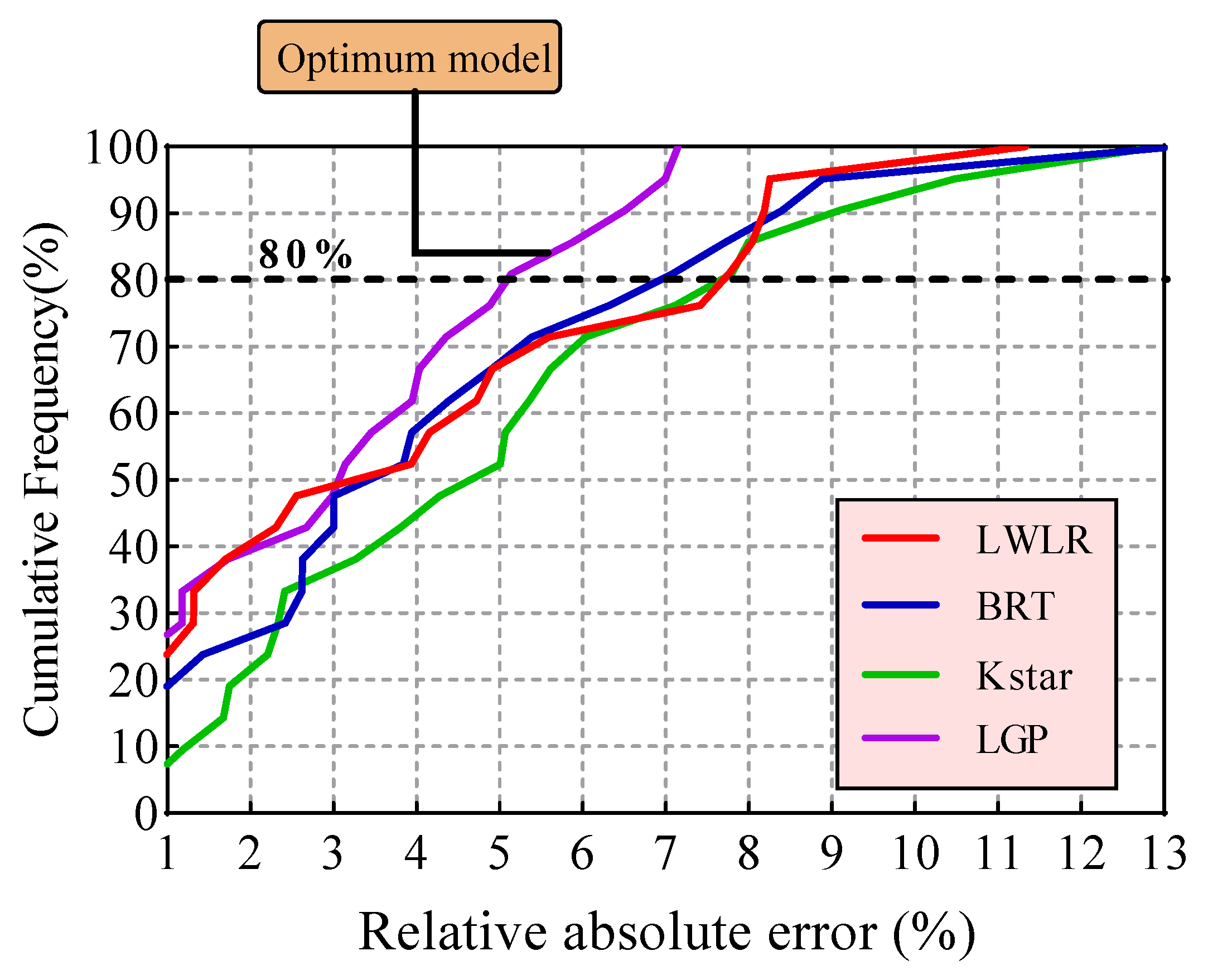
4. Results and Discussion
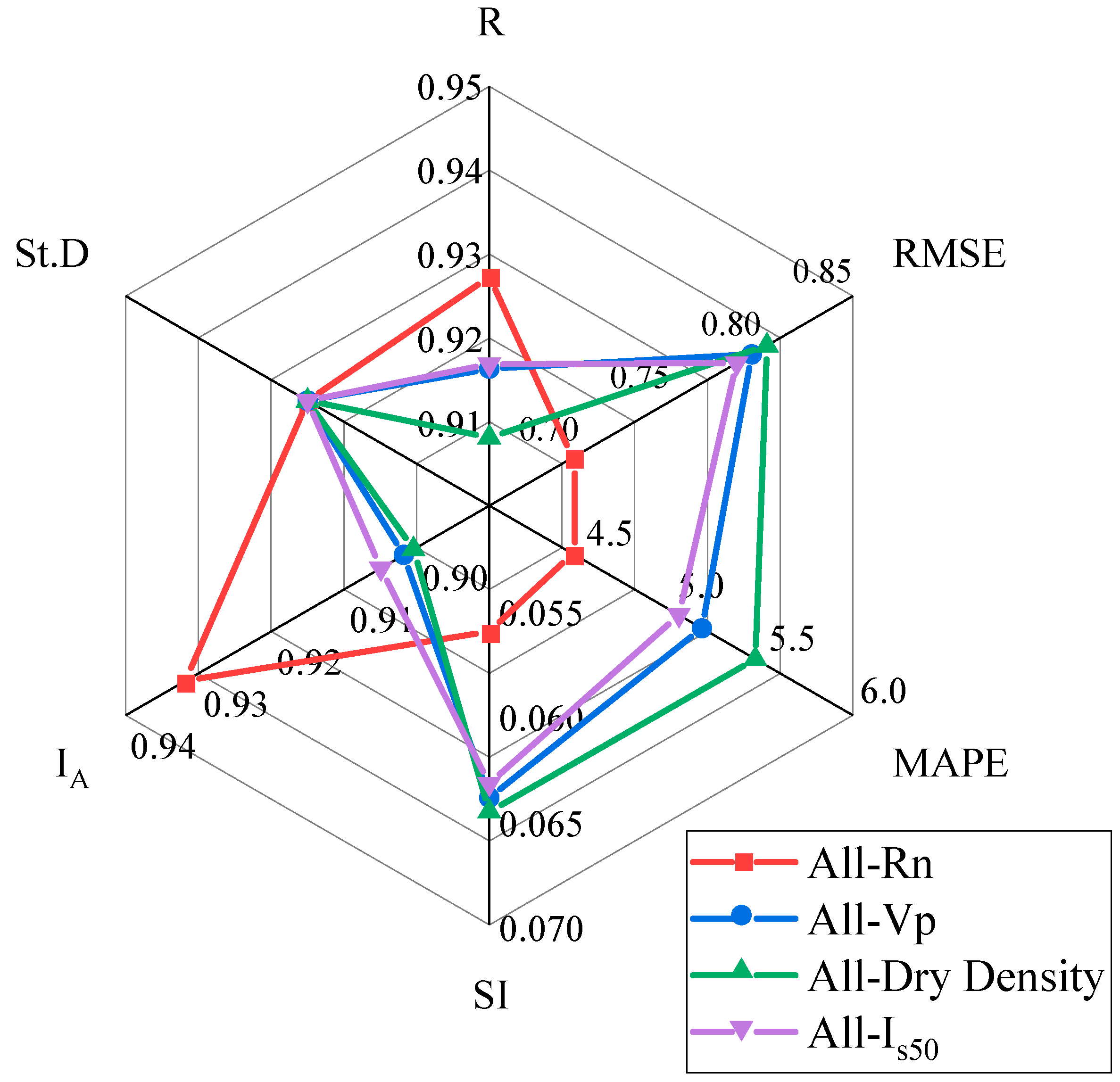
5. Sensitivity Analysis
6. Conclusions
- Based on the results, all developed models’ performance capacity was suitable and acceptable. Accordingly, all proposed models can be used with confidence for future research on predictions of other issues in the field of rock mechanics.
- Among the proposed models, the KStar (R = 0.9984 and RMSE = 0.0865) model predicted BI with the best performance in the training phase, while the best performance for the testing phase was achieved by the LGP (R = 0.9529 and RMSE = 0.4838) model. In addition, both LWLR (R = 0.9490 and RMSE = 0.6607) and BRT (R = 0.9433 and RMSE = 0.6875), ranking second and third, respectively, lead to desired results for modeling BI values.
- The authors recommend increasing the accuracy of BI modeling as a possible future study, examining the ensemble of stacked models to integrate the advantages of standalone data-driven models.
- Sensitivity analysis demonstrated that dry density (D) was the most influential parameter with respect to BI.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rickman, R.; Mullen, M.J.; Petre, J.E.; Grieser, W.V.; Kundert, D. A practical use of shale petrophysics for stimulation design optimization: All shale plays are not clones of the Barnett Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008. [Google Scholar]
- Miskimins, J.L. The impact of mechanical stratigraphy on hydraulic fracture growth and design considerations for horizontal wells. Bulletin 2012, 91, 475–499. [Google Scholar]
- Jahed Armaghani, D.; Asteris, P.G.; Askarian, B.; Hasanipanah, M.; Tarinejad, R.; Huynh, V.V. Examining hybrid and single SVM models with different kernels to predict rock brittleness. Sustainability 2020, 12, 2229. [Google Scholar] [CrossRef] [Green Version]
- Hajiabdolmajid, V.; Kaiser, P. Brittleness of rock and stability assessment in hard rock tunnelling. Tunn. Undergr. Space Technol. 2003, 18, 35–48. [Google Scholar] [CrossRef]
- Rybacki, E.; Reinicke, A.; Meier, T.; Makasi, M.; Dresen, G. What controls the mechanical properties of shale rocks?–Part I: Strength and Young’s modulus. J. Pet. Sci. Eng. 2015, 135, 702–722. [Google Scholar] [CrossRef]
- Rybacki, E.; Meier, T.; Dresen, G. What controls the mechanical properties of shale rocks?—Part II: Brittleness. J. Pet. Sci. Eng. 2016, 144, 39–58. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.P. Brittleness and the mechanical winning of coal. Min. Sci. Technol. 1986, 3, 173–180. [Google Scholar] [CrossRef]
- Sun, D.; Lonbani, M.; Askarian, B.; Jahed Armaghani, D.; Tarinejad, R.; Pham, B.T.; Huynh, V.V. Investigating the Applications of Machine Learning Techniques to Predict the Rock Brittleness Index. Appl. Sci. 2020, 10, 1691. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Guo, H.; Koopialipoor, M.; Armaghani, D.J.; Tahir, M.M. Investigating the effective parameters on the risk levels of rockburst phenomena by developing a hybrid heuristic algorithm. Eng. Comput. 2020, 37, 1679–1694. [Google Scholar] [CrossRef]
- Yagiz, S. Utilizing rock mass properties for predicting TBM performance in hard rock condition. Tunn. Undergr. Space Technol. 2008, 23, 326–339. [Google Scholar] [CrossRef]
- Ebrahimabadi, A.; Goshtasbi, K.; Shahriar, K.; Cheraghi Seifabad, M. A model to predict the performance of roadheaders based on the Rock Mass Brittleness Index. J. S. Afr. Inst. Min. Metall. 2011, 111, 355–364. [Google Scholar]
- Yagiz, S. Assessment of brittleness using rock strength and density with punch penetration test. Tunn. Undergr. Space Technol. 2009, 24, 66–74. [Google Scholar] [CrossRef]
- Altindag, R. Assessment of some brittleness indexes in rock-drilling efficiency. Rock Mech. Rock Eng. 2010, 43, 361–370. [Google Scholar] [CrossRef]
- Morley, A. Strength of Material, Longmans, 11th ed.; Green: London, UK, 1954. [Google Scholar]
- Ramsay, J.G. Folding and Fracturing of Rocks; Mc Graw Hill B. Co.: New York, NY, USA, 1967; Volume 568. [Google Scholar]
- Obert, L.; Duvall, W.I. Rock Mechanics and the Design of Structures in Rock; Wiley: Hoboken, NJ, USA, 1967. [Google Scholar]
- Yagiz, S.; Gokceoglu, C. Application of fuzzy inference system and nonlinear regression models for predicting rock brittleness. Expert Syst. Appl. 2010, 37, 2265–2272. [Google Scholar] [CrossRef]
- Wang, Y.; Watson, R.; Rostami, J.; Wang, J.Y.; Limbruner, M.; He, Z. Study of borehole stability of Marcellus shale wells in longwall mining areas. J. Pet. Explor. Prod. Technol. 2014, 4, 59–71. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Zhou, H.; Zhang, C.; Xu, R.; Lu, J. Evaluation methodology of brittleness of rock based on post-peak stress–strain curves. Rock Mech. Rock Eng. 2015, 48, 1787–1805. [Google Scholar] [CrossRef]
- Hucka, V.; Das, B. Brittleness determination of rocks by different methods. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1974, 11, 389–392. [Google Scholar] [CrossRef]
- Lawn, B.R.; Marshall, D.B. Hardness, toughness, and brittleness: An indentation analysis. J. Am. Ceram. Soc. 1979, 62, 347–350. [Google Scholar] [CrossRef]
- Khandelwal, M.; Faradonbeh, R.S.; Monjezi, M.; Armaghani, D.J.; Bin Abd Majid, M.Z.; Yagiz, S. Function development for appraising brittleness of intact rocks using genetic programming and non-linear multiple regression models. Eng. Comput. 2017, 33, 13–21. [Google Scholar] [CrossRef]
- Altindag, R. The role of rock brittleness on analysis of percussive drilling performance. In Proceedings of the 5th National Rock Mechanics, Isparta, Turkey, 30–31 October 2000; pp. 105–112. [Google Scholar]
- Nejati, H.R.; Moosavi, S.A. A new brittleness index for estimation of rock fracture toughness. J. Min. Environ. 2017, 8, 83–91. [Google Scholar]
- Koopialipoor, M.; Noorbakhsh, A.; Noroozi Ghaleini, E.; Jahed Armaghani, D.; Yagiz, S. A new approach for estimation of rock brittleness based on non-destructive tests. Nondestruct. Test. Eval. 2019, 34, 354–375. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Koopialipoor, M.; Marto, A.; Yagiz, S. Application of several optimization techniques for estimating TBM advance rate in granitic rocks. J. Rock Mech. Geotech. Eng. 2019, 11, 779–789. [Google Scholar] [CrossRef]
- Dehghan, S.; Sattari, G.H.; Chelgani, S.C.; Aliabadi, M.A. Prediction of uniaxial compressive strength and modulus of elasticity for Travertine samples using regression and artificial neural networks. Min. Sci. Technol. 2010, 20, 41–46. [Google Scholar] [CrossRef]
- Yagiz, S.; Yazitova, A.; Karahan, H. Application of differential evolution algorithm and comparing its performance with literature to predict rock brittleness for excavatability. Int. J. Min. Reclam. Environ. 2020, 34, 672–685. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Jamei, M.; Chu, X. A novel hybrid wavelet-locally weighted linear regression (W-LWLR) model for electrical conductivity (EC) prediction in water surface. J. Contam. Hydrol. 2020, 232, 103641. [Google Scholar] [CrossRef]
- Jiang, H.; Mohammed, A.S.; Kazeroon, R.A.; Sarir, P. Use of the Gene-Expression Programming Equation and FEM for the High-Strength CFST Columns. Appl. Sci. 2021, 11, 10468. [Google Scholar] [CrossRef]
- Asteris, P.G.; Rizal, F.I.M.; Koopialipoor, M.; Roussis, P.C.; Ferentinou, M.; Armaghani, D.J.; Gordan, B. Slope Stability Classification under Seismic Conditions Using Several Tree-Based Intelligent Techniques. Appl. Sci. 2022, 12, 1753. [Google Scholar] [CrossRef]
- Massalov, T.; Yagiz, S.; Adoko, A.C. Application of Soft Computing Techniques to Estimate Cutter Life Index Using Mechanical Properties of Rocks. Appl. Sci. 2022, 12, 1446. [Google Scholar] [CrossRef]
- Qian, Y.; Aghaabbasi, M.; Ali, M.; Alqurashi, M.; Salah, B.; Zainol, R.; Moeinaddini, M.; Hussein, E.E. Classification of Imbalanced Travel Mode Choice to Work Data Using Adjustable SVM Model. Appl. Sci. 2021, 11, 11916. [Google Scholar] [CrossRef]
- Kaunda, R.B.; Asbury, B. Prediction of rock brittleness using nondestructive methods for hard rock tunnelling. J. Rock Mech. Geotech. Eng. 2016, 8, 533–540. [Google Scholar] [CrossRef] [Green Version]
- Hatheway, A.W. The complete ISRM suggested methods for rock characterization, testing and monitoring; 1974–2006. Environ. Eng. Geosci. 2009, 15, 47–48. [Google Scholar] [CrossRef]
- Geroge, D.; Mallery, P. SPSS for Windows Step by Step: A Simple Guide and Reference; Allyn and Bacon: Boston, MA, USA, 2003. [Google Scholar]
- Nie, N.H.; Bent, D.H.; Hull, C.H. SPSS: Statistical Package for the Social Sciences; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Kobayashi, M.; Sakata, S. Mallows’ Cp criterion and unbiasedness of model selection. J. Econom. 1990, 45, 385–395. [Google Scholar] [CrossRef]
- Gilmour, S.G. The interpretation of Mallows’s Cp-statistic. J. R. Stat. Soc. Ser. D Stat. 1996, 45, 49–56. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Claeskens, G.; Hjort, N.L. Model Selection and Model Averaging; Cambridge Books: Cambridge, UK, 2008. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Gandomi, A.H.; Mohammadzadeh, D.; Pérez-Ordóñez, J.L.; Alavi, A.H. Linear genetic programming for shear strength prediction of reinforced concrete beams without stirrups. Appl. Soft Comput. 2014, 19, 112–120. [Google Scholar] [CrossRef]
- Atkeson, C.G.; Moore, A.W.; Schaal, S. Locally Weighted Learning for Control. Artif. Intell. Rev. 1997, 11, 75–113. [Google Scholar] [CrossRef]
- Jamei, M.; Ahmadianfar, I. Prediction of scour depth at piers with debris accumulation effects using linear genetic programming. Mar. Georesources Geotechnol. 2020, 38, 468–479. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Jamei, M.; Chu, X. Prediction of local scour around circular piles under waves using a novel artificial intelligence approach. Mar. Georesources Geotechnol. 2019, 39, 44–55. [Google Scholar] [CrossRef]
- Wang, J.; Yu, L.C.; Lai, K.R.; Zhang, X. Locally weighted linear regression for cross-lingual valence-arousal prediction of affective words. Neurocomputing 2016, 194, 271–278. [Google Scholar] [CrossRef]
- Pourrajab, R.; Ahmadianfar, I.; Jamei, M.; Behbahani, M. A meticulous intelligent approach to predict thermal conductivity ratio of hybrid nanofluids for heat transfer applications. J. Therm. Anal. Calorim. 2020, 146, 611–628. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. (NY) 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Machine, P. Practical Machine Learning Tools and Techniques. In Data Mining; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Williams, T.P.; Gong, J. Predicting construction cost overruns using text mining, numerical data and ensemble classifiers. Autom. Constr. 2014, 43, 23–29. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Hasanipanah, M.; Monjezi, M.; Shahnazar, A.; Jahed Armaghanid, D.; Farazmand, A. Feasibility of indirect determination of blast induced ground vibration based on support vector machine. Measurement 2015, 75, 289–297. [Google Scholar] [CrossRef]
- Parsajoo, M.; Armaghani, D.J.; Mohammed, A.S.; Khari, M.; Jahandari, S. Tensile strength prediction of rock material using. Transp. Geotech. 2021, 31, 100652. [Google Scholar] [CrossRef]
- non-destructive tests: A comparative intelligent study. Transp. Geotech. 2021, 31, 100652. [CrossRef]
- Asteris, P.G.; Mamou, A.; Hajihassani, M.; Hasanipanah, M.; Koopialipoor, M.; Le, T.T.; Kardani, N.; Armaghani, D.J. Soft computing based closed form equations correlating L and N-type Schmidt hammer rebound numbers of rocks. Transp. Geotech. 2021, 29, 100588. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, M.D.; Nguyen-Thoi, T.; Ho, L.S.; Koopialipoor, M.; Quoc, N.K.; Armaghani, D.J.; Van Le, H. A novel approach for classification of soils based on laboratory tests using Adaboost, Tree and ANN modeling. Transp. Geotech. 2020, 27, 100508. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Zhu, S.; Jahed Armaghani, D.; Khandelwal, M.; Mohamad, E.T. Estimating TBM advance rate in hard rock condition using XGBoost and Bayesian optimization. Undergr. Space 2020, 6, 506–515. [Google Scholar] [CrossRef]
- Harandizadeh, H.; Jahed Armaghani, D.; Hasanipanah, M.; Jahandari, S. A novel TS Fuzzy-GMDH model optimized by PSO to determine the deformation values of rock material. Neural Comput. Appl. 2022, in press. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Amnieh, H.B. A fuzzy rule-based approach to address uncertainty in risk assessment and prediction of blast-induced flyrock in a quarry. Nat. Resour. Res. 2020, 29, 669–689. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Amnieh, H.B. Developing a new uncertain rule-based fuzzy approach for evaluating the blast-induced backbreak. Eng. Comput. 2020, 37, 1879–1893. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Keshtegar, B.; Thai, D.K.; Troung, N.-T. An ANN adaptive dynamical harmony search algorithm to approximate the flyrock resulting from blasting. Eng. Comput. 2020, 38, 1257–1269. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Meng, D.; Keshtegar, B.; Trung, N.T.; Thai, D.K. Nonlinear models based on enhanced Kriging interpolation for prediction of rock joint shear strength. Neural Comput. Appl. 2020, 33, 4205–4215. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Zhang, W.; Jahed Armaghani, D.; Rad, H.N. The potential application of a new intelligent based approach in predicting the tensile strength of rock. IEEE Access 2020, 8, 57148–57157. [Google Scholar] [CrossRef]
- Zhu, W.; Nikafshan Rad, H.; Hasanipanah, M. A chaos recurrent ANFIS optimized by PSO to predict ground vibration generated in rock blasting. Appl. Soft. Comput. 2021, 108, 107434. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Jamei, M.; Mohammed, A.S.; Nait Amar, M.; Hocine, O.; Khedher, K.M. Intelligent prediction of rock mass deformation modulus through three optimized cascaded forward neural network models. Earth Sci. Inform. 2022, in press. [Google Scholar] [CrossRef]
- Babyak, M.A. What you see may not be what you get: A brief, nontechnical introduction to overfitting in regression-type models. Psychosom. Med. 2004, 66, 411–421. [Google Scholar]
- Hill, T.; Lewicki, P. Statistics: Methods and Applications: A Comprehensive Reference for Science, Industry, and Data Mining; StatSoft, Inc.: Tulsa, OK, USA, 2006. [Google Scholar]
- Yagiz, S.; Ghasemi, E.; Adoko, A.C. Prediction of Rock Brittleness Using Genetic Algorithm and Particle Swarm Optimization Techniques. Geotech. Geol. Eng. 2018, 36, 3767–3777. [Google Scholar] [CrossRef]





| Parameters | Vp (m/s) | Dry Density (g/cm3) | Is50 (MPa) | BI | |
|---|---|---|---|---|---|
| Minimum | 20 | 2910 | 2.38 | 0.8722 | 10.12 |
| Maximum | 59 | 7943 | 2.75 | 6.59 | 16.75 |
| Mean | 37.16 | 4975 | 2.536 | 3.441 | 12.61 |
| Std. Deviation | 10.12 | 1199 | 0.079 | 1.118 | 1.554 |
| Range | 39 | 5033 | 0.37 | 5.718 | 6.626 |
| Skewness | 0.3951 | 0.2449 | 0.1161 | 0.1294 | 0.7339 |
| Kurtosis | −0.76 | −0.605 | −0.3473 | 0.3369 | 0.2216 |
| Number of Variables | Variables | MSE | R2 | Adjusted R2 | Mallows’ Cp | Akaike’s AIC | Amemiya’s PC |
|---|---|---|---|---|---|---|---|
| 2 | Vp/D | 0.652 | 0.736 | 0.730 | 36.387 | −33.419 | 0.276 |
| 3 | 0.530 | 0.788 | 0.781 | 15.611 | −50.109 | 0.227 | |
| 4 | 0.463 | 0.817 | 0.808 | 5.000 | −60.552 | 0.201 |
| Models | Setting of Parameter | |
|---|---|---|
| LGP | Function set | +, −, ×, ÷, √, power, sin, cos |
| Population size | 300 | |
| Mutation frequency % | 85 | |
| Crossover frequency % | 50 | |
| Number of replication | 10 | |
| Block mutation rate % | 20 | |
| Instruction mutation rate % | 20 | |
| Instruction data mutation rate % | 60 | |
| Homologous crossover % | 90 | |
| Program size | 64–256 | |
| LWLR | • µ = 4 | |
| KStar | • Global blend = 30 | |
| BRT | • Function: “Bag”, Learning cycles = 50, MinLeafSize = 1 | |
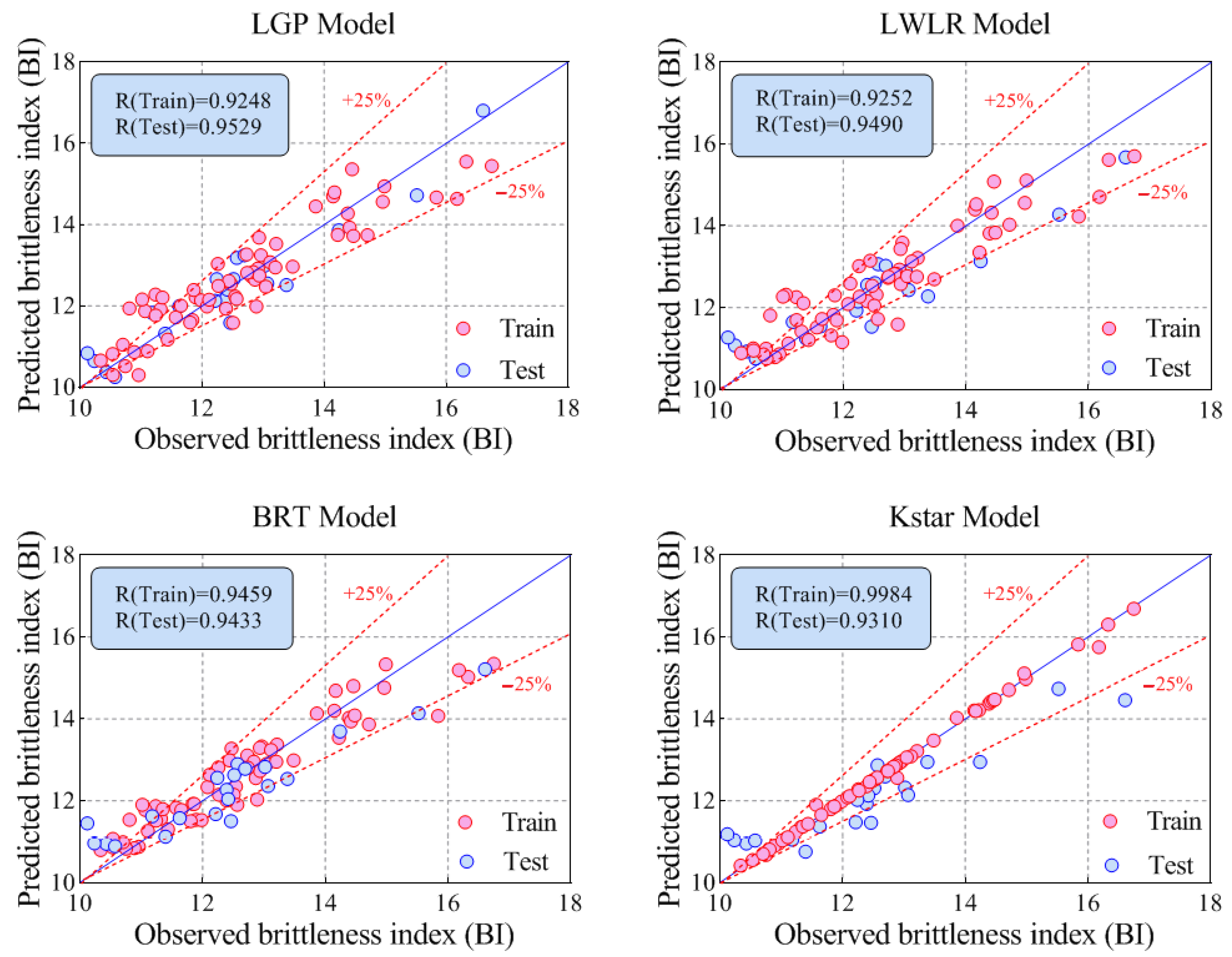
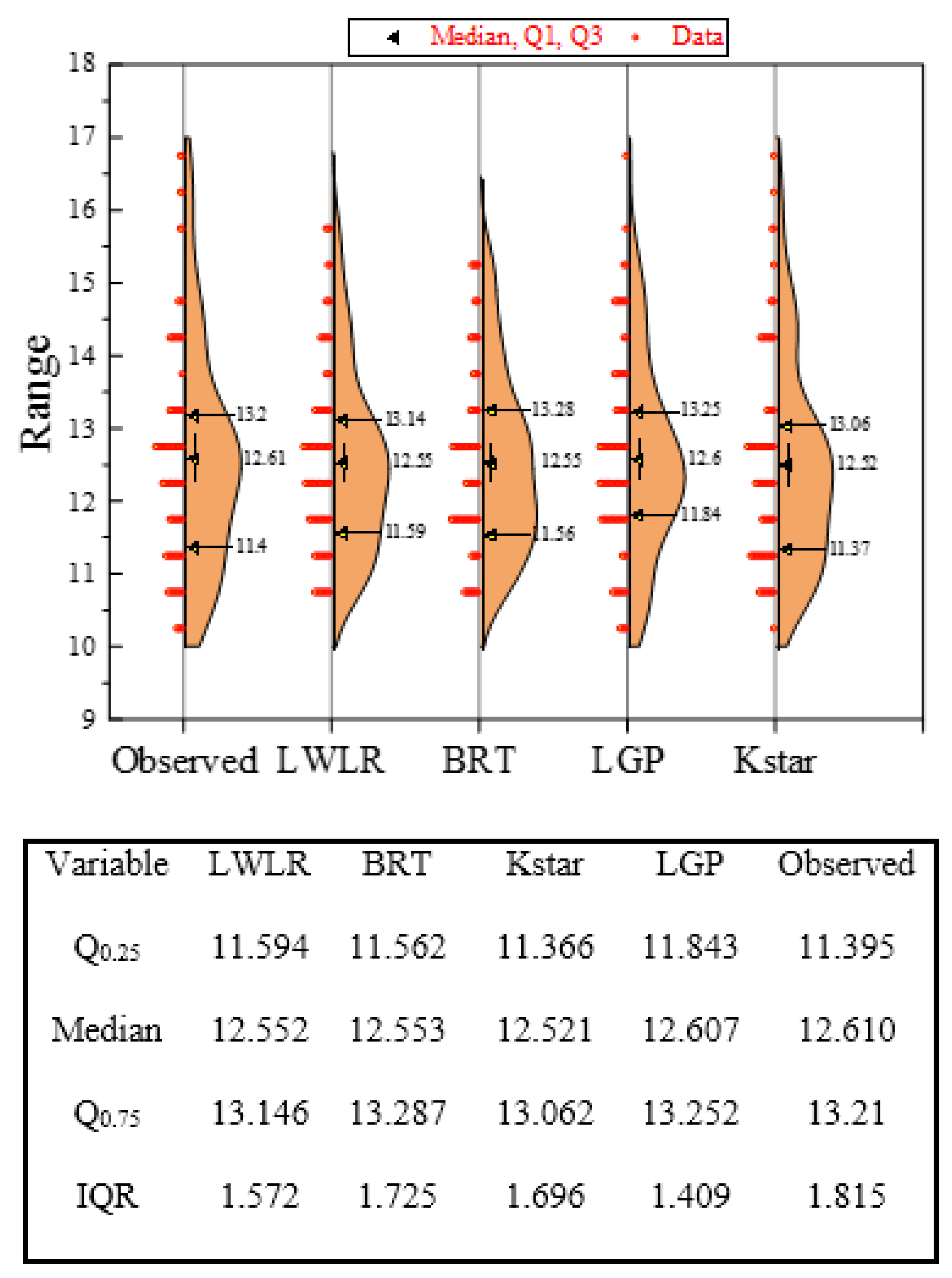
| Metrics | LGP | K-Star | BRT | LWLR | |
|---|---|---|---|---|---|
| Training | R | 0.9248 | 0.9984 | 0.9459 | 0.9252 |
| RMSE | 0.5867 | 0.0865 | 0.5297 | 0.5960 | |
| MAPE% | 3.6279 | 0.2564 | 3.1569 | 3.4088 | |
| SI | 0.0463 | 0.0068 | 0.0418 | 0.0470 | |
| IA | 0.9560 | 0.9992 | 0.9628 | 0.9531 | |
| St.D | 1.3339 | 1.5195 | 1.2640 | 1.2828 | |
| Testing | R | 0.9529 | 0.9310 | 0.9433 | 0.9490 |
| RMSE | 0.4838 | 0.7933 | 0.6875 | 0.6607 | |
| MAPE% | 3.2155 | 5.0573 | 4.3884 | 4.1549 | |
| SI | 0.0389 | 0.0638 | 0.0553 | 0.0532 | |
| IA | 0.9744 | 0.9095 | 0.9324 | 0.9400 | |
| St.D | 1.5059 | 1.0861 | 1.1116 | 1.1686 |
| Metric | All-Rn | All-Vp | All-Dry Density | All-Is50 | All |
|---|---|---|---|---|---|
| R | 0.9273 | 0.9163 | 0.9081 | 0.9169 | 0.9433 |
| RMSE | 0.6959 | 0.7944 | 0.8027 | 0.7861 | 0.6875 |
| MAPE | 4.4592 | 5.1695 | 5.4642 | 5.0433 | 4.3884 |
| SI | 0.0560 | 0.0639 | 0.0646 | 0.0633 | 0.0553 |
| IA | 0.9318 | 0.9018 | 0.9004 | 0.9049 | 0.9324 |
| St.D | 1.6277 | 1.6277 | 1.6277 | 1.6277 | 1.6277 |
| Rank | 4.0000 | 3.0000 | 1.0000 | 2.0000 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamei, M.; Mohammed, A.S.; Ahmadianfar, I.; Sabri, M.M.S.; Karbasi, M.; Hasanipanah, M. Predicting Rock Brittleness Using a Robust Evolutionary Programming Paradigm and Regression-Based Feature Selection Model. Appl. Sci. 2022, 12, 7101. https://doi.org/10.3390/app12147101
Jamei M, Mohammed AS, Ahmadianfar I, Sabri MMS, Karbasi M, Hasanipanah M. Predicting Rock Brittleness Using a Robust Evolutionary Programming Paradigm and Regression-Based Feature Selection Model. Applied Sciences. 2022; 12(14):7101. https://doi.org/10.3390/app12147101
Chicago/Turabian StyleJamei, Mehdi, Ahmed Salih Mohammed, Iman Ahmadianfar, Mohanad Muayad Sabri Sabri, Masoud Karbasi, and Mahdi Hasanipanah. 2022. "Predicting Rock Brittleness Using a Robust Evolutionary Programming Paradigm and Regression-Based Feature Selection Model" Applied Sciences 12, no. 14: 7101. https://doi.org/10.3390/app12147101
APA StyleJamei, M., Mohammed, A. S., Ahmadianfar, I., Sabri, M. M. S., Karbasi, M., & Hasanipanah, M. (2022). Predicting Rock Brittleness Using a Robust Evolutionary Programming Paradigm and Regression-Based Feature Selection Model. Applied Sciences, 12(14), 7101. https://doi.org/10.3390/app12147101










