Full-Field Strain Determination for Additively Manufactured Parts Using Radial Basis Functions
Abstract
:1. Introduction
2. Surface Strain Determination
2.1. Strain Computation in Surfaces
2.2. Radial Basis Functions
2.3. Application of Radial Basis Functions for Strain Determination
3. Evaluation of Strain Determination Using RBFs
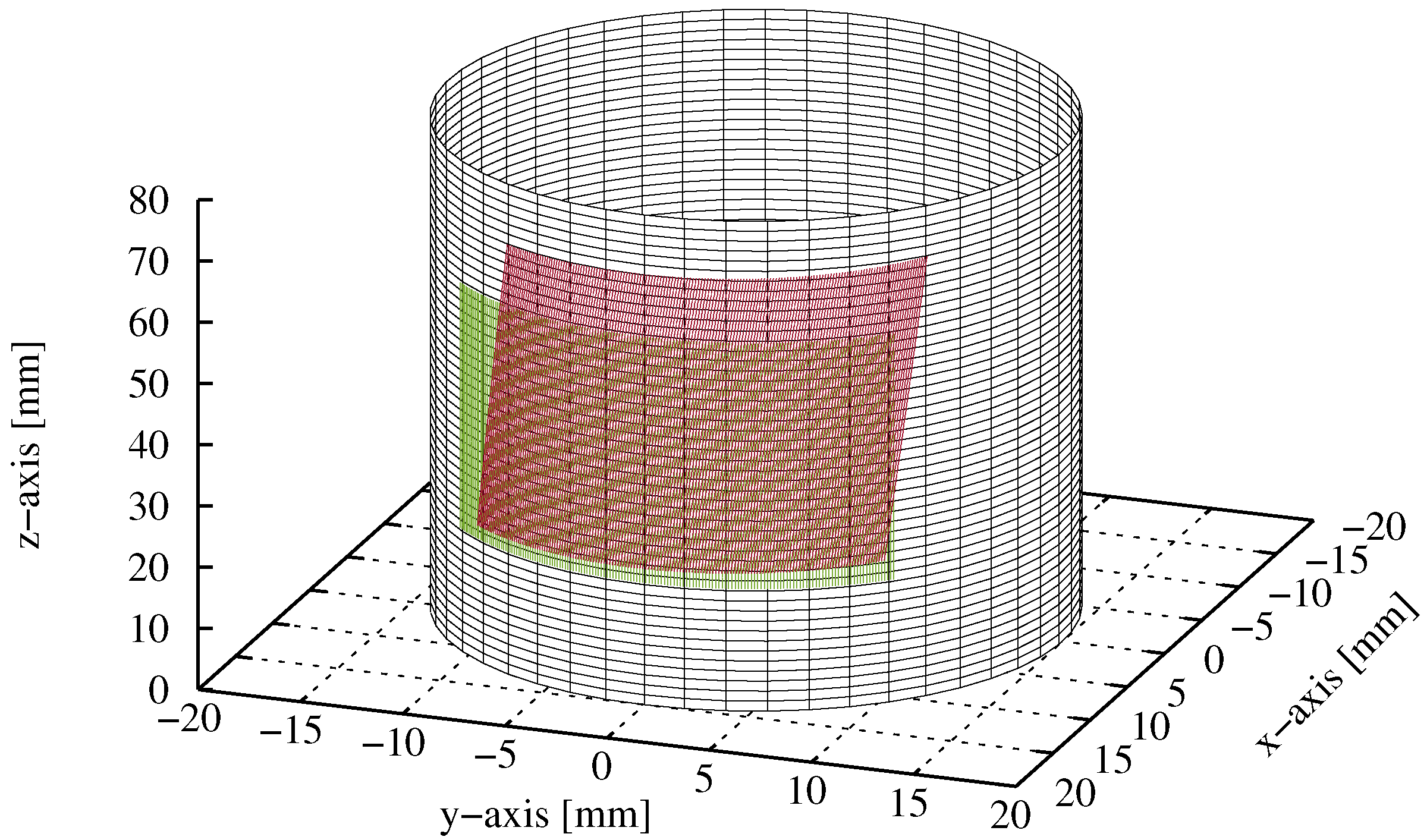
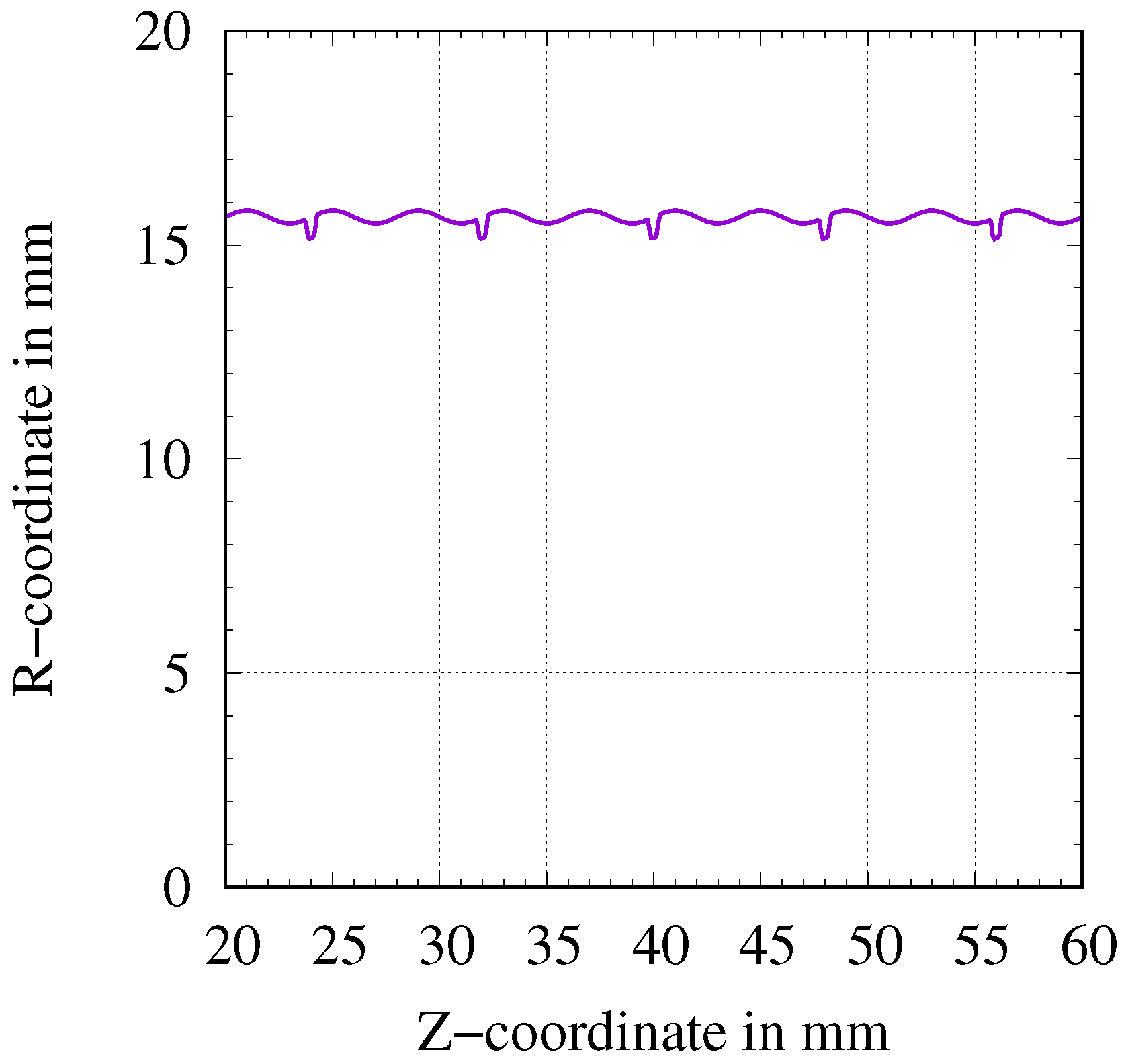
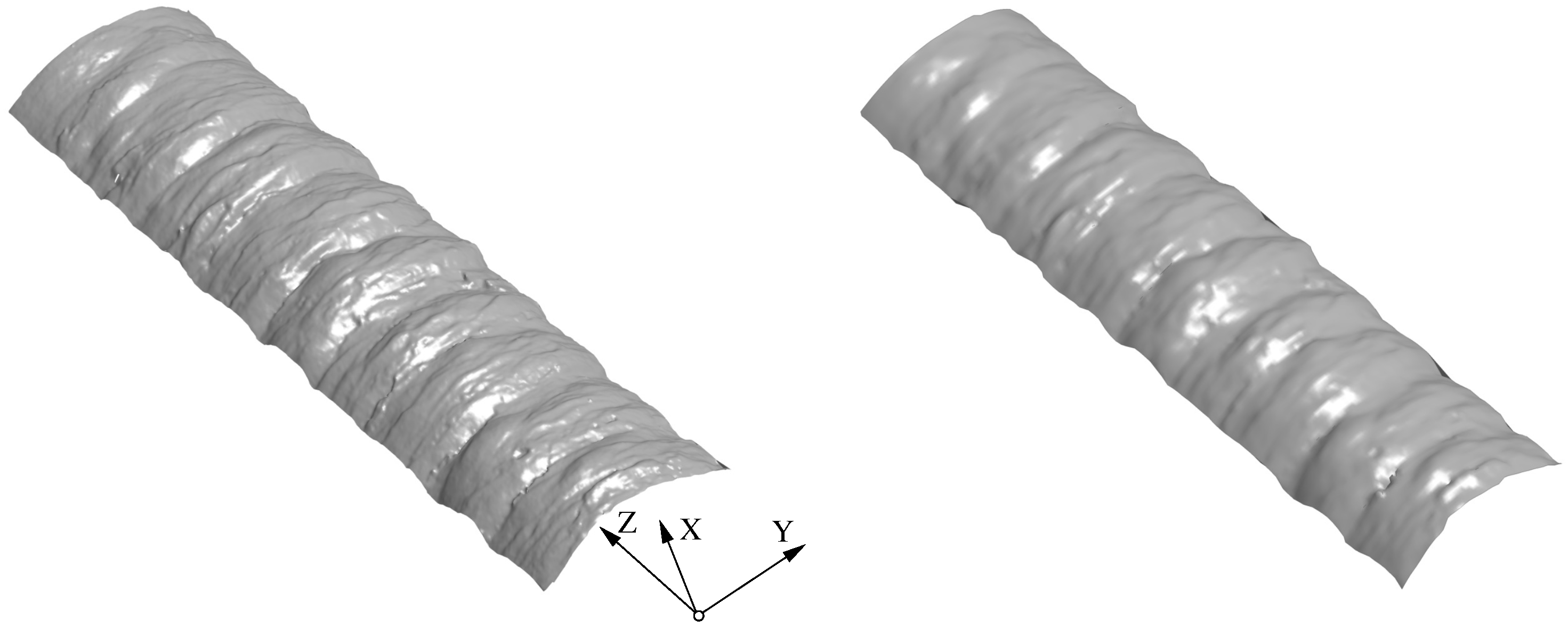
3.1. Verification Examples of WAAM-Produced Cylindrical Components
3.1.1. Tension and Torsion of a Cylindrical Tube
3.1.2. Tension and Torsion of a Tube with Rough Surface
3.2. Real Application Example of a Tube under Tension and Torsion
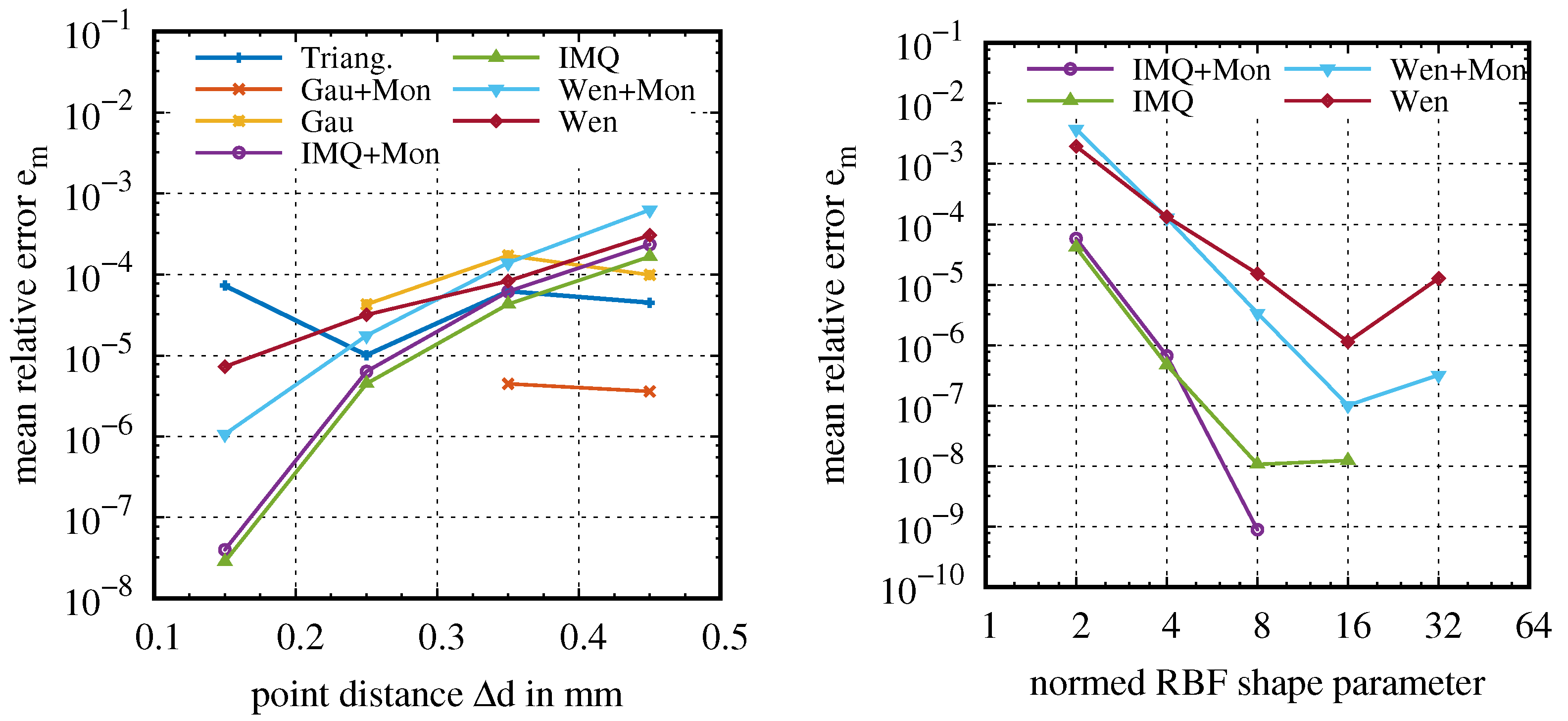
3.2.1. Comparison of Triangulation Concept and RBF (Torsional Case)
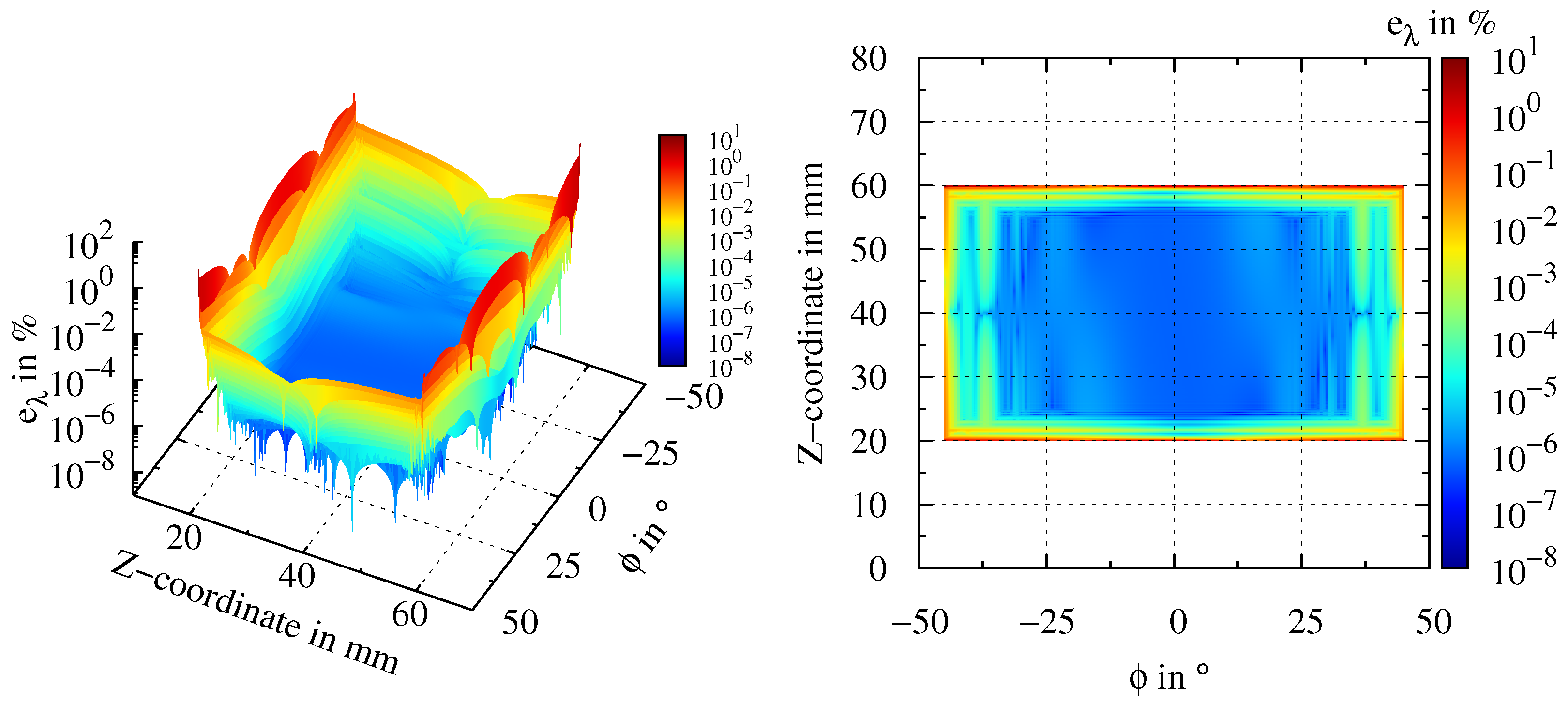
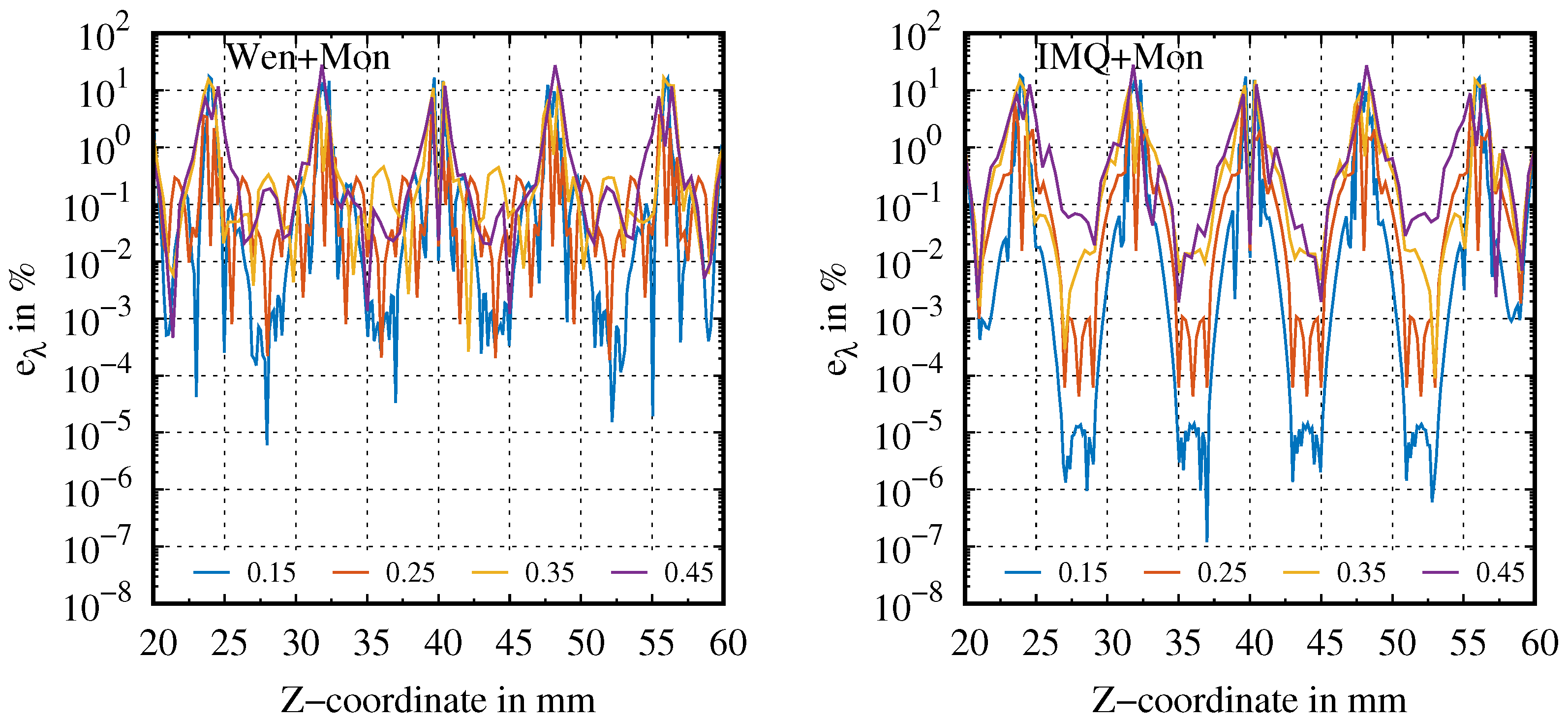
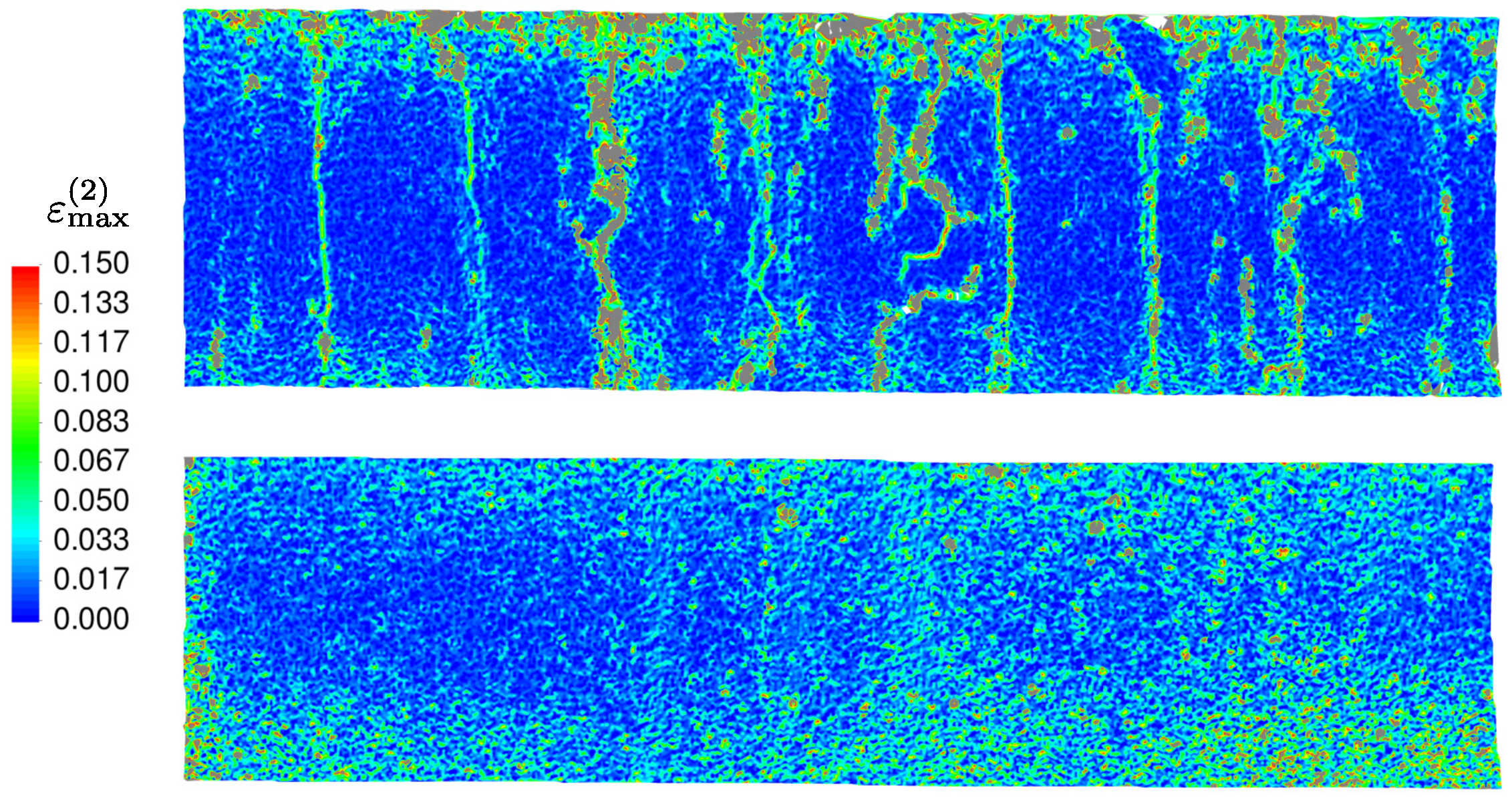
3.2.2. Rough Versus Smooth Surface Properties
3.2.3. Smoothing Data
3.2.4. Principal Directions
3.3. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DIC | Digital image correlation |
| IMQ | Inverse multi-quadrics |
| LLS | Linear least-square |
| PDE | Partial differential equations |
| px | Pixel |
| RBF | Radial basis functions |
| WAAM | Wire arc additive manufacturing |
Appendix A. Properties of Radial Basis Functions
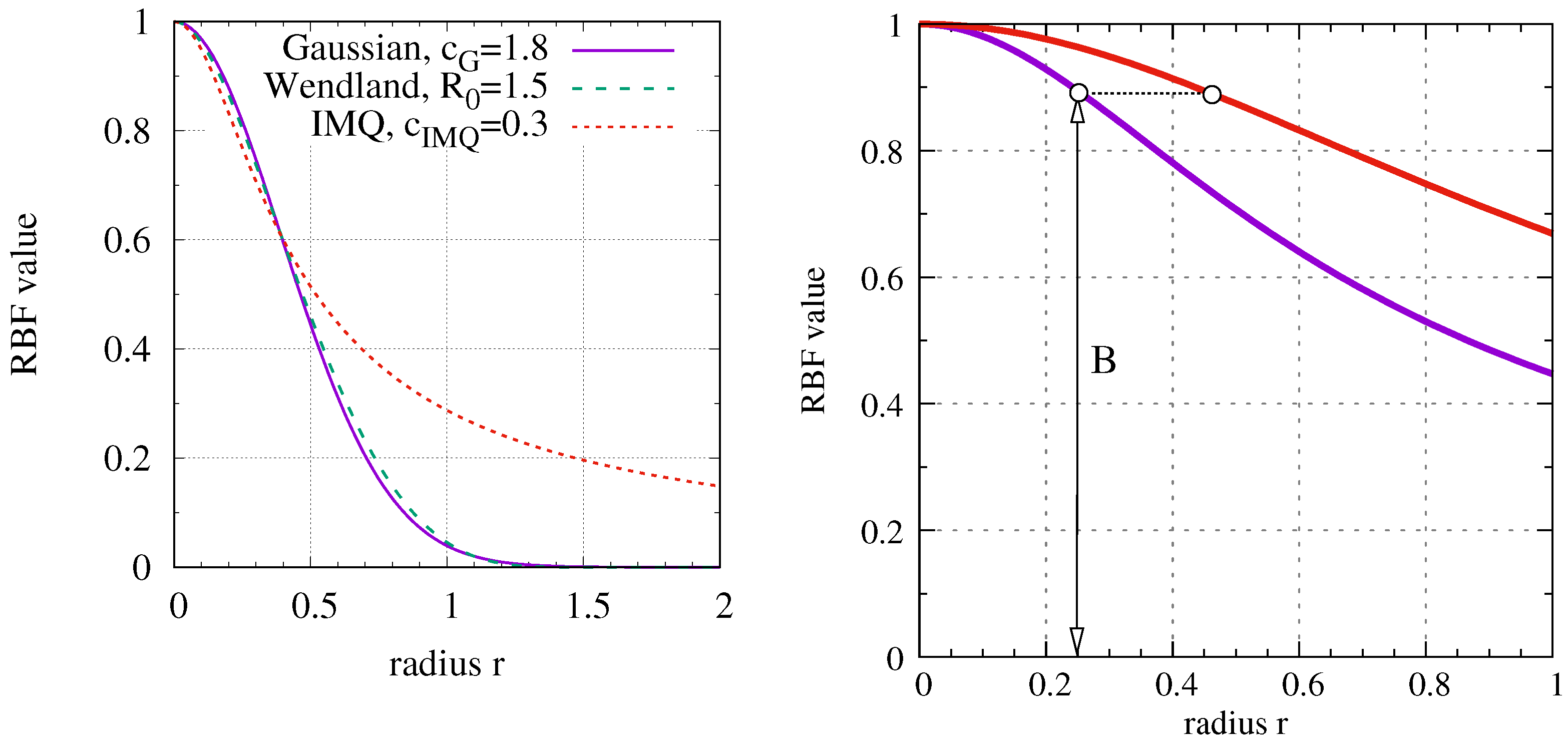
References
- Grédiac, M.; Hild, F. (Eds.) Full-Field Measurments and Identification in Solid Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Cunha, F.G.; Santos, T.G.; Xavier, J. In Situ Monitoring of Additive Manufacturing Using Digital Image Correlation: A Review. Materials 2021, 14, 1511. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H.W. Image Correlation for Shape, Motion and Deformation Measurements; Springer: New York, NY, USA, 2009. [Google Scholar]
- Hartmann, S.; Rodriguez, S. Verification examples for strain and strain-rate determination of digital image correlation systems. In Advances in Mechanics of Materials and Structural Analysis. Advanced Structured Materials; Number 80 in Advanced Structured Materials; Altenbach, H., Jablonski, F., Müller, W., Naumenko, K., Schneider, P., Eds.; Springer: Cham, Switzerland, 2018; pp. 135–174. [Google Scholar]
- Hsu, F.P.K.; Schwab, C.; Rigamonti, D.; Humphrey, J.D. Identification of response functions from axisymmetric membrane inflation tests: Implications for biomechanics. Int. J. Solids Struct. 1994, 31, 3375–3386. [Google Scholar] [CrossRef]
- Orteu, J.J. 3-D computer vision in experimental mechanics. Opt. Lasers Eng. 2009, 47, 282–291. [Google Scholar] [CrossRef] [Green Version]
- Buhmann, M.D. Radial Basis Functions, 1st ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Biancolini, M.E. Fast Radial Basis Functions for Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Groth, C.; Biancolini, M.E.; Costa, E.; Cella, U. Validation of high fidelity computational methods for aeronautical FSI analyses. Flex. Eng. Towar. Green Aircr. LNACM 2020, 92, 29–48. [Google Scholar]
- Costa, E.; Groth, C.; Lavedrine, J.; Caridi, D.; Dupain, G.; Biancolini, M.E. Unsteady FSI analysis of a square array of tubes in water crossflow. Flex. Eng. Towar. Green Aircr. LNACM 2020, 92, 129–152. [Google Scholar]
- De Boer, A.; Van der Schoot, M.S.; Bijl, H. Mesh deformation based on radial basis function interpolation. Comput. Struct. 2007, 85, 784–795. [Google Scholar] [CrossRef]
- Jamshidi, A.A.; Kirby, M.J. Examples of compactly supported functions for radial basis approximations. In Proceedings of the International Conference on Machine Learning: Models, Technologies & Applications, MLMTA 2006, Las Vegas, NV, USA, 26–29 June 2006; pp. 1–6. [Google Scholar]
- Trejo-Caballero, G.; Rostro-Gonzalez, H.; Garcia-Capulin, C.; Ibarra-Manzano, O.; Avina-Cervantes, J.; Torres-Huitzil, C. Automatic curve fitting based on radial basis functions and a hierarchical genetic algorithm. Math. Probl. Eng. 2015, 2015, 731207. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liu, G. A point interpolation meshless method based on radial basis functions. Int. J. Numer. Methods Eng. 2002, 54, 1623–1648. [Google Scholar] [CrossRef]
- Wang, L. Radial basis functions methods for boundary value problems: Performance comparison. Eng. Anal. Bound. Elem. 2017, 84, 191–205. [Google Scholar] [CrossRef]
- Fasshauer, G.E. Solving differential equations with radial basis functions: Multilevel methods and smoothing. Adv. Comput. Math. 1999, 11, 139–159. [Google Scholar] [CrossRef]
- Treutler, K.; Wesling, V. The current state of research of Wire Arc Additive Manufacturing (WAAM): A Review. Appl. Sci. 2021, 11, 8619. [Google Scholar] [CrossRef]
- Itskov, M. Tensor Algebra and Tensor Analysis for Engineers; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods: An overview and recent developments. Comput. Methods Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef] [Green Version]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Carr, J.C.; Beatson, R.K.; Cherrie, J.B.; Mitchell, T.J.; Fright, W.R.; McCallum, B.C.; Evans, T.R. Reconstruction and representation of 3D objects with radial basis functions. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 01, Los Angeles, CA, USA, 12–17 August 2001; pp. 67–76. [Google Scholar]
- Holmström, K. An adaptive radial basis algorithm (ARBF) for expensive black-box global optimization. J. Glob. Optim. 2008, 41, 447–464. [Google Scholar] [CrossRef]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics. In Encyclopedia of Physics; Springer: Berlin/Heidelberg, Germany, 1965; Volume III. [Google Scholar]
- Fosdick, R.L. Dynamically Possible Motions of Incompressible, Isotropic, Simple Materials. Arch. Ration. Mech. Anal. 1968, 29, 272–288. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Ellis Horwood: Chichester, UK, 1984. [Google Scholar]
- Hartmann, S. Numerical Studies on the Identification of the Material Parameters of Rivlin’s Hyperelasticity using Tension-Torsion Tests. Acta Mech. 2001, 148, 129–155. [Google Scholar] [CrossRef]
- Shewchuk, J.R. Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator. In Applied Computational Geometry: Towards Geometric Engineering; Lecture Notes in Computer Science; Lin, M.C., Manocha, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1148, pp. 203–222. [Google Scholar]
- Shewchuk, J.R. Delaunay Refinement Algorithms for Triangular Mesh Generation. Comput. Geom. Theory Appl. 2002, 22, 21–74. [Google Scholar] [CrossRef] [Green Version]
- Anderson, E.; Bai, Z.; Bischof, C.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; Ostrouchov, S.; et al. LAPACK User’s Guide; SIAM Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Coll, A.; Ribó, R.; Pasenau, M.; Escolano, E.; Perez, J.S.; Melendo, A.; Monros, A.; Gárate, J. GiD v.14 User Manual. CIMNE. 2018. Available online: www.gidhome.com (accessed on 15 October 2021).








| Gaussian | |||
| Wendland [20] | |||
| Inverse Multi-Quadrics |
| Gau | Gau + Mon | Wen | Wen + Mon | IMQ | IMQ + Mon | |
|---|---|---|---|---|---|---|
| 0.15 | ||||||
| 0.25 | ||||||
| 0.35 | ||||||
| 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hartmann, S.; Müller-Lohse, L.; Tröger, J.-A. Full-Field Strain Determination for Additively Manufactured Parts Using Radial Basis Functions. Appl. Sci. 2021, 11, 11434. https://doi.org/10.3390/app112311434
Hartmann S, Müller-Lohse L, Tröger J-A. Full-Field Strain Determination for Additively Manufactured Parts Using Radial Basis Functions. Applied Sciences. 2021; 11(23):11434. https://doi.org/10.3390/app112311434
Chicago/Turabian StyleHartmann, Stefan, Lutz Müller-Lohse, and Jendrik-Alexander Tröger. 2021. "Full-Field Strain Determination for Additively Manufactured Parts Using Radial Basis Functions" Applied Sciences 11, no. 23: 11434. https://doi.org/10.3390/app112311434
APA StyleHartmann, S., Müller-Lohse, L., & Tröger, J.-A. (2021). Full-Field Strain Determination for Additively Manufactured Parts Using Radial Basis Functions. Applied Sciences, 11(23), 11434. https://doi.org/10.3390/app112311434







