Stiffness-Based Cell Setup Optimization for Robotic Deburring with a Rotary Table
Abstract
:Featured Application
Abstract
1. Introduction
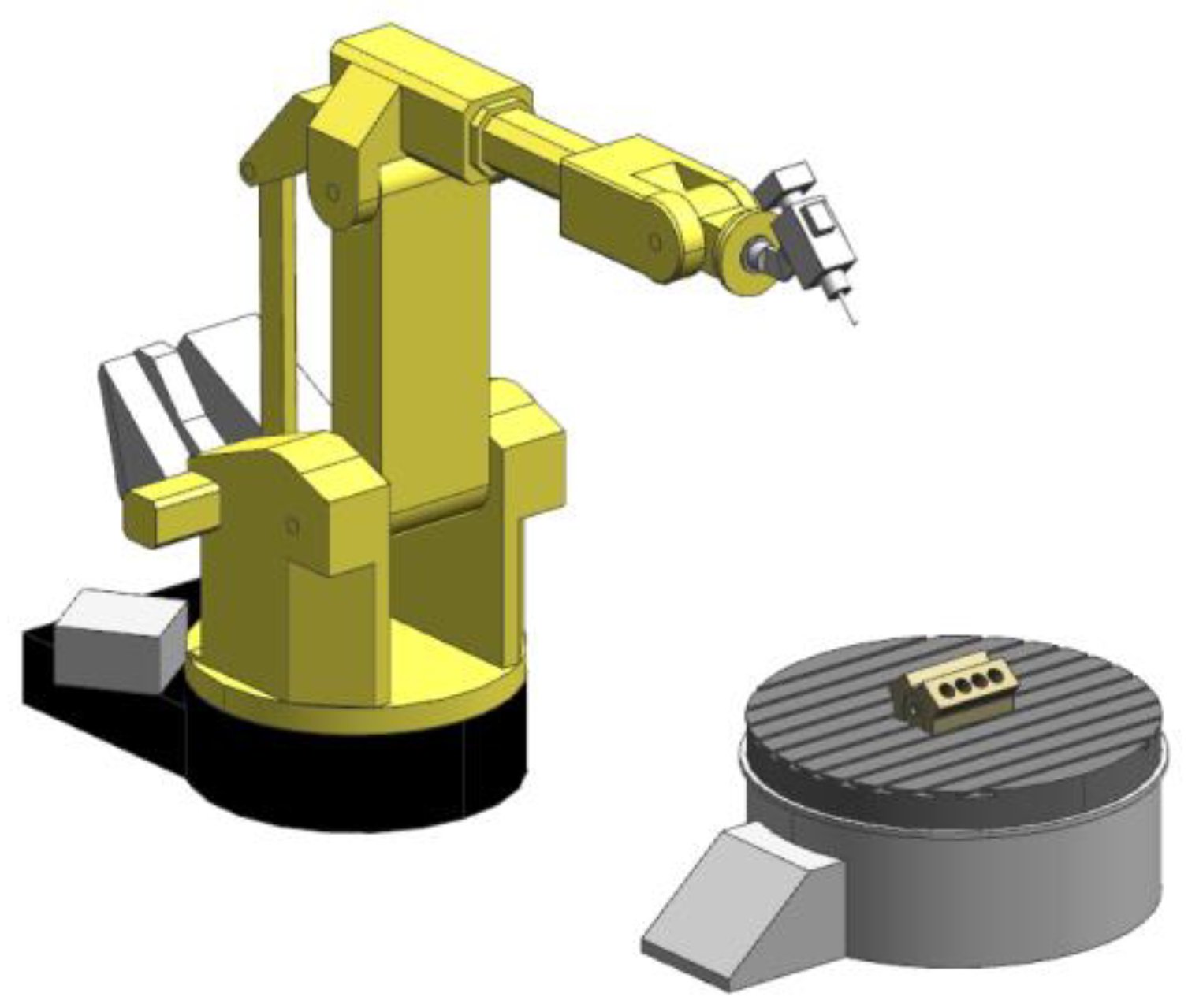
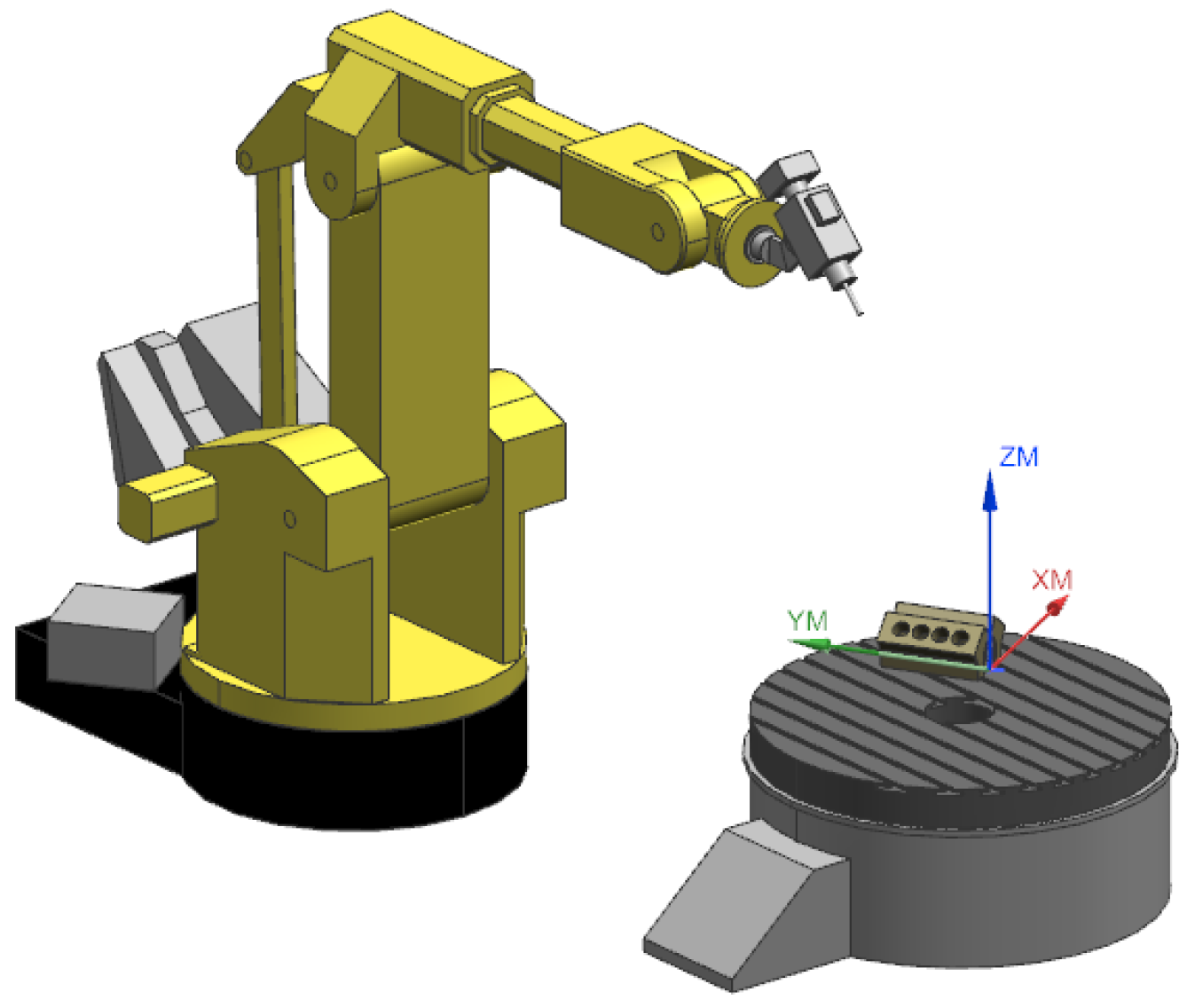
2. Robotic Deburring Cell
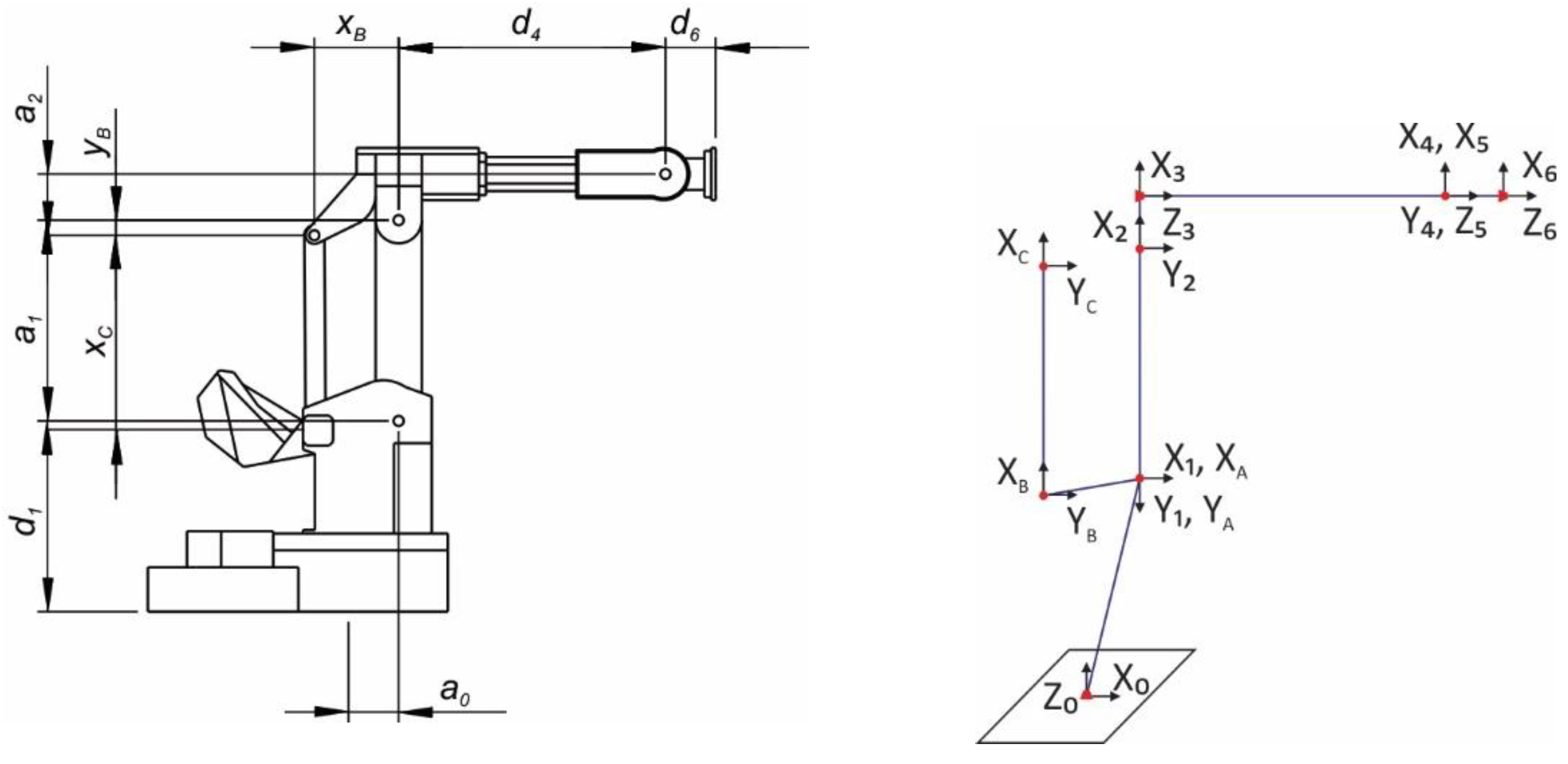
2.1. Kinematic Model of Robot ACMA XR701
2.2. Kinematic Model of the Deburring Head
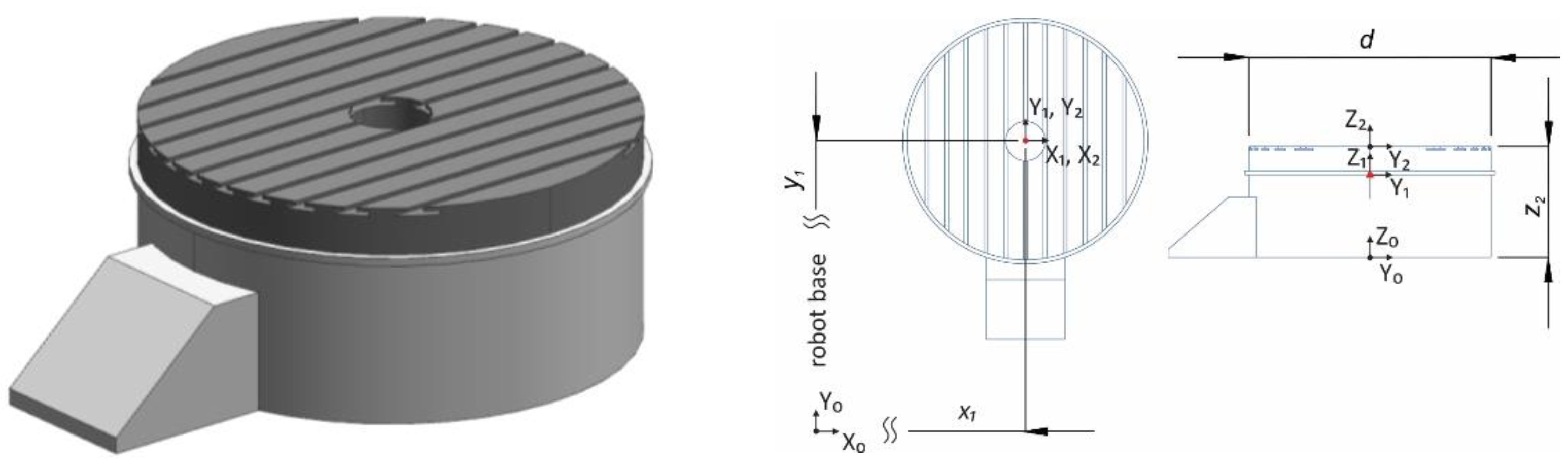
2.3. Kinematic Model of the Rotary Table
2.4. Workpiece Offset
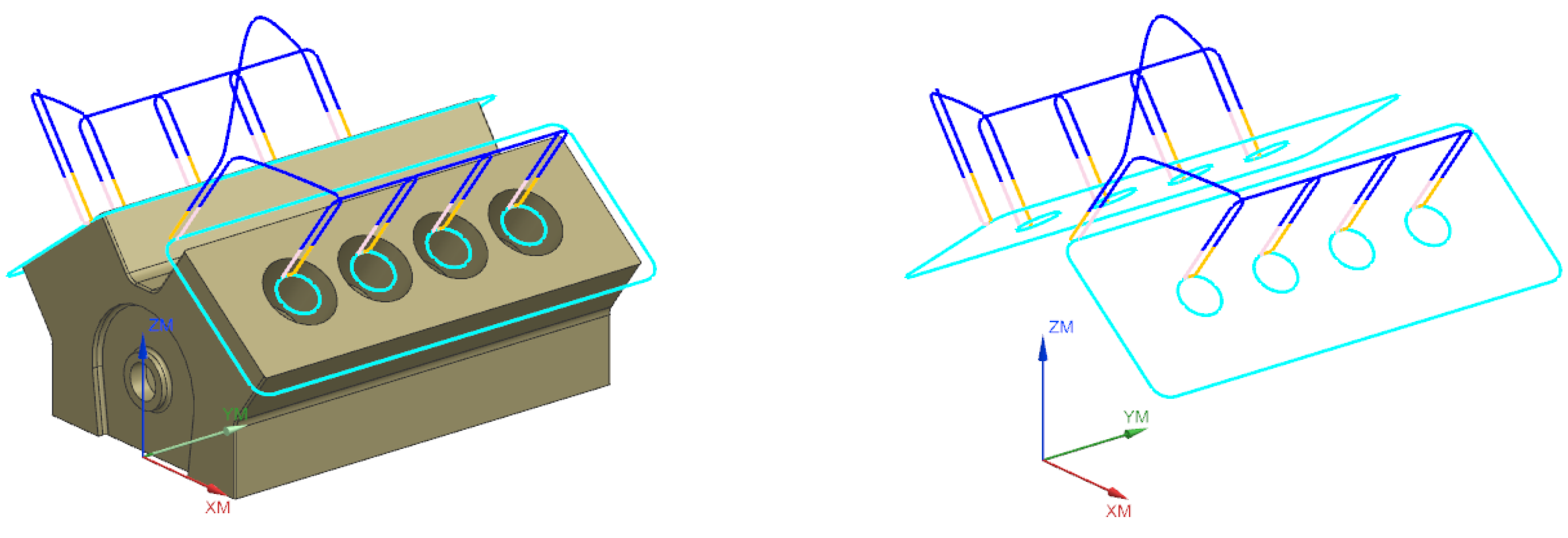
2.5. Deburring Toolpath
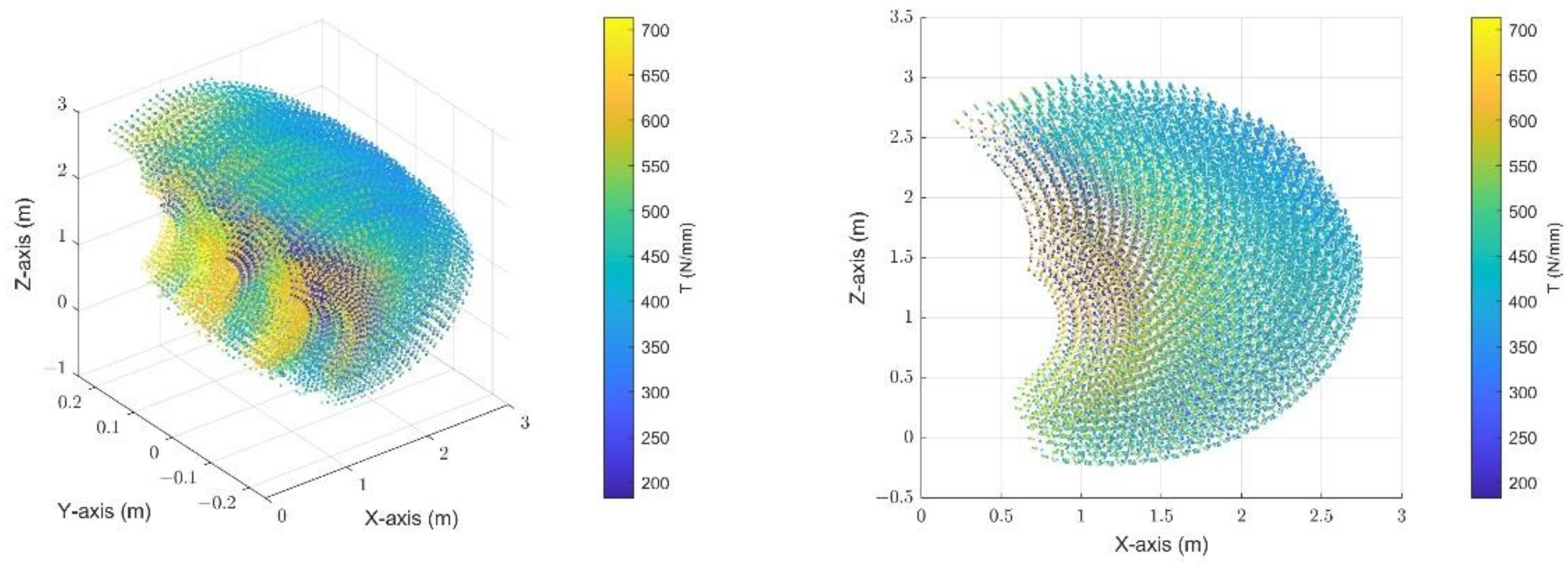
3. Stiffness Model
4. Optimization of Robotic Deburring
4.1. Workpiece Initial Placement
4.1.1. Variables, Search Space and Population Size
4.1.2. Nonlinear Constraints
4.1.3. GA Objective Function
4.1.4. Objective Function Constraints
4.2. Tracking the Toolpath
4.2.1. Rotary Table Constraints
4.2.2. Current Table Configuration
5. Results and Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Verl, A.; Valente, A.; Melkote, S.; Brecher, C.; Ozturk, E.; Tunc, L.T. Robots in machining. CIRP Ann.-Manuf. Technol. 2019, 68, 799–822. [Google Scholar] [CrossRef]
- Kubela, T.; Pochyly, A.; Singule, V. Assessment of industrial robots accuracy in relation to accuracy improvement in machining processes. In Proceedings of the Power Electronics and Motion Control Conference (PEMC), 2016 IEEE International, Varna, Bulgaria, 25–28 September 2016; pp. 720–725. [Google Scholar]
- Cordes, M.; Hintze, W. Offline simulation of path deviation due to joint compliance and hysteresis for robot machining. Int. J. Adv. Manuf. Technol. 2017, 90, 1075–1083. [Google Scholar] [CrossRef]
- Wang, G.; Dong, H.; Guo, Y.; Ke, Y. Dynamic cutting force modeling and experimental study of industrial robotic boring. Int. J. Adv. Manuf. Technol. 2015, 179–190. [Google Scholar] [CrossRef]
- Guo, Y.J.; Dong, H.Y.; Wang, G.F.; Ke, Y.L. Vibration analysis and suppression in robotic boring process. Int. J. Mach. Tools Manuf. 2016, 101, 102–110. [Google Scholar] [CrossRef]
- Jasiewicz, M.; Miądlicki, K. An integrated CNC system for chatter suppression in turning. Adv. Prod. Eng. Manag. 2020, 15, 318–330. [Google Scholar] [CrossRef]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Control of imperfect dynamical systems. Nonlinear Dyn. 2019, 98, 2989–2999. [Google Scholar] [CrossRef]
- Beschi, M.; Mutti, S.; Nicola, G.; Faroni, M.; Magnoni, P.; Villagrossi, E.; Pedrocchi, N. Optimal robot motion planning of redundant robots in machining and additive manufacturing applications. Electronics 2019, 8, 1437. [Google Scholar] [CrossRef] [Green Version]
- Abele, E.; Bauer, J.; Rothenbücher, S.; Stelzer, M.; Von Stryk, O. Prediction of the Tool Displacement by Coupled Models of the Compliant Industrial Robot and the Milling Process. In Proceedings of the Intl. Conference on Process Machine Interactions, Hannover, Germany, 3–4 September 2008. [Google Scholar]
- Reinl, C.; Friedmann, M.; Bauer, J.; Pischan, M.; Abele, E.; Stryk, O.v. Model-based off-line compensation of path deviation for industrial robots in milling applications. In Proceedings of the 2011 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Budapest, Hungary, 3–7 July 2011; pp. 367–372. [Google Scholar]
- Sörnmo, O.; Olofsson, B.; Robertsson, A.; Johansson, R. Increasing time-efficiency and accuracy of robotic machining processes using model-based adaptive force control. IFAC Proc. Vol. 2012, 45, 543–548. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, C.; Halbauer, M.; Euhus, D.; Overbeck, D. Milling with industrial robots: Strategies to reduce and compensate process force induced accuracy influences. In Proceedings of the 2012 IEEE 17th International Conference on Emerging Technologies & Factory Automation (ETFA 2012), Krakow, Poland, 17–21 September 2012; pp. 1–4. [Google Scholar]
- Moeller, C.; Schmidt, H.C.; Koch, P.; Boehlmann, C.; Kothe, S.; Wollnack, J.; Hintze, W. Real Time Pose Control of an Industrial Robotic System for Machining of Large Scale Components in Aerospace Industry Using Laser Tracker System. SAE Int. J. Aerosp. 2017, 10, 100–108. [Google Scholar] [CrossRef] [Green Version]
- Sabourin, L.; Robin, V.; Gogu, G.; Fauconnier, J.M. Improving the capability of a redundant robotic cell for cast parts finishing. Ind. Robot.: Int. J. 2012, 39, 381–391. [Google Scholar] [CrossRef]
- Villagrossi, E. Robot Dynamics Modelling and Control for Machining Applications; Università degli Studi di Brescia: Brescia, Italy, 2016. [Google Scholar]
- Domroes, F.; Krewet, C.; Kuhlenkoetter, B. Application and analysis of force control strategies to deburring and grinding. Mod. Mech. Eng. 2013, 3, 8. [Google Scholar] [CrossRef] [Green Version]
- Song, H.-C.; Song, J.-B. Precision robotic deburring based on force control for arbitrarily shaped workpiece using CAD model matching. Int. J. Precis. Eng. Manuf. 2013, 14, 85–91. [Google Scholar] [CrossRef]
- Burghardt, A.; Szybicki, D.; Kurc, K.; Muszyńska, M. Optimization of process parameters of edge robotic deburring with force control. Int. J. Appl. Mech. Eng. 2016, 21, 987–995. [Google Scholar] [CrossRef] [Green Version]
- Bottin, M.; Cocuzza, S.; Massaro, M. Variable stiffness mechanism for the reduction of cutting forces in robotic deburring. Appl. Sci. 2021, 11, 2883. [Google Scholar] [CrossRef]
- Burek, J.; Płodzień, M.; Żyłka, Ł.; Sułkowicz, P. High-performance end milling of aluminum alloy: Influence of different serrated cutting edge tool shapes on the cutting force. Adv. Prod. Eng. Manag. 2019, 14, 494–506. [Google Scholar] [CrossRef]
- Vosniakos, G.C.; Matsas, E. Improving feasibility of robotic milling through robot placement optimisation. Robot. Comput.-Integr. Manuf. 2010, 26, 517–525. [Google Scholar] [CrossRef]
- Farzanehkaloorazi, M.; Bonev, I.A.; Birglen, L. Simultaneous path placement and trajectory planning optimization for a redundant coordinated robotic workcell. Mech. Mach. Theory 2018, 130, 346–362. [Google Scholar] [CrossRef]
- Qin, H.; Li, Y.; Xiong, X. Workpiece Pose Optimization for Milling with Flexible-Joint Robots to Improve Quasi-Static Performance. Appl. Sci. 2019, 9, 1044. [Google Scholar] [CrossRef] [Green Version]
- Bu, Y.; Liao, W.; Tian, W.; Zhang, J.; Zhang, L. Stiffness analysis and optimization in robotic drilling application. Precis. Eng. 2017, 49, 388–400. [Google Scholar] [CrossRef]
- Zhang, J.; Liao, W.; Bu, Y.; Tian, W.; Hu, J. Stiffness properties analysis and enhancement in robotic drilling application. Int. J. Adv. Manuf. Technol. 2020, 106, 5539–5558. [Google Scholar] [CrossRef]
- Liao, Z.-Y.; Li, J.-R.; Xie, H.-L.; Wang, Q.-H.; Zhou, X.-F. Region-based toolpath generation for robotic milling of freeform surfaces with stiffness optimization. Robot. Comput.-Integr. Manuf. 2020, 64, 101953. [Google Scholar] [CrossRef]
- Cvitanic, T.; Nguyen, V.; Melkote, S.N. Pose optimization in robotic machining using static and dynamic stiffness models. Robot. Comput.-Integr. Manuf. 2020, 66, 101992. [Google Scholar] [CrossRef]
- Xiong, G.; Ding, Y.; Zhu, L.M. Stiffness-based pose optimization of an industrial robot for five-axis milling. Robot. Comput.-Integr. Manuf. 2019, 55, 19–28. [Google Scholar] [CrossRef]
- Gotlih, J.; Karner, T.; Gotlih, K.; Brezočnik, M. Accuracy improvement of robotic machining based on robot’s structural properties. Int. J. Adv. Manuf. Technol. 2020, 108, 1309–1329. [Google Scholar] [CrossRef]
- Dumas, C.; Caro, S.; Cherif, M.; Garnier, S.; Furet, B. Joint stiffness identification of industrial serial robots. Robotica 2012, 30, 649–659. [Google Scholar] [CrossRef] [Green Version]
- Hui, Z.; Jianjun, W.; Zhang, G.; Zhongxue, G.; Zengxi, P.; Hongliang, C.; Zhenqi, Z. Machining with flexible manipulator: Toward improving robotic machining performance. In Proceedings of the Proceedings, 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; pp. 1127–1132. [Google Scholar]
- Tyapin, I.; Hovland, G.; Brogårdh, T. Method for estimating combined controller, joint and link stiffnesses of an industrial robot. In Proceedings of the 2014 IEEE International Symposium on Robotic and Sensors Environments (ROSE) Proceedings, Timisoara, Romania, 16–18 October 2014. [Google Scholar]
- Klimchik, A.; Furet, B.; Caro, S.; Pashkevich, A. Identification of the manipulator stiffness model parameters in industrial environment. Mech. Mach. Theory 2015, 90, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Li, T.; Chu, M.; Xuan, J.-Q.; Xu, S.-H. Review on kinematics calibration technology of serial robots. Int. J. Precis. Eng. Manuf. 2014, 15, 1759–1774. [Google Scholar] [CrossRef]
- Friedrich, J.; Hinze, C.; Renner, A.; Verl, A.; Lechler, A. Estimation of stability lobe diagrams in milling with continuous learning algorithms. Robot. Comput.-Integr. Manuf. 2017, 43, 124–134. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, D.; Ge, Y.J. Design optimization of a spatial six degree-of-freedom parallel manipulator based on artificial intelligence approaches. Robot. Comput.-Integr. Manuf. 2010, 26, 180–189. [Google Scholar] [CrossRef]
- Mahler, J.; Liang, J.; Niyaz, S.; Laskey, M.; Doan, R.; Liu, X.; Ojea, J.A.; Goldberg, K. Dex-Net 2.0: Deep Learning to Plan Robust Grasps with Synthetic Point Clouds and Analytic Grasp Metrics. In Proceedings of the Robotics: Science and Systems 2017, Cambridge, MA, USA, 12–16 July 2017. [Google Scholar]
- Klimchik, A.; Pashkevich, A. Serial vs. quasi-serial manipulators: Comparison analysis of elasto-static behaviors. Mech. Mach. Theory 2017, 107, 46–70. [Google Scholar] [CrossRef]
- Kuss, A.; Drust, M.; Verl, A. Detection of workpiece shape deviations for tool path adaptation in robotic deburring systems. In Proceedings of the 49th CIRP Conference on Manufacturing Systems (CIRP-CMS 2016), Stuttgart, Germany, 25–27 May 2016; pp. 545–550. [Google Scholar]
- Brunete, A.; Gambao, E.; Koskinen, J.; Heikkilä, T.; Kaldestad, K.B.; Tyapin, I.; Hovland, G.; Surdilovic, D.; Hernando, M.; Bottero, A.; et al. Hard material small-batch industrial machining robot. Robot. Comput.-Integr. Manuf. 2018, 54, 185–199. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, H.; Ding, H. Spindle configuration analysis and optimization considering the deformation in robotic machining applications. Robot. Comput.-Integr. Manuf. 2018, 54, 83–95. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, H.; Ding, H. Posture optimization methodology of 6R industrial robots for machining using performance evaluation indexes. Robot. Comput.-Integr. Manuf. 2017, 48, 59–72. [Google Scholar] [CrossRef]
- Gotlih, J.; Karner, T.; Gotlih, K.; Brezocnik, M. Experiment Based Structural Stiffness Calibration of a Virtual Robot Model. In DAAAM International Scientific Book 2018; DAAAM International: Vienna, Austria, 2018; pp. 131–140. [Google Scholar]
- Klimchik, A.; Magid, E.; Caro, S.; Waiyakan, K.; Pashkevich, A. Stiffness of serial and quasi-serial manipulators: Comparison analysis. In Proceedings of the 2016 International Conference on Measurement Instrumentation and Electronics (Icmie 2016), Munich, Germany, 6–8 June 2016. [Google Scholar]
- Chen, C.; Peng, F.Y.; Yan, R.; Li, Y.T.; Wei, D.Q.; Fan, Z.; Tang, X.W.; Zhu, Z.R. Stiffness performance index based posture and feed orientation optimization in robotic milling process. Robot. Comput.-Integr. Manuf. 2019, 55, 29–40. [Google Scholar] [CrossRef]





| 1 | 0.2500 | 0.9500 | 0 | |
| 2 | 1.0000 | 0 | 0 | |
| 3 | 0.2300 | 0 | 0 | |
| 4 | 0 | 1.3294 | 0 | |
| 5 | 0 | 0 | 0 | |
| 6 | 0 | 0 | 0.2500 | 0 |
| A | 0 | 0 | 0 | 0 | 0 | 0 |
| B | −0.42 | 0.075 | 0 | 0 | 0 | |
| C | 1 | 0 | 0 | 0 | 0 | 0 |
| min. | 0 | 50 | 30 | 200 | 120 | 0 |
| max. | 0 | 65 | 155 | 200 | 120 | 0 |
| step | 0 | 5 | 5 | 50 | 30 | 0 |
| 1 | Initialize generation with random individuals from |
| 2 | For each individual |
| 2.1 | Evaluate |
| 3 | Until convergence, do |
| 3.1 | Reproduction of best individuals from (based on ) |
| 3.2 | Crossover of random individuals from |
| 3.3 | Mutation of random individuals from |
| 3.4 | ← create new generation |
| 3.5 | For each individual |
| 3.5.1 | Evaluate |
| 3.5.2 | For each individual |
| 3.5.2.1 | Evaluate |
| 4 | Retrun best individual from |
| LB | 1.255 | 0.190 | 0 | 0 | 0 | |
| UB | 2.375 | 1.310 | 0 | 0 | 0 |
| Outer Edges | Bore 1 Edges | Bore 1–4 | Traverse | |
|---|---|---|---|---|
| Table rotation (°) | 0.12 | 0.05 | 5.07 | 147.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gotlih, J.; Brezocnik, M.; Karner, T. Stiffness-Based Cell Setup Optimization for Robotic Deburring with a Rotary Table. Appl. Sci. 2021, 11, 8213. https://doi.org/10.3390/app11178213
Gotlih J, Brezocnik M, Karner T. Stiffness-Based Cell Setup Optimization for Robotic Deburring with a Rotary Table. Applied Sciences. 2021; 11(17):8213. https://doi.org/10.3390/app11178213
Chicago/Turabian StyleGotlih, Janez, Miran Brezocnik, and Timi Karner. 2021. "Stiffness-Based Cell Setup Optimization for Robotic Deburring with a Rotary Table" Applied Sciences 11, no. 17: 8213. https://doi.org/10.3390/app11178213
APA StyleGotlih, J., Brezocnik, M., & Karner, T. (2021). Stiffness-Based Cell Setup Optimization for Robotic Deburring with a Rotary Table. Applied Sciences, 11(17), 8213. https://doi.org/10.3390/app11178213







