Design Optimization of Centrifugal Microfluidic “Lab-on-a-Disc” Systems towards Fluidic Larger-Scale Integration
Abstract
:1. Introduction
2. Rotational Flow Control
2.1. Pressures
2.2. Critical Spin Rate
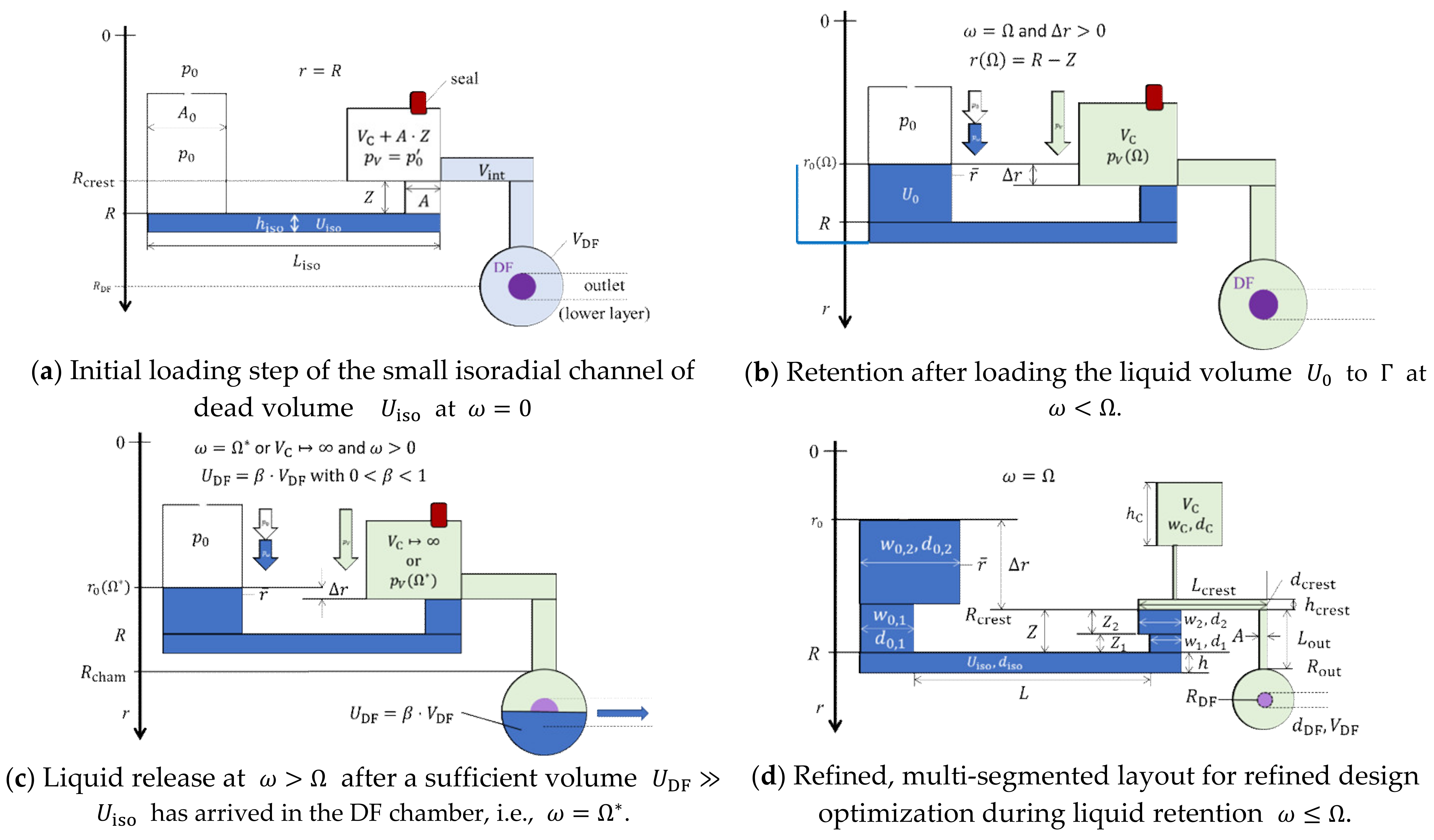
2.3. Example: Centrifugo-Pneumatic Siphon Valves
2.4. Operational Robustness
2.5. Laboratory Unit Operations
3. Design Optimization
3.1. Multiplexing
3.2. Parameter Space
3.3. Performance Metrics & Design Criteria
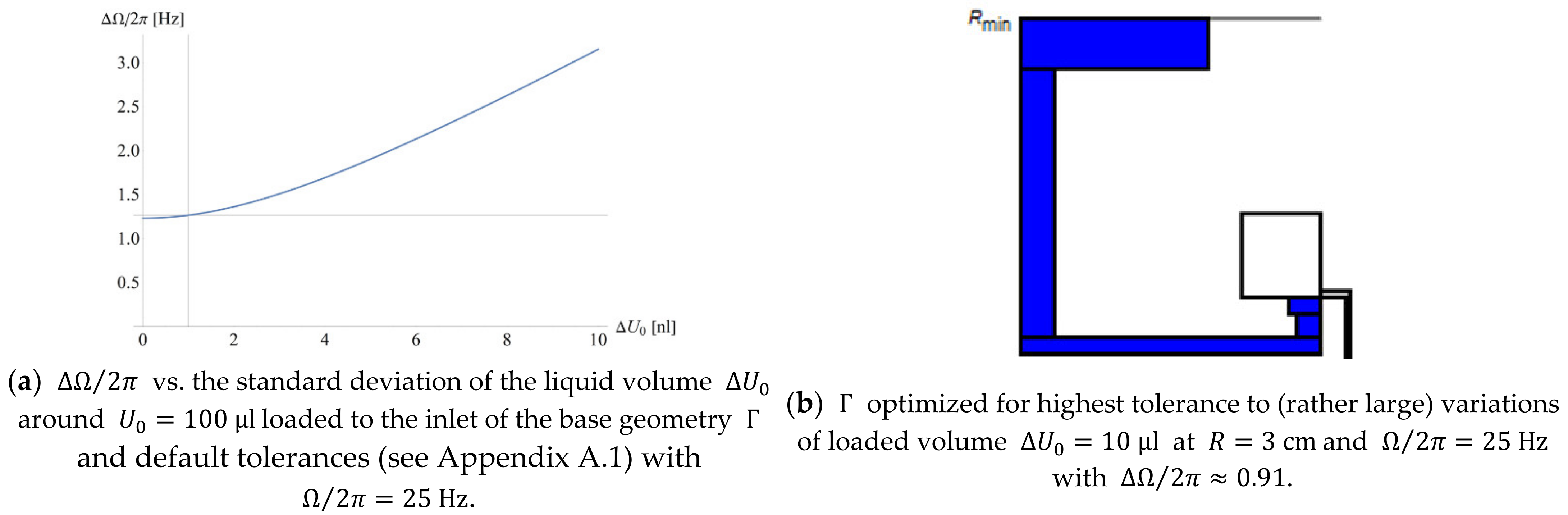
3.3.1. Band Width
3.3.2. Refined Geometry
3.3.3. Retention Rate and Field Strength
3.3.4. Concurrent Valving
3.3.5. Radial Space
3.3.6. Spatial Footprint
3.3.7. Definition of Liquid Volumes
3.3.8. Ambient Pressure
3.3.9. Manufacturing-Process Limitations and Costs
3.3.10. Multi-Parameter Optimization
3.3.11. General Design Guidelines
4. Summary and Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Default Valve Geometry
- Lateral structuring ;
- Vertical structuring ;
- Precision of liquid volume ;
- Ambient pressure .
Appendix A.2. Computation of Results
References
- Manz, A.; Graber, N.; Widmer, H.Á. Miniaturized total chemical analysis systems: A novel concept for chemical sensing. Sens. Actuators B Chem. 1990, 1, 244–248. [Google Scholar] [CrossRef]
- Reyes, D.R.; Iossifidis, D.; Auroux, P.A.; Manz, A. Micro total analysis systems. 1. introduction, theory, and technology. Anal. Chem. 2002, 74, 2623–2636. [Google Scholar] [CrossRef] [PubMed]
- Auroux, P.A.; Iossifidis, D.; Reyes, D.R.; Manz, A. Micro total analysis systems. 2. analytical standard operations and applications. Anal. Chem. 2002, 74, 2637–2652. [Google Scholar] [CrossRef] [PubMed]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Craighead, H. Future lab-on-a-chip technologies for interrogating individual molecules. Nature 2006, 442, 387–393. [Google Scholar] [CrossRef]
- Jamil, E.A.; Sorger, P.K.; Jensen, K.F. Cells on chips. Nature 2006, 442, 403–411. [Google Scholar] [CrossRef]
- Janasek, D.; Franzke, J.; Manz, A. Scaling and the design of miniaturized chemical-analysis systems. Nature 2006, 442, 374–380. [Google Scholar] [CrossRef]
- Schembri, C.T.; Ostoich, V.; Lingane, P.J.; Burd, T.L.; Buhl, S.N. Portable simultaneous multiple analyte whole-blood analyzer for point-of-care testing. Clin. Chem. 1992, 38, 1665–1670. [Google Scholar] [CrossRef]
- Schembri, C.T.; Burd, T.L.; Kopf-Sill, A.R.; Shea, L.R.; Braynin, B. Centrifugation and capillarity integrated into a multiple analyte whole-blood analyzer. J. Autom. Chem. 1995, 17, 99–104. [Google Scholar] [CrossRef]
- Abaxis (Piccolo Express). Available online: https://www.abaxis.com (accessed on 14 June 2021).
- Andersson, P.; Jesson, G.; Kylberg, G.; Ekstrand, G.; Thorsén, G. Parallel nanoliter microfluidic analysis system. Anal. Chem. 2007, 79, 4022–4030. [Google Scholar] [CrossRef] [Green Version]
- Inganas, M.; Derand, H.; Eckersten, A.; Ekstrand, G.; Honerud, A.K.; Jesson, G.; Thorsen, G.; Soderman, T.; Andersson, P. Integrated microfluidic compact disc device with potential use in both centralized and point-of-care laboratory settings. Clin. Chem. 2005, 51, 1985–1987. [Google Scholar] [CrossRef] [PubMed]
- Gyros Protein Technologies. Available online: https://www.gyrosproteintechnologies.com(accessed on 14 June 2021).
- Madou, M.J.; Kellogg, G.J. The LabCD (TM): A centrifuge-based microfluidic platform for diagnostics. In Systems and Technologies for Clinical Diagnostics and Drug Discovery; International Society for Optics and Photonics: Bellingham, DC, USA, 1998; Volume 3259, pp. 80–93. [Google Scholar] [CrossRef]
- Shea, M. ADMET assays on tecan’s labCD-ADMET system. J. Assoc. Lab. Autom. 2003, 8, 74–77. [Google Scholar] [CrossRef]
- Smith, S.; Mager, D.; Perebikovsky, A.; Shamloo, E.; Kinahan, D.; Mishra, R.; Delgado, S.M.T.; Kido, H.; Saha, S.; Ducrée, J.; et al. CD-based microfluidics for primary care in extreme point-of-care settings. Micromachines 2016, 7, 22. [Google Scholar] [CrossRef] [Green Version]
- Kong, L.X.; Perebikovsky, A.; Moebius, J.; Kulinsky, L.; Madou, M. Lab-on-a-CD: A fully integrated molecular diagnostic system. J. Assoc. Lab. Autom. 2016, . 21, 323–355. [Google Scholar] [CrossRef] [Green Version]
- Maguire, I.; O’Kennedy, R.; Ducrée, J.; Regan, F. A review of centrifugal microfluidics in environmental monitoring. Anal. Methods 2018, 10, 1497–1515. [Google Scholar] [CrossRef]
- Gorkin, R.; Park, J.; Siegrist, J.; Amasia, M.; Lee, B.S.; Park, J.M.; Kim, J.; Kim, H.; Madou, M.; Cho, Y.K. Centrifugal microfluidics for biomedical applications. Lab Chip 2010, 10, 1758–1773. [Google Scholar] [CrossRef] [Green Version]
- Burger, R.; Amato, L.; Boisen, A. Detection methods for centrifugal microfluidic platforms. Biosens. Bioelectron. 2016, 76, 54–67. [Google Scholar] [CrossRef]
- Ducrée, J.; Haeberle, S.; Lutz, S.; Pausch, S.; von Stetten, F.; Zengerle, R. The centrifugal microfluidic Bio-Disk platform. J. Micromech. Microeng. 2007, 17, S103–S115. [Google Scholar] [CrossRef]
- Lutz, S.; Mark, D.; Roth, G.; Zengerle, R.; von Stetten, F. Centrifugal microfluidic platforms for molecular diagnostics. Clin. Chem. Lab. Med. 2011, 49, S608. [Google Scholar]
- Tang, M.; Wang, G.; Kong, S.-K.; Ho, H.-P. A review of biomedical centrifugal microfluidic platforms. Micromachines 2016, 7, 26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duffy, D.C.; Gillis, H.L.; Lin, J.; Sheppard, N.F.; Kellogg, G.J. Microfabricated centrifugal microfluidic systems: Characterization and multiple enzymatic assays. Anal. Chem. 1999, 71, 4669–4678. [Google Scholar] [CrossRef]
- Azimi-Boulali, J.; Madadelahi, M.; Madou, M.J.; Martinez-Chapa, S.O. Droplet and particle generation on centrifugal microfluidic platforms: A review. Micromachines 2020, 11, 603. [Google Scholar] [CrossRef] [PubMed]
- Strohmeier, O.; Keller, M.; Schwemmer, F.; Zehnle, S.; Mark, D.; von Stetten, F.; Zengerle, R.; Paust, N. Centrifugal microfluidic platforms: Advanced unit operations and applications. Chem. Soc. Rev. 2015, 44, 6187–6229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aeinehvand, M.M.; Magaña, P.; Aeinehvand, M.S.; Aguilar, O.; Madou, M.J.; Martinez-Chapa, S.O. Ultra-rapid and low-cost fabrication of centrifugal microfluidic platforms with active mechanical valves. Rsc. Adv. 2017, 7, 55400–55407. [Google Scholar] [CrossRef]
- Aeinehvand, M.M.; Weber, L.; Jiménez, M.; Palermo, A.; Bauer, M.; Loeffler, F.F.; Ibrahim, F.; Breitling, F.; Korvink, J.; Madou, M.; et al. Elastic reversible valves on centrifugal microfluidic platforms. Lab Chip 2019, 19, 1090–1100. [Google Scholar] [CrossRef]
- Hess, J.F.; Zehnle, S.; Juelg, P.; Hutzenlaub, T.; Zengerle, R.; Paust, N. Review on pneumatic operations in centrifugal microfluidics. Lab Chip 2019, 19, 3745–3770. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.V.; Nguyen, V.D.; Nguyen, H.Q.; Chau, T.H.T.; Lee, E.Y.; Seo, T.S. Nucleic acid diagnostics on the total integrated lab-on-a-disc for point-of-care testing. Biosens. Bioelectron. 2019, 141. [Google Scholar] [CrossRef]
- Rombach, M.; Hin, S.; Specht, M.; Johannsen, B.; Lüddecke, J.; Paust, N.; Zengerle, R.; Roux, L.; Sutcliffe, T.; Peham, J.R.; et al. RespiDisk: A point-of-care platform for fully automated detection of respiratory tract infection pathogens in clinical samples. Analyst 2020, 145, 7040–7047. [Google Scholar] [CrossRef]
- Homann, A.R.; Niebling, L.; Zehnle, S.; Beutler, M.; Delamotte, L.; Rothmund, M.-C.; Czurratis, D.; Beller, K.-D.; Zengerle, R.; Hoffmann, H.; et al. A microfluidic cartridge for fast and accurate diagnosis of Mycobacterium tuberculosis infections on standard laboratory equipment. Lab Chip 2021, 21, 1540–1548. [Google Scholar] [CrossRef]
- Madadelahi, M.; Acosta-Soto, L.F.; Hosseini, S.; Martinez-Chapa, S.O.; Madou, M.J. Mathematical modeling and computational analysis of centrifugal microfluidic platforms: A review. Lab Chip 2020, 20, 1318–1357. [Google Scholar] [CrossRef]
- Miyazaki, C.M.; Carthy, E.; Kinahan, D.J. Biosensing on the centrifugal microfluidic Lab-on-a-Disc platform. Processes 2020, 8, 1360. [Google Scholar] [CrossRef]
- Mian , A.; Kieffer-Higgins, S.G.; Corey , G.D. Devices and Methods for Using Centripetal Acceleration to Drive Fluid Movement in a Microfluidics System. Patent No. US6319469B1, 18 December 1996. [Google Scholar]
- Burstein Technologies, Inc. [archived]. Available online: https://web.archive.org/web/20061209052345/http://www.bursteintechnologies.com (accessed on 31 May 2021).
- Biosurfit, SA. Available online: https://www.biosurfit.com (accessed on 14 June 2021).
- Spindiag GmbH. Available online: http://www.spindiag.de (accessed on 14 June 2021).
- RotaPrep Inc. Available online: https://rotaprep.com/ (accessed on 19 April 2021).
- LaMotte Chemical Products, Co. Available online: https://www.lamotte.com (accessed on 14 June 2021).
- Radisens Diagnostics. Available online: http://www.radisens.com (accessed on 14 June 2021).
- Blusense Diagnostics. Available online: https://blusense-diagnostics.com (accessed on 14 June 2021).
- SpinX Technologies. Available online: https://web.archive.org/web/20040414090409/http://www.spinx-technologies.com (accessed on 14 June 2021).
- Clime, L.; Daoud, J.; Brassard, D.; Malic, L.; Geissler, M.; Veres, T. Active pumping and control of flows in centrifugal microfluidics. Microfluid. Nanofluid. 2019, 23, 29. [Google Scholar] [CrossRef]
- Brassard, D.; Geissler, M.; Descarreaux, M.; Tremblay, D.; Daoud, J.; Clime, L.; Mounier, M.; Charlebois, D.; Veres, T. Extraction of nucleic acids from blood: Unveiling the potential of active pneumatic pumping in centrifugal microfluidics for integration and automation of sample preparation processes. Lab Chip 2019, 19, 1941–1952. [Google Scholar] [CrossRef] [PubMed]
- Abi-Samra, K.; Hanson, R.; Madou, M.; Gorkin, R.A. Infrared controlled waxes for liquid handling and storage on a CD-microfluidic platform. Lab Chip 2011, 11, 723–726. [Google Scholar] [CrossRef]
- Kong, L.X.; Parate, K.; Abi-Samra, K.; Madou, M. Multifunctional wax valves for liquid handling and incubation on a microfluidic CD. Microfluid. Nanofluid. 2015, 18, 1031–1037. [Google Scholar] [CrossRef]
- Torres Delgado, S.M.; Kinahan, D.J.; Nirupa Julius, L.A.; Mallette, A.; Ardila, D.S.; Mishra, R.; Miyazaki, C.M.; Korvink, J.G.; Ducrée, J.; Mager, D. Wirelessly powered and remotely controlled valve-array for highly multiplexed analytical assay automation on a centrifugal microfluidic platform. Biosens. Bioelectron. 2018, 109, 214–223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kinahan, D.J.; Renou, M.; Kurzbuch, D.; Kilcawley, N.A.; Bailey, E.; Glynn, M.T.; McDonagh, C.; Ducrée, J. Baking powder actuated centrifugo-pneumatic valving for automation of multi-step bioassays. Micromachine 2016, 7, 175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haeberle, S.; Brenner, T.; Zengerle, R.; Ducrée, J. Centrifugal extraction of plasma from whole blood on a rotating disk. Lab Chip 2006, 6, 776–781. [Google Scholar] [CrossRef]
- Steigert, J.; Brenner, T.; Grumann, M.; Riegger, L.; Lutz, S.; Zengerle, R.; Ducrée, J. Integrated siphon-based metering and sedimentation of whole blood on a hydrophilic lab-on-a-disk. Biomed. Microdevices 2007, 9, 675–679. [Google Scholar] [CrossRef] [PubMed]
- Kinahan, D.J.; Kearney, S.M.; Kilcawley, N.A.; Early, P.L.; Glynn, M.T.; Ducrée, J. Density-gradient mediated band extraction of leukocytes from whole blood using centrifugo-pneumatic siphon valving on centrifugal microfluidic discs. PLoS ONE 2016, 11. [Google Scholar] [CrossRef]
- Dimov, N.; Gaughran, J.; Mc Auley, D.; Boyle, D.; Kinahan, D.J.; Ducrée, J. Centrifugally Automated Solid-Phase Purification of RNA. In Proceedings of the 2014 IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS), San Francisco, CA, USA, 26–30 January 2014; pp. 260–263. [Google Scholar] [CrossRef]
- Gaughran, J.; Boyle, D.; Murphy, J.; Kelly, R.; Ducrée, J. Phase-selective graphene oxide membranes for advanced microfluidic flow control. Microsyst. Nanoeng. 2016, 2, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Zehnle, S.; Rombach, M.; Zengerle, R.; von Stetten, F.; Paust, N. Network simulation-based optimization of centrifugopneumatic blood plasma separation. Biomicrofluidics 2017, 11. [Google Scholar] [CrossRef] [Green Version]
- Al-Faqheri, W.; Thio, T.H.G.; Qasaimeh, M.A.; Dietzel, A.; Madou, M.; Al-Halhouli, A. Particle/cell separation on microfluidic platforms based on centrifugation effect: A review. Microfluid. Nanofluid. 2017, 21. [Google Scholar] [CrossRef]
- Mark, D.; Haeberle, S.; Metz, T.; Lutz, S.; Ducrée, J.; Zengerle, R.; von Stetten, F. Aliquoting structure for centrifugal microfluidics based on a new pneumatic valve. In Proceedings of the 2008 IEEE 21st International Conference on Micro Electro Mechanical Systems, Tucson, AZ, USA, 13–17 January 2008; pp. 611–614. [Google Scholar] [CrossRef] [Green Version]
- Schwemmer, F.; Hutzenlaub, T.; Buselmeier, D.; Paust, N.; von Stetten, F.; Mark, D.; Zengerle, R.; Kosse, D. Centrifugo-pneumatic multi-liquid aliquoting-parallel aliquoting and combination of multiple liquids in centrifugal microfluidics. Lab Chip 2015, 15, 3250–3258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keller, M.; Wadle, S.; Paust, N.; Dreesen, L.; Nuese, C.; Strohmeier, O.; Zengerle, R.; von Stetten, F. Centrifugo-thermopneumatic fluid control for valving and aliquoting applied to multiplex real-time PCR on off-the-shelf centrifugal thermocycler. Rsc. Adv. 2015, 5, 89603–89611. [Google Scholar] [CrossRef] [Green Version]
- Grumann, M.; Geipel, A.; Riegger, L.; Zengerle, R.; Ducrée, J. Batch-mode mixing on centrifugal microfluidic platforms. Lab Chip 2005, 5, 560–565. [Google Scholar] [CrossRef] [PubMed]
- Ducrée, J.; Brenner, T.; Haeberle, S.; Glatzel, T.; Zengerle, R. Multilamination of flows in planar networks of rotating microchannels. Microfluid. Nanofluid. 2006, 2, 78–84. [Google Scholar] [CrossRef]
- Burger, R.; Kinahan, D.; Cayron, H.; Reis, N.; Garcia da Fonseca, J.; Ducrée, J. Siphon-induced droplet break-off for enhanced mixing on a centrifugal platform. Inventions 2020, 5, 1. [Google Scholar] [CrossRef] [Green Version]
- Ducrée, J.; Haeberle, S.; Brenner, T.; Glatzel, T.; Zengerle, R. Patterning of flow and mixing in rotating radial microchannels. In Microfluid. Nanofluid. 2006, 2, 97–105. [Google Scholar] [CrossRef]
- Strohmeier, O.; Keil, S.; Kanat, B.; Patel, P.; Niedrig, M.; Weidmann, M.; Hufert, F.; Drexler, J.; Zengerle, R.; von Stetten, F. Automated nucleic acid extraction from whole blood, B. subtilis, E. coli, and Rift Valley fever virus on a centrifugal microfluidic LabDisk. Rsc. Adv. 2015, 5, 32144–32150. [Google Scholar] [CrossRef]
- Karle, M.; Miwa, J.; Roth, G.; Zengerle, R.; von Stetten, F. A novel microfluidic platform for continuous dna extraction and purification using laminar flow magnetophoresis. In Proceedings of the 2009 IEEE 22nd International Conference on Micro Electro Mechanical Systems, Sorrento, Italy, 25–29 January 2009; pp. 276–279. [Google Scholar] [CrossRef]
- Kido, H.; Micic, M.; Smith, D.; Zoval, J.; Norton, J.; Madou, M. A novel, compact disk-like centrifugal microfluidics system for cell lysis and sample homogenization. Colloids Surf. B Biointerfaces 2007, 58, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Haeberle, S.; Zengerle, R.; Ducrée, J. Centrifugal generation and manipulation of droplet emulsions. Microfluid. Nanofluid. 2007, 3, 65–75. [Google Scholar] [CrossRef]
- Schuler, F.; Schwemmer, F.; Trotter, M.; Wadle, S.; Zengerle, R.; von Stetten, F.; Paust, N. Centrifugal step emulsification applied for absolute quantification of nucleic acids by digital droplet RPA. Lab Chip 2015, 15, 2759–2766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schuler, F.; Trotter, M.; Geltman, M.; Schwemmer, F.; Wadle, S.; Dominguez-Garrido, E.; Lopez, M.; Cervera-Acedo, C.; Santibanez, P.; von Stetten, F.; et al. Digital droplet PCR on disk. Lab Chip 2016, 16, 208–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brennan, D.; Coughlan, H.; Clancy, E.; Dimov, N.; Barry, T.; Kinahan, D.; Ducrée, J.; Smith, T.J.; Galvin, P. Development of an on-disc isothermal in vitro amplification and detection of bacterial RNA. Sens. Actuators B Chem. 2017, 239, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Delgado, S.M.T.; Kinahan, D.J.; Sandoval, F.S.; Julius, L.A.N.; Kilcawley, N.A.; Ducrée, J.; Mager, D. Fully automated chemiluminescence detection using an electrified-Lab-on-a-Disc (eLoaD) platform. Lab Chip 2016, 16, 4002–4011. [Google Scholar] [CrossRef] [Green Version]
- Zehnle, S.; Schwemmer, F.; Bergmann, R.; von Stetten, F.; Zengerle, R.; Paust, N. Pneumatic siphon valving and switching in centrifugal microfluidics controlled by rotational frequency or rotational acceleration. Microfluid. Nanofluid. 2015, 19, 1259–1269. [Google Scholar] [CrossRef]
- Ducrée, J. Systematic review of centrifugal valving based on digital twin modelling towards highly integrated Lab-on-a-Disc systems. Nat. Microsyst. Nanoeng. 2021. [Google Scholar] [CrossRef]
- Digital Twin. Available online: https://en.wikipedia.org/wiki/Digital_twin (accessed on 25 May 2021).
- Marr, B. What Is Digital Twin Technology-And Why Is It So Important? Available online: https://www.forbes.com/sites/bernardmarr/2017/03/06/what-is-digital-twin-technology-and-why-is-it-so-important/ (accessed on 25 May 2021).
- Grieves, M.; Vickers, J. Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems. In Transdisciplinary Perspectives on Complex Systems: New Findings and Approaches; Kahlen, F.-J., Flumerfelt, S., Alves, A., Eds.; Springer International Publishing: Berlin, Germany, 2017; pp. 85–113. [Google Scholar] [CrossRef]
- Thorsen, T. Microfluidic Large-Scale Integration. Science 2002, 298, 580–584. [Google Scholar] [CrossRef] [Green Version]
- Ducrée, J. Secure air traffic control at the hub of multiplexing on the centrifugo-pneumatic Lab-on-a-Disc platform. Micromachines 2021, 700. [Google Scholar] [CrossRef]
- Ducrée, J. Efficient development of integrated Lab-On-A-Chip systems featuring operational robustness and nanufacturability. Micromachines 2019, 10, 886. [Google Scholar] [CrossRef] [Green Version]
- Reyes, D.R.; Heeren, H.v.; Guha, S.; Herbertson, L.H.; Tzannis, A.P.; Ducrée, J.; Bissig, H.; Becker, H. Accelerating innovation and commercialization through standardization of microfluidic-based medical devices. Lab Chip 2021, 21, 9–21. [Google Scholar] [CrossRef]
- Ducrée, J. Efficient development of microfluidic solutions for bioanalytical “point-of-use” testing towards high-technology-readiness levels—a platform-based design-for-manufacture approach. Multidiscip. Digit. Publ. Inst. Proc. 2019, 2, 1097. [Google Scholar] [CrossRef] [Green Version]
- Ducrée, J. Anti-Counterfeit Technologies for Centrifugal Microfluidic “Lab-on-a-Disc” Systems: An Analysis. Preprints 2021. (in preparation). [Google Scholar]
- Ducrée, J.; Etzrodt, M.; Bartling, S.; Walshe, R.; Harrington, T.; Wittek, N.; Posth, S.; Wittek, K.; Ionita, A.; Prinz, W.; et al. Unchaining collective intelligence for science, research and technology development by blockchain-boosted community participation. Front. Blockchain 2021, 4. [Google Scholar] [CrossRef]
- Ducrée, J. Research–a blockchain of knowledge? Blockchain Res. Appl. 2020, 1. [Google Scholar] [CrossRef]
- Ducrée, J.; Gravitt, M.; Walshe, R.; Bartling, S.; Etzrodt, M.; Harrington, T. Open platform concept for blockchain-enabled crowdsourcing of technology development and supply chains. Front. Blockchain 2020, 3. [Google Scholar] [CrossRef]
- Ducrée, J.; Etzrodt, M.; Gordijn, B.; Gravitt, M.; Bartling, S.; Walshe, R.; Harrington, T. Blockchain for Organising Effective Grass-Roots Actions on a Global Commons: Saving The Planet. Front. Blockchain 2020, 3, 33. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ducrée, J. Design Optimization of Centrifugal Microfluidic “Lab-on-a-Disc” Systems towards Fluidic Larger-Scale Integration. Appl. Sci. 2021, 11, 5839. https://doi.org/10.3390/app11135839
Ducrée J. Design Optimization of Centrifugal Microfluidic “Lab-on-a-Disc” Systems towards Fluidic Larger-Scale Integration. Applied Sciences. 2021; 11(13):5839. https://doi.org/10.3390/app11135839
Chicago/Turabian StyleDucrée, Jens. 2021. "Design Optimization of Centrifugal Microfluidic “Lab-on-a-Disc” Systems towards Fluidic Larger-Scale Integration" Applied Sciences 11, no. 13: 5839. https://doi.org/10.3390/app11135839
APA StyleDucrée, J. (2021). Design Optimization of Centrifugal Microfluidic “Lab-on-a-Disc” Systems towards Fluidic Larger-Scale Integration. Applied Sciences, 11(13), 5839. https://doi.org/10.3390/app11135839






