1. Introduction
Periodic structures can be defined as structures consisting of a series of repeating segments with the same physical properties and sizes. Theoretical investigations of such structures have usually been carried out by the assumption of infinite dimensions [
1,
2,
3,
4,
5]. However, certain features of periodic structures may also manifest even in the case of structures of finite dimensions if they include a sufficient number of segments.
One of specific features of periodic structures are band gaps in their frequency spectra. Band gaps define frequency ranges within which signals cannot propagate within these structures. The locations and the widths of these gaps in the frequency spectra are strongly dependent on the size of the unit cell and such material properties as modulus of elasticity [
6,
7,
8]. These special features of periodic structures can be employed for very efficient vibration damping. On the other hand, active vibration damping methods include techniques that use piezoelectric materials. Structures with active piezoelectric elements enable one the conversion of mechanical vibrations to electrical vibrations and thus to control damping properties of the system. Therefore, only the balance between passive and active damping allows one to maximise the effectiveness of the damping process.
Additionally, while modeling periodic structures, the influence of features resulting from the application of a particular numerical model, on the results of calculations, should be taken into account carefully. Almost every computational model of a discretised structure (finite element method (FEM) or time domain spectral finite element method (TDSFEM) models), has certain characteristics of a periodic structure. Therefore, it is worth to analyse if certain features of periodic structures may be utilised in a directed manner in order to make practical use of the unusual behaviour of such structures. This approach may potentially allow to reduce, or enhance, periodic properties of the computational model.
In this paper, the authors propose to combine all the aspects mentioned above. They propose a special numerical model of the beam with active piezoelectric elements, by means of which the dynamic characteristics of the beam can be analysed and the width of band gaps can be controlled.
2. Numerical Model
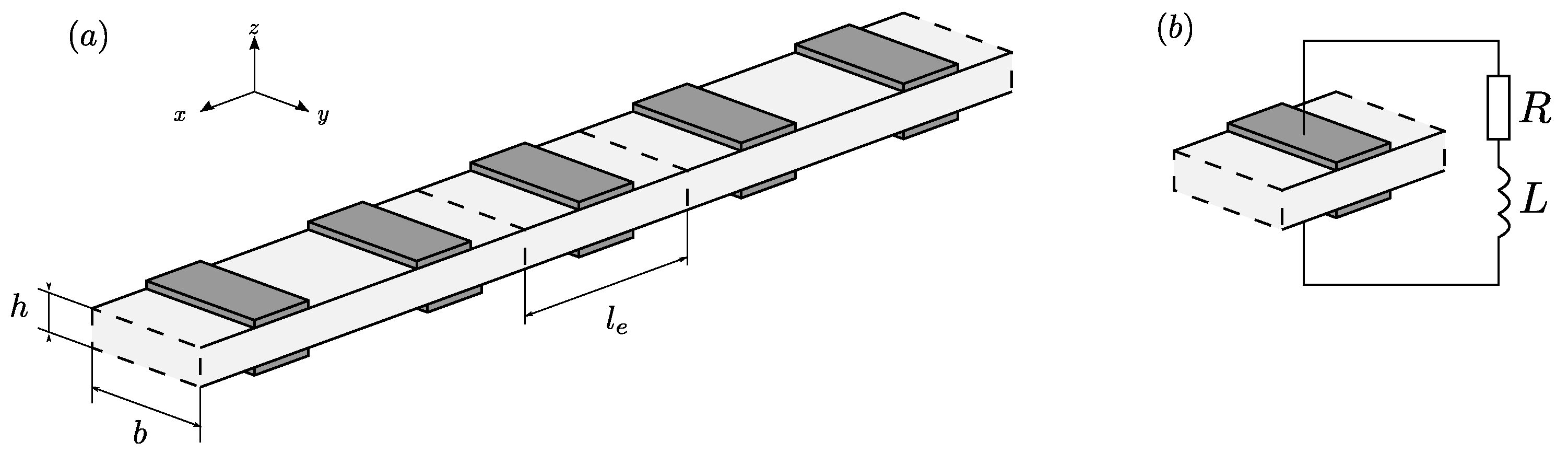
The structure under consideration, presented in
Figure 1, is a sequence of 50 unit cells, consisting of an aluminium beam with piezoelectric rectangular strips (from APC International, Ltd., Cat.No. 70-1000, item 721) attached on both sides. Each pair of piezoelements is connected to the RLC resonant circuit with a controlled inductance.
The material parameters taken into calculations were as follows: for aluminium E = 67.5 GPa, kg/m3 and and for piezoelectric material E = 63 GPa, kg/m3, and piezoelectric electro-mechanical coupling coefficient . The geometry of the analysed beam was as follows: the length m, the width m, the height m, the single RLC element length was m.
Numerical modelling of the piezoelectric material properties was based on the approach proposed in the literature [
9,
10]. The authors presented there a formulae for calculation of the effective Young’s modulus of the piezoelectric element being an element of a resonant circuit. The piezoelectric material has frequency-dependent stiffness and damping, and the frequency itself depends on the parameters of the resonance circuit. Therefore, the effective Young’s modulus of the piezoelectric material in the resonant circuit can be described by the equation:
where
is the effective Young’s modulus of the piezoelectric material in a closed circuit mode,
is the effective Young’s modulus of the piezoelectric material in an open circuit mode,
is the electro-mechanical coupling coefficient of thee piezoelectric material,
is the capacitance of the piezoelectric element, and
is the impedance of a resonant circuit. In the carried out numerical calculations, PZT impedance has been taken into account as an electrical circuit parameter. The impedance of the aluminium beam itself has been neglected because the aluminium beam is not a part of a controlled electrical circuit. In the presented paper, changes in the vibration characteristics of the aluminium beam with attached, actively controlled PZT elements have been analysed.
The displacement and deformation fields of the analysed beam structure have been assumed according to the Timoshenko theory. The mathematical formulae can be expressed by [
11,
12]:
where
and
are respectively the longitudinal and transverse components of the element displacements expressed in the global coordinate system, while the independent rotation
around the
y axis and the lateral displacement
are nodal displacements, defined in neutral element axis.
Following the standard FEM procedures, the inertia matrix
M and the stiffness matrix
K were evaluated:
where
is the density of the material,
is the matrix of elasticity coefficients, and
and
are the shape function and strain-displacement matrices, respectively.
The presented numerical simulations have been obtained by the use of the classical Finite Element Method (FEM), the Frequency Domain Spectral Element Method (FDSFEM, details have been widely presented by Doyle in [
13], the interested Reader is encouraged to follow the source) or the Time Domain Spectral Finite element Method (TDSFEM) approach.
In the classical FEM approach, the unit cell has been divided into three finite elements while in the case of the spectral approach the unit cell has been represented by one finite element, as shown in
Figure 2.
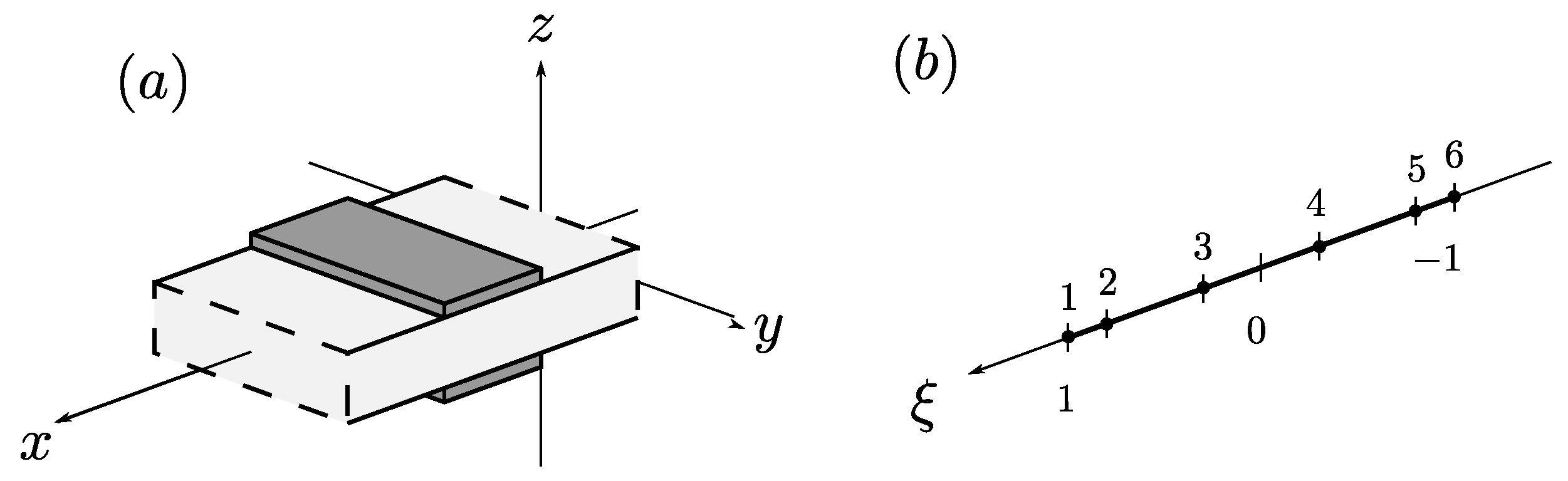
The main difference of the TDSFEM in comparison to the FEM is that in the TDSFEM approach the element nodes are not equally distributed. Coordinates of the nodes are defined as roots of a certain orthogonal polynomial:
which in the analysed case has been
—the second order Chebyshev polynomial. The element nodes in the element coordinate system may be calculated as follows:
Such a definition of node distribution allows one to use higher order shape functions without the risk of causing the Runge effect. The node distribution used in the calculations performed for this paper has been shown in
Figure 3.
The stiffness and inertia matrices corresponding to the piezoelectric element within the respective integration limits have been joined with the stiffness and inertia matrices of the aluminium element respectively, as shown in
Figure 4. The procedure has been precisely described in [
14] for the case of passive periodic structures being a beam and rod with a sequence of drilled holes.
The aforementioned mathematical operations ensures that the stiffness matrix of the piezoelectric element is dependent on the frequency, therefore it is possible to actively control the mechanical responses of the analysed element by frequency variation.
3. Numerical Analysis
In order to examine whether the proposed numerical approach is appropriate, a series of numerical experiments were carried out to verify the impact of the resonance circuit parameters on the physical properties (the width and placement of band gaps) of the periodic beam. During calculations the periodic boundary conditions were assumed.
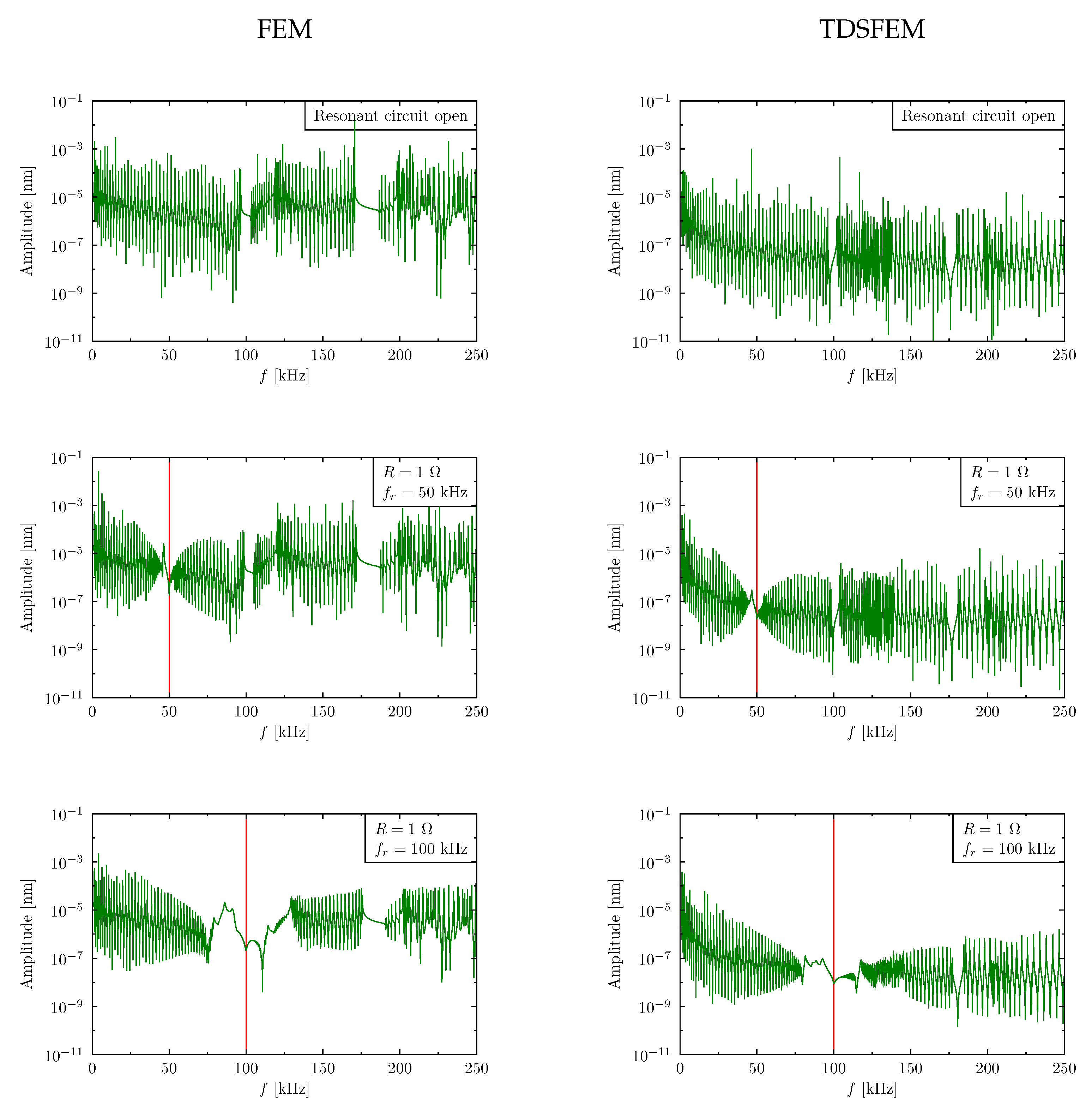
The graphs shown in
Figure 5 represent frequency response functions in the ranges from 0 to 250 kHz for the periodic beam with a resonant circuit being: open, closed or tuned to the specific frequency. The left column of
Figure 5 shows the results obtained by the use of the FEM, the right hand side column of this Figure—by the TDSFEM [
12] respectively. It may be noticed that there appeared two natural band gaps in given frequency ranges for the passive structure. Tuning the PZT circuits to the resonant frequency introduced an artificial band gap in the range of that frequency. However tuning the circuits to the frequency in the range of the natural periodic beam band gap, with the inactive PZT element, significantly widened the band gap. It should be also mentioned that for a lower range of the frequency spectra both the FEM and the TDSFEM results were quite similar, but in a higher frequency range the FEM results were distorted. The reason for that has been widely discussed in [
14], where several features of the numerical models have been addressed.
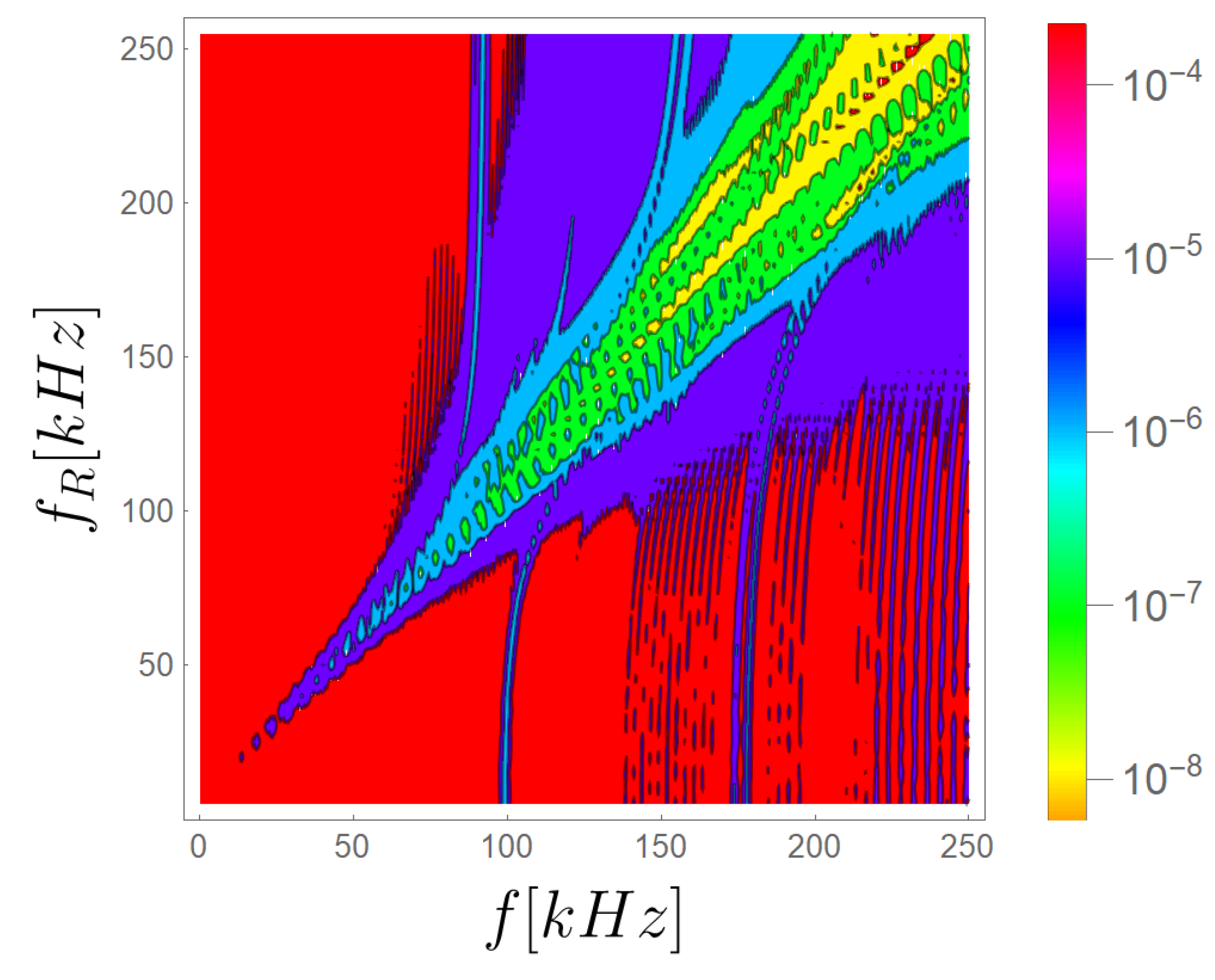
Figure 6 shows the influence of the PZT circuits resonance frequency on the width of beam band gaps. This example was calculated with the TDSFEM. In this case it has been demonstrated how changes in the resonant frequency of PZT circuits allows one to control the ranges of blocked frequencies in the case of forced vibrations. Red colour represents frequency ranges that will propagate freely in the structure, the other colours (blue, green and yellow) represent different levels of attenuation.
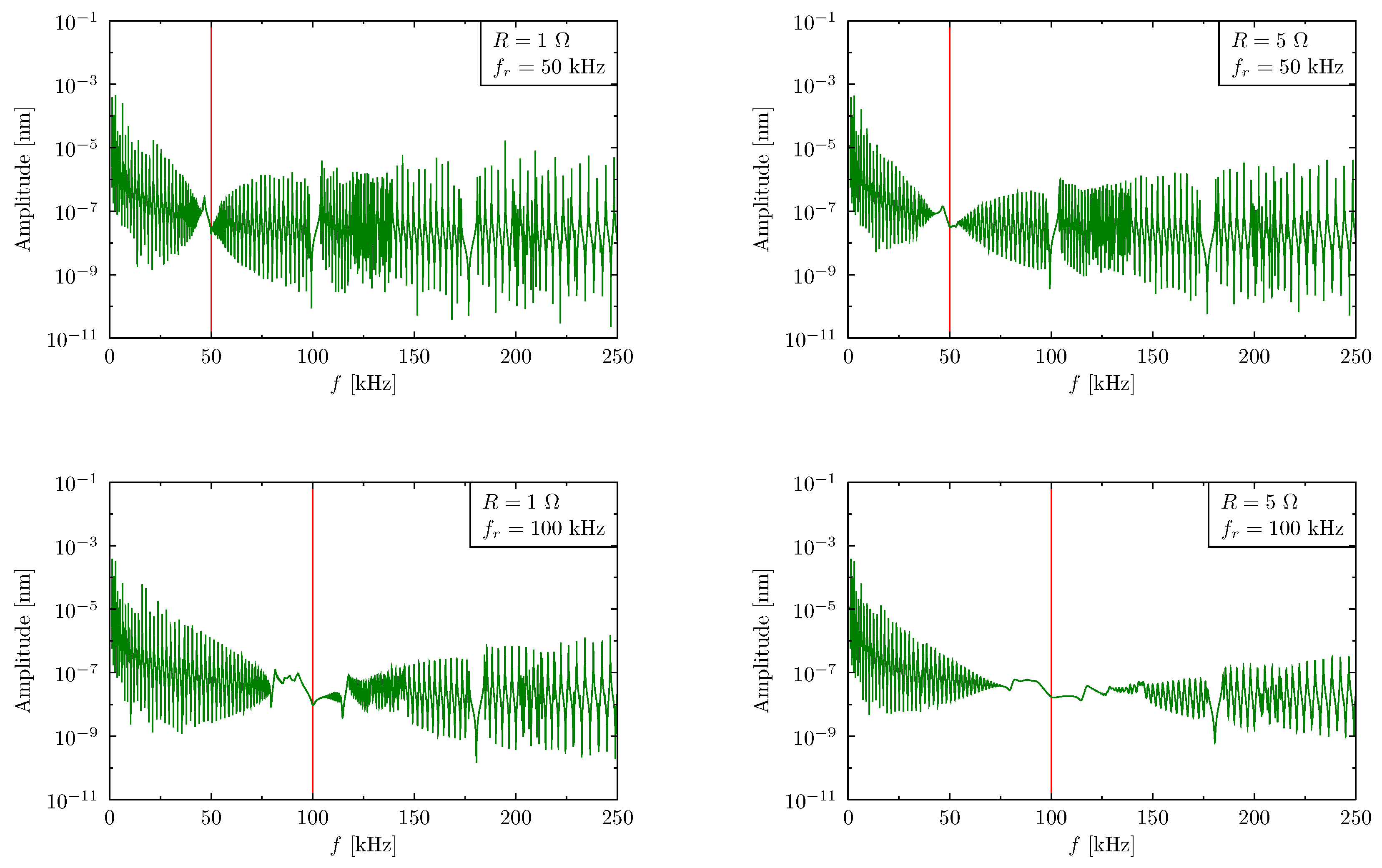
The graphs presented in
Figure 7 illustrate the effect of changes in the electrical resistance on the active periodic structure frequency band gaps. Here the TDSFEM has been used. The figures shown on the left hand side present the results calculated for 1 Ω RLC circuit resistance, the right hand-side—5 Ω respectively. As it can be noticed higher values of the resistance in the RLC circuit increased the energy dissipation and, as a result, widens the band gap. This effect is more significant in case, when the resonant frequency of the RLC circuit is equal to the passive structure frequency band gap. It it may be noticed in the bottom right graph from
Figure 7.
Wave Propagation
This subsection presents the results of the analysis of changes in the propagating elastic waves in the modelled active periodical beam. For modelling the discussed structure the shape functions based on the FDSFEM [
13] was used and the node distribution the same as in the TDSFEM [
15] was adopted. Such a combination of the two totally different methods enabled a thorough analysis of the influence of frequency-dependent changes in the Young’s modulus of piezoelectric material—Equation (
1). The amplitude at both ends of the beam was determined. The aim of a such calculation programme was to analyse the changes of the propagating wave. The analysed periodic beam with active piezoelectric elements was excited to transverse vibrations at one end with the sinusoidal signal (eight pulses) modulated by the Hanning window, by the force of a
N amplitude. Two excitation frequencies
kHz and
kHz have been chosen; the first one from the frequency range of normal behaviour of the periodic beam, and the second within the passive band gap of the periodic structure.
Next
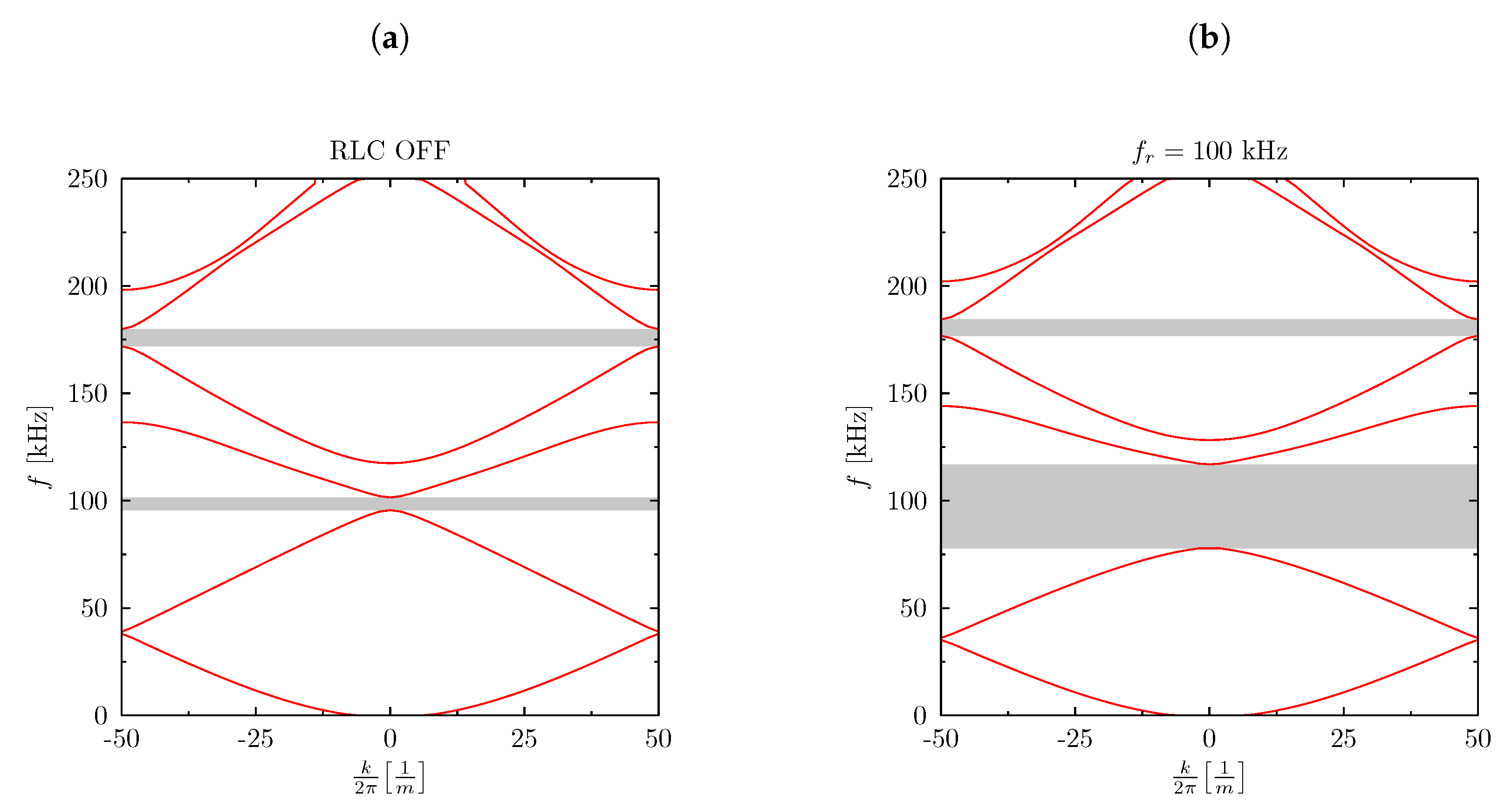
Figure 8 shows the dispersion curves determined for the analysed periodical beam in the first Brillouin zone [
16,
17]. These curves have been determined by the use of the Bloch reduction method [
18] by taking into account the relation from Equation (
1). The graph in
Figure 8a shows the first Brillouin zone of the passive system. One can notice the red lines meaning the vibrations of the propagating wave. The frequency ranges, marked with grey areas, at which there is no wave propagation are visible, i.e., there are no corresponding wave vectors. On the second chart in
Figure 8b there is the first Brillouin zone of the system with each RLC circuit tuned to 100 kHz (frequency from the range of the band gap). RLC circuits create an area of anti-resonant vibrations independent of the wave vector that effectively widens the area of the grey fields of blocked wave propagation.
Flexural wave propagation in an electromechanical periodic structure has been presented in
Figure 9. The presented results represent six cases—the open RLC circuit (
Figure 9a,b), the RLC tuned to the frequency of
kHz (
Figure 9c,d) and the RLC tuned to the frequency of
kHz (
Figure 9e,f) for both 50 kHz and 100 kHz excitation signals—left and right column, respectively. It may be concluded that the active RLC circuits with the resonant frequency equal to the excitation carrier frequency had the features of an active vibration damper.
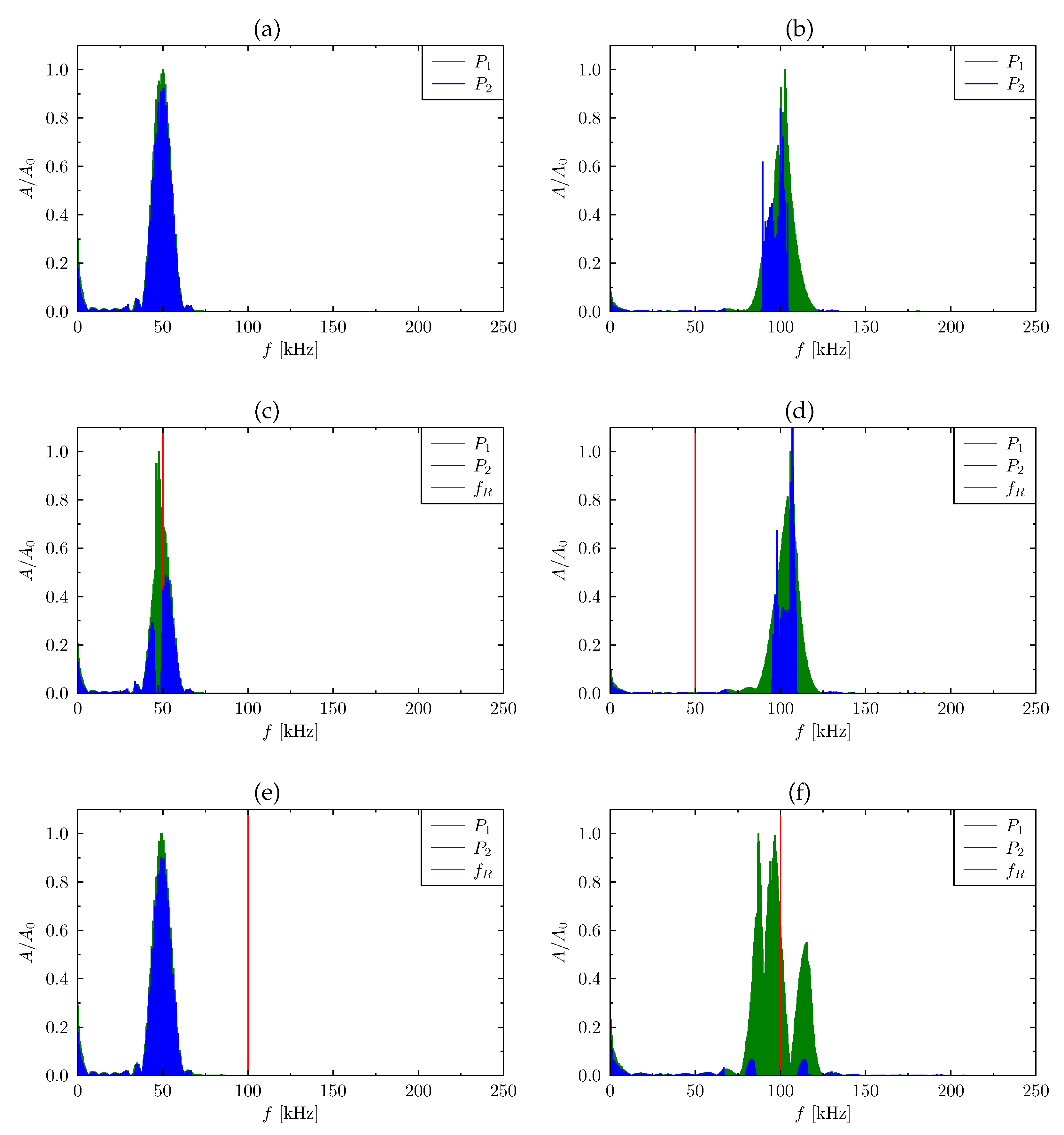
To illustrate the damping character of an active periodic beam with the piezoelectric RLC circuits the following set of results was gathered (
Figure 10). Here the vibration spectra before and after passing through the structure have been shown. The green colours show the spectra of vibration measured before passing through the structure (
), the blue after passing through the structure (
). The red line represents the tuned resonant frequency (
) of the RLC circuit. The left hand side column represents the data calculated for 50 kHz excitation signal, the right hand side column for 100 kHz respectively.
In the case of the passive system (
Figure 10a,b), the wave of the carrier frequency of
kHz was free to propagate itself, there was no remarkable change in the amplitude magnitude (
Figure 10a). In case of the wave of the carrier frequency of
kHz it may be noticed that some amount of the energy was blocked due to the presence of band gaps for this spectrum range as the band gap was a barrier for propagation of waves of these frequencies. However, the natural band gap was of relatively small width, therefore a certain amount of wave energy could propagate through the band gap.
The diagram below (
Figure 10c,d) shows the changes in the excitation spectrum in the active periodic beam with the RLC circuits tuned to
kHz. As it can be noticed, the excitation wave (of the carrier frequency of
kHz) at that frequency was unable to propagate freely due to the dissipation of energy on the electrical resistance band gap that appears. Although the band gap was very narrow the amplitude of the wave decreased in a significant manner. On the other hand for this
kHz no significant changes were observed in the amplitude of the excitation signal of the carrier frequency of
kHz in comparison to the amplitude registered for the passive system.
Finally, tuning of the RLC circuit to the frequency of
kHz (
Figure 10e,f) did not cause any changes in the wave propagation of the excitation wave of the frequency of
kHz (also comparing to the passive structure). However, this value of the
kHz caused a significant widening of the band gap. The amplitude of the wave after passing through the structure with band gap decreased tenfold. It was caused by the synergy of the natural periodic structure band gap with energy dissipation caused by the active RLC circuit and its electrical resistance.
4. Conclusions
In this paper numerical investigations of a beam structural element built out of periodically arranged elementary cells with active piezoelectric elements has been performed. For this analysis the authors propose numerical models based on the use of the finite element method (FEM) and the spectral finite element methods defined in the frequency domain (FDSFEM) and the time domain (TDSFEM). The application of different modelling methods allow the authors to formulate conclusions that result from the calculations performed.
The FEM is the most common method and generally gives correct results. However, for high-frequency analysis problems it is necessary to use either a heavily dense grid or higher-order approximation polynomials. This leads to a correspondingly large sizes of the problems to be solved or a Runge effect. There is another reason why the FEM can be disadvantageous in the applications related to periodic structures—numerical models themselves show periodic characteristics [
6,
15]. Thus, it is easy to predict that the results obtained may have features typical to periodic structures resulting not only from the geometry of finite elements, but also from the features of the numerical models. The consequent misinterpretation of results may be simply dangerous.
Due to the above mentioned characteristics of the FEM, the study proposes to utilise the TDSFEM method. The unquestionable advantage of the TDSFEM method is its ability to employ higher order approximation polynomials, which results in higher calculation accuracy. Additionally, an un-uniform distribution of nodes in single finite elements enables one to obtain a diagonal form of the inertia matrix, which significantly reduces the time of numerical calculations. All presented amplitude-frequency characteristics of the analysed periodic beam structural element, taking into account the dependence of the PZT Young’s modulus on the frequency, have been determined by this method.
While in the case of determination of the amplitude-frequency characteristics of the active periodic beam, the use of the TDSFEM allowed the authors to obtain results at a satisfactory level, the calculations for changes in the propagation of elastic wave required another modification of the modelling method. In order to precisely map changes in Young’s modulus for the value of PZT material for each analysed frequency, it was necessary to use the FDSFEM method. Modification of the method involved the use of non-uniform mesh of nodes in the finite elements known from the TDSFEM and shape functions from the FDSFEM. In this way the changes in propagation of elastic waves in the active periodic beam structural element have been modelled.
After all numerical tests performed it may be concluded that periodic structures with active piezoelectric elements incorporated into the RLC resonance circuit can be successfully used to attenuate vibrations in a controlled manner. A resonant circuit with piezoelectric elements causes the appearance of an additional band gap in the spectrum of mechanical vibrations in the vicinity of the natural frequency of the RLC resonance system. Adjusting the resonance frequencies of the RLC systems to the frequency of the naturally present band gap in the spectrum of mechanical vibrations results in a significant widening of the band gap, which leads to effective vibration damping in this frequency range.
Although the proposed approach clearly demonstrates that there is a possibility of active control of band gaps, it should be added that the problem still requires a number of analyses and will definitely be the subject of further scientific considerations of the authors.