1. Introduction
Electromagnetic wave amplification by non-linear wave mixing has been studied for decades with most of the research focusing on the field of non-linear optics. It has been well-established that a low power input wave can be amplified via mixing with a high-intensity pump wave, in a medium that demonstrates a high degree of non-linearity. The fundamental theory of intra-cavity non-linear optical amplification is about the energy transfer from the pump wave-energized resonator to the input wave as a consequence of non-linear optical coupling [
1,
2,
3]. The more elaborate theory of non-linear wave amplification involves a dispersion analysis that takes into account the frequency dependence of the non-linearity of the interaction medium. However, based on our in-depth investigations, a direct gain factor maximization approach via a non-linear constrained optimization algorithm is lacking. The background research about the theory of non-linear wave mixing has been mostly experimental rather than computational, especially for the purpose of optical amplification. The major reason of this tendency is that this topic is usually studied in the micrometer- or nanometer-wavelength range, but the required interaction medium length to observe a strong non-linear effect is in the millimeter or centimeter range [
4]. This requires a tremendous computational cost for acquiring meaningful results, particularly for wave amplification purposes.
Another incentive for the experimental investigation of the topic is the desire to discover new materials that exhibit unusually high non-linearity under excitation. More recently, researchers focus on determining the resonance frequencies of the non-linear electrical response of commonly used materials in photonics such as graphene and gallium nitride. This approach has been mostly successful and resulted in an improvement of efficiencies in many applications in photonics. However, for the purpose of optical amplification, achieving a resonant non-linear optical response usually fails as the dielectric absorption around any non-linear resonance peak is quite strong to prevent significant amplification. Moreover, the well-established concept of optical parametric amplification yields a negligible gain factor in a few micrometers-long resonator. The required interaction medium length for high-gain optical parametric amplification is usually in the order of centimeters. Therefore, optical amplification by non-linear wave mixing is not so feasible for utilization in micro-resonators, optical transistors, micro-modulators, and many other device models in integrated photonics such as those mentioned in [
5,
6]. However, if one can perform super-gain optical parametric amplification in the micrometer scale, much more powerful macroscale devices can be produced for high-power applications, by engineering the individual micro-scale devices to operate in an array form to maximize optical interference, such as high-power welding machines and super-intensity lasers that are employed in particle accelerators and fusion reactors. A major scientific advancement can be in the field of optical antennas via supercontinuum generation for achieving ultra-wideband operation.
In this article, we have performed a numerical analysis that provides evidence for the high-gain amplification of a low-power stimulus wave, via intense pump waves of ultrashort duration, inside a several micrometers long micro-resonator, by maximizing the electric energy density of the pump wave in the resonator.
Since the order of amplification that can be achieved via non-linear wave mixing depends on the amount of stored electric energy density and the pump wave-initiated polarization density, which acts as a non-linear coupling coefficient, we will first present the energy storage dynamics for a resonator and we will recall the definitions of the electric polarization density and the gain factor of an amplification process. Then we will present the basic background for wave propagation in non-linear dispersive media and we will formulate our energy maximization (optimization) problem based on the partial differential equations given to express wave propagation in non-linear dispersive media. Finally, we will present two numerical experiments and analyze their results.
2. Polarization Density and the Cavity Quality (Q) Factor
The Q factor indicates the amount of the stored energy inside a resonator for a given round trip loss. A high Q value usually signifies that the resonator is low loss, i.e., has a low loss factor, which means that high energy can be trapped efficiently in the resonator. The Q factor depends on the resonator length, the reflectivities of the resonator walls, the frequency of the propagating wave, the total absorption coefficient of the interaction medium between the resonator walls, and any sort of diffraction or scattering loss that may take place inside a resonator. The Q factor of a resonator is defined as:
,
,
The electric energy density in a resonator depends on the magnitude of the electric field and the polarizability of the interaction medium. For a given resonator configuration, the stored electric energy density in a homogenous isotropic interaction medium is given as [
7]:
,
,
,
The electrical polarization density (
P) in an interaction medium is a microscopic parameter that indicates both the volume density of electrons and the displacement of an electron with respect to the position of the nucleus [
3]. For a given electron density of a medium, the more an electron is allowed to displace from its initial position (and the nucleus) the higher the polarization density becomes. It is a measure of the electrical excitability of a material by an incident electromagnetic wave [
1]. Polarization density is an important parameter for energy storage in a resonator as more energy can be stored in a cavity with a highly polarizable interaction medium. This is because, as each electron displaces further from the nucleus, their potential energy becomes higher, and an abundance of electrons in the medium will lead to a higher potential energy being stored in the medium [
4]. For a highly non-linear medium, the polarization density itself depends on the magnitude of the electric field [
1,
4]. For these reasons, we will frequently use the term polarization density in our analyses.
3. Wave Propagation in Non-Linear Dispersive Media
As previously stated, non-linear interaction takes place when a wave that propagates in a medium have a very high intensity. This degree of non-linearity inducing high intensities is usually possible with ultra-short duration pulses and can be practically generated from a mode locked laser or a Q-switched laser, which have durations on the scale of picoseconds or femtoseconds. Since such high-intensity pulses have ultra-short durations, we must perform a dispersion analysis.
Impulse response of the polarization density of many dielectric media last much longer in duration than the pulse durations of such high intensity pulses [
8,
9].
The inclusion of dispersion in the analysis means that we need to solve for the polarization density of the interaction medium separately. In fact, it is much more accurate to solve the wave equation in parallel with the non-linear electron cloud motion equation for a non-linear dispersive medium, since parameters such as the resonance frequency, damping rate, atom density, and atomic diameter have typical values for most solid media, which makes the simulation results more realistic. To determine the time variation of the electric field in a non-linear dispersive medium, we need to solve the following equations (see
Figure 1) [
1]:
,
In Equation (4) we have accounted up to the third order of the polarization density as higher order terms are negligibly small. For a dielectric medium, the electric conductivity is almost zero
Some typical values for solid dielectric media are [
1];
, , Electromagnetic wave amplification by non-linear wave mixing involves two waves, namely the low intensity stimulus (input) wave to be amplified, and the high-intensity pump wave. Let us first consider the high-intensity pump wave
without the presence of the low intensity stimulus wave
. In this case, the pair of equations that model the propagation of
is given as:
,
Now assume that
and
are simultaneously propagating in the same medium, in that case the pair of equations that describe the total electric field propagation is written as:
Our aim is to solve for the low amplitude wave
in the presence of the high-amplitude wave
, i.e., we want to solve for the stimulus wave
when there is an energy coupling from
. To model this problem, we subtract Equation (5a,b) from Equation (6a,b) respectively [
1], which yields:
Equations (5a,b) and (7a,b) show that
and
are coupled to each other. The pump wave
acts as a source field distribution for electromagnetic wave propagation, with the stimulus wave
acting as the carrier distribution in reference to the model presented in [
10]. Based on Equation (7a,b), we will examine if it is feasible to amplify the low-intensity electric field
, via energy coupling from the microresonator that is energized by the high-intensity electric field
(see
Figure 2).
From Equation (7a), we can see that the stimulus wave has a source term , which is the polarization density of the stimulus wave. The source term is also dependent on the source term (polarization density) of the high-intensity pump wave . This means that in order to solve for the stimulus wave , we need to solve for the pump wave as the equations for the stimulus wave and the pump wave are coupled to each other via the coupling term . Therefore, the stimulus wave can be solved by simultaneously solving all these four equations (Equations (5a,b) and (7a,b)).
Our goal is to maximize the stimulus wave magnitude at a given stimulus wave frequency; max(
). In order to achieve this, we will make a dispersion analysis that is based on the high-intensity pump wave frequency. By sweeping the excitation frequency of the pump wave (
) in a large spectral interval that extends from the far-infrared region to the near-ultraviolet region, we can investigate the pump wave frequency dependent variation of the maximum stimulus wave magnitude for
, and we can select the optimal pump wave frequency value that maximizes the magnitude of the stimulus wave for
. Mathematically our optimization problem can be stated as:
where
If we are using
N ultrashort high-intensity pulse excitations to amplify the low-intensity stimulus wave,
Then the dispersion analysis-based optimization problem is stated as follows:
Note that in this case the pump wave comprises N ultrashort pulses instead of a single ultrashort pulse. Therefore, we have a multiparameter optimization problem.
The physics behind the efficient amplification of the stimulus wave involves the simultaneous maximization of the stored electric energy density and the polarization density originated by the pump wave in the resonator (see
Figure 3). This can be explained in two steps, first we need to maximize the stored energy in the cavity in order to transfer a high amount of energy to the stimulus wave. Second, we need to maximize the polarization density of the pump wave, which acts as the energy coupling coefficient based on Equation (7b).
Even if we maximize the stored electric energy density in a resonator, if the non-linear coupling coefficient is not high, then we cannot efficiently transfer the accumulated energy into the stimulus wave and high-gain amplification of the stimulus wave does not occur.
In order to perform the optimization of the stimulus wave magnitude at a given stimulus wave frequency , we need an efficient optimization algorithm. In the next section, we will use the computationally efficient quasi-Newton Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm to perform the maximization of the stimulus wave magnitude at a desired frequency.
4. Optimization of Optical Parametric Amplification Gain Factor in a Micro-Resonator
Assume that we are using N ultrashort high power pulses to amplify the stimulus wave. These ultrashort pulses have similar pulse energies so that each of them affects the amplification performance in the same degree. The ultrashort high-power pulses are summed up to form the pump wave. At a given spatial input point, the pump wave and the stimulus wave are given as:
We want to tune the frequencies (
of these ultrashort pulses so that the gain factor is maximized. In order to do that, we use the BFGS algorithm, so that the Hessian matrix of each iteration is recursively updated. The BFGS algorithm is one of the quasi-Newton methods that are used to compute the Hessian matrix. Recursive computation reduces the computational cost of the optimization by eliminating the need to compute the second derivative at each iteration. We will use the BFGS algorithm because of its accuracy and simplicity. The most general form of the quasi-Newton method is given as [
11]:
Quasi-Newton methods, like steepest descent, require only the gradient of the objective function to be supplied at each iteration. The Hessian is updated by analyzing successive gradient vectors. The whole BFGS algorithm is as described below [
11].
Given a starting point , convergence tolerance ε > 0, inverse Hessian approximation ;
|
| while; |
| Compute search direction |
| ; |
| Setwhereis computed from a line search procedure to satisfy the Wolfe conditions. |
| Defineand |
| Computeusing; |
| (BFGS) |
| Where |
|
| end (while) |
The step size
can be computed from a line search procedure to satisfy the Wolfe conditions:
Alternatively, the step size
can be computed from the so-called backtracking approach [
11]:
| Choose |
| repeat until |
|
| end |
Since our problem is the amplification of a stimulus (input) wave via non-linear wave mixing with a high-power pump wave, for this problem, the optimization parameters are the frequencies of the N ultrashort pulses that constitute the total pump wave. Assume that is the low power stimulus wave to be amplified, and is the high-power pump wave, which is the combination of N ultrashort pulses. The general formulation for the maximization of the stimulus wave magnitude (gain factor) is summarized as follows:
Optimization parameters: , Cost function to be maximized:
Constraints: ,
This problem is a constrained optimization problem, we can convert this problem into an unconstrained optimization problem by modifying the cost function via the addition of penalty functions. In the case of a maximization problem, these penalty functions yield a decrease in the cost function when the constraints are violated. In our case, the penalty for violating the constraints is adjusted to yield a quadratic decrease:
Augmented cost function: (penalty function method)
q: positive valued penalty exponent,
L: Positive valued penalty constant,
: penalty coefficients
The convergence rate of the BFGS algorithm is super-linear, but our formulated problem is a non-linear optimization problem (non-linear programming). Therefore, the convergence is not reached immediately. Furthermore, the recursive computation of the Hessian matrix slows down the convergence rate. For these reasons, the computation of the optimum frequency values takes a great amount of time.
5. Finite-Difference Time-Domain Solution of the Gain Factor Optimization Problem in Optical Parametric Amplification
Equations (5a,b) and (7a,b) can be discretized using the finite-difference time-domain (FDTD) method as stated in Equations (18a,b) and (18c,d), for every iteration k of our optimization problem. Our initial goal is to discretize Equation (5a,b) in order to get
i.e., the value of
at a certain spatial coordinate at the next time step. Since
and
are coupled to each other, initially we attempt to solve for
and then substitute its value into the wave equation for
. These two equations are solved recursively for every time step and for all spatial points in a given one-dimensional solution domain. In order to increase the accuracy of our obtained solution, we should select
and
as small as we can [
12,
13]. Then we may proceed on the discretization of Equation (7a,b) and substitute the previously obtained value of
from Equation (5a,b), for the solution of
in Equation (7a,b). Finally, we update the values of the optimization parameters based on the BFGS algorithm, and we repeat the entire procedure for every iteration of the optimization process until the desired gain factor is achieved (see
Figure 4).
FDTD Equations:x: spatial coordinate,
t: time,
k: iteration number,
,
Cost function:
Augmented cost function: (penalty function method)
Wolfe conditions for
:
6. Numerical Experiments
6.1. Double-Frequency Tuning for Gain Factor Optimization
Assume that a 250 THz (
= 1.2 μm) infra-red stimulus wave
and a high power pump wave
that is composed of two high-intensity ultrashort pulses (frequencies are to be determined) are propagating inside a low-loss (high Q) cavity that has two reflecting walls (see
Figure 5). The wall on the left side can be thought as an optical isolator, which fully transmits from its left side and almost fully reflects from its right side. The wall on the right side represents an optical band-pass filter with a frequency-dependent reflection coefficient
Both waves are generated at x = 0 μm, at the time instant t = 0 s. The waves and the parameters of the gain medium are as given below:
Our problem: find the optimal pump wave pulse frequencies
that maximize the magnitude of the monochromatic stimulus wave in the cavity (
), for 10 THz <
(THz to UV), and for
, such that
Our aim is to maximize the magnitude of the stimulus wave at its original frequency
(monochromatic form). This is a precaution against any degree of spectral broadening that the stimulus wave may go through while being amplified. Therefore, our cost function is chosen as (at any spatial point
inside the cavity):
Boundary and excitation conditions:
where
Absorbing boundary condition (perfectly matched layer): Optical isolator condition: full reflection at
Optical bandpass filter condition: frequency dependent reflection at
Cost function to be maximized:
where
Optimization algorithm (BFGS): In order to satisfy the Wolfe conditions, the step size at each iteration is chosen as:
where
is just a constant (
) and
is the step size at iteration k. This formula (Equation (19)) was determined by trial and error and was found to satisfy Wolfe’s conditions automatically at each iteration. This saves us from the huge computational cost of running another iteration loop to determine the step size at each iteration of the optimization process. In this simulation C = 1.445. Based on the above formulations, the maximum stimulus wave amplitude that has been reached in the cavity (for 0 < t < 10 ps) is determined as
, which corresponds to the frequencies
(see
Table 1), or to the free space wavelengths
as the ultrashort pulses can be practically generated outside the resonator. In this simulation, the gain factor of the amplification is defined as:
where
is chosen as an intra-cavity point
and
As we can see from
Table 1, the optimal ultrashort pulse frequencies correspond to very high stored electric energy density and high polarization density. The stored electric energy density and the polarization density must be simultaneously high for a significant stimulus wave amplification. The stored electric energy density indicates the achievable order of stimulus wave amplification [
14,
15], and the polarization density acts as a coupling coefficient, which is a measure of how much stored electric energy can be coupled to the stimulus wave.
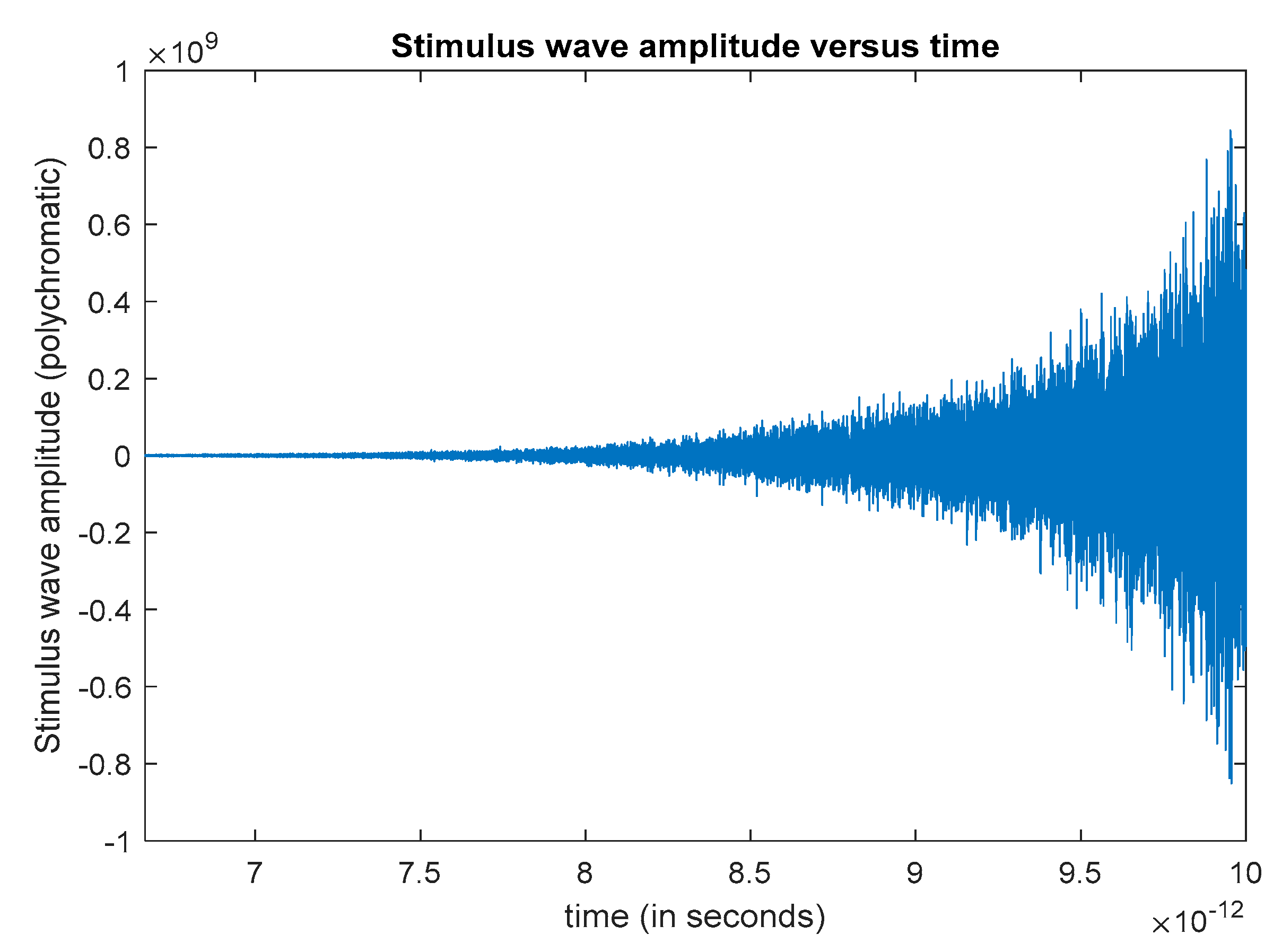
The time variation of the spectrally broadened (polychromatic) stimulus wave between t = 6.6 picoseconds and t = 10 picoseconds is shown in
Figure 6. From the figure, we can see that the polychromatic stimulus wave reaches an amplitude of approximately
.
6.2. Triple-Frequency Tuning for Gain Factor Optimization
Assume that a 300 THz (
1 μm) infra-red stimulus wave
and a high-power pump wave
that is composed of three ultrashort pulses (frequencies are to be determined), are generated to propagate in a micro-resonator with two reflecting walls. The wall on the left side can be thought as an optical isolator, which fully transmits from its left side and almost fully reflects from its right side. The wall on the right side represents an optical band-pass filter with a frequency-dependent reflection coefficient
(see
Figure 7). Both waves are generated at x = 0 μm and at the time instant t = 0 ps. The waves and the parameters of the gain medium are as given below:
Our problem: Find the optimal pump wave pulse frequencies
that maximize the magnitude of the monochromatic stimulus wave in the cavity (
), for 50 THz <
,
, such that
It is important to emphasize that our aim is to maximize the magnitude of the stimulus wave at its original frequency
(monochromatic form). This is a precaution against any degree of spectral broadening that the stimulus wave may go through while being amplified. A plain attempt to maximize the magnitude of the stimulus wave (
) independent of the original excitation frequency (
), may result in an amplified stimulus wave with different frequency components. In fact, these different frequency components might be even much more dominant than the original excitation frequency of the stimulus wave. Therefore, our cost function is chosen as (at any spatial point
)
Boundary and excitation conditions: Absorbing boundary condition (perfectly matched layer): Optical isolator condition: full reflection at ;
Optical bandpass filter condition: frequency-dependent reflection at
;
Augmented cost function to be maximized:
Optimization algorithm (BFGS): In order to satisfy the Wolfe conditions, the step size at each iteration is chosen as:
where
is just a constant (
) and
is the step size at iteration k. In this simulation C = 1.45. Based on the above formulations, the maximum stimulus wave amplitude that has been reached in the cavity (for 0 < t < 40 ps) is determined as
, which corresponds to the frequencies
(see
Table 2), or to the free-space wavelengths
as the ultrashort pulses can be practically generated outside the resonator. In this simulation, the gain factor of the amplification is defined as:
where
is chosen as an intra-cavity point
and
As we can see from
Table 2, the optimal ultrashort pulse frequencies correspond to a very high stored electric energy density and a high polarization density. If we have a look at
Table 2, we can see that the stored electric energy density and the polarization density must be simultaneously high for a significant stimulus wave amplification. The stored electric energy density indicates the achievable order of stimulus wave amplification. The polarization density serves as an energy-coupling coefficient and is a measure of the stored electric energy that can be coupled to the stimulus wave.
7. Verification of Our Computational Model
Our numerical model is verified by using the experimentally validated formulas of the topics sum frequency generation via non-linear wave mixing and optical amplification via non-linear wave mixing as described in the examples below.
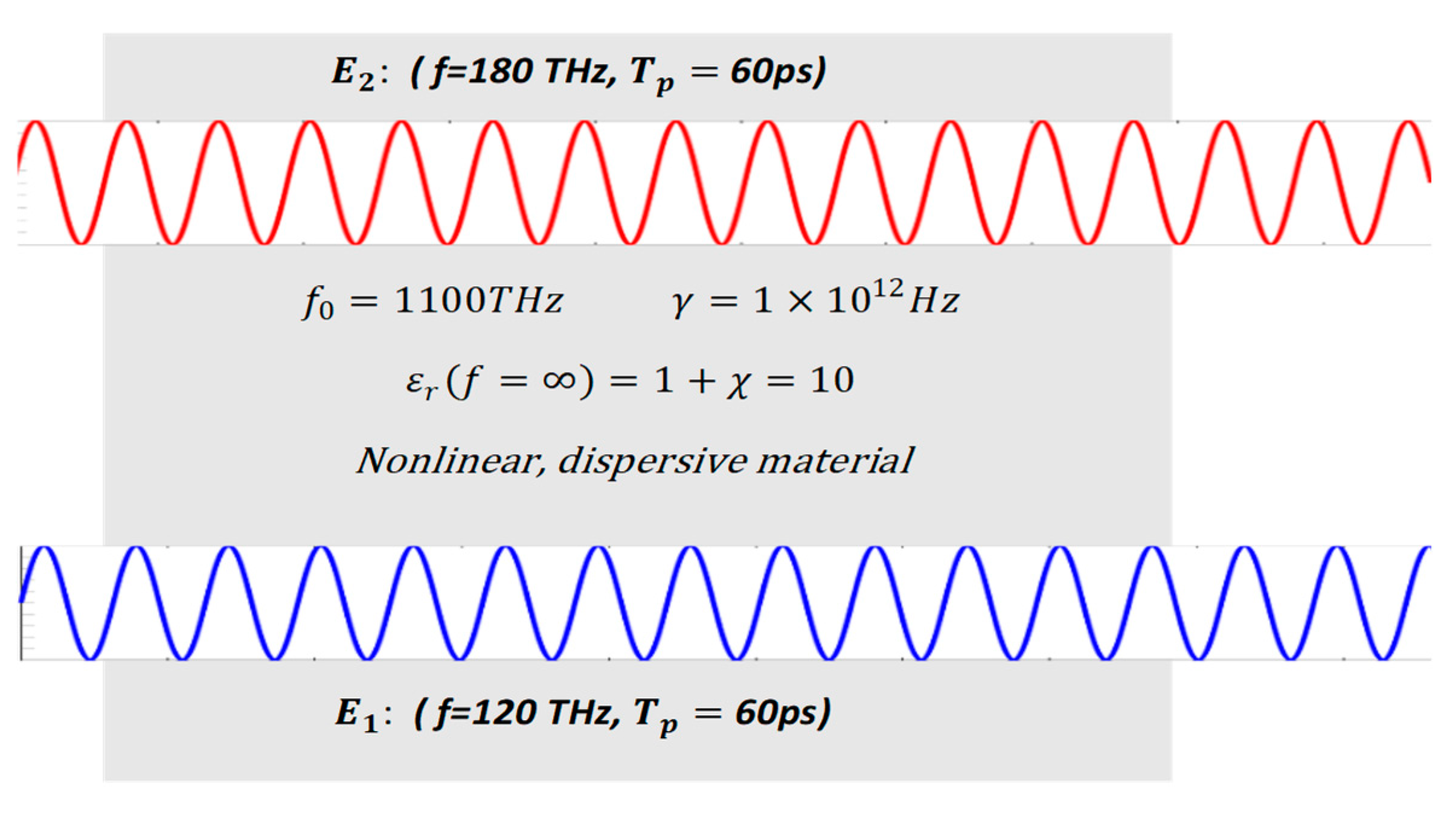
Example 1. Sum frequency generation via non-linear wave mixing (frequency up-conversion)
This example is about the generation of a higher frequency component, by mixing of two monochromatic waves with frequenciesandvia non-linear coupling, such that.
The pump wave
is originated at x = 2.5 μm, with an amplitude of
V/m and a frequency of 180 THz.
The input wave
is originated at x = 2.5 μm, with an amplitude of
V/m and a frequency of 120 THz (see
Figure 8).
The experimentally verified theoretical formula for frequency up-conversion efficiency is given as [
1,
4]
Our computational model, which is based on the non-linear electron motion equation, is implemented via FDTD discretization. Coupled with the wave equation, the total wave
is computed from:
For a time interval of
, the computational formula for frequency up-conversion efficiency is:
In this example, we have used the following values for each efficiency formula:
L = length of the interaction media = 3.33 (from x = 3.33 to 6.66 )
, n=
d = material non-linearity coefficient =
(The theoretical and the computational results agree for this value of
d for a sample pump wave amplitude of
(see
Figure 9). Our aim is to see if the results also agree for all the other pump wave amplitudes for this value of d)
= pump wave amplitude (varied from )
= input wave amplitude = (
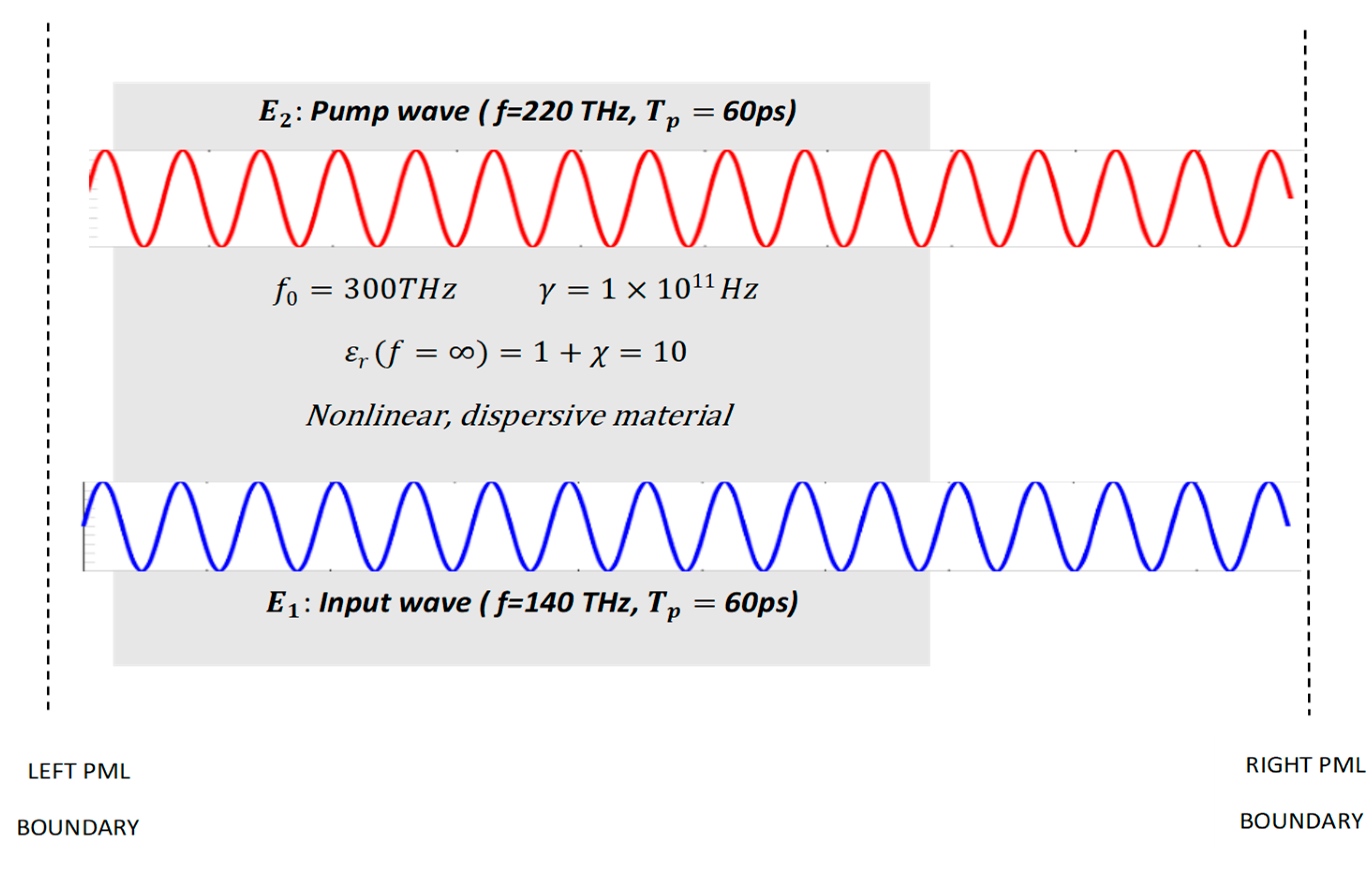
Example 2. Optical amplification via non-linear wave mixing (parametric amplification).
The high-intensity pump wave
is generated at x = 2.5 μm. It has an amplitude of
V/m and a frequency of 220 THz.
The input wave
is generated at x = 2.5 μm. It has an amplitude of
V/m and a frequency of 140 THz (see
Figure 10)).
Range of independent simulation variables:
Our goal is to amplify the input wave via energy coupling from the high-power pump wave. The computational results are obtained by solving (21a,b) and by computing the ratio of the spectral intensity of the input wave for
at
to the input wave intensity for
at
:
The experimentally verified theoretical formula for parametric amplification, which is derived from the solution of the non-linear wave equation that is based on material non-linearity coefficient, is given as [
1,
4]:
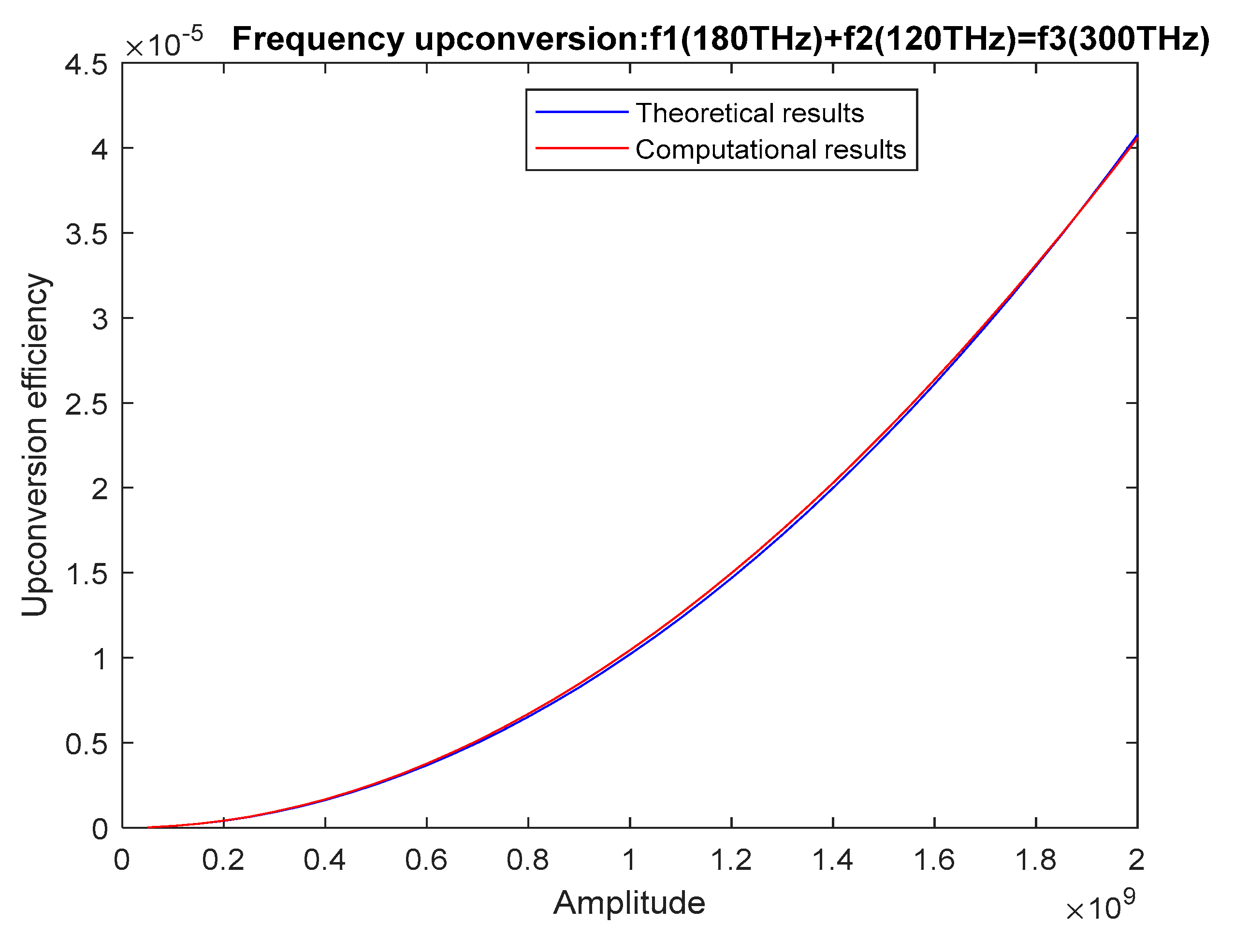
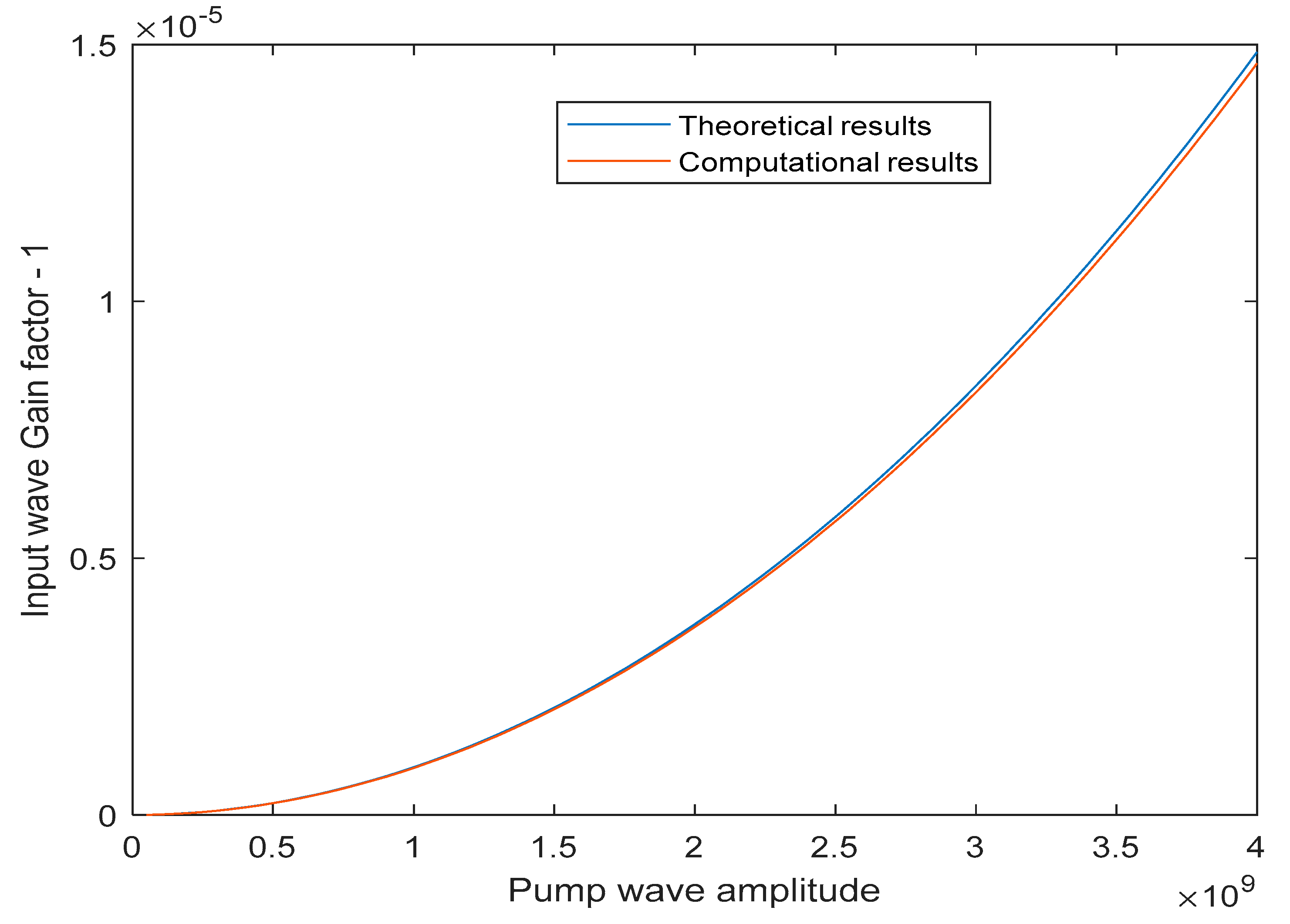
The resulting amplification of the input wave (gain factor) is plotted with respect to the pump wave amplitude based on both the theoretical and the computational formulations (see
Figure 11). Notice that the gain factor increases quadratically with the pump wave amplitude. The resulting gain is quite small, as parametric amplification practically requires an interaction medium length on the order of centimeters [
16,
17,
18,
19,
20], whereas in this example we have an interaction medium length of 5 μm.
8. Discussion
It is important to note that although the presented algorithm is very accurate in obtaining the highest gain factor and determining the optimal frequencies for the ultrashort pump wave pulses, the parameters of the gain medium may limit the maximum achievable gain factor. For example, in our presented numerical experiments, the background permittivity values were set as
and
respectively, these values correspond to the background permittivity of many solid dielectric media in the near infra-red and the visible frequency range. A very large gain factor is also achievable for smaller values of the background permittivity at the expense of a slight increase in ultrashort pump wave intensity to compensate for the decreased stored energy in the micro-resonator. Similarly, for a gain material with a higher background permittivity, the required pump wave intensity can be lowered in order to achieve the same gain factor. Another important parameter that heavily influences the gain factor is the polarization damping rate or simply the damping rate
. A damping rate that is greater than
slows down the rate of amplification via non-linear wave mixing and results in a lower gain factor [
21].
The frequencies of the ultrashort pump wave pulses can be practically tuned from the far IR (infrared) range to the near UV (ultraviolet) range. Commercial IR laser sources such as the Neodymium-YAG laser, or the Helium-Neon laser can be used in the near IR range and also in the visible range via frequency doubling. A visible laser light can be used in combination with a near IR laser light to generate a UV laser light via the process of sum frequency generation. A far IR laser light and even a THz laser light can be generated using two near IR laser lights of slightly different frequencies, through difference frequency generation process.
Optical amplification via non-linear wave mixing offers the advantage of wide-band amplification of a monochromatic stimulus wave, practically in a frequency interval ranging from the far IR to the near UV part of the spectrum [
1,
4,
19]. Hence, the numerical algorithm presented in
Figure 4, can be used to amplify a monochromatic stimulus wave of any frequency that lies between the far IR to the near UV part of the spectrum.
Our main aim in this article is to show that super-gain optical parametric amplification can be achieved in a simple fabry-perot type micro-resonator. For more complicated resonators including microring and microdisc resonators, the one-dimensional model presented in this article must be extended to a two-dimensional model. Our algorithm, which is presented in
Figure 4, can be extended to a two-dimensional or a three-dimensional micro-resonator analysis using the technique that is presented in the article referenced in [
22]. This article explains how, using FDTD, Maxwell’s 2-D and 3-D curl equations in vector form can be effectively stepped in time simultaneously with a system of auxiliary differential equations, in order to create an integrated model that is capable of accurately simulating a medium involving instantaneous non-linearity, dispersive non-linearity, and multiple linear dispersions. Concerning implementation, the Greene-Taflove algorithm given in [
22] can easily be incorporated into our algorithm during the discretization of the equations via finite difference time domain method. Hence the algorithm presented in this article can be employed in the analysis of arbitrary-shaped 2-D and 3-D micro-resonators.
9. Conclusions
For high-gain stimulus wave amplification via non-linear coupling in a micro-resonator, a high stored energy and a high polarization density is required. In order to maximize the intracavity energy and the polarization density, for a given resonance frequency (, the frequencies of the high-intensity ultrashort pulses that comprise the pump wave must be tuned accordingly. This can be accomplished via a computationally cost-efficient optimization algorithm such as the quasi-Newton BFGS algorithm. The optimization algorithm must be embedded in the numerical discretization method by choosing the stimulus wave magnitude as the cost function and by modifying it according to the problem constraints.
If the optimal frequencies of the high-intensity ultrashort pulses are set, it is possible to amplify a low-intensity stimulus wave with a very large gain coefficient even inside a micrometer-scale resonator.