Collision-Free Path Planning Method for Robots Based on an Improved Rapidly-Exploring Random Tree Algorithm
Abstract
Featured Application
Abstract
1. Introduction
| Algorithm 1 Basic-RRT algorithm. |
| 1: InitTree(); |
| 2: for 1 to n do |
| 3: RandomSample(i); |
| 4: NearestNeighbor(); |
| 5: Extend(); |
| 6: if CollisionFree() then |
| 7: AddNewNode(); |
| 8: end if |
| 9: if Distance( then |
| 10: return T; |
| 11: end if |
| 12: end for |
| 13: return ; |
| Algorithm 2 GoalBiasedSample() |
| 1: RandomNumber; RandomNumber |
| 2: if k then |
| 3: ; |
| 4: else |
| 5: RandomSample(); |
| 6: end if |
| 7: return ; |
2. The NC-RRT Method
2.1. The Method of Gradually Changing the Sampling Area
| Algorithm 3 CSA-RRT algorithm. |
| 1: InitTree(); |
| 2: ; |
| 3: for 1 to n do |
| 4: RandomSample(i); |
| 5: if Distance then |
| 6: continue; |
| 7: end if |
| 8: NearestNeighbor(); |
| 9: Extend(); |
| 10: if CollisionFree() then |
| 11: AddNewNode(); |
| 12: Distance; |
| 13: else |
| 14: ; |
| 15: continue; |
| 16: end if |
| 17: if Distance( then |
| 18: return T; |
| 19: end if |
| 20: end for |
| 21: return ; |
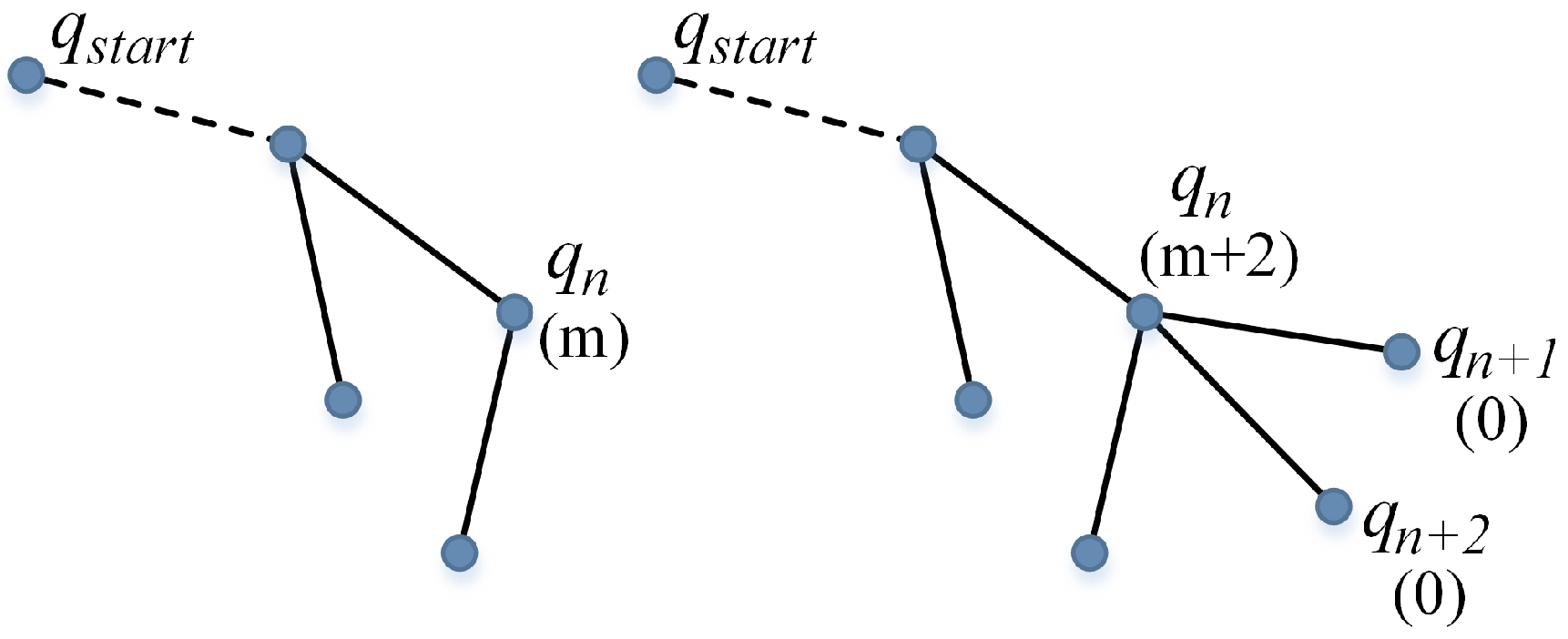
2.2. The Node Control Mechanism
| Algorithm 4 NC-RRT algorithm. |
| 1: InitTree(); |
| 2: ; |
| 3: ; |
| 4: 1; |
| 5: for 1 to n do |
| 6: RandomSample(i); |
| 7: if Distance then |
| 8: continue; |
| 9: end if |
| 10: LessThanControl(); |
| 11: NearestNeighbor(); |
| 12: Extend(); |
| 13: if CollisionFree() then |
| 14: AddNewNode(); |
| 15: ; |
| 16: BranchNodeUpdate(); |
| 17: Distance; |
| 18: ; |
| 19: else |
| 20: ; |
| 21: c; (c |
| 22: continue; |
| 23: end if |
| 24: if Distance( then |
| 25: return T; |
| 26: end if |
| 27: end for |
| 28: return ; |
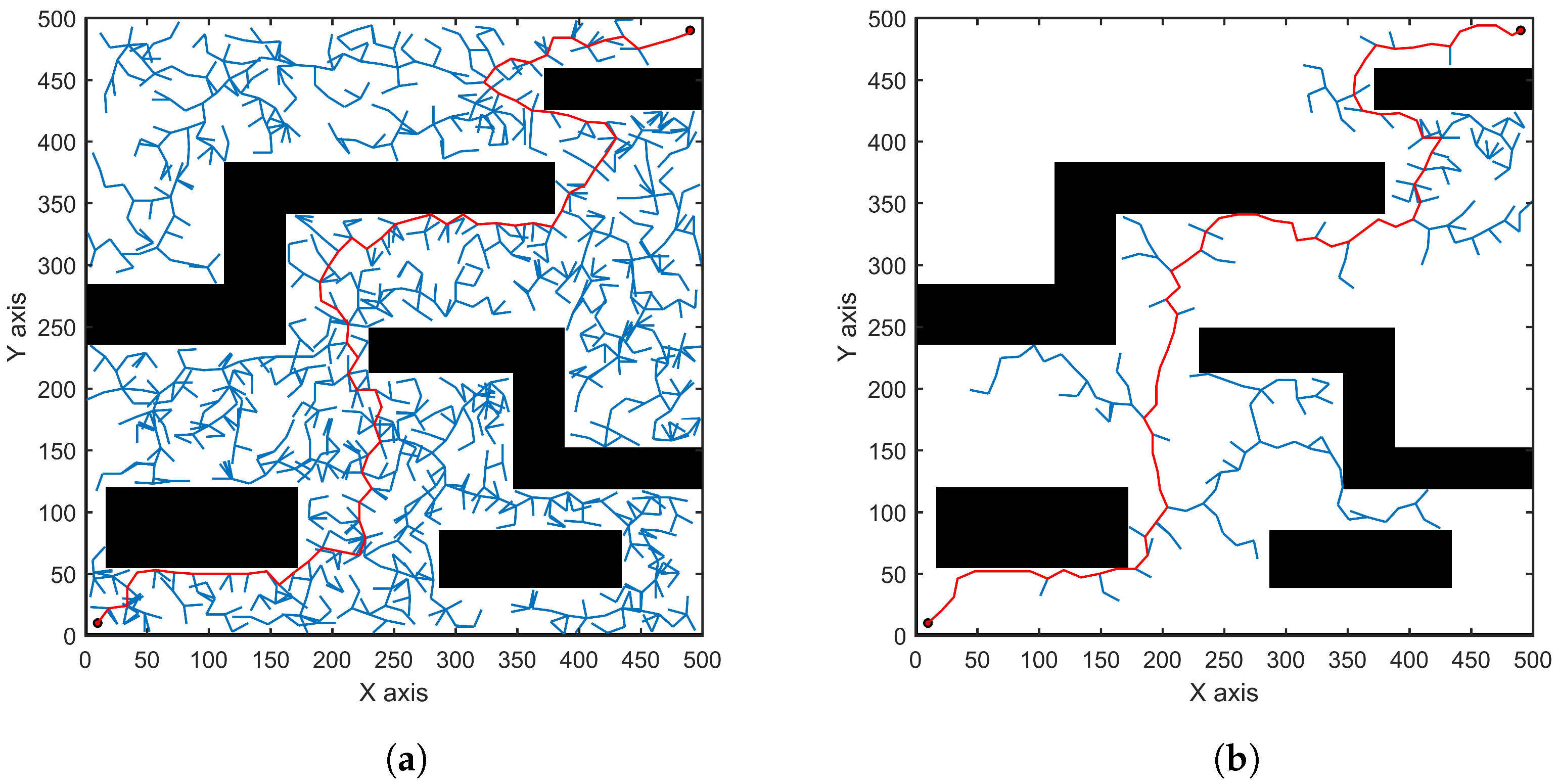
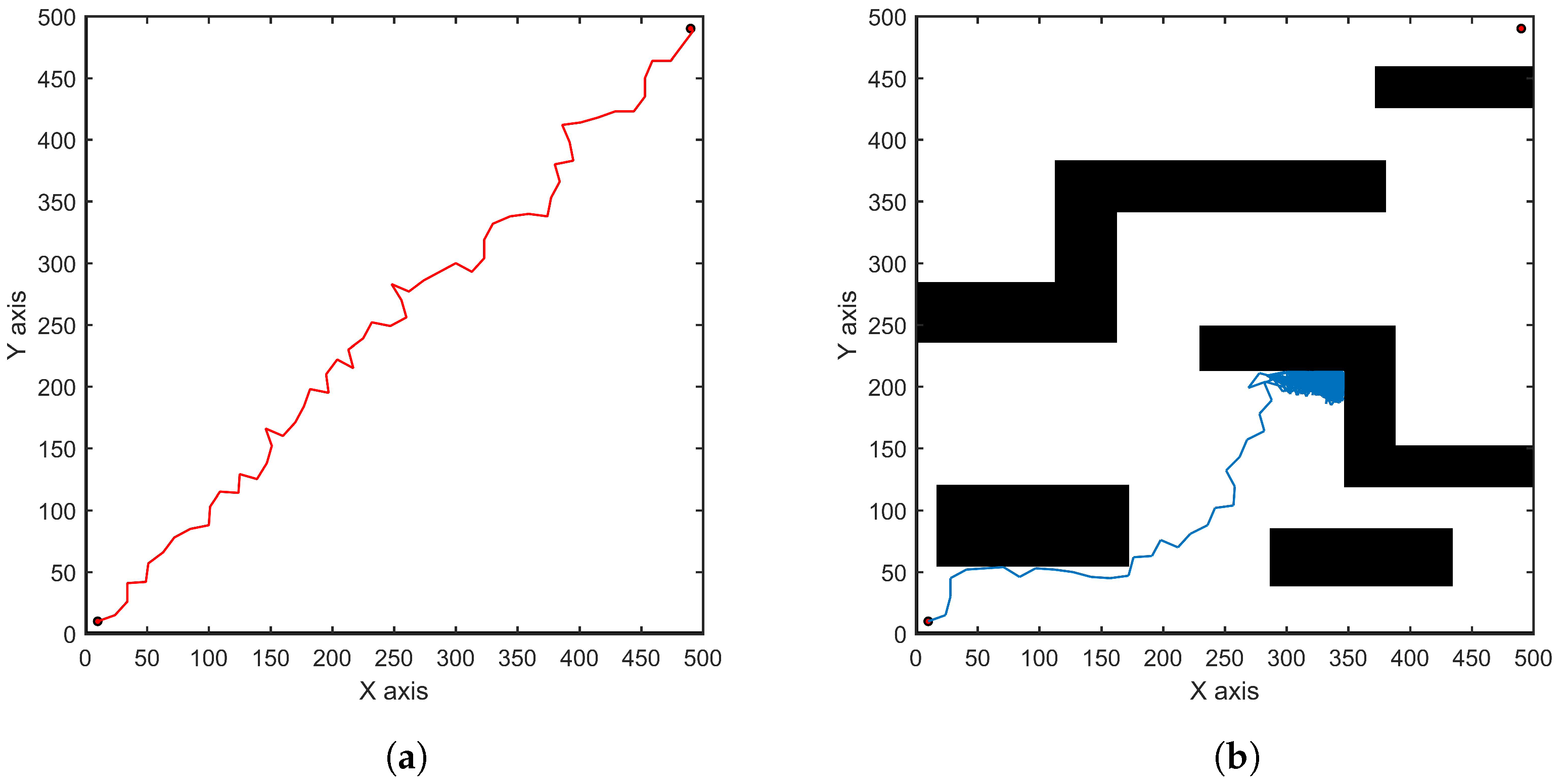
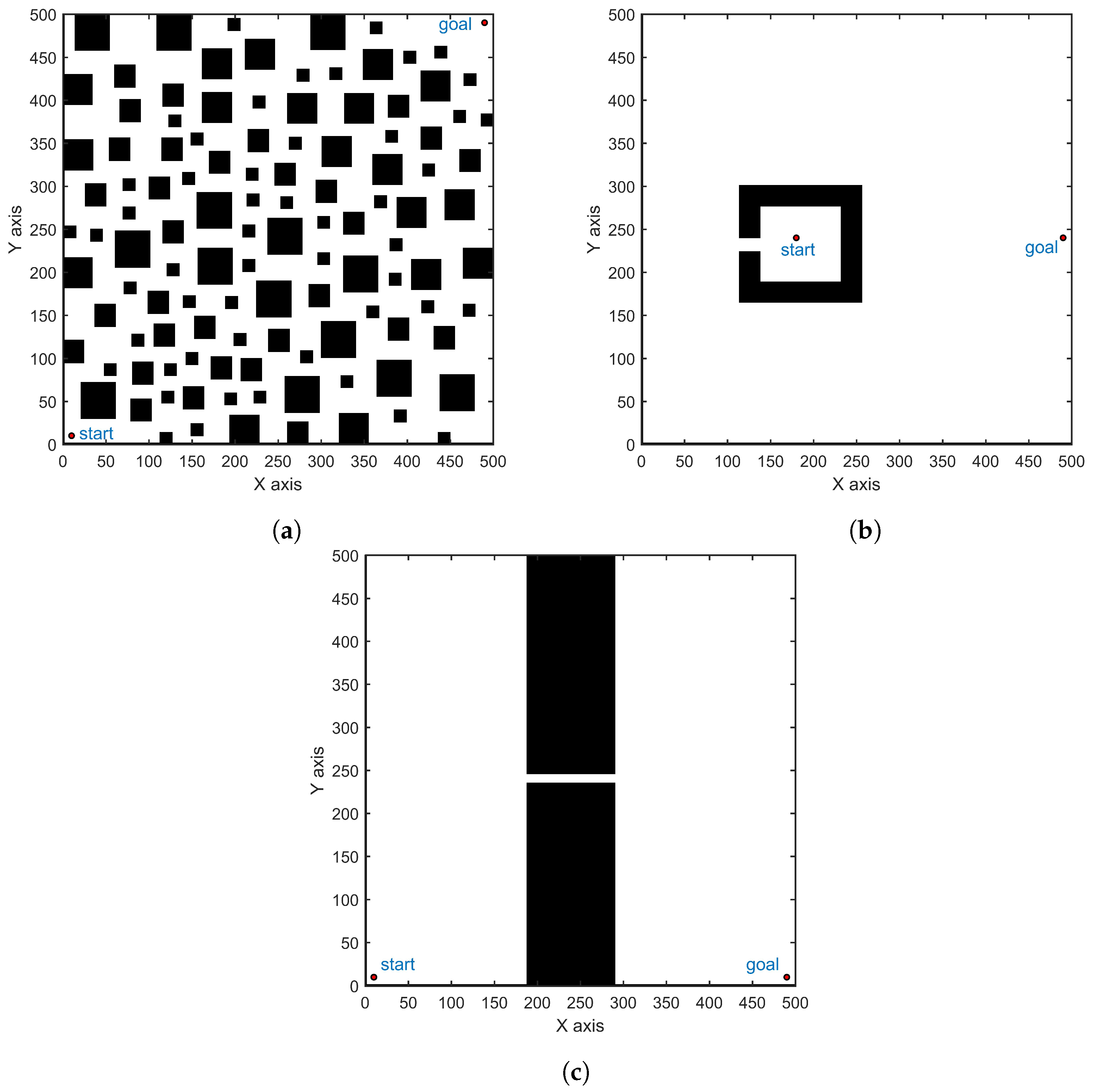
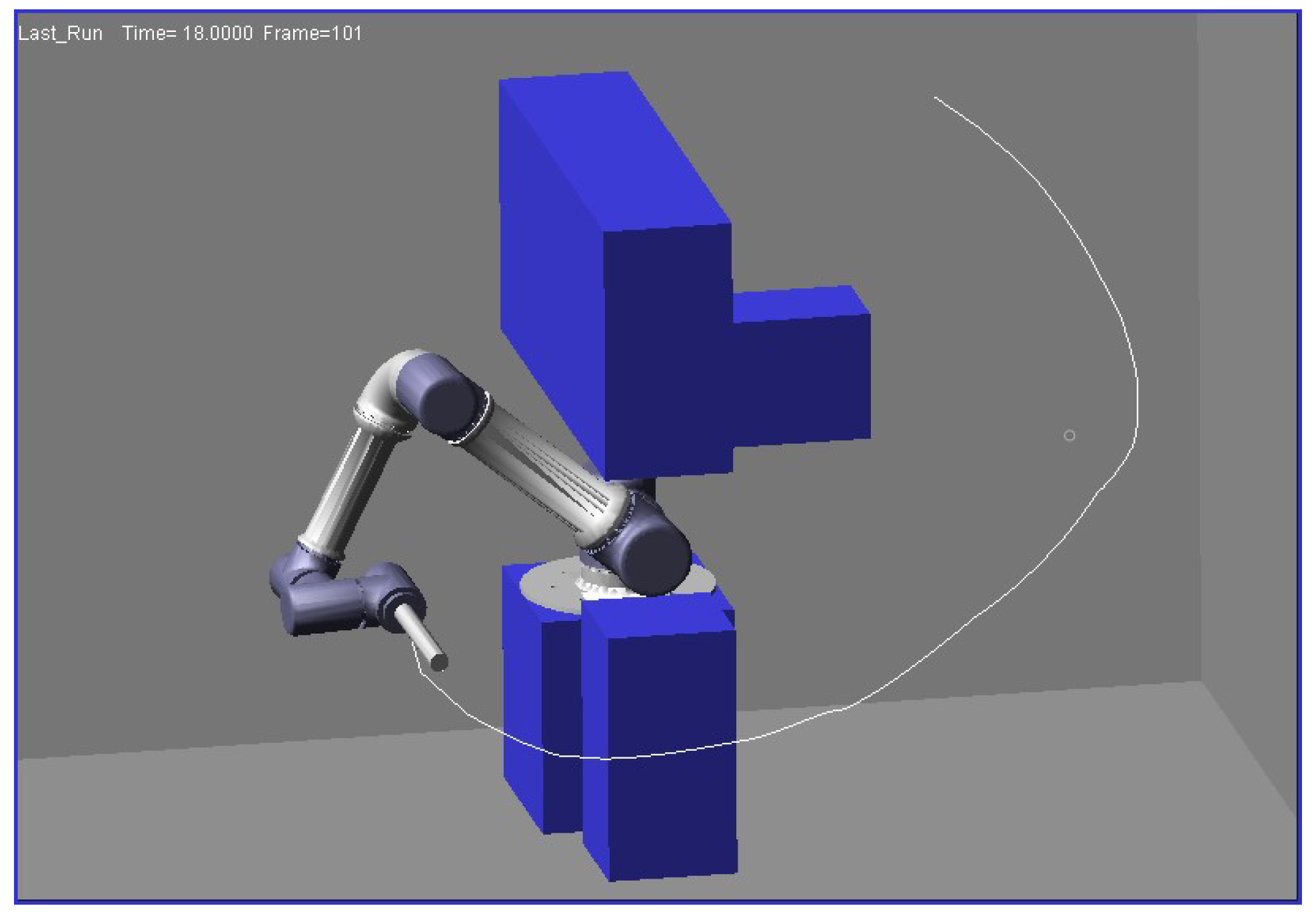
3. Simulation and Analysis
3.1. Simulations in a Two-Dimensional Environment
3.2. Simulation of the 6-DOF Manipulator
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| C-space | Configuration space |
| RRT | Rapidly-exploring Random Tree |
| PRM | Probabilistic Roadmap Method |
| CSA-RRT | Gradually Changing the Sampling Area-RRT |
| NC-RRT | Node Control-RRT |
| DOF | Degree-Of-Freedom |
References
- Barraquand, J.; Kavraki, L.; Latombe, J.C.; Motwani, R.; Li, T.Y.; Raghavan, P. A random sampling scheme for path planning. Int. J. Robot. Res. 1997, 16, 759–774. [Google Scholar] [CrossRef]
- Hsu, D.; Latombe, J.C.; Kurniawati, H. On the probabilistic foundations of probabilistic roadmap planning. Int. J. Robot. Res. 2006, 25, 627–643. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-exploring random trees: A new tool for path planning. Comput. Sci. Dept. Oct. 1998, 98. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.35.1853 (accessed on 19 February 2020).
- Amato, N.M.; Wu, Y. A randomized roadmap method for path and manipulation planning. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 1, pp. 113–120. [Google Scholar]
- Kavraki, L.E.; Svestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M. Sampling-based robot motion planning: A review. IEEE Access 2014, 2, 56–77. [Google Scholar] [CrossRef]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The robot that won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.; Dolan, J.; Duggins, D.; Galatali, T.; Geyer, C.; et al. Autonomous driving in urban environments: Boss and the urban challenge. In The DARPA Urban Challenge; Springer: Berlin, Germany, 2009; pp. 1–59. [Google Scholar]
- Yang, K.; Sukkarieh, S. An analytical continuous-curvature path-smoothing algorithm. IEEE Trans. Robot. 2010, 26, 561–568. [Google Scholar] [CrossRef]
- Wei, K.; Ren, B. A method on dynamic path planning for robotic manipulator autonomous obstacle avoidance based on an improved RRT algorithm. Sensors 2018, 18, 571. [Google Scholar] [CrossRef] [PubMed]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Nasir, J.; Islam, F.; Malik, U.; Ayaz, Y.; Hasan, O.; Khan, M.; Muhammad, M.S. RRT*-SMART: A rapid convergence implementation of RRT. Int. J. Adv. Robot. Syst. 2013, 10, 299. [Google Scholar] [CrossRef]
- Qureshi, A.H.; Iqbal, K.F.; Qamar, S.M.; Islam, F.; Ayaz, Y.; Muhammad, N. Potential guided directional-RRT* for accelerated motion planning in cluttered environments. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; pp. 519–524. [Google Scholar]
- Weghe, M.V.; Ferguson, D.; Srinivasa, S.S. Randomized path planning for redundant manipulators without inverse kinematics. In Proceedings of the 2007 7th IEEE-RAS International Conference on Humanoid Robots, Pittsburgh, PA, USA, 29 November–1 December 2007; pp. 477–482. [Google Scholar]
- Kuffner, J.J.; LaValle, S.M. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the 2000 ICRA, Millennium Conference, IEEE International Conference on Robotics and Automation, Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 995–1001. [Google Scholar]
- Kang, G.; Kim, Y.B.; Lee, Y.H.; Oh, H.S.; You, W.S.; Choi, H.R. Sampling-based motion planning of manipulator with goal-oriented sampling. Intell. Serv. Robot. 2019, 12, 265–273. [Google Scholar] [CrossRef]
- Burns, B.; Brock, O. Single-query motion planning with utility-guided random trees. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3307–3312. [Google Scholar]
- Kim, D.H.; Choi, Y.S.; Kim, S.H.; Wu, J.; Yuan, C.; Luo, L.P.; Lee, J.Y.; Han, C.S. Adaptive rapidly-exploring random tree for efficient path planning of high-degree-of-freedom articulated robots. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 3361–3367. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Zheng, J.; Yu, J. Path Planning of Industrial Robot Based on Improved RRT Algorithm in Complex Environments. IEEE Access 2018, 6, 53296–53306. [Google Scholar] [CrossRef]
- Boor, V.; Overmars, M.H.; Van Der Stappen, A.F. The Gaussian sampling strategy for probabilistic roadmap planners. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; pp. 1018–1023. [Google Scholar]
- Sun, Z.; Hsu, D.; Jiang, T.; Kurniawati, H.; Reif, J.H. Narrow passage sampling for probabilistic roadmap planning. IEEE Trans. Robot. 2005, 21, 1105–1115. [Google Scholar]
- Zhong, C.; Liu, H. A region-specific hybrid sampling method for optimal path planning. Int. J. Adv. Robot. Syst. 2016, 13, 71. [Google Scholar] [CrossRef]
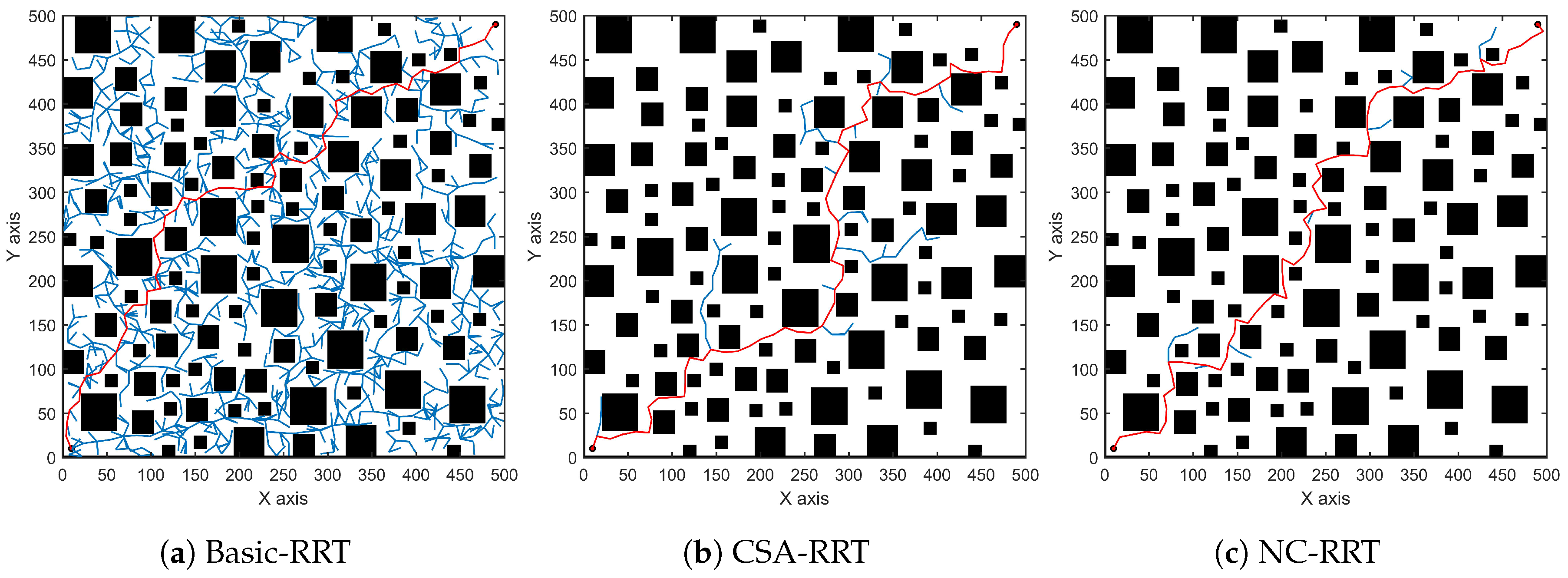
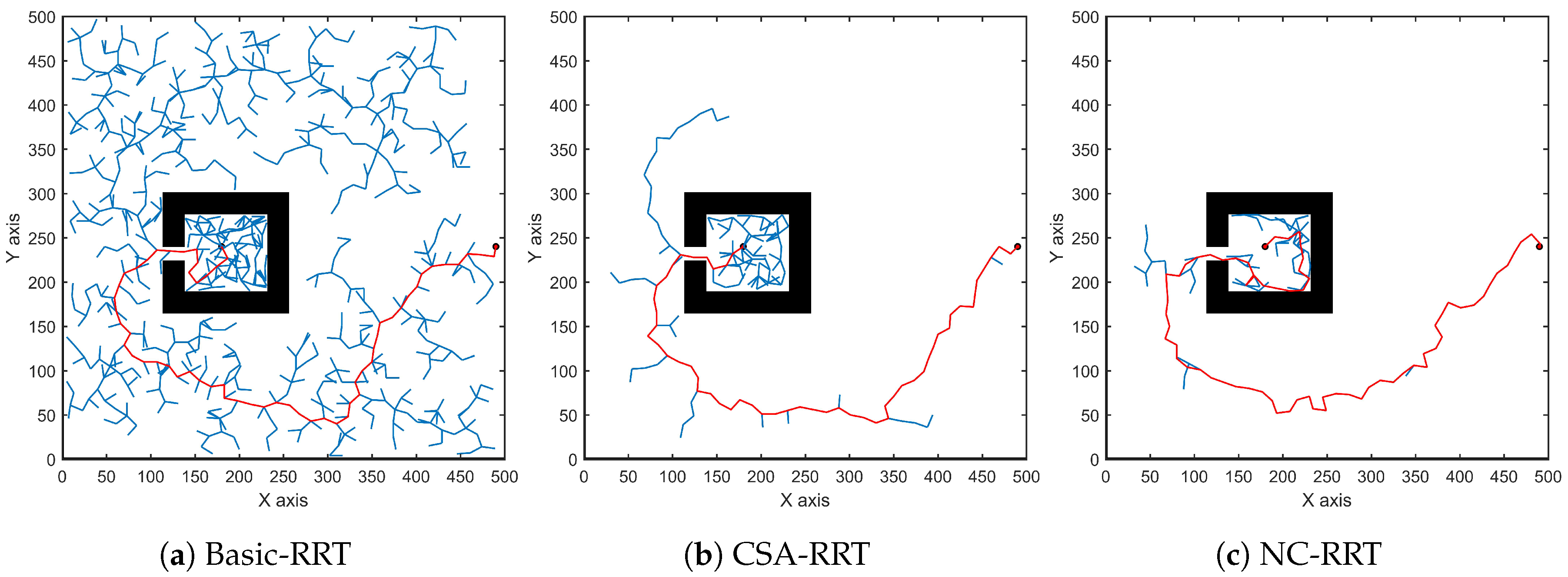
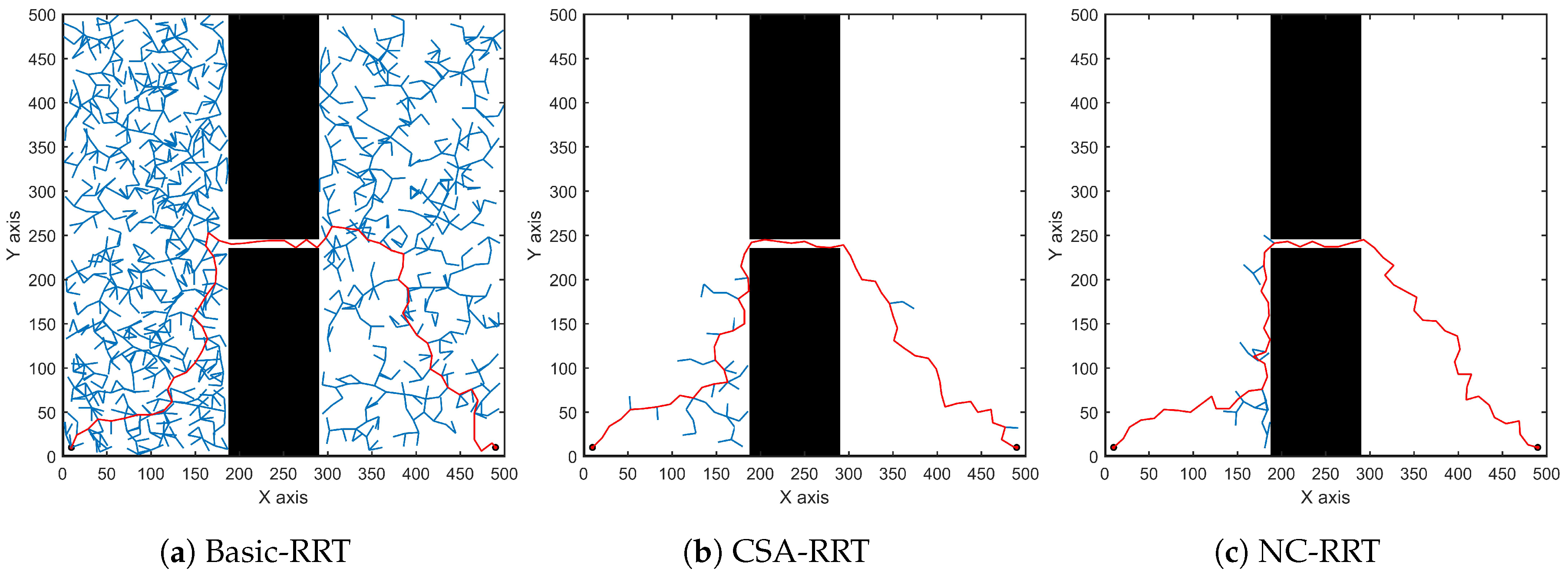
| Algorithm | Average Computational Time (s) | Average Number of Nodes in the Tree | Average Number of Collision Detections | Average Path Length | The Success Rate of the Algorithm |
|---|---|---|---|---|---|
| Basic-RRT | 0.463 | 844.520 | 38,026 | 954.369 | 96% |
| CSA-RRT | 0.058 | 92.900 | 4860.1 | 915.982 | 100% |
| NC-RRT | 0.055 | 82.860 | 3941.7 | 977.667 | 100% |
| Algorithm | Average Computational Time (s) | Average Number of Nodes in the Tree | Average Number of Collision Detections | Average Path Length | The Success Rate of the Algorithm |
|---|---|---|---|---|---|
| Basic-RRT | 0.471 | 928.680 | 35,821 | 865.236 | 84% |
| CSA-RRT | 0.118 | 122.909 | 9705.3 | 805.751 | 88% |
| NC-RRT | 0.159 | 126.817 | 9214.6 | 992.595 | 88% |
| Algorithm | Average Computational Time (s) | Average Number of Nodes in the Tree | Average Number of Collision Detections | Average Path Length | The Success Rate of the Algorithm |
|---|---|---|---|---|---|
| Basic-RRT | 0.550 | 1145.600 | 40,159 | 871.825 | 78% |
| CSA-RRT | 0.106 | 172.732 | 8867.2 | 868.609 | 82% |
| NC-RRT | 0.117 | 126.245 | 6746.4 | 942.615 | 98% |
| Algorithm | Basic-RRT | CSA-RRT | NC-RRT |
|---|---|---|---|
| Average computational time (s) | 3.658 | 1.541 | 1.469 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Luo, X.; Han, B.; Chen, Y.; Liang, G.; Zheng, K. Collision-Free Path Planning Method for Robots Based on an Improved Rapidly-Exploring Random Tree Algorithm. Appl. Sci. 2020, 10, 1381. https://doi.org/10.3390/app10041381
Wang X, Luo X, Han B, Chen Y, Liang G, Zheng K. Collision-Free Path Planning Method for Robots Based on an Improved Rapidly-Exploring Random Tree Algorithm. Applied Sciences. 2020; 10(4):1381. https://doi.org/10.3390/app10041381
Chicago/Turabian StyleWang, Xinda, Xiao Luo, Baoling Han, Yuhan Chen, Guanhao Liang, and Kailin Zheng. 2020. "Collision-Free Path Planning Method for Robots Based on an Improved Rapidly-Exploring Random Tree Algorithm" Applied Sciences 10, no. 4: 1381. https://doi.org/10.3390/app10041381
APA StyleWang, X., Luo, X., Han, B., Chen, Y., Liang, G., & Zheng, K. (2020). Collision-Free Path Planning Method for Robots Based on an Improved Rapidly-Exploring Random Tree Algorithm. Applied Sciences, 10(4), 1381. https://doi.org/10.3390/app10041381





