Basic Analysis of Uncertainty Sources in the CFD Simulation of a Shell-and-Tube Latent Thermal Energy Storage Unit
Abstract
1. Introduction
2. Materials and Methods
2.1. Set-Up
2.2. Boundary and Initial Conditions
2.3. Numerical Model
2.4. Mesh and Solver
2.5. Sensitivity Analysis
3. Results
3.1. Validation and Independency Studies
3.2. Sensitivity Analysis
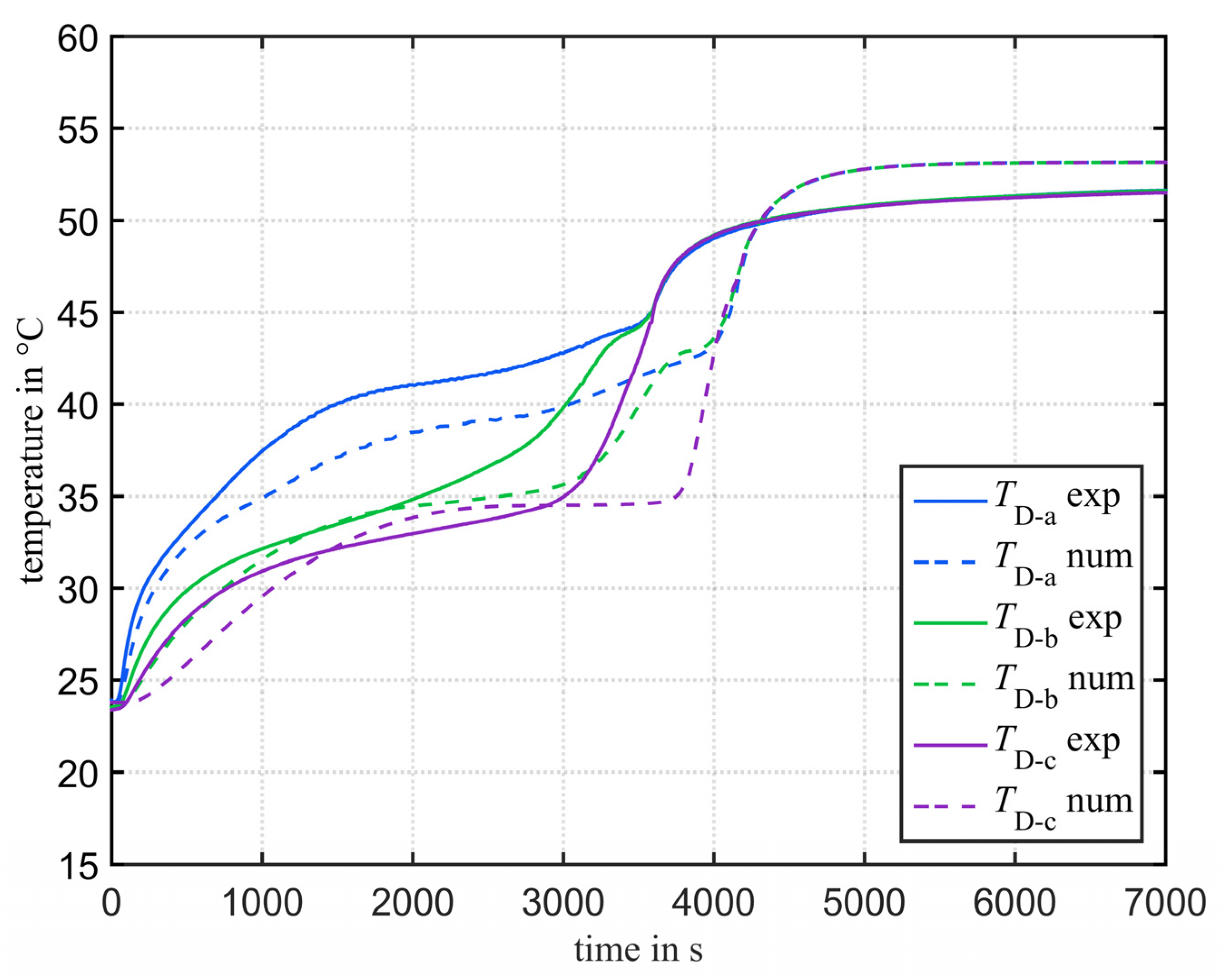
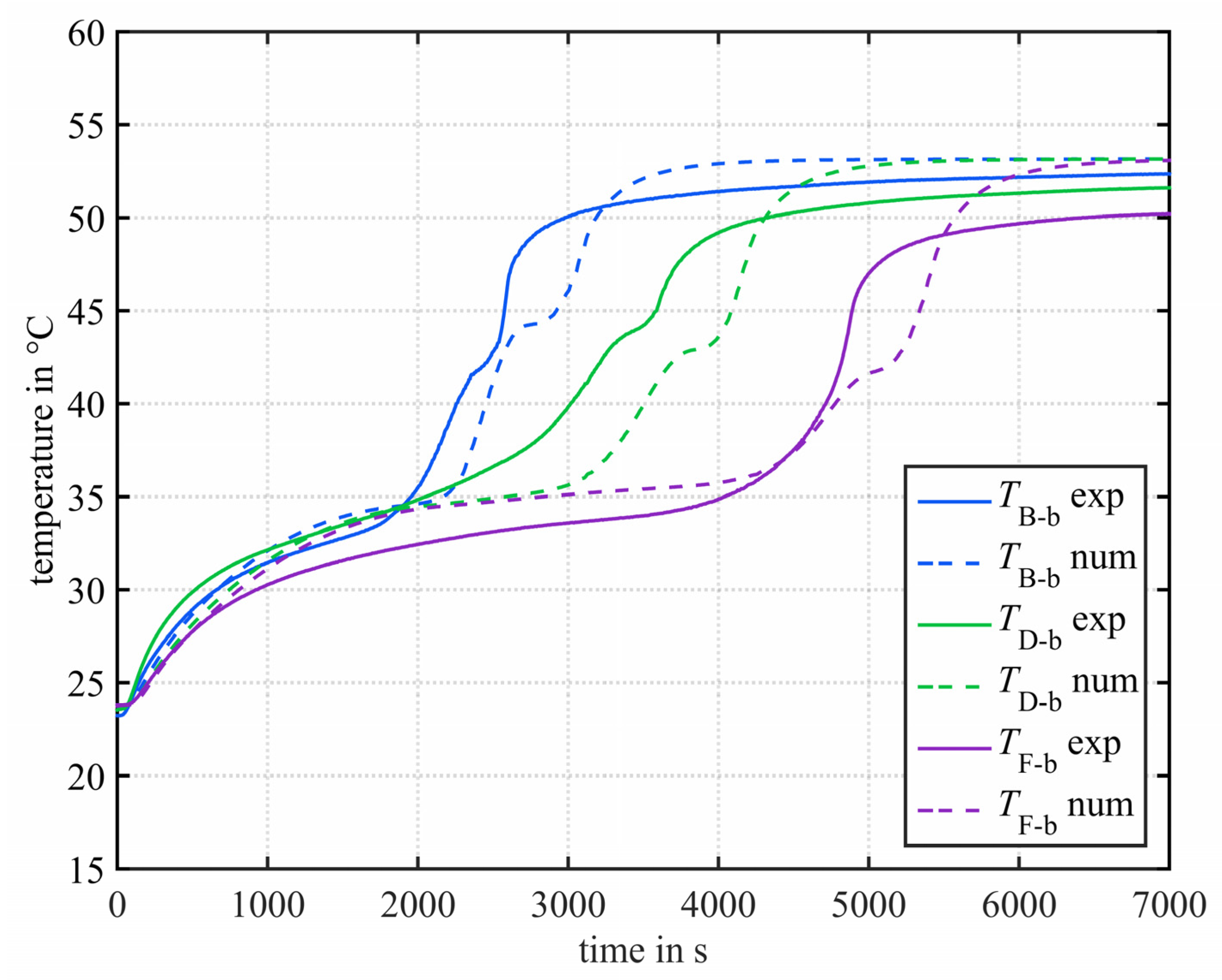
3.2.1. Temperature Measuring Position
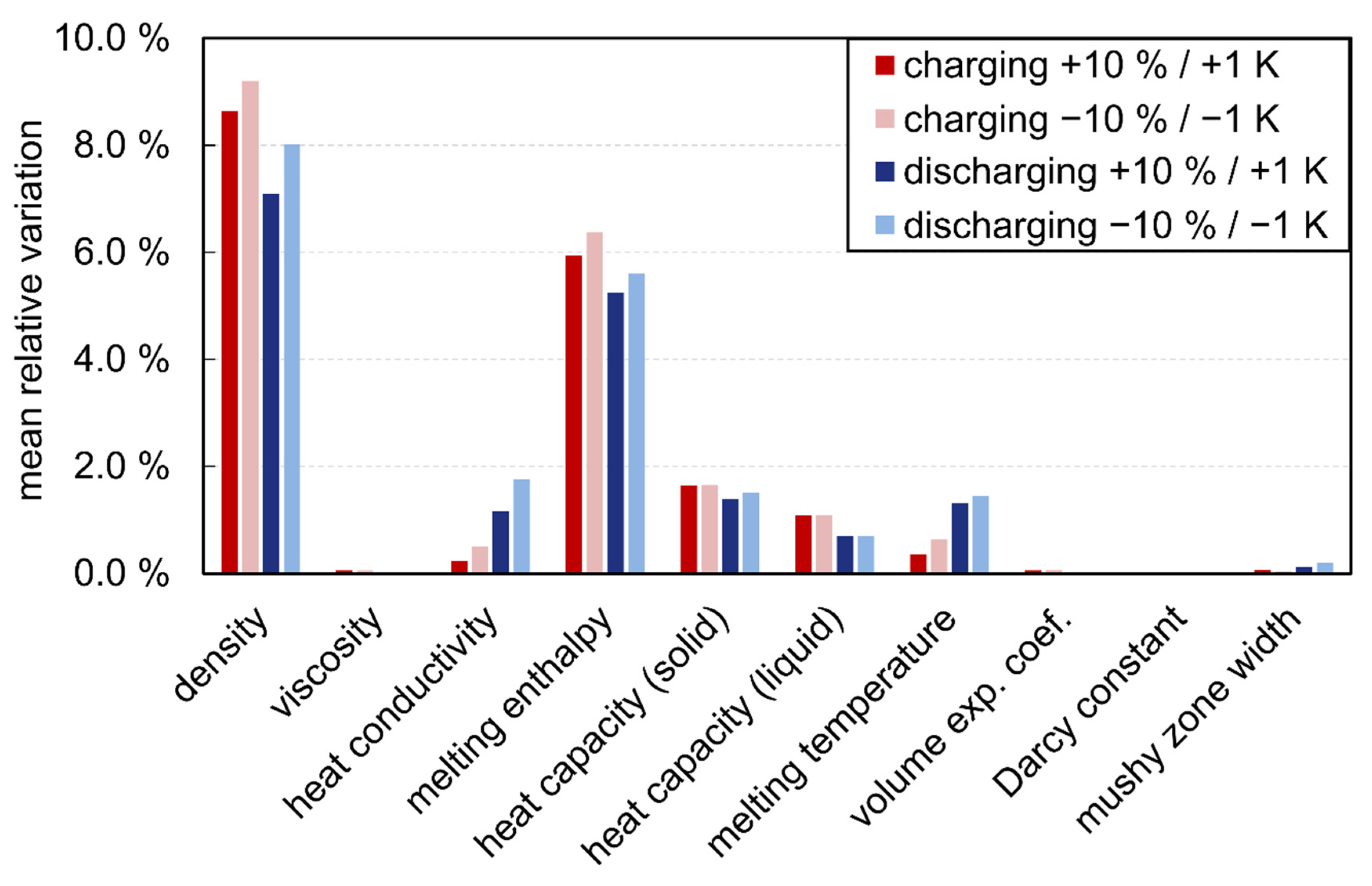
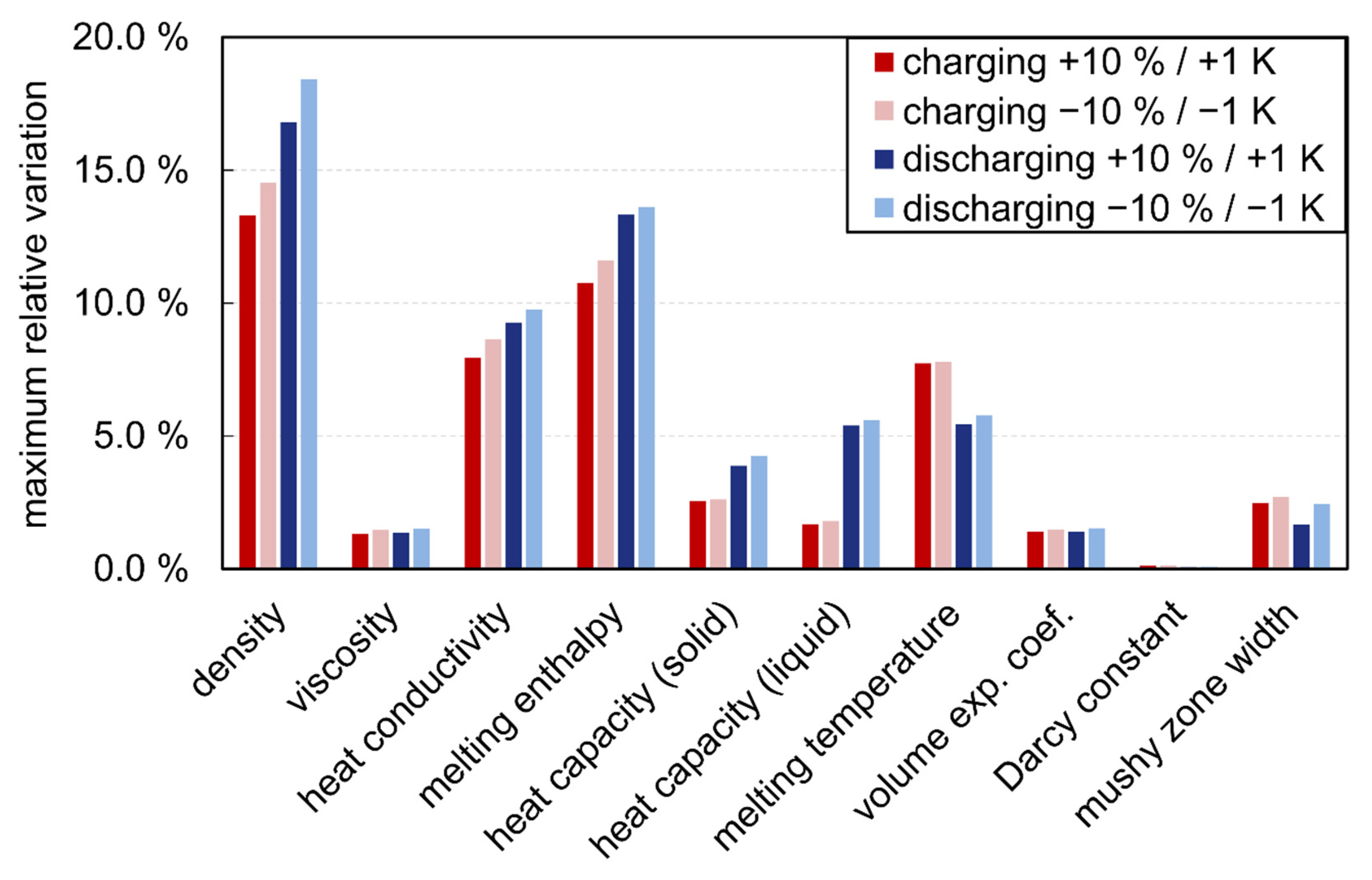
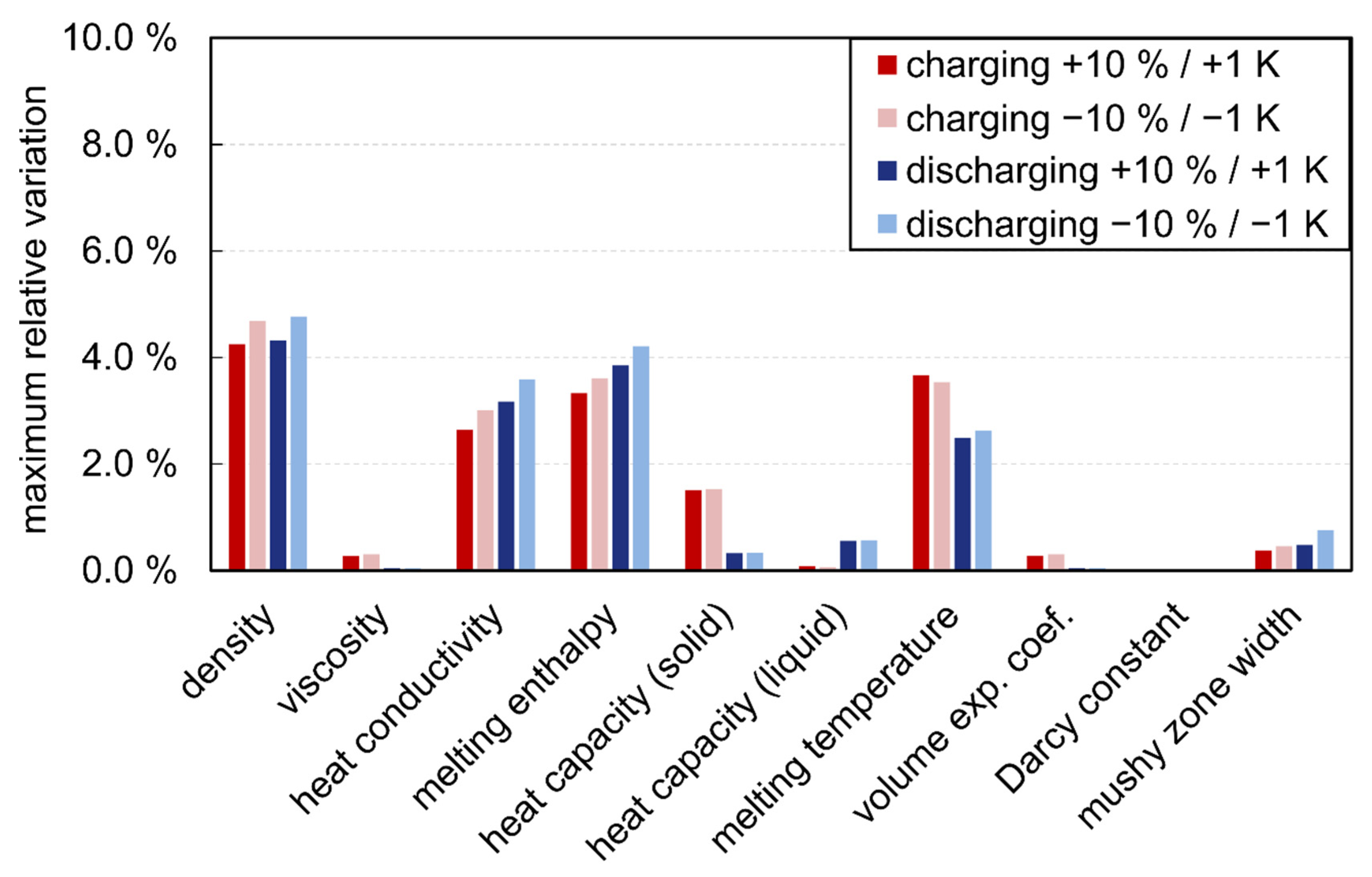
3.2.2. Material Properties
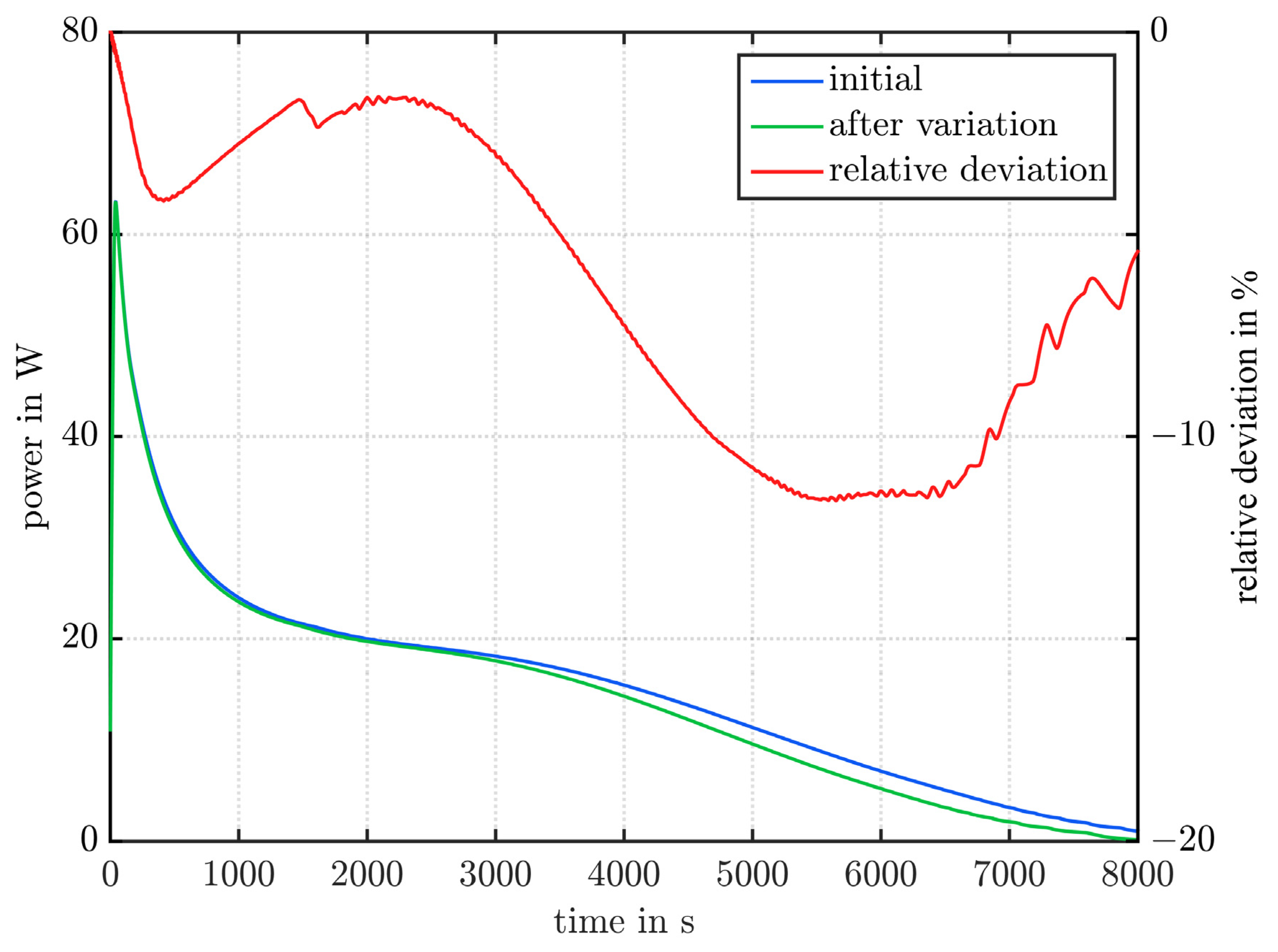
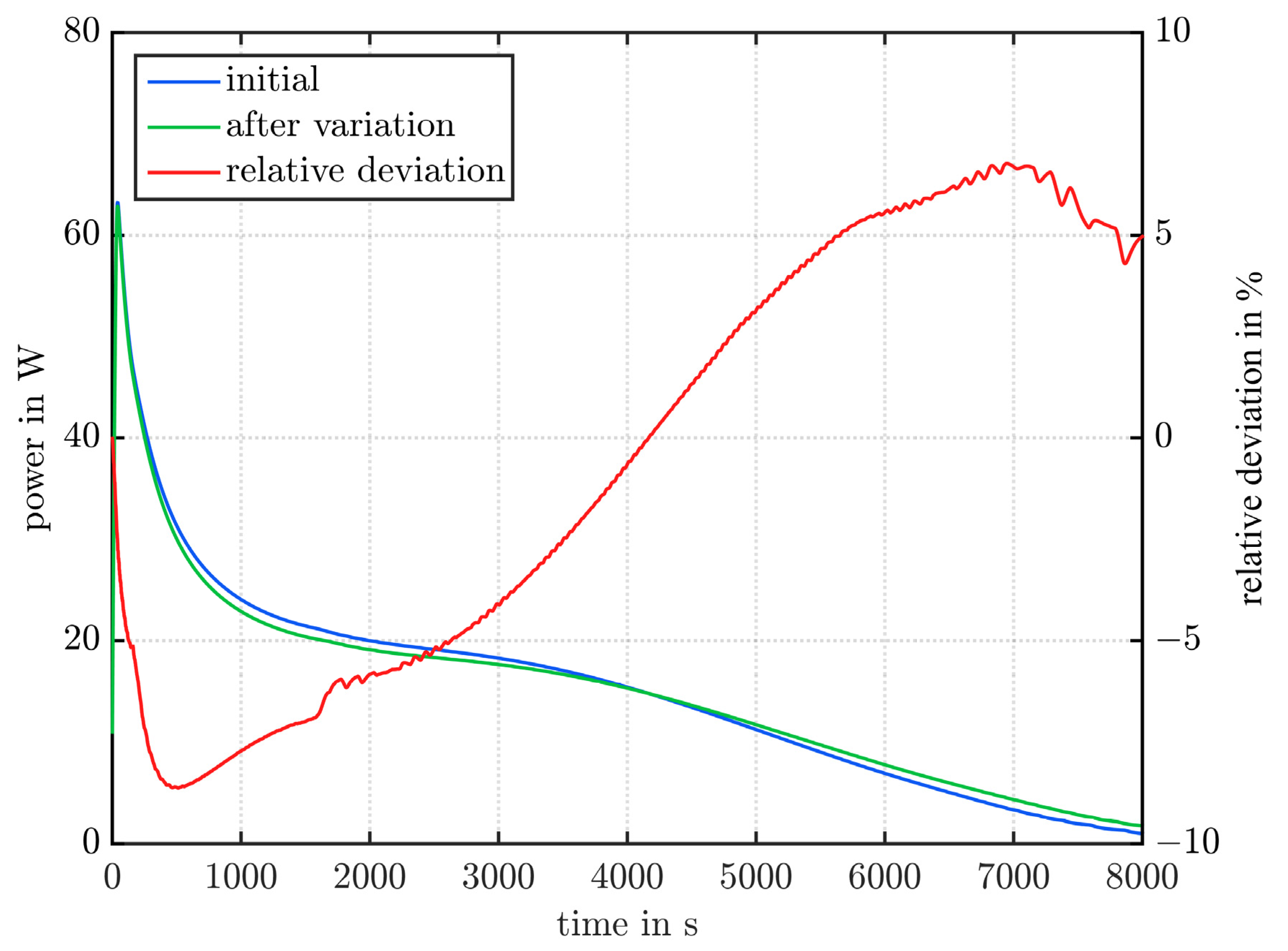
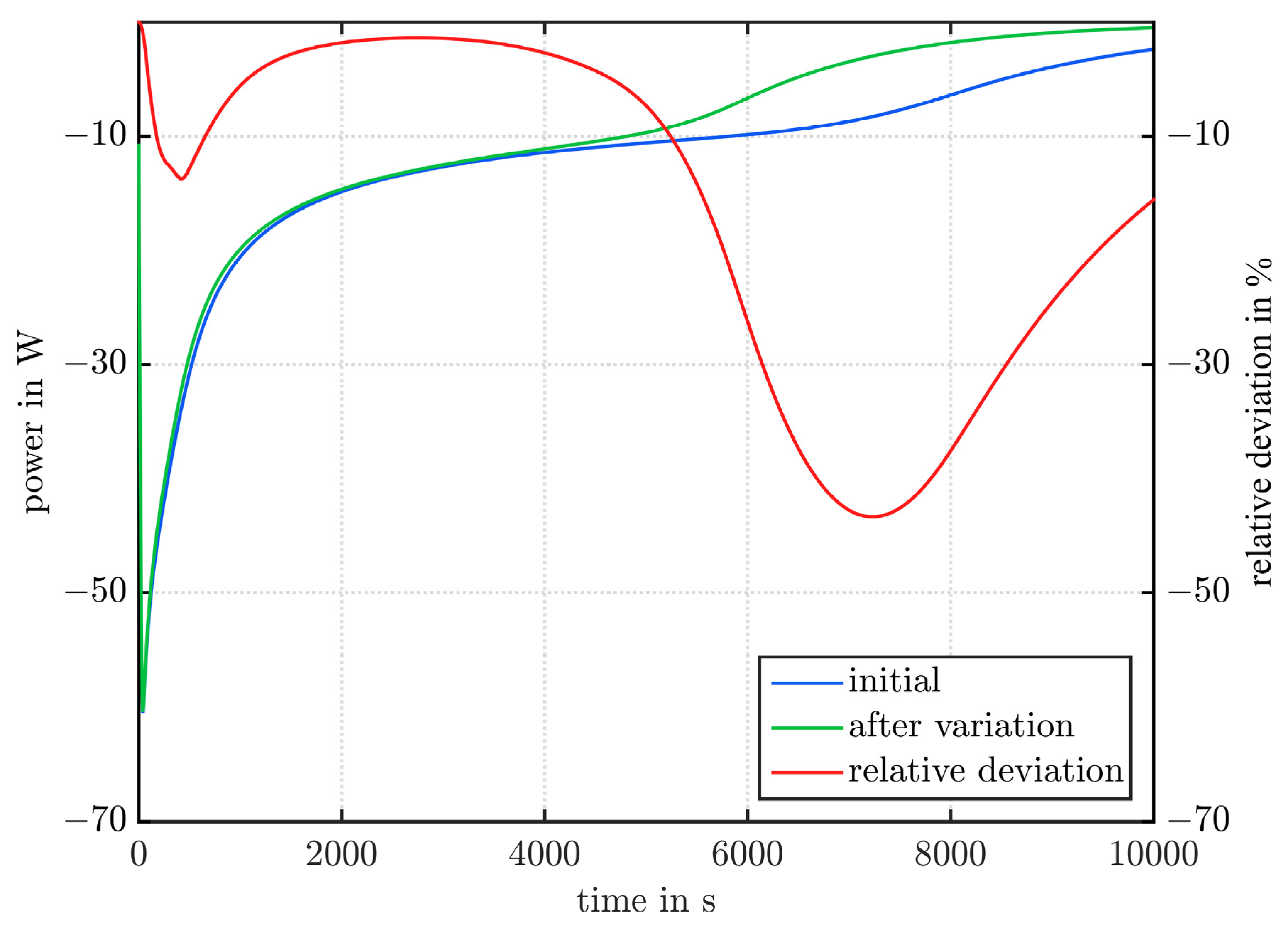
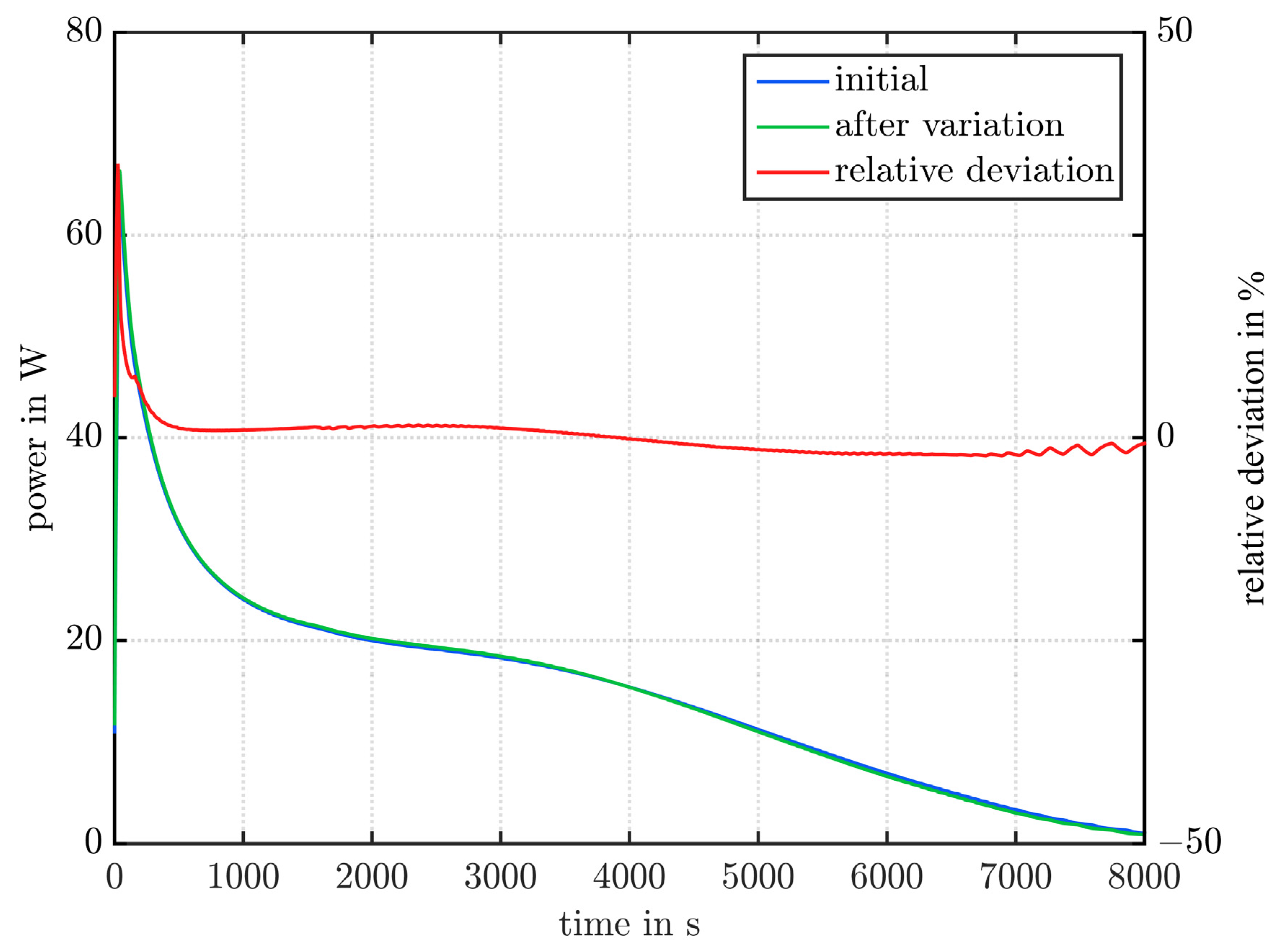
- Material properties that have no, or only little effect, if they are varied like indicated here: only has an influence that is always below 1% (maximum of 0.12%). Here, one has to keep in mind that is varied by several orders of magnitude in literature, and not only by ±10%.
- Material properties that have an influence on the power and the global liquid fraction, but none on the mean power (i.e., the total heat transferred): the material properties and mainly influence the maximum deviations and not the mean power. The reason why also has a slight influence on the average output is that the storage system can still absorb or release a certain amount of sensible heat at the end of charging and discharging.
- Material properties that also influence the mean power (i.e., the total heat transferred): all remaining material properties ( ) also affect the mean power when varied, but and only slightly.
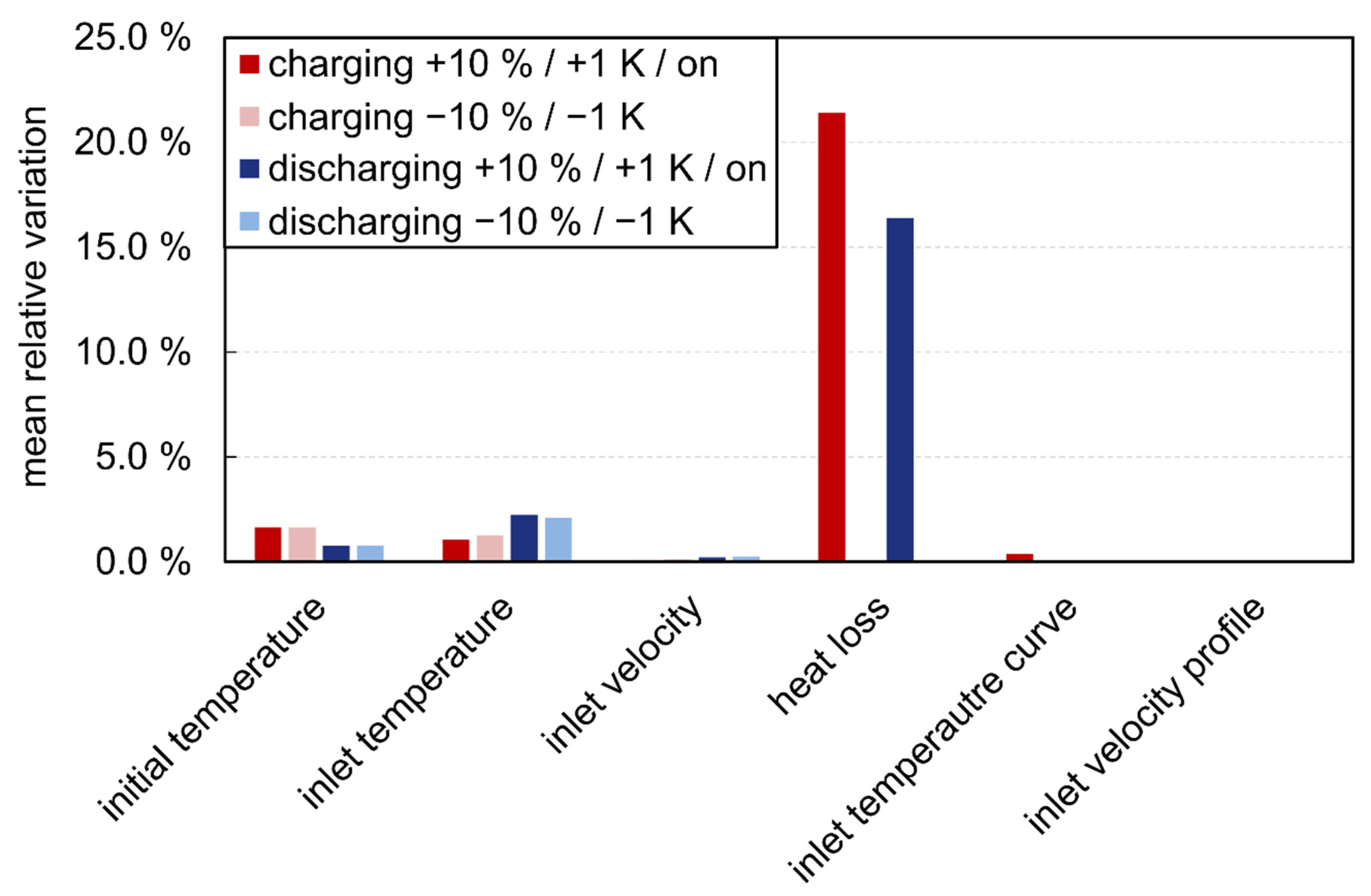
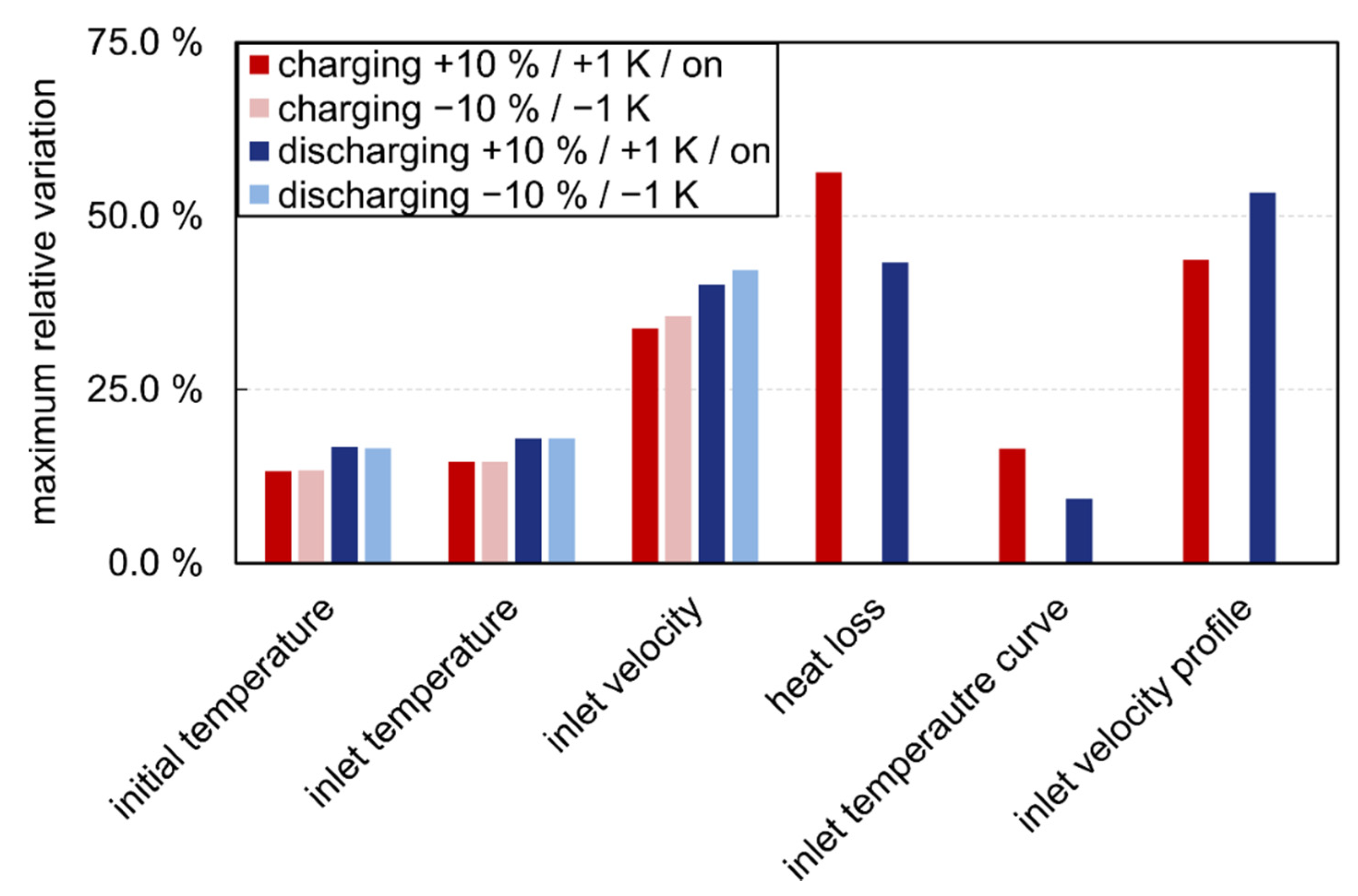
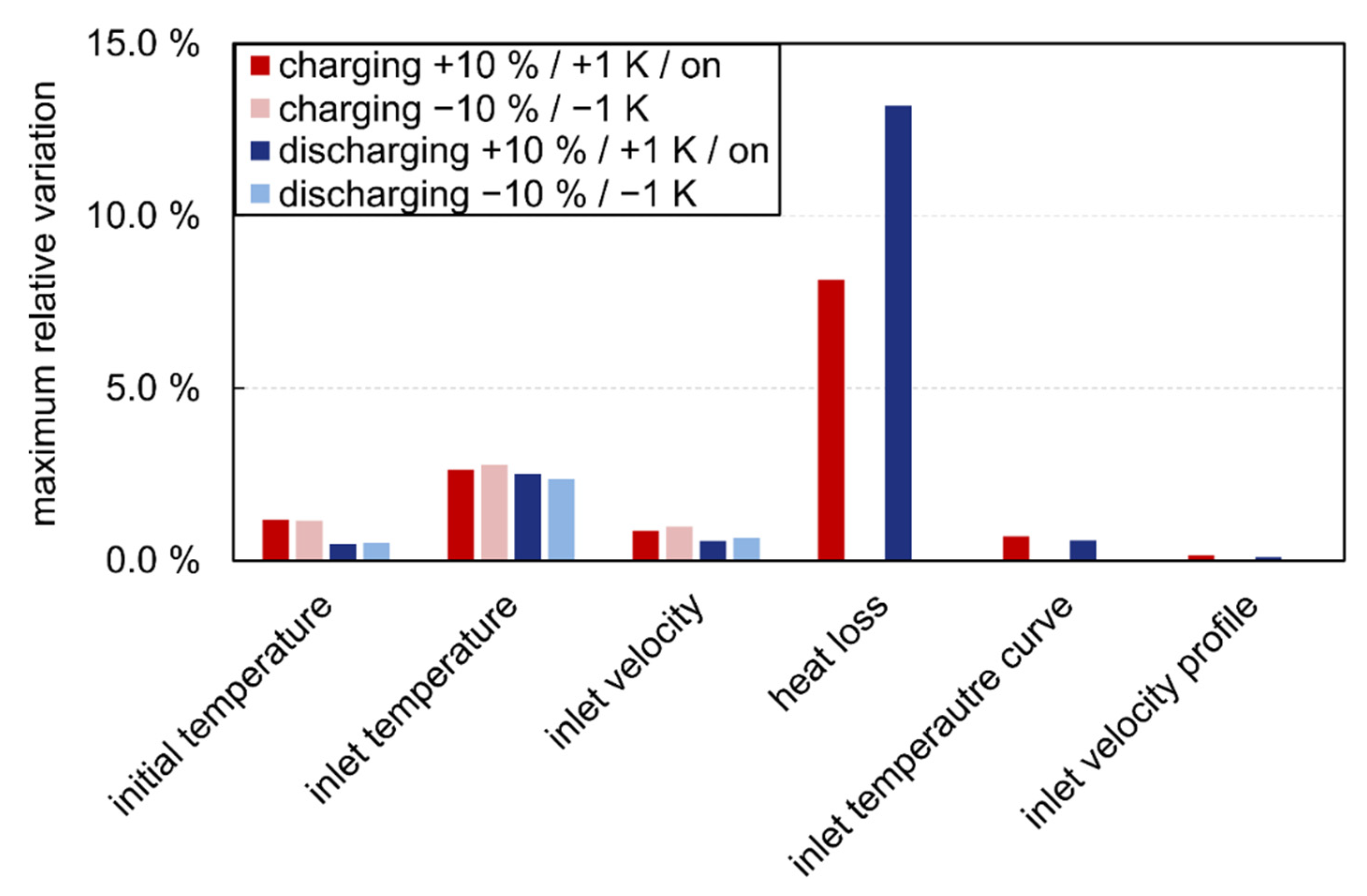
3.2.3. Boundary and Initial Conditions
4. Comparison with Previous Studies
5. Conclusions
- The variation of the material properties had a very large effect on the power and the global liquid fraction. In conclusion, uncertainties in the material properties may affect the results of a CFD simulation of a LTESS significantly.
- The material properties can be subdivided into three groups:
- ○
- Material properties that have no or only little effect: only has an influence that is always below 1% (maximum of 0.12%), but one has to keep in mind that it is varied by several orders of magnitude in literature.
- ○
- Material properties that have an influence on the power and the global liquid fraction slope, but none on the mean power: the material properties and mainly influence the maximum deviations and not the mean power.
- ○
- Material properties that also influence the mean power: all remaining material properties ( ) also affect the mean power when varied, but and only slightly.
- (up to 21.4%), (up to 9.2%) and (up to 6.4%) have the largest influence on the mean power.
- The ranking of the parameters and the magnitude of the influence is sometimes distinctively different in studies found in literature.
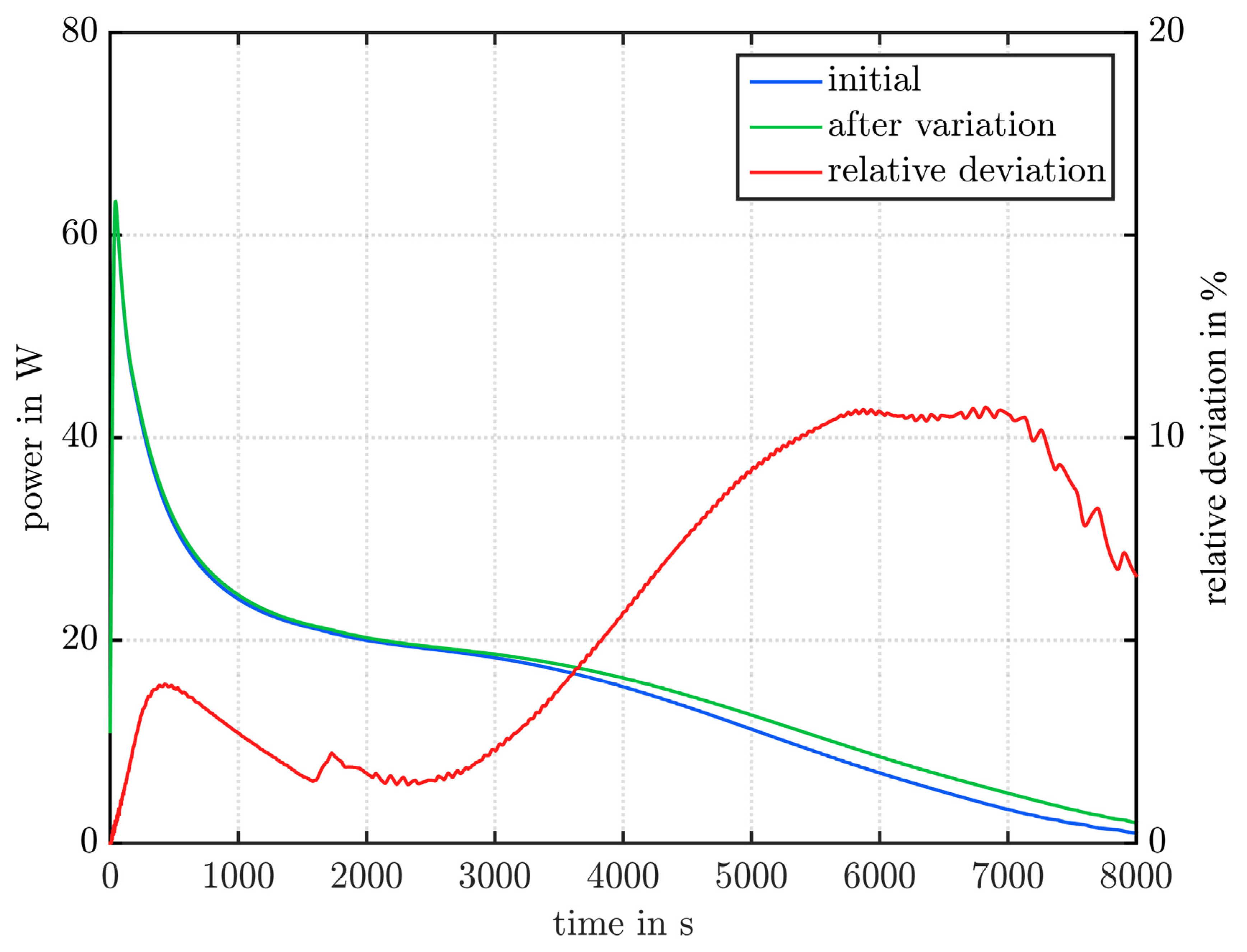
- Comparing the maximum deviation of the power can be misleading as the deviation may only occur as a short peak, and has no effect on the overall performance.
- For the investigated storage configuration and orientation, a radial variation of the temperature measurement position had a much higher impact than a vertical variation. A displacement of the measuring point in radial direction by already led to a maximum deviation in the measured temperature of more than 5 K.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| lateral Surface of the storage unit | ||
| specific heat capacity | ||
| large constant in the Darcy term | ||
| small constant in the Darcy term | ||
| Darcy term | ||
| air channel thickness | ||
| gravitational acceleration | ||
| specific enthalpy | ||
| specific latent heat of fusion | ||
| pressure | ||
| heat flux | ||
| thermal resistance | ||
| temperature | ||
| mushy zone width | ||
| time | ||
| overall heat transfer coefficient | ||
| velocity | ||
| velocity vector | ||
| volume flow | ||
| variable | ||
| deviation | ||
| Greek symbols | ||
| convective heat transfer coefficient | ||
| global liquid fraction | ||
| thermal expansion coefficient | ||
| thermal conductivity | ||
| stress tensor (without pressure) | ||
| dynamic viscosity | ||
| density | ||
| Subscripts | ||
| reference point | ||
| ambient | ||
| charging | ||
| temporal curve | ||
| discharging | ||
| extern | ||
| Heat Transfer Fluid | ||
| inner | ||
| inlet | ||
| initial | ||
| liquid, liquidus | ||
| heat loss | ||
| melting | ||
| maximum | ||
| mean | ||
| Plexiglas | ||
| spatial profile | ||
| reference case/simulation | ||
| solid, solidus | ||
| variation | ||
| wall | ||
| related to the variable y | ||
| Abbreviations | ||
| abs | absolute value | |
| CFD | Computational Fluid Dynamics | |
| DSC | Differential Scanning Calorimetry | |
| HTF | Heat Transfer Fluid | |
| LTESS | Latent Thermal Energy Storage System | |
| max | maximum value | |
| PCM | Phase Change Material | |
| PISO | Pressure-Implicit with Splitting of Operators | |
| PRESTO! | PREssure STaggering Option | |
| QUICK | Quadratic Upstream Interpolation for Convective Kinematics | |
| SIMPLE | Semi-Implicit Method for Pressure Linked Equations | |
| VVM | Variable Viscosity Method |
Appendix A
| Subfield | Parameter | Value |
|---|---|---|
| solution method | pressure-velocity coupling | PISO extrapolated |
| discretization (pressure) | PRESTO! | |
| discretization (momentum) | QUICK | |
| discretization (energy) | QUICK | |
| discretization (time) | first order implicit | |
| residuals | continuity | |
| x-velocity | ||
| y-velocity | ||
| energy | ||
| simulation parameter | time step | 0.2 s |
| 0.001 |
| Point B-b | Point D-a | Point D-b | Point D-c | Point F-b | Mean | Unit | ||
|---|---|---|---|---|---|---|---|---|
| radial +1 mm | mean | −0.33 | −0.67 | −0.38 | −0.21 | −0.41 | −0.40 | K |
| maximum | 4.30 | 2.24 | 2.84 | 5.21 | 2.16 | 3.35 | K | |
| standard deviation | 0.74 | 0.84 | 0.62 | 0.70 | 0.49 | 0.68 | K | |
| radial −1 mm | mean | 0.38 | 1.01 | 0.44 | 0.26 | 0.49 | 0.52 | K |
| maximum | 3.61 | 3.10 | 2.09 | 4.32 | 1.47 | 2.92 | K | |
| standard deviation | 0.74 | 1.10 | 0.60 | 0.68 | 0.48 | 0.72 | K | |
| vertical +1 mm | mean | 0.03 | 0.02 | 0.02 | 0.02 | 0.03 | 0.03 | K |
| maximum | 0.32 | 0.33 | 0.30 | 0.44 | 0.37 | 0.35 | K | |
| standard deviation | 0.07 | 0.05 | 0.05 | 0.07 | 0.06 | 0.06 | K | |
| vertical −1 mm | mean | −0.03 | −0.02 | −0.02 | −0.02 | −0.03 | −0.03 | K |
| maximum | 0.32 | 0.33 | 0.30 | 0.44 | 0.37 | 0.35 | K | |
| standard deviation | 0.07 | 0.05 | 0.05 | 0.07 | 0.06 | 0.06 | K |
| Charging | Discharging | |||
|---|---|---|---|---|
| +10% +1 K on | −10% −1 K off | +10% +1 K on | −10% −1 K off | |
| 8.64% | −9.20% | 7.09% | −8.02% | |
| 1.64% | −1.65% | 1.39% | −1.51% | |
| 1.08% | −1.09% | 0.70% | −0.70% | |
| 0.24% | −0.50% | 1.16% | −1.76% | |
| 5.94% | −6.37% | 5.24% | −5.60% | |
| −0.05% | 0.05% | 0.00% | 0.00% | |
| 0.05% | −0.06% | 0.00% | 0.00% | |
| −0.01% | 0.01% | 0.00% | 0.00% | |
| 0.36% | −0.63% | 1.31% | −1.45% | |
| −0.06% | 0.04% | 0.12% | −0.20% | |
| inlet velocity | 0.09% | −0.12% | 0.21% | −0.25% |
| initial temperature | −1.64% | 1.64% | 0.79% | −0.79% |
| inlet temperature | 1.05% | −1.27% | −2.23% | 2.10% |
| heat loss | 21.42% | − | −16.39% | − |
| inlet temperature curve | 0.40% | − | 0.06% | − |
| inlet velocity profile | 0.01% | − | −0.04% | − |

References
- Steinmann, W.-D.; Jockenhöfer, H.; Bauer, D. Thermodynamic Analysis of High-Temperature Carnot Battery Concepts. Energy Technol. 2020, 8, 1900895. [Google Scholar] [CrossRef]
- Mehling, H.; Cabeza, L.F. Heat and Cold Storage with PCM; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Faden, M.; Höhlein, S.; Wanner, J.; König-Haagen, A.; Brüggemann, D. Review of Thermophysical Property Data of Octadecane for Phase-Change Studies. Materials 2019, 12, 2974. [Google Scholar] [CrossRef] [PubMed]
- Dutil, Y.; Rousse, D.R.; Salah, N.B.; Lassue, S.; Zalewski, L. A review on phase-change materials: Mathematical modeling and simulations. Renew. Sustain. Energy Rev. 2011, 15, 112–130. [Google Scholar] [CrossRef]
- Voller, V.R.; Markatos, N.C.; Cross, M. Techniques for account for the moving interface in convection/diffusion phase change. In Numerical Methods in Thermal Problems; Lewis, R.W., Morgan, K., Eds.; Pineridge Press: Swansea, UK, 1985; pp. 595–609. [Google Scholar]
- Morgan, K. A numerical analysis of freezing and melting with convection. Comput. Methods Appl. Mech. Eng. 1981, 28, 275–284. [Google Scholar] [CrossRef]
- Gartling, D.K. Finite Element Analysis of Convection Heat Transfer Problems in Phase Change. In Computer Methods in Fluids; Morgan, K., Taylor, C., Brebbia, C.A., Eds.; Pentech: London, UK, 1980; pp. 257–284. [Google Scholar]
- Brent, A.D.; Voller, V.R.; Reid, K.J. Enthalpy-porosity technique for modeling convection-diffusion phase change: Application to the melting of a pure metal. Numer. Heat Transf. Part A Appl. 1988, 13, 297–318. [Google Scholar]
- Kheirabadi, A.C.; Groulx, D. The effect of the mushy-zone constant on simulated phase change heat transfer. In Proceedings of the CHT-15: 6th International Symposium on Advances in Computational Heat Transfer, Begell House, Danbury, CT, USA, 25–29 May 2015; p. 22. [Google Scholar]
- Beust, C.; Franquet, E.; Bédécarrats, J.-P.; Garcia, P.; Pouvreau, J. Influence of the modeling parameters on the numerical CFD simulation of a shell-and-tube latent heat storage system with circular fins. In SOLARPACES 2018: International Conference on Concentrating Solar Power and Chemical Energy Systems; AIP Publishing: Melville, NY, USA, 2019; p. 200007. [Google Scholar]
- Fadl, M.; Eames, P.C. Numerical investigation of the influence of mushy zone parameter Amush on heat transfer characteristics in vertically and horizontally oriented thermal energy storage systems. Appl. Therm. Eng. 2019, 151, 90–99. [Google Scholar] [CrossRef]
- Arena, S.; Casti, E.; Gasia, J.; Cabeza, L.F.; Cau, G. Numerical simulation of a finned-tube LHTES system: Influence of the mushy zone constant on the phase change behaviour. Energy Procedia 2017, 126, 517–524. [Google Scholar] [CrossRef]
- Shmueli, H.; Ziskind, G.; Letan, R. Melting in a vertical cylindrical tube: Numerical investigation and comparison with experiments. Int. J. Heat Mass Transf. 2010, 53, 4082–4091. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Kleijn, C.R.; Richardson, I.M. Sensitivity of numerical predictions to the permeability coefficient in simulations of melting and solidification using the enthalpy-porosity method. Energies 2019, 12, 4360. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Hu, H.; Argyropoulos, S.A. Mathematical modelling of solidification and melting: A review. Model. Simul. Mater. Sci. Eng. 1996, 4, 371–396. [Google Scholar] [CrossRef]
- Voller, V.R.; Swaminathan, C.R.; Thomas, B.G. Fixed grid techniques for phase change problems: A review. Int. J. Numer. Methods Eng. 1990, 30, 875–898. [Google Scholar] [CrossRef]
- Voller, V.R. An overview of numerical methods for solving phase change problems. In Advances in Numerical Heat Transfer; Minkowycz, W.J., Sparrow, E.M., Eds.; Taylor & Francis: New York, NY, USA, 1997; pp. 341–380. [Google Scholar]
- König-Haagen, A.; Franquet, E.; Faden, M.; Brüggemann, D. Influence of the convective energy formulation for melting problems with enthalpy methods. Int. J. Therm. Sci. 2020, 158, 106477. [Google Scholar] [CrossRef]
- Tittelein, P.; Gibout, S.; Franquet, E.; Johannes, K.; Zalewski, L.; Kuznik, F.; Dumas, J.-P.; Lassue, S.; Bédécarrats, J.-P.; David, D. Simulation of the thermal and energy behaviour of a composite material containing encapsulated-PCM: Influence of the thermodynamical modelling. Appl. Energy 2015, 140, 269–274. [Google Scholar] [CrossRef]
- König-Haagen, A.; Franquet, E.; Pernot, E.; Brüggemann, D. A comprehensive benchmark of fixed-grid methods for the modeling of melting. Int. J. Therm. Sci. 2017, 118, 69–103. [Google Scholar] [CrossRef]
- Galione, P.A.; Lehmkuhl, O.; Rigola, J.; Oliva, A. Fixed-grid numerical modeling of melting and solidification using variable thermo-physical properties—Application to the melting of n-Octadecane inside a spherical capsule. Int. J. Heat Mass Transf. 2015, 86, 721–743. [Google Scholar] [CrossRef]
- Ben-David, O.; Levy, A.; Mikhailovich, B.; Azulay, A. 3D numerical and experimental study of gallium melting in a rectangular container. Int. J. Heat Mass Transf. 2013, 67, 260–271. [Google Scholar] [CrossRef]
- Günther, E.; Hiebler, S.; Mehling, H.; Redlich, R. Enthalpy of phase change materials as a function of temperature: Required accuracy and suitable measurement methods. Int. J. Thermophys. 2009, 30, 1257–1269. [Google Scholar] [CrossRef]
- Arkar, C.; Medved, S. Influence of accuracy of thermal property data of a phase change material on the result of a numerical model of a packed bed latent heat storage with spheres. Thermochim. Acta 2005, 438, 192–201. [Google Scholar] [CrossRef]
- Feng, G.; Huang, K.; Xie, H.; Li, H.; Liu, X.; Liu, S.; Cao, C. DSC test error of phase change material (PCM) and its influence on the simulation of the PCM floor. Renew. Energy 2016, 87, 1148–1153. [Google Scholar] [CrossRef]
- Dolado, P.; Mazo, J.; Lázaro, A.; Marín, J.M.; Zalba, B. Experimental validation of a theoretical model: Uncertainty propagation analysis to a PCM-air thermal energy storage unit. Energy Build. 2012, 45, 124–131. [Google Scholar] [CrossRef]
- Mazo, J.; el Badry, A.T.; Carreras, J.; Delgado, M.; Boer, D.; Zalba, B. Uncertainty propagation and sensitivity analysis of thermo-physical properties of phase change materials (PCM) in the energy demand calculations of a test cell with passive latent thermal storage. Appl. Therm. Eng. 2015, 90, 596–608. [Google Scholar] [CrossRef]
- Soni, V.; Kumar, A.; Jain, V.K. Modeling of PCM melting: Analysis of discrepancy between numerical and experimental results and energy storage performance. Energy 2018, 150, 190–204. [Google Scholar] [CrossRef]
- Zsembinszki, G.; Moreno, P.; Solé, C.; Castell, A.; Cabeza, L.F. Numerical model evaluation of a PCM cold storage tank and uncertainty analysis of the parameters. Appl. Therm. Eng. 2014, 67, 16–23. [Google Scholar] [CrossRef]
- Longeon, M.; Soupart, A.; Fourmigué, J.-F.; Bruch, A.; Marty, P. Experimental and numerical study of annular PCM storage in the presence of natural convection. Appl. Energy 2013, 112, 175–184. [Google Scholar] [CrossRef]
- Rösler, F. Modellierung und Simulation der Phasenwechselvorgänge in Makroverkapselten Latenten Thermischen Speichern; Logos Verlag Berlin GmbH: Berlin, Germany, 2014. [Google Scholar]
- VDI. VDI-Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Voller, V.R.; Swaminathan, C.R. General source-based method for solidification phase change. Numer. Heat Transf. Part B Fundam. 1991, 19, 175–189. [Google Scholar] [CrossRef]
- Fluent, A. Ansys Fluent 15 User’s Guide; ANSYS: Canonsburg, PA, USA, 2013. [Google Scholar]
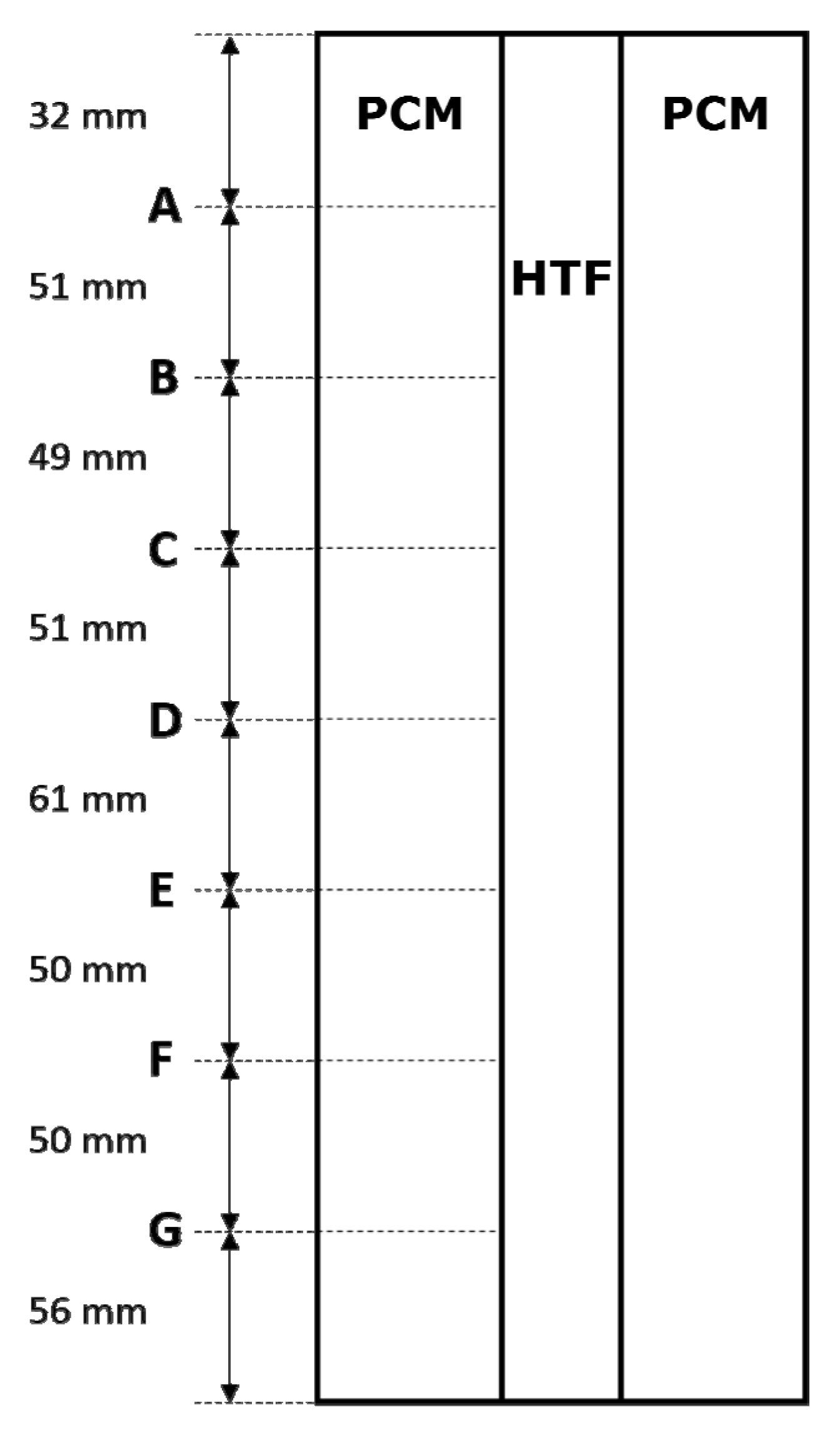
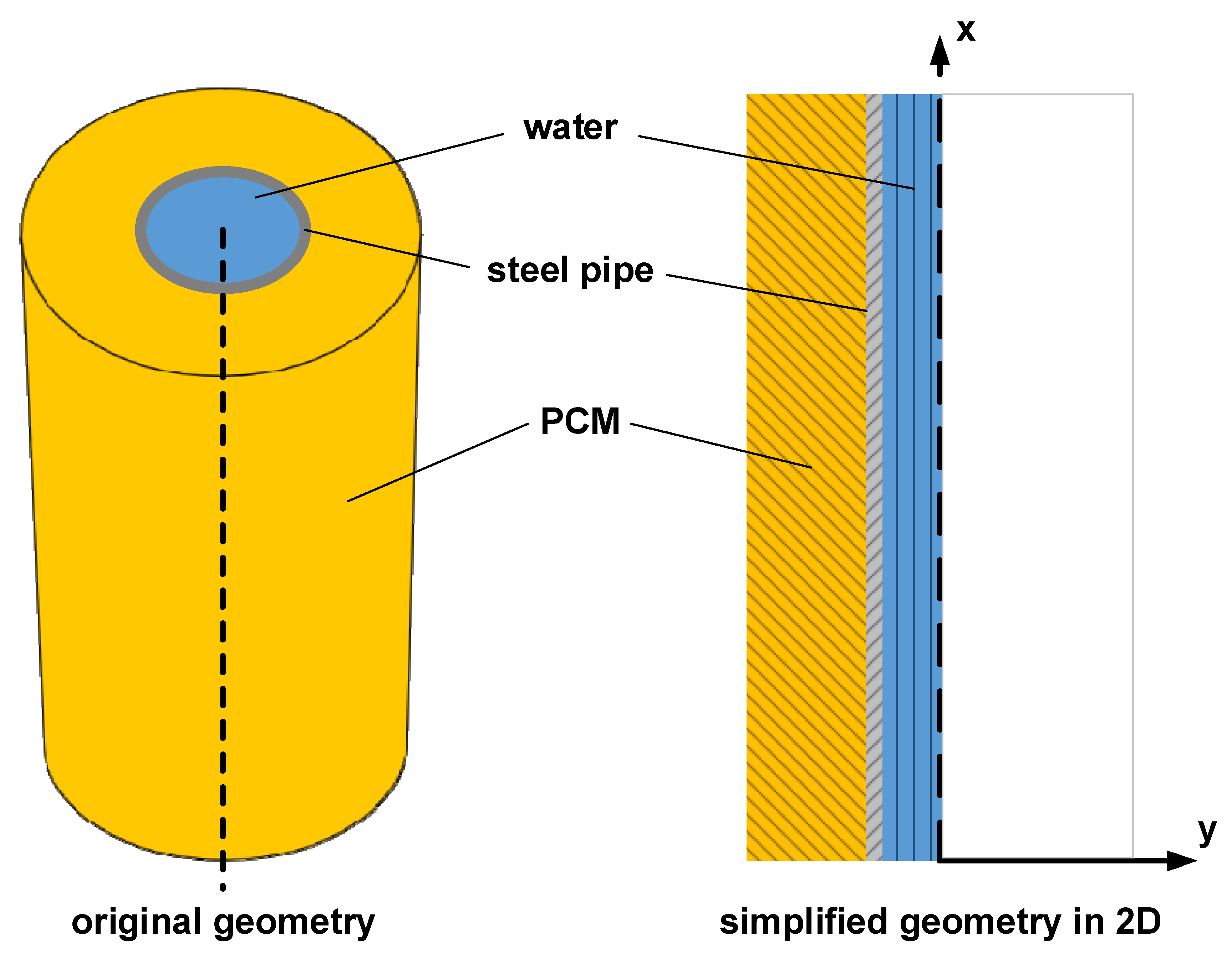


| Measuring Point Identifiers | Radius in mm | Height in mm |
|---|---|---|
| B-b | 16 | 317 |
| D-a | 13 | 217 |
| D-b | 16 | 217 |
| D-c | 19 | 217 |
| F-b | 16 | 106 |
| Physical Properties | Value | Unit | Source |
|---|---|---|---|
| 760 | [31] | ||
| 5.0 | [32] | ||
| 2.1 | [32] | ||
| 0.2 | [31] | ||
| 220 | [32] | ||
| 34.5 | [32] | ||
| 36.0 | [32] | ||
| see Equation (1) | own measurements | ||
| 0.001 | [31] |
| Variable | Value | Unit |
|---|---|---|
| 23.79 | ||
| 47.15 | ||
| 53.17 | ||
| 18.51 | ||
| 8000 | ||
| 10,000 | ||
| 0 |
| Material Properties, Initial and Boundary Conditions | Variation |
|---|---|
| on/off | |
| on/off | |
| on/off |
| Study | Output | 1. | 2. | 3. | 4. | 5. |
|---|---|---|---|---|---|---|
| Dolado et al. [27] | mean power deviation | |||||
| Zsembinszki et al. [30] | mean absolute power deviation | * | * | |||
| mean power deviation | ** | ** | *** | |||
| Mazo et al. [28] | saving in yearly energy consumption | |||||
| this study | mean power deviation | on/off | ||||
| maximum power deviation | on/off | On/off | ||||
| maximum global liquid fraction deviation | on/off |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
König-Haagen, A.; Mühlbauer, A.; Marquardt, T.; Caron-Soupart, A.; Fourmigué, J.-F.; Brüggemann, D. Basic Analysis of Uncertainty Sources in the CFD Simulation of a Shell-and-Tube Latent Thermal Energy Storage Unit. Appl. Sci. 2020, 10, 6723. https://doi.org/10.3390/app10196723
König-Haagen A, Mühlbauer A, Marquardt T, Caron-Soupart A, Fourmigué J-F, Brüggemann D. Basic Analysis of Uncertainty Sources in the CFD Simulation of a Shell-and-Tube Latent Thermal Energy Storage Unit. Applied Sciences. 2020; 10(19):6723. https://doi.org/10.3390/app10196723
Chicago/Turabian StyleKönig-Haagen, Andreas, Adam Mühlbauer, Tom Marquardt, Adèle Caron-Soupart, Jean-François Fourmigué, and Dieter Brüggemann. 2020. "Basic Analysis of Uncertainty Sources in the CFD Simulation of a Shell-and-Tube Latent Thermal Energy Storage Unit" Applied Sciences 10, no. 19: 6723. https://doi.org/10.3390/app10196723
APA StyleKönig-Haagen, A., Mühlbauer, A., Marquardt, T., Caron-Soupart, A., Fourmigué, J.-F., & Brüggemann, D. (2020). Basic Analysis of Uncertainty Sources in the CFD Simulation of a Shell-and-Tube Latent Thermal Energy Storage Unit. Applied Sciences, 10(19), 6723. https://doi.org/10.3390/app10196723





