Determination of Axial Force in Tie Rods of Historical Buildings Using the Model-Updating Technique
Abstract
1. Introduction
- The tie rods are generally located at elevated positions;
- High-accuracy displacement sensors should be used due to small vertical displacements. These should be placed on a previously-determined referent location;
- The strain gauge installation can be complicated at elevated positions.
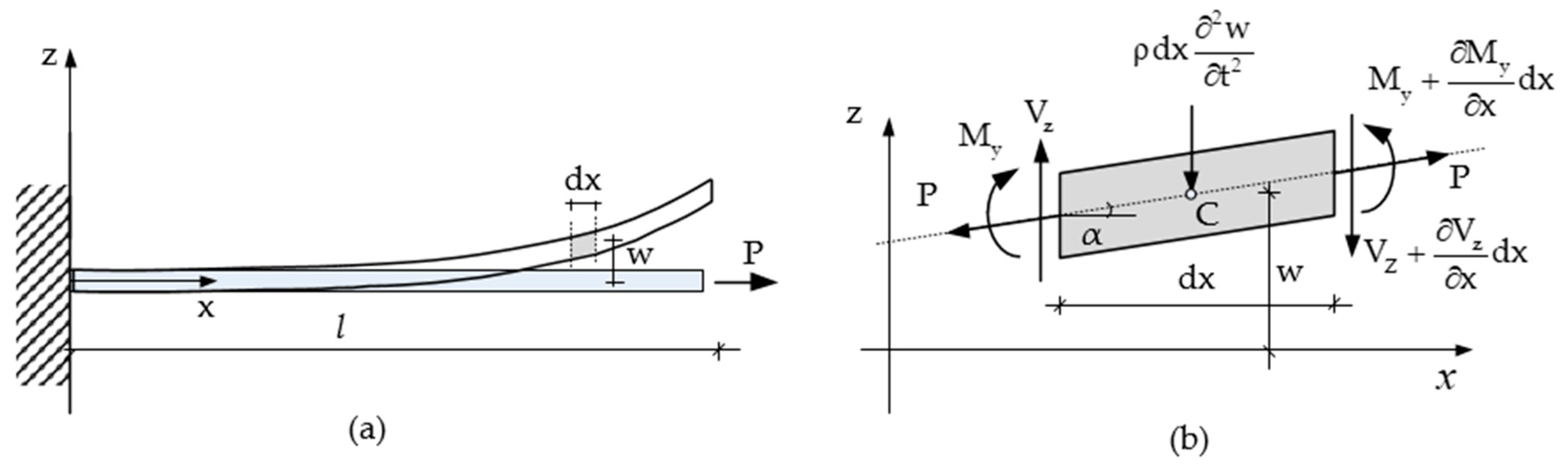
2. Analytical Solution for Lateral Tie Rod Vibration
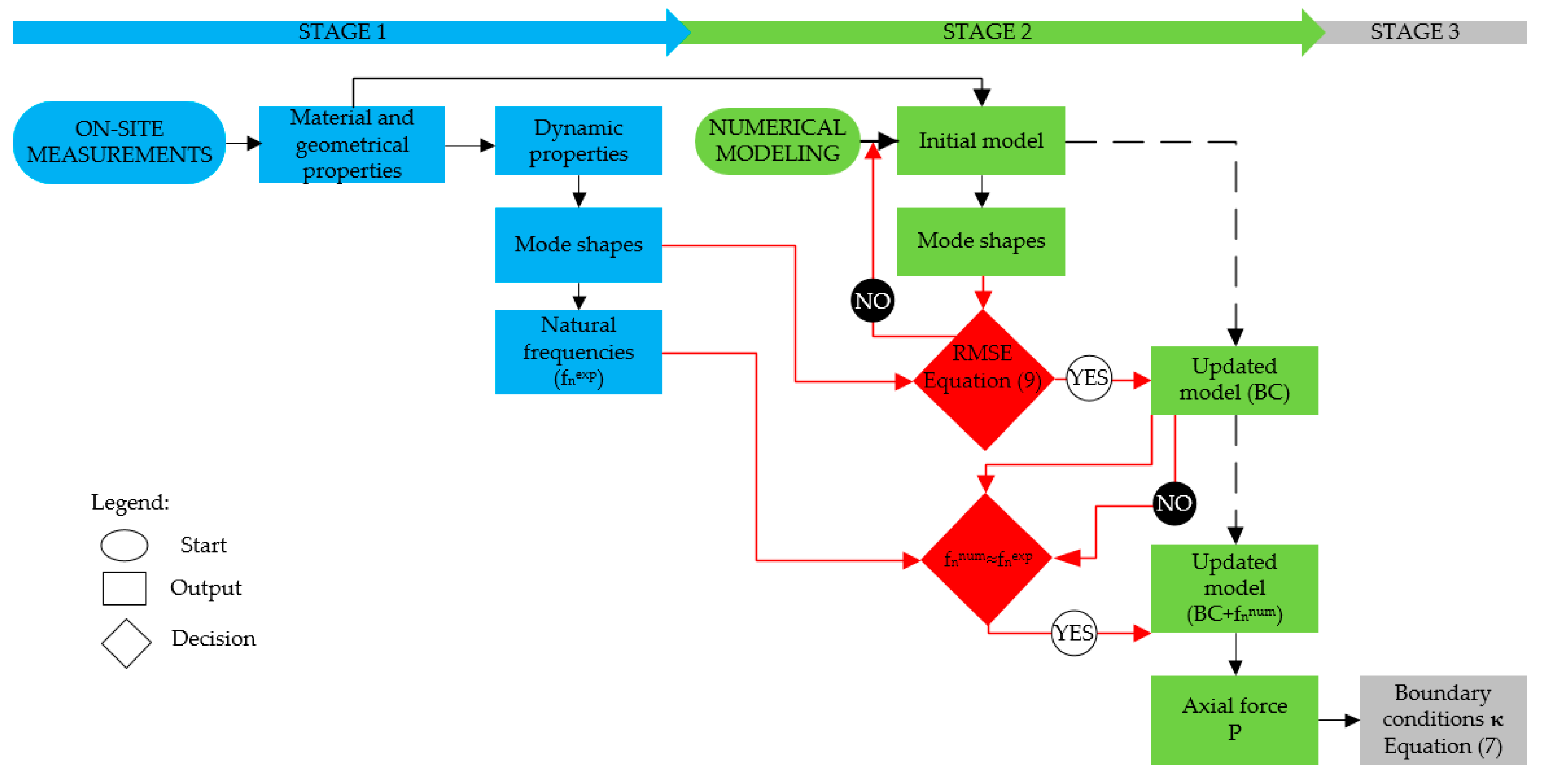
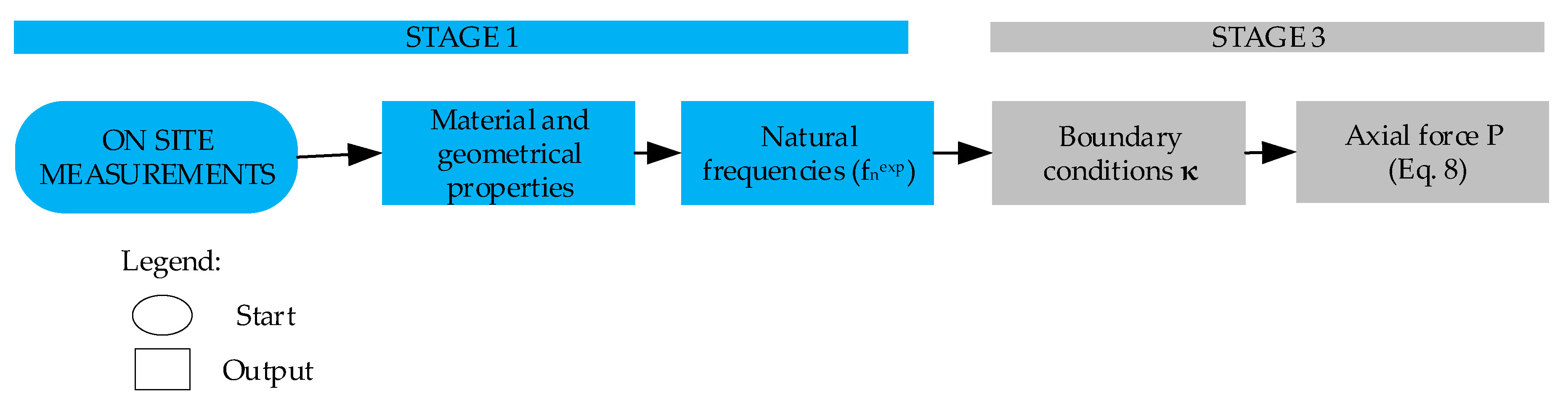
3. Methodology for Boundary Conditions and Axial Load Identification
4. Case Study Using the Proposed Methodology
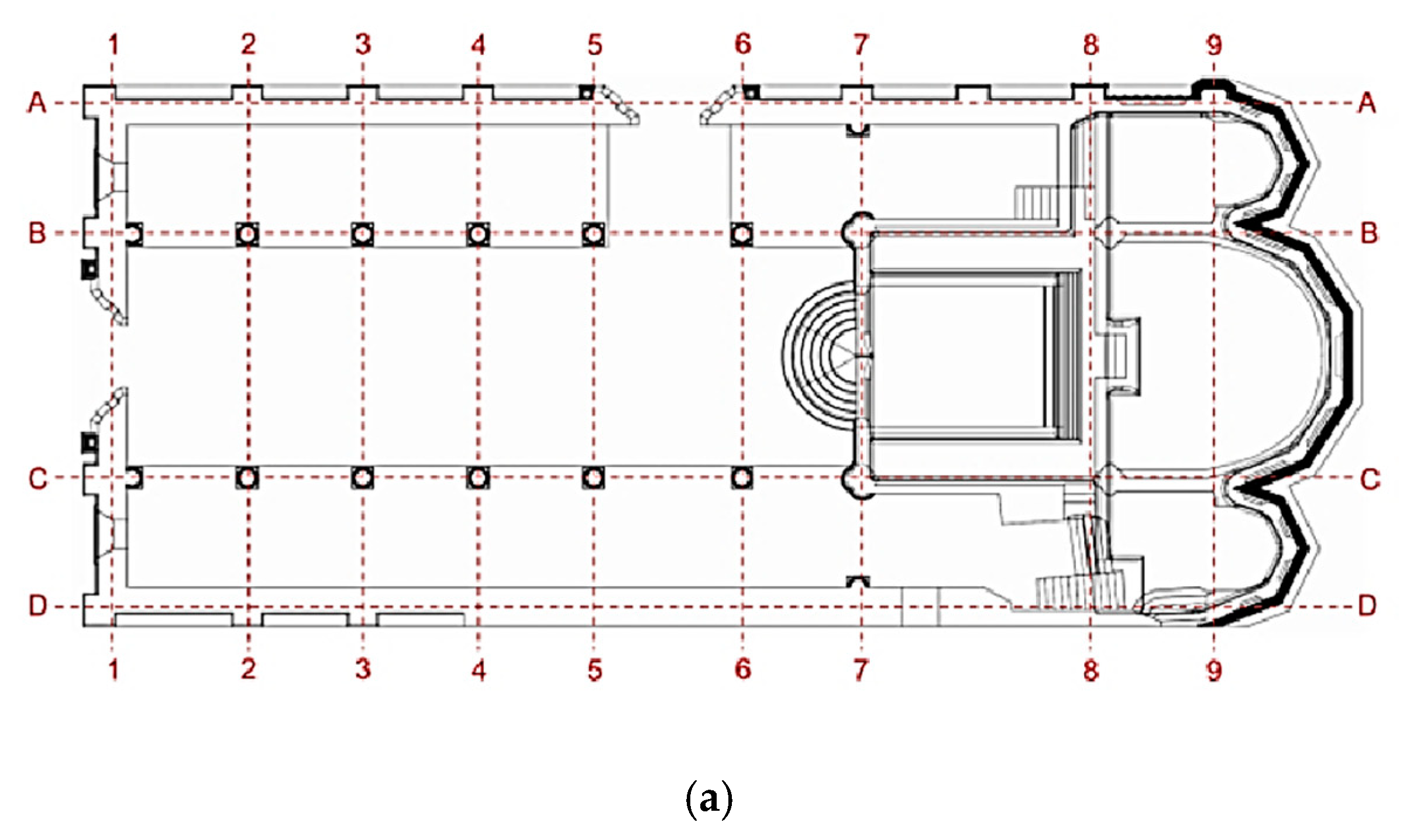
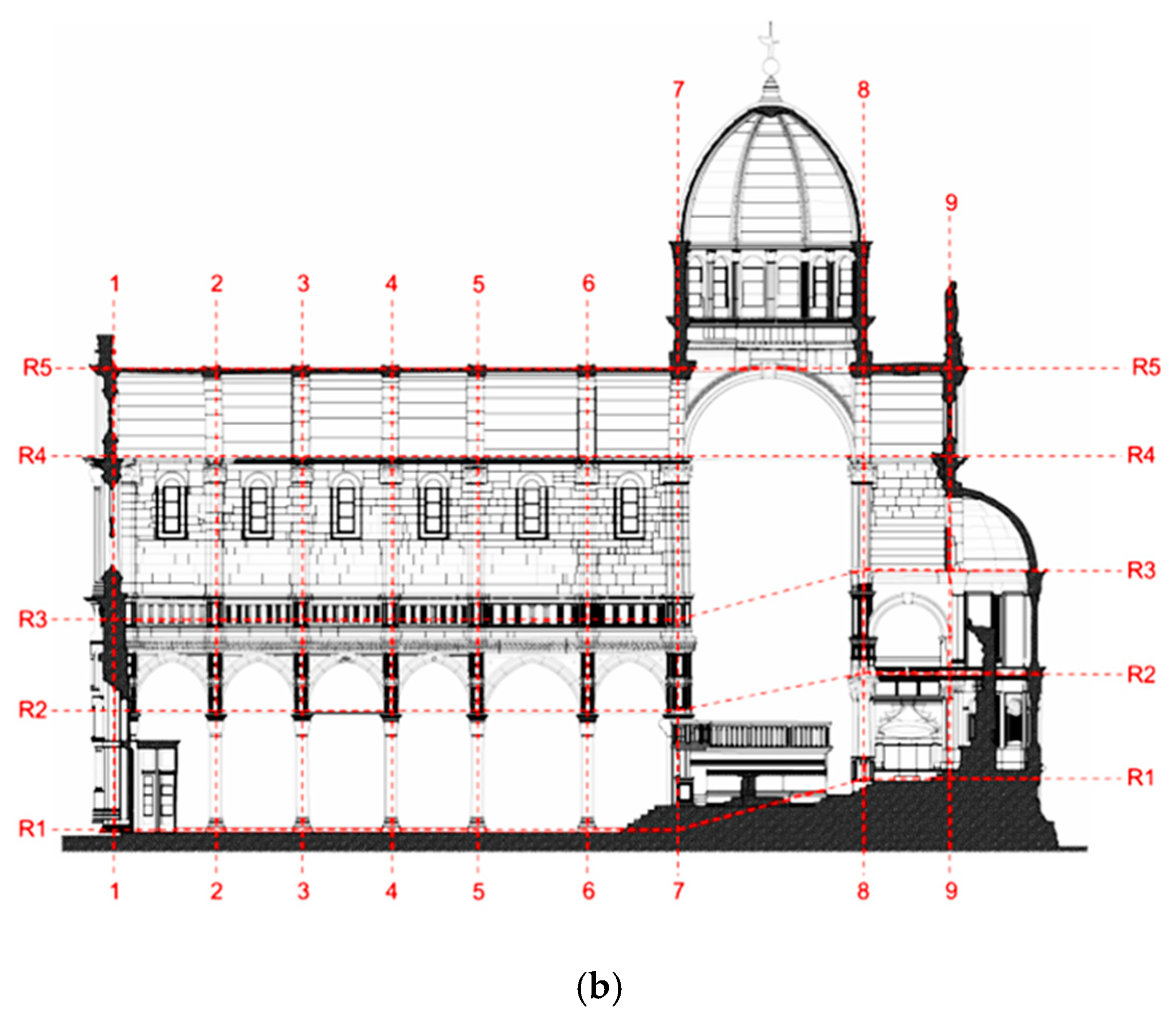
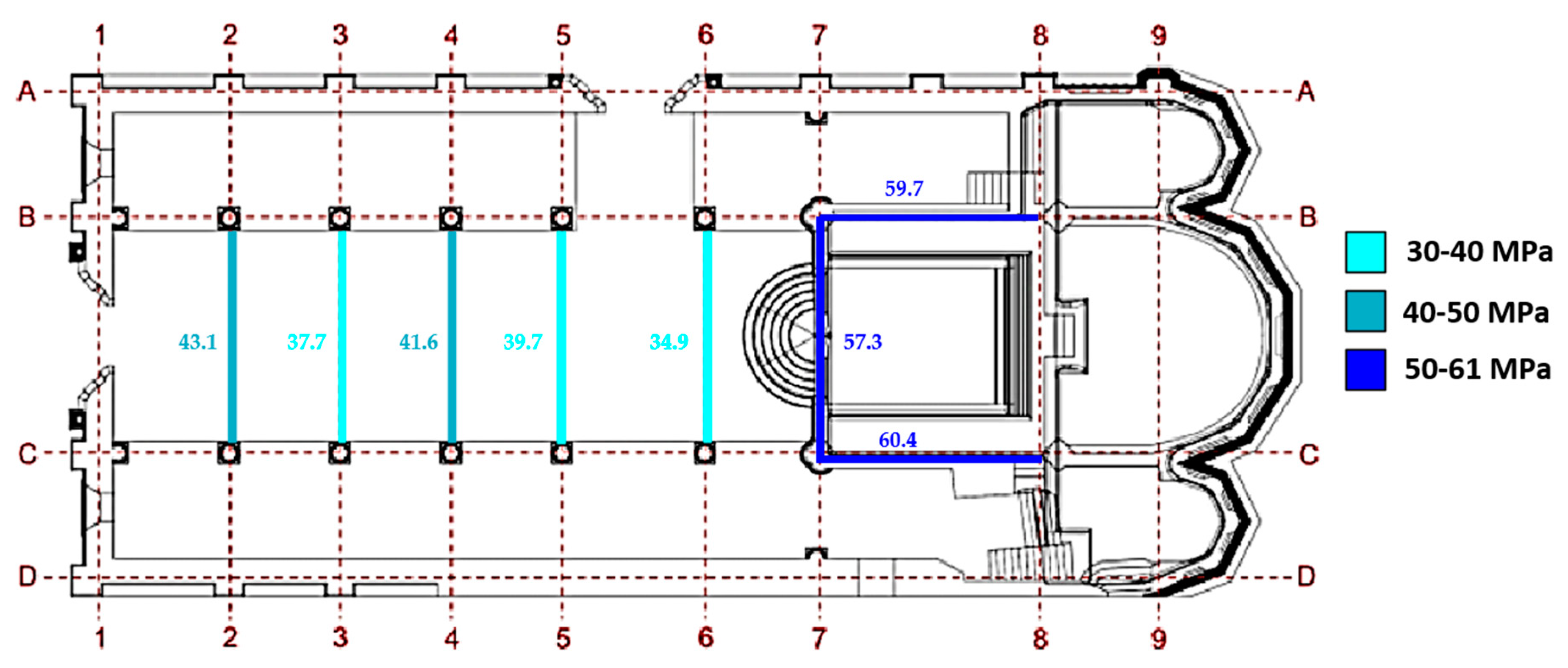
4.1. Description of Structure
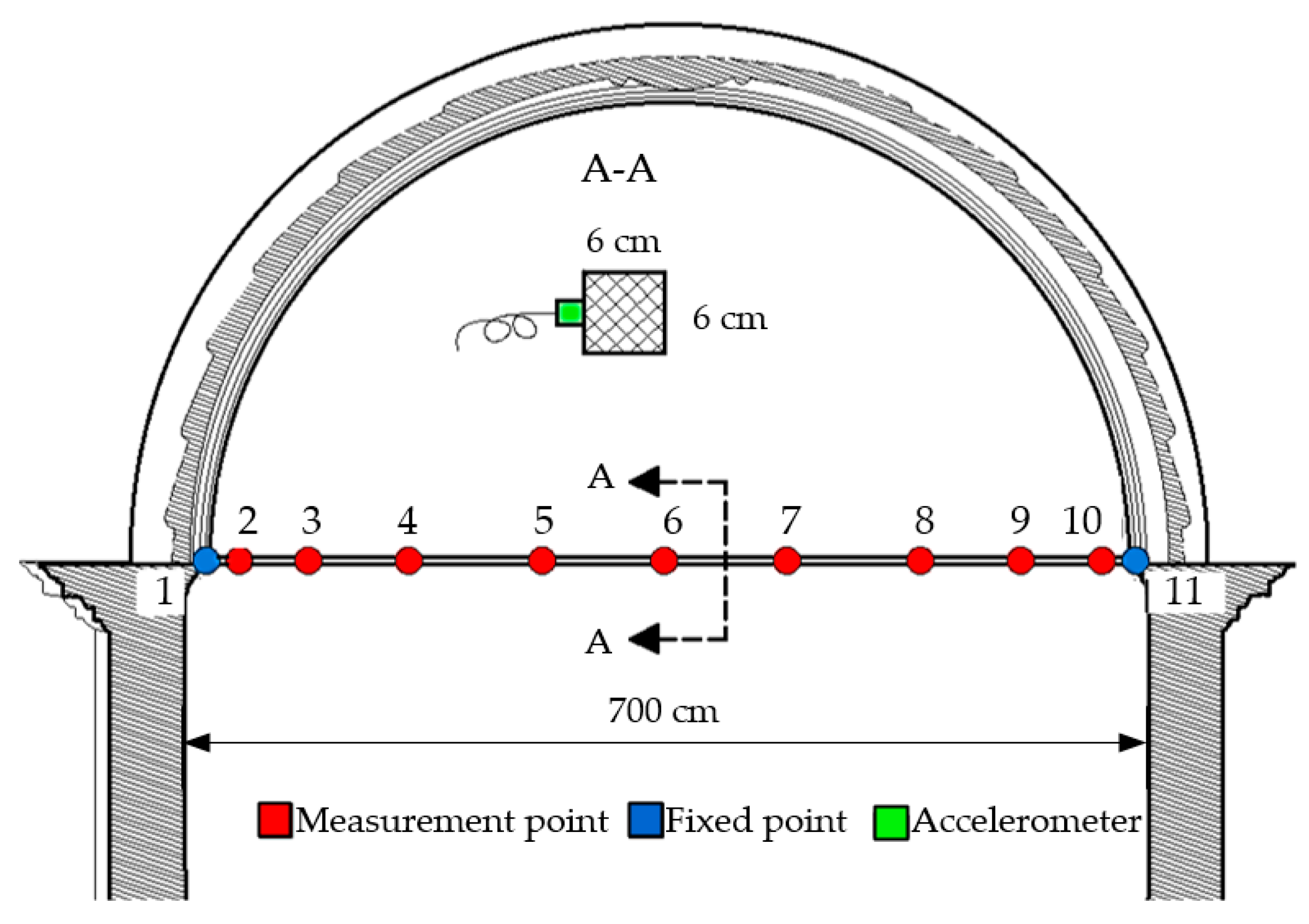
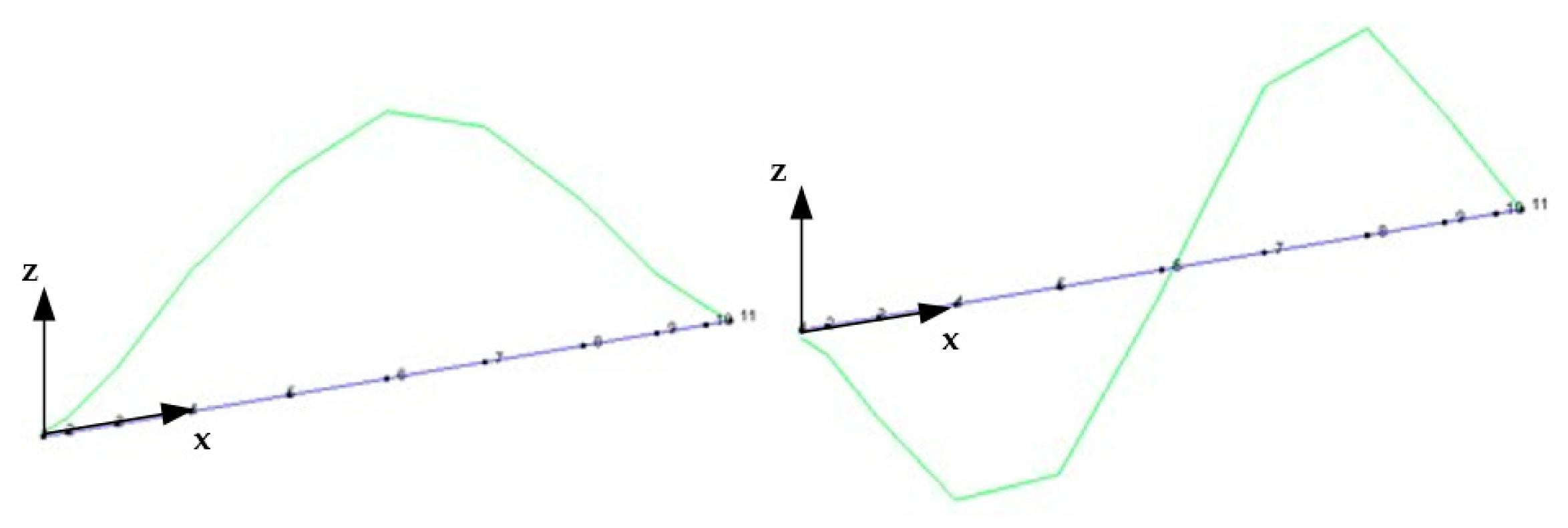
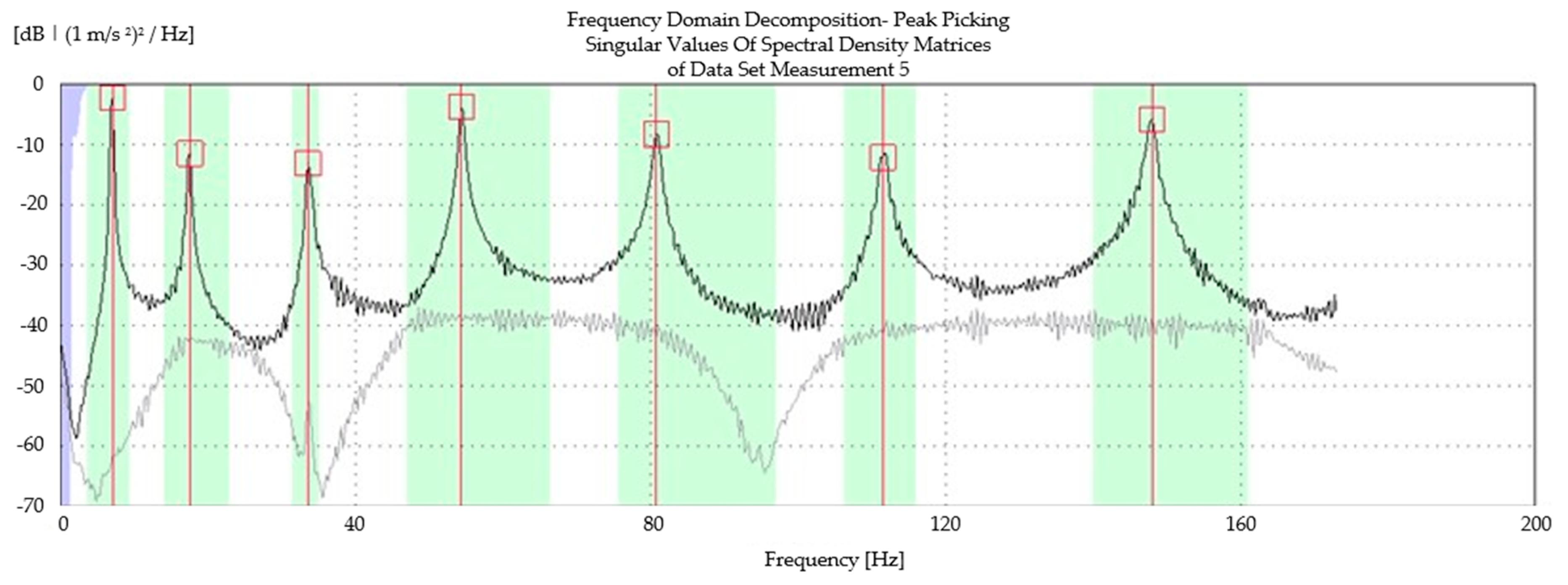
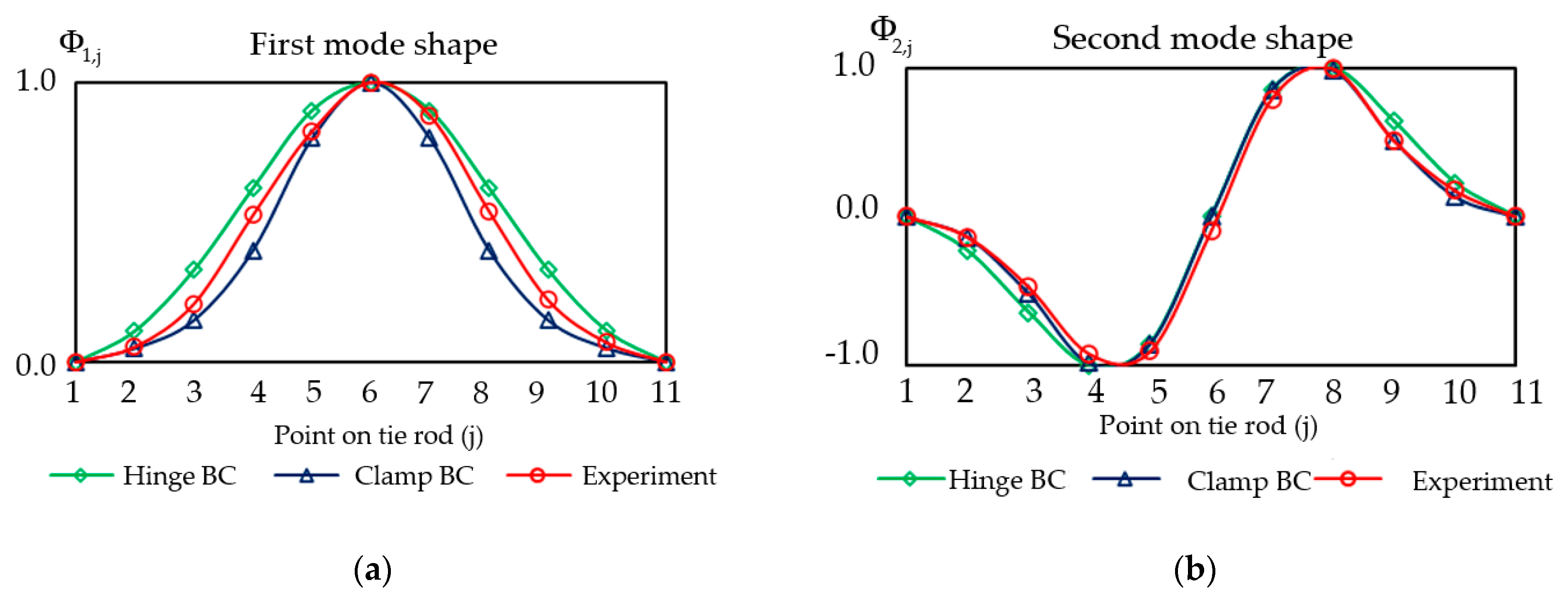
4.2. Experimental Identification of Dynamic Properties of Tie Rods
4.3. Numerical Simulation
4.3.1. Initial Model
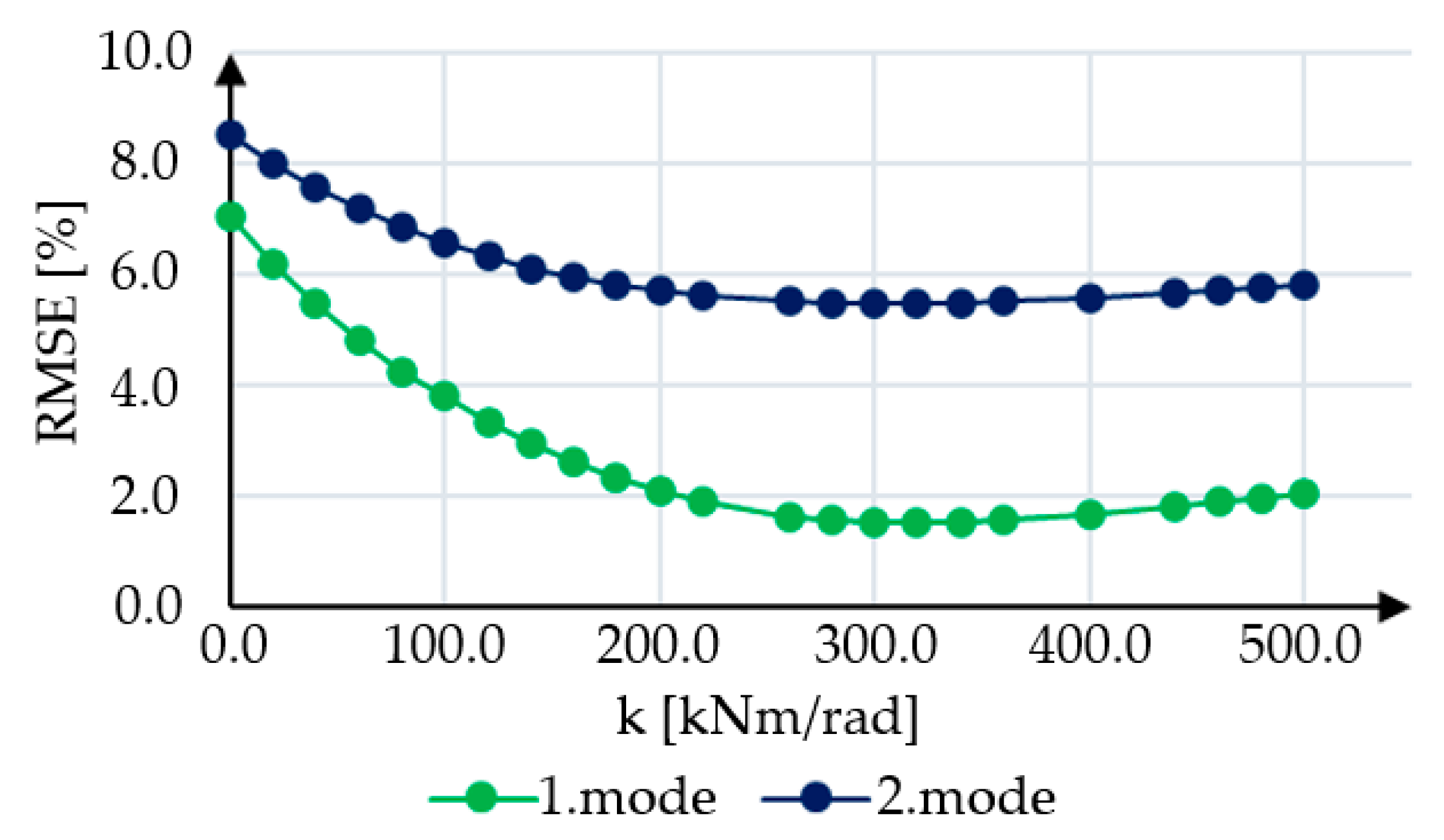
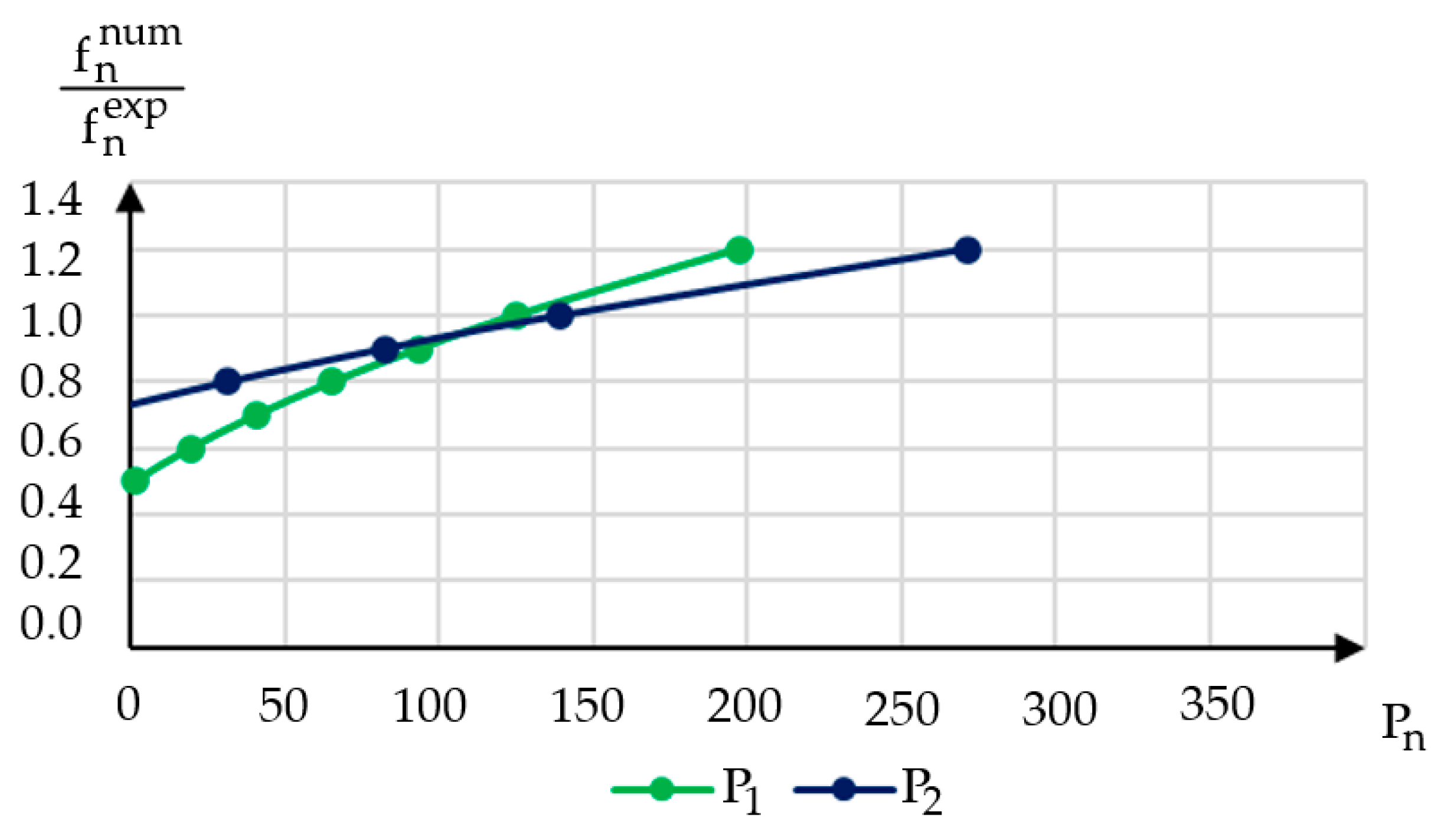
4.3.2. Updated Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, S.; Reynders, E.; Maes, K.; De Roeck, G. Vibration-based estimation of axial force for a beam member with uncertain boundary conditions. J. Sound Vib. 2013, 332, 795–806. [Google Scholar] [CrossRef]
- Li, D.S.; Yuan, Y.Q.; Li, K.P.; Li, H.N. Experimental axial force identification based on modified Timoshenko beam theory. Struct. Monit. Maint. 2017, 4, 153–173. [Google Scholar]
- Li, S.; Josa, I.; Cavero, E. Post Earthquake Evaluation of Axial Forces and Boundary Conditions for High-Tension Bars. In Proceedings of the 16th World Conference of Earthquake, Santiago, Chile, 3–9 January 2017. [Google Scholar]
- Calderini, C.; Piccardo, P.; Vecchiattini, R. Experimental Characterization of Ancient Metal Tie-Rods in Historic Masonry Buildings. Int. J. Arch. Herit. 2019, 13, 416–428. [Google Scholar] [CrossRef]
- Briccoli, S.B.; Ugo, T. Experimental Methods for Estimating in Situ Tensile Force in Tie-Rods. J. Eng. Mech. 2001, 127, 1275–1283. [Google Scholar]
- Tullini, N.; Rebecchi, G.; Laudiero, F. Bending tests to estimate the axial force in tie-rods. Mech. Res. Commun. 2012, 44, 57–64. [Google Scholar] [CrossRef]
- Tullini, N. Bending tests to estimate the axial force in slender beams with unknown boundary conditions. Mech. Res. Commun. 2013, 53, 15–23. [Google Scholar] [CrossRef]
- Duvnjak, I.; Damjanović, D.; Krolo, J. Structural health monitoring of cultural heritage structures: Applications on Peristyle of Diocletian’s palace in Split. In Proceedings of the 8th European Workshop on Structural Health Monitoring, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Collini, L.; Garziera, R.; Riabova, K. Vibration Analysis for Monitoring of Ancient Tie-Rods. Shock. Vib. 2017, 2017, 7591749. [Google Scholar] [CrossRef]
- Lai, J.-W.; Mahin, S. Strongback System: A Way to Reduce Damage Concentration in Steel-Braced Frames. J. Struct. Eng. 2015, 141, 04014223. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Calderini, C. The dynamical identification of the tensile force in ancient tie-rods. Eng. Struct. 2005, 27, 846–856. [Google Scholar] [CrossRef]
- Casas, J. A Combined Method for Measuring Cable Forces: The Cable-Stayed Alamillo Bridge, Spain. Struct. Eng. Int. 1994, 4, 235–240. [Google Scholar] [CrossRef]
- Geier, R.; De Roeck, G.; Flesch, R. Accurate cable force determination using ambient vibration measurements. Struct. Infrastruct. Eng. 2006, 2, 43–52. [Google Scholar] [CrossRef]
- Irawan, R.; Priyosulistyo, H.; Suhendro, B. Evaluation of Forces on a Steel Truss Structure Using Modified Resonance Frequency. Procedia Eng. 2014, 95, 196–203. [Google Scholar] [CrossRef]
- Gentilini, C.; Marzani, A.; Mazzotti, M. Nondestructive characterization of tie-rods by means of dynamic testing, added masses and genetic algorithms. J. Sound Vib. 2013, 332, 76–101. [Google Scholar] [CrossRef]
- Blasi, C.; Sorace, S. Determining the Axial Force in Metallic Rods. Struct. Eng. Int. 1994, 4, 241–246. [Google Scholar] [CrossRef]
- Sorace, S. Parameter Models for Estimating In-Situ Tensile Force in Tie-Rods. J. Eng. Mech. 1996, 122, 818–825. [Google Scholar] [CrossRef]
- Vasić, M. A Multidisciplinary Approach for the Structural Assessment of Historical Construction with Tie-Rods. Ph.D. Thesis, Politecnico di Milano, Milano, Italy, 2015. [Google Scholar]
- Stokey, W.F. Vibration of systems having distributed mass and elasticity. In Harris’ Shock and Vibration Handbook, 5th ed.; Harris, C.M., Piersol, A.G., Eds.; McGraw-Hill1: New York, NY, USA, 2002; Volume 15, pp. 238–287. [Google Scholar]
- Nugroho, G.; Priyosulistyo, H.; Suhendro, B. Evaluation of Tension Force Using Vibration Technique Related to String and Beam Theory to Ratio of Moment of Inertia to Span. Procedia Eng. 2014, 95, 225–231. [Google Scholar] [CrossRef]
- Rak, M.; Krolo, J.; Herceg, L.; Čalogović, V.; Šimunić, Ž. Monitoring for special civil engineering facilities. Građevinar 2010, 62, 897–904. [Google Scholar]
- Zhang, L.; Brincker, R.P. Andersen, An overview of major developments and issues in modal identification. In Proceedings of the IMAC XXII: A Conference on Structural Dynamics, Dearborn, MI, USA, 26–29 January 2004; pp. 1–8. [Google Scholar]
- Cakir, F. Determination of dynamic parameters of double- layered brick arches. Građevinar 2015, 67, 123–130. [Google Scholar]
- Bakhshizade, A.; Ashory, M.R. Root mean square error criterion using operational deflection shape curvature for structural damage detection. Math. Models Eng. 2015, 1, 96–101. [Google Scholar]
- Gelo, D.; Meštrović, M. Discrete dome model for St. Jacob cathedral in Šibenik. Građevinar 2016, 68, 687–696. [Google Scholar]
- Orlowitz, E.; Brandt, A. Comparison of experimental and operational modal analysis on a laboratory test plate. Measurement 2017, 102, 121–130. [Google Scholar] [CrossRef]
- Amabili, M.; Carra, S.; Collini, L.; Garziera, R.; Panno, A. Estimation of tensile force in tie-rods using a frequency-based identification method. J. Sound Vib. 2010, 329, 2057–2067. [Google Scholar] [CrossRef]
- Gentile, C.; Poggi, C.; Ruccolo, A.; Vasic, M. Dynamic assessment of the axial force in the tie-rods of the Milan Cathedral. Procedia Eng. 2017, 199, 3362–3367. [Google Scholar] [CrossRef]



| Boundary Condition | Static System | Coefficient | ||
|---|---|---|---|---|
| 1st Mode | 2nd Mode | nth Mode | ||
| Hinge–hinge |  | 3.142 | 6.283 | |
| Clamp–clamp |  | 4.730 | 7.853 | |
| Clamp–hinge |  | 3.927 | 7.069 | |
| Clamp–free |  | 1.875 | 4.694 | |
| Tie Rod | L (m) | h (mm) | b (mm) | (Hz) | (Hz) |
|---|---|---|---|---|---|
| 2B‒C | 6.84 | 55 | 55 | 7.25 | 17.94 |
| 3B‒C | 6.71 | 64 | 64 | 7.56 | 19.00 |
| 4B‒C | 6.81 | 60 | 60 | 7.31 | 18.69 |
| 5B‒C | 6.87 | 68 | 68 | 7.31 | 19.56 |
| 6B‒C | 6.90 | 61 | 61 | 6.94 | 17.50 |
| 7B‒C | 6.95 | 56 | 56 | 8.25 | 18.88 |
| 7‒8B | 6.97 | 56 | 56 | 8.13 | 19.38 |
| 7‒8C | 6.98 | 60 | 60 | 8.63 | 19.38 |
| RMSE Values | ||
|---|---|---|
| Mode Number | Hinge–Hinge | Clamp–Clamp |
| 1 | 7.06 | 9.15 |
| 2 | 8.50 | 10.66 |
| Mode Number | (Hz) | (Hz) | Relative Error (%) |
|---|---|---|---|
| 1 | 4.83 | 6.94 | 30.20 |
| 2 | 13.95 | 17.50 | 20.29 |
| Mode Number | (Hz) | P (kN) | σ (MPa) | κ |
|---|---|---|---|---|
| 1 | 6.94 | 122.8 | 33.0 | 3.534 |
| 2 | 17.5 | 137.2 | 36.9 | 6.777 |
| 2B‒C | 3B‒C | 4B-C | 5B-C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mode Num. | κ | Pn (kN) | σn (MPa) | Pn (kN) | σn (MPa) | Pn (kN) | σn (MPa) | Pn (kN) | σn (MPa) |
| 1 | 3.534 | 115.8 | 38.3 | 149.6 | 36.5 | 132.1 | 36.7 | 159.4 | 34.5 |
| 2 | 6.777 | 144.7 | 47.8 | 158.8 | 38.8 | 167.7 | 46.6 | 207.9 | 45.0 |
| Mean values | 130.3 | 43.1 | 154.2 | 37.7 | 149.9 | 41.6 | 183.6 | 39.7 | |
| 6B‒C | 7B‒C | 7‒8B | 7‒8C | ||||||
| Mode Num. | κ | Pn (kN) | σn (MPa) | Pn (kN) | σn (MPa) | Pn (kN) | σn (MPa) | Pn (kN) | σn (MPa) |
| 1 | 3.534 | 122.8 | 33.0 | 170.8 | 54.5 | 166.3 | 53.0 | 215.2 | 59.8 |
| 2 | 6.777 | 137.2 | 36.9 | 188.7 | 60.2 | 208.1 | 66.4 | 219.6 | 61.0 |
| Mean values | 130.0 | 34.9 | 179.8 | 57.3 | 187.2 | 59.7 | 217.4 | 60.4 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duvnjak, I.; Ereiz, S.; Damjanović, D.; Bartolac, M. Determination of Axial Force in Tie Rods of Historical Buildings Using the Model-Updating Technique. Appl. Sci. 2020, 10, 6036. https://doi.org/10.3390/app10176036
Duvnjak I, Ereiz S, Damjanović D, Bartolac M. Determination of Axial Force in Tie Rods of Historical Buildings Using the Model-Updating Technique. Applied Sciences. 2020; 10(17):6036. https://doi.org/10.3390/app10176036
Chicago/Turabian StyleDuvnjak, Ivan, Suzana Ereiz, Domagoj Damjanović, and Marko Bartolac. 2020. "Determination of Axial Force in Tie Rods of Historical Buildings Using the Model-Updating Technique" Applied Sciences 10, no. 17: 6036. https://doi.org/10.3390/app10176036
APA StyleDuvnjak, I., Ereiz, S., Damjanović, D., & Bartolac, M. (2020). Determination of Axial Force in Tie Rods of Historical Buildings Using the Model-Updating Technique. Applied Sciences, 10(17), 6036. https://doi.org/10.3390/app10176036






