Abstract
A review of developments, trends, and challenges in synthesis, design, and operation optimization of ship energy systems is presented in this article. For better understanding of the context of this review, pertinent terms are defined, including the three levels of optimization: synthesis, design, and operation (SDO). The static and dynamic optimization problems are stated mathematically in single- and multiobjective form. The need for intertemporal optimization is highlighted. The developments in ship energy systems optimization throughout the years is clearly presented by means of journal articles, giving the main characteristics of each article. After the review of what has been done up to now, ideas for future work are given. Further research needs for optimization of ship energy systems are mentioned: further development of methodology for synthesis optimization and SDO optimization, including transients, uncertainty, reliability, and maintenance scheduling. Hints are given for expansion of the system border in order to include aspects belonging to other disciplines, such as electrical and control engineering as well as hull and propulsor optimization, thus, opening a way to the holistic ship optimization.
1. Introduction
Scientists and engineers continuously strive for the improvement of their theories and constructions. This is how the efficiency, e.g., of internal combustion engines increased from about 6% at the beginning of the 20th century to more than 50% at present or that of gas turbines increased from negative values at the end of 19th century to more than 40% at present. In today’s complex world, when economic growth, prudent use of energy resources, and protection of the environment are all imperative but often competing with each other, improvement is not enough; there is a need of optimization, i.e., achievement of the best result under given circumstances.
Optimization as a concept is known since the antiquity. In the question “why optimization?,” Aristotle (384–322 B.C.) in his Second Book of Physics, gave the answer
“Because the goal is not the last, but the best.”
Mathematically, optimization is defined as the process of finding the conditions (decision variables) that give the minimum or maximum of a function, called “objective function” [1]. In the second half of the 20th century, with the development of computers and software capable of solving the complex problems thus formulated, it started being applied in real-world problems.
Recent and rather comprehensive reviews of optimization of energy systems have appeared in Refs. [2,3], either primarily [2] or exclusively [3] for land installations. The focus of the present article is a review of developments, trends, and challenges in optimization of energy systems installed on ships. Since the components and the structure of ship energy systems are the same or very similar to those of land installations, reference to [2,3] will be made as appropriate, in order to avoid repetition. However, there are also aspects pertinent to the ship energy systems as, e.g., the autonomous character (no external supply of energy while traveling) and the need for increased reliability (no substitute, if the system fails) that have to be taken into consideration.
The structure of the text is as follows.
In Section 2, the context in which the terms energy system, integrated energy system, and intertemporal optimization are used in this article is clarified; the levels synthesis, design, and operation (SDO) optimization are explained; and the limits of this review are specified.
In Section 3, the problems of intertemporal static and dynamic SDO optimization of energy systems are stated mathematically and solution methods are mentioned in brief. Additionally, the multiobjective optimization is stated.
In Section 4, the results of journal articles search on optimization of ship energy systems are presented. In order to follow the historical development, the articles are presented in a table in chronological order with the type of optimization performed (synthesis, design, and operation) and indication as to whether dynamic optimization is performed. The treatment of time in optimization, the objective functions, and the algorithms used are also mentioned. Section 4 is supported with Appendix A, where the main characteristics of each article are written.
In Section 5, further research needs and challenges in the optimization of ship energy systems are mentioned, i.e., open issues on synthesis optimization, extension of synthesis to working fluids, inclusion of transients, uncertainty, reliability and maintenance in SDO optimization, optimization in modeling, and modeling for optimization.
In Section 6, functional and physical expansion of the system to be optimized is suggested in order to include electrical and control engineering aspects, as well as hull and propulsors, opening a way towards holistic ship optimization.
The article closes with general remarks followed by the aforementioned Appendix A and a comprehensive but not exhaustive list of references.
2. Concepts, Definitions, and Limits of the Present Article
It is useful, before proceeding, to define certain terms clearly and to specify the subjects that are inside and outside the limits of the article.
2.1. The Energy System and Its Optimization Levels
In general terms, an energy system is any system that transforms energy from one form to another or to other forms or transfers energy from one place to another or from one body to another. This article deals with complex systems of interconnected components that convert primary energy to forms of energy useful on ships, i.e., mechanical, electric, and thermal energy. A diesel engine, a gas turbine, a heat exchanger, etc., fall under the general definition of an energy system, but the optimization of those as individual components, which is certainly applicable, is beyond the limits of the present text; instead, they are considered as components of a more general system.
In the past, the propulsion, electric, and thermal loads were served by separate units: main engine(s) for propulsion, diesel generator sets for electric loads, and combustion boilers for thermal loads. The need for better exploitation of the chemical energy of fuels led to integrated energy systems, i.e., systems that, with proper interconnection of components, aim at covering as many types of loads as possible from the same primary energy source. While improvements and optimization of individual components, a never-ending endeavor, continue increasing their efficiency gradually, system integration and optimization can lead to step-function increase of the total energy efficiency. This is a challenging field, and it is certainly inside the limits of the article.
The optimization of an energy system either on land or on a ship can be considered at three levels as initially defined in [4,5,6] and further elaborated in [7,8]:
- Synthesis optimization. The term synthesis refers to the components that appear in a system and their functional interconnections. With synthesis optimization, the optimal configuration of the system is determined and the flow diagram of the system can be drawn.
- Design optimization. The word design here is used to imply the technical characteristics (specifications) of the components and the properties of the substances entering and exiting each component at the design point (nominal load) of the system. One may argue that design includes synthesis too. However, in order to distinguish the three levels of optimization, the word “design” will be used with the particular meaning given here.
- Operation optimization. For a given system (i.e., one in which the synthesis and design are known) under specified conditions, the optimal operating state at each instant of time is requested, as it is defined by the operating properties of components and substances in the system (speed of revolution, power output, mass flow rates, pressures, temperatures, composition of fluids, etc.).
It is understood that each level cannot be considered in complete isolation from the others. Consequently, the complete optimization problem, taking into consideration that an energy system operates under conditions that change with time, can be stated by the following question:
What is the synthesis of the system, the design specifications of the components, and the operating state at each instant of time that lead to an overall optimum?
2.2. Intertemporal Optimization
In many publications, design optimization is performed at a single set of conditions, usually called design point. However, the ship and, consequently, its energy system, operates at conditions that change with time due to, e.g., weather state, load carried, mission requirements, cost of fuel, etc. Thus, if only a single operating point is considered, most probably a suboptimal system will be obtained. Instead, intertemporal optimization is needed, having the following meaning [2,7]:
Intertemporal optimization is the optimization that takes into consideration the various operating conditions that a system encounters throughout its life time and determines the operating state at each instant of time that results in the overall minimum or maximum of the general objective function.
The term operating mode appearing in [2] has been replaced here with the term operating state, because the word mode is used with other meanings on ships, e.g., regular cruising, full-speed, in port, loading/unloading, or gas mode of operation (for dual fuel engines). Thus, an operating mode may include various operating states.
3. Mathematical Statement and Solution Methods of the Optimization Problem
The synthesis, design, and operation (SDO) optimization problem can be static or dynamic. The mathematical statement of each type is presented in this section in brief, in order to make the subject of this review clear, but details are avoided in order not to deviate largely from the main goal. Instead, related references are cited for more detailed presentation.
3.1. The Static Optimization Problem
3.1.1. Mathematical Statement and Solution Methods of the Static Optimization Problem
In general terms, the optimization problem is stated as follows:
subject to equality and inequality constraints
where x is the set of independent variables.
For the complete SDO optimization, it is convenient to write the objective function in the form [2,5,6]
where
- v
- set of independent variables for operation optimization (load factors of components, mass flow rates, pressures and temperatures of streams, etc.),
- w
- set of independent variables for design optimization (nominal capacities of components, mass flow rates, pressures and temperatures of streams, etc.),
- z
- set of independent variables for synthesis optimization; there is only one variable of this type for each component, indicating whether the component exists in the optimal configuration or not; it may be a binary (0,1), an integer, or a continuous variable such as the rated power of a component, with zero value indicating the nonexistence of a component in the final configuration.
If optimization is performed not on all three levels (SDO) but on one or two of those, Equation (4) is simplified accordingly.
It is usual in optimization theory to express the objective as minimization of a function. If maximization is the goal, the whole formulation can remain the same, since
A practical procedure for solution of the SDO optimization problem is the following: a set of values is selected for the design and synthesis independent variables (w,z), the operation optimization problem is solved starting with an initial set of values of v, and the objective function is evaluated. The set (w,z) is updated and the iterative procedure is repeated until convergence. With the increase of computing capacity, it has been possible to work on all three levels simultaneously, i.e., to handle all the independent variables at a single step. Further details will be given in following sections.
For updating the values of the independent variables, various methods have been developed, which are classified in three broad categories: (i) search methods, (ii) calculus methods, and (iii) stochastic or evolutionary methods. Search methods do not use derivatives of the objective function with respect to the variables, they are implemented relatively easily, but they may be slow in locating the optimum, compared to the calculus methods. Calculus methods are much faster, but they require continuity of the objective function and the derivatives, a requirement that often is not satisfied in optimization problems of energy systems. In such cases, stochastic or evolutionary methods can be applied, that have also the additional advantage of locating the global optimum in problems with many local optima. Complete formulation of methods appears in publications such as Refs. [9,10,11,12,13,14,15,16,17].
3.1.2. Intertemporal Static Optimization
In Equations (1)–(4), time is not involved and consequently, operation optimization can be performed at a single operating point, e.g., the nominal loading condition (design point). However, as stated in Section 2.2, in reality, intertemporal optimization is needed. This can be achieved, while keeping the mathematical statement of Equation (4), with the following approach.
It is considered that the operating profile of the system for the time period that the optimization is to be performed (e.g., day, week, season, the whole life cycle of the ship) is known, i.e., all forms of power needed on board (mechanical, electric, and thermal) are known functions of time and of variables related to the operation of the ship. A discretization of the profile is performed: the whole time period is divided in N time intervals of duration in such a way that a steady-state operation can be considered in each interval, i.e., the loads remain constant at a value in good approximation to the real profile. The transients are ignored under the assumption that their duration is negligible in comparison to the whole operating period. Of course, larger N and shorter lead to better approximation of the real with the discretized profile.
Next, a time decomposition is assumed, i.e., it is considered that the operation in a time interval does not affect and it is not affected by the operation in other intervals. Then, the solution procedure described after Equation (5) is followed, with the operation optimization being performed for one interval after the other. Each interval is characterized by its own set of operation-independent variables, vn. Applications of this solution method appear in several publications, such as Refs. [5,6,18,19].
However, the conditions for time decomposition are not always satisfied. If, e.g., the duration of the trip from port A to port B is fixed, the speed of the ship in a time interval affects the speed in other time intervals. If time decomposition is not applicable, the operation optimization problem cannot be solved for one interval after the other, as described in the preceding, but there is need to handle all the operation-independent variables at a single step [7,8]. The dimensionality of the problem (number of independent variables) increases significantly and the solution may be inefficient or impossible. In such a case, the best way out is the application of dynamic optimization, which is the subject of next section.
3.2. Dynamic Optimization
3.2.1. Mathematical Statement of the Dynamic Optimization Problem
In dynamic optimization, the variables as functions of time are requested that give minimum (or maximum) to the objective function, which is called functional. Convenient for optimization of energy systems is the Bolza form of the functional, which consists of the function Q at the end of the time interval under consideration, tf, and the integral of the function F over the time horizon [t0, tf] [20,21,22]
where
- J
- scalar objective functional
- z
- differential state profile vector
- y
- algebraic state profile vector
- u
- control (independent variables) profile vector
- w
- time-independent variables vector
- tf
- final time.
If the optimization is or can be considered as discrete in time, the mathematical statement takes a discrete form and the integral in Equation (6) is replaced by a summation:
The time period [t0, tf] is divided in N time intervals of duration . In Equation (7), the variables are discrete vector sequences (e.g., ).
The mathematical formulation includes equality and inequality constraints consisting of differential and algebraic equations (DAE formulation). Details are not included here, but they can be found in the aforementioned publications, while adaptation and application to energy systems of ships appear in [8,23].
3.2.2. Solution Methods of the Dynamic Optimization Problem
The methods developed for the solution of the dynamic optimization problem are classified in two main categories: indirect methods and direct methods.
The indirect methods include calculus of variations (COV) [24,25] and dynamic programming (DP) [26]. As explained in [2,23], they are not particularly useful for optimization of energy systems, as they are considered here.
The direct methods convert the original problem, which is continuous in time, to a discrete one. They are divided in two subcategories: sequential methods and simultaneous methods. Detailed description is avoided here, but it can be found in related publications [21,22,27,28], while application examples on energy systems on land, airplanes, or ships appear in [8,23,29,30,31,32].
3.2.3. Intertemporal Dynamic Optimization
In the way the problem is stated by Equations (6) and (7), the dynamic optimization is intertemporal anyway [2]. However, we can use the term intertemporal dynamic optimization, whenever we need to make a distinction between optimization in a short time horizon, as is the case of transients, and in a long time horizon, such as a round trip, 1 year, or the whole life cycle of a ship. For brevity, the word intertemporal will be omitted, if the description of the particular problem makes the type of dynamic optimization clear.
3.3. Multiobjective Optimization
In the preceding formulations, Equations (1)–(7), the optimization has one objective only. In reality, there may be two or more desirable goals simultaneously and often competing with each other. For example, it is desirable to have a system of low cost, high efficiency, and low emissions. However, a system of minimum cost may not have maximum efficiency or minimum emissions. In such cases, the system obtained by optimization with a single objective most probably will not satisfy other objectives. In order to address problems of this type, multiobjective (or multicriteria) optimization methods have been developed [33,34,35,36]. In general terms, the problem is stated mathematically with the objective function
where is the i-th objective function, accompanied by constraints, Equations (2) and (3).
The simplest way of formulating and solving a multiobjective optimization problem is to define the objective function F as a weighted summation of the individual objectives
where wi are the weighting factors, often subjective. Then the problem is reduced to one of a single objective and can be solved with methods available for problems of Equations (1)–(7).
More elaborate methods exist, as, e.g., methods that select as optimal solution a point on the Pareto front, such as the point with minimum distance from the ideal one or the point of maximum distance from the nonideal one.
No matter what is the method, the system obtained usually does not satisfy each objective in separate, but it is the result of a compromise, more or less subjective. Applications on ship energy systems will be presented in Section 4.4.
4. Historical Development of Optimization of Ship Energy Systems
4.1. Articles Published in Journals
In order to investigate the development of optimization of ship energy systems, a search for related articles in numerous journals has been performed in the period March–April 2020 using keywords, with no restrictions on the publication year. In addition, the reference list of each article thus located has been searched for articles on optimization of ship energy systems, as they are defined in Section 2.1. In total, 57 articles have been found. Being interested in the development of the field with time, the articles are written in chronological order in Table 1, while main characteristics for each article are written in Appendix A, in the same order as in Table 1.

Table 1.
Journal articles on optimization of energy systems of ships by the year of publication. (Explanations of symbols and abbreviations are written after Section 7 Closure.).
Presentations in conferences are not included because on one hand, they are not easily accessible to persons who have not participated in a conference, and on the other hand, significant and well written presentations are often recommended for submission to journals, where they appear 1–2 years after the conference.
The number of each article in the list of references is given in the second column of the table, while the third column gives the year of publication. The system under optimization is written in abbreviated form in the fourth column. The next three columns indicate the type of optimization (synthesis, design, and operation), while the last one indicates whether dynamic optimization is performed.
For a broad overview, it is interesting to note the number of articles per type of optimization performed, whether and how time is taken into consideration, what is the optimization objective, and which are the optimization algorithms used. These subjects will be presented in the following subsections in brief.
4.2. Type of Optimization Performed
The type of optimization and the number of articles in each type are given in Table 2, where the letters S, D, and O stand for synthesis, design, and operation optimization, respectively. The percentages are depicted also in the pie chart of Figure 1.

Table 2.
Type of optimization and number of articles.
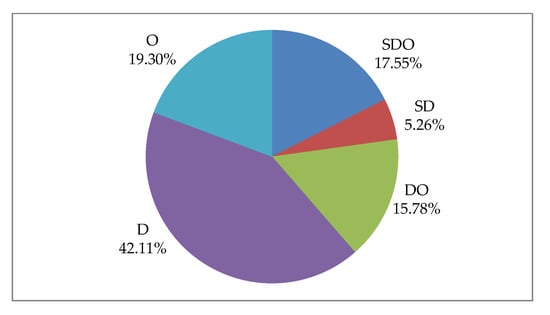
Figure 1.
Distribution of number of articles to optimization types.
Even though the first two articles in Table 1 applied triple optimization (SDO), only 10 articles in total have been published since 2008 with SDO optimization, while the highest percentage (42.11%) applied design optimization only.
4.3. Design Point Versus Optimization based on Operating Profile–Time in Optimization
Design optimization at a single operating state (design or nominal point) is relatively easy, because there is no need to consider partial load performance of equipment, and the dimensionality of the optimization problem (number of independent variables) remains relatively low. In addition, if the optimization objective is a thermodynamic one, e.g., maximization of efficiency or minimization of fuel consumption, there is no need to consider time. However, time of operation either in steady state or under variable conditions is needed, if the economic performance of the system is assessed, even with operation at a single point.
The problem becomes more complex, if the optimization is performed considering various operating states. Table 3 gives information on these issues, as they are treated in the articles of Table 1.

Table 3.
Consideration of operating conditions in optimization and number of articles.
The simplest problem, optimization at a single operating point (design) point is the most frequent in Table 3 (35.09%). The operating profile is approximated with a number of operating states in 18 articles, while an hourly profile is considered in 6 articles. In each state or hour, the various loads (propulsion, electric, and thermal) are given together with the duration, usually in number of hours in a period, e.g., in a round trip or in a typical year of operation of the ship. An alternative way is the consideration of the frequency of occurrence of the various loads in discrete values in a certain period, e.g., in a typical year of operation. Four articles follow this approach.
Speed optimization of the ship in real time is performed in two articles under environmental conditions changing with time. The whole route is divided in n time steps.
Instead of discrete loads, load profiles continuous in time for a certain period are considered in seven articles.
Only six articles apply dynamic optimization (No. 14, 24, 32, 46, 48, and 56). One article (No. 20) applies dynamic simulation of the system, while the transient behavior of the system is simulated after design, in order to guarantee stable operation after transients.
4.4. Objective Functions
Both single- and multiobjective optimization appears in the articles of Table 1. In order to have a concise picture, the objective functions grouped by type are written in Table 4, together with the articles that apply each objective function.

As seen in Table 4, several objective functions have been used, while multiobjective optimization starts gaining ground with a variety of objective functions and their combinations.
4.5. Optimization Algorithms
The continuous increase of the interest in applying optimization and of the complexity of optimization problems leads to a continuous improvement of existing and development of new optimization methods and algorithms. The algorithms used in the articles of Table 1 are presented in Table 5.

Table 5.
Algorithms and/or software used in the articles of Table 1.
In Ref. [2], a list of algorithms is included that have been applied for optimization of energy systems on land. Many of those algorithms appear also in Table 5, while there are algorithms in Table 5 that do not appear in Ref. [2]. Cross-fertilization between the two similar fields (land–ship energy systems) can be very fruitful.
5. Further Research Needs and Challenges in Optimization of Ship Energy Systems
5.1. Synthesis Optimization
5.1.1. On the Possibility of Finding the Optimal Configuration
In the usual practice, the system configuration is determined by the designers based on their knowledge and experience, while their ingenuity and inspiration can be of vital importance in creating new systems. It is interesting and useful to copy here a paragraph from Ref. [89]:
“Given the multitude of energy system types and the variations in each type, one may question whether it is ever possible to replace the experienced designer’s mental process with an algorithm consisting of a set of formulae and rules. On the other hand, in today’s complex world, this same multitude of types and variations makes it rather impossible even for an experienced designer to evaluate all possible alternatives. Consequently, an automated procedure, if properly used, can be of invaluable help to the designer.”
The preceding thoughts justify the impetus for development and application of methods for synthesis optimization of energy systems. The related activity for energy systems on land started in the 1980s, while applications on ships appeared in the first decade of 2000. Characteristic classes and examples of methods for land installations are presented in [2,3], while here, we will be restricted to systems on ships.
5.1.2. Methods and Applications of Synthesis Optimization of Ship Energy Systems–Challenges and Opportunities
As indicated in Table 2, only 13 of the 57 articles address the synthesis optimization problem. In 11 of these articles the superconfiguration (the term “superstructure” is used in the literature on land systems, but it is avoided here, because it has a different meaning on ships) approach is followed, i.e., all the envisioned components are possible candidates for the system and a synthesis independent variable is associated with each component. It may be a binary variable (0, 1) indicating whether a component exists or not in the optimal configuration, a continuous variable (e.g., the nominal power of equipment) with zero value indicating nonexistence of the component in the optimal configuration, as well as integer variables indicating connections between components.
In No. 4 [39] the optimum ORC process layout and fluid are determined out of a number of fluids available, while the method includes four processes: (a) at subcritical and supercritical pressures, (b) with any degree of superheating, (c) with or without internal recuperator, and (d) with and without preheater. Broadly speaking, this is similar to the superconfiguration approach.
Completely different is the method applied in No. 17 [51]. The HEATSEP method [90] is used for optimization of the heat exchanger network of the ORC system. The method has been developed for land installations, but it can very well be used for systems on ships.
With the continuous increase of interest in and need of integrated energy systems on ships, the installation of pollution abatement equipment, and the appearance of renewable energy equipment on board, the application of synthesis (together with design and operation) optimization will be not a luxury but a necessity. The interested reader is kindly referred to recent reviews in [2,3] for methods and applications of synthesis optimization, primarily on land installations, but they can be applied on ship systems too.
With the superconfiguration approach, the optimal configuration inevitably is restricted by the initial superconfiguration. In order to avoid such a restriction, superconfiguration-free (superstructure-free in the terminology of land systems) methods have been and continue being developed [3,91,92,93].
It can be said that, in spite of the progress, methodologically, the problem of synthesis optimization has not been solved in its generality. Thus, the field is open to further research and development.
5.1.3. SDO Optimization Including Synthesis Optimization of Working Fluids
As indicated in Table 1, the Organic Rankine Cycle (ORC) is often the subject of optimization. In these works, the working fluid is predetermined or several available working fluids are investigated, and the combination of fluid and system with the best performance is finally selected.
A different and very interesting approach is followed in [94]: The fluid is synthesized during the optimization procedure by computer-aided molecular design using several molecular groups (e.g., –CH3, –CH2–, =CH2, =CH–, etc.). The aim of the optimization is to determine the optimal combination of the molecular groups and thermodynamic variables that maximize the power output generated by the ORC for specified heat source and heat sink. In this particular application, the synthesis of the system is fixed. The complete SDO optimization can be further developed to include molecular synthesis of the working fluid(s).
5.2. SDO Optimization Including Transients
Transients are mentioned in four of the articles of Table 1. In No. 20 [54], the system is so designed that it reaches stable operation after transient conditions (change of ship speed and, consequently, power output of the main engines) in a reasonable length of time. In No. 24 [58], optimization is performed for a cycle of 120 min of the ship including start-up, acceleration, full speed ahead, deceleration, and stop. In No. 33 [66], transients are taken into consideration in building the model of the experimental facility (cooling network), which then was used in order to optimize the total heat exchanger inventory allocation. In No. 56 [87], transients of load, electric voltage, and temperature of the cooling fluid are taken into consideration for optimal control. However, there is a long way to go from these applications to the compete SDO optimization of a ship energy system for the whole life cycle that includes interrelated periods of practically steady-state operation as well as operation during transient conditions.
An idea of how such a complex problem can be addressed is given in Refs. [31,32]. The energy system of an aircraft is optimized for a whole trip that consists of the phases take-off, flight, and landing. Each phase is characterized by a different set of differential and algebraic equations. Adaptation and further development of the methodology for optimization over much longer time periods, as is the operation of a ship, are needed.
5.3. Optimization with Uncertainty Considerations
The objective function and the model of the system, both technical and economic, include a multitude of parameters. Many of those may have values not known with certainty. For example, uncertainty may exist regarding the future operation of the ship and, consequently, the load profile, the cost of fuel, the weather conditions, etc. Therefore, it is not sufficient to solve the optimization problem for one set of conditions, i.e., for one set of parameter values only. There is need of at least a parametric study or sensitivity analysis with respect to crucial parameters, which is performed relatively easily, i.e., the optimization problem is solved for several values of the parameters and the effect on the optimal solution is recorded. This is the procedure followed in most of the articles in Table 1.
Even though more demanding, uncertainties can be taken into consideration during the optimization procedure. There are two approaches for optimization under uncertainty [95]: stochastic programming and robust optimization. The subject with related methodology is presented thoroughly in [95,96,97,98,99,100]. Examples with applications on ship energy systems are as follows:
In No. 15 [49], the uncertainty due to the intermittent PV generation caused by the irradiation and the swinging of the ship is taken into consideration with an interval optimization method in order to determine the optimal size of the battery unit and the load of the diesel generator.
In No. 24 [58], a load power prediction model based on multiresolution analysis of wavelet neural network (MRA-WNN) is established to predict the electric load of the ship under load uncertainty. The model is then used for optimization of load allocation among the sources of electric energy.
In No. 36 [69], the uncertainty of the hourly global irradiation and its effect on the power output of the PV system are taken into account by the probability density function in a two-stage stochastic mixed integer nonlinear programming method in order to determine the optimal size of the hybrid electric power system of an oil tanker.
The complete SDO optimization taking uncertainties into consideration remains to be developed and applied.
5.4. Optimization with Consideration of System Reliability
The word ‘reliability’ is used here with the following meaning [101]:
“Reliability is the probability that an item will perform a required function under stated conditions for a stated period of time.”
Usually, the problem of energy systems optimization is solved assuming that the equipment is always available for operation, except of periods for scheduled maintenance. If redundancy is required, modifications of the system are performed after optimization. However, with such an approach, the final system most probably will be nonoptimal.
An example of a different approach is given in Ref. [102]. The method is first developed theoretically introducing reliability and availability in the mathematical model of the system using the state-space method, while decisions in case of partial failure of equipment are taken by applying the Intelligent Functional Approach [5,6]. The method was then applied for SDO optimization of a cogeneration system with and without consideration of reliability. It is interesting to note that introduction of reliability changed the optimal system significantly at all three levels (synthesis, design, and operation) and that if reliability (and consequently the failure probability of equipment) is not considered, then the economic performance of the system, as it is expressed by its net present value, is overestimated.
A literature search can give also other applications of land energy systems optimization including reliability (examples are given in [2]), but applications on ship energy systems have not been located (a note of caution: the word reliability may appear in many publications, but without real consideration in mathematical terms). It is worth applying these methods on ship energy systems too. The similarity between energy systems on land and on board will facilitate this effort.
5.5. Optimization of Maintenance Schedule in Itself or Embedded in SDO Optimization
In articles of Table 1 that include cost estimation, maintenance cost is estimated either as a fixed percentage of the capital cost of the system or as a linear function of the mechanical or electric energy produced with no consideration of the maintenance strategy, being tacitly assumed that maintenance will take place at fixed and prespecified periods, as is the usual practice on ships. However, with the continuous expansion of data acquisition systems on board, condition-based maintenance can be a realistic option for certain equipment, while reliability-centered maintenance could be considered, even though more demanding in application. Maintenance after failure (run till failure) should rather be excluded as an option on ships, for safety reasons.
The aforementioned indicate that the maintenance strategy itself can be the subject of optimization. Since such an application on ships has not been found, an example referring to a land installation is mentioned here, in order to make the subject more clear. In [103], a network of compressors with fixed synthesis and design operating in parallel in an air separation plant is considered and the operation and maintenance schedule are optimized simultaneously. Objective function is the minimization of the total startup, shutdown, and power consumption costs of the compressors as well as the procurement cost of products from external sources. Three different maintenance policies are considered: (i) fixed maintenance plan, (ii) flexible maintenance plan through the simultaneous optimization of operational and maintenance tasks, and (iii) flexible maintenance plan considering maintenance workforce limitations. Optimization is performed for policies (ii) and (iii) in separate.
Optimization of maintenance scheduling either in itself or embedded in the whole SDO optimization of ship energy systems is an interesting endeavor. Taking into consideration that maintenance and reliability are directly interrelated, SDO optimization of ship energy systems including both reliability and maintenance scheduling is even more interesting and challenging.
5.6. Optimization in Modeling and Modeling for Optimization
It is interesting to mention that optimization can be used also for development of the model of a system, no matter whether the model will be used for optimization or not. Such an application is described in No. 33 [66]. The purpose was to develop the model of experimental facility representing the cooling network of an integrated energy system of a notional all-electric ship. The parameters appearing in the equations of the model were calculated using experimental data and applying multiobjective optimization. Three objectives were considered: (i) maximization of the Index of Agreement (IA), (ii) maximization of the modeling efficiency (ME), and (iii) minimization of the root-mean-square error (RMSE). In the particular work, the model was then used for optimization of the system.
Care should be exercised in building the model of a system that will be used for optimization, for the following reason. At each iterative step during the numerical solution, the optimizer calls the model of the system, which may consist of hundreds or even thousands of algebraic and/or differential equations, in order to evaluate the objective function. There may be thousands of iterations that may require computational capacity not available or unacceptably long convergence time. This is why, there is often need to develop reduced models and to consider modeling and optimization not as sequential tasks but in an integrated approach [95].
6. Functional and Physical Expansion of the System Boundary
6.1. Inclusion of Electrical and Control Engineering Aspects
It is clear from the preceding that subjects related to electrical and control engineering have been considered beyond the limits of this review.
However, with the continuous expansion of electrification of ships, the advent of hybrid systems including thermal and/or electric energy storage, the coming of renewables on board, and the need for integration of many energy technologies, there will be increasing need of an interdisciplinary approach. Many articles in Table 1 include in their study photovoltaics, supercapacitors, batteries, and cold ironing (i.e., shore connection for electricity supply while in port) together with diesel engines, gas turbines, and steam turbines. Thus, the border of the system under study is continuously expanding. Examples of optimization from the electrical and control engineering point of view are presented in Refs. [104,105,106,107,108], while multiphysics approach is followed in No. 56 [87], where the electric power system is modeled along with the cooling system and interactions between the two systems are considered in developing the control system.
6.2. Towards Holistic Ship Optimization
In No. 37 [70], the system to be optimized is not restricted to the energy system (in this case, photovoltaic panels and a battery), but it includes also the hull and the propulsor (water jet) in a multidisciplinary approach. The characteristics of the hull, the water jet, and the energy system as well as their interrelationships are taken into consideration in formulating several optimization problems as stated in Appendix A.
Extension to electrical and control engineering aspects and inclusion of hull and propulsor in optimization give us a hint for future endeavors: by expanding the functional and physical border of the system to be optimized further, we go towards the holistic ship optimization (Principle of holism as stated by Aristotle in his book Metaphysics “the whole is more than the sum of its parts.”), i.e., optimization of the whole ship as a complex system with all its subsystems (hull, total energy system, propulsors, accommodation equipment, deck machinery, navigation equipment, etc.) for its whole life cycle [109,110].
7. Closure
Optimization of energy systems on land started being applied in the 1970s with continuous development since that time. The triple optimization (synthesis, design, and operation), in particular, has been formally stated and started being developed and applied about 20 years later, again on land installations. If the journal article search performed with this opportunity has not missed related contributions, optimization of energy systems on ships appeared in the first decade of the 21st century. Significant developments in methodologies, algorithms, and applications have been achieved up to now, while further research needs and challenges are required, as explained in Section 5 and Section 6; it is worth summarizing those here:
- Synthesis optimization is always a challenging endeavor: how to support and/or replace the designer’s experience, ingenuity, and inspiration with a computer code?
- Further development of both superconfiguration-based and superconfiguration-free methods for synthesis optimization is needed.
- Synthesis optimization of working fluids has appeared recently on land installations. Its incorporation in the synthesis optimization of the whole system is worth pursuing.
- There is need of further development of methods for SDO optimization of ship energy systems taking into consideration
- transients,
- uncertainties (e.g., in operating profile, cost of fuel, weather conditions, etc.),
- reliability–availability of equipment,
- combinations of the preceding.
- Interdisciplinary approach needs to be followed, so that aspects not only of mechanical engineering but also of other disciplines such as electrical and control engineering are taken into consideration in optimization.
- The border of the system to be optimized needs to be further and further expanded, with the aim of including the ship as a whole.
The preceding makes it rather clear that there are many interesting and challenging subjects that need to be addressed, and there are areas for further development of methodology combined with applications on ship energy systems.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Symbols and Abbreviations
| A | Heat transfer area |
| AC | Alternating current |
| AM-CCPS | Adaptive Multicontext Cooperatively Coevolving Particle Swarm Optimization Algorithm |
| APC | Absorption Power Cycle |
| AR | Absorption Refrigeration |
| BOG | Boil-Off Gas |
| COBYLA | Constraint Optimization BY Linear Approximation |
| COGES | Combined Gas turbine, Electric generator and Steam turbine |
| CPP | Controllable Pitch Propeller |
| D | Design |
| DC | Direct current |
| DDP | Deterministic Dynamic Programming |
| DE | Diesel engine |
| DF | Dual fuel |
| DG | Diesel-generator |
| DSOx | Desulphurization |
| DNOx | Denitrification |
| total exergy supplied to the system | |
| EEDI | Energy Efficiency Design Index |
| EEOI | Energy Efficiency Operational Indicator |
| EG | Exhaust gas |
| EGR | Exhaust gas recirculation |
| ESS | Energy storage system |
| FC | Fuel cell |
| fmincon | Find minimum of constrained nonlinear multivariable function |
| FPP | Fixed pitch propeller |
| GAMS | General Algebraic Modeling System |
| GE | Genetic Algorithm |
| GHG | Greenhouse gas |
| GRG | Generalized Reduced Gradient |
| GT | Gas turbine |
| GWP | Global Warming Potential |
| GUROBI | Zonghao Gu, Edward Rothberg, Robert Bixby |
| HESS | Hybrid Energy Storage System |
| HRSG | Heat Recovery Steam Generator |
| IES | Integrated Energy System |
| INTLAB | Interval Laboratory |
| ISCA | Improved Sine Cosine Algorithm |
| JCW | Jacket cooling water |
| JW | Jacket water |
| KC | Kalina cycle |
| LNG | Liquefied natural gas |
| MCFC | Molten Carbonate Fuel Cell |
| MCR | Maximum Continuous Rating |
| MIDACO | Mixed Integer Distributed Ant Colony Optimization Solver |
| MINLP | Mixed Integer Nonlinear Programming |
| MOPSO | Multiobjective Particle Swarm Optimization |
| Nlopt | Nonlinear optimization |
| NSGA | Nondominated Sorting Genetic Algorithm |
| NPV | Net present value |
| O | Operation |
| ORC | Organic Rankine Cycle |
| PEM | Proton exchange membrane |
| PSO | Particle swarm optimization |
| PT | Power turbine |
| PV | Photovoltaics |
| PWC | Present worth cost |
| Ren | Renewable |
| RO | Reverse osmosis |
| S | Synthesis |
| SCBC | Supercritical CO2 Brayton cycle |
| SQP | Sequential Quadratic Programming |
| StrGA | Struggle Genetic Algorithm |
| U | Overall heat transfer coefficient |
| Net power output | |
| WHR | Waste heat recovery |
| WJ | Water jet |
Appendix A. Main Characteristics of Journal Articles on Optimization of Ship Energy Systems
Main characteristics of articles on optimization of energy systems of ships published in journals are written in this Appendix. The articles are written in chronological order, as in Table 1. In order to save space, only the authors’ names, the journal, and year of publication are given here for each article, while complete publication details are written in the References.
Two numbers are written before the author(s) names: the first one is the number of the article in Table 1 and the second one, in bracket, is the number in the References.
- [37] Dimopoulos, G.G.; Frangopoulos, C.A. International Journal of Thermodynamics 2008. System: superconfiguration of a COGES system of an LNG carrier with high-power gas turbines, moderate power gas turbines, HRSG units of single pressure, HRSG units of double pressure, one steam turbine. SDO optimization. Five operating states. Objective: maximize NPV. Service speed among the independent variables. Solution with two levels: A synthesis and design and (B) operation with time decomposition. Algorithm: a hybrid of Particle Swarm Optimization (PSO) and Struggle Genetic Algorithm (StrGA).
- [18] Dimopoulos, G.G.; Kougioufas, A.V.; Frangopoulos, C.A. Energy 2008. System: superconfiguration of a COGES system of a cruise liner with high-power gas turbines, moderate power gas turbines, HRSG units of single pressure, HRSG units of double pressure, and one steam turbine. SDO optimization. Solution with two levels: A synthesis and design and B operation with time decomposition. Three operating states. Objective: minimize total annualized cost. Algorithm: a hybrid of Particle Swarm Optimization (PSO) and Struggle Genetic Algorithm (StrGA).
- [38] Dimopoulos, G.G.; Stefanatos, I.C.; Kakalis, N.M.P. Energy 2013. System: steam methane prereformer for marine molten carbonate fuel cells (MCFC) fueled by liquefied natural gas (LNG). Design optimization at nominal operating conditions. Objective: minimization of the total irreversibility of the system subject to design, space, technical, and operational constraints. Algorithm: SQP implemented in gPROMS software.
- [39] Larsen, U.; Pierobon, L.; Haglind, F.; Gabrielii, C. Energy 2013. System: ORC with heat from exhaust gases of a diesel engine of MCR 72,240 kW. Synthesis and design (boiler pressure only) optimization: determine the optimum working fluid, boiler pressure, and Rankine process layout. Objective: maximize thermal efficiency. Algorithm: GA.
- [40] Larsen, U.; Nguyen, T.; Knudsen, T.; Haglind, F. Energy 2014. System: Kalina cycle with heat from exhaust gases of a large diesel engine. Design optimization (at nominal conditions) of four variations of the cycle: Reference cycle, Split cycle, Reference cycle with reheat, Split cycle with reheat. Objective: maximize net power output (equivalent to maximum efficiency, because the inlet and outlet temperatures of the exhaust gases are considered fixed). Algorithm: GA.
- [41] Baldi, F.; Larsen, U.; Gabrielii, C. Ocean Engineering 2015. System: initial—two diesel main engines driving one propeller and one shaft generator and two DG sets of a Panamax product/chemical tanker. Retrofit: ORC operating on exhaust gas heat of the main engines. Design and operation optimization. Discretized annual load profile. Objective: minimization of fuel consumption. Economic evaluation is performed after optimization, for the optimal system. Algorithm: GA.
- [19] Kalikatzarakis, M.; Frangopoulos, C.A. International Journal of Thermodynamics 2015. System: ORC with heat from the cooling circuit (charge air, cylinder cooling water, and lubricating oil). Evaluation criteria: technical, economic, environmental. Design and operation optimization at two levels. Four operating modes. Objectives: Operation—maximize the net savings in each one of the four modes of operation considered. Design—maximize NPV. Algorithm: at each level, GA determines a near optimal solution, while GRG2 determines the optimal solution.
- [42] Lan, H.; Wen, S.; Ying-Yi Hong, Y.-Y.; Yu, D.C.; Zhang, L. Applied Energy 2015. System: PV, DG set, and battery on an oil tanker. Electricity production only (propulsion by steam turbine). Design optimization (sizing of PV and battery, while the power of the DG set is predetermined so that it covers the loads completely). Five operating states (electric load) are considered. Biobjective: minimize total cost and minimize CO2 emissions. Algorithm: Multiobjective Particle Swarm Optimization (MOPSO) combined with elitist Nondominated Sorting Genetic Algorithm (NSGA-II).
- [43] Soffiato, M.; Frangopoulos, C.A.; Manente, G.; Rech S.; Lazzaretto, A. Energy Conversion and Management 2015. System: ORC operating on low-temperature waste heat of main engines of an LNG carrier. Design optimization of each of the alternative configurations and selection of the best one. Objective: maximization of the net power output. Method: HEATSEP for the heat exchangers part. Software: MATLAB Simulink and fmincon MATLAB function with SQP.
- [44] Solem, S.; Fagerholt, K.; Erikstad, S.O.; Patricksson, Ø. Journal of Marine Science and Technology 2015. System: a set of DG sets (diesel-electric machinery). Synthesis design and operation optimization considering lifetime of 20 years, divided in time periods and operational states. The number (configuration), the nominal power, and the load of each DG set throughout the lifetime are determined. Objective function: minimize (investment + operation costs). NOx tax is included, if applicable. Algorithm: commercial solver by means of the branch and bound technique.
- [45] Baldi, F.; Ahlgren, F.; Melino, F.; Gabrielii, C.; Andersson, K. Energy Conversion and Management 2016. System: four diesel engines connected to two propeller shafts, four diesel-generator sets, exhaust gas boilers, two auxiliary boilers, and one compression chiller of a cruise ship. Operation optimization. In addition to the current system, the installation of a shaft generator/motor on each of the two propeller shafts is studied. Objective: minimization of fuel consumption. The engines are grouped in engines of equal size and performance. In each group, the operating engines are equally loaded. Independent variables: the number of operating engines in each group (integer) and the total load of each group (continuous). Algorithm: the problem is of MINLP. SQP of MATLAB is used for the nonlinear part and a branch-and-bound method is applied for handling the integer variables.
- [46] Benvenuto, G.; Trucco, A.; Campora, U. Journal of Engineering for the Maritime Environment 2016. System: WHR system consisting of a power turbine and double-pressure Rankine cycle of a Suezmax crude oil tanker. Design optimization at nominal conditions and performance evaluation at off-design conditions. Objective: maximize total efficiency (including the power of the diesel engine). Method: systematic variation of certain variables, in a range of values of each one. One variable at a time. No optimization algorithm was used.
- [47] Dimopoulos, G.G.; Stefanatos, I.C.; Kakalis, N.M.P. Energy Conversion and Management 2016. System: molten carbonate fuel cell (MCFC) simple or combined with steam cycle cogeneration system of an offshore supply vessel. Design optimization. Objective: maximization of exergetic efficiency. Algorithm: SQP implemented in gPROMS software.
- [48] Wang, K.; Yan, X.; Yuan, Y.; Li, F. Transportation Research-Part D 2016. System: main engine of a cruise ship on the Yangtze river. Speed optimization only in real time. Before applying optimization, wavelet neural network is used to predict wind speed and water depth for a short time ahead. Objective: minimize fuel consumption of main and auxiliary engines, as well as cost of sailing time from port A to port B, converted to equivalent fuel consumption. Method: dynamic optimization (details of algorithm are not given).
- [49] Wen, S.; Lan, H.; Hong, Y.-Y.; Yu, D.C.; Zhang, L.; Cheng, P. Applied Energy 2016. Experimental work in the laboratory: performance evaluation of PV on a swinging platform. System: PV modules, diesel generator, and a NaS battery as ESS. Five loading conditions are considered pertinent to an oil tanker. Design (battery sizing only) and operation optimization. Objective: minimize cost of fuel + cost of battery. Independent variables are the power output of the diesel generator and the capacity of the battery. Method: interval optimization. Algorithm: INTLAB-Version 5.5 with MATLAB.
- [50] Yang, M.-H. Energy 2016. System: transcritical ORC using heat from exhaust gas, cylinder cooling water, scavenge air cooling water, and lubricating oil from a marine diesel engine of 68,640 kW in a merchant ship. Various fluids are investigated. Design optimization. Objective: minimize levelized energy cost (LEC). Independent variables: pressure and temperature of the working fluid at the inlet of the expander. Solution procedure: first derivative of LEC with respect to each independent variable equal to zero.
- [51] Kalikatzarakis, M.; Frangopoulos, C.A. Journal of Engineering for the Maritime Environment 2017. System: ORC with heat from the cooling circuit (charge air, cylinder cooling water, and lubricating oil) of a containership. SDO optimization: four operating states. Partial load performance of the ME. The HEATSEP method is used for optimization of the heat exchanger network. Objective: maximize NPV. Algorithm: GA determines a near optimal solution, while GRG2 determines the optimal solution.
- [52] Kyriakidis, F.; Sørensen, K.; Singh, S.; Condra, T. Energy Conversion and Management 2017. System: combination of EGR with Rankine cycle using heat from the cooling circuits and exhaust gases of the two-stroke ME (MCR 23,000 kW). Two configurations are studied: (1) with double-pressure steam turbine and (2) with triple-pressure steam turbine. Design optimization. No partial load performance. Objective: maximize net power output. Algorithms: SQP for configuration 1 and GA for configuration 2.
- [53] Nemati, A.; Sadeghi, M.; Yari, M. Desalination 2017. System: two-stage ORC using heat only of the exhaust gases of the diesel engine and reverse osmosis desalination unit. Design optimization at nominal point. Biobjective: maximize exergetic efficiency and minimize total unit product cost. Algorithm: GA.
- [54] Rech, S.; Zandarin, S.; Lazzaretto, A.; Frangopoulos, C.A. Applied Energy 2017. System: three configurations of ORC operating on waste heat of Marine Diesel Engines. Modeling: design and off-design, steady-state, and dynamic models. Design and operation optimization taking partial load into consideration. Alternative configurations are compared. Four operating states. Objective: maximization of the net power output of the ORC. The system is so designed that it reaches stable operation after transient conditions (change of ship speed and, consequently, power output of the main engines) in a reasonable length of time.
- [55] Sharma, O.P.; Kaushik, S.C.; Manjunath, K. Thermal Science and Engineering Progress 2017. System: supercritical CO2 regenerative recompression Brayton cycle (RRCBC) with heat from marine gas turbine. Energy and exergy analysis. Optimization: only the pressure ratio for maximizing efficiency at design point is determined by drawing related diagrams.
- [56] Wen, S.; Lan, H.; Yu, D.C.; Fu, Q.; Hong, Y.-Y.; Yu, L.; Yang, R. Energy 2017. System: diesel generator and PV with hybrid energy storage comprising lead-acid battery, Li-ion battery, and supercapacitor in an oil tanker. The motion of the ship, including rolling, is taken into consideration in calculating the electric power produced by the PVs. Method of analysis: a frequency analysis of the imbalanced power, i.e., the power not covered by the PVs, is performed by Discrete Fourier Transform (DFT). Three types of storage technologies are considered for the HESS: lead-acid battery, which has high energy density, is suitable for mitigating the relatively slowly varying component of imbalanced power. Lithium ion batteries respond faster and exhibit high cycle efficiencies. Therefore, they can be used to accommodate the component of variation of imbalanced power corresponding to the middle-frequency range. Owing to its excellent performance and rapid response, a supercapacitor is employed to smooth out the most dramatic power surges. Design optimization. Profile continuous in time. Objective: minimize total cost of the ESS. Independent variables: the cut-off frequencies, which affect the rated power and capacity of each storage technology. Algorithm: PSO.
- [57] Ancona, M.A.; Baldi, F.; Bianchi, M.; Branchini, L.; Melino, F.; A. Peretto, A.; Rosati, J. Energy Conversion and Management 2018. System: four diesel engines connected to two propeller shafts, four diesel-generator sets, exhaust gas boilers, two auxiliary boilers, and one compression chiller on a cruise ship. Operation optimization. In addition to the current system, alternative configurations have been considered: (a) mechanical propulsion with thermal storage, (b) electric propulsion, (c) electric propulsion with thermal storage, and (d) electric propulsion with thermal storage and absorption chiller. Objective: maximization of efficiency (minimization of fuel consumption). Independent variables: the load of each engine. In case of thermal storage, the volume of the storage tank is an independent variable too. Algorithm: Energy Grids Optimizer (EGO) using a GA.
- [58] Gao, D.; Wang, X.; Wang, T.; Wang, Y.; Xu, X. Energies 2018. System: two diesel generators, AC/DC, DC/DC, DC/AC converters, lithium batteries, DC bus, propeller, and propulsion controller. Experimental setting only. Examples of ships mentioned: ferries and water buses. Multiobjective operation optimization. The optimal load allocation among the two diesel generators and the batteries is determined for a single operation cycle of 120 min of the ship including start-up, acceleration, full speed ahead, deceleration, and stop. Objectives: minimize fuel consumption, minimize emissions, and maximize endurance (as it is expressed by the difference between the initial and final state of charge of the batteries: minimum difference). Algorithm: improved NSGA-II Algorithm.
- [59] Kwak, D.-H.; Heo, J.-H.; Park, S.-H.; Seo, S.-J.; Kim, J.-K. Energy 2018. System: small-scale boil-off gas reliquefaction plant on an LNG-fueled ship. Design optimization at nominal conditions. Objective: minimization of the work required per unit mass of BOG reliquefied. Algorithm and software: GA in MATLAB.
- [60] Nour Eddine, A.; Chalet D.; Faure X.; L. Aixala, L.; Chess, P. Energy 2018. System: experimental set up with automotive engine, simulating performance of a marine engine. Two thermoelectric materials were tested. The clamping pressure was changed in a certain region, and the point of maximum power was determined. The effect of load resistance and voltage of the thermoelectric generator were investigated. Not a formal, mathematical optimization.
- [7] Sakalis, G.N.; Frangopoulos, C.A. Applied Energy 2018. System: superconfiguration including diesel engines, bottoming Rankine cycle, exhaust gas boiler, auxiliary boilers, and DG sets. SDO optimization. Four operating states. Objective: minimize PWC. Algorithm: GA. One-step solution of the problem.
- [61] Tang, R.; Li, X.; Lai, J.J.A.E. Applied Energy 2018. System: photovoltaic/battery/diesel/ cold-ironing hybrid energy system. Operation optimization: optimal power flow dispatching. Hourly load profile for 3 days. Objective: minimize total cost of electric energy. Algorithm: Adaptive Multicontext Cooperatively Coevolving Particle Swarm Optimization Algorithm (AM-CCPSO).
- [62] Tang, R.; Wu, Z.; Li, X. Energy 2018. System: photovoltaic/battery/diesel/cold-ironing hybrid energy system. Operation optimization: optimal power flow dispatching during cold ironing. Hourly load profile for 3 days. Objective: minimize total cost of electric energy. Method: optimal control and model predictive control (MPC) methods.
- [63] Trivyza, N.; Rentizelas, A.; Theotokatos, G. Energy Conversion and Management 2018. System: main and auxiliary engines of various types and fuels, boilers of various fuels, MCFCs, WHR, emission abatement technologies in an Aframax tanker. SD optimization. Operation by predetermined rules. Operation profiles for propulsion, electric, and thermal loads are considered in the form of frequency of occurrence. Four objectives: (i) minimize life cycle cost, (ii) minimize life cycle CO2 emissions, (ii) minimize life cycle SOx emissions, (ii) minimize life cycle NOx emissions. Decision variables: (a) type of fuel, type of engine, and nominal power of each engine; for both main and auxiliary engines; (b) type of boilers, number of boilers, and fuel type; (c) existence of energy efficiency technologies; and (d) existence of emission abatement technologies. Algorithm: Nondominated Sorting Genetic Algorithm NSGA-II.
- [64] Wang, K.; Yan, X.; Yuan, Y. Journal of Engineering for the Maritime Environment 2018. System: two dual fuel main engines with shaft generators and two DG sets in a bulk carrier. Design and operation optimization. Single-point optimization for four different power requirements. Three objectives: (i) fuel consumption, (ii) CO2 emissions, and (iii) power safety margin: (P-Q)/P, where P the available electric power and Q the electric load. Nominal power output of the main engines and the DG sets are design-independent variables, while the speed of the vessel, rotational speed of the main engines, and the load of the generators are operation-independent variables. Algorithm: PSO.
- [65] Wang, K.; Yan, X.; Yan, Y.; Jiang, X.; Lin, X.; Negenborn, R.R. Transportation Research-Part D 2018. Further development of previous work (No. 14). System: main engine in a cruise ship on the Yangtze river. Speed optimization only in real time. A whole route is divided into n legs with n time steps. The optimal speed is determined for each step. Changes in the environmental conditions at each step are taken into consideration. Constraint on the whole sailing time from port A to port B is considered. Objective: minimize EEOI. Method: model predictive control and dynamic optimization. Algorithm: PSO.
- [66] Yang, S.; Chagas, M.B.; Ordonez, J.C. Applied Thermal Engineering 2018. System: laboratory experimental facility of an integrated energy system (IES) cooling network of a notional all-electric ship. Graph theory was used to represent the network. The network model was formulated and solved in MATLAB. The equations were solved using the adaptive backward differentiation formula for transient cases and trust-region Newton method for steady-state solutions. First optimization: building the model of the system. Performance parameters were estimated using experimental data. Objective: maximize the Index of Agreement (IA) and modeling efficiency (ME) and minimize the root-mean-square error (RMSE). Algorithm: Mixed Integer Distributed Ant Colony Optimization solver (MIDACO). The design space towards global optimum is updated by the oracle penalty method. The case also was investigated wherein all three metrics were considered simultaneously by solving a multiobjective optimization problem with Utopia–Nadir Balance concept. Second optimization: integrative thermodynamic optimization: the system is considered as a whole. The total heat exchanger inventory allocation throughout the IES was optimized by minimizing the maximum temperature in the system. Parametric sweeps were conducted instead of using sophisticated optimization techniques to obtain clear physical insights into the evolution of system architecture towards the optimum with respect to the parameters of interest.
- [67] Al-Falahi, M.D.A.; Jayasinghe, S.D.G.; Enshaei, H. Energy 2019. System: two diesel-generator sets and one battery pack in all-electric short-haul ferry. Operation optimization. Four operating states during a round trip of 60–100 min. Objective function: minimization of the operating cost, as expressed by minimization of fuel consumption. Independent variables: power output of each DG set and charging power of the battery pack. Algorithm: hybrid of Grey Wolf Optimizer and Fuzzy Logic expert system. GWO determines the power output of each DG set, while FL determines the charging power of the battery pack. Iteration between GWO and FL is performed until convergence.
- [68] Bordin, C.; O. Mo, O. Journal of Energy Storage 2019. System: battery for electricity storage operating with diesel or gas generators in all-electric ship. Design and operation optimization in terms of battery choice, sizing, and energy flows management among the different energy units. A load profile is considered (hour, day, week, etc.) that is repeated throughout the typical year. Objective function: minimize total cost (investment + operation). Algorithm: Mixed Integer Linear Programming.
- [69] Dolatabadi, A.; Ebadi, R.; Mohammadi-Ivatloo, B. Journal of Operation and Automation in Power Engineering 2019. System: HESS—hybrid power system with energy storage (ESS), photovoltaics (PV), and diesel generator in oil tanker. The stochastic character of solar radiation is taken into consideration. Design optimization (sizing of the HESS). The load profile is approximated with five periods of steady-state operation. The operation is rule-based. Objective: minimize the annualized cost of the system that includes capital, fuel, maintenance, and emissions cost. Only the size of PV (kW) and battery (kWh) are determined. Algorithm: MINLP problem implemented in GAMS 23.6 software and solved using the SBB solver. GAMS: General Algebraic Modeling System.
- [70] Esmailian, E.; Gholami, H.; Røstvik, H.N.; Menhaj, M.B. Energy Conversion and Management 2019. System to be optimized: hull, water jet, and building integrated photovoltaic (BIPV) system including a battery of a planing craft with water jet propulsion operating in a river. Design optimization. Six optimization problems are formulated and solved. Objectives: (i) lifetime fuel consumption, (ii) overall propulsive efficiency, (iii) total ship resistance, (iv) GHG emissions across the entire operating range, and (v) total cost. Two of the five objectives are selected for each optimization problem in a biobjective optimization. Algorithm: Nondominated Sorting Genetic Algorithm (NSGA-II).
- [71] Jaurola, M.; Hedin, A.; Tikkanen, S.; Huhtala, K. Journal of Marine Science and Technology 2019. System: diesel-mechanical with shaft generator or hybrid electric power system including a battery, with the shaft generator being able to operate as motor in fishing boat. Operation optimization. Series of six steady-state operation modes. Objective: minimize fuel consumption. Independent variables: the power output of each component. Algorithms: combined use of NLopt and COBYLA.
- [72] Jaurola, M.; Hedin, A.; Tikkanen, S.; Huhtala, K. Journal of Marine Science and Technology 2019. Extension of the previous work that includes comparison among different options of propeller (FPP and CPP) and propulsion control (pitch, speed, or both).
- [73] Jianyun, Z.; Li, C.; Lijuan, X.; Bin, W. Energy 2019. System: plug-in hybrid electric propulsion systems (HEPSs), including the diesel engines, motors, battery modules, and gearboxes in tug ship. Design optimization: determine the size of major components of the system. Rule-based energy management. Two operating modes are considered: transit mode and loading mode. Biobjective: (i) minimize fuel consumption and (ii) minimize GHG emissions. Algorithm: NSGA-II.
- [74] Kim, D.; Hwang, C.; Gundersen, T.; Lim, Y. Energy 2019. System: alternative BOG reliquefaction systems in LNG carrier. The ship has high pressure gas injection engines for propulsion and duel fuel DG sets. Design optimization. Comparison of alternative configurations of the BOG reliquefaction systems. Objective: minimization of the total annual cost. Algorithm: PSO.
- [75] Koo, J.; Oh, S.-R.; Choi, Y.-U.; Jung, J.-H.; Park, K. Energies 2019. System: ORC exploiting the low temperature of the LNG (“cold” energy) for condensing the working fluid in LNG-powered ship with two alternatives: high-pressure DF engine and medium-pressure DF engine. Jacket cooling water is the heat source. Three alternative configurations are studied for each alternative (high-pressure DF engine and medium-pressure DF engine) with nine alternative working fluids. Design optimization. Objective: where the net power output of the ORC system and the total exergy supplied to the ORC system by the LNG streams. Algorithm: PSO.
- [76] Marques, C.H. Belchior, C.R.P.; Caprace, J.-D. Ocean Engineering 2019. Theory. System: slow speed diesel engines and propellers in LNG carrier. Constant weather conditions are considered. SDO optimization. Strength and cavitation of propeller blades is estimated along the way. Objective: maximize NPV. Algorithm: not clearly specified.
- [77] Marques, C.H. Belchior, C.R.P.; Caprace, J.-D. Ocean Engineering 2019. Application. System: slow speed diesel engines and propellers in LNG carrier. Constant weather conditions are considered. SDO optimization. Strength and cavitation of propeller blades is estimated along the way. Objective: maximize NPV. Algorithm: Differential Evolution Optimization Algorithm.
- [78] Ouyang, T.; Su, Z.; Huang, G.; Zhao, Z.; Wang, Z.; Chen, N.; Haozhong, H. Energy Conversion and Management 2019. System: dual loop ORC system, absorption refrigeration unit, Exhaust gas purification unit (desulfurization and denitrification) based on photocatalytic oxidation in bulk carrier. Design optimization. Objective: maximize the equivalent power output of the combined system (net power of the dual loop ORC + equivalent power of the absorption refrigeration (electric power that would be required by a compression refrigeration unit). Decision variables: mixture ratios of the high temperature and low temperature ORC, evaporation pressure, and condensation temperature of the high temperature ORC. Algorithm: GA. EEDI, EEOI, energy and exergy efficiencies, and reduction of SOx and NOx are calculated after optimization.
- [8] Sakalis, G.N.; Tzortzis, G.J.; Frangopoulos, C.A. Energies 2019. Static problem. System: superconfiguration including gas turbines, bottoming Rankine cycle, exhaust gas boiler, auxiliary boilers, and DG sets. SDO optimization. Four operating states. Objective: minimize PWC. Algorithm: GA. One-step solution of the problem. Dynamic problem. System: superconfiguration including gas turbines, 2- and 4-stroke diesel engines, bottoming Rankine cycle, auxiliary boiler, and DG sets. Dynamic SDO optimization. Initially continuous and then discretized load profile. Mixed Integer Dynamic Optimization Problem (MIDO). Objective: maximize NPV. Algorithm: Direct sequential method combined with NLP solver implanted in gPROMS software.
- [79] Trivyza, N.L.; Rentizelas, A.; Theotokatos, G. Energy 2019. System: DG sets, MCFCs, thermal boilers, WHR, and carbon capture technology in cruise ship with electric propulsion. Operation profiles for electric and thermal loads are considered. SD optimization. Load profiles are considered in the form of frequency of occurrence. Operation with predetermined rules. Two objectives: (i) minimize life cycle cost and (ii) minimize life cycle CO2 emissions. Four scenarios are examined regarding the policy on CO2. Algorithm: Nonsorting Genetic Algorithm NSGA-II.
- [23] Tzortzis, G.J.; Frangopoulos, C.A. Journal of Engineering for the Maritime Environment 2019. System: superconfiguration with 4-stroke diesel engines, DG sets, HRSG, steam turbine, and auxiliary boiler in LNG carrier. Dynamic SDO optimization. The speed of the ship and, consequently, the propulsion power, is under optimization. Electric and thermal loads are calculated as functions of the brake power of the main engines during the travel, while they are considered constant and known in port. Additionally, the weather conditions along the route are taken into consideration. A mixed integer-nonlinear programming problem is formulated. Initially continuous and then discretized load profile. Objective: minimize PWC. Solution method: direct sequential. Algorithm: CVP-SS software: gPROMS.
- [80] Yan, Y.; Zhang, H.; Long, Y.; Wang, Y.; Liang, Y.; Song, X.; Yu, J.J.Q. Journal of Cleaner Production 2019. System: superconfiguration including diesel engine with exhaust gas after treatment facilities, gas turbine, dual-fuel engine, EGBs, wind turbines and PV panels with battery, and compression chiller in cruise ship. SDO optimization. Objectives: (i) minimize total annual cost and (ii) minimize size (space occupied and weight). They are considered in separate or together (multiobjective optimization). Operation profile: operation state is divided into three types: (i) navigation, (ii) port stay and sea stay, and (iii) maneuvering, which accounts for 59%, 33%, and 8% of the operation period, respectively. Three typical days to represent winter, summer, and mid-season with a duration of 182, 62, and 121 days, respectively. Hourly profile of each load in each typical day. Algorithms: GUROBI 8.1.0 for the single-objective problem and augmented ε-constraint method for the biobjective problem.
- [81] Bolbot, V.; Trivyza, N.L.; Theotokatos, G.; Boulougouris, E.; Rentizelas, A.; Vassalos, D. Energy 2020. System: alternative systems with diesel or dual fuel engines and various fuels in cruise ship. Each combination is optimized in separate. Design optimization: the operating profile in the form of frequency of occurrence of loads is considered. Objectives: (i) life cycle cost and (ii) lifetime CO2 emissions. Independent variables for each alternative configuration: number of DG sets and nominal power output of each set. The blackout frequency and the unavailability of a generator (safety metrics) are estimated for the optimal plant. Algorithm: Nonsorting Genetic Algorithm II (NSGA-II).
- [82] Chen, H.; Zhang, Z.; Guan, C.; Gao, H. Energy 2020. System: hydrogen fuel cell stack with battery and supercapacitors for electric energy storage (HESS: hybrid energy storage system) in passenger boat. Design and operation optimization: sizing of the system and power allocation (power flow between the fuel cell and the storage system). Objective function: weighted summation of the battery degradation, power quality as expressed by voltage fluctuation, useful energy losses (in place of energy efficiency), and device cost. Algorithm: Whale Optimization Algorithm.
- [83] Feili, M; Ghaebi, H.; Parikhani, T.; Rostamzadeh, H. Thermal Science and Engineering Progress 2020. System: absorption power cycle (APC), i.e., Kalina cycle, and a humidification- dehumidification desalination (HDH) unit. APC uses heat from the cooling water and HDH heat from exhaust gases of the main engine. Multiobjective design optimization. Objectives: maximize energy efficiency, maximize exergy efficiency, and minimize unit cost of fresh water. Finally, one objective function is formulated as a properly weighted summation of the individual objectives. Algorithm: GA.
- [84] Feng, Y.; Du, Z.; Shreka, M.; Zhu, Y.; Zhou, S.; Zhang, W. Energy Conversion and Management 2020. System: supercritical CO2 Brayton cycle (SCBC) combined with Kalina cycle (KC) with heat from the exhaust gas of MAN 8S90ME-C10.2 low-speed two-stroke diesel engine. At load of the diesel engine lower than 85%, only the KC recovers energy from the exhaust gas. Design optimization at nominal point of the engine. Single objective: maximize net power output of each cycle in separate. Biobjective: (i) maximize efficiency and (ii) maximize Wnet/UA for each cycle converted in a single objective with the weighted sum function. Instead of formal optimization, each objective is drawn as a function of various parameters. Certain graphs reveal an optimal point.
- [85] Letafat, A.; Rafiei, M.; Sheikh, M.; Mosayeb Afshari-Igder, M.; Banaei, M.; Boudjadar, J.; Khooban, M.H. Journal of Energy Storage 2020. System: PEM fuel cells and battery in ferry boat. Cold-ironing at harbor. Optimization of sizing of fuel cells and battery and operation optimization (power from fuel cells, from cold-ironing, and from/to battery for a 24-h round trip). Propulsion and electric load for each hour of a 24-h round trip. Objective: total daily cost (capital and operation). Algorithm: Improved Sine Cosine Algorithm (ISCA), while Harmony Search is used to prevent SCA from being trapped in local optima.
- [86] Tian, Z.; Yue, Y.; Zhang, Y.; Gu, B.; Gao, W. Energies 2020. System: three ORC cycles combined. They use heat from the JCW and exhaust gas for evaporation and LNG to be burned in the main engine for condensation of the fluids. Design optimization at full load of the main engine. Only two independent variables: pressures of evaporator and condenser. Various fluids are investigated. Two objectives: (i) maximize energy and exergy efficiencies and (ii) minimize (system investment/payback period). The standard Technique for Order Preference by Similarity to Ideal Situation (TOPSIS) method attempts to choose alternatives that have the shortest distance from the ideal solution. Algorithm: NSGA-II.
- [87] Trinklein, E.H.; Parker, G.; McCoy, T. Energy 2020. System: gas turbine-generator, power electronics, cooling circuit, and thermal and electric energy storage. Operation optimization: optimal control. Objective: minimize exergy destruction of the whole system, excluding the gas turbine-generator at each control update. Method: model predictive control. The optimization executes the ship simulation within a call to the nonlinear optimization algorithm fmincon. A multiphysics-based model is used: the electric power system is modeled along with the cooling system and interactions between the two shipboard systems are considered.
- [88] Wu, P.; Bucknall, R. International Journal of Hydrogen Energy, 2020. System: fuel cell and battery propulsion system in coastal ferry. Voyage duration: 1 h. Shore connection is available in all ports. Design and operation optimization. Electric power profile for 3500 s. Solution: inner layer solves the optimal power split problem for given sizing of components. The external layer optimizes the average voyage cost and GWP emissions concurrently. The decision variables of the external layer are a vector of the fuel cell and battery module sizing parameters. The trade-off between the two objectives needs to be determined manually based on the Pareto front. Biobjective: (i) minimize average voyage cost and (ii) minimize GWP emissions. Algorithms: Deterministic Dynamic Programming (DDP) for the inner layer and Nondominated Sorting Genetic Algorithm II for the external layer.
References
- Stoecker, W.F. Design of Thermal Systems, 3rd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1989. [Google Scholar]
- Frangopoulos, C.A. Recent developments and trends in optimization of energy systems. Energy 2018, 164, 1011–1020. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Z.; Sharma, S.; Mian, A.; Lin, T.-E.; Tsatsaronis, G.; Maréchal, F.; Yang, Y. A Review of evaluation, optimization and synthesis of energy systems: Methodology and application to thermal power plants. Energies 2019, 12, 73. [Google Scholar] [CrossRef]
- Frangopoulos, C.A. Optimal Synthesis and Operation of Thermal Systems by the Thermoeconomic Functional Approach. In Analysis and Design of Energy Systems: Thermodynamic Analysis of Industrial Processes, ASME Winter Annual Meeting, San Francisco, CA, USA, 10–15 December 1989; Bajura, R.A., von Spakovsky, M.R., Geskin, E.S., Eds.; ASME: New York, NY, USA, 2020; AES-Volume 10-3, pp. 49–59, Published also in J. Eng. Gas Turb. Power 1992, 114, 707–714. [Google Scholar]
- Frangopoulos, C.A. Intelligent Functional Approach: A method for analysis and optimal synthesis-design-operation of complex systems. In A Future for Energy, Proceedings of Florence World Energy Research Symposium, Florence, Italy, 28 May–1 June 1990; Stecco, S.S., Moran, M.J., Eds.; Pergamon Press: Oxford, UK, 1991; pp. 805–815, Published also in Int. J. Energy-Environ.-Econ. 1991, 1, 267–274. [Google Scholar]
- Frangopoulos, C.A. Optimization of synthesis-design-operation of a cogeneration system by the Intelligent Functional Approach. In A Future for Energy; pp. 597–609, Published also in Int. J. Energy-Environ.-Econ. 1991, 1, 275–287.
- Sakalis, G.N.; Frangopoulos, C.A. Intertemporal optimization of synthesis, design and operation of integrated energy systems of ships: General method and application on a system with Diesel main engine. Appl. Energy 2018, 226, 991–1008. [Google Scholar] [CrossRef]
- Sakalis, G.N.; Tzortzis, G.J.; Frangopoulos, C.A. Intertemporal static and dynamic optimization of synthesis, design and operation of integrated energy systems of ships. Energies 2019, 12, 893. [Google Scholar] [CrossRef]
- Papalambros, P.Y.; Wilde, D.J. Principles of Optimal Design: Modeling and Computation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ravindran, A.; Ragsdell, K.M.; Reklaitis, G.V. Engineering Optimization: Methods and Applications, 2nd ed.; John Wiley and Sons, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Rao, S.S. Engineering Optimization: Theory and Practice, 4th ed.; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison–Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Van Laarhoven, P.; Aarts, E. Simulated Annealing: Theory and Applications; D. Reidel: Boston, MA, USA, 1987. [Google Scholar]
- Freeman, J.A.; Skapura, D.M. Neural Networks; Addison-Wesley: Reading, MA, USA, 1992. [Google Scholar]
- Sakawa, M. Fuzzy Sets and Interactive Multiobjective Optimization; Plenum Press: New York, NY, USA, 1993. [Google Scholar]
- Sciubba, E.; Melli, R. Artificial Intelligence in Thermal Systems Design: Concepts and Applications; Nova Science Publishers, Inc.: Commack, NY, USA, 1998. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Swarm Intelligence; Morgan Kaufmann Publishers: San Francisco, CA, USA, 2001. [Google Scholar]
- Dimopoulos, G.G.; Kougioufas, A.V.; Frangopoulos, C.A. Synthesis, design and operation optimization of a marine energy system. Energy 2008, 33, 180–188. [Google Scholar] [CrossRef]
- Kalikatzarakis, M.; Frangopoulos, C.A. Multi-criteria selection and thermo-economic optimization of organic Rankine cycle system for a marine application. Int. J. Thermodyn. 2015, 18, 133–141. [Google Scholar] [CrossRef]
- Allgor, R.J.; Barton, P.I. Mixed Integer Dynamic Optimization. Comput. Chem. Eng. 1997, 21, 451–456. [Google Scholar] [CrossRef]
- Biegler, L.T.; Cervantes, A.M.; Wachter, M.A. Advances in simultaneous strategies for dynamic process optimization. Chem. Eng. Sci. 2002, 57, 575–593. [Google Scholar] [CrossRef]
- Biegler, L.T.; Grossman, I.E. Retrospective on optimization. Comput. Chem. Eng. 2004, 28, 1169–1192. [Google Scholar] [CrossRef]
- Tzortzis, G.J.; Frangopoulos, C.A. Dynamic optimization of synthesis, design and operation of marine energy systems. Proc. IMechE Part M J. Eng. Marit. Environ. 2019, 233, 454–473. [Google Scholar] [CrossRef]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Processes; Interscience: New York, NY, USA, 1962. [Google Scholar]
- Gelfand, I.M.; Fomin, S.V.; Silverman, R.A. Calculus of Variations; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957; Republished by Dover; 2003. [Google Scholar]
- Vassiliadis, V.S.; Sargent, R.W.H.; Pantelides, C.C. Solution of a class of multistage dynamic optimization problems. 1. Problems without path constraints. Ind. Eng. Chem. Res. 1994, 33, 2111–2122. [Google Scholar] [CrossRef]
- Vassiliadis, V.S.; Sargent, R.W.H.; Pantelides, C.C. Solution of a class of multistage dynamic optimization problems. 2. Problems with path constraints. Ind. Eng. Chem. Res. 1994, 33, 2123–2133. [Google Scholar] [CrossRef]
- Vallianou, V.A.; Frangopoulos, C.A. Dynamic Operation Optimization of a Trigeneration System. Int. J. Thermodyn. 2012, 15, 239–247. [Google Scholar]
- Kim, K.; von Spakovsky, M.R.; Wang, M.; Nelson, D.J. A hybrid multi-level optimization approach for the dynamic synthesis/design and operation/control under uncertainty of a fuel cell system. Energy 2011, 36, 3933–3943. [Google Scholar] [CrossRef]
- Munoz, J.R.; von Spakovsky, M.R. A decomposition approach for the large scale synthesis/design optimization of highly coupled, highly dynamic energy systems. Int. J. Appl. Thermodyn. 2001, 4, 19–33. [Google Scholar]
- Munoz, J.R.; von Spakovsky, M.R. The application of decomposition to the large scale synthesis/design optimization of aircraft energy systems. Int. J. Appl. Thermodyn. 2001, 4, 61–76. [Google Scholar]
- Cohon, J.L. Multiobjective Programming and Planning; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Eschenauer, H.; Koski, J.; Osyczka, A. Multicriteria Design Optimization: Procedures and Applications; Springer: Berlin, Germany, 1990. [Google Scholar]
- Kalyanmoy, D. Multi-Objective Optimization using Evolutionary Algorithms; John Wiley and Sons, Inc.: New York, NY, USA, 2009. [Google Scholar]
- Seyedali, M.; Dong, J.S. Multi-Objective Optimization Using Artificial Intelligence Techniques; Springer: Berlin, Germany, 2019. [Google Scholar]
- Dimopoulos, G.G.; Frangopoulos, C.A. Synthesis, design and operation optimization of the marine energy system for a liquefied natural gas carrier. Int. J. Thermodyn. 2008, 11, 203–211. [Google Scholar]
- Dimopoulos, G.G.; Stefanatos, I.C.; Kakalis, N.M.P. Exergy analysis and optimisation of a steam methane pre-reforming system. Energy 2013, 58, 17–27. [Google Scholar] [CrossRef]
- Larsen, U.; Pierobon, L.; Haglind, F.; Gabrielii, C. Design and optimization of organic Rankine cycles for waste heat recovery in marine applications using the principles of natural selection. Energy 2013, 55, 803–812. [Google Scholar] [CrossRef]
- Larsen, U.; Nguyen, T.; Knudsen, T.; Haglind, F. System analysis and optimisation of a Kalina split-cycle for waste heat recovery on large marine diesel engines. Energy 2014, 64, 484–494. [Google Scholar] [CrossRef]
- Baldi, F.; Larsen, U.; Gabrielii, C. Comparison of different procedures for the optimization of a combined Diesel Engine and organic Rankine cycle system based on ship operational profile. Ocean Eng. 2015, 110, 85–93. [Google Scholar] [CrossRef]
- Lan, H.; Wen, S.; Ying-Yi Hong, Y.-Y.; Yu, D.C.; Zhang, L. Optimal sizing of hybrid PV/diesel/battery in ship power system. Appl. Energy 2015, 158, 26–34. [Google Scholar] [CrossRef]
- Soffiato, M.; Frangopoulos, C.A.; Manente, G.; Rech, S.; Lazzaretto, A. Design optimization of ORC systems for waste heat recovery on board a LNG carrier. Energy Convers. Manag. 2015, 92, 523–534. [Google Scholar] [CrossRef]
- Solem, S.; Fagerholt, K.; Erikstad, S.O.; Patricksson, Ø. Optimization of diesel electric machinery system configuration in conceptual ship design. J. Mar. Sci. Technol. 2015, 20, 406–416. [Google Scholar] [CrossRef]
- Baldi, F.; Ahlgren, F.; Melino, F.; Gabrielii, C.; Andersson, K. Optimal load allocation of complex ship power plants. Energy Convers. Manag. 2016, 124, 344–356. [Google Scholar] [CrossRef]
- Benvenuto, G.; Trucco, A.; Campora, U. Optimization of waste heat recovery from the exhaust of marine diesel engines. Proc. IMechE Part M J. Eng. Marit. Environ. 2016, 230, 83–94. [Google Scholar] [CrossRef]
- Dimopoulos, G.G.; Stefanatos, I.C.; Kakalis, N.M.P. Exergy analysis and optimisation of a marine molten carbonate fuel cell system in simple and combined cycle configuration. Energy Convers. Manag. 2016, 107, 10–21. [Google Scholar] [CrossRef]
- Wang, K.; Yan, X.; Yuan, Y.; Li, F. Real-time optimization of ship energy efficiency based on the prediction technology of working condition. Transp. Res. Part D 2016, 46, 81–93. [Google Scholar] [CrossRef]
- Wen, S.; Lan, H.; Hong, Y.-Y.; Yu, D.C.; Zhang, L.; Cheng, P. Allocation of ESS by interval optimization method considering impact of ship swinging on hybrid PV/diesel ship power system. Appl. Energy 2016, 175, 158–167. [Google Scholar] [CrossRef]
- Yang, M.-H. Optimizations of the waste heat recovery system for a large marine diesel engine based on transcritical Rankine cycle. Energy 2016, 113, 1109–1124. [Google Scholar] [CrossRef]
- Kalikatzarakis, M.; Frangopoulos, C.A. Thermo-economic optimization of synthesis, design and operation of a marine organic Rankine cycle system. Proc. IMechE Part M J. Eng. Marit. Environ. 2017, 231, 137–152. [Google Scholar] [CrossRef]
- Kyriakidis, F.; Sørensen, K.; Singh, S.; Condra, T. Modeling and optimization of integrated exhaust gas recirculation and multi−stage waste heat recovery in marine engines. Energy Convers. Manag. 2017, 151, 286–295. [Google Scholar] [CrossRef]
- Nemati, A.; Sadeghi, M.; Yari, M. Exergoeconomic analysis and multi-objective optimization of a marine engine waste heat driven RO desalination system integrated with an organic Rankine cycle using zeotropic working fluid. Desalination 2017, 422, 113–123. [Google Scholar] [CrossRef]
- Rech, S.; Zandarin, S.; Lazzaretto, A.; Frangopoulos, C.A. Design and off-design models of single and two-stage ORC systems on board a LNG carrier for search of the optimal performance and control strategy. Appl. Energy 2017, 204, 221–241. [Google Scholar] [CrossRef]
- Sharma, O.P.; Kaushik, S.C.; Manjunath, K. Thermodynamic analysis and optimization of a supercritical CO2 regenerative recompression Brayton cycle coupled with a marine gas turbine for shipboard waste heat recovery. Therm. Sci. Eng. Prog. 2017, 3, 62–74. [Google Scholar] [CrossRef]
- Wen, S.; Lan, H.; Yu, D.C.; Fu, Q.; Hong, Y.-Y.; Yu, L.; Yang, R. Optimal sizing of hybrid energy storage sub-systems in PV/diesel ship power system using frequency analysis. Energy 2017, 140, 198–208. [Google Scholar] [CrossRef]
- Ancona, M.A.; Baldi, F.; Bianchi, M.; Branchini, L.; Melino, F.; Peretto, A.; Rosati, J. Efficiency improvement on a cruise ship: Load allocation optimization. Energy Convers. Manag. 2018, 164, 42–58. [Google Scholar] [CrossRef]
- Gao, D.; Wang, X.; Wang, T.; Wang, Y.; Xu, X. An Energy optimization strategy for hybrid power ships under load uncertainty based on load power prediction and improved NSGA-II Algorithm. Energies 2018, 11, 1699. [Google Scholar] [CrossRef]
- Kwak, D.-H.; Heo, J.-H.; Park, S.-H.; Seo, S.-J.; Kim, J.-K. Energy-efficient design and optimization of boil-off gas (BOG) re-liquefaction process for liquefied natural gas (LNG)-fuelled ship. Energy 2018, 148, 915–929. [Google Scholar] [CrossRef]
- Nour Eddine, A.; Chalet, D.; Faure, X.; Aixala, L.; Chess, P. Optimization and characterization of a thermoelectric generator prototype for marine engine application. Energy 2018, 143, 682–695. [Google Scholar] [CrossRef]
- Tang, R.; Li, X.; Lai, J.J.A.E. A novel optimal energy-management strategy for a maritime hybrid energy system based on large-scale global optimization. Appl. Energy 2018, 228, 254–264. [Google Scholar] [CrossRef]
- Tang, R.; Wu, Z.; Li, X. Optimal operation of photovoltaic/battery/diesel/cold-ironing hybrid energy system for maritime application. Energy 2018, 162, 697–714. [Google Scholar] [CrossRef]
- Trivyza, N.; Rentizelas, A.; Theotokatos, G. A novel multi-objective decision support method for ship energy systems synthesis to enhance sustainability. Energy Convers. Manag. 2018, 168, 128–149. [Google Scholar] [CrossRef]
- Wang, K.; Yan, X.; Yuan, Y. Optimizing ship energy efficiency: Application of particle swarm optimization algorithm. Proc. IMechE Part M J. Eng. Marit. Environ. 2018, 232, 379–391. [Google Scholar] [CrossRef]
- Wang, K.; Yan, X.; Yan, Y.; Jiang, X.; Lin, X.; Negenborn, R.R. Dynamic optimization of ship efficiency considering time-varying environmental factors. Transp. Res. Part D 2018, 62, 685–698. [Google Scholar] [CrossRef]
- Yang, S.; Chagas, M.B.; Ordonez, J.C. Modeling, cross-validation, and optimization of a shipboard integrated energy system cooling network. Appl. Therm. Eng. 2018, 145, 516–527. [Google Scholar] [CrossRef]
- Al-Falahi, M.D.A.; Jayasinghe, S.D.G.; Enshaei, H. Hybrid algorithm for optimal operation of hybrid energy systems in electric ferries. Energy 2019, 187, 115923. [Google Scholar] [CrossRef]
- Bordin, C.; Mo, O. Including power management strategies and load profiles in the mathematical optimization of energy storage sizing for fuel consumption reduction in maritime vessels. J. Energy Stor. 2019, 23, 425–441. [Google Scholar] [CrossRef]
- Dolatabadi, A.; Ebadi, R.; Mohammadi-Ivatloo, B. A two-stage stochastic programming model for the optimal sizing of hybrid pv/diesel/battery in hybrid electric ship system. J. Oper. Autom. Power Eng. 2019, 7, 16–26. [Google Scholar]
- Esmailian, E.; Gholami, H.; Røstvik, H.N.; Menhaj, M.B. A novel method for optimal performance of ships by simultaneous optimisation of hull-propulsion-BIPV systems. Energy Convers. Manag. 2019, 197, 111879. [Google Scholar] [CrossRef]
- Jaurola, M.; Hedin, A.; Tikkanen, S.; Huhtala, K. TOpti: A flexible framework for optimising energy management for various ship machinery topologies. J. Mar. Sci. Technol. 2019, 24, 1183–1196. [Google Scholar] [CrossRef]
- Jaurola, M.; Hedin, A.; Tikkanen, S.; Huhtala, K. A TOpti simulation for finding fuel saving by optimising propulsion control and power management. J. Mar. Sci. Technol. 2019. [CrossRef]
- Jianyun, Z.; Li, C.; Lijuan, X.; Bin, W. Bi-objective optimal design of plug-in hybrid electric propulsion system for ships. Energy 2019, 177, 247–261. [Google Scholar] [CrossRef]
- Kim, D.; Hwang, C.; Gundersen, T.; Lim, Y. Process design and economic optimization of boil-off-gas reliquefaction systems for LNG carriers. Energy 2019, 173, 1119–1129. [Google Scholar] [CrossRef]
- Koo, J.; Oh, S.-R.; Choi, Y.-U.; Jung, J.-H.; Park, K. Optimization of an Organic Rankine Cycle system for an LNG-powered ship. Energies 2019, 12, 1933. [Google Scholar] [CrossRef]
- Marques, C.H.; Belchior, C.R.P.; Caprace, J.-D. An early-stage approach to optimise a marine energy system for liquefied natural gas carriers: Part A—Developed approach. Ocean Eng. 2019, 181, 161–172. [Google Scholar] [CrossRef]
- Marques, C.H.; Belchior, C.R.P.; Caprace, J.-D. An early-stage approach to optimise a marine energy system for liquefied natural gas carriers: Part B—Application. Ocean Eng. 2019, 174, 96–107. [Google Scholar] [CrossRef]
- Ouyang, T.; Su, Z.; Huang, G.; Zhao, Z.; Wang, Z.; Chen, N.; Haozhong, H. Modeling and optimization of a combined cooling, cascaded power and flue gas purification system in marine diesel engines. Energy Convers. Manag. 2019, 200, 112102. [Google Scholar] [CrossRef]
- Trivyza, N.L.; Rentizelas, A.; Theotokatos, G. Impact of carbon pricing on the cruise ship energy systems optimal configuration. Energy 2019, 175, 952–966. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, H.; Long, Y.; Wang, Y.; Liang, Y.; Song, X.; Yu, J.J.Q. Multi-objective design optimization of combined cooling, heating and power system for cruise ship application. J. Clean. Prod. 2019, 233, 264–279. [Google Scholar] [CrossRef]
- Bolbot, V.; Trivyza, N.L.; Theotokatos, G.; Boulougouris, E.; Rentizelas, A.; Vassalos, D. Cruise ships power plant optimisation and comparative analysis. Energy 2020, 196, 117061. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Guan, C.; Gao, H. Optimization of sizing and frequency control in battery/ supercapacitor hybrid energy storage system for fuel cell ship. Energy 2020, 197, 117285. [Google Scholar] [CrossRef]
- Feili, M.; Ghaebi, H.; Parikhani, T.; Rostamzadeh, H. Exergoeconomic analysis and optimization of a new combined power and freshwater system driven by waste heat of a marine diesel engine. Therm. Sci. Eng. Prog. 2020, 18, 100513. [Google Scholar] [CrossRef]
- Feng, Y.; Du, Z.; Shreka, M.; Zhu, Y.; Zhou, S.; Zhang, W. Thermodynamic analysis and performance optimization of the supercritical carbon dioxide Brayton cycle combined with the Kalina cycle for waste heat recovery from a marine low-speed diesel engine. Energy Convers. Manag. 2020, 206, 112483. [Google Scholar] [CrossRef]
- Letafat, A.; Rafiei, M.; Sheikh, M.; Mosayeb Afshari-Igder, M.; Banaei, M.; Boudjadar, J.; Khooban, M.H. Simultaneous energy management and optimal components sizing of a zero-emission ferry boat. J. Energy Stor. 2020, 28, 101215. [Google Scholar] [CrossRef]
- Tian, Z.; Yue, Y.; Zhang, Y.; Gu, B.; Gao, W. Multi-objective thermo-economic optimization of a Combined Organic Rankine Cycle (ORC) system based on waste heat of dual fuel marine engine and LNG cold energy recovery. Energies 2020, 13, 1397. [Google Scholar] [CrossRef]
- Trinklein, E.H.; Parker, G.; McCoy, T. Modeling, optimization, and control of ship energy systems using exergy methods. Energy 2020, 191, 116542. [Google Scholar] [CrossRef]
- Wu, P.; Bucknall, R. Hybrid fuel cell and battery propulsion system modelling and multi-objective optimisation for a coastal ferry. Int. J. Hydrogen Energy 2020, 45, 3193–3208. [Google Scholar] [CrossRef]
- Frangopoulos, C.A.; von Spakovsky, M.R.; Sciubba, E. A brief review of methods for the design and synthesis optimization of energy systems. Int. J. Appl. Thermodyn. 2002, 5, 151–160. [Google Scholar]
- Toffolo, A.; Lazzaretto, A.; Morandin, M. The HEATSEP method for the synthesis of thermal systems: An application to the S-Graz cycle. Energy 2010, 35, 976–981. [Google Scholar] [CrossRef]
- Voll, P.; Lampe, M.; Wrobel, G.; Bardow, A. Superstructure-free synthesis and optimization of distributed industrial energy supply systems. Energy 2012, 45, 424–435. [Google Scholar] [CrossRef]
- Wang, L.; Voll, P.; Lampe, M.; Yang, Y.; Bardow, A. Superstructure-free synthesis and optimization of thermal power plants. Energy 2015, 91, 700–711. [Google Scholar] [CrossRef]
- Lazzaretto, A.; Manente, G.; Toffolo, A. SYNTHSEP: A general methodology for the synthesis of energy system configurations beyond superstructures. Energy 2018, 147, 924–949. [Google Scholar] [CrossRef]
- White, M.T.; Oyewunmi, O.A.; Haslam, A.J.; Markides, C.N. Industrial waste-heat recovery through integrated computer-aided working-fluid and ORC system optimisation using SAFT-γ Mie. Energy Convers. Manag. 2017, 150, 851–869. [Google Scholar] [CrossRef]
- Mitsos, A.; Asprion, N.; Floudas, C.A.; Bortz, M.; Baldea, M.; Bonvin, D.; Caspari, A.; Schäfer, P. Challenges in Process Optimization for New Feedstocks and Energy Sources. Comput. Chem. Eng. 2018, 113, 209–221. [Google Scholar] [CrossRef]
- Sahinidis, N.V. Optimization under uncertainty: State-of-the-art and opportunities. Comput. Chem. Eng. 2004, 28, 971–983. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Apap, R.M.; Calfa, B.A.; García-Herreros, P.; Zhang, Q. Recent advances in mathematical programming techniques for the optimization of process systems under uncertainty. Comput. Chem. Eng. 2016, 91, 3–14. [Google Scholar] [CrossRef]
- Charitopoulos, V.M.; Dua, V. A unified framework for model-based multi-objective linear process and energy optimisation under uncertainty. Appl. Energy 2017, 186, 539–548. [Google Scholar] [CrossRef]
- Ning, C.; You, F. Data-driven stochastic robust optimization: General computational framework and algorithm leveraging machine learning for optimization under uncertainty in the big data era. Comput. Chem. Eng. 2018, 111, 115–133. [Google Scholar] [CrossRef]
- Ning, C.; You, F. Optimization under uncertainty in the era of big data and deep learning: When machine learning meets mathematical programming. Comput. Chem. Eng. 2019, 125, 434–448. [Google Scholar] [CrossRef]
- Villemeur, A. Reliability, Availability, Maintainability and Safety Assessment: Vol. 1: Methods and Techniques; John Wiley & Sons: Chichester, UK, 1992. [Google Scholar]
- Frangopoulos, C.A.; Dimopoulos, G.G. Effect of Reliability Considerations on the Optimal Synthesis, Design and Operation of a Cogeneration System. Energy 2004, 29, 309–329. [Google Scholar] [CrossRef]
- Kopanos, G.M.; Xenos, D.P.; Cicciotti, M.; Pistikopoulos, E.N.; Thornhill, N.F. Optimization of a network of compressors in parallel: Operational and maintenance planning—The air separation plant case. Appl. Energy 2015, 146, 453–470. [Google Scholar] [CrossRef]
- Zahedi, B.; Norum, L.E.; Ludvigsen, K.B. Optimized efficiency of all-electric ships by dc hybrid power systems. J. Power Sources 2014, 255, 341–354. [Google Scholar] [CrossRef]
- Kanellos, F.D.; Prousalidis, J.M.; Tsekouras, G.J. Control system for fuel consumption minimization-gas emission limitation of full electric propulsion ship power systems. Proc. IMechE Part M J. Eng. Marit. Environ. 2014, 228, 17–28. [Google Scholar] [CrossRef]
- Kanellos, F.D.; Anvari-Moghaddam, A.; Guerrero, J.M. A cost-effective and emission-aware power management system for ships with integrated full electric propulsion. Electr. Power Syst. Res. 2017, 150, 63–75. [Google Scholar] [CrossRef]
- Manasa, B.; Vaisakh, K. Optimal shipboard power management by classical and differential evolution methods. Int. Res. J. Eng. Technol. 2019, 6, 269–279. [Google Scholar]
- Fang, S.; Xu, Y. Multi-objective robust energy management for all-electric shipboard microgrid under uncertain wind and wave. Electr. Power Energy Syst. 2020, 117, 105600. [Google Scholar] [CrossRef]
- Papanikolaou, A. Holistic ship design optimization. Comput. Aided Design 2010, 42, 1028–1044. [Google Scholar] [CrossRef]
- Skoupas, S.; Zaraphonitis, G.; Papanikolaou, A. Parametric design and optimisation of high-speed Ro-Ro Passenger ships. Ocean Eng. 2019. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).