1. Introduction
The urgent need for the reduction of greenhouse gas (GHG) emissions requires efficient and integrated energy communities in order to decrease the final energy demand and to sustain energy transitions towards renewable energy sources (RES). This introduces a big research challenge for the design and optimization of future energy systems, given the multi-level and inter-sectorial dimension of the problem. With this aim, energy models have paramount importance. At present, energy models focus on specific aspects of an energy system, and they typically neglect the interconnections between different layers and elements of the overall system. A model that is aimed at analyzing an integrated energy system, including both technical and economic characteristics, can follow two different approaches: bottom-up or top-down [
1]. Top-down models give more attention to the economic aspects, including less details in the representation of the energy technologies. Bottom-up models, instead, are based on models with an in-depth description of the technological aspects of the energy systems, but they neglect the economic implications at a wider level [
1]. In [
1], the authors propose an integrated modelling approach to overcome the modelling limitations that are previously described. They suggest a combination of a top-down and bottom-up approach in order to create the nexus between several energy models. Brouwer et al. [
2] state that the Nexus concept must be applied to consider integrated systems, and to support sustainable development, because it is necessary to take into account energy resources, water, food, land and climate at the same time. Thus, it is evident how much the problem of the representation of multi-energy and multi-sector systems can be complex. The purpose of this work is indeed to highlight the critical aspects of integrated energy systems (IES) modelling, such as composites infrastructure with IES, including different subsystems (e.g., power plants, buildings, transportation, etc.) and energy carriers, such as electricity, natural gas, heating/cooling. Integrated energy systems are intelligent energy systems, which enable the production, transmittance, storage, and usage of energy in a systematic, integrated, and optimally managed way. They allow for the coexistence of different carriers and efficient energy cascade utilization [
3]. Integrated energy systems, when optimized as an overall system, show the advantage of a better allocation of resources, and they can also guarantee increased resilience [
4]. The latter is indeed a very interesting topic for IES, and Moslehi and Reddy [
5] propose a methodology to assess the resilience of an integrated energy system in order to make it sustainable, intending it to be more reliable, robust, adaptable, and self-sufficient. In the following the most critical issues to be addressed when modelling integrated energy systems are reported, and an overview of the main findings that are available in the literature is presented.
3. Scalability
Given the definition of integrated energy systems, it is evident that modelling IES implies the consideration of different subsystems, and the size of the problem can significantly grow, depending on the analyzed system. Thus, scalability is an important issue when addressing the representation of IES, in order to be able to handle a growing amount of data and information, and different peculiar characteristics of the subsystems. At a bigger scale, as stated by Beuzekom et al. [
6], the trade-off between the necessary level of detail and the computability of the model has to be considered. Furthermore, with the short-term dynamics of renewable resources, as well as the long-term evolution of fossil fuels, technology prices have to be incorporated in the model. Even Pina et al. [
7] highlight the importance of time scale when representing such systems, and they propose the combination of long-term models with short-term models. The first ones are used for resources planning (e.g., to optimize the investment in generation capacity) and they employ a time step of a few years up to 50 years, while the second ones, which represent the daily operation of the system, help to set proper constraints for the upper level optimization, and employ a time step ranging between 15 min to 1 h. The authors demonstrate that the inclusion of short-term electricity supply and demand dynamics in the long-term energy systems modeling is paramount for capturing the behavior of complex systems, especially including renewable energy sources.
As far as the demand side is concerned, Cayla and Maizi [
8] tackle the problem of energy demand heterogeneity in long-term energy planning models. They suggest the disaggregation of energy demand, and to also take into account non-technical variables (e.g., occupant behavior in households) that have been generally neglected at such a scale, and they demonstrate the improvement in the prediction results. Indeed, many different aspects need to be considered, in order to include all of the influencing elements (e.g., occupant behavior, building features, etc.) when the energy demand is represented. Frayssinet et al. [
9] state that at an urban scale, in order to know the building’s energy demand, a huge amount of information is needed. For example, the occupants are responsible for a large demand diversity, which is not simply the sum of the demand of single buildings. In addition, the influence of the urban environment on building energy demand cannot be neglected. In particular, at the urban scale, a top-down (where the city is studied as an entity) or a bottom-up (where any end users can be distinguished) approach can be employed in the modelling process. Within the latter, there are the so-called micro-simulation models, defined as those models that are fully detailed. The authors highlight that such models can introduce a lot of uncertainty at the urban scale, because the uncertainty on the input parameters have a higher impact on the solution than model simplifications [
9].
With more detail, buildings can be modelled by the means of physically based models (white box approach), reduced-order models (grey box approach) or statistical learning methods (black box approach) [
10]. When the number of buildings to be represented is big, a white box approach is very difficult to follow. There are different attempts in literature aimed at finding a simplified way to represent the building behavior at neighborhood, district and urban scale. R-C (resistance–capacitance) models are often used for their simplicity, even if they only give a rough estimate of the energy use. Reduced-order grey box models can behave better, but the estimation of parameters should be continuously updated [
9,
11]. For example Heidarinejad et al. [
12] developed effective urban-scale reduced-order building energy models by checking the most influent variables for the heat transfer process. Kontokosta and Tull [
13], instead, developed a data-driven predictive model for energy use in buildings at urban scale. They demonstrated that the model is able to predict electricity consumption using actual data from a relatively small subset of buildings, while the prediction is a bit more complicated for natural gas use, because of the more complex infrastructure involved. Allegrini et al. [
14] analyzed the existing simulations tools used to represent district scale energy systems, and they showed how the different instruments face the representation of the various aspects characterizing an energy system (i.e., external air flow, short- and long-wave radiation, building thermal behavior, users’ behavior, building energy system, thermal storages, electrical and gas network, district plant, wind power, photovoltaic, ground source, transportation, embodied energy, spatial resolution). The approach can be detailed or simplified, or some aspects can be neglected or included in the representation by coupling with other simulation tools. Their results show that generally, tools with a very detailed approach are applied for a well-defined and restricted scope, while a simplified approach allows a broader representation of energy aspects. In [
6] a list of available smart city modelling tools can be found, with a detailed description of the main features of each model and technical specifications.
Concluding, the scalability issue, related to modelling integrated large scale energy systems, deals especially with a proper time resolution choice and a detailed and heterogeneous demand representation (see
Figure 1). The model structure is, indeed, influenced by the detail of representation and scale of the problem.
4. Uncertainty
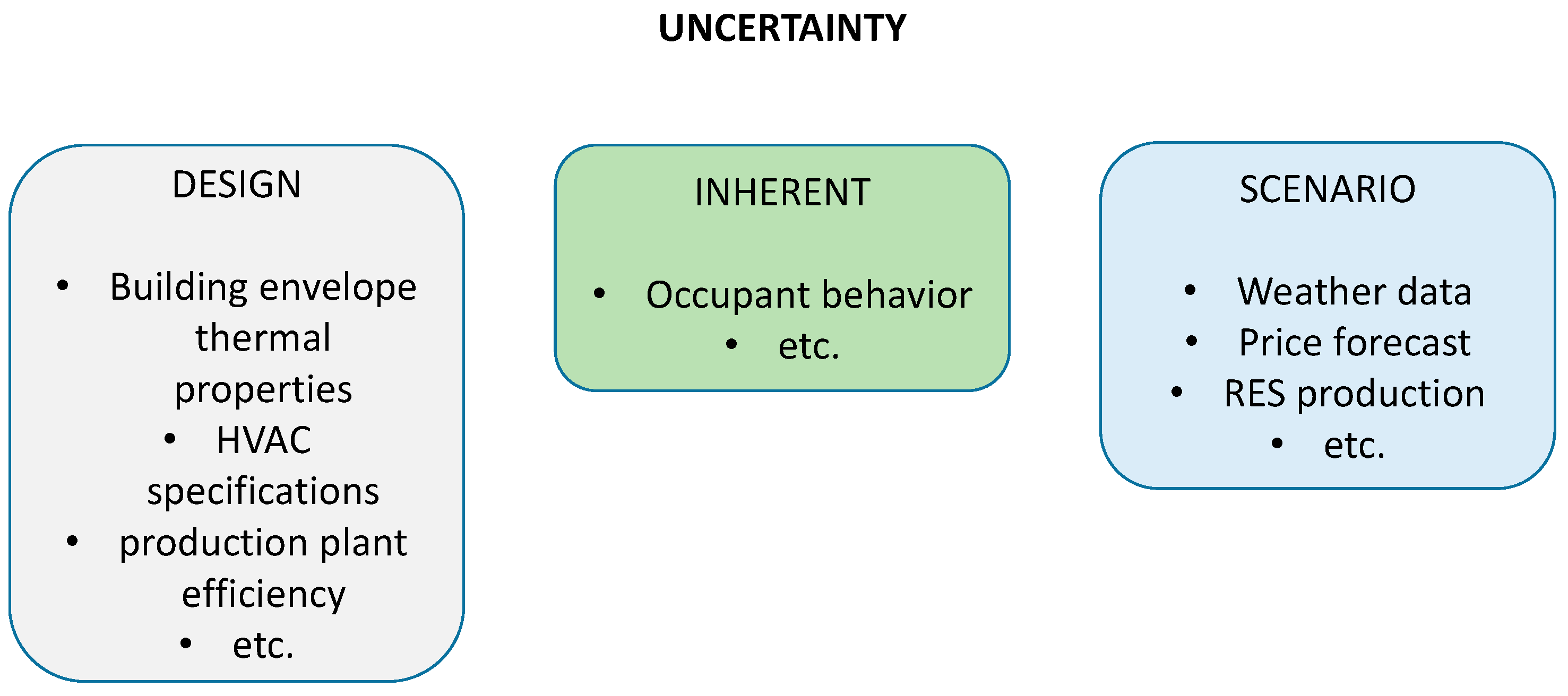
Another important issue occurring when representing complex energy systems is related with the uncertainties due to inexact knowledge over the parameters having an influence on the energy performance of the considered system. These parameters can be classified as (
Figure 2) design parameters (e.g., building envelope thermal properties, technical specification/efficiency of the production systems), inherent uncertain parameters (e.g., occupants/users behavior) and scenario parameters (e.g., varying economic conditions or weather data). Uncertainties can also be introduced by a discrepancy between the simulation model and reality, because of missing physical aspects in the representation or numerical approximations. Tian et al. [
15] present an in-depth review about uncertainty analysis in building simulations. They define two different quantification approaches: (i) forward and (ii) inverse uncertainty quantification. Forward uncertainty analysis (uncertainty propagation) quantifies the uncertainty in the system outputs propagated from uncertain input variables through mathematical models, while inverse uncertainty analysis (model calibration) calculates unknown variables through mathematical models that are calibrated on measurement data [
15]. Furthermore an uncertainty can be aleatory (e.g., occupancy presence), i.e., due to an inherent variation of the system, and impossible to be reduced, or epistemic (e.g., lighting), which depends on a lack of knowledge.
As far as the forward uncertainty quantification method, it can be based on probabilistic approaches or non-probabilistic approaches. The probabilistic approach uses rigorous probability theory and it can be sampling-based (where the deterministic model is treated as a black box model trained on data coming from the deterministic model with different inputs, e.g., Monte Carlo methods) or non-sampling-based (including perturbation methods, moment equations, spectral representations methods, and classical stochastic differential equations). The non-probabilistic approach is used in the case of a lack of information or data; it includes, for example, fuzzy models [
15]. On the other hand, the inverse quantification method is used to infer unknown input parameters in a model through a mathematical formulation, given the measurement data. It includes Frequentist techniques and Bayesian techniques [
15]. Further information about this characterization can be found in [
15].
There are different studies about uncertainty in buildings simulations. For example, Macdonald [
16] focuses on uncertainties due to building envelope thermo-physical properties, casual gains, and infiltration rates, while Wang [
17] concentrates on uncertainty due to infiltrations, thermal bridges, HVAC (Heating Ventilation and Air Conditioning) systems, and occupancy. In the followings, some more details about the most relevant sources of uncertainty in the building simulation are provided:
Weather data: a representative year based on historical data is generally used for weather data in a building simulation; it is derived from measurement; however, available meteorological measurements are not always suitable for representing the microclimatic conditions around the building (e.g., presence of vegetation) [
15]. Furthermore, the energy consumption in buildings are more closely related to future climatic trends than with historical data; thus, climate projections are needed, as available, for example, in [
18].
Building envelope: the uncertainty on thermal properties are related, both to measurement errors, and to environmental conditions [
15]. Clarke and Pinney [
19] studied in detail the uncertainty due to the unknown properties of the construction materials. Besides the materials, the infiltration rate, thermal bridges, and convective heat transfer coefficient are the parameters that most greatly affect building energy performances.
HVAC systems: they are generally represented in a fairly ideal way, and aspects such as oversizing, ageing, and maintenance are neglected, even if they influence the overall energy performance.
Occupant behavior: occupant behavior is accounted as one of the major uncertainty sources, producing variations in building energy predictions of around 30% [
20]. Moreover, occupant presence may not be the best element for predicting internal loads [
21].
Considering, instead, the electric power system, Rezaee Jordehi [
22] classifies the main uncertain parameters as technical parameters (which can be operational or topological) or economic parameters (i.e., macro-economic or micro-economic parameters). Indeed, the most important sources of uncertainty come from load forecasting errors, photovoltaic and wind power generation estimation, charging/discharging behavior of electric vehicles, and forecasted electricity price.
Thus, there are different sources of uncertainty in an integrated energy system, and they have to be determined and included in the evaluations, in order to obtain reliable results.
5. Robustness
An integrated energy system is defined as robust on the basis of its ability to tolerate perturbations. When a system undergoes a robust design optimization process, the system response is maximized, while the system variability is minimized. Indeed, robust optimization takes into account the possible uncertainties of the system, in order to obtain a better optimal solution that is not affected by unforeseen variations in the boundary conditions or input variables. Robust optimization is intended to protect against parameters of ambiguity and stochastic uncertainty, which can affect the feasibility of the solution or the objective value. Static robust optimization addresses the uncertainty affecting the solution feasibility by seeking a solution that is feasible for any realization (i.e., the worst case optimization). In case of uncertainty affecting the objective value, the robust optimization looks for a solution that performs well for any realization [
23].
Robust optimization differs from stochastic optimization for the way in which the uncertainty is treated. In stochastic optimization, the probability distribution of uncertain data is assumed as known, while in robust optimization, it is not known, but there are boundaries that fix the uncertainty that is set [
24]. Gorissen et al. [
24] describe the steps to be followed to implement a robust optimization. Firstly the uncertainty parameters and their uncertainty sets are chosen. Then, an optimal solution is calculated, and its distance from the optimal objective has to be quantified by setting proper boundaries. The adjustable variables and decision rules can be varied if the solution is not robust enough.
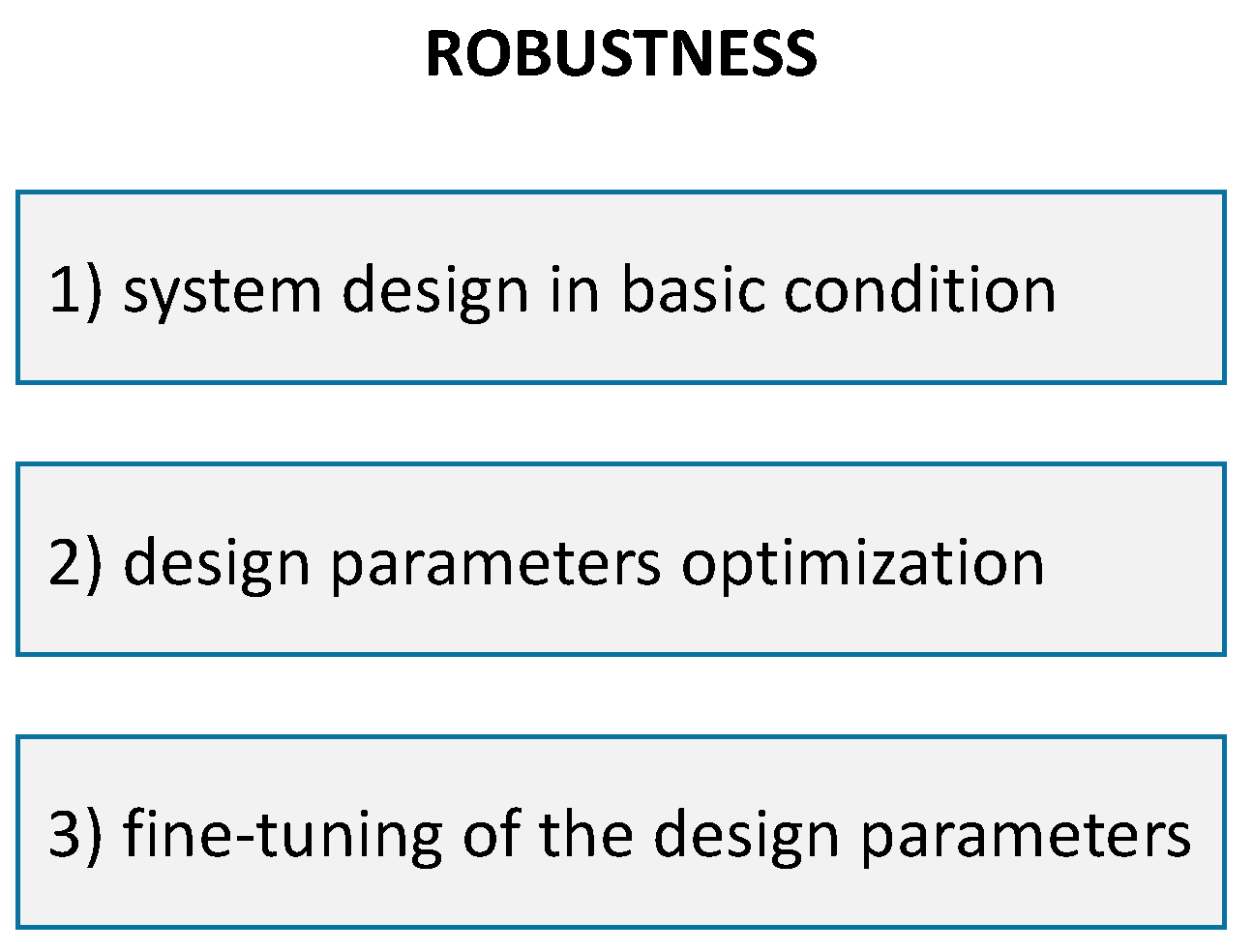
In [
25], the robust design methodology of Taguchi (the father of robust design) is described as being composed of three stages (
Figure 3): system design in the basic condition; design parameter optimization in order to meet the target; fine-tuning of the design parameters. The method accounts for noise factors beyond the control of the designer, which can be modeled deterministically, probabilistically, or possibilistically. From a broader perspective, there are two approaches to robust optimization: a deterministic approach, which uses numerical techniques, or a simulation optimization, which uses noisy functions that are obtained through simulation (e.g., Monte Carlo techniques). More details about the mathematical formulation of robust optimization methods can be found in [
24,
25].
Several works dealt with the robust optimization of energy systems, focusing on different aspects. For example, Buso et al. [
26] apply robust design in order to reduce the uncertainty effect on energy performance due to occupant behavior. Results show that robustness by varying occupants’ behavior increased with increasing thermal mass, and with the decreasing transparent area of the envelope. Bahramara and Golpîra [
27], instead, formulate a microgrid operation problem in a robust manner by taking into account the presence of electric vehicles and the uncertain behavior of the drivers. The optimization process is developed in two stages: in the first one, the microgrid addresses power trading with the main grid, and in the second one, the optimal scheduling of the microgrid resources is obtained, while including robustness through penalty factors in the objective function. Even Zhang et al. [
28] refer to microgrids, especially since they use robust optimization on multi-microgrids to improve operational and economic performance. Indeed, in this configuration, the microgrids interact not only with the main grid, but also among themselves. Their results show that the proposed model can diminish the cost increase caused by uncertainty. Zhou et al. [
29] consider local energy communities, composed of distributed energy sources and users, and apply robust optimization in order to handle the uncertainties and to determine the day-ahead scheduling strategy for the community operating within ancillary service markets.
Therefore robust optimization has paramount importance in designing good integrated energy systems, because it allow issues that have been introduced by the unavoidable presence of uncertainty in IES to be overcome.
6. Optimal Control
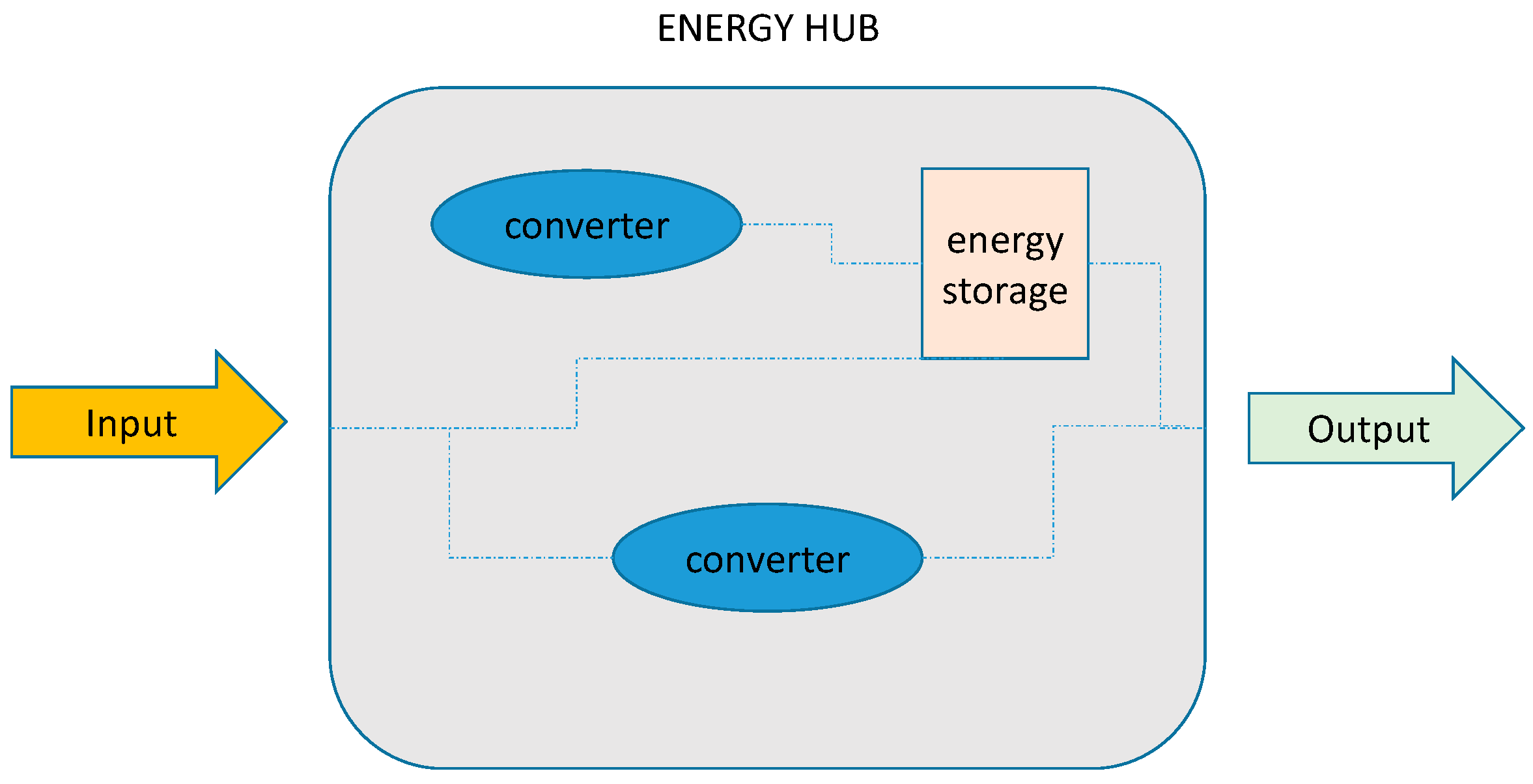
Another critical aspect when considering integrated energy systems deals with their management, because different energy carriers and energy sectors have to interact. The concept of the energy hub is introduced, and it is defined as “a framework where production, conversion, storage, and consumption of different energy carriers is done” [
30]. An energy hub can have different scales (e.g., a city or a house), but the common idea is that at this level, a system can be effectively designed and managed, in order to obtain a more efficient use of resources and better performance. An energy hub is composed of four elements (
Figure 4): input, output, storage, and conversion systems [
31]. The inputs are the different energy carriers/energy sources. The converters are used to convert energy carriers in other carriers, or to use them as output. The energy storage systems are meant to store energy when a surplus is available to be used later when it is needed. The outputs are typically the users’ demands and they can be different, for example, heating or cooling demand, or electricity demand. Furthermore more energy hubs, also from different sectors, can be connected among them (e.g., micro residential energy hubs with industrial energy hubs) and in this case, a macro-hub is created. The management of macro-hubs is generally done in two steps: firstly, the performance of each hub is optimized, and then the overall system is considered (optimal energy flow) [
30]. The concept of smart management of an energy hub is in agreement with the concept of a smart grid, indicating a smart match and the management of supply and demand, performed thanks to the necessary information and communication technology. In this context, energy storage systems and demand side management (DSM) programs have especially paramount roles. Demand side management is intended as all those programs that are aimed at changing the final users’ energy demand, in order to match it with the energy supply. Li and Pye [
32] studied the role of DSM in an integrated energy system, including energy production, residential sector, and transportation sector. They highlighted that demand-side control increases the system flexibility, enabling the integration of more renewable energy, while decreasing the need for storage systems.
Indeed, the optimal control of the integrated system can lead to a more efficient use of the available resources. Several studies have analyzed, for example, the possibility of the load management of a cluster of buildings, and various positive effects have been highlighted (e.g., peak shaving, costs reduction) when buildings are interconnected and can exchange energy among themselves [
33]. Smart control systems can be classified as: (i) agent-based control; (ii) model-based predictive control, and (iii) learning-based control (
Figure 5). The first category is represented by agent-based technology, which can be effectively used to control integrated systems that are composed of more elements, where each element is represented by an agent with its own optimal control [
33]. Optimal control can be also achieved by means of Model Predictive Control (MPC), whose relevance is continuously increasing. MPC allows for control by taking into account the future system dynamics, thanks to a model that simulates the system behavior. MPC has been widely used, both at the system level and at the component level. In [
34], an MPC for an integrated energy system is presented, where storage systems, forecasts on energy prices, and operational constraints are considered. The authors considered different prediction horizons and showed how costs can decrease while the time horizon increases. Even in buildings, MPC is often considered as a control system that is useful in the DSM context, or to obtain better comfort performance in the case of low thermal inertia buildings (e.g., thermally activated buildings, TABS) [
35]. Mirakhorli and Dong [
36] present a price-based MPC for a residential building energy management system, which controls the air conditioner, electric vehicle, water heater, and battery energy storage system. The controller shows the ability to guarantee peak shaving of the integrated system and lower operation costs. In [
37], a robust MPC is described as being aimed at optimizing microgrids in the presence of uncertainty, which has great relevance towards system performance, as described in the previous section. Eventually, learning-based control systems are those controls that do not have any need of modelling the systems, because they learn their behavior on the basis of their dynamics [
35]. They belong to artificial intelligence methods, such as fuzzy logic, neural networks, and reinforcement learning. The last category is especially gaining more and more attention. Reinforcement learning is defined as a machine learning technique where the control action taken is aimed at maximizing the obtained reward. It is generally formulated as a Markov Decision Process [
38]. In [
39], an example of reinforcement learning control for the HVAC system in a building is proposed. The authors state that, unlike heuristic control that requires specific knowledge of individual buildings, reinforcement learning control guarantees optimality through self-advancement on given goals and cost functions. It is also able to adapt to occupant behaviors that are otherwise difficult to predict [
39].
Furthermore the combination of optimal control and optimal design has paramount importance, in order to optimize the overall integrated system. Indeed in this way, a better performance can be achieved, rather than optimizing the design and control in separate stages. Evins [
40] presents a bi-level optimization process that is used to select and size the components of an energy center while determining their optimal operation. In this approach, the optimization process consists of a design level where it is also nested at the operational level. Such a method allows for assumptions to be avoided in control strategies or design, because the two aspects are strictly connected. In [
41], three different levels are considered for the optimal integrated design and control of a building: building level, plant level, and operational level. The method is applied to a case study, and it is shown that the multi-level optimization approach can exploit synergies between different areas of design and account for operational issues.
It is then evident that an effective smart control system is strongly necessary for an IES. It has to be included in the system-design stage and cannot be based on simple rules, but it has to take into account the optimal interactions of sub-systems and future dynamics.