Evaluation of Standardised (ISO) Leaching Tests for Assessing Leaching and Solid–Solution Partitioning of Perfluoroalkyl Substances (PFAS) in Soils
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Soils
2.3. Spiking and Aging of Soils
2.4. Rinsing of Equipment
2.5. Test Set-Up
2.6. Up-Flow Percolation Test (ISO 21268-3:2019)
2.7. Batch Test ISO 21268-2:2019
2.8. PFAS Analysis
2.9. Data Analysis
2.9.1. Calculations
Batch Test
Percolation Test
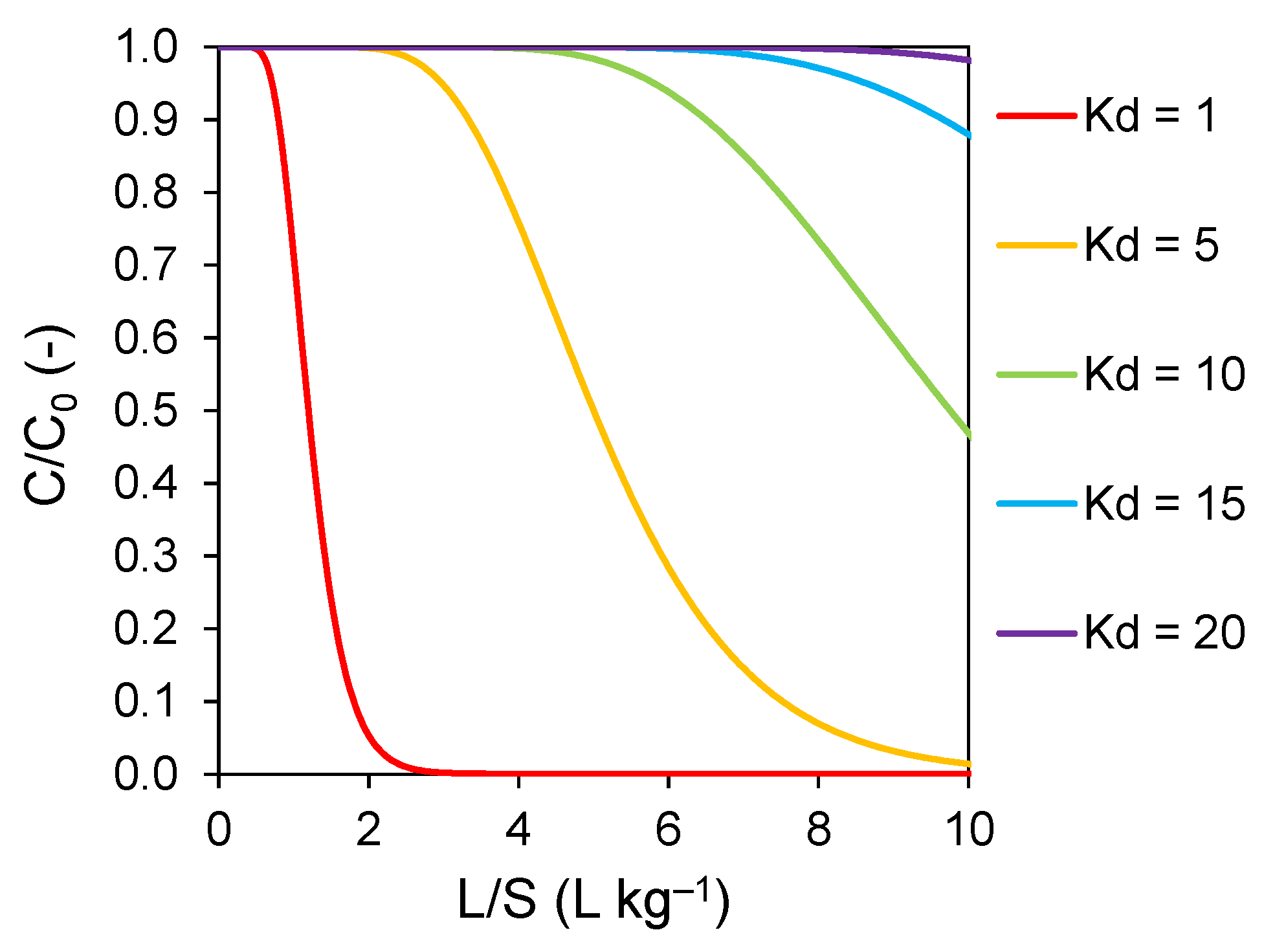
2.9.2. Modelling Leaching Behaviour of PFAS in Percolation Tests
3. Results and Discussion
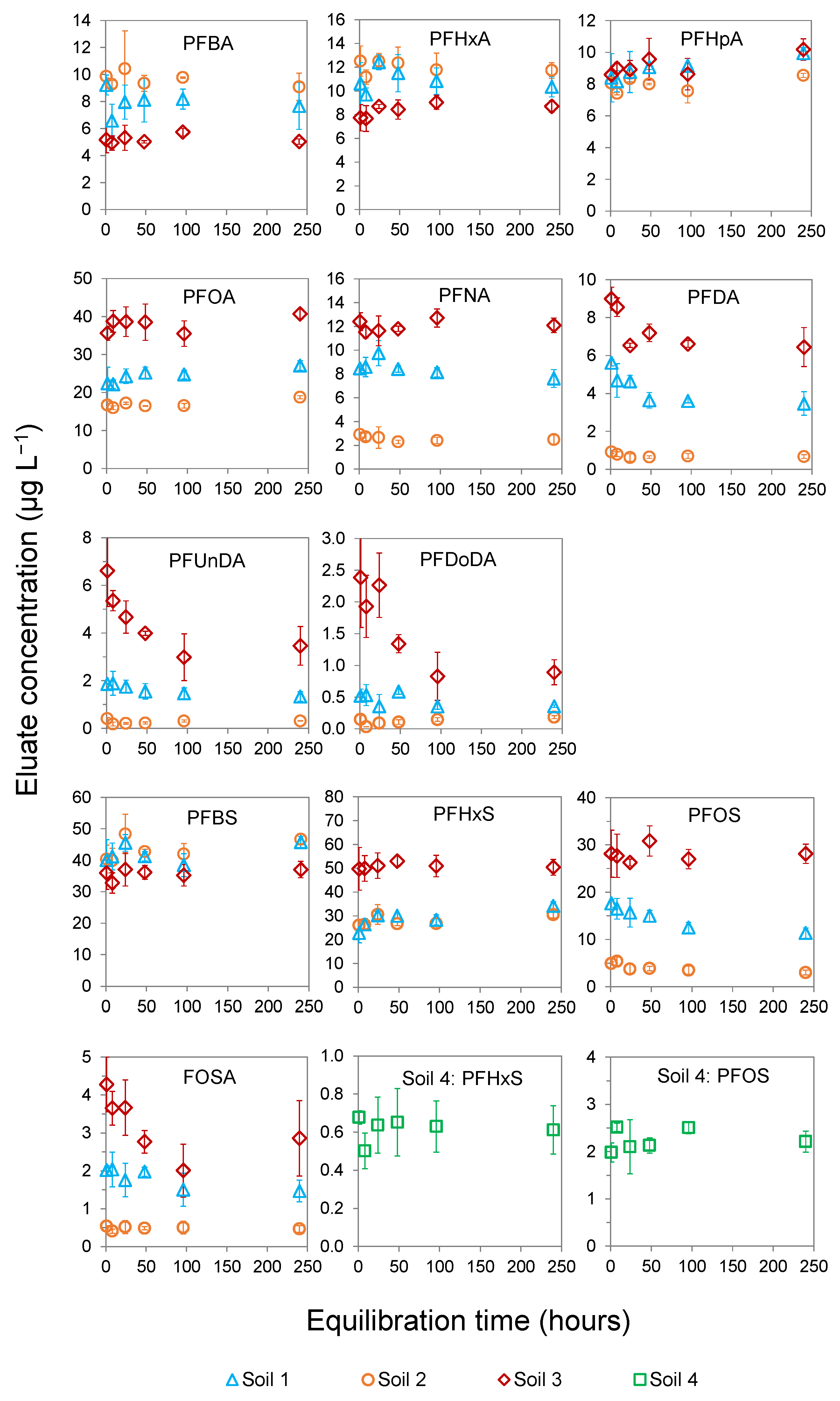
3.1. Desorption Kinetics of PFAS in Batch Test ISO 21268-2:2019
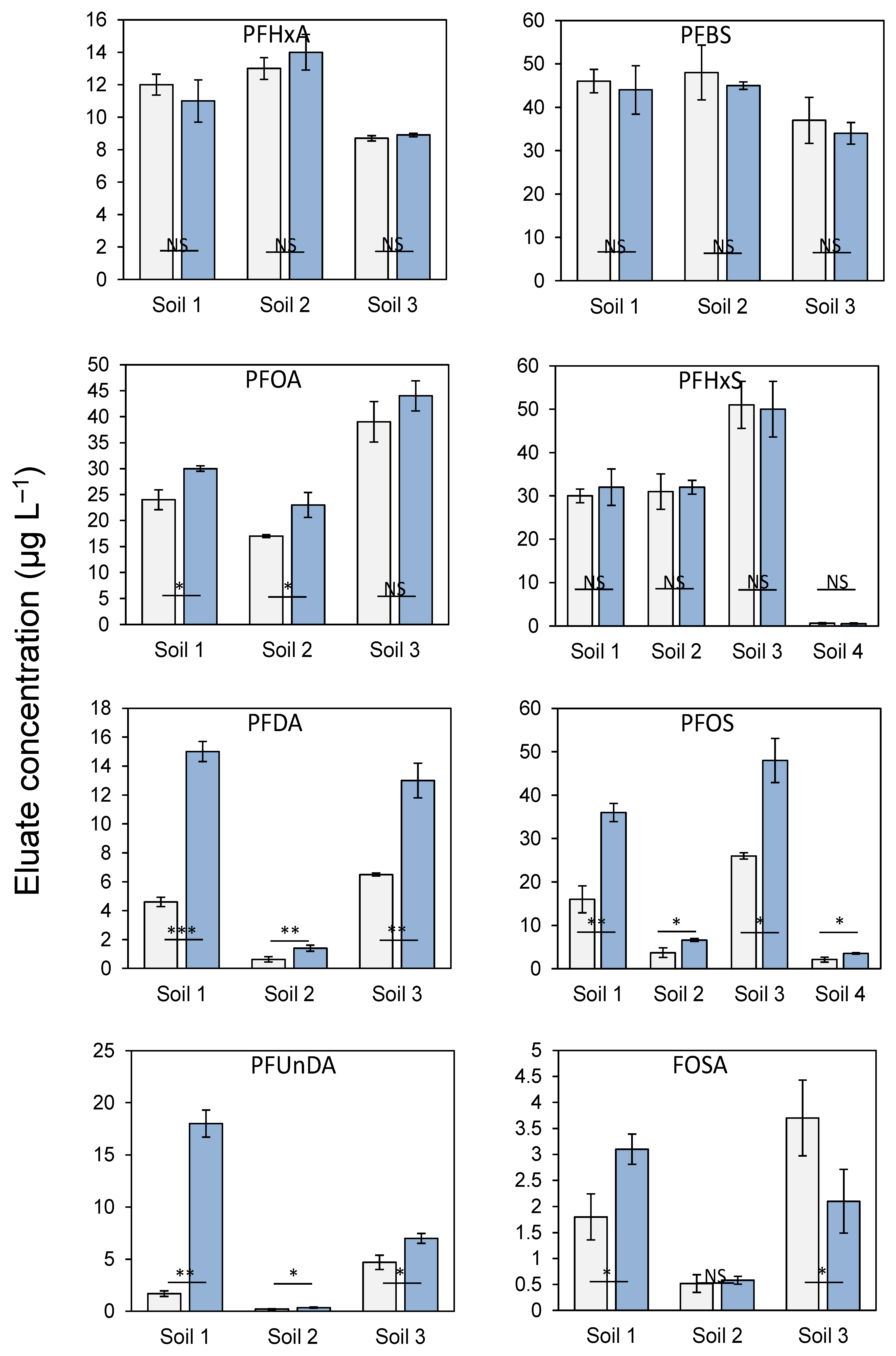
3.2. Comparing Deionized Water and 1 mM CaCl2 as Leachants in Batch Tests
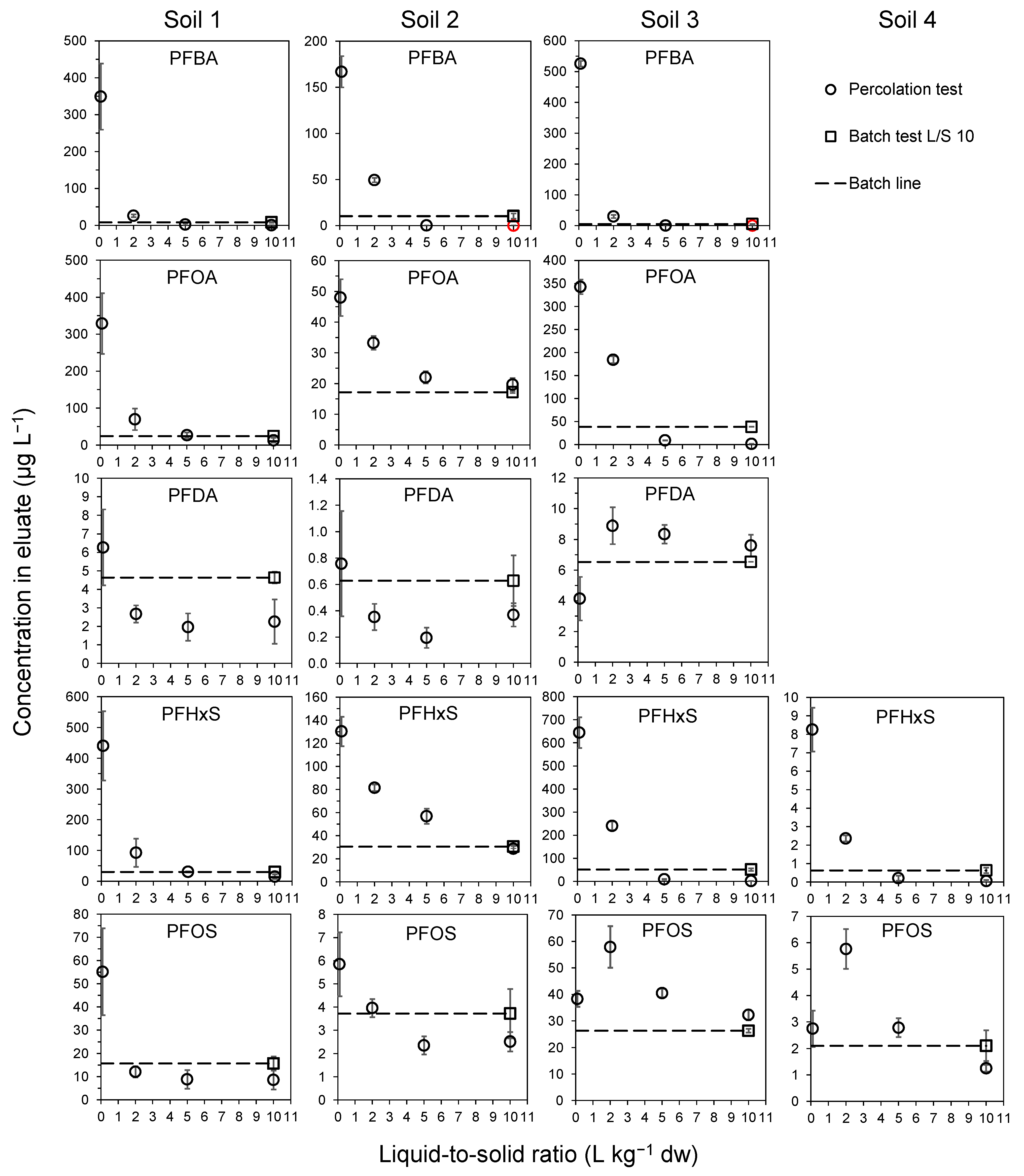
3.3. Up-Flow Percolation Test ISO 21268-3
3.4. Determining Solid–Solution Partitioning (Kd) of PFAS in Percolation and Batch Tests
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rankin, K.; Mabury, S.A.; Jenkins, T.M.; Washington, J.W. A North American and Global Survey of Perfluoroalkyl Substances in Surface Soils: Distribution Patterns and Mode of Occurrence. Chemosphere 2016, 161, 333–341. [Google Scholar] [CrossRef] [PubMed]
- Brusseau, M.L.; Anderson, R.H.; Guo, B. PFAS Concentrations in Soils: Background Levels versus Contaminated Sites. Sci. Total Environ. 2020, 740, 140017. [Google Scholar] [CrossRef] [PubMed]
- Grunfeld, D.A.; Gilbert, D.; Hou, J.; Jones, A.M.; Lee, M.J.; Kibbey, T.C.G.; O’Carroll, D.M. Underestimated Burden of Per- and Polyfluoroalkyl Substances in Global Surface Waters and Groundwaters. Nat. Geosci. 2024, 17, 340–346. [Google Scholar] [CrossRef]
- Filipovic, M.; Woldegiorgis, A.; Norström, K.; Bibi, M.; Lindberg, M.; Österås, A.H. Historical Usage of Aqueous Film Forming Foam: A Case Study of the Widespread Distribution of Perfluoroalkyl Acids from a Military Airport to Groundwater, Lakes, Soils and Fish. Chemosphere 2015, 129, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Gobelius, L.; Hedlund, J.; Dürig, W.; Tröger, R.; Lilja, K.; Wiberg, K.; Ahrens, L. Per-and Polyfluoroalkyl Substances in Swedish Groundwater and Surface Water: Implications for Environmental Quality Standards and Drinking Water Guidelines. Environ. Sci. Technol. 2018, 52, 4340–4349. [Google Scholar] [CrossRef]
- Glüge, J.; Scheringer, M.; Cousins, I.T.; Dewitt, J.C.; Goldenman, G.; Herzke, D.; Lohmann, R.; Ng, C.A.; Trier, X.; Wang, Z. An Overview of the Uses of Per-And Polyfluoroalkyl Substances (PFAS). Environ. Sci. Process. Impacts. 2020, 22, 2345–2373. [Google Scholar] [CrossRef]
- Li, S.; Oliva, P.; Zhang, L.; Goodrich, J.A.; McConnell, R.; Conti, D.V.; Chatzi, L.; Aung, M. Associations between Per-and Polyfluoroalkyl Substances (PFAS) and County-Level Cancer Incidence between 2016 and 2021 and Incident Cancer Burden Attributable to PFAS in Drinking Water in the United States. J. Expo. Sci. Environ. Epidemiol. 2025, 35, 425–436. [Google Scholar] [CrossRef]
- Guelfo, J.L.; Higgins, C.P. Subsurface Transport Potential of Perfluoroalkyl Acids at Aqueous Film-Forming Foam (AFFF)-Impacted Sites. Environ. Sci. Technol. 2013, 47, 4164–4171. [Google Scholar] [CrossRef]
- Guelfo, J.L.; Korzeniowski, S.; Mills, M.A.; Anderson, J.; Anderson, R.H.; Arblaster, J.A.; Conder, J.M.; Cousins, I.T.; Dasu, K.; Henry, B.J.; et al. Environmental Sources, Chemistry, Fate, and Transport of Per- and Polyfluoroalkyl Substances: State of the Science, Key Knowledge Gaps, and Recommendations Presented at the August 2019 SETAC Focus Topic Meeting. Environ. Toxicol. Chem. 2021, 40, 3234–3260. [Google Scholar] [CrossRef]
- Nguyen, T.M.H.; Bräunig, J.; Thompson, K.; Thompson, J.; Kabiri, S.; Navarro, D.A.; Kookana, R.S.; Grimison, C.; Barnes, C.M.; Higgins, C.P.; et al. Influences of Chemical Properties, Soil Properties, and Solution PH on Soil-Water Partitioning Coefficients of Per- And Polyfluoroalkyl Substances (PFASs). Environ. Sci. Technol. 2020, 54, 15883–15892. [Google Scholar] [CrossRef]
- Mejia-Avendaño, S.; Zhi, Y.; Yan, B.; Liu, J. Sorption of Polyfluoroalkyl Surfactants on Surface Soils: Effect of Molecular Structures, Soil Properties, and Solution Chemistry. Environ. Sci. Technol. 2020, 54, 1513–1521. [Google Scholar] [CrossRef] [PubMed]
- Milinovic, J.; Lacorte, S.; Vidal, M.; Rigol, A. Sorption Behaviour of Perfluoroalkyl Substances in Soils. Sci. Total Environ. 2015, 511, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Brusseau, M.L. Differential Sorption of Short-Chain versus Long-Chain Anionic Per- and Poly-Fluoroalkyl Substances by Soils. Environments 2023, 10, 175. [Google Scholar] [CrossRef]
- Campos-Pereira, H.; Kleja, D.B.; Ahrens, L.; Enell, A.; Kikuchi, J.; Pettersson, M.; Gustafsson, J.P. Effect of PH, Surface Charge and Soil Properties on the Solid–Solution Partitioning of Perfluoroalkyl Substances (PFASs) in a Wide Range of Temperate Soils. Chemosphere 2023, 321, 138133. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.L.; Anschutz, A.J.; Smolen, J.M.; Simcik, M.F.; Penn, R.L. The Adsorption of Perfluorooctane Sulfonate onto Sand, Clay, and Iron Oxide Surfaces. J. Chem. Eng. Data 2007, 52, 1165–1170. [Google Scholar] [CrossRef]
- Campos-Pereira, H.; Kleja, D.B.; Sjöstedt, C.; Ahrens, L.; Klysubun, W.; Gustafsson, J.P. The Adsorption of Per- and Polyfluoroalkyl Substances (PFASs) onto Ferrihydrite Is Governed by Surface Charge. Environ. Sci. Technol. 2020, 54, 15722–15730. [Google Scholar] [CrossRef]
- Shafique, U.; Dorn, V.; Paschke, A.; Schüürmann, G. Adsorption of Perfluorocarboxylic Acids at the Silica Surface. Chem. Commun. 2017, 53, 589–592. [Google Scholar] [CrossRef]
- Knight, E.R.; Janik, L.J.; Navarro, D.A.; Kookana, R.S.; McLaughlin, M.J. Predicting Partitioning of Radiolabelled 14C-PFOA in a Range of Soils Using Diffuse Reflectance Infrared Spectroscopy. Sci. Total Environ. 2019, 686, 505–513. [Google Scholar] [CrossRef]
- AS 4439-3:2019; Wastes, Sediments and Contaminated Soils, Part 3. Preparation of Leachates-Bottle Leaching Procedure. Standards Australia: Sydney, Australia, 2019.
- USEPA. Method 1311: Toxicity Characteristic Leaching Procedure; United State Environmental Protection Agency (USEPA): Washington, DC, USA; Research Triangle Park: Durham, NC, USA, 1992.
- USEPA. Method 1320: Multiple Extraction Procedure. EPA SW-846: Test Methods for Evaluating Solid Waste, Physical/Chemical Methods; United State Environmental Protection Agency (USEPA): Washington, DC, USA; Research Triangle Park: Durham, NC, USA, 1992.
- USEPA. Method 1314: Liquid-Solid Partitioning as a Function of Liquid-Solid Ratio for Constituents in Solid Materials Using an Up-Flow Percolation Column Procedure; United State Environmental Protection Agency (USEPA): Washington, DC, USA; Research Triangle Park: Durham, NC, USA, 2017.
- ISO 21268-2:2019; Soil Quality—Leaching Procedures for Subsequent Chemical and Ecotoxicological Testing of Soil and Soil-like Materials Part 2: Batch Test Using a Liquid to Solid Ratio of 10 l/Kg Dry Matter. The International Organization for Standardization: Geneva, Switzerland, 2019.
- ISO 21268-3:2019; Soil Quality—Leaching Procedures for Subsequent Chemical and Ecotoxicological Testing of Soil and Soil-like Materials Part 3: Up-Flow Percolation Test. The International Organization for Standardization: Geneva, Switzerland, 2019.
- Löv, Å.; Larsbo, M.; Sjöstedt, C.; Cornelis, G.; Gustafsson, J.P.; Kleja, D.B. Evaluating the Ability of Standardised Leaching Tests to Predict Metal(Loid) Leaching from Intact Soil Columns Using Size-Based Elemental Fractionation. Chemosphere 2019, 222, 453–460. [Google Scholar] [CrossRef]
- Grathwohl, P.; Susset, B. Comparison of Percolation to Batch and Sequential Leaching Tests: Theory and Data. Waste Manag. 2009, 29, 2681–2688. [Google Scholar] [CrossRef]
- Kabiri, S.; Tucker, W.; Navarro, D.A.; Bräunig, J.; Thompson, K.; Knight, E.R.; Nguyen, T.M.H.; Grimison, C.; Barnes, C.M.; Higgins, C.P.; et al. Comparing the Leaching Behavior of Per- and Polyfluoroalkyl Substances from Contaminated Soils Using Static and Column Leaching Tests. Environ. Sci. Technol. 2022, 56, 368–378. [Google Scholar] [CrossRef] [PubMed]
- van Glubt, S.; Brusseau, M.L.; Yan, N.; Huang, D.; Khan, N.; Carroll, K.C. Column versus Batch Methods for Measuring PFOS and PFOA Sorption to Geomedia. Environ. Pollut. 2021, 268, 115917. [Google Scholar] [CrossRef] [PubMed]
- Aly, Y.H.; McInnis, D.P.; Lombardo, S.M.; Arnold, W.A.; Pennell, K.D.; Hatton, J.; Simcik, M.F. Enhanced Adsorption of Perfluoro Alkyl Substances for in Situ Remediation. Environ. Sci. Water Res. Technol. 2019, 5, 1867–1875. [Google Scholar] [CrossRef]
- Higgins, C.P.; Luthy, R.G. Sorption of Perfluorinated Surfactants on Sediments. Environ. Sci. Technol. 2006, 40, 7251–7256. [Google Scholar] [CrossRef]
- Campos Pereira, H.; Ullberg, M.; Kleja, D.B.; Gustafsson, J.P.; Ahrens, L. Sorption of Perfluoroalkyl Substances (PFASs) to an Organic Soil Horizon—Effect of Cation Composition and pH. Chemosphere 2018, 207, 183–191. [Google Scholar] [CrossRef] [PubMed]
- ISO 10390:2021; Soil, Treated Biowaste and Sludge—Determination of pH. The International Organization for Standardization: Geneva, Switzerland, 2021.
- ISO 11277:2020; Soil Quality—Determination of Particle Size Distribution in Mineral Soil Material—Method by Sieving and Sedimentation. The International Organization for Standardization: Geneva, Switzerland, 2020.
- Martz, M.; Heil, J.; Marschner, B.; Stumpe, B. Effects of Soil Organic Carbon (SOC) Content and Accessibility in Subsoils on the Sorption Processes of the Model Pollutants Nonylphenol (4-n-NP) and Perfluorooctanoic Acid (PFOA). Sci. Total Environ. 2019, 672, 162–173. [Google Scholar] [CrossRef]
- EN 1484:1997; Water Analysis—Guidelines for the Determination of Total Organic Carbon (TOC) and Dissolved Organic Carbon (DOC). CEN, The European Committee for Standardization: Brussels, Belgium, 1997.
- ISO 11885:2007; Water Quality—Determination of Selected Elements by Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES). The International Organization for Standardization: Geneva, Switzerland, 2007.
- ISO 10304-1:2007; Water Quality—Determination of Dissolved Anions by Liquid Chromatography of Ions Part 1: Determination of Bromide, Chloride, Fluoride, Nitrate, Nitrite, Phosphate and Sulfate. The International Organization for Standardization: Geneva, Switzerland, 2007.
- Lath, S.; Knight, E.R.; Navarro, D.A.; Kookana, R.S.; McLaughlin, M.J. Sorption of PFOA onto Different Laboratory Materials: Filter Membranes and Centrifuge Tubes. Chemosphere 2019, 222, 671–678. [Google Scholar] [CrossRef]
- Sörengård, M.; Franke, V.; Tröger, R.; Ahrens, L. Losses of Poly- and Perfluoroalkyl Substances to Syringe Filter Materials. J Chromatogr A 2020, 1609, 460430. [Google Scholar] [CrossRef]
- Higgins, C.P.; Field, J.A.; Criddle, C.S.; Luthy, R.G. Quantitative Determination of Perfluorochemicals in Sediments and Domestic Sludge. Environ. Sci. Technol. 2005, 39, 3946–3956. [Google Scholar] [CrossRef]
- Ahrens, L.; Yamashita, N.; Yeung, L.W.Y.; Taniyasu, S.; Horii, Y.; Lam, P.K.S.; Ebinghaus, R. Partitioning Behavior of Per- and Polyfluoroalkyl Compounds between Pore Water and Sediment in Two Sediment Cores from Tokyo Bay, Japan. Environ. Sci. Technol. 2009, 43, 6969–6975. [Google Scholar] [CrossRef]
- Sörengård, M.; Kikuchi, J.; Wiberg, K.; Lutz, A. Spatial Distribution and Load of Per- and Polyfluoroalkyl Substances (PFAS) in Background Soils in Sweden. Chemosphere 2022, 295, 133944. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Leij, F.J.; Skaggs, T.H.; Toride, N.; Bradford, S.A.; Pontedeiro, E.M. Exact Analytical Solutions for Contaminant Transport in Rivers 1. The Equilibrium Advection-Dispersion Equation. J. Hydrol. Hydromech. 2013, 61, 146–160. [Google Scholar] [CrossRef]
- Ramírez-Sabag, J.; López-Falcón, D.A. How To Use Solutions of Advection-Dispersion Equation to Describe Reactive Solute Transport Through Porous Media. Geofis. Int. 2021, 60, 229–240. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Alves, W.J. Analytical Solutions of the One-Dimensional Convective-Dispersive Solute Transport Equation. In Technical Bulletin Number 1661 United States Department of Agriculture; USDA: Washington, DC, USA, 1982. Available online: https://www.ars.usda.gov/arsuserfiles/20361500/pdf_pubs/P0753.pdf (accessed on 20 May 2025).
- Röhler, K.; Haluska, A.A.; Susset, B.; Liu, B.; Grathwohl, P. Long-Term Behavior of PFAS in Contaminated Agricultural Soils in Germany. J. Contam. Hydrol. 2021, 241, 103812. [Google Scholar] [CrossRef] [PubMed]
- Parfitt, R.L.; Childs, C.W. Estimation of Forms of Fe and Al—A Review, and Analysis of Contrasting Soils by Dissolution and Mossbauer Methods. Soil Res. 1988, 26, 121–144. [Google Scholar] [CrossRef]
- Cousins, I.T.; Dewitt, J.C.; Glüge, J.; Goldenman, G.; Herzke, D.; Lohmann, R.; Ng, C.A.; Scheringer, M.; Wang, Z. The High Persistence of PFAS Is Sufficient for Their Management as a Chemical Class. Environ. Sci. Process. Impacts 2020, 22, 2307–2312. [Google Scholar] [CrossRef] [PubMed]
- Zhi, Y.; Liu, J. Sorption and Desorption of Anionic, Cationic and Zwitterionic Polyfluoroalkyl Substances by Soil Organic Matter and Pyrogenic Carbonaceous Materials. Chem. Eng. J. 2018, 346, 682–691. [Google Scholar] [CrossRef]
- Borthakur, A.; Olsen, P.; Dooley, G.P.; Cranmer, B.K.; Rao, U.; Hoek, E.M.V.; Blotevogel, J.; Mahendra, S.; Mohanty, S.K. Dry-Wet and Freeze-Thaw Cycles Enhance PFOA Leaching from Subsurface Soils. J. Hazard. Mater. Lett. 2021, 2, 100029. [Google Scholar] [CrossRef]
- Erkoç, Ş.; Erkoç, F. Structural and Electronic Properties of PFOS and LiPFOS. J. Mol. Struct. Theochem. 2001, 549, 289–293. [Google Scholar] [CrossRef]
- Xiao, F.; Zhang, X.; Penn, L.; Gulliver, J.S.; Simcik, M.F. Effects of Monovalent Cations on the Competitive Adsorption of Perfluoroalkyl Acids by Kaolinite: Experimental Studies and Modeling. Environ. Sci. Technol. 2011, 45, 10028–10035. [Google Scholar] [CrossRef]
- Rayne, S.; and Forest, K. A New Class of Perfluorinated Acid Contaminants: Primary and Secondary Substituted Perfluoroalkyl Sulfonamides Are Acidic at Environmentally and Toxicologically Relevant pH Values. J. Environ. Sci. Health Part A 2009, 44, 1388–1399. [Google Scholar] [CrossRef] [PubMed]
- Høisæter, Å.; Breedveld, G.D. Leaching Potential of Per- and Polyfluoroalkyl Substances from Source Zones with Historic Contamination of Aqueous Film Forming Foam—A Surfactant Mixture Problem. Environ. Adv. 2022, 8, 100222. [Google Scholar] [CrossRef]
- Kalbe, U.; Piechotta, C.; Bandow, N. Comparing PFAS Analysis in Batch Leaching and Column Leaching Tests. Environ. Sci. Pollut. Res. 2024, 31, 65233–65251. [Google Scholar] [CrossRef]
- Capitain, C.; Schüßler, M.; Bugsel, B.; Zweigle, J.; Vogel, C.; Leube, P.; Zwiener, C. Implementation of Matrix-Matched Semiquantification of PFAS in AFFF-Contaminated Soil. Environ. Sci. Technol. 2025, 59, 7338–7347. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Finkel, M.; Grathwohl, P. Mass Transfer Principles in Column Percolation Tests: Initial Conditions and Tailing in Heterogeneous Materials. Materials 2021, 14, 4708. [Google Scholar] [CrossRef]
- ISO 21268-1:2019; Soil Quality—Leaching Procedures for Subsequent Chemical and Ecotoxicological Testing of Soil and Soil-like Materials Part 1: Batch Test Using a Liquid to Solid Ratio of 2 l/Kg Dry Matter. The International Organization for Standardization: Geneva, Switzerland, 2019.
- USEPA. Method 1316—Liquid-Solid Partitioning as a Function of Liquid-Solid Ratio Using a Parallel Batch Extraction Procedure; United State Environmental Protection Agency (USEPA): Washington, DC, USA; Research Triangle Park: Durham, NC, USA, 2017.
- Brusseau, M.L.; Yan, N.; Van Glubt, S.; Wang, Y.; Chen, W.; Lyu, Y.; Dungan, B.; Carroll, K.C.; Holguin, F.O. Comprehensive Retention Model for PFAS Transport in Subsurface Systems. Water Res. 2019, 148, 41–50. [Google Scholar] [CrossRef]


| Soil | Site | Soil Type/Horizon | Treatment |
|---|---|---|---|
| 1 | Paskalampa | Spodosol/E | Spiking and aging |
| 2 | Paskalampa | Spodosol/Bs | Spiking and aging |
| 3 | Arboga | Cambisol/A | Spiking and aging |
| 4 | Arboga | Cambisol/A | None (field contaminated) |
| Soil | TOC (%) a | pH (H2O) b | Feox c (mmol kg−1) | Alox − Alp d (mmol kg−1) | CEC e (cmol+ kg–1) | Sand f (%) | Silt f (%) | Clay f (%) | Textural Class |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.1 | 4.6 | 2.5 | 1.9 | 1.8 | 53 | 40 | 7 | Sandy loam |
| 2 | 2.2 | 5.5 | 130 | 500 | 1.7 | 54 | 42 | 4 | Sandy loam |
| 3 | 1.3 | 5.5 | 110 | 31 | 8.6 | 27 | 44 | 29 | Clay |
| 4 | 1.7 | 6.9 | 130 | 42 | 13 | 24 | 26 | 50 | Clay |
| Soil | Soil 1 | Soil 2 | Soil 3 | Soil 4 |
|---|---|---|---|---|
| Compound | ||||
| PFBA | 98 ± 68 | 109 ± 27 | 126 ± 71 | ND |
| PFHxA | 153 ± 23 | 145 ± 31 | 115 ± 43 | ND |
| PFHpA | 160 ± 81 | 103 ± 9.7 | 136 ± 10 | ND |
| PFOA | 521 ± 294 | 323 ± 22 | 452 ± 88 | ND |
| PFNA | 253 ± 89 | 166 ± 44 | 144 ± 17 | 4.1 ± 0.9 |
| PFDA | 297 ± 87 | 256 ± 66 | 187 ± 104 | 3.8 ± 3.3 |
| PFUnDA | 394 ± 140 | 295 ± 38 | 356 ± 214 | ND |
| PFDoDA | 293 ± 89 | 163 ± 121 | 259 ± 142 | ND |
| PFBS | 681 ± 431 | 415 ± 153 | 597 ± 331 | ND |
| PFHxS | 676 ± 427 | 405 ± 46 | 568 ± 122 | 6.0 ± 1.1 |
| PFOS | 631 ± 238 | 540 ± 72 | 678 ± 28 | 63 ± 8.1 |
| FOSA | 445 ± 120 | 316 ± 31 | 373 ± 78 | ND |
| Kd | Batch (L/S 10) (%) | Percolation (L/S 0–10) (%) |
|---|---|---|
| 1 | 91 | 100 |
| 5 | 67 | 100 |
| 10 | 50 | 86 |
| 20 | 33 | 49 |
| 50 | 17 | 20 |
| Soil | L/S (L kg−1) | PFBA | PFHxA | PFHpA | PFOA | PFNA | PFDA | PFUnDA | PFDoDA | PFBS | PFHxS | PFOS | FOSA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Soil 1 | 0–0.1 | 0.25 ± 0.09 | 0.40 ± 0.16 | 0.64 ± 0.25 | 1.6 ± 0.5 | 6.5 ± 1.6 | 51.7 ± 20.3 | 368 ± 154 | 729 ± 306 | 0.77 ± 0.21 | 1.6 ± 0.5 | 12.3 ± 3.8 | 1826 ± 1065 |
| 0.1–2 | 1.6 ± 0.7 | 2.0 ± 1.3 | 3.6 ± 2.6 | 7.4 ± 4.8 | 26.8 ± 11.1 | 112 ± 21 | 479 ± 108 | 1314 ± 771 | 3.5 ± 1.5 | 8.0 ± 6.4 | 52.2 ± 11.9 | 765 ± 324 | |
| 2–5 | 10.7 ± 11.5 | 11.5 ± 5.8 | 12.1 ± 3.1 | 13.4 ± 7.9 | 41.7 ± 30.0 | 167 ± 79 | 672 ± 146 | 3149 ± 1055 | 30.3 ± 20.2 | 13.7 ± 4.0 | 80.8 ± 48.6 | 854 ± 553 | |
| 5–10 | <LoQ | 29.7 ± 7.2 | 32.4 ± 14.5 | 20.5 ± 3.7 | 32.8 ± 17.9 | 164 ± 115 | 1037 ± 81 | <LoQ | 110 ± 48 | 23.9 ± 4.6 | 82.8 ± 58.1 | 715 ± 180 | |
| Batch (10) | 2.5 ± 2.2 | 2.3 ± 0.6 | 8.5 ± 2.5 | 11.5 ± 1.7 | 16.1 ± 2.7 | 54.2 ± 4.4 | 219 ± 33 | 952 ± 392 | 5.0 ± 0.9 | 12.4 ± 1.2 | 31.3 ± 8.0 | 256 ± 77 | |
| Soil 2 | 0–0.1 | 0.61 ± 0.07 | 0.84 ± 0.06 | 1.8 ± 0.2 | 6.8 ± 0.9 | 50.1 ± 13.3 | 395 ± 161 | 3468 ± 1140 | <LoQ | 0.89 ± 0.04 | 3.1 ± 0.3 | 95.6 ± 21.6 | <LoQ |
| 0.1–2 | <0 | 1.0 ± 0.2 | 1.70.2 | 8.7 ± 0.7 | 76.7 ± 7.6 | 761 ± 187 | 2647 ± 802 | <LoQ | 1.0 ± 0.1 | 3.9 ± 0.2 | 136 ± 14 | <LoQ | |
| 2–5 | <LoQ | <0 | <0 | 10.2 ± 1.1 | 106 ± 12 | 1466 ± 588 | <LoQ | <LoQ | <0 | 2.7 ± 0.5 | 228 ± 34 | <LoQ | |
| 5–10 | <LoQ | <0 | <0 | 7.1 ± 1.5 | 103 ± 9 | 721 ± 203 | <LoQ | <LoQ | <0 | <0 | 210 ± 32 | <LoQ | |
| Batch (10) | <0 | 1.6 ± 0.6 | 2.4 ± 0.3 | 8.8 ± 0.3 | 56.8 ± 19.0 | 423 ± 126 | 1423 ± 247 | 2792 ± 1884 | <0 | 3.4 ± 1.8 | 143 ± 41.3 | 645 ± 202 | |
| Soil 3 | 0–0.1 | 0.19 ± 0.00 | 0.20 ± 0.00 | 0.46 ± 0.03 | 1.3 ± 0.1 | 5.0 ± 0.2 | 48.7 ± 15.6 | 892 ± 217 | 1589 ± 93 | 0.44 ± 0.07 | 0.84 ± 0.1 | 17.7 ± 1.3 | <LoQ |
| 0.1–2 | 1.4 ± 0.4 | 0.83 ± 0.23 | 1.3 ± 0.1 | 1.2 ± 0.1 | 2.8 ± 0.2 | 20.2 ± 2.7 | 178 ± 39 | 752 ± 92 | 1.9 ± 0.3 | <0 | 10.7 ± 1.7 | 1587 | |
| 2–5 | 39.8 ± 37.6 | <0 | <0 | <0 | <0 | 18.8 ± 1.6 | 179 ± 7 | 725 ± 284 | 66.8 ± 24.4 | <0 | 12.3 ± 0.5 | 1011 | |
| 5–10 | <LoQ | <0 | <0 | <0 | <0 | 16.7 ± 1.5 | 138 ± 25 | 384 ± 78 | 288 ± 133 | <0 | 11.2 ± 0.5 | 393 | |
| Batch (10) | 14.2 ± 4.1 | 3.2 ± 0.2 | 5.3 ± 1.0 | 1.8 ± 1.3 | 2.5 ± 1.3 | 18.6 ± 0.5 | 67.3 ± 12.2 | 109 ± 31 | 6.3 ± 2.4 | 1.2 ± 1.2 | 15.8 ± 0.7 | 94.9 ± 23.2 | |
| Soil 4 | 0–0.1 | - | - | - | - | - | - | - | - | - | 0.68 ± 0.1 | 23.8 ± 5.4 | - |
| 0.1–2 | - | - | - | - | - | - | - | - | - | 1.3 ± 0.2 | 10.2 ± 1.5 | - | |
| 2–5 | - | - | - | - | - | - | - | - | - | 5.5 ± 3.0 | 17.8 ± 2.7 | - | |
| 5–10 | - | - | - | - | - | - | - | - | - | <0 | 33.0 ± 2.8 | - | |
| Batch (10) | - | - | - | - | - | - | - | - | - | <0 | 21.6 ± 9.4 | - |
| Kd Used as Input in Simulations | |||||||
|---|---|---|---|---|---|---|---|
| L/S | 1 | 5 | 10 | 15 | 20 | 30 | 50 |
| 0–0.1 | 1.2 | 5.2 | 10 | 15 | 20 | 30 | 50 |
| 0.1–2 | 1.0 | 4.2 | 9.2 | 14 | 19 | 29 | 49 |
| 2–5 | 1.3 | 2.5 | 6.8 | 12 | 17 | 27 | 47 |
| 5–10 | - | 2.6 | 4.3 | 8.1 | 13 | 23 | 43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kleja, D.B.; Campos-Pereira, H.; Kikuchi-McIntosh, J.; Pettersson, M.; Golovko, O.; Enell, A. Evaluation of Standardised (ISO) Leaching Tests for Assessing Leaching and Solid–Solution Partitioning of Perfluoroalkyl Substances (PFAS) in Soils. Environments 2025, 12, 179. https://doi.org/10.3390/environments12060179
Kleja DB, Campos-Pereira H, Kikuchi-McIntosh J, Pettersson M, Golovko O, Enell A. Evaluation of Standardised (ISO) Leaching Tests for Assessing Leaching and Solid–Solution Partitioning of Perfluoroalkyl Substances (PFAS) in Soils. Environments. 2025; 12(6):179. https://doi.org/10.3390/environments12060179
Chicago/Turabian StyleKleja, Dan B., Hugo Campos-Pereira, Johannes Kikuchi-McIntosh, Michael Pettersson, Oksana Golovko, and Anja Enell. 2025. "Evaluation of Standardised (ISO) Leaching Tests for Assessing Leaching and Solid–Solution Partitioning of Perfluoroalkyl Substances (PFAS) in Soils" Environments 12, no. 6: 179. https://doi.org/10.3390/environments12060179
APA StyleKleja, D. B., Campos-Pereira, H., Kikuchi-McIntosh, J., Pettersson, M., Golovko, O., & Enell, A. (2025). Evaluation of Standardised (ISO) Leaching Tests for Assessing Leaching and Solid–Solution Partitioning of Perfluoroalkyl Substances (PFAS) in Soils. Environments, 12(6), 179. https://doi.org/10.3390/environments12060179






