Effect of Orientation and Vegetation over the Embankment Crest for Energy Reduction at Downstream
Abstract
1. Introduction
2. Materials and Methods
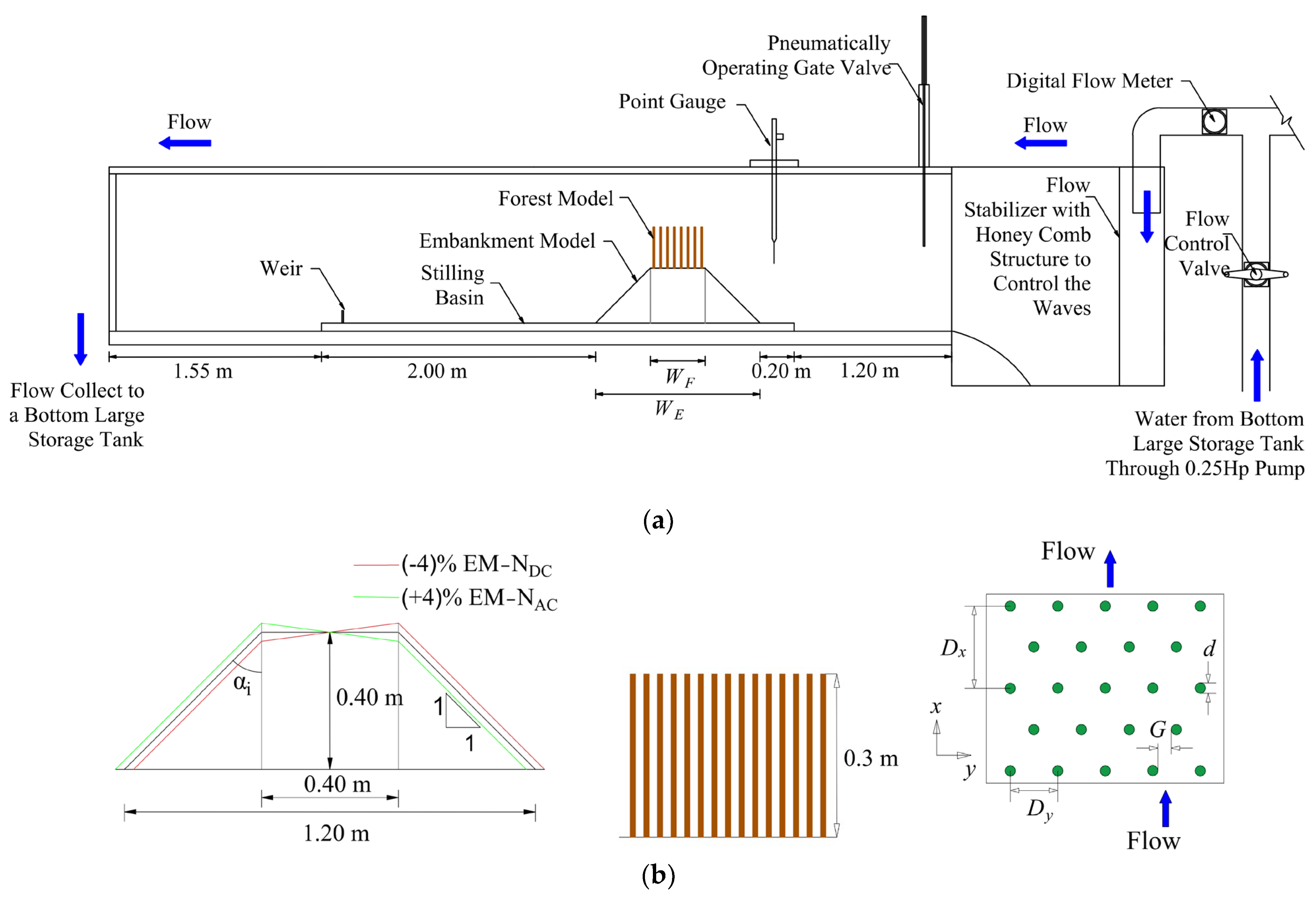
2.1. Experimental Conditions
2.1.1. Scaling of the Model
2.1.2. Flume Characteristics and Flow Conditions
2.1.3. Setup of the Physical Model
2.2. Experimental Procedure and Data Analysis
2.2.1. Initial Condition
2.2.2. Measurement of the Water Depth and Velocity
2.2.3. Normalized Parameters Used for the Analysis
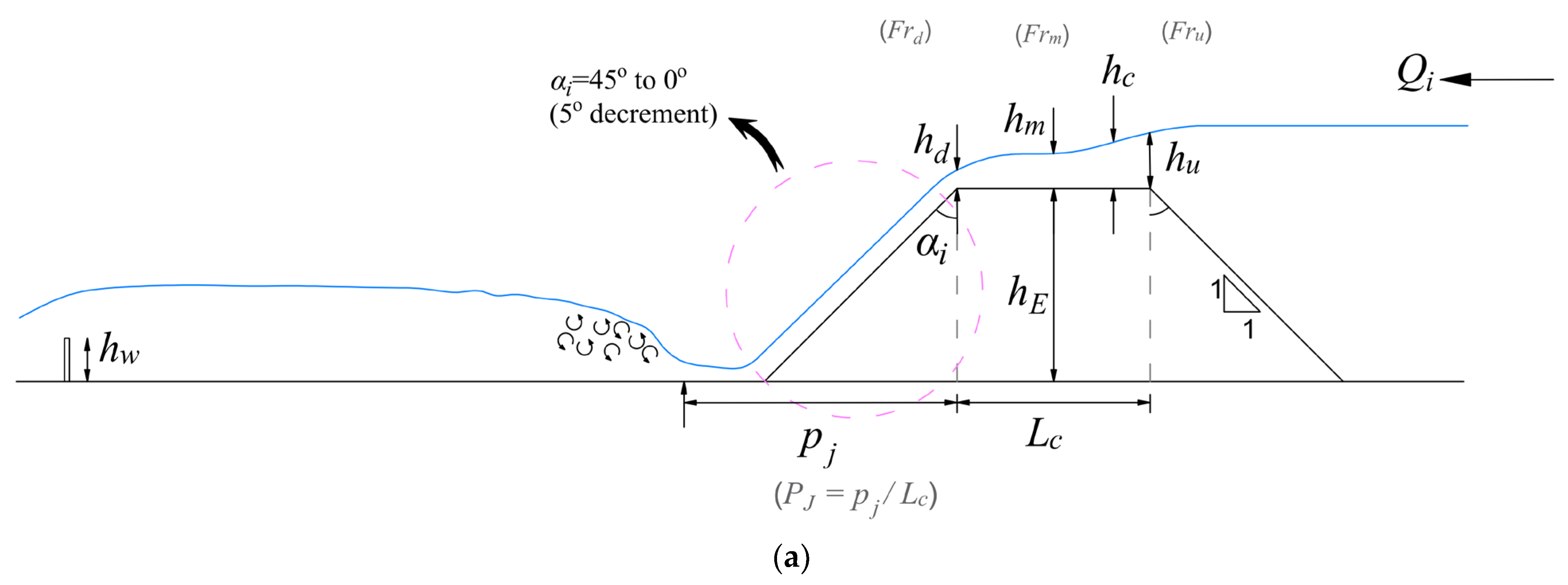
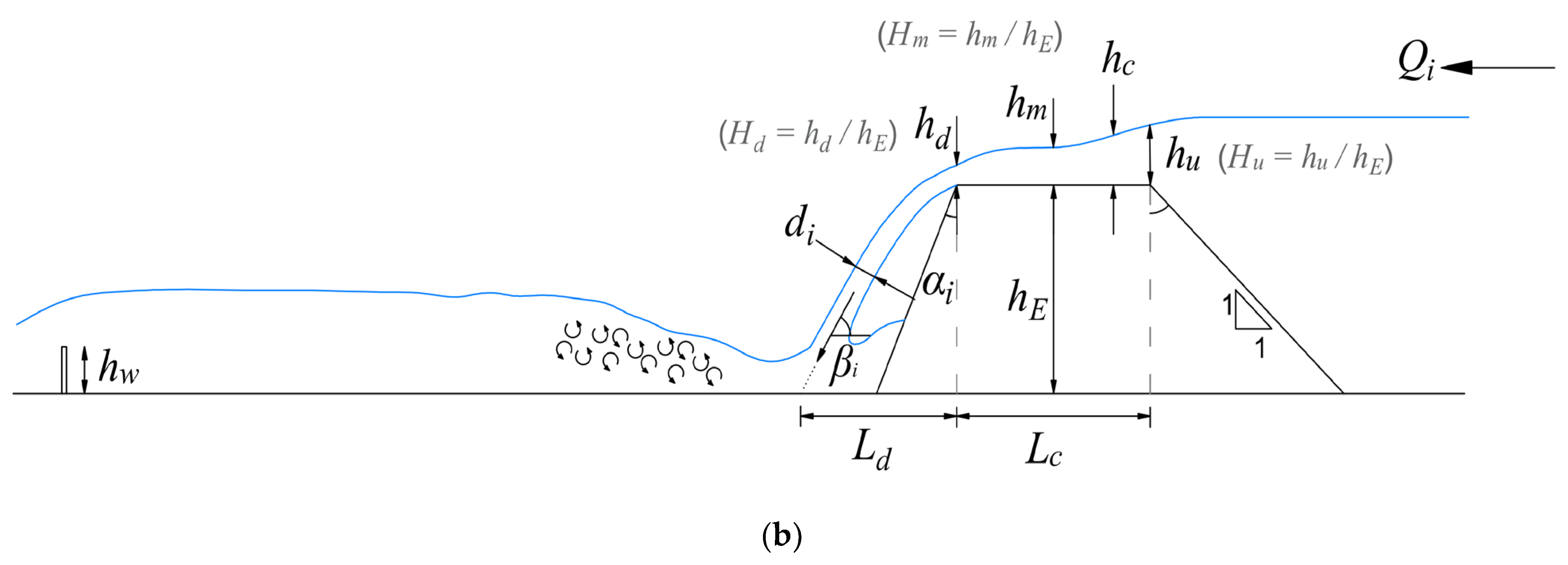
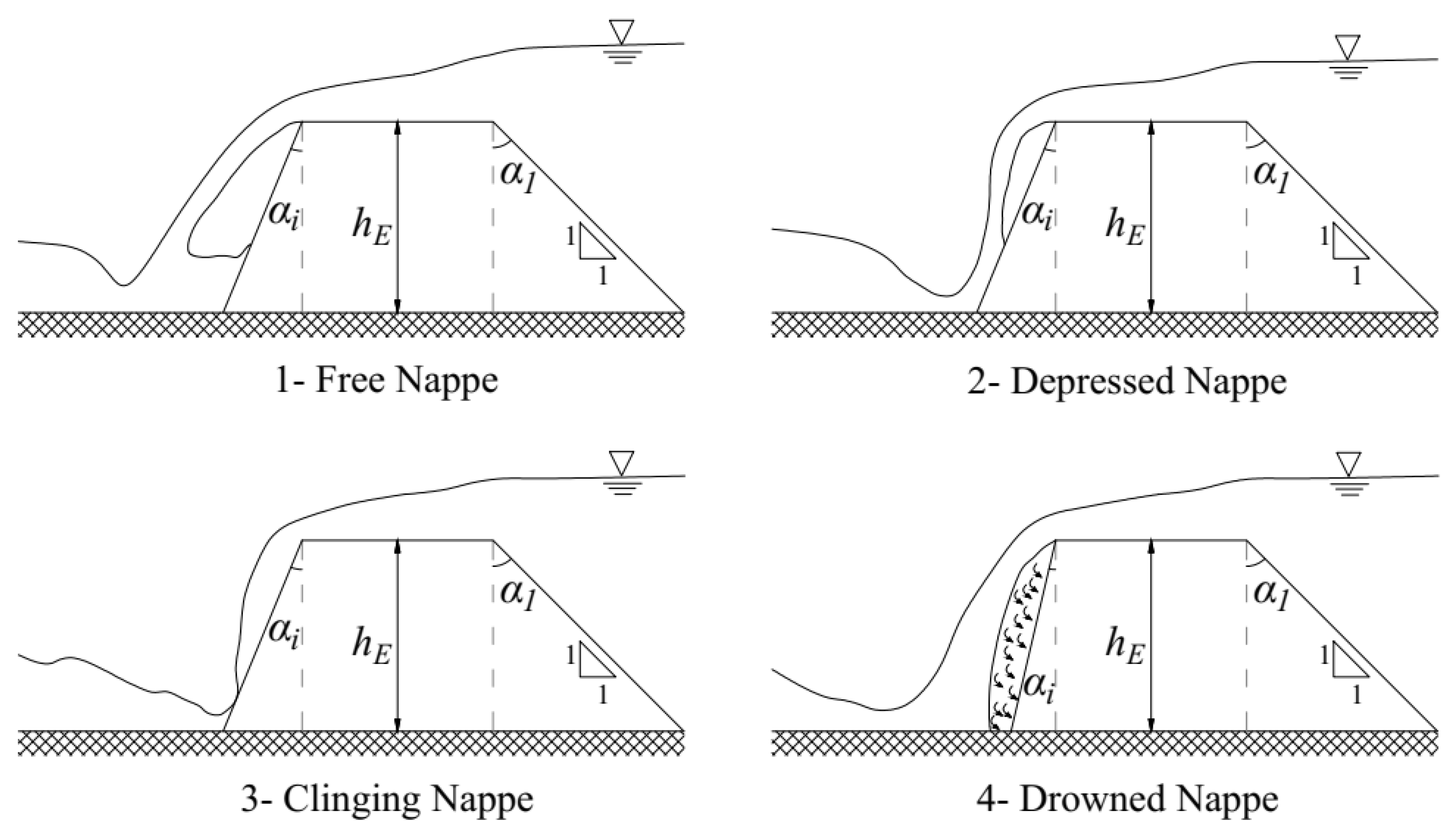
2.2.4. Nappe Flow and Its Properties
2.2.5. Position of the Hydraulic Jump
2.2.6. Energy Loss and Head Loss
3. Results
3.1. Flow Properties at EM Crest
3.1.1. Changes in the Flow Structure by Overtopping and Nappe Flow Formation
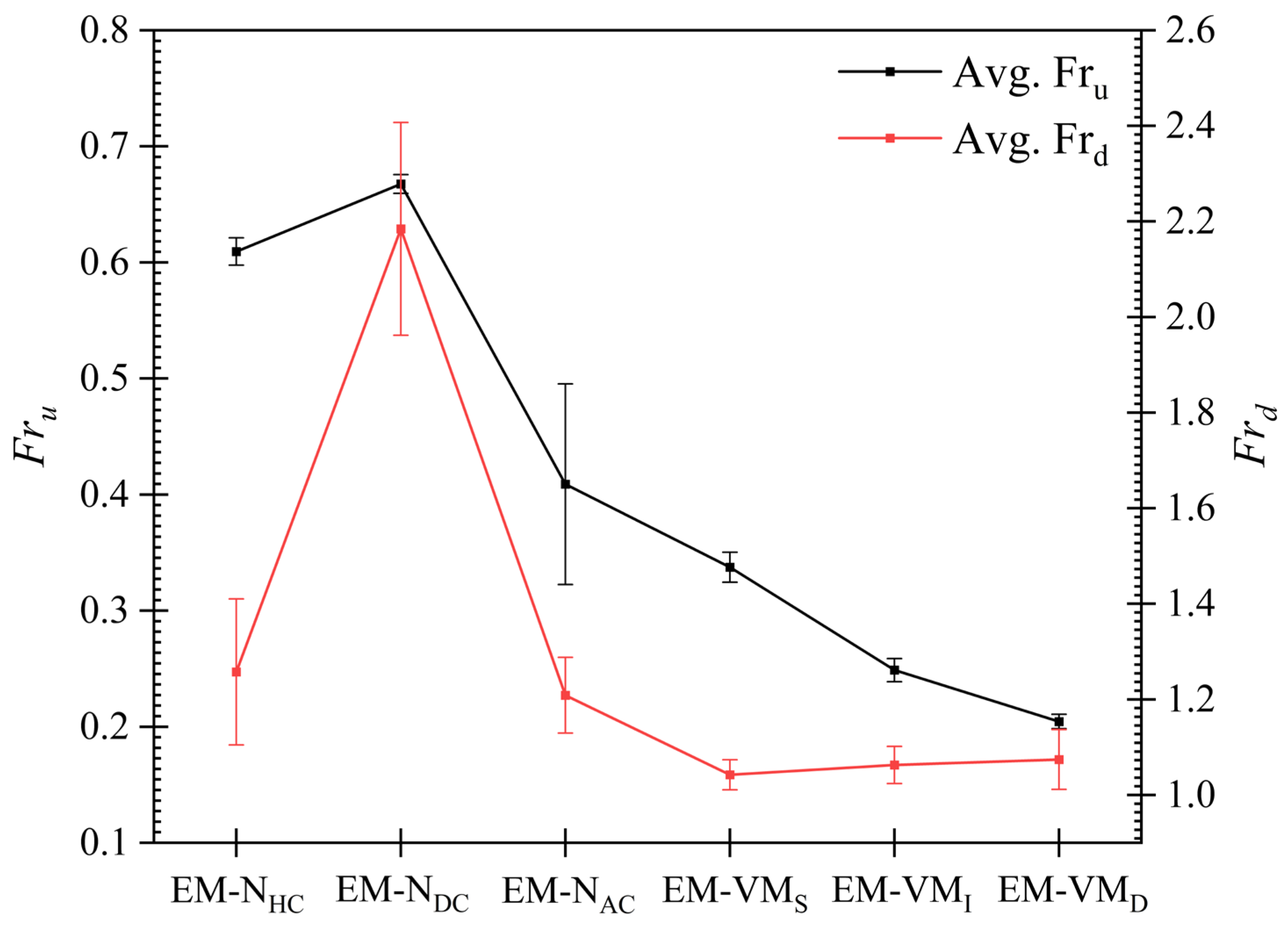
3.1.2. Froude Number and Critical Depth
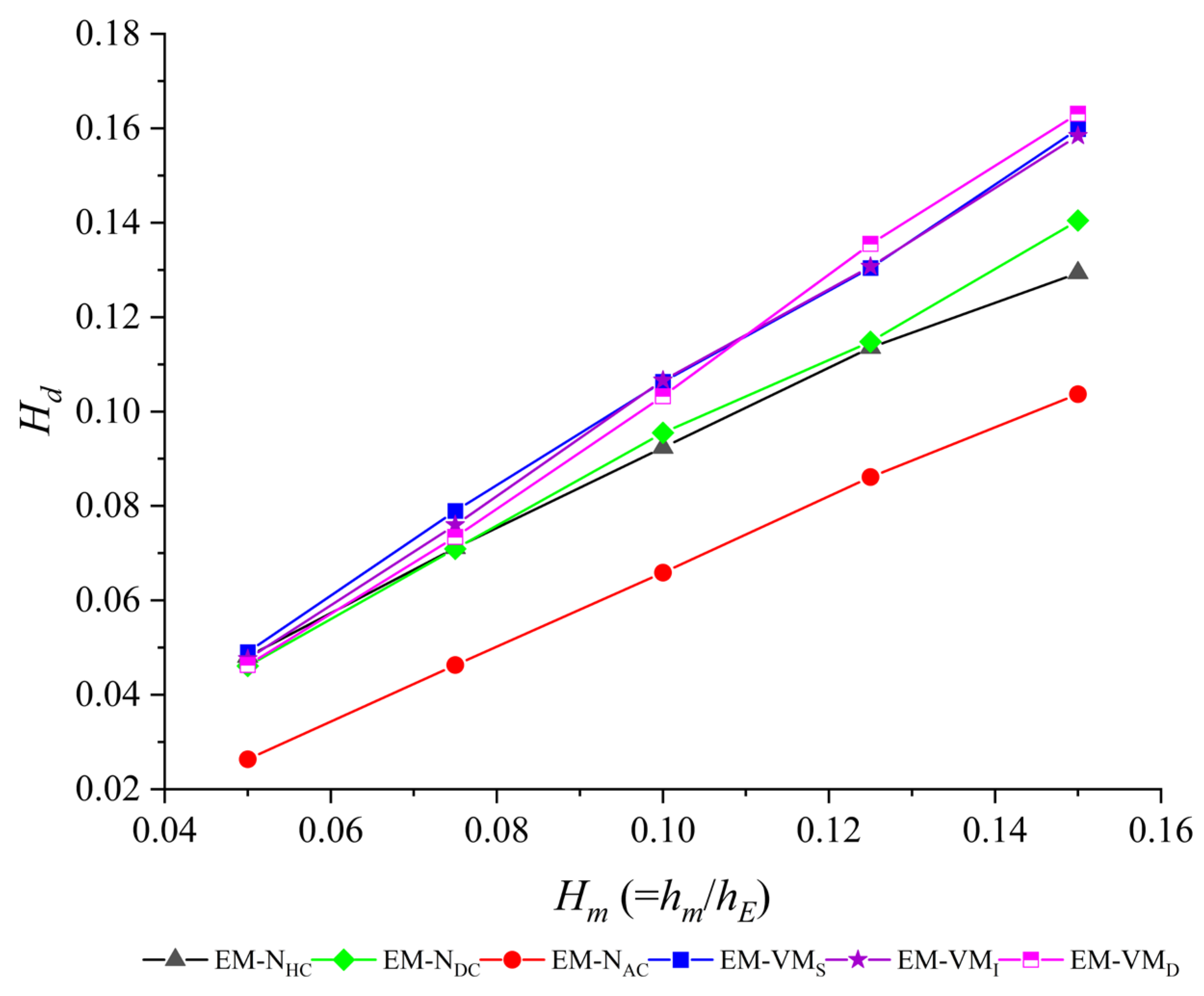
3.1.3. Effect of the Crest Orientation and Geometry on the Water Depth at Downstream
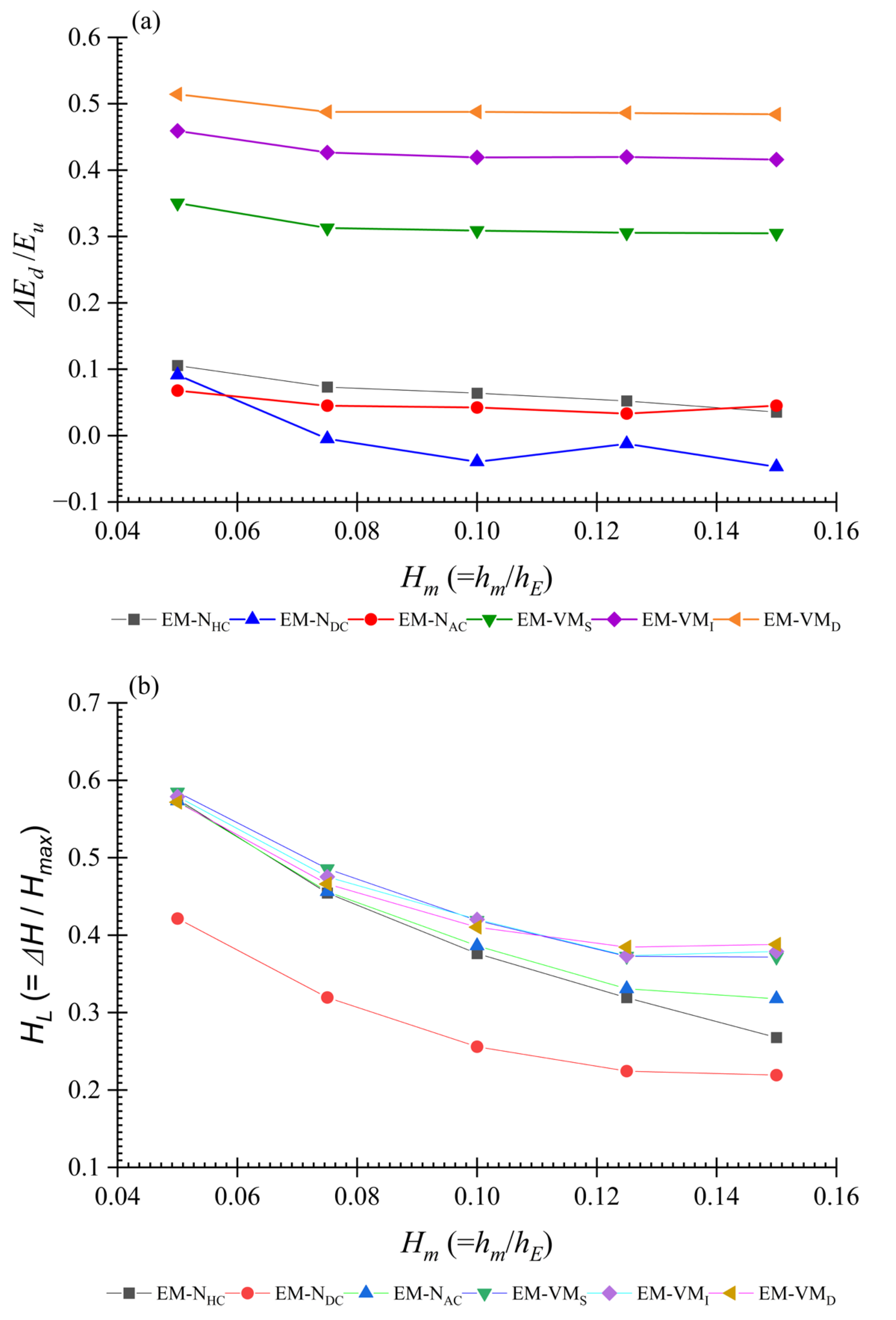
3.1.4. Energy Reduction over the Embankment Crest by Overtopping and at the Downstream Plunge Pool
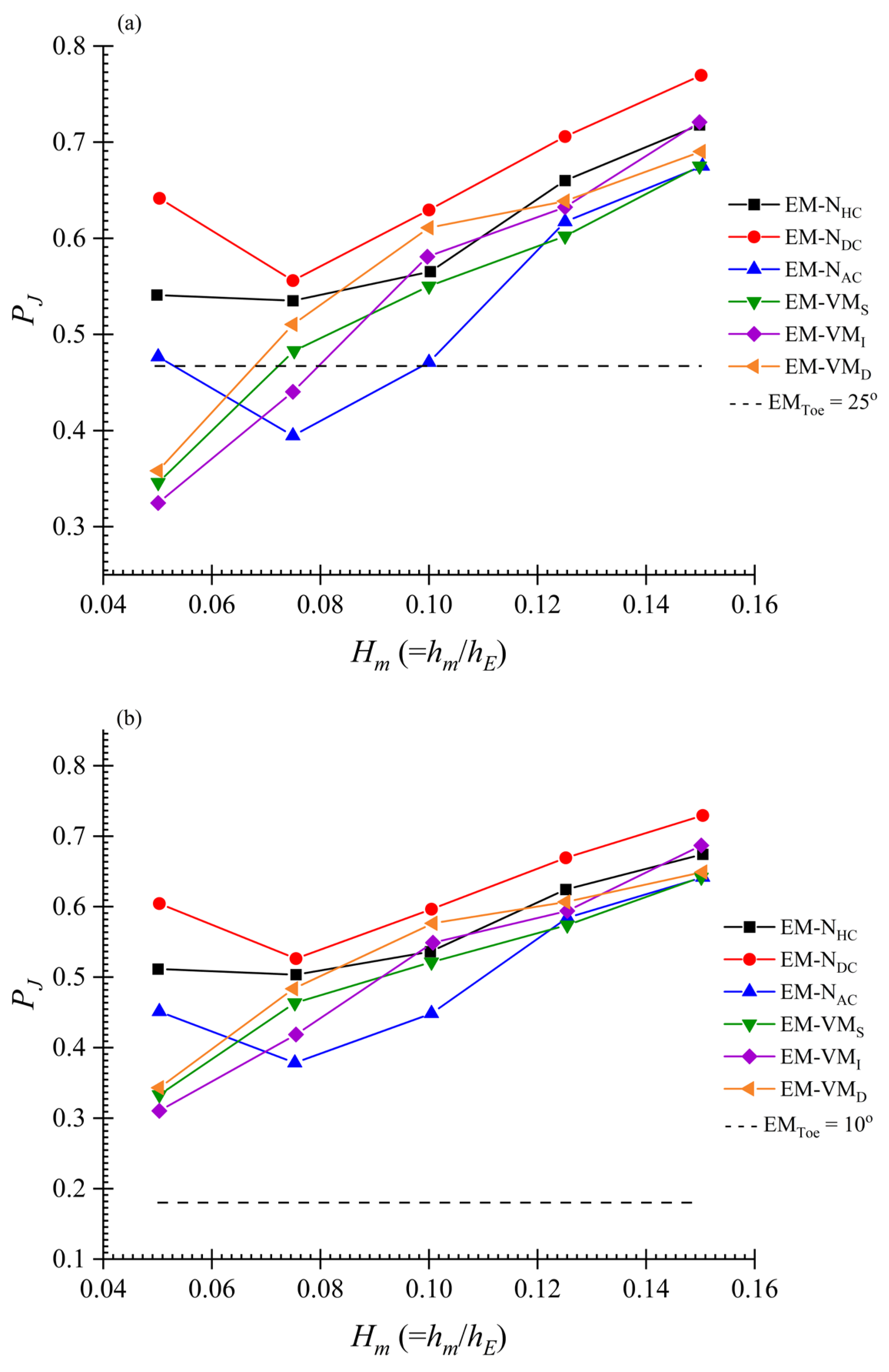
3.1.5. Position of the Hydraulic Jump at Downstream
3.2. Nappe Flow Properties
Variation of the Nappe Flow Drop Length, Thickness, and Impinging Jet Angle
4. Discussion
4.1. Flow Structures and Their Characteristics
4.2. Vegetation over the Crest of the Embankment, Energy Reduction, and Head Loss
Use of Vegetation as a Countermeasure to Reduce the Destructive Energy of Tsunami
5. Summary
- The overtopping flow from an embankment creates a nappe flow, impinging the jet and steepening the downward slope downstream. Changes in the crest geometry can significantly affect the nappe formation condition. With the ascending slope, the flow structure and geometry over the crest have further controlled nappe flow formation. In descending slope, the nappe flow formation was quicker while increasing overtopping flow. In the EM-NDC case, when the downstream surface slope varied from 45° to 30°, depressed and clinging nappe occurred. This phenomenon was not observed in other cases. In no vegetation cases (EM-NHC, EM-NAC, EM-NDC), the energy reduction and the head losses are comparatively low concerning the cases with vegetation patches (EM-VMS, EM-VMI, EM-VMD) at the crest. The created plunge pool by the secondary structure, the downstream (weir), absorbs the potential energy of the impact of jet impingement using the provided water cushion. The energy absorption by the water cushion of the plunge pool can be further evaluated with mobile bed condition experiments concerning the scouring depth.
- Vegetation at the crest further delays the overtopping flow by increasing the water depth in front of the vegetation while increasing the discharge corresponding to the selected overtopping depth. This tailwater depth increases majorly depending on the vegetation model’s density (G/d ratio). The G/d ratios of vegetation models were 1.33, 0.59, and 0.29 for EM-VMS, EM-VMI, and EM-VMD, respectively. When density increased, energy reduction at the downstream brink edge was raised, where maximum energy reduction at the downstream brink edge occurred by the EM-VMD greater than 0.5 (Figure 5). Additionally, the head loss downstream was increased concerning the density of the vegetation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EM | embankment model |
| EM-NAC | embankment model with +4.0% ascending crest (no vegetation over the crest) |
| EM-NDC | embankment model with −4.0% descending crest (no vegetation over the crest) |
| EM-NHC | embankment model with horizontal crest (no vegetation over the crest) |
| EM-VMD | embankment model with horizontal crest (dense vegetation model over the crest, G/d = 0.29) |
| EM-VMI | embankment model with horizontal crest (intermediate vegetation model over the crest, G/d = 0.59) |
| EM-VMS | embankment model with horizontal crest (sparse vegetation model over the crest, G/d = 1.33) |
| GEJT | Great East Japan Tsunami |
| IOT | Indian Ocean Tsunami |
| VM | vegetation model |
| The following symbols are used in this paper: | |
| co-efficient used to calculate the velocity fluctuations | |
| angle of the downstream surface slope of the EM measured from downstream brink edge | |
| angle of the nappe flow impinging jet | |
| critical angle of the downstream surface slope of the EM measured from downstream brink edge | |
| specific energy loss over the downstream brink edge of the EM crest | |
| head loss (m) | |
| D | center to center distance of stems in the vegetation model (m) |
| Dx | center to center distance of stems in the vegetation model into x-direction (m) |
| Dy | center to center distance of stems in the vegetation model into y-direction (m) |
| specific energy | |
| specific energy at the downstream brink edge over the EM crest | |
| specific energy at the upstream brink edge over the EM crest | |
| G | distance between the stems in the cross-stream direction in the vegetation model (m) |
| Froude number | |
| normalized critical water depth over the embankment crest | |
| normalized water depth of the downstream brink edge of the embankment crest | |
| dam height (m), and this is equal to the | |
| normalized total head loss at the plunge pool | |
| normalized overtopping depth measured at the mid-section of the EM | |
| maximum head at the upstream of the EM | |
| normalized water depth of the upstream brink edge of the embankment crest | |
| normalized position of the hydraulic jump at the downstream plunge pool of the EM | |
| crest length of the EM (m) | |
| nappe flow impinging jet drop length measured from downstream brink edge (m) | |
| length of the model (m) | |
| length of the prototype (m) | |
| length scale | |
| flow rate through the model (m3/s) | |
| Reynolds numbers | |
| depth-averaged velocity of the flow (m/s) | |
| Weber number | |
| width of the vegetation model over the crest of the embankment model (m) | |
| width of the channel (m)/width of the embankment model (m) | |
| diameter of the stem in vegetation model (m) | |
| thickness of the nappe flow impinging jet (mm) | |
| number of wooden stems in a square meter of the vegetation model (No.cm) | |
| gravitational acceleration (m/s−2) | |
| depth of water flow (m) | |
| critical water depth over the embankment crest (m) | |
| water depth of the downstream brink edge of the embankment crest (m) | |
| critical brink depth at downstream brink edge of the EM (m) | |
| height of the embankment model at the center (m) | |
| overtopping depth measured at the mid-section of the crest of the EM in the initial case (m) | |
| Manning’s roughness coefficient | |
| position of the hydraulic jump in plunge pool measured from the downstream brink edge (m) | |
| elevation of the bottom of the model from reference line (m) | |
References
- Dissanayaka, K.D.C.R.; Tanaka, N.; Vinodh, T.L.C. Integration of Eco-DRR and hybrid defense system on mitigation of natural disasters (Tsunami and Coastal Flooding): A review. Nat. Hazards 2021, 110, 1–28. [Google Scholar] [CrossRef]
- Igarashi, Y.; Tanaka, N.; Zaha, T. Changes in flow structures and energy reduction through compound tsunami mitigation system with embankment and lined piles. Ocean Eng. 2018, 164, 722–732. [Google Scholar] [CrossRef]
- Rahman, M.A.; Tanaka, N.; Rashedunnabi, A.H.M. Flume experiments on flow analysis and energy reduction through a compound tsunami mitigation system with a seaward embankment and landward vegetation over a mound. Geosciences 2021, 11, 90. [Google Scholar] [CrossRef]
- Shuto, N.; Fujima, K. A short history of tsunami research and countermeasures in Japan. Proc. Jpn. Acad. Ser B Phys. Biol. Sci. 2009, 85, 267–275. [Google Scholar] [CrossRef]
- Shuto, N.; Imamura, F.; Koshimura, S.; Satake, K.; Matsutomi, H. Encyclopedia of Tsunamis (Tsunami no Jiten); Asakura Publishing: Tokyo, Japan, 2007; p. 350. [Google Scholar]
- Tsujimoto, G.; Kakinoki, T.; Mineura, R.; Uno, K.; Yamada, F. Scouring mechanism behind seawall from tsunami overflow and optimum conditions to reduce tsunami energy with an artificial trench. Coast. Eng. Proc. 2015, 1, 38. [Google Scholar] [CrossRef]
- Zaha, T.; Tanaka, N.; Kimiwada, Y. Flume experiments on optimal arrangement of hybrid defense system comprising an embankment, moat, and emergent vegetation to mitigate inundating tsunami current. Ocean Eng. 2019, 173, 45–57. [Google Scholar] [CrossRef]
- Allsop, N.W.H.A.; Kortenhaus, A.; Morris, M.W. Failure Mechanisms for Flood Defense Structures. FLOODsite Rep. T04-06-01, FLOODsite Consortium 2007. Available online: www.floodsite.net (accessed on 12 May 2022).
- Japan Forest Agency. Annual Report on Forest and Forestry in Japan; Fiscal Year 2011 (Summary). 2012. Available online: https://www.data.go.jp/data/en/dataset/maff_20140918_0070 (accessed on 4 April 2022).
- Kato, F.; Suwa, Y.; Watanabe, K.; Hatogai, S. Mechanism of coastal dike failure induced by the Great East Japan Earthquake Tsunami. In Proceedings of the 33rd ICCE, Santander, Spain, 1–6 July 2012. 9p. [Google Scholar]
- Tokida, K.; Tanimoto, R. Lessons for countermeasures using earth structures against tsunami obtained in the 2011 Off the Pacific Coast of Tohoku Earthquake. Soils Found. 2014, 54, 523–543. [Google Scholar] [CrossRef]
- Tanaka, N.; Yagisawa, J.; Yasuda, S. Breaking pattern and critical breaking condition of Japanese pine trees on coastal sand dunes in huge tsunami caused by Great East Japan Earthquake. Nat. Hazards 2013, 65, 423–442. [Google Scholar] [CrossRef]
- Iimura, K.; Tanaka, N. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean Eng. 2012, 54, 223–232. [Google Scholar] [CrossRef]
- Matsuba, S.; Mikami, T.; Jayaratne, R.; Shibayama, T.; Esteban, M. Analysis of tsunami behavior and the effect of coastal forest in reducing tsunami force around the coastal dikes. Coast. Eng. Proc. 2014, 1, 37. [Google Scholar] [CrossRef]
- Tanaka, N.; Jinadasa, K.B.S.N.; Mowjood, M.I.M.; Fasly, M.S.M. Coastal vegetation planting projects for tsunami disaster mitigation: Effectiveness evaluation of new establishments. Landsc. Ecol. Eng. 2011, 7, 127–135. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Undular hydraulic jump formation and energy loss in a flow through emergent vegetation of varying thickness and density. Ocean Eng. 2017, 141, 308–325. [Google Scholar] [CrossRef]
- Ali, S.; Uijttewaal, W.S.J. Form drag due to vegetated weirlike obstacles interpreted as expansion loss. In Proceedings of the 33rd International Association for Hydro-Environment Engineering and Research (IAHR) World Congress, Vancouver, Canada, 9–14 August 2009; pp. 139–146. [Google Scholar]
- Ali, S.; Uijttewaal, W.S.J. Flow resistance of vegetated weir-like obstacles during high water stages. In Proceedings of the River Flow, Bundesanstalt für Wasserbau, Braunschweig, Germany, 8–10 September 2010; pp. 293–299. [Google Scholar]
- Abdalla, M.G.; Shamaa, M.T. Experimental Investigation of Nappe Profile and Pool Depth for Broad-Crested Weirs. Int. J. Eng. Res. Gen. Sci. 2016, 4, 1–18, ISSN 2091-2730. [Google Scholar]
- Strusińska-Correia, A. Tsunami mitigation in Japan after the 2011 Tōhoku Tsunami. Int. J. Disaster Risk Reduct. 2017, 22, 397–411. [Google Scholar] [CrossRef]
- Zhu, T. Breach Growth in Clay Dikes. Ph.D. Thesis, University of Technology, Delft, The Netherlands, 2006. ISBN 10: 90-9020964-6. [Google Scholar]
- Daneshfaraz, R.; Dasineh, M.; Ghaderi, A.; Sadeghfam, S. Numerical modelling of hydraulic properties of slopped broad crested weir. AUT J. Civ. Eng. 2020, 4, 229–240. [Google Scholar] [CrossRef]
- Emiroglu, M.E.; Baylar, A. The effect of broad-crested weir shape on air entrainment. J. Hydraul. Res. 2003, 41, 649–655. [Google Scholar] [CrossRef]
- Imanin, H.; Mohammadian, A.; Hoshyar, P. Experimental and numerical study of flow over a broad-crested weir under different hydraulic head ratios. Flow Meas. Instrum. 2021, 80, 102004. [Google Scholar] [CrossRef]
- Tanaka, S.; Istiyanto, D.C.; Kuribayashi, D. (Eds.) ICHARM Planning and Design of Tsunami-Mitigative Coastal Vegetation Belts; Technical Note of PWRI No. 4177; International Centre for Water Hazard and Risk Management under the Auspices of UNESCO (ICHARM) and Public Works Research Institute (PWRI): Ibaraki-ken, Japan, 2010. [Google Scholar]
- Peakall, J.; Warburton, J. Surface tension in small hydraulic river models–the significance of the Weber number. J. Hydrol. 1996, 35, 199–212. [Google Scholar]
- Spiske, M.; Weiss, R.; Bahlburg, H.; Roskosch, J.; Amijaya, H. The TsuSedMod inversion model applied to the deposits of the 2004 Sumatra and 2006 Java tsunami and implications for estimating flow parameters of palaeo-tsunami. Sediment Geol. 2010, 224, 29–37. [Google Scholar] [CrossRef]
- Detailed Design Report for Infrastructure for Coastal Line, Colombo Suburban Railway Project (CSRP). Available online: https://csrp.lk/backend/documents/1-%2020-CL-DD-F-RE-%20Detailed%20Design%20Report%20-%202020-09-web.pdf (accessed on 22 January 2022).
- De Costa, R.; Tanaka, N. Inland forest as a trapping function against tsunami borne large broken or washed-out trees. Landsc. Ecol. Eng. 2020, 16, 97–112. [Google Scholar] [CrossRef]
- Tanaka, N.; Yasuda, S.; Iimura, K.; Yagisawa, J. Combined effects of coastal forest and sea embankment on reducing the washout region of houses in the Great East Japan tsunami. J. Hydro-Environ. Res. 2014, 8, 270–280. [Google Scholar] [CrossRef]
- Tanaka, N.; Sasaki, Y.; Mowjood, M.I.M.; Jinadasa, K.B.S.N.; Homchuen, S. Coastal vegetation structures and their functions in tsunami protection: Experience of the recent Indian Ocean tsunami. Landsc. Ecol. Eng. 2007, 3, 33–45. [Google Scholar] [CrossRef]
- Thuy, N.B.; Nandasena, N.A.K.; Hai Dang, V.; Tanaka, N.; Quoc Viet, H.; Giay, C. Simplified formulae for designing coastal forest against tsunami run-up: One-dimensional approach. Mar. Geophys. Geol. 2018, 92, 327–346. [Google Scholar] [CrossRef]
- Shuto, N. The effectiveness and limit of tsunami control forests. Coast. Eng. Jpn. 1987, 30, 143–153. [Google Scholar] [CrossRef]
- Tanaka, N.; Yagisawa, J. Flow structures and sedimentation characteristics around clump-type vegetation. J. Hydro-Environ. Res. 2010, 4, 15–25. [Google Scholar] [CrossRef]
- Takemura, T.; Tanaka, N. Flow structures and drag characteristics of a colony-type emergent roughness model mounted on a flat plate in uniform flow. Fluid Dyn. Res. 2007, 39, 694–710. [Google Scholar] [CrossRef]
- Arora, K.R. Fluid Mechanics, Hydraulics, and Hydraulic Machines; Standard Publishers Distribution: Delhi, India, 1973. [Google Scholar]
- Dey, S.; Kumar, B.R. Hydraulics of free overfall in-shape channels. Sadhana 2002, 27 Pt 3, 353–363. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; p. 728. [Google Scholar]
- Anjum, N.; Tanaka, N. Experimental study on flow analysis and energy loss around discontinued vertically layered vegetation. Environ. Fluid Mech. 2020, 20, 791–817. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of Nappe Flow Regime above Stepped Chutes and Spillways. Trans.-Inst. Eng. Aust. Civ. Eng. Ce 1994, 36, 69. [Google Scholar]
- Foster, M.; Fell, R.; Spannagle, M. The statistics of embankment dam failures and accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Tracy, H.J. Discharge Characteristics of Broad-Crested Weirs; Geological Survey Circular 397; United States Department of the Interior: Reston, VA, USA, 1957. [Google Scholar]
- Chanson, H. The Hydraulics of Open Channel Flow: An Introduction: Basic Principles, Sediment Motion, Hydraulic Modelling, Design of Hydraulic Structures, 2nd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2004; ISBN 9780080472973. [Google Scholar]
- Hamadan, L.; Nahi, T.N. Comparison of Flow over Broad Crested Weir in Laboratory and by a Numerical Method. Wasit J. Eng. Sci. 2018, 6, 82–90. [Google Scholar] [CrossRef]
- Rahman, M.A.; Tanaka, N.; Reheman, N. Experimental study on reduction of scouring and tsunami energy through a defense system consisting of a seaward embankment followed by vertically double layered vegetation. Ocean. Eng. 2021, 234, 108816. [Google Scholar] [CrossRef]
- Rahman, M.A.; Tanaka, N. Countermeasure against local scouring and tsunami damage by downstream forest behind a coastal embankment. Appl. Ocean. Res. 2022, 120, 103070. [Google Scholar] [CrossRef]
- Rashedunnabi, A.H.M.; Tanaka, N. Energy reduction of a tsunami current through a hybrid defense system comprising a sea embankment followed by a coastal forest. Geosciences 2019, 9, 247. [Google Scholar]
- Song, J.; De Risi, R.; Goda, K. Influence of Flow Velocity on Tsunami Loss Estimation. Geosciences 2017, 7, 114. [Google Scholar] [CrossRef]
- Adam, A.M.; Ruff, J.F.; AlQaser, G.; Abt, S.R. Characteristics of B-jump with different toe locations. J. Hydraul. Eng. 1993, 119, 938–948. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hayashi, K.; Hashimoto, H. Drag coefficient for unsubmerged rigid vegetation stems in open channel flows. J. Hydraul. Res. 2009, 47, 691–699. [Google Scholar] [CrossRef]
- Samarakoon, M.B.; Tanaka, N.; Yagisawa, J. Effects of local scouring and saturation of soil due to flooding on maximum resistive bending moment for overturning Robinia pseudoacacia. Landsc. Ecol. Eng. 2013, 9, 11–25. [Google Scholar] [CrossRef]
- Tanaka, N.; Sasaki, Y.; Mowjood, M.I.M. Effects of sand dune and vegetation in the coastal area of Sri Lanka at the Indian Ocean tsunami. In Advances in Geosciences: Volume 6: Hydrological Science (HS); World Scientific Co.: Singapore, 2006; pp. 149–159. ISBN 9789812708915. [Google Scholar]
- Antonellini, M.; Mollema, P.N. Impact of groundwater salinity on vegetation species richness in the coastal pine forests and wetlands of Ravenna, Italy. Ecol. Eng. 2010, 36, 1201–1211. [Google Scholar] [CrossRef]



| Exp. Case | Normalized Overtopping Depth (Hm) | Re | We |
|---|---|---|---|
| EM-NHC | 0.05, 0.075, 0.10, 0.125, 0.15 | 7.52 × 103–4.30 × 104 | 18.6–84.6 |
| EM-NAC | 0.05, 0.075, 0.10, 0.125, 0.15 | 7.76 ×103–4.24 × 104 | 14.5–81.2 |
| EM-NDC | 0.05, 0.075, 0.10, 0.125, 0.15 | 8.01 × 103–4.45 × 104 | 19.3–94.5 |
| EM-VMS | 0.05, 0.075, 0.10, 0.125, 0.15 | 7.13 × 103–4.13 × 104 | 15.9–76.1 |
| EM-VMI | 0.05, 0.075, 0.10, 0.125, 0.15 | 6.91 × 103–4.14 × 104 | 13.5–76.4 |
| EM-VMD | 0.05, 0.075, 0.10, 0.125, 0.15 | 6.76 × 103–4.11 × 104 | 12.8–75.3 |
| Exp. Case | Normalized Overtopping Depth (Hm) | Dx (mm) | Dy (mm) | G (mm) | d (mm) | WF (mm) | Slope | Porosity (Pr) % |
|---|---|---|---|---|---|---|---|---|
| EM-NHC | 0.05, 0.075, 0.10, 0.125, 0.15 | - | - | - | - | - | - | - |
| EM-NAC | 0.05, 0.075, 0.10, 0.125, 0.15 | - | - | - | - | - | +4.0 | - |
| EM-NDC | 0.05, 0.075, 0.10, 0.125, 0.15 | - | - | - | - | - | −4.0 | - |
| EM-VMS | 0.05, 0.075, 0.10, 0.125, 0.15 | 96.1 | 55.5 | 49.5 | 12.0 | 400 | - | 86.8 |
| EM-VMI | 0.05, 0.075, 0.10, 0.125, 0.15 | 66.2 | 38.2 | 36.2 | 12.0 | 400 | - | 92.2 |
| EM-VMD | 0.05, 0.075, 0.10, 0.125, 0.15 | 53.5 | 30.9 | 24.9 | 12.0 | 400 | - | 95.7 |
| Exp. Case | Discharge | ||||||
|---|---|---|---|---|---|---|---|
| EM-NHC | 4.19 | 0.45 | 2.01 | 2.77 | 1.93 | 1.88 | 0.58 |
| 8.97 | 0.64 | 3.11 | 4.44 | 3.20 | 2.82 | 0.49 | |
| 14.36 | 0.78 | 4.16 | 6.11 | 4.38 | 3.70 | 0.43 | |
| 19.79 | 0.89 | 5.11 | 7.57 | 5.43 | 4.44 | 0.38 | |
| 26.06 | 1.01 | 6.17 | 9.04 | 6.52 | 5.17 | 0.35 | |
| EM-NAC | 4.19 | 0.45 | 3.65 | 4.54 | 1.93 | 1.86 | 0.58 |
| 8.97 | 0.63 | 5.09 | 6.17 | 3.20 | 2.84 | 0.49 | |
| 14.36 | 0.75 | 6.22 | 7.64 | 4.38 | 3.82 | 0.43 | |
| 19.79 | 0.86 | 7.79 | 9.09 | 5.43 | 4.59 | 0.38 | |
| 26.06 | 0.93 | 8.20 | 10.37 | 6.52 | 5.62 | 0.35 | |
| EM-NDC | 4.19 | 0.80 | 1.32 | 2.56 | 1.93 | 1.05 | 0.58 |
| 8.97 | 0.97 | 2.33 | 4.16 | 3.20 | 1.85 | 0.49 | |
| 14.36 | 1.09 | 3.39 | 5.71 | 4.38 | 2.64 | 0.43 | |
| 19.79 | 1.15 | 4.44 | 7.07 | 5.43 | 3.45 | 0.38 | |
| 26.06 | 1.26 | 5.50 | 8.61 | 6.52 | 4.15 | 0.35 | |
| EM-VMS | 4.19 | 0.43 | 0.06 | 4.26 | 1.93 | 1.96 | 0.58 |
| 8.97 | 0.57 | 0.09 | 6.62 | 3.20 | 3.16 | 0.49 | |
| 14.36 | 0.68 | 0.12 | 9.00 | 4.38 | 4.25 | 0.43 | |
| 19.79 | 0.76 | 0.15 | 11.10 | 5.43 | 5.22 | 0.38 | |
| 26.06 | 0.82 | 0.17 | 13.29 | 6.52 | 6.39 | 0.35 | |
| EM-VMI | 4.19 | 0.44 | 0.08 | 5.22 | 1.93 | 1.91 | 0.58 |
| 8.97 | 0.59 | 0.13 | 8.15 | 3.20 | 3.04 | 0.49 | |
| 14.36 | 0.67 | 0.17 | 10.98 | 4.38 | 4.27 | 0.43 | |
| 19.79 | 0.76 | 0.21 | 13.62 | 5.43 | 5.23 | 0.38 | |
| 26.06 | 0.82 | 0.25 | 16.23 | 6.52 | 6.34 | 0.35 | |
| EM-VMD | 4.19 | 0.45 | 0.10 | 5.86 | 1.93 | 1.85 | 0.58 |
| 8.97 | 0.61 | 0.16 | 9.26 | 3.20 | 2.94 | 0.49 | |
| 14.36 | 0.70 | 0.21 | 12.62 | 4.38 | 4.13 | 0.43 | |
| 19.79 | 0.73 | 0.25 | 15.52 | 5.43 | 5.42 | 0.38 | |
| 26.06 | 0.80 | 0.30 | 18.56 | 6.52 | 6.52 | 0.35 |
| Crest Exposer Condition | Critical Angle (Degrees) | Normalized Overtopping Depth (Hm) | Critical Brink Depth, (cm) |
|---|---|---|---|
| Horizontal Crest without Vegetation (EM-NHC) | 30 | 0.15 | 5.17 |
| Ascending Crest (+4%) (EMN-NAC) | 25 | 0.10 | 3.82 |
| Descending Crest (−4%) (EM-NDC) | 30 | 0.10 | 2.64 |
| Sparse Vegetation (EM-VMS) (G/d = 1.33, dn = 180) | 30 | 0.125 | 5.22 |
| Intermediate Vegetation (EM-VMI) (G/d = 0.59, dn = 380) | 30 | 0.125 | 5.23 |
| Dense Vegetation (EM-VMD) (G/d = 0.29, dn = 580) | 35 | 0.15 | 6.52 |
| Hm (=hm/hE) | Nappe Flow Drop Length (Ld) (mm) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EM-NHC | EM-NAC | EM-NDC | EM-VMS | EM-VMI | EM-VMD | |||||||
| 25° | 10° | 25° | 10° | 25° | 10° | 25° | 10° | 25° | 10° | 25° | 10° | |
| 0.05 | 97 | 174 | 141 | 146 | 106 | 289 | 66 | 120 | 83 | 115 | 89 | 114 |
| 0.075 | 115 | 187 | 157 | 156 | 225 | 240 | 143 | 172 | 137 | 169 | 128 | 159 |
| 0.10 | 223 | 221 | 178 | 176 | 246 | 253 | 210 | 228 | 204 | 227 | 190 | 218 |
| 0.125 | 263 | 245 | 211 | 197 | 279 | 278 | 236 | 246 | 223 | 242 | 228 | 228 |
| 0.15 | 272 | 289 | 249 | 263 | 289 | 294 | 252 | 249 | 246 | 246 | 240 | 242 |
| Hm (=hm/hE) | Nappe Flow Thickness (djet) (mm) | |||||||||||
| EM-NHC | EM-NAC | EM-NDC | EM-VMS | EM-VMI | EM-VMD | |||||||
| 25° | 10° | 25° | 10° | 25° | 10° | 25° | 10° | 25° | 10° | 25° | 10° | |
| 0.05 | 10 | 10 | 9 | 10 | 8 | 8. | 11 | 12 | 13 | 11 | 14 | 13 |
| 0.075 | 14 | 16 | 17 | 16 | 14 | 13 | 17 | 16 | 16 | 17 | 17 | 17 |
| 0.10 | 26 | 26 | 25 | 24 | 22 | 23 | 23 | 24 | 26 | 28 | 27 | 27 |
| 0.125 | 33 | 34 | 33 | 33 | 32 | 32 | 34 | 35 | 35 | 36 | 33 | 36 |
| 0.15 | 40 | 42 | 41 | 42 | 38 | 39 | 50 | 44 | 45 | 44 | 46 | 45 |
| Hm (=hm/hE) | Impinging Jet Angle (βi) | |||||||||||
| EM-NHC | EM-NAC | EM-NDC | EM-VMS | EM-VMI | EM-VMD | |||||||
| 25° | 10° | 25° | 10° | 25° | 10° | 25° | 10° | 25° | 10° | 25° | 10° | |
| 0.05 | 82 | 80 | 73 | 73 | 76 | 58 | 82 | 81 | 82 | 82 | 83 | 82 |
| 0.075 | 78 | 74 | 76 | 77 | 71 | 66 | 80 | 76 | 81 | 77 | 79 | 76 |
| 0.10 | 72 | 73 | 75 | 75 | 69 | 64 | 75 | 75 | 75 | 74 | 75 | 75 |
| 0.125 | 70 | 69 | 73 | 73 | 64 | 63 | 72 | 71 | 72 | 71 | 71 | 74 |
| 0.15 | 65 | 66 | 69 | 69 | 63 | 62 | 71 | 71 | 70 | 70 | 70 | 69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dissanayaka, K.D.C.R.; Tanaka, N.; Hasan, M.K. Effect of Orientation and Vegetation over the Embankment Crest for Energy Reduction at Downstream. Geosciences 2022, 12, 354. https://doi.org/10.3390/geosciences12100354
Dissanayaka KDCR, Tanaka N, Hasan MK. Effect of Orientation and Vegetation over the Embankment Crest for Energy Reduction at Downstream. Geosciences. 2022; 12(10):354. https://doi.org/10.3390/geosciences12100354
Chicago/Turabian StyleDissanayaka, Kannangara D. C. R., Norio Tanaka, and Md. Kamrul Hasan. 2022. "Effect of Orientation and Vegetation over the Embankment Crest for Energy Reduction at Downstream" Geosciences 12, no. 10: 354. https://doi.org/10.3390/geosciences12100354
APA StyleDissanayaka, K. D. C. R., Tanaka, N., & Hasan, M. K. (2022). Effect of Orientation and Vegetation over the Embankment Crest for Energy Reduction at Downstream. Geosciences, 12(10), 354. https://doi.org/10.3390/geosciences12100354








