Abstract
A simple analytical model is presented in this work to investigate reflection coefficients due to the interactions of waves with rectangular submerged obstacles/and submarine trenches. Our intention in this work is to present a simple analytical model to simulate and study water-wave scattering by evaluating reflection coefficients. Further, our challenge is to present an analytical model that can easily investigate simultaneously the effects of rectangular submerged obstacles/and submarine trenches on wave scattering. Furthermore, reflection coefficients are investigated for different immersion ratios and relative lengths simultaneously for submarine trenches/and rectangular submerged obstacles. In addition, to ensure the validity of the presented model, our results are well compared with those of the literature. Finally, a comparison of reflection coefficients associated with the interactions of waves with rectangular submerged obstacles/and submarine trenches are presented to investigate the most efficient breakwater, and to highlight the importance of the presented model.
1. Introduction
Preserve infrastructures and resources in coastal and marine environment are an interesting challenge in coastal and ocean engineering. For these reasons, the investigation of water-wave propagation over a structure/or trenched bottom is an important topic in coastal and ocean science. Further, the reflection and transmission coefficients are crucial hydrodynamic parameters that can evaluate efficiently the efficiency of the adopted breakwaters. Furthermore, this topic has been investigated widely in the literature by adopting the linear potential theory. Moreover, the investigations on wave-structure interactions are divided into three group: Scientists or researchers that are interested in studying wave-structure interactions theoretically [1,2], a second group that is interested in investigating the interaction of waves and structures in a numerical wave tank (NWT) [3,4,5], and a third group that is interested in conducting research on wave-structure interaction experimentally [6,7]. Additionally, breakwaters can be presented as bottom submerged breakwaters, submerged plate breakwaters, submarine trench, and seawall breakwaters.
This research paper studies scattering water waves using bottom submerged breakwaters and submarine trench. For this reason, it is interested in shining light on the state-of-the-art methods associated with the topic investigated in this research paper. First, Szmidt [8] used the finite difference method to compute the reflection coefficient associated with rectangular submerged bottom breakwaters in a numerical wave tank (NWT). Next, Ouyang [9] studied a series of submerged bottom breakwaters using a computational approach based on the regularized meshless method (RMM). Then, Bragg offered some reflections on a train of surface water waves from a succession of impermeable submerged bottom breakwaters. Further, by presenting a number of experiment measurements by Hsu [10], he studied scattering water waves by rectangle, cosine, and triangle sand breakwaters, and the investigation showed that the rectangular sand breakwaters provide the maximum reflection, according to a series of experimental data that the author presented. Recently, submerged rectangular breakwater was investigated by Chioukh [11] using an efficient numerical method (ISBM) to compute the reflection and transmission coefficients applied to study wave-submerged rectangular breakwater. Later, Loukili et al. [12] compared the analytical model with the numerical approach presented by Chioukh [11]. Additionally, the comparison has shown a good agreement between analytical and numerical approaches. Furthermore, water-wave scattering by a trenched bottom can be an interesting tool to reflect waves and protect the coastal and marine environment. Moreover, wave propagation over variable-depth geometries was initially studied by Kreisel [13]. Apart from that, Lassiter [14] investigated the complementary issue of dispersion of water waves caused by the interactions with a rectangular trench, where the condition of the velocity potential and horizontal velocity must be continuous along the vertical lines before and after the trench, to formulate the problem in terms of complementary variational integrals of Schwinger’s type, from which he was able to derive reflection and transmission coefficients. Next, by writing solutions in two subregions made up of an infinite rectangular region of constant depth and a finite rectangular region of the trench, Lee and Ayer [15] used a matching procedure to solve the rectangular trench problem. They then calculated the reflection and transmission coefficients numerically. Moreover, they performed several experiments in a wave tank and compared the outcomes to those calculated theoretically. Shortly afterwards, Miles [16] formulated the trench problem for long waves and then used a conformal mapping approach to solve it for normal incidence of the wave train. Recently, Bender and Dean [17], Xie et al. [18] and Liu et al. [19] considered various kinds of trench problems. Bender and Dean [17] investigated the problem of wave propagation over two-dimensional trenches and shoals. Thereafter, the issue of long-wave reflection by a rectangular barrier with two trenches was investigated by Xie et al. [18]. In addition, Liu et al. [19] investigated wave reflection by a rectangular breakwater with two scour trenches by formulating the problem in terms of a modified mild-slope equation (MMSE), and then the reflection coefficient was obtained analytically. Recently, multi-term Galerkin approximations have been used to investigate obliquely incident water-wave diffraction by an asymmetric trench [20,21], a numerical method that has been widely used lately.
In this work, our challenge is to present a simple analytical model that can simulate and study simultaneously the interactions of waves with rectangular submerged obstacles/and submarine trenches. Further, the intention is to highlight the advantages of a simple analytical model that can investigate the effect of the hydrodynamics parameters on the reflection coefficients due to the interactions of waves with rectangular submerged obstacles/and submarine trenches. The advantages of this approach are that it is simple and easy to manipulate. Further, it is based on a domain connection by connecting the domains via continuity conditions, and this procedure leads to a good definition of the domain of study, and avoids the problem of singularities associated with classical numerical approaches. On the other hand, the limitation of this approach is that it is limited to just the intermediate zone, and hence it is incapable of treating waves-structure interactions in the case of deep zones.
To realize the goals and the challenge of this research paper, this work is divided into four main sections. After introducing the topic of this research in Section 1, the theoretical formulation of the problem is presented in Section 2. Thereafter, results and discussion are presented in Section 3 to illustrate the goals of this research paper. Finally, conclusions and additional perspectives are given in Section 4.
2. Theoretical Formulation of the Problem
The aim of this section is to introduce the formulation of the problem based on a theoretical approach. Further, the objective is to present an analytical model to compute the reflection and transmission coefficients associated with the interactions of waves with rectangular submerged obstacles/and submarine trenches simultaneously. By expressing the continuity of velocity potential and horizontal velocity at the obstacle’s edges (see Figure 1 and Figure 2), the reflection and transmission coefficients are easily calculated. The advantages of this technical approach are easy to implement and can be used to compute the reflection and transmission coefficients for both rectangular submerged obstacles/and submarine trenches simultaneously.
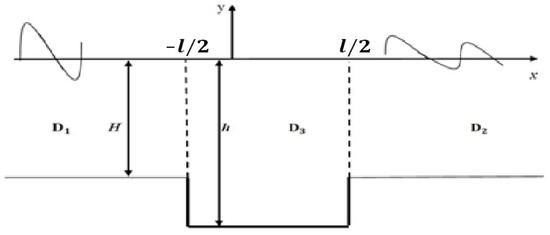
Figure 1.
Configuration of submarine trench breakwater.
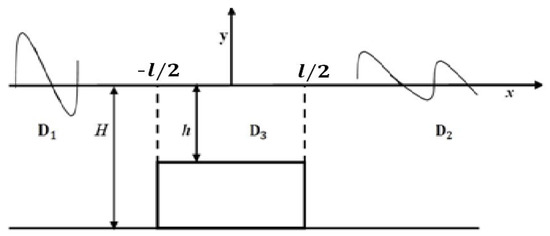
Figure 2.
Configuration of bottom rectangular submerged breakwater.
The velocity potential at each subdomain is written as
- -
- at the subdomain
- -
- at the subdomain
- -
- at the subdomain
a, R, Tr and respectively stand for amplitude of the incident wave, the reflection and the transmission coefficients.
The horizontal velocity and the velocity potential wave, the reflect defined at x = and x = as
- At the position x =
- At the position x =
where, following the expression of the connection conditions at the positions x = and x = , we get an algebraic system as
where:
The additional factors in Formulas (4)–(7) are added to simplify the integration of the Equations (9)–(11) as
By combining the set of Equation (8), we get
Formulas (15) and (16) are then injected into the second and fourth equations of the system (8), yielding
with more explicitly,
After that, we get a matrix system as
The formulation of the reflection and transmission coefficients can be obtained as a result of the matrix system’s resolution.
where:
The expression is verified theoretically, which confirms the conservation of energy associated with water-wave propagations. Further, this expression can be used as an error indicator for numerical approaches by evaluating .For more details, , and verify the dispersion relations such as
From Equations (25) and (26), we can write
Further, Equation (27) can be re-written as
where , stands for the immersion ration.
For the sake of clarity, Equation (27) is resolved numerically using the Newton–Raphson method [22].
3. Results and Discussions
The outcomes of this study are divided into two main subsections. The first subsection is dedicated to validation tests to ensure the validity of the present model used in this investigation. The second subsection is incorporated to assess and study the effect of the immersion ratio and relative length on the reflection coefficients for the two used cases simultaneously, namely the interaction of water waves with rectangular submerged obstacles/and submarine trenches.
3.1. Validation Tests
To ensure the validity of the approach used in this work, two tables are presented in this subsection. Table 1 is presented to compare our outcomes with the results of the literature in the case of the interaction of waves with submarine trenches for the hydrodynamic parameters h/H = 3, et l/H = 5. Table 2 is depicted to compare the analytical and numerical method based on the improved version of the meshless method (ISBM) [12], in the case of rectangular submerged breakwater by fixing the relative lengths and varying the immersion ratios: h/H = 0.25, 0.5, 0.75. In addition, a partial verification of the accuracy of the results is achieved by the current analytical approach, by verifying the energy conservation that is expressed as .

Table 1.
Comparison of our results with those of the literature for the immersion ratio: h/H = 3, and relative length l/H = 5 (in the case of submarine trenches).

Table 2.
Comparison of analytical and the numerical approach [12] for different immersion ratios and relative lengths (for the case of rectangular breakwater).
By comparing our results with those of the literature and checking the energy conservation for the different immersion ratios, we conclude that the analytical model presented in this work is accurate and efficient for the interactions of waves with rectangular submerged obstacles/and submarine trenches.
Further, the convergence of the approach adopted in this work is associated with the convergence of the dispersion equation (Equation (27)) that is resolved by the Newton Raphson method [22]. Our numerical experiments indicate that the Newton–Raphson method converges when KH is beyond the range [3]; outside of this range, the method happened to be unstable. For more details, this outcome proves the incapacity of this approach to treat wave-structure interactions in the case of deep-water zones.
3.2. Reflection Coefficients Investigations
In this subsection, the aim is to illustrate the efficiency of the analytical model presented in this work, namely to study the effects of the hydrodynamic parameters on the reflection coefficients associated with the interactions of waves with submerged rectangular breakwaters/and submarine trenches. For these reasons, the reflection coefficients are assessed for the different immersion ratios h/H and the relative lengths l/d (where). Firstly, our intention is to assess the effects of the hydrodynamic parameters on the reflection coefficients for the case of the interactions of waves with submerged rectangular breakwaters. Namely, in Figure 3, the reflection coefficients are assessed for the different immersion ratios (h/H = 0.25, 0.5, 0.75) by fixing the relative length at l/d = 1, and 2. Further, in Figure 4, the reflection coefficients are investigated for the different relative lengths (l/h = 2, 4, 6) by fixing the immersion ratios at h/H = 0.20, and 0.80.
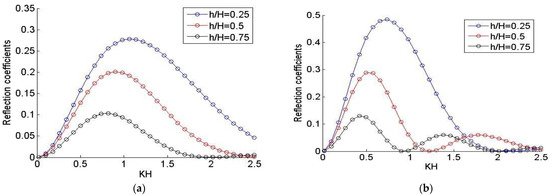
Figure 3.
Variations of reflection coefficients by fixing the relative length at (a) l/d = 1, (b) l/d = 2, and varying the immersion ratio: h/H = 0.25, 0.5, 0.75.
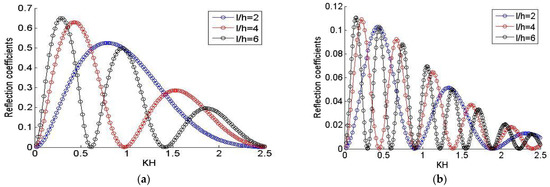
Figure 4.
Variations of reflection coefficients by fixing the immersion ratio at (a) h/H = 0.20, (b) h/H = 0.80, and varying the relative length: l/h = 2, 4, 6.
Secondly, the purpose is to study the effects of the hydrodynamic parameters on the reflection coefficients for the case of the interactions of waves with submarine trench breakwater. Namely, in Figure 5, the reflection coefficients are assessed for the different immersion ratios (h/H = 1.25, 1.5, 1.75) and fixing the relative lengths at l/d = 0.5 and 0.85. Further, in Figure 6, the reflection coefficients are investigated for the different relative lengths (l/h = 0.5, 0.8, 1.15) and fixing the immersion ratios at h/H = 1.25, and 1.75.
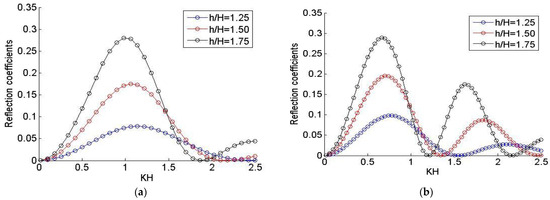
Figure 5.
Variations of reflection coefficients by fixing the relative lengths at (a) l/d = 0.5, (b) l/d = 0.85 and varying the immersion ratios: h/H = 1.25, 1.5, 1.75.
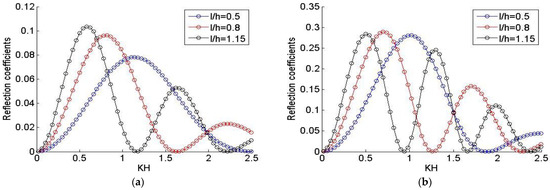
Figure 6.
Variations of reflection coefficients by fixing the immersion ratios at (a) h/H = 1.25, (b) h/H = 1.75 and varying the relative lengths: l/h = 0.5, 0.8, 1.15.
Finally, Figure 7 shows comparisons of the reflection variations due to wave-submerged rectangular breakwaters/and submarine trenches. The investigations are illustrated at the first time in the Figure 7a, by fixing the immersion ratio at h/H = 0.5, and the relative length at l/h = 1 for the rectangular submerged breakwater, and the immersion ratio at h/H = 1.5, and the relative length l/h = 1/3 for the submarine trench. For further investigation, in the Figure 7b the immersion ratio is fixed at h/H = 0.5 and the rela-tive length at l/h = 2 for the rectangular submerged breakwater, and immersion ratio at h/H = 1.5, and the relative length l/h = 2/3 for the submarine trench.
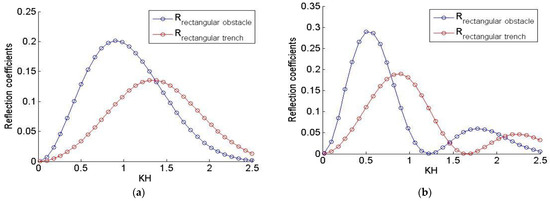
Figure 7.
Comparisons of the reflection variations due to wave-submerged rectangular breakwater/and submarine trenches: (a): h/H = 0.5, and l/h = 1 for rectangular breakwater, h/H = 1.5, and l/h = 1/3 for the submarine trench, (b): h/H = 0.5, and l/h = 2 for rectangular breakwater, h/H = 1.5, and l/h = 2/3 for the submarine trench.
The Justification for these hydrodynamics values is that, the correspondence is performed by replacing the h-parameter associated with the rectangular submerged breakwater (Figure 2) by the equivalent of 3h associated with the submarine trench breakwater (Figure 1).
The outcomes of this subsection prove the efficiency of the present model to study simultaneously the interactions of waves with submerged rectangular breakwaters/and submarine trenches. Furthermore, Figure 3 and Figure 4 describe the effect of the immersion ratios, and the relative lengths on the reflection coefficients associated with the interactions of waves with submerged rectangular breakwater. In addition, Figure 5 and Figure 6 describe also the effect of the immersion ratios, and the relative lengths on the reflection coefficients associated with the interactions of waves with submarine trenches. By fixing the relative lengths and varying the immersion ratios in Figure 3 and Figure 5, the results show that the reflection coefficients decrease when the immersion ratio increases. In addition, Figure 4 and Figure 6 describe the effect of the relative lengths on the reflection coefficients simultaneously for the interactions of waves with submerged rectangular breakwater and wave-submarine trenches; by fixing the immersion ratio and varying the relative lengths, the results show that the reflection coefficients increase when the relative length increases. Moreover, the results of all figures show that, as we increase the relative lengths, the oscillation aspect of the reflection coefficients increases. Furthermore, in the case of wave-submarine trench interactions, the maximum of the reflection coefficient is still constant when the immersion ratio reaches h/H = 1.75.
Finally, Figure 7 is dedicated to comparing the reflection coefficients associated with the interactions of waves with submerged rectangular breakwater and wave-submarine trenches. The upshot of this figure proves that the reflection coefficients of the submerged rectangular breakwater go one better than the reflection coefficients associated with the submarine trench.
4. Conclusions and Perspectives
This research paper has addressed many challenges. First, a simple analytical model is presented and illustrates the advantages of treating simultaneously the problem of wave-submerged rectangular breakwaters and wave-trench breakwaters. Secondly, the reflection coefficients associated with the interactions of wave-submerged rectangular breakwaters and trench breakwaters have been thoroughly investigated. Namely, the investigation covered the effect of the relative length and the immersion ratio on the reflection coefficients. The results of this research paper show that the relative length and the immersion ratio are the key parameters of the study. Further, the reflection coefficients increase when the relative length increases, while the reflection coefficients decrease when the immersion ratio increases. This conclusion is observed for both the case of the wave-submerged rectangular breakwater and wave-trench breakwaters. Finally, the simplicity of the present simple analytical model allowed us to compare the reflection coefficients associated with the wave-submerged rectangular breakwater and wave-trench breakwaters.
In the future, we will endeavor to investigate the problem studied in this work for the different hydrodynamic parameters in the presence of the currents.
Author Contributions
Conceptualization, M.L., D.D., S.P., K.K. and N.A.; methodology, M.L., D.D., S.P., K.K. and N.A.; software, M.L., D.D., S.P., K.K. and N.A.; validation M.L., D.D., S.P., K.K. and N.A.; formal analysis, M.L., D.D., S.P., K.K. and N.A.; investigation, M.L., D.D., S.P., K.K. and N.A.; resources, M.L., D.D., S.P., K.K. and N.A.; writing—original draft preparation, M.L., D.D., S.P., K.K. and N.A.; writing—review and editing, M.L., D.D., S.P., K.K. and N.A.; visualization, M.L., D.D., S.P., K.K. and N.A.; supervision, M.L., D.D., S.P., K.K. and N.A.; project administration, M.L., D.D., S.P., K.K. and N.A.; funding acquisition, M.L., D.D., S.P., K.K. and N.A. All authors have read and agreed to the published version of the manuscript.
Funding
The work of D.D. has been supported by the French National Research Agency, through the Investments for Future Program (ref. ANR-18-EURE-0016—Solar Academy).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to express their gratitude to the referees who helped us to improve our manuscript quality.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Errifaiy, M.; Naasse, S.; Chahine, C. Analytical determination of the reflection coefficient by the evanescent modes model during the wave6—Solar Academy). Comptes Rendus Mécan. 2016, 344, 479–486. [Google Scholar] [CrossRef]
- Naasse, S.; Errifaiy, M.; Chakib, C. Analytical study of the effect of the geometrical parameters during the interaction of regular wavehorizontal plate-current. Acta Oceanol. Sin. 2019, 38, 10–20. [Google Scholar] [CrossRef]
- Loukili, M.; Dutykh, D.; Kotrasova, K.; Ning, D. Numerical Stability Investigations of the Method of Fundamental Solutions Applied to Wave-Current Interactions Using Generating-Absorbing Boundary Conditions. Symmetry 2021, 13, 1153. [Google Scholar] [CrossRef]
- Loukili, M.; Kotrasova, K.; Bouaine, A. A Generating—Absorbing Boundary Condition Applied to Wave—Current Interactions Using the Method of Fundamental Solutions. Civ. Environ. Eng. 2021, 17, 343–352. [Google Scholar] [CrossRef]
- Loukili, M.; Kotrasova, K.; Mouhid, M. Computerized Decision Aid Applied to Meshless Method for the Use Case: Wave-Structure Interactions. In Proceedings of the International Conference on Decision Aid Sciences and Application (DASA), Online, 8–9 November 2020; pp. 33–36. [Google Scholar]
- Brossard, J.; Chagdali, M. Experimental investigation of the harmonic generation by waves over a submerged plate. Coast. Eng. 2001, 42, 277–290. [Google Scholar] [CrossRef]
- Brossard, J.; Perret, G.; Blonce, L.; Diedhiou, A. Higher harmonics induced by a submerged horizontal plate and a submergedrectangular step in a wave flume. Coast. Eng. 2009, 56, 11–22. [Google Scholar] [CrossRef]
- Szmidt, K. Finite difference analysis of surface wave scattering by underwater rectangular obstacles. Arch. Hydro-Eng. Environ. Mech. 2010, 57, 179–198. [Google Scholar]
- Ouyang, H.T.; Chen, K.H.; Tsai, C.M. Wave characteristics of Bragg reflections from a train of submerged bottom breakwaters. J. Hydro-Environ. Res. 2016, 11, 91–100. [Google Scholar] [CrossRef]
- Hsu, T.W.; Chang, H.K.; Hsieh, C.M. Bragg reflection of waves by different shapes of artificial bars. China Ocean. Eng. 2002, 16, 21–30. [Google Scholar]
- Chioukh, N.; Çevik, E.; Yüksel, Y. Reflection and transmission of regular waves from/through single and double perforated thinwalls. China Ocean Eng. 2017, 31, 466–475. [Google Scholar] [CrossRef]
- Loukili, M.; Dutykh, D.; Nadjib, C.; Ning, D.; Kotrasova, K. Analytical and Numerical Investigations Applied to Study the Reflections and Transmissions of a Rectangular Breakwater Placed at the Bottom of a Wave Tank. Geosciences 2021, 11, 430. [Google Scholar] [CrossRef]
- Kreisel, H. Surface waves. Q. Appl. Math. 1949, 7, 21–44. [Google Scholar] [CrossRef]
- Lassiter, J.B. The Propagation of Water Waves over Sediment Pockets. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1972. [Google Scholar]
- Lee, J.J.; Ayer, R.M. Wave propagation over a rectangular trench. J. Fluid Mech. 1981, 110, 335–347. [Google Scholar] [CrossRef]
- Miles, J.W. On surface wave diffraction by a trench. J. Fluid Mech. 1982, 115, 315–325. [Google Scholar] [CrossRef]
- Bender, C.J.; Dean, R.G. Wave transformation by two dimensional bathymetric anomalies with sloped transitions. Coast. Eng. 2003, 56, 61–84. [Google Scholar] [CrossRef]
- Xie, J.J.; Liu, H.W.; Lin, P. Analytical solution for long wave reflection by a rectangular obstacle with two scour trenches. ASCE J. Eng. Mech. 2011, 137, 919–930. [Google Scholar] [CrossRef]
- Liu, H.W.; Fu, D.J.; Sun, X.L. Analytic solution to the modified mild-slope equation for reflection by a rectangular breakwaterwith scour trenches. ASCE J. Eng. Mech. 2013, 139, 39–58. [Google Scholar] [CrossRef]
- Paul, S.; Sasmal, A.; De, S. Interaction of oblique waves with an ice sheet over an asymmetric trench. Ocean Eng. 2019, 193, 106613. [Google Scholar] [CrossRef]
- Sasmal, A.; De, S. Analysis of oblique wave diffraction by rectangular thick barrier in the presence of surface tension. Indian J. Phys. 2022, 96, 2051–2063. [Google Scholar] [CrossRef]
- Yang, X. Chapter 2—Analysis of Algorithms. In Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014; pp. 23–44. [Google Scholar]
- Kirby, J.T.; Dalrymple, R.A. Propagation of obliquely incident water waves over a trench. J. Fluid Mech. 1983, 133, 47–63. [Google Scholar] [CrossRef]
- Chakraborty, R.; Mandal, B.N. Water wave scattering by a rectangular trench. J. Eng. Math. 2014, 89, 101–112. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).